Voltage and Frequency Regulation in Interconnected Power Systems via a (1+PDD2)-(1+TI) Cascade Controller Optimized by Mirage Search Optimizer
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Contributions
- The development and implementation of a robust (1+PDD2)-(1+TI) controller to improve frequency and voltage stability in a dual-area interconnected power system;
- The application of the Mirage Search Optimization (MSO) algorithm to fine-tune the parameters of the proposed controller, offering a creative and high-performance approach to LFC and AVR optimization;
- A comprehensive comparison demonstrating the exceptional effectiveness of the MSO algorithm over several advanced optimization techniques, including ChOA, DOA, PSO, GTO, and GBO;
- In-depth analysis of the proposed controller’s performance and robustness under multiple scenarios, including sudden load changes at t = 0, random load fluctuations, commonly exhibit nonlinearities in power systems (such as Generation Rate Constraints (GRC) and Governor Dead Band (GDB)), time-varying reference voltages in both areas, and ±20% to ±40% variations in system parameters.
- Section 2: outlines the architecture of the studied system and describes its components;
- Section 3: presents the proposed MSO algorithm with details the configuration of the designed controller;
- Section 4: discusses the simulation results under various test scenarios;
- Section 5: concludes the paper with final observations and recommendations.
2. Representation of a Two-Area Interconnected Power Network
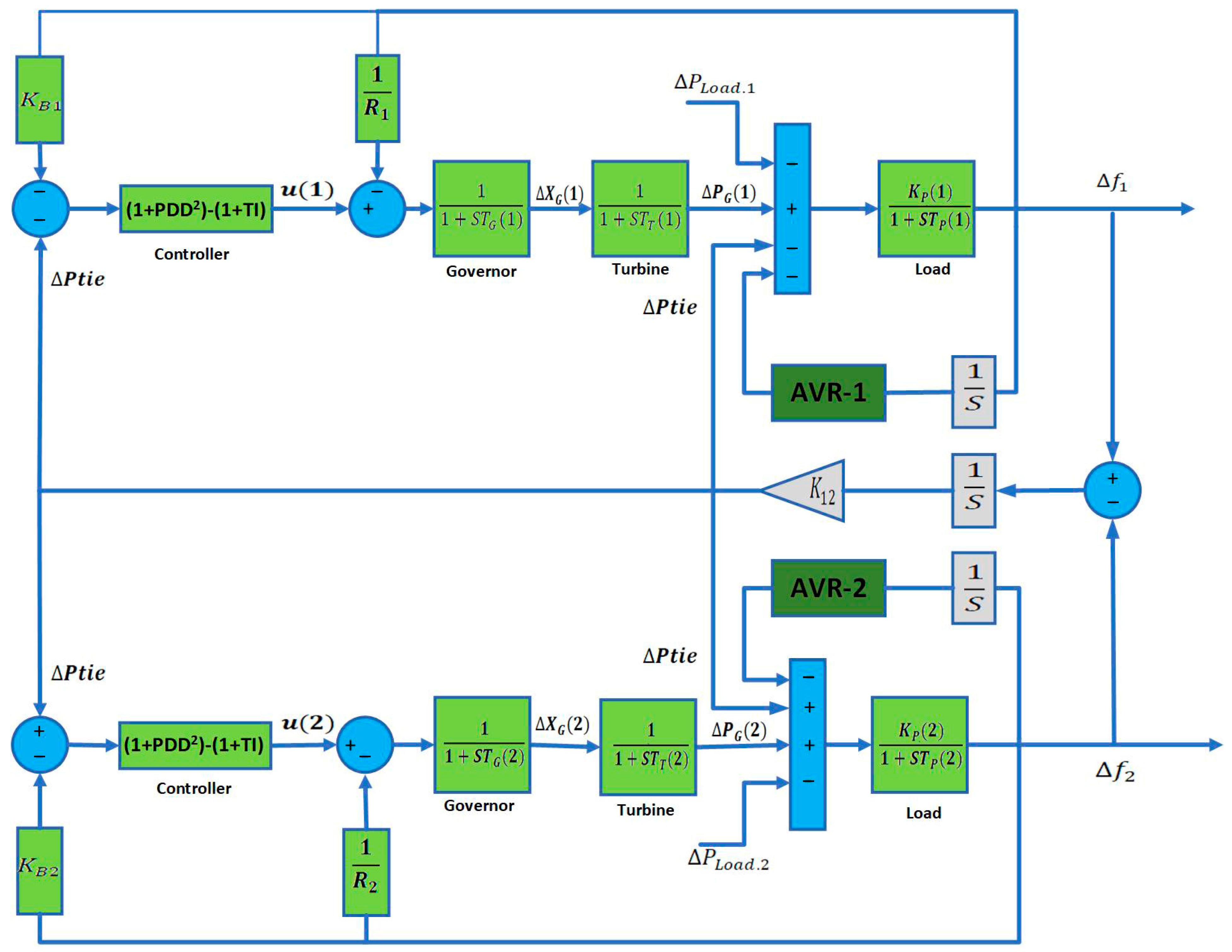
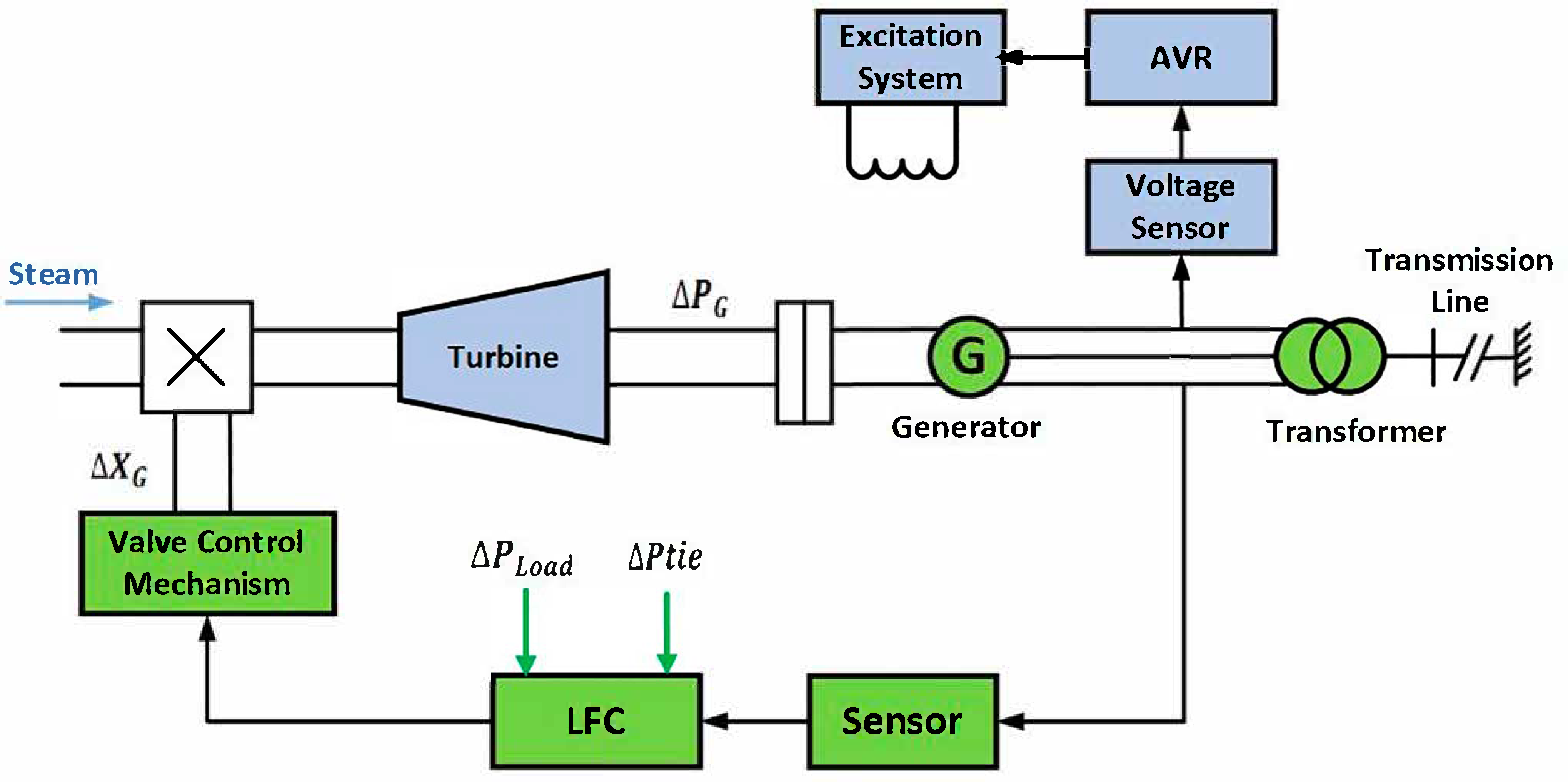
2.1. Dual-Area Interconnected Power System
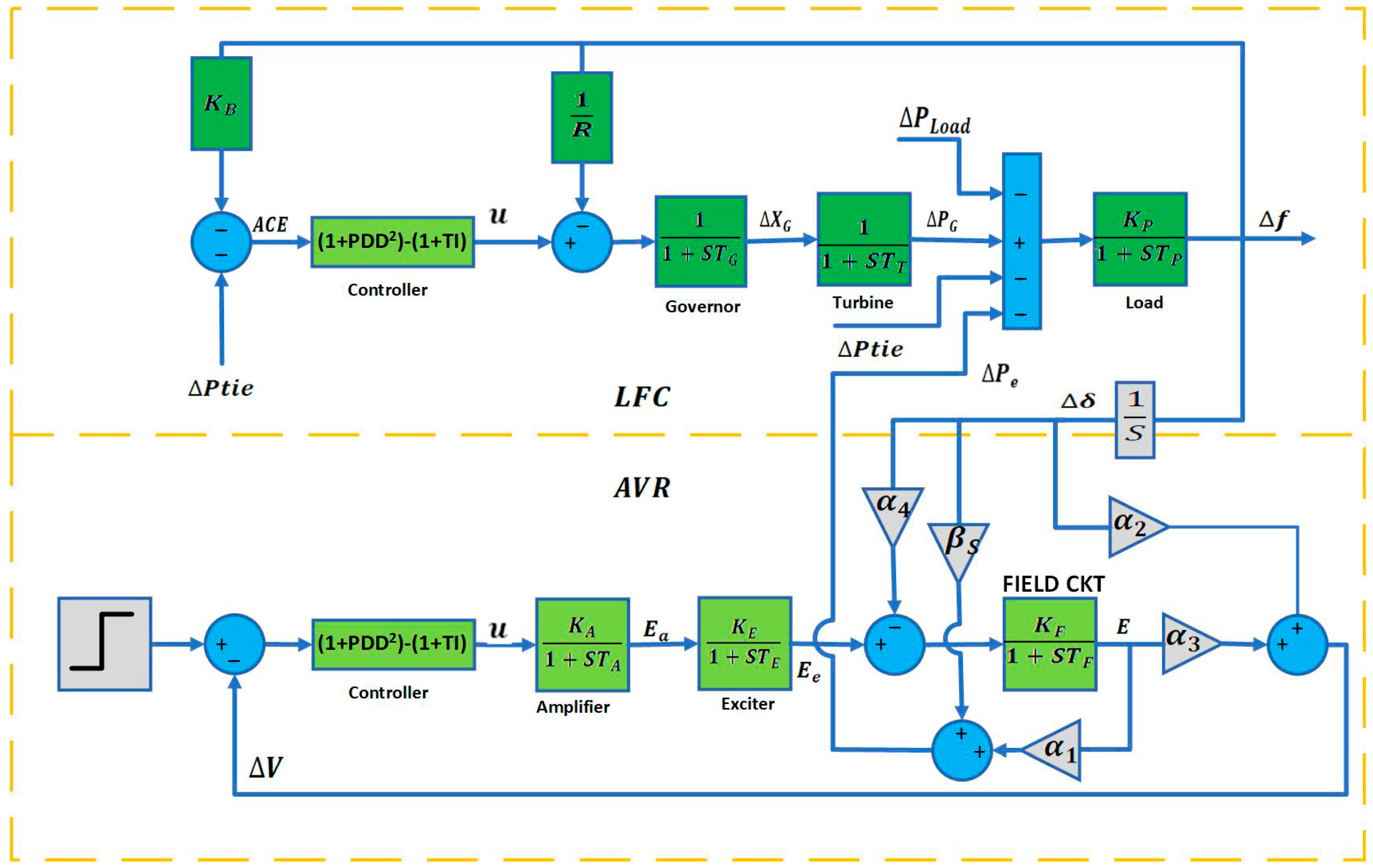
2.2. Automatic Voltage Regulation
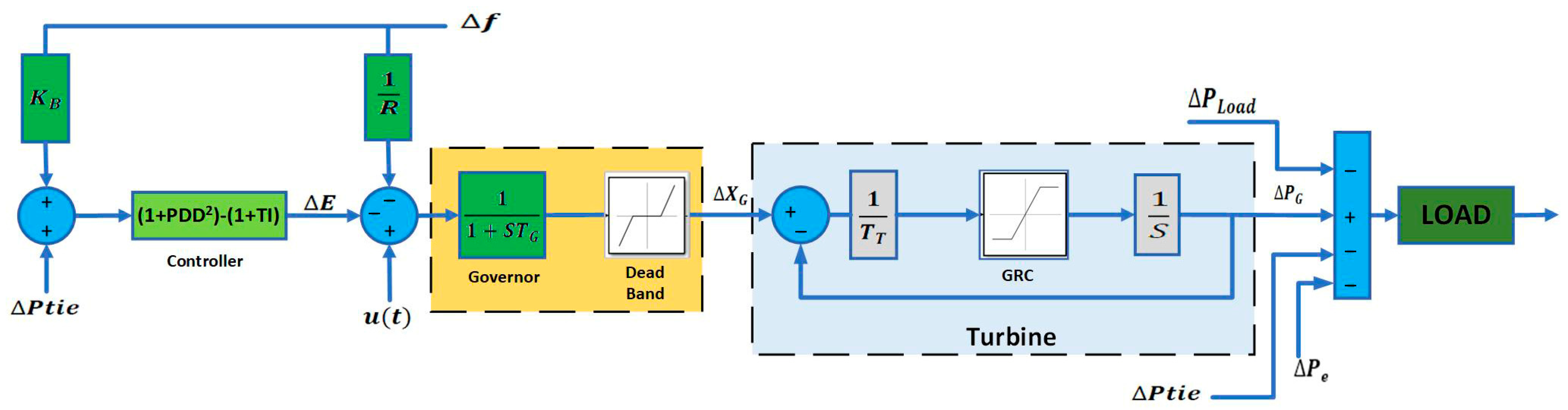
2.3. Load Frequency Control
2.4. Integrated AVR-LFC Power System
2.5. Mathematical Representation of the Power System
3. Control Methodology and Problem Overview
3.1. MSO Algorithm
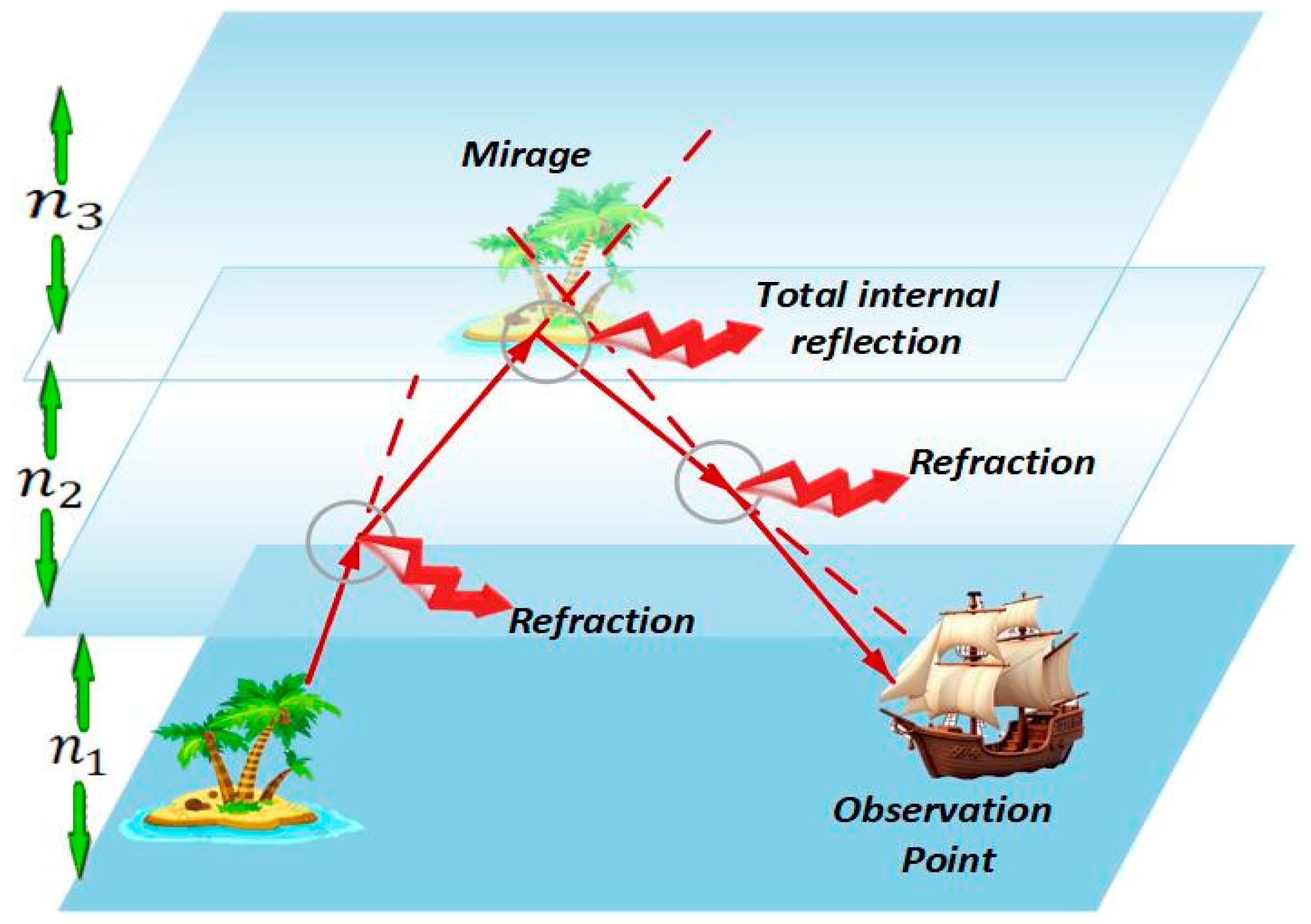
3.1.1. Motivation
- A superior mirage occurs when warm air lies above cooler air, reversing the normal temperature gradient. This causes light rays to bend downward, making distant objects appear above the horizon. These are often observed over cold surfaces, such as polar regions or cold seas, and metaphorically suggest seeing beyond immediate limits.
- An inferior mirage forms when hot air is near the ground and cooler air lies above it. This causes light to bend upward, creating a distorted or floating image. A common example is the shimmering illusion seen on roads during hot weather. It symbolizes seeing only a partial or misleading view of reality.
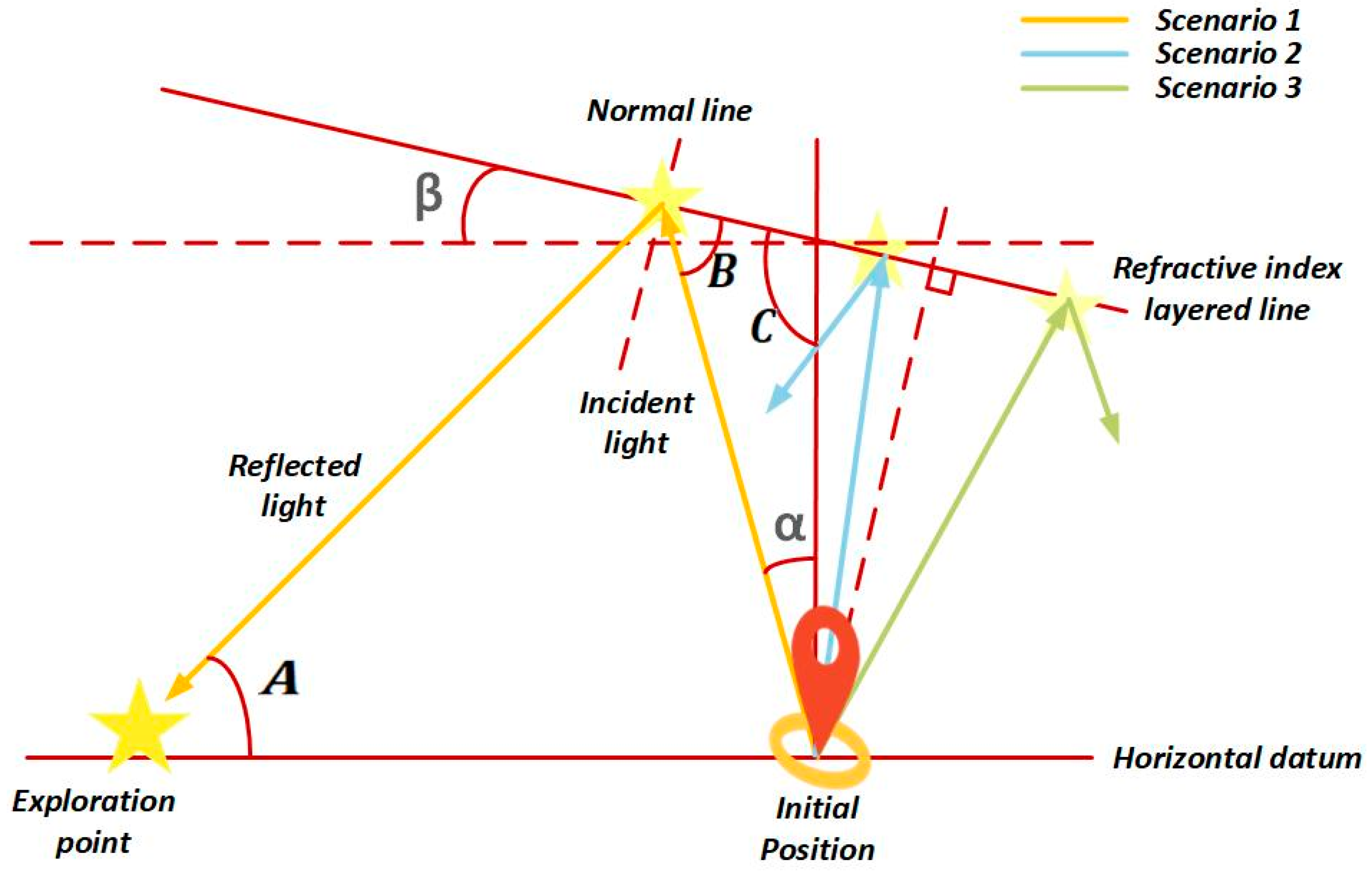
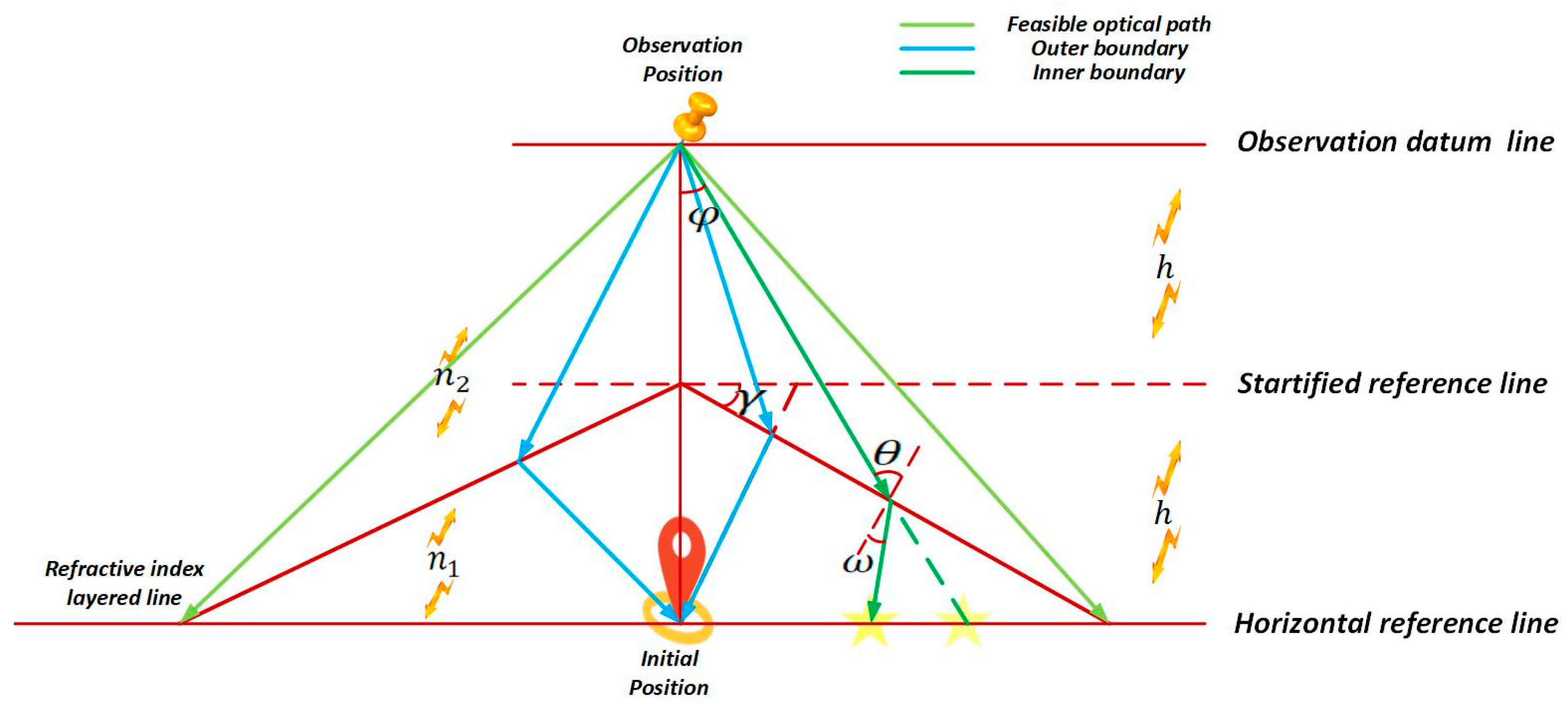
3.1.2. Mathematical Model
Formulating the Starting Solution Set
Superior Mirage Strategy
Inferior Mirage Strategy
Equilibrium Between Exploration and Exploitation
3.1.3. Execution of the MSO Algorithm
3.1.4. Computational Complexity
- (a)
- Time complexity
- (b)
- Space complexity
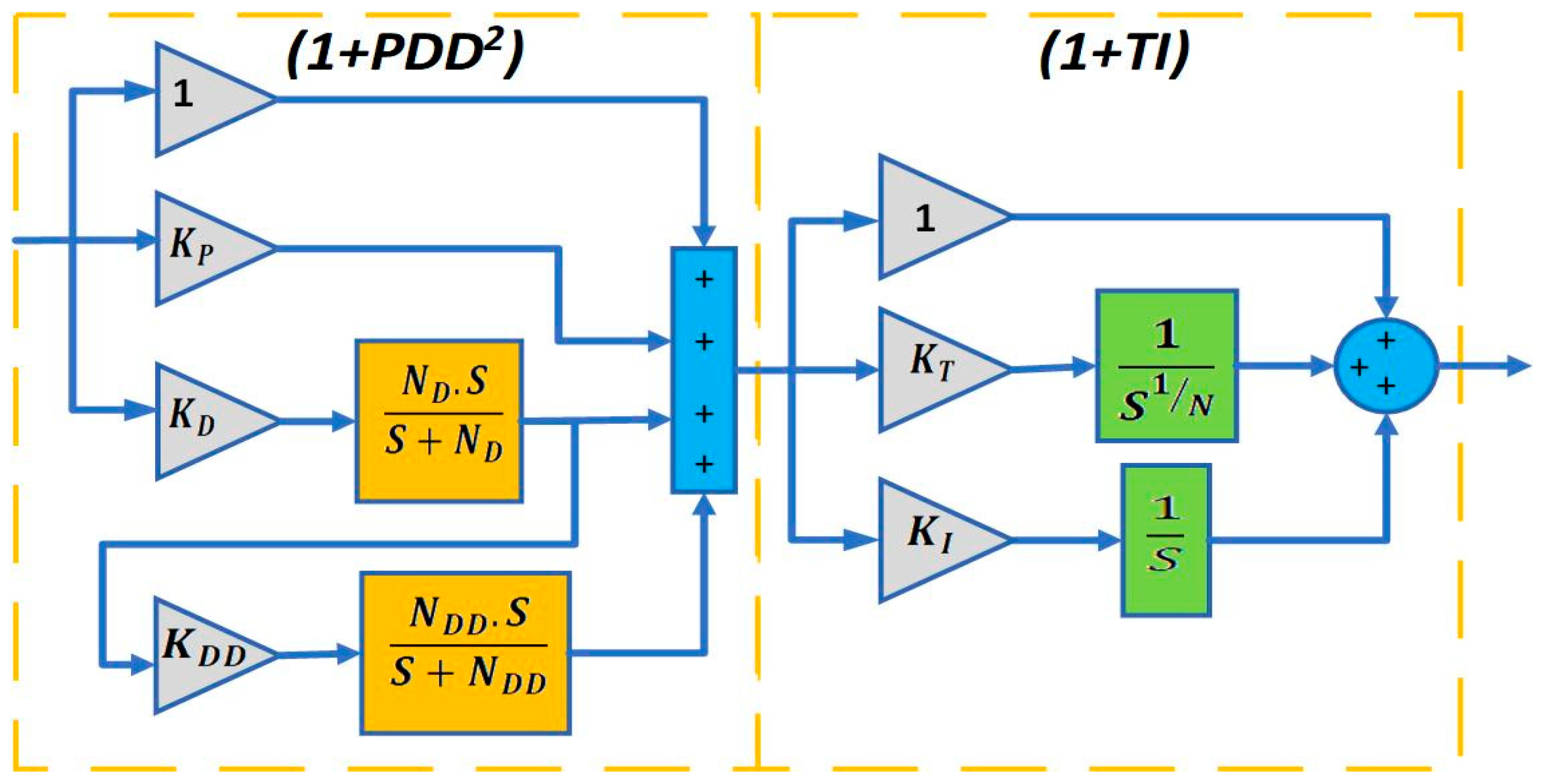
3.2. The Precise Design of the Proposed (1+PDD2)-(1+TI) Regulator
4. Simulation Results and Analysis
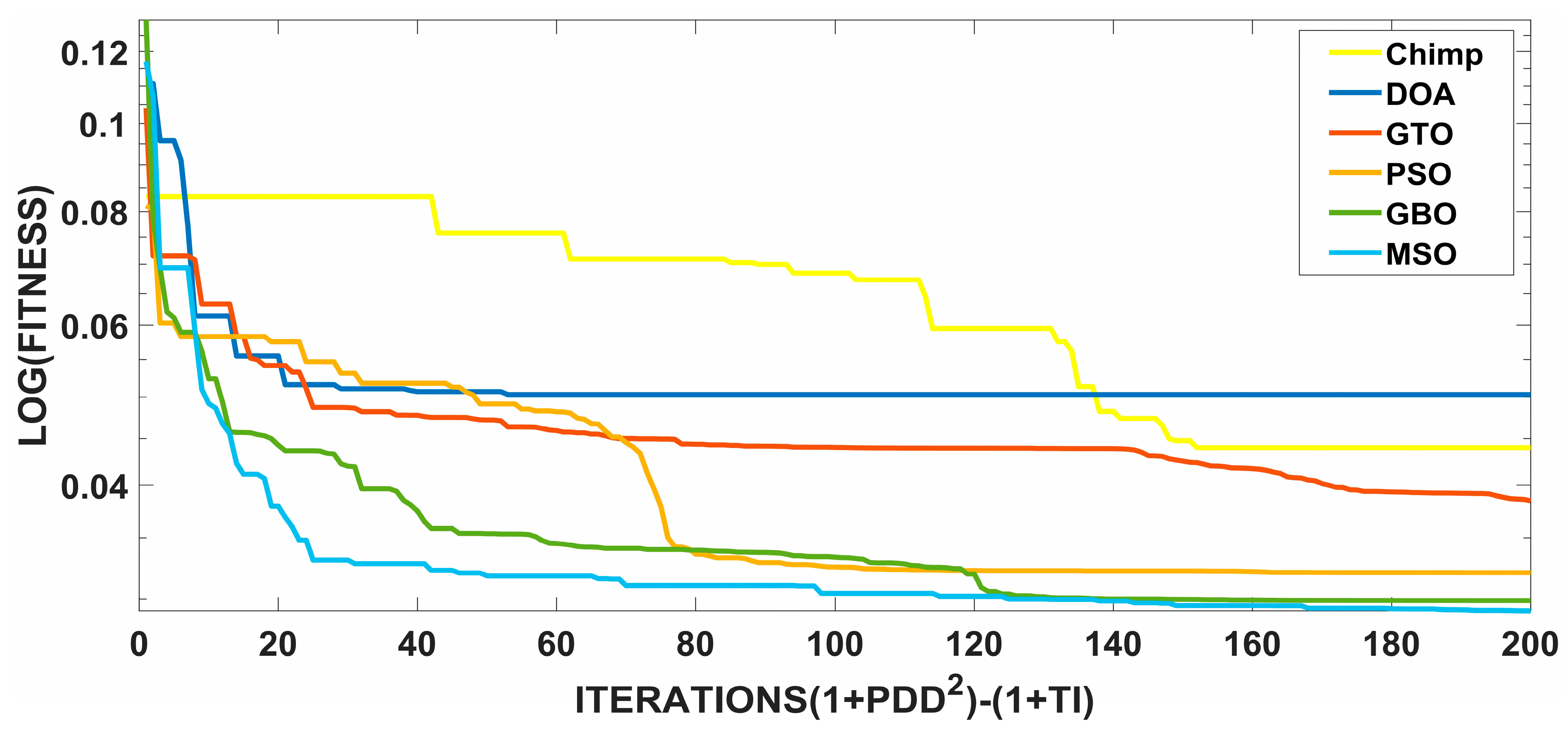
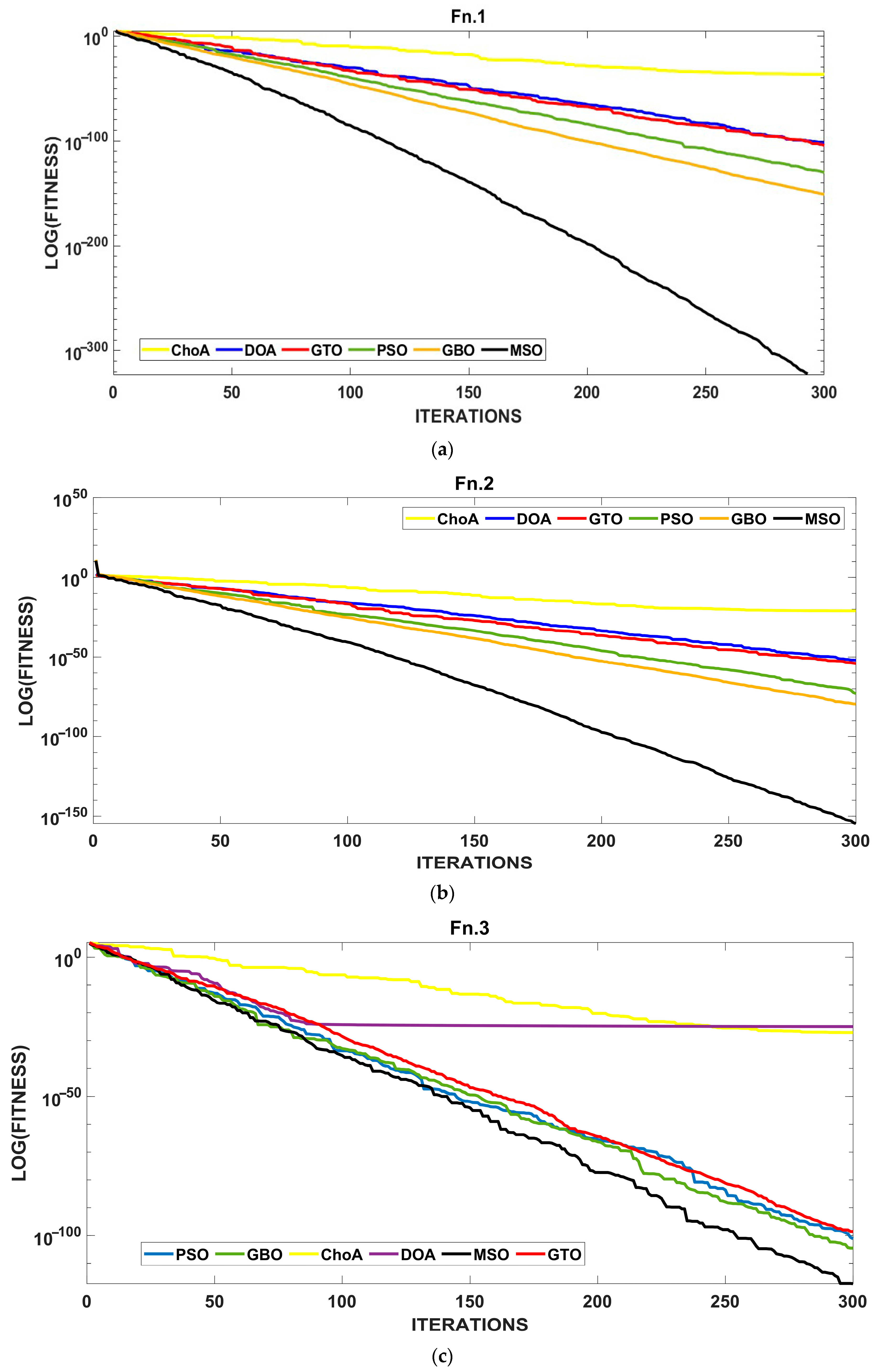
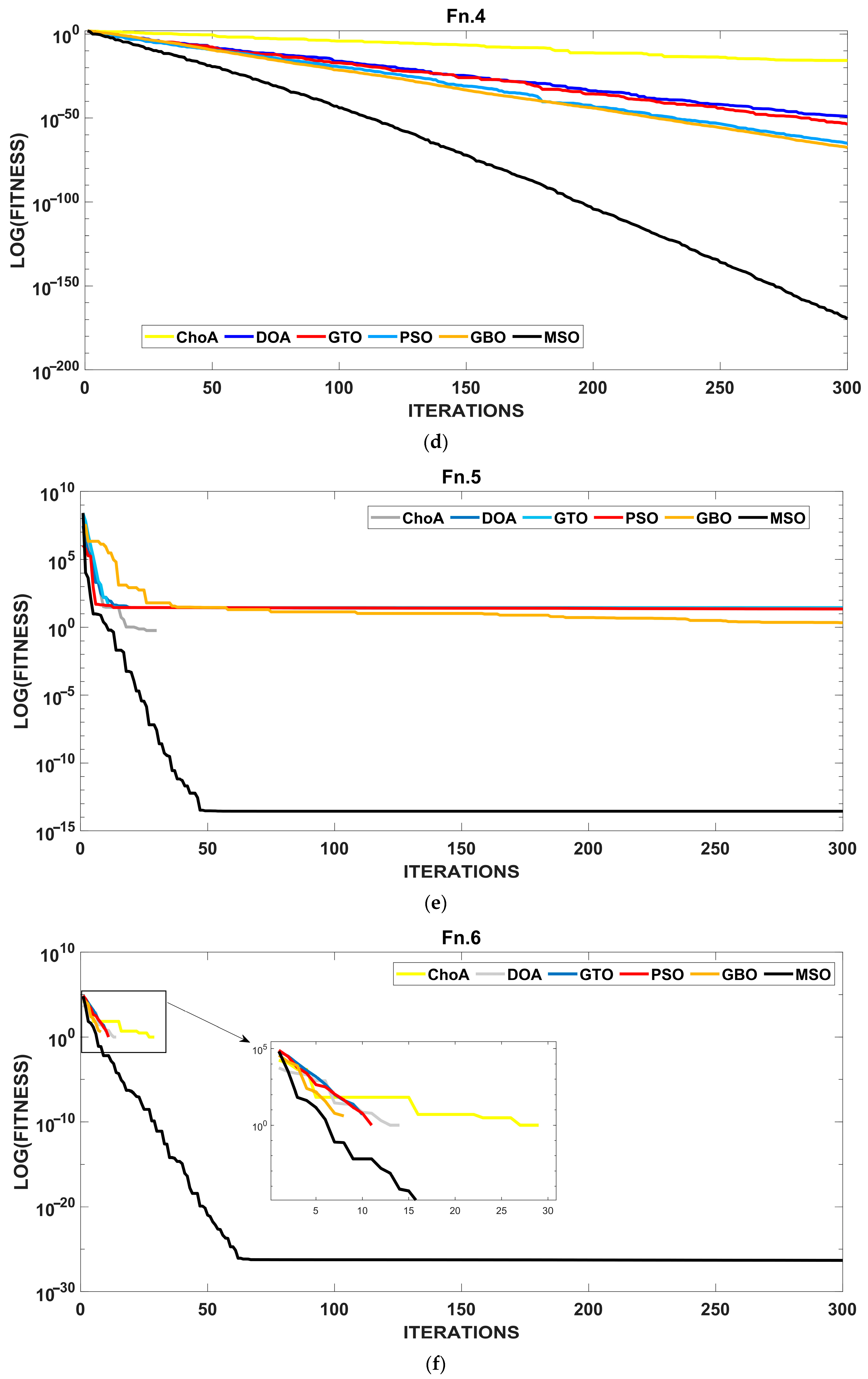
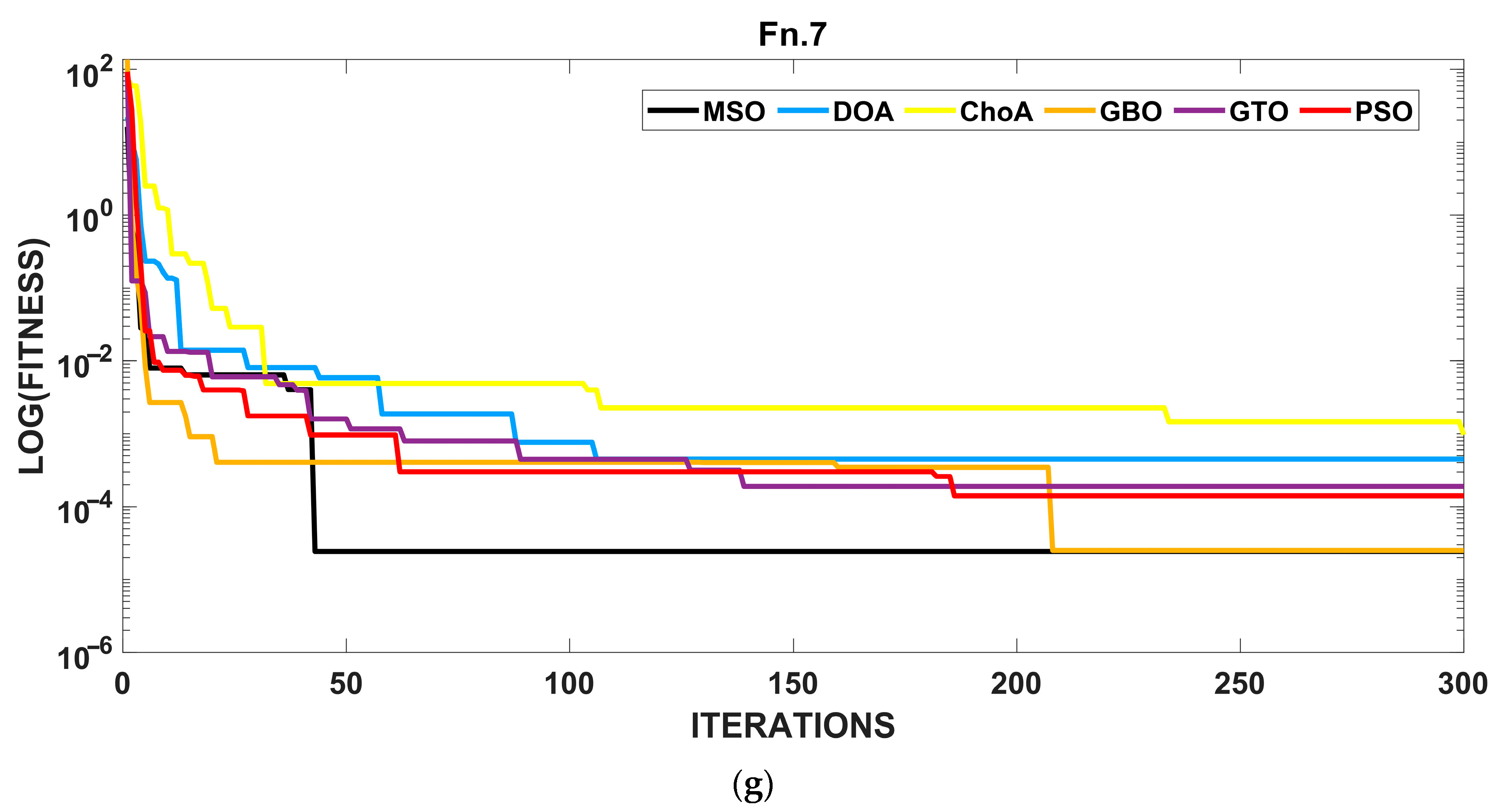
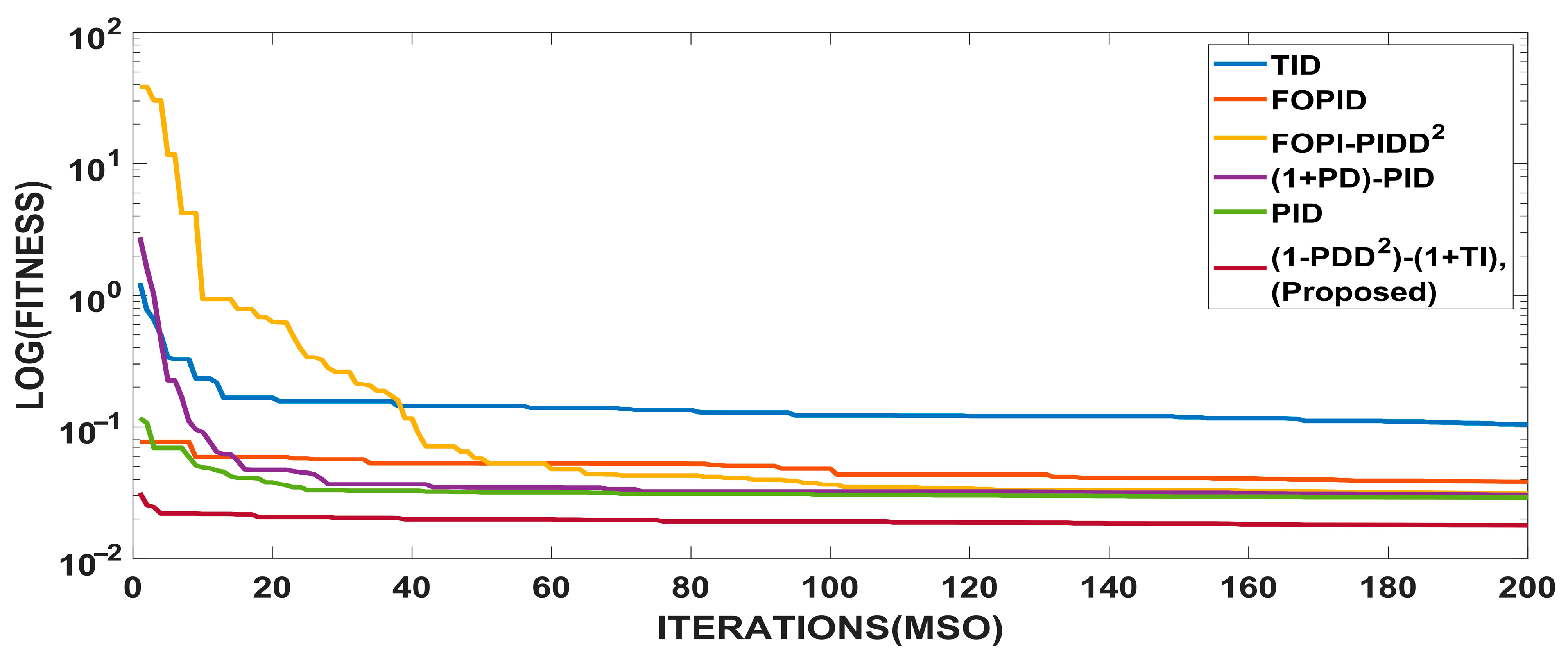
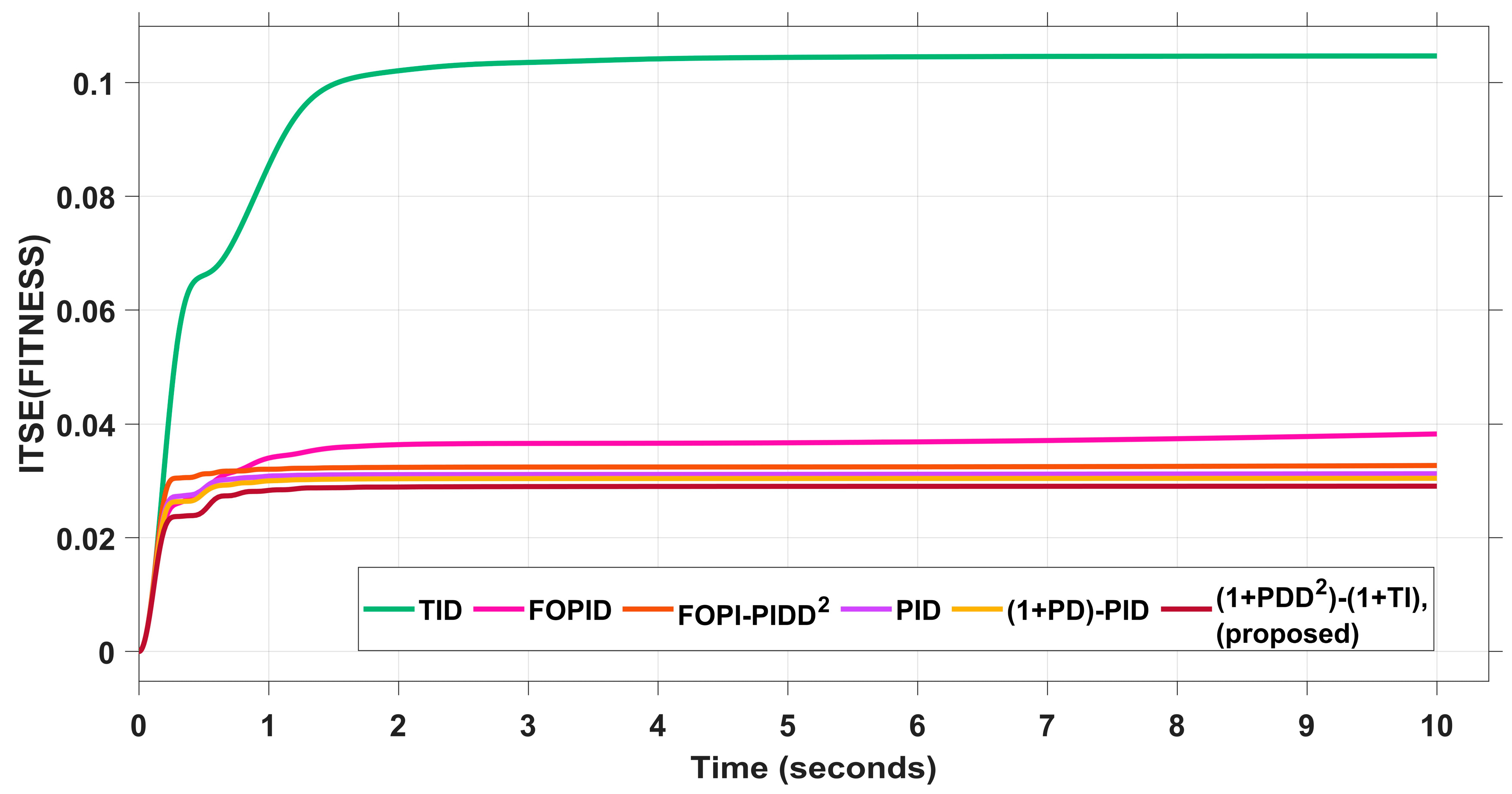
4.1. Evaluating the Effectiveness of the MSO Algorithm
4.2. Robustness Analysis of the Proposed (1+PDD2)-(1+TI) Controller
- Scenario I: A sudden change in demanded load is introduced at t = 0 s, with a 2% increase in Area 1 and a 1.5% increase in Area 2;
- Scenario II: Random load disturbances are applied to the system to assess its dynamic response under unpredictable conditions;
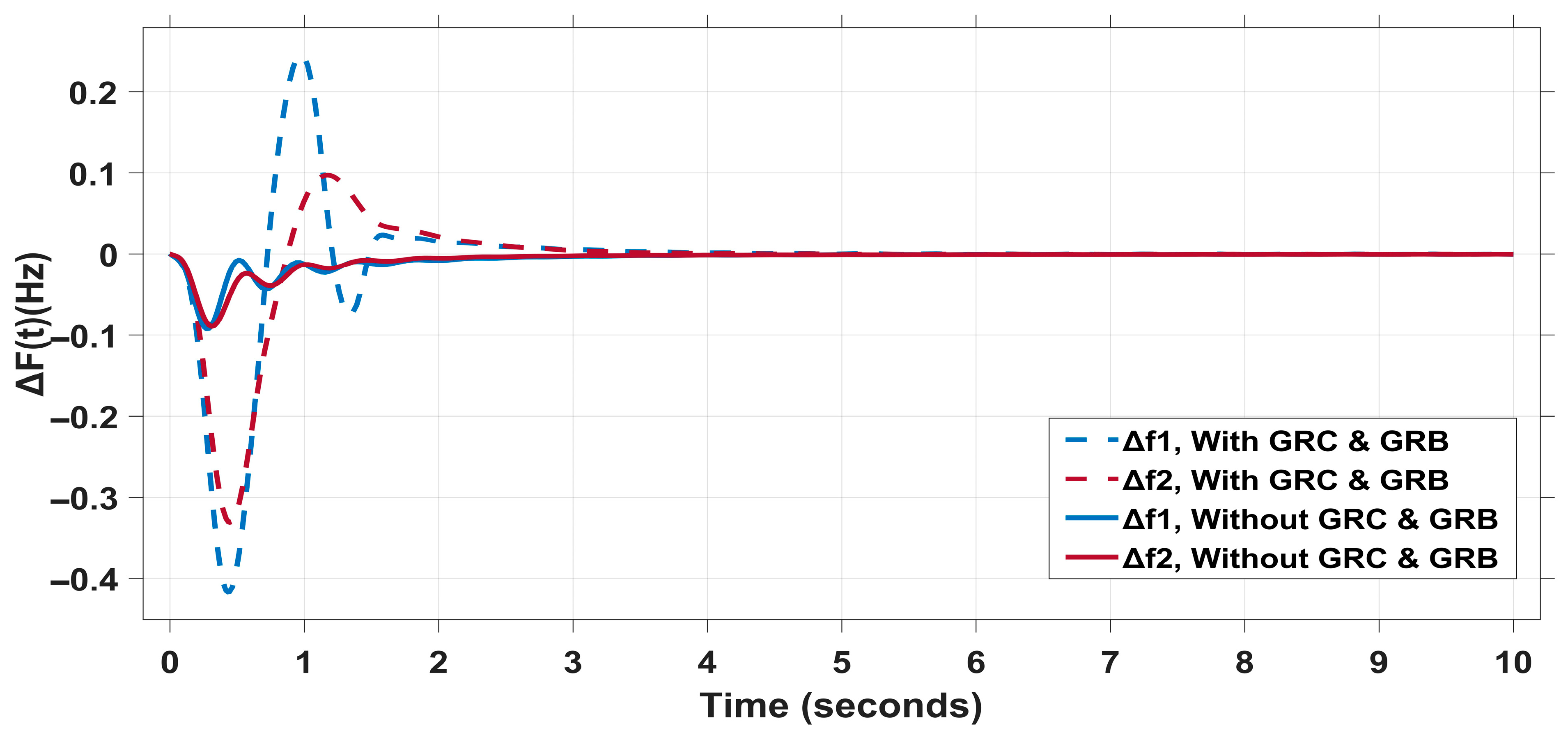
- Scenario III: The performance of controller is evaluated in the presence of typical system nonlinearities, such as Generation Rate Constraint (GRC) and Governor Dead Band (GDB);
- Scenario IV: A time-varying reference voltage is provided to examine how well the controller tracks dynamic reference signals;
- Scenario V: A sensitivity analysis is proceeded to assess the system’s strength against system parameters changes.
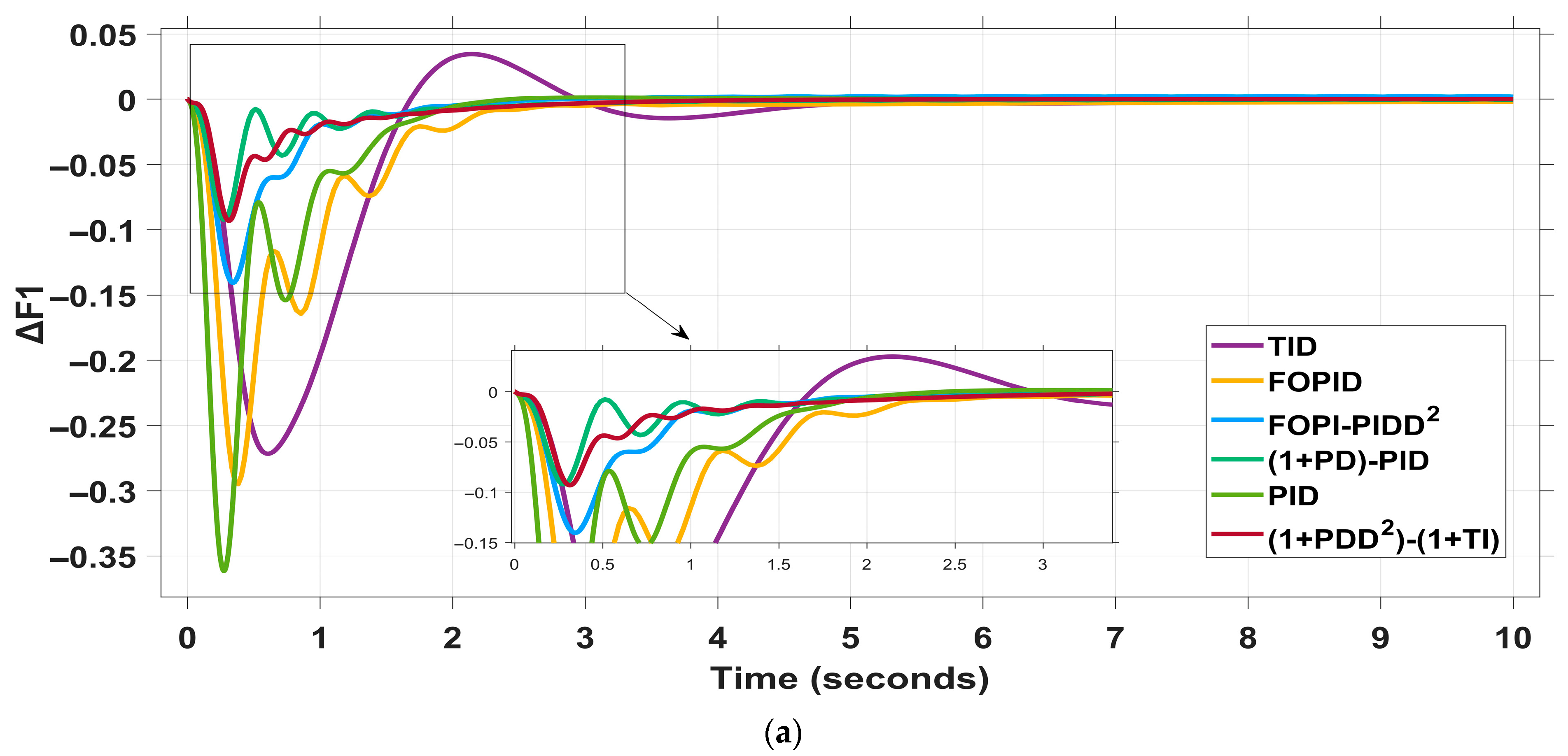
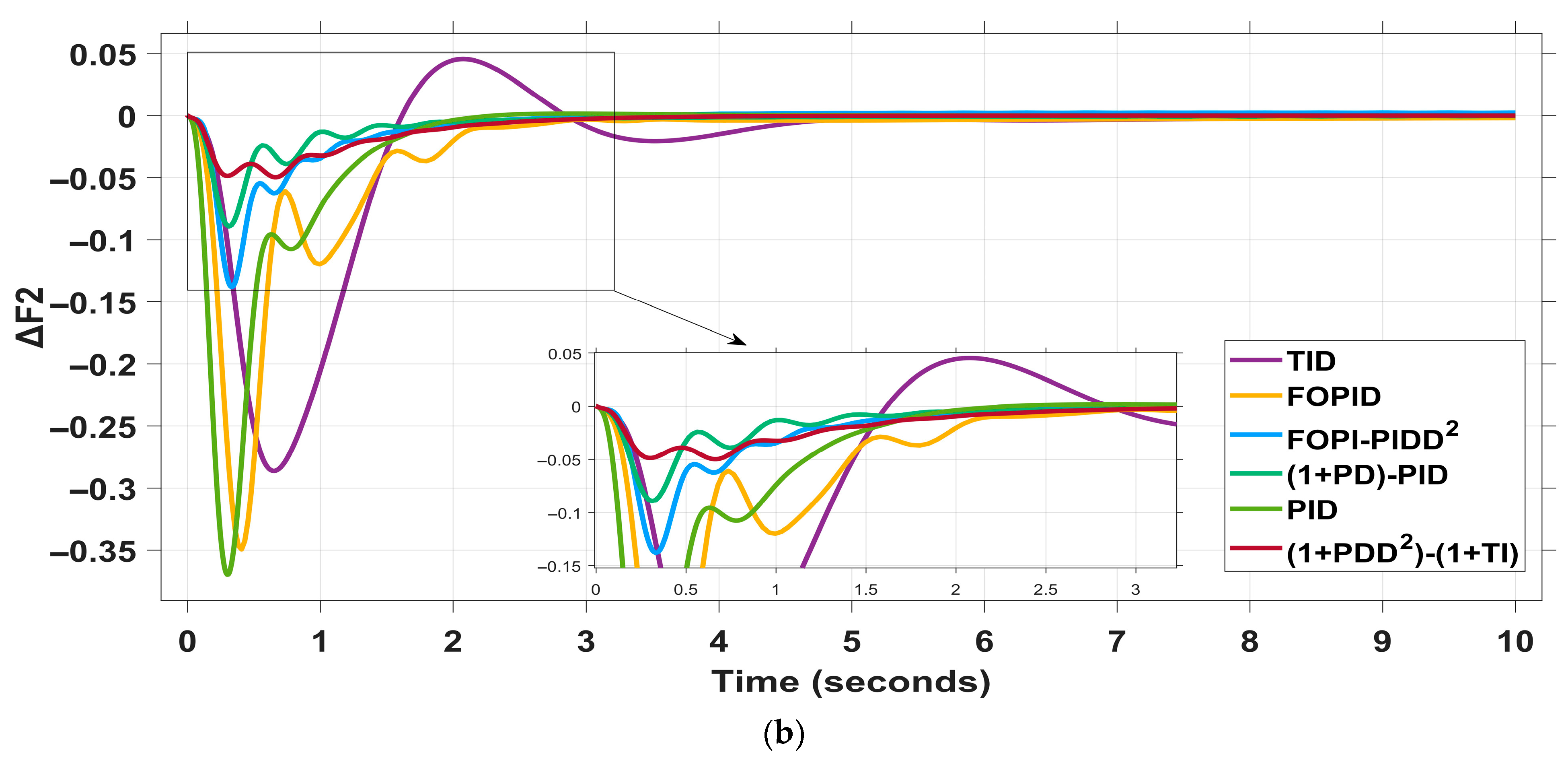
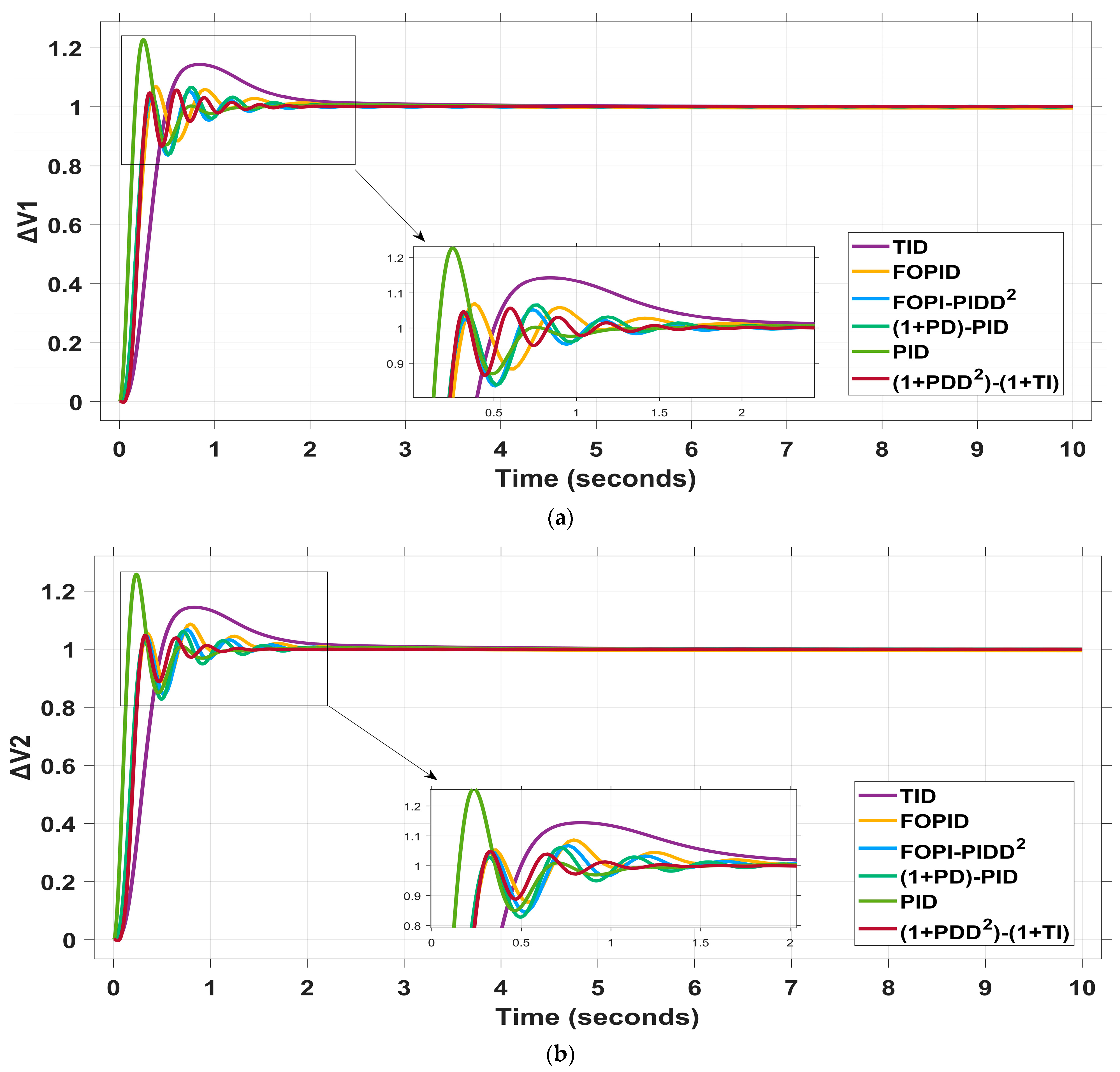
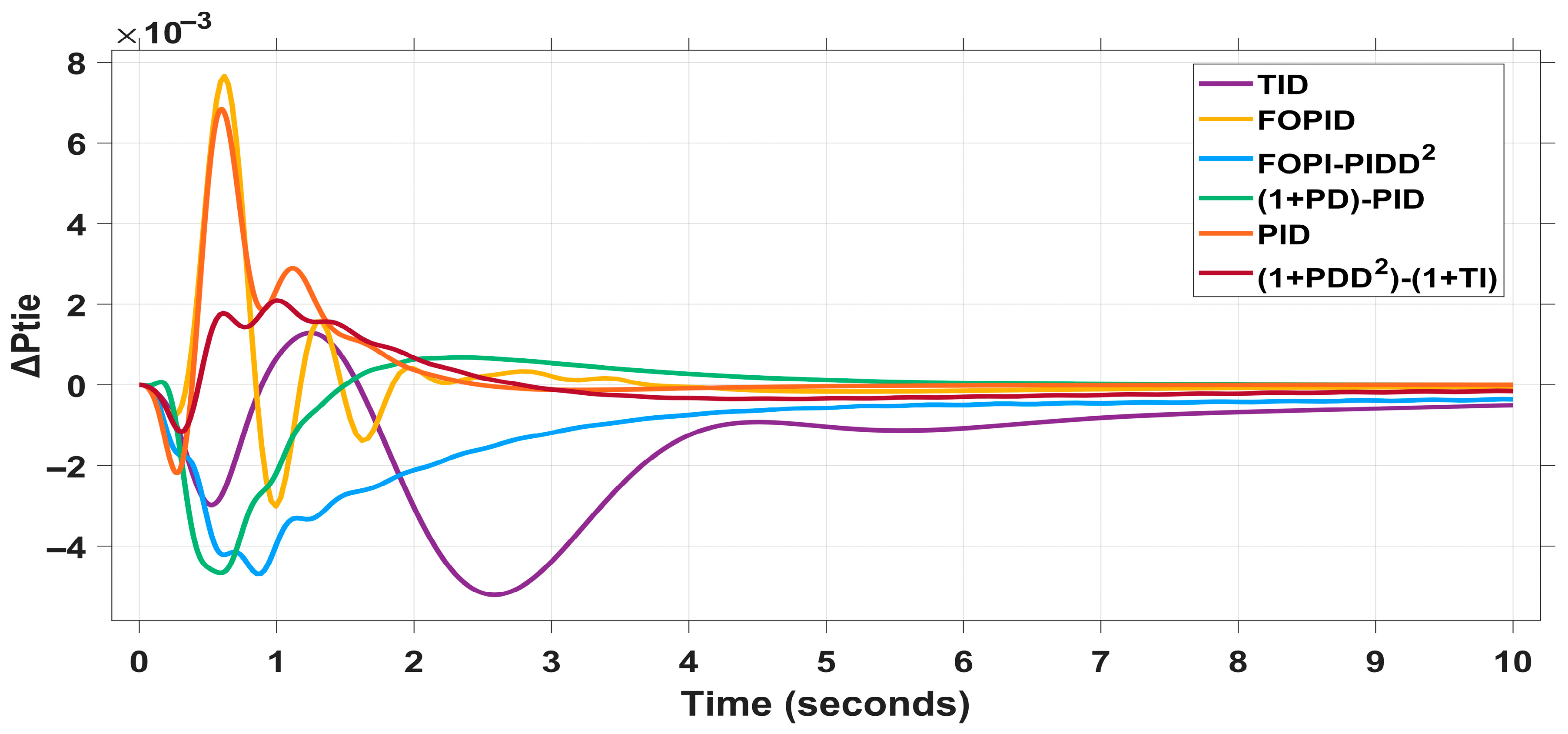
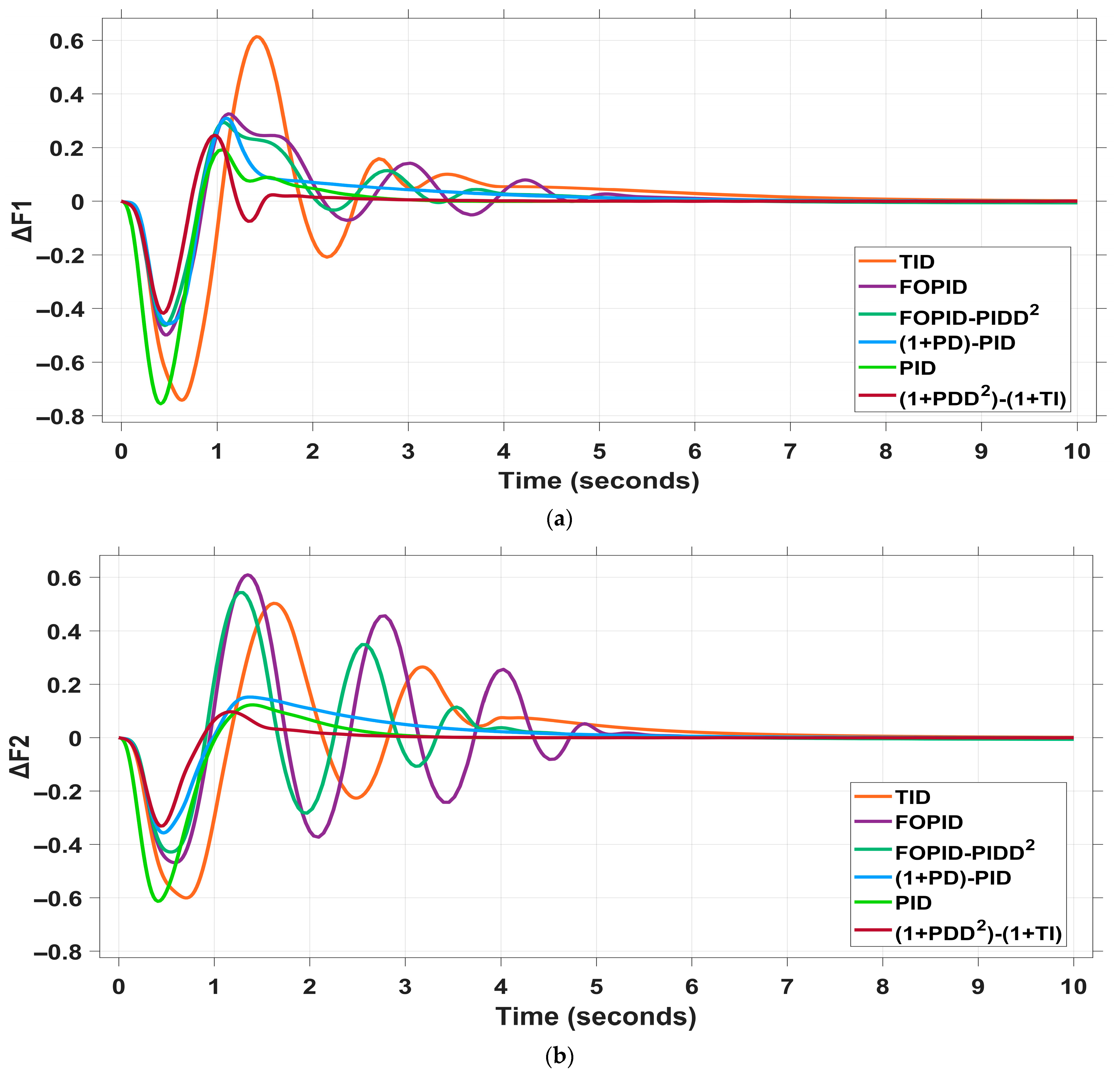
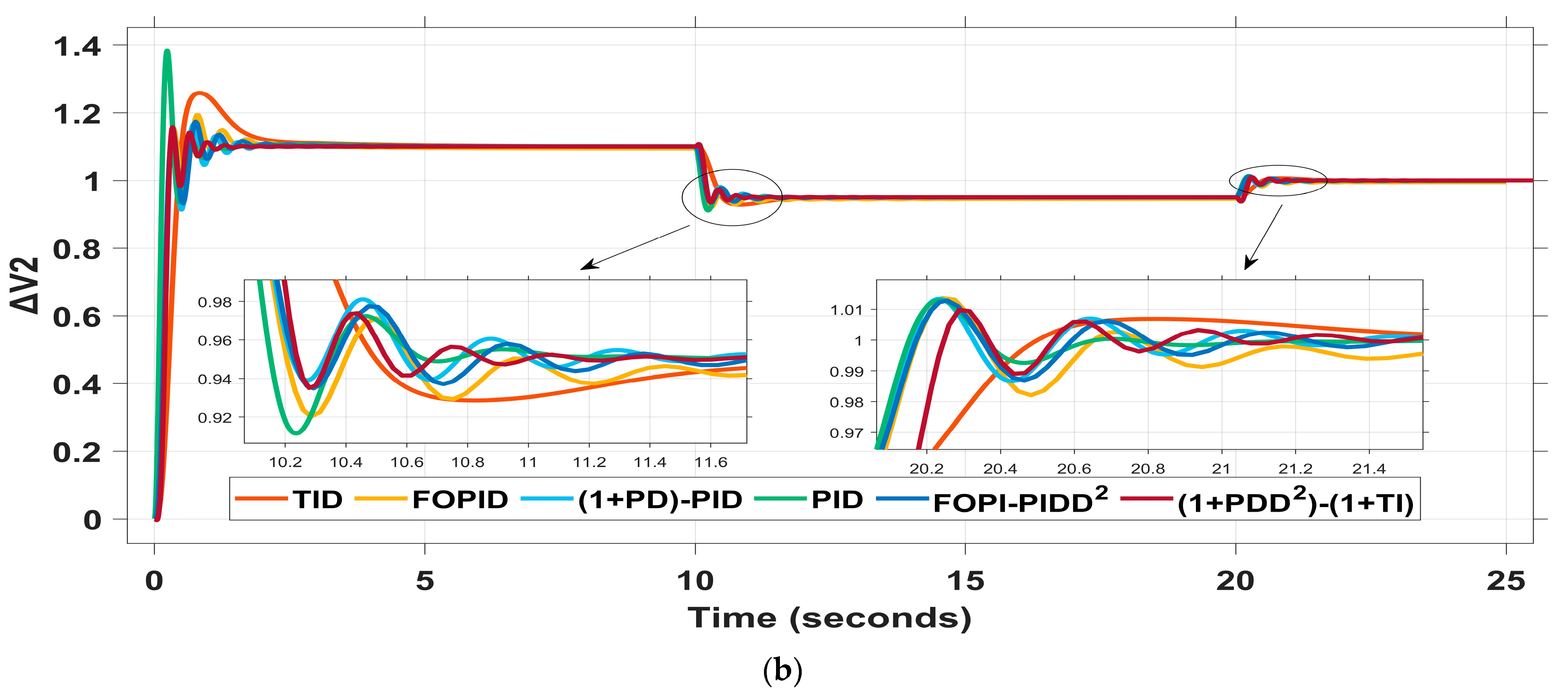
4.2.1. Scenario I: 2% Load Increase in Area 1 and 1.5% Load Increase in Area 2
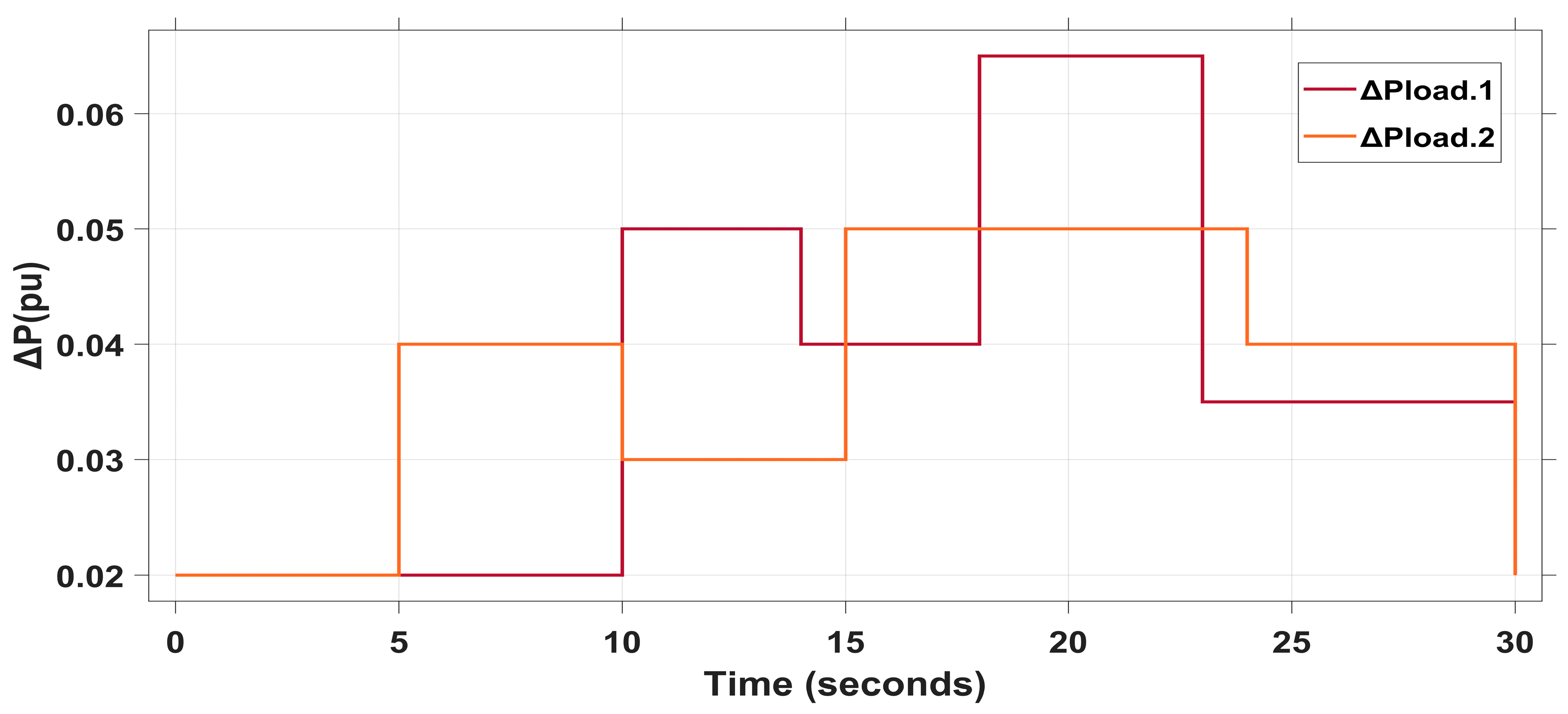
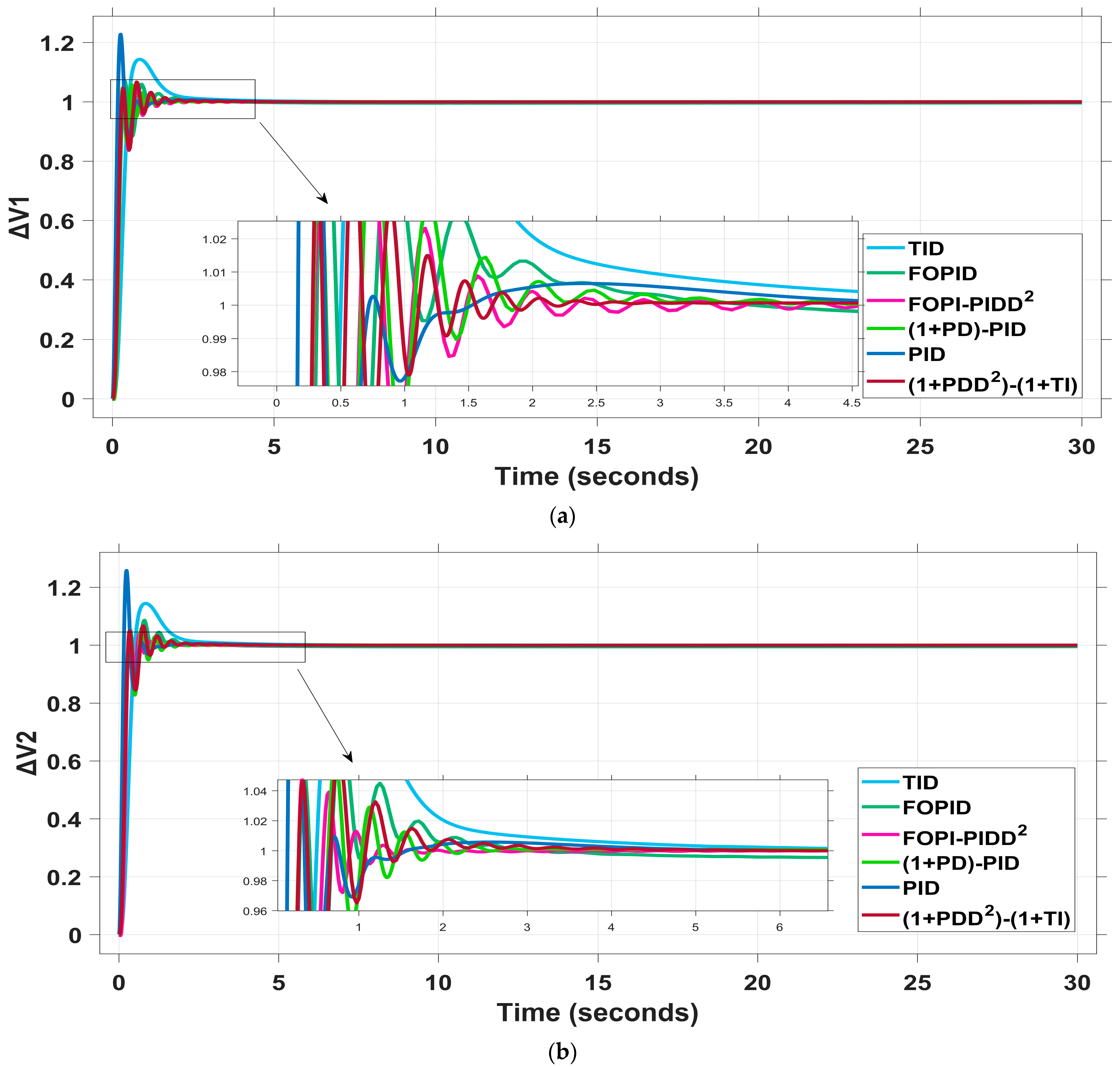
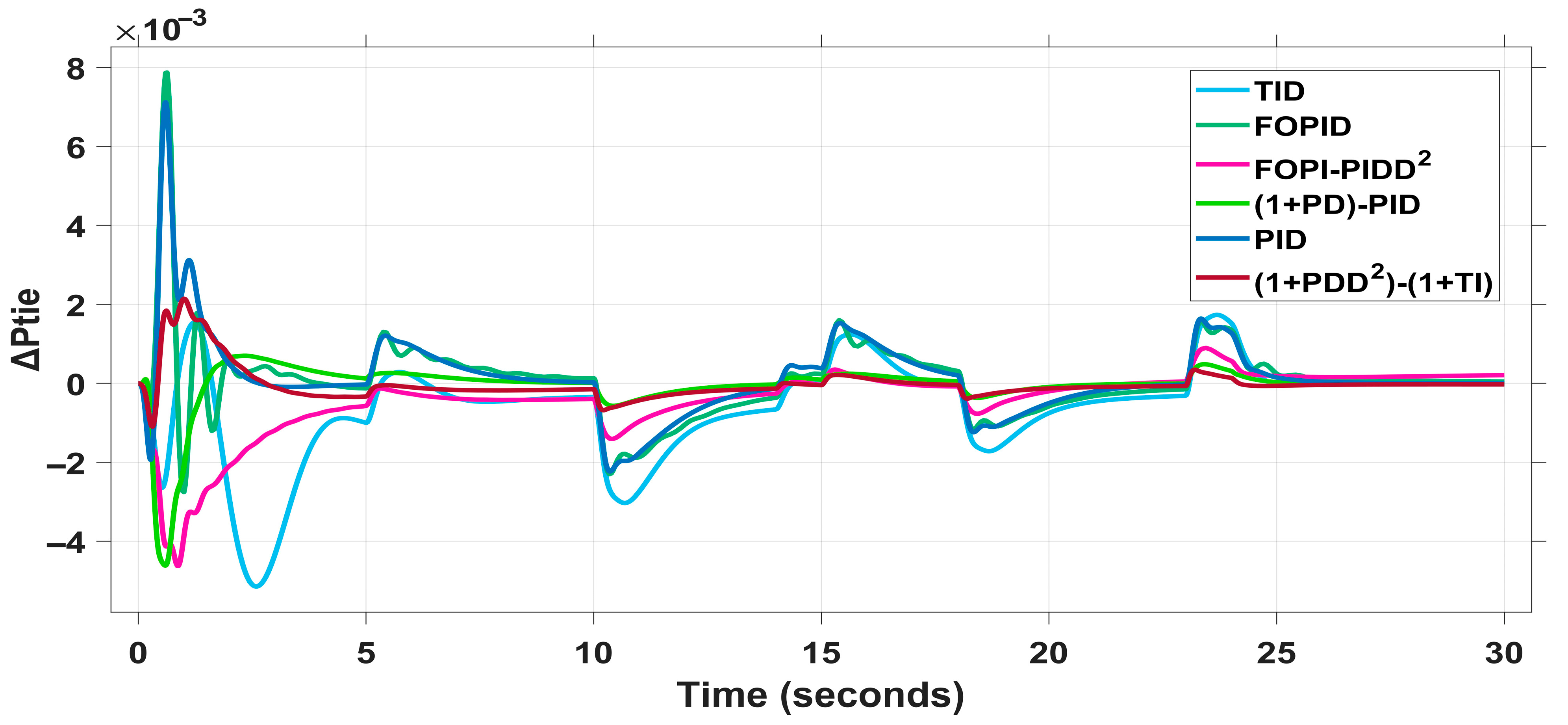
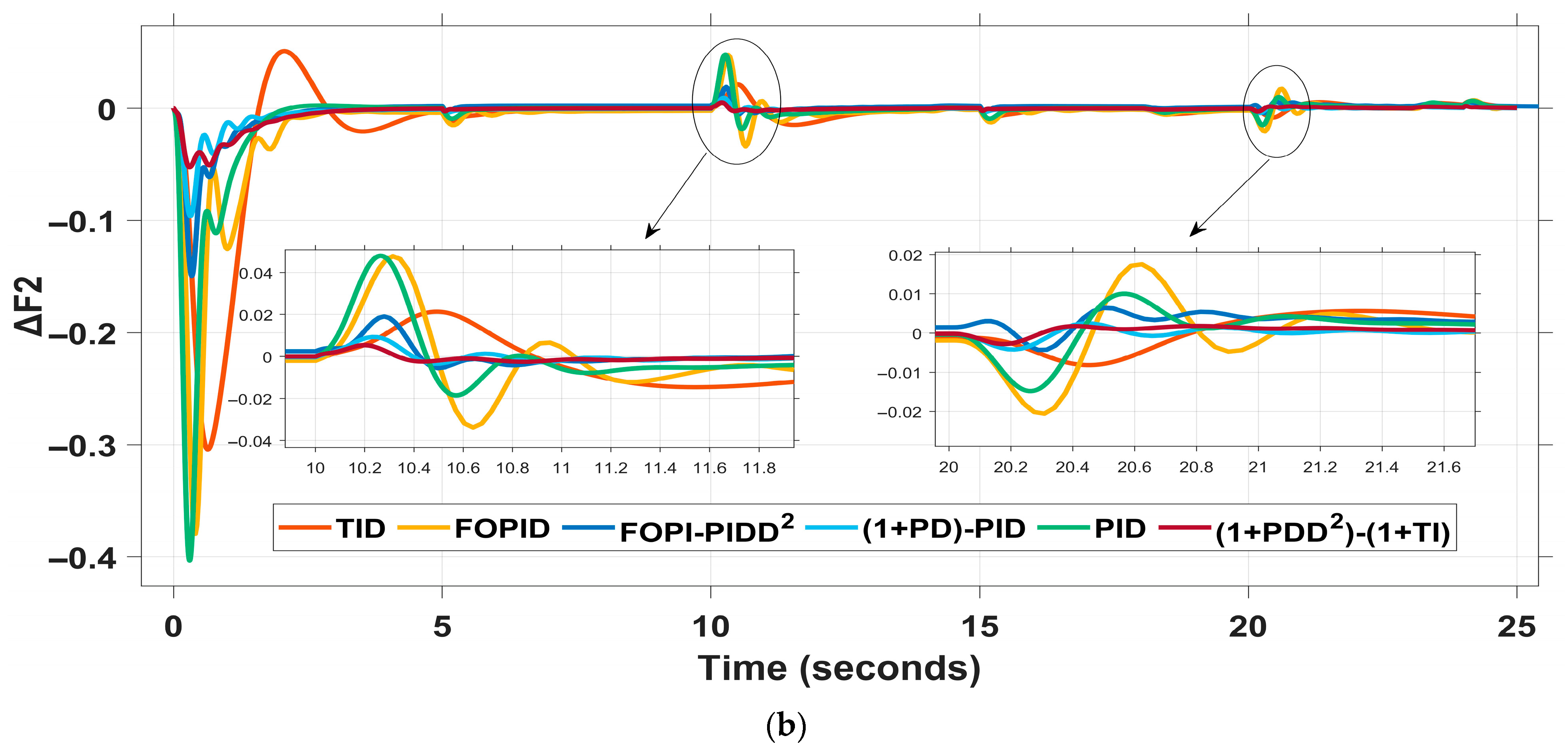
4.2.2. Scenario II: Random Load Variation in Both Areas
4.2.3. Scenario III: Impact of Typical System Nonlinearities
4.2.4. Scenario IV: Time-Varying Desired Output Voltage
4.2.5. Scenario V: Sensitivity Analysis of the System Under Parametric Variations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wadi, M.; Shobole, A.; Elmasry, W.; Kucuk, I. Load frequency control in smart grids: A review of recent developments. Renew. Sustain. Energy Rev. 2024, 189, 114013. [Google Scholar] [CrossRef]
- Nahas, N.; Abouheaf, M.; Darghouth, N.; Md Sharaf, A. A multi-objective AVR-LFC optimization scheme for multi-area power systems. Electr. Power Syst. Res. 2021, 200, 107467. [Google Scholar] [CrossRef]
- Micev, M.; Ćalasan, M.; Radulović, M. Optimal tuning of the novel voltage regulation controller considering the real model of the automatic voltage regulation system. Heliyon 2023, 9, e18707. [Google Scholar] [CrossRef] [PubMed]
- Nahas, N.; Abouheaf, M.; Sharaf, A.; Gueaieb, W. A self-adjusting adaptive AVR-LFC Scheme for Synchronous Generators. IEEE Trans. Power Syst. 2019, 34, 5073–5075. [Google Scholar] [CrossRef]
- Shimizu, K.; Masuta, T.; Ota, Y.; Yokoyama, A. Load frequency control in power system using vehicle-to-grid system considering the customer convenience of electric vehicles. In Proceedings of the 2010 International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–8. [Google Scholar]
- Shimizu, K.; Masuta, T.; Ota, Y.; Yokoyama, A. A new load frequency control method in power system using vehicle-to-grid system considering users’ convenience. In Proceedings of the 17th Power Systems Computation Conference, Stockholm, Sweden, 22–26 August 2011; pp. 22–26. [Google Scholar]
- Masuta, T.; Yokoyama, A. Supplementary load frequency control by use of a number of both electric vehicles and heat pump water heaters. IEEE Trans. Smart Grid 2012, 3, 1253–1262. [Google Scholar] [CrossRef]
- Hajam, F.H.; Mufti, M.-D. An intelligent two-level control of Ultrabattery for improved automatic generation control of a multi-source deregulated power system. Int. J. Energy Res. 2021, 45, 7933–7960. [Google Scholar] [CrossRef]
- Sharma, M.; Dhundhara, S.; Arya, Y.; Prakash, S. Frequency stabilization in deregulated energy system using coordinated operation of fuzzy controller and redox flow battery. Int. J. Energy Res. 2020, 45, 7457–7475. [Google Scholar] [CrossRef]
- Dekaraja, B.; Saikia, L.C. Performance of redox flow battery in combined frequency and voltage control of multi-area multisource system using CFOPDN-FOPIDN controller. Int. Trans. Electr. Energy Syst. 2021, 31, e12782. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, C.; Zeng, T.; Lv, C.; Chan, S.H. Modeling and energy management of a photovoltaic-fuel cell-battery hybrid electric vehicle. Energy Storage 2019, 1, e61. [Google Scholar] [CrossRef]
- Tu, T.; Rajarathnam, G.P.; Vassallo, A.M. Synergic integration of desalination and electric vehicle loads with hybrid micro-grid sizing and control: An Island case study. Energy Storage 2020, 2, e104. [Google Scholar] [CrossRef]
- Topno, P.N.; Chanana, S. Differential evolution algorithm based tilt integral derivative control for LFC problem of an interconnected hydro-thermal power system. J. Vib. Control 2017, 24, 3952–3973. [Google Scholar] [CrossRef]
- Khokhar, B.; Dahiya, S.; Parmar, K.P.S. Load Frequency Control of a Multi-Microgrid System Incorporating Electric Vehicles. Electr. Power Compon. Syst. 2021, 49, 867–883. [Google Scholar] [CrossRef]
- Elmelegi, A.; Mohamed, E.A.; Aly, M.; Ahmed, E.M.; Mohamed, A.A.A.; Elbaksawi, O. Optimized Tilt Fractional Order Cooperative Controllers for Preserving Frequency Stability in Renewable Energy-Based Power Systems. IEEE Access 2021, 9, 8261–8277. [Google Scholar] [CrossRef]
- Morsali, J.; Zare, K.; Tarafdar Hagh, M. Comparative performance evaluation of fractional order controllers in LFC of two-area diverse-unit power system with considering GDB and GRC effects. J. Electr. Syst. Inf. Technol. 2018, 5, 708–722. [Google Scholar] [CrossRef]
- Mohamed, E.A.; Ahmed, E.M.; Elmelegi, A.; Aly, M.; Elbaksawi, O.; Mohamed, A.A.A. An Optimized Hybrid Fractional Order Controller for Frequency Regulation in Multi-Area Power Systems. IEEE Access 2020, 8, 213899–213915. [Google Scholar] [CrossRef]
- Ali, M.; Kotb, H.; Aboras, K.M.; Abbasy, N.H. Design of Cascaded PI-Fractional Order PID Controller for Improving the Frequency Response of Hybrid Microgrid System Using Gorilla Troops Optimizer. IEEE Access 2021, 9, 150715–150732. [Google Scholar] [CrossRef]
- Prakash, A.; Murali, S.; Shankar, R.; Bhushan, R. HVDC tie-link modeling for restructured AGC using a novel fractional order cascade controller. Electr. Power Syst. Res. 2019, 170, 244–258. [Google Scholar] [CrossRef]
- Saha, A.; Saikia, L.C. Load frequency control of a wind-thermal-split shaft gas turbine-based restructured power system integrating FACTS and energy storage devices. Int. Trans. Electr. Energy Syst. 2019, 29, e2756. [Google Scholar] [CrossRef]
- Mohamed, T.H.; Shabib, G.; Abdelhameed, E.H.; Khamies, M.; Qudaih, Y. Load Frequency Control in Single Area System Using Model Predictive Control and Linear Quadratic Gaussian Techniques. Int. J. Electr. Energy 2015, 3, 141–143. [Google Scholar] [CrossRef]
- Elkasem, A.H.A.; Khamies, M.; Hassan, M.H.; Agwa, A.M.; Kamel, S. Optimal Design of TD-TI Controller for LFC Considering Renewables Penetration by an Improved Chaos Game Optimizer. Fractal Fract. 2022, 6, 220. [Google Scholar] [CrossRef]
- Abubakr, H.; Vasquez, J.C.; Mohamed, T.H.; Guerrero, J.M. The concept of direct adaptive control for improving voltage and frequency regulation loops in several power system applications. Int. J. Electr. Power Energy Syst. 2022, 140, 108068. [Google Scholar] [CrossRef]
- Mojumder, H.M.R.; Roy, N.K. PID, LQR, and LQG Controllers to Maintain the Stability of an AVR System at Varied Model Parameters. In Proceedings of the 2021 5th International Conference on Electrical Engineering and Information & Communication Technology (ICEEICT), Dhaka, Bangladesh, 18–20 November 2021; pp. 1–6. [Google Scholar]
- Lai, H.B.; Tran, A.T.; Huynh, V.; Amaefule, E.N.; Tran, P.T.; Phan, V.D. Optimal linear quadratic Gaussian control-based frequency regulation with communication delays in power system. Int. J. Electr. Comput. Eng. 2022, 12, 157–165. [Google Scholar] [CrossRef]
- Bhutto, D.K.; Ansari, J.; Zameer, H. Implementation of AI Based Power Stabilizer Using Fuzzy and Multilayer Perceptron In MatLab. In Proceedings of the 2020 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 29–30 January 2020; pp. 1–8. [Google Scholar]
- Hosseinimoghadam, S.M.S.; Dashtdar, M.; Dashtdar, M.; Roghanian, H. Security control of islanded micro-grid based on adaptive neuro-fuzzy inference system. Sci. Bull. Ser. C Electr. Eng. Comput. Sci. 2020, 1, 189–204. [Google Scholar]
- Modabbernia, M.; Alizadeh, B.; Sahab, A.; Moghaddam, M.M. Designing the Robust Fuzzy PI and Fuzzy Type-2 PI Controllers by Metaheuristic Optimizing Algorithms for AVR System. IETE J. Res. 2020, 68, 3540–3554. [Google Scholar] [CrossRef]
- Bhutto, A.A.; Chachar, F.A.; Hussain, M.; Bhutto, D.K.; Bakhsh, S.E. Implementation of probabilistic neural network (PNN) based automatic voltage regulator (AVR) for excitation control system in Matlab. In Proceedings of the 2019 2nd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 30–31 January 2019; pp. 1–5. [Google Scholar]
- Kalyan, C.N.S.; Goud, B.S.; Reddy, C.R.; Bajaj, M.; Sharma, N.K.; Alhelou, H.H.; Siano, P.; Kamel, S. Comparative Performance Assessment of Different Energy Storage Devices in Combined LFC and AVR Analysis of Multi-Area Power System. Energies 2022, 15, 629. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; García-Bustos, J.E.; Castillo-López, E.I. Switched Fractional Order Model Reference Adaptive Control for an Automatic Voltage Regulator. IFAC-PapersOnLine 2020, 53, 3731–3736. [Google Scholar] [CrossRef]
- Safiullah, S.; Rahman, A.; Ahmad Lone, S. Optimal control of electrical vehicle incorporated hybrid power system with second order fractional-active disturbance rejection controller. Optim. Control Appl. Methods 2021, 44, 905–934. [Google Scholar] [CrossRef]
- Aljaifi, T.; Bawazir, A.; Abdellatif, A.; Pauline, O.; Yee, L.C.; Abdullah, H. Applying genetic algorithm to optimize the PID controller parameters for an effective automatic voltage regulator. Commun. Comput. Appl. Math. 2019, 1, 10–15. [Google Scholar]
- Yegireddy, N.K.; Panda, S.; Papinaidu, T.; Yadav, K.P.K. Multi-objective non dominated sorting genetic algorithm-II optimized PID controller for automatic voltage regulator systems. J. Intell. Fuzzy Syst. 2018, 35, 4971–4975. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S.; Padmanaban, S.; Blaabjerg, F.; Chittathuru, D. Small-Signal Stability Analysis of Hybrid Power System with Quasi-Oppositional Sine Cosine Algorithm Optimized Fractional Order PID Controller. IEEE Access 2020, 8, 155971–155986. [Google Scholar] [CrossRef]
- Kamel, S.; Elkasem, A.H.A.; Korashy, A.; Ahmed, M.H. Sine Cosine Algorithm for Load Frequency Control Design of Two Area Interconnected Power System with DFIG Based Wind Turbine. In Proceedings of the 2019 International Conference on Computer, Control, Electrical, and Electronics Engineering (ICCCEEE), Khartoum, Sudan, 21–23 September 2019. [Google Scholar]
- Ghosh, A.; Ray, A.K.; Nurujjaman; Jamshidi, M. Voltage and frequency control in conventional and PV integrated power systems by a particle swarm optimized Ziegler–Nichols based PID controller. SN Appl. Sci. 2021, 3, 314. [Google Scholar] [CrossRef]
- Ebrahim, M.A.; Ali, A.M.; Hassan, M.M. Frequency and voltage control of multi area power system via novel particle swarm optimization techniques. Int. J. Comput. Res. 2017, 24, 427–474. [Google Scholar]
- Mokeddem, D.; Mirjalili, S. Improved Whale Optimization Algorithm applied to design PID plus second-order derivative controller for automatic voltage regulator system. J. Chin. Inst. Eng. 2020, 43, 541–552. [Google Scholar] [CrossRef]
- Taher, S.A.; Fini, M.H.; Aliabadi, S.F. Fractional order PID controller design for LFC in electric power systems using imperialist competitive algorithm. Ain Shams Eng. J. 2014, 5, 121–135. [Google Scholar] [CrossRef]
- Mahmoud, E. Design of neural network predictive controller based on imperialist competitive algorithm for automatic voltage regulator. Neural Comput. Appl. 2019, 31, 5017–5027. [Google Scholar]
- Chatterjee, S.; Mukherjee, V. PID controller for automatic voltage regulator using teaching–learning based optimization technique. Int. J. Electr. Power Energy Syst. 2016, 77, 418–429. [Google Scholar] [CrossRef]
- Yeboah, S.J. Gravitational Search Algorithm Based Automatic Load Frequency Control for Multi-Area Interconnected Power System. Turk. J. Comput. Math. Educ. (TURCOMAT) 2021, 12, 4548–4568. [Google Scholar]
- Alhelou, H.H.; Hamedani-Golshan, M.E.; Zamani, R.; Heydarian-Forushani, E.; Siano, P. Challenges and opportunities of load frequency control in conventional, modern and future smart power systems: A comprehensive review. Energies 2018, 11, 2497. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]
- Al-Hinai, A.; Alyammahi, H.; Haes Alhelou, H. Coordinated intelligent frequency control incorporating battery energy storage system, minimum variable contribution of demand response, and variable load damping coefficient in isolated power systems. Energy Rep. 2021, 7, 8030–8041. [Google Scholar] [CrossRef]
- Panda, S.; Mohanty, B.; Hota, P.K. Hybrid BFOA-PSO algorithm for automatic generation control of linear and nonlinear interconnected power systems. Appl. Soft Comput. 2013, 13, 4718–4730. [Google Scholar] [CrossRef]
- Ramesh, M.; Yadav, A.K.; Pathak, P.K. Artificial Gorilla troops optimizer for frequency regulation of wind contributed Microgrid System. ASME J. Comput. Nonlinear Dyn. 2022, 18, 011005. [Google Scholar] [CrossRef]
- Sah, S.V.; Prakash, V.; Pathak, P.K.; Yadav, A.K. Fractional Order AGC Design for Power Systems via Artificial Gorilla Troops Optimizer. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022. [Google Scholar]
- Daoud, M.S.; Shehab, M.; Al-Mimi, H.M.; Abualigah, L.; Abu Zitar, R.; Shambour, M.K.Y. Gradient-Based Optimizer (GBO): A Review, Theory, Variants, and Applications. Arch. Comput. Methods Eng. 2023, 30, 2431–2449. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S. Mirage Search Optimization. MATLAB Central File Exchange. 2025. Available online: https://www.mathworks.com/matlabcentral/fileexchange/180042-mirage-search-optimization (accessed on 25 April 2025).
- Alharbi, M.; Ragab, M.; AboRas, K.M.; Kotb, H.; Dashtdar, M.; Shouran, M.; Elgamli, E. Innovative AVR-LFC Design for a Multi-Area Power System Using Hybrid Fractional-Order PI and PIDD2 Controllers Based on Dandelion Optimizer. Mathematics 2023, 11, 1387. [Google Scholar] [CrossRef]
- Çelik, E.; Öztürk, N.; Arya, Y.; Ocak, C. (1+PD)-PID cascade controller design for performance betterment of load frequency control in diverse electric power systems. Neural Comput. Appl. 2021, 33, 15433–15456. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Biswal, A.; Sekhar, G.T.C. Design and analysis of tilt integral derivative controller with filter for load frequency control of multi-area interconnected power systems. ISA Trans. 2016, 61, 251–264. [Google Scholar] [CrossRef]
- Zeidan, M.A.; Hammad, M.R.; Megahed, A.I.; AboRas, K.M.; Alkuhayli, A.; Gowtham, N. Enhancement of a hybrid electric shipboard microgrid’s frequency stability with triangulation topology aggregation optimizer-based 3DOF-PID-TI controller. IEEE Access 2024, 12, 66625–66645. [Google Scholar] [CrossRef]
- Dev, A.; Bhatt, K.; Mondal, B.; Kumar, V.; Bajaj, M.; Tuka, M.B. Enhancing load frequency control and automatic voltage regulation in Interconnected power systems using the Walrus optimization algorithm. Sci. Rep. 2024, 14, 27839. [Google Scholar] [CrossRef]
- Saadat, H. Power System Analysis, 3rd ed.; PSA Publishing: Williamsport, PA, USA, 2011. [Google Scholar]
- Rajbongshi, R.; Saikia, L.C. Combined control of voltage and frequency of multi-area multisource system incorporating solar thermal power plant using LSA optimised classical controllers. IET Gener. Transm. Distrib. 2017, 11, 2489–2498. [Google Scholar] [CrossRef]
- Anand, S.; Dev, A.; Sarkar, M.K.; Banerjee, S. Non-fragile approach for frequency regulation in power system with event-triggered control and communication delays. IEEE Trans. Ind. Appl. 2021, 57, 2187–2201. [Google Scholar] [CrossRef]
- Hasanien, H.M.; El-Fergany, A.A. Salp swarm algorithm-based optimal load frequency control of hybrid renewable power systems with communication delay and excitation cross coupling effect. Electr. Power Syst. Res. 2019, 176, 105938. [Google Scholar] [CrossRef]
- Chen, G.; Liu, X.; Ren, X.; Xia, J.; Park, J.H. Asynchronous-based countermeasure for stealthy attack on aperiodic sampled-data control systems. IEEE Trans. Autom. Control 2025, 1–8. [Google Scholar] [CrossRef]







| Model | Transfer Function | Parameters | Nominal Values | Parameter Description |
|---|---|---|---|---|
| Amplifier | , | 10, 0.1 | Gains and time constants of amplifier, exciter, generator and sensor | |
| Exciter | , | 1, 0.4 | ||
| Generator (Field CKT) | , | 1, 1 | ||
| Sensor | , | 1, 0.01 |
| Model | Transfer Function | Parameters | Nominal Values Area 1 | Nominal Values Area 2 | Parameter Description |
|---|---|---|---|---|---|
| Governor | , | 1, 0.08 | 1, 0.072 | Governor, Turbine, and Load gains and time constants | |
| Turbine | , | 1, 0.3 | 1, 0.33 | ||
| Load | , | 120, 20 | 112.5, 25 | ||
| 0.41 | 0.37 | Frequency bias coefficients | |||
| R | 2.4 | 2.7 | Governor speed regulation parameters |
| Area | α1 | α2 | α3 | α4 | βS | |
|---|---|---|---|---|---|---|
| 1 | 0.3 | 0.1 | 0.5 | 1.4 | 1.5 | 0.55 |
| 2 | 0.3 | 0.1 | 0.5 | 1.4 | 1.5 |
| Parameters | ChOA | DOA | GTO | PSO | GBO | MSO | |
|---|---|---|---|---|---|---|---|
| LFC1 | KP | 0 | 3.15 | 4.99 | 5 | 4.48 | 4.49 |
| KD | 5 | 5 | 4.99 | 5 | 4.87 | 2.05 | |
| KDD | 7.95 × 10−5 | 0.1 | 0.02 | 0 | 0.025 | 0.05 | |
| ND | 142.93 | 202.02 | 500 | 500 | 135.11 | 351.78 | |
| NDD | 370.18 | 223.71 | 100 | 100 | 481.46 | 204.23 | |
| KT | 0.02 | 2.65 | 5 | 0 | 2.31 | 4.024 | |
| NT | 1 | 10 | 1.012 | 10 | 1.30 | 1.91 | |
| KI | 5 | 3.46 | 2.62 | 5 | 4.99 | 3.15 | |
| AVR1 | KP | 0 | 4.96 | 2.25 | 4.99 | 0.52 | 4.62 |
| KD | 2.16 | 4.23 | 0.74 | 0.99 | 0.37 | 1.15 | |
| KDD | 42.14 × 10−5 | 0.03 | 93.06 × 10−4 | 0.02 | 21.2 × 10−4 | 40.78 × 10−5 | |
| ND | 423.36 | 494.57 | 100.65 | 500 | 364.87 | 481.22 | |
| NDD | 100 | 500 | 500 | 500 | 496.52 | 190.67 | |
| KT | 0.12 | 4.80 | 1.87 | 5 | 4.49 | 0.74 | |
| NT | 1.08 | 1.37 | 9.88 | 10 | 9.87 | 9.96 | |
| KI | 5 | 2.15 | 0.29 | 0 | 0.57 | 0.17 | |
| LFC2 | KP | 96.96 × 10−5 | 5 | 4.99 | 5 | 4.35 | 4.02 |
| KD | 5 | 4.96 | 4.99 | 5 | 2.48 | 4.32 | |
| KDD | 89.66 × 10−4 | 0.1 | 98.81 × 10−3 | 57.35 × 10−4 | 12.37 × 10−5 | 0.05 | |
| ND | 206.28 | 456.97 | 100.02 | 100 | 313.58 | 251.57 | |
| NDD | 253.15 | 196.01 | 100 | 112.78 | 133.39 | 344.77 | |
| KT | 58.83 × 10−4 | 5 | 4.99 | 1.93 | 4.99 | 0.58 | |
| NT | 1.21 | 9.53 | 1.25 | 10 | 9.85 | 3.76 | |
| KI | 4.73 | 3.39 | 5 | 5 | 4.97 | 4.81 | |
| AVR2 | KP | 0 | 0 | 2.07 | 5 | 1.40 | 4.92 |
| KD | 0.79 | 1.80 | 0.71 | 1.03 | 0.55 | 1.23 | |
| KDD | 0 | 0 | 18.92 × 10−4 | 13.77 × 10−3 | 16.25 × 10−4 | 16.96 × 10−4 | |
| ND | 139.51 | 500 | 148.27 | 500 | 496.31 | 354.09 | |
| NDD | 500 | 107.50 | 317.20 | 500 | 124.01 | 465.33 | |
| KT | 2.55 | 0 | 1.39 | 5 | 3.13 | 0.64 | |
| NT | 1.65 | 2.98 | 10 | 10 | 9.99 | 7.28 | |
| KI | 19.02 × 10−5 | 5 | 0.35 | 0.06 | 0.36 | 0.16 | |
| Fitness | ITSE | 0.044 | 0.05 | 0.03 | 0.033 | 0.03 | 0.028 |
| Test Functions | ChOA | DOA | GTO | PSO | GBO | MSO | |
|---|---|---|---|---|---|---|---|
| 0 | |||||||
| 9.63 | 7.85 | 6.78 | 2.76 | 2.16 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | |||
| Total consumption time for all test function | 0.6091161 | 0.6109206 | 0.5104028 | 0.7284502 | 0.5891876 | 0.5266098 | |
| Controller | ΔF1 | ΔF2 | ΔPtie | ΔV1 | ΔV2 | ITSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MOS | MUS | ST | MOS | MUS | ST | MOS ) | MUS ) | ST | MOS | ST | MOS | ST | ||
| TID | 0.034 | −0.596 | 8 | 0.045 | −0.286 | 8 | 1.2 | −5.2 | 10 | 1.14 | 3.7 | 1.14 | 3.7 | 0.104 |
| FOPID | 0 | −0.295 | 6 | 0 | −0.369 | 6.5 | 7.6 | −3 | 5 | 1.08 | 4 | 1.08 | 3.9 | 0.038 |
| FOPI-PIDD2 | 0 | −0.14 | 10 | 0 | −0.137 | 10 | 0 | −4.6 | 8 | 1.05 | 3.8 | 1.06 | 3.9 | 0.031 |
| (1+PD)-PID | 0 | −0.093 | 4 | 0 | −0.089 | 3 | 0.67 | −4.6 | 6 | 1.07 | 3.5 | 1.02 | 2.5 | 0.031 |
| PID | 0 | −0.358 | 5 | 0 | −0.349 | 5 | 6.8 | −2.17 | 4.5 | 1.2 | 3 | 1.2 | 2.7 | 0.029 |
| (1+PDD2)-(1+TI) (proposed) | 0 | −0.093 | 3 | 0 | −0.048 | 2.22 | 2.15 | −1.18 | 4 | 1.04 | 2.2 | 1.4 | 2.2 | 0.028 |
| Controller | ITSE | Total ITSE | |||
|---|---|---|---|---|---|
| ΔF1 | ΔF2 | ΔV1 | ΔV2 | ||
| TID | 0.1152 | 0.0876 | 0.0729 | 0.0514 | 0.3271 |
| FOPID | 0.0444 | 0.0368 | 0.0296 | 0.0213 | 0.1321 |
| FOPI-PIDD2 | 0.02953 | 0.02038 | 0.01726 | 0.01145 | 0.07862 |
| (1+PD)-PID | 0.02973 | 0.02264 | 0.01678 | 0.01052 | 0.07967 |
| PID | 0.02211 | 0.01584 | 0.01297 | 0.00831 | 0.05923 |
| (1+PDD2)-(1+TI) (proposed) | 0.01460 | 0.01114 | 0.00985 | 0.00572 | 0.04131 |
| (1+PDD2)-(1+TI) (Proposed Controller) | ΔF1 | ΔF2 | ΔPtie | ITSE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MOS | MUS | ST | MOS | MUS | ST | MOS ) | MUS ) | ST | ||
| Without GRC and GRB | 0 | −0.093 | 3 | 0 | −0.089 | 2.22 | 2.15 | −1.18 | 4 | 0.028 |
| With GRC and GRB | 0.241 | −0.417 | 5 | 0 | −0.331 | 6.5 | 4.1 | −3.6 | 5 | 0.038 |
| Controller | ITSE | Total ITSE | |||
|---|---|---|---|---|---|
| ΔF1 | ΔF2 | ΔV1 | ΔV2 | ||
| TID | 0.0976 | 0.0792 | 0.0615 | 0.0478 | 0.2861 |
| FOPID | 0.0422 | 0.0339 | 0.0258 | 0.0176 | 0.1195 |
| FOPI-PIDD2 | 0.02800 | 0.01877 | 0.01628 | 0.01136 | 0.07441 |
| (1+PD)-PID | 0.02740 | 0.01925 | 0.01567 | 0.01082 | 0.07314 |
| PID | 0.02044 | 0.01533 | 0.01047 | 0.00812 | 0.05436 |
| (1+PDD2)-(1+TI) (proposed) | 0.01214 | 0.01041 | 0.00893 | 0.00684 | 0.03832 |
| Parameter | Variation | ΔF1 | ΔF2 | ΔPtie | |||
|---|---|---|---|---|---|---|---|
| MUS (Hz) | ST (s) | MUS (Hz) | ST (s) | MOS ) (PU) | MUS ) (PU) | ||
| Nominal | 0% | −0.093 | 3.8 | −0.048 | 2.22 | 2.15 | −1.18 |
| KG | +40% +20% | −0.083 −0.088 | 4.1 4 | −0.070 −0.074 | 4.2 4 | 1.89 1.94 | −1.92 −1.74 |
| −20% −40% | −0.122 −0.125 | 4.4 4.6 | −0.111 −0.116 | 4 4.1 | 2.7 2.9 | −1.94 −1.98 | |
| TG.1 | +40% +20% | −0.120 −0.115 | 4 4 | −0.097 −0.092 | 4.3 4 | 2.8 2.61 | −2.98 −2.85 |
| −20% −40% | −0.098 −0.095 | 4 4.2 | −0.088 −0.084 | 4 4.2 | 2.16 2.19 | −1.47 −1.59 | |
| KT | +40% +20% | −0.085 −0.088 | 4 4 | −0.070 −0.076 | 3.7 3.5 | 1.69 1.73 | −2.02 −1.94 |
| −20% −40% | −0.115 −0.119 | 4.4 4.7 | −0.109 −0.113 | 4.5 4.6 | 2.61 2.72 | −1.51 −1.63 | |
| TT.1 | +40% +20% | −0.116 −0.106 | 4.1 4 | −0.093 −0.091 | 4.4 4.1 | 2.37 2.29 | −2.21 −2.12 |
| −20% −40% | −0.079 −0.070 | 4 4 | −0.087 −0.086 | 4 4.5 | 2 1.94 | −0.44 −0.31 | |
| KP.1 | +40% +20% | 0.084 −0.09 | 4 4 | 0.091 −0.089 | 4.5 4 | 2.23 2.18 | −1.36 −1.31 |
| −20% −40% | −0.094 0.098 | 4 4.1 | −0.088 −0.083 | 4 4.1 | 2.1 2.08 | −0.97 −0.80 | |
| TP.1 | +40% +20% | −0.095 −0.093 | 4.6 4.4 | −0.084 −0.088 | 4.2 4 | 2.09 2.11 | −0.96 −1.01 |
| −20% −40% | −0.089 −0.086 | 4 4.1 | −0.09 −0.094 | 4.4 4.5 | 2.17 2.21 | −1.33 −1.51 | |
| TG.2 | +40% +20% | −0.097 −0.093 | 4.3 4.1 | −0.099 −0.094 | 4.2 4.1 | 2.01 2.06 | −0.77 −0.81 |
| −20% −40% | −0.091 −0.088 | 4.4 4.7 | −0.084 −0.079 | 3.9 4.2 | 2.24 2.33 | −1.57 −1.69 | |
| TT.2 | +40% +20% | −0.095 −0.093 | 4 4 | −0.16 −0.1 | 4.3 4.1 | 2.56 2.44 | −0.49 −0.65 |
| −20% −40% | −0.091 −0.088 | 4 4.1 | −0.078 −0.071 | 4 4 | 2.16 2.18 | −1.95 −2.27 | |
| KP.2 | +40% +20% | −0.096 −0.093 | 4.4 4 | −0.086 −0.088 | 4.2 4 | 2.02 2.08 | −0.78 −0.97 |
| −20% −40% | −0.092 −0.094 | 4 4.2 | −0.09 −0.093 | 4 4 | 2.25 2.36 | −1.48 −1.68 | |
| TP.2 | +40% +20% | −0.096 −0.092 | 4.2 4 | −0.091 −0.089 | 4.1 4 | 2.40 2.23 | −1.63 −1.42 |
| −20% −40% | −0.092 −0.097 | 4 4.1 | −0.088 −0.086 | 4 4.4 | 2.06 1.98 | −0.95 −0.89 | |
| Parameter | Variation | ΔF1 | ΔF2 | ΔPtie | ΔV1 | ΔV2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ST (s) | ST (s) | MOS ) (PU) | MOS | MOS (PU) | MUS (PU) | ST (s) | MOS (PU) | MUS (PU) | ST (s) | ||
| Nominal | 0% | 3 | 2.22 | 2.15 | −1.18 | 1.04 | 0.85 | 2.2 | 1.04 | 0.89 | 2.2 |
| KA | +40% +20% | 4.8 4.5 | 7 5 | 2.30 2.21 | −1.32 −1.24 | 1.10 1.08 | 0.78 0.81 | 3.2 2.9 | 1.10 1.08 | 0.73 0.81 | 3.4 2.9 |
| −20% −40% | 4.6 5 | 4 5 | 2.04 1.91 | −1.07 −1.01 | 1.06 1.05 | 0.88 0.93 | 2 1.8 | 1.07 1.08 | 0.87 0.94 | 2 1.7 | |
| TA | +40% +20% | 4.9 4.5 | 6.8 4.5 | 2.31 2.21 | −1.11 −1.15 | 1.3 1.1 | 0.76 0.81 | 3.3 2.9 | 1.19 1.1 | 0.80 0.82 | 3.3 2.9 |
| −20% −40% | 4.2 4.4 | 3.9 4.5 | 2.06 1.93 | −1.17 −1.15 | 1.4 1.7 | 0.86 0.88 | 2 1.8 | 1.3 1.42 | 0.86 0.90 | 1.7 1.5 | |
| KE | +40% +20% | 4.8 4.4 | 4.7 4.1 | 2.32 2.21 | −1.29 −1.21 | 1.11 1.08 | 0.74 0.81 | 3.2 2.9 | 1.12 1.08 | 0.73 0.81 | 3.4 2.9 |
| −20% −40% | 4.1 4.3 | 4 4.5 | 2.04 1.93 | −1.07 −0.98 | 1.06 1.04 | 0.87 0.92 | 2 1.9 | 1.06 1.01 | 0.87 0.91 | 2 1.4 | |
| TE | +40% +20% | 4.6 4 | 4.9 4 | 2.08 2.11 | −1.02 −1.11 | 1.11 1.08 | 0.89 0.86 | 2.5 2.4 | 1.16 1.09 | 0.94 0.86 | 2.7 2.4 |
| −20% −40% | 4.4 5 | 4 4.7 | 2.14 2.11 | −1.22 −1.30 | 1.06 1.03 | 0.82 0.78 | 2.4 2.6 | 1.06 1.02 | 0.82 0.72 | 2.4 2.8 | |
| KF | +40% +20% | 4.8 4.5 | 4.6 4.1 | 2.29 2.21 | −1.31 −1.24 | 1.1 1.08 | 0.73 0.81 | 3.5 3.2 | 1.11 1.08 | 0.77 0.81 | 3.4 2.9 |
| −20% −40% | 4 4.3 | 4 4.4 | 2.04 1.97 | −1.09 −1.02 | 1.06 1.02 | 0.88 0.91 | 2 1.5 | 1.06 1.03 | 0.88 0.94 | 2 1.7 | |
| TF | +40% +20% | 4.5 4 | 4.7 4 | 2.02 2.08 | −1.07 −1.13 | 107 1.07 | 0.92 0.87 | 1.7 2 | 1.07 1.07 | 0.91 0.87 | 1.8 2 |
| −20% −40% | 4 4.4 | 4 4.1 | 2.18 2.27 | −1.23 −1.28 | 1.07 1.07 | 0.80 0.72 | 2.4 2.8 | 1.07 1.07 | 0.81 0.74 | 2.4 2.9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AboRas, K.M.; Elkassas, A.M.; Megahed, A.I.; Kotb, H. Voltage and Frequency Regulation in Interconnected Power Systems via a (1+PDD2)-(1+TI) Cascade Controller Optimized by Mirage Search Optimizer. Mathematics 2025, 13, 2251. https://doi.org/10.3390/math13142251
AboRas KM, Elkassas AM, Megahed AI, Kotb H. Voltage and Frequency Regulation in Interconnected Power Systems via a (1+PDD2)-(1+TI) Cascade Controller Optimized by Mirage Search Optimizer. Mathematics. 2025; 13(14):2251. https://doi.org/10.3390/math13142251
Chicago/Turabian StyleAboRas, Kareem M., Ali M. Elkassas, Ashraf Ibrahim Megahed, and Hossam Kotb. 2025. "Voltage and Frequency Regulation in Interconnected Power Systems via a (1+PDD2)-(1+TI) Cascade Controller Optimized by Mirage Search Optimizer" Mathematics 13, no. 14: 2251. https://doi.org/10.3390/math13142251
APA StyleAboRas, K. M., Elkassas, A. M., Megahed, A. I., & Kotb, H. (2025). Voltage and Frequency Regulation in Interconnected Power Systems via a (1+PDD2)-(1+TI) Cascade Controller Optimized by Mirage Search Optimizer. Mathematics, 13(14), 2251. https://doi.org/10.3390/math13142251





