Hypergeometric Functions as Activation Functions: The Particular Case of Bessel-Type Functions
Abstract
1. Introduction
2. Hypergeometric Functions
3. Hypergeometric Functions as Multi-Parametric Activation Functions
- If we consider , we have (jointly with the properties of the hypergeometric functions) that (6) is continuously differentiable, which allows the application of gradient-based optimization methods.
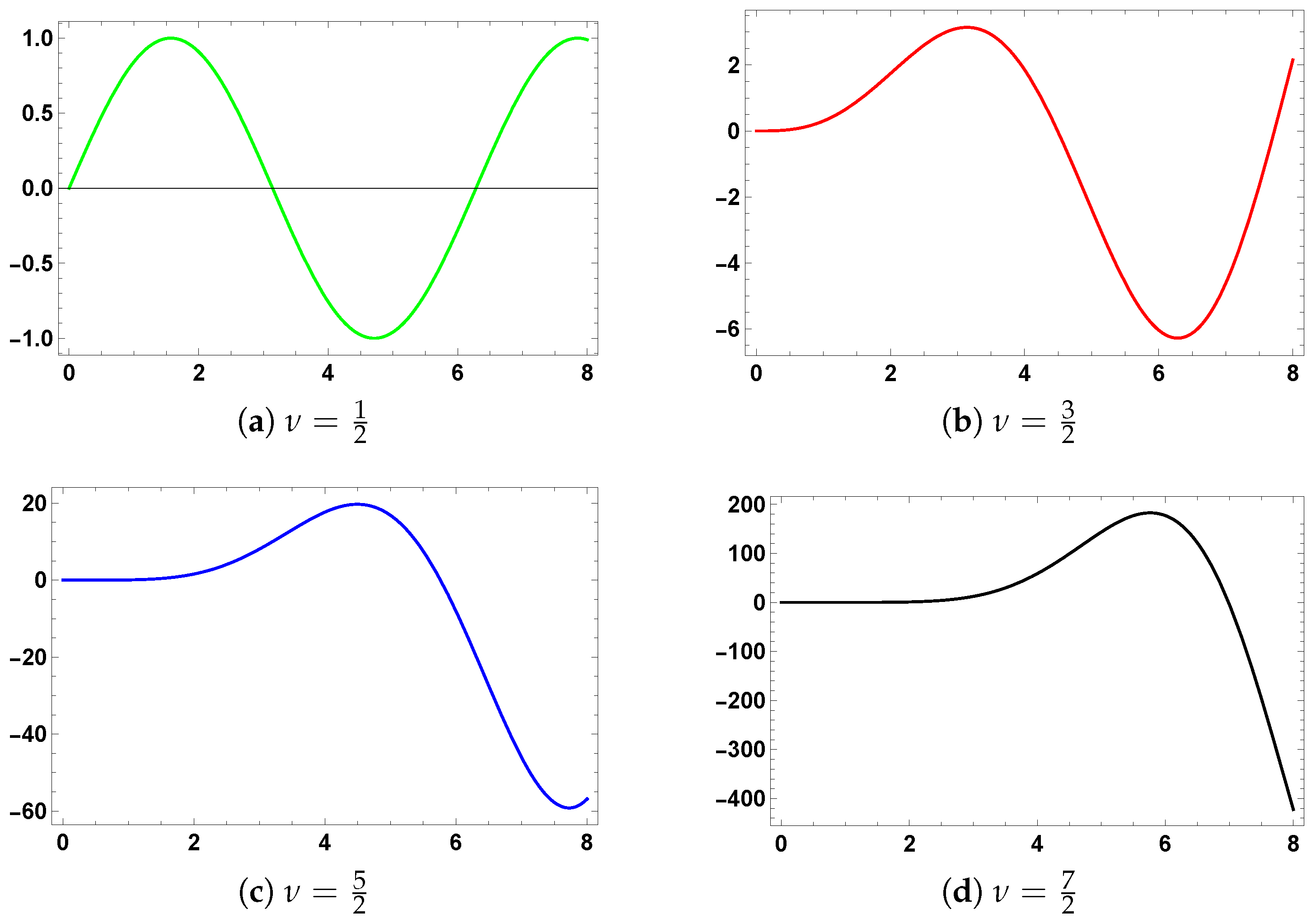
Bessel-Type Functions as Activation Functions
4. Numerical Experiments and Results
4.1. Case Study 1—MNIST Classification
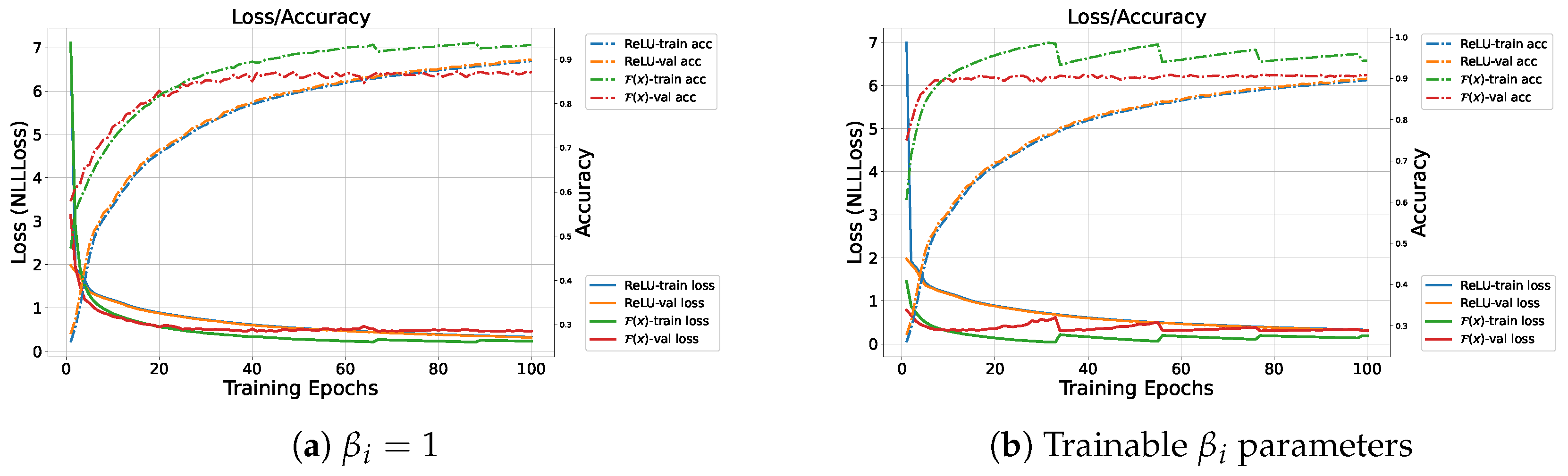
4.1.1. FC Model with Bessel-Type Activation Functions
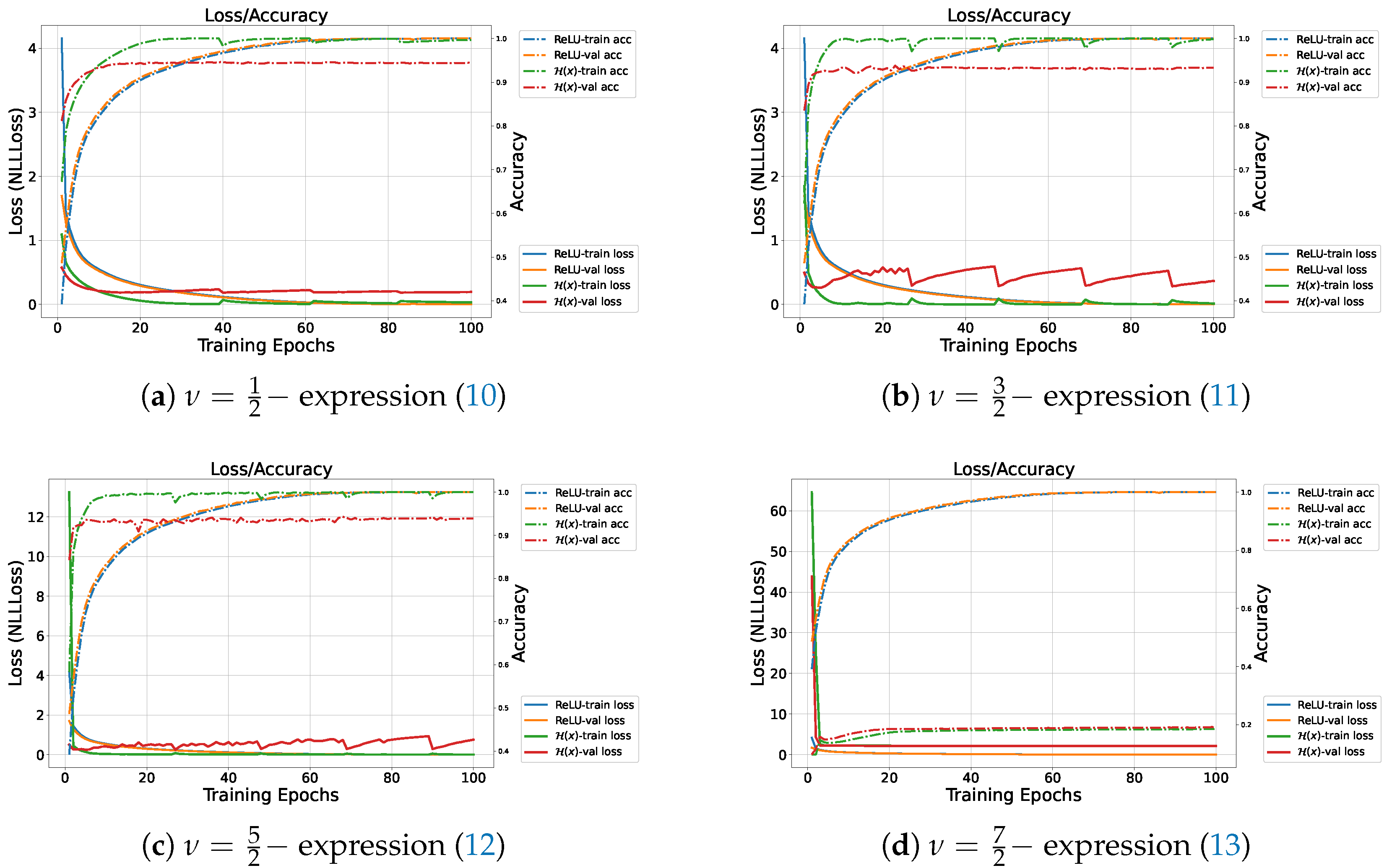
4.1.2. CNN Model with Bessel-Type Activation Functions
4.2. Case Study 2—STL10 Dataset and Deep CNN Architectures
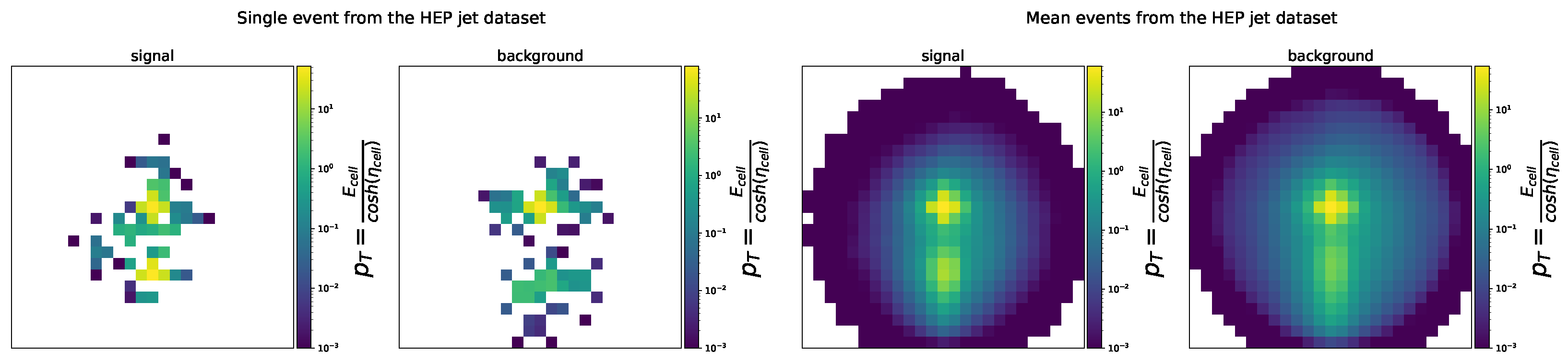
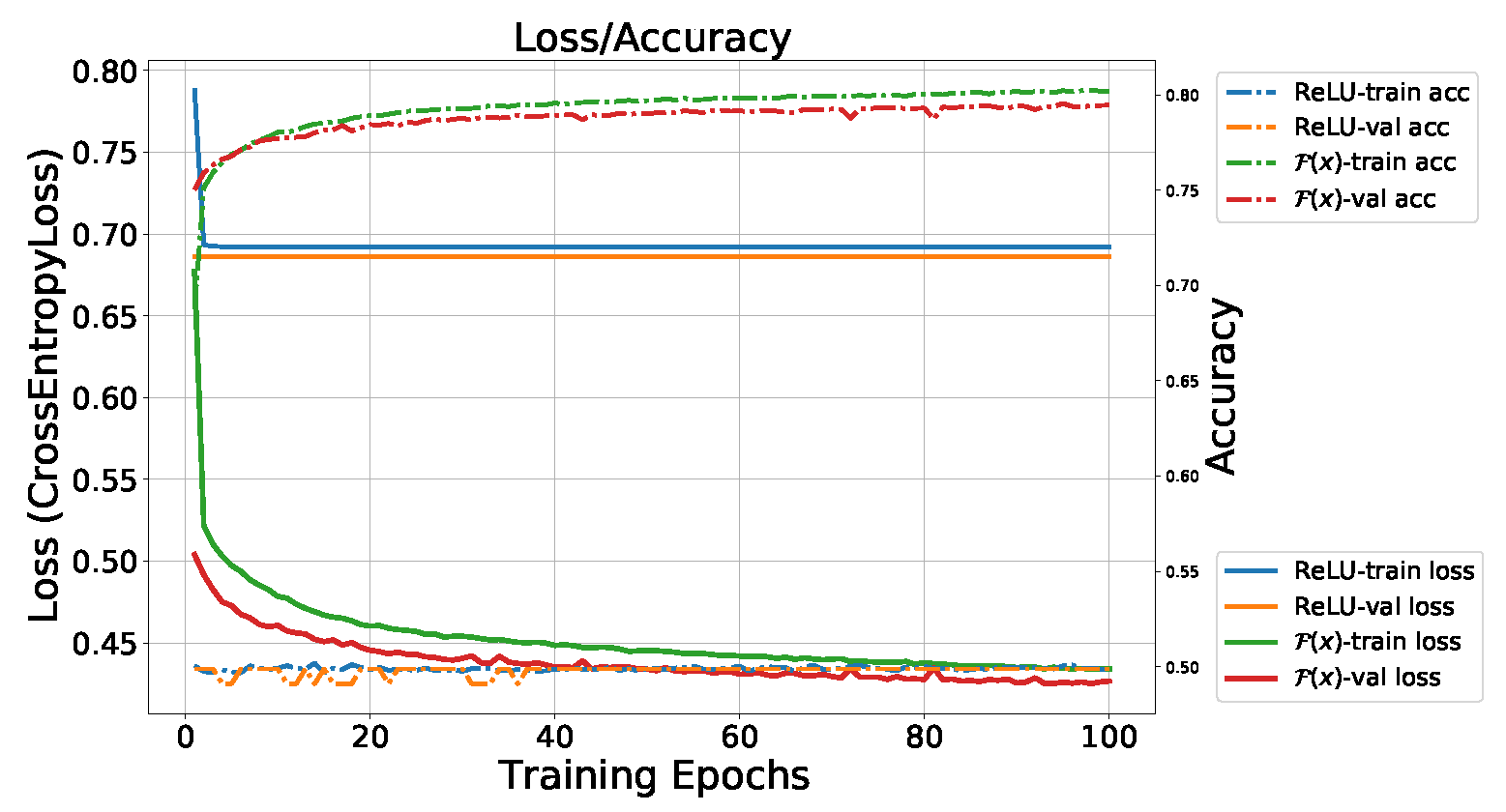
4.3. Case Study 3—High Energy Physics Jet Image Dataset
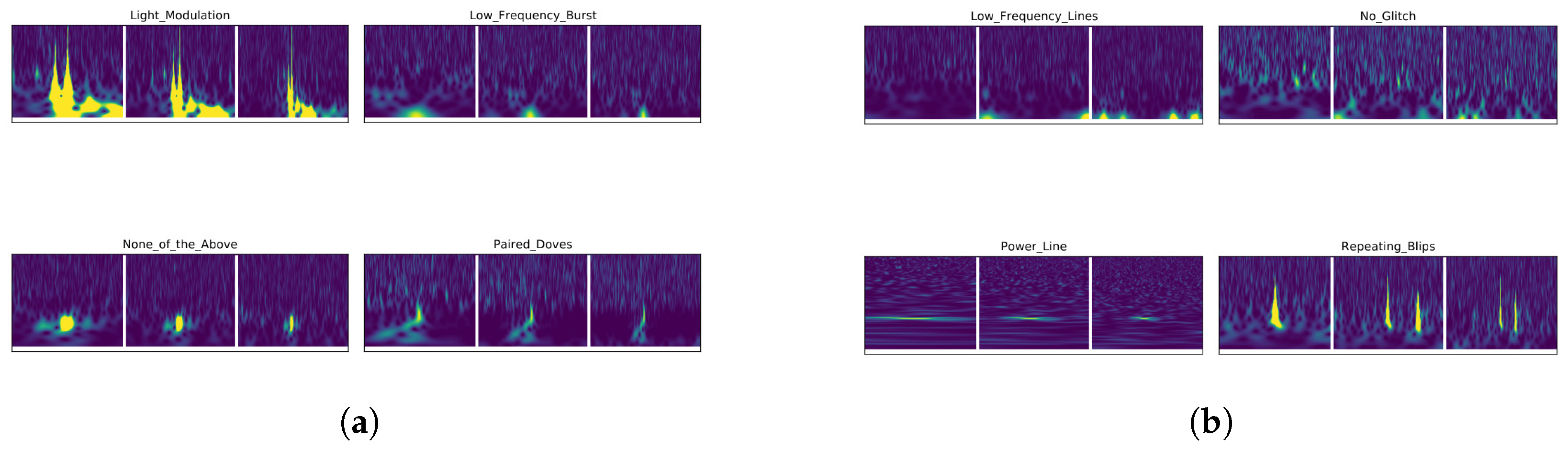
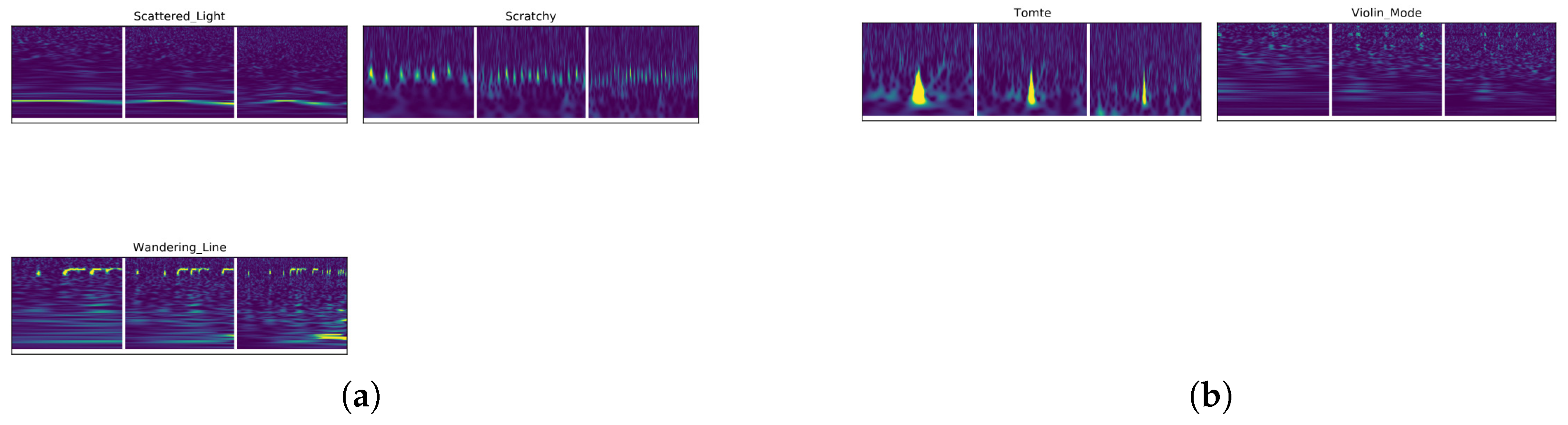
4.4. Case Study 4—Gravity Spy Glitch Dataset
5. Conclusions
6. Technical Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maguolo, G.; Nanni, L.; Ghidoni, S. Ensemble of convolutional neural networks trained with different activation functions. Expert Syst. Appl. 2021, 166, 114048. [Google Scholar] [CrossRef]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. J. Mach. Learn. Res. 2011, 15, 315–323. [Google Scholar]
- Maas, A.; Hannum, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the 30 th International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; Volume 30, p. 3. [Google Scholar]
- Clevert, D.-A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (ELUs). In Proceedings of the 4th International Conference on Learning Representations (ICLR), San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-normalizing neural networks. Adv. Neural Inf. Process. Syst. 2017, 2017, 972–981. [Google Scholar]
- Bilgili, E.; Göknar, C.I.; Ucan, O.N. Cellular neural network with trapezoidal activation function. Int. J. Circ. Theory Appl. 2005, 33, 393–417. [Google Scholar] [CrossRef]
- Özdemir, N.; Iskender, B.; Özgür, N.Y. Complex valued neural network with Möbius activation function. Commun. Nonlinear Sci. 2011, 16, 4698–4703. [Google Scholar] [CrossRef]
- Jalab, H.A.; Ibrahim, R.W. New activation functions for complex-valued neural network. Int. J. Phys. Sci. 2011, 6, 1766–1772. [Google Scholar]
- Sathasivam, S. Boltzmann machine and new activation function comparison. Appl. Math. Sci. 2011, 5, 3853–3860. [Google Scholar]
- Bingham, G.; Miikkulainen, R. Discovering parametric activation functions. arXiv 2020, arXiv:2006.03179v4. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Agostinelli, F.; Hoffman, M.; Sadowski, P.; Baldi, P. Learning activation functions to improve deep neural networks. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Scardapane, S.; Vaerenbergh, S.V.; Uncini, A. Kafnets: Kernel-based nonparametric activation functions for neural networks. Neural Netw. 2018, 110, 19–32. [Google Scholar] [CrossRef] [PubMed]
- Manessi, F.; Rozza, A. Learning Combinations of Activation Functions. In Proceedings of the 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 61–66. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for Activation Functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Zamora-Esquivel, J.; Vargas, A.C.; Camacho-Perez, J.R.; Meyer, P.L.; Cordourier, H.; Tickoo, O. Adaptive activation functions using fractional calculus. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 2006–2013. [Google Scholar]
- Pearson, J. Computation of Hypergeometric Functions. Master’s Thesis, University of Oxford, Oxford, UK, 2009. [Google Scholar]
- Vieira, N. Quaternionic convolutional neural networks with trainable Bessel activation functions. Complex Anal. Oper. Theory 2023, 17, 82. [Google Scholar] [CrossRef]
- Vieira, N. Bicomplex neural networks with hypergeometric activation functions. Adv. Appl. Clifford Algebr. 2023, 33, 20. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series. Volume 3: More Special Functions; Gould, G.G., Translator; Gordon and Breach Science Publishers: New York, NY, USA, 1990. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th ed.; National Bureau of Standards, Wiley-Interscience Publication; John Wiley & Sons: New York, NY, USA, 1972. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Smith, L.N. A disciplined approach to neural network hyper-parameters: Part 1—learning rate, batch size, momentum, and weight decay. arXiv 2018, arXiv:1803.09820. [Google Scholar]
- Kaiming, H.; Xiangyu, Z.; Shaoqing, R.; Jian, S. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.T.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. In Computer Vision—ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11218. [Google Scholar]
- de Oliveira, L.; Kagan, M.; Mackey, L.; Nachman, B.; Schwartzman, A. Jet-Images—Deep Learning Edition. J. High Energy Phys. 2016, 2016, 69. [Google Scholar] [CrossRef]
- Zevin, M.; Coughlin, S.; Bahaadini, S.; Besler, E.; Rohani, N.; Allen, S.; Cabero, M.; Crowston, K.; Katsaggelos, A.K.; Larson, S.L.; et al. Gravity Spy: Integrating advanced LIGO detector characterization, machine learning, and citizen science. Class. Quantum Gravity 2017, 34, 064003. [Google Scholar] [CrossRef] [PubMed]





| General Activation Functions | Activation Function Inside the Class | Identity | Binary Step | ReLU | GELU |
| ELU | SELU | PReLU | Inverse Tangent | ||
| Softsing | Bent Identity | Sinusoid | Sinc | ||
| Gaussian | |||||
| Activation Functions Outside the Class | Sigmoid | Hyperbolic Tangent | SoftPlus | SNQL | |
| SiLu | |||||
| CNN Architecture | # Layers/# Parameters | Micro-Avg | Macro-Avg | # Epochs |
|---|---|---|---|---|
| ResNet18 with ReLU | 18 /11 | 0.57 | 0.62 | 98 |
| ResNet18 with (see (14)) | 18 /11 | 0.88 | 0.88 | 76 |
| ResNet34 with ReLU | 34 /21 | 0.87 | 0.88 | 98 |
| ResNet34 with (see (14)) | 34 /21 | 0.83 | 0.85 | 79 |
| ShuffleNetV2 with ReLU | 164 /1.2 | 0.51 | 0.54 | 20 |
| ShuffleNetV2 with (see (14)) | 164 /1.2 | 0.83 | 0.83 | 6 |
| Resnet18 | Resnet34 | ShuffleNetV2 | ||||
|---|---|---|---|---|---|---|
| Class | ReLU | ReLU | ReLU | |||
| Airplane | 0.78 | 0.94 | 0.91 | 0.95 | 0.39 | 0.93 |
| Bird | 0.54 | 0.81 | 0.85 | 0.73 | 0.56 | 0.76 |
| Car | 0.48 | 0.94 | 0.92 | 0.94 | 0.44 | 0.90 |
| Cat | 0.51 | 0.80 | 0.83 | 0.73 | 0.54 | 0.73 |
| Deer | 0.48 | 0.88 | 0.89 | 0.84 | 0.64 | 0.83 |
| Dog | 0.59 | 0.82 | 0.82 | 0.80 | 0.54 | 0.78 |
| Horse | 0.71 | 0.89 | 0.91 | 0.83 | 0.59 | 0.79 |
| Monkey | 0.68 | 0.88 | 0.88 | 0.86 | 0.61 | 0.84 |
| Ship | 0.79 | 0.92 | 0.89 | 0.92 | 0.65 | 0.90 |
| Truck | 0.63 | 0.88 | 0.87 | 0.87 | 0.44 | 0.82 |
| CNN Architecture | # Layers/# Parameters | Micro-Avg | Macro-Avg | # Epochs |
|---|---|---|---|---|
| ResNet18 with ReLU | 18/11 | 0.88 | 0.87 | 100 |
| ResNet18 with (see (14)) | 18/11 | 0.88 | 0.88 | 90 |
| ResNet34 with ReLU | 34/21 | 0.88 | 0.88 | 100 |
| ResNet34 with (see (14)) | 34/21 | 0.91 | 0.91 | 98 |
| ShuffleNet v2 with ReLU | 164/1.2 | 0.52 | 0.57 | 100 |
| ShuffleNet v2 with (see (14)) | 164/1.2 | 0.86 | 0.86 | 84 |
| Resnet18 | Resnet34 | ShuffleNetV2 | ||||
|---|---|---|---|---|---|---|
| Class | ReLU | ReLU | ReLU | |||
| Airplane | 0.94 | 0.60 | 0.94 | 0.96 | 0.72 | 0.89 |
| Bird | 0.80 | 0.41 | 0.85 | 0.89 | 0.52 | 0.85 |
| Car | 0.94 | 0.85 | 0.95 | 0.96 | 0.60 | 0.93 |
| Cat | 0.79 | 0.47 | 0.85 | 0.86 | 0.42 | 0.82 |
| Deer | 0.86 | 0.37 | 0.90 | 0.91 | 0.68 | 0.89 |
| Dog | 0.80 | 0.45 | 0.85 | 0.87 | 0.46 | 0.82 |
| Horse | 0.88 | 0.69 | 0.92 | 0.93 | 0.55 | 0.86 |
| Monkey | 0.88 | 0.49 | 0.91 | 0.92 | 0.59 | 0.91 |
| Ship | 0.95 | 0.64 | 0.94 | 0.96 | 0.50 | 0.94 |
| Truck | 0.88 | 0.71 | 0.90 | 0.93 | 0.69 | 0.89 |
| CNN Architecture | # Layers/# Parameters | Micro-Avg | Macro-Avg | # Epochs |
|---|---|---|---|---|
| ResNet18 | 18/11 | 57% | 62% | 98 |
| ResNet18 with | 18/11 | 88% | 88% | 76 |
| ResNet34 | 34/21 | 87% | 88% | 98 |
| ResNet34 with | 34/21 | 83% | 85% | 79 |
| ShuffleNet v2 | 164/1.2 | 51% | 54% | 20 |
| ShuffleNet v2 with | 164/1.2 | 83% | 83% | 6 |
| Resnet18 | Resnet34 | ShuffleNetV2 | ||||
|---|---|---|---|---|---|---|
| Glitch | ReLU | ReLU | ReLU | |||
| 1080Lines | 0.03 | 0.91 | 0.96 | 0.78 | 0.92 | 0.85 |
| 1400Ripples | 0.02 | 0.30 | 0.88 | 0.81 | 0.36 | 0.22 |
| Air Compressor | 0.01 | 0.15 | 0.32 | 0.01 | 0.42 | 0.47 |
| Blip | 0.94 | 0.98 | 0.99 | 0.94 | 0.99 | 0.96 |
| Chirp | 0.02 | 0.09 | 0.14 | 0.24 | 0.27 | 0.19 |
| Extremely Loud | 0.90 | 0.94 | 0.91 | 0.97 | 0.95 | 0.94 |
| Helix | 0.53 | 0.95 | 0.98 | 0.95 | 0.97 | |
| Koi Fish | 0.46 | 0.87 | 0.70 | 0.85 | 0.98 | 0.96 |
| Light Modulation | 0.66 | 0.69 | 0.38 | 0.38 | 0.49 | 0.77 |
| Low Frequency Burst | 0.50 | 0.60 | 0.59 | 0.16 | 0.20 | 0.87 |
| Low Frequency Lines | 0.70 | 0.37 | 0.12 | 0.20 | 0.17 | 0.37 |
| No Glitch | 0.32 | 0.06 | 0.57 | 0.11 | 0.28 | 0.14 |
| None of the Above | 0.04 | 0.17 | 0.16 | 0.08 | 0.23 | 0.19 |
| Paired Doves | 0.01 | 0.32 | 0.13 | 0.10 | 0.33 | 0.29 |
| Power Line | 0.56 | 0.42 | 0.19 | 0.17 | 0.11 | 0.92 |
| Repeating Blips | 0.87 | 0.83 | 0.94 | 0.69 | 0.87 | 0.69 |
| Scattered Light | 0.27 | 0.93 | 0.74 | 0.90 | 0.87 | 0.94 |
| Scratchy | 0.50 | 0.90 | 0.95 | 0.89 | 0.98 | 0.86 |
| Tomte | 0.03 | 0.65 | 0.85 | 0.55 | 0.46 | 0.42 |
| Violin Mode | 0.25 | 0.87 | 0.91 | 0.80 | 0.82 | 0.88 |
| Wandering Line | 0.08 | 0.21 | 0.30 | 0.46 | 0.03 | 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vieira, N.; Freitas, F.; Figueiredo, R.; Georgieva, P. Hypergeometric Functions as Activation Functions: The Particular Case of Bessel-Type Functions. Mathematics 2025, 13, 2232. https://doi.org/10.3390/math13142232
Vieira N, Freitas F, Figueiredo R, Georgieva P. Hypergeometric Functions as Activation Functions: The Particular Case of Bessel-Type Functions. Mathematics. 2025; 13(14):2232. https://doi.org/10.3390/math13142232
Chicago/Turabian StyleVieira, Nelson, Felipe Freitas, Roberto Figueiredo, and Petia Georgieva. 2025. "Hypergeometric Functions as Activation Functions: The Particular Case of Bessel-Type Functions" Mathematics 13, no. 14: 2232. https://doi.org/10.3390/math13142232
APA StyleVieira, N., Freitas, F., Figueiredo, R., & Georgieva, P. (2025). Hypergeometric Functions as Activation Functions: The Particular Case of Bessel-Type Functions. Mathematics, 13(14), 2232. https://doi.org/10.3390/math13142232







