Convection in a Rapidly Rotating Spherical Shell: Newton’s Method Using Implicit Coriolis Integration
Abstract
1. Introduction
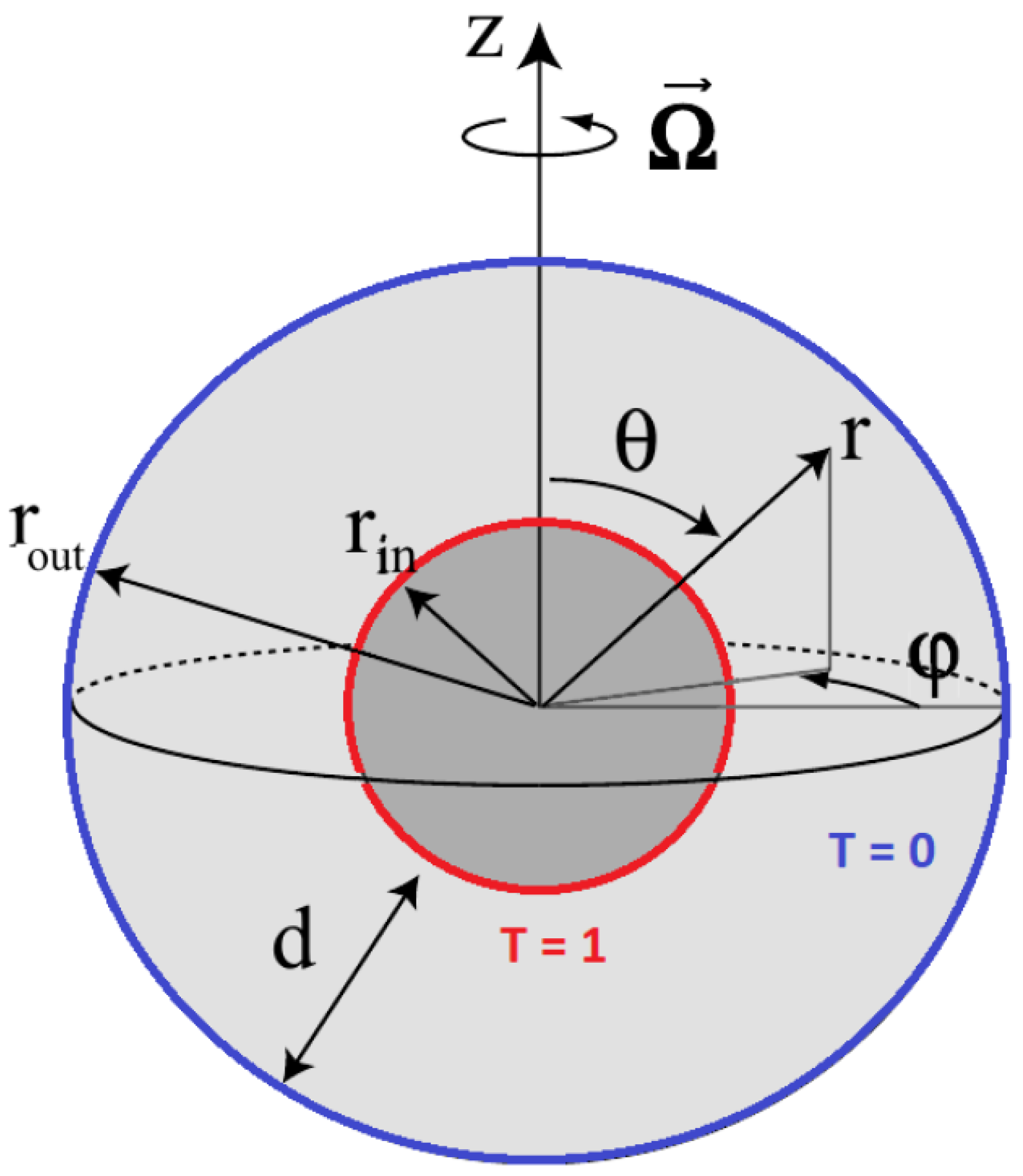
2. Physical Description
2.1. Governing Equations
2.2. Overview
3. Numerical Methods
3.1. Spatial Representation
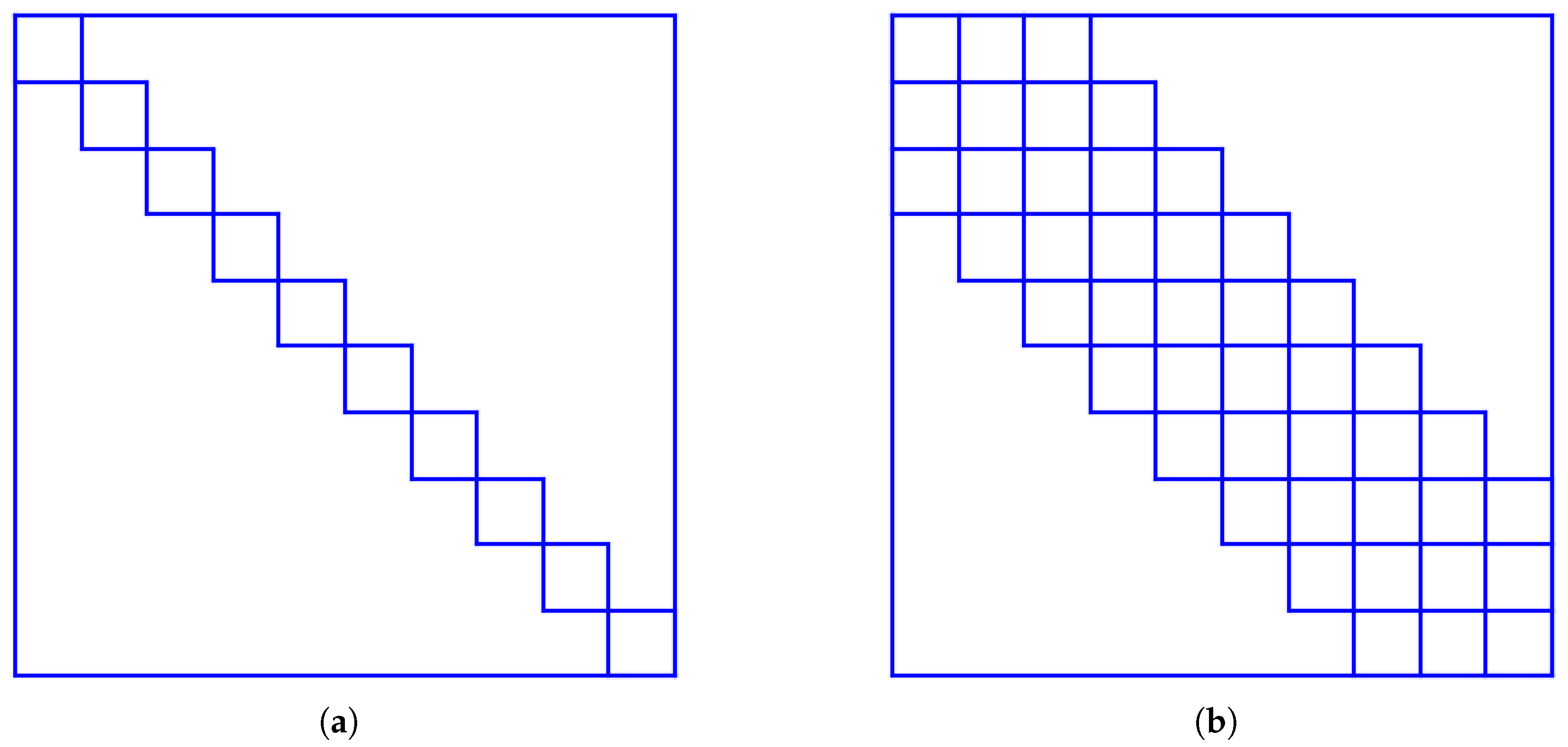
3.2. Implicit Coriolis Integration
- The spectral coefficients and both appear in both equations.
- While each m can be treated independently, components ℓ, , and are coupled.
- The real and imaginary parts of and are coupled via the imaginary coefficient .
3.3. Newton Method
3.4. Traveling Waves
3.5. Continuation
3.6. Turning Points
4. Branch Following
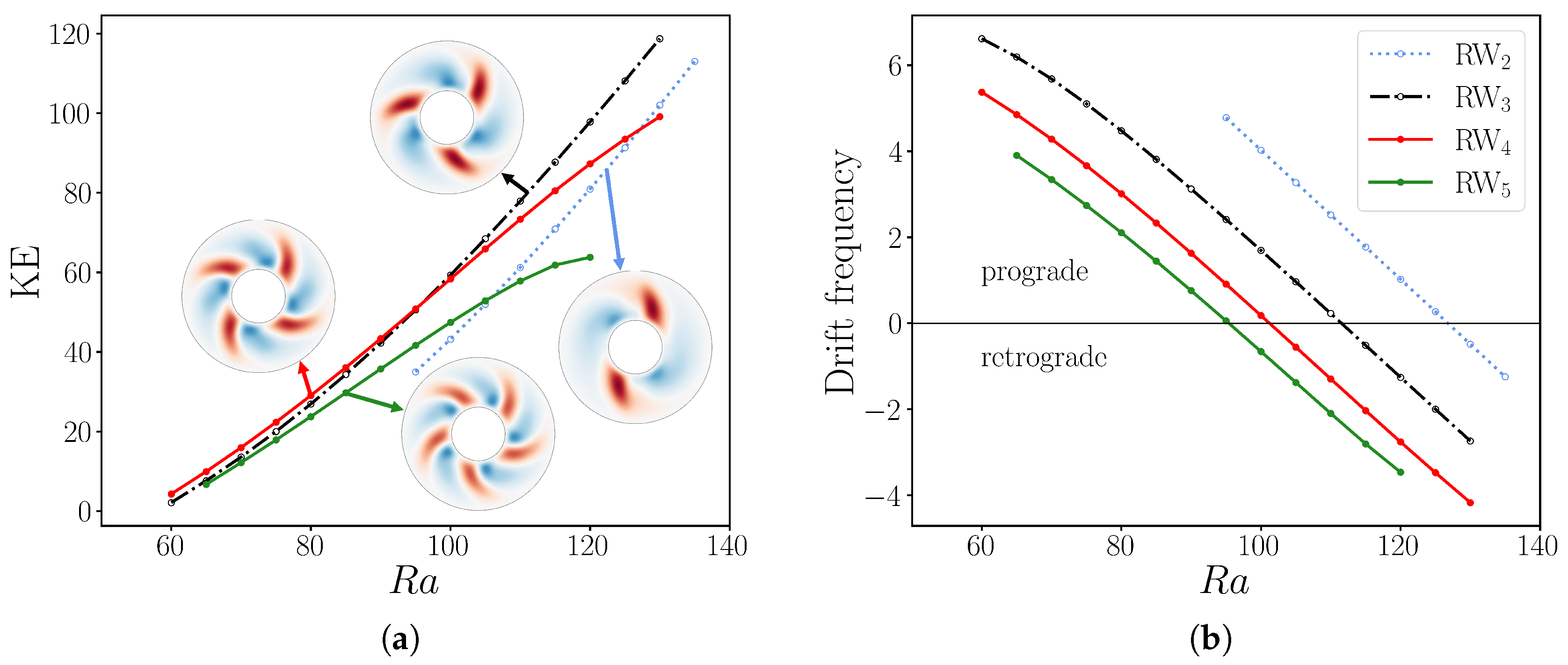
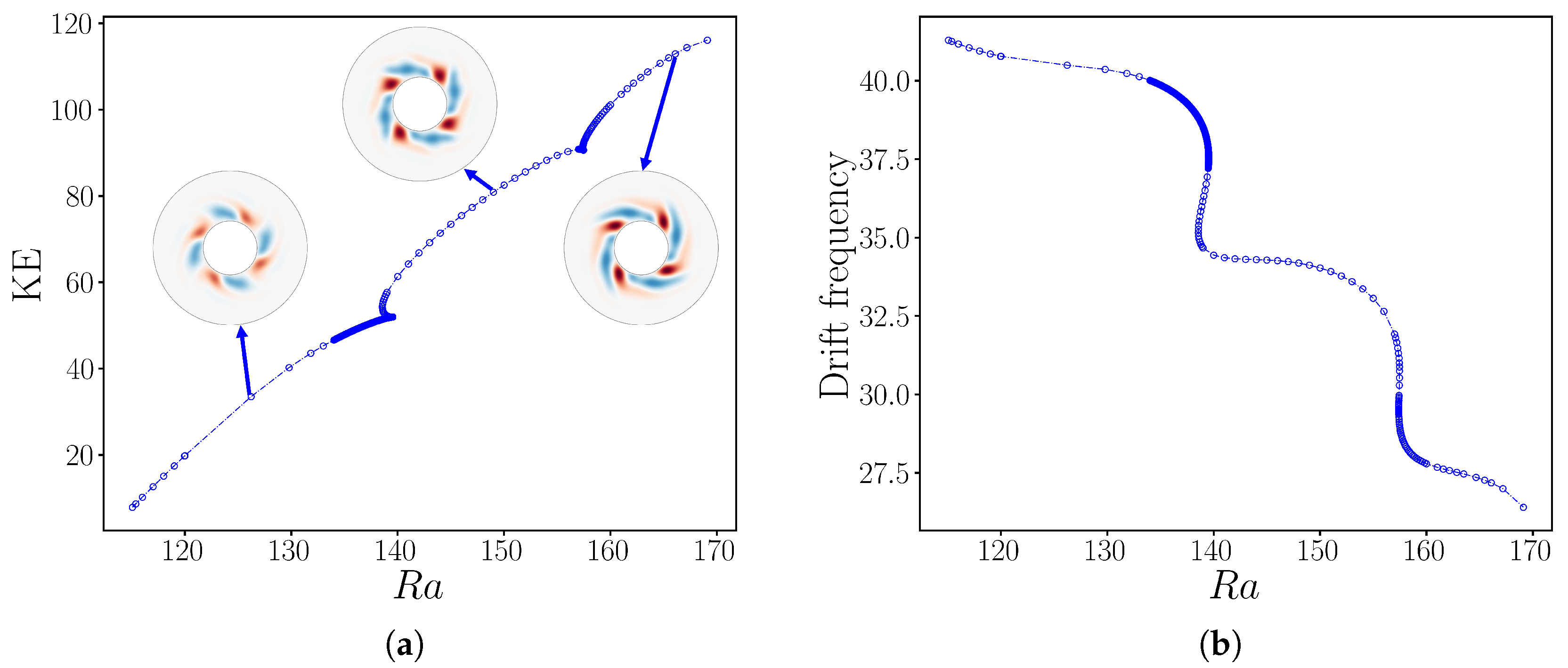
4.1. Continuation in Rayleigh Number
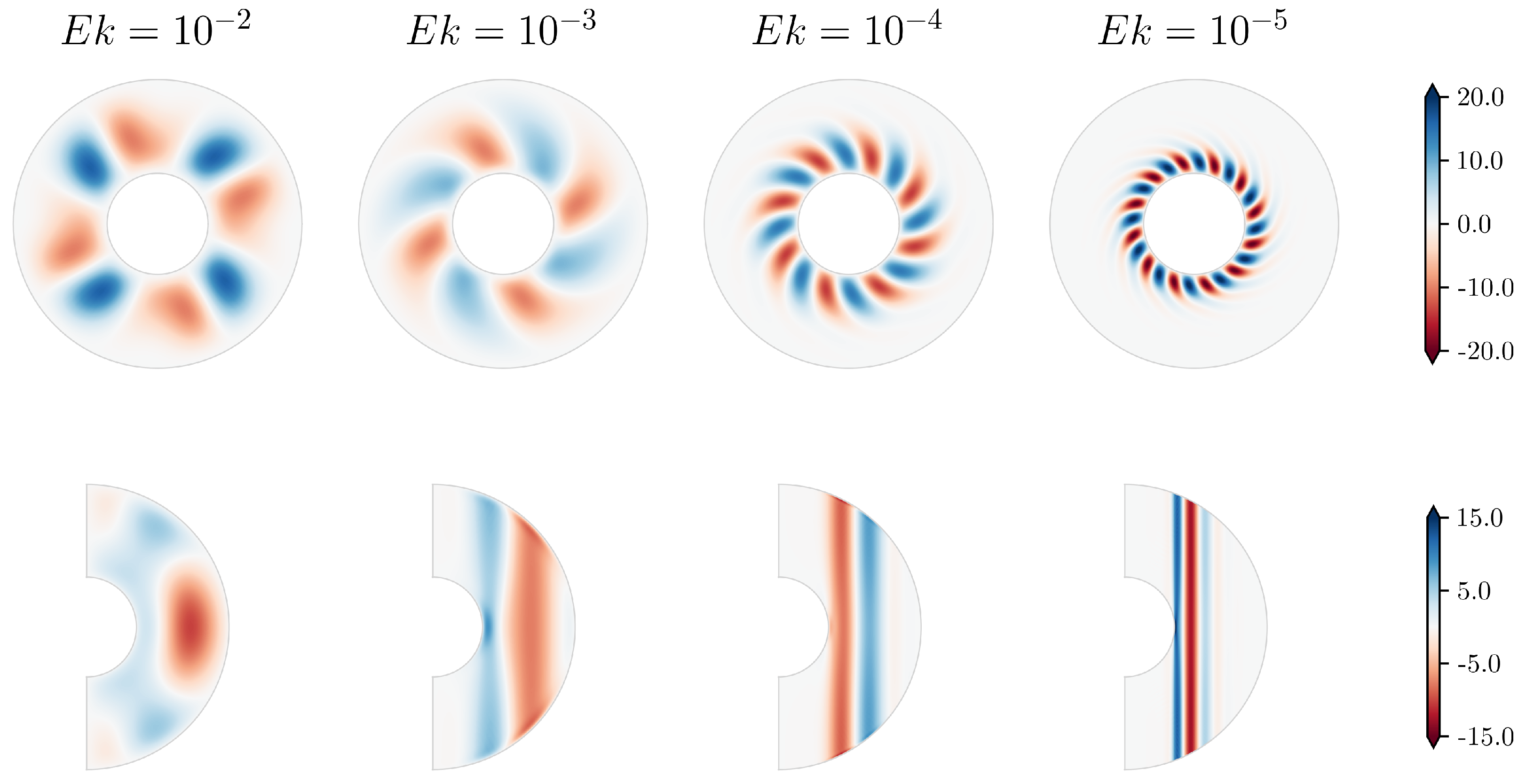
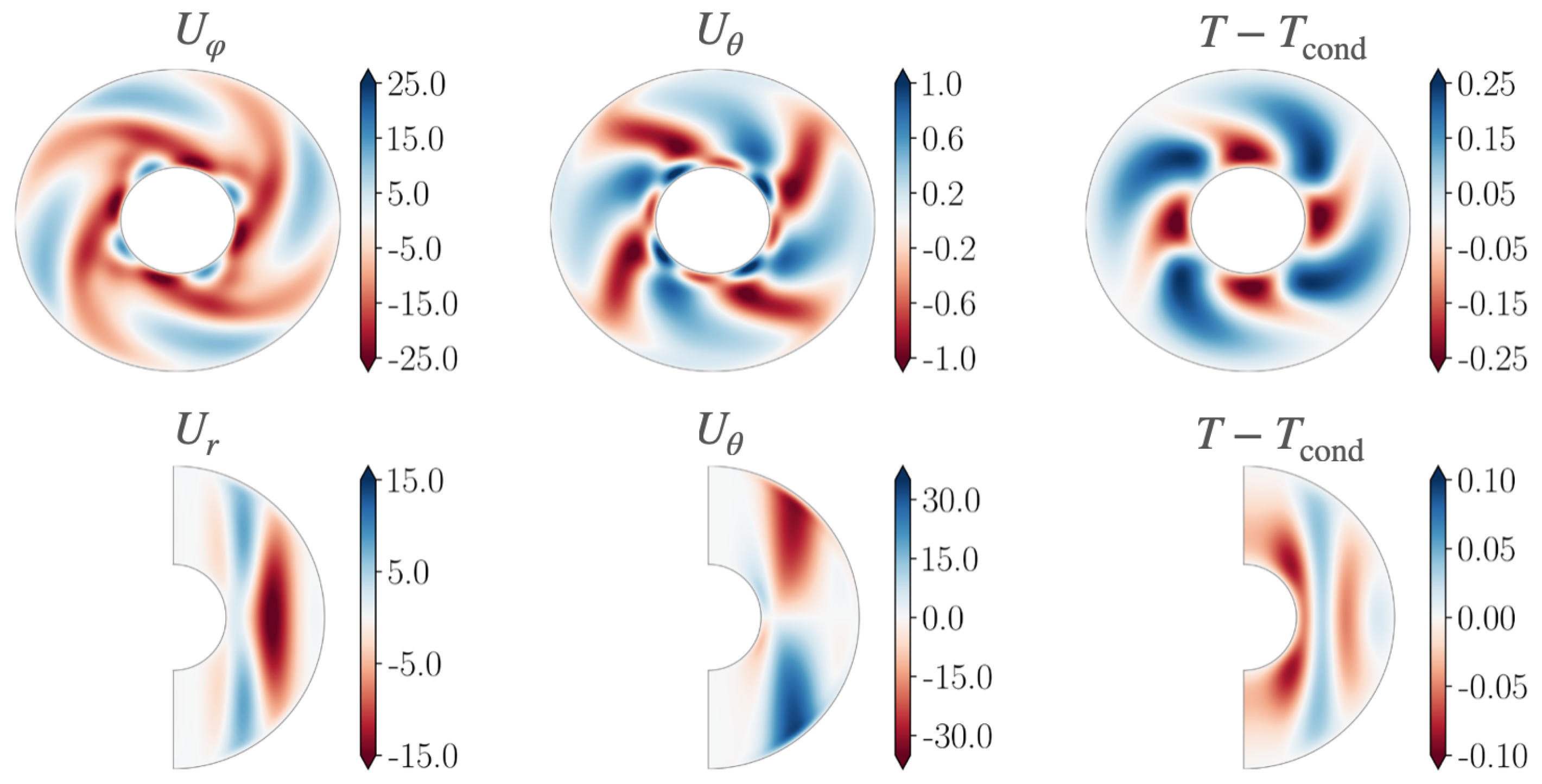
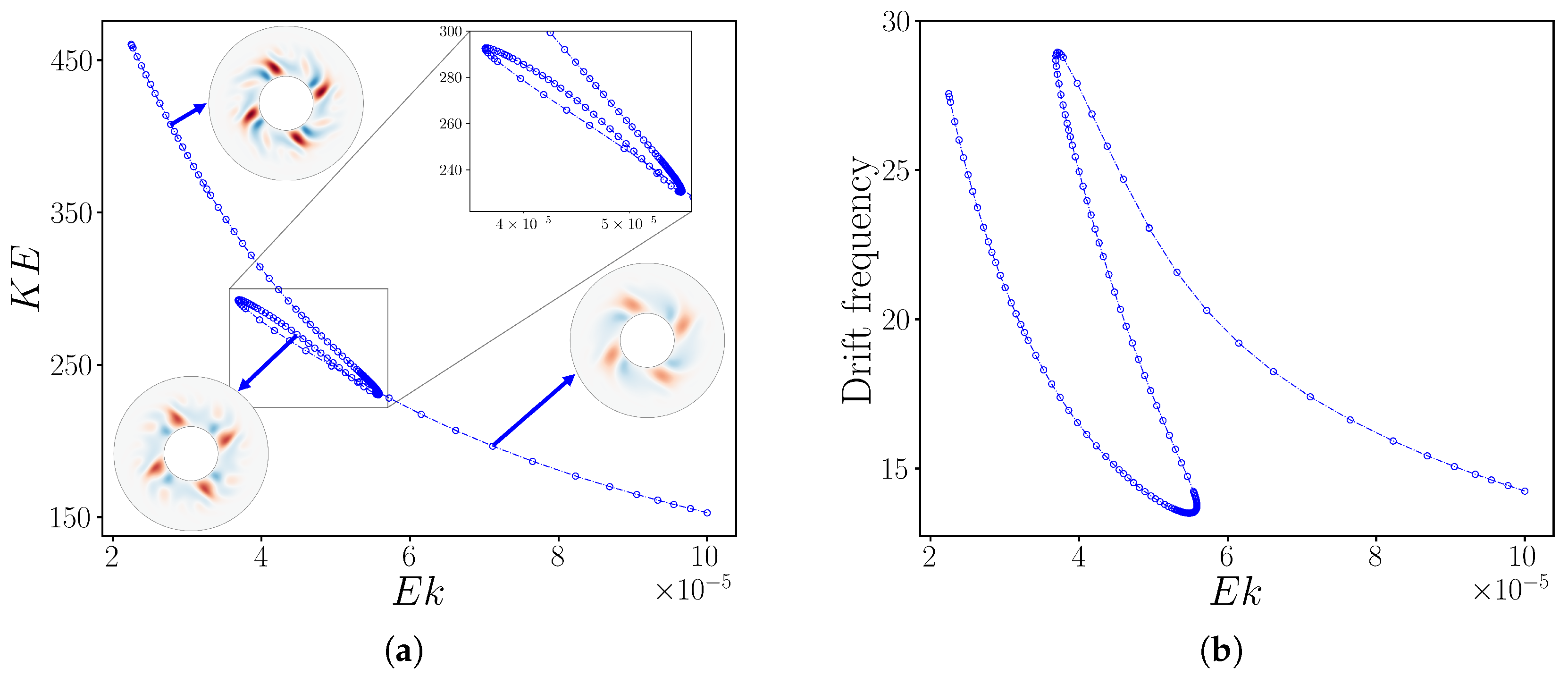
4.2. Continuation in Ekman Number and in Resolution
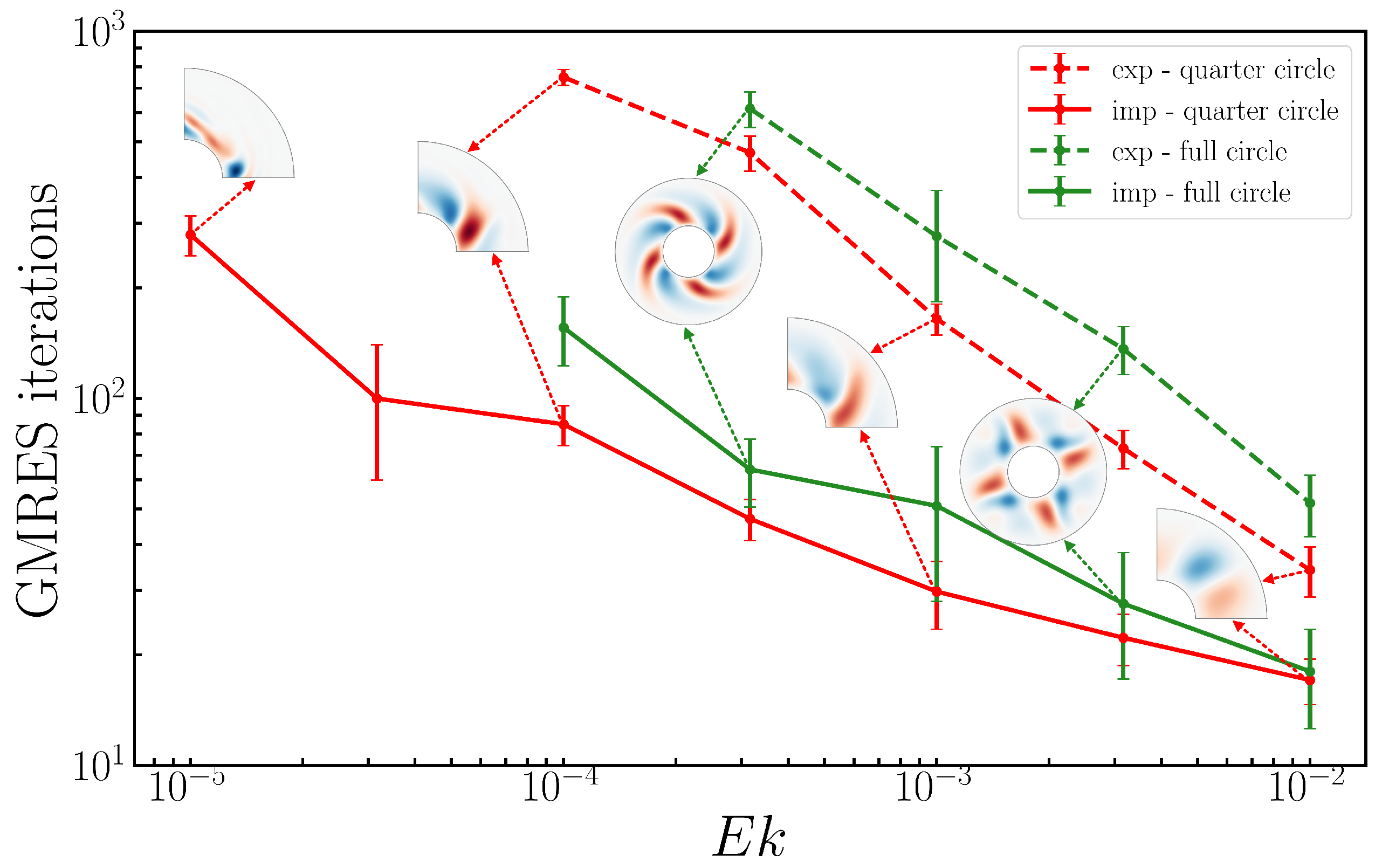
5. Timing Comparisons
6. Discussion
6.1. Differences with Other Methods
6.2. Relevance for Geophysics
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
- Roberts, P.H. On the thermal instability of a rotating-fluid sphere containing heat sources. Phil. Trans. R. Soc. Lond. A 1968, 263, 93–117. [Google Scholar]
- Busse, F. Thermal instabilities in rapidly rotating systems. J. Fluid Mech. 1970, 44, 441–460. [Google Scholar] [CrossRef]
- Zhang, K.K.; Busse, F.H. On the onset of convection in rotating spherical shells. Geophys. Astrophys. Fluid Dyn. 1987, 39, 119–147. [Google Scholar] [CrossRef]
- Jones, C.A.; Soward, A.M.; Mussa, A.I. The onset of thermal convection in a rapidly rotating sphere. J. Fluid Mech. 2000, 405, 157–179. [Google Scholar] [CrossRef]
- Dormy, E.; Soward, A.; Jones, C.; Jault, D.; Cardin, P. The onset of thermal convection in rotating spherical shells. J. Fluid Mech. 2004, 501, 43–70. [Google Scholar] [CrossRef]
- Net, M.; Garcia, F.; Sánchez, J. On the onset of low-Prandtl-number convection in rotating spherical shells: Non-slip boundary conditions. J. Fluid Mech. 2008, 601, 317–337. [Google Scholar] [CrossRef]
- Skene, C.S.; Tobias, S.M. Weakly nonlinear analysis of the onset of convection in rotating spherical shells. Geophys. Astrophys. Fluid Dyn. 2024, 1–22. [Google Scholar] [CrossRef]
- Ruelle, D. Bifurcations in the presence of a symmetry group. Arch. Rat. Mech. Anal. 1973, 51, 136–152. [Google Scholar] [CrossRef]
- Ecke, R.; Zhong, F.; Knobloch, E. Hopf bifurcation with broken reflection symmetry in rotating Rayleigh-Bénard convection. Europhys. Lett. 1992, 19, 177. [Google Scholar] [CrossRef]
- Chossat, P.; Lauterbach, R. Methods in Equivariant Bifurcations and Dynamical Systems; World Scientific: Singapore, 2000. [Google Scholar]
- Busse, F. Convective flows in rapidly rotating spheres and their dynamo action. Phys. Fluids 2002, 14, 1301–1314. [Google Scholar] [CrossRef]
- Hindman, B.W.; Jain, R. Radial trapping of thermal Rossby waves within the convection zones of low-mass stars. Astrophys. J. 2022, 932, 68. [Google Scholar] [CrossRef]
- Dormy, E. Rapidly Rotating Magnetohydrodynamics and the Geodynamo. Annu. Rev. Fluid Mech. 2025, 57. [Google Scholar] [CrossRef]
- Pothérat, A.; Horn, S. Seven decades of exploring planetary interiors with rotating convection experiments. Comptes Rendus Phys. 2025, 25, 233. [Google Scholar]
- Zhang, K. Convection in a rapidly rotating spherical shell at infinite Prandtl number: Transition to vacillating flows. Phys. Earth Planet. Inter. 1992, 72, 236–248. [Google Scholar] [CrossRef]
- Simitev, R.; Busse, F. Patterns of convection in rotating spherical shells. New J. Phys. 2003, 5, 97. [Google Scholar] [CrossRef]
- Feudel, F.; Seehafer, N.; Tuckerman, L.S.; Gellert, M. Multistability in rotating spherical shell convection. Phys. Rev. E 2013, 87, 023021. [Google Scholar] [CrossRef][Green Version]
- Feudel, F.; Tuckerman, L.S.; Gellert, M.; Seehafer, N. Bifurcations of rotating waves in rotating spherical shell convection. Phys. Rev. E 2015, 92, 053015. [Google Scholar] [CrossRef]
- Garcia, F.; Net, M.; Sánchez, J. Continuation and stability of convective modulated rotating waves in spherical shells. Phys. Rev. E 2016, 93, 013119. [Google Scholar] [CrossRef]
- Cardin, P.; Olson, P. Chaotic thermal convection in a rapidly rotating spherical shell: Consequences for flow in the outer core. Phys. Earth Planet. Inter. 1994, 82, 235–259. [Google Scholar] [CrossRef]
- Aubert, J.; Brito, D.; Nataf, H.C.; Cardin, P.; Masson, J.P. A systematic experimental study of rapidly rotating spherical convection in water and liquid gallium. Phys. Earth Planet. Inter. 2001, 128, 51–74. [Google Scholar] [CrossRef]
- Jones, C.A. Thermal and compositional convection in the outer core. Core Dyn. 2007, 8, 131–185. [Google Scholar]
- Aurnou, J.M.; Horn, S.; Julien, K. Connections between nonrotating, slowly rotating, and rapidly rotating turbulent convection transport scalings. Phys. Rev. Res. 2020, 2, 043115. [Google Scholar] [CrossRef]
- Olson, P. Laboratory experiments on the dynamics of the core. Phys. Earth Planet. Inter. 2011, 187, 139–156. [Google Scholar] [CrossRef]
- Glatzmaier, G.A. Numerical simulations of stellar convective dynamos. I. the model and method. J. Comput. Phys. 1984, 55, 461–484. [Google Scholar] [CrossRef]
- Christensen, U.; Aubert, J.; Cardin, P.; Dormy, E.; Gibbons, S.; Glatzmaier, G.; Grote, E.; Honkura, Y.; Jones, C.; Kono, M.; et al. A numerical dynamo benchmark. Phys. Earth Planet. Inter. 2001, 128, 25–34. [Google Scholar] [CrossRef]
- Jones, C.; Boronski, P.; Brun, A.; Glatzmaier, G.; Gastine, T.; Miesch, M.; Wicht, J. Anelastic convection-driven dynamo benchmarks. Icarus 2011, 216, 120–135. [Google Scholar] [CrossRef]
- Futterer, B.; Krebs, A.; Plesa, A.C.; Zaussinger, F.; Hollerbach, R.; Breuer, D.; Egbers, C. Sheet-like and plume-like thermal flow in a spherical convection experiment performed under microgravity. J. Fluid Mech. 2013, 735, 647–683. [Google Scholar] [CrossRef]
- Zaussinger, F.; Haun, P.; Szabo, P.S.B.; Travnikov, V.; Al Kawwas, M.; Egbers, C. Rotating spherical gap convection in the GeoFlow International Space Station (ISS) experiment. Phys. Rev. Fluids 2020, 5, 063502. [Google Scholar] [CrossRef]
- Travnikov, V.; Egbers, C. Numerical investigation of atmospherelike flows in a spherical geometry. Phys. Rev. E 2021, 104, 065110. [Google Scholar] [CrossRef]
- Tuckerman, L.S. Transformations of matrices into banded form. J. Comput. Phys. 1989, 84, 360–376. [Google Scholar] [CrossRef]
- Marti, P.; Calkins, M.; Julien, K. A computationally efficient spectral method for modeling core dynamics. Geochem. Geophys. Geosystems 2016, 17, 3031–3053. [Google Scholar] [CrossRef]
- Kuang, W.; Bloxham, J. Numerical modeling of magnetohydrodynamic convection in a rapidly rotating spherical shell: Weak and strong field dynamo action. J. Comput. Phys. 1999, 153, 51–81. [Google Scholar] [CrossRef]
- Hollerbach, R. A spectral solution of the magneto-convection equations in spherical geometry. Int. J. Numer. Methods Fluids 2000, 32, 773–797. [Google Scholar] [CrossRef]
- Sprague, M.; Julien, K.; Knobloch, E.; Werne, J. Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 2006, 551, 141–174. [Google Scholar] [CrossRef]
- Stellmach, S.; Hansen, U. An efficient spectral method for the simulation of dynamos in Cartesian geometry and its implementation on massively parallel computers. Geochem. Geophys. Geosyst. 2008, 9. [Google Scholar] [CrossRef]
- Julien, K.; van Kan, A.; Miquel, B.; Knobloch, E.; Vasil, G. Rescaled Equations of Fluid Motion for Well-Conditioned Direct Numerical Simulations of Rapidly Rotating Convection. arXiv 2024, arXiv:2410.02702. [Google Scholar]
- van Kan, A.; Julien, K.; Miquel, B.; Knobloch, E. Bridging the Rossby number gap in rapidly rotating thermal convection. J. Fluid Mech. 2025, 1010, A42. [Google Scholar] [CrossRef]
- García González, F.; Net Marcé, M.; Garcia-Archilla, B.; Sánchez Umbría, J. A comparison of high-order time integrators for thermal convection in rotating spherical shells. J. Comput. Phys. 2010, 229, 7997–8010. [Google Scholar] [CrossRef]
- Garcia, F.; Sánchez, J.; Dormy, E.; Net, M. Oscillatory Convection in Rotating Spherical Shells: Low Prandtl Number and Non-Slip Boundary Conditions. SIAM J. Appl. Dyn. Syst. 2015, 14, 1787–1807. [Google Scholar] [CrossRef]
- Feudel, F.; Bergemann, K.; Tuckerman, L.S.; Egbers, C.; Futterer, B.; Gellert, M.; Hollerbach, R. Convection patterns in a spherical fluid shell. Phys. Rev. E 2011, 83, 046304. [Google Scholar] [CrossRef][Green Version]
- Feudel, F.; Tuckerman, L.S.; Zaks, M.; Hollerbach, R. Hysteresis of dynamos in rotating spherical shell convection. Phys. Rev. F 2017, 2, 053902. [Google Scholar] [CrossRef]
- Schaeffer, N. Efficient spherical harmonic transforms aimed at pseudospectral numerical simulations. Geochem. Geophys. Geosyst. 2013, 14, 751–758. [Google Scholar] [CrossRef]
- Sánchez, J.; Net, M.; Garcıa-Archilla, B.; Simó, C. Newton–Krylov continuation of periodic orbits for Navier–Stokes flows. J. Comput. Phys. 2004, 201, 13–33. [Google Scholar] [CrossRef]
- Garcia, F.; Sánchez, J.; Net, M. Antisymmetric Polar Modes of Thermal Convection in Rotating Spherical Fluid Shells at High Taylor Numbers. Phys. Rev. Lett. 2008, 101, 194501. [Google Scholar] [CrossRef]
- Sánchez, J.; Garcia, F.; Net, M. Computation of azimuthal waves and their stability in thermal convection in rotating spherical shells with application to the study of a double-Hopf bifurcation. Phys. Rev. E 2013, 87, 033014. [Google Scholar] [CrossRef]
- Tuckerman, L.S.; Langham, J.; Willis, A. Order-of-magnitude speedup for steady states and traveling waves via Stokes preconditioning in Channelflow and Openpipeflow. In Computational Modelling of Bifurcations and Instabilities in Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–31. [Google Scholar]
- Gastine, T.; Wicht, J.; Barik, A.; Duarte, L. Formulation of the (magneto)-hydrodynamics Problem. Available online: https://magic-sph.github.io/ (accessed on 30 May 2025).
- Marques, F.; Mercader, I.; Batiste, O.; Lopez, J.M. Centrifugal effects in rotating convection: Axisymmetric states and three-dimensional instabilities. J. Fluid Mech. 2007, 580, 303–318. [Google Scholar] [CrossRef][Green Version]
- Satake, H.; Tagawa, T. Influence of Centrifugal Buoyancy in Thermal Convection within a Rotating Spherical Shell. Symmetry 2022, 14, 2021. [Google Scholar] [CrossRef]
- Ishioka, K. A New Recurrence Formula for Efficient Computation of Spherical Harmonic Transform. J. Meteorol. Soc. Jpn. 2018, 96, 241–249. [Google Scholar] [CrossRef]
- Schaeffer, N.; Jault, D.; Nataf, H.C.; Fournier, A. Turbulent geodynamo simulations: A leap towards Earth’s core. Geophys. J. Int. 2017, 211, 1–29. [Google Scholar] [CrossRef]
- Lago, R.; Gastine, T.; Dannert, T.; Rampp, M.; Wicht, J. MagIC v5. 10: A two-dimensional message-passing interface (MPI) distribution for pseudo-spectral magnetohydrodynamics simulations in spherical geometry. Geosci. Model Dev. 2021, 14, 7477–7495. [Google Scholar] [CrossRef]
- Garcia, F.; Sánchez, J.; Net, M. Numerical simulations of thermal convection in rotating spherical shells under laboratory conditions. Phys. Earth Planet. Inter. 2014, 230, 28–44. [Google Scholar] [CrossRef]
- Gottlieb, D.; Orszag, S.A. Numerical Analysis of Spectral Methods: Theory and Applications; SIAM: Philadelphia, PA, USA, 1977. [Google Scholar]
- Saad, Y.; Schultz, M.H. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Tuckerman, L.S. Steady-state solving via Stokes preconditioning; Recursion relations for elliptic operators. In Proceedings of the 11th International Conference on Numerical Methods in Fluid Dynamics, Williamsburg, VA, USA, 27 June 1988; Springer: Berlin/Heidelberg, Germany, 1989; pp. 573–577. [Google Scholar]
- Mamun, C.K.; Tuckerman, L.S. Asymmetry and Hopf bifurcation in spherical Couette flow. Phys. Fluids 1995, 7, 80–91. [Google Scholar] [CrossRef]
- Bergeon, A.; Henry, D.; Benhadid, H.; Tuckerman, L.S. Marangoni convection in binary mixtures with Soret effect. J. Fluid Mech. 1998, 375, 143–177. [Google Scholar] [CrossRef]
- Nore, C.; Tuckerman, L.S.; Daube, O.; Xin, S. The 1:2 mode interaction in exactly counter-rotating von Kármán swirling flow. J. Fluid Mech. 2003, 477, 51–88. [Google Scholar] [CrossRef]
- Meca, E.; Mercader, I.; Batiste, O.; Ramírez-Piscina, L. Blue sky catastrophe in double-diffusive convection. Phys. Rev. Lett. 2004, 92, 234501. [Google Scholar] [CrossRef]
- Batiste, O.; Knobloch, E.; Alonso, A.; Mercader, I. Spatially localized binary-fluid convection. J. Fluid Mech. 2006, 560, 149–158. [Google Scholar] [CrossRef]
- Borońska, K.; Tuckerman, L.S. Extreme multiplicity in cylindrical Rayleigh-Bénard convection. II. Bifurcation diagram and symmetry classification. Phys. Rev. E 2010, 81, 036321. [Google Scholar] [CrossRef]
- Mercader, I.; Batiste, O.; Alonso, A.; Knobloch, E. Convectons, anticonvectons and multiconvectons in binary fluid convection. J. Fluid Mech. 2011, 667, 586–606. [Google Scholar] [CrossRef]
- Beaume, C.; Bergeon, A.; Kao, H.C.; Knobloch, E. Convectons in a rotating fluid layer. J. Fluid Mech. 2013, 717, 417–448. [Google Scholar] [CrossRef]
- Torres, J.F.; Henry, D.; Komiya, A.; Maruyama, S. Bifurcation analysis of steady natural convection in a tilted cubical cavity with adiabatic sidewalls. J. Fluid Mech. 2014, 756, 650–688. [Google Scholar] [CrossRef]
- Huepe, C.; Metens, S.; Dewel, G.; Borckmans, P.; Brachet, M.E. Decay rates in attractive Bose-Einstein condensates. Phys. Rev. Lett. 1999, 82, 1616. [Google Scholar] [CrossRef]
- Huepe, C.; Tuckerman, L.S.; Métens, S.; Brachet, M.E. Stability and decay rates of nonisotropic attractive Bose-Einstein condensates. Phys. Rev. A 2003, 68, 023609. [Google Scholar] [CrossRef][Green Version]
- Tuckerman, L.S. Laplacian preconditioning for the inverse Arnoldi method. Commun. Comput. Phys. 2015, 18, 1336–1351. [Google Scholar] [CrossRef]
- Lanczos, C. Trigonometric interpolation of empirical and analytical functions. J. Math. Phys. 1938, 17, 123–199. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Marcus, P.S. Simulation of Taylor-Couette flow. Part 1. Numerical methods and comparison with experiment. J. Fluid Mech. 1984, 146, 45–64. [Google Scholar] [CrossRef]
- Duguet, Y.; Pringle, C.C.; Kerswell, R.R. Relative periodic orbits in transitional pipe flow. Phys. Fluids 2008, 20, 114102. [Google Scholar] [CrossRef]
- Gibson, J.F.; Halcrow, J.; Cvitanović, P. Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 2009, 638, 243–266. [Google Scholar] [CrossRef]
- Zheng, Z.; Tuckerman, L.S.; Schneider, T.M. Natural convection in a vertical channel. Part 1. Wavenumber interaction and Eckhaus instability in a narrow domain. J. Fluid Mech. 2024, 1000, A28. [Google Scholar] [CrossRef]
- Zheng, Z.; Tuckerman, L.S.; Schneider, T.M. Natural convection in a vertical channel. Part 2. Oblique solutions and global bifurcations in a spanwise-extended domain. J. Fluid Mech. 2024, 1000, A29. [Google Scholar] [CrossRef]
- Zheng, Z.; Tuckerman, L.S.; Schneider, T.M. Natural convection in a vertical channel. Part 3. Bifurcations of many (additional) unstable equilibria and periodic orbits. arXiv 2025, arXiv:2504.05524. [Google Scholar]
- Schmiegel, A. Transition to Turbulence in Linearly Stable Shear Flows. Ph.D. Thesis, Philipps-Universität Marburg, Marburg, Germany, 1999. Available online: http://archiv.ub.uni-marburg.de/diss/z2000/0062/ (accessed on 30 May 2025).
- Pringle, C.C.; Duguet, Y.; Kerswell, R.R. Highly symmetric travelling waves in pipe flow. Phil. Trans. R. Soc. Lond. A 2009, 367, 457–472. [Google Scholar] [CrossRef]
- Borońska, K.; Tuckerman, L.S. Extreme multiplicity in cylindrical Rayleigh-Bénard convection. I. Time dependence and oscillations. Phys. Rev. E 2010, 81, 036320. [Google Scholar] [CrossRef] [PubMed]
- Cvitanovic, P.; Eckhardt, B. Periodic orbit expansions for classical smooth flows. J. Phys. A-Math. 1991, 24, L237. [Google Scholar] [CrossRef]
- Kawahara, G.; Uhlmann, M.; Van Veen, L. The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 2012, 44, 203–225. [Google Scholar] [CrossRef]
- Lathrop, D.P.; Fineberg, J.; Swinney, H.L. Transition to shear-driven turbulence in Couette-Taylor flow. Phys. Rev. A 1992, 46, 6390. [Google Scholar] [CrossRef] [PubMed]
- Dong, S. Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 2007, 587, 373–393. [Google Scholar] [CrossRef]
- Huisman, S.G.; Van Der Veen, R.C.; Sun, C.; Lohse, D. Multiple states in highly turbulent Taylor–Couette flow. Nat. Commun. 2014, 5, 3820. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D.; Sun, C. High-Reynolds number Taylor-Couette turbulence. Annu. Rev. Fluid Mech. 2016, 48, 53–80. [Google Scholar] [CrossRef]
- Eckhardt, B.; Doering, C.R.; Whitehead, J.P. Exact relations between Rayleigh-Bénard and rotating plane Couette flow in two dimensions. J. Fluid Mech. 2020, 903, R4. [Google Scholar] [CrossRef]

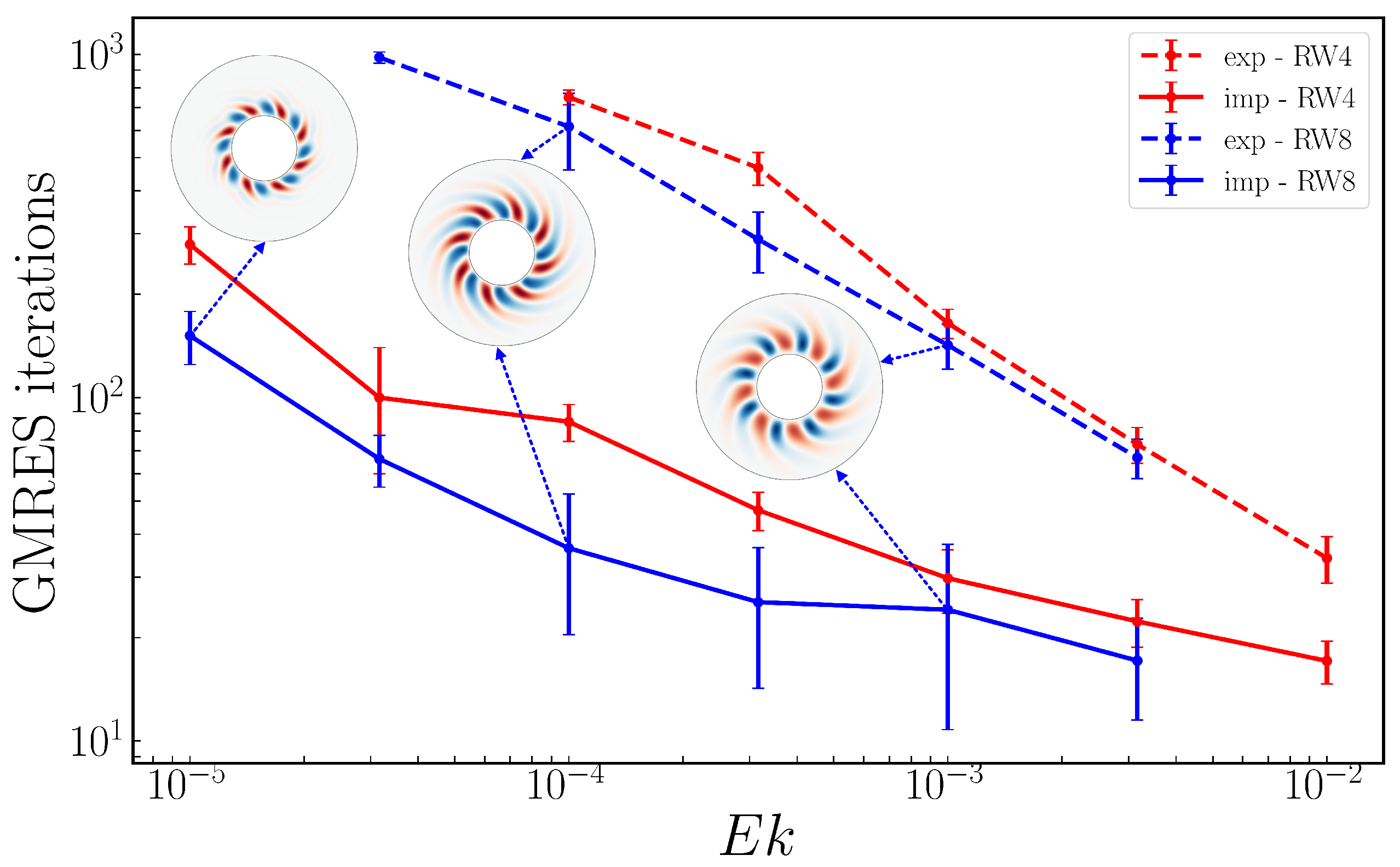
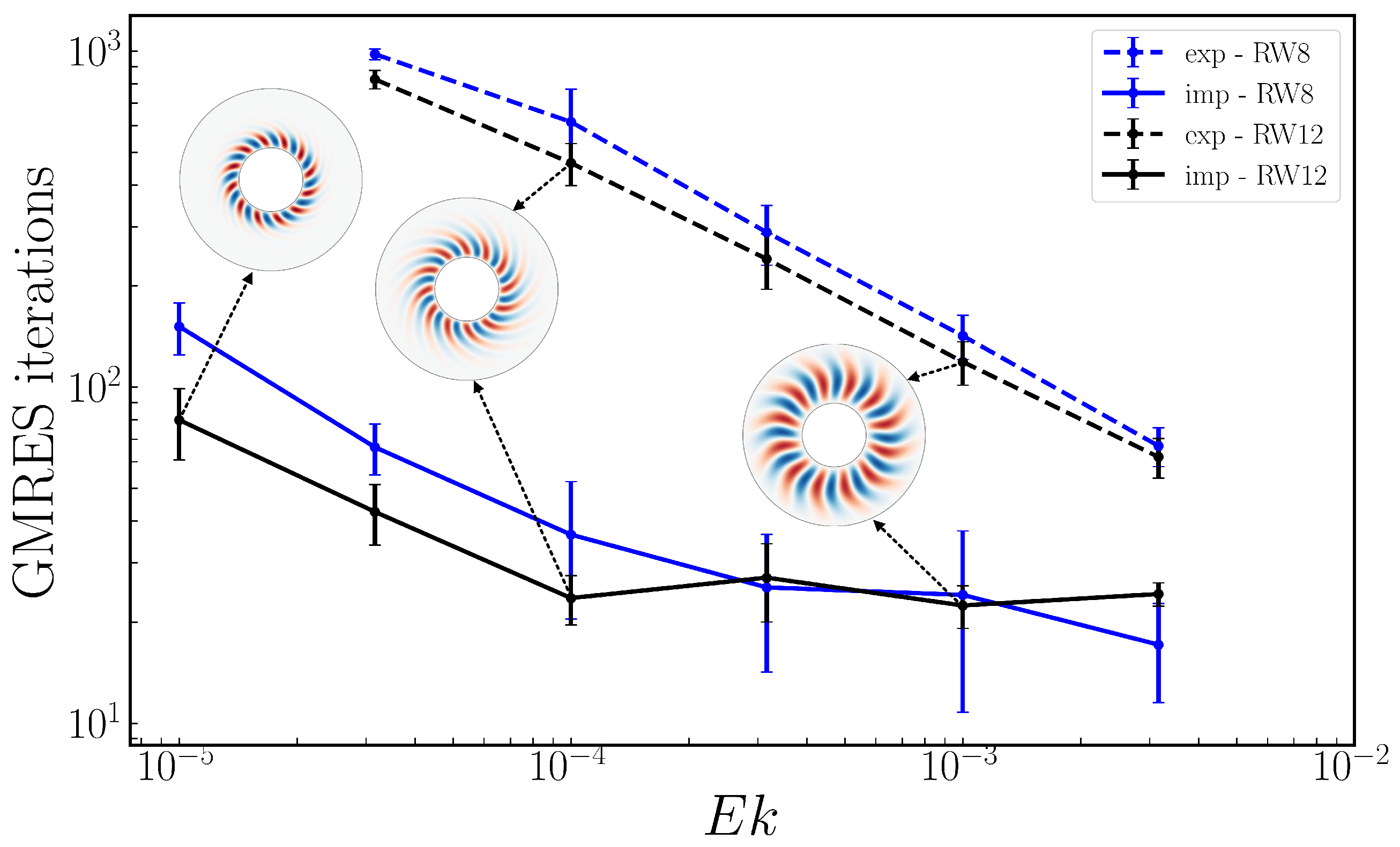
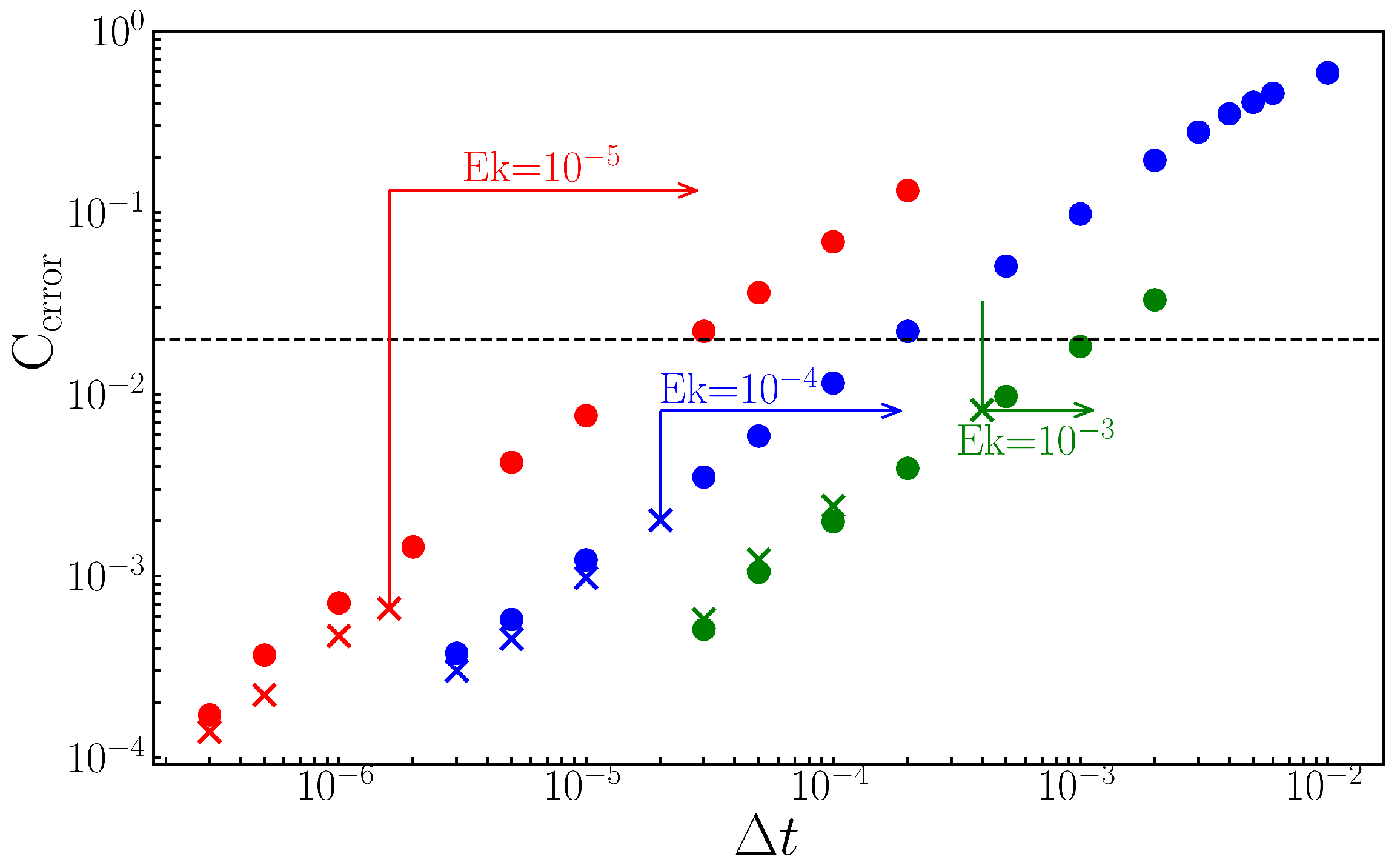
| Ek | Ra | M | (Nr, Nθ, Nφ × M) | Cexact | Explicit Diverges | 2% Error | Ratio |
|---|---|---|---|---|---|---|---|
| 120 | 4 | 3 | |||||
| 130 | 8 | 9 | |||||
| 140 | 12 | 17 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez Sembla, J.C.; Rambert, C.; Feudel, F.; Tuckerman, L.S. Convection in a Rapidly Rotating Spherical Shell: Newton’s Method Using Implicit Coriolis Integration. Mathematics 2025, 13, 2113. https://doi.org/10.3390/math13132113
Gonzalez Sembla JC, Rambert C, Feudel F, Tuckerman LS. Convection in a Rapidly Rotating Spherical Shell: Newton’s Method Using Implicit Coriolis Integration. Mathematics. 2025; 13(13):2113. https://doi.org/10.3390/math13132113
Chicago/Turabian StyleGonzalez Sembla, Juan Cruz, Camille Rambert, Fred Feudel, and Laurette S. Tuckerman. 2025. "Convection in a Rapidly Rotating Spherical Shell: Newton’s Method Using Implicit Coriolis Integration" Mathematics 13, no. 13: 2113. https://doi.org/10.3390/math13132113
APA StyleGonzalez Sembla, J. C., Rambert, C., Feudel, F., & Tuckerman, L. S. (2025). Convection in a Rapidly Rotating Spherical Shell: Newton’s Method Using Implicit Coriolis Integration. Mathematics, 13(13), 2113. https://doi.org/10.3390/math13132113






