A Novel Stochastic SVIR Model Capturing Transmission Variability Through Mean-Reverting Processes and Stationary Reproduction Thresholds

Abstract

This study presents a stochastic SVIR epidemic model in which disease transmission rates fluctuate randomly over time, driven by independent, mean-reverting processes with multiplicative noise. These dynamics capture environmental variability and behavioral changes affecting disease spread. We derive analytical expressions for the conditional moments of the transmission rates and establish the existence of their stationary distributions under broad conditions. By averaging over these distributions, we define a stationary effective reproduction number that enables a probabilistic classification of outbreak scenarios. Specifically, we estimate the likelihood of disease persistence or extinction based on transmission uncertainty. Sensitivity analyses reveal that the shape and intensity of transmission variability play a decisive role in epidemic outcomes. Monte Carlo simulations validate our theoretical findings, showing strong agreement between empirical distributions and theoretical predictions. Our results underscore how randomness in disease transmission can fundamentally alter epidemic trajectories, offering a robust mathematical framework for risk assessment under uncertainty.

1. Introduction

Understanding the long-term dynamics of infectious diseases in populations subject to environmental uncertainty is a central problem in mathematical epidemiology [1]. Traditional deterministic models, while foundational, are insufficient for capturing the complex reality that transmission mechanisms often vary due to a multitude of unpredictable factors, including seasonal cycles, behavioral responses, environmental changes, and public health interventions [2]. To incorporate this variability, stochastic epidemic models have been developed, wherein randomness is typically introduced by perturbing key parameters (most notably the transmission rate) through additive white noise or time-dependent deterministic functions [3]. While such models represent a step toward realism, they often fall short because they fail to capture important features such as heavy-tailed fluctuations, long memory effects, and sudden extreme events that are frequently observed in real epidemic data [4,5].

In classical stochastic models, transmission rates are often perturbed by additive Gaussian white noise, resulting in dynamics of the form $\beta ⇝\beta +\sigma \mathbb{B}\left(t\right)$, where $\mathbb{B}\left(t\right)$ is standard Brownian motion [6]. This formulation implies that the transmission rate can grow without bound or become negative, an evident violation of biological feasibility [7]. Even if restricted artificially to the positive domain, such models ignore the empirical observation that transmission rates fluctuate around natural baseline levels, shaped by long-term behavioral and ecological equilibria [8]. For instance, contact rates may increase during flu season but gradually decline due to awareness campaigns or adaptive behaviors such as social distancing [9].

Additive noise models typically assume independent increments in perturbations, meaning that they lack temporal memory [10]. In real epidemics, however, changes in transmission are often temporally correlated [11]. For example, a surge in infection may prompt sustained behavioral changes, such as mask-wearing or lockdowns, leading to long-term reductions in contact rates [12]. Likewise, seasonal environmental factors like temperature and humidity exert persistent effects on transmission dynamics [13]. Thus, models that treat perturbations as memoryless may misrepresent the autocorrelated structure of real-world transmission [14].

The most significant mathematical limitation of traditional stochastic models with additive noise is the lack of stationary behavior in the perturbed parameters [15]. When the transmission rate evolves as a Brownian motion or a non-reverting diffusion, its distribution spreads over time, and no stationary distribution exists [16]. This renders long-term analysis intractable, precluding the use of ergodic theorems and invariant measure theory to study endemic equilibria or extinction thresholds [17].

To overcome these limitations, we replace the classical modeling of stochastic transmission with mean-reverting stochastic differential equations of the Ornstein–Uhlenbeck type [18]. Specifically, we assume that the transmission rate $\beta \left(t\right)$ evolves according to

$$\mathrm{d}\beta \left(t\right)=a\left(b-\beta \left(t\right)\right)\mathrm{d}t+c\beta \left(t\right)\mathrm{d}\mathbb{B}\left(t\right),$$

(1)

where $a>0$ denotes the speed of reversion, $b>0$ is the baseline transmission level, and $c>0$ scales the stochastic perturbation. This equation captures the essential epidemiological characteristic that, while transmission fluctuates in response to exogenous shocks, it tends to return to a characteristic level in the absence of sustained forcing [19].

From a mathematical standpoint, modeling the transmission rate $\beta \left(t\right)$ using mean-reverting stochastic differential equations with multiplicative noise offers several significant advantages [20]. First, under appropriate parameter conditions, the process $\beta \left(t\right)$ remains strictly positive almost surely, which ensures biological consistency by preventing negative transmission rates [21]. Second, such processes admit explicit stationary distributions that allow for a rigorous analysis of long-term behavior [22]. Third, the ergodic nature of this process guarantees convergence in distribution to the stationary law, enabling the application of ergodic theorems [23,24,25,26].

To elucidate the advantages of incorporating mean-reverting stochastic transmission rates, we investigate how environmental and behavioral variability influences the long-term dynamics of a stochastic SVIR (susceptible–vaccinated–infected–recovered) epidemic model [27,28,29]. The model is formulated on a complete filtered probability space $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P})$, where the filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ satisfies the usual conditions of right-continuity and completeness. The state variables $S\left(t\right)$, $V\left(t\right)$, $I\left(t\right)$, and $R\left(t\right)$ denote the respective sizes of the susceptible, vaccinated, infected, and recovered populations at time t, and evolve as ${\mathbb{R}}_{+}^4$-valued càdlàg, ${\mathcal{F}}_t$-adapted processes. The stochastic evolution of the epidemic is then described by the following system of coupled stochastic differential equations:

$$\begin{array}{cc}\hfill \mathrm{d}S\left(t\right)& =\left(qA-{\beta }_1\left(t\right)S\left(t\right)I\left(t\right)-uS\left(t\right)\right)\mathrm{d}t,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \mathrm{d}V\left(t\right)& =\left(pA-{\beta }_2\left(t\right)V\left(t\right)I\left(t\right)-uV\left(t\right)\right)\mathrm{d}t,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \mathrm{d}I\left(t\right)& =\left(\left({\beta }_1\left(t\right)S\left(t\right)+{\beta }_2\left(t\right)V\left(t\right)\right)I\left(t\right)-(u+{\gamma }_1+{\gamma }_2)I\left(t\right)\right)\mathrm{d}t,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \mathrm{d}R\left(t\right)& =\left({\gamma }_{2}I\left(t\right)-uR\left(t\right)\right)\mathrm{d}t,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \mathrm{d}{\beta }_1\left(t\right)& =a_1\left(b_1-{\beta }_1\left(t\right)\right)\mathrm{d}t+c_1{\beta }_1\left(t\right)\mathrm{d}{\mathbb{B}}_1\left(t\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \mathrm{d}{\beta }_2\left(t\right)& =a_2\left(b_2-{\beta }_2\left(t\right)\right)\mathrm{d}t+c_2{\beta }_2\left(t\right)\mathrm{d}{\mathbb{B}}_2\left(t\right).\hfill \end{array}$$

(7)

Here, $A>0$ is the constant recruitment rate into the population. A proportion $q\in [0,1]$ of new individuals enter the susceptible class, while the remaining $p=1-q$ are vaccinated at birth. The parameter $u>0$ is the natural mortality rate. The disease-induced death rate and recovery rate are given by ${\gamma }_1>0$ and ${\gamma }_2>0$, respectively. Infection transmission is modeled through mass-action incidence, with time-varying stochastic transmission rates ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$ for the susceptible and vaccinated classes, respectively.

The dynamics of ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$ are governed by stochastic differential equations of the form (6) and (7), incorporating a mean-reverting drift and multiplicative Brownian noise. The deterministic drift terms $a_i(b_i-{\beta }_i)$ ($i=1,2$) model the mean-reversion mechanism, where the transmission rates ${\beta }_i\left(t\right)$ tend to revert to baseline levels $b_i$ over time in the absence of noise. Here, $a_i$ is a constant that governs the speed of mean reversion. The diffusion terms $c_i{\beta }_i\mathrm{d}{\mathbb{B}}_i\left(t\right)$ capture continuous stochastic fluctuations arising from environmental or behavioral variability, with ${\mathbb{B}}_1\left(t\right)$ and ${\mathbb{B}}_2\left(t\right)$ representing independent standard Brownian motions. Figure 1 illustrates the mean-reverting behavior driven by the deterministic pull term $a_i(b_i-{\beta }_i)$ and the stochastic multiplicative noise $c_i{\beta }_i\left(t\right)\mathrm{d}{\mathbb{B}}_i\left(t\right)$.

Building upon earlier studies of SVIR epidemic models, the authors in [30] investigated a stochastic SVIR framework incorporating saturated incidence rates and logistic population growth. They established sufficient conditions for disease extinction and ergodicity. Subsequently, ref. [31] introduced an extended version of the SVIR model and examined the conditions under which the disease persists or dies out. In [32], the model was further generalized to account for transport-induced infections, media influence, and Lévy noise. The authors derived rigorous criteria for both extinction and persistence in this context. Additionally, ref. [33] explored the role of heterogeneous vaccination strategies in disease transmission by formulating a discrete-time Markov chain SVIR model. They derived the epidemic threshold and investigated various probabilistic characteristics of the system.

Compared to the aforementioned recent studies, the key innovation of our work lies in the rigorous formulation and analysis of a bivariate SVIR model incorporating ergodic stochastic transmission rates governed by inverse gamma distributions. By modeling the time-varying transmission rates ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$ as solutions to geometric mean-reverting stochastic differential equations with multiplicative noise, we show that (under some meaningful conditions) each rate admits a unique stationary distribution. We identify this invariant distribution as the inverse gamma law with explicitly computable shape and scale parameters. This provides a fully tractable stochastic structure of the transmission process, enabling the exact characterization of the stationary effective reproduction number ${\mathcal{R}}_{\infty }$. Unlike classical models that rely on fixed or mean-field estimates of ${\mathcal{R}}_0$, our formulation captures intrinsic stochastic fluctuations and their long-term epidemiological impact. Moreover, we derive an analytically computable expression for $\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)$, offering a novel probabilistic threshold condition for disease persistence based on the convolution of inverse gamma laws.

The paper is organized as follows. Section 2 establishes foundational results by presenting key lemmas and exploring the asymptotic behavior of the stochastic transmission processes ${\beta }_i\left(t\right)$, thereby setting the stage for the subsequent analysis. In Section 3, we develop the main theoretical contributions, including a novel classification framework for the long-term dynamics of the SVIR model driven by mean-reverting stochastic transmission rates. Section 4 offers numerical simulations that illustrate and validate the theoretical findings. Finally, Section 5 concludes the paper with a summary of the key insights, a discussion of limitations, and suggestions for future research directions.

2. Asymptotic Properties of Mean-Reverting Stochastic Transmission Rates ${\mathit{\beta }}_{\mathit{i}}$

First, the processes ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$ admit unique strong solutions that remain strictly positive for all $t\ge 0$ due to the multiplicative noise structure and linear drift (see Theorem 4.4 in [34]). Given the continuity and local Lipschitz properties of the drift coefficients in the equations for $S\left(t\right),V\left(t\right),I\left(t\right),R\left(t\right)$, and the fact that the transmission rates ${\beta }_1\left(t\right),{\beta }_2\left(t\right)$ are well-behaved adapted stochastic processes, the full system admits a unique strong solution up to an explosion time. Moreover, standard arguments using linear boundedness of the drift and the non-negativity of initial conditions imply that the solution remains in ${\mathbb{R}}_{+}^6$ and is non-explosive for all finite time $t\ge 0$. Therefore, the full system is well-posed and models a biologically meaningful evolution of the disease dynamics under stochastic transmission rates.

Now, we present the explicit analytical expressions for the solutions of the processes ${\beta }_1$ and ${\beta }_2$.

Lemma 1. 

Let ${\beta }_i\left(t\right)$ (i = 1, 2) satisfy the stochastic differential Equations (2) and (5). Then, the unique strong solution is given by

$${\beta }_i\left(t\right)=e^{-a_{i}t+{\displaystyle \frac{1}{2}}{c}_i^{2}t+c_i{\mathbb{B}}_i\left(t\right)}\left[{\beta }_i\left(0\right)+a_i{b}_i{\int }_0^t{e}^{a_{i}s-{\displaystyle \frac{1}{2}}{c}_i^{2}s-c_i{\mathbb{B}}_i\left(s\right)}\mathrm{d}s\right].$$

Proof. 

Let us introduce the stochastic integrating factor

$${\mu }_i\left(t\right):=exp\left(a_{i}t-{\displaystyle \frac{1}{2}}{c}_i^{2}t-c_i{\mathbb{B}}_i\left(t\right)\right),$$

and define the product process ${\tilde{\beta }}_i\left(t\right):={\mu }_i\left(t\right){\beta }_i\left(t\right)$. By Itô’s product rule, we have

$$\mathrm{d}\left({\tilde{\beta }}_i\left(t\right)\right)={\mu }_i\left(t\right)\mathrm{d}{\beta }_i\left(t\right)+{\beta }_i\left(t\right)\mathrm{d}{\mu }_i\left(t\right)+\mathrm{d}{\langle {\mu }_i,{\beta }_i\rangle }_t.$$

Using Itô’s formula applied to ${\mu }_i\left(t\right)$, we compute

$$\mathrm{d}{\mu }_i\left(t\right)=a_i{\mu }_i\left(t\right)\mathrm{d}t-c_i{\mu }_i\left(t\right)\mathrm{d}{\mathbb{B}}_i\left(t\right),$$

and, recalling the dynamics of ${\beta }_i\left(t\right)$, the differential becomes

$${\mu }_i\left(t\right)\mathrm{d}{\beta }_i\left(t\right)={\mu }_i\left(t\right)a_i(b_i-{\beta }_i\left(t\right))\mathrm{d}t+{\mu }_i\left(t\right)c_i{\beta }_i\left(t\right)\mathrm{d}{\mathbb{B}}_i\left(t\right),$$

$${\beta }_i\left(t\right)\mathrm{d}{\mu }_i\left(t\right)={\beta }_i\left(t\right)a_i{\mu }_i\left(t\right)\mathrm{d}t-{\beta }_i\left(t\right)c_i{\mu }_i\left(t\right)\mathrm{d}{\mathbb{B}}_i\left(t\right),$$

$$\mathrm{d}{\langle {\mu }_i,{\beta }_i\rangle }_t=(-c_i{\mu }_i\left(t\right))\left(c_i{\beta }_i\left(t\right)\right)\mathrm{d}t=-c_i^2{\mu }_i\left(t\right){\beta }_i\left(t\right)\mathrm{d}t.$$

Summing all three contributions yields

$$\begin{array}{cc}\hfill \mathrm{d}\left({\tilde{\beta }}_i\left(t\right)\right)& ={\mu }_i\left(t\right)a_i(b_i-{\beta }_i\left(t\right))\mathrm{d}t+{\mu }_i\left(t\right)c_i{\beta }_i\left(t\right)\mathrm{d}{\mathbb{B}}_i\left(t\right)\hfill \\ \hfill & +{\beta }_i\left(t\right)a_i{\mu }_i\left(t\right)\mathrm{d}t-{\beta }_i\left(t\right)c_i{\mu }_i\left(t\right)\mathrm{d}{\mathbb{B}}_i\left(t\right)-c_i^2{\mu }_i\left(t\right){\beta }_i\left(t\right)\mathrm{d}t.\hfill \end{array}$$

Observe that the stochastic integrals cancel exactly, and the drift terms simplify

$${\mu }_i\left(t\right)a_i(b_i-{\beta }_i\left(t\right))+{\beta }_i\left(t\right)a_i{\mu }_i\left(t\right)-c_i^2{\mu }_i\left(t\right){\beta }_i\left(t\right)=a_i{b}_i{\mu }_i\left(t\right),$$

so that

$$\mathrm{d}\left({\tilde{\beta }}_i\left(t\right)\right)=a_i{b}_i{\mu }_i\left(t\right)\mathrm{d}t.$$

This is a deterministic differential equation for ${\tilde{\beta }}_i\left(t\right)$, which integrates directly to give

$${\tilde{\beta }}_i\left(t\right)={\beta }_i\left(0\right)+a_i{b}_i{\int }_0^t{\mu }_i\left(s\right)\mathrm{d}s.$$

Substituting back the definition of ${\tilde{\beta }}_i\left(t\right)={\mu }_i\left(t\right){\beta }_i\left(t\right)$, we obtain

$${\beta }_i\left(t\right)={\mu }_i{\left(t\right)}^{-1}\left[{\beta }_i\left(0\right)+a_i{b}_i{\int }_0^t{\mu }_i\left(s\right)\mathrm{d}s\right],$$

which gives the explicit representation of the solution. Writing out ${\mu }_i{\left(t\right)}^{-1}$ explicitly yields

$${\beta }_i\left(t\right)=exp\left(-a_{i}t+{\displaystyle \frac{1}{2}}{c}_i^{2}t+c_i{\mathbb{B}}_i\left(t\right)\right)\left[{\beta }_i\left(0\right)+a_i{b}_i{\int }_0^{t}exp\left(a_{i}s-{\displaystyle \frac{1}{2}}{c}_i^{2}s-c_i{\mathbb{B}}_i\left(s\right)\right)\mathrm{d}s\right],$$

which completes the derivation of the explicit solution for ${\beta }_i\left(t\right)$.   □

In the next two lemmas, we investigate the analytical structure and moment dynamics of the mean-reverting stochastic processes ${\beta }_i\left(t\right)$. We begin by deriving their explicit solutions and conditional expectations, and then proceed to analyze the conditional second moment $\mathbb{E}[{\beta }_i^2\left(t\right)\mid {\beta }_i\left(s\right)]$, which plays a crucial role in characterizing the asymptotic behavior and variance of the processes.

Lemma 2. 

Let ${\{{\beta }_1\left(t\right),{\beta }_2\left(t\right)\}}_{t\ge 0}$ denote the unique solution to Equations (6) and (7). Then, for any $0\le s<t$, the process ${\beta }_i\left(t\right)$ admits the following mild (integral) representation:

$${\beta }_i\left(t\right)=\left({\beta }_i\left(s\right)-b_i\right)e^{-a_i(t-s)}+b_i+{\int }_s^t{c}_i{e}^{-a_i(t-u)}{\beta }_i\left(u\right)\mathrm{d}{\mathbb{B}}_i\left(u\right).$$

Furthermore, we have

$$\mathbb{E}[{\beta }_i\left(t\right)\mid {\beta }_i\left(s\right)]=\left({\beta }_i\left(s\right)-b_i\right)e^{-a_i(t-s)}+b_i.$$

Proof. 

We define the deterministic integrating factor

$$\varphi \left(t\right):=e^{a_i(t-s)},$$

which satisfies ${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\varphi \left(t\right)=a_i\varphi \left(t\right)$. Applying Itô’s product rule to the process $\varphi {\left(t\right)}^{-1}{\beta }_i\left(t\right)=e^{-a_i(t-s)}{\beta }_i\left(t\right)$, we have

$$\begin{array}{cc}\hfill \mathrm{d}\left(e^{-a_i(t-s)}{\beta }_i\left(t\right)\right)& =-a_i{e}^{-a_i(t-s)}{\beta }_i\left(t\right)\mathrm{d}t+e^{-a_i(t-s)}\left(a_i(b_i-{\beta }_i\left(t\right))\mathrm{d}t+c_i{\beta }_i\left(t\right)\mathrm{d}{\mathbb{B}}_i\left(t\right)\right)\hfill \\ \hfill & =-a_i{e}^{-a_i(t-s)}{\beta }_i\left(t\right)\mathrm{d}t+a_i{b}_i{e}^{-a_i(t-s)}\mathrm{d}t-a_i{e}^{-a_i(t-s)}{\beta }_i\left(t\right)\mathrm{d}t+c_i{e}^{-a_i(t-s)}{\beta }_i\left(t\right)\mathrm{d}{\mathbb{B}}_i\left(t\right)\hfill \\ \hfill & =a_i{b}_i{e}^{-a_i(t-s)}\mathrm{d}t+c_i{e}^{-a_i(t-s)}{\beta }_i\left(t\right)\mathrm{d}{\mathbb{B}}_i\left(t\right).\hfill \end{array}$$

Integrating both sides from s to t, we find

$$e^{-a_i(t-s)}{\beta }_i\left(t\right)-{\beta }_i\left(s\right)=a_i{b}_i{\int }_s^t{e}^{-a_i(u-s)}\mathrm{d}u+{\int }_s^t{c}_i{e}^{-a_i(u-s)}{\beta }_i\left(u\right)\mathrm{d}{\mathbb{B}}_i\left(u\right).$$

Multiplying both sides by $e^{a_i(t-s)}$ yields

$${\beta }_i\left(t\right)={\beta }_i\left(s\right)e^{-a_i(t-s)}+a_i{b}_i{\int }_s^t{e}^{-a_i(t-u)}\mathrm{d}u+{\int }_s^t{c}_i{e}^{-a_i(t-u)}{\beta }_i\left(u\right)\mathrm{d}{\mathbb{B}}_i\left(u\right).$$

Evaluating the deterministic integral, we obtain

$$a_i{b}_i{\int }_s^t{e}^{-a_i(t-u)}\mathrm{d}u=b_i(1-e^{-a_i(t-s)}),$$

so the expression simplifies to

$${\beta }_i\left(t\right)=\left({\beta }_i\left(s\right)-b_i\right)e^{-a_i(t-s)}+b_i+{\int }_s^t{c}_i{e}^{-a_i(t-u)}{\beta }_i\left(u\right)\mathrm{d}{\mathbb{B}}_i\left(u\right),$$

as required. To compute the conditional expectation $\mathbb{E}[{\beta }_i\left(t\right)\mid {\beta }_i\left(s\right)]$, we exploit the independence of the Brownian increment ${\mathbb{B}}_i\left(t\right)-{\mathbb{B}}_i\left(s\right)$ from ${\mathcal{F}}_s=\sigma \{{\beta }_i\left(r\right):r\le s\}$. Noting that the stochastic integral is a local martingale with zero mean under conditioning on the past, it follows that

$$\mathbb{E}[{\beta }_i\left(t\right)\mid {\beta }_i\left(s\right)]=\left({\beta }_i\left(s\right)-b_i\right)e^{-a_i(t-s)}+b_i.$$

   □

Remark 1. 

The conditional expectation of ${\beta }_i\left(t\right)$ given its past value ${\beta }_i\left(s\right)$ decays exponentially to the mean level $b_i$ with rate $a_i>0$, consistent with the mean-reverting property of the process.

Lemma 3. 

Let ${\{{\beta }_1\left(t\right),{\beta }_2\left(t\right)\}}_{t\ge 0}$ denote the unique solution to Equations (6) and (7). Assume that $c_i^2\ne 2a_i$ and $c_i^2\ne a_i$; then,

$$\begin{array}{cc}\hfill \mathbb{E}[{\beta }_i^2\left(t\right)\mid {\beta }_i\left(s\right)={\beta }_{i0}]& ={\beta }_{i0}^2{e}^{(c_i^2-2a_i)(t-s)}+{\displaystyle \frac{2a_i{b}_i^2}{2a_i-c_i^2}}\left(1-e^{(c_i^2-2a_i)(t-s)}\right)\hfill \end{array}$$

(8)

$$\begin{array}{cc}& +{\displaystyle \frac{2a_i{b}_i({\beta }_{i0}-b_i)}{a_i-c_i^2}}\left(e^{(c_i^2-a_i)(t-s)}-e^{-a_i(t-s)}\right).\hfill \end{array}$$

(9)

Proof. 

We define the integrating factor as

$${\Phi }_i\left(t\right):=exp\left(-a_i(t-s)+c_i({\mathbb{B}}_i\left(t\right)-{\mathbb{B}}_i\left(s\right))-\frac{1}{2}{c}_i^2(t-s)\right),$$

which allows us to express the solution explicitly in the mild form

$${\beta }_i\left(t\right)={\Phi }_i\left(t\right)\left({\beta }_{i0}+a_i{b}_i{\int }_s^t{\Phi }_i^{-1}\left(u\right)\mathrm{d}u\right).$$

To compute the conditional second moment, we consider the square

$${\beta }_i^2\left(t\right)={\Phi }_i^2\left(t\right){\left({\beta }_{i0}+a_i{b}_i{\int }_s^t{\Phi }_i^{-1}\left(u\right)\mathrm{d}u\right)}^2.$$

We analyze $\mathbb{E}\left[{\Phi }_i^2\left(t\right)\right]$, noting that the Brownian increment ${\mathbb{B}}_i\left(t\right)-{\mathbb{B}}_i\left(s\right)\sim \mathcal{N}(0,t-s)$. Hence, ${\Phi }_i^2\left(t\right)$ is a log-normal random variable and its expectation can be computed using the moment-generating function of the normal distribution:

$$\mathbb{E}\left[{\Phi }_i^2\left(t\right)\right]=exp\left(-2a_i(t-s)+2c_i^2(t-s)-c_i^2(t-s)\right)=exp\left(-(2a_i-c_i^2)(t-s)\right).$$

Substituting this into the expansion of ${\beta }_i^2\left(t\right)$, taking expectations, and using the independence structure of stochastic integrals with respect to Brownian motion yields the following closed-form expression:

$$\begin{array}{cc}\hfill \mathbb{E}[{\beta }_i^2\left(t\right)\mid {\beta }_i\left(s\right)={\beta }_{i0}]& ={\beta }_{i0}^2{e}^{(c_i^2-2a_i)(t-s)}+{\displaystyle \frac{2a_i{b}_i^2}{2a_i-c_i^2}}\left(1-e^{(c_i^2-2a_i)(t-s)}\right)\hfill \\ \hfill & +{\displaystyle \frac{2a_i{b}_i({\beta }_{i0}-b_i)}{a_i-c_i^2}}\left(e^{(c_i^2-a_i)(t-s)}-e^{-a_i(t-s)}\right).\hfill \end{array}$$

   □

Remark 2. 

The exponential term $e^{(c_i^2-2a_i)(t-s)}$ in (8) captures the interplay between the stochastic forcing (through the noise intensity $c_i$) and the deterministic damping (through the rate $a_i$). If $c_i^2<2a_i$, the second moment decays exponentially over time, indicating that the damping dominates the noise, and this contributes to the stability and boundedness of the process. Conversely, if $c_i^2>2a_i$, the second moment grows exponentially, suggesting that noise overwhelms damping, leading to potential instability or unbounded growth.

We now turn to the asymptotic behavior of the process. It is straightforward to show that the first moment converges to the deterministic equilibrium,

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\mathbb{E}\left[{\beta }_i\left(t\right)\right]=b_i,\end{array}$$

(10)

while the second moment tends to

$$\underset{t\to \infty }{lim}\mathbb{E}\left[{\beta }_i^2\left(t\right)\right]={\displaystyle \frac{2a_i{b}_i^2}{2a_i-c_i^2}}.$$

Consequently, the stationary variance is given by

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\mathrm{Var}\left[{\beta }_i\left(t\right)\right]={\displaystyle \frac{b_i^2{c}_i^2}{2a_i-c_i^2}}.\end{array}$$

(11)

Remark 3. 

Equations (10) and (11) characterize the long-term fluctuations in ${\beta }_i\left(t\right)$ around its equilibrium level $b_i$, with the trade-off between the stabilizing drift strength $a_i$ and the volatility parameter $c_i$ governing the magnitude of the variability.

3. Invariant Distribution of ${\mathbf{\beta }}_{\mathbf{i}}$ and Dynamical Classification of the SVIR Model

This section centers on the ergodic properties of the stochastic transmission rate processes ${\beta }_i$ (i = 1,2), which are subsequently employed to approximate the probability that the effective reproduction number in the steady state exceeds the critical threshold of one.

3.1. Invariant Distribution of Stochastic Transmission Rate Processes ${\beta }_i$

Theorem 1. 

Let ${\{{\beta }_1\left(t\right),{\beta }_2\left(t\right)\}}_{t\ge 0}$ denote the unique solution to Equations (6) and (7). Assume that $c_i^2<2a_i$ and $c_i^2\ne a_i$; then, the bivariate process $({\beta }_1\left(t\right),{\beta }_2\left(t\right))$ admits a unique invariant probability measure $\mu ({\beta }_1,{\beta }_2)$ supported on ${(0,\infty )}^2$, given by the following product measure:

$$\mu ({\beta }_1,{\beta }_2)={\mu }_1\left({\beta }_1\right)\otimes {\mu }_2\left({\beta }_2\right),$$

where each marginal ${\mu }_i$ is the inverse gamma distribution with shape parameter ${\alpha }_i=1+{\displaystyle \frac{2a_i}{c_i^2}}$ and scale parameter ${\theta }_i={\displaystyle \frac{2a_i{b}_i}{c_i^2}}$. Explicitly, for $i=1,2$,

$${\mu }_i\left({\beta }_i\right)={\displaystyle \frac{1}{\Gamma \left(1+\frac{2a_i}{c_i^2}\right)}}{\left({\displaystyle \frac{2a_i{b}_i}{c_i^2}}\right)}^{1+{\displaystyle \frac{2a_i}{c_i^2}}}{\beta }_i^{-2-{\displaystyle \frac{2a_i}{c_i^2}}}exp\left(-{\displaystyle \frac{2a_i{b}_i}{c_i^2{\beta }_i}}\right),{\beta }_i>0.$$

Hence, in the stationary regime, each ${\beta }_i\left(t\right)\sim \mathrm{InvGamma}\left(1+{\displaystyle \frac{2a_i}{c_i^2}},{\displaystyle \frac{2a_i{b}_i}{c_i^2}}\right)$.

Proof. 

Since the stochastic differential equations for ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$ are independent, it suffices to analyze each process separately. To determine its invariant measure, we study the stationary Fokker–Planck equation for the probability density $p_i\left({\beta }_i\right)$, which takes the following form:

$$0=-{\displaystyle \frac{\mathrm{d}}{\mathrm{d}{\beta }_i}}\left[a_i(b_i-{\beta }_i)p_i\left({\beta }_i\right)\right]+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\mathrm{d}}^2}{\mathrm{d}{\beta }_i^2}}\left[c_i^2{\beta }_i^2{p}_i\left({\beta }_i\right)\right],{\beta }_i>0.$$

We seek a solution of the form

$$p_i\left({\beta }_i\right)=K_i{\beta }_i^{-m_i}exp\left(-{\displaystyle \frac{n_i}{{\beta }_i}}\right),$$

where $K_i>0$ is a normalization constant and $m_i,n_i>0$ are parameters to be identified. We compute

$$p_i^{\prime }\left({\beta }_i\right)=\left(-{\displaystyle \frac{m_i}{{\beta }_i}}+{\displaystyle \frac{n_i}{{\beta }_i^2}}\right)p_i\left({\beta }_i\right),p_i^{\prime \prime }\left({\beta }_i\right)=\left({\displaystyle \frac{m_i(m_i+1)}{{\beta }_i^2}}-{\displaystyle \frac{2m_i{n}_i}{{\beta }_i^3}}+{\displaystyle \frac{n_i^2}{{\beta }_i^4}}\right)p_i\left({\beta }_i\right).$$

Substituting into the stationary Fokker–Planck equation and matching powers of ${\beta }_i$, we obtain

$$m_i=1+{\displaystyle \frac{2a_i}{c_i^2}},n_i={\displaystyle \frac{2a_i{b}_i}{c_i^2}}.$$

Hence, the stationary density is given by

$$p_i\left({\beta }_i\right)=K_i·{\beta }_i^{-1-\left(1+{\displaystyle \frac{2a_i}{c_i^2}}\right)}exp\left(-{\displaystyle \frac{2a_i{b}_i}{c_i^2{\beta }_i}}\right),$$

which corresponds to the inverse gamma distribution

$$\mathrm{InvGamma}({\alpha }_i,{\theta }_i),\mathrm{with}{\alpha }_i=1+{\displaystyle \frac{2a_i}{c_i^2}},{\theta }_i={\displaystyle \frac{2a_i{b}_i}{c_i^2}}.$$

The normalization constant $K_i$ is

$$K_i={\displaystyle \frac{1}{\Gamma \left({\alpha }_i\right)}}{\theta }_i^{{\alpha }_i}.$$

Since ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$ are independent, the joint invariant density is the product $p_1\left({\beta }_1\right)·p_2\left({\beta }_2\right)$, supported on ${(0,\infty )}^2$. The uniqueness of the invariant measure follows from classical ergodic results for positive recurrent, irreducible diffusions on $(0,\infty )$.    □

3.2. Gamma Approximation of Disease Persistence Probability Under Stochastic Transmission Rates

First, we analyze the disease-free equilibrium (DFE) of the deterministic compartmental model defined by Equations (2)–(5). Under the assumption of constant recruitment rate A and uniform natural removal rate u, the DFE corresponds to a steady-state configuration in which no infection persists in the population. This equilibrium is obtained by solving the system in the absence of infection ($I=R=0$), leading to

$$S^0={\displaystyle \frac{qA}{u}},V^0={\displaystyle \frac{pA}{u}},I^0=0,R^0=0.$$

Assuming that the conditions of Theorem 1 are satisfied, we introduce the notion of the stationary effective reproduction number, denoted as ${\mathcal{R}}_{\infty }$. This quantity represents the expected number of secondary infections produced by a single infected individual introduced into a population at the DFE, averaged over the stationary distributions of the stochastic processes governing transmission. Formally, we define

$${\mathcal{R}}_{\infty }:={\displaystyle \frac{1}{u+{\gamma }_1+{\gamma }_2}}\left(S^0{\int }_0^{\infty }{\beta }_1\mathrm{d}{\mu }_1\left({\beta }_1\right)+V^0{\int }_0^{\infty }{\beta }_2\mathrm{d}{\mu }_2\left({\beta }_2\right)\right),$$

where ${\mu }_1$ and ${\mu }_2$ denote the invariant probability distributions (stationary measures) of the stochastic processes ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$, respectively. Substituting the expressions for $S^0$ and $V^0$, we obtain

$${\mathcal{R}}_{\infty }={\displaystyle \frac{A}{u(u+{\gamma }_1+{\gamma }_2)}}\left(q{\int }_0^{\infty }{\beta }_1\mathrm{d}{\mu }_1\left({\beta }_1\right)+p{\int }_0^{\infty }{\beta }_2\mathrm{d}{\mu }_2\left({\beta }_2\right)\right).$$

According to Theorem 1, the expectations under these distributions are

$$\mathbb{E}\left[{\beta }_1\right]={\displaystyle \frac{{\theta }_1}{{\alpha }_1-1}},\mathbb{E}\left[{\beta }_2\right]={\displaystyle \frac{{\theta }_2}{{\alpha }_2-1}}.$$

Substituting into the previous expression yields

$${\mathcal{R}}_{\infty }={\displaystyle \frac{A}{u(u+{\gamma }_1+{\gamma }_2)}}\left(q·{\displaystyle \frac{{\theta }_1}{{\alpha }_1-1}}+p·{\displaystyle \frac{{\theta }_2}{{\alpha }_2-1}}\right).$$

To streamline notation and facilitate subsequent stochastic analysis, we define

$$K:={\displaystyle \frac{A}{u(u+{\gamma }_1+{\gamma }_2)}},Z:=q{\beta }_{\infty ,1}+p{\beta }_{\infty ,2},$$

where ${\beta }_{\infty ,1}\sim {\mu }_1$ and ${\beta }_{\infty ,2}\sim {\mu }_2$ denote independent random variables distributed according to the respective invariant measures. Then,

$${\mathcal{R}}_{\infty }=KZ.$$

This formulation naturally leads to a probabilistic characterization of the system’s behavior, particularly the likelihood of disease persistence, expressed as

$$\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)=\mathbb{P}(KZ\ge 1).$$

Although the distribution of Z, as a linear combination of inverse gamma variables, lacks a closed-form expression, it is amenable to moment-matching techniques. In particular, we approximate in the following theorem the distribution of Z by a gamma distribution whose parameters are determined by matching the first two moments, thereby enabling tractable approximations of quantities such as $\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)$.

Theorem 2. 

Let ${\{{\beta }_1\left(t\right),{\beta }_2\left(t\right)\}}_{t\ge 0}$ denote the unique solution to Equations (6) and (7). Assume that $c_i^2<2a_i$ and $c_i^2\ne a_i$. Then, the probability of disease persistence, i.e., the probability that ${\mathcal{R}}_{\infty }\ge 1$, is approximated by

$$\begin{array}{c}\hfill \mathbb{P}({\mathcal{R}}_{\infty }\ge 1)\approx {\displaystyle \frac{\Gamma \left(k,\frac{1}{K\theta }\right)}{\Gamma \left(k\right)}},\end{array}$$

(12)

where $\Gamma (k,x)$ is the upper incomplete gamma function, and the shape and scale parameters of the Gamma approximation are given by

$$k={\displaystyle \frac{{\left(\mathbb{E}\left[Z\right]\right)}^2}{\mathrm{Var}\left(Z\right)}},\theta ={\displaystyle \frac{\mathrm{Var}\left(Z\right)}{\mathbb{E}\left[Z\right]}},$$

with

$$\begin{array}{cc}\hfill \mathbb{E}\left[Z\right]& =q·{\displaystyle \frac{{\theta }_1}{{\alpha }_1-1}}+p·{\displaystyle \frac{{\theta }_2}{{\alpha }_2-1}},\hfill \\ \hfill \mathrm{Var}\left(Z\right)& =q^2·{\displaystyle \frac{{\theta }_1^2}{{({\alpha }_1-1)}^2({\alpha }_1-2)}}+p^2·{\displaystyle \frac{{\theta }_2^2}{{({\alpha }_2-1)}^2({\alpha }_2-2)}}.\hfill \end{array}$$

Proof. 

Using the independence of ${\beta }_{\infty ,1}$ and ${\beta }_{\infty ,2}$, the mean and variance of Z are computed as

$$\mathbb{E}\left[Z\right]=q\mathbb{E}\left[{\beta }_{\infty ,1}\right]+p\mathbb{E}\left[{\beta }_{\infty ,2}\right],\mathrm{Var}\left(Z\right)=q^2\mathrm{Var}\left[{\beta }_{\infty ,1}\right]+p^2\mathrm{Var}\left[{\beta }_{\infty ,2}\right].$$

The moments of an inverse gamma distribution $\mathrm{InvGamma}({\alpha }_i,{\theta }_i)$ exist only for ${\alpha }_i>2$, and are given by

$$\mathbb{E}\left[{\beta }_{\infty ,i}\right]={\displaystyle \frac{{\theta }_i}{{\alpha }_i-1}},\mathrm{Var}\left[{\beta }_{\infty ,i}\right]={\displaystyle \frac{{\theta }_i^2}{{({\alpha }_i-1)}^2({\alpha }_i-2)}}.$$

Substituting these into the expressions for $\mathbb{E}\left[Z\right]$ and $\mathrm{Var}\left(Z\right)$, we obtain

$$\mathbb{E}\left[Z\right]={\displaystyle \frac{q{\theta }_1}{{\alpha }_1-1}}+{\displaystyle \frac{p{\theta }_2}{{\alpha }_2-1}},\mathrm{Var}\left(Z\right)={\displaystyle \frac{q^2{\theta }_1^2}{{({\alpha }_1-1)}^2({\alpha }_1-2)}}+{\displaystyle \frac{p^2{\theta }_2^2}{{({\alpha }_2-1)}^2({\alpha }_2-2)}}.$$

Since the distribution of Z is not closed-form, we approximate it using a gamma distribution $Z^{\prime }\sim \Gamma (k,\theta )$ by matching its first two moments. The parameters are defined by

$$\mathbb{E}\left[Z^{\prime }\right]=k\theta =\mathbb{E}\left[Z\right],\mathrm{Var}\left(Z^{\prime }\right)=k{\theta }^2=\mathrm{Var}\left(Z\right),$$

which implies that

$$\theta ={\displaystyle \frac{\mathrm{Var}\left(Z\right)}{\mathbb{E}\left[Z\right]}},k={\displaystyle \frac{{\left(\mathbb{E}\left[Z\right]\right)}^2}{\mathrm{Var}\left(Z\right)}}.$$

By this approximation,

$$\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)=\mathbb{P}\left(Z\ge {\displaystyle \frac{1}{K}}\right)\approx \mathbb{P}\left(Z^{\prime }\ge {\displaystyle \frac{1}{K}}\right).$$

The cumulative distribution function of $Z^{\prime }$ is expressed in terms of the lower incomplete gamma function, so the tail probability satisfies

$$\mathbb{P}\left(Z^{\prime }\ge {\displaystyle \frac{1}{K}}\right)=1-F_{Z^{\prime }}\left({\displaystyle \frac{1}{K}}\right)={\displaystyle \frac{\Gamma \left(k,\frac{1}{K\theta }\right)}{\Gamma \left(k\right)}},$$

where $\Gamma (k,x)={\int }_x^{\infty }{t}^{k-1}{e}^{-t}dt$ is the upper incomplete gamma function and $\Gamma \left(k\right)$ is the gamma function. This equality follows from the change of variables

$$t={\displaystyle \frac{x}{\theta }}\Rightarrow dx=\theta dt,$$

which transforms the tail integral into the standard upper incomplete gamma integral:

$$\begin{array}{cc}\hfill \mathbb{P}\left(Z^{\prime }\ge {\displaystyle \frac{1}{K}}\right)& ={\int }_{{\displaystyle \frac{1}{K}}}^{\infty }{\displaystyle \frac{1}{\Gamma \left(k\right){\theta }^k}}{x}^{k-1}{e}^{-x/\theta }dx\hfill \\ & ={\displaystyle \frac{1}{\Gamma \left(k\right)}}{\int }_{{\displaystyle \frac{1}{K\theta }}}^{\infty }{t}^{k-1}{e}^{-t}dt={\displaystyle \frac{\Gamma \left(k,\frac{1}{K\theta }\right)}{\Gamma \left(k\right)}}.\hfill \end{array}$$

Hence, the probability that the effective reproduction number exceeds unity is approximated by the ratio of upper incomplete gamma to gamma functions:

$$\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)\approx {\displaystyle \frac{\Gamma \left(k,\frac{1}{K\theta }\right)}{\Gamma \left(k\right)}}.$$

This completes the approximation of the persistence probability via the effective reproduction number distribution.    □

Example 1. 

Using the parameters $A=50,u=0.1,{\gamma }_1=0.1,{\gamma }_2=0.2,q=0.5,p=0.5$, and stochastic transmission rates ${\beta }_1$ and ${\beta }_2$ governed by inverse gamma distributions with parameters ${\alpha }_1=3,{\theta }_1=0.004,{\alpha }_2=3,{\theta }_2=0.002$ (derived from $a_i=1.0$, $b_1=0.002$, $b_2=0.001$, $c_i=1.0$), we define the scaling constant:

$$K={\displaystyle \frac{A}{u(u+{\gamma }_1+{\gamma }_2)}}={\displaystyle \frac{50}{0.1\times (0.1+0.1+0.2)}}=1250.$$

Using Monte Carlo simulation with one million samples from the inverse gamma distributions for ${\beta }_1$ and ${\beta }_2$, we compute samples of the effective reproduction number ${\mathcal{R}}_{\infty }$ (the MATLAB-2015 code utilized for the simulations can be found in Appendix A). The estimated probability that the effective reproduction number exceeds the epidemic threshold, $\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)$, is found to be approximately

$$\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)\approx 0.836249,$$

indicating an 83.6% chance that the epidemic persists under these stochastic transmission dynamics.

Corollary 1. 

Let ${\mathcal{R}}_{\infty }=KZ$, where

$$Z:=q{\beta }_{\infty ,1}+p{\beta }_{\infty ,2},$$

and assume that ${\beta }_{\infty ,1}\sim \mathrm{InvGamma}({\alpha }_1,{\theta }_1)$, ${\beta }_{\infty ,2}\sim \mathrm{InvGamma}({\alpha }_2,{\theta }_2)$ are independent inverse gamma-distributed random variables with shape parameters ${\alpha }_i>2$. Let $Z^{\prime }\sim \Gamma (k,\theta )$ be a gamma-distributed random variable matching the first and second moments of Z, where

$$k={\displaystyle \frac{{\left(\mathbb{E}\left[Z\right]\right)}^2}{\mathrm{Var}\left(Z\right)}},\theta ={\displaystyle \frac{\mathrm{Var}\left(Z\right)}{\mathbb{E}\left[Z\right]}}.$$

Then, the probability that the epidemic goes extinct, that is, ${\mathcal{R}}_{\infty }<1$, is approximately given by

$$\mathbb{P}({\mathcal{R}}_{\infty }<1)\approx {\displaystyle \frac{\gamma \left(k,\frac{1}{K\theta }\right)}{\Gamma \left(k\right)}}=1-{\displaystyle \frac{\Gamma \left(k,\frac{1}{K\theta }\right)}{\Gamma \left(k\right)}}$$

where $\gamma (k,x)$ and $\Gamma (k,x)$ are the lower and upper incomplete gamma functions, respectively.

Example 2. 

Based on Example 1, we have $\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)\approx 0.836249$. Consequently, by the complement rule, we obtain $\mathbb{P}({\mathcal{R}}_{\infty }<1)\approx 1-0.836249=0.163751$. This indicates that there is approximately a 16.4% chance that the effective reproduction number under stationary transmission dynamics is strictly less than one. In epidemiological terms, this means that, in about $16\%$ of the stochastic scenarios, the disease will tend to die out in the long run.

3.3. Accuracy and Error Quantification of the Approximation

The accuracy of the gamma approximation (12) fundamentally hinges on its ability to match the first two moments of the random variable Z. However, it inherently fails to capture higher-order moments such as skewness and kurtosis, defined, respectively, by

$$\mathrm{Skewness}\left(Z\right)={\displaystyle \frac{\mathbb{E}\left[{(Z-\mathbb{E}\left[Z\right])}^3\right]}{\mathrm{Var}{\left(Z\right)}^{3/2}}},\mathrm{Kurtosis}\left(Z\right)={\displaystyle \frac{\mathbb{E}\left[{(Z-\mathbb{E}\left[Z\right])}^4\right]}{\mathrm{Var}{\left(Z\right)}^2}}.$$

These higher moments are critical in characterizing the tail behavior of the distribution, and their omission constitutes the primary source of approximation error, especially when estimating tail probabilities related to persistence. From a theoretical standpoint, classical Berry–Esseen-type inequalities, suitably adapted for gamma approximations (see, e.g., ref. [35]), provide an upper bound on the maximal deviation between the true cumulative distribution function (CDF) of Z and the gamma approximation. Specifically, there exists a universal constant C such that

$$\underset{x}{sup}\left|F_Z\left(x\right)-F_{\Gamma }\left(x\right)\right|\le C{\displaystyle \frac{\left|\mathrm{Skewness}\right(Z\left)\right|}{\sqrt{k}}},$$

where $F_Z$ and $F_{\Gamma }$ denote the CDFs of Z and its gamma approximation, respectively, and k is the gamma shape parameter. This inequality indicates that the approximation accuracy improves as the shape parameter k increases and the skewness of Z decreases.

When considering the persistence probability itself, expressed as a tail probability,

$$\left|\mathbb{P}\left(Z\ge {\displaystyle \frac{1}{K}}\right)-{\displaystyle \frac{\Gamma \left(k,\frac{1}{K\theta }\right)}{\Gamma \left(k\right)}}\right|\le \epsilon ,$$

the error term $\epsilon$ depends intricately on the higher-order central moments of Z, the mixture proportion q, and the position of the threshold $1/K$. Notably, the approximation error tends to increase as the threshold moves further into the tail region, where the gamma distribution’s lighter tails underestimate the true persistence probability.

In the limiting regime where the shape parameters ${\alpha }_i\to \infty$, the inverse gamma components become less skewed and more symmetric, resulting in the mixture Z being better approximated by a gamma distribution. Similarly, when the mixture weight q approaches the extremes 0 or 1, the mixture effectively reduces to a single component distribution, which significantly enhances the accuracy by avoiding bimodality.

Empirical evidence from simulation studies, as illustrated in Figure 2, corroborates these theoretical points: the approximation error is minimal for shape parameters ${\alpha }_i>3$ and for mixture weights away from the central region $q=0.5$, where bimodality in the mixture distribution is most pronounced. Across all tested scenarios, the gamma approximation consistently tends to underestimate persistence probabilities due to its inherently lighter tails.

4. Sensitivity Analysis and Computational Validation of Theoretical Results

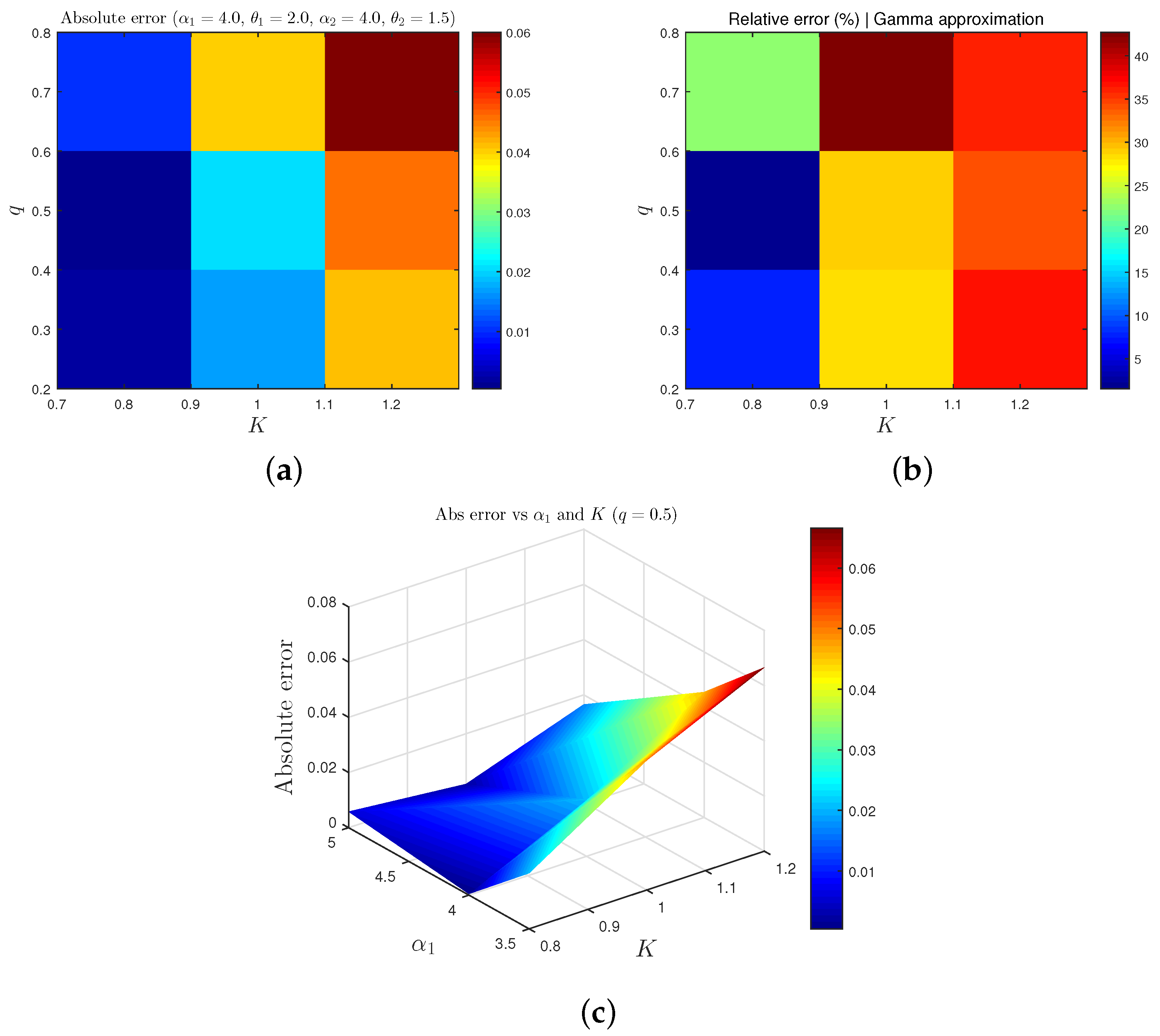
In this section, we focus on a detailed sensitivity analysis of key parameters influencing the probabilities $\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)$ and $\mathbb{P}({\mathcal{R}}_{\infty }<1)$, which determine the likelihood of epidemic persistence or extinction in the long term. Specifically, we examine how variations in the shape and scale parameters of the inverse gamma distributions associated with the stochastic transmission rates ${\beta }_{\infty ,1}$ and ${\beta }_{\infty ,2}$, as well as the weight parameters q and p, affect the effective reproduction number ${\mathcal{R}}_{\infty }$.

We then proceed to numerically classify the dynamical behavior of the SVIR epidemic model through trajectory simulations, which incorporate the long-term ergodic behavior of the stochastic transmission rates. By simulating numerous sample paths under different parameter configurations, we are able to assess how stochastic fluctuations in the transmission dynamics shape the qualitative evolution of the epidemic.

4.1. Sensitivity Analysis

We begin by analyzing how variations in key parameters influence the probability $\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)$, which quantifies the likelihood of epidemic persistence. The surface plots in Figure 3 illustrate the behavior of $\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)$ as a function of the shape and scale parameters $b_1$ and $c_1$ of the inverse gamma distribution characterizing the stochastic transmission rate ${\beta }_1\left(t\right)$, while keeping the parameters of ${\beta }_2\left(t\right)$ and the scaling constant K fixed. The plots are generated for three representative values of the parameter $a_1\in \{0.5,1.0,2.0\}$, which influence the overall shape of the inverse gamma distribution. The results indicate that increasing the shape parameter or decreasing the scale parameter reduces $\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)$, thereby increasing the probability of disease extinction. This behavior aligns with the intuition that a reduced variability or tighter concentration of transmission rates favors epidemic control.

In Figure 4, we further investigate the extinction probability $\mathbb{P}({\mathcal{R}}_{\infty }<1)$ by examining its sensitivity to three sets of key parameters. First, we assess the influence of the shape parameters ${\alpha }_1$ and ${\alpha }_2$, which are shown to control the concentration of the inverse gamma distributions of ${\beta }_{\infty ,1}$ and ${\beta }_{\infty ,2}$. An increase in ${\alpha }_i$ results in a more peaked distribution, leading to reduced transmission variability and thus a higher chance of epidemic extinction. Second, we explore the role of the scale parameters ${\theta }_1$ and ${\theta }_2$, which modulate both the mean and the variance of the transmission rates. Larger values of ${\theta }_i$ lead to greater dispersion, which tends to elevate the likelihood of persistence due to amplified stochastic effects. Finally, we consider the impact of the weighting coefficients q and p, which determine the relative contributions of the two stochastic transmission components to the overall effective reproduction number ${\mathcal{R}}_{\infty }$. Adjusting these weights alters the balance between the two sources of infection pressure and can significantly influence the extinction probability.

Collectively, these results highlight the nuanced interplay between parameter uncertainty and epidemic outcomes. They underscore that even in the presence of randomness, careful parameter tuning (especially of the distributional characteristics of the transmission rates) can enhance disease control efforts.

4.2. Empirical Verification of Stationary Distributions of ${\beta }_i$

Figure 5 provides a comparison between the empirical and theoretical stationary distributions of the stochastic transmission rates ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$, offering strong numerical support for the assumed ergodic inverse gamma behavior. In the left panel, the histogram represents the empirical distribution of ${\beta }_1\left(t\right)$ generated from long-run simulations after discarding the transient phase, ensuring convergence to the stationary regime. This histogram closely aligns with the orange curve corresponding to the theoretical inverse gamma probability density function, suggesting that the stochastic differential equation governing ${\beta }_1\left(t\right)$ indeed admits an inverse gamma stationary distribution. Similarly, the right panel displays the results for ${\beta }_2\left(t\right)$, where the empirical distribution matches well with the inverse gamma PDF shown in blue, reinforcing the same conclusion.

The parameters $a_1=a_2=1.0$, $b_1=0.002$, $b_2=0.001$, and $c_1=c_2=1.0$ were selected to ensure consistent shape behavior while allowing for variation in scale, which directly influences the tail behavior and variance of the distribution. The strong agreement observed in both panels between the simulated empirical distributions and the theoretical inverse gamma densities confirms not only the ergodicity of the transmission processes but also the structural robustness of the inverse gamma assumption across the considered parameter regimes. This consistency indicates that the inverse gamma law remains a reliable stationary approximation for the stochastic transmission rates, even under varying dynamical and noise conditions.

From a modeling perspective, this result is conceptually important because it demonstrates internal consistency: the long-term behavior of the stochastic transmission rates governed by the chosen mean-reverting dynamics aligns with an analytically tractable and interpretable distribution. While this does not constitute empirical validation, it offers theoretical justification for adopting the inverse gamma law as a stationary approximation, which, in turn, enables explicit analytical expressions for quantities like the effective reproduction number ${\mathcal{R}}_{\infty }$. This analytical tractability is essential for conducting rigorous probabilistic and sensitivity analyses within the model framework.

Figure 6 explores the influence of the diffusion coefficient $c_1$ on the stationary behavior of the stochastic transmission rate ${\beta }_1\left(t\right)$. Using fixed values $a_1=1$ and $b_1=0.002$, we simulate three distinct cases that vary only by the diffusion intensity $c_1$, thereby isolating its role in determining the existence and shape of the stationary distribution.

In the first scenario, $c_1=0.70$, yielding $c_1^2=0.49<2a_1=2.00$, the theoretical conditions for the existence of a stationary inverse gamma distribution are satisfied. The resulting histogram aligns well with the corresponding inverse gamma density, confirming the theoretical prediction. In the second case, $c_1=1.20$, where $c_1^2=1.44<2a_1$, the process remains within the stationary regime, and the empirical distribution again matches the inverse gamma density, though the distribution exhibits increased variance and heavier tails due to the higher diffusion intensity.

In contrast, the third case with $c_1=1.90$ leads to $c_1^2=3.61>2a_1=2.00$, violating the theoretical condition for stationarity. As expected, the empirical histogram shows clear divergence from the inverse gamma shape, indicating that the process may not admit a stationary distribution in this regime. The absence of a matching theoretical curve highlights the loss of ergodicity and the onset of instability in the dynamics of ${\beta }_1\left(t\right)$.

Figure 7 examines how changes in the diffusion coefficient $c_2$ impact the stationary distribution of the stochastic transmission rate ${\beta }_2\left(t\right)$ under the fixed parameters $a_2=1$ and $b_2=0.001$. We consider three representative cases by varying $c_2$ in order to assess whether the process remains within the stationary inverse gamma regime.

In the first case, $c_2=0.60$, corresponding to $c_2^2=0.36<2a_2=2.00$, the theoretical condition for the existence of an inverse gamma stationary distribution is satisfied (see Theorem 1). The close agreement between the simulated histogram and the corresponding theoretical density confirms that the process has reached its stationary regime. This numerical evidence supports the ergodicity of the transmission rate process and illustrates the model’s capacity to capture stable long-term stochastic dynamics in the transmission rate, consistent with the theoretical predictions.

For the second case, $c_2=1.40$, the squared diffusion intensity is $c_2^2=1.96$, which still falls below the critical threshold $2a_2$. Here again, the empirical histogram aligns well with the inverse gamma density, though with a greater spread and heavier tails, as expected due to increased stochastic fluctuations. This supports the robustness of the stationary regime under moderate diffusion.

However, in the third case, where $c_2=2.00$ and hence $c_2^2=4>2a_2$, the theoretical condition for stationarity is violated. The resulting histogram deviates significantly from the inverse gamma shape, indicating that the process likely lacks a stationary distribution in this regime. The loss of convergence and increasing variability reflect a breakdown in the balance between drift and diffusion, pushing the system beyond the bounds of ergodic stability.

4.3. Stochastic Dynamics and Sample Trajectories of the SVIR Model

Figure 8 illustrates representative trajectories of the stochastic SVIR model defined by Equations (2)–(5), where the transmission rates ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$ evolve as stochastic processes governed by inverse gamma-driven dynamics according to Equations (6) and (7). The simulation uses the following parameter values: $a_1=a_2=1.0$, $b_1=0.002$, $b_2=0.001$, $c_1=0.4$, $c_2=0.3$, $q=p=0.5$, $A=50$, $u=0.1$, ${\gamma }_1=0.001$, and ${\gamma }_2=0.002$. These choices ensure that both ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$ admit stationary inverse gamma distributions, preserving the ergodicity of the transmission mechanisms. The sample paths of the SVIR compartments over time reflect the dynamic interplay between vaccination, infection, and recovery processes under stochastic fluctuations. Despite the noise in the transmission rates, the trajectories exhibit persistent epidemic behavior, with infected individuals remaining present over a long time horizon. Quantitatively, the estimated probability that the effective reproduction number exceeds one, $\mathbb{P}({\mathcal{R}}_{\infty }>1)$, is computed as approximately $0.753873$. This high probability suggests that, under the given parameter configuration, the system is likely to sustain the epidemic in the long run, consistent with the observed persistence in the sample paths.

Figure 9 presents representative trajectories of the SVIR epidemic model governed by the stochastic system (2)–(5), with t the following parameter configuration: $a_1=a_2=1.0$, $b_1=0.002$, $b_2=0.001$, $c_1=0.4$, $c_2=0.3$, $q=p=0.5$, $A=4.5$, $u=0.1$, ${\gamma }_1=0.001$, and ${\gamma }_2=0.002$. These settings maintain the ergodicity and stationarity of the transmission processes, allowing for a well-defined analysis of long-term dynamics. The trajectories reveal a clear trend toward the extinction of the epidemic, with the number of infected individuals gradually declining and eventually approaching zero over time. This behavior is consistent with a low reproduction potential of the disease under the influence of the chosen stochastic transmission structure. This is further corroborated by the numerical estimate of the probability $\mathbb{P}({\mathcal{R}}_{\infty }<1)$, which is approximately $0.9368$. This high extinction probability strongly indicates that the epidemic is unlikely to persist in the long run under the current parameter regime. The decline in ${\mathcal{R}}_{\infty }$ is primarily driven by the reduced scaling factor $A=4.5$, which effectively lowers the overall transmission intensity despite the inherent stochasticity in ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$.

5. Conclusions

In this study, we carried out a probabilistic analysis of a stochastic SVIR epidemic model, where the transmission rates ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$ evolve according to ergodic stochastic differential equations with inverse gamma stationary distributions. Our primary objective was to understand how stochastic fluctuations and heterogeneity in disease transmission influence the long-term dynamics of the epidemic, particularly in determining whether the disease persists or dies out.

From a theoretical standpoint, we derived sufficient conditions for the existence of stationary distributions of the stochastic transmission processes. Specifically, we showed that the processes ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$ admit stationary inverse gamma distributions when the diffusion coefficients satisfy $c_i^2<2a_i$ and $c_i^2\ne a_i$ for $i=1,2$. We analytically characterized these stationary distributions and demonstrated that, under such conditions, the effective reproduction number ${\mathcal{R}}_{\infty }$ becomes a well-defined random variable whose distribution governs the probabilistic thresholds of epidemic persistence or extinction. Furthermore, we provided approximations for $\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)$ and $\mathbb{P}({\mathcal{R}}_{\infty }<1)$, highlighting their dependence on the inverse gamma parameters and the mixing weights q and p used to combine the two transmission pathways.

The theoretical findings were supported by some numerical examples. Monte Carlo simulations of the stochastic processes demonstrated that the empirical distributions of ${\beta }_1\left(t\right)$ and ${\beta }_2\left(t\right)$, computed over long time horizons, closely match their theoretical inverse gamma stationary distributions. This numerical agreement provides strong evidence of the ergodic behavior predicted by the theoretical analysis, confirming that the processes converge in distribution to their respective invariant measures. Sensitivity analyses using three-dimensional surface plots demonstrated that increasing the shape parameters $a_i$ or reducing the scale and diffusion parameters $b_i$, $c_i$ results in a lower variance of ${\beta }_i\left(t\right)$, enhancing predictability and increasing the probability of extinction. Conversely, larger values of $b_i$ or $c_i$ amplify transmission variability, raising the risk of disease persistence.

In addition, we showed that the overall transmission strength, modulated by the parameter A, plays a crucial role in shaping epidemic outcomes. Simulations of the full SVIR model revealed contrasting scenarios: for a high input rate ($A=50$), the probability of persistence $\mathbb{P}({\mathcal{R}}_{\infty }\ge 1)$ was approximately 0.7538, indicating a likely outbreak. In contrast, for  ($A=4.5$), the extinction probability $\mathbb{P}({\mathcal{R}}_{\infty }<1)$ increased to 0.9368, suggesting effective epidemic control.

In summary, our findings establish that modeling transmission rates as stochastic processes with inverse gamma stationary distributions offers a nuanced and adaptable framework for capturing epidemic dynamics under uncertainty. Both rigorous theoretical analysis and numerical simulations underscore the pivotal role of transmission variability in influencing disease outcomes, including persistence and extinction scenarios.

Future work may extend this model to account for time-varying vaccination strategies, spatial heterogeneity, and contact network structures. Additionally, integrating real epidemic data through advanced statistical inference techniques could further enhance the model’s applicability to real-world public health planning and epidemic forecasting.