A Comprehensive Review of Image Restoration Research Based on Diffusion Models
Abstract
1. Introduction
2. Definition of the Diffusion Model and Its Improvement
2.1. Definition of Diffusion Models
2.1.1. Denoising Diffusion Probabilistic Models
2.1.2. Score-Based Generative Models
2.1.3. Stochastic Differential Equations
2.2. Common Improvements to Diffusion Models
2.2.1. Restructuring the Network
2.2.2. Accelerated Sampling Process
3. Diffusion Model-Based Image Restoration Method
3.1. Conditional Guided Image Restoration
3.2. Pre-Training-Based Image Restoration
3.3. Estimation-Based Image Restoration
3.3.1. Image Restoration Based on Posterior Estimation
3.3.2. Blind Image Kernel Estimate
3.4. Image Restoration Based on Image Domain Transformation
3.4.1. Image Restoration Based on Potential Space and Decomposition Space
3.4.2. Image Restoration Based on Data Domain Synthesis
3.5. Projection-Based Image Restoration
4. Applications of Diffusion Models in Super-Resolution Reconstruction and Frequency-Selective Image Restoration
4.1. Super-Resolution Reconstruction
4.2. Image Restoration Based on Frequency Selection
4.2.1. Image Deblurring
4.2.2. Image Inpainting
4.2.3. Image Deraining, Desnowing, and Dehazing
4.2.4. Image Denoising
4.2.5. Low-Light Enhancement
5. Dataset and Evaluation Metrics
5.1. Datasets
5.2. Evaluation Metrics
6. Conclusions
- (1)
- Efficient sampling
- (2)
- Model Compression
- Model pruning: removing unimportant parameters by estimating the importance score of each parameter.
- Knowledge distillation: transferring complex teacher model content to student model species. For example, Salimans et al. [124] proposed a strategy of progressive distillation, which iteratively compresses the knowledge of the original model into a student model with fewer sampling steps through multiple rounds of teacher–student training. Each round of distillation halves the sampling steps by aligning the outputs and dynamically adjusts the noise schedule to maintain generation quality, effectively addressing the issue of slow sampling speeds caused by multi-step iteration. Addressing the limitations of traditional diffusion model knowledge distillation methods that rely on original training data, Xiang et al. [125] proposed a data-free knowledge distillation framework (DKDM). This method utilizes the pre-trained diffusion model itself to generate synthetic training samples, designs a noise-conditional generation strategy, and incorporates adversarial feature matching with multi-scale feature consistency constraints, achieving efficient distillation for student models of arbitrary architectures.
- Low-rank decomposition: decomposing a tensor with a huge number of parameters into multiple low-rank tensors. All of the above methods work on model compression from the structure of the diffusion model itself, but very little work has been conducted to design a model compression strategy for the image restoration aspect of the diffusion-based model, so this direction needs to be studied urgently.
- Model Lightweighting: Two common techniques are used in the lightweighting process: half-precision floating-point quantization (FP16) and 8-bit integer quantization (INT8). FP16 converts the model weights and activation values from 32-bit single-precision floating point (FP32) to 16-bit half-precision floating point (FP16) with almost no loss of precision, and is suitable for most network architectures, effectively increasing the model’s running speed by approximately 2×. INT8 maps FP32 weight values to INT8 (−128–127), significantly reducing memory footprint and increasing computation speed by 3–4×. However, it often exhibits a significant loss of precision for sensitive tasks such as image super-resolution, making it unable to fully guarantee image restoration quality.
- Conditional Diffusion Model Sparsification: This method significantly reduces the model size and improves inference speed while maintaining conditional control capabilities by removing redundant weights, entire neurons, or attention heads, while striving to maintain generation quality.
- (3)
- Model Structure
- (4)
- Evaluation Index
- (5)
- Multi-Modal Fusion
- (6)
- Specific scenes
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ouyang, X.; Chen, Y.; Zhu, K.; Agam, G. Image restoration refinement with Uformer GAN. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–18 June 2024; pp. 5919–5928. [Google Scholar] [CrossRef]
- Rama, P.; Pandiaraj, A.; Angayarkanni, V.; Prakash, Y.; Jagadeesh, S. Advancement in Image Restoration Through GAN-based Approach. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24–28 June 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Masmoudi, Y.; Ramzan, M.; Khan, S.A.; Habib, M. Optimal feature extraction and ulcer classification from WCE image data using deep learning. Soft Comput. 2022, 26, 7979–7992. [Google Scholar] [CrossRef]
- Habib, M.; Ramzan, M.; Khan, S.A. A deep learning and handcrafted based computationally intelligent technique for effective COVID-19 detection from X-ray/CT-scan imaging. J. Grid Comput. 2022, 20, 23. [Google Scholar] [CrossRef]
- Muslim, H.S.M.; Khan, S.A.; Hussain, S.; Jamal, A.; Qasim, H.S.A. A knowledge-based image enhancement and denoising approach. Comput. Math. Organ. Theory 2019, 25, 108–121. [Google Scholar] [CrossRef]
- Li, M.; Fu, Y.; Zhang, T.; Wen, G. Supervise-assisted self-supervised deep-learning method for hyperspectral image restoration. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 7331–7344. [Google Scholar] [CrossRef]
- Monroy, B.; Bacca, J.; Tachella, J. Generalized recorrupted-to-recorrupted: Self-supervised learning beyond gaussian noise. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, TN, USA, 11–15 June 2025; pp. 28155–28164. [Google Scholar]
- Li, X.; Ren, Y.; Jin, X.; Lan, C.; Wang, X.; Zeng, W.; Wang, X.; Chen, Z. Diffusion Models for Image Restoration and Enhancement–A Comprehensive Survey. arXiv 2023, arXiv:2308.09388. [Google Scholar] [CrossRef]
- Luo, Z.; Gustafsson, F.K.; Zhao, Z.; Sjölund, J.; Schön, T.B. Taming diffusion models for image restoration: A review. arXiv 2024, arXiv:2409.10353. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Sohl-Dickstein, J.; Weiss, E.; Maheswaranathan, N.; Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 7–9 July 2015; pp. 2256–2265. Available online: https://proceedings.mlr.press/v37/sohl-dickstein15.html (accessed on 10 May 2025).
- Song, Y.; Ermon, S. Generative modeling by estimating gradients of the data distribution. Adv. Neural Inf. Process. Syst. 2019, 32, 6392. Available online: https://papers.nips.cc/paper/2019/file/3001ef257407d5a371a96dcd947c7d93-MetaReview.html (accessed on 10 May 2025).
- Song, Y.; Ermon, S. Improved techniques for training score-based generative models. Adv. Neural Inf. Process. Syst. 2020, 33, 12438–12448. [Google Scholar]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-based generative modeling through stochastic differential equations. arXiv 2020, arXiv:2011.13456. [Google Scholar] [CrossRef]
- Song, Y.; Durkan, C.; Murray, I.; Ermon, S. Maximum likelihood training of score-based diffusion models. Adv. Neural Inf. Process. Syst. 2021, 34, 1415–1428. [Google Scholar]
- Rezende, D.; Mohamed, S. Variational inference with normalizing flows. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 7–9 July 2015; pp. 1530–1538. Available online: https://proceedings.mlr.press/v37/rezende15.html (accessed on 10 May 2025).
- Welling, M.; Teh, Y.W. Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Citeseer, Bellevue, WA, USA, 28 June–2 July 2011; pp. 681–688. Available online: https://icml.cc/virtual/2021/test-of-time/11808 (accessed on 10 May 2025).
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar] [CrossRef]
- Nichol, A.Q.; Dhariwal, P. Improved denoising diffusion probabilistic models. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 8162–8171. Available online: https://proceedings.mlr.press/v139/nichol21a.html (accessed on 10 May 2025).
- Yang, X.; Shih, S.M.; Fu, Y.; Zhao, X.; Ji, S. Your vit is secretly a hybrid discriminative-generative diffusion model. arXiv 2022, arXiv:2208.07791. [Google Scholar] [CrossRef]
- Nichol, A.; Dhariwal, P.; Ramesh, A.; Shyam, P.; Mishkin, P.; McGrew, B.; Sutskever, I.; Chen, M. Glide: Towards photorealistic image generation and editing with text-guided diffusion models. arXiv 2021, arXiv:2112.10741. [Google Scholar] [CrossRef]
- Lee, K.; Liu, H.; Ryu, M.; Watkins, O.; Du, Y.; Boutilier, C.; Abbeel, P.; Ghavamzadeh, M.; Gu, S.S. Aligning text-to-image models using human feedback. arXiv 2023, arXiv:2302.12192. [Google Scholar] [CrossRef]
- Song, J.; Meng, C.; Ermon, S. Denoising diffusion implicit models. arXiv 2020, arXiv:2010.02502. [Google Scholar] [CrossRef]
- Lu, C.; Zhou, Y.; Bao, F.; Chen, J.; Li, C.; Zhu, J. Dpm-solver: A fast ode solver for diffusion probabilistic model sampling in around 10 steps. Adv. Neural Inf. Process. Syst. 2022, 35, 5775–5787. [Google Scholar]
- Lyu, Z.; Xu, X.; Yang, C.; Lin, D.; Dai, B. Accelerating diffusion models via early stop of the diffusion process. arXiv 2022, arXiv:2205.12524. [Google Scholar] [CrossRef]
- Xia, B.; Zhang, Y.; Wang, S.; Wang, Y.; Wu, X.; Tian, Y.; Yang, W.; Van Gool, L. Diffir: Efficient diffusion model for image restoration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 13095–13105. [Google Scholar] [CrossRef]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 8748–8763. Available online: https://icml.cc/virtual/2021/oral/9194 (accessed on 10 May 2025).
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. 2013. Available online: https://iclr.cc/virtual/2024/test-of-time/21444 (accessed on 10 May 2025).
- Saharia, C.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image super-resolution via iterative refinement. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 4713–4726. [Google Scholar] [CrossRef]
- Saharia, C.; Chan, W.; Chang, H.; Lee, C.; Ho, J.; Salimans, T.; Fleet, D.; Norouzi, M. Palette: Image-to-image diffusion models. In Proceedings of the ACM SIGGRAPH 2022 Conference Proceedings, Vancouver, BC, Canada, 7–11 August 2022; pp. 1–10. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, X.; Li, D.; Wang, X.; Wang, J.; Li, H. A unified conditional framework for diffusion-based image restoration. Adv. Neural Inf. Process. Syst. 2023, 36, 49703–49714. [Google Scholar]
- Fei, B.; Lyu, Z.; Pan, L.; Zhang, J.; Yang, W.; Luo, T.; Zhang, B.; Dai, B. Generative diffusion prior for unified image restoration and enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 9935–9946. [Google Scholar] [CrossRef]
- Feng, B.T.; Smith, J.; Rubinstein, M.; Chang, H.; Bouman, K.L.; Freeman, W.T. Score-based diffusion models as principled priors for inverse imaging. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 10520–10531. [Google Scholar] [CrossRef]
- Sun, H.; Bouman, K.L. Deep probabilistic imaging: Uncertainty quantification and multi-modal solution characterization for computational imaging. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 2628–2637. [Google Scholar] [CrossRef]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using real nvp. arXiv 2016, arXiv:1605.08803. [Google Scholar] [CrossRef]
- Niu, A.; Zhang, K.; Pham, T.X.; Sun, J.; Zhu, Y.; Kweon, I.S.; Zhang, Y. Cdpmsr: Conditional diffusion probabilistic models for single image super-resolution. arXiv 2023, arXiv:2302.12831. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar] [CrossRef]
- Gao, S.; Liu, X.; Zeng, B.; Xu, S.; Li, Y.; Luo, X.; Liu, J.; Zhen, X.; Zhang, B. Implicit diffusion models for continuous super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 10021–10030. [Google Scholar] [CrossRef]
- Guo, L.; Wang, C.; Yang, W.; Huang, S.; Wang, Y.; Pfister, H.; Wen, B. Shadowdiffusion: When degradation prior meets diffusion model for shadow removal. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 14049–14058. [Google Scholar] [CrossRef]
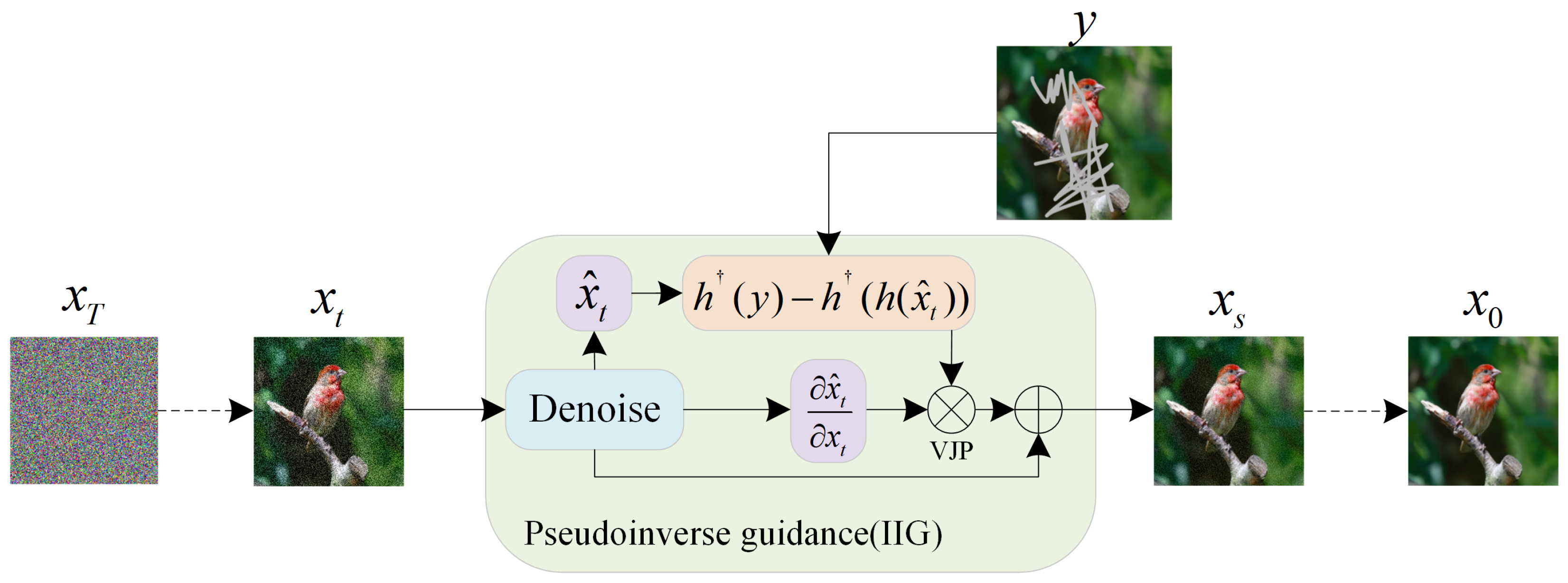
- Chung, H.; Kim, J.; Mccann, M.T.; Klasky, M.L.; Ye, J.C. Diffusion posterior sampling for general noisy inverse problems. arXiv 2022, arXiv:2209.14687. [Google Scholar] [CrossRef]
- Song, J.; Vahdat, A.; Mardani, M.; Kautz, J. Pseudoinverse-guided diffusion models for inverse problems. In Proceedings of the International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023; Available online: https://iclr.cc/virtual/2023/poster/11030 (accessed on 10 May 2025).
- Chung, H.; Kim, J.; Kim, S.; Ye, J.C. Parallel diffusion models of operator and image for blind inverse problems. In Proceedings of the CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; Volume 1, p. 3. [Google Scholar] [CrossRef]
- Murata, N.; Saito, K.; Lai, C.H.; Takida, Y.; Uesaka, T.; Mitsufuji, Y.; Ermon, S. Gibbsddrm: A partially collapsed gibbs sampler for solving blind inverse problems with denoising diffusion restoration. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 25501–25522. Available online: https://icml.cc/virtual/2023/oral/25492 (accessed on 10 May 2025).
- Van Dyk, D.A.; Park, T. Partially collapsed Gibbs samplers: Theory and methods. J. Am. Stat. Assoc. 2008, 103, 790–796. [Google Scholar] [CrossRef]
- Luo, Z.; Gustafsson, F.K.; Zhao, Z.; Sjölund, J.; Schön, T.B. Refusion: Enabling large-size realistic image restoration with latent-space diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1680–1691. [Google Scholar] [CrossRef]
- Kawar, B.; Elad, M.; Ermon, S.; Song, J. Denoising diffusion restoration models. Adv. Neural Inf. Process. Syst. 2022, 35, 23593–23606. [Google Scholar]
- Kawar, B.; Song, J.; Ermon, S.; Elad, M. Jpeg artifact correction using denoising diffusion restoration models. arXiv 2022, arXiv:2209.11888. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, J.; Zhang, J. Zero-shot image restoration using denoising diffusion null-space model. arXiv 2022, arXiv:2212.00490. [Google Scholar] [CrossRef]
- Yang, T.; Ren, P.; Xie, X.; Zhang, L. Synthesizing realistic image restoration training pairs: A diffusion approach. arXiv 2023, arXiv:2303.06994. [Google Scholar] [CrossRef]
- Wei, M.; Shen, Y.; Wang, Y.; Xie, H.; Qin, J.; Wang, F.L. Raindiffusion: When unsupervised learning meets diffusion models for real-world image deraining. arXiv 2023, arXiv:2301.09430. [Google Scholar] [CrossRef]
- Zhang, S.; Ren, W.; Tan, X.; Wang, Z.J.; Liu, Y.; Zhang, J.; Zhang, X.; Cao, X. Semantic-aware dehazing network with adaptive feature fusion. IEEE Trans. Cybern. 2021, 53, 454–467. [Google Scholar] [CrossRef]
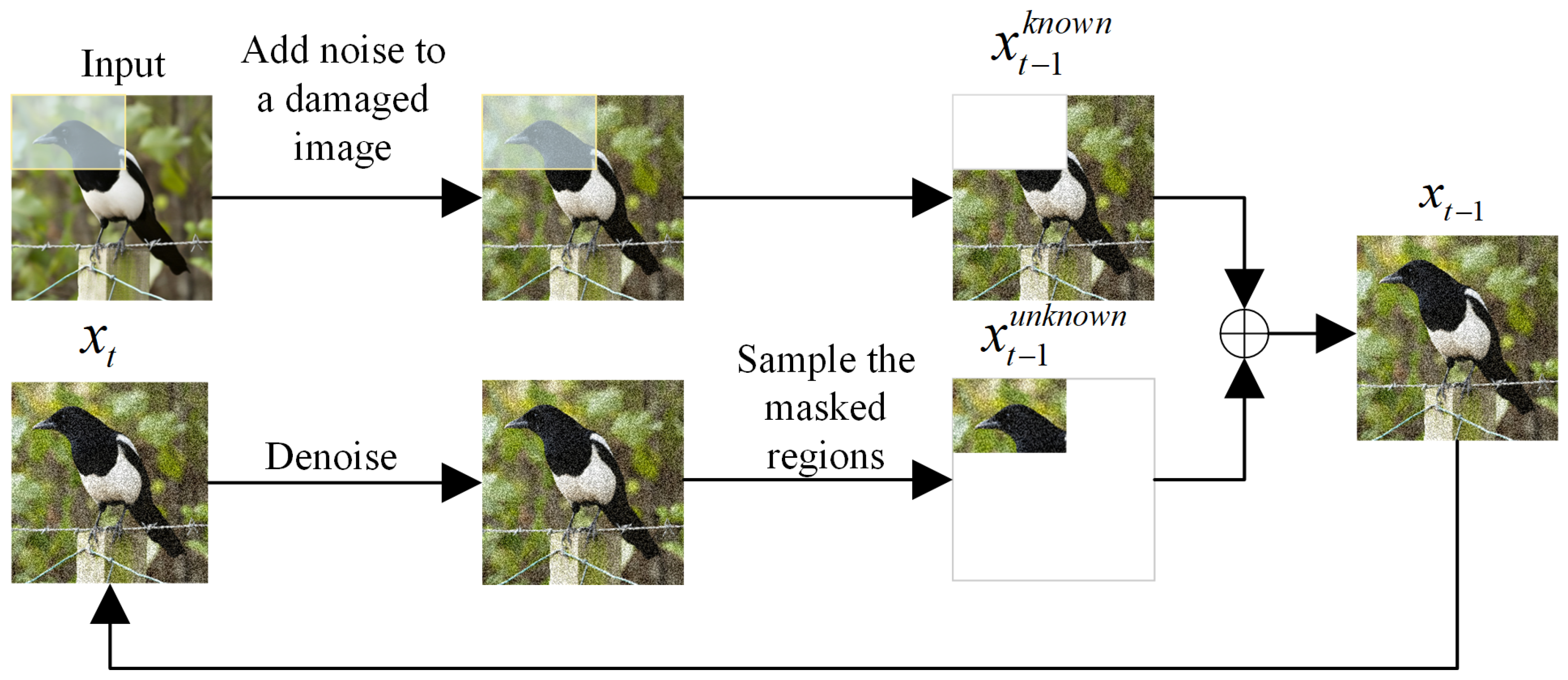
- Lugmayr, A.; Danelljan, M.; Romero, A.; Yu, F.; Timofte, R.; Van Gool, L. Repaint: Inpainting using denoising diffusion probabilistic models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11461–11471. [Google Scholar] [CrossRef]
- Choi, J.; Kim, S.; Jeong, Y.; Gwon, Y.; Yoon, S. Ilvr: Conditioning method for denoising diffusion probabilistic models. arXiv 2021, arXiv:2108.02938. [Google Scholar] [CrossRef]
- Ho, J.; Saharia, C.; Chan, W.; Fleet, D.J.; Norouzi, M.; Salimans, T. Cascaded diffusion models for high fidelity image generation. J. Mach. Learn. Res. 2022, 23, 1–33. [Google Scholar]
- Li, H.; Yang, Y.; Chang, M.; Chen, S.; Feng, H.; Xu, Z.; Li, Q.; Chen, Y. Srdiff: Single image super-resolution with diffusion probabilistic models. Neurocomputing 2022, 479, 47–59. [Google Scholar] [CrossRef]
- Wang, J.; Yue, Z.; Zhou, S.; Chan, K.C.; Loy, C.C. Exploiting diffusion prior for real-world image super-resolution. Int. J. Comput. Vis. 2024, 132, 5929–5949. [Google Scholar] [CrossRef]
- Shang, S.; Shan, Z.; Liu, G.; Wang, L.; Wang, X.; Zhang, Z.; Zhang, J. Resdiff: Combining cnn and diffusion model for image super-resolution. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 8975–8983. [Google Scholar] [CrossRef]
- Dos Santos, M.; Laroca, R.; Ribeiro, R.O.; Neves, J.; Proença, H.; Menotti, D. Face super-resolution using stochastic differential equations. In Proceedings of the 2022 35th SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Natal, Brazil, 24–27 October 2022; Volume 1, pp. 216–221. [Google Scholar] [CrossRef]
- Sahak, H.; Watson, D.; Saharia, C.; Fleet, D. Denoising diffusion probabilistic models for robust image super-resolution in the wild. arXiv 2023, arXiv:2302.07864. [Google Scholar] [CrossRef]
- Whang, J.; Delbracio, M.; Talebi, H.; Saharia, C.; Dimakis, A.G.; Milanfar, P. Deblurring via stochastic refinement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16293–16303. [Google Scholar] [CrossRef]
- Ren, M.; Delbracio, M.; Talebi, H.; Gerig, G.; Milanfar, P. Multiscale structure guided diffusion for image deblurring. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 10721–10733. [Google Scholar] [CrossRef]
- Delbracio, M.; Milanfar, P. Inversion by direct iteration: An alternative to denoising diffusion for image restoration. arXiv 2023, arXiv:2303.11435. [Google Scholar] [CrossRef]
- Kawar, B.; Vaksman, G.; Elad, M. Snips: Solving noisy inverse problems stochastically. Adv. Neural Inf. Process. Syst. 2021, 34, 21757–21769. [Google Scholar]
- Zhang, G.; Ji, J.; Zhang, Y.; Yu, M.; Jaakkola, T.S.; Chang, S. Towards Coherent Image Inpainting Using Denoising Diffusion Implicit Models. 2023. Available online: https://icml.cc/virtual/2023/poster/24127 (accessed on 10 May 2025).
- Chung, H.; Sim, B.; Ye, J.C. Come-closer-diffuse-faster: Accelerating conditional diffusion models for inverse problems through stochastic contraction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12413–12422. [Google Scholar] [CrossRef]
- Fabian, Z.; Tinaz, B.; Soltanolkotabi, M. Diracdiffusion: Denoising and incremental reconstruction with assured data-consistency. Proc. Mach. Learn. Res. 2024, 235, 12754. [Google Scholar]
- Mardani, M.; Song, J.; Kautz, J.; Vahdat, A. A variational perspective on solving inverse problems with diffusion models. arXiv 2023, arXiv:2305.04391. [Google Scholar] [CrossRef]
- Özdenizci, O.; Legenstein, R. Restoring vision in adverse weather conditions with patch-based denoising diffusion models. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10346–10357. [Google Scholar] [CrossRef]
- Luo, Z.; Gustafsson, F.K.; Zhao, Z.; Sjölund, J.; Schön, T.B. Image restoration with mean-reverting stochastic differential equations. arXiv 2023, arXiv:2301.11699. [Google Scholar] [CrossRef]
- Chan, M.A.; Young, S.I.; Metzler, C.A. SUD2: Supervision by Denoising Diffusion Models for Image Reconstruction. arXiv 2023, arXiv:2303.09642. [Google Scholar] [CrossRef]
- Xie, Y.; Yuan, M.; Dong, B.; Li, Q. Diffusion model for generative image denoising. arXiv 2023, arXiv:2302.02398. [Google Scholar] [CrossRef]
- Yue, Y.; Yu, M.; Yang, L.; Liu, T. Joint Conditional Diffusion Model for image restoration with mixed degradations. Neurocomputing 2025, 626, 129512. [Google Scholar] [CrossRef]
- Yue, C.; Peng, Z.; Ma, J.; Zhang, D. Enhanced control for diffusion bridge in image restoration. In Proceedings of the ICASSP 2025—2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hyderabad, India, 6–11 April 2025; pp. 1–5. [Google Scholar] [CrossRef]
- Jiang, H.; Luo, A.; Fan, H.; Han, S.; Liu, S. Low-light image enhancement with wavelet-based diffusion models. ACM Trans. Graph. (TOG) 2023, 42, 1–14. [Google Scholar] [CrossRef]
- Lv, X.; Zhang, S.; Wang, C.; Zheng, Y.; Zhong, B.; Li, C.; Nie, L. Fourier priors-guided diffusion for zero-shot joint low-light enhancement and deblurring. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–18 June 2024; pp. 25378–25388. [Google Scholar] [CrossRef]
- Nguyen, C.M.; Chan, E.R.; Bergman, A.W.; Wetzstein, G. Diffusion in the dark: A diffusion model for low-light text recognition. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 4146–4157. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, K.; Zhang, Y.; Luo, W.; Stenger, B.; Lu, T.; Kim, T.K.; Liu, W. LLDiffusion: Learning degradation representations in diffusion models for low-light image enhancement. Pattern Recognit. 2025, 166, 111628. [Google Scholar] [CrossRef]
- Luo, Z.; Gustafsson, F.K.; Zhao, Z.; Sjölund, J.; Schön, T.B. Controlling vision-language models for multi-task image restoration. arXiv 2023, arXiv:2310.01018. [Google Scholar] [CrossRef]
- Zheng, D.; Wu, X.M.; Yang, S.; Zhang, J.; Hu, J.F.; Zheng, W.S. Selective hourglass mapping for universal image restoration based on diffusion model. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–18 June 2024; pp. 25445–25455. [Google Scholar] [CrossRef]
- Agustsson, E.; Timofte, R. Ntire 2017 challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 126–135. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Yang, J.; An, W.; Guo, Y. Flickr1024: A large-scale dataset for stereo image super-resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27–28 October 2019. [Google Scholar] [CrossRef]
- Karras, T.; Laine, S.; Aila, T. A style-based generator architecture for generative adversarial networks. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4217–4228. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive growing of gans for improved quality, stability, and variation. arXiv 2017, arXiv:1710.10196. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Alberi-Morel, M.L. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In Proceedings of the British Machine Vision Conference 2012, Surrey, UK, 3–7 September 2012. [Google Scholar] [CrossRef]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In International Conference on Curves and Surfaces; Springer: Berlin/Heidelberg, Germany, 2010; pp. 711–730. [Google Scholar] [CrossRef]
- Matsui, Y.; Ito, K.; Aramaki, Y.; Fujimoto, A.; Ogawa, T.; Yamasaki, T.; Aizawa, K. Sketch-based manga retrieval using manga109 dataset. Multimed. Tools Appl. 2017, 76, 21811–21838. [Google Scholar] [CrossRef]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar] [CrossRef]
- Wang, X.; Yu, K.; Dong, C.; Loy, C.C. Recovering realistic texture in image super-resolution by deep spatial feature transform. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 606–615. [Google Scholar] [CrossRef]
- Cai, J.; Zeng, H.; Yong, H.; Cao, Z.; Zhang, L. Toward real-world single image super-resolution: A new benchmark and a new model. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 3086–3095. [Google Scholar] [CrossRef]
- Wei, P.; Xie, Z.; Lu, H.; Zhan, Z.; Ye, Q.; Zuo, W.; Lin, L. Component divide-and-conquer for real-world image super-resolution. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 101–117. [Google Scholar] [CrossRef]
- Nah, S.; Hyun Kim, T.; Mu Lee, K. Deep multi-scale convolutional neural network for dynamic scene deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3883–3891. [Google Scholar] [CrossRef]
- Rim, J.; Lee, H.; Won, J.; Cho, S. Real-world blur dataset for learning and benchmarking deblurring algorithms. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 184–201. [Google Scholar] [CrossRef]
- Nah, S.; Baik, S.; Hong, S.; Moon, G.; Son, S.; Timofte, R.; Mu Lee, K. Ntire 2019 challenge on video deblurring and super-resolution: Dataset and study. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, W.; Lu, X.; Shen, J.; Ling, H.; Xu, T.; Shao, L. Human-aware motion deblurring. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 5572–5581. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Yang, J. Stacked conditional generative adversarial networks for jointly learning shadow detection and shadow removal. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1788–1797. [Google Scholar] [CrossRef]
- Qu, L.; Tian, J.; He, S.; Tang, Y.; Lau, R.W. Deshadownet: A multi-context embedding deep network for shadow removal. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4067–4075. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, L.; Pei, S.; Fu, H.; Qin, J.; Zhang, Q.; Wan, L.; Feng, W. From synthetic to real: Image dehazing collaborating with unlabeled real data. In Proceedings of the 29th ACM International Conference on Multimedia, Virtual, 20–24 October 2021; pp. 50–58. [Google Scholar] [CrossRef]
- Ancuti, C.O.; Ancuti, C.; Sbert, M.; Timofte, R. Dense-haze: A benchmark for image dehazing with dense-haze and haze-free images. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1014–1018. [Google Scholar] [CrossRef]
- Li, B.; Ren, W.; Fu, D.; Tao, D.; Feng, D.; Zeng, W.; Wang, Z. Benchmarking single-image dehazing and beyond. IEEE Trans. Image Process. 2018, 28, 492–505. [Google Scholar] [CrossRef] [PubMed]
- Golodetz, S.; Cavallari, T.; Lord, N.A.; Prisacariu, V.A.; Murray, D.W.; Torr, P.H. Collaborative large-scale dense 3d reconstruction with online inter-agent pose optimisation. IEEE Trans. Vis. Comput. Graph. 2018, 24, 2895–2905. [Google Scholar] [CrossRef]
- Liu, Y.F.; Jaw, D.W.; Huang, S.C.; Hwang, J.N. Desnownet: Context-aware deep network for snow removal. IEEE Trans. Image Process. 2018, 27, 3064–3073. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Fang, H.Y.; Ding, J.J.; Tsai, C.C.; Kuo, S.Y. JSTASR: Joint size and transparency-aware snow removal algorithm based on modified partial convolution and veiling effect removal. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 754–770. [Google Scholar] [CrossRef]
- Zhang, H.; Sindagi, V.; Patel, V.M. Image de-raining using a conditional generative adversarial network. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 3943–3956. [Google Scholar] [CrossRef]
- Fu, X.; Huang, J.; Zeng, D.; Huang, Y.; Ding, X.; Paisley, J. Removing rain from single images via a deep detail network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3855–3863. [Google Scholar] [CrossRef]
- Qian, R.; Tan, R.T.; Yang, W.; Su, J.; Liu, J. Attentive generative adversarial network for raindrop removal from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2482–2491. [Google Scholar] [CrossRef]
- Li, R.; Cheong, L.F.; Tan, R.T. Heavy rain image restoration: Integrating physics model and conditional adversarial learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 1633–1642. [Google Scholar] [CrossRef]
- Wang, T.; Yang, X.; Xu, K.; Chen, S.; Zhang, Q.; Lau, R.W. Spatial attentive single-image deraining with a high quality real rain dataset. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 12270–12279. [Google Scholar] [CrossRef]
- Gu, S.; Lugmayr, A.; Danelljan, M.; Fritsche, M.; Lamour, J.; Timofte, R. Div8k: Diverse 8k resolution image dataset. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 3512–3516. [Google Scholar] [CrossRef]
- López-Cifuentes, A.; Escudero-Vinolo, M.; Bescós, J.; García-Martín, Á. Semantic-aware scene recognition. Pattern Recognit. 2020, 102, 107256. [Google Scholar] [CrossRef]
- Huang, G.B.; Mattar, M.; Berg, T.; Learned-Miller, E. Labeled faces in the wild: A database forstudying face recognition in unconstrained environments. In Proceedings of the Workshop on Faces in ‘Real-Life’ Images: Detection, Alignment, and Recognition, Marseille, France, 17 October 2008; Available online: https://inria.hal.science/inria-00321923/ (accessed on 10 May 2025).
- Choi, Y.; Uh, Y.; Yoo, J.; Ha, J.W. Stargan v2: Diverse image synthesis for multiple domains. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8188–8197. [Google Scholar] [CrossRef]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Proceedings Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 416–423. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Buades, A.; Li, X. Color demosaicking by local directional interpolation and nonlocal adaptive thresholding. J. Electron. Imaging 2011, 20, 023016. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar] [CrossRef]
- Ding, K.; Ma, K.; Wang, S.; Simoncelli, E.P. Image quality assessment: Unifying structure and texture similarity. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 2567–2581. [Google Scholar] [CrossRef]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. Adv. Neural Inf. Process. Syst. 2017, 30, 6629–6640. Available online: https://proceedings.neurips.cc/paper/2017/hash/8a1d694707eb0fefe65871369074926d-Abstract.html (accessed on 10 May 2025).
- Bińkowski, M.; Sutherland, D.J.; Arbel, M.; Gretton, A. Demystifying mmd gans. arXiv 2018, arXiv:1801.01401. [Google Scholar] [CrossRef]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “completely blind” image quality analyzer. IEEE Signal Process. Lett. 2012, 20, 209–212. [Google Scholar] [CrossRef]
- Blau, Y.; Mechrez, R.; Timofte, R.; Michaeli, T.; Zelnik-Manor, L. The 2018 PIRM challenge on perceptual image super-resolution. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar] [CrossRef]
- Salimans, T.; Ho, J. Progressive distillation for fast sampling of diffusion models. arXiv 2022, arXiv:2202.00512. [Google Scholar] [CrossRef]
- Xiang, Q.; Zhang, M.; Shang, Y.; Wu, J.; Yan, Y.; Nie, L. Dkdm: Data-free knowledge distillation for diffusion models with any architecture. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, TN, USA, 11–15 June 2025; pp. 2955–2965. Available online: https://cvpr.thecvf.com/virtual/2025/poster/33250 (accessed on 12 June 2025).
- Bao, F.; Nie, S.; Xue, K.; Cao, Y.; Li, C.; Su, H.; Zhu, J. All are worth words: A vit backbone for diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 22669–22679. [Google Scholar] [CrossRef]


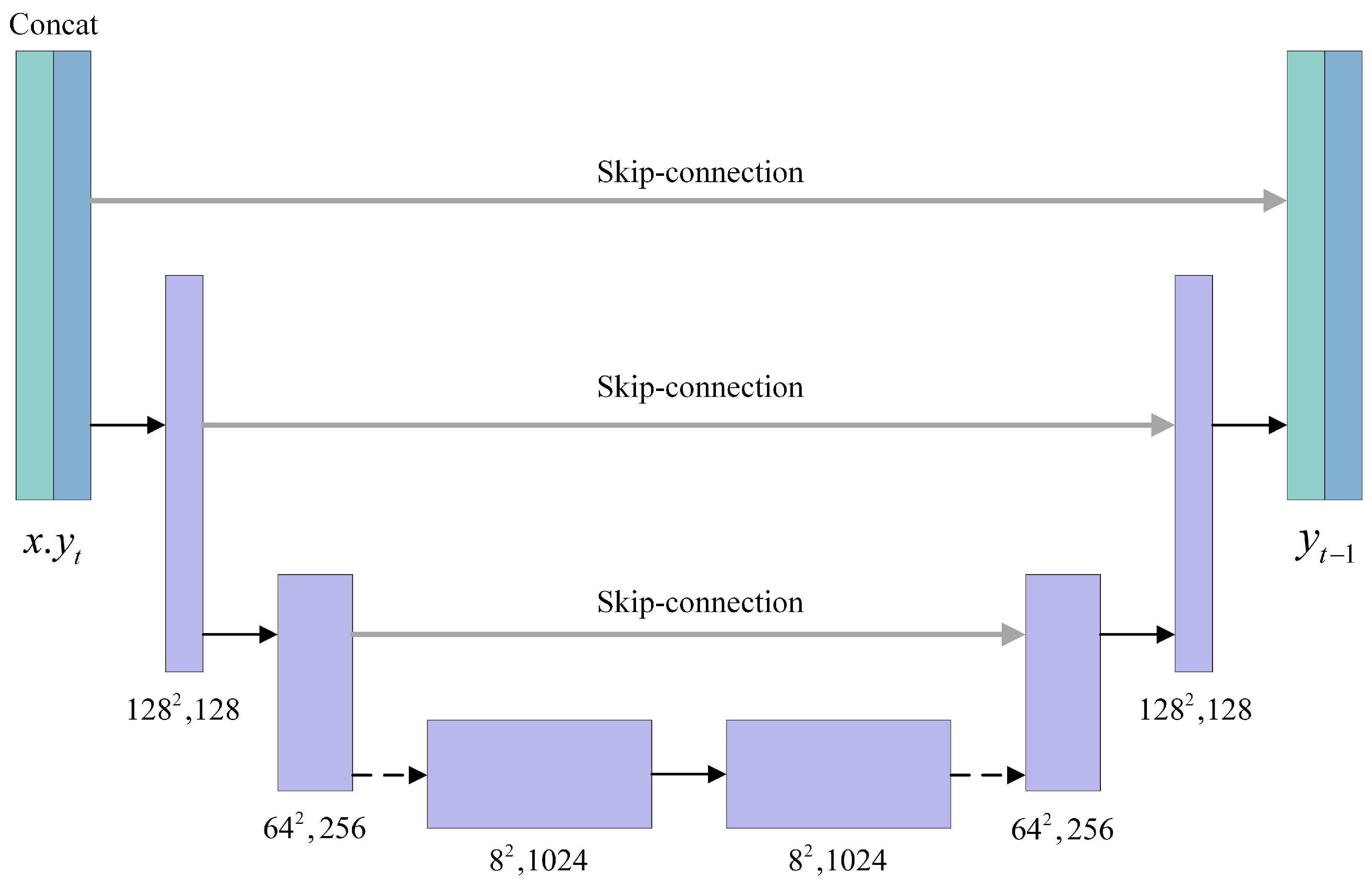



| Model | Year | Structure | Method | Contribute | Limitation |
|---|---|---|---|---|---|
| SR3 [29] | 2022 | U-Net | Channel concatenation is performed in DDPM, followed by iterative upsampling. More text here to show wrapping. Even more text. | The first use of DDPM for SR work. This contribution could be a bit longer to demonstrate how text wraps. | Cannot effectively handle severely degraded LR images. This limitation might also be a sentence or two. |
| SRdiff [57] | 2022 | CNN + ResNet | DDPM uses the LR image encoding as input for both forward diffusion and reverse SR image reconstruction. | Using a pre-trained encoder to extract information from the LR image. | Sensitive to conditional guidance. |
| CDPMSR [36] | 2023 | U-Net | The LR image is passed through a pre-trained SR model, generating a conditional vector. | First-time use of conditional diffusion models for single i-mage SR reconstruction. | Sensitive to noise in the input image. |
| Res-diff [59] | 2024 | CNN + U-Net | Adopt a residual learning strategy to fuse features from a pre-trained CNN and the diffusion model. | Fusing features extracted by two models to enhance task performance. | Limited effectiveness in real-world complex scenes. |
| SDE-SR [60] | 2022 | U-Net | Encode facial features into vectors and reconstruct them using an SDE solver. | This is the first application of SDE to facial super-resolution. | Training HR images is time-consuming. |
| LDM [18] | 2022 | U-Net + GAN | Diffusion occurs in the latent space. | Image attributes are controlled by the latent vector’s dimensions. | Image quality is limited by training data. |
| CDM [56] | 2022 | U-Net | Multiple diffusion models are cascaded, each generating different image detail levels. | Leveraging multi-level image details to generate high-quality images. | Involves multiple diffusion models |
| SR3+ [61] | 2023 | U-Net + CNN | Encode the LR image into a conditional vector, used at each time step of reverse generation. | Real-world SR image reconstruction tasks are addressed. | Sensitive to the real-world training set. |
| IDM [40] | 2023 | U-Net + CNN | Implicit diffusion processes use continuous ODEs. | Generate super-resolution images at continuous scales. | Generated images show artifacts. |
| Stable-SR [58] | 2024 | U-Net | Utilize feature maps at different scales to fine-tune the pre-trained Stable Diffusion. | Enhance the model’s adaptability to real-world images. | Additional training is required for specific scenarios. |
| ILVR [55] | 2021 | U-Net + CNN | Projection contrast, apply the error vector to the latent space, and iteratively adjust the latent variables. | Select the conditional injection method based on the task and conditional information. | The diversity of the images is insufficient. |
| Model | Year | Structure | Method | Contribute | Limitation |
|---|---|---|---|---|---|
| Deblur-DPM [62] | 2022 | U-Net + CNN | A DDPM generates and refines a blurry image to produce the final output. | Effectively handles various types of blur. | The model exhibits weak generalization performance. |
| DG-DPM [63] | 2022 | U-Net + CNN | Conditional guidance directs a diffusion model’s deblurring process. | Processes real-world blurred images. | Image details are lost or artifacts are present. |
| BlindDPS [44] | 2023 | U-Net + CNN | Two parallel diffusion models separately model the blur kernel and the image. | Handles blind deblurring without prior knowledge. | Overly reliant on blur kernel data. |
| DiffIR [26] | 2023 | U-Net + Transformer | Image priors from pre-training guide DIRformer’s deblurring. | Transformer structure improves restoration results. | Overly reliant on specific-scenario data. |
| InDI [64] | 2023 | CNN | An inversion network learns alternative deblurring to diffusion models. | The model is simple and quick to train. | Restorations are prone to artifacts. |
| SNIPS [65] | 2021 | U-Net | Spectral SVD reduces dimensions; then a network restores images. | Without any prior knowledge. | Model training converges poorly. |
| DDRM [48] | 2022 | U-Net | Obtains accurate restored images with fewer sampling steps. | Improves the inference efficiency of the model. | Restored images still have blur. |
| Gibbs-DDRM [45] | 2023 | U-Net + CNN | Sampling divides variables into fixed and sampled subsets. | Effectively reduces the computational cost. | The model is complex and prone to overfitting. |
| Model | Year | Structure | Method | Contribute | Limitation |
|---|---|---|---|---|---|
| Repaint [54] | 2022 | U-Net + CNN | Degraded image regions are separately noised; their fusion is the denoising input. | Diffusion models are first applied to image inpainting. | Overly reliant on occluded region complexity. |
| COPAINT [66] | 2023 | U-Net + CNN | Conditional guidance uses damaged image mask features. | DDIM is first applied to image inpainting. | Sensitive to occlusion masks. |
| Palette [30] | 2022 | U-Net + CNN | Image inpainting uses image translation conditioned on a target style. | Restored image details and texture improved. | Reliant on target style image. |
| CCDF [67] | 2022 | U-Net | Stochastic SDE contraction theory explains and optimizes conditional diffusion. | Decrease the iterations of the diffusion process. | The model fails to speed up diffusion. |
| Dirac-Diffusion [68] | 2024 | U-Net + CNN | Incremental reconstruction ensures step-wise consistency. | Improves the robustness of the model. | Sensitive to constraint settings. |
| RED-Diff [69] | 2023 | U-Net + CNN | Variational inference is used to optimizes the diffusion model. | Effectively handles linear inverse problems and improves interpretability. | The model tends to overfit easily. |
| Model | Year | Structure | Method | Contribute | Limitation |
|---|---|---|---|---|---|
| Weather-Diff [70] | 2023 | U-Net + CNN | The diffusion model inputs small image patches. | First use of diffusion models for adverse-weather image restoration. | Inappropriate patch division yields poor restorations. |
| Rain-Diffusion [52] | 2023 | U-Net + CNN | Cycle-consistent pairs train a degraded conditional diffusion model. | This is the first use of diffusion models for image deraining. | The model tends to overfit easily. |
| Refusion [47] | 2023 | U-Net + CNN | Latent vectors are compressed, reduced, and then diffused. | Achieves large-scale real-world image dehazing. | The model struggles with varied restoration. |
| IR-SDE [71] | 2023 | CNN | Image generation is described by a mean-reverting SDE. | First use of mean-reverting SDE for deraining and dehazing. | Severely degraded images are challenging. |
| SUD2 [72] | 2023 | U-Net | Training is conducted with fewer training data pairs. | The restoration effect is better for complex scenes. | Sensitive to DDPM training quality. |
| Application | Model | PSNR | SSIM | LPIPS | FID |
|---|---|---|---|---|---|
| Image Super-Resolution | SR3 [29] | 26.4 | 0.762 | - | 5.2 |
| Res-diff [59] | 27.94 | 0.72 | - | 106.71 | |
| LDM [18] | 25.8 | 0.74 | - | 4.4 | |
| Stable-SR [58] | 24.17 | 0.62 | 0.30 | 24.10 | |
| Image Deblurring | DeblurDPM [62] | 33.23 | 0.963 | 0.078 | 17.46 |
| DiffIR [26] | 33.20 | 0.963 | - | - | |
| InDI [64] | 31.49 | 0.946 | 0.058 | 3.55 | |
| DDRM [45] | 35.64 | 0.95 | 0.71 | 20 | |
| Image Inpainting | Repaint [54] | - | - | 0.12 | - |
| COPAINT [66] | - | - | 0.18 | - | |
| Palette [30] | - | - | - | 5.2 | |
| DiracDiffusion [68] | 28.92 | 0.8958 | 0.1676 | 38.25 | |
| Image Deraining | WeatherDiff [70] | 30.71 | 0.93 | - | - |
| Raindiffusion [52] | 36.85 | 0.97 | - | - | |
| IR-SDE [71] | 38.30 | 0.98 | 0.014 | 7.9 | |
| Image Desnowing | WeatherDiff [70] | 35.83 | 0.96 | - | - |
| IR-SDE [71] | 31.65 | 0.90 | 0.047 | 18.64 | |
| Image Dehazing | DA-CLIP [80] | 31.39 | 0.98 | - | - |
| DiffUIR [81] | 31.14 | 0.90 | - | - | |
| IR-SDE [71] | 30.70 | 0.90 | 0.064 | 6.32 | |
| Image Denoising | DA-CLIP [80] | 24.36 | 0.58 | 0.272 | 64.71 |
| IR-SDE [71] | 28.09 | 0.79 | 0.101 | 36.49 | |
| DDRM [45] | 25.21 | 0.66 | 12.43 | 20 | |
| Low-Light Enhancement | WaveDiff [76] | 28.86 | 0.876 | 0.207 | 45.359 |
| DiD [78] | 23.97 | 0.84 | 0.12 | - | |
| LLDiffusion [79] | 31.77 | 0.902 | 0.040 | - |
| Application | Dataset | Year | Training Set | Test Set | Characteristic |
|---|---|---|---|---|---|
| Image Super-Resolution | DIV2K [82] | 2017 | 800 | 100 | 2 K resolution |
| Flickr2K [83] | 2017 | 2650 | - | 2 K resolution | |
| Set5 [86] | 2012 | - | 5 | 5 image classes | |
| Set14 [87] | 2012 | - | 14 | 14 image classes | |
| Manga109 [88] | 2015 | - | 109 | 109 comic images | |
| Urban100 [89] | 2015 | - | 100 | 100 urban images | |
| OST300 [90] | 2018 | - | 300 | Outdoor scene images | |
| DIV8K [111] | 2019 | 1304 | 100 | 8 K resolution | |
| RealSR [91] | 2019 | 565 | 30 | Real-world images | |
| DRealSR [92] | 2020 | 884 | 83 | Large-scale dataset | |
| Image Deblurring | GoPro [93] | 2017 | 2103 | 1111 | 1280 × 720 blur images |
| HIDE [96] | 2019 | 6397 | 2025 | Clear and blurred image pairs | |
| RealBlur [94] | 2020 | 3758 | 980 | 182 different scenes | |
| Image Inpainting | ImageNet [85] | 2010 | 1,281,167 | 100,000 | 1000 classes of images |
| Places365 [112] | 2019 | 1,800,000 | 36,000 | 434 classes of scenes | |
| LFW [113] | 2008 | 13,233 | - | 1080 website facial images | |
| FFHQ [84] | 2019 | 70,000 | - | face images | |
| Celeba-HQ [86] | 2018 | 30,000 | - | face images | |
| AFHQ [114] | 2020 | 15,000 | - | animal face images | |
| CelebA [86] | 2015 | 202,599 | - | images | |
| Image Deraining Desnowing and Dehazing | RainDrop [108] | 2018 | 1119 | - | Various rainy scenes |
| Outdoor-Rain [109] | 2019 | 9000 | 1500 | Outdoor rainy images | |
| DDN-data [107] | 2017 | 9100 | 4900 | Real-world clear/rainy image pairs | |
| SPA-data [110] | 2019 | 295,000 | 1000 | Various natural rainy scenes | |
| CSD [103] | 2021 | 8000 | 2000 | Large-scale snowy dataset | |
| Snow100k [104] | 2017 | 50,000 | 50,000 | 1369 real snowy scene images | |
| SRRS [105] | 2020 | 25,000 | - | Online real-world scenes | |
| Haze-4K [100] | 2021 | 4000 | - | Indoor-outdoor hazy scenes | |
| Dense-Haze [101] | 2019 | 33 | - | Outdoor hazy scenes | |
| RESIDE [102] | 2019 | 443,950 | 5342 | Real-world hazy images | |
| Image Denoising | CBSD68 [115] | 2001 | - | 68 | Various noise levels |
| McMaster [116] | 2011 | - | 18 | Crop size: |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, H.; Li, Y.; Zhang, H. A Comprehensive Review of Image Restoration Research Based on Diffusion Models. Mathematics 2025, 13, 2079. https://doi.org/10.3390/math13132079
Li J, Wang H, Li Y, Zhang H. A Comprehensive Review of Image Restoration Research Based on Diffusion Models. Mathematics. 2025; 13(13):2079. https://doi.org/10.3390/math13132079
Chicago/Turabian StyleLi, Jun, Heran Wang, Yingjie Li, and Haochuan Zhang. 2025. "A Comprehensive Review of Image Restoration Research Based on Diffusion Models" Mathematics 13, no. 13: 2079. https://doi.org/10.3390/math13132079
APA StyleLi, J., Wang, H., Li, Y., & Zhang, H. (2025). A Comprehensive Review of Image Restoration Research Based on Diffusion Models. Mathematics, 13(13), 2079. https://doi.org/10.3390/math13132079






