Quasi-Irreducibility of Nonnegative Biquadratic Tensors

Abstract

While the adjacency tensor of a bipartite 2-graph is a nonnegative biquadratic tensor, it is inherently reducible. To address this limitation, we introduce the concept of quasi-irreducibility in this paper. The adjacency tensor of a bipartite 2-graph is quasi-irreducible if that bipartite 2-graph is not bi-separable. This new concept reveals important spectral properties: although all M⁺-eigenvalues are M⁺⁺-eigenvalues for irreducible nonnegative biquadratic tensors, the M⁺-eigenvalues of a quasi-irreducible nonnegative biquadratic tensor can be either M⁰-eigenvalues or M⁺⁺-eigenvalues. Furthermore, we establish a max-min theorem for the M-spectral radius of a nonnegative biquadratic tensor.

1. Introduction

Nonnegative biquadratic tensors emerge naturally in the spectral analysis of bipartite 2-graphs and multilayer networks, two important extensions of classical graph theory that significantly enhance modeling capabilities for complex systems. Bipartite 2-graphs [1] are characterized by a vertex set partitioned into two distinct classes, with connections permitted only between (not within) these groups. Each hyperedge in such graphs connects exactly two vertices from each partition, making this structure particularly valuable for modeling optimization problems including optimal assignments and co-clustering applications. Multilayer networks [2,3], on the other hand, provide a more flexible framework by incorporating multiple relationship types across different network layers. These layers may encode diverse interaction modalities or temporal evolution patterns, rendering them particularly useful in domains ranging from social network analysis to transportation systems and biological network modeling.

Very recently, Cui and Qi [4] studied the spectral properties of nonnegative biquadratic tensors. They showed that a nonnegative biquadratic tensor has at least one M⁺-eigenvalue, i.e., an M-eigenvalue with a pair of nonnegative M-eigenvectors. The largest M-eigenvalue of a nonnegative biquadratic tensor is an M⁺-eigenvalue. It is also the M-spectral radius of that tensor. All the M⁺-eigenvalues of an irreducible nonnegative biquadratic tensor are M⁺⁺-eigenvalues, i.e., M-eigenvalues with positive M-eigenvector pairs. For an irreducible nonnegative biquadratic tensor, the largest M⁺-eigenvalue has a max-min characterization, while the smallest M⁺-eigenvalue has a min-max characterization. A Collatz algorithm for computing the largest M⁺-eigenvalues was proposed, and numerical results were reported in [4]. These results enriched the theories of nonnegative tensors.

Irreducibility plays an important role in the theoretical analysis of nonnegative matrices and tensors. However, for nonnegative tensors arising from spectral hypergraph theory, irreducibility is too strong [1]. Then, weak irreducibility introduced by Friedland, Gaubert, and Han [5] was adopted as an alternative. However, we found that the direct extension of weak irreducibility to biquadratic tensors is too weak to produce useful results. Consequently, in this paper, we propose the concept of quasi-irreducibility, which provides a more appropriate framework for studying biquadratic tensors. Our definition is motivated by bipartite 2-graphs and the concepts of x- and y-reducibility proposed in [6].

In particular, we establish that the M⁺-eigenvalues of quasi-irreducible nonnegative biquadratic tensors can be precisely classified as either M⁰-eigenvalues or M⁺⁺-eigenvalues. This finding generalizes the known result for irreducible nonnegative biquadratic tensors (all the M⁺-eigenvalues are M⁺⁺-eigenvalues) to the broader class of reducible cases. Furthermore, we generalize the max-min theorem for the M-spectral radius from irreducible to reducible nonnegative biquadratic tensors.

In the next section, we present some preliminary knowledge for this paper. In Section 3, we study bipartite 2-graphs. We introduce quasi-irreducibility and M⁰-eigenvalues of nonnegative biquadratic tensors in Section 4. We show there that the adjacency tensors of bipartite 2-graphs that are not bi-separable are quasi-irreducible. We further prove that M⁺-eigenvalues of quasi-irreducible nonnegative biquadratic tensors are either M⁰-eigenvalues or M⁺⁺-eigenvalues. In Section 5, we establish a max-min theorem for the M-spectral radius of a nonnegative biquadratic tensor. In Section 6, we discuss the problem of computing the largest M-eigenvalue of a nonnegative biquadratic tensor.

2. Preliminaries

Let m and n be integers greater than 1. Denote $\left[n\right]:=\{1,\dots ,n\}$. A real fourth-order tensor $\mathcal{A}=\left(a_{i_1{j}_1{i}_2{j}_2}\right)\in {\mathbb{R}}^{m\times n\times m\times n}$ is said to be a biquadratic tensor. If for $i_1,i_2\in \left[m\right]$ and $j_1,j_2\in \left[n\right]$,

$$a_{i_1{j}_1{i}_2{j}_2}=a_{i_2{j}_2{i}_1{j}_1},$$

then $\mathcal{A}$ is said to be weakly symmetric. Furthermore, if for $i_1,i_2\in \left[m\right]$ and $j_1,j_2\in \left[n\right]$,

$$a_{i_1{j}_1{i}_2{j}_2}=a_{i_2{j}_1{i}_1{j}_2}=a_{i_1{j}_2{i}_2{j}_1},$$

then $\mathcal{A}$ is said to be symmetric. Let $BQ(m,n)$ and $NBQ(m,n)$ denote the sets of all biquadratic tensors and nonnegative biquadratic tensors in ${\mathbb{R}}^{m\times n\times m\times n}$, respectively.

A biquadratic tensor $\mathcal{A}\in BQ(m,n)$ is said to be positive semi-definite if for any $\mathbf{x}\in {\mathbb{R}}^m$ and $\mathbf{y}\in {\mathbb{R}}^n$,

$$f(\mathbf{x},\mathbf{y})\equiv \langle \mathcal{A},\mathbf{x}\circ \mathbf{y}\circ \mathbf{x}\circ \mathbf{y}\rangle \equiv {\displaystyle \sum _{i_1,i_2=1}^m}{\displaystyle \sum _{j_1,j_2=1}^n}{a}_{i_1{j}_1{i}_2{j}_2}{x}_{i_1}{y}_{j_1}{x}_{i_2}{y}_{j_2}\ge 0,$$

(1)

and it is said to be positive definite if for any $\mathbf{x}\in {\mathbb{R}}^m, {\mathbf{x}}^{\top }\mathbf{x}=1$ and $\mathbf{y}\in {\mathbb{R}}^n, {\mathbf{y}}^{\top }\mathbf{y}=1$,

$$f(\mathbf{x},\mathbf{y})>0.$$

The biquadratic tensor $\mathcal{A}$ is called an SOS (sum-of-squares) biquadratic tensor if $f(\mathbf{x},\mathbf{y})$ can be written as a sum of squares.

In 2009, Qi, Dai, and Han [7] introduced M-eigenvalues and M-eigenvectors for symmetric biquadratic tensors during their investigation of the strong ellipticity condition of the elastic tensor in solid mechanics. Recently, Qi and Cui [6] generalized M-eigenvalues to general (nonsymmetric) biquadratic tensors. This definition was motivated by the study of covariance tensors in statistics [8], which are not symmetric (only weakly symmetric), yet it remains positive semi-definite.

Suppose that $\mathcal{A}=\left(a_{i_1{j}_1{i}_2{j}_2}\right)\in BQ(m,n)$. A real number $\lambda$ is said to be an M-eigenvalue of $\mathcal{A}$ if there are real vectors $\mathbf{x}={(x_1,\dots ,x_m)}^{\top }\in {\mathbb{R}}^m,\mathbf{y}={(y_1,\dots ,y_n)}^{\top }\in {\mathbb{R}}^n$ such that the following equations are satisfied: For any $i\in \left[m\right]$,

$${\displaystyle \sum _{i_1=1}^m}{\displaystyle \sum _{j_1,j_2=1}^n}{a}_{i_1{j}_{1}i{j}_2}{x}_{i_1}{y}_{j_1}{y}_{j_2}+{\displaystyle \sum _{i_2=1}^m}{\displaystyle \sum _{j_1,j_2=1}^n}{a}_{i{j}_1{i}_2{j}_2}{y}_{j_1}{x}_{i_2}{y}_{j_2}=2\lambda x_i;$$

(2)

for any $j\in \left[n\right]$,

$${\displaystyle \sum _{i_1,i_2=1}^m}{\displaystyle \sum _{j_1=1}^n}{a}_{i_1{j}_1{i}_{2}j}{x}_{i_1}{y}_{j_1}{x}_{i_2}+{\displaystyle \sum _{i_1,i_2=1}^m}{\displaystyle \sum _{j_2=1}^n}{a}_{i_{1}j{i}_2{j}_2}{x}_{i_1}{x}_{i_2}{y}_{j_2}=2\lambda y_j;$$

(3)

and

$${\mathbf{x}}^{\top }\mathbf{x}={\mathbf{y}}^{\top }\mathbf{y}=1.$$

(4)

Then, $\mathbf{x}$ and $\mathbf{y}$ are called the corresponding M-eigenvectors. We may rewrite Equations (2) and (3) as ${\displaystyle \frac{1}{2}}\mathcal{A}·\mathbf{y}\mathbf{x}\mathbf{y}+{\displaystyle \frac{1}{2}}\mathcal{A}\mathbf{x}\mathbf{y}·\mathbf{y}=\lambda \mathbf{x}$ and ${\displaystyle \frac{1}{2}}\mathcal{A}\mathbf{x}·\mathbf{x}\mathbf{y}+{\displaystyle \frac{1}{2}}\mathcal{A}\mathbf{x}\mathbf{y}\mathbf{x}·=\lambda \mathbf{y}$, respectively.

The following theorem was established in [6].

Theorem 1.

Suppose that $\mathcal{A}\in BQ(m,n)$. Then, $\mathcal{A}$ always has M-eigenvalues. Furthermore, $\mathcal{A}$ is positive semi-definite if and only if all of its M-eigenvalues are nonnegative, and $\mathcal{A}$ is positive definite if and only if all of its M-eigenvalues are positive.

Let $\mathcal{A}\in BQ(m,n)$ and ${\lambda }_{max}\left(\mathcal{A}\right)$ be the largest M-eigenvalue of $\mathcal{A}$. Then, we have

$${\lambda }_{max}\left(\mathcal{A}\right)=max\{f(\mathbf{x},\mathbf{y}):{\mathbf{x}}^{\top }\mathbf{x}={\mathbf{y}}^{\top }\mathbf{y}=1 ,\mathbf{x}\in {\mathbb{R}}^m, \mathbf{y}\in {\mathbb{R}}^n\}.$$

(5)

We define the M-spectral radius of $\mathcal{A}$, denoted by ${\rho }_M\left(\mathcal{A}\right)$, to be the maximum absolute value among all M-eigenvalues of $\mathcal{A}$. Suppose that $\lambda$ is an M-eigenvalue of $\mathcal{A}$ associated with a pair of nonnegative M-eigenvectors $\mathbf{x}\in {\mathbb{R}}_{+}^m$ and $\mathbf{y}\in {\mathbb{R}}_{+}^n$. Then, $\lambda$ is also nonnegative, i.e., $\lambda \ge 0$. We call $\lambda$ an M⁺-eigenvalue of $\mathcal{A}$. Furthermore, if both $\mathbf{x}$ and $\mathbf{y}$ are positive, we call $\lambda$ an M⁺⁺-eigenvalue of $\mathcal{A}$.

The following theorems, which form the weak Perron–Frobenius theorem of irreducible nonnegative biquadratic tensors, were established in [4].

Theorem 2.

Let $\mathcal{A}=\left(a_{i_1{j}_1{i}_2{j}_2}\right)\in NBQ(m,n)$, where $m,n\ge 2$. Then, we have

$${\rho }_M\left(\mathcal{A}\right)={\lambda }_{max}\left(\mathcal{A}\right),$$

(6)

and ${\lambda }_{max}\left(\mathcal{A}\right)$ is an M⁺-eigenvalue of $\mathcal{A}$. Consequently, $\mathcal{A}$ has at least one M⁺-eigenvalue.

Theorem 3.

Suppose that $\mathcal{A}=\left(a_{i_1{j}_1{i}_2{j}_2}\right)\in NBQ(m,n)$ is irreducible, where $m,n\ge 2$. Assume that λ is an M⁺ eigenvalue of $\mathcal{A}$ with nonnegative M-eigenvector $\{\overline{\mathbf{x}},\overline{\mathbf{y}}\}$. Then, λ is a positive M⁺⁺-eigenvalue. Consequently, $\mathcal{A}$ has at least one M⁺⁺-eigenvalue.

3. Bipartite 2-Graphs

A bipartite hypergraph $G=(S,T,E)$ has two vertex sets $S=\{u_1,u_2,\dots ,u_m\}$, $T=\{v_1,v_2,\dots ,v_n\}$ and an edge set $E=\{e_1,e_2,\dots ,e_p\}$. An edge $e_l=(s_l,t_l)$ of G consists of a subset $s_l\subset S$ and a subset $t_l\subset T$. Assume that there are no two edges with the same subset pair of S and T. Bipartite hypergraphs are useful in the study of uniform hypergraphs [1,9,10].

Suppose that we have a bipartite hypergraph $G=(S,T,E)$. If for all edges $e_l=(s_l,t_l), l\in \left[p\right]$, $s_l$ and $t_l$ have the same cardinality k, then G is called a bipartite uniform hypergraph or a bipartite k-graph. In particular, a bipartite 1-graph is simply called a bipartite graph, which has been studied extensively. We now study bipartite 2-graphs.

Let $G=(S,T,E)$ be a bipartite 2-graph. We may express G by a biquadratic tensor $\mathcal{A}=\left(a_{i_1{j}_1{i}_2{j}_2}\right)\in NBQ(m,n)$ as follows:

$$a_{i_1{j}_1{i}_2{j}_2}=\left\{\begin{array}{cc}1,& \mathrm{if}{e}_{i_1{j}_1{i}_2{j}_2}=(s_{i_1{i}_2},t_{j_1{j}_2})\in E;\hfill \\ 0,& \mathrm{otherwise},\hfill \end{array}\right.$$

(7)

where $s_{i_1{i}_2}=(i_1,i_2)$ and $t_{j_1{j}_2}=(j_1,j_2)$. Then, $\mathcal{A}$ is a symmetric nonnegative biquadratic tensor. If, in addition, there is a nonnegative valued function $\phi :E\to {\mathbb{R}}_{+}$ for the weighted graph $G=(S,T,E,\phi )$, we may define the adjacency tensor $\mathcal{A}$ as follows:

$$a_{i_1{j}_1{i}_2{j}_2}=\left\{\begin{array}{cc}\phi \left(e_{i_1{j}_1{i}_2{j}_2}\right),& \mathrm{if}{e}_{i_1{j}_1{i}_2{j}_2}=(s_{i_1{i}_2},t_{j_1{j}_2})\in E;\hfill \\ 0,& \mathrm{otherwise},\hfill \end{array}\right.$$

(8)

where $s_{i_1{i}_2}=(i_1,i_2)$ and $t_{j_1{j}_2}=(j_1,j_2)$. Then, $\mathcal{A}$ is still a nonnegative biquadratic tensor.

Based on [4], a biquadratic tensor $\mathcal{A}=\left(a_{i_1{j}_1{i}_2{j}_2}\right)\in BQ(m,n)$ is reducible if it is either x-reducible, i.e., there is a nonempty proper index subset $J_x⊊\left[m\right]$ and a proper index $j\in \left[n\right]$ such that

$$a_{i_{2}j{i}_{1}j}+a_{i_{1}j{i}_{2}j}=0,\forall i_1\in J_x,\forall i_2\notin J_x,$$

(9)

or it is y-reducible, i.e., there is a proper index $i\in \left[m\right]$ and a nonempty proper index subset $J_y⊊\left[n\right]$ such that

$$a_{i{j}_{1}i{j}_2}+a_{i{j}_{2}i{j}_1}=0,\forall j_1\in J_y,\forall j_2\notin J_y.$$

(10)

Then, based on the definition of bipartite 2-graphs, their adjacency tensors are always reducible. Actually, according to our definition, for the entries of the adjacency tensor $\mathcal{A}=\left(a_{i_1{j}_1{i}_2{j}_2}\right)$ of a bipartite 2-graph G, we always have $a_{i_1{j}_1{i}_2{j}_2}=0$ if either $i_1=i_2$ or $j_1=j_2$. Therefore, the adjacency tensor $\mathcal{A}$ is always both x-reducible and y-reducible. Consequently, as in the nonnegative cubic tensor case, we have to consider weaker conditions.

Given a bipartite 2-graph $G=(S,T,E,\phi )$, we may also define its signless Laplacian biquadratic tensor as follows:

$$\mathcal{Q}={\mathcal{D}}^0+{\mathcal{D}}^x+{\mathcal{D}}^y+\mathcal{A}\in NBQ(m,n),$$

(11)

where $D^0=\left(d_{i_1{j}_1{i}_2{j}_2}^0\right)\in NBQ(m,n)$ is a diagonal biquadratic tensor with diagonal elements

$$d_{i_1{j}_1{i}_2{j}_2}^0=\left\{\begin{array}{cc}{\displaystyle \sum _{i_2^{\prime }=1}^m}{\displaystyle \sum _{j_2^{\prime }=1}^n}{a}_{i_1{j}_1{i}_2^{\prime }{j}_2^{\prime }},& \mathrm{if}{i}_1=i_2\mathrm{and}{j}_1=j_2;\hfill \\ 0,& \mathrm{otherwise},\hfill \end{array}\right.$$

(12)

and $D^x=\left(d_{i_1{j}_1{i}_2{j}_2}^x\right)\in NBQ(m,n)$ and $D^y=\left(d_{i_1{j}_1{i}_2{j}_2}^y\right)\in NBQ(m,n)$ are defined by

$$d_{i_1{j}_1{i}_2{j}_2}^x=\left\{\begin{array}{cc}{\displaystyle \sum _{i_2^{\prime }=1}^m}{a}_{i_1{j}_1{i}_2^{\prime }{j}_2},& \mathrm{if}{i}_1=i_2;\hfill \\ 0,& \mathrm{otherwise},\hfill \end{array}\right.$$

(13)

$$d_{i_1{j}_1{i}_2{j}_2}^y=\left\{\begin{array}{cc}{\displaystyle \sum _{j_2^{\prime }=1}^n}{a}_{i_1{j}_1{i}_2{j}_2^{\prime }},& \mathrm{if}{j}_1=j_2;\hfill \\ 0,& \mathrm{otherwise},\hfill \end{array}\right.$$

(14)

for all $i,i_1,i_2\in \left[m\right]$ and $j,j_1,j_2\in \left[n\right]$, respectively.

Similarly, we can define its Laplacian biquadratic tensor as follows:

$$\mathcal{L}={\mathcal{D}}^0-{\mathcal{D}}^x-{\mathcal{D}}^y+\mathcal{A}\in BQ(m,n).$$

(15)

Building upon the preceding definitions, we obtain the following lemma.

Lemma 1.

Given a weighted bipartite 2-graph $G=(S,T,E,\phi )$ with $\phi \ge 0$ and the adjacency matrix given by (8), both the signless Laplacian biquadratic tensor defined by (11) and the Laplacian biquadratic tensor defined by (15) are positive semi-definite and SOS.

Proof. 

For any $\mathbf{x}\in {\mathbb{R}}^m$ and $\mathbf{y}\in {\mathbb{R}}^n$, we have the following:

$$\begin{array}{cc}\hfill \mathcal{Q}\mathbf{x}\mathbf{y}\mathbf{x}\mathbf{y}=& ({\mathcal{D}}^0+{\mathcal{D}}^x+{\mathcal{D}}^y+\mathcal{A})\mathbf{x}\mathbf{y}\mathbf{x}\mathbf{y}\hfill \\ \hfill =& {\displaystyle \sum _{i_1,i_2=1}^m}{\displaystyle \sum _{j_1,j_2=1}^n}\left(a_{i_1{j}_1{i}_2{j}_2}{x}_{i_1}^2{y}_{j_1}^2+a_{i_1{j}_1{i}_2{j}_2}{x}_{i_1}{x}_{i_2}{y}_{j_1}^2+a_{i_1{j}_1{i}_2{j}_2}{x}_{i_1}^2{y}_{j_1}{y}_{j_2}+a_{i_1{j}_1{i}_2{j}_2}{x}_{i_1}{x}_{i_2}{y}_{j_1}{y}_{j_2}\right)\hfill \\ \hfill =& {\displaystyle \frac{1}{4}}{\displaystyle \sum _{i_1,i_2=1}^m}{\displaystyle \sum _{j_1,j_2=1}^n}{a}_{i_1{j}_1{i}_2{j}_2}{(x_{i_1}+x_{i_2})}^2{(y_{j_1}+y_{j_2})}^2.\hfill \end{array}$$

Similarly, we have the following:

$$\begin{array}{c}\hfill \mathcal{L}\mathbf{x}\mathbf{y}\mathbf{x}\mathbf{y}={\displaystyle \frac{1}{4}}{\displaystyle \sum _{i_1,i_2=1}^m}{\displaystyle \sum _{j_1,j_2=1}^n}{a}_{i_1{j}_1{i}_2{j}_2}{(x_{i_1}-x_{i_2})}^2{(y_{j_1}-y_{j_2})}^2.\end{array}$$

This completes the proof. □

Let us further examine the application backgrounds of bipartite 2-graphs $G=(S,T,E)$. We may think that S is a set of persons and T is a set of tools. Suppose that a working group requires exactly two persons, $i_1$ and $i_2$, and two tools, $j_1$ and $j_2$. While a working group consists of two persons and two tools, there exist compatibility constraints that prevent arbitrary pairs of persons and tools from forming valid groups. If two persons $i_1,i_2$ and two tools $j_1$ and $j_2$ can form a working group, then we say that edge $(i_1,i_2,j_1,j_2)$ is in E. We say that S is T-bi-separable if there exist a proper partition $(S_1,S_2)$ of S and two vertices $j_1,j_2\in T$ such that for all $i_1\in S_1$ and $i_2\in S_2$, $(i_1,i_2,j_1,j_2)\notin E$. Similarly, we say that T is S-bi-separable if there exist a proper partition $(T_1,T_2)$ of T and two vertices $i_1,i_2\in S$ such that for all $j_1\in T_1$ and $j_2\in T_2$, $(i_1,i_2,j_1,j_2)\notin E$. If S is T-bi-separable or T is S-bi-separable, then we say that G is bi-separable.

4. Quasi-Irreducible Nonnegative Biquadratic Tensors

Let $\mathcal{A}=\left(a_{i_1{j}_1{i}_2{j}_2}\right)\in NBQ(m,n)$. We say that $\mathcal{A}$ is quasi-reducible if it is either x-quasi-reducible, i.e., there is a nonempty proper index subset $J_x⊊\left[m\right]$ and two distinct indices $j_1,j_2\in \left[n\right]$, $j_1\ne j_2$ such that

$$a_{i_2{j}_1{i}_1{j}_2}+a_{i_1{j}_1{i}_2{j}_2}=0,\forall i_1\in J_x,\forall i_2\notin J_x,$$

(16)

or it is y-quasi-reducible, i.e., there are two distinct indices $i_1,i_2\in \left[m\right]$, $i_1\ne i_2$ and a nonempty proper index subset $J_y⊊\left[n\right]$ such that

$$a_{i_1{j}_1{i}_2{j}_2}+a_{i_1{j}_2{i}_2{j}_1}=0,\forall j_1\in J_y,\forall j_2\notin J_y.$$

(17)

We say that $\mathcal{A}$ is quasi-irreducible if it is not quasi-reducible.

In fact, if $j_1=j_2$ in Equation (16), then x-quasi-reducible becomes the x-reducible in [4]. Similarly, if $i_1=i_2$ in Equation (17), then y-quasi-reducible becomes the y-reducible in [4]. Take $m=n=2$ as an example. $\mathcal{A}\in NBQ(2,2)$ is x-reducible if

$$a_{1121}+a_{2111}>0\mathrm{and}{a}_{1222}+a_{2212}>0,$$

while $\mathcal{A}$ is x-quasi-reducible if

$$a_{1122}+a_{2112}>0\mathrm{and}{a}_{1221}+a_{2211}>0.$$

Thus, these two definitions are fundamentally distinct, with neither being a special case of the other. Our definition of quasi-irreducibility naturally encompasses hyperedges in bipartite 2-graphs, which in fact motivated our formulation. We illustrate the distinction between irreducible and quasi-irreducible nonnegative biquadratic tensors in the following two examples. Notably, an irreducible nonnegative biquadratic tensor may not be quasi-irreducible, and a quasi-irreducible nonnegative biquadratic tensor may not be irreducible.

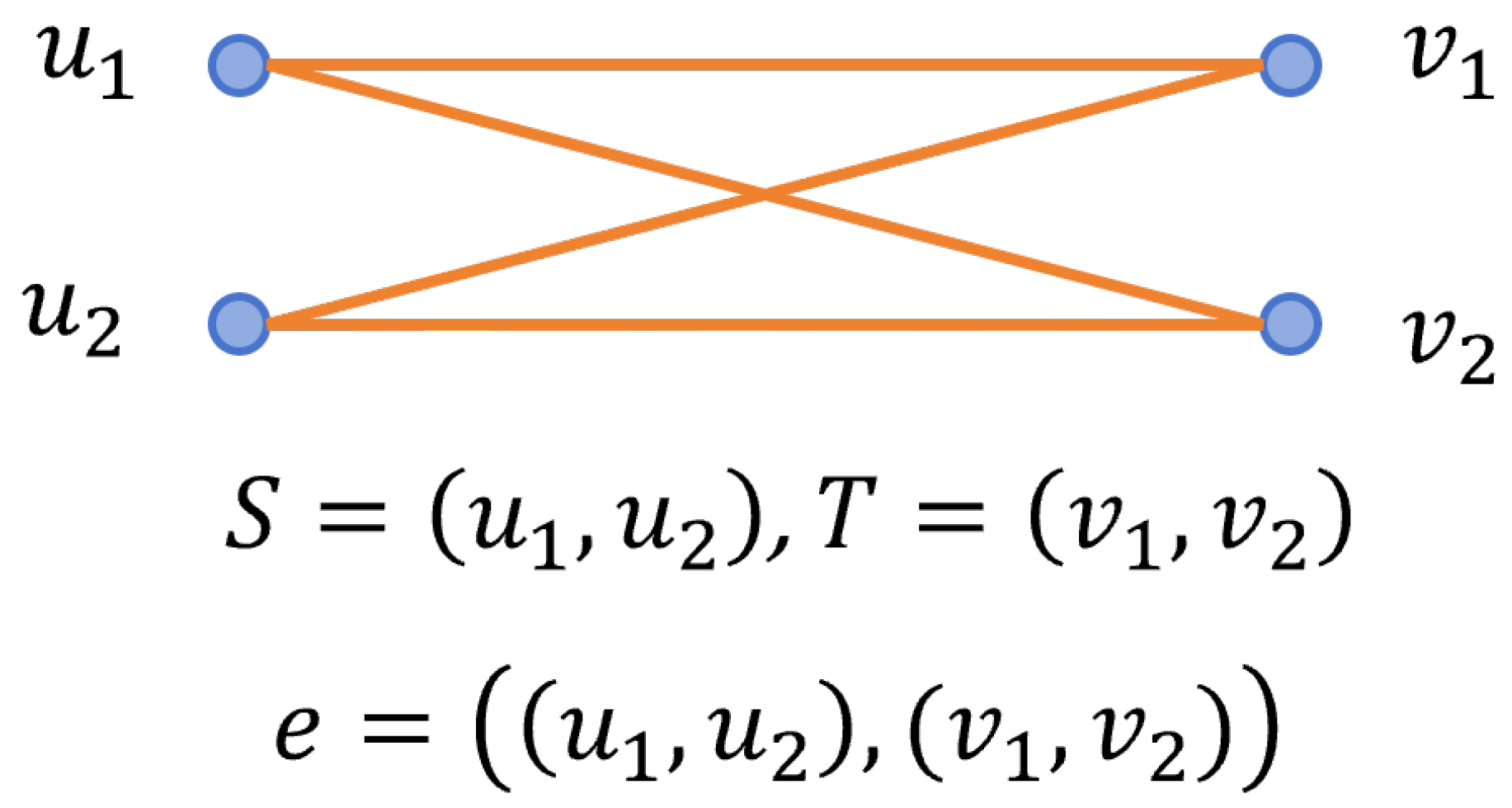
Example 1.

Let $S=\{u_1,u_2\}$, $T=\{v_1,v_2\}$, $e_1=(u_1,u_1,v_1,v_2)$, $e_2=(u_2,u_2,v_1,v_2)$, and $E=\{e_1,e_2\}$. Then, the adjacency tensor of G satisfies $\mathcal{A}=\left(a_{i_1{j}_1{i}_2{j}_2}\right)\in NBQ(2,2)$, $a_{1112}=a_{1211}=a_{2122}=a_{2221}=1$, and all other entries are equal to zero. It follows from (9) and (10) that $\mathcal{A}$ is irreducible. However, $\mathcal{A}$ is quasi-reducible since $a_{i_1{j}_1{i}_2{j}_2}=0$ for all $i_1\ne i_2$ and $j_1\ne j_2$.

Example 2.

Let $S=\{u_1,u_2\}$ and $T=\{v_1,v_2\}$ denote two sets of vertices, and let $e=(u_1,u_2,v_1,v_2)$ denote an edge, with $E=\left\{e\right\}$. Consider the bipartite 2-graph demonstrated in Figure 1 with $G=\{S,T,E\}$.

Then, the adjacency tensor $\mathcal{A}$ of G satisfies $a_{1122}=a_{1221}=a_{2112}=a_{2211}=1$, and all other entries are equal to zero. It follows from (16) and (17) that $\mathcal{A}$ is quasi-irreducible. However, $\mathcal{A}$ is reducible since $a_{i_1{j}_1{i}_2{j}_2}=0$ for all $i_1=i_2$ or $j_1=j_2$.

Very recently, Chen and Bu [2] studied the application backgrounds of biquadratic tensors on multilayer graphs/networks. As demonstrated in [3], the adjacency tensors of such multilayer networks constitute weakly symmetric biquadratic tensors. In this framework, intra-layer connectivity corresponds to the x-irreducibility of the adjacency tensor, while inter-layer connectivity relates to its y-irreducibility. Notably, a multilayer network is hyper-connected if and only if its corresponding adjacency tensor is irreducible.

However, these conventional definitions may impose overly strict conditions for certain multilayer network structures. To address this limitation, Chen and Bu [2] introduced three specialized network types: layer-coupled, vertex-coupled, and hyper-coupled multilayer networks. These classifications exhibit fundamental connections to the x-quasi-irreducibility, y-quasi-irreducibility, and quasi-irreducibility properties of their associated adjacency tensors proposed in this mauscript, respectively.

Properties of Quasi-Irreducible Biquadratic Tensors

We have the following propositions on bipartite 2-graphs that are not bi-separable.

Proposition 1.

Suppose that a bipartite 2-graph $G=(S,T,E)$ is not bi-separable, where $\left|S\right|\ge 2$ and $\left|T\right|\ge 2$, and $\mathcal{A}$ is the adjacency tensor of G. Then, $\mathcal{A}$ is a quasi-irreducible biquadratic tensor.

Proof. 

Based on the definition given in (7) in Section 2, we have $\mathcal{A}\in NBQ(m,n)$, where $m,n\ge 2$. Suppose that $\mathcal{A}$ is x-quasi-reducible. Then, there are two indices $i_1,i_2\in \left[m\right]$, such that T is S-separable. This contradicts our assumption on G. Thus, $\mathcal{A}$ is x-quasi-irreducible. Similarly, we may show that $\mathcal{A}$ is y-quasi-irreducible. Hence, $\mathcal{A}$ is quasi-irreducible. □

Proposition 2.

Suppose that the bipartite 2-graph $G=(S,T,E)$ is not bi-separable, where $\left|S\right|\ge 2$ and $\left|T\right|\ge 2$, and $\mathcal{Q}$ is the signless Laplacian tensor of G. Thus, we draw the following conclusions.

(i) 

${\mathcal{D}}^x$ is x-irreducible, y-reducible, and quasi-reducible;

(ii) 

${\mathcal{D}}^y$ is y-irreducible, x-reducible, and quasi-reducible;

(iii) 

${\mathcal{D}}^0$ is x- and y-reducible and x- and y-quasi-reducible;

(iv) 

$\mathcal{Q}$ is irreducible and quasi-irreducible.

Proof. 

It follows from Proposition 1 that $\mathcal{A}$ is quasi-reducible. Consequently, for any nonempty proper index subset $J_x⊊\left[m\right]$ and two distinct indices $j_1,j_2\in \left[n\right]$, $j_1\ne j_2$, we have

$$a_{i_2{j}_1{i}_1{j}_2}+a_{i_1{j}_1{i}_2{j}_2}>0,\exists i_1\in J_x, \exists i_2\notin J_x,$$

(18)

and for any two distinct indices $i_1,i_2\in \left[m\right]$, $i_1\ne i_2$ and nonempty proper index subset $J_y⊊\left[n\right]$, we have

$$a_{i_1{j}_1{i}_2{j}_2}+a_{i_1{j}_2{i}_2{j}_1}>0,\exists j_1\in J_y, \exists j_2\notin J_y.$$

(19)

(i) Based on Equation (19), for any proper index $i\in \left[m\right]$ and nonempty proper index subset $J_y⊊\left[n\right]$, there exist $j_1\in J_y$ and $j_2\notin J_y$ such that

$$d_{i{j}_{1}i{j}_2}^x+d_{i{j}_{2}i{j}_1}^x={\displaystyle \sum _{i_2=1}^m}{a}_{i{j}_1{i}_2{j}_2}+a_{i{j}_2{i}_2{j}_1}\ge \sum _{i_2\ne i}{a}_{i{j}_1{i}_2{j}_2}+a_{i{j}_2{i}_2{j}_1}>0.$$

This shows that ${\mathcal{D}}^x$ is x-irreducible. Furthermore, based on Equation (19), we have $d_{i_1{j}_1{i}_2{j}_2}^x=0$ for any $i_1\ne i_2$. Consequently, ${\mathcal{D}}^x$ is y-reducible and quasi-reducible, respectively.

(ii) Based on Equation (18), for any proper index $j\in \left[n\right]$ and nonempty proper index subset $J_x⊊\left[m\right]$, there exist $i_1\in J_x$ and $i_2\notin J_x$ such that

$$d_{i_{1}j{i}_{2}j}^y+d_{i_{2}j{i}_{1}j}^y={\displaystyle \sum _{j_2=1}^m}{a}_{i_{1}j{i}_2{j}_2}+a_{i_{2}j{i}_1{j}_2}\ge \sum _{j_2\ne j}{a}_{i_{1}j{i}_2{j}_2}+a_{i_{2}j{i}_1{j}_2}>0.$$

This shows that ${\mathcal{D}}^y$ is y-irreducible. Furthermore, based on Equation (18), we have $d_{i_1{j}_1{i}_2{j}_2}^y=0$ for any $j_1\ne j_2$. Consequently, ${\mathcal{D}}^y$ is x-reducible and quasi-reducible, respectively.

(iii) Given that ${\mathcal{D}}^0$ is a diagonal biquadratic tensor, the conclusion holds.

(iv) It follows directly from $\mathcal{Q}=\mathcal{A}+{\mathcal{D}}^0+{\mathcal{D}}^x+{\mathcal{D}}^y$ that $\mathcal{A}$ is quasi-irreducible, ${\mathcal{D}}^x$ is x-irreducible, and ${\mathcal{D}}^y$ is y-irreducible; therefore, the conclusion holds.

This completes the proof. □

Suppose that $\lambda$ is an M-eigenvalue of $\mathcal{A}$. If $\mathcal{A}$ has a pair of M-eigenvectors, $\mathbf{x}\in {\mathbb{R}}^m$ and $\mathbf{y}\in {\mathbb{R}}^n$, such that either $\left|\mathrm{supp}\right(\mathbf{x}\left)\right|=1$ or $\left|\mathrm{supp}\right(\mathbf{y}\left)\right|=1$, then we call $\lambda$ an $M^0$-eigenvalue of $\mathcal{A}$. Now we are ready to present the main result of this section.

Theorem 4.

Suppose that $\mathcal{A}=\left(a_{i_1{j}_1{i}_2{j}_2}\right)\in NBQ(m,n)$ is quasi-irreducible, and λ is an $M^{+}$ eigenvalue of $\mathcal{A}$. Then, λ is either an $M^0$ eigenvalue or an $M^{++}$ eigenvalue of $\mathcal{A}$.

Proof. 

Based on the definition of M-eigenvalues and M-eigenvectors, we obtain the following:

$$\mathcal{A}\overline{\mathbf{x}}\overline{\mathbf{y}}·\overline{\mathbf{y}}+\mathcal{A}·\overline{\mathbf{y}}\overline{\mathbf{x}}\overline{\mathbf{y}}=2\lambda \overline{\mathbf{x}}\mathrm{and}\mathcal{A}\overline{\mathbf{x}}\overline{\mathbf{y}}\overline{\mathbf{x}}·+\mathcal{A}\overline{\mathbf{x}}·\overline{\mathbf{x}}\overline{\mathbf{y}}=2\lambda \overline{\mathbf{y}}.$$

Furthermore, based on the properties of nonnegative biquadratic tensors, $\lambda$ is an $M^{+}$ eigenvalue of $\mathcal{A}$. Now, assuming that $\lambda$ is not an $M^0$ eigenvalue, we now prove that $\lambda$ is an $M^{++}$ eigenvalue by showing that $\overline{\mathbf{x}}>{\mathbf{0}}_m$ and $\overline{\mathbf{y}}>{\mathbf{0}}_n$ utilizing the method of contradiction.

Suppose that $\overline{\mathbf{x}}\ngtr {\mathbf{0}}_m$. Let $J_x=\left[m\right]\setminus \mathrm{supp}\left(\overline{\mathbf{x}}\right)$. Then, $J_x$ is a nonempty set. For any $i\in J_x$, we have the following:

$$\begin{array}{ccc}& & {\displaystyle \sum _{i_1=1}^m}{\displaystyle \sum _{j_1,j_2=1}^n}{a}_{i_1{j}_{1}i{j}_2}{\overline{x}}_{i_1}{\overline{y}}_{j_1}{\overline{y}}_{j_2}+{\displaystyle \sum _{i_2=1}^m}{\displaystyle \sum _{j_1,j_2=1}^n}{a}_{i{j}_1{i}_2{j}_2}{\overline{x}}_{i_2}{\overline{y}}_{j_1}{\overline{y}}_{j_2}\hfill \\ & =& \sum _{i_1\notin J_x}\sum _{j_1,j_2\in \mathrm{supp}\left(\overline{\mathbf{y}}\right)}{a}_{i_1{j}_{1}i{j}_2}{\overline{x}}_{i_1}{\overline{y}}_{j_1}{\overline{y}}_{j_2}+\sum _{i_2\notin J_x}\sum _{j_1,j_2\in \mathrm{supp}\left(\overline{\mathbf{y}}\right)}{a}_{i{j}_1{i}_2{j}_2}{\overline{x}}_{i_2}{\overline{y}}_{j_1}{\overline{y}}_{j_2}\hfill \\ & =& 0.\hfill \end{array}$$

This shows that $a_{i{j}_1{i}_2{j}_2}=0$ for all $i\in J_x$, $i_2\notin J_x$, and $j_1,j_2\in \mathrm{supp}\left(\overline{\mathbf{y}}\right)$. As $\lambda$ is not an M⁰ eigenvalue, we have $\left|\mathrm{supp}\left(\overline{\mathbf{y}}\right)\right|\ge 2$. This leads to a contradiction with the assumption that $\mathcal{A}$ is quasi-irreducible. Hence, $\overline{\mathbf{x}}>{\mathbf{0}}_m$. Similarly, we could show that $\overline{\mathbf{y}}>{\mathbf{0}}_n$. Therefore, we conclude that $\lambda >0$ and that it is an M⁺⁺-eigenvalue. □

The above theorem, together with Theorem 2, forms the weak Perron–Frobenius theorem of quasi-irreducible nonnegative biquadratic tensors.

The next example shows that a quasi-irreducible nonnegative biquadratic tensor may have no M⁺⁺ eigenvalue.

Example 3.

Let $\mathcal{A}\in NBQ(2,2)$ be defined by $a_{1111}=1$, $a_{2222}=2$, $a_{1212}=3$, $a_{1122}=a_{1221}=a_{2112}=a_{2211}=1$, and all other elements are zeros. Then, we may verify that $\mathcal{A}$ is reducible, but quasi-reducible. Furthermore, the M⁺-eigenvalues of $\mathcal{A}$ are

$$0,1.0000,2.0000,3.0000,$$

and the corresponding eigenvectors are as follows:

$$\begin{array}{cc}\hfill \left\{\begin{array}{c}\mathbf{x}={(0,1)}^{\top },\\ \mathbf{y}={(1,0)}^{\top }.\end{array}\right.& \left\{\begin{array}{c}\mathbf{x}={(1,0)}^{\top },\\ \mathbf{y}={(1,0)}^{\top },\end{array}\right.\left\{\begin{array}{c}\mathbf{x}={(0,1)}^{\top },\\ \mathbf{y}={(0,1)}^{\top },\end{array}\right.\left\{\begin{array}{c}\mathbf{x}={(1,0)}^{\top },\\ \mathbf{y}={(0,1)}^{\top }.\end{array}\right.\end{array}$$

5. A Max-Min Theorem for Nonnegative Biquadratic Tensors

We denote

$$S_{+}^{m-1}=\{\mathbf{x}\in {\mathbb{R}}_{+}^m:\sum x_i^2=1\}$$

as the nonnegative section of the unit sphere surface in the m-dimensional space and

$$S_{++}^{m-1}=\{\mathbf{x}\in {\mathbb{R}}_{++}^m:\sum x_i^2=1\}$$

as the relative interior set of $S_{+}^{m-1}$. For any $\mathbf{x}\in {\mathbb{R}}^m$ and $\mathbf{y}\in {\mathbb{R}}^n$, let

$$\mathbf{g}={\displaystyle \frac{1}{2}}(\mathcal{A}·\mathbf{y}\mathbf{x}\mathbf{y}+\mathcal{A}\mathbf{x}\mathbf{y}·\mathbf{y}),\mathbf{h}={\displaystyle \frac{1}{2}}(\mathcal{A}\mathbf{x}·\mathbf{x}\mathbf{y}+\mathcal{A}\mathbf{x}\mathbf{y}\mathbf{x}·).$$

(20)

Let $\mathcal{A}\in NBQ(m,n)$ be quasi-irreducible. We define the following two functions for all $\mathbf{x}\in {\mathbb{R}}_{+}^m\setminus \left\{{\mathbf{0}}_m\right\}$ and $\mathbf{y}\in {\mathbb{R}}_{+}^n\setminus \left\{{\mathbf{0}}_n\right\}$.

$$\begin{array}{c}\hfill v(\mathbf{x},\mathbf{y})=\underset{\begin{array}{c}i:x_i>0,\\ j:y_j>0\end{array}}{min}\left\{{\displaystyle \frac{g_i}{x_i}},{\displaystyle \frac{h_j}{y_j}}\right\},u(\mathbf{x},\mathbf{y})=\underset{\begin{array}{c}i:x_i>0,\\ j:y_j>0\end{array}}{max}\left\{{\displaystyle \frac{g_i}{x_i}},{\displaystyle \frac{h_j}{y_j}}\right\}.\end{array}$$

(21)

Then $v(\mathbf{x},\mathbf{y})\le u(\mathbf{x},\mathbf{y})$. Here, we require the indices $i,j$ to be subsets of $\left[m\right]$ and $\left[n\right]$, respectively, to avoid the indeterminate form ${\displaystyle \frac{0}{0}}$. As illustrated in Example 3, an M⁺-eigenvalue may not necessarily be an $M^{++}$-eigenvalue. We also define the following:

$${\rho }_{\ast }=\underset{\mathbf{x}\in S_{+}^{m-1},\mathbf{y}\in S_{+}^{n-1}}{inf}u(\mathbf{x},\mathbf{y})\mathrm{and}{\rho }^{*}=\underset{\mathbf{x}\in S_{+}^{m-1},\mathbf{y}\in S_{+}^{n-1}}{sup}v(\mathbf{x},\mathbf{y})$$

(22)

Based on Theorem 2, ${\lambda }_{max}\left(\mathcal{A}\right)$ is attainable and coincides with the M-spectral radius ${\rho }_M\left(\mathcal{A}\right)$ of $\mathcal{A}$, and ${\lambda }_{max}\left(\mathcal{A}\right)$ is an M⁺-eigenvalue of $\mathcal{A}$. The following theorem shows that the value ${\rho }^{*}$ is attainable and is equal to ${\rho }_M\left(\mathcal{A}\right)$.

Theorem 5.

Suppose that $\mathcal{A}=\left(a_{i_1{j}_1{i}_2{j}_2}\right)\in NBQ(m,n)$. Then, we have

$${\rho }^{*}={\lambda }_{max}\left(\mathcal{A}\right)={\rho }_M\left(\mathcal{A}\right).$$

Proof. 

Let $\overline{\mathbf{x}},\overline{\mathbf{y}}$ denote the optimal solutions to problem (5). Then, $v(\overline{\mathbf{x}},\overline{\mathbf{y}})={\lambda }_{max}\left(\mathcal{A}\right)={\rho }_M\left(\mathcal{A}\right)$, which shows that ${\rho }^{*}\ge {\lambda }_{max}\left(\mathcal{A}\right)$. Next, we prove that ${\rho }^{*}={\lambda }_{max}\left(\mathcal{A}\right)$ using the method of contradiction.

Suppose that ${\rho }^{*}>{\lambda }_{max}\left(\mathcal{A}\right)$. Then, for any $ϵ>0$, there are $\tilde{\mathbf{x}}\in S_{+}^{m-1}$ and $\tilde{\mathbf{y}}\in S_{+}^{n-1}$ such that $v(\tilde{\mathbf{x}},\tilde{\mathbf{y}})\ge {\rho }^{*}-ϵ$. By choosing $ϵ={\displaystyle \frac{1}{2}}({\rho }^{*}-{\lambda }_{max}\left(\mathcal{A}\right))$, we obtain

$$v(\tilde{\mathbf{x}},\tilde{\mathbf{y}})\ge {\displaystyle \frac{1}{2}}({\rho }^{*}+{\lambda }_{max}\left(\mathcal{A}\right)).$$

Therefore, it follows that ${\tilde{g}}_i\ge {\displaystyle \frac{1}{2}}({\rho }^{*}+{\lambda }_{max}\left(\mathcal{A}\right)){\tilde{x}}_i^{*}$ and ${\tilde{h}}_j\ge {\displaystyle \frac{1}{2}}({\rho }^{*}+{\lambda }_{max}\left(\mathcal{A}\right)){\tilde{y}}_j^{*}$ for all $i\in \left[m\right]$ and $j\in \left[n\right]$. Consequently, we have $\mathcal{A}\tilde{\mathbf{x}}\tilde{\mathbf{y}}\tilde{\mathbf{x}}\tilde{\mathbf{y}}={\tilde{\mathbf{g}}}^{\top }\tilde{\mathbf{x}}={\tilde{\mathbf{h}}}^{\top }\tilde{\mathbf{y}}\ge {\displaystyle \frac{1}{2}}({\rho }^{*}+{\lambda }_{max}\left(\mathcal{A}\right))$. This contradicts the definition of ${\lambda }_{max}$ in (5). Thus, we conclude that ${\rho }^{*}={\lambda }_{max}\left(\mathcal{A}\right)$. This completes the proof. □

6. Conclusions and Open Problems

Inspired by the bipartite 2-graphs and reducibility concepts in [6], in this paper, we introduced quasi-irreducibility for biquadratic tensors, yielding two main results: a complete classification of M⁺-eigenvalues as M⁰ and M⁺⁺-eigenvalues for such tensors, and a max-min theorem for their M-spectral radius.

Suppose $\mathcal{A}\in BQ(m,n)$. Then, computing its largest M-eigenvalue is an NP-hard problem, as proven in [11]. However, the situation differs when $\mathcal{A}\in NBQ(m,n)$. This parallels the case for cubic tensors: while computing the spectral radius of a general high-order cubic tensor is NP-hard, efficient algorithms exist for nonnegative cubic tensors [1]. This contrast highlights the following open problems.

Problem 1: Finding the largest M-eigenvalue of a nonnegative biquadratic tensor $\mathcal{A}\in NBQ(m,n)$. Theoretically, is this problem polynomial-time solvable? Practically, are there efficient algorithms to solve this problem?

Based on Theorem 2, the largest M-eigenvalue of a nonnegative biquadratic tensor is an M⁺-eigenvalue. This is the first step in solving this problem.

We now consider a subproblem of Problem 1.

Problem 2: Finding the largest M-eigenvalue of an irreducible nonnegative biquadratic tensor $\mathcal{A}\in NBQ(m,n)$. Theoretically, is this problem polynomial-time solvable? Practically, are there efficient algorithms to solve this problem?

Based on Theorem 3, the largest M-eigenvalue of an irreducible nonnegative biquadratic tensor is an M⁺⁺-eigenvalue. A Collatz algorithm was proposed in [4] to solve this problem.

Based Theorem 5, can we also construct a Collatz algorithm to solve Problem 1?

This paper raised another subproblem of Problem 1.

Problem 3: Finding the largest M-eigenvalue of a quasi-irreducible nonnegative biquadratic tensor $\mathcal{A}\in NBQ(m,n)$. Theoretically, is this problem polynomial-time solvable? Practically, are there efficient algorithms to solve this problem?

Theorem 4 indicates that for a quasi-irreducible nonnegative biquadratic tensor, the largest M-eigenvalue ${\lambda }_{max}\left(\mathcal{A}\right)$ is either an M⁰-eigenvalue or an M⁺⁺-eigenvalue. Can we utilize this information to solve Problem 3?