Probabilistic Selling with Unsealing Strategy: An Analysis in Markets with Vertical-Differentiated Products
Abstract
1. Introduction
- How does the retailer’s decision to unseal and resell high-quality and low-quality goods separately affect the profitability and consumer surplus relative to a scenario where the goods remain sealed and sold through the retailer?
- How does the introduction of a manufacturer-operated direct sales channel for probabilistic goods influence the retailer’s unsealing strategy, and what are the resulting implications for market equilibrium, pricing structures, and consumer surplus?
2. Literature Review
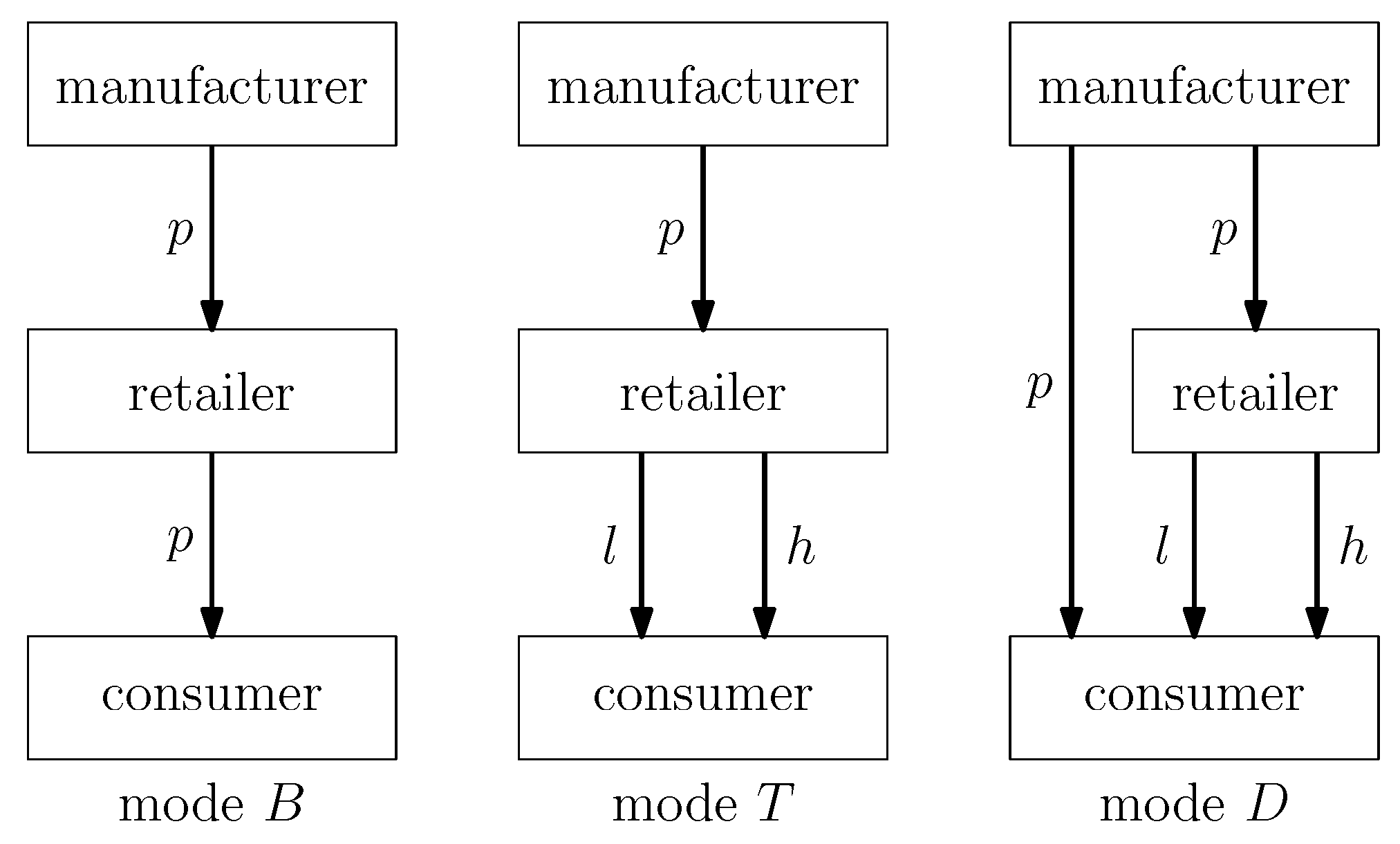
3. Model
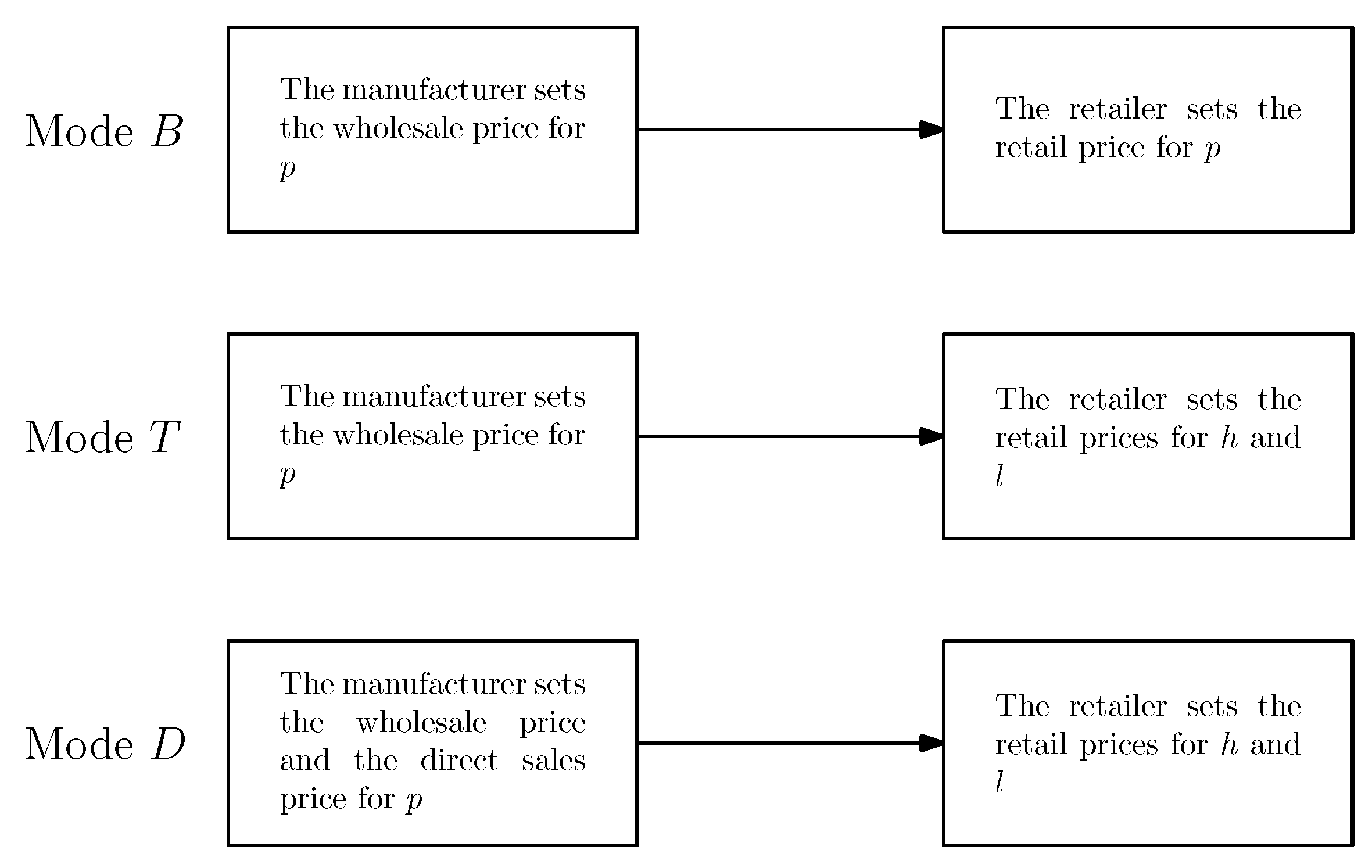
- In mode B, the manufacturer first sets the wholesale price for the probabilistic good, and the retailer then sets the retail price for the probabilistic good .
- In mode T, the manufacturer first sets the wholesale price , after which the retailer unseals the probabilistic good and sets retail prices for the high-quality and low-quality products and , respectively. The unsealing step fundamentally transforms the market from a probabilistic offering to a deterministic one, shifting demand dynamics.
- In mode D, the manufacturer first to determine both the direct retail price for probabilistic goods (sold to consumers) and the wholesale price for probabilistic goods (supplied to the retailer). The retailer then unseals the supplied probabilistic good and sets retail prices for the high-quality and low-quality products and , respectively.
3.1. Mode B
3.2. Mode T
- 1.
- The profits remains identical to the case where probabilistic goods are excluded, that is,
- 2.
- The demand for probabilistic goods at equilibrium is zero, that is, .
3.3. Mode D
4. Analysis
4.1. Asymptotic Behaviors
- 1.
- In mode T, taking , then the cost becomes ; the prices become , , and ; the demands become and ; the profits become and .
- 2.
- In mode D, taking , then the cost becomes ; the prices become , , , and ; the demands become , , and ; the profits become and .
- 1.
- In mode T, taking , then the cost becomes ; the prices become , , and ; the demands become and ; the profits become and .
- 2.
- In mode D, taking , then the cost becomes ; the prices become , , , and ; the demands become , , and ; the profits become and .
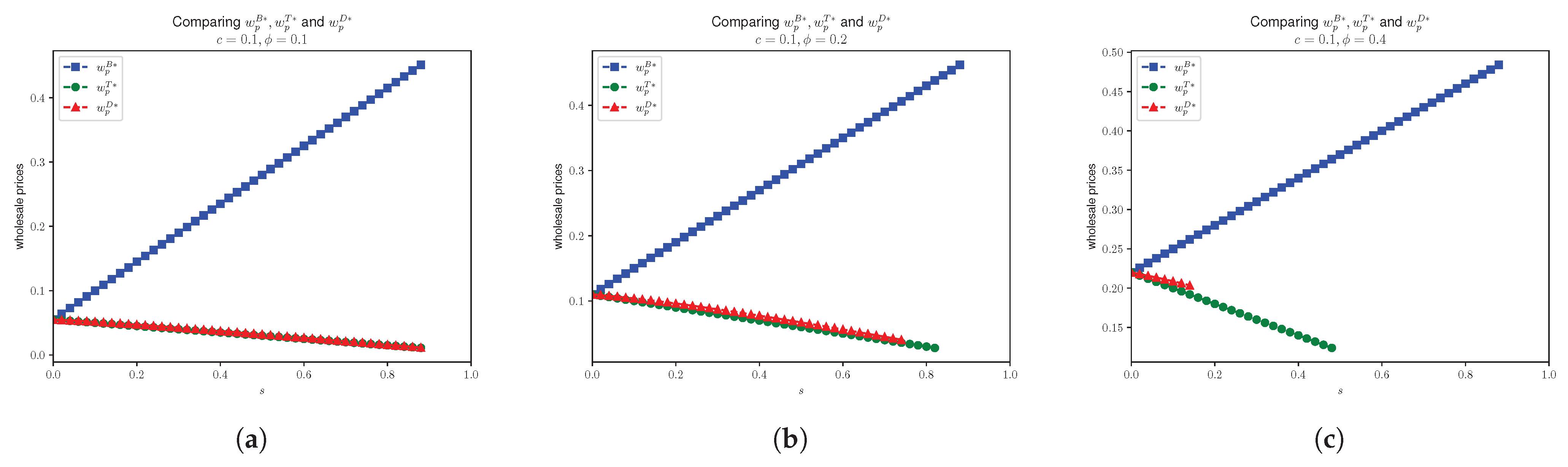
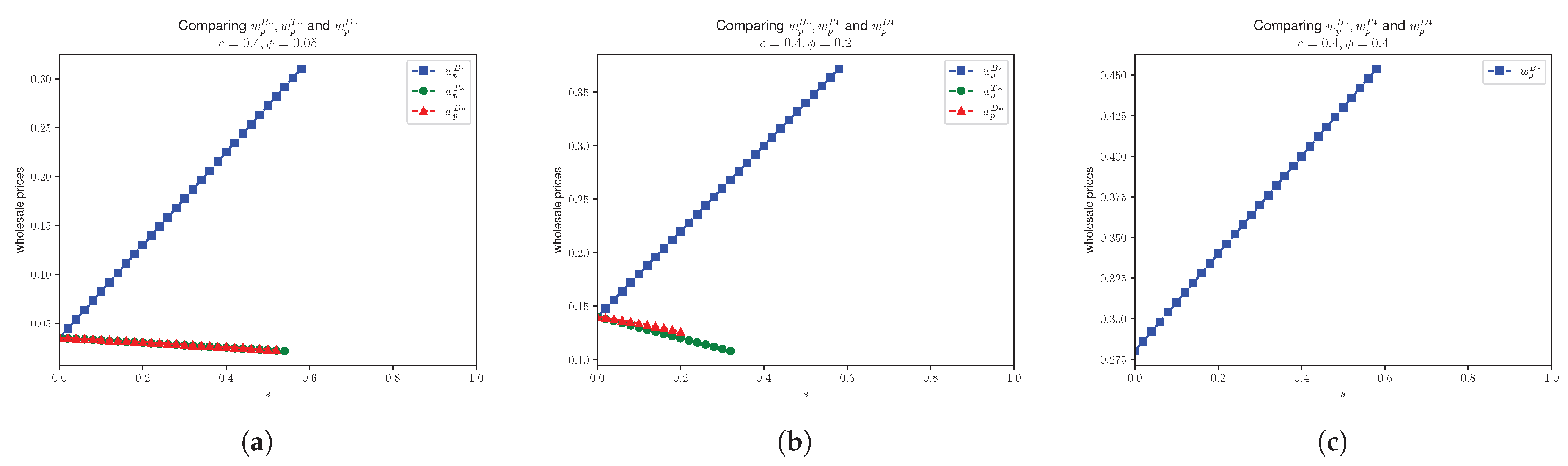
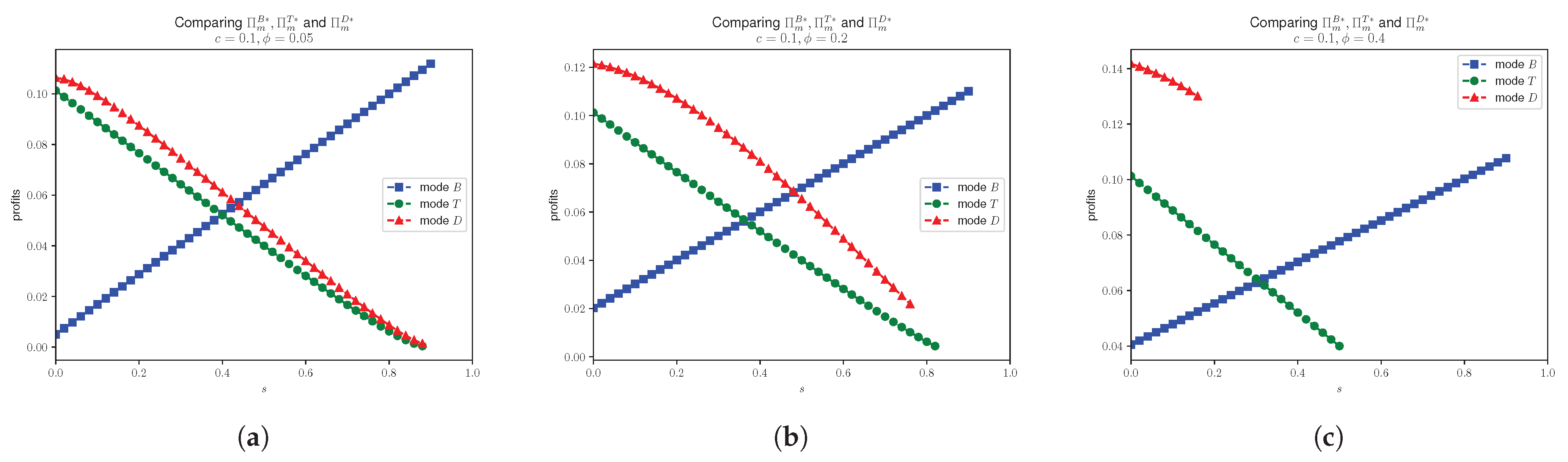
4.2. Effects of Unsealing Probabilistic Goods on Prices and Demands
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- .
- 1.
- ;
- 2.
- ;
- 3.
- .
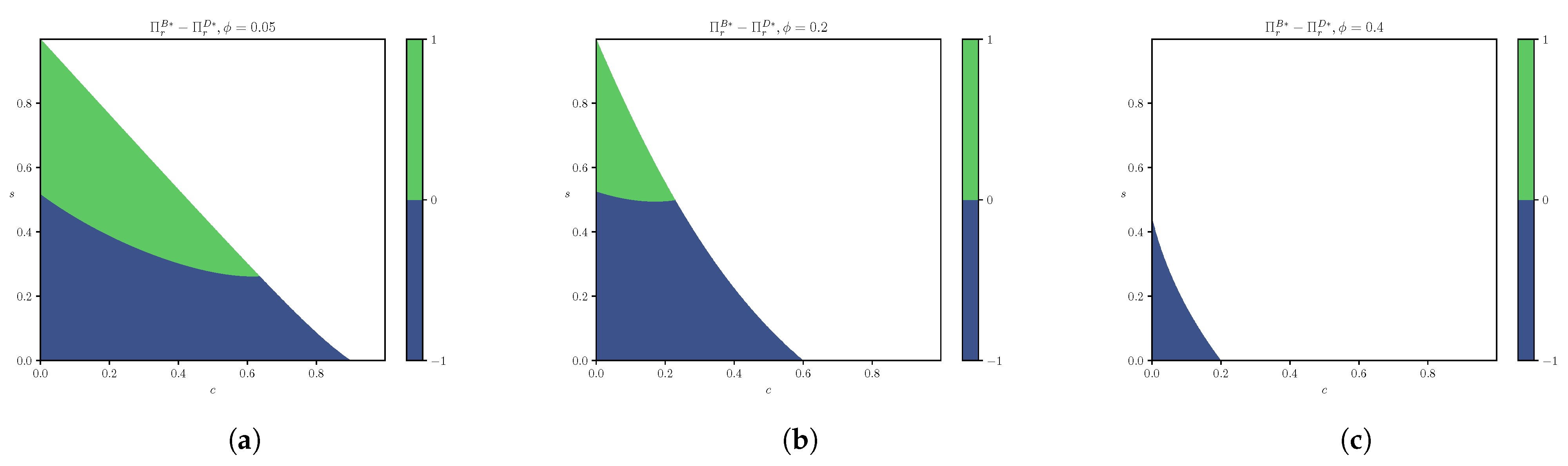
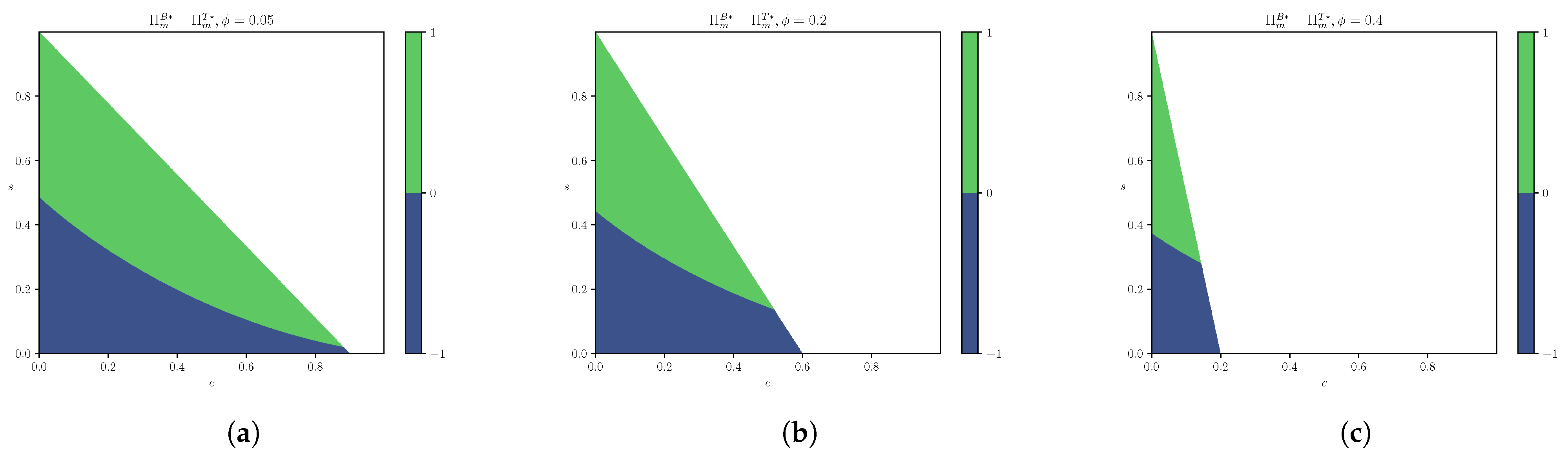
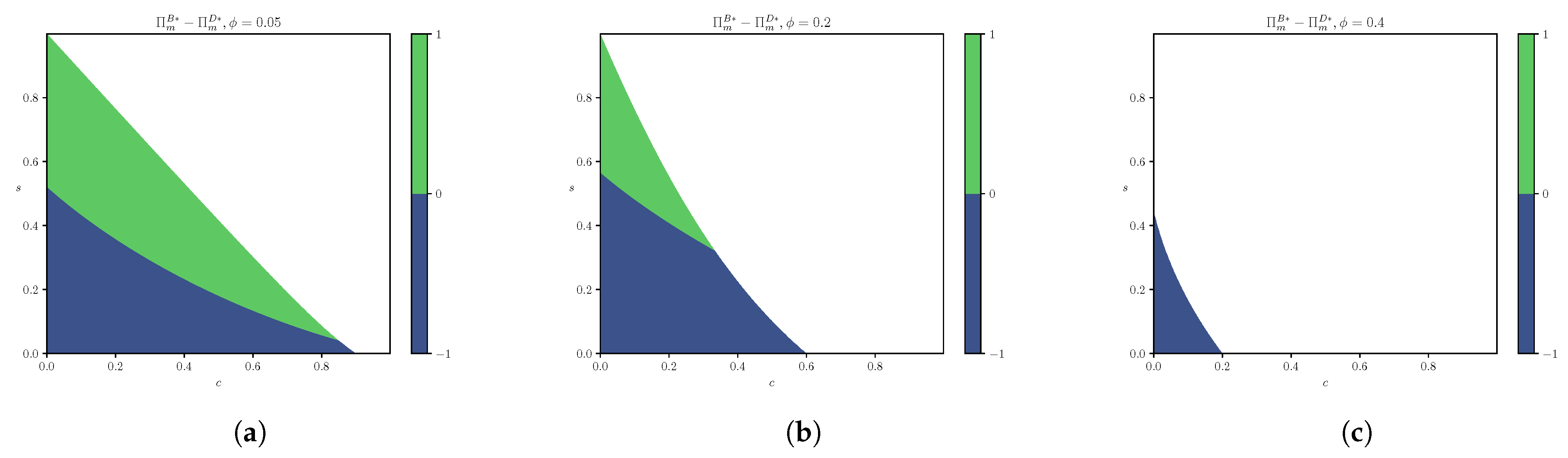
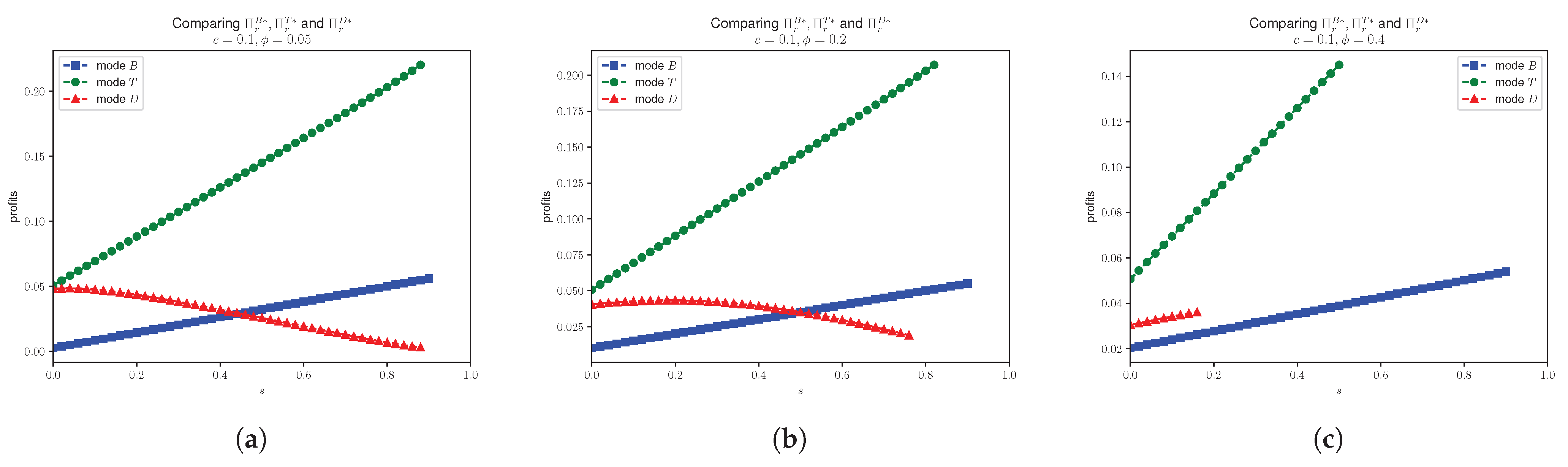
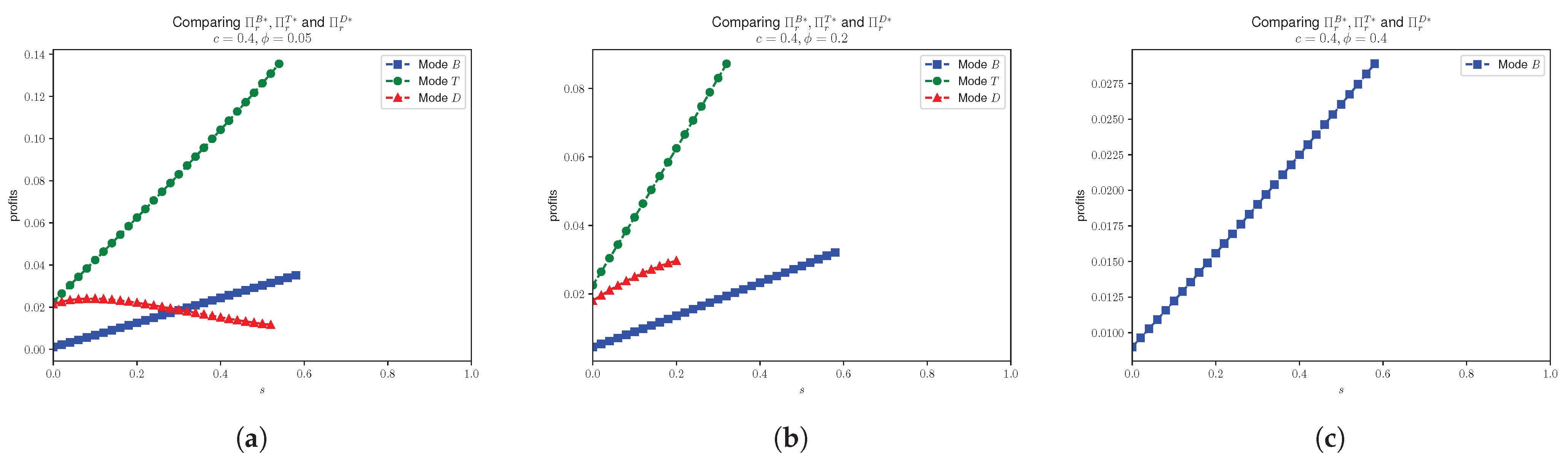
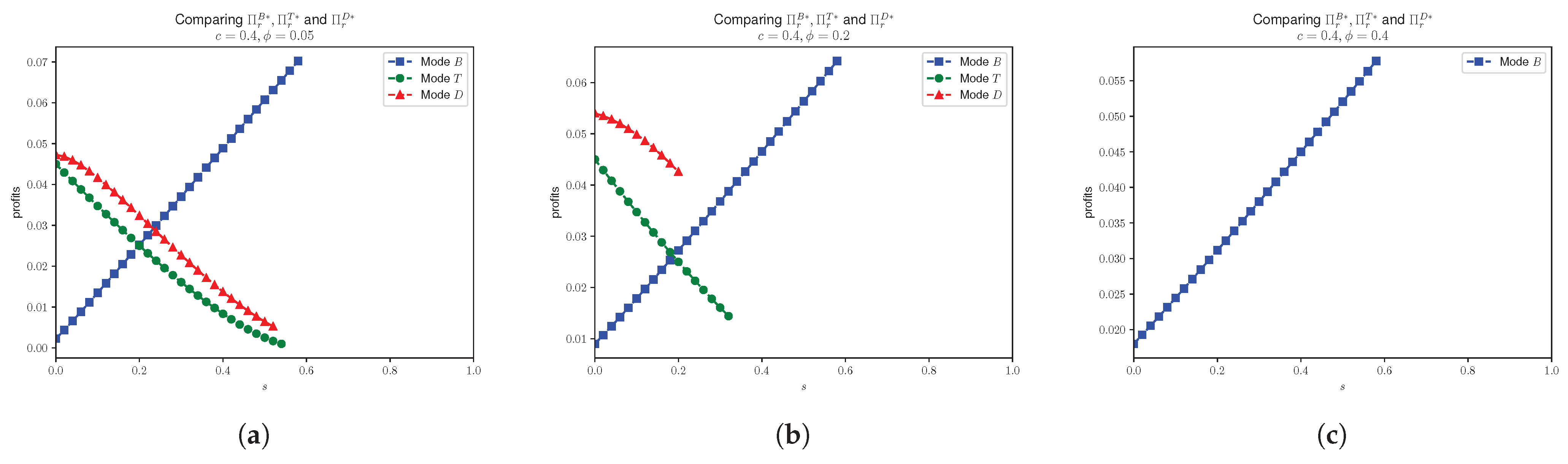
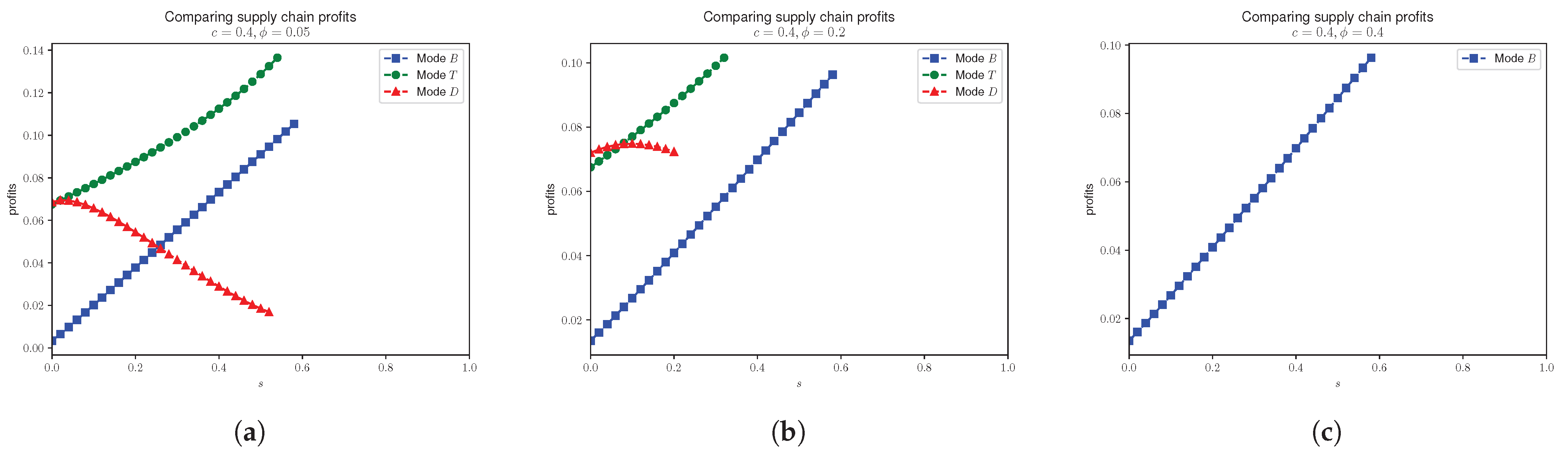
4.3. Effects of Unsealing Probabilistic Goods on Profits
- 1.
- ;
- 2.
- ;
- 3.
- ;
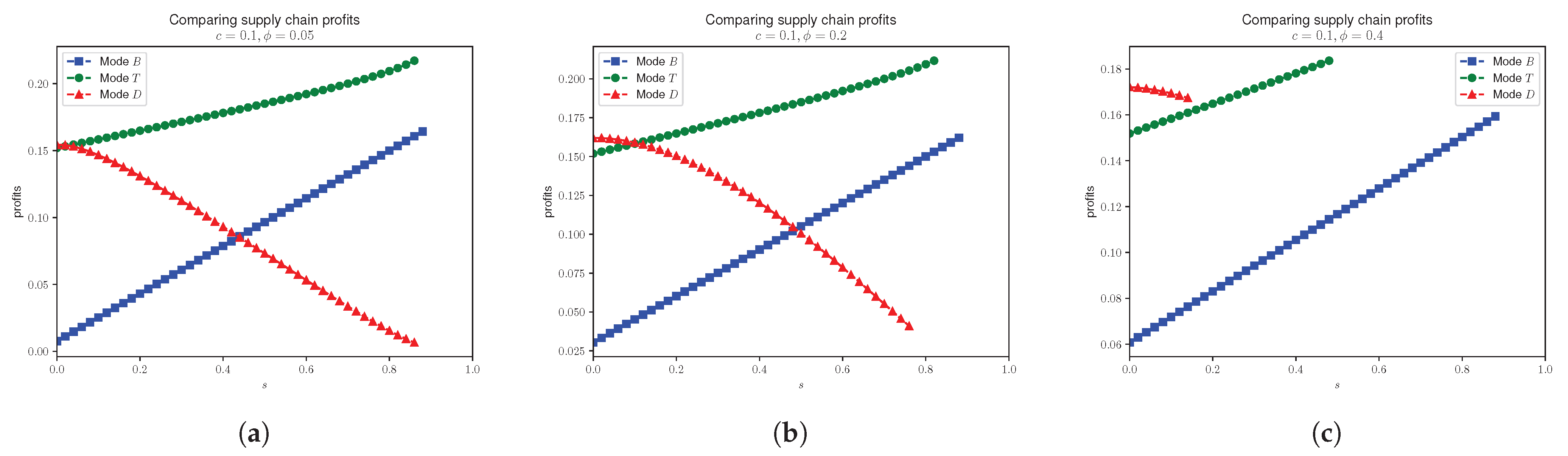
4.4. Probabilistic Selling Effects on Consumer Surplus
5. Conclusions and Future Research
5.1. Conclusions
5.2. Limitations and Future Research
- Risk-neutral consumers, who may not show real-world behavior where risk preferences influence purchasing decisions.
- The absence of operational costs, such as unsealing, logistics, and inventory constraints, which are critical in practical scenarios.
- A uniform distribution of willingness to pay, simplifying consumer heterogeneity in quality and price sensitivity.
- The model does not capture dynamic factors like brand reputation, repeated consumer interactions, or market competition.
- Introducing consumer risk attitudes: examining how risk-averse or risk-seeking consumers affect demand, pricing, and unsealing strategies.
- Incorporating operational costs: modeling unsealing costs, logistics, and inventory constraints to better understand their impact on profitability and channel coordination.
- Using alternative distributions: replacing the uniform distribution with more realistic distributions to capture nuanced consumer heterogeneity in preferences.
- Extending to competitive dynamics: analyzing multi-player frameworks with multiple manufacturers and retailers to study strategic interactions, brand reputation, and repeated market competition.
5.3. Managerial Implications
5.3.1. Manufacturers
- Adopt a dual-channel strategy: Combine direct-to-consumer and indirect channels to keep pricing authority while allowing retailers to unseal probabilistic goods. This reduces profit loss and maximizes consumer surplus.
- Strengthen direct-to-consumer channels: Reduce reliance on intermediaries to align with brand values, build consumer trust, and minimize reputational risks from unauthorized unsealing practices in secondary markets.
- Optimize market positioning: Proactively address uncertainties in probabilistic goods by balancing transparency (e.g., disclosing probabilities) with pricing control to maintain brand integrity.
5.3.2. Retailers
- Implement ethical pricing strategies: Avoid exploiting consumer uncertainty by ensuring fair pricing for unsealed goods. For instance, applying slight premium pricing to high-quality unsealed products can lower uncertainty and better align with consumers’ perceived value.
- Avoid unauthorized altering: Disclose unsealing processes transparently to maintain market fairness and prevent reputational harm from unethical practices.
5.3.3. Regulators
- Mandate disclosure requirements: (1) Require clear communication of probabilities and unsealing processes to comply with consumer protection rules; (2) use blockchain technology to track the occurrence and authenticity of probabilistic goods.
- Enforce compliance and integrity: (1) Conduct regular independent audits to verify declared probabilities and unsealing practices; (2) implement penalties for misrepresentation or non-compliance with disclosed terms.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proofs
- Case 1:From this case, we have that the prices must satisfy and . Then, the optimal price must also satisfy and . On the other hand, the profits for the manufacturer and retailer areandFrom the Stackleberg equilibrium, maximizing the retailer’s profit with respect to and , the Hessian isand , so we have that the Hessian is negative definite. So, solving the first-order derivatives givesand we obtainThen, inserting the optimal values and to Equation (A1), we have , and therefore, maximizing with respect to , we haveSo, the optimal selling price is thenFrom , we have . Also, is the necessary condition for and . In this case, we haveand
- Case 2:From this case, we have that the prices must satisfy and . On the other hand, the profits for the manufacturer and retailer areandSo, the Hessian isand ; this means the solution of the first-order derivative is not optimal. On the other hand, as we have , this suggests that the profit of the retailer is convex in the direction. Furthermore, the profit of the retailer is concave in the direction as . Since we have that , so taking to this boundary point for the retailer’s profit function, we haveNow, maximizing the profit with respect to , we obtain . Next, we optimize the manufacturer’s profitwith respect to . But, , indicating that is convex. So, we need to check the bounds of as the maximum is at the boundary. From , we have . So, we haveAnd the manufacturer’s profit is maximized when . And therefore the profits areandNote that we need ; this is equivalent to . As , the condition is equivalent to , which means .
- Case 1:We have the profit functions asandThen, we have the Hessian H aswe have ; then,and also, . Therefore, we have that the is negative definite. Taking the first-order derivatives to be zero, we haveand we obtainNext, inserting , , and into Equation (A23), we have , and then maximizing with respect to , we haveTherefore, we haveSubstitute the values , , and for the demands, we haveSimilarly, we have the profitsand
- Case 2:Following similar steps in Proposition 2, one can conclude that the retailer’s decision algins with Case 1.
- Case 1:We have the profit functions asandSo, we have the Hessian asand ; we have that the is negative definite. Hence, we haveThen, we insert the optimal value back into the manufacturer’s profit function , and similarly, we have obtained the optimal and .Then, we have obtained the optimal profit for the retailer and the manufacturer aswhereandwhere
- Case 2:We follow the similar steps, as shown in mode T, and we have that the retailer’s decision will align with Case 1, that is, the retailer will fulfill all the demands for the consumers, and the order quantity of the probabilistic goods is .
References
- Fay, S.; Xie, J. Probabilistic goods: A creative way of selling products and services. Mark. Sci. 2008, 27, 674–690. [Google Scholar] [CrossRef]
- Sun, Y.; Yuan, Z.; Cheng, H. Obsessed with surprise? The effects of probabilistic selling on online consumers’ repurchase intention. J. Strateg. Mark. 2024, 32, 690–711. [Google Scholar] [CrossRef]
- Buechel, E.C.; Li, R. Mysterious consumption: Preference for horizontal (vs. vertical) uncertainty and the role of surprise. J. Consum. Res. 2023, 49, 987–1013. [Google Scholar] [CrossRef]
- Miao, X.; Niu, B.; Yang, C.; Feng, Y. Examining the gamified effect of the blindbox design: The moderating role of price. J. Retail. Consum. Serv. 2023, 74, 103423. [Google Scholar] [CrossRef]
- Chen, N.; Elmachtoub, A.N.; Hamilton, M.L.; Lei, X. Loot Box Pricing and Design. Manag. Sci. 2021, 67, 4809–4825. [Google Scholar] [CrossRef]
- Xiao, L.Y. Regulating loot boxes as gambling? Towards a combined legal and self-regulatory consumer protection approach. Interact. Entertain. Law Rev. 2021, 4, 27–47. [Google Scholar] [CrossRef]
- Xiao, L.Y.; Henderson, L.L.; Nielsen, R.K.; Newall, P.W. Regulating gambling-like video game loot boxes: A public health framework comparing industry self-regulation, existing national legal approaches, and other potential approaches. Curr. Addict. Rep. 2022, 9, 163–178. [Google Scholar] [CrossRef]
- Leahy, D. Rocking the boat: Loot boxes in online digital games, the regulatory challenge, and the EU’s unfair commercial practices directive. J. Consum. Policy 2022, 45, 561–592. [Google Scholar] [CrossRef]
- Jiang, Y. Price discrimination with opaque products. J. Revenue Pricing Manag. 2007, 6, 118–134. [Google Scholar] [CrossRef]
- Zhang, Z.; Joseph, K.; Subramaniam, R. Probabilistic selling in quality-differentiated markets. Manag. Sci. 2015, 61, 1959–1977. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Q. The entropy complexity of an asymmetric dual-channel supply chain with probabilistic selling. Entropy 2018, 20, 543. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Jin, S. Joint pricing and inventory decision under a probabilistic selling strategy. Oper. Res. 2022, 22, 1209–1233. [Google Scholar] [CrossRef]
- Cai, G.; Chen, Y.J.; Wu, C.C.; Hsiao, L. Probabilistic selling, channel structure, and supplier competition. Decis. Sci. 2013, 44, 267–296. [Google Scholar] [CrossRef]
- Zhang, Y.; Hua, G.; Wang, S.; Zhang, J.; Fernandez, V. Managing demand uncertainty: Probabilistic selling versus inventory substitution. Int. J. Prod. Econ. 2018, 196, 56–67. [Google Scholar] [CrossRef]
- Fay, S.; Xie, J. Timing of product allocation: Using probabilistic selling to enhance inventory management. Manag. Sci. 2015, 61, 474–484. [Google Scholar] [CrossRef]
- Fay, S. Selling an opaque product through an intermediary: The case of disguising one’s product. J. Retail. 2008, 84, 59–75. [Google Scholar] [CrossRef]
- Huang, Y.S.; Wu, T.Y.; Fang, C.C.; Tseng, T.L. Decisions on probabilistic selling for consumers with different risk attitudes. Decis. Anal. 2021, 18, 121–138. [Google Scholar] [CrossRef]
- Li, Q.; Tang, C.S.; Xu, H. Mitigating the double-blind effect in opaque selling: Inventory and information. Prod. Oper. Manag. 2020, 29, 35–54. [Google Scholar] [CrossRef]
- Zheng, Q.; Pan, X.A.; Carrillo, J.E. Probabilistic selling for vertically differentiated products with salient thinkers. Mark. Sci. 2019, 38, 442–460. [Google Scholar] [CrossRef]
- Chen, T.; Yang, F.; Guo, X. Probabilistic selling in a distribution channel with vertically differentiated products. J. Oper. Res. Soc. 2024, 75, 1076–1091. [Google Scholar] [CrossRef]
- He, Y.; Rui, H. Probabilistic selling in vertically differentiated markets: The role of substitution. Prod. Oper. Manag. 2022, 31, 4191–4204. [Google Scholar] [CrossRef]
- Jerath, K.; Netessine, S.; Veeraraghavan, S.K. Revenue management with strategic customers: Last-minute selling and opaque selling. Manag. Sci. 2010, 56, 430–448. [Google Scholar] [CrossRef]
- Huang, T.; Yu, Y. Sell probabilistic goods? A behavioral explanation for opaque selling. Mark. Sci. 2014, 33, 743–759. [Google Scholar] [CrossRef]
- Huang, T.; Yin, Z. Dynamic probabilistic selling when customers have boundedly rational expectations. Manuf. Serv. Oper. Manag. 2021, 23, 1597–1615. [Google Scholar] [CrossRef]
- Fay, S.; Xie, J. The economics of buyer uncertainty: Advance selling vs. probabilistic selling. Mark. Sci. 2010, 29, 1040–1057. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J. Probabilistic selling and manufacturer encroachment in retail markets with vertical-differentiated products. Int. Trans. Oper. Res. 2022, 29, 3051–3080. [Google Scholar] [CrossRef]
- Ren, H.; Huang, T. Opaque selling and inventory management in vertically differentiated markets. Manuf. Serv. Oper. Manag. 2022, 24, 2543–2557. [Google Scholar] [CrossRef]
- Xu, S.; Tang, H.; Huang, Y. Inventory competition and quality improvement decisions in dual-channel supply chains with data-driven marketing. Comput. Ind. Eng. 2023, 183, 109452. [Google Scholar] [CrossRef]
- Bolton, G.E.; Ockenfels, A. ERC: A theory of equity, reciprocity, and competition. Am. Econ. Rev. 2000, 91, 166–193. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 363–391. [Google Scholar] [CrossRef]
- Von Stackelberg, H. Market Structure and Equilibrium; Springer Science & Business Media: Cham, Switzerland, 2010. [Google Scholar]
- Yang, G.; Wang, Y.; Liu, M. Optimal Policy for Probabilistic Selling with Three-Way Revenue Sharing Contract under the Perspective of Sustainable Supply Chain. Sustainability 2023, 15, 3771. [Google Scholar] [CrossRef]
- Yang, G.; Tian, L.; Cai, M.; Cao, J.; Gong, Z. Vertically probabilistic selling mechanism under asymmetric quality-tier competition: An analytical exploration. Int. J. Prod. Econ. 2025, 286, 109633. [Google Scholar] [CrossRef]
- Hou, R.; Zhao, Y.; Zhu, M.; Lin, X. Price and quality decisions in a vertically-differentiated supply chain with an “Online-to-Store” channel. J. Retail. Consum. Serv. 2021, 62, 102593. [Google Scholar] [CrossRef]
- Xu, S.; Tang, H.; Lin, Z. Inventory and Ordering Decisions in Dual-Channel Supply Chains Involving Free Riding and Consumer Switching Behavior with Supply Chain Financing. Complexity 2021, 2021, 5530124. [Google Scholar] [CrossRef]
- Xu, S.; Tang, H.; Huang, Y. Decisions of pricing and delivery-lead-time in dual-channel supply chains with data-driven marketing using internal financing and contract coordination. Ind. Manag. Data Syst. 2023, 123, 1005–1051. [Google Scholar] [CrossRef]
- Niu, B.; Li, J.; Zhang, J.; Cheng, H.K.; Tan, Y. Strategic analysis of dual sourcing and dual channel with an unreliable alternative supplier. Prod. Oper. Manag. 2019, 28, 570–587. [Google Scholar] [CrossRef]
- Guan, X.; Mantrala, M.; Bian, Y. Strategic information management in a distribution channel. J. Retail. 2019, 95, 42–56. [Google Scholar] [CrossRef]
- Zhang, T.; Feng, X.; Wang, N. Manufacturer encroachment and product assortment under vertical differentiation. Eur. J. Oper. Res. 2021, 293, 120–132. [Google Scholar] [CrossRef]
- Gan, T. Gacha game: When prospect theory meets optimal pricing. arXiv 2022, arXiv:2208.03602. [Google Scholar]
- Xiao, L.Y. Loot box state of play 2023: Law, regulation, policy, and enforcement around the world. Gaming Law Rev. 2024, 28, 450–483. [Google Scholar] [CrossRef]
- Commission, E. Commission Staff Working Document Fitness Check on EU Consumer Law on Digital Fairness. Available online: https://commission.europa.eu/document/707d7404-78e5-4aef-acfa-82b4cf639f55_en (accessed on 12 June 2025).
| Study | Initial Product Type | Product Differentiation | Supply Chain | Unsealing | Problem Type |
|---|---|---|---|---|---|
| [1] | Both | Horizontal | Profit | ||
| [15] | Both | Horizontal | Profit, Inventory, Welfare | ||
| [10] | Both | Vertical | Profit, Welfare | ||
| [14] | Both | Vertical | Profit, Behavioral | ||
| [18] | Both | Horizontal | Profit, Behavioral, Inventory | ||
| [21] | Both | Vertical | Profit, Behavioral | ||
| [26] | Both | Vertical | Yes | Profit, Channel | |
| [20] | Both | Vertical | Yes | Profit, Channel | |
| This Study | Probabilistic | Vertical | Yes | Yes | Profit, Channel |
| Notation | Explanation |
|---|---|
| i | , where h, l, and p denote the high-quality product, low-quality product, and probabilistic good, respectively |
| x | , where m and r denote the manufacturer and the retailer, respectively |
| y | , where B, T, and D denote the base mode, transparent mode, and direct mode, respectively |
| The consumer willingness-to-pay measure | |
| The probability of high-quality product from the probabilistic good | |
| The unit cost of product i | |
| c | The unit cost of high-quality product |
| The quality product i | |
| s | The quality of low-quality product |
| The retail price of product i | |
| The wholesale price of product i | |
| The profit of x in Mode y |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che, P.H.; Chen, Y. Probabilistic Selling with Unsealing Strategy: An Analysis in Markets with Vertical-Differentiated Products. Mathematics 2025, 13, 2036. https://doi.org/10.3390/math13122036
Che PH, Chen Y. Probabilistic Selling with Unsealing Strategy: An Analysis in Markets with Vertical-Differentiated Products. Mathematics. 2025; 13(12):2036. https://doi.org/10.3390/math13122036
Chicago/Turabian StyleChe, Pak Hou, and Yue Chen. 2025. "Probabilistic Selling with Unsealing Strategy: An Analysis in Markets with Vertical-Differentiated Products" Mathematics 13, no. 12: 2036. https://doi.org/10.3390/math13122036
APA StyleChe, P. H., & Chen, Y. (2025). Probabilistic Selling with Unsealing Strategy: An Analysis in Markets with Vertical-Differentiated Products. Mathematics, 13(12), 2036. https://doi.org/10.3390/math13122036







