A Surrogate Piecewise Linear Loss Function for Contextual Stochastic Linear Programs in Transport
Abstract
1. Introduction
2. Literature Review
3. Problem Statement
3.1. Contextual Stochastic Optimization
3.2. Sequential Learning and Optimization
3.3. SLO Performance Evaluation
4. Methodology
4.1. Model Statement
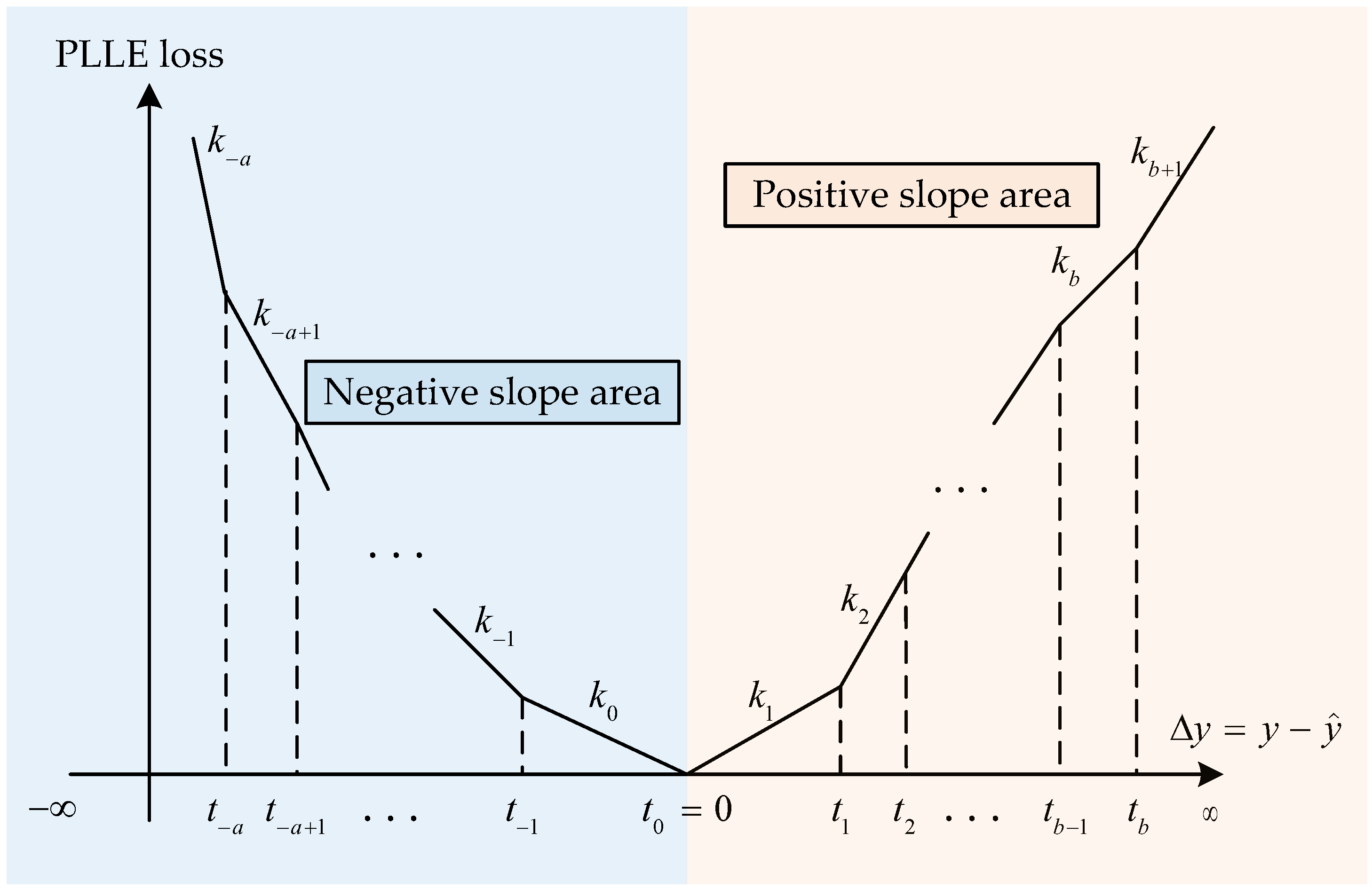
4.2. Piecewise Linear Loss Function
4.3. Optimization of Loss Function Parameters
| Algorithm 1: The improved GA for optimizing PLLF |
 |
4.4. Evaluation Method
5. Case Study
5.1. Problem Setting
5.1.1. Optimization Problem Statement
5.1.2. Data Split and Learning Setting
5.1.3. Parameters Setting
5.2. Experimental Results
5.2.1. Linear Regression Model
5.2.2. XGBoost Model
5.2.3. Neural Network Model
5.3. Discussion of the Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSO | Contextual Stochastic Optimization |
| GA | Genetic Algorithm |
| i.i.d. | Independent and Identically Distributed |
| KKT | Karush–Kuhn–Tucker |
| ML | Machine Learning |
| MSE | Mean Squared Error |
| PLLF | Piecewise Linear Loss Function |
| R&D | Research and Development |
| ReLU | Rectified Linear Unit |
| SA | Simulated Annealing |
| SLO | Sequential Learning and Optimization |
| SPO | Smart Predict-then-Optimize |
References
- Bertsimas, D.; Kallus, N. From predictive to prescriptive analytics. Manag. Sci. 2020, 66, 1025–1044. [Google Scholar] [CrossRef]
- Saki, S.; Soori, M. Artificial Intelligence, Machine Learning and Deep Learning in Advanced Transportation Systems, A Review. Multimodal Transp. 2025, 100242. [Google Scholar] [CrossRef]
- Liu, Z.; Lyu, C.; Huo, J.; Wang, S.; Chen, J. Gaussian process regression for transportation system estimation and prediction problems: The deformation and a hat kernel. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22331–22342. [Google Scholar] [CrossRef]
- Sadana, U.; Chenreddy, A.; Delage, E.; Forel, A.; Frejinger, E.; Vidal, T. A survey of contextual optimization methods for decision-making under uncertainty. Eur. J. Oper. Res. 2025, 320, 271–289. [Google Scholar] [CrossRef]
- Ferjani, A.; Yaagoubi, A.E.; Boukachour, J.; Duvallet, C. An optimization-simulation approach for synchromodal freight transportation. Multimodal Transp. 2024, 3, 100151. [Google Scholar] [CrossRef]
- Bengio, Y. Using a financial training criterion rather than a prediction criterion. Int. J. Neural Syst. 1997, 8, 433–443. [Google Scholar] [CrossRef]
- Mandi, J.; Kotary, J.; Berden, S.; Mulamba, M.; Bucarey, V.; Guns, T.; Fioretto, F. Decision-focused learning: Foundations, state of the art, benchmark and future opportunities. J. Artif. Intell. Res. 2024, 80, 1623–1701. [Google Scholar] [CrossRef]
- Elmachtoub, A.N.; Grigas, P. Smart “Predict, then Optimize”. Manag. Sci. 2022, 68, 9–26. [Google Scholar] [CrossRef]
- Wilder, B.; Dilkina, B.; Tambe, M. Melding the data-decisions pipeline: Decision-focused learning for combinatorial optimization. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1658–1665. [Google Scholar]
- Amos, B.; Kolter, J.Z. Optnet: Differentiable optimization as a layer in neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 136–145. [Google Scholar]
- Liu, Z.; Wang, Y.; Cheng, Q.; Yang, H. Analysis of the information entropy on traffic flows. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18012–18023. [Google Scholar] [CrossRef]
- Hong, Q.; Tian, X.; Li, H.; Liu, Z.; Wang, S. Sample Distribution Approximation for the Ship Fleet Deployment Problem Under Random Demand. Mathematics 2025, 13, 1610. [Google Scholar] [CrossRef]
- Ito, S.; Fujimaki, R. Optimization beyond prediction: Prescriptive price optimization. In Proceedings of the the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1833–1841. [Google Scholar]
- Basso, R.; Kulcsár, B.; Sanchez-Diaz, I. Electric vehicle routing problem with machine learning for energy prediction. Transp. Res. Part B Methodol. 2021, 145, 24–55. [Google Scholar] [CrossRef]
- Chen, X.; Owen, Z.; Pixton, C.; Simchi-Levi, D. A statistical learning approach to personalization in revenue management. Manag. Sci. 2022, 68, 1923–1937. [Google Scholar] [CrossRef]
- Donti, P.; Amos, B.; Kolter, J.Z. Task-based end-to-end model learning in stochastic optimization. Adv. Neural Inf. Process. Syst. 2017, 30, 5490–5500. [Google Scholar]
- Wallar, A.; Van Der Zee, M.; Alonso-Mora, J.; Rus, D. Vehicle rebalancing for mobility-on-demand systems with ride-sharing. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 4539–4546. [Google Scholar]
- Yan, R.; Yang, Y.; Du, Y. Stochastic optimization model for ship inspection planning under uncertainty in maritime transportation. Electron. Res. Arch. 2023, 31, 103–122. [Google Scholar] [CrossRef]
- Tian, X.; Yan, R.; Liu, Y.; Wang, S. A smart predict-then-optimize method for targeted and cost-effective maritime transportation. Transp. Res. Part B Methodol. 2023, 172, 32–52. [Google Scholar] [CrossRef]
- Chu, H.; Zhang, W.; Bai, P.; Chen, Y. Data-driven optimization for last-mile delivery. Complex Intell. Syst. 2023, 9, 2271–2284. [Google Scholar] [CrossRef]
- Huang, D.; Zhang, J.; Liu, Z.; He, Y.; Liu, P. A novel ranking method based on semi-SPO for battery swapping allocation optimization in a hybrid electric transit system. Transp. Res. Part E Logist. Transp. Rev. 2024, 188, 103611. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1996, 9, 155–161. [Google Scholar]
- Loh, W.Y. Classification and regression trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Choi, T.M.; Wallace, S.W.; Wang, Y. Big data analytics in operations management. Prod. Oper. Manag. 2018, 27, 1868–1883. [Google Scholar] [CrossRef]
- Dai, H.; Khalil, E.B.; Zhang, Y.; Dilkina, B.; Song, L. Learning combinatorial optimization algorithms over graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 6351–6361. [Google Scholar]
- Chen, B.; Chao, X. Dynamic inventory control with stockout substitution and demand learning. Manag. Sci. 2020, 66, 5108–5127. [Google Scholar] [CrossRef]
- Wang, C.; Peng, X.; Zhao, L.; Zhong, W. Refinery planning optimization based on smart predict-then-optimize method under exogenous price uncertainty. Comput. Chem. Eng. 2024, 188, 108765. [Google Scholar] [CrossRef]
- Alrasheedi, A.F.; Alnowibet, K.A.; Alshamrani, A.M. A smart predict-and-optimize framework for microgrid’s bidding strategy in a day-ahead electricity market. Electr. Power Syst. Res. 2024, 228, 110016. [Google Scholar] [CrossRef]
- Shapiro, J. Genetic algorithms in machine learning. In Advanced Course on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1999; pp. 146–168. [Google Scholar]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. In Breakthroughs in Statistics: Methodology and Distribution; Springer: Berlin/Heidelberg, Germany, 1992; pp. 492–518. [Google Scholar]



| No. | Study/Year | Use Case | Uncertain Variable | Optimization Objective |
|---|---|---|---|---|
| 1 | Donti et al. (2017) [16] | Inventory stocking | Stochastic demand | Minimize operational cost |
| 2 | Wallar et al. (2018) [17] | Ride-sharing fleet rebalancing | Spatial–temporal demand distribution | Minimize passenger delay and waiting time |
| 3 | Bertsimas & Kallus (2020) [1] | Media inventory management | Demand and auxiliary signals | Maximize profit under uncertainty |
| 4 | Basso et al. (2021) [14] | Electric vehicle routing | Energy consumption | Minimize route energy; ensure feasibility under uncertainty |
| 5 | Yan et al. (2023) [18] | Port state control inspection | Ship condition | Maximize service efficiency |
| 6 | Elmachtoub & Grigas (2022) [8] | Shortest path routing | Edge cost | Minimize travel time |
| 7 | Tian et al. (2023) [19] | Ship maintenance planning | Probability of ship deficiencies | Minimize total operational cost (inspection, repair, risk) |
| 8 | Chu et al. (2023) [20] | Online food delivery optimization | Travel time under uncertainty | Minimize delivery delay; improve assignment accuracy |
| 9 | Huang et al. (2024) [21] | Electric bus battery allocation | State of charge | Minimize service delay; improve allocation efficiency |
| 10 | Hong et al. (2025) [12] | Ship deployment scheduling | Cargo transport demand | Maximize enterprise profit |
| Name | Symbol | Value |
|---|---|---|
| Population size | P | 40 |
| Number of generations | G | 15 |
| Crossover rate | 0.7 | |
| Mutation rate | 0.1 | |
| Mutation scale factor | 0.5 | |
| Mutation decay exponent | 1.5 | |
| Loss interval indices | ||
| Breakpoints of loss | ||
| Dataset size | N | 1000 |
| Train–test split | - | 80%/20% |
| Number of features | d | 1 to 5 |
| Noise ratio | 0.5, 1.0, 2.0 | |
| Effective information ratio | 0.6, 0.8, 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, Q.; Jia, M.; Tian, X.; Liu, Z.; Wang, S. A Surrogate Piecewise Linear Loss Function for Contextual Stochastic Linear Programs in Transport. Mathematics 2025, 13, 2033. https://doi.org/10.3390/math13122033
Hong Q, Jia M, Tian X, Liu Z, Wang S. A Surrogate Piecewise Linear Loss Function for Contextual Stochastic Linear Programs in Transport. Mathematics. 2025; 13(12):2033. https://doi.org/10.3390/math13122033
Chicago/Turabian StyleHong, Qi, Mo Jia, Xuecheng Tian, Zhiyuan Liu, and Shuaian Wang. 2025. "A Surrogate Piecewise Linear Loss Function for Contextual Stochastic Linear Programs in Transport" Mathematics 13, no. 12: 2033. https://doi.org/10.3390/math13122033
APA StyleHong, Q., Jia, M., Tian, X., Liu, Z., & Wang, S. (2025). A Surrogate Piecewise Linear Loss Function for Contextual Stochastic Linear Programs in Transport. Mathematics, 13(12), 2033. https://doi.org/10.3390/math13122033








