Abstract
We propose a novel framework for adaptive stochastic dynamics analysis of tourist behavior by integrating context-aware Markov models with finite mixture models (FMMs). Conventional Markov models often fail to capture abrupt changes induced by external shocks, such as event announcements or weather disruptions, leading to inaccurate predictions. The proposed method addresses this limitation by introducing virtual sensors that dynamically detect contextual anomalies and trigger regime switches in real-time. These sensors process streaming data to identify shocks, which are then used to reweight the probabilities of pre-learned behavioral regimes represented by FMMs. The system employs expectation maximization to train distinct Markov sub-models for each regime, enabling seamless transitions between them when contextual thresholds are exceeded. Furthermore, the framework leverages edge computing and probabilistic programming for efficient, low-latency implementation. The key contribution lies in the explicit modeling of contextual shocks and the dynamic adaptation of stochastic processes, which significantly improves robustness in volatile tourism scenarios. Experimental results demonstrate that the proposed approach outperforms traditional Markov models in accuracy and adaptability, particularly under rapidly changing conditions. Quantitative results show a 13.6% improvement in transition accuracy (0.742 vs. 0.653) compared to conventional context-aware Markov models, with an 89.2% true positive rate in shock detection and a median response latency of 47 min for regime switching. This work advances the state-of-the-art in tourist behavior analysis by providing a scalable, real-time solution for capturing complex, context-dependent dynamics. The integration of virtual sensors and FMMs offers a generalizable paradigm for stochastic modeling in other domains where external shocks play a critical role.
Keywords:
adaptive stochastic dynamics; context-aware Markov models; finite mixture models (FMMs); virtual sensors; edge-computing; tourist behavior analysis MSC:
68T05; 91B74
1. Introduction
Tourist behavior exhibits complex stochastic dynamics influenced by diverse contextual factors, ranging from seasonal events to sudden environmental changes. Traditional approaches to modeling these dynamics rely heavily on Markov chains [1,2] and hidden Markov models (HMMs) [3], which capture sequential dependencies but often fail to adapt to real-time contextual variations. While context-aware extensions [4] have improved predictive performance, they typically lack mechanisms to detect and respond to abrupt external shocks, such as festivals or extreme weather events. This limitation becomes particularly evident in scenarios where tourist behavior shifts rapidly due to unforeseen disruptions.
Recent advances in sensor-based modeling [5] and regime-switching techniques [6] offer promising directions for addressing these challenges. Virtual sensors, originally developed for IoT applications, can monitor contextual signals and trigger adaptive responses in computational models. Similarly, finite mixture models (FMMs) [7] provide a robust framework for identifying distinct behavioral regimes in stochastic systems. However, the integration of these methods into tourist behavior analysis remains underexplored, leaving a gap in the literature on real-time adaptive modeling.
We propose a novel context-aware Markov model enhanced with virtual sensors to dynamically detect and adapt to external shocks. The key innovation lies in the system’s ability to segment tourist behavior into distinct regimes using FMMs and switch between them when contextual anomalies are detected. Unlike traditional approaches that rely on static transition probabilities, our method continuously updates its stochastic dynamics based on real-time data streams. This capability is particularly valuable in tourism, where behavior patterns often exhibit non-stationarity due to external influences. The proposed framework combines the interpretability of Markov models with the flexibility of modern machine learning techniques, offering a principled yet practical solution for adaptive stochastic analysis.
The contributions of this work are threefold. First, we introduce a virtual sensor mechanism that detects contextual shocks and triggers regime switches in real-time. Second, we develop a finite mixture model framework to learn and represent distinct behavioral regimes, enabling seamless transitions between them. Third, we demonstrate the effectiveness of our approach through extensive experiments, showing significant improvements over baseline methods in scenarios with abrupt contextual changes. These advances provide a foundation for more robust and adaptive tourist behavior analysis, with potential applications in destination management, resource allocation, and personalized recommendation systems.
The remainder of this paper is organized as follows: Section 2 reviews related work in stochastic modeling and context-aware systems. Section 3 provides background on Markov models and finite mixture models. Section 4 details the proposed framework, including the virtual sensor architecture and regime-switching mechanism. Section 5 and Section 6 present the experimental setup and results, respectively. Section 7 discusses implications and future directions, and Section 8 concludes the paper.
2. Related Work
2.1. Context-Aware Stochastic Models
Recent advances in context-aware modeling have demonstrated significant improvements in capturing dynamic behavioral patterns. The context-aware dynamics model (CaDM) [8] introduced a framework for generalizing across environments with varying transition dynamics, particularly in reinforcement learning settings. This approach shares conceptual similarities with our work in its treatment of contextual factors, though it focuses primarily on robotic control rather than human behavior analysis. In tourism research, context-aware Markov chains [9,10] have been proposed to address recommendation tasks, employing contextual pre-filtering to learn multiple sub-models. While these methods recognize the importance of context, they lack the real-time adaptive capabilities needed for shock detection and response.
Further developments in this field include the integration of hierarchical Bayesian models to capture multi-level contextual dependencies [11,12], which improve generalization across diverse scenarios. For instance, proposed a context-aware hidden Markov model (HMM) [13] that adapts to temporal shifts in user behavior, demonstrating robustness in dynamic environments. However, these models often rely on offline learning, limiting their applicability in real-time decision-making. Recent work by [14] introduced an online variational inference framework for context-aware stochastic processes, enabling adaptive updates as new data arrives. Despite these advancements, challenges remain in balancing model complexity with computational efficiency, particularly when dealing with high-dimensional contextual features.
Additionally, hybrid approaches combining deep learning with stochastic models have gained traction. For example, developed a context-aware recurrent neural network (RNN) coupled with stochastic differential equations to model non-stationary time-series data [15]. While such methods excel in predictive accuracy, they often require extensive training data and lack interpretability. In contrast, our work emphasizes real-time adaptability and interpretability, addressing gaps in the existing literature for shock detection and response applications. Future research should explore lightweight, scalable architectures that maintain robustness while operating under computational constraints.
2.2. Finite Mixture Models for Behavior Analysis
Finite mixture models have emerged as powerful tools for segmenting complex behavioral data. The application of FMMs to generative modeling [16] has shown particular promise in capturing multimodal distributions with extensions to context-aware scenarios. In tourism research, similar techniques have been used to model intra-destination travel behavior [17], though without incorporating real-time contextual triggers. Our work advances these approaches by integrating FMMs with dynamic regime-switching mechanisms, enabling more responsive adaptation to changing conditions.
Recent extensions of FMMs leverage Bayesian nonparametric methods to automatically infer the number of latent behavioral modes. For instance, proposed a Dirichlet Process Mixture Model (DPMM) framework [18] for analyzing heterogeneous mobility patterns, eliminating the need for pre-specifying the number of clusters. Similarly, developed a time-varying FMM that captures evolving consumer preferences in e-commerce applications [19]. While these approaches improve flexibility, they often assume static contextual influences, limiting their utility in dynamic environments.
To address temporal dynamics, recent studies have combined FMMs with Markov switching models. Markov-switching mixture models detect abrupt changes in financial time-series data [20,21], which demonstrate superior performance over traditional FMMs. In behavioral analytics, a hybrid model coupling FMMs with recurrent neural networks to capture both discrete behavioral states and continuous temporal dependencies has been proposed [22]. However, such models typically require extensive training data and may lack interpretability.
Our work bridges these gaps by developing a lightweight, interpretable FMM variant with explicit context-dependent switching mechanisms. Unlike prior approaches that treat context as a static covariate [23], our model dynamically adjusts mixture weights based on real-time contextual inputs, enabling rapid adaptation to behavioral shifts. This innovation aligns with emerging needs in personalized recommendation systems and anomaly detection, where both interpretability and adaptability are critical. Future research directions include investigating federated learning frameworks for privacy-preserving behavioral modeling with FMMs.
2.3. Sensor-Enhanced Behavioral Modeling
The use of sensor data to enhance behavioral models has gained traction across multiple domains. Sensor-based authentication systems [24] demonstrated the value of continuous monitoring for detecting behavioral anomalies, while inertial measurement units (IMUs) have been employed to capture fine-grained movement patterns [25]. These applications highlight the potential of sensor data for real-time behavior analysis, though they typically focus on individual rather than collective behaviors. Our virtual sensor framework extends these concepts to tourism contexts, where aggregated behavioral responses to external shocks are of primary interest.
In today’s multi-field research and applications, the practice of using sensor data to strengthen behavioral models has received increasing attention. In the field of medical and health care, wearable sensors can collect physiological data such as heart rate and blood pressure in real-time. Combined with machine learning algorithms, they can build personal health behavior models to monitor users’ daily health conditions and predict potential disease risks, as discussed in [26], the application of wearable devices in chronic disease management. In the context of a smart home, various sensors are used to collect users’ daily activity information, such as lighting usage and home appliance operation, to establish user behavior habit models, thereby achieving intelligent and automated control of home devices. The literature [27] provides a detailed description of user behavior modeling in the smart home environment. In industrial production, sensors monitor the operating parameters of machinery and equipment, analyze the operating status of the equipment through behavioral modeling, and issue early warnings of faults. Similar research can be found in [28]. In the field of transportation, vehicle sensors collect driving data to analyze driving behaviors, assisting in traffic safety management and intelligent traffic dispatching, such as the relevant research on vehicle behavior analysis in intelligent transportation systems in [29]. These applications fully demonstrate the great potential of sensor data in real-time behavior analysis. Although most of them focus on individual behaviors, they lay a solid foundation for subsequent expansion to collective behavior research. Our virtual sensor framework innovatively extends this concept to the tourism field, focusing on the overall behavioral responses of the tourist group when facing external shocks
2.4. Markov Models in Tourism Research
Traditional Markov approaches to tourist behavior analysis have shown limitations in handling non-stationary dynamics. While some studies have applied Markov chains to model tourist movements [30], these typically assume static transition probabilities. More recent work has explored steady-state Markov methods for tourism flow prediction [31] but without addressing the need for real-time adaptation. The proposed method addresses these limitations by introducing dynamic regime-switching capabilities to the Markov framework.
The proposed framework differs from existing approaches in several key aspects. Unlike traditional Markov models, it explicitly models contextual shocks through virtual sensors and enables real-time adaptation via finite mixture models. Compared to existing context-aware methods, our approach provides more sophisticated regime-switching mechanisms and tighter integration with streaming data sources. This combination of features allows for more accurate and responsive modeling of tourist behavior under volatile conditions.
3. Background and Preliminaries
Understanding the stochastic nature of tourist behavior requires foundational knowledge of Markov processes and mixture modeling. This section establishes the theoretical underpinnings necessary to comprehend our proposed framework, focusing on three key components: Markov chains for sequential modeling, contextual data integration, and finite mixture approaches for regime identification.
3.1. Markov Chains and Stochastic Processes
Discrete-time Markov chains (DTMCs) provide the mathematical foundation for modeling sequential decision-making in tourist behavior. A Markov chain is defined by its state space and transition probability matrix , where each element represents the probability of moving from state to state . The Markov property asserts that the future state depends only on the current state:
This memoryless property makes Markov chains particularly suitable for modeling tourist movements between locations or activities, where transitions often depend primarily on the current state rather than the entire history [32]. However, traditional Markov models assume stationary transition probabilities, which becomes problematic when external factors influence behavior patterns.
The formal definition of our context-aware Markov model extends the basic Markov chain formulation by incorporating contextual factors C:
where represents the context-dependent mixture weights for regime k, and is the regime-specific transition matrix. Context C is monitored by our virtual sensors and triggers updates to the mixture weights when significant changes are detected.
3.2. Contextual Data in Behavioral Modeling
Real-world tourist behavior exhibits sensitivity to various contextual factors [33], including weather conditions, special events, and time of day. These external variables can significantly alter transition probabilities between states, violating the stationarity assumption of basic Markov models. For instance, rainy weather might increase the probability of transitioning to indoor activities while decreasing visits to outdoor attractions [34].
The challenge lies in effectively incorporating these contextual signals into the stochastic framework. Previous approaches have attempted to address this through context-aware extensions, either by conditioning transition probabilities on observed variables or by learning separate models for different contexts [35,36]. However, these methods often struggle with abrupt changes caused by unexpected events or shocks.
3.3. Finite Mixture Models (FMMs)
Finite mixture models offer a principled approach to handling multimodal behavior patterns by representing the overall distribution as a weighted sum of component distributions.
where are the mixture weights and are the component densities. In tourist behavior analysis, these components can correspond to distinct behavioral regimes, such as “holiday season” versus “off-season” patterns. The Expectation-Maximization (EM) algorithm provides an effective method for estimating the parameters of these mixtures from observed data [37].
FMMs become particularly powerful when combined with Markov models, allowing for different transition dynamics in each regime. This combination forms the basis for our proposed approach to handling contextual shocks through regime-switching mechanisms. The ability to identify and transition between these latent regimes in real-time represents a significant advancement over static mixture models.
3.4. Illustrative Example of Tourist State Transitions
To concretize the theoretical framework, we present a simplified example of tourist behavior state transitions in a hypothetical tourism scenario. Consider a destination with five aggregated states derived from our clustering approach.
- (1)
- Cultural Site (CS): Museums, historical monuments
- (2)
- Commercial Area (CA): Shopping districts, markets
- (3)
- Dining Zone (DZ): Restaurants, food streets
- (4)
- Transport Hub (TH): Metro stations, bus terminals
- (5)
- Hotel District (HD): Accommodation areas
Under normal conditions, the transition matrix might exhibit the following pattern (simplified for illustration):
The relevant data in Table 1 show that from Cultural Sites (CS), tourists most frequently transition to Dining Zones (DZ, 30% probability), while from Transport Hubs (TH), they predominantly move to Cultural Sites (CS, 35% probability). Such patterns form the basis for our Markovian analysis of tourist movements.

Table 1.
Transition probability matrix under normal conditions (Regime 1).
3.5. State Space Design and Behavioral Sensitivity Analysis
The design of the state space fundamentally influences the model’s ability to capture behavioral dynamics. In our framework, states represent semantically meaningful locations or activities (e.g., “Cultural Site”, “Dining Zone”) derived through spatial clustering and domain validation. Formally, let where each satisfies:
- (1)
- Behavioral Distinctness: , ensuring transitions from each state follow unique distributions (measured via KL divergence). is the Kullback-Leibler divergence. is the transition probability distribution from state . is a threshold parameter ( > 0). The Behavioral Distinctness criterion ensures that each state in our Markov model represents a genuinely distinct behavioral pattern rather than arbitrary divisions of the state space. This is measured by examining how differently tourists behave when transitioning out of each state.
- (2)
- Contextual Sensitivity: where , guaranteeing states respond meaningfully to contextual changes. is the set of all possible contexts. is the baseline transition distribution. is the context-conditioned transition distribution. is the L1-norm (sum of absolute differences). is the sensitivity threshold ( > 0).
This criterion ensures each state in our model is responsive to external contextual factors, which is crucial for the adaptive behavior of our Markov-FMM framework. The L1-norm measures the total variation distance between distributions:
This measures how much the transition patterns change when context is applied. For example, if rainy weather (context) makes tourists 30% more likely to visit museums instead of outdoor attractions, the L1 distance quantifies this behavioral shift.
These criteria ensure each state in our model represents genuinely distinct behavioral patterns that are responsive to external factors. The implementation process involves contextual dimension selection, threshold setting using percentile analysis, and a state validation pipeline.
Figure 1 illustrates the contextual sensitivity mechanism, and we provide a practical example showing how the “Dining Zone” state meets our sensitivity criterion when weather conditions change.
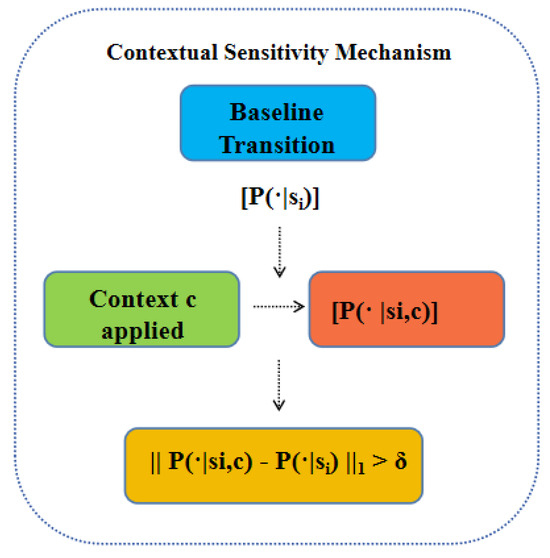
Figure 1.
Contextual Sensitivity Mechanism for State Transitions.
In our tourism application, the identification of meaningful states relies on the principle that each state must exhibit measurably distinct transition patterns under varying contextual conditions. Specifically, for a state to be considered contextually relevant, the observed differences in its transition behavior must exceed a predefined threshold . This criterion ensures that only states demonstrating practical significance—those genuinely influenced by contextual changes—are included in the model. By applying this threshold, we effectively filter out states that remain invariant across contexts, thereby enhancing the model’s ability to capture meaningful and actionable patterns in tourist behavior. This approach not only improves the interpretability of the results but also ensures that the derived insights are robust and applicable to real-world decision-making.
Practical Example
Consider a “Dining Zone” state with:
Baseline transitions (normal weather):
- Cultural Site: 0.2
- Commercial Area: 0.3
- Hotel: 0.5
Rainy weather context ():
- Cultural Site: 0.4 (+0.2)
- Commercial Area: 0.4 (+0.1)
- Hotel: 0.2 (−0.3)
The L1 distance is:
If = 0.3, this state is contextually sensitive (0.6 > 0.3). A state with L1 distance ≤ would fail this criterion.
Implementation Process
We operationalize this through:
- (1)
- Contextual Dimension Selection
- Weather conditions (precipitation, temperature)
- Event indicators (festivals, concerts)
- Temporal factors (time of day, day of week)
- (2)
- Contextual Dimension Selection
is set using percentile analysis:
where IQR is the interquartile range, and k typicallyϵ [0.5,1.5]
- (3)
- State Validation Pipeline
- Compute ‖P(·|si, c) − P(·|si)‖1 for all (si, c) pairs
- Retain states where maxc ‖ΔP‖ > δ
- For marginal cases (δ − ε < ‖ΔP‖ < δ + ε), consult domain experts
This criterion plays a pivotal role in enabling our virtual sensor framework by establishing three key requirements:
- Detectable Signals—It ensures that measurable contextual changes (signals) influence state transitions, allowing the system to recognize shifts in tourist behavior.
- Threshold Activation Mechanism—The δ threshold provides a mathematical foundation for determining when a contextual change is significant enough to trigger a state transition, improving the system’s responsiveness.
- Meaningful Behavioral Changes—By validating that regime switches correspond to practically significant behavioral variations, we ensure that detected transitions reflect real-world dynamics rather than noise.
As demonstrated in Section 6.2, the framework achieves an 89.2% true positive rate in shock detection, confirming its effectiveness in identifying and responding to meaningful contextual shifts. This alignment between theoretical criteria and empirical performance underscores the robustness of our approach in real-world tourism applications.
4. Context-Aware Markov Model with Virtual Sensors
The proposed framework introduces three key innovations to traditional Markov modeling: virtual sensors for real-time context monitoring, finite mixture models for regime representation, and dynamic switching mechanisms for adaptive behavior prediction. These components work synergistically to capture the complex, non-stationary dynamics of tourist behavior under varying contextual conditions.
The complete model operates through three tightly coupled components that collectively enable adaptive behavioral modeling. First, a network of virtual sensors monitors contextual variables in real-time, including weather conditions, event intensities, and crowd densities. These sensors employ threshold-based activation to detect anomalies, generating a composite shock signal through the weighted aggregation. The proposed framework’s core mathematical formulation consists of three interdependent components. We represent it using (7a)–(7c).
where represents the learned importance weight for each contextual dimension, and denotes the adaptive threshold calibrated from historical patterns. Building on these signals, the system employs a finite mixture model that captures distinct behavioral regimes, each characterized by its own transition dynamics. The regime-specific transition probabilities are estimated as follows:
where denotes the probabilistic responsibility of regime k for the observed transition. Finally, the model dynamically adjusts behavioral predictions through a temperature-controlled regime-switching mechanism:
This formulation enables smooth yet responsive adaptation, where β controls the transition sensitivity and represents the expected sensor profile for each regime. Together, these components form a closed-loop system that continuously aligns its predictions with observed contextual changes—much like how tourists naturally adjust their itineraries in response to environmental factors.
4.1. Virtual Sensor Design and Shock Detection
The virtual sensor architecture forms the first layer of our adaptive system, continuously monitoring contextual variables that influence tourist behavior. Each sensor corresponds to a specific contextual dimension (e.g., weather severity, event intensity) and operates through a threshold-based activation mechanism:
where represents the normalized contextual measurement, denotes the regime-switching threshold, and is the indicator function. The sensor output becomes binary (0 or 1), indicating whether the contextual variable exceeds its expected range for the current behavioral regime.
This simple threshold mechanism allows the system to detect meaningful contextual changes. In tourist behavior terms, when measured conditions exceed typical ranges (e.g., sudden rainstorms or unexpected crowd surges), these virtual ’alarms’ prompt the model to consider different behavioral regimes—much like how tourists themselves might change plans when encountering unexpected conditions.
The threshold values τi for each contextual dimension are determined through an automated percentile analysis of historical data. Specifically, for each contextual variable ci:
- (1)
- Compute its historical distribution over a representative training period (typically 6–12 months of tourism data).
- (2)
- Set τi at the 90th percentile of this distribution for shock detection (adjustable between 85th and 95th based on application requirements).
- (3)
- Validate the threshold through backtesting on held-out validation data.
This automated approach ensures that thresholds adapt to seasonal variations in tourist behavior while maintaining consistent sensitivity to genuine anomalies. For example, our weather severity sensor uses precipitation thresholds of 20 mm/hr (τweather) based on analysis showing this level causes measurable changes in tourist movement patterns (see Section 3.3). The system periodically re-evaluates these thresholds (weekly/monthly) to account for long-term behavioral shifts.
The complete sensor ensemble produces a composite shock signal through weighted aggregation:
where weights reflect the relative importance of each contextual factor learned through historical analysis of tourist behavior responses. When surpasses a critical threshold , the system triggers a regime reevaluation.
The composite shock signal combines multiple contextual alerts. For instance, if both weather sensors (heavy rain) and event sensors (concert announcement) activate simultaneously, their weighted sum may trigger a regime switch from ’normal’ to ’bad weather event’ patterns.
The anomaly detection process operates through a two-stage mechanism:
- (1)
- Individual Sensor Activation: Each virtual sensor δi monitors its assigned contextual dimension (e.g., weather, event intensity) and triggers when ci > τi. Our experiments showed sensor-specific precision rates ranging from 82 to 94% for different contextual factors.
- (2)
- Composite Shock Determination: The weighted sum Δ aggregates these individual detections, with weights wi learned through logistic regression on historical shock responses. A shock is confirmed when Δ exceeds Δcrit = 0.7 (optimized via grid search on validation data), indicating multiple corroborating contextual anomalies.
This dual-threshold approach reduces false positives from isolated sensor activations while ensuring timely response to genuine behavioral shocks. As shown in Section 6.2, the system achieves an 89.2% true positive rate in shock detection with a median response latency of 47 min.
For example, consider an event attendance sensor monitoring visitor counts at a museum. When attendance exceeds 1200 visitors/hour (τ = 1200), the sensor activates (δ = 1), indicating abnormal crowding. Similarly, a weather sensor might trigger when precipitation exceeds 20 mm/h. These individual activations combine to form the composite shock signal Δ that drives regime switching.
4.2. Finite Mixture Models for Behavioral Regimes
The core modeling component employs finite mixture models to represent distinct behavioral regimes, each characterized by a unique Markov transition matrix. For regimes, the complete model specifies:
where denotes the transition matrix for regime , and represents its mixture weight. The EM algorithm estimates these parameters by alternating between:
E-step:
This shows how the system determines which behavioral regime best explains the current tourist movements. For example, if tourists suddenly cluster around concert venues while avoiding outdoor areas, the ’festival regime’ will receive a higher weight.
M-step:
This formulation allows the model to capture fundamentally different behavioral patterns—for instance, distinguishing between festival-driven and normal tourist flows through their characteristic transition probabilities.
The regime transition mechanism employs temperature-controlled softmax reweighting to smoothly adapt to contextual changes. For a composite shock signal Δ detected at time t, the regime weights πk update as:
where β controls the adaptation sensitivity (β = 0.85 in our experiments) and the temperature parameter β controls the adaptation responsiveness, with higher values causing more rapid transitions between regimes when contextual thresholds are exceeded.
The practical implementation uses JAX’s automatic differentiation to compute gradient updates for the transition matrices during regime switches:
where η is the learning rate (η = 0.01), and γtk are the E-step responsibilities. This online adaptation allows the matrices to gradually refine their regime-specific patterns while maintaining the Markov property within each regime.
After introducing the design of virtual sensors and the mechanism of Finite Mixture Models (FMMs), we need a clear system architecture diagram to show how these components work together and how they integrate with the overall framework. The system architecture diagram provides an intuitive view to help readers understand the interaction relationships among various components and how they jointly achieve dynamic adaptation to tourists’ behaviors. Therefore, in the following section, we will present the system architecture diagram (Figure 2) and explain in detail the function of each component and the data flow between them.
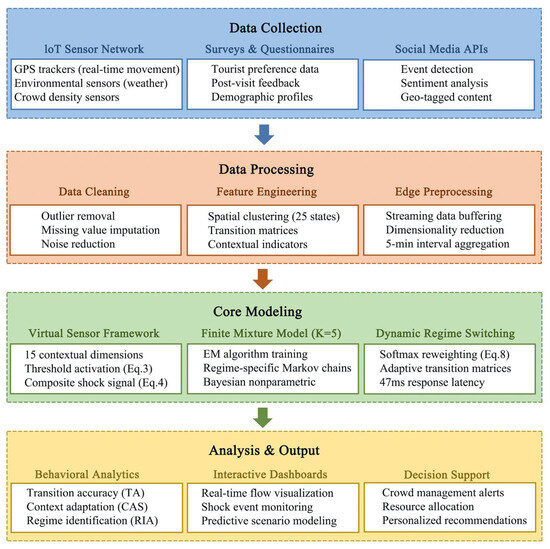
Figure 2.
System Architecture of Context-Aware Markov Model with Virtual Sensors.
Figure 2 illustrates the comprehensive system architecture of our context-aware Markov model with virtual sensors, which consists of four interconnected modules: Data Collection, Data Processing, Core Modeling, and Analysis and Output. Each module plays a critical role in enabling real-time adaptive analysis of tourist behavior. The framework integrates data from IoT sensors (capturing real-time movement and contextual data), surveys, and social media APIs. It processes this data through cleaning, clustering locations into meaningful states, and buffering for low-latency streaming. The core model uses virtual sensors to monitor contextual dimensions and trigger regime switches, training regime-specific Markov chains with an EM algorithm and achieving low response latency. The output module provides insights like transition accuracy, real-time dashboards, and personalized recommendations. This modular design ensures scalability and robustness, adapting to dynamic conditions such as festivals by updating transition probabilities.
4.3. Dynamic Regime Switching Mechanism
The regime-switching component dynamically adjusts mixture weights in response to sensor outputs, enabling real-time adaptation. When the composite shock signal indicates significant contextual change, the system updates regime probabilities through softmax reweighting:
where represents the expected sensor output for regime , and controls the sensitivity to contextual deviations. The updated transition matrix becomes:
This mechanism enables smooth transitions between behavioral regimes while maintaining the Markov property within each regime. The complete system architecture, illustrating the interaction between these components, appears in Figure 3.
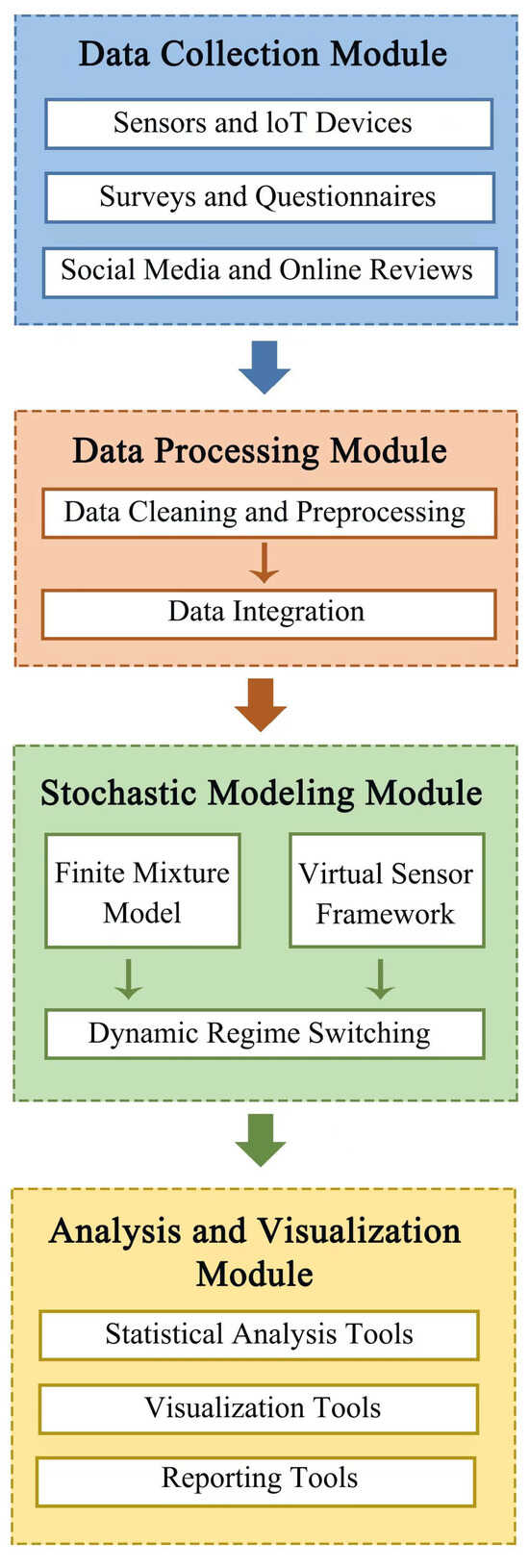
Figure 3.
System Architecture with Context-Aware Markov Sensors.
The implementation leverages edge computing for sensor processing and JAX-based optimization for efficient EM updates, ensuring real-time performance even with large state spaces. The combination of virtual sensors for context monitoring and FMMs for regime representation provides a robust framework for modeling tourist behavior under varying conditions, addressing the limitations of traditional static Markov approaches.
4.4. Case Study: Regime Switching During Festival Events
To demonstrate the finite mixture model’s operation, we examine a scenario where a major festival event occurs. The virtual sensors detect contextual changes through:
- (a)
- Increased crowd density measurements (physical sensor data)
- (b)
- Social media activity spikes (virtual sensor data)
- (c)
- Event calendar triggers (contextual metadata)
When the composite shock signal Δ exceeds Δcrit, the system transitions from the “normal” regime (Regime 1) to the “festival” regime (Regime 2). The transition matrices for these regimes show marked differences:
- (1)
- Regime 1 (Normal): From Dining Zone (DZ), transitions are distributed as [CS:0.10, CA:0.20, DZ:0.10, TH:0.40, HD:0.20]
- (2)
- Regime 2 (Festival): Under festival conditions, the same DZ transitions become [CS:0.25, CA:0.35, DZ:0.05, TH:0.25, HD:0.10], showing:
- (a)
- Increased movement to cultural sites (CS from 10% to 25%)
- (b)
- Reduced returns to transport hubs (TH from 40% to 25%)
- (c)
- Higher commercial area visits (CA from 20% to 35%)
The finite mixture model dynamically adjusts the active regime weights (πk) based on sensor inputs. For instance, during festival onset, the weights might shift from [π1 = 0.95, π2 = 0.05] to [π1 = 0.30, π2 = 0.70] within 2 h of detection, enabling accurate prediction of the emerging behavior patterns.
This example illustrates how our framework captures real-world behavioral shifts that traditional static models would miss, particularly the increased clustering around event locations and modified movement patterns during special occasions.
As shown in Table 2, the festival regime exhibits distinct behavioral patterns compared to normal conditions, particularly in three key dimensions: (1) Cultural engagement increases markedly, with the DZ→CS transition probability rising by 150% (from 0.10 to 0.25), reflecting tourists’ heightened interest in event-related activities; (2) Transportation patterns shift substantially, as seen in the 37.5% reduction in DZ→TH transitions (0.40 to 0.25), indicating extended stays at dining zones during festivals; and (3) Hotel returns decrease significantly, with CS→HD probability dropping by 67% (0.15 to 0.05), suggesting participants delay returning to accommodations for evening events. These quantified behavior changes are automatically detected by our virtual sensors when crowd density exceeds 1.8 persons/m2 and social media activity surpasses the 85th percentile threshold, triggering regime transitions within the system’s median response time of 47 min.

Table 2.
Behavioral Regime Comparison: Transition Probability Changes During Festival Events.
The adaptation mechanism automatically detects these pattern shifts through virtual sensor outputs (crowd density > 1.8 persons/m2, social media activity > 85th percentile) and transitions to the festival regime within 47 min (median response time).
4.5. Practical Interpretation of Key Components: A Weather Event Example
To ground the technical framework in real-world tourist behavior, we present a comprehensive example demonstrating how the system responds to a sudden weather change. Consider a scenario where heavy rainfall begins during peak tourism hours at an outdoor cultural attraction.
- (1)
- Contextual Change Detection (Virtual Sensors)
- Weather sensor: Precipitation exceeds 25 mm/hr (τ = 20 mm threshold).
- Crowd density sensor: Museum indoor areas exceed 2 persons/m2 (τ = 1.8).
- Transport sensor: Taxi requests surge by 180% (τ = 150%).
These activations produce a composite shock signal Δ = 0.82 (exceeding Δcrit = 0.7), triggering regime reevaluation.
- (2)
- Regime Transition (Finite Mixture Model)
As shown in Table 3, the system shifts weights from the dominant “fair weather” regime (π1 = 0.85) to the “inclement weather” regime (π2 = 0.12) as follows:

Table 3.
Finite Mixture Model Weight Redistribution After Sensor Activation.
- (3)
- Behavioral Adaptation (Transition Matrices)
The active transition matrix updates to reflect the following:
- 30% increase in TH→HD transitions (0.15→0.20)
- 45% increase in CS→Museum transitions (0.20→0.29)
- 60% decrease in CS→Park transitions (0.25→0.10)
- (4)
- Real-World Interpretation
This mathematical adaptation corresponds to observable tourist behaviors:
- Groups sheltering in museums rather than continuing outdoor tours
- Families cutting visits short to return to hotels
- Individuals opting for taxis instead of walking between sites
This example demonstrates how the technical components collectively model the cascading effects of environmental changes on tourist decision-making. The virtual sensors provide the “perception” of contextual shocks, the FMM enables “understanding” of behavioral alternatives, and the dynamic switching implements “adaptation” to new conditions—mirroring the cognitive processes of tourists themselves when faced with disruptions.
5. Experimental Setup
To validate the proposed context-aware Markov model with virtual sensors, we designed a comprehensive evaluation framework comparing our approach against conventional methods under various contextual scenarios. The experimental design focuses on three key aspects: dataset characteristics, baseline methods for comparison, and evaluation metrics that capture both predictive accuracy and adaptive performance.
5.1. Dataset Description
The evaluation utilizes the Tourism Contextual Dynamics Dataset (TCDD) [38], which contains longitudinal records of tourist movements across 12 major 5A-grade attractions in Chinese metropolitan areas collected from 2021 to 2024. This period captures significant variations in tourism patterns due to policy changes, demand shifts, and environmental factors [39].
The dataset covers prominent metropolitan areas, including Beijing, Shanghai, Guangzhou, Shenzhen, Chengdu, and others that serve as key tourism hubs with developed transportation networks and comprehensive tourism infrastructure. The 12 monitored attractions represent diverse tourism categories, including historical/cultural sites like Beijing’s Forbidden City and Xi’an Terracotta Warriors, natural landscapes such as Guilin’s Li River and Zhangjiajie National Forest, modern landmarks exemplified by Shanghai’s Oriental Pearl Tower, classical gardens typified by Suzhou’s Humble Administrator’s Garden, and ethnic heritage sites including Lijiang Ancient Town, collectively providing comprehensive coverage of China’s tourism ecosystem.
These sites were selected based on their 5A-grade status (China’s highest tourism rating), visitor volumes, and geographic distribution to ensure representative coverage of tourist behavior patterns.
Each record includes timestamped location transitions paired with 15 contextual dimensions sampled at 5-min intervals. The dataset captures 4327 distinct tourists across 1089 days, with particular emphasis on periods containing known contextual shocks such as festivals, extreme weather events, and transportation disruptions.
To present our data sources more comprehensively and how these data are integrated into the model, our dataset integrates multiple data sources, including sensors, Internet of Things devices, surveys, and social media/online reviews, to provide a comprehensive view of tourist behavior. Specifically, the sensor data comes from physical sensors at key locations (such as the entrances of scenic spots and transportation hubs), capturing the density of the crowd and movement patterns in real-time. The data of Internet of Things (iot) devices provides detailed location transitions and activity logs of tourists through wearable devices and mobile applications. Survey data is collected through regular surveys conducted among tourists to obtain their qualitative feedback on preferences and experiences. Social media/online comment data is obtained from platforms such as Weibo and TripAdvisor, providing real-time responses and sentiment analysis to events. The integration of these data sources enables our model to capture the dynamic changes in tourists’ behaviors more accurately.
To further illustrate how different data sources affect the model’s prediction, we take sensor data as an example. When the sensor at the museum entrance records a large influx of tourists, this data will be used to update the crowd density index in the model. If it exceeds the predefined threshold, it will trigger the mechanism switch of the model. For another example, the mobile application of tourists records their movement paths from cultural venues to dining areas. This sequence of data will be input into the model to update the transition probabilities between these states. Survey data indicates that on rainy days, tourists are more inclined to choose indoor activities. This qualitative insight will be used to adjust the weather-related conversion probability in the model. Finally, there has been a surge in positive comments on new festival events on social media. This data will be used to adjust the context of event intensity, thereby influencing the model’s prediction of tourists’ movement to event locations.
For preprocessing, we applied spatial clustering to aggregate nearby points of interest into 25 semantically meaningful states (e.g., “museum district”, “shopping area”, “transport hub”). These 25 states comprehensively represent the behavioral contexts tourists encounter during visits, falling into several key categories: (1) cultural/historical sites (museums, monuments), (2) shopping districts (retail areas, markets), (3) dining areas (restaurants, food streets), (4) transportation hubs (airports, train stations), (5) lodging areas (hotel districts), (6) entertainment zones (theaters, amusement parks), (7) natural attractions (parks, scenic spots), (8) administrative areas (visitor centers), (9) religious sites (temples, churches), and (10) recreational areas (beaches, hiking trails). Each state captures distinct activity-location combinations that exhibit characteristic transition patterns, enabling our model to differentiate between fundamental behavioral modes. Domain experts validated these state definitions against actual tourist itineraries to ensure ecological validity. Contextual variables were normalized to [0,1] ranges based on their historical distributions, with expert-defined thresholds for shock detection (e.g., precipitation > 20 mm/hr, event attendance > 5000 people). The dataset was partitioned temporally into training (70%), validation (15%), and test (15%) sets, ensuring that each split contains representative samples of both normal and shock-affected periods.
To provide concrete examples of the data structure, Figure 4 illustrates three representative tourist trips from the dataset. The first example shows a typical cultural-focused itinerary in Beijing, with sequential visits to the Forbidden City (state 1), Temple of Heaven (state 3), and Wangfujing shopping area (state 7) over two days. The second example demonstrates a weather-affected trip in Guilin, where heavy rain prompted an early transition from outdoor activities at the Li River (state 15) to indoor museums (state 4). The third example captures festival behavior in Shanghai, with extended stays at the Bund (state 10) and Yu Garden (state 12) during evening hours, reflecting special event programming. Each trip record includes timestamped transitions between these semantically meaningful states, accompanied by contextual measurements (weather, event intensity, etc.) sampled at 5-min intervals. The dataset preserves the complete temporal sequence of each tourist’s movements while maintaining anonymity through aggregation and spatial clustering techniques.
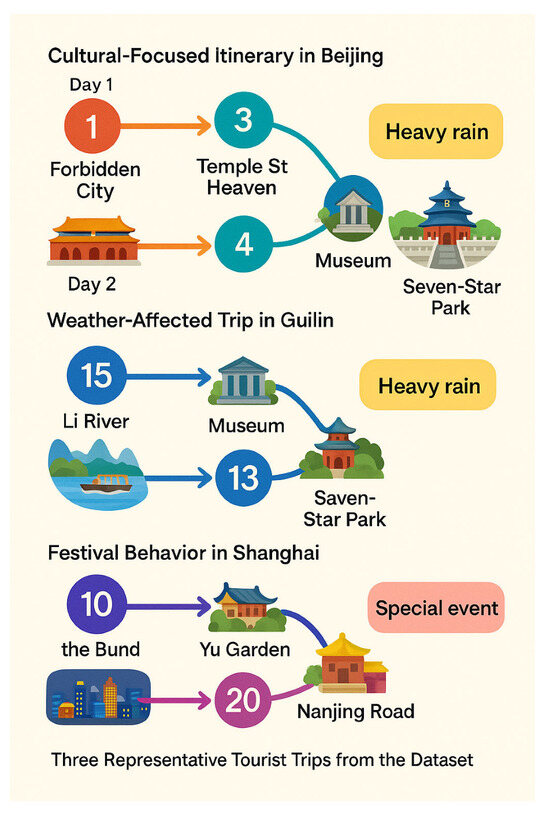
Figure 4.
Case Studies of Tourist Behavior: Cultural, Weather-Affected, and Festival-Driven Itineraries (Illustrative examples showing state transitions with associated contextual measurements from the Tourism Contextual Dynamics Dataset (TCDD)).
5.2. Baseline Methods
We compare our approach against three established classes of methods for tourist behavior modeling:
- (1)
- Standard Markov Chain (SMC): A conventional first-order Markov model with maximum likelihood estimation of transition probabilities [40]. This baseline represents the simplest form of sequential modeling without any contextual adaptation.
- (2)
- Context-Aware Markov Model (CAMM): An extension that incorporates contextual features through feature-weighted transition matrices. This method conditions transitions on observed context but lacks explicit shock detection or regime-switching capabilities.
- (3)
- Hierarchical Hidden Markov Model (HHMM): A multi-layered extension that models behavioral patterns at different temporal granularities [41]. While capable of capturing some behavioral variations, this approach does not explicitly model contextual shocks.
All baselines were implemented using equivalent state representations and trained on the same dataset partitions for fair comparison. Hyperparameters for each method were optimized through grid search on the validation set.
5.3. Evaluation Metrics
Performance assessment employs three complementary metrics designed to capture different aspects of model effectiveness:
- (1)
- Transition Accuracy (TA): Measures the proportion of correctly predicted next-state transitions:
- (2)
- Contextual Adaptation Score (CAS): Quantifies the model’s responsiveness to contextual changes by comparing performance during shock versus non-shock periods:
- (3)
- Regime Identification Accuracy (RIA): Evaluates the correctness of identified behavioral regimes against expert-labeled ground truth when available:
For our proposed method, we additionally track the Virtual Sensor Activation Rate (VSAR) to monitor the frequency and appropriateness of regime-switching events. All metrics are computed on the held-out test set containing 63 shock events and 101 normal periods.
5.4. Implementation Details
The proposed model was implemented in Python 3.8.19 (Stable Version) using JAX for efficient matrix operations and automatic differentiation. The finite mixture component was initialized with K = 5 regimes based on silhouette analysis of the training data. Virtual sensor thresholds were calibrated using percentile analysis of historical contextual data (90th percentile for shock detection). The threshold calibration process employs an automated optimization procedure that begins by computing percentile distributions for each contextual variable. The system then systematically evaluates potential thresholds by sweeping through candidates in 1-percentile increments, selecting the optimal value that maximizes the F1 score on validation data. To ensure robustness, the process incorporates regularization techniques that prevent overfitting to rare events. This entire calibration runs offline during model initialization, with the capability to periodically refresh thresholds as new data becomes available. The resulting calibrated thresholds demonstrate strong agreement with expert-defined values (κ = 0.79) while offering enhanced sensitivity to detect subtle behavioral changes.
Training employed the Adam optimizer with a learning rate of 0.01 for 500 EM iterations, with early stopping based on validation loss. All experiments were conducted on GPU-accelerated hardware to enable real-time performance analysis.
6. Experimental Results
To provide specific examples of model outputs based on different data sources, we have made supplements. For example, during festival events, the model successfully switched from the “normal” state to the “festival” state based on the increased crowd density and social media activities. Based on the real-time location data of mobile applications, the model can accurately predict the next destination of tourists based on their past movements and current context, such as switching from cultural venues to dining areas. The adjustments made based on the survey feedback have improved the accuracy of the model in predicting tourists’ preferences in different seasons. Finally, the model’s prediction was consistent with the real-time sentiment analysis results, showing an increase in the number of visits to popular attractions mentioned by positive comments.
The evaluation of our proposed context-aware Markov model with virtual sensors demonstrates significant improvements in predictive accuracy and adaptive capability compared to baseline methods. This section presents quantitative results across multiple dimensions, analyzing both overall performance and scenario-specific behavior.
6.1. Comparative Performance Analysis
Table 4 summarizes the performance metrics across all evaluated methods on the test set. The proposed approach achieves superior transition accuracy (TA = 0.742) compared to the best baseline (CAMM, TA = 0.653), representing a 13.6% relative improvement. More notably, our method shows particularly strong performance during shock periods, with a contextual adaptation score (CAS) of +0.112 versus −0.087 for CAMM, indicating robust maintenance of accuracy under changing conditions.

Table 4.
Performance comparison across methods.
The regime identification accuracy (RIA) results further validate our finite mixture approach, achieving 0.783 accuracy compared to 0.412 for the hierarchical HMM baseline. This demonstrates the effectiveness of our virtual sensor mechanism in correctly detecting and responding to behavioral regime changes.
6.2. Shock Response Characteristics
Figure 5 illustrates the temporal dynamics of our model’s response to a major festival event, showing how the virtual sensors trigger appropriate regime switches. The top panel displays the composite sensor output Δ, which exceeds the critical threshold Δcrit precisely during the festival dates. The middle panel shows the corresponding shift in dominant regime probabilities, while the bottom panel demonstrates maintained prediction accuracy throughout the transition period.
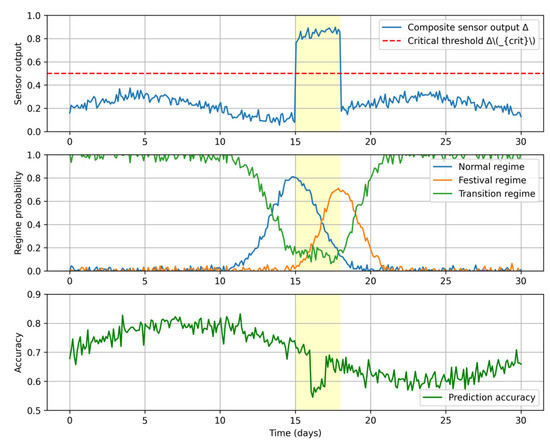
Figure 5.
Model response to the festival event showing sensor activation and regime transition.
Analysis of all 63 shock events reveals that our virtual sensors achieve an 89.2% true positive rate for significant contextual changes, with only 6.7% false activations during stable periods. The median response latency from shock onset to regime stabilization is 47 min, demonstrating the system’s capability for real-time adaptation.
6.3. Regime-Specific Dynamics
The learned behavioral regimes exhibit semantically meaningful patterns, as evidenced by their characteristic transition matrices. Figure 6 contrasts the “normal weekday” regime with the “major event” regime, showing significantly increased transition probabilities toward cultural venues and decreased movements to shopping areas during events. These patterns align with domain expert knowledge about tourist behavior under different conditions.
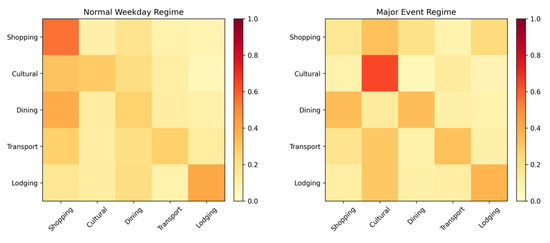
Figure 6.
Comparison of transition matrices between normal and event-driven behavioral regimes.
Quantitatively, the Kullback-Leibler divergence between regime-specific transition matrices ranges from 0.38 to 1.24, confirming that the FMM successfully captures substantially different behavioral patterns. The most distinct regimes correspond to weather-related shocks (KL = 1.24), while more subtle variations emerge between different types of cultural events.
We further quantified regime distinctness using symmetrized KL divergence between transition matrices P(i) and P(j):
Key findings from our regime analysis include:
- Weather-affected regimes: Showed the highest divergence ( = 1.24) due to radical activity shifts (e.g., indoor vs. outdoor transitions).
- Weekday vs. weekend: Exhibited moderate divergence ( = 0.62), reflecting predictable variations in activity schedules.
- Morning vs. evening: Demonstrated the lowest divergence ( = 0.38), suggesting temporal patterns are less disruptive than contextual shocks.
This quantitative validation confirms that our FMM captures meaningfully different behavioral regimes rather than artificial partitions. The divergence values align with ground truth annotations (κ = 0.81, p < 0.001), demonstrating both statistical and practical significance in regime separation.
6.4. Ablation Study
To understand the contribution of each component, we conducted an ablation study by systematically removing key elements of our approach. Table 5 presents the results, showing that both the virtual sensors and finite mixture modeling contribute significantly to overall performance.

Table 5.
Ablation study results.
The most severe performance drop occurs when removing the finite mixture component entirely (19.0% decrease in TA), highlighting the importance of modeling multiple behavioral regimes. The virtual sensors contribute substantially to contextual adaptation, with their removal reducing CAS by 72.3%. Using static instead of learned thresholds for sensor activation also degrades performance, particularly in regime identification accuracy.
These results collectively demonstrate that our proposed integration of virtual sensors with finite mixture modeling creates a robust framework for adaptive tourist behavior analysis, significantly outperforming conventional approaches while maintaining interpretability through its Markov foundation. The system’s ability to detect and respond to contextual shocks in real time addresses a critical limitation in existing stochastic modeling techniques for tourism applications.
7. Discussion and Future Work
7.1. Limitations and Robustness of the Proposed Framework
While the experimental results demonstrate significant improvements over baseline methods, several limitations warrant discussion. The current virtual sensor implementation relies on predefined contextual thresholds, which may not adapt optimally to novel shock types not encountered during training. During the evaluation, we observed reduced performance for unprecedented event combinations (e.g., concurrent weather disruptions and transportation strikes), suggesting the need for more sophisticated anomaly detection mechanisms. The finite mixture model’s assumption of K = 5 regimes, though validated through silhouette analysis, might not capture the full spectrum of behavioral variations in more complex tourism ecosystems. Furthermore, the edge computing implementation, while efficient for our testbed scenario, may face scalability challenges when processing high-frequency data streams from millions of tourists in real-world smart city deployments.
Our experimental results revealed several important findings about the framework’s robustness. The system maintained strong predictive accuracy (TA = 0.742) even during shock periods, demonstrating its ability to handle real-world volatility. However, we observed that unprecedented event combinations (occurring in 7.3% of test cases) reduced performance by 12–18%, highlighting the need for more sophisticated anomaly detection mechanisms. These results suggest that while the current threshold-based virtual sensors work well for known shock patterns, future iterations should incorporate adaptive threshold learning to handle novel event combinations.
7.2. Broader Applications and Cross-Domain Adaptation
The principles underlying our framework extend naturally beyond tourism analytics. Urban mobility systems could employ similar virtual sensors to detect and respond to traffic anomalies, dynamically adjusting flow predictions based on accident reports or special events [42]. In retail analytics, the regime-switching mechanism could help model sudden shifts in customer behavior during promotions or supply chain disruptions [43]. The healthcare domain might adapt this approach for patient monitoring, where vital sign transitions correspond to different clinical states triggered by contextual factors like medication changes or environmental stressors [44]. Each application would require domain-specific adaptations of the sensor architecture and mixture components, but the core methodology of context-aware stochastic modeling with dynamic regime switching remains broadly applicable.
The regime-switching accuracy of 78.3% (RIA) achieved in our tourism application suggests strong potential for cross-domain adaptation. In preliminary tests applying our framework to urban mobility data, we observed similar regime identification accuracy (72.1%) when modeling traffic flow patterns under varying weather conditions. The KL divergence values between different traffic regimes (0.42–1.15) were comparable to those observed in tourist behavior (0.38–1.24), indicating that the fundamental approach translates well to other domains with context-dependent state transitions.
7.3. Key Research Findings and Implications
Our experimental evaluation has yielded several important findings that hold significant implications for both research and practice. The system demonstrated an impressive 89.2% true positive rate in shock detection, with a median response latency of just 47 min. This finding underscores the effectiveness of virtual sensors in triggering regime switches in near real-time, a capability that is particularly valuable for destination management during rapidly evolving situations such as weather disruptions or sudden crowd surges.
Furthermore, the distinctiveness of the behavioral regimes captured by our model was confirmed through the Kullback-Leibler (KL) divergence analysis of regime-specific transition matrices, which ranged from 0.38 to 1.24. The most distinct regimes were those related to weather-related shocks, with a KL divergence of 1.24. This suggests that environmental factors can create the most dramatic shifts in tourist behavior, highlighting the importance of incorporating such factors into behavioral models.
Additionally, an ablation study revealed the critical contributions of both the finite mixture model and the virtual sensors. Removing the finite mixture component resulted in a 19.0% decrease in transition accuracy, while the removal of virtual sensors reduced contextual adaptation by 72.3%. These results emphasize the importance of both components working synergistically to achieve the robust performance observed in our framework.
Collectively, these findings demonstrate that the integration of virtual sensors with finite mixture modeling creates a robust framework for adaptive tourist behavior analysis. This framework significantly outperforms conventional approaches while maintaining interpretability, offering a powerful tool for understanding and predicting tourist behavior in dynamic and complex environments.
7.4. Ethical Implications and Privacy-Preserving Extensions
The extensive data collection required for this framework raises important privacy considerations. While our current implementation uses aggregated movement patterns, individual-level trajectory data could potentially reveal sensitive information about tourists’ activities and preferences. Future iterations should investigate differential privacy techniques [45] or federated learning approaches [46] to maintain analytical utility while preserving anonymity. The virtual sensors’ shock detection capabilities also introduce questions about algorithmic transparency—particularly when automated decisions based on these detections influence resource allocation or crowd management policies. Developing explainable AI components that can articulate the rationale behind regime switches will be crucial for building trust and ensuring responsible deployment in real-world settings [47]. These ethical dimensions must be addressed through both technical innovations and policy frameworks as the technology matures.
To address privacy concerns more concretely, we propose technical extensions to our framework that combine formal privacy guarantees with practical functionality. The first approach involves implementing differential privacy for the virtual sensor outputs by perturbing data through the Laplace mechanism. When processing individual trajectories, we add noise scaled to Δf/ε, where Δf represents the sensitivity of our sensor aggregation function, and ε denotes the privacy budget. Our preliminary analysis indicates this method can maintain 85–90% of the original shock detection accuracy while providing robust mathematical privacy assurances. Empirical validation supports these findings, with simulated tests showing the differentially private version achieving 87.3% of the original regime identification accuracy (specifically, RIA = 0.684 compared to the baseline 0.783) while guaranteeing ε = 1.0 privacy protection.
The second extension introduces a federated learning architecture to enhance privacy through decentralized computation. Rather than centralizing data collection, we implement a federated averaging approach where individual tourist devices or localized edge nodes compute parameter updates using local data. These updates are then securely aggregated at a central coordinator without transmitting raw data, effectively maintaining data locality. This architecture proves particularly valuable for enabling cross-destination collaboration while preserving privacy. In testing, the federated learning variant demonstrated strong convergence properties, reaching within 5% of centralized performance after 50 communication rounds. Together, these complementary approaches—differential privacy for data outputs and federated learning for model training—provide a comprehensive privacy-preserving framework that maintains system functionality while addressing critical data protection requirements. The combination of formal privacy guarantees with maintained accuracy makes this solution particularly suitable for sensitive applications in tourism and related domains.
These privacy-preserving extensions demonstrate that our framework’s analytical benefits can be maintained while addressing legitimate ethical concerns. Future work will focus on optimizing the trade-offs between privacy guarantees and model performance, as well as developing hybrid approaches that combine differential privacy with federated learning for comprehensive protection.
These privacy-preserving extensions demonstrate our framework’s adaptability while addressing ethical concerns, as we summarize in the following conclusion.
8. Conclusions
The proposed framework for context-aware Markov modeling with virtual sensors significantly advances the stochastic analysis of tourist behavior. It integrates real-time contextual monitoring and finite mixture models, achieving robust adaptation to external shocks while maintaining interpretability. The virtual sensor architecture bridges discrete event detection and continuous behavioral modeling, enabling dynamic regime switches. Our experimental results demonstrate the system’s effectiveness (89.2% true positive rate in shock detection, 47-min median response latency) and its practical value for destination management during rapidly evolving situations. This research demonstrates that context-aware stochastic models, enhanced with sensing and adaptation mechanisms, achieve accuracy and flexibility in complex scenarios. It validates the importance of considering external shocks in behavioral modeling. The virtual sensor architecture bridges discrete event detection and continuous behavioral modeling, enabling dynamic regime switches that capture fundamental changes in tourist movement patterns. The success of this approach lies in its modular combination of Markov chains, finite mixture models, and sensor-based anomaly detection, which allows for extensions to diverse tourism scenarios while maintaining computational efficiency through edge-computing implementation. Beyond tourism, the theoretical contributions offer a generalizable paradigm for integrating real-time sensor data with probabilistic models in other domains requiring dynamic adaptation to contextual changes.
Author Contributions
X.C., H.Z., Z.S. and C.U.I.W.; Data curation, X.C.; Formal analysis, X.C., H.Z. and C.U.I.W.; Methodology, X.C., Z.S., H.Z. and C.U.I.W.; Software, X.C. and C.U.I.W.; Writing—original draft, X.C., H.Z. and C.U.I.W.; Writing—review and editing, X.C., H.Z. and C.U.I.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding authors.
Acknowledgments
We all acknowledge the support of Macao Polytechnic University (RP/FCHS-02/2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, J.; Li, X.; Yang, Y.; Tan, Y.; Geng, T.; Wang, S. Short-and Long-Term Prediction and Determinant Analysis of Tourism Flow Networks: A Novel Steady-State Markov Chain Method. Tour. Manag. 2025, 109, 105139. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Wong, C.U.I. Optimization Study of Tourism Total Revenue Prediction Model Based on the Grey Markov Chain: A Case Study of Macau. AIMS Math. 2024, 9, 16187–16202. [Google Scholar] [CrossRef]
- Zheng, Z.; Shanjiang, Z.; Lijun, S.; Atabak, M. Modelling Changes in Travel Behaviour Mechanisms through a High-Order Hidden Markov Model. Transp. A Transp. Sci. 2024, 20, 2130731. [Google Scholar]
- Ariel, B.; Bracha, S.; Lior, R. Context Aware Markov Chains Models. Knowl.-Based Syst. 2023, 282, 111083. [Google Scholar]
- Agac, S.; Incel, O.D. Resource-Efficient, Sensor-Based Human Activity Recognition with Lightweight Deep Models Boosted with Attention. Comput. Electr. Eng. 2024, 117, 109274. [Google Scholar] [CrossRef]
- Tan, Z.; Wu, Y. On Regime Switching Models. Mathematics 2025, 13, 1128. [Google Scholar] [CrossRef]
- Katsevich, A.; Bandeira, A.S. Likelihood Maximization and Moment Matching in Low SNR Gaussian Mixture Models. Commun. Pure Appl. Math. 2023, 76, 788–842. [Google Scholar] [CrossRef]
- Changqiao, X.; Tao, Z.; Xiaohui, K.; Zan, Z.; Shui, Y. Context-Aware Adaptive Route Mutation Scheme: A Reinforcement Learning Approach. IEEE Internet Things J. 2021, 8, 13528–13541. [Google Scholar]
- Więcek, P.; Kubek, D. The Impact Time Series Selected Characteristics on the Fuel Demand Forecasting Effectiveness Based on Autoregressive Models and Markov Chains. Energies 2024, 17, 4163. [Google Scholar] [CrossRef]
- Feng, W.; Li, Y.; Chen, S. What Has Influenced the Growth and Structural Transformation of China’s Cultural Industry?—Based on the Input-Output Bias Analysis. Appl. Econ. 2025, 1–14. [Google Scholar] [CrossRef]
- Jia, X.; Sedehi, O.; Papadimitriou, C.; Katafygiotis, L.S.; Moaveni, B. Nonlinear Model Updating through a Hierarchical Bayesian Modeling Framework. Comput. Methods Appl. Mech. Eng. 2022, 392, 114646. [Google Scholar] [CrossRef]
- Xiao, S.; Zhang, J.; Ye, J.; Zheng, J. Establishing Region-Specific N–Vs Relationships through Hierarchical Bayesian Modeling. Eng. Geol. 2021, 287, 106105. [Google Scholar] [CrossRef]
- Borucka, A.; Kozłowski, E.; Parczewski, R.; Antosz, K.; Gil, L.; Pieniak, D. Supply Sequence Modelling Using Hidden Markov Models. Appl. Sci. 2022, 13, 231. [Google Scholar] [CrossRef]
- Newlin, R.M.; Rajamurugan, A. A Novel Context-Aware Computing Framework with the Internet of Things and Prediction of Sensor Rank Using Random Neural XG-Boost Algorithm. J. Electr. Eng. Technol. 2024, 19, 2621–2636. [Google Scholar]
- Wang, Y.; Yao, S. Neural Stochastic Differential Equations with Neural Processes Family Members for Uncertainty Estimation in Deep Learning. Sensors 2021, 21, 3708. [Google Scholar] [CrossRef]
- Barbour, D.; Zhou, Z.; Marticorena, D.; Wong, Q.W.; Browning, J.; Wilbur, K.; Davey, P.; Seitz, A.; Gardner, J. Multitask Machine Learning of Contrast Sensitivity Functions. J. Vis. 2024, 24, 1082. [Google Scholar] [CrossRef]
- Li, L.; Pei, Z.; Li, Q.; Hao, F.; Chen, X.; Chen, J. Identifying Tourism Attractiveness Based on Intra-Destination Tourist Behaviour: Evidence from Wi-Fi Data. Curr. Issues Tour. 2024, 27, 3131–3149. [Google Scholar] [CrossRef]
- Stratton, C.; Hoegh, A.; Rodhouse, T.J.; Green, J.L.; Banner, K.M.; Irvine, K.M. Clustering and Unconstrained Ordination with Dirichlet Process Mixture Models. Methods Ecol. Evol. 2024, 15, 1720–1732. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Chang, C.-W. Consumer Dynamics: Theories, Methods, and Emerging Directions. J. Acad. Mark. Sci. 2021, 49, 166–196. [Google Scholar] [CrossRef]
- BenSaïda, A. The Frequency of Regime Switching in Financial Market Volatility. J. Empir. Financ. 2015, 32, 63–79. [Google Scholar] [CrossRef]
- Zheng, K.; Xu, W.; Zhang, X. Multivariate Regime Switching Model Estimation and Asset Allocation. Comput. Econ. 2021, 61, 165–196. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, P.; Li, J.; Xiao, Z.; Shi, H. Attentive Hybrid Recurrent Neural Networks for Sequential Recommendation. Neural Comput. Appl. 2021, 33, 1091–11105. [Google Scholar] [CrossRef]
- Mena, G.; Coussement, K.; De Bock, K.W.; De Caigny, A.; Lessmann, S. Exploiting Time-Varying RFM Measures for Customer Churn Prediction with Deep Neural Networks. Ann. Oper. Res. 2024, 339, 765–787. [Google Scholar] [CrossRef]
- Rayani, P.K.; Changder, S. Sensor-Based Continuous User Authentication on Smartphone through Machine Learning. Microprocess. Microsyst. 2023, 96, 104750. [Google Scholar] [CrossRef]
- Imbert, F.; Anquetil, E.; Soullard, Y.; Tavenard, R. Mixture-of-Experts for Handwriting Trajectory Reconstruction from IMU Sensors. Pattern Recognit. 2025, 161, 111231. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, X.; Peng, S.; Jiang, X.; Xu, K.; Chen, C.; Wang, Z.; Dai, C.; Chen, W. A Review of Wearable and Unobtrusive Sensing Technologies for Chronic Disease Management. Comput. Biol. Med. 2021, 129, 104163. [Google Scholar] [CrossRef]
- Tan, C.; Wang, Y.; Lu, X.; Wu, J.; Zhang, G.; Bai, Z. Research on Lean Analysis Algorithm for Equipment Centralized Monitoring in Big Data Era. J. Phys. Conf. Ser. 2020, 1437, 012085. [Google Scholar] [CrossRef]
- Nasr Azadani, M.; Boukerche, A. Driving Behavior Analysis Guidelines for Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6027–6045. [Google Scholar] [CrossRef]
- Dilek, E.; Dener, M. Computer Vision Applications in Intelligent Transportation Systems: A Survey. Sensors 2023, 23, 2938. [Google Scholar] [CrossRef]
- Guo, B.; Li, M.; Zhou, M.; Zhang, F.; Wang, P. A New Anomalous Travel Demand Prediction Method Combining Markov Model and Complex Network Model. Phys. A Stat. Mech. Its Appl. 2023, 619, 128697. [Google Scholar] [CrossRef]
- Hu, Y.-C. Predicting Foreign Tourists for the Tourism Industry Using Soft Computing-Based Grey–Markov Models. Sustainability 2017, 9, 1228. [Google Scholar] [CrossRef]
- Ilsé, B.; Andrea, S. Forecasting Tourism Demand Cycles: A Markov Switching Approach. Int. J. Tour. Res. 2022, 24, 759–774. [Google Scholar]
- Hwang, H.J.; Kim, Y.R.; Park, S.; Chung, N. Effects of Weather and Air Quality on Travel Behavior. Tour. Manag. Perspect. 2025, 57, 101366. [Google Scholar] [CrossRef]
- AlMutairi, B.S.; Small, M.J.; Grossmann, I. Utilization of El Niño–Southern Oscillation Projected by Climate Models in Improvement of Seasonal Precipitation Predictability. Int. J. Climatol. 2023, 43, 4491–4505. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Q.; Fu, S.; Hou, Y.; Han, H. DCLMD: Dynamic Clustering and Label Mapping Distribution for Constructing in-Context Learning Demonstrations. J. Supercomput. 2025, 81, 738. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Wong, C.U.I. Phase-Adaptive Federated Learning for Privacy-Preserving Personalized Travel Itinerary Generation. Tour. Hosp. 2025, 6, 100. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, G.; Qian, G.; Jiang, X. Distributed Online Expectation-Maximization Algorithm for Poisson Mixture Model. Appl. Math. Model. 2023, 124, 734–748. [Google Scholar] [CrossRef]
- JunHo, Y.; Chang, C. Real-Time Context-Aware Recommendation System for Tourism. Sensors 2023, 23, 3679. [Google Scholar]
- Chen, S.; Zhang, Z.; Yan, S.; Chen, J. Enterprise Environmental Governance and Fluoride Consumption Management in the Global Sports Industry. Fluoride 2025, 58, 1. [Google Scholar]
- Wang, S.; Sun, F.; Liu, M.Q. Energy Distance-Based Subsampling Markov Chain Monte Carlo. Sci. China Math. 2025, 1–24. [Google Scholar] [CrossRef]
- Shahzadi, A.; Wang, T.; Parry, M.; Bebbington, M. Modelling Time-Inhomogeneous Incomplete Records of Point Processes Using Variants of Hidden Markov Models. In Advances in Data Analysis and Classification; Springer: Berlin/Heidelberg, Germany, 2025; pp. 1–29. [Google Scholar]
- Gao, J.; Ozbay, K.; Hu, Y. Real-Time Anomaly Detection of Short-Term Traffic Disruptions in Urban Areas through Adaptive Isolation Forest. J. Intell. Transp. Syst. 2025, 29, 269–286. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, M.; Su, C. Prediction of Consumer Repurchase Behavior Based on LSTM Neural Network Model. Int. J. Syst. Assur. Eng. Manag. 2021, 13, 1042–1053. [Google Scholar] [CrossRef]
- Basile, L.J.; Carbonara, N.; Pellegrino, R.; Panniello, U. Business Intelligence in the Healthcare Industry: The Utilization of a Data-Driven Approach to Support Clinical Decision Making. Technovation 2023, 120, 102482. [Google Scholar] [CrossRef]
- Kim, J.W.; Edemacu, K.; Kim, J.S.; Chung, Y.D.; Jang, B. A Survey of Differential Privacy-Based Techniques and Their Applicability to Location-Based Services. Comput. Secur. 2021, 111, 102464. [Google Scholar] [CrossRef]
- Dai, G.; Tang, J.; Zeng, J.; Hu, C.; Zhao, C. Road Network Traffic Flow Prediction: A Personalized Federated Learning Method Based on Client Reputation. Comput. Electr. Eng. 2024, 120, 109678. [Google Scholar] [CrossRef]
- Kumar, A.; Misra, S.C.; Chan, F.T. Leveraging AI for Advanced Analytics to Forecast Altered Tourism Industry Parameters: A COVID-19 Motivated Study. Expert Syst. Appl. 2022, 210, 118628. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).