Adaptive Fixed-Time NN-Based Tracking Control for a Type of Stochastic Nonlinear Systems Subject to Input Saturation
Abstract
1. Introduction
- (1)
- The fixed-time convergence and the input saturation restriction are investigated simultaneously. Although the adaptive fixed-time tracking control schemes have been developed in [21,24], they have not taken into consideration the input constraint. This implies that the proposed control scheme in [21,24] could not solve the input saturation problem.
- (2)
- The adaptive NN fixed-time controller is designed. The diffusion terms of the considered systems are unknown; the NN approximation method is used to deal with unknown functions. Together with Gaussian error function being utilized to tackle the input saturation issue, the adaptive fixed-time controller is constructed under the framework of the backstepping approach. The adaptive neural network fixed-time control algorithm can achieve the control goal; that is, all the variables of the investigated system are bounded in probability and the tracking error fluctuates around the origin without violating input saturation restriction.
2. Problem and Preliminaries
3. Controller Design and Stability Analysis
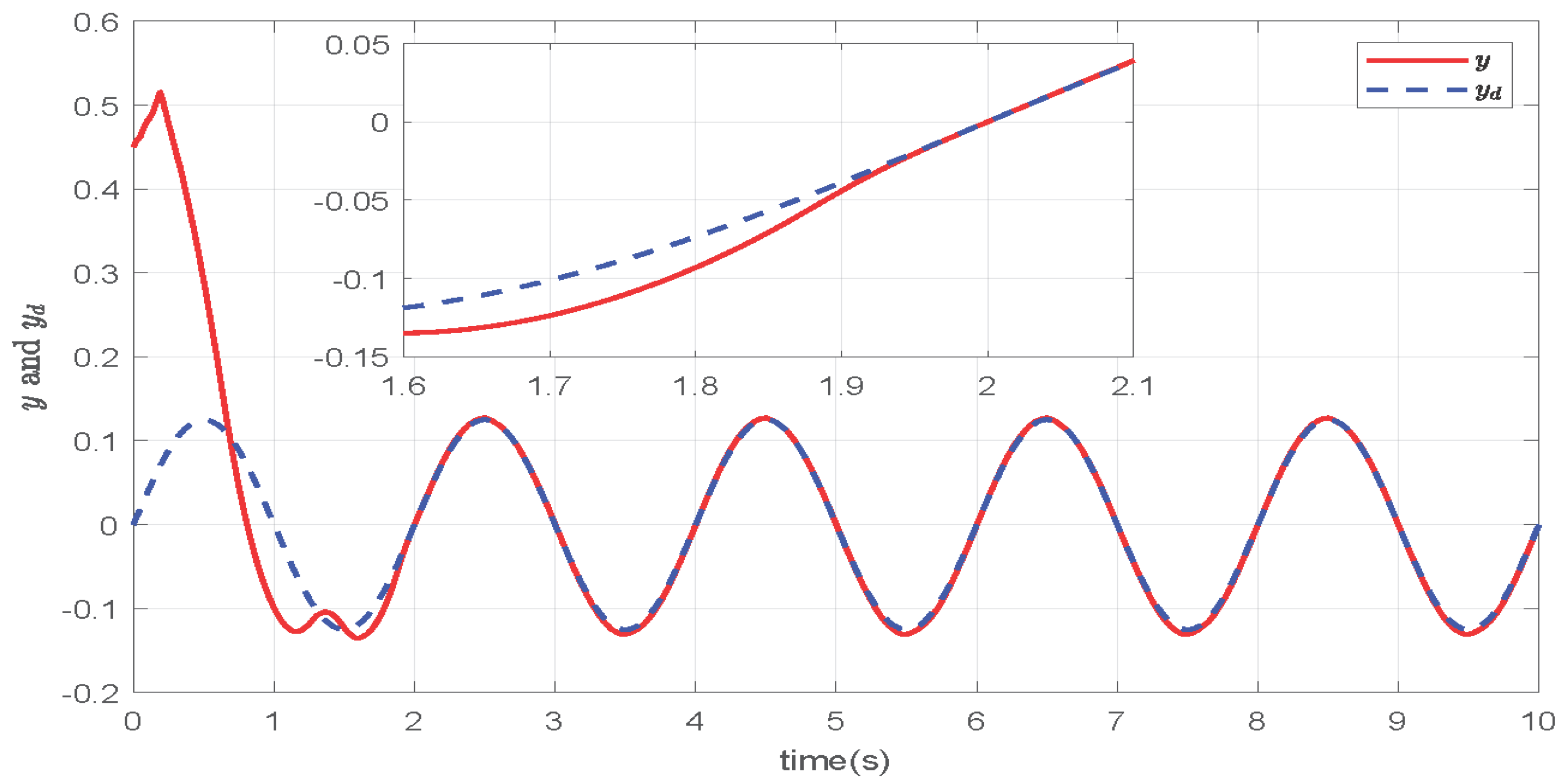
4. Simulation Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tao, B. A tool for the global stabilization of stochastic nonlinear systems. IEEE Trans. Autom. Control 2017, 62, 1946–1951. [Google Scholar]
- Khoo, S.; Yin, J.; Man, Z.; Yu, X. Finite-time stabilization of stochastic nonlinear systems in strict-feedback form. Automatica 2013, 49, 1403–1410. [Google Scholar] [CrossRef]
- Jiang, M.M.; Xie, X.J. Finite-time stabilization of stochastic low-order nonlinear systems with FT-SISS inverse dynamics. Int. J. Robust Nonlinear Control 2018, 28, 1960–1972. [Google Scholar] [CrossRef]
- Sun, Y.M.; Chen, B.; Lin, C.; Wang, H.; Zhou, S. Adaptive neural control for a class of stochastic nonlinear systems by backstepping approach. Inf. Sci. 2016, 369, 748–764. [Google Scholar] [CrossRef]
- Fang, L.D.; Ding, S.; Ma, L.; Zhu, D. Finite-time state-feedback control for a class of stochastic constrained nonlinear systems. J. Frankl. Inst. 2022, 359, 7415–7437. [Google Scholar] [CrossRef]
- Fang, L.D.; Ma, L.; Park, J.H.; Ding, S. Finite-time stabilization for a class of stochastic output-constrained systems by output feedback. Int. J. Robust Nonlinear Control 2022, 32, 1256–1271. [Google Scholar] [CrossRef]
- Cui, M.Y.; Xie, X.J.; Wu, J. Dynamics modeling and tracking control of robot manipulators in random vibration environment. IEEE Trans. Autom. Control 2013, 50, 1540–1545. [Google Scholar] [CrossRef]
- Liu, X.C.; Guan, X.Q.; Wu, Z.J. Simulation of stochastic vibration of maglev track inspection vehicle. Mech. Syst. Signal Process. 2007, 21, 1927–1935. [Google Scholar] [CrossRef]
- Gu, J.B.; Wang, H.; Li, W.Q. Decentralized tracking of large-Scale stochastic nonlinear systems via output-feedback. IEEE Access 2022, 10, 82346–82354. [Google Scholar] [CrossRef]
- Li, W.Q. Mean-nonovershooting control of stochastic nonlinear systems. IEEE Trans. Autom. Control 2021, 66, 5756–5771. [Google Scholar] [CrossRef]
- Yakoub, Z.; Naifar, O.; Ivanov, D. Unbiased identification of fractional order system with unknown time-delay using bias compensation method. Mathematics 2022, 10, 3028. [Google Scholar] [CrossRef]
- Kahouli, O.; Jmal, A.; Naifar, O.; Nagy, A.M.; Ben Makhlouf, A. New result for the analysis of Katugampola fractional-order systems-application to identification problems. Mathematics 2022, 10, 1814. [Google Scholar] [CrossRef]
- Sui, S.; Li, Y.M.; Tong, S.C. Adaptive fuzzy control design and applications of uncertain stochastic nonlinear systems with input saturation. Neurocomputing 2015, 156, 42–51. [Google Scholar] [CrossRef]
- Min, H.F.; Shi, S.; Feng, H. Adaptive stabilization of constrained stochastic nonlinear systems with input saturation: A combined BLF and NN approach. Trans. Inst. Meas. Control 2024, 46, 1520–1528. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, F. Observer-based finite-time control of stochastic non-strict-feedback nonlinear systems. Int. J. Control Autom. Syst. 2021, 19, 655–665. [Google Scholar] [CrossRef]
- Wang, F.; You, Z.Y. A fast finite-time neural network control of stochastic nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 7443–7452. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Wang, X.; Yu, D. Adaptive fuzzy nonsingular fixed-time control for a class of MIMO nonstrict feedback system. IEEE Trans. Fuzzy Syst. 2023, 31, 4039–4050. [Google Scholar] [CrossRef]
- Huang, B.; Li, A.J.; Guo, Y.; Wang, C.Q. Fixed-time attitude tracking control for spacecraft without unwinding. Acta Astronaut. 2018, 151, 818–827. [Google Scholar] [CrossRef]
- Yu, J.; Yu, S.; Li, J.; Yan, Y. Fixed-time stability theorem of stochastic nonlinear systems. Int. J. Control 2019, 92, 2194–2220. [Google Scholar] [CrossRef]
- Long, Z.Z.; Zhou, W.; Fang, L.D.; Zhu, D.H. Fixed-Time Stabilization of a Class of Stochastic Nonlinear Systems. Actuators 2024, 13, 3. [Google Scholar] [CrossRef]
- Liang, Y.J.; Li, Y.X.; Hou, Z.S. Adaptive fixed-time tracking control for stochastic pure-feedback nonlinear systems. Int. J. Adapt. Control Signal Process. 2021, 35, 1712–1731. [Google Scholar] [CrossRef]
- Yao, Y.G.; Tan, J.Q.; Wu, J.; Zhang, X. Fixed-time synchronization of stochastic memristor-based neural networks with adaptive control. Neural Netw. 2020, 569, 527–543. [Google Scholar]
- Yao, Y.G.; Tan, J.Q.; Wu, J.; Zhang, X. Event-triggered fixed-time adaptive neural dynamic surface control for stochastic non-triangular structure nonlinear systems. Inf. Sci. 2021, 569, 527–543. [Google Scholar] [CrossRef]
- Wang, N.; Fu, Z.M.; Tao, F.Z.; Song, S.Z.; Ma, M. Adaptive fuzzy fixed-time control for a class of strict-feedback stochastic nonliear systems. Syst. Sci. Control Eng. 2022, 10, 142–153. [Google Scholar] [CrossRef]
- Wang, C.; Lin, Y. Decentralized adaptive tracking control for a class of interconnected nonlinear time-varing systems. Automatica 2015, 54, 16–24. [Google Scholar] [CrossRef]
- Carlen, E.A.; Lieb, E.H.; Loss, M. A sharp analog of young inequality on sn and related entropy inequalities. J. Geom. Anal. 2004, 14, 487–520. [Google Scholar] [CrossRef]
- Dong, Y.; Yu, Z.X.; Li, S.G. Adaptive output feedback tracking control for switched non-strict-feedback non-linear systems with unknown control direction and asymmetric saturation actuators. IET Control Theory Appl. 2017, 11, 2539–2548. [Google Scholar] [CrossRef]













Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, D.; Long, Z.; Fang, L. Adaptive Fixed-Time NN-Based Tracking Control for a Type of Stochastic Nonlinear Systems Subject to Input Saturation. Mathematics 2025, 13, 2018. https://doi.org/10.3390/math13122018
Zhu D, Long Z, Fang L. Adaptive Fixed-Time NN-Based Tracking Control for a Type of Stochastic Nonlinear Systems Subject to Input Saturation. Mathematics. 2025; 13(12):2018. https://doi.org/10.3390/math13122018
Chicago/Turabian StyleZhu, Daohong, Zhenzhen Long, and Liandi Fang. 2025. "Adaptive Fixed-Time NN-Based Tracking Control for a Type of Stochastic Nonlinear Systems Subject to Input Saturation" Mathematics 13, no. 12: 2018. https://doi.org/10.3390/math13122018
APA StyleZhu, D., Long, Z., & Fang, L. (2025). Adaptive Fixed-Time NN-Based Tracking Control for a Type of Stochastic Nonlinear Systems Subject to Input Saturation. Mathematics, 13(12), 2018. https://doi.org/10.3390/math13122018




