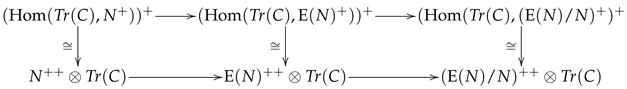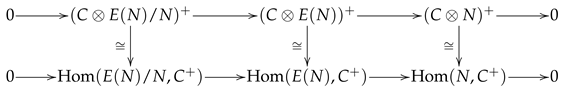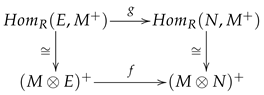Subinjectivity Relative to Cotorsion Pairs

Abstract

In this paper, we define and study the $\mathcal{X}$-subinjectivity domain of a module M where $\mathcal{X}=(\mathcal{A},\mathcal{B})$ is a complete cotorsion pair, which consists of those modules N such that, for every extension K of N with $K/N$ in $\mathcal{A}$, any homomorphism $f:N\to M$ can be extended to a homomorphism $g:K\to M$. This approach allows us to characterize some classical rings in terms of these domains and generalize some known results. In particular, we classify the rings with $\mathcal{X}$-indigent modules—that is, the modules whose $\mathcal{X}$-subinjectivity domains are as small as possible—for the cotorsion pair $\mathcal{X}=(\mathcal{FC},\mathcal{FI})$, where $\mathcal{FI}$ is the class of FP-injective modules. Additionally, we determine the rings for which all (simple) right modules are either $\mathcal{X}$-indigent or FP-injective. We further investigate $\mathcal{X}$-indigent Abelian groups in the category of torsion Abelian groups for the well-known example of the flat cotorsion pair $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$, where $\mathcal{FL}$ is the class of flat modules.

1. Introduction

Throughout, R will denote an associative ring with unity, and the modules will be unital right R-modules unless otherwise stated. As usual, Mod-R denotes the category of all the right R-modules, and ${\mathcal{I}}_0,{\mathcal{P}}_0,\mathcal{FI},\mathcal{FC},\mathcal{FL},\mathcal{EC}$, $\mathcal{PI}$, and $\mathcal{PP}$ denote the classes of all the injective, projective, FP-injective, finitely covered (or FP-projective), flat, cotorsion, pure-injective, and pure-projective modules, respectively. Auslander–Bridger transpose and a character module of a module M are denoted by $Tr\left(M\right)$, and $M^{+}$, respectively.

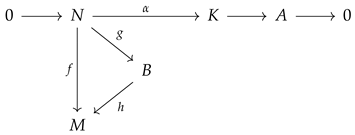
The notions of subinjectivity and pure-subinjectivity were introduced in [1,2], respectively. In contrast to the notion of relative injectivity, an R-module M is called N-subinjective if, for every extension K of N and every homomorphism $f:N\to M$, there exists a homomorphism $g:K\to M$ such that $g{\mid }_N=f$. The class of modules N such that M is N-subinjective is called the subinjectivity domain of M and denoted by ${\underline{\mathcal{I}}}^{-1}\left(M\right)$. In [2], inspired by the notion of subinjectivity, M is called N-pure-subinjective if we replace every extension from the above definition by just taking every pure extension. The class of modules N such that M is N-pure-subinjective is called the pure-subinjectivity domain of M and denoted by ${\underline{\mathcal{PI}}}^{-1}\left(M\right)$. Indigent modules are introduced in [1] as the ones having their subinjectivity domains as small as possible, i.e., consisting of injective modules only. The existence of indigent modules for an arbitrary ring is unknown. There are examples of rings over which indigent modules do exist, for example Noetherian and Artinian serial rings (see [1,3]), but, other than that, little is known about these types of rings. Recently, many studies have been conducted on indigent modules along with their generalizations and rings that have exactly two feasible subinjectivity domains: injective modules and all modules; these are the so-called rings without a right-subinjective middle class (see [3,4,5]).

We will denote by ${\mathcal{C}}^{\perp }=\{X:{Ext}_R^1(C,X)=0$ for all $C\in \mathcal{C}\}$ the right-orthogonal class of $\mathcal{C}$, and by ${}^{\perp }\mathcal{C}=\{X:{Ext}_R^1(X,C)=0$ for all $C\in \mathcal{C}\}$ the left-orthogonal class of $\mathcal{C}$. A cotorsion pair is a pair of classes $(\mathcal{A},\mathcal{B})$ in Mod-R such that ${\mathcal{A}}^{\perp }=\mathcal{B}$ and ${}^{\perp }\mathcal{B}=\mathcal{A}$. If $\mathcal{C}$ is any class of R-modules, then $\mathcal{X}={(}^{\perp }\left({\mathcal{C}}^{\perp }\right),{\mathcal{C}}^{\perp })$ and $\mathcal{Y}={(}^{\perp }\mathcal{C},{{(}^{\perp }\mathcal{C})}^{\perp })$ are easily seen to be cotorsion pairs, called cogenerated and generated cotorsion pairs, respectively, by class $\mathcal{C}$.

Recall (see, for example, [6]) that, given a class $\mathcal{B}$, a $\mathcal{B}$-preenvelope of a module M is a homomorphism $\alpha :M\to B$ such that the homomorphism of Abelian groups ${Hom}_R(B,B^{\prime })\to {Hom}_R(M,B^{\prime })$ is an epimorphism for every module $B^{\prime }$ of $\mathcal{B}$. The preenvelope is said to be special if it is a monomorphism and its cokernel holds in ${}^{\perp }\mathcal{B}$, and it is said to be an envelope provided that every $f:B\to B$ with $f\alpha =f$ is an automorphism. Dually, we have the definition of (special) $\mathcal{B}$-precovers and covers. A cotorsion pair $(\mathcal{A},\mathcal{B})$ is called perfect(complete) if every right R-module has a $\mathcal{B}$-envelope and an $\mathcal{A}$-cover (a special $\mathcal{B}$-preenvelope and a special $\mathcal{A}$-precover). Class $\mathcal{B}$ is said to be preenveloping, special preenveloping, or enveloping provided that every module has a $\mathcal{B}$-preenvelope, a special $\mathcal{B}$-preenvelope, or a $\mathcal{B}$-envelope, respectively. The dual concepts are those of precovering, special precovering, and covering classes.

Cotorsion pairs were introduced by Salce [7] in the 1970s within the framework of Abelian groups. This theory gained significant momentum following Hovey’s [8] discovery of a bijective correspondence between Abelian model structures and cotorsion pairs in Abelian categories. Many examples of cotorsion pairs and the corresponding model structures have been illustrated so far. A famous example of a cotorsion pair is given by the pair $(\mathcal{FL},\mathcal{EC})$, where $\mathcal{FL}$ is the class of flat objects (see [6]). It gave rise to the celebrated Flat Cover Conjecture by Enochs, which was solved in [9] in the case of module categories and in [10] for Grothendieck categories.

It is well known that a right R-module F is flat if and only if each short exact sequence $0\to M\to N\to F\to 0$ in Mod-R is pure. Flat modules are known to be the left part of the so-called flat cotorsion pair $(\mathcal{FL},\mathcal{EC})$ (see [6] (Lemma 7.1.4)). Note that $\mathcal{FL}={}^{\perp }\mathcal{PI}$, so $(\mathcal{FL},\mathcal{EC})$ is generated by $\mathcal{PI}$—that is, $\mathcal{PI}\subseteq \mathcal{EC}$—and the character module of any module is cotorsion. Then, $(\mathcal{FL},\mathcal{EC})$ is complete and perfect. Inspired by this approach in [11], purity relative to a cotorsion pair is defined as follows: a short exact sequence $0\to X\to Y\to Z\to 0$ in Mod-R is called pure relative to the cotorsion pair $(\mathcal{A},\mathcal{B})$ (or $\mathcal{A}$-pure) if $Z\in \mathcal{A}$. In particular, $X\subseteq Y$ is an $\mathcal{A}$-pure submodule whenever $0\to X\to Y\to Y/X\to 0$ is $\mathcal{A}$-pure.

Motivated by this notion of purity relative to a cotorsion pair, we propose a new approach to relative subinjectivity in terms of cotorsion pairs. In Section 2, starting from a complete cotorsion pair $\mathcal{X}=(\mathcal{A},\mathcal{B})$ in Mod-R, we first investigate a general context by introducing $\mathcal{X}$-subinjectivity. Given two right modules M and N, we say that M is N-$\mathcal{X}$-subinjective if, for every extension K of N with $K/N$ in $\mathcal{A}$, any homomorphism $f:N\to M$ can be extended to a homomorphism $g:K\to M$. The $\mathcal{X}$-subinjectivity domain of M (denoted ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$) consists of those modules N such that M is N-$\mathcal{X}$-subinjective. If we take $\mathcal{X}=($Mod-$R,{\mathcal{I}}_0)$, the $\mathcal{X}$-subinjectivity domains are simply the usual subinjectivity domains of modules. For any cotorsion pair $(\mathcal{A},\mathcal{B})$, we always have ${\mathcal{I}}_0\subseteq \mathcal{B}$. This motivates us to undertake a general study of this situation. It is easy to verify that ${\underline{\mathcal{I}}}^{-1}\left(M\right)\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. Subinjectivity and $\mathcal{X}$-subinjectivity domains coincide for all modules if and only if every module in $\mathcal{B}$ is injective. Moreover, if $\mathcal{PI}\subseteq \mathcal{B}$, then we have ${\underline{\mathcal{I}}}^{-1}\left(M\right)\subseteq {\underline{\mathcal{PI}}}^{-1}\left(M\right)\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. But, they need not be equal. It is clear that $\mathcal{B}$ is contained in the $\mathcal{X}$-subinjectivity domain of any module, so the following relations are clear: $\mathcal{B}\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)=\{N:M$ is N-$\mathcal{X}$-subinjective$\} \subseteq$ Mod-R.

Likewise, in light of usual subinjectivity, for any complete cotorsion pair $\mathcal{X}=(\mathcal{A},\mathcal{B})$, we ask how small ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$ can be. We observe that the $\mathcal{X}$-subinjectivity domain of any module must contain at least class $\mathcal{B}$. Hence, inspired by the works [1,4], in Section 3, we call a module M $\mathcal{X}$-indigent if the $\mathcal{X}$-subinjectivity domain of such modules consists of only class $\mathcal{B}$. It is natural to wonder about the existence of $\mathcal{X}$-indigent modules; we actually prove that every ring has an $\mathcal{X}$-indigent module $F={\prod }_{C\in \mathcal{C}}Tr{\left(C\right)}^{+}$ if the cotorsion pair $\mathcal{X}=(\mathcal{A},\mathcal{B})$ is cogenerated by a set $\mathcal{C}$ of some finitely presented modules. It turns out that $F={\prod }_{C\in \mathcal{C}}Tr{\left(C\right)}^{+}$ is indigent if and only if every module in $\mathcal{B}$ is injective (i.e., $\mathcal{A}-GLD\left(R\right)=0$). In particular, taking $\mathcal{X}=(\mathcal{FC},\mathcal{FI})$, we prove that R is right-Noetherian if and only if $F={\prod }_{C\in \mathcal{C}}{C}^{+}$ is indigent, where $\mathcal{C}$ is a complete set of finitely presented modules. On the other hand, if we let $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$ be the flat cotorsion pair that is generated by class $\mathcal{PI}$ of all the pure injective modules, we show that R is right-perfect if and only if every (nonzero) right module is $\mathcal{X}$-indigent. Naturally, the first question that arises is whether such $\mathcal{X}$-indigent modules exist over all rings. We have not been able to answer this question entirely, but, in the category of torsion Abelian groups, we prove that an Abelian group A is $\mathcal{X}$-indigent if and only if for every prime p and every positive integer N there is an integer $n\ge N$ such that A has a direct summand isomorphic to ${\mathbb{Z}}_{p^n}$. We do not know the complete description of $\mathcal{X}$-indigent Abelian groups, but an $\mathcal{X}$-indigent Abelian group must contain a subgroup isomorphic to a p-localization ${\mathbb{Z}}_{\left(p\right)}$ of $\mathbb{Z}$ for every prime p.

The last section deals with the particular complete cotorsion pair $\mathcal{X}=(\mathcal{FC},\mathcal{FI})$, which is the cotorsion pair cogenerated by a set of representatives of all finitely presented right R-modules. We know that there is an $\mathcal{X}$-indigent module over any ring R. This suggests the question of how close the class of $\mathcal{X}$-indigent right R-modules can be to Mod-R. We prove that every right R-module is $\mathcal{X}$-indigent if and only if R is a (von Neumann) regular ring. If R is not regular, then no FP-injective module is $\mathcal{X}$-indigent. Our aim is mainly to examine the rings whose every (simple) right module is either FP-injective or $\mathcal{X}$-indigent. We show that every simple right module is FP-injective or $\mathcal{X}$-indigent if and only if either R is a right-SAP ring or there exists a unique $\mathcal{X}$-indigent simple right R-module S (up to isomorphism). Furthermore, in this case, if R is not right-SAP, then R is either right-semihereditary or right-FP-injective. We are able to show that, if R is a left-perfect right-coherent ring that is not nonsingular, then every simple right R-module is FP-injective or $\mathcal{X}$-indigent if and only if R is either a right-SAP ring or $R=S\times T$, where S is a semisimple Artinian ring and T is an indecomposable matrix ring over a local QF-ring. Finally, if R is a left-perfect ring that has at least one finitely presented singular simple left R-module with $Z\left(R_R\right)\ne 0$, we prove that every right R-module is FP-injective or $\mathcal{X}$-indigent if and only if R is a fully saturated QF-ring.

2. Generalities on Subinjectivity Relative to a Cotorsion Pair

It is well known that a right R-module F is flat if and only if each short exact sequence $0\to M\to N\to F\to 0$ in Mod-R is pure. Inspired by this approach, in [11], purity relative to a cotorsion pair is defined as follows: a short exact sequence $0\to X\to Y\to Z\to 0$ in Mod-R is called pure relative to the cotorsion pair $(\mathcal{A},\mathcal{B})$ if $Z\in \mathcal{A}$. Motivated by this notion of purity relative to a cotorsion pair, in this section, we propose a new approach which is, in some sense, the opposite to injectivity in terms of cotorsion pairs.

Through this section, and unless otherwise specified, $\mathcal{X}=(\mathcal{A},\mathcal{B})$ will denote a complete cotorsion pair in Mod-R.

Definition 1. 

Given right modules M and N, we say that M is N-$\mathcal{X}$-subinjective if, for every extension K of N with $K/N$ in $\mathcal{A}$, any homomorphism $f:N\to M$ can be extended to a homomorphism $g:K\to M$.

The $\mathcal{X}$-subinjectivity domain of M (denoted by ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$) consists of those modules N such that M is N-$\mathcal{X}$-subinjective.

If we take $\mathcal{X}=($Mod-$R,{\mathcal{I}}_0)$, the $\mathcal{X}$-subinjectivity domains are simply the usual subinjectivity domains of modules. We always have ${\mathcal{I}}_0\subseteq \mathcal{B}$. This motivates us to a general study of this situation.

Our next lemma provides an alternative characterization of the $\mathcal{X}$-subinjectivity domain ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$ of a module M.

Proposition 1. 

Let $M,N\in$ Mod-R. Then, the following conditions are equivalent:

(1) 

$N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

(2) 

For every homomorphism $f:N\to M$ and every special $\mathcal{B}$-preenvelope $h:N\to B$ of N, there exists a homomorphism $g:B\to M$ such that $gh=f$.

(3) 

For every homomorphism $f:N\to M$, there exists a special $\mathcal{B}$-preenvelope $h:N\to B$ of N and a homomorphism $g:B\to M$ such that $gh=f$.

(4) 

For every homomorphism from $f:N\to M$, there exists a $\mathcal{B}$-extension B of N such that f can be extended to a homomorphism from B to M.

(5) 

Every homomorphism $f:N\to M$ factors through a module B of $\mathcal{B}$; that is, there are homomorphisms $g:N\to B$ and $h:B\to M$ such that $f=hg$.

Moreover, if $\mathcal{X}$ is perfect, then the above conditions are equivalent to

(6) 

For every homomorphism $f:N\to M$, there exists a $\mathcal{B}$-envelope $h:N\to E$ of N and a homomorphism $g:B\to M$ such that $gh=f$.

Proof. 

The implications $\left(1\right)\Rightarrow \left(2\right)$ and $\left(3\right)\Rightarrow \left(4\right)\Rightarrow \left(5\right)$ are clear.

$\left(2\right)\Rightarrow \left(3\right)$ is also clear since $\mathcal{X}$ is complete.

$\left(5\right)\Rightarrow \left(1\right)$ Let $f:N\to M$ be any homomorphism, and consider the situation

where $hg=f$ is the factorization given by the hypothesis.

Since $B\in \mathcal{B}$ and $A\in \mathcal{A}={}^{\perp }\mathcal{B}$, g can be extended to some $t:K\to B$, and then $ht$ is the desired extension of f.

Finally, if $\mathcal{X}$ is perfect, then $\mathcal{B}$ is an enveloping class [12] (Corollary 1.19). Moreover, since ${\mathcal{I}}_0\subseteq \mathcal{B}$, any $\mathcal{B}$-envelope is also a special preenvelope by [12] (Lemma 1.9). Thus, $\left(3\right)\Rightarrow \left(6\right)$ and $\left(6\right)\Rightarrow \left(4\right)$ follow easily. □

As a consequence of Proposition 1, one sees by the following proposition that a module M is M-$\mathcal{X}$-subinjective if and only if it is contained in the right part of a complete cotorsion pair $\mathcal{X}$.

Proposition 2. 

The following conditions are equivalent for a module M:

(1) 

$M\in \mathcal{B}$.

(2) 

${\underline{\mathcal{IX}}}^{-1}\left(M\right)=$ Mod-R.

(3) 

$M\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

(4) 

${\underline{\mathcal{IX}}}^{-1}\left(M\right)$ is closed under submodules.

Proof. $\left(1\right)\Rightarrow \left(2\right)$ Let $M\in \mathcal{B}$ and $N\in$ Mod-R. We claim that $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. Since $\mathcal{X}$ is complete, there exists a short exact sequence $0\to N\to B\to A\to 0$ with $B\in \mathcal{B}$ and $A\in \mathcal{A}$. If we apply $Ho{m}_R(-,M)$ to this exact sequence, we obtain the sequence $0\to Ho{m}_R(A,M)\to Ho{m}_R(B,M)\to Ho{m}_R(N,M)\to Ex{t}_R^1(A,M)$. Since $A\in \mathcal{A}$ and $M\in \mathcal{B}$, $Ex{t}_R^1(A,M)=0$. So, the claim follows by Proposition 1.

$\left(2\right)\Rightarrow \left(3\right)$ and $\left(2\right)\Rightarrow \left(4\right)$ are clear.

$\left(3\right)\Rightarrow \left(1\right)$ Assume that $M\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. Then, M is M-$\mathcal{X}$-subinjective. Let $1_M:M\to M$ be the identity map, and consider the short exact sequence $0\to M\to B\to A\to 0$ with $B\in \mathcal{B}$ and $A\in \mathcal{A}$. If we apply $Ho{m}_R(-,M)$, then we obtain the exact sequence $0\to Ho{m}_R(A,M)\to Ho{m}_R(B,M)\to Ho{m}_R(M,M)\to 0$. Thus, $0\to M\to B$ splits, so $M\in \mathcal{B}$.

$\left(4\right)\Rightarrow \left(3\right)$ Let M be a module and $f:M\to B$ be a monic $\mathcal{B}$-preenvelope of M. Since $B\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, by hypothesis, $M\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. □

Let $M\in$ Mod-R. It is clear that $\mathcal{B}$ is contained in the $\mathcal{X}$-subinjectivity domain of any module. This, together with Proposition 2, provides the following relations:

$$\mathcal{B}\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)=\{N:M\mathrm{is} N\text{-}\mathcal{X}\text{-subinjective}\}\subseteq \text{Mod-}R$$

Likewise, in light of Proposition 2, we ask how small ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$ can be.

Corollary 1. 

${\bigcap }_{M\in \mathit{\text{Mod-}}R}{\underline{\mathcal{I}\mathcal{X}}}^{-1}\left(M\right)=\mathcal{B}$.

Proof. 

Note that $N\in {\underline{\mathcal{IX}}}^{-1}\left(N\right)$ if and only if $N\in \mathcal{B}$. □

In the following result, we highlight some standard properties of $\mathcal{X}$-subinjectivity domains in relation to direct products. Thus, we recall the concept of equivalence of modules with respect to a class: two right R-modules M and N will be said to be $\mathcal{B}$-equivalent if $M\oplus B=N\oplus B^{\prime }$ for some B and $B^{\prime }$ in $\mathcal{B}$.

Lemma 1. 

The following statements are true:

(1) 

${\underline{\mathcal{IX}}}^{-1}\left({\prod }_{i\in I}{M}_i\right)={\cap }_{i\in I}{\underline{\mathcal{IX}}}^{-1}\left(M_i\right)$ for any family of right R-modules ${\left\{M_i\right\}}_{i\in I}$.

(2) 

${\underline{\mathcal{IX}}}^{-1}\left(M\right)={\underline{\mathcal{IX}}}^{-1}\left(N\right)$ for $\mathcal{B}$-equivalent modules M and N.

Proof. 

It is immediate from the definitions. □

We always have ${\underline{\mathcal{I}}}^{-1}\left(M\right)\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. Moreover, if $\mathcal{PI}\subseteq \mathcal{B}$, then we have ${\underline{\mathcal{I}}}^{-1}\left(M\right)$ $\subseteq {\underline{\mathcal{PI}}}^{-1}\left(M\right)\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. But, they need not be equal. For example, if we have a non-pure-injective module M such that $M\in \mathcal{B}$, by the previous proposition, $M\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, but $M\notin {\underline{\mathcal{PI}}}^{-1}\left(M\right)$; otherwise, it would be pure-injective.

It is natural to consider when the $\mathcal{X}$-subinjectivity and $\mathcal{Y}$-subinjectivity domains relative to cotorsion theories $\mathcal{X}$ and $\mathcal{Y}$ may coincide for certain modules.

Lemma 2. 

Let $\mathcal{X}=(\mathcal{A},\mathcal{B})$ and $\mathcal{Y}=(\mathcal{C},\mathcal{D})$ be complete cotorsion pairs, $M\in$ Mod-R and $\mathcal{B}\subseteq \mathcal{D}$. Then,

(1) 

${\underline{\mathcal{IX}}}^{-1}\left(M\right)\subseteq {\underline{\mathcal{IY}}}^{-1}\left(M\right)$.

(2) 

${\underline{\mathcal{IX}}}^{-1}\left(M\right)={\underline{\mathcal{IY}}}^{-1}\left(M\right)$ if and only if $\mathcal{D}\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Proof. $\left(1\right)$ Let M be a module and $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. So, there exists a $Ho{m}_R(-,M)$-exact sequence $0\to N\to B\to A\to 0$ such that $B\in \mathcal{B}$ since $\mathcal{B}\subseteq \mathcal{D}$, $N\in {\underline{\mathcal{IY}}}^{-1}\left(M\right)$ by Proposition 1.

$\left(2\right)$ Assume that $\mathcal{D}\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. We have ${\underline{\mathcal{IX}}}^{-1}\left(M\right)\subseteq {\underline{\mathcal{IY}}}^{-1}\left(M\right)$ by (1). On the other hand, let $N\in {\underline{\mathcal{IY}}}^{-1}\left(M\right)$. So, there exists a $Ho{m}_R(-,M)$-exact sequence $0\to N\to D\to C\to 0$ such that $D\in \mathcal{D}$, and also by hypothesis $D\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. Let $0\to N\to B\to A\to 0$ be any short exact sequence with $B\in \mathcal{B}$ and $A\in \mathcal{A}$, and consider the following pushout diagram:

By applying the functor $Ho{m}_R(-,M)$ to the above diagram, we have the following exact diagram:

Since $D\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, $\gamma$ is epic. Also, ${\alpha }^{\ast }$ is epic by the hypothesis since $N\in {\underline{\mathcal{IY}}}^{-1}\left(M\right)$. This means that ${\delta }^{\ast }$ is an epimorphism, so $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Conversely, it is clear that, if ${\underline{\mathcal{IX}}}^{-1}\left(M\right)={\underline{\mathcal{IY}}}^{-1}\left(M\right)$, then $\mathcal{D}\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. □

Recall that the $\mathcal{A}$-dimension of a right module A is defined by $\mathcal{A}-dim\left(A\right)=inf\{n:Ex{t}_R^{n+1}(A,B)=0$ for every $B\in \mathcal{B}\}$. The $\mathcal{A}-GLD\left(R\right)=$sup$\{\mathcal{A}-dim(A):A$ is a right R-module}.

As an easy consequence of Lemma 2, we can consider when the subinjectivity and $\mathcal{X}$-subinjectivity domains may coincide for certain modules or for all modules.

Corollary 2. 

The following conditions are equivalent:

(1) 

Every module in $\mathcal{B}$ is injective.

(2) 

$\mathcal{A}=$Mod-R.

(3) 

For every R-module M, ${\underline{\mathcal{IX}}}^{-1}\left(M\right)={\underline{\mathcal{I}}}^{-1}\left(M\right)$.

(4) 

For every R-module M, ${\underline{\mathcal{IX}}}^{-1}\left(M\right)\subseteq {\underline{\mathcal{I}}}^{-1}\left(M\right)$.

(5) 

$\mathcal{A}-GLD\left(R\right)=0$.

It is not known whether or not the subinjectivity domains are closed under extensions or cokernels of monomorphisms. In general, we need to assume the condition that the short exact sequences are $Ho{m}_R(-,\mathcal{B})$-exact.

Proposition 3. 

If $0\to K\to N\to C\to 0$ is a $Hom(-,\mathcal{B})$-exact sequence and $K,C\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, then $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Proof. 

Choose $\mathcal{B}$-precovers of K and C, $K\to B_K$, and $C\to B_C$. Since the exact sequence of the statement is $Hom(-,\mathcal{B})$-exact, we can apply the Horseshoe Lemma to get the following commutative diagram with splitting second row

Therefore, applying $Hom(-,M)$, we get the commutative diagram with exact rows

where the first and third columns are exact because $K,C\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. Thus, f is an epimorphism and $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. □

Lemma 3. 

The following conditions are equivalent:

(1) 

For every short exact sequence $0\to A\to B\to D\to 0$, which is $Ho{m}_R(-,\mathcal{B})$-exact, if $A,B\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, then $D\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

(2) 

For every special $\mathcal{B}$-preenvelope $A\to B$ of A, if $A\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, then $B/A\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

(3) 

For every special $\mathcal{B}$-preenvelope $A\to B$ of A with $A\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, the pushout of B over A holds in ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Proof. $\left(1\right)\Rightarrow \left(2\right)$ is clear.

$\left(2\right)\Rightarrow \left(1\right)$ Consider an exact sequence $0\to A\to B\to C\to 0$, which is $Ho{m}_R(-,\mathcal{B})$-exact with $A,B\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$; we claim that $C\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. Consider the following pushout diagram:

where $f:A\to D$ is a special $\mathcal{B}$-preenvelope of A. Then, ${\displaystyle \frac{D}{A}}\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ by the assumption. Since ${\displaystyle \frac{D}{A}}$ and B in ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$, $E\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ by the previous result. Now, $0\to A\to B\to C\to 0$ is $Ho{m}_R(-,\mathcal{B})$-exact and $D\in \mathcal{B}$, so there exists $h:B\to D$ such that $hg=f$. Then, by the Homotopy Lemma, there is $h^{\prime }:C\to E$ such that $d{h}^{\prime }=1_C$; that is, $0\to D\to E\to C\to 0$ splits. Therefore, C is isomorphic to a direct summand of E, where $C\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

$\left(2\right)\iff \left(3\right)$ Consider the following diagram where D is the pushout of B over A:

Then, $0\to B\to D\to C\to 0$ is $Ho{m}_R(-,\mathcal{B})$-exact. If $A\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, then $C\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, so $D\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. Conversely, if $D\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, then $C\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ since $0\to B\to D\to C\to 0$ splits. □

It is easy to see that, if ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$ is closed under cokernels of monomorphisms for any right module M, then $\mathcal{B}$ is also closed under cokernels of monomorphisms. For the converse, we have the following.

Proposition 4. 

Class $\mathcal{B}$ is closed under cokernels of monomorphisms if and only if for every module M and every short exact sequence $0\to A\to B\to C\to 0$ with $A\in \mathcal{B}$ and $B\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, necessarily $C\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Proof. 

We first show that $\mathcal{B}$ is closed under cokernels of monomorphisms. Consider the short exact sequence $0\to A\to B\to C\to 0$ with $A,B\in \mathcal{B}$. Clearly, we have $B\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ for every right module M, so, by the hypothesis, $C\in {\underline{\mathcal{IX}}}^{-1}\left(C\right)$; that is, $C\in \mathcal{B}$.

Conversely, let $B\to B^{\prime }$ be a special $\mathcal{B}$-preenvelope of B and consider the following pushout diagram:

Since $\mathcal{B}$ is closed under cokernels of monomorphisms, we have $D\in \mathcal{B}$. Applying the functor $Ho{m}_R(-,M)$, we obtain the following diagram:

Since $B\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, g is epic, f is epic too. Therefore, $C\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. □

Proposition 5. 

Let $0\to A\to B\to M\to 0$ be a short exact sequence with $B\in \mathcal{B}$. Then, ${}^{\perp }A\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Moreover, if $B\to M$ is a $\mathcal{B}$-precover, then ${\underline{\mathcal{IX}}}^{-1}\left(M\right)\cap {}^{\perp }B\subseteq {}^{\perp }A$.

Proof. 

Let $N\in {}^{\perp }A$ considering any homomorphism $f:N\to M$ and the pullback

Since $N{\in }^{\perp }A$, the sequence

$$0\to A\to P\to N\to 0$$

splits and then there exists $s:N\to P$ such that $hs=1_N$. Therefore, $gs:N\to B$ is such that $\beta gs=fhs=f$, so f factors through $B\in \mathcal{B}$ and then $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ by Proposition 1.

On the other hand, let $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)\cap {}^{\perp }B$ and $N\to B^{\prime }$ be a $\mathcal{B}$-preenvelope. Applying $Hom(B^{\prime },-)$ and $Hom(-,N)$, we have the following diagram:

Since $N\in {}^{\perp }B$, $Ex{t}_R^1(N,B)=0$. Moreover, since $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, g is epic. Also, $B\to M$ being a $\mathcal{B}$-precover implies that f is epic. This means that h is epic, so $Ex{t}_R^1(N,A)=0$. Thus, $N\in {}^{\perp }A$. □

By Proposition 5, if a module M is a homomorphic image of a module in $\mathcal{B}$, then ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$ contains the class of projective modules.

Proposition 6. 

The following conditions are equivalent for a module M:

(1) 

M is a homomorphic image of a module in $\mathcal{B}$.

(2) 

There exists a module K such that ${}^{\perp }K\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

(3) 

${\mathcal{P}}_0\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

(4) 

Any projective precover P of M is in ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Proof. $\left(1\right)\Rightarrow \left(2\right)$ follows from Proposition 5.

$\left(2\right)\Rightarrow \left(3\right)\Rightarrow \left(4\right)$ are clear.

$\left(4\right)\Rightarrow \left(1\right)$ Let $f:P\to M$ be a projective precover of M. Since $P\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, there exists a $\mathcal{B}$ preenvelope $g:P\to B$ and a homomorphism $h:B\to M$ such that $hg=f$. Since f is epic, h is epic. This completes the proof. □

Now, we investigate in a similar manner to Proposition 6, when the domains contain the class of pure-projective modules. Thus, for the next result, we recall the known fact that every module has a pure-projective precover.

Proposition 7. 

The following conditions are equivalent for a module M:

(1) 

M is a pure quotient of a module in $\mathcal{B}$.

(2) 

$\mathcal{PP}\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

(3) 

Any pure-projective precover P of M is in ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

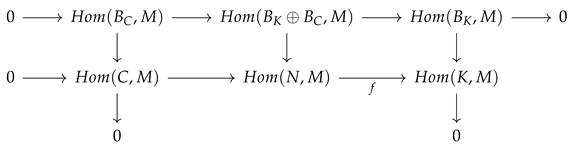
In general, for any module M and a cotorsion pair $\mathcal{X}=(\mathcal{A},\mathcal{B})$, ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$ is not closed under homomorphic images. For example, consider the module $F={\prod }_{C\in \mathcal{C}}Tr{\left(C\right)}^{+}$ that will be described in Proposition 11. In this case, we have ${\underline{\mathcal{IX}}}^{-1}\left(F\right)=\mathcal{B}$. Even if $\mathcal{X}$ is complete, class $\mathcal{B}$ need not be closed under homomorphic images and thus happens to be ${\underline{\mathcal{IX}}}^{-1}\left(F\right)$.

Proposition 8. 

The following are equivalent:

(1) 

$\mathcal{B}$ is closed under homomorphic images.

(2) 

For any $M\in$ Mod-$R,$ ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$ is closed under homomorphic images.

Proof. $\left(1\right)\Rightarrow \left(2\right)$ Let M be a right module and $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ and $K\subseteq N$. Let $f:{\displaystyle \frac{N}{K}}\to M$ be any homomorphism. Consider the pushout diagram:

with $L\in \mathcal{B}$ and ${\displaystyle \frac{L}{N}}\in \mathcal{A}$. Since $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, there exists $\phi :L\to M$ such that $\phi {\alpha }_1=f{\pi }_1$. Since $f{\pi }_1\left(K\right)=\phi {\alpha }_1\left(K\right)=0$, ${\alpha }_1\left(K\right)\subseteq Ker\phi$. Thus, by the factor theorem, there exists $\psi :T\to M$ such that $\psi {\alpha }_2=f$. By the hypothesis, $T\in \mathcal{B}$, so ${\displaystyle \frac{N}{K}}\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ by Proposition 1.

$\left(2\right)\Rightarrow \left(1\right)$ Let $N\in \mathcal{B}$ and $K\subseteq N$. Then, $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ for every module M and then $N/K\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ for every module M by the hypothesis. Therefore, $N/K\in \mathcal{B}$. □

Example 1. 

As the class of cotorsion Abelian groups is closed under homomorphic images and there is no nonzero homomorphism from a cotorsion to a cotorsion-free Abelian group, it is easy to see that, if $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$, then ${\underline{\mathcal{IX}}}^{-1}\left(G\right)=\{N:Ho{m}_{\mathbb{Z}}(N,G)=0\}$ for any cotorsion-free Abelian group G (for example, ${\mathbb{Z}}_{\left(p\right)}$). In particular, ${\underline{\mathcal{IX}}}^{-1}\left(\mathbb{Z}\right)$ is the class of all Abelian groups that do not contain any direct summand isomorphic to $\mathbb{Z}$.

Let $\mathcal{C}$ be a class of some finitely presented left R-modules. A ring R is called $\mathcal{C}$-semihereditary if, whenever $0\to K\to P\to C\to 0$ is exact, $C\in \mathcal{C}$, P is finitely generated projective and K is finitely generated; then, K is projective. Let $\mathcal{C}$ be the class of all finitely presented right R modules; then, the ring R is $\mathcal{C}$-semihereditary if and only if R is right-semihereditary (see [13]).

Corollary 3. 

Suppose $\mathcal{X}=(\mathcal{A},\mathcal{B})$ is cogenerated by a class $\mathcal{C}$ of some finitely presented right modules. The following conditions are equivalent:

(1) 

R is a $\mathcal{C}$-semihereditary ring.

(2) 

$\mathcal{B}$ is closed under homomorphic images.

(3) 

For any $M\in$ Mod-R, ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$ is closed under homomorphic images.

(4) 

Every right R-module has a monic $\mathcal{B}$-cover.

(5) 

Every $A\in \mathcal{A}$ has projective dimension at most 1.

Proof. $\left(1\right)\iff \left(2\right)\iff \left(4\right)\iff \left(5\right)$ Follow by [13] (Theorem 4.3).

$\left(2\right)\iff \left(3\right)$ Follows by 8. □

3. Indigent Modules Relative to Cotorsion Pairs

Recall first that modules for which the subinjectivity domain is as small as possible are called indigent modules. For a complete cotorsion pair $\mathcal{X}=(\mathcal{A},\mathcal{B})$, modules for which the $\mathcal{X}$-subinjectivity domain is as small as possible will be called $\mathcal{X}$-indigent. The $\mathcal{X}$-subinjectivity domain of such modules will consist of only class $\mathcal{B}$.

By (1) in Lemma 1, it follows easily that

Proposition 9. 

If a module M is $\mathcal{X}$-indigent, then $M\oplus N$ is $\mathcal{X}$-indigent for any module N.

The proof of the following is obvious from the definitions.

Proposition 10. 

Let $\mathcal{X}=(\mathcal{A},\mathcal{B})$ be a complete cotorsion pair. The following conditions are equivalent:

(1) 

$\mathcal{B}=$Mod-R.

(2) 

Every (nonzero) R-module is $\mathcal{X}$-indigent.

(3) 

There exists an $\mathcal{X}$-indigent module in $\mathcal{B}$.

(4) 

$\left\{0\right\}$ is an $\mathcal{X}$-indigent module.

(5) 

There exists an $\mathcal{X}$-indigent module and nonzero direct summands of $\mathcal{X}$-indigent modules are $\mathcal{X}$-indigent.

(6) 

There exists an $\mathcal{X}$-indigent module and nonzero quotients of $\mathcal{X}$-indigent modules are $\mathcal{X}$-indigent.

In the rest of this note, unless otherwise stated, $\mathcal{B}$ is a proper subclass of Mod-R.

Let M be a finitely presented right R-module; that is, M has a free presentation $F_1\to F_0\to M\to 0$, where $F_0$ and $F_1$ are finitely generated free modules. If we apply the functor $Ho{m}_R(-,R)$ to this presentation, we obtain the sequence $0\to M^{\ast }\to F_0^{\ast }\to F_1^{\ast }\to Tr\left(M\right)\to 0$, where $Tr\left(M\right)$ is the cokernel of the dual map $F_0^{\ast }\to F_1^{\ast }$. Note that $Tr\left(M\right)$ is a finitely presented left R-module. The left R-module $Tr\left(M\right)$ is called an Auslander–Bridger transpose of the right R-module M (see [14] (§5)).

The following proposition shows that $\mathcal{X}$-indigent modules exist for any ring if $\mathcal{X}=(\mathcal{A},\mathcal{B})$ is a complete cotorsion pair cogenerated by a set of some finitely presented modules $\mathcal{C}$.

Proposition 11. 

Let $\mathcal{X}=(\mathcal{A},\mathcal{B})$ be a complete cotorsion pair cogenerated by a set of some finitely presented right modules $\mathcal{C}$. Then, $F={\prod }_{C\in \mathcal{C}}Tr{\left(C\right)}^{+}$ is $\mathcal{X}$-indigent.

Proof. 

Let $N\in {\underline{\mathcal{IX}}}^{-1}\left(F\right)$. Then, $N\in {\underline{\mathcal{IX}}}^{-1}\left(Tr{\left(C\right)}^{+}\right)$ for every $C\in \mathcal{C}$ by (1) in Proposition 1; that is, $Tr{\left(C\right)}^{+}$ is N-$\mathcal{X}$-subinjective for every $C\in \mathcal{C}$. Now, consider the exact sequence $0\to N\to B\to A\to 0$ with $B\in \mathcal{B}$ and $A\in \mathcal{A}$.

Since $Tr{\left(C\right)}^{+}$ is N-$\mathcal{X}$-subinjective, the rows of the following commutative diagram, where the vertical isomorphisms are obtained by applying twice the adjunction $(\otimes ,Hom)$, are exact:

The second row being exact means that the sequence

$$0\to N\otimes Tr\left(C\right)\to B\otimes Tr\left(C\right)\to A\otimes Tr\left(C\right)\to 0$$

is exact for any $C\in \mathcal{C}$. Thus, since $C\in \mathcal{C}$ is finitely presented, it follows by [15] (Corollary 5.1) that

$$0\to C\otimes A^{+}\to C\otimes B^{+}\to C\otimes N^{+}\to 0$$

is exact for any $C\in \mathcal{C}$, and then, holding again that C is finitely presented, we get the commutative diagram with exact rows

from which it follows that

$$0\to Hom(C,N)\to Hom(C,B)\to Hom(C,A)\to 0$$

is exact for any $C\in \mathcal{C}$. That is, $Ex{t}_R^1(C,N)=0$ for any $C\in \mathcal{C}$, where $N\in \mathcal{B}$ by the fact that $\mathcal{C}$ is a cogenerating set for $\mathcal{X}$. □

Remark 1. 

By (2) in Lemma 1, we see that ${\underline{\mathcal{IX}}}^{-1}\left(Tr{\left(C\right)}^{+}\right)$ is independent of the chosen free presentation of C since all the modules $Tr{\left(C\right)}^{+}$ are $\mathcal{B}$-equivalent. That is why we have not been more precise in our use of $Tr\left(C\right)$ throughout this paper.

Proposition 12. 

Let $\mathcal{X}=(\mathcal{A},\mathcal{B})$ be a complete cotorsion pair cogenerated by a set of some finitely presented right modules $\mathcal{C}$. The following conditions are equivalent:

(1) 

$\mathcal{A}-GLD\left(R\right)=0$.

(2) 

Every module in $\mathcal{B}$ is injective.

(3) 

$F={\prod }_{C\in \mathcal{C}}Tr{\left(C\right)}^{+}$ is indigent.

Proof. $\left(1\right)\iff \left(2\right)$ Immediate.

$\left(2\right)\Rightarrow \left(3\right)$ Follows by Corollary 2 and Proposition 11.

$\left(3\right)\Rightarrow \left(2\right)$ Let $N\in \mathcal{B}$ and consider the exact sequence

$$0\to N\to E\left(N\right)\to E\left(N\right)/N\to 0.$$

We claim that

$$0\to Hom(E(N)/N,F)\to Hom(E(N),F)\to Hom(N,F)\to 0$$

is also exact.

Since $N\in \mathcal{B}$, $Ex{t}_R^1(C,B)=0$ for any $C\in \mathcal{C}$,

$$0\to Hom(C,N)\to Hom(C,E(N\left)\right)\to Hom(C,E(N)/N)\to 0$$

is exact for any $C\in \mathcal{C}$. So, by [15] (Corollary 5.1),

$$0\to N\otimes Tr\left(C\right)\to E\left(N\right)\otimes Tr\left(C\right)\to E\left(N\right)/N\otimes Tr\left(C\right)\to 0$$

is exact, and, by [15] (Lemma 5.1),

$$0\to Hom(Tr\left(C\right),{(E\left(N\right)/N)}^{+})\to Hom(Tr\left(C\right),E{\left(N\right)}^{+})\to Hom(Tr\left(C\right),N^{+})\to 0$$

is exact. But, every $C\in \mathcal{C}$ is finitely presented, so we get the following commutative diagram with exact rows:

which induces the commutative diagram with exact rows

Since every module is pure in its double dual and $Tr{\left(C\right)}^{+}$ is pure-injective, we see that h, $\psi$, and f are epimorphisms. But, g is also epic, so $fg=\varphi \psi$ is epic and then $\varphi$ is necessarily an epimorphism (for any $C\in \mathcal{C}$). Hence,

$$0\to \mathrm{Hom}\left(\mathrm{E}\right(N)/N,F)\to \mathrm{Hom}\left(\mathrm{E}\right(N),F)\to \mathrm{Hom}(N,F)\to 0$$

is exact; that is, F is N-subinjective, and then N is injective since F is indigent. □

Remark 2. 

The cotorsion pair $\mathcal{X}=(\mathcal{FC},\mathcal{FI})$ is cogenerated by a complete set $\mathcal{C}$ of representatives of all finitely presented modules. Then, all modules $Tr{\left(C\right)}^{+}$ of Proposition 11 are represented in $\mathcal{C}$, so $F={\prod }_{C\in \mathcal{C}}{C}^{+}$ is $\mathcal{X}$-indigent but not indigent in general.

If we assume that $F={\prod }_{C\in \mathcal{C}}{C}^{+}$ is indigent, we have an analogous result of Proposition 12, which characterizes the right-Noetherian rings.

Corollary 4. 

Let $\mathcal{X}=(\mathcal{FC},\mathcal{FI})$. The following are equivalent:

(1) 

R is right-Noetherian.

(2) 

Every FP-injective right module is injective.

(3) 

Every $\mathcal{X}$-indigent right module is indigent.

(4) 

$F={\prod }_{C\in \mathcal{C}}{C}^{+}$ is indigent.

Proof. $\left(1\right)\iff \left(2\right)$ [16] (Theorem 3).

$\left(1\right)\iff \left(4\right)$ [3] (Corollary 5).

$\left(2\right)\Rightarrow \left(3\right)$ If M is $\mathcal{X}$-indigent, then ${\underline{\mathcal{IX}}}^{-1}\left(M\right)=\mathcal{FI}={\mathcal{I}}_0$.

On the other hand, ${\mathcal{I}}_0\subseteq {\underline{\mathcal{I}}}^{-1}\left(M\right)\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, so indeed ${\underline{\mathcal{I}}}^{-1}\left(M\right)={\mathcal{I}}_0$ and then M is indigent.

$\left(3\right)\Rightarrow \left(4\right)$ $F={\prod }_{C\in \mathcal{C}}{C}^{+}$ is $\mathcal{X}$-indigent by Proposition 11. □

Let $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$ be the flat cotorsion pair that is generated by class $\mathcal{PI}$ of all pure injective modules. It is well known by [17] (Proposition 3.3.1) that R is right-perfect if and only if every right R-module is cotorsion. Thus, a ring R is right-perfect if and only if every (nonzero) right module is $\mathcal{X}$-indigent. Naturally, the first question that arises is whether such $\mathcal{X}$-indigent modules exist over all rings. Although we have not been able to answer this question entirely, we have some results for the existence of flat or cotorsion $\mathcal{X}$-indigent modules.

Remark 3. 

Let $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$ be the flat cotorsion pair and R be a von Neumman regular ring that is not semisimple. Then, Mod-R has no cotorsion $\mathcal{X}$-indigent module. Indeed, if there exists a cotorsion $\mathcal{X}$-indigent right module M, then ${\underline{\mathcal{IX}}}^{-1}\left(M\right)=\mathcal{EC}$ (because M is $\mathcal{X}$-indigent) and ${\underline{\mathcal{IX}}}^{-1}\left(M\right)=$ Mod-R (because M is cotorsion). Therefore, our cotorsion pair is $(\mathcal{FL},Mod\text{-}R)$. But, every right R-module is flat, so ${\mathcal{FL}}^{\perp }=Mod\text{-}{R}^{\perp }={\mathcal{I}}_0$ and then ${\mathcal{I}}_0=$ Mod-R, so R is semisimple, which is a contradiction.

Proposition 13. 

Let $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$ be the flat cotorsion pair over a commutative ring R. If there is an $\mathcal{X}$-indigent flat module, then $R/A$ is cotorsion for any finitely generated ideal A that contains a regular element.

Proof. 

If A contains a regular element, then $Ho{m}_R(R/A,R)=0$. Thus, by considering the isomorphism $Ho{m}_R(R/A,R^{\left(I\right)})\cong Ho{m}_R{(R/A,R)}^{\left(I\right)}$, we have $Ho{m}_R(R/A,R^{\left(I\right)})=0$. Let F be a flat and $\mathcal{X}$-indigent module and consider any epimorphism $\pi :R^{\left(I\right)}\to F$. Since $R/A$ is finitely presented and $\pi$ is pure, any homomorphism from $R/A$ to F can be lifted to $R^{\left(I\right)}$. Thus, $Ho{m}_R(R/A,F)=0$ by the fact that $Ho{m}_R(R/A,R^{\left(I\right)})=0$. Thus, $R/A\in {\underline{\mathcal{IX}}}^{-1}\left(F\right)$, so $R/A$ is cotorsion. □

Remark 4. 

Let $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$ be the flat cotorsion pair.

(1) Assume that R is a commutative Noetherian domain. If there is an $\mathcal{X}$-indigent flat module, by Proposition 13, every proper cyclic module is cotorsion.

(2) Assume that R is a commutative Noetherian domain with Krull dimension $\ge 1$. Then, by [18] (Proposition 2.8), any cyclic R-module $R/I$ is cotorsion if and only if $R/I$ is a complete semilocal ring. If R has some factor ring that is not completely semilocal, then not every cyclic module needs to be cotorsion. Thus, we see that there are commutative Noetherian domains with no $\mathcal{X}$-indigent flat modules.

Proposition 14. 

If an Abelian group A is $\mathcal{X}$-indigent, where $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$, then, for every prime number p, the reduced part of $T_p\left(A\right)$ is unbounded; that is, for every integer N, there is $n\ge N$ such that A has a direct summand isomorphic to ${\mathbb{Z}}_{p^n}$.

Proof. 

We can assume that A is reduced. Suppose the contrary, that there is a prime number p and a natural number N such that, for every direct summand of A isomorphic to ${\mathbb{Z}}_{p^n}$, $n<N$. Therefore, for the basic subgroup B of the p-component $T_p\left(A\right)$ of the torsion part $T\left(A\right)$ of A, we have $p^{N}B=0$. Then, $T_p\left(A\right)\cong B\oplus T_p\left(A\right)/B$. Since $T_p\left(A\right)$ is reduced, $T_p\left(A\right)/B=0$, so $p^N{T}_p\left(A\right)=p^{N}B=0$. Then, for every homomorphism $f:{⨁}_{n=1}^{\infty }{\mathbb{Z}}_{p^n}\to A$, $p^{N}Imf\subseteq p^N{T}_p\left(A\right)=0$; therefore, f can be extended to some homomorphism $g:{\prod }_{n=1}^{\infty }{\mathbb{Z}}_{p^n}\to Imf\subseteq A$ since $Imf$ is cotorsion. So, A is ${⨁}_{n=1}^{\infty }{\mathbb{Z}}_{p^n}$-$\mathcal{X}$-subinjective. But, ${⨁}_{n=1}^{\infty }{\mathbb{Z}}_{p^n}$ is not cotorsion by [19] (Corollary 8.4). Thus, A is not $\mathcal{X}$-indigent, a contradiction. □

Proposition 15. 

Let $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$ and A be an Abelian group such that, for every prime p, the reduced part of $T_p\left(A\right)$ is unbounded. If A is C-$\mathcal{X}$-subinjective for some torsion group C, then C is cotorsion.

Proof. 

Without loss of generality, we may assume that A is reduced. Let A be C-$\mathcal{X}$-subinjective for some torsion group C. We can assume that C is reduced as well. Then, A is $C_p$-$\mathcal{X}$-subinjective for each p-component of C. If $C_p$ is unbounded, then its basic subgroup $B_p$ is also unbounded. There is an epimorphism $f:C\to B_p$ by [19] (Theorem 6.10). Since $T_p\left(A\right)$ is unbounded and reduced, its basic subgroup is unbounded. Therefore, there is a homomorphism $g:B_p\to T_p\left(A\right)$ such that $Im\left(g\right)$ is unbounded. Since $T_p\left(A\right)$ is C-$\mathcal{X}$-subinjective, the homomorphism $g\circ f:C\to T_p\left(A\right)$ can be extended to a homomorphism $\varphi :c\left(C\right)\to T_p\left(A\right)$, where $c\left(C\right)$ is the cotorsion envelope of C. Since cotorsion groups are closed under factor groups, $Im\left(\varphi \right)$ must be cotorsion. However, $Im\left(g\right)\subseteq Im\left(\varphi \right)$, so $Im\left(\varphi \right)$ is unbounded, and therefore it is not cotorsion by [19] (Corollary 8.4). This contradiction shows that $C_p$ is bounded.

Now, if $C_p\ne 0$ only for a finite number of p’s, then C is cotorsion by [19] (Corollary 8.4). Suppose that $C_p\ne 0$ for infinitely many p’s. For each p with $C_p\ne 0$, there is an epimorphism $f_p:C_p\to B_p$, where $B_p$ is a basic subgroup of $C_p$ and a nonzero homomorphism $g_p:B_p\to T_p\left(A\right)$. Then, the p-component ${(Imh)}_p$ of $Imh$ is not zero for infinite number of p, where $h=⨁(g_p\circ f_p):C=⨁C_p\to A=⨁A_p$. Since A is C-$\mathcal{X}$-subinjective, h can be extended to a homomorphism $u:c\left(C\right)\to A$, where $c\left(C\right)$ is the cotorsion envelope of C. Then, $Imu$ is cotorsion and ${(Imu)}_p\ne 0$ for infinitely many p’s. Therefore, $Imu={⨁}_{p\in P}{(Imu)}_p\ne {\prod }_{p\in P}{(Imu)}_p$ and $K=\left({\prod }_{p\in P}{(Imu)}_p\right)/Imu$ is torsion-free and divisible. Then, ${\prod }_{p\in P}{(Imu)}_p\cong Imu\oplus K$. But, ${\prod }_{p\in P}{(Imu)}_p$ is reduced. Contradiction. So, C is cotorsion. □

As a consequence of Propositions 14 and 15, we have the following.

Corollary 5. 

Let $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$, and let $\mathcal{T}$ denote the class of all torsion Abelian groups. For an Abelian group A, ${\underline{\mathcal{IX}}}^{-1}\left(A\right)\cap \mathcal{T}=\mathcal{EC}\cap \mathcal{T}$ if and only if, for every prime p, the reduced part of $T_p\left(A\right)$ is unbounded.

Remark 5. 

Let $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$ be the flat cotorsion pair. We do not know the complete description of $\mathcal{X}$-indigent Abelian groups, but an $\mathcal{X}$-indigent Abelian group must contain a subgroup isomorphic to the p-localization ${\mathbb{Z}}_{\left(p\right)}$ of $\mathbb{Z}$ for every prime p. In fact, if A is an Abelian group that does not contain such a subgroup for some prime p, then, for every homomorphism $f:{\mathbb{Z}}_{\left(p\right)}\to A$, $Imf$ will be zero or a torsion group that is isomorphic to ${\mathbb{Z}}_{p^n}$ for some integer n. In either case, $Im\left(f\right)$ is cotorsion, so f always factors through a cotorsion module; that is, A is ${\mathbb{Z}}_{\left(p\right)}$-$\mathcal{X}$-subinjective, where A is not $\mathcal{X}$-indigent since ${\mathbb{Z}}_{\left(p\right)}$ is not cotorsion.

This being the case, the following comes to mind: if we add torsion-free groups of rank 1 as direct summands, can we obtain an $\mathcal{X}$-indigent group?

The example below shows that these are also insufficient.

Example 2. 

Let $B=T\oplus \left({⨁}_{i\in I}{R}_i\right)$, where T is a reduced torsion group with unbounded $T_p$ for all primes p and ${\left\{R_i\right\}}_{i\in I}$ is the complete set of nonisomorphic torsion-free groups of rank 1. Then, B is not $\mathcal{X}$-indigent.

To prove it, we will prove that B is A-$\mathcal{X}$-subinjective, where A is the following non-cotorsion group found by Corner. By [19] (Page: 437, Exercise 5), there is a torsion-free group A of rank 2 such that all torsion-free factor groups of rank 1 are divisible, all subgroups of rank 1 are free, and $\mathit{End}A\cong \mathbb{Z}$. A is countable; therefore, A is slender by [19] (Chapter 13, Lemma 2.3). Then, A is not algebraically compact (= pure-injective) by [19] (Page: 489, Property (d)); therefore, A is not cotorsion since cotorsion torsion-free groups are algebraically compact by [19] (Chapter 9, Lemma 8.1). Now, to show that B is A-$\mathcal{X}$-subinjective, let $f:A\to B$ be any homomorphism and C be a cotorsion envelope of A. Each $R_i$ is reduced and $Im\left({\pi }_{i}f\right)$ is divisible, where ${\pi }_i:B\to R_i$ is the canonical projection, so ${\pi }_{i}f=0$ for each i and then $Imf\subseteq T$. Clearly, ${(Imf)}_p\ne 0$ for only finitely many primes p, and $r_p(Imf)=2$ for each p. So, $Imf$ is bounded and therefore is cotorsion. Then, f can be extended to $g:C\to Imf\subseteq B$. So, B is A-$\mathcal{X}$-subinjective and A is not cotorsion; that is, B is not $\mathcal{X}$-indigent.

 Question. 

Provide a description of an $\mathcal{X}$-indigent Abelian group.

We think that a group of the form $T\oplus A$, where T is a reduced torsion group with unbounded $T_p$ for all primes p, and A is a direct sum of nonisomorphic indecomposable torsion-free groups of finite rank, is $\mathcal{X}$-indigent.

Remark 6. 

Let $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$ be the flat cotorsion pair in the category of Abelian groups.

(1) There is no $\mathcal{X}$-indigent torsion-free Abelian group. Indeed, let F be a torsion-free group that is not cotorsion and T be a torsion group that is not cotorsion. Since $Hom(T,F)=0$, then F is T-$\mathcal{X}$-subinjective; therefore, F is not $\mathcal{X}$-indigent.

(2) There is no $\mathcal{X}$-indigent torsion Abelian group by Remark 5.

Remark 7. 

Let $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$. The Abelian group $G={\oplus }_p{\mathbb{Z}}_p$, where p ranges over all primes, is indigent by [4] (Theorem 27). On the other hand, G is not $\mathcal{X}$-indigent by Proposition 14.

We conclude this section by presenting examples of $\mathcal{X}$-subinjectivity domains that are neither minimal nor maximal.

Remark 8. 

For the cotorsion pair $\mathcal{X}=(\mathcal{FL},\mathcal{EC})$, we have the following examples of Abelian groups that are neither $\mathcal{X}$-indigent nor cotorsion: $\mathbb{Z}$, non-cotorsion torsion groups, and module B of Example 2.

Remark 9. 

For the cotorsion pair $\mathcal{X}=(\mathcal{FC},\mathcal{FI})$ in Mod-R, the right module $M={\prod }_{C\in \mathcal{C}}{C}^{+}$, where $\mathcal{C}$ is the complete set of representatives of all cyclically presented modules, is neither $\mathcal{X}$-indigent nor FP-injective. Note that divisible right R-modules are the right part of the cotorsion pair cogenerated by cyclically presented modules. So, it can be easily seen by Lemma 2 that ${\underline{\mathcal{IX}}}^{-1}\left(M\right)\subseteq$ {divisible modules}. On the other hand, let N be a divisible right R-module and consider the exact sequence $0\to N\to E\left(N\right)\to E\left(N\right)/N\to 0$.

Since N is divisible, the above exact sequence is $RD$-exact; hence, for any $C\in \mathcal{C}$, the rows of the following commutative diagram, where the vertical isomorphisms are obtained by applying the adjunction $(\otimes ,Hom)$, are exact:

The second row being exact means that $N\in {\underline{\mathcal{IX}}}^{-1}\left(C^{+}\right)$ for any $C\in \mathcal{C}$. So, we conclude by Lemma 1 that $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

4. Cotorsion Pair Cogenerated by the Class of All Finitely Presented Modules

It is well known that a right R-module M is FP-injective if and only if each short exact sequence $0\to M\to N\to L\to 0$ in Mod-R is pure. FP-injective modules are known to be the right part of the complete cotorsion pair $\mathcal{X}=(\mathcal{FC},\mathcal{FI})$. Note that $\mathcal{FI}$ is also the right-orthogonal class of finitely presented modules, so $\mathcal{X}=(\mathcal{FC},\mathcal{FI})$ is cogenerated by the class of all finitely presented modules. From now on, $\mathcal{X}$ will always refer to the cotorsion pair $\mathcal{X}=(\mathcal{FC},\mathcal{FI})$.

From Proposition 1, N is FP-injective if and only if $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ for any module M if and only if $N\in {\underline{\mathcal{IX}}}^{-1}\left(M^{+}\right)$ for any finitely presented module M. The following two results will be used throughout this section.

Proposition 16. 

The following conditions are equivalent for a module M:

(1) 

M is FP-injective.

(2) 

${\underline{\mathcal{IX}}}^{-1}\left(M\right)=$ Mod-R.

(3) 

$M\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Moreover, if R is a right-coherent ring, then the above conditions equivalent to

(4) 

$\mathcal{FC}\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

(5) 

FP-projective precovers of M are in ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

(6) 

$\mathcal{PP}\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

(7) 

Pure-projective precovers of M are in ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Proof. $\left(1\right)\iff \left(2\right)\iff \left(3\right)$ follow from Proposition 2.

$\left(2\right)\Rightarrow \left(4\right)\Rightarrow \left(5\right)$ Clear.

$\left(5\right)\Rightarrow \left(6\right)$ If $f:F\to M$ is an FP-projective precover, then, for any pure-projective module P, the unique morphism $P\oplus F\to M$ induced by f and $0:P\to M$ is also an FP-projective precover of M, so, by hypothesis, $P\oplus F\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. But, ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$ is closed under direct summands, so we conclude.

$\left(6\right)\iff \left(7\right)$ Follows from Proposition 7.

$\left(7\right)\Rightarrow \left(1\right)$ The hypothesis implies by Proposition 7 that M is a pure-quotient of an FP-injective module. Therefore, there is a pure exact sequence

$$0\to K\to N\to M\to 0$$

(1)

with N FP-injective. For any finitely presented module F, we get the exact sequence

$$0\to Hom(F,K)\to Hom(F,N)\to Hom(F,M)\to Ex{t}^1(F,K)\to Ex{t}^1(F,N)=0,$$

and $Hom(F,N)\to Hom(F,M)\to 0$ is also exact, so $Ex{t}^1(F,K)=0$ and K is FP-injective.

But, since R is right-coherent, K being FP-injective implies that $Ex{t}^n(F,K)=0\forall n$, and from $\left(1\right)$ we also have the exact sequence

$$0=Ex{t}^1(F,N)\to Ex{t}^1(F,M)\to Ex{t}^2(F,K)=0,$$

so, necessarily, $Ex{t}^1(F,M)=0$, and then M is FP-injective. □

Proposition 17. 

The following conditions are equivalent for a module M:

(1) 

M is a homomorphic image of an FP-injective module.

(2) 

${\mathcal{P}}_0\subseteq {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

(3) 

For any projective right module P and any submodule K of P, if $P/K\in {}^{\perp }M$, then $K\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Proof. $\left(1\right)\iff \left(2\right)$ follows from Proposition 6.

$\left(3\right)\Rightarrow \left(2\right)$ is clear by taking $K=P$.

$\left(2\right)\Rightarrow \left(3\right)$ Let P be a projective right module. Consider $0\to K\to P\to P/K\to 0$ with $P/K\in {}^{\perp }M$. By applying $Hom(-,M)$, we obtain $0\to Hom(P/K,M)\to Hom(P,M)\to Hom(K,M)\to Ex{t}^1(P/K,M)$. Since $Ex{t}^1(P/K,M)=0$, $Hom(P,M)\to Hom(K,M)$ is epic. This means that, for any $f:K\to M$, there exists a homomorphism $g:P\to M$ such that $g\alpha =f$, where $\alpha :K\to P$. To show that $K\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, let $h:P\to E$ be a special FP-injective preenvelope of P. Since $P\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, there exists a homomorphism $\varphi :E\to M$ such that $\varphi h=g$. So, $f=g\alpha =\left(\varphi h\right)\alpha$, where $K\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. □

Recall that R is QF if and only if every injective (resp. projective) right module is projective (resp. injective). Now, we characterize QF rings in terms of subinjectivity domains relative to the cotorsion pair $\mathcal{X}=(\mathcal{FC},\mathcal{FI})$ and subprojectivity domains ${\underline{\mathcal{P}}}^{-1}\left(N\right)$.

Theorem 1. 

The following conditions are equivalent for a ring R:

(1) 

R is QF.

(2) 

For any two modules M and N, $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ if and only if $M\in {\underline{\mathcal{P}}}^{-1}\left(N\right)$.

Proof. $\left(1\right)\Rightarrow \left(2\right)$ Consider the natural epimorphism $\pi :P\to M$ with P projective, and let $g:N\to E$ be an FP-injective special preenvelope of N. Suppose that $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. To prove that $M\in {\underline{\mathcal{P}}}^{-1}\left(N\right)$, let $f:N\to M$ be any homomorphism. Since $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, there exists $h:E\to M$ such that $hg=f$. Since R is QF, E is projective. So, there exists a homomorphism $\varphi :E\to P$ such that $\pi \varphi =h$, where $f=hg=\pi \varphi g$. Thus, $M\in {\underline{\mathcal{P}}}^{-1}\left(N\right)$.

Now, suppose that $M\in {\underline{\mathcal{P}}}^{-1}\left(N\right)$. We claim that $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. Let $f:N\to M$ be any morphism and $\pi :P\to M$ be any epimorphism with P projective. Since $M\in {\underline{\mathcal{P}}}^{-1}\left(N\right)$, there exists a homomorphism $h:N\to P$ such that $\pi h=f$. Consider the following diagram:

where $\alpha :N\to E$ is any special FP-injective preenvelope of N. Since R is QF, P is FP-injective, so there exists a homomorphism $\phi :E\to P$ such that $\phi \alpha =h$. So, $f=\pi h=\left(\pi \phi \right)\alpha$, where $\pi \phi :E\to M$ and where $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

$\left(2\right)\Rightarrow \left(1\right)$ Let E be an FP-injective module. Then, $E\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ for every right module M. By assumption, $M\in {\underline{\mathcal{P}}}^{-1}\left(E\right)$ for every M. So, E is projective, where R is QF. □

Clearly, the subinjectivity domain ${\underline{\mathcal{I}}}^{-1}\left(M\right)$ of a module M is contained in ${\underline{\mathcal{IX}}}^{-1}\left(M\right)$. But, they need not be equal.

Example 3. 

Let R be a non-Noetherian ring, and $M={⨁}_{i\in I}{E}_i$ be an arbitrary direct sum of injective modules $E_i$. Since M is FP-injective, $M\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$. On the other hand, since M need not be injective, $M\notin {\underline{\mathcal{I}}}^{-1}\left(M\right)$.

As an easy consequence of Proposition 2, we have the following result.

Remark 10. 

Let M be a module. Then, ${\underline{\mathcal{IX}}}^{-1}\left(M\right)={\underline{\mathcal{I}}}^{-1}\left(M\right)$ if and only if $\mathcal{FI}\subseteq {\underline{\mathcal{I}}}^{-1}\left(M\right)$.

Let M be a left R-module and N be a right R-module. Recall that N is absolutely M-pure if $N{\otimes }_{R}M\to K{\otimes }_{R}M$ is a monomorphism for every (resp. FP-injective) extension K of N. For a module M, the absolutely pure domain of M, $\mathcal{A}p\left(M\right)$, is defined to be the collection of all modules N such that N is absolutely M-pure. M is said to be f-indigent if its absolutely pure domain is as small as possible, namely consisting of exactly the FP-injective modules (see [20]).

Proposition 18. 

Let M be a right R-module and N be a left R-module. Then,

(1) 

$N\in {\underline{\mathcal{IX}}}^{-1}\left(M^{+}\right)$ if and only if $N\in \mathcal{A}p\left(M\right)$.

(2) 

M is f-indigent if and only if $M^{+}$ is $\mathcal{X}$-indigent.

Proof. (1) Let $N\to E$ be any FP-injective extension of N, and consider the following diagram:

Hence, f is epic if and only if g is epic. Therefore, $N\in {\underline{\mathcal{IX}}}^{-1}\left(M^{+}\right)$ if and only if $N\in \mathcal{A}p\left(M\right)$.

(2) Easily follows by (1). □

Proposition 19. 

Let N be a finitely presented right R-module and M a right R-module. Then,

(1) 

$N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ if and only if $N\in \mathcal{A}p\left(M^{+}\right)$.

(2) 

$N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ if and only if $N\in {\underline{\mathcal{IX}}}^{-1}\left(M^{++}\right)$.

(3) 

If $N^{++}\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, then $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Proof. (1) Let $N\in \mathcal{A}p\left(M^{+}\right)$; i.e., N is absolutely $M^{+}$-pure. Let $N\to E$ be an $FP$-injective precover of N. Since N is finitely presented, we can consider the following diagram with isomorphic columns:

Since the first row is exact, the second row is also exact. Thus, it follows that

$$0\to Hom(E/N,M)\to Hom(E,M)\to Hom(N,M)\to 0$$

is exact; that is, $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$.

Conversely, if $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, the second row above must be exact, as well as the first row. Thus, $N\in \mathcal{A}p\left(M^{+}\right)$.

(2) follows easily by (1) and Proposition 18.

(3) If $N^{++}\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$, then $N^{++}\in \mathcal{A}p\left(M^{+}\right)$ by (1). Let $0\to N\to N^{++}\to N^{++}/N\to 0$ be a short exact sequence, and consider the pushout of $N\to N^{++}$ and $N\to E\left(N\right)$. If we apply $-\otimes M^{+}$ to this pushout, we get the commutative diagram

Since N is pure in $N^{++}$, $\psi$ is monic. On the other hand, since $N^{++}\in \mathcal{A}p\left(M^{+}\right)$, $\varphi$ is monic. So, $\varphi \psi =gf$ is monic, where f is monic and $N\in \mathcal{A}p\left(M^{+}\right)$ ([20] (Proposition 2.2). Thus, $N\in {\underline{\mathcal{IX}}}^{-1}\left(M\right)$ by (1). □

Now, applying Proposition 17, we find characterizations of FP-injective rings in terms of the existence of an $\mathcal{X}$-indigent module, which is the homomorphic image of an FP-injective module.

Proposition 20. 

The following conditions are equivalent for a ring R:

(1) 

$R_R$ is FP-injective.

(2) 

Every right R-module is a homomorphic image of an FP-injective module.

(3) 

For any projective right module P and any submodule K of P, if $P/K$ is projective, then K is FP-injective.

(4) 

For any projective right module P and any submodule K of P, if $P/K$ is flat, then K is FP-injective.

(5) 

There exists an $\mathcal{X}$-indigent module that is homomorphic image of an FP-injective module.

Proof. $\left(1\right)\iff \left(2\right)$ Clear.

$\left(2\right)\iff \left(3\right)$ Proposition 17.

$\left(1\right)\Rightarrow \left(4\right)$ If $P/K$ is flat, then the sequence

$$0\to K\to P\to P/K\to 0$$

is pure, so K is $FP$-injective if and only if P is FP-injective. But, R is FP-injective, so every projective module is FP-injective.

$\left(4\right)\Rightarrow \left(3\right)$ Nothing to prove.

$\left(2\right)\Rightarrow \left(5\right)$ Clear by the existence of an $\mathcal{X}$-indigent module.

$\left(5\right)\Rightarrow \left(1\right)$ Assume that there exists an $\mathcal{X}$-indigent module that is also homomorphic image of an FP-injective module. So, ${\underline{\mathcal{IX}}}^{-1}\left(M\right)=\mathcal{FI}\supseteq {\mathcal{P}}_0$, where every projective module is FP-injective. □

We know that there is an $\mathcal{X}$-indigent module over any ring R by Proposition 11. This suggests the question of how close can the class of $\mathcal{X}$-indigent right R-modules be to Mod-R. By Proposition 10, every right R-module is $\mathcal{X}$-indigent if and only if every right R-module is FP-injective; i.e., R is right (von Neumann) regular ring. If R is not regular, then no FP-injective module is $\mathcal{X}$-indigent.

Now, we examine rings whose every simple right module is either FP-injective or $\mathcal{X}$-indigent. Note that right-SAP rings (the rings whose simple right modules are FP-injective; see [21]) are natural examples of this type of ring.

Lemma 4. 

The following conditions are equivalent for a ring R:

(1) 

Every simple right module is FP-injective or $\mathcal{X}$-indigent.

(2) 

Either R is a right-SAP ring or there exists a unique $\mathcal{X}$-indigent simple right R-module S (up to isomorphism).

Proof. 

Let R be a ring whose every simple right module is FP-injective or $\mathcal{X}$-indigent. Suppose R is not right-SAP. Let S be a simple right R-module that is not FP-injective. Thus, by assumption, S is $\mathcal{X}$-indigent. If $S^{\prime }$ is another simple right R-module such that $S^{\prime }\ncong S$, then, clearly, $S^{\prime }\in {\underline{\mathcal{IX}}}^{-1}\left(S\right)$. This establishes that $S^{\prime }$ is an FP-injective right R-module. It turns out that R has at most one isomorphism class of non-FP-injective simple right module which is $\mathcal{X}$-indigent. Conversely, if R is right-SAP, then there is nothing to prove. On the other hand, let T be a simple right module that is not FP-injective. If $T\ncong S$, $T\in {\underline{\mathcal{IX}}}^{-1}\left(S\right)$; that is, T is FP-injective, a contradiction. Thus, $T\cong S$, and (1) follows. □

In the remainder of this paper, alongside the newly proposed approach, we employ the techniques presented by Durgun in [3,20], which are applicable to certain classes of rings.

Proposition 21. 

Let R be a ring such that every simple right R-module is FP-injective or $\mathcal{X}$-indigent. If R is not right-SAP, then R is either right-semihereditary or right-FP-injective.

Proof. 

Suppose that every non-FP-injective simple right R-module is $\mathcal{X}$-indigent. Since R is not right-SAP ring, there exists a unique $\mathcal{X}$-indigent simple right R-module S up to isomorphism by Lemma 4. If $Hom\left(E\right(R),S)=0$, then, for any submodule K of $E\left(R\right)$, consider $E\left(R\right)/K$. By applying $Hom(-,S)$ to the epimorphism $E\left(R\right)\to E\left(R\right)/K$, we get the exact sequence $0\to Hom\left(E\right(R)/K,S)\to Hom\left(E\right(R),S)=0$. So, $Hom\left(E\right(R)/K,S)=0$, where $E\left(R\right)/K$ is FP-injective by the $\mathcal{X}$-indigency of S. This shows that R is right-semihereditary by [22] (Theorem 2.2). On the other hand, if $Hom\left(E\right(R),S)\ne 0$, then S is a homomorphic image of an (FP-)injective right module $E\left(R\right)$, so R is right-FP-injective by Proposition 20. □

Over a commutative ring, for any simple module S, we always have $S\cong S^{+}$. It is well known that a ring R is right-Kasch if each simple right R-module embeds in a projective right R-module. Dually, a ring R is called in [23] right-dual-Kasch if each simple right R-module is a homomorphic image of an injective right R-module.

Corollary 6. 

Let R be a commutative coherent ring such that every simple R-module is FP-injective or $\mathcal{X}$-indigent. Then, R satisfies only one of the following cases:

(1) 

R is a V-ring.

(2) 

R is a semihereditary ring.

(3) 

R is an IF and dual-Kasch ring.

Proof. 

Let R be a ring whose every simple module is FP-injective or $\mathcal{X}$-indigent. By Lemma 4, either R is an SAP ring or there exists a unique $\mathcal{X}$-indigent simple R-module T (up to isomorphism). In case R is an SAP ring, every simple right R-module is FP-injective. Over a commutative ring R for a simple module S, $S\cong S^{+}$, so S is flat if and only if it is injective. Thus, R is a V-ring. The latter case implies by Proposition 21 that R is either semihereditary or FP-injective. Since the latter case implies that R is not semihereditary, by the proof of Proposition 21, $Hom\left(E\right(R),S)\ne 0$, meaning that R is dual-Kasch. On the other hand, let E be an injective right R-module. Since R is coherent, $E^{+}$ is flat, so $E^{+}\in \mathcal{A}p\left(S\right)$ by [20] (Lemma 3.1). In this case, since the simple module T is f-indigent by Proposition 18, $E^{+}$ is FP-injective, so E is flat. Thus, R is an IF ring. □

Theorem 2. 

Let R be a left-perfect right-coherent ring with $Z\left(R_R\right)\ne 0$. The following are equivalent:

(1) 

Every simple right R-module is FP-injective or $\mathcal{X}$-indigent.

(2) 

One of the following statements holds:

(i) R is a right-SAP ring;

(ii) $R=S\times T$, where S is semisimple Artinian ring and T is an indecomposable matrix ring over a local QF-ring.

Proof. $\left(1\right)\Rightarrow \left(2\right)$ Let R be a ring whose every simple right module is FP-injective or $\mathcal{X}$-indigent, which is not right-SAP. Since R is not nonsingular, R is not right-semihereditary. So, by Proposition 21, R must be right-FP-injective. Since R is right-coherent and right-FP-injective, R is left-IF ring by [24] (Theorem 3.10). Thus, R is QF by left-perfectness. In this case, since R is right-Noetherian, by Corollary 4, R has no simple subinjective middle class. Thus, by [3] (Theorem 18), there is a ring direct sum $R=S\times T$, where S is semisimple Artinian ring and T is an indecomposable matrix ring over a local QF-ring.

$\left(2\right)\Rightarrow \left(1\right)$ In case R is a right-SAP ring, every simple right R-module is FP-injective, and the task is complete. If we assume 2-(ii), R is right-Noetherian. The rest follows by [3] (Theorem 18) and Corollary 4. □

Corollary 7. 

Let R be a commutative ring. The following are equivalent:

(1) 

Every simple module is (FP-)injective or $\mathcal{X}$-indigent.

(2) 

Every simple module is flat or f-indigent.

Moreover, if R is Noetherian, then the above is equivalent to

(3) 

R is a V-ring or there is a ring direct sum $R=S\times T$, where S is semisimple Artinian ring and T is either a local QF ring or a DVR.

Proof. $\left(1\right)\iff \left(2\right)$ follows by the isomorphism $S\cong S^{+}$ for any simple module S and Proposition 18.

$\left(2\right)\iff \left(3\right)$ follows by [20] (Theorem 5.2) and [3] (Corollary 19). □

The weak global dimension of R, $wD\left(R\right)\le 1$ if and only if every submodule of a flat right (left) R-module is flat if and only if every (finitely generated) right (left) ideal is flat (see [25] (9.24)).

Proposition 22. 

Let R be a non-regular right-coherent ring. Assume that every right R-module is FP-injective or $\mathcal{X}$-indigent. Then, R satisfies only one of the following cases:

(1) 

R is right-semihereditary;

(2) 

R is left-coherent two-sided IF and left-Kasch ring.

Proof. 

By hypothesis, R has a singular simple left module S. Since S is singular, S is non-flat, so $S^{+}$ is not FP-injective. So, the hypothesis implies that $S^{+}$ is $\mathcal{X}$-indigent, where S is f-indigent by Proposition 18(2). On the other hand, R is either right-semihereditary or right-FP-injective by Proposition 21.

From the latter case, R is right-FP-injective. Since in this case R is not right-semihereditary, $wD\left(R\right)\nleqq 1$ by right coherence of R. So, there exists a finitely generated left ideal I that is not flat; that is, $I^{+}\notin \mathcal{A}p\left(S\right)$. Since S is finitely presented, by [20] (Corollary 2.1), $I\notin {\underline{\mathcal{P}}}^{-1}\left(S\right)$. This means that $Hom(S,I)\ne 0$, so $Hom(S,R)\ne 0$. This shows that R is left-Kasch, so the f-indigent module S embeds in ${}_{\mathrm{R}}R$. Thus, by [20] (Corollary 3.1), R is left-IF. Now, we claim also that R is right-IF. First we show that every non-flat left R-module is f-indigent. Let M be a non-flat left module. Then, $M^{+}$ is not FP-injective, so, by hypothesis, $M^{+}$ is $\mathcal{X}$-indigent; this means that M is f-indigent by Proposition 18. Thus, being right-IF and left-coherent comes from [20] (Lemma 4.1). □

Theorem 3. 

Let R be a non-regular left-perfect ring that has at least one finitely presented singular simple left R-module. Assume that every right R-module is FP-injective or $\mathcal{X}$-indigent. Then, R satisfies only one of the following cases:

(1) 

R is hereditary Artinian serial.

(2) 

R is QF fully saturated ring.

Proof. 

First, we claim that every non-projective simple left R-module is f-indigent. Let S be a non-projective simple left module. Then, $S^{+}$ is not FP-injective, so, by the hypothesis, $S^{+}$ is $\mathcal{X}$-indigent. This means that S is f-indigent by Proposition 18. Thus, R is left-$\sum -CS$ by [20] (Corollary 4.1). On the other hand, by hypothesis, R has a finitely presented singular simple left module T. Existence of a finitely presented f-indigent module T is provided by [20] (Proposition 4.2) such that R is right-coherent. On the other hand, R is either right-semihereditary or right-FP-injective by Proposition 21. The former case provides that $wD\left(R\right)\le 1$, and, together with left-perfectness, we can deduce that R is left-hereditary. Since R is left-$\sum -CS$, R is hereditary Artinian serial ring on both sides by [26] (Corollary 3.2). The latter case provides by Proposition 22 that R is left-Kasch. Being left-Kasch and left-$\sum -CS$, R is QF. In this case, the hypothesis implies by Corollary 4 that R has no subinjective middle class. Thus, R is right fully saturated by [4] (Lemma 15). □

Corollary 8. 

Let R be a left-perfect ring that has at least one finitely presented singular simple left R-module with $Z\left(R_R\right)\ne 0$. The following are equivalent:

(1) 

Every right R-module is FP-injective or $\mathcal{X}$-indigent.

(2) 

R is a fully saturated QF-ring.

Proof. $\left(1\right)\Rightarrow \left(2\right)$ Since we assume that R is not nonsingular, the hypothesis and Theorem 3 imply that R is QF fully saturated ring, and we conclude.

$\left(2\right)\Rightarrow \left(1\right)$ If we assume (2), then R is right-Noetherian. The rest follows by [27] (Theorem 18) and Corollary 4. □

Corollary 9. 

Let R be a non-regular left-perfect ring that has at least one finitely presented singular simple right R-module. The following are equivalent:

(1) 

Every right R-module is FP-injective or $\mathcal{X}$-indigent.

(2) 

Every right R-module is injective or indigent.

(3) 

There is a ring decomposition $R\cong S\times T$, where S is a semisimple Artinian ring and T is an indecomposable ring that is either

(i) right fully saturated QF-ring;

(ii) hereditary Artinian serial ring with $J{\left(T\right)}^2$ = 0.

Proof. $\left(1\right)\iff \left(2\right)$ is clear since (1) implies by Theorem 3 that R is right-Noetherian.

$\left(2\right)\iff \left(3\right)$ follows by [27] (Theorem 3.2). □

5. Conclusions

This work links cotorsion theory with the well-known subinjectivity concept and extends the classical results into one unified framework. We introduce a new concept of a module M opposed to injectivity in terms of complete cotorsion pair $\mathcal{X}=(\mathcal{A},\mathcal{B})$, referred to as the $\mathcal{X}$-subinjectivity domain of M. This approach not only confirms the known results about usual subinjectivity but also applies to more general cases involving any complete cotorsion pair. This allows us to characterize some classical rings in terms of these domains and generalize some known results. In addition, we consider the modules whose $\mathcal{X}$-subinjectivity domains are as small as possible, called $\mathcal{X}$-indigent. We have established the existence of $\mathcal{X}$-indigent modules for any cotorsion pair cogenerated by the class of all finitely presented modules. Additionally, we determine the rings for which all (simple) right modules are either $\mathcal{X}$-indigent or FP-injective. Although we have not been able to provide an example of an $\mathcal{X}$-indigent Abelian group for the cotorsion pair generated by the class of pure-injective modules, we have included significant results and posed questions regarding what such a structure might look like should it exist.

Overall, the notions of relative subinjectivity and indigency constitute a significant area of study for specific cotorsion pairs, and we believe they will serve as valuable tools in addressing some important questions that arise through the use of such cotorsion pairs. This has important implications for future research in module and ring theory and lays the foundation for new applications involving cotorsion theories. These results broaden the classical understanding of subinjectivity and cotorsion theory and open new avenues for further research in module theory and homological algebra, particularly in the study of category theory.