Abstract
With the rapid development and convergence of systems science, cryptography, and data science, chaos-based image information security has emerged as a prominent research area, drawing considerable attention from researchers in computer science, physics, and related disciplines. This paper aims to review the fundamental concepts of chaos, as well as chaos-based image encryption, watermarking, and steganography. Building on this foundation, we analyze the evaluation standards, advancements, and applications of chaos-based image information security. Additionally, we propose several potential areas of focus for the future of chaos-based image information security, encouraging interested readers to pay attention to these crucial developments. Our analysis suggests that chaos can be effectively employed in plaintext image encryption, and that chaos-based watermarking and hiding techniques also hold promise.
MSC:
65P20
1. Introduction
In general, chaos refers to seemingly random and unpredictable behavior that arises in deterministic systems, a concept first proposed by Li and Yorke in 1975 [1]. These deterministic systems are a specific category of complex systems characterized by rich dynamical properties. Chaos was initially applied to image information security by Fridrich in 1998 [2]. Today, chaos-based methods are primarily utilized in a diverse range of areas such as image plaintext encryption, image steganography, and image watermarking, as illustrated in Figure 1.
Figure 1.
The main contents reviewed in chaotic image security.
Plaintext data is a critical component of information, referring to raw data that has not been encrypted or concealed. This type of data is mainly characterized by high readability, ease of understanding, sensitivity, and convenient transmission. When comparing plaintext textual data to plaintext image data, it’s evident that image data typically has a larger volume and exhibits stronger pixel correlation. This makes it challenging to apply traditional text encryption techniques, such as the Data Encryption Standard (DES) and the Advanced Encryption Standard (AES), directly to image encryption scenarios [3].
In the realm of data security, another significant issue that needs addressing is data copyright ownership. Current research in this area primarily focuses on two techniques: “watermarking” and “steganography”. Although both are classified as information-hiding technologies, they have distinct objectives and applications. The primary goal of “steganography” is to discreetly embed secret information, such as text, files, or codes, into images or other carriers [4]. This allows for the covert transmission of information, ensuring that third parties remain unaware of the concealed data within the images. On the other hand, “watermarking” technology essentially focuses on embedding visible or imperceptible identifying markers within images to protect copyright, verify authenticity, and track sources [5]. While steganography and watermarking share some technical similarities, they differ significantly in their core objectives and contexts of application.
This paper aims to review the technological development and applications of chaos theory in areas such as plaintext image encryption, image steganography, and copyright protection. It presents the latest research achievements and development trends identified by researchers in this field. The main structure of the paper is as follows: Section 2 provides an overview of the concepts, properties, and developments related to chaos. Section 3 describes chaos-based image encryption, detailing the basic processes and advancements in this area. Section 4 presents recent results in information hiding techniques, specifically focusing on “watermarking” and “steganography”. Section 5 highlights some emerging research areas in chaos-based image information security from the authors’ perspective. Finally, Section 6 concludes the paper with a summary of the main findings.
2. Systems and Theory of Chaos
Chaos arises from unpredictable behavior in deterministic systems, reflecting a unity between order and disorder, as well as determinism and randomness. In this section, we will explore chaos by examining different types and properties. Typically, chaotic systems can be classified into discrete and continuous categories based on the continuity of their states, and into self-organizing and coupled systems depending on their internal coupling. Additionally, this article provides a separate explanation of memristive chaotic systems, which have gained popularity recently due to their memory function.
2.1. Discrete Chaotic Maps
This review discusses various discrete maps based on existing results. Such typical systems can be categorized as follows:
(1) Logistic map: a simple one-dimensional iterative model introduced by biologist Robert May in 1976 [6], which exhibits complex period-doubling and chaotic behavior. The main formula of this approach is:
where represents the system parameter. In the case of , this map denotes a chaotic behavor. The bifurcation, Lyapunov exponential and initial value sensitivity plot ( = 4) for system (1) are illustrated in Figure 2a, Figure 2b and Figure 2c, respectively.
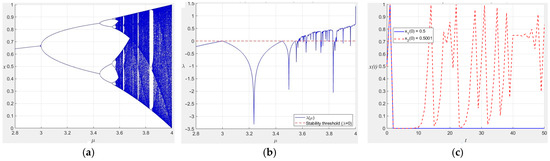
Figure 2.
Characteristic visualization of Logistic map. (a) Bifurcation, (b) Lyapunov exponential, (c) initial value sensitivity plot when = 4.
As can be seen in Figure 2a, when is small (e.g., < 3), the system tends to stabilize the single-valued output; as increases, it shows the phenomenon of cycle multiplication; when reaches about 3.57, the system enters into the chaotic region. It visualizes the transition process of the system from order (stable and periodic) to chaos, reflecting the strong dependence of the system behavior on the parameter. The transition of the system from stability to chaos (the Lyapunov exponent λ changes from negative to positive) and the fluctuation of λ in the chaotic region can be seen in Figure 2b, which quantifies the sensitivity of the system to the initial value. From Figure 2c, it can be seen that even if the initial conditions are only slightly different, the state of the system can become completely different after long-term evolution.
(2) Hénon map: Different from the Logistic map, the two-dimensional map, proposed by the French astronomer Hénon in 1964 [7], is discretely represented as:
where and denote the system parameters, and for the case of and , the map is chaotic. The bifurcation, Lyapunov exponential and initial value sensitivity diagram for system (2) are illustrated in Figure 3a, Figure 3b and Figure 3c, respectively.
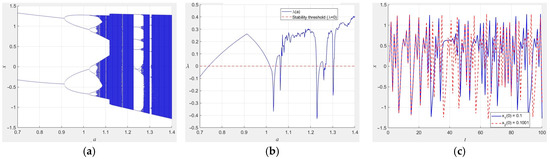
Figure 3.
Characteristic visualization of Logistic map. (a) Bifurcation where b = 0.3, (b) Lyapunov exponential where b = 0.3, (c) initial value sensitivity plot when a = 1.4 and b = 0.3.
The three diagrams in Figure 3 illustrate the nature of the chaos that collectively portrays the Hénon map from different dimensions: driven by deterministic rules, the system exhibits a complex, unpredictable and long-term behavior due to small perturbations in the parameters or initial values.
(3) Tent map [8]: Succeeding, we define a piecewise-defined tent map, topologically conjugate to the logistic map, as follows:
where the system parameter ranges from 0 to 2. The bifurcation, Lyapunov exponential and initial value sensitivity diagram for system (3) are illustrated in Figure 4a, Figure 4b and Figure 4c, respectively.
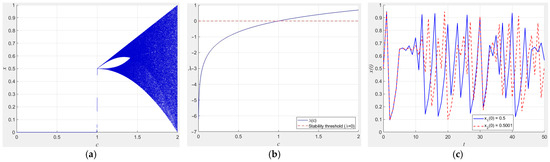
Figure 4.
Characteristic visualization of Logistic map. (a) Bifurcation, (b) Lyapunov exponential, (c) initial value sensitivity diagram when c = 1.9.
The three plots in Figure 4 illustrate the complex and chaotic nature of the dynamics of the Tent map, which exhibits rich dynamics ranging from ordered to chaotic in different parameter intervals.
2.2. Continuous Chaotic Systems
Unlike discrete maps, continuous chaotic systems are time-dependent based on observed series. Such typical systems can be categorized as follows:
(1) Lorenz system: This is proposed by Lorenz in 1963 [9] in “deterministic nonperiodic flow”, marking chaos research’s start. The main classical dynamical equations of this system read:
where a denotes the fluid’s Prandtl number, b is the Rayleigh number, and c signifies a spatial constant. In the case of a = 10, b = 28, and c = 8/3, the system associated with Equation (4) presents a chaotic one. Figure 5a–c show the phase diagram, Lyapunov exponential plot and initial sensitivity diagram of Lorenz system respectively.
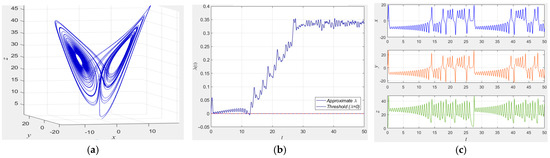
Figure 5.
Characteristic visualization of Lorenz system. (a) Bifurcation, (b) Lyapunov exponential where a = 10, b = 8/3 and c = 28, (c) time series diagram.
Figure 5a shows the classical butterfly shape of the Lorenz attractor, reflecting the chaotic nature of the system. In Figure 5b, positive Lyapunov exponent verifies the chaotic properties of the Lorenz system. Figure 5c shows the evolution of the x, y, and z variables over time, reflecting the non-periodic and stochastic nature of the system.
(2) Chen system: Prof. Chen in 1999 [10] established this system, which is not topologically equivalent to the Lorenz system and exhibits more complex behavior. The corresponding dynamical equations are written as:
where a, b, and c denote the main systems’ factors. For the case of a = 35, b = 3, and c = 28, the system provided in Equation (5) follows a chaotic behavior.
(3) Chua system: This circuit system, as introduced in Ref. [11], is able to characterize the quantitative dynamics of arbitrary 3-order nonlinear systems via an odd-symmetric piecewise-linear function. For this system, the corresponding state equations read:
where the piecewise nonlinear function is defined by: . For the case of a = 10, b = 14.87, and , the system presented in Equation (6) is chaotic.
2.3. Coupled Map Lattice
Coupled chaos expands both discrete and continuous chaos by increasing dimensionality through connections between systems. Notably, Kaneko’s coupled-map lattice (CML) [12] models the correlations between time and space nodes through the process of coupling, demonstrating spatiotemporal chaos via temporal iteration and spatial interconnection. For example, a unidirectional CML system can be represented by:
where x denotes the system state, n represents the iteration number, ε is the coupling strength, and i signifies the lattice index. f represents the local mapping function of a single node, denotes the result of the i-th lattice point at the n-th iteration, based on its own current state after the f function mapping. In recent decades, we have seen improved CMLs like one-way coupled-map lattices (OCML) [13], global nonlocal collapsible mapping lattices (GNCML) [14], multiple dynamic coupled map lattices (MDCML) [15], improved sinusoidal dynamic non-adjacent coupled mapping lattices (ISDNCML) [16], and non-adjacent coupled dynamic parameter mapping lattices (NCMLP) [17]. Due to their higher dimensions and improved dynamics, these CMLs are extensively utilized in the field of image information security.
2.4. Memristor Chaotic System
The memristor is a nonlinear device whose resistance is mainly determined by the flow of charge, allowing it to “remember” charge through resistance measurement. It was originally proposed by Chua et al. in 1971 [18] and was physically implemented in 2008 [19]. Memristors fall into two categories: magnetic flux-controlled memristors (MFCMs) and charge-controlled memristors (CCMs). Due to their nonlinearity and memory effects, memristors are commonly employed to create chaotic systems. In recent years, several novel memristor-based chaotic systems have emerged. For instance, in 2020, Wan et al. [20] developed a five-dimensional memristor hyperchaotic system featuring hidden behavior, utilizing a flux-controlled memristor model. In 2022, Ramamoorthy et al. [21] introduced a magneton memristor into the Sprott B system, resulting in a proposed four-dimensional hyperchaotic memristor system. Additionally, Li et al. [22] recently presented a memristor-based Hopfield neural network (HNN) capable of generating complex multi-vortex attractors.
2.5. Properties of Chaos
Chaos is a distinctive behavior observed in nonlinear systems and exhibits complex characteristics as follows:
(1) Intrinsic Stochasticity: Deterministic equations could lead to “disorderly” aperiodic solutions, which are fundamentally different from the extrinsic stochasticity found in random signals.
(2) Sensitivity to Initial Conditions: In chaotic systems, even slight differences in initial states could result in vastly different trajectories over time.
(3) Lyapunov Exponent (LE): The Lyapunov exponent measures [23] how quickly nearby trajectories converge or diverge in phase space, and it contributes to the instability of chaotic attractors. For a continuous dynamical system in an n-dimensional phase space, the LE can be defined in the following form:
where denotes a vector in some direction in the phase space of the system at the initial moment t = 0, denotes the corresponding vector in the phase space based on the initial vector after the evolution at time t.
In addition to the previously mentioned properties, chaotic systems also show characteristics such as boundedness, ergodicity, fractal dimensionality, and universality. In the realm of chaos-based image analysis, most research and applications depend on the inherent stochasticity and sensitivity of chaotic systems [24].
2.6. Performance Evaluation of Chaotic Systems
The visualization tool to measure the performance of the above chaotic system is as follows:
(1) Phase diagram: visualization of system dynamics behavior (e.g., attractor morphology). However, it is difficult to visualize for high-dimensional systems, relying on initial values. Recent experiments have utilized PCA/t-SNE [25] to achieve dimensionality reduction and assist in understanding complex system trajectories.
(2) Bifurcation diagram: Clearly present system behavioral transitions under parameter changes (e.g., chaotic windows). But it is computationally intensive and may miss the subtle bifurcation structure. Recently, experiments have been conducted to sample the dense area of encrypted bifurcations to improve computational efficiency and accuracy [26].
(3) Diagram of Lyapunov index: It can quantitatively determine the chaos (positive exponential) and intensity. However, it is computationally complex for high-dimensional systems and the results depend on numerical methods. Recent experiments have used the QR decomposition method [27] to improve the high-dimensional LE calculation.
(4) Initial value sensitivity: It allows direct verification of the butterfly effect (initial value differences leading to trajectory separation). However, it is only for specific initial values and global analysis is insufficient. Recent stability through statistical phase space partitioning, covering global initial values and overcoming the shortcomings of insufficient global analysis [28].
(5) Time series diagram: Visualize the trend of variable evolution. However, it is difficult to distinguish between chaos and noise, and it is difficult to infer high-dimensional dynamics. Recent experiments to distinguish chaos from noise by deterministic structures [29].
(6) NIST test: It is a tool for testing the randomness of binary sequences generated by random number generators in cryptographic applications. Among them, the NIST SP 800-22 random number test set contains 15 test items, such as frequency test, run test, discrete Fourier transform test, etc., which can test the randomness of an arbitrarily long binary sequence, and evaluate the randomness of the sequence by calculating the p-value, and determine the sequence to be non-random if the p-value < 0.01.
2.7. Chaotic System Exploitation Nethods and Examples
Chaotic systems are widely used in many fields, and those obtained by different development methods have their own advantages and disadvantages in practical applications. The following compares and analyses the advantages and limitations of chaotic systems corresponding to common development methods. A comparative analysis of these categories is provided in Table 1.

Table 1.
Chaotic system exploitation methods and examples.
In conclusion, the development methods of chaotic systems are varied and involve knowledge and techniques from various fields such as mathematics and physics. By continuously exploring new development methods and constructing new chaotic systems, it helps to gain a deeper understanding of the phenomenon of chaos and its potential application in various fields.
3. Chaos-Based Image Encryption
Chaotic systems disrupt the spatial and statistical properties of images for security purposes, which enhances their resistance to attacks. The effectiveness of image encryption relies on several factors, including the dataset used, the design of the system, and whether the domain is spatial or frequency-based. Recognizing the importance of these elements in improving encryption performance, this chapter examines image datasets, chaotic encryption techniques, and the methods for their evaluation.
3.1. Image Database
The image datasets analyzed in this paper are categorized into four main types as follows:
(1) Standard Test Image Datasets: This category includes well-known images such as Lena, Baboon, and Peppers, along with popular datasets like Kodak, which contains 24 lossless true-color images (available at https://www.kaggle.com/sherylmehta/kodak-dataset, accessed on 5 May 2025), and USC-SIPI, created by the Signal and Image Processing Institute at the University of Southern California in TIFF format (accessible at http://sipi.usc.edu/database, accessed on 5 May 2025).
(2) Natural Scene Image Datasets: These datasets include COCO, ImageNet, and PASCAL VOC, characterized by high resolution, complex backgrounds, a large number of images, and diverse content. The COCO dataset (accessible at http://cocodataset.org, accessed on 5 May 2025), released by Microsoft Research in 2014, consists of over 330,000 varied images capturing daily life. ImageNet, developed by a Stanford University team, focuses on addressing large-scale image classification challenges.
(3) Medical Image Datasets: This category primarily contains grayscale and color medical images, similar to those found in datasets like the Medical Segmentation Decathlon dataset and the COVID-19 Radiography Database. For instance, the Medical Segmentation Decathlon dataset (accessible at http://medicaldecathlon.com, accessed on 5 May 2025), established in 2019, includes 2633 images, and the medical image datasets may feature similar types of images.
(4) Remote Sensing Image Datasets: These datasets are essentially defined by multi-precision, multi-temporal, multi-semantic, and multi-band features, along with large volumes of data, substantial image sizes, high resolution, and rich details. Examples include the USC-SIPI dataset and the RSOD dataset. The USC-SIPI dataset (accessible at https://sipi.usc.edu/database/database.php, accessed on 5 May 2025), developed by the Signal and Image Processing Institute at the University of Southern California, was first released in 1977 and has since undergone multiple updates.
3.2. Spatial Domain Techniques
For chaotic image encryption, most operations are performed in the spatial domain, and these techniques can be classified into four categories: scrambling, diffusion, encoding, and substitution. A comparative analysis of these categories is provided in Table 2.

Table 2.
Comparison of the characteristics and performance of different types of spatial domain techniques.
3.2.1. Scrambling Technique
The spatial disambiguation technique in image encryption reorganizes pixel positions without changing their values. For example, universal row and column scrambling operations can be visualized in Figure 6.
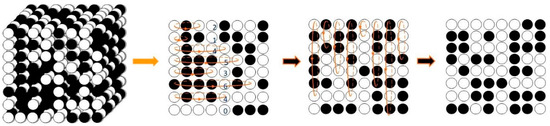
Figure 6.
The main contents reviewed in chaotic image information security.
These disordering obscure visual patterns in plaintext images, reduce pixel interdependencies, and increase image randomness. The integration of a chaotic system further enhances this randomness, making it more challenging for an attacker to recover the original image even if they obtain the ciphertext. Classical chaotic algorithms used for scrambling include the phantom square transform, the game of life, the Hilbert curve, and the magic square transform, among others.
3.2.2. Diffusion Technique
Diffusion differs from scrambling in that it modifies pixel values rather than their positions. It propagates the values of plaintext pixels across all ciphertext pixels, ensuring that changes to any single pixel appropriately affect the entire encrypted image. When combined with a chaotic system, the pixel values in the ciphertext mainly rely on both the image and chaotic dynamics. This diffusion technique weakens interpixel dependencies in the plaintext, thereby enhancing the algorithm’s security and randomness.
In chaotic image encryption algorithms, scrambling is typically combined with diffusion, making both techniques essential components of modern image encryption methods. For instance, Xie et al. [33] combined a block-level scrambling scheme with a bit-level file manager diffusion technique to establish a novel image encryption algorithm (as illustrated in Figure 7). Sun et al. [34] first scrambled the bits of plaintext images via chaotic sequences and then diffused the scrambled image using the Fibonacci Q-matrix and a central diffusion algorithm.
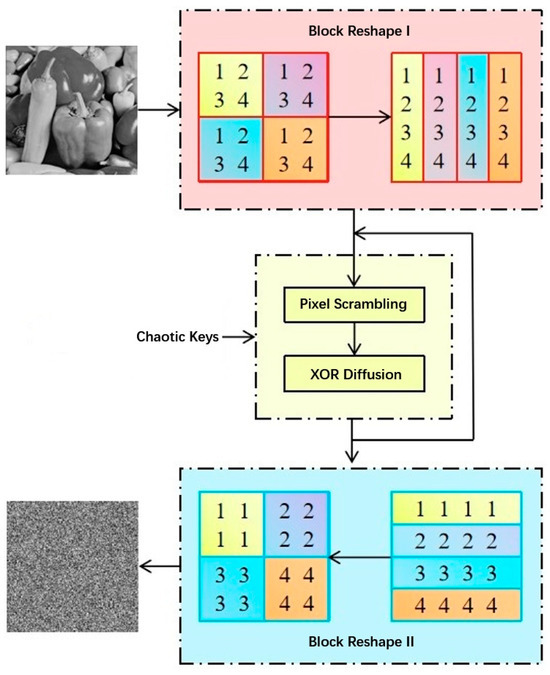
Figure 7.
The basic scrambling-diffusion encryption algorithm.
The following will explain in detail how to use diffusion in Chaos:
(1) Chaotic sequence generation associated with pixel values: Many chaotic image encryption algorithms first utilize chaotic maps such as Logistic, Tent, Lorenz system to generate chaotic sequences, which are sensitive to the initial value and are ergodic. By quantizing the value of the chaotic sequence and matching it with the pixel value of the image, and then changing the pixel value through addition, multiplication, or dissimilarity, the pixel value is broken to realize the diffusion of the pixel value by breaking the original dependency relationship between the pixels [35].
(2) Chaos-based chunk diffusion: In order to improve the encryption efficiency and security, the image can be chunked, and chaos diffusion can be utilized within each chunk. For example, the coupled chaotic sequence extracts the plaintext information to control the key generation to encrypt the plaintext, and encrypts and diffuses it in chunks by utilizing the binary characteristics [36]. In each sub-block, the pixel update rule is determined according to the chaotic sequence, so that the pixels in the sub-block are fully diffused and there is a correlation between the sub-blocks.
(3) Multilayered diffusion and the fusion of chaos: To strengthen the diffusion effect, multi-layer diffusion can be used. For example, the chaos-based heuristic three-layer diffusion (CHTD) method first reduces the pixel correlation by using spiral and chaotic substitution [37], then enhances the security by block-based substitution, and finally increases the randomness and irregularity by using chaos-based heuristic and three-layer primitive function diffusion. It ensures that the ciphertext is highly randomized and effectively resists statistical and differential attacks.
(4) Applications of Chaos in Parallel and Partitioned Diffusion Strategies: In scenarios where encryption speed needs to be increased, parallel and partitioned diffusion strategies combined with chaos are used to achieve efficient and secure encryption. For example, the plaintext image is divided into three parts and acted on the upper and lower parts or the left and right parts using a parallel CBC-based diffusion method to achieve O(W + H) time complexity. In diffusion, the centre ranks information interaction enhances the avalanche effect to resist differential attacks [38].
3.2.3. Encoding Technique
The fundamental principle of encoding-based image encryption algorithms is to transform the original structure of a plaintext image into a different format, thereby improving the algorithm’s security. Common encoding methods used in chaotic image encryption mainly include DNA coding, Gray coding, and RNA coding. Generally, encoding serves as an enhancement to the scrambling and diffusion encryption systems found in chaotic image encryption [39,40,41,42,43].
3.2.4. Substitution Technique
Another broadly utilized technique in chaotic image encryption is substitution. In this context, substitution involves generating a new pixel value through a specific method and then replacing the pixel values of the image with these chaos-related values. Recent studies have particularly focused on the generation of S-boxes and the corresponding substitution process [44,45,46,47,48].
3.3. Frequency Domain Transform
Frequency-domain image encryption (FDIE) is a technique that utilizes frequency-domain transform methods from signal processing, such as the discrete Fourier transform (DFT), discrete cosine transform (DCT), and discrete wavelet transform (DWT), to convert image data from the spatial domain to the frequency domain. This conversion allows for encryption by altering frequency-domain coefficients. Compared to algorithms that operate in the spatial domain, FDIE is more robust and resistant to interference, enabling selective encryption. Recently, significant advancements have been made in DFT [49,50,51], DCT [52,53,54], DWT [55,56], and Fractional Fourier Transform (FrFT) [57,58,59] and so on. A comparative analysis of these categories is provided in Table 3.

Table 3.
Comparison of the characteristics and performance of different types of frequency domain techniques.
3.4. Performance Analysis
To evaluate the robustness and security of chaotic image encryption algorithms, the following statistical analysis and attack tests are usually utilized:
(1) Key space: It must be sufficiently large (≥2128 bits) to thwart brute-force attacks.
(2) Key sensitivity: A robust encryption algorithm demonstrates high sensitivity meaning that even minor modifications to the key result in significantly different decryption outputs.
(3) Algorithm complexity: This refers to the algorithm’s ability to ensure security and resistance against attacks. There should be a delicate balance between robustness (against brute-force and statistical cracking) and efficiency (the practical computational overhead involved).
(4) Histogram: Encrypted images should exhibit a uniform pixel-value distribution, known as a flat histogram. This characteristic helps prevent statistical leakage, which is commonly seen in the uneven histogram of plaintext images.
(5) Correlation Coefficient (CC) [60]: This metric measures pixel-wise similarity between the original and encrypted images. In the case of the original image, there are strong correlations (i.e., CC ≈ 1) in the horizontal, vertical, and diagonal directions. Conversely, the CC of the encrypted image is weak (CC ≈ 0).
(6) Information entropy [61]: This measure reflects the unpredictability and uncertainty of the information source. A higher information entropy indicates greater uncertainty. The theoretical critical value for information entropy is herein set as 8.
(7) Mean Squared Error (MSE) [62]: MSE calculates the average of the squared differences between corresponding pixels in two images. It is commonly utilized to assess the avalanche effect by determining the MSE between images, indicating a remarkable difference between them.
(8) Differential attack analysis [63]: This analysis tests the sensitivity of subtle changes in standard images. It employs parameters like Unified Average Change Intensity (UACI) and Normalized Pixel Change Rate (NPCR). The theoretical critical values for the UACI and NPCR in order are 33.4635% and 99.6094%.
(9) Noise attack test [64]: Images transmitted over physical channels commonly suffer from noise corruption (e.g., Gaussian noise or impulse noise). A robust algorithm must withstand such interferences to ensure the quality of the decrypted image.
(10) Clipping attack test [65]: This test simulates partial data loss during transmission or storage by cropping or truncating ciphertexts. It evaluates the integrity of the decrypted image under such conditions, measuring resistance to information loss.
(11) Chosen-Plaintext Attack (CPA) [66]: Plaintext attacks mainly consist of chosen-plaintext attack (CPA) and known-plaintext attack (KPA). In CPA, attackers could utilize an encryption machine temporarily; on the other hand, an adversary could have passive access to some plaintext-ciphertext pairs in KPA. Consequently, CPA poses a greater threat, as attackers have control over the encryption inputs, and CPA-resistant cryptosystems also resist KPA.
4. Watermarking and Steganography
Chaotic image encryption primarily focuses on the plain-text information and visual security. However, specific concepts such as watermarking and image hiding, which are less visible, are also crucial and hold significant potential applications in information security.
4.1. Watermarking Technique
Digital watermarking serves as an active authentication technique, embedding copyright information into a host image via specific algorithms. Based on their functional requirements and recoverability, digital watermarks can be generally classified into three categories: robust, fragile, and reversible. A comparative analysis of these categories is provided in Table 4.

Table 4.
Comparison of functions and characteristics of different types of digital watermarks.
4.1.1. Robust Watermarking
Robust watermarking techniques aim to ensure that the watermark information can still be accurately extracted from a watermarked image, even after potential attacks such as cropping, rotation, noise, and filtering. Similar to encryption methods, robust watermarking can be categorized into spatial-domain and frequency-domain embedding based on the embedding domain. Traditionally, researchers have focused on enhancing the attack resistance of watermarking algorithms while also considering security [67,68,69] (as illustrated in Figure 8).
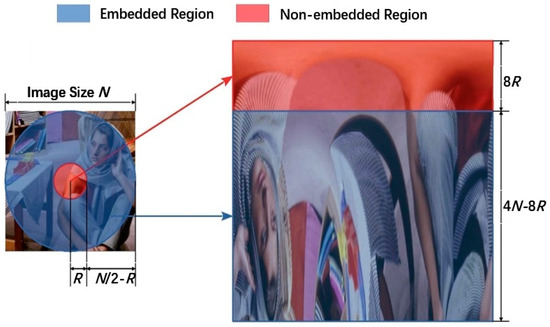
Figure 8.
The selected region for embedding watermark.
In chaos-based robust watermarking, researchers utilize chaotic systems to pre-scramble watermark information before embedding. This approach enhances the security of watermark extraction [70,71]. Particularly, some researchers have also proposed zero-watermarking algorithms, where features extracted from the host image are combined with the watermark information to form a watermark signature, all while leaving the original image untouched [72,73].
4.1.2. Fragile Watermarking
While robust watermarking emphasizes resistance to various attacks, fragile watermarking is highly sensitive to content changes, making it suitable for scenarios where the fidelity and authenticity of image content are paramount. Generally, fragile watermarking is used to verify the integrity of images, enabling the prompt detection and localization of any modifications after tampering occurs. In research on fragile watermarking, the focus is typically on improving the accuracy of tamper localization [74,75,76,77,78], often with the use of chaos-based techniques. For instance, Liu et al. [79] proposed a specific approach that maps the differences between the host image and a chaotic pattern into a binary watermark, which is then embedded in the Least Significant Bits (LSB) of the host image. In 2024, Feng et al. [80] established a hyperchaotic modulation framework based on the Latin square principle, constructing a novel three-dimensional hyperchaotic system for enhanced security. This watermarking system supported copyright authentication and tamper localization and demonstrated high detection accuracy against various tampering attacks.
4.1.3. Reversible Watermarking
Reversible watermarking is designed to embed watermark information while allowing for the complete restoration of the original host image during extraction. This results in lossless watermarking, making it particularly valuable in scenarios where maintaining high fidelity and integrity of the original image is crucial. So far, researchers have proposed various methods to enhance both visual quality and tamper resistance [81,82,83,84,85,86].
4.2. Steganography Technique
While watermarking provides copyright protection through explicit embedding, it often faces a conflict between invisibility and robustness, which limits its application. In contrast, steganography focuses on taking advantage of statistical redundancy in the carrier image to conceal secret data, ensuring the visibility [87]. The primary challenge of steganography lies in increasing the amount of embedded data while minimizing anomalies in higher-order statistical features [88]. Image steganography can be divided into two categories: adaptive and static methods. A comparative analysis of these categories is provided in Table 5.

Table 5.
Comparison of the characteristics and performance of different types of steganography technique.
The strength of adaptive methods mainly lies in their ability to finely tune security and imperceptibility; however, they typically come with high computational overhead [89,90]. On the other hand, static approaches rely on deterministic operations using preset rules (such as LSB substitution [91] and fixed-frequency-domain embedding). These methods are easier to implement but are more vulnerable to attacks from statistical analysis and steganography detection tools [92]. To address the inherent limitations of these two paradigms, recent research has shown significant advancements in cross-domain convergence and technological innovation [93,94,95,96].
It is worth mentioning that current security research in steganographic systems is evolving from a single embedding stage to full-link protection. This shift promotes the integration of steganography with chaos-based cryptography. For instance, Li et al. [97] developed an Artificial Immune System (AIS)-based steganographic post-processing framework. This framework uses immuno-evolution to optimize images, thereby reducing detectability against both handcrafted and deep-learning steganalysis tools. Additionally, advancements in chaotic system engineering [98] inspired Yang et al. [99] to segment stereoscopic medical images into regions of interest (ROI) and background regions. They employed chaotic sequences for key generation and guided data embedding through a multidimensional chaotic time-based binary coded sequence (nD-CTBCS) system. This approach significantly enhanced both the security of data hiding and the reversibility through auxiliary information compression.
4.3. Performance Analysis
In analyzing the performance of watermarking and steganography techniques, four core evaluation dimensions are essential: concealment, robustness, capacity, and computational efficiency. These can be displayed in more detail as follows:
(1) Concealment is a crucial metric used to assess whether watermarking and steganography techniques are able to embed information without drawing attention. The main evaluation methods include Peak Signal-to-Noise Ratio (PSNR) [100], Structural Similarity (SSIM) [101], Signal-to-Noise Ratio (SNR), and histogram analysis [102]. Additionally, other metrics could numerically evaluate the visual invisibility of embeddings, such as Normalized Correlation Coefficient (NCC), Weighted Peak Signal-to-Noise Ratio (WPSNR), Euclidean Distance (ED), and Image Fidelity (IF); however, these are less frequently employed [103,104].
(2) Robustness measures the ability of watermarking and steganography techniques to recover information effectively after facing various attacks [105]. The primary metrics for robustness include the NCC and bit error rate (BER). An NCC value greater than 0.7 is typically considered indicative of effective recovery, while a BER value of less than 5% is usually acceptable.
(3) Capacity refers to the maximum amount of information that can be embedded in a unit carrier while maintaining invisibility and robustness. It is quantified using the term “Bits Per Pixel (BPP),” which is defined as the ratio of the total number of bits embedded to the total number of carrier pixels.
(4) Computational Efficiency evaluates the processing speed and resource consumption of watermarking and steganography techniques based on algorithm complexity or experimental outcomes. This dimension directly measures the actual running time and reflects the algorithm’s performance in a specific environment [106,107].
5. Recent Developments in Chaos-Based Image Security
In this section, we will review the fundamental chaos-based image information techniques and introduce some related topics featuring significant novelties and developments. These topics can be broadly categorized into the implementation of algorithms on Field Programmable Gate Arrays (FPGAs), quantum algorithm design, attack resistance and recovery analysis, deep learning, and neural network algorithms.
5.1. FPGA Implements of Algorithms
The implementation of image security algorithms based on FPGAs has demonstrated considerable advantages in terms of speed and complexity. This is due to the powerful parallel processing capabilities of FPGAs, which allow them to handle multiple pixels or image blocks simultaneously. In 2001, Sobhy et al. [108] introduced a chaotic encryption algorithm based on the Lorenz system implemented on an FPGA. The following year, Utami et al. [109] constructed a chaotic encryption system on an FPGA using digital filter overflow and modulo functions to demonstrate the effective application of FPGAs in chaotic encryption systems. Building on this work, Balakrishnan et al. [110] proposed a hybrid image encryption system based on the Haar integer wavelet transform in 2002, which utilized only 4,025 logic elements and took just 0.28 ms to encrypt an image. Moreover, Boutros et al. [111], aiming at Internet of Things (IoT) applications, achieved hardware acceleration of their proposed algorithm on the FPGA. For a 512 × 512 image, they reached an impressive frequency of 135 MHz, with an encryption frame rate of 256 fps. Mohamed et al. [112] proposed a real-time image encryption and decryption system based on the FPGA-Zynq, utilizing four distinct chaotic systems to generate high-quality keys while occupying minimal hardware resources. This system achieved an operational frequency of up to 142.8 MHz and a throughput of 3408 Mb/s. In their chaotic encryption algorithm, Marwan et al. [113] achieved a maximum efficiency of 110.8 MHz. Additionally, Moghimi Moghaddam et al. [114] proposed a parallel image encryption algorithm called PCCIE, based on chaos theory, to address the internal memory limitations of FPGAs through a parallel system structure. In 2024, Ahmet et al. [115] presented a real-time hybrid medical image encryption algorithm based on memristor chaos implemented on a low-cost PYNQ-Z1 FPGA board. Guang et al. [116] also proposed the application of a parametrically controllable symmetric multi-scroll chaotic system on the FPGA. Beyond these examples, FPGAs have been extensively employed to accelerate chaotic image encryption algorithms, yielding significant performance improvements [117,118,119,120,121,122] (as illustrated in Figure 9).

Figure 9.
The FPGA experimental environment.
Furthermore, FPGAs play a crucial role in enhancing watermarking and steganography techniques. For instance, Arumugham et al. [123] proposed a secure carrier solution for medical images by combining the Integer Wavelet Transform (IWT), Singular Value Decomposition (SVD), and chaotic encryption to embed patient information as watermarks into DICOM images using an FPGA implementation. In 2021, Kaibou et al. [124] proposed a chaotic encryption digital watermarking system based on the co-design of hardware and software that enables real-time and secure watermarking operations. Two years later, Sun et al. [125] established an FPGA-based image encryption-steganography algorithm utilizing a novel chaotic system with a linear equilibrium point. In the same year, another color image steganography algorithm, which combined an unbalanced hyperchaotic system, was also implemented on the FPGA. Following that, Li et al. [126] developed a chaos-based digital watermarking algorithm for medical image copyright protection, scheduled for FPGA implementation in 2025.
5.2. Quantum Image Algorithm Design
5.2.1. Quantum Computing in Image Security
Given the increasing complexity and high resource consumption typically associated with current image processing algorithms, the integration of quantum computing with traditional digital image processing methods presents a promising solution. The unique characteristics of quantum computing, particularly entanglement and parallelism, enable quantum image processing algorithms to outperform their classical counterparts significantly. In 2012, Akhshani et al. [127] introduced an innovative image encryption algorithm utilizing the quantum logistic map, marking the first application of chaotic mapping in quantum image encryption technology. This groundbreaking work spurred a growing interest among researchers in chaos-based quantum image encryption and steganography techniques over the following years. For instance, in 2019, Jiang et al. [128] developed a quantum implementation circuit of the two-dimensional Henon chaotic map using a quantum arithmetic unit and proposed a quantum image encryption algorithm grounded in the GQIR model. Following this, Abd EL-Latif et al. [129] created a pseudorandom number generator (PRNG) based on the controlled alternate quantum walk technology (CAQW), which utilized the generated chaotic sequence to control the encryption of quantum color images through controlled gates. In 2023, Wang et al. [130] introduced a quantum image steganography algorithm employing the HSI color-space embedding technique, aiming to enhance both the security and efficiency of sensitive information concealment.
Recently, Liu et al. [131] presented a fractional four-dimensional quantum game chaotic map alongside a synchronization control system to mitigate uncertainties in quantum games. When applied to image encryption, this approach demonstrated robust security, demonstrating the potential of chaos theory in quantum image encryption. Further advancing the field, Rehman et al. [132] proposed an encryption scheme that combines a one-dimensional sine-based chaotic map with quantum coding, leveraging a quantum coherence-inspired PRNG to produce unpredictable code streams and thus enhancing security. Khan et al. [133] introduced a two-phase chaotic confusion-diffusion architecture comprising four modules, designed to encrypt the pixel positions and intensities of quantum-encoded images at both the qubit and pixel levels, thus propelling the evolution of quantum image encryption. In parallel research, Dong et al. [134] integrated quantum measurement uncertainty with chaotic systems, generating random sequences through a single-qubit circuit and manipulating qubit rotation angles for encryption, effectively harnessing the capabilities of quantum computing. Additionally, Liu et al. [135] employed multi-dimensional chaotic keys from a four-dimensional system to encrypt image pixel values and utilized the Arnold transform to manage pixel positions, successfully overcoming periodic interference while augmenting system complexity. Another significant advancement was made by Yan et al. [136], who utilized fractional wavelet decomposition to segregate images into high- and low-frequency components, subsequently scrambling them with a chaotic system and fractal matrix model, thereby enhancing encryption effectiveness. In 2025, Li et al. [137] proposed a quantum reversible color-to-grayscale conversion scheme that generates true random numbers via a two-dimensional quantum walk for bitwise XOR encryption and designs a bidirectional conversion process for lossless reversible image transformation, marking a notable contribution to the field of quantum image encryption. In summary, quantum technology has emerged as a pivotal force in advancing image security, opening new avenues for ensuring the security of chaotic image information.
5.2.2. Quantum Decryption Attacks and Robustness Analysis
The development of quantum computing technology poses a potential threat to traditional encryption systems, and the robustness of quantum image encryption algorithms needs to be specifically evaluated against quantum decryption attacks. Table 6 combines known attack models with existing algorithmic properties to sort out the attack resistance of current research.

Table 6.
Types of quantum decryption attacks and robustness analysis of typical quantum image encryption algorithms.
The robustness of the above algorithms relies on chaotic high-dimensionality and quantum unclonability. Existing studies are under-optimised for quantum phase estimation attacks and need to be combined with dynamic quantum gates to enhance security.
5.3. Attack-Resistance and Image Recovery
Chaos-based techniques enhance image security through the use of random pseudo-random signals. However, this approach is insufficient to counteract all threats to images, particularly in terms of active disruption and passive leakage. Active attacks specifically target data integrity and authenticity and typically manifest in three distinct forms. The first is content-level tampering, which includes deepfakes, face replacement, and copy-paste operations that directly alter the semantic content of images. The second form involves geometric perturbations, such as rotation, scaling, and cropping, which disturb the structural consistency and feature distribution of images. Finally, semantic-level pollution introduces imperceptible perturbations—such as adversarial examples—into model inputs, misleading deep neural networks (DNNs) into making erroneous decisions, thus posing significant threats to inference security and reliability.
To address the multidimensional challenges posed by active attacks, investigators have developed various image security techniques and reconstruction frameworks that prioritize robustness and recovery. In 2023, Jiang et al. [53] proposed a color image watermarking algorithm leveraging a multilayer perceptron and Cauchy distribution, further enhanced by quaternion transformations to ensure robustness against rotation, filtering, and compression. Building on this foundation, Liu et al. [138] integrated Discrete Wavelet Transform (DWT) with SPH-T coding to enable accurate tamper detection and high-quality self-recovery. Wu et al. [139] then advanced the field with the development of the DEAR network, which incorporates embedding, attention, and refinement modules to effectively remove artifacts and restore details in sparse-view image reconstruction, thereby improving overall quality. Additionally, Shen et al. [140] introduced MTC-CSNet, which combines convolutional networks and Transformer architectures to achieve superior reconstruction and enhanced perturbation resistance under compression. Furthermore, Sekar et al. [141] proposed a two-stage compressive sensing framework tailored for medical images, integrating self-similarity modeling and structural similarity optimization to enhance detail preservation. Yang et al. [142] designed ADMM-CSNet, which unraveled the alternating direction method of multipliers into a trainable network suited for end-to-end compressed image reconstruction, demonstrating promising applications in both medical and industrial fields.
In contrast to active attacks, passive attacks focus on unauthorized access to and inference of concealed information within digital media, often stealthily and persistently. Attackers frequently employ frequency domain analysis and compressed sensing inversion to deduce watermark data or the original content, resulting in data leakage. To mitigate these threats, Xiao et al. [143] proposed a secure solution that combines screen-cam-resistant watermarking with dynamic image decryption, specifically addressing vulnerabilities related to screen capture leakage and inspiring further research on screen-cam robustness. Similarly, Zhang et al. [144] decomposed satellite images into bit-planes, combining compression encoding with neural networks to achieve high compression ratios and precise reconstruction. Lin et al. [145] designed a robust image encryption framework that integrates YCbCr separation, block-level DCT quantization, and Latin square scrambling to enhance compression. Additionally, Ibrahim et al. [146] introduced an encryption algorithm that was capable of combining fractional-order β chaotic mapping with multi-level scrambling to improve resistance against statistical analysis and brute-force attacks.
Beyond content security, model and system-level data security represent critical areas of research. Luo et al. [147] proposed a dynamic invalidation verification protocol for deep model watermarking, aimed at preventing unauthorized reuse and theft of intellectual property. Additionally, Shang et al. [148] introduced a clock-skew-based identity authentication protocol tailored for lightweight IoT applications, which effectively resists various attacks while accommodating the constraints of edge devices. Furthermore, Zhang et al. [149] developed the SED deduplication scheme, which operates without relying on a trusted key server, supports dynamic updates, and is designed to resist collusion attacks. Building on this foundation, Xue et al. [150] proposed a blockchain-based data sharing mechanism that integrates machine learning with hierarchical identity-based encryption. This combination allows for flexible authorization and efficient key updates, making it well-suited for collaborative multi-party environments.
In the realm of cloud computing and multi-user retrieval scenarios, Cheng et al. [151] introduced CLPAEKS, a scheme that supports multi-keyword retrieval and offers full keyword selection attack resistance. This innovation was capable of enhancing trapdoor privacy and ciphertext security in encrypted data queries, particularly within industrial internet frameworks. Wang et al. [152] designed a quantum image watermark-based authentication and recovery mechanism, featuring a dual-layer tamper detection system that improves robustness and traceability in the face of various malicious attacks. Lastly, Daoui et al. [153] merged hyperchaotic systems with deep image generation models, such as CodeFormer and DeOldify, exhibiting significant performance improvements in secure transmission and tamper recovery of color face images. This approach offers a novel paradigm for trustworthy facial image communication. Table 7 provides a summary of several representative investigations and their key contributions under various threat scenarios.

Table 7.
Summary of representative research works in digital media security.
5.4. Deep Learning and Neural Network Method
With the rapid advancement of artificial intelligence technologies, deep learning and neural networks have demonstrated remarkable capabilities in feature learning and representation, particularly in the realm of image security. A growing number of researchers are merging chaotic image security techniques with deep learning to develop more efficient and intelligent solutions for image protection.
In the field of image encryption, the integration of DNNs with chaotic systems and various encryption algorithms has led to the creation of high-performance approaches. In 2016, Huang et al. [154] pioneered the application of neural network theory within cellular automata to construct a hyperchaotic system, subsequently utilizing this system for image scrambling. Concurrently, Zhou et al. [155] capitalized on the parallel computation and local diffusion features of cellular neural networks to propose a parallel group encryption algorithm based on the Feistel framework, significantly enhancing overall encryption performance. To elevate both encryption strength and resistance to potential attacks, Wang et al. [156] designed an encryption algorithm that integrates a DNN, where the network’s weight matrix is derived from scrambled discrete cosine transform (DCT) coefficient matrices. This approach enabled the accurate reconstruction of the original image through the deep network’s decryption unit, demonstrating robust resistance against brute-force and cropping attacks. Similarly, Feng et al. [157] combined chaotic image encryption with convolutional neural networks (CNNs), leveraging the nonlinear mapping characteristics of chaotic sequences alongside the feature extraction capabilities of CNNs to achieve enhanced encryption intensity. Their method exhibited outstanding performance in terms of both security and encryption/decryption efficiency.
However, many of these methods predominantly focus on image encryption in isolation. In specific application scenarios, enhanced transmission performance is equally vital. To address this need, Mou et al. [158] developed a compression-encryption algorithm that remains agnostic to the type or size of multiple images. By integrating a backpropagation neural network with the knight’s tour problem, they achieved a hybrid encryption mechanism applicable to multiple images. In addition, Li et al. [159] enhanced the performance of their compression algorithm by incorporating the particle swarm optimization algorithm into the BP (backpropagation) network. To overcome the challenges posed by large-scale remote sensing images, they introduced a block-based, multi-threaded parallel encryption method, effectively fusing neural networks with chaotic encryption to achieve high-precision compression and reconstruction, alongside strong resilience to attacks. Building upon this groundwork, Li et al. [22] further advanced the field by developing an end-to-end image compression-encryption network based on a self-attention mechanism. This innovative network integrates a bidirectional recurrent multi-scroll memristive neural network system, thereby facilitating simultaneous image compression and encryption. The proposed method exhibited promising results concerning reconstruction accuracy and encryption efficiency. Within the spectrum of neural network-based image processing techniques, the Vision Transformer (ViT) stands out as a computer vision architecture rooted in the Transformer model. It exhibits exceptional performance across various image-related tasks [160,161,162]. Table 8 provides a comparative overview of DNN-based image security techniques versus traditional encryption methods, highlighting differences in implementation strategies, security, and efficiency.

Table 8.
Comparison between traditional encryption and deep neural network based security techniques.
In addition, DNNs and chaotic encryption technologies have demonstrated significant potential in areas such as tampering detection and copyright authentication [167,168]. Huang et al. [169] proposed an innovative watermarking technique that utilizes neural networks in conjunction with image features. By analyzing the fractal dimension of the image, they generated a watermark image that was subsequently encrypted using the Arnold transformation to bolster security. Afsharizadeh et al. [170] introduced attack simulation and holographic reconstruction within DNNs, which enabled the watermarking network to be trained for enhanced robustness and imperceptibility. This method capitalizes on the strong feature extraction capabilities of neural networks to elevate the performance of watermark embedding. Moreover, Chen et al. [171] trained a neural network model specifically designed to resist overlay network attacks, resulting in a robust watermarking system characterized by high resilience.
The integration of DNNs with chaotic encryption, compression, transmission, and watermark authentication has led to substantial advancements in relevant research. As model architectures are further optimized and training mechanisms are continuously improved, chaotic image security techniques based on DNNs are anticipated to play an increasingly vital role in ensuring image data integrity, enhancing transmission efficiency, and improving resistance to diverse attacks.
6. Conclusions
This article provides a systematic review of the fundamental concepts of chaos and its applications in chaotic image information security, encompassing image encryption, watermarking, and steganography. Through a thorough analysis of evaluation standards, advancements, and practical applications, we aim to demonstrate the notable advantages and broad prospects of chaotic image information security. Theoretically, chaotic image information security expands the scope of traditional cryptographic methods by harnessing the unpredictability and ergodicity of chaotic systems, establishing a novel paradigm for image data protection and secure communication. On the application front, chaotic image information security has displayed significant potential and superior performance across various domains, including secure image transmission, copyright protection, and tampering detection. Furthermore, the paper methodically examines the integration of chaotic systems with other cutting-edge technologies in image information security, such as neural networks, FPGAs, and quantum information. These hybrid approaches take advantage of the unique characteristics of chaos, such as sensitivity to initial conditions, topological transitivity, and pseudo-randomness, fostering interdisciplinary collaborations and propelling further advancements in image information security methodologies. Overall, chaos-based image information security emerges as a highly promising technique for safeguarding image data. Looking ahead, we will delve deeper into the challenges confronting chaos-based image information security technology and place greater emphasis on multidisciplinary integration strategies to enhance its security and efficiency.
Author Contributions
Conceptualization, H.Z. and J.S.; methodology, H.Z.; software, X.F.; validation, P.Y., J.S. and X.F.; formal analysis, P.Y.; writing—original draft preparation, H.Z.; writing—review and editing, P.Y., J.S. and X.F.; funding acquisition, H.Z. and P.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by National Natural Science Foundation of China, grant number 61702356, and Natural Science Foundation of Shanxi Province, grant numbers 20210302124050 and 202203021221074.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
The authors would like to express their sincere gratitude to the following graduate students from the College of Computer Science and Technology and the School of Software at Taiyuan University of Technology (namely, Lu Chen-chen, Li Pei-zhen, Li Shi-yi, Guo Yi-ting, Xu Ting-ting, Geng Yu-jie, Du Fu-ya, Kang Zhi-jie, Wang Xiao-qing, Li Zhen-yu, Nan Shi-xian, Cai Hong, Zhang Yu-zhou, Gao Ya-jun, Jiang Mei-ru, Wang Wan-ting and Chang Rui-yun) for their unwavering dedication and invaluable assistance in the preparation of this review article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Li, T.Y.; Yorke, J.A. Period Three Implies Chaos. Am. Math. Mon. 1975, 82, 985. [Google Scholar] [CrossRef]
- Fridrich, J. Symmetric Ciphers Based on Two-Dimensional Chaotic Maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Z.D.; Fang, J.A. Image Encryption Using Chaotic Coupled Map Lattices with Time-Varying Delays. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2456–2468. [Google Scholar] [CrossRef]
- Katzenbeisser, S.; Petitcolas, F.A.P. Defining Security in Steganographic Systems. In Proceedings of the Security and Watermarking of Multimedia Contents 2022, San Jose, CA, USA, 29 April 2002. [Google Scholar]
- Cox, I.J.; Miller, M.L. A Review of Watermarking and the Importance of Perceptual Modeling. In Proceedings of the SPIE Electronic Imaging ‘97, Storage and Retrieval for Image and Video Databases, San Jose, CA, USA, 8–14 February 1997. [Google Scholar]
- Rani, M.; Agarwal, R. A New Experimental Approach to Study the Stability of Logistic Map. Chaos Solitons Fractals 2009, 41, 2062–2066. [Google Scholar] [CrossRef]
- Hénon, M. A Two-Dimensional Mapping with a Strange Attractor. Commun. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Silva, L.; Rocha, J.L.; Silva, M.T. Bifurcations of 2-Periodic Nonautonomous Stunted Tent Systems. Int. J. Bifurc. Chaos 2017, 27, 1730020. [Google Scholar] [CrossRef]
- Lorenz, E. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet Another Chaotic Attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Matsumoto, T.; Chua, L.O.; Komuro, M. The double scroll family. IEEE Trans. Circuits Syst. 1985, 32, 797–818. [Google Scholar] [CrossRef]
- Kaneko, K. Pattern Dynamics in Spatiotemporal Chaos: Pattern Selection, Diffusion of Defect and Pattern Competition Intermittency. Phys. D Nonlinear Phenom. 1989, 34, 1–41. [Google Scholar] [CrossRef]
- Rhouma, R.; Meherzi, S.; Belghith, S. OCML-Based Colour Image Encryption. Chaos Solitons Fractals 2009, 40, 309–318. [Google Scholar] [CrossRef]
- Khellat, F.; Ghaderi, A.; Vasegh, N. Li-Yorke Chaos and Synchronous Chaos in A Globally Nonlocal Coupled Map Lattice. Chaos Solitons Fractals 2011, 44, 934–939. [Google Scholar] [CrossRef]
- Tao, Y.; Cui, W.; Zhang, Z. Spatiotemporal Chaos in Multiple Dynamically Coupled Map Lattices and Its Application in A Novel Image Encryption Algorithm. J. Inf. Secur. Appl. 2020, 55, 102650. [Google Scholar] [CrossRef]
- Liu, P.; Wang, X.; Su, Y.; Liu, H.; Unar, S. Globally Coupled Private Image Encryption Algorithm Based on Infinite Interval Spatiotemporal Chaotic System. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 2511–2522. [Google Scholar] [CrossRef]
- Du, L.; Teng, L.; Liu, H.; Lu, H. Multiple Face Images Encryption Based on A New Non-Adjacent Dynamic Coupled Mapping Lattice. Expert Syst. Appl. 2024, 238, 121728. [Google Scholar] [CrossRef]
- Chua, L. Memristor-The Missing Circuit Element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.; Snider, G.; Stewart, D.; Williams, R. The Missing Memristor Found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Wan, Q.; Zhou, Z.; Ji, W.; Wang, C.; Yu, F. Dynamic Analysis and Circuit Realization of a Novel No-Equilibrium 5D Memristive Hyperchaotic System with Hidden Extreme Multistability. Complexity 2020, 2020, 7106861. [Google Scholar] [CrossRef]
- Ramamoorthy, R.; Rajagopal, K.; Leutcho, G.; Krejcar, O.; Namazi, H.; Hussain, I. Multistable Dynamics and Control of a New 4D Memristive Chaotic Sprott B System. Chaos Solitons Fractals 2022, 156, 111834. [Google Scholar] [CrossRef]
- Li, P.; Feng, X.; Lu, H.; Zhou, S.; Zhang, H. SAECNet: Self-Attention Encryption and Compression Network Based on Bidirectional Cyclic Multi-Scroll Memristor Neural Network. IEEE Internet Things J. 2025. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.; Swinney, H.; Vastano, J. Determining Lyapunov Exponents from a Time Series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Arora, S.; Hu, W.; Kothari, P.K. An Analysis of the T-SNE Algorithm for Data Visualization. In Proceedings of the Conference on Learning Theory, Stockholm, Sweden, 6–9 July 2018; PMLR: London, UK; pp. 1455–1462. [Google Scholar]
- Zhang, Q.; Su, C.; Luo, Q.; Grebogi, C.; Huang, Z.; Jiang, J. Adaptive Whole-Brain Dynamics Predictive Method: Relevancy to Mental Disorders. Research 2025, 8, 0648. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Q. Constructing N-Dimensional Discrete Non-Degenerate Hyperchaotic Maps Using QR Decomposition. Chaos Solitons Fractals 2023, 174, 113915. [Google Scholar] [CrossRef]
- Che, Y.; Cheng, C.; Liu, Z.; Zhang, Z. Fast Basin Stability Estimation for Dynamic Systems under Large Perturbations with Sequential Support Vector Machine. Phys. D Nonlinear Phenom. 2020, 405, 132381. [Google Scholar] [CrossRef]
- Marwan, N.; Kraemer, K.H. Trends in Recurrence Analysis of Dynamical Systems. Eur. Phys. J. Spec. Top. 2023, 232, 5–27. [Google Scholar] [CrossRef]
- Huang, L.; Yao, W.; Xiang, J.; Zhang, Z. Heterogeneous and Homogenous Multistabilities in a Novel 4D Memristor-Based Chaotic System with Discrete Bifurcation Diagrams. Complexity 2020, 2020, 2408460. [Google Scholar] [CrossRef]
- Farjami, A.A.; Yaghoobi, M.; Kardehi Moghaddam, R. Extended Cascade Chaotic Systems and Estimation Parameters with New Chaotic Grey Wolf Algorithm. J. Exp. Theor. Artif. Intell. 2024, 36, 1187–1211. [Google Scholar] [CrossRef]
- Thoa, T.T.; Pei, Y. Chaotic Evolution Algorithm with Multiple Chaotic Systems. In Proceedings of the 2020 59th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Chiang Mai, Thailand, 23–26 September 2020; IEEE: Piscataway, NJ, USA; pp. 814–819. [Google Scholar]
- Xie, H.; Gao, Y.; Zhang, H. An Image Encryption Algorithm Based on Novel Block Scrambling Scheme and Josephus Sequence Generator. Multimedia Tools Appl. 2023, 82, 16431–16453. [Google Scholar] [CrossRef]
- Sun, J.; Li, C.; Wang, Z.; Wang, Y.A. Memristive Fully Connect Neural Network and Application of Medical Image Encryption Based on Central Diffusion Algorithm. IEEE Trans. Ind. Inform. 2023, 20, 3778–3788. [Google Scholar] [CrossRef]
- Mondal, B.; Singh, J.P. A Lightweight Image Encryption Scheme Based on Chaos and Diffusion Circuit. Multimed. Tools Appl. 2022, 81, 34547–34571. [Google Scholar] [CrossRef]
- Liu, L.; Hao, S.; Lin, J.; Wang, Z.; Hu, X.; Miao, S. Image Block Encryption Algorithm Based on Chaotic Maps. IET Signal Process. 2018, 12, 22–30. [Google Scholar] [CrossRef]
- Manivannan, D.; Murugan, B. Image Encryption Using Chaos Based Heuristic Diffusion. SN Comput. Sci. 2023, 4, 239. [Google Scholar] [CrossRef]
- Ge, B.; Shen, Z.; Zhang, J. Fast Chaotic Image Encryption Algorithm Using a Novel Divide and Conquer Diffusion strategy. IEEE Access 2022, 10, 95986–96005. [Google Scholar] [CrossRef]
- Wang, S.; Peng, Q.; Du, B. Chaotic Color Image Encryption Based on 4D Chaotic Maps and DNA Sequence. Opt. Laser Technol. 2022, 148, 107753. [Google Scholar] [CrossRef]
- Chen, X.; Mou, J.; Cao, Y.; Banerjee, S. Chaotic Multiple-Image Encryption Algorithm Based on Block Scrambling and Dynamic DNA Coding. Int. J. Bifurc. Chaos 2023, 33, 2350190. [Google Scholar] [CrossRef]
- Zou, C.; Wang, X.; Zhou, C.; Xu, S.; Huang, C. A Novel Image Encryption Algorithm Based on DNA Strand Exchange and Diffusion. Appl. Math. Comput. 2022, 430, 127291. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Banerjee, S.; Cao, Y.; Xiong, L.; Chen, X. An Effective Multiple-Image Encryption Algorithm Based On 3D Cube and Hyperchaotic Map. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 1535–1551. [Google Scholar] [CrossRef]
- Zhou, S.; Wei, Y.; Zhang, Y.; Lu, H.; Zhang, H. Image Encryption Algorithm Based on the Dynamic RNA Computing and a New Chaotic Map. Integration 2025, 101, 102336. [Google Scholar] [CrossRef]
- Wang, W.; Sun, J.; Wang, G.; Zhang, H. Fisher-Yates Scrambling Algorithm Combined with S-Box Color Image Encryption Technology Based On 3D-SCCM Chaotic System. Multimed. Tools Appl. 2023, 82, 45233–45258. [Google Scholar] [CrossRef]
- Nan, S.; Feng, X.; Wu, Y.; Zhang, H. Remote Sensing Image Compression and Encryption Based on Block Compressive Sensing And 2D-LCCCM. Nonlinear Dyn. 2022, 108, 2705–2729. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Li, B.; Banerjee, S.; Sun, B. Multi-Image Hybrid Encryption Algorithm Based on Pixel Substitution and Gene Theory. Fractals 2023, 31, 2340111. [Google Scholar] [CrossRef]
- Zhou, S.; Qiu, Y.; Wang, X.; Zhang, Y. Novel Image Cryptosystem Based on New 2D Hyperchaotic Map and Dynamical Chaotic S-Box. Nonlinear Dyn. 2023, 111, 9571–9589. [Google Scholar] [CrossRef]
- Alexan, W.; Alexan, N.; Gabr, M. Multiple-Layer Image Encryption Utilizing Fractional-Order Chen Hyperchaotic Map and Cryptographically Secure Prngs. Fractal Fract. 2023, 7, 287. [Google Scholar] [CrossRef]
- Shao, Z.; Tang, Y.; Liang, M.; Shang, Y.; Wang, F.; Wang, Y. Double Image Encryption Based on Symmetry of 2D-DFT And Equal Modulus Decomposition. Multimed. Tools Appl. 2021, 80, 8973–8998. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, J.; Wang, J. An Image Compression Encryption Based on the Semi-Tensor Product and the DFT Measurement Matrix. Optik 2023, 288, 171175. [Google Scholar] [CrossRef]
- Wang, M.; Fu, X.; Yan, X.; Teng, L. A New Chaos-Based Image Encryption Algorithm Based on Discrete Fourier Transform and Improved Joseph Traversal. Mathematics 2024, 12, 638. [Google Scholar] [CrossRef]
- Cao, F.; Guo, D.; Wang, T.; Yao, H.; Li, J.; Qin, C. Universal Screen-Shooting Robust Image Watermarking with Channel-Attention in DCT Domain. Expert Syst. Appl. 2024, 238, 122062. [Google Scholar] [CrossRef]
- Jiang, M.R.; Feng, X.F.; Wang, C.P.; Fan, X.L.; Zhang, H. Robust Color Image Watermarking Algorithm Based on Synchronization Correction with Multi-Layer Perceptron and Cauchy Distribution Model. Appl. Soft Comput. 2023, 140, 110271. [Google Scholar] [CrossRef]
- Lone, P.N.; Mir, U.H.; Gaffar, A. Hyperchaotic Image Encryption Using DNA Coding and Discrete Cosine Transform. J. Frankl. Inst. 2023, 360, 13318–13338. [Google Scholar] [CrossRef]
- Chowdhury, R.S.; Jana, J.; Tripathi, S.; Bhaumik, J. Improved DWT And IDWT Architectures for Image Compression. Microprocess. Microsyst. 2024, 104, 104990. [Google Scholar] [CrossRef]
- Feng, X.F.; Yang, J.; Wu, Y.F.; Zhang, H. Robust Encryption and Compression of Sequential Images Using STP-CS And 2D-EPHM: A Novel Hybrid Symmetric-Asymmetric Approach. Vis. Comput. 2025. [Google Scholar] [CrossRef]
- Gao, L.; Qi, L.; Guan, L. The Property of Frequency Shift In 2D-FRFT Domain with Application to Image Encryption. IEEE Signal Process. Lett. 2021, 28, 185–189. [Google Scholar] [CrossRef]
- Tao, L.; Liang, X.; Wu, Z.; Han, L.; Zhu, J. Plaintext Related Optical Image Hybrid Encryption Based on Fractional Fourier Transform and Generalized Chaos of Multiple Controlling Parameters. J. Grid Comput. 2023, 21, 17. [Google Scholar] [CrossRef]
- Wang, M.M.; Song, X.G.; Zhou, N.R.; Liu, S.H. Novel 1-D Enhanced Log-Logistic Chaotic Map and Asymmetric Generalized Gaussian Apertured Frft for Image Encryption. Chaos Solitons Fractals 2024, 187, 115443. [Google Scholar] [CrossRef]
- Ma, Y.; Zhou, N.R. Quantum Color Image Compression and Encryption Algorithm Based on Fibonacci Transform. Quantum Inf. Process. 2023, 22, 39. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, C.; Cui, M.; Luo, Y.; Wu, T.; Liang, X. Joint Compressed Sensing and JPEG Coding Based Secure Compression Scheme In OFDM-PON. Opt. Commun. 2022, 510, 127901. [Google Scholar] [CrossRef]
- Sara, U.; Akter, M.; Uddin, M.S. Image Quality Assessment Through FSIM, SSIM, MSE And PSNR-A Comparative Study. J. Comput. Commun. 2019, 7, 8–18. [Google Scholar] [CrossRef]
- Biban, G.; Chugh, R.; Panwar, A. Image Encryption Based on 8D Hyperchaotic System Using Fibonacci Q-Matrix. Chaos Solitons Fractals 2023, 170, 113396. [Google Scholar] [CrossRef]
- Sun, Y.J.; Zhang, H.; Wang, C.P.; Li, Z.Y.; Wang, X.Y. Networked Chaotic Map Model and Its Applications in Color Multiple Image Encryption. IEEE Photonics J. 2020, 12, 7801218. [Google Scholar] [CrossRef]
- Gao, Y.J.; Xie, H.W.; Zhang, J.; Zhang, H. A Novel Quantum Image Encryption Technique Based on Improved Controlled Alternated Quantum Walks and Hyperchaotic System. Phys. A Stat. Mech. Its Appl. 2022, 598, 127334. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, X.Q.; Wang, X.Y.; Yan, P.F. Novel Multiple Images Encryption Algorithm Using CML System and DNA Encoding. IET Image Process. 2020, 14, 518–529. [Google Scholar] [CrossRef]
- Affes, M.; Meziou, M.S.; Ghorbel, F. Robust Color Watermarking Method Based on Clifford Transform; Springer International Publishing: Cham, Switzerland, 2016; pp. 453–464. [Google Scholar]
- Zhang, X.; Zhang, W.; Sun, W.; Sun, X.; Jha, S. A Robust 3-D Medical Watermarking Based on Wavelet Transform for Data Protection. Comput. Syst. Sci. Eng. 2022, 41, 1043–1056. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.Y.; Chen, Y.L.; Lu, C.; Yan, P. Fast image reconstruction method using radial harmonic Fourier moments and its application in digital watermarking. J. Frankl. Inst. 2025, 362, 107391. [Google Scholar] [CrossRef]
- Jiang, M.R.; Feng, X.F.; Wang, C.P.; Li, Z.; Zhang, H. Robust and Blind Watermarking Algorithm for Chaotic System Encryption Based on Discrete Cosine Transform-Singular Value Decomposition. J. Electron. Imaging 2023, 32, 013020. [Google Scholar] [CrossRef]
- Lu, C.C.; Feng, X.; Teng, L.; Wang, C.; Zhang, H. Blind Watermarking Algorithm with 2D-SCCM Chaotic System Encryption Based on SURF And Rhfms. Phys. Scr. 2024, 99, 035247. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Xia, Z.; Zhang, C. Ternary Radial Harmonic Fourier Moments Based Robust Stereo Image Zero-Watermarking Algorithm. Inf. Sci. 2019, 470, 109–120. [Google Scholar] [CrossRef]
- Fan, D.; Li, Y.; Gao, S.; Chi, W.; Lv, C. A Novel Zero Watermark Optimization Algorithm Based on Gabor Transform and Discrete Cosine Transform. Concurr. Comput. Pract. Exp. 2022, 34, e5689. [Google Scholar] [CrossRef]
- Azeroual, A.; Afdel, K. A Fragile Watermarking Scheme for Image Authentication Using Wavelet Transform, International Conference on Image and Signal Processing; Springer International Publishing: Cham, Switzerland, 2016; pp. 337–345. [Google Scholar]
- Ahmadi, S.B.; Zhang, G.; Rabbani, M.; Boukela, L.; Jelodar, H. An Intelligent and Blind Dual Color Image Watermarking for Authentication and Copyright Protection. Appl. Intell. 2021, 51, 1701–1732. [Google Scholar] [CrossRef]
- Bhalerao, S.; Ansari, I.A.; Kumar, A. A Secure Image Watermarking for Tamper Detection and Localization. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 1057–1068. [Google Scholar] [CrossRef]
- Peng, F.; Liao, T.; Long, M.; Li, J.; Zhang, W.; Zhou, Y. Semi-Fragile Reversible Watermarking For 3D Models Using Spherical Crown Volume Division. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 6531–6543. [Google Scholar] [CrossRef]
- Hurrah, N.N.; Khan, E.; Khan, U. CADEN: Cellular Automata and DNA Based Secure Framework for Privacy Preserving in Iot Based Healthcare. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 2631–2643. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.H.; Yao, H.X.; Gao, W.; Liu, Y. An Image Fragile Watermark Scheme Based on Chaotic Image Pattern and Pixel-Pairs. Appl. Math. Comput. 2007, 185, 869–882. [Google Scholar] [CrossRef]
- Feng, X.F.; Jiang, M.R.; Zhang, H.; Wang, C. Robust Multifunctional Watermarking System Based Zero-Watermarking and Polar Harmonic Fourier Moments. J. Frankl. Inst. 2024, 361, 319–340. [Google Scholar] [CrossRef]
- Dragoi, I.C.; Coltuc, D. Local-Prediction-Based Difference Expansion Reversible Watermarking. IEEE Trans. Image Process. 2014, 23, 1779–1790. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Yuan, X.; Liu, T.; Huang, G.; Lin, Z.; Li, J. FRRW: A Feature Extraction-Based Robust and Reversible Watermarking Scheme Utilizing Zernike Moments and Histogram Shifting. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101698. [Google Scholar] [CrossRef]
- Tang, Y.; Li, K.; Wang, C.; Bian, S.; Huang, Q. A Two-Stage Robust Reversible Watermarking Using Polar Harmonic Transform for High Robustness and Capacity. Inf. Sci. 2024, 654, 119786. [Google Scholar] [CrossRef]
- Garcia, H.; Feregrino, U.; Menendez, O.; Williams, R. Evaluation of A Framework for Robust Image Reversible Watermarking. Appl. Sci. 2022, 12, 7242. [Google Scholar] [CrossRef]
- Zhan, C.; Leng, L.; Chang, C.C.; Horng, J. Reversible Image Fragile Watermarking with Dual Tampering Detection. Electronics 2024, 13, 1884. [Google Scholar] [CrossRef]
- Qi, W.; Guo, S.; Hu, W. Generic Reversible Visible Watermarking Via Regularized Graph Fourier Transform Coding. IEEE Trans. Image Process. 2021, 31, 691–705. [Google Scholar] [CrossRef]
- Meng, L.; Jiang, X.; Sun, T. A Review of Coverless Steganography. Neurocomputing 2024, 566, 126945. [Google Scholar] [CrossRef]
- Melman, A.; Evsutin, O. Image Data Hiding Schemes Based on Metaheuristic Optimization: A Review. Artif. Intell. Rev. 2023, 56, 15375–15447. [Google Scholar] [CrossRef]
- Kadhim, I.J.; Premaratne, P.; Vial, P.J.; Halloran, B. Comprehensive Survey of Image Steganography: Techniques, Evaluations, And Trends in Future Research. Neurocomputing 2019, 335, 299–326. [Google Scholar] [CrossRef]
- Muhuri, P.K.; Ashraf, Z.; Goel, S. A Novel Image Steganographic Method Based on Integer Wavelet Transformation and Particle Swarm Optimization. Appl. Soft Comput. 2020, 92, 106257. [Google Scholar] [CrossRef]
- Sun, J.Y.; Cai, H.; Wang, G.; Gao, Z.; Zhang, H. FPGA Image Encryption-Steganography Using A Novel Chaotic System with Line Equilibria. Digit. Signal Process. 2023, 134, 103889. [Google Scholar]
- Kombrink, M.; Geradts, Z.; Worring, M. Image Steganography Approaches and Their Detection Strategies: A Survey. ACM Comput. Surv. 2024, 57, 1–40. [Google Scholar] [CrossRef]
- Tahiri, M.; Bencherqui, A.; Karmouni, H.; Amakdouf, H.; Mirjalili, S.; Motahhir, S.; Abouhawwash, M.; Askar, S.; Sayyouri, M.; Qjidaa, H. Implementation of A Steganography System Based on Hybrid Square Quaternion Moment Compression in IoMT. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101604. [Google Scholar] [CrossRef]
- Tai, W.L.; Yeh, C.M.; Chang, C.C. Reversible Data Hiding Based on Histogram Modification of Pixel Differences. IEEE Trans. Circuits Syst. Video Technol. 2009, 19, 906–910. [Google Scholar]
- Yin, Z.; Xiang, Y.; Zhang, X. Reversible Data Hiding in Encrypted Images Based on Multi-MSB Prediction and Huffman Coding. IEEE Trans. Multimed. 2019, 22, 874–884. [Google Scholar] [CrossRef]
- Jiang, R.; Zhou, H.; Zhang, W.; Yu, N. Reversible Data Hiding in Encrypted Three-Dimensional Mesh Models. IEEE Trans. Multimed. 2017, 20, 55–67. [Google Scholar] [CrossRef]
- Li, W.; Wang, H.; Chen, Y.; Abdullahi, S.; Luo, J. Constructing Immunized Stego-Image for Secure Steganography Via Artificial Immune System. IEEE Trans. Multimed. 2023, 25, 8320–8333. [Google Scholar] [CrossRef]
- Cao, W.; Cai, H.; Hua, Z. N-Dimensional Chaotic Map with Application in Secure Communication. Chaos Solitons Fractals 2022, 163, 112519. [Google Scholar] [CrossRef]
- Yang, Y.; Chang, R.; Feng, X.; Li, P.; Chen, Y.; Zhang, H. An n-Dimensional Chaotic Map with Application in Reversible Data Hiding for Medical Images. Entropy 2024, 26, 254. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Luo, X.; Guo, Y.; Qin, C.; Liu, F. Multiple Robustness Enhancements for Image Adaptive Steganography in Lossy Channels. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 2750–2764. [Google Scholar] [CrossRef]
- Brunet, D.; Vrscay, E.R.; Wang, Z. On The Mathematical Properties of the Structural Similarity Index. IEEE Trans. Image Process. 2011, 21, 1488–1499. [Google Scholar] [CrossRef]
- Qin, C.; Qian, X.; Hong, W.; Zhang, H. An Efficient Coding Scheme for Reversible Data hiding In Encrypted Image with Redundancy Transfer. Inf. Sci. 2019, 487, 176–192. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Barni, M. A Survey of Deep Neural Network Watermarking Techniques. Neurocomputing 2021, 461, 171–193. [Google Scholar] [CrossRef]
- Krasula, L.; Le Callet, P.; Fliegel, K.; Klima, M. Quality Assessment of Sharpened Images: Challenges, Methodology, And Objective Metrics. IEEE Trans. Image Process. 2017, 26, 1496–1508. [Google Scholar] [CrossRef]
- Li, Q.; Wang, X.; Ma, B.; Wang, X.; Wang, C.; Gao, S.; Shi, Y. Concealed Attack for Robust Watermarking Based on Generative Model and Perceptual Loss. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 5695–5706. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, X.; Zhang, L.; Qin, Z.; Sun, X.; Ren, K. A Privacy-Preserving and Copy-Deterrence Content-Based Image Retrieval Scheme in Cloud Computing. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2594–2608. [Google Scholar] [CrossRef]
- Yin, Z.; Ji, Y.; Luo, B. Reversible Data Hiding in JPEG Images with Multi-Objective Optimization. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 2343–2352. [Google Scholar] [CrossRef]
- Sobhy, M.I.; Shehata, A.R. Chaotic Algorithms for Data Encryption. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001; Volume 2, pp. 997–1000. [Google Scholar]
- Utami, D.; Suwastio, H.; Sumadjudin, B. FPGA Implementation of Digital Chaotic Cryptography. In Proceedings of the EurAsia-ICT 2002: Information and Communication Technology, Shiraz, Iran, 29–31 October 2002; Volume 2510, pp. 239–247. [Google Scholar]
- Balakrishnan, R.; Rengarajan, A.; Rayappan, J.B.B. Hybrid Image Crypto System for Secure Image Communication-A VLSI Approach. Microprocess. Microsyst. 2017, 50, 1–13. [Google Scholar]
- Boutros, A.; Hesham, S.; Georgey, B.; Abd El Ghany, M. Hardware Acceleration of Novel Chaos-Based Image Encryption for IOT Application. In Proceedings of the 2017 29th International Conference on Microelectronics, Beirut, Lebanon, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Gafsi, M.; Hajjaji, M.A.; Malek, J.; Mtibaa, A. FPGA Hardware Acceleration of An Improved Chaos-Based Cryptosystem for Real-Time Image Encryption and Decryption. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 7001–7022. [Google Scholar] [CrossRef]
- Fetteha, M.A.; Sayed, W.S.; Said, L.A. A Lightweight Image Encryption Scheme Using DNA Coding and Chaos. Electronics 2023, 12, 4895. [Google Scholar] [CrossRef]
- Moghimi Moghaddam, S.S.; Rashtchi, V.; Azarpeyvand, A. Parallel Chaos-Based Image Encryption Algorithm: High-Level Synthesis and FPGA Implementation. J. Supercomput. 2024, 80, 10985–11013. [Google Scholar] [CrossRef]
- Demirkol, A.S.; Sahin, M.E.; Karakaya, B.; Ulutas, H.; Ascoli, A.; Tetzlaff, R. Real Time Hybrid Medical Image Encryption Algorithm Combining Memristor-Based Chaos with DNA Coding. Chaos Solitons Fractals 2024, 183, 114923. [Google Scholar] [CrossRef]
- Guang, Y.; Ding, Q. Dynamics Analysis of A Novel Parametrically Controllable Symmetric Multi-Scroll Chaotic System and FPGA Design of An Image Encryption System. Chaos Solitons Fractals 2024, 188, 115572. [Google Scholar] [CrossRef]
- Vijayakumar, M.; Ahilan, A. An Optimized Chaotic S-Box for Real-Time Image Encryption Scheme Based On 4-Dimensional Memristive Hyperchaotic Map. Ain Shams Eng. J. 2024, 15, 102620. [Google Scholar] [CrossRef]
- Yang, C.H.; Chien, Y.S. FPGA Implementation and Design of A Hybrid Chaos-AES Color Image Encryption Algorithm. Symmetry 2020, 12, 189. [Google Scholar] [CrossRef]
- Cai, H.; Sun, J.; Gao, Z.; Zhang, H. A Novel Multi-Wing Chaotic System with FPGA Implementation and Application in Image Encryption. J. Real-Time Image Process. 2022, 19, 775–790. [Google Scholar] [CrossRef]
- Amdouni, R.; Gafsi, M.; Abbassi, N.; Hajjaji, M.; Mtibaa, A. Robust Hardware Implementation of A Block-Cipher Scheme Based on Chaos and Biological Algebraic Operations. Multimed. Tools Appl. 2023, 82, 37097–37130. [Google Scholar] [CrossRef]
- Vinoth Raj, R.; Siva Janakiraman, S.; Rengarajan, A. Reconfigurable Color Medical Image Encryptor Using Hardware Accelerated Chao(S)-Box Triplets. J. Real-Time Image Process. 2023, 20, 1–26. [Google Scholar]
- Deng, Q.; Wang, C.; Sun, Y.; Deng, Z.; Yang, G. Memristive Tabu Learning Neuron Generated Multi-Wing Attractor with FPGA Implementation and Application in Encryption. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 300–310. [Google Scholar] [CrossRef]
- Arumugham, S.; Rajagopalan, S.; Rayappan, J.; Amirtharajan, R. Tamper-Resistant Secure Medical Image Carrier: An IWT–SVD–Chaos–FPGA Combination. Arab. J. Sci. Eng. 2019, 44, 9561–9580. [Google Scholar] [CrossRef]
- Kaibou, R.; Azzaz, M.S.; Benssalah, M.; Teguig, D.; Hamil, H.; Merah, A.; Akrour, M. Real-Time FPGA Implementation of A Secure Chaos-Based Digital Crypto-Watermarking System in The DWT Domain Using Co-Design Approach. J. Real-Time Image Process. 2021, 18, 2009–2025. [Google Scholar] [CrossRef]
- Sun, J.Y.; Cai, H.; Gao, Z.B.; Wang, C.; Zhang, H. A Novel Non-Equilibrium Hyperchaotic System and Application on Color Image Steganography with FPGA Implementation. Nonlinear Dyn. 2023, 111, 3851–3868. [Google Scholar] [CrossRef]
- Li, S.Y.; Wu, G.Y.; Sun, J.Y.; Yan, P.; Zhang, H. Novel 3D-PCHCS Design and Application on Ophthalmic Medical Image Copyright Protection with FPGA Implementation. J. Real-Time Image Process. 2025, 22, 33. [Google Scholar] [CrossRef]
- Akhshani, A.; Akhavan, A.; Lim, S.C.; Hassan, Z. An Image Encryption Scheme Based on Quantumlogistic Map. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4653–4661. [Google Scholar] [CrossRef]
- Jiang, N.; Dong, X.; Hu, H.; Ji, Z.; Zhang, W. Quantum Image Encryption Based on Henon Mapping. Int. J. Theor. Phys. 2019, 58, 979–991. [Google Scholar] [CrossRef]
- Abd EL-Latif, A.A.; Abd-El-Atty, B.; Venegas-Andraca, S.E. Controlled Alternate Quantum walk-Based Pseudo-Random Number Generator and Its Application to Quantum Color Image encryption. Phys. A Stat. Mech. Its Appl. 2020, 547, 123869. [Google Scholar] [CrossRef]
- Sun, J.Y.; Wang, W.T.; Yan, P.F.; Zhang, H. Quantum Steganography Scheme and Circuit Design Based on The Synthesis of Three Grayscale Images in The HSI Color Space. Quantum Inf. Process. 2023, 22, 349. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, B.; Yao, Y.; Wang, X. The Synchronisation Control of Fractional 4-D Quantum Game Chaotic Map with Its Application in Image Encryption. Appl. Intell. 2025, 55, 343. [Google Scholar] [CrossRef]
- Rehman, M.U. Quantum-Enhanced Chaotic Image Encryption: Strengthening Digital Data Security with 1-D Sine-Based Chaotic Maps and Quantum Coding. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 101980. [Google Scholar] [CrossRef]
- Khan, M.S.; Ahmad, J.; Al-Dubai, A.; Pitropakis, N.; Ghaleb, B.; Ullah, A.; Khan, M.; Buchanan, W. Chaotic Quantum Encryption to Secure Image Data in Post Quantum Consumer Technology. IEEE Trans. Consum. Electron. 2024, 70, 7087–7100. [Google Scholar] [CrossRef]
- Dong, Y.; Yin, C.; Xu, C.; Yan, R. A Quantum Image Encryption Method for Dual Chaotic Systems Based on Quantum Logistic Mapping. Phys. Scr. 2024, 99, 015103. [Google Scholar] [CrossRef]
- Liu, X.D.; Chen, Q.H.; Zhao, R.S.; Liu, G.; Guan, S.; Wu, L.; Fan, X. Quantum Image Encryption Algorithm Based on Four-Dimensional Chaos. Front. Phys. 2024, 12, 1230294. [Google Scholar] [CrossRef]
- Yan, X.; Teng, L.; Su, Y. A Novel Chaotic Image Encryption Is Based on Fractional Wavelet Decomposition and Quantum Transform Model. Phys. Scr. 2024, 99, 055217. [Google Scholar] [CrossRef]
- Li, N.; Tang, Z. A Quantum Reversible Color-To-Grayscale Conversion Scheme via Image Encryption Based on True Random Numbers and Two-Dimensional Quantum Walks. Signal Process. 2025, 233, 109949. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, X. Adaptive Feature Calculation and Diagonal Mapping for Successive Recovery of Tampered Regions. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 2617–2630. [Google Scholar] [CrossRef]
- Wu, W.; Guo, X.; Chen, Y.; Wang, S.; Chen, J. Deep Embedding-Attention-Refinement for Sparse-View CT Reconstruction. IEEE Trans. Instrum. Meas. 2022, 72, 4501111. [Google Scholar] [CrossRef]
- Shen, M.; Gan, H.; Ma, C.; Ning, C.; Li, H.; Liu, F. MTC-CSNet: Marrying Transformer and Convolution for Image Compressed Sensing. IEEE Trans. Cybern. 2024, 54, 4949–4961. [Google Scholar] [CrossRef] [PubMed]
- Sekar, R.; Ravi, G. Taylor Sun Flower Optimization-Based Compressive Sensing for Image Compression and Recovery. Comput. J. 2023, 66, 873–887. [Google Scholar]
- Yang, Y.; Sun, J.; Li, H.; Xu, Z. ADMM-CSNet: A Deep Learning Approach for Image Compressive Sensing. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 521–538. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Zhang, Y.; Hua, Z.; Xiao, Z.; Weng, J. Client-Side Embedding of Screen-Shooting Resilient Image Watermarking. IEEE Trans. Inf. Forensics Secur. 2024, 19, 5357–5372. [Google Scholar] [CrossRef]
- Zhang, W.; Li, D.; Zhang, H.; Yu, P.; Gao, W. Lightweight Bit-Depth Recovery Network for Gaofen Satellite Multispectral Image Compression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 18635–18651. [Google Scholar] [CrossRef]
- Lin, Y.; Xie, Z.; Chen, T.; Cheng, X.; Wen, H. Image Privacy Protection Scheme Based on High-Quality Reconstruction DCT Compression and Nonlinear Dynamics. Expert Syst. Appl. 2024, 257, 124891. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Natiq, H.; Alkhayyat, A.; Farhan, A.; Al-Saidi, N.; Baleanu, D. Image Encryption Algorithm Based on New Fractional Beta Chaotic Maps. Comput. Model. Eng. Sci. 2022, 132, 119–131. [Google Scholar] [CrossRef]
- Luo, H.; Li, L.; Zhang, X. Secure Neural Network Watermarking Protocol Against Evidence Exposure Attack. IEEE Trans. Multimed. 2025. [Google Scholar] [CrossRef]
- Shang, C.; Cao, J.; Zhu, T.; Zhang, Y.; Niu, B.; Li, H. CADFA: A Clock Skew-Based Active Device Fingerprint Authentication Scheme for Class-1 Iot Devices. IEEE Syst. J. 2024, 18, 590–599. [Google Scholar] [CrossRef]
- Zhang, D.; Le, J.; Mu, N.; Wu, J.; Liao, X. Secure and Efficient Data Deduplication in Joint Cloud Storage. IEEE Trans. Cloud Comput. 2021, 11, 156–167. [Google Scholar] [CrossRef]
- Xue, L.; Liu, D.; Huang, C.; Shen, X.; Zhuang, W.; Sun, R.; Ying, B. Blockchain-Based Data Sharing with Key Update for Future Networks. IEEE J. Sel. Areas Commun. 2022, 40, 3437–3451. [Google Scholar] [CrossRef]
- Cheng, L.; Meng, F. Certificateless Public Key Authenticated Searchable Encryption with Enhanced Security Model in IIoT Applications. IEEE Internet Things J. 2022, 10, 1391–1400. [Google Scholar] [CrossRef]
- Wang, M.X.; Yang, H.M.; Jiang, D.H.; Yan, B.; Pan, J.; Wang, T. A Novel Quantum Image Watermarking Scheme for Tamper Localization and Self-Recovery. Quantum Inf. Process. 2022, 21, 277. [Google Scholar] [CrossRef]
- Daoui, A.; Yamni, M.; Altameem, T.; Ahmad, M.; Hammad, M.; Plawiak, P.; Tadeusiewicz, R.; Abd El-Latif, A. Aucfsr: Authentication and Color Face Self-Recovery Using Novel 2D Hyperchaotic System and Deep Learning Models. Sensors 2023, 23, 8957. [Google Scholar] [CrossRef]
- Huang, Q.; Zhao, X.; Li, G. Research on the application of Video encryption technology based on 7 dimensional CNN hyper chaos. In Proceedings of the 2018 10th International Conference on Measuring Technology and Mechatronics Automation, Changsha, China, 25–26 February 2018; pp. 448–451. [Google Scholar]
- Zhou, S. Image Encryption Technology Research Based on Neural Network. In Proceedings of the 2015 International Conference on Intelligent Transportation, Big Data and Smart City, Halong Bay, Vietnam, 19–20 December 2015; pp. 462–465. [Google Scholar]
- Wang, C.; Zhang, Y. A Novel Image Encryption Algorithm with Deep Neural Network. Signal Process. 2022, 196, 108536. [Google Scholar] [CrossRef]
- Feng, L.; Du, J.; Fu, C.; Song, W. Image Encryption Algorithm Combining Chaotic Image Encryption and Convolutional Neural Network. Electronics 2023, 12, 3455. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Banerjee, S.; Zhang, Y. Color-Gray Multi-Image Hybrid Compression–Encryption Scheme Based on BP Neural Network and Knight Tour. IEEE Trans. Cybern. 2023, 53, 5037–5047. [Google Scholar] [CrossRef]
- Li, P.; Feng, X.; Zhou, S.; Yan, P.; Zhang, H. Compression and Encryption for Remote Sensing Image Based On PSO-BP And 2D-MCCM. Phys. Scr. 2024, 99, 085268. [Google Scholar] [CrossRef]
- Feng, Q.; Li, P.; Lu, Z.; Li, C.; Wang, Z.; Duan, C.; Huang, F.; Weng, J.; Yu, P. Evit: Privacy-Preserving Image Retrieval Via Encrypted Vision Transformer in Cloud Computing. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 7467–7483. [Google Scholar] [CrossRef]
- Nagamori, T.; Shiota, S.; Kiya, H. Efficient Fine-Tuning with Domain Adaptation for Privacy-Preserving Vision Transformer. arXiv 2024, arXiv:2401.05126. [Google Scholar] [CrossRef]
- Amin, A.; Hasan, K.; Ullah, S.; Hong, L. AI-Driven Secure Data Sharing: A Trustworthy and Privacy-Preserving Approach. In Proceedings of the 2025 International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA, 17–20 February 2025. [Google Scholar]
- Fan, L.; Li, M.; Hu, Z.; Hong, Y.; Kong, D. DNGG: Medical Image Lossless Encryption Via Deep Network Guided Generative. IEEE Signal Process. Lett. 2025, 32, 1331–1335. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Z.; Qin, Z.; Zhou, E.; Zhu, G.; Qin, Z.; Choo, K. Backdoor Attack on Deep Learning-Based Medical Image Encryption and Decryption Network. IEEE Trans. Inf. Forensics Secur. 2023, 19, 280–292. [Google Scholar] [CrossRef]
- Li, Y.; Gao, W.; Li, G.; Ma, S. Saliency Segmentation Oriented Deep Image Compression with Novel Bit Allocation. IEEE Trans. Image Process. 2024, 34, 16–29. [Google Scholar] [CrossRef]
- Zhang, Y.; Ni, J.; Su, W. Hifimsfa: Robust and High-Fidelity Image Watermarking Using Attention Augmented Deep Network. IEEE Signal Process. Lett. 2025, 32, 781–785. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Y.; Wang, G. Adaptor: Improving The Robustness and Imperceptibility of Watermarking By The Adaptive Strength Factor. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 6260–6272. [Google Scholar] [CrossRef]
- Li, Y.; Liao, X.; Wu, X. Screen-Shooting Resistant Watermarking with Grayscale Deviation Simulation. IEEE Trans. Multimed. 2024, 26, 10908–10923. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, W. Digital Watermarking Based on Neural Network and Image Features. In Proceedings of the 2009 Second International Conference on Information and Computing Science, Manchester, UK, 21–22 May 2009; Volume 2, pp. 238–240. [Google Scholar]
- Afsharizadeh, M.; Mohammadi, M. Prediction-Based Reversible Image Watermarking Using Artificial Neural Networks. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 896–910. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, T.; Liu, C.; Yu, S.; Zhou, W. High-Frequency Matters: Attack and Defense for Image-Processing Model Watermarking. IEEE Trans. Serv. Comput. 2024, 17, 1565–1579. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).