Three-Step Iterative Methodology for the Solution of Extended Ordered XOR-Inclusion Problems Incorporating Generalized Cayley–Yosida Operators
Abstract
1. Introduction
2. Prerequisites and Formulation of SEOXORIP
- (i)
- (ii)
- (iii)
- (iv)
- (i)
- (ii)
- If then
- (iii)
- (iv)
- If then if and only if
- (v)
- If , and w are comparable to each other, then
- (ix)
- If , and w are comparable to each other, then
- (vi)
- ;
- (vii)
- If then
- (i)
- A comparison mapping if, for every and , then and
- (ii)
- A strong comparison mapping if f is a comparison mapping and if and only if for any
- (iii)
- A -ordered compression mapping if f is a comparison mapping and
- (i)
- A -ordered compression mapping associated with f in the first component if there exists a constant such that
- (ii)
- A -ordered compression mapping associated with g in the second component if there exists a constant such that
- (i)
- It is well known that the generalized Yosida approximation operator is Lipschitz-type continuous with constant
- (ii)
- Similarly, the generalized Cayley operator is Lipschitz-type continuous with constant
SEOXORIP and the Existence of Its Solution
3. Three-Step Iterative Scheme and Its Convergence
| Algorithm 1: Three-Step Iterative Algorithm for the Approximate Solution of SEOXORIP |
| Let , ; let and be single-valued mappings. Let be a -Lipschitz continuous mapping with constants and let be a generalized -strongly accretive mapping with respect to . Then, Initially: Choose and . Step I: Let and We define Step III: If the accuracy is satisfactory and and , satisfy step I, then stop; if not, set and return to step I. |
- (i)
- and ;
- (ii)
- hold.
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adamu, A.; Abass, H.H.; Ibrahim, A.I.; Kilicman, A. An accelerated Halpern-type algorithm for solving variational inclusion problems with applications. Bangmod J. Math. Comput. Sci. 2022, 8, 37–55. [Google Scholar] [CrossRef]
- Adamu, A.; Deepho, J.; Ibrahim, A.H.; Abubakar, A.B. Approximation of zeros of sum of Monotone Mappings with Applications to Variational Inequalities Problems and image processing. Nonlinear Fun. Anal. Appl. 2021, 262, 411–432. [Google Scholar]
- Taiwo, A.; Reich, S.; Agarwal, R.P. Tseng-Type Algorithms for Solving Variational Inequalities Over the Solution Sets of Split Variational Inclusion Problems with An Application to A Bilevel Optimization Problem. J. Appl. Numer. Optim. 2024, 6, 41–57. [Google Scholar]
- Lin, L.-J.; Chen, Y.-D.; Chuang, C.-S. Solutions for a variational inclusion problem with applications to multiple sets split feasibility problems. Fixed Point Theory Appl. 2013, 2013, 333. [Google Scholar] [CrossRef][Green Version]
- Fang, Y.-P.; Huang, N.-J. H-monotone operator and resolvent operator technique for variational inclusions. Appl. Math. Comput. 2003, 145, 795–803. [Google Scholar] [CrossRef]
- Fang, Y.-P.; Huang, N.-J. H-accretive operators and resolvent operator technique for solving variational inclusions in Banach spaces. Appl. Math. Lett. 2004, 17, 647–653. [Google Scholar] [CrossRef]
- Xia, F.-Q.; Huang, N.-J. Variational inclusions with a general H-monotone operator in Banach spaces. Comput. Math. Appl. 2007, 54, 24–30. [Google Scholar] [CrossRef]
- Ding, X.P.; Xia, F.Q. A new class of completely generalized quasivariational inclusions in Banach spaces. J. Comput. Appl. Math. 2002, 147, 369–383. [Google Scholar] [CrossRef]
- Amann, H. On the number of solutions of nonlinear equations in ordered Banach spaces. J. Funct. Anal. 1972, 11, 346–384. [Google Scholar] [CrossRef]
- Li, H.G. Approximation solution for general nonlinear ordered variational inequalities and ordered equations in ordered Banach space. Nonlinear Anal. Forum 2008, 13, 205–214. [Google Scholar]
- Ali, I.; Ahmad, R.; Wen, C.F. Cayley Inclusion problem involving XOR-operation. Mathematics 2019, 7, 302. [Google Scholar] [CrossRef]
- Li, H.G.; Li, L.P.; Jin, M.M. A class of nonlinear mixed ordered ininclusion problems for ordered (αA,λ)-ANODM set-valued mappings with strong compression mapping. Fixed Point Theory Appl. 2014, 2014, 79. [Google Scholar] [CrossRef]
- Li, H.G. A nonlinear inclusion problem involving (α,λ)-NODM set-valued mappings in ordered Hilbert space. Appl. Math. Lett. 2012, 25, 1384–1388. [Google Scholar] [CrossRef]
- Glowinski, G.; Le Tallec, P. Augmented Lagrangian and Operator Splitting Methods in Nonlinear Mechanics; SIAM: Philadelphia, PA, USA, 1989. [Google Scholar]
- Noor, M.A. New approximation schemes for general variational inequalities. J. Math. Anal. Appl. 2000, 251, 217–229. [Google Scholar] [CrossRef]
- Noor, M.A. A predictor-corrector algorithm for general variational inequalities. Appl. Math. Lett. 2001, 14, 53–58. [Google Scholar] [CrossRef]
- Noor, M.A. Three-step iterative algorithms for multivaled quasi-variational inclusions. J. Math. Anal. Appl. 2001, 255, 589–604. [Google Scholar] [CrossRef]
- Ahmad, I.; Rahaman, M.; Ahmad, R.; Ali, I. Convergence analysis and stability of perturbed three-step iterative algorithm for generalized mixed ordered quasi-variational inclusion involving XOR operator. Optimization 2020, 69, 821–845. [Google Scholar] [CrossRef]
- Ali, I.; Wang, Y.; Ahmad, R. Convergence and Stability of a Three-Step Iterative Algorithm for the Extended Cayley–Yosida Inclusion Problem in 2-Uniformly Smooth Banach Spaces: Convergence and Stability Analysis. Mathematics 2024, 12, 1977. [Google Scholar] [CrossRef]
- Schaefer, H.H. Banach Lattices and Positive Operators; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Aubin, J.P.; Cellina, A. Differential Inclusions; Springer: Berlin, Germany, 1984. [Google Scholar]
- Kazmi, K.R.; Khan, F.A.; Shahzad, M. A system of generalized variational inclusions involving generalized H(·,·)-accretive mapping in real q-uniformly smooth Banach spaces. Appl. Math. Comput. 2011, 217, 9679–9688. [Google Scholar] [CrossRef]
- Salahuddin. System of Generalized Mixed Nonlinear Ordered Variational Inclusions. Numer. Algebra Control. Optim. 2019, 9, 445–460. [Google Scholar] [CrossRef]
- Du, Y.H. Fixed points of increasing operators in ordered Banach spaces and applications. Appl. Anal. 1990, 38, 1–20. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, R.; Iqbal, J. A resolvent approach for solving a set-valued variational inclusion problem using weak-RRD set-valued mapping. Korean J. Math. 2016, 16, 199–213. [Google Scholar] [CrossRef]
- Osilike, M.O. Stability results for the Ishikawa fixed point iteration procedure. Ind. J. Pure Appl. Math. 1995, 26, 937–945. [Google Scholar]
- Nadler, S.B., Jr. Multi-valued contraction mappings. Pac. J. Math. 1969, 30, 475–488. [Google Scholar] [CrossRef]
- Arifuzzaman; Irfan, S.S.; Ahmad, I. Convergence Analysis for Cayley Variational Inclusion Problem Involving XOR and XNOR Operations. Axioms 2025, 14, 149. [Google Scholar] [CrossRef]


| No. of | For | For | For |
|---|---|---|---|
| Iterations | |||
| n = 1 | (−1,2) | (3,−2) | (4,−1) |
| n = 2 | (−0.49930, 0.81207) | (0.23862, 0.24273) | (−0.72659, 2.10466) |
| n = 3 | (−0.45165, 0.71122) | (−0.44464,1.89461) | (−0.43555, 0.89865) |
| n = 4 | (−0.46018, 0.80844 ) | (−0.33075 , 0.90799) | (−0.43376, 0.89865) |
| n = 5 | (−0.45581, 0.80425) | (−0.33841, 0.75610) | (−0.46637, 0.82427) |
| n = 10 | (−0.44173, 0.76545) | (−0.36189, 0.69389) | (−0.4845, 0.74925) |
| n = 15 | (−0.43366, 0.73856) | (−0.36339, 0.63498) | (−0.48451, 0.71074) |
| n = 20 | (−0.42794, 0.71821) | (−0.36241, 0.60042) | (−0.48211, 0.68513) |
| n = 25 | (−0.42341, 0.70210) | (−0.36087, 0.57680) | (−0.47936, 0.66615) |
| n = 30 | (−0.41972, 0.68884) | (−0.35921, 0.55919) | (−0.47668, 0.65118) |
| n = 35 | (−0.41659, 0.67762) | (−0.35758, 0.54531) | (−0.47417, 0.63887) |
| n = 40 | (−0.41389, 0.66791) | (−0.35604, 0.53394) | (−0.47186, 0.62845) |
| n = 45 | (−0.41149, 0.65938) | (−0.35458, 0.52436) | (−0.46972, 0.61943) |
| n = 55 | (−0.40742, 0.64494) | (−0.35194, 0.50891) | (−0.46591 0.60444) |
| n = 70 | (−0.40252, 0.62779) | (−0.34853, 0.49157) | (−0.46113, 0.58701) |
| n = 80 | (−0.39981, 0.61841) | (−0.34656, 0.48248) | (−0.45835 0.57760) |
| n = 90 | (−0.39742, 0.61020) | (−0.34479, 0.47473) | (−0.45588, 0.56946) |
| n = 100 | (−0.39523, 0.60290) | (−0.34318, 0.46796) | (−0.45365, 0.56228) |
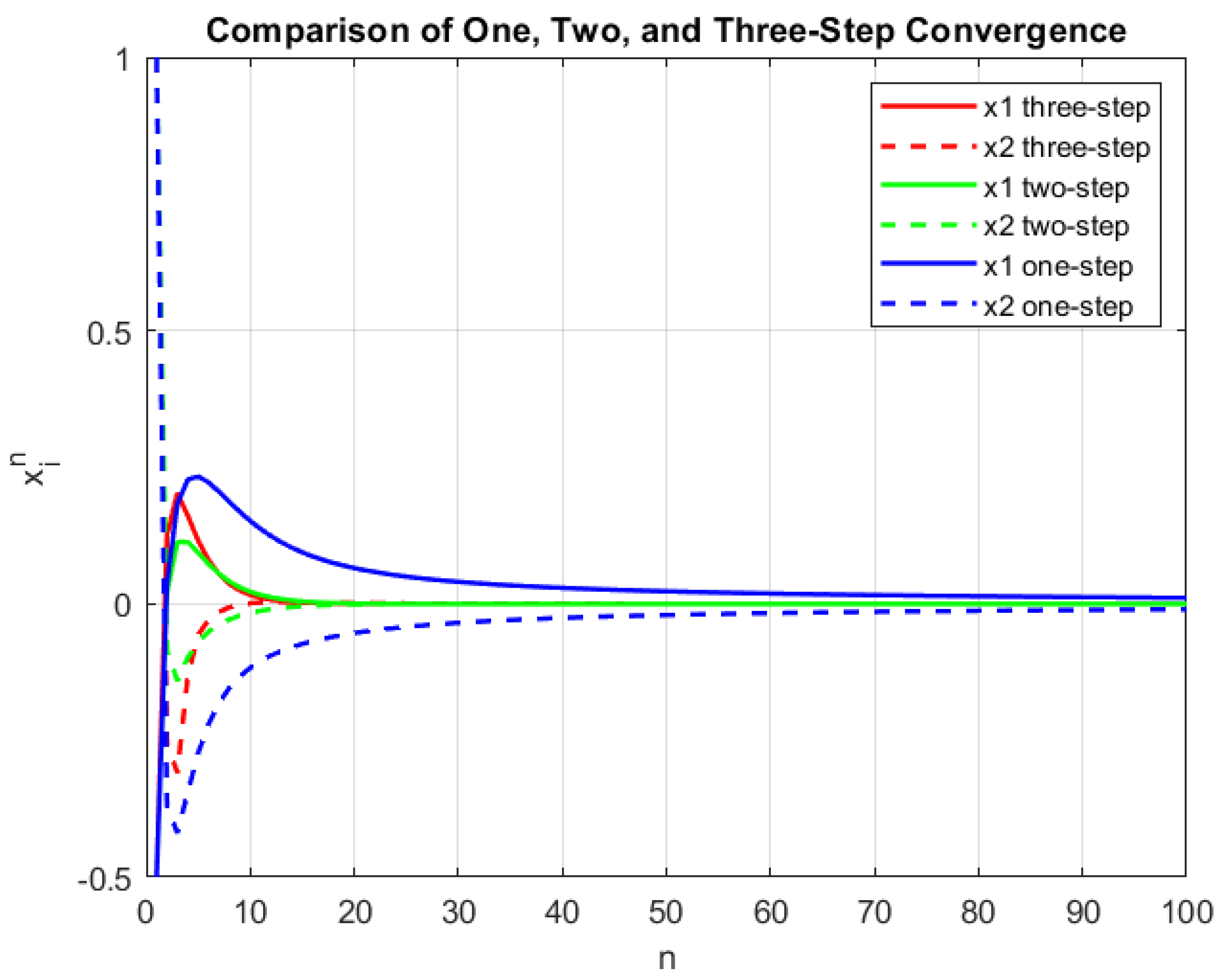
| No. ofIterations | Three-Step Iterative Algorithm | Two-Step Iterative Algorithm | One Step Iterative Algorithm |
|---|---|---|---|
| n = 1 | (−0.5,1) | (−0.5,1) | (−0.5,1) |
| n = 2 | (0.12570, −0.25747) | (0.02153, −0.08605) | (0.03702, −0.37147) |
| n = 3 | (0.20262, −0.30925) | (0.11337, −0.14096) | (0.18311, −0.41916) |
| n = 4 | (0.16102, −0.13137) | (0.11288, −0.0982) | (0.22754, −0.34455) |
| n = 5 | (0.11547, −0.05666) | (0.09339, −0.06932) | (0.2329, −0.27319) |
| n = 10 | (0.01631, 0.00114) | (0.02223, −0.01653) | (0.15164, −0.11691) |
| n = 15 | (0.00225, 0.00301) | (0.00459, −0.00439) | (0.09413, −0.07328) |
| n = 20 | (0.00017, 0.00172) | (0.00071 −0.00100) | (0.06543, −0.05345) |
| n = 25 | (0, 0.00093) | (0.00013, −0.0001) | (0.04982, −0.04209) |
| n = 30 | (0, 0.00052) | (0, 0.00016) | (0.04026, −0.03471) |
| n = 35 | (0, 0.00029) | (0, 0.00013) | (0.03382, −0.02954) |
| n = 40 | (0, 0.00016) | (0, 0.00009) | (0.02918, −0.02571) |
| n = 45 | (0, 0.00009) | (0, 0.00006) | (0.02566, −0.02276) |
| n = 55 | (0, 0) | (0, 0.00003) | (0.02069, 0) |
| n = 70 | (0, 0) | (0, 0) | (0.01604, 0) |
| n = 80 | (0, 0) | (0, 0) | (0.01395, −0.01262) |
| n = 90 | (0, 0) | (0, 0) | (0.01234, −0.0112) |
| n = 100 | (0, 0) | (0, 0) | (0.01107, −0.01006) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filali, D.; Ali, I.; Ali, M.S.; Eljaneid, N.H.E.; Alshaban, E.; Khan, F.A. Three-Step Iterative Methodology for the Solution of Extended Ordered XOR-Inclusion Problems Incorporating Generalized Cayley–Yosida Operators. Mathematics 2025, 13, 1969. https://doi.org/10.3390/math13121969
Filali D, Ali I, Ali MS, Eljaneid NHE, Alshaban E, Khan FA. Three-Step Iterative Methodology for the Solution of Extended Ordered XOR-Inclusion Problems Incorporating Generalized Cayley–Yosida Operators. Mathematics. 2025; 13(12):1969. https://doi.org/10.3390/math13121969
Chicago/Turabian StyleFilali, Doaa, Imran Ali, Montaser Saudi Ali, Nidal H. E. Eljaneid, Esmail Alshaban, and Faizan Ahmad Khan. 2025. "Three-Step Iterative Methodology for the Solution of Extended Ordered XOR-Inclusion Problems Incorporating Generalized Cayley–Yosida Operators" Mathematics 13, no. 12: 1969. https://doi.org/10.3390/math13121969
APA StyleFilali, D., Ali, I., Ali, M. S., Eljaneid, N. H. E., Alshaban, E., & Khan, F. A. (2025). Three-Step Iterative Methodology for the Solution of Extended Ordered XOR-Inclusion Problems Incorporating Generalized Cayley–Yosida Operators. Mathematics, 13(12), 1969. https://doi.org/10.3390/math13121969






