A Forward–Backward–Forward Algorithm for Quasi-Variational Inequalities in the Moving Set Case
Abstract
1. Introduction
Outline of the Paper
2. Preliminaries
3. A Dynamical System of Forward–Backward–Forward Type
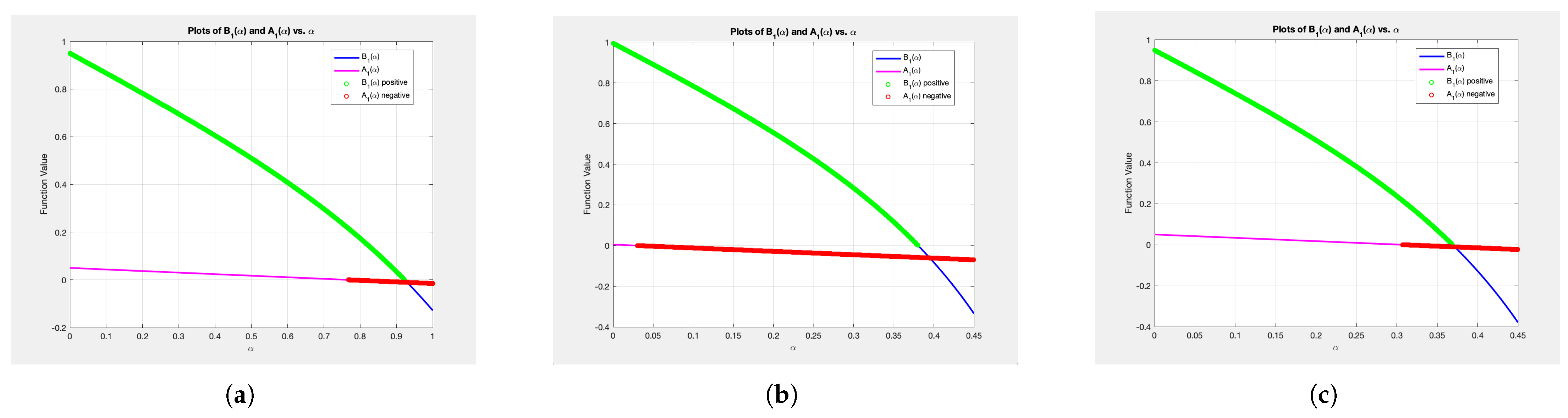
- (a)
- and for Graph 1;
- (b)
- and for Graph 2;
- (c)
- and for Graph 3.
4. A Forward–Backward–Forward Algorithm
| Algorithm 1 Forward-Backward-Forward Algorithm |
| Initialization: Choose the starting point and the step size . Set . |
| Step 1: Compute . |
| If or , then STOP: is a solution. |
| Step 2: Set , update n to and go to Step 1. |
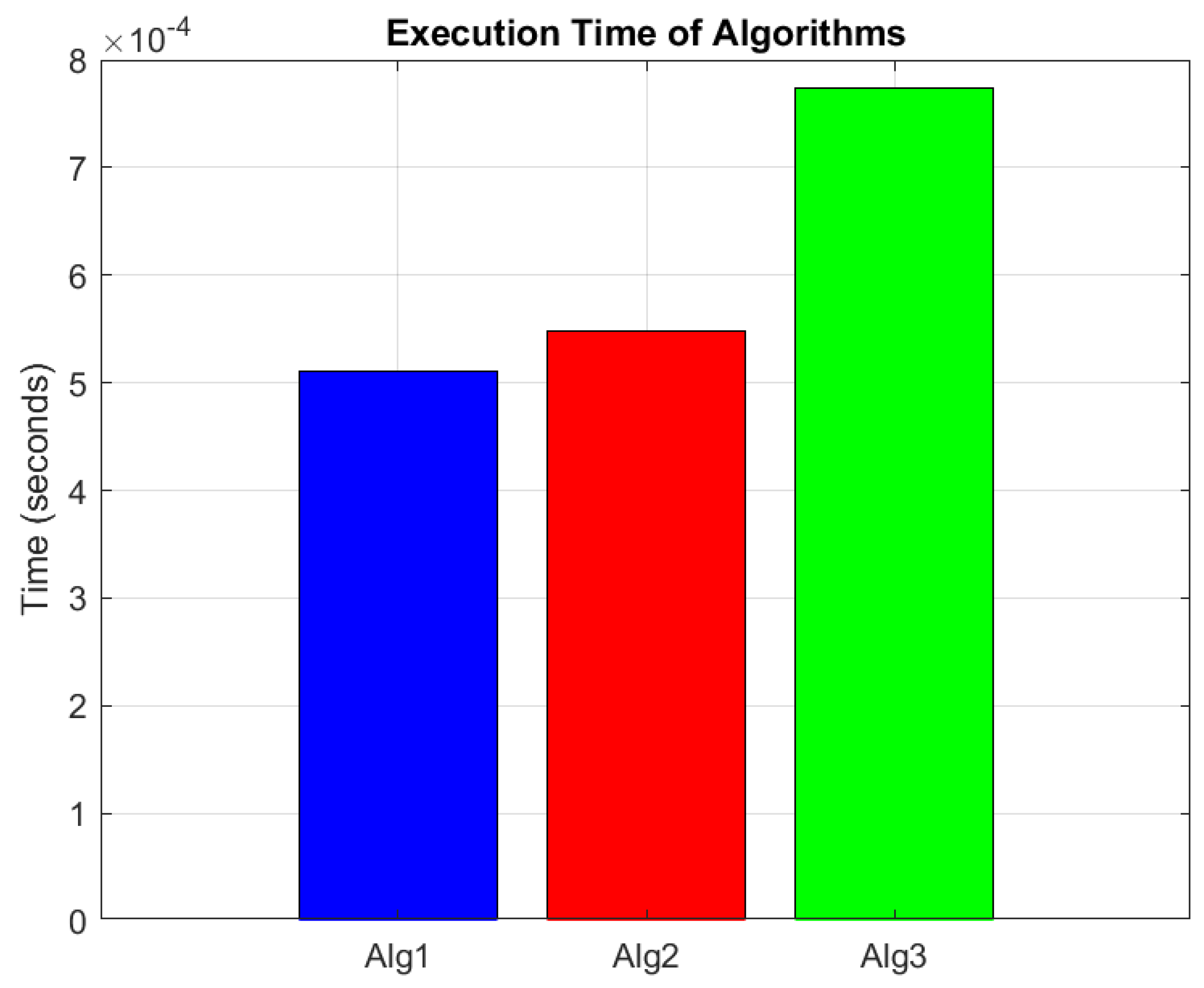
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VI | Variational inequality |
| QVI | Quasi-variational inequality |
References
- Cavazzuti, E.; Pappalardo, M.; Passacantando, M. Nash Equilibria, Variational Inequalities, and Dynamical Systems. J. Optim. Theory Appl. 2002, 114, 491–506. [Google Scholar] [CrossRef]
- Facchinei, F.; Pang, J.S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer: New York, NY, USA, 2003. [Google Scholar]
- Kinderlehrer, D.; Stampacchia, G. An Introduction to Variational Inequalities and Their Applications; Classics in Applied Mathematics (Book 31); Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1987. [Google Scholar]
- Baiocchi, A.; Capelo, A. Variational and Quasi-Variational Inequalities; Wiley: NewYork, NY, USA, 1984. [Google Scholar]
- Bensoussan, A.; Goursat, M.; Lions, J.L. Contrôle impulsionnel et inéquations quasi-variationnelles stationnaries. Comptes Rendus L’Académie Sci. Paris Ser. A 1973, 276, 1279–1284. [Google Scholar]
- Mosco, U. Implicit variational problems and quasi variational inequalities. In Nonlinear Operators and the Calculus of Variations: Summer School Held in Bruxelles, 8–9 September 1975; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1976; Volume 543, pp. 83–156. [Google Scholar]
- Bliemer, M.; Bovy, P. Quasi-variational inequality formulation of the multiclass dynamic traffic assignment problem. Transp. Res. Part B Methodol. 2003, 37, 501–519. [Google Scholar] [CrossRef]
- Harker, P.T. Generalized Nash games and quasivariational inequalities. Eur. J. Oper. Res. 1991, 54, 81–94. [Google Scholar] [CrossRef]
- Kocvara, M.; Outrata, J.V. On a class of quasi-variational inequalities. Optim Methods Softw. 1995, 5, 275–295. [Google Scholar] [CrossRef]
- Pang, J.S.; Fukushima, M. Quasi-variational inequalities, generalized Nash equilibria and Multi-leader-follower games. Comput. Manag. Sci. 2005, 1, 21–56. [Google Scholar] [CrossRef]
- Wei, J.Y.; Smeers, Y. Spatial oligopolistic electricity models with Cournot generators and regulated transmission prices. Oper. Res. 1999, 47, 102–112. [Google Scholar]
- Yao, J.C. The generalized quasi-variational inequality problem with applications. J. Math. Anal. Appl. 1991, 158, 139–160. [Google Scholar] [CrossRef]
- Alizadeh, Z.; Jalilzadeh, A. Convergence Analysis of Non-Strongly-Monotone Stochastic Quasi-Variational Inequalities. arXiv 2024, arXiv:2401.03076. [Google Scholar]
- Antipin, A.S.; Jaćimović, M.; Mijajlović, N. Extragradient method for solving quasivariational inequalities. Optimization 2017, 67, 103–112. [Google Scholar] [CrossRef]
- Antipin, A.S.; Mijajlović, N.; Jaćimović, M. A Second-Order Continuous Method for Solving Quasi-Variational Inequalities. Comput. Math. Math. Phys. 2011, 51, 1856–1863. [Google Scholar] [CrossRef]
- Antipin, A.S.; Mijajlović, N.; Jaćimović, M. A Second-Order Iterative Method for Solving Quasi-Variational Inequalities. Comput. Math. Math. Phys. 2013, 53, 258–264. [Google Scholar] [CrossRef]
- Barbagallo, A. Existence results for a class of quasi-variational inequalities and applications to a noncooperative model. Optimization 2024, 1–22. [Google Scholar] [CrossRef]
- Dey, S.; Reich, S. A dynamical system for solving inverse quasi-variational inequalities. Optimization 2024, 73, 1681–1701. [Google Scholar] [CrossRef]
- Facchinei, F.; Kanzow, C.; Karl, S.; Sagratella, S. The semismooth Newton method for the solution of quasi-variational inequalities. Comput. Optim. Appl. 2015, 62, 85–109. [Google Scholar] [CrossRef]
- Facchinei, F.; Kanzow, C.; Sagratella, S. Solving quasi-variational inequalities via their KKT conditions. Math. Program. 2014, 144, 369–412. [Google Scholar] [CrossRef]
- Lara, F.; Marcavillaca, R.T. Bregman proximal point type algorithms for quasiconvex minimization. Optimization 2022, 73, 497–515. [Google Scholar] [CrossRef]
- Mijajlović, N.; Jaćimović, M. Three-step approximation methods from continuous and discrete perspective for quasi-variational inequalities. Comput. Math. Math. Phys. 2024, 64, 605–613. [Google Scholar] [CrossRef]
- Mijajlović, N.; Jaćimović, M. Strong convergence theorems by an extragradient-like approximation methods for quasi-variational inequalities. Optim. Lett. 2023, 17, 901–916. [Google Scholar] [CrossRef]
- Mijajlović, N.; Jaćimović, M.; Noor, M.A. Gradient-type projection methods for quasi-variational inequalities. Optim. Lett. 2019, 13, 1885–1896. [Google Scholar] [CrossRef]
- Mijajlović, N.; Jaćimović, M. Some Continuous Methods for Solving Quasi-Variational Inequalities. Comput. Math. Math. Phys. 2018, 58, 190–195. [Google Scholar] [CrossRef]
- Mijajlović, N.; Jaćimović, M. Proximal methods for solving quasi-variational inequalities. Comput. Math. Math. Phys. 2015, 55, 1981–1985. [Google Scholar] [CrossRef]
- Nguyen, L.V. An existence result for strongly pseudomonotone quasi-variational inequalities. Ric. Mat. 2023, 72, 803–813. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Qin, X. Some Results on Strongly Pseudomonotone Quasi-Variational Inequalities. Set-Valued Var. Anal. 2020, 28, 239–257. [Google Scholar] [CrossRef]
- Noor, M.A.; Noor, K.I. Some new iterative schemes for solving general quasi variational inequalities. Le Matematiche 2024, 79, 327–370. [Google Scholar]
- Shehu, Y. Linear Convergence for Quasi-Variational Inequalities with Inertial Projection-Type Method. Numer. Funct. Anal. Optim. 2021, 42, 1865–1879. [Google Scholar] [CrossRef]
- Shehu, Y.; Gibali, A.; Sagratella, S. Inertial Projection-Type Methods for Solving Quasi-Variational Inequalities in Real Hilbert Spaces. J. Optim. Theory Appl. 2020, 184, 877–894. [Google Scholar] [CrossRef]
- Yao, Y.; Adamu, A.; Shehu, Y. Strongly convergent inertial forward-backward-forward algorithm without on-line rule for variational inequalities. Acta Math. Sci. 2024, 44, 551–566. [Google Scholar] [CrossRef]
- Yao, Y.; Jolaoso, L.O.; Shehu, Y. C-FISTA type projection algorithm for quasi-variational inequalities. Numer. Algor. 2025, 98, 1781–1798. [Google Scholar] [CrossRef]
- Banert, S.; Bot, R.I. A forward-backward-forward differential equation and its asymptotic properties. J. Convex Anal. 2018, 25, 371–388. [Google Scholar]
- Tseng, P. A modified forward-backward splitting method for maximal monotone mappings. SIAM J. Control Optim. 2000, 38, 431–446. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Shehu, Y.; Jiang, B. Double inertial Forward–Backward–Forward method with adaptive step-size for variational inequalities with quasi-monotonicity. Commun. Nonlinear Sci. Numer. Simul. 2024, 132, 107924. [Google Scholar] [CrossRef]
- Yin, T.C.; Hussain, N. A Forward-Backward-Forward Algorithm for Solving Quasimonotone Variational Inequalities. J. Funct. Spaces 2022, 2022, 7117244. [Google Scholar] [CrossRef]
- Bot, R.I.; Csetnek, E.R.; Vuong, P.T. The Forward-Backward-Forward Method from continuous and discrete perspective for pseudo-monotone variational inequalities in Hilbert spaces. Eur. J. Oper. Res. 2020, 287, 49–60. [Google Scholar] [CrossRef]
- Bot, R.I.; Mertikopoulos, P.; Staudigl, M.; Vuong, P.T. Minibatch forward- backward-forward methods for solving stochastic variational inequalities. Stoch. Syst. 2021, 11, 112–139. [Google Scholar] [CrossRef]
- Izuchukwu, C.; Shehu, Y.; Yao, J.C. New inertial forward-backward type for variational inequalities with Quasi-monotonicity. J. Glob. Optim. 2022, 84, 441–464. [Google Scholar] [CrossRef]
- Attouch, H.; Czarnecki, M.-O.; Peypouquet, J. Coupling Forward-Backward with Penalty Schemes and Parallel Splitting for Constrained Variational Inequalities. SIAM J. Optim. 2011, 21, 1251–1274. [Google Scholar] [CrossRef]
- Ryazantseva, I.P. First-order methods for certain quasi-variational inequalities in a Hilbert space. Comput. Math. Math. Phys. 2007, 47, 183–190. [Google Scholar] [CrossRef]
- Vasil’ev, F.P. Optimization Methods; Faktorial Press: Moscow, Russia, 2002. [Google Scholar]
- Nesterov, Y.; Scrimali, L. Solving strongly monotone variational and quasi-variational inequalities. Discret. Contin. Dyn. Syst. 2011, 31, 1383–1396. [Google Scholar] [CrossRef]
- Noor, M.A.; Oettli, W. On general nonlinear complementarity problems and quasi-equilibria. Le Matematiche 1994, 49, 313–331. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mijajlović, N.; Zajmović, A.; Jaćimović, M. A Forward–Backward–Forward Algorithm for Quasi-Variational Inequalities in the Moving Set Case. Mathematics 2025, 13, 1956. https://doi.org/10.3390/math13121956
Mijajlović N, Zajmović A, Jaćimović M. A Forward–Backward–Forward Algorithm for Quasi-Variational Inequalities in the Moving Set Case. Mathematics. 2025; 13(12):1956. https://doi.org/10.3390/math13121956
Chicago/Turabian StyleMijajlović, Nevena, Ajlan Zajmović, and Milojica Jaćimović. 2025. "A Forward–Backward–Forward Algorithm for Quasi-Variational Inequalities in the Moving Set Case" Mathematics 13, no. 12: 1956. https://doi.org/10.3390/math13121956
APA StyleMijajlović, N., Zajmović, A., & Jaćimović, M. (2025). A Forward–Backward–Forward Algorithm for Quasi-Variational Inequalities in the Moving Set Case. Mathematics, 13(12), 1956. https://doi.org/10.3390/math13121956





