On Exact Non-Traveling Wave Solutions to the Generalized Nonlinear Kadomtsev–Petviashvili Equation in Plasma Physics and Fluid Mechanics

Abstract

The Kadomtsev–Petviashvili (KP) equation serves as a powerful model for investigating various nonlinear wave phenomena in fluid dynamics, plasma physics, optics, and engineering. In this paper, by combining the method of separation of variables with the modified generalized exponential rational function method (mGERFM), abundant explicit exact non-traveling wave solutions for a (3+1)-dimensional generalized form of the equation are constructed. The proposed method utilizes a transformation approach to reduce the original equation to a simpler form. The derived solutions include several arbitrary functions, which enable the construction of a wide variety of exact solutions to the model. These solutions are expressed through diverse functional forms, such as exponential, trigonometric, and Jacobi elliptic functions. To the best of the author’s knowledge, these results are novel and have not been documented in prior studies. This study enhances understanding of wave dynamics in the equation and provides a practical method applicable to other related equations.

1. Introduction

Partial differential equations (PDEs) are essential mathematical tools used to model a wide range of phenomena across various scientific and engineering disciplines [1,2,3,4]. From fluid dynamics and heat transfer to wave propagation and quantum mechanics, PDEs provide the mathematical language to describe how physical quantities evolve in space and time. However, finding exact solutions to these equations is still a major challenge, and developing effective, reliable methods remains a key goal in applied mathematics [5,6,7].

Among all differential equations, nonlinear evolution equations are particularly valuable for modeling real-world systems, where elements constantly affect one another in complicated ways [8,9,10,11,12,13]. In this paper, we study the generalized (3+1)-dimensional nonlinear KP equation, given by [14,15,16,17]

$${\left(u_t+{\sigma }_1{u}_{xxx}+{\sigma }_{2}u{u}_x\right)}_x+{\sigma }_3{u}_{xx}+{\sigma }_4{u}_{yy}+{\sigma }_5{u}_{zz}+{\sigma }_6{u}_{xy}+{\sigma }_7{u}_{xz}+{\sigma }_8{u}_{yz}=0,$$

(1)

where $u=u(x,y,z,t)$ represents the dependent variable, and ${\sigma }_i(i=1,2,\dots ,8)$ are real constants that govern the specific physical context. This equation generalizes several important models in mathematical physics, and by selecting specific values for the constants ${\sigma }_i$, Equation (1) reduces to various well-known classical models, such as

I: For ${\sigma }_1=1$, ${\sigma }_2=-6$, and ${\sigma }_3={\sigma }_4={\sigma }_5={\sigma }_6={\sigma }_7={\sigma }_8=0$, Equation (1) reduces to the classical Korteweg–de Vries (KdV) equation [18,19,20]

$$u_t+u_{xxx}-6u{u}_x=0,$$

(2)

which describes the behavior of shallow water waves in fluid mechanics and is widely used to explain several physical and engineering phenomena.

II: For ${\sigma }_1=1$, ${\sigma }_2=6$, ${\sigma }_4=-\lambda$, and ${\sigma }_3={\sigma }_5={\sigma }_6={\sigma }_7={\sigma }_8=0$, Equation (1) becomes the (2+1)-dimensional KP equation [21,22]

$${\left(u_t+u_{xxx}+6u{u}_x\right)}_x-\lambda u_{yy}=0,$$

(3)

where $\lambda =\pm 1$. Equation (3) is called the KPI equation when $\lambda =1$, and the KPII equation when $\lambda =-1$. The KPII equation is known to be completely integrable.

III: For ${\sigma }_1=1$, ${\sigma }_2=6$, ${\sigma }_4={\sigma }_5=\pm 3$, and ${\sigma }_3={\sigma }_6={\sigma }_7={\sigma }_8=0$, Equation (1) simplifies to the (3+1)-dimensional KP equation [23]

$${\left(u_t+u_{xxx}+6u{u}_x\right)}_x\pm 3\left(u_{yy}+u_{zz}\right)=0,$$

(4)

which describes three-dimensional solitons in weakly dispersive media, including fluid mechanics and plasma physics. Equation (4) is referred to as the (3+1)-dimensional KPI equation when the “−” sign is used, and the (3+1)-dimensional KPII equation when the “+” sign is used.

In recent years, many researchers have expressed significant interest in developing methods to derive exact wave solutions for the (3+1)-dimensional evolution Equation (1). Using generalized Bell’s polynomials and multidimensional Riemann theta functions, the authors construct multiperiodic periodic waves, including cnoidal waves (one-periodic) and two-periodic waves with two-dimensional surface patterns [14]. They also analyze the asymptotic behavior of these waves and establish a rigorous connection between periodic waves and soliton solutions through a limiting procedure. The work of [15] investigates Equation (1) using the Hirota method, where the authors derive breather-wave, lump-wave, and lump wave-soliton solutions, analyzing the effects of dispersion, nonlinearity, and perturbed parameters on dark breather and lump waves. The study also explores fusion and fission phenomena between lump waves and solitons under specific conditions, providing insights into nonlinear wave interactions in fluid dynamics. In [16], the authors derive mixed lump-stripe waves, bright and dark mixed rogue wave-stripe solutions, and dark rogue waves to the model using symbolic computation. The study explores fission and fusion phenomena between lumps and stripe waves, as well as interactions between rogue waves and stripe waves, analyzing the effects of dispersion, nonlinearity, and perturbed parameters. Graphical representations illustrate the dynamic behaviors of these waves, including the merging of stripe waves and the influence of various parameters on wave interactions. This paper of [17] investigates the model using symbolic computation and the Hirota method, where the authors derive mixed interaction solutions, including local waves, solitary waves, breather waves, exploding waves, and periodic waves. The study explores the effects of dispersion, nonlinearity, and other parameters on wave interactions, demonstrating how localized waves can amplify solitary waves and how parameter adjustments stabilize breather waves while also introducing new exploding and periodic wave patterns. In their study, the authors of [24] systematically investigate a (3+1)-dimensional generalized KP equation using the Hirota bilinear method. They derive explicit N-soliton solutions as well as bright and dark multi-soliton solutions. The work further explores various breather solutions and hybrid solutions, including the construction of bright and dark lump solutions and line rogue wave solutions through a long wave limit analysis.

The search for exact solutions to Equation (1) is a challenging but crucial endeavor. Such solutions not only provide a deeper understanding of the underlying physics but also serve as benchmarks for numerical methods and can be used to construct more complex solutions. This paper presents a novel approach to derive explicit non-traveling wave solutions to Equation (1). We combine a generalized variable separation method [25,26,27,28,29] with the mGERFM, which has been proposed by Ghanbari [30]. The variable separation method allows us to reduce the original PDE to a set of lower-dimensional equations, while the mGERFM provides a powerful tool for solving these reduced equations. This combined approach enables us to construct a variety of new explicit solutions, expressed in terms of elementary and special functions. The structure of the paper is as follows: In Section 2, we detail the application of the generalized variable separation technique, leading to a reduced equation. Section 3 then outlines the use of the mGERFM to solve this reduced equation and derive explicit solutions. Finally, we present a conclusion summarizing our findings and outlining potential future directions.

2. The First Reduction Procedure for Equation (1)

In this section, we explore a generalized variable separation method that allows us to derive non-traveling exact solutions to Equation (1) within the specified framework outlined below.

Theorem 1.

In accordance with the specified transformation

$$u(x,y,z,t)=\psi (\xi ,t)+q(y,z,t),$$

(5)

where $\xi =\alpha x+\Theta (y,z,t)$, the function $q(y,z,t)$ is defined as follows:

$$q(y,z,t)=-{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.$$

(6)

Moreover, the function $\Theta (y,z,t)$ can be expressed in two forms:

$${\Theta }_1(y,z,t)=f_1\left(\left({\displaystyle \frac{{\sigma }_8}{2\sqrt{{\sigma }_8^2-4{\sigma }_4{\sigma }_5}}}+{\displaystyle \frac{1}{2}}\right)y-{\displaystyle \frac{z{\sigma }_4}{\sqrt{{\sigma }_8^2-4{\sigma }_4{\sigma }_5}}},t\right)+f_2\left(t\right)\left({\displaystyle \frac{\left(-{\sigma }_8+\sqrt{{\sigma }_8^2-4{\sigma }_4{\sigma }_5}\right)}{2{\sigma }_4}}y+z\right)+f_3\left(t\right),$$

(7)

or can alternatively be represented as

$${\Theta }_2(y,z,t)=f_3\left(t\right)y+f_4\left(t\right)z+f_5\left(t\right),$$

(8)

where $f_1,\dots ,f_6$ are arbitrary functions. Under this transformation, Equation (1) is subsequently transformed into the following new partial differential equation:

$${\psi }_t(\xi ,t)+{\alpha }^3{\sigma }_1{\psi }_{\xi \xi \xi }(\xi ,t)+\alpha {\sigma }_2\psi (\xi ,t){\psi }_{\xi }(\xi ,t)=0.$$

(9)

Proof. 

First, by inserting the symbolic structure Equation (5) into Equation (1), it is simplified as

$$\begin{array}{c}\hfill {\varrho }_1{\psi }_{\xi }+{\varrho }_2{\psi }_{\xi \xi }+{\varrho }_3+\alpha {\psi }_{\xi t}+{\alpha }^4{\sigma }_1{\psi }_{\xi \xi \xi \xi }+{\alpha }^2{\sigma }_2\left(\psi {\psi }_{\xi \xi }+{\psi }_{\xi }^2\right)=0,\end{array}$$

(10)

where

$$\begin{array}{cc}\hfill {\varrho }_1& ={\sigma }_4{\Theta }_{y,y}+{\sigma }_8{\Theta }_{y,z}+{\sigma }_5{\Theta }_{z,z},\hfill \\ \hfill {\varrho }_2& =q{\alpha }^2{\sigma }_2+{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3,\hfill \\ \hfill {\varrho }_3& ={\sigma }_4{q}_{y,y}+{\sigma }_5{q}_{z,z}+{\sigma }_8{q}_{y,z}.\hfill \end{array}$$

(11)

Now, our primary goal is to identify the necessary conditions for transforming Equation (10) into a simplified form that admits exact solutions. For this purpose, we focus on the situation where ${\varrho }_1,{\varrho }_2$, and ${\varrho }_3$ all vanish in Equation (10). Using Maple to solve the coupled PDE system for $\Theta (y,z,t)$ and $q(y,z,t)$ together, we find two possible solutions for $\Theta (y,z,t)$ as

$${\Theta }_1\left(y,z,t\right)=f_1\left(\left({\displaystyle \frac{{\sigma }_8}{2\sqrt{{\sigma }_8^2-4{\sigma }_4{\sigma }_5}}}+{\displaystyle \frac{1}{2}}\right)y-{\displaystyle \frac{z{\sigma }_4}{\sqrt{{\sigma }_8^2-4{\sigma }_4{\sigma }_5}}},t\right)+f_2\left(t\right)\left({\displaystyle \frac{\left(-{\sigma }_8+\sqrt{{\sigma }_8^2-4{\sigma }_4{\sigma }_5}\right)}{2{\sigma }_4}}y+z\right)+f_3\left(t\right),$$

(12)

or,

$${\Theta }_2\left(y,z,t\right)=f_4\left(t\right)y+f_5\left(t\right)z+f_6\left(t\right),$$

(13)

where $f_1$ is an arbitrary function of two variables, and $f_2$ through $f_6$ are free functions of the single variable t.

At the same time, the explicit expression for $q\left(y,z,t\right)$ is derived as follows:

$$q\left(y,z,t\right)=-{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.$$

(14)

Considering these results, Equation (10) is simplified as

$${\alpha }^3{\sigma }_1{\psi }_{\xi \xi \xi \xi }+\alpha {\sigma }_2\left({\psi }_{\xi \xi }\psi +{\psi }_{\xi }^2\right)+{\psi }_{\xi t}=0.$$

(15)

By integrating Equation (15) with respect to $\xi$ and removing the integration constant, the desired result in Equation (9) is obtained. □

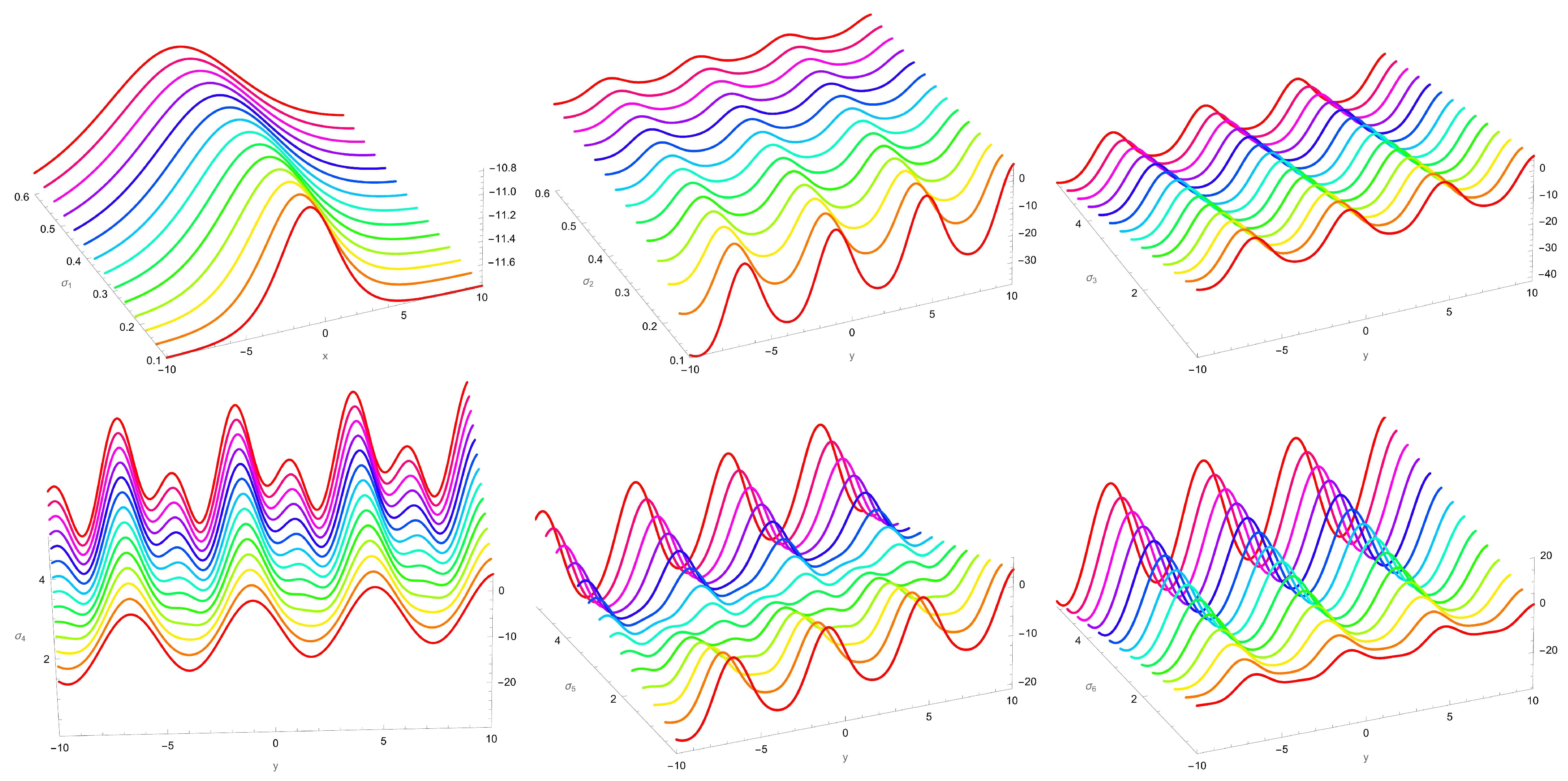
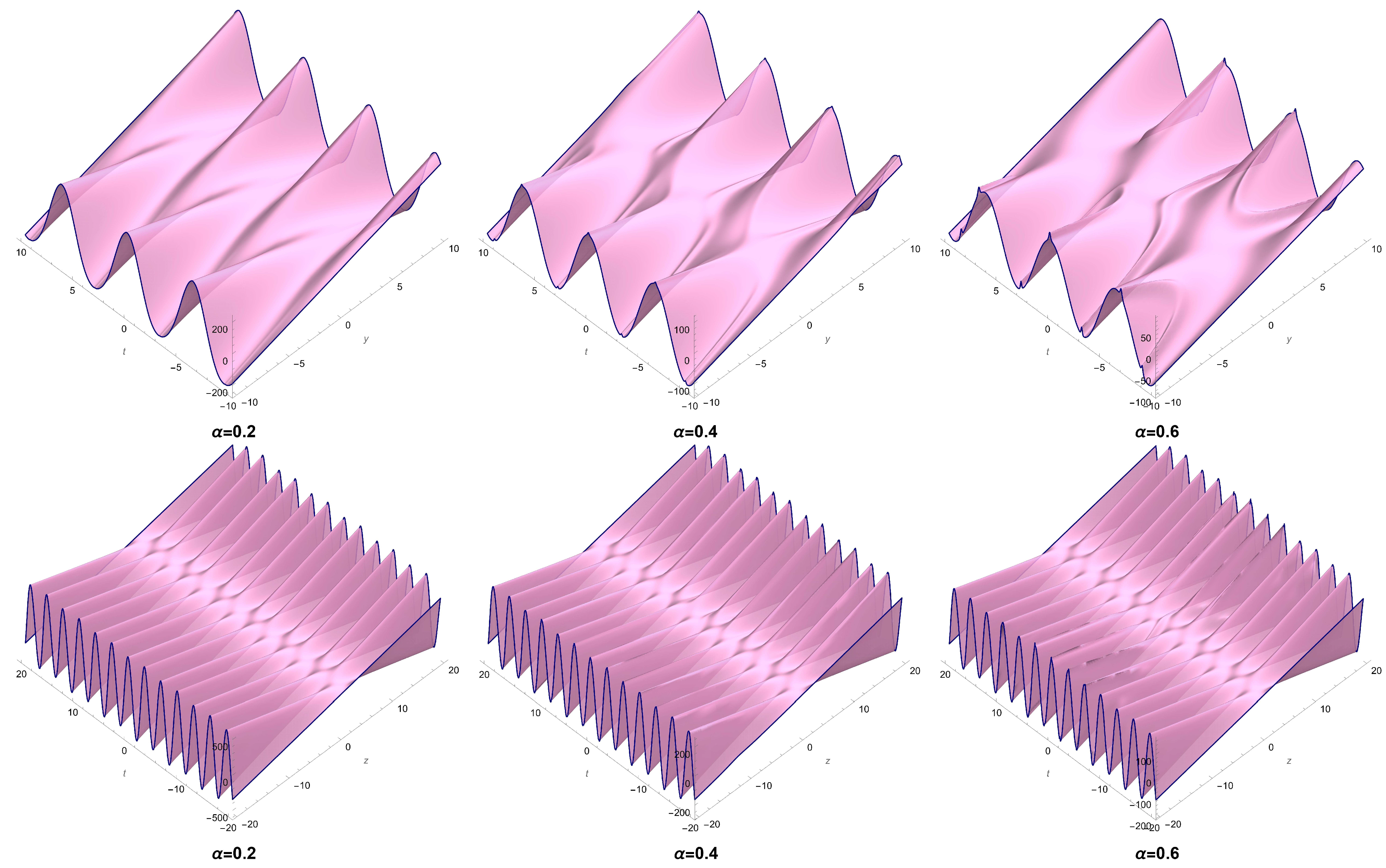
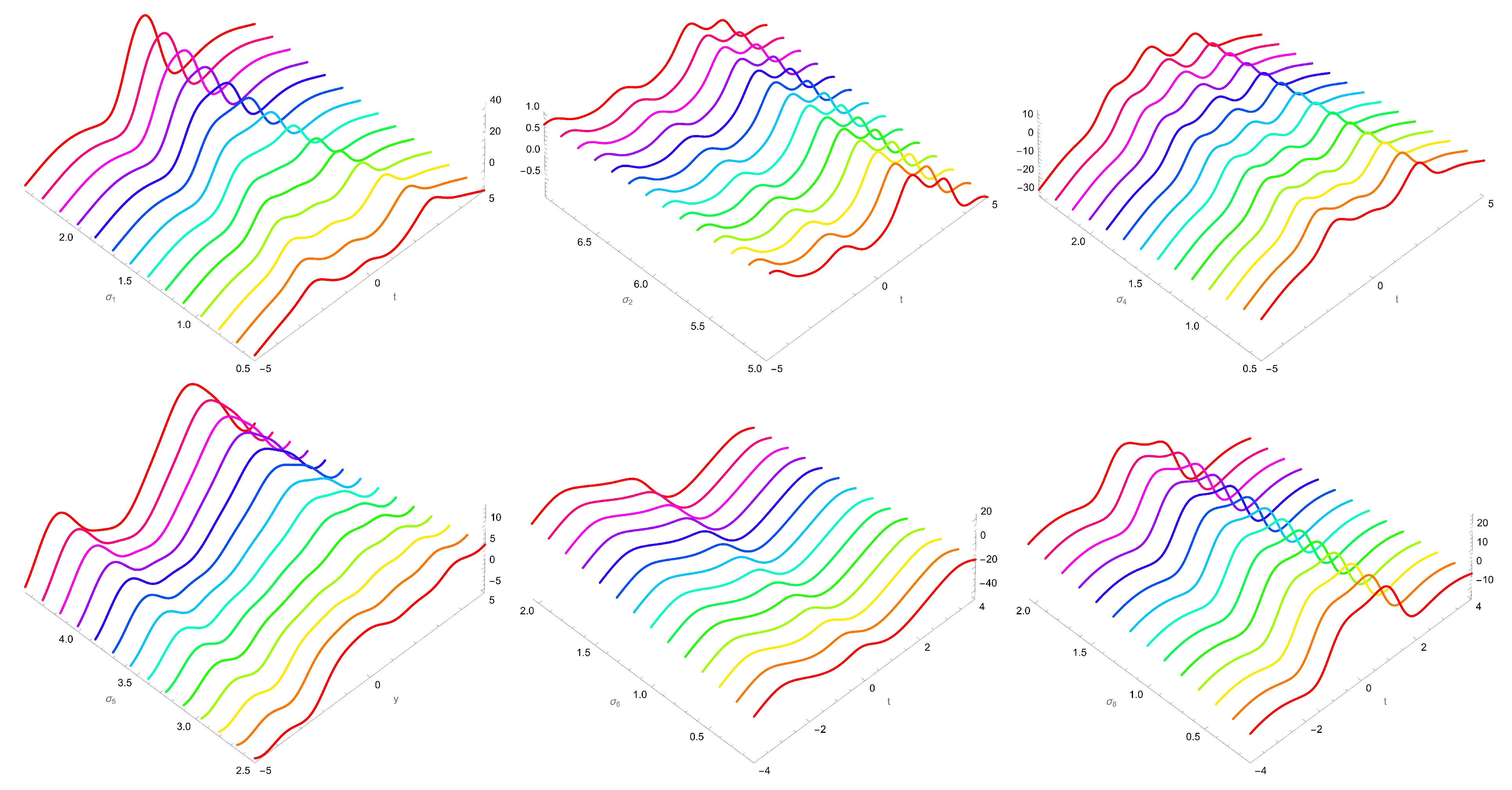
2.1. The Soliton Solutions for Equation (9)

To analyze Equation (9) with the mGERFM technique, we introduce a wave ansatz of the form $\psi \left(\xi ,t\right)=\phi \left(\vartheta \right)$, along with

$$\vartheta =\kappa \xi +\omega t.$$

(16)

Under this transformation, the equation becomes

$${\kappa }^3{\alpha }^3{\sigma }_1{\phi }^{\prime \prime \prime }\left(\vartheta \right)+\alpha \kappa {\sigma }_2{\phi }^{\prime }\left(\vartheta \right)\phi \left(\vartheta \right)+\omega {\phi }^{\prime }\left(\vartheta \right)=0.$$

(17)

After integrating Equation (17) in $\vartheta$ and performing algebraic simplifications, including elimination of the integration constant, we arrive at

$$2{\alpha }^3{\kappa }^3{\sigma }_1{\phi }^{\prime \prime }\left(\vartheta \right)+\alpha \kappa {\sigma }_2{\phi }^2\left(\vartheta \right)+2\omega \phi \left(\vartheta \right)=0.$$

(18)

In the subsequent parts, we investigate two effective analytical methods for solving Equation (18). Furthermore, it is worth noting that certain particular solutions to either Equation (9) or Equation (18) can also be obtained via direct integration.

Our solution approach for Equation (18) begins with applying an analytical technique called the mGERFM. Based on mGERFM, the solution of the equation is expressed in the following symbolic form:

$$\phi \left(\vartheta \right)={\epsilon }_0+\sum _{j=1}^{\mathbf{n}}{\epsilon }_j{\left({\displaystyle \frac{{\Lambda }^{\prime }\left(\vartheta \right)}{\Lambda \left(\vartheta \right)}}\right)}^j,$$

(19)

where

$$\Lambda \left(\vartheta \right)={\displaystyle \frac{{\lambda }_1{\mathrm{e}}^{{\tau }_1\vartheta }+{\lambda }_2{\mathrm{e}}^{{\tau }_2\vartheta }}{{\lambda }_3{\mathrm{e}}^{{\tau }_3\vartheta }+{\lambda }_4{\mathrm{e}}^{{\tau }_4\vartheta }}},$$

(20)

or,

$$\Lambda \left(\vartheta \right)={\displaystyle \frac{{\lambda }_1\mathbf{CN}\left({\tau }_1\vartheta \right|\ell )+{\lambda }_2\mathbf{SN}\left({\tau }_2\vartheta \right|\ell )}{{\lambda }_3\mathbf{CN}\left({\tau }_3\vartheta \right|\ell )+{\lambda }_4\mathbf{SN}\left({\tau }_4\vartheta \right|\ell )}}.$$

(21)

The value of $\mathbf{n}$ in Equation (19) is determined by the balance rules specified in Equation (18). Moreover, $\mathbf{SN}$ and $\mathbf{CN}$ are Jacobi elliptic functions of modulus ℓ.

From Equation (18), we obtain the relation $2\mathbf{n}=\mathbf{n}+2$, which simplifies to $\mathbf{n}=2$. Consequently, Equation (19) reduces to

$$\phi \left(\vartheta \right)={\epsilon }_0+{\epsilon }_1\left({\displaystyle \frac{{\Lambda }^{\prime }\left(\vartheta \right)}{\Lambda \left(\vartheta \right)}}\right)+{\epsilon }_2{\left({\displaystyle \frac{{\Lambda }^{\prime }\left(\vartheta \right)}{\Lambda \left(\vartheta \right)}}\right)}^2.$$

(22)

We organize our findings according to applications of two symbolic structures (20) and (21) applied to Equation (22) via mGERFM.

By incorporating Equations (20) and (22) in Equation (18), we obtain the following solutions for the unknown parameters:

• Set 1: Letting $[{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4]=[1,-1,2,0]$ and $[{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4]=[2,0,0,0]$ in Equation (20) gives

  $$\Lambda \left(\vartheta \right)={\mathrm{e}}^{\vartheta }sinh\vartheta .$$

  (23)
• Case 1-1: In this case, the rest of the parameters can be attained as

  $$\begin{array}{c}\hfill \omega =4{\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0=-{\displaystyle \frac{8{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_1={\displaystyle \frac{24{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

  (24)

  where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (23), we have

$$\phi \left(\vartheta \right)=-{\displaystyle \frac{8{\kappa }^2{\alpha }^2{\sigma }_1\left({\mathrm{e}}^{4\vartheta }+4{\mathrm{e}}^{2\vartheta }+1\right)}{{\sigma }_2{\left({\mathrm{e}}^{2\vartheta }-1\right)}^2}}.$$

Combining this solution with Equation (16), the wave solution for Equation (18) is constructed as

$${\psi }_1\left(\xi ,t\right)=-{\displaystyle \frac{8{\kappa }^2{\alpha }^2{\sigma }_1\left({\mathrm{e}}^{4\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}+4{\mathrm{e}}^{2\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}+1\right)}{{\sigma }_2{\left({\mathrm{e}}^{2\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}-1\right)}^2}}.$$

(25)

As a result, from Equations (5) and (25), we can derive a non-soliton solution for Equation (1) as

$$\begin{array}{cc}\hfill u_1& =-{\displaystyle \frac{8{\kappa }^2{\alpha }^2{\sigma }_1\left({\mathrm{e}}^{4\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}+4{\mathrm{e}}^{2\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}+1\right)}{{\sigma }_2{\left({\mathrm{e}}^{2\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}-1\right)}^2}}\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}},\hfill \end{array}$$

(26)

where the function $\Theta \left(y,z,t\right)$ can be taken to one of the two forms introduced in Equation (12) or (13). The same assumption regarding $\Theta \left(y,z,t\right)$ is applied consistently throughout this subsection of the paper.

• Case 1-2: In this case, the rest of the parameters can be attained as

  $$\begin{array}{c}\hfill \omega =-4{\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0=0,{ϵ}_1={\displaystyle \frac{24{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

  (27)

  where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (23), we have

$$\phi \left(\vartheta \right)=-{\displaystyle \frac{48{\kappa }^2{\alpha }^2{\sigma }_1{\mathrm{e}}^{2\vartheta }}{{\sigma }_2{\left({\mathrm{e}}^{2\vartheta }-1\right)}^2}}.$$

Combining this solution with Equation (16), the wave solution for Equation (18) is expressed as

$${\psi }_2\left(\xi ,t\right)=-{\displaystyle \frac{48{\kappa }^2{\alpha }^2{\sigma }_1{\mathrm{e}}^{2\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}}{{\sigma }_2{\left({\mathrm{e}}^{2\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}-1\right)}^2}}.$$

(28)

As a result, using Equations (5) and (28), we can derive a non-soliton solution for Equation (1) as

$$\begin{array}{cc}\hfill u_2& =-{\displaystyle \frac{48{\kappa }^2{\alpha }^2{\sigma }_1{\mathrm{e}}^{2\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}}{{\sigma }_2{\left({\mathrm{e}}^{2\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}-1\right)}^2}}-{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(29)

Set 2: Letting $[{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4]=[\dot{\iota },-\dot{\iota },2,0]$ and $[{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4]=[-1-\dot{\iota },-1+\dot{\iota },0,0]$ in Equation (20) gives

$$\Lambda \left(\vartheta \right)={\mathrm{e}}^{-\vartheta }sin\vartheta .$$

(30)

Case 2-1: In this case, the remaining parameters can be obtained as follows:

$$\begin{array}{c}\hfill \omega =-4{\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0=-{\displaystyle \frac{16{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_1=-{\displaystyle \frac{24{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

(31)

where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (30), one achieves

$$\phi \left(\vartheta \right)=-{\displaystyle \frac{4{\kappa }^2{\alpha }^2{\sigma }_1}{{\sigma }_2}}\left(1+3{cot}^2\vartheta \right).$$

Combining this solution with Equation (16), the wave solution for Equation (18) can be formulated as

$${\psi }_3\left(\xi ,t\right)=-{\displaystyle \frac{4{\kappa }^2{\alpha }^2{\sigma }_1}{{\sigma }_2}}\left(1+3{cot}^2\left(\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)\right)\right).$$

(32)

Hence, using Equations (5) and (32), a non-soliton solution for Equation (1) can be established in the following manner:

$$\begin{array}{cc}\hfill u_3& =-{\displaystyle \frac{4{\kappa }^2{\alpha }^2{\sigma }_1}{{\sigma }_2}}\left(1+3{cot}^2\left(\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)\right)\right)\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(33)

Case 2-2: In this case, the remaining parameters can be obtained as follows:

$$\begin{array}{c}\hfill \omega =4{\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0=-{\displaystyle \frac{24{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_1=-{\displaystyle \frac{24{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

(34)

where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (30), one achieves

$$\phi \left(\vartheta \right)=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}{csc}^2\vartheta .$$

Combining this solution with Equation (16), the wave solution for Equation (18) is expressed as

$${\psi }_4\left(\xi ,t\right)=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}{csc}^2\left(\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)\right).$$

(35)

Hence, using Equations (5) and (35), a non-soliton solution for Equation (1) can be established in the following manner:

$$\begin{array}{cc}\hfill u_4& =-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}{csc}^2\left(\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)\right)\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(36)

Set 3: Letting $[{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4]=[-\dot{\iota },\dot{\iota },1,1]$ and $[{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4]=[2\dot{\iota },0,2\dot{\iota },0]$ in Equation (20) gives

$$\Lambda \left(\vartheta \right)=tan\vartheta .$$

(37)

Case 3-1: In this case, the rest of the parameters can be attained as

$$\begin{array}{c}\hfill \omega =16{\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0={ϵ}_1=0,{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

(38)

where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (37), one gets

$$\phi \left(\vartheta \right)=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}{sec}^2\vartheta {csc}^2\vartheta .$$

Combining this solution with Equation (16), the wave solution for Equation (18) can be formulated as

$${\psi }_5\left(\xi ,t\right)=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}{sec}^2\left(\kappa \left(16{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)\right){csc}^2\left(\kappa \left(16{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)\right).$$

(39)

Consequently, from Equations (5) and (39), a non-soliton solution for Equation (1) can be established in the following manner:

$$\begin{array}{cc}\hfill u_5& =-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1\left({sec}^2\left(\kappa \left(16{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)\right){csc}^2\left(\kappa \left(16{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)\right)\right)}{{\sigma }_2}}\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(40)

Case 3-2: In this case, the rest of the parameters can be attained as

$$\begin{array}{c}\hfill \omega =-16{\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0={\displaystyle \frac{32{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_1=0,{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

(41)

where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (37), one gets

$$\phi \left(\vartheta \right)=-{\displaystyle \frac{4{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}\left(3{cot}^2\vartheta +3{tan}^2\vartheta -2\right).$$

Combining this solution with Equation (16), the wave solution for Equation (18) can be formulated as

$${\psi }_6\left(\xi ,t\right)=-{\displaystyle \frac{4{\alpha }^2{\kappa }^2{\sigma }_1\left(3{cot}^2\left(\kappa \left(-16{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)\right)+3{tan}^2\left(\kappa \left(-16{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)\right)-2\right)}{{\sigma }_2}}.$$

(42)

Consequently, from Equations (5) and (42), a non-soliton solution for Equation (1) can be established in the following manner:

$$\begin{array}{cc}\hfill u_6& =-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1\left(3{cot}^2\left(\kappa \left(-16{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)\right)+3{tan}^2\left(\kappa \left(-16{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)\right)-2\right)}{{\sigma }_2}}\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(43)

Set 4: Letting $[{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4]=[2,0,1,1]$ and $[{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4]=[2,0,2,0]$ in Equation (20) gives

$$\Lambda \left(\vartheta \right)={\mathrm{e}}^{\vartheta }\mathrm{sech}\vartheta .$$

(44)

Case 4-1: In this case, the remaining parameters can be obtained as follows:

$$\begin{array}{c}\hfill \omega =4{\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0=-{\displaystyle \frac{8{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_1={\displaystyle \frac{24{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

(45)

where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (44), we obtain

$$\phi \left(\vartheta \right)=-{\displaystyle \frac{8{\alpha }^2{\kappa }^2{\sigma }_1\left({\mathrm{e}}^{4\vartheta }-4{\mathrm{e}}^{2\vartheta }+1\right)}{{\sigma }_2{\left({\mathrm{e}}^{2\vartheta }+1\right)}^2}}.$$

Combining this solution with Equation (16), the wave solution for Equation (18) is expressed as

$${\psi }_7\left(\xi ,t\right)=-{\displaystyle \frac{8{\alpha }^2{\kappa }^2{\sigma }_1\left({\mathrm{e}}^{4\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}-4{\mathrm{e}}^{2\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}+1\right)}{{\sigma }_2{\left({\mathrm{e}}^{2\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}+1\right)}^2}}.$$

(46)

Hence, from Equations (5) and (46), a non-soliton solution for Equation (1) can be established in the following manner:

$$\begin{array}{cc}\hfill u_7& =-{\displaystyle \frac{8{\alpha }^2{\kappa }^2{\sigma }_1\left({\mathrm{e}}^{4\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}-4{\mathrm{e}}^{2\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}+1\right)}{{\sigma }_2{\left({\mathrm{e}}^{2\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}+1\right)}^2}}\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(47)

To analyze solution $u_7(x,y,z,t)$, we first utilize the structure introduced in Equation (12) for the existing function $\Theta (y,z,t)$. To this end, let us consider the functions $f_1(x,t)$, $f_2\left(t\right)$, and $f_3\left(t\right)$, such as

$$\begin{array}{c}\hfill f_1(x,t)=sin\left(x\right)+cos\left(t\right),f_2\left(t\right)=sin\left(0.5t\right),f_3\left(t\right)=sin\left(t\right).\end{array}$$

(48)

In this case, the solution describes a system with periodic and harmonic interactions. The term $f_1(x,t)$ introduces spatial and temporal oscillations, representing wave-like behavior in both space and time. The function $f_2\left(t\right)$ adds a slower temporal modulation, while $f_3\left(t\right)$ contributes a standard sinusoidal variation. Together, these functions create resonant and quasi-periodic dynamics, making $u_7$ suitable for modeling systems with standing waves, harmonic oscillators, or wave interference phenomena, where periodic interactions and frequency mixing are dominant features. Several dynamics of solution (47) for some values of $\alpha$ across different directions are displayed in Figure 1. In this plot, we considered Equation (48) in Equation (12) along with taking ${\sigma }_1=0.6,{\sigma }_2=0.2,{\sigma }_3=0.5,{\sigma }_4=0.7,{\sigma }_5=0.1,{\sigma }_6=0.1,{\sigma }_7=0.2,{\sigma }_8=1.2$, and $\kappa =1.2$.

Now, let us consider the solution $u_7$ using the structure introduced in Equation (13). To this end, we examine the functions $f_4(x,t)$, $f_5\left(t\right)$, and $f_6\left(t\right)$, defined as follows:

$$\begin{array}{cccc}\hfill f_4\left(t\right)& =sin\left(t\right),f_5\left(t\right)\hfill & \hfill =sin\left(t\right)cos\left(t\right),f_6\left(t\right)& =cos\left(t\right).\hfill \end{array}$$

(49)

Upon these assumptions, we obtain a specific solution to the (3+1)-dimensional nonlinear evolution equation. This particular solution represents a non-traveling wave, meaning its profile does not propagate with a constant speed. Instead, the wave’s shape evolves and oscillates in place, influenced by the interplay of the sinusoidal functions in both space and time. The spatial component, $sin\left(x\right)$, suggests a periodic variation along the x-axis, while the time-dependent terms, $sin\left(t\right)cos\left(t\right)$ and $cos\left(t\right)$, introduce temporal oscillations in the wave’s amplitude and overall structure. Physically, this could correspond to a wave whose height or intensity fluctuates rhythmically at a fixed location, perhaps driven by some external periodic force or internal resonance within the system. The specific form of these oscillations, determined by the chosen functions, reveals the intricate balance between the nonlinear, dispersive, and perturbed effects captured by the original evolution equation. Several dynamics of solution (47) for some values of $\alpha$ across different directions are displayed in Figure 2. In this plot, we consider Equation (48) in Equation (12) along with keeping the other constants.

Now, we analyze the sensitivity of the solution (47), based on the selection of Equation (48) with respect to different ${\sigma }_i$’s together with $\alpha =0.6,\kappa =1.2$ in Figure 3.

• Case 4-2: In this case, the remaining parameters can be obtained as follows:

  $$\begin{array}{c}\hfill \omega =-4{\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0=0,{ϵ}_1={\displaystyle \frac{24{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

  (50)

  where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (44), we acquire

$$\phi \left(\vartheta \right)={\displaystyle \frac{48{\alpha }^2{\kappa }^2{\sigma }_1{\mathrm{e}}^{2\vartheta }}{{\sigma }_2{\left({\mathrm{e}}^{2\vartheta }+1\right)}^2}}.$$

Combining this solution with Equation (16), the wave solution for Equation (18) can be formulated as

$${\psi }_8\left(\xi ,t\right)={\displaystyle \frac{48{\alpha }^2{\kappa }^2{\sigma }_1{\mathrm{e}}^{2\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}}{{\sigma }_2{\left({\mathrm{e}}^{2\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}+1\right)}^2}}.$$

(51)

Hence, from Equations (5) and (51), a non-soliton solution for Equation (1) can be established in the following manner:

$$\begin{array}{cc}\hfill u_8& ={\displaystyle \frac{48{\alpha }^2{\kappa }^2{\sigma }_1{\mathrm{e}}^{2\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}}{{\sigma }_2{\left({\mathrm{e}}^{2\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}+1\right)}^2}}-{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(52)

The solution $u_8$ exhibits rich dynamic properties due to its dependence on the function $\Theta (y,z,t)$ and the interplay of exponential and hyperbolic terms. The first term in $u_8$ represents a soliton-like structure modulated by the exponential function ${\mathrm{e}}^{2\kappa (-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta (y,z,t))}$, which governs the wave’s amplitude and propagation. The denominator ${\left({\mathrm{e}}^{2\kappa (·)}+1\right)}^2$ ensures a localized, bell-shaped profile, typical of solitary waves. The second term introduces nonlinear interactions through partial derivatives of $\Theta (y,z,t)$, such as ${\Theta }_y$, ${\Theta }_z$, and ${\Theta }_t$, which influence the wave’s dispersion and phase dynamics. By incorporating the functions

$$\begin{array}{c}\hfill f_1(x,t)=sin\left(x\right)tanh\left(t\right),f_2\left(t\right)=tanh\left(t\right),f_3\left(t\right)=sin\left(t\right),\end{array}$$

(53)

the solution gains additional temporal and spatial modulation. For instance, $tanh\left(t\right)$ introduces a smooth transition between states, while $sin\left(t\right)$ and $sin\left(x\right)$ introduce periodic oscillations. These features make $u_8$ a versatile solution capable of modeling complex wave phenomena, including wavefront interactions, amplitude modulation, and phase transitions in nonlinear systems. The described dynamic properties of solution (47) for some values of $\alpha$ across different directions are displayed in Figure 4. In this plot, we consider Equation (53) in Equation (12), along with the parameter values ${\sigma }_1=0.2$, ${\sigma }_2=0.3$, ${\sigma }_3=0.3$, ${\sigma }_4=0.2$, ${\sigma }_5=0.1$, ${\sigma }_6=0.2$, ${\sigma }_7=0.2$, ${\sigma }_8=0.8$, and $\kappa =1.2$.

Now, taking

$$\begin{array}{c}\hfill f_4\left(t\right)=0.5sin\left(2t\right),f_5\left(t\right)=1.2e^{-0.3t},f_6\left(t\right)=0.4t^2.\end{array}$$

(54)

into account in Equation (13), the solution $u_8$ represents a nonlinear wave with dynamic behavior influenced by the function ${\Theta }_2(y,z,t)$. The term $f_4\left(t\right)=0.5sin\left(2t\right)$ introduces periodic oscillations in the y-direction, modeling a wave with a frequency of 2 and an amplitude of $0.5$. The term $f_5\left(t\right)=1.2e^{-0.3t}$ describes an exponentially decaying component in the z-direction, representing a damping effect with a decay rate of $0.3$. Finally, $f_6\left(t\right)=0.4t^2$ introduces a quadratic growth in time, capturing a nonlinear temporal evolution. Together, these functions create a solution $u_8$ that exhibits a combination of periodic, decaying, and growing behaviors, making it suitable for modeling complex physical phenomena such as damped oscillatory waves, nonlinear wavefront propagation, or wave interactions in dissipative media. The interplay of these terms highlights the rich dynamics of the system, including amplitude modulation, dispersion, and energy dissipation.

Several dynamics of solution (52) for some values of $\alpha$ across different directions are displayed in Figure 5. In this plot, we consider Equation (54) in Equation (13) along with keeping the other constants.

In Figure 6, we study the sensitivity of the solution (52), based on the selection of Equation (53) with respect to different ${\sigma }_i$’s together with $\alpha =0.4,\kappa =0.9$.

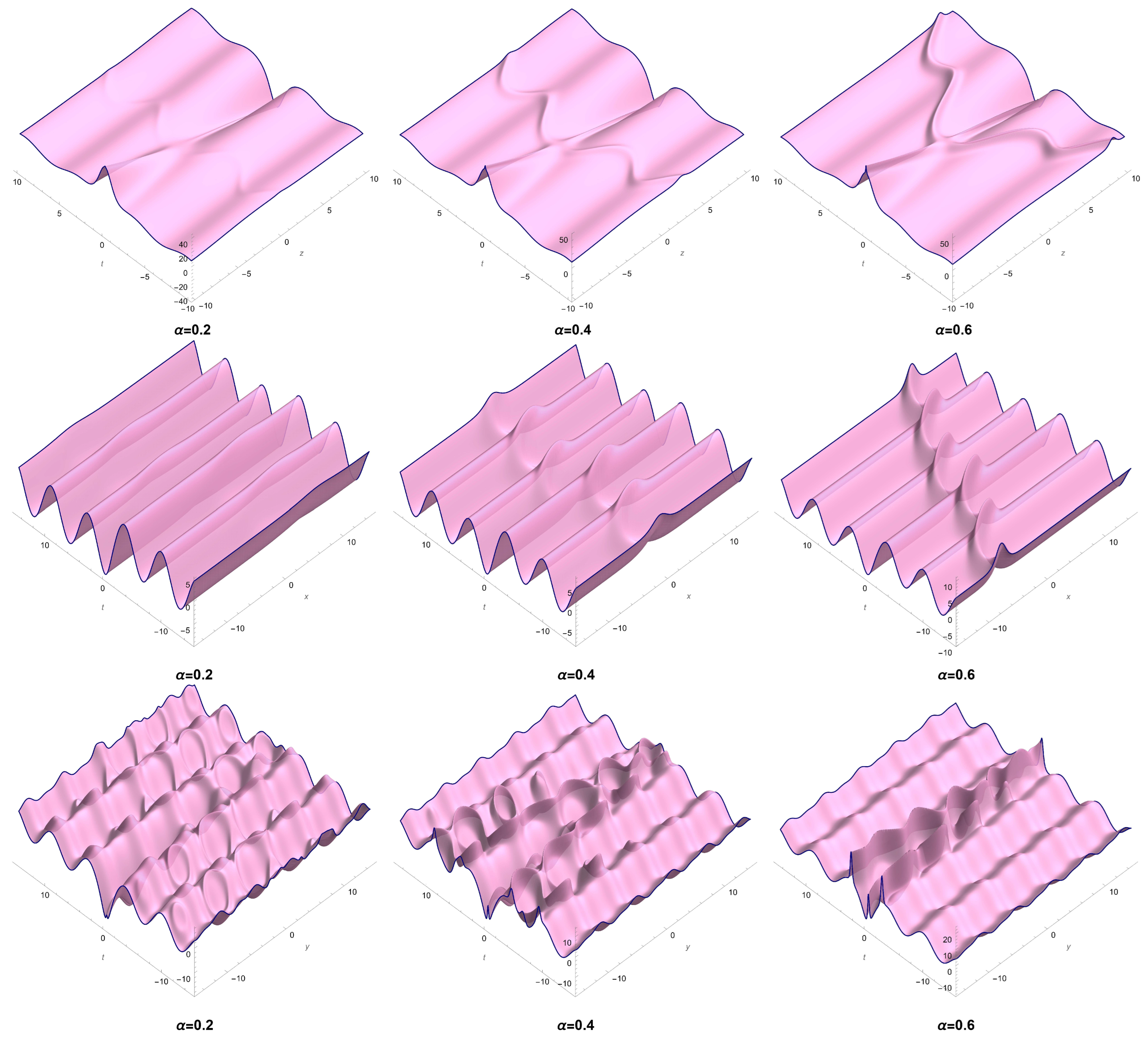
• Set 5: Letting $[{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4]=[1,1,2,0]$ and $[{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4]=[1-\dot{\iota },1+\dot{\iota },0,0]$ in Equation (20) gives

  $$\Lambda \left(\vartheta \right)={\mathrm{e}}^{\vartheta }\cos \vartheta$$

  (55)
• Case 5-1: In this case, the rest of the parameters can be attained as

  $$\begin{array}{c}\hfill \omega =-4{\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0=-{\displaystyle \frac{16{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_1={\displaystyle \frac{24{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

  (56)

  where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (55), it reads

$$\phi \left(\vartheta \right)=-{\displaystyle \frac{4{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}\left(3{sec}^2\vartheta -2\right).$$

Combining this solution with Equation (16), the wave solution for Equation (15) is constructed as

$${\psi }_9\left(\xi ,t\right)=-{\displaystyle \frac{4{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}\left(3{sec}^2\left(\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)\right)-2\right).$$

(57)

Therefore, from Equations (5) and (57), we derive a non-soliton solution for Equation (1) as follows:

$$\begin{array}{cc}\hfill u_9& =-{\displaystyle \frac{4{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}\left(3{sec}^2\left(\kappa \left(-4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)\right)-2\right)\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(58)

Case 5-2: In this case, the rest of the parameters can be attained as

$$\begin{array}{c}\hfill \omega =4{\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0=-{\displaystyle \frac{24{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_1={\displaystyle \frac{24{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

(59)

where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (55), it reads

$$\phi \left(\vartheta \right)=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}{sec}^2\vartheta .$$

Combining this solution with Equation (16), the wave solution for Equation (18) can be formulated as

$${\psi }_{10}\left(\xi ,t\right)=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}{sec}^2\left(\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)\right).$$

(60)

Therefore, from Equations (5) and (60), we derive a non-soliton solution for Equation (1) as follows:

$$\begin{array}{cc}\hfill u_{10}& =-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}{sec}^2\left(\kappa \left(4{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)\right)\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(61)

Set 6: Letting $[{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4]=[1,1,1,0]$ and $[{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4]=[-1,0,0,0]$ in Equation (20) gives

$$\Lambda \left(\vartheta \right)=1+{\mathrm{e}}^{-\vartheta }.$$

(62)

Case 6-1: In this case, the rest of the parameters can be attained as

$$\begin{array}{c}\hfill \omega ={\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0=-{\displaystyle \frac{2{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_1=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

(63)

where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (55), it reads

$$\phi \left(\vartheta \right)={\displaystyle \frac{2{\alpha }^2{\kappa }^2{\sigma }_1\left(-{\mathrm{e}}^{2\vartheta }+4{\mathrm{e}}^{\vartheta }-1\right)}{{\sigma }_2{\left(1+{\mathrm{e}}^{\vartheta }\right)}^2}}.$$

Combining this solution with Equation (16), the wave solution for Equation (18) is expressed as

$${\psi }_{11}\left(\xi ,t\right)={\displaystyle \frac{2{\alpha }^2{\kappa }^2{\sigma }_1\left(-{\mathrm{e}}^{2\kappa \left({\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}+4{\mathrm{e}}^{\kappa \left({\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}-1\right)}{{\sigma }_2{\left(1+{\mathrm{e}}^{\kappa \left({\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}\right)}^2}}.$$

(64)

Therefore, from Equations (5) and (64), we derive a non-soliton solution for Equation (1) as follows

$$\begin{array}{cc}\hfill u_{11}(x,y,z,t)& ={\displaystyle \frac{2{\alpha }^2{\kappa }^2{\sigma }_1\left(-{\mathrm{e}}^{2\kappa \left({\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}+4{\mathrm{e}}^{\kappa \left({\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}-1\right)}{{\sigma }_2{\left(1+{\mathrm{e}}^{\kappa \left({\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}\right)}^2}}\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(65)

Case 6-2: In this case, the rest of the parameters can be attained as

$$\begin{array}{c}\hfill \omega =-{\alpha }^3{\kappa }^3{\sigma }_1,{ϵ}_0=0,{ϵ}_1=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{ϵ}_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\end{array}$$

(66)

where $\alpha$ and $\kappa$ are free-chosen parameters.

Taking the obtained results into account in Equations (22) and (55), it reads

$$\phi \left(\vartheta \right)={\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1{\mathrm{e}}^{\vartheta }}{{\sigma }_2{\left(1+{\mathrm{e}}^{\vartheta }\right)}^2}}.$$

Combining this solution with Equation (16), the wave solution for Equation (18) can be formulated as

$${\psi }_{12}\left(\xi ,t\right)={\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1{\mathrm{e}}^{\kappa \left(-{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}}{{\sigma }_2{\left(1+{\mathrm{e}}^{\kappa \left(-{\alpha }^3{\kappa }^2{\sigma }_{1}t+\xi \right)}\right)}^2}}.$$

(67)

Therefore, from Equations (5) and (67), we derive a non-soliton solution for Equation (1) as follows:

$$\begin{array}{cc}\hfill u_{12}& ={\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1{\mathrm{e}}^{\kappa \left(-{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}}{{\sigma }_2{\left(1+{\mathrm{e}}^{\kappa \left(-{\alpha }^3{\kappa }^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)}\right)}^2}}-{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(68)

By incorporating Equations (21) and (22) in Equation (18), we obtain the following solutions for the unknown parameters:

• Case 7: In this case, the unknown parameters are obtained as

  $$\begin{array}{cc}\hfill \kappa & ={\displaystyle \frac{\sqrt{{\epsilon }_0{\sigma }_2}\sqrt{4{\ell }^2+\sqrt{16{\ell }^4-16{\ell }^2+1}-2}}{2{\tau }_3\alpha \sqrt{3{\sigma }_1}}},\hfill \\ \hfill \omega & ={\displaystyle \frac{\sqrt{3}{\epsilon }_0^{\frac{3}{2}}{\sigma }_2^{\frac{3}{2}}\sqrt{4{\ell }^2+\sqrt{16{\ell }^4-16{\ell }^2+1}-2}\left(16{\ell }^4+4\sqrt{16{\ell }^4-16{\ell }^2+1}{\ell }^2-16{\ell }^2-2\sqrt{16{\ell }^4-16{\ell }^2+1}+1\right)}{18{\tau }_3\sqrt{{\sigma }_1}}},\hfill \\ \hfill {\epsilon }_1& =0,{\epsilon }_2=-{\displaystyle \frac{{\epsilon }_0\left(4{\ell }^2+\sqrt{16{\ell }^4-16{\ell }^2+1}-2\right)}{{\tau }_3^2}},{\lambda }_2=0,{\lambda }_4=0,{\tau }_1=0,\hfill \end{array}$$

  (69)

  where $\alpha$, ${\epsilon }_0(>0)$ and ${\tau }_3\ne 0$ are free-chosen parameters.

Taking the obtained results into account in Equation (21), we have

$$\Lambda \left(\vartheta \right)={\displaystyle \frac{{\lambda }_1}{{\lambda }_3\mathbf{CN}\left({\tau }_3\vartheta |\ell \right)}}.$$

(70)

Further, Equation (22) turns to

$$\phi \left(\vartheta \right)={\epsilon }_0\left(1-\left(4{\ell }^2-2+\sqrt{16{\ell }^4-16{\ell }^2+1}\right){\displaystyle \frac{{\mathbf{SN}}^2\left({\tau }_3\vartheta |\ell \right){\mathbf{DN}}^2\left({\tau }_3\vartheta |\ell \right)}{{\mathbf{CN}}^2\left({\tau }_3\vartheta |\ell \right)}}\right).$$

Combining this solution with Equation (16), the wave solution for Equation (15) is constructed as

$${\psi }_{13}\left(\xi ,t\right)={\epsilon }_0\left(1-\left(4{\ell }^2-2+\sqrt{16{\ell }^4-16{\ell }^2+1}\right){\displaystyle \frac{{\mathbf{SN}}^2\left({\tau }_3\left(\kappa \xi +\omega t\right)|\ell \right){\mathbf{DN}}^2\left({\tau }_3\left(\kappa \xi +\omega t\right)|\ell \right)}{{\mathbf{CN}}^2\left({\tau }_3\left(\kappa \xi +\omega t\right)|\ell \right)}}\right).$$

(71)

So, from Equations (5) and (71), we can derive a non-soliton solution for Equation (1) as

$$\begin{array}{cc}\hfill u_{13}& ={\epsilon }_0\left(1-\left(∆\right){\displaystyle \frac{{\mathbf{SN}}^2\left({\tau }_3\left(\alpha \kappa x+\kappa \Theta \left(y,z,t\right)+\omega t\right)|\ell \right){\mathbf{DN}}^2\left({\tau }_3\left(\alpha \kappa x+\kappa \Theta \left(y,z,t\right)+\omega t\right)|\ell \right)}{{\mathbf{CN}}^2\left({\tau }_3\left(\alpha \kappa x+\kappa \Theta \left(y,z,t\right)+\omega t\right)|\ell \right)}}\right)\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}},\hfill \end{array}$$

(72)

where $∆=4{\ell }^2-2+\sqrt{16{\ell }^4-16{\ell }^2+1}$, and $\kappa ,\omega$ are given in Equation (69).

Two special cases of solution (72)

□

For $\ell =0$ in Equation (72), we get

$$\begin{array}{cc}\hfill u& ={\epsilon }_0{\mathrm{sech}}^2\left({\displaystyle \frac{\sqrt{{\epsilon }_0{\sigma }_2}\left(3\Theta \left(y,z,t\right)+\left(3x-t{\epsilon }_0{\sigma }_2\right)\alpha \right)}{6\alpha \sqrt{3{\sigma }_1}}}\right)\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(73)

□

For $\ell =1$ in Equation (72), we get

$$\begin{array}{cc}\hfill u& ={\epsilon }_0\left(3{\mathrm{sech}}^2\left({\displaystyle \frac{\sqrt{{\epsilon }_0{\sigma }_2}\left(\Theta \left(y,z,t\right)+\left(t{\epsilon }_0{\sigma }_2+x\right)\alpha \right)}{2\alpha \sqrt{{\sigma }_1}}}\right)-2\right)\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(74)

The solution $u_{13}$ presented in (72) exhibits rich and complex dynamic properties due to its dependence on Jacobi elliptic functions ($\mathbf{SN}$, $\mathbf{CN}$, $\mathbf{DN}$) and the interplay of spatial and temporal components. In this case, within the framework of Equation (12), we consider the specific functional forms

$$\begin{array}{c}\hfill f_1(x,t)=sin\left(x\right)tanh\left(t\right),f_2\left(t\right)=tanh\left(t\right),f_3\left(t\right)=sin\left(t\right).\end{array}$$

(75)

The inclusion of $tanh\left(t\right)$ and $sin\left(t\right)$ in the functions $f_1(x,t)$, $f_2\left(t\right)$, and $f_3\left(t\right)$ introduces a combination of smooth transitions and periodic oscillations, which modulate the wave’s amplitude and phase over time. The term $sin\left(x\right)tanh\left(t\right)$ in $f_1(x,t)$ suggests a spatially periodic structure that evolves smoothly in time, while $tanh\left(t\right)$ and $sin\left(t\right)$ in $f_2\left(t\right)$ and $f_3\left(t\right)$ contribute to temporal damping and harmonic oscillations, respectively. The solution $u_{13}$ captures nonlinear wave phenomena, including amplitude modulation, wavefront interactions, and phase transitions, driven by the interplay of the elliptic functions and the functional forms of $\Theta (y,z,t)$. The parameter $∆$, which depends on the elliptic modulus ℓ, further influences the wave’s shape and propagation, allowing for the modeling of both periodic and localized wave structures. This solution is particularly suited for describing systems with nonlinear dispersion, wave damping, and harmonic interactions, such as nonlinear optics, fluid dynamics, and plasma physics, where the balance between nonlinearity and dispersion plays a critical role in shaping wave dynamics.

The described dynamic properties of solution (72) for some values of $\alpha$ across different directions are displayed in Figure 7.

In this plot, we have considered Equation (75) in Equation (12), along with the parameter values ${\sigma }_1=0.2$, ${\sigma }_2=0.9$, ${\sigma }_3=0.3$, ${\sigma }_4=0.2$, ${\sigma }_5=0.1$, ${\sigma }_6=0.2$, ${\sigma }_7=0.1$, ${\sigma }_8=0.3$, along with ${\epsilon }_0=1,\ell =0$ and $\kappa =0.1$.

Moreover, in Figure 8, we study the sensitivity of the solution (72), based on the selection of Equation (75) with respect to different ${\sigma }_i$’s together with $\alpha =0.9,\kappa =1.6$.

• Case 8: In this case, the unknown parameters are obtained as

  $$\begin{array}{cc}\hfill \omega & =4{\alpha }^3{\kappa }^3{\tau }_4^2{\sigma }_1\sqrt{{\ell }^4+14{\ell }^2+1},{\epsilon }_0=-{\displaystyle \frac{4{\alpha }^2\left(2{\ell }^2+\sqrt{{\ell }^4+14{\ell }^2+1}+2\right){\tau }_4^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},\hfill \\ \hfill {\epsilon }_1& =0,{\epsilon }_2=-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}},{\lambda }_2=0,{\lambda }_3=0,{\tau }_1=0,\hfill \end{array}$$

  (76)

  where $\alpha$, $\kappa$ and ${\tau }_4\ne 0$ are free-chosen parameters.

Taking the obtained results into account in Equation (21), we have

$$\Lambda \left(\vartheta \right)={\displaystyle \frac{{\lambda }_1}{{\lambda }_4\mathbf{SN}\left({\tau }_4\vartheta |\ell \right)}}.$$

(77)

Further, Equation (22) turns to

$$\phi \left(\vartheta \right)=-{\displaystyle \frac{4{\alpha }^2\left(2{\ell }^2+\sqrt{{\ell }^4+14{\ell }^2+1}+2\right){\tau }_4^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1{\tau }_4^2\mathbf{CN}{\left({\tau }_4\xi |\ell \right)}^2\mathbf{DN}{\left({\tau }_4\xi |\ell \right)}^2}{{\sigma }_2\mathbf{SN}{\left({\tau }_4\xi |\ell \right)}^2}}.$$

Combining this solution with Equation (16), the wave solution for Equation (18) can be formulated as

$${\psi }_{14}\left(\xi ,t\right)=-{\displaystyle \frac{4{\kappa }^2{\alpha }^2{\tau }_4^2{\sigma }_1\left(2{\ell }^2+\sqrt{{\ell }^4+14{\ell }^2+1}+2\right)}{{\sigma }_2}}-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1{\tau }_4^2\mathbf{CN}{\left({\tau }_4\left(\kappa \xi +\omega t\right)|\ell \right)}^2\mathbf{DN}{\left({\tau }_4\left(\kappa \xi +\omega t\right)|\ell \right)}^2}{{\sigma }_2\mathbf{SN}{\left({\tau }_4\left(\kappa \xi +\omega t\right)|\ell \right)}^2}}.$$

(78)

Thus, from Equations (5) and (78), we can derive a non-soliton solution for Equation (1) as

$$\begin{array}{cc}\hfill u_{14}& =-{\displaystyle \frac{4{\alpha }^2\left(2{\ell }^2+\sqrt{{\ell }^4+14{\ell }^2+1}+2\right){\tau }_4^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}-{\displaystyle \frac{12{\alpha }^2{\kappa }^2{\sigma }_1{\tau }_4^2\mathbf{CN}{\left({\tau }_4∆|\ell \right)}^2\mathbf{DN}{\left({\tau }_4∆|\ell \right)}^2}{{\sigma }_2\mathbf{SN}{\left({\tau }_4∆|\ell \right)}^2}}\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}},\hfill \end{array}$$

(79)

where $∆=\kappa \alpha +\kappa \Theta \left(y,z,t\right)+\omega t$, and $\kappa ,\omega$ are given in Equation (76).

Two special cases of solution (79)

□

For $\ell =0$ in Equation (79), we get

$$\begin{array}{cc}\hfill u& =-{\displaystyle \frac{12\alpha {\sigma }_1^2{\tau }_4^2{\kappa }^2}{{\sigma }_2}}{csc}^2\left({\tau }_4\kappa \left(4{\alpha }^3{\kappa }^2{\tau }_4^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)\right)\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(80)

□

For $\ell =1$ in Equation (79), we get

$$\begin{array}{cc}\hfill u& =-{\displaystyle \frac{4{\tau }_4^2{\alpha }^2{\kappa }^2{\sigma }_1}{{\sigma }_2}}\left(3{\mathrm{sech}}^2\left({\tau }_4\kappa \left(16{\alpha }^3{\kappa }^2{\tau }_4^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)\right){\mathrm{csch}}^2\left({\tau }_4\kappa \left(16{\alpha }^3{\kappa }^2{\tau }_4^2{\sigma }_{1}t+\alpha x+\Theta \left(y,z,t\right)\right)\right)+8\right)\hfill \\ & -{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\hfill \end{array}$$

(81)

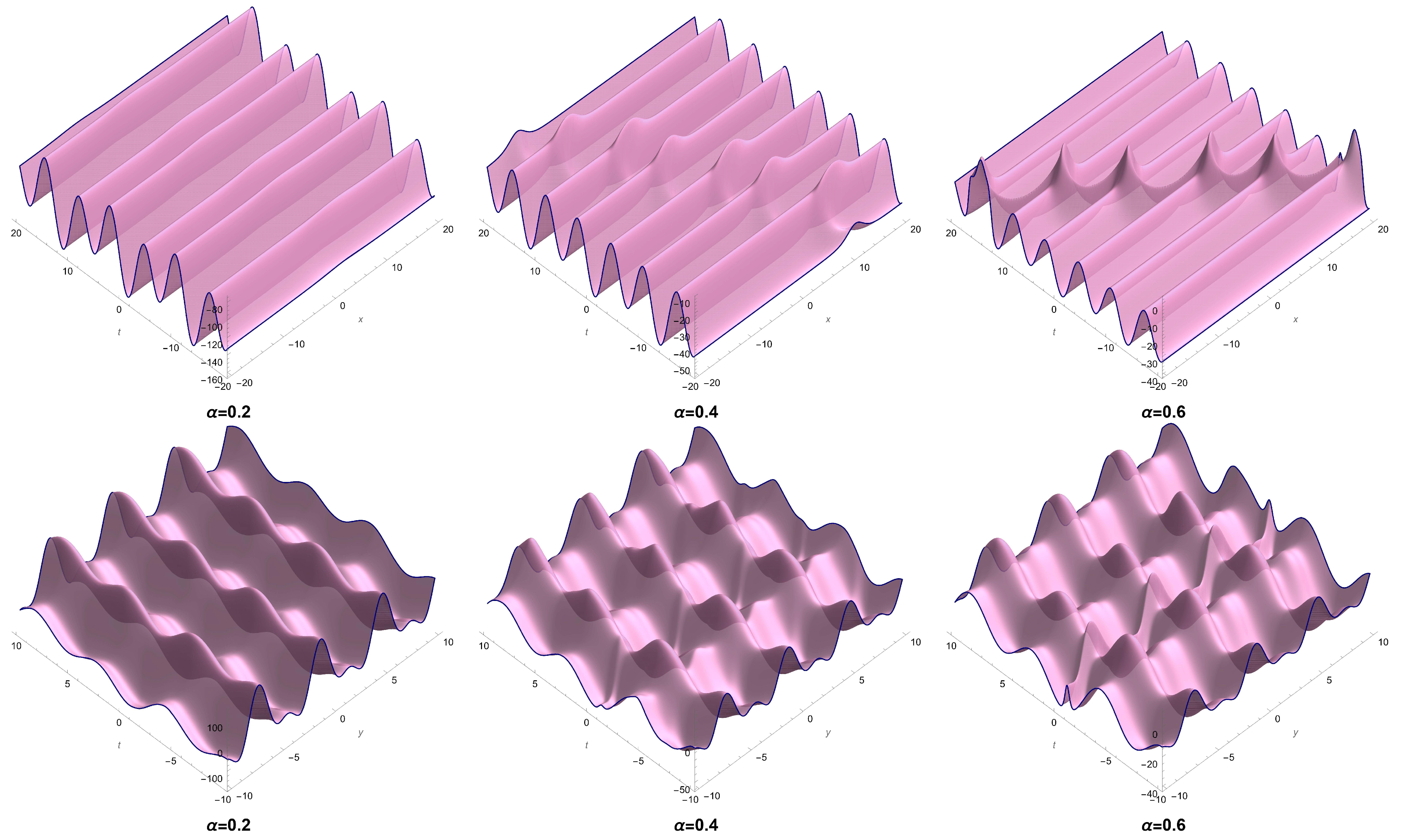
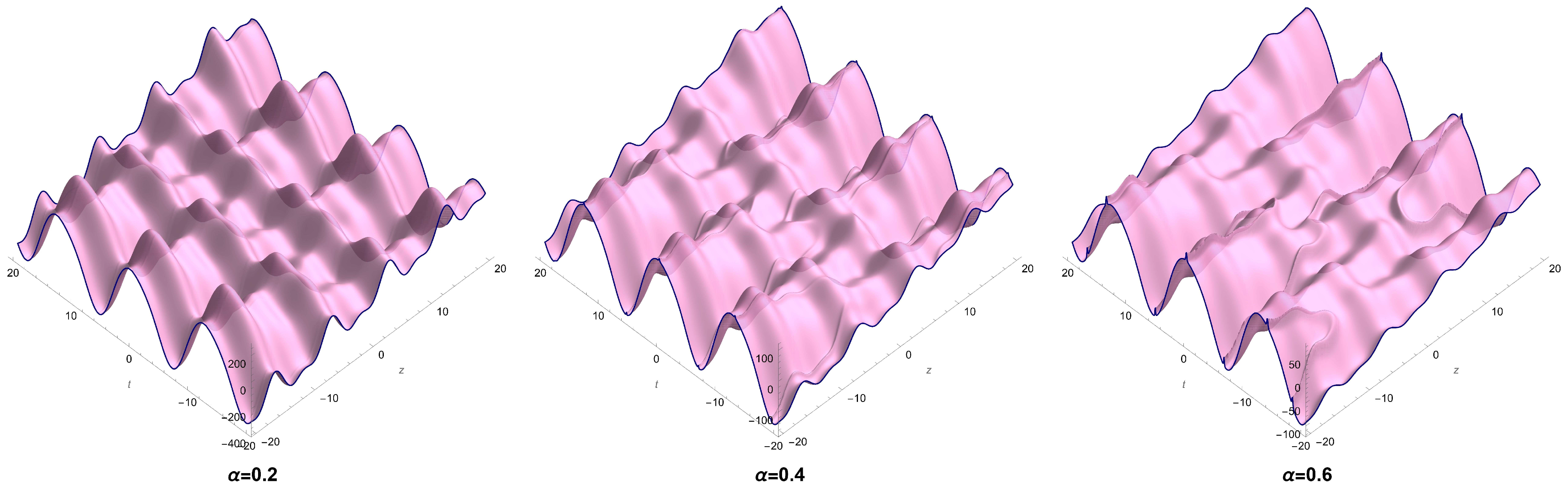
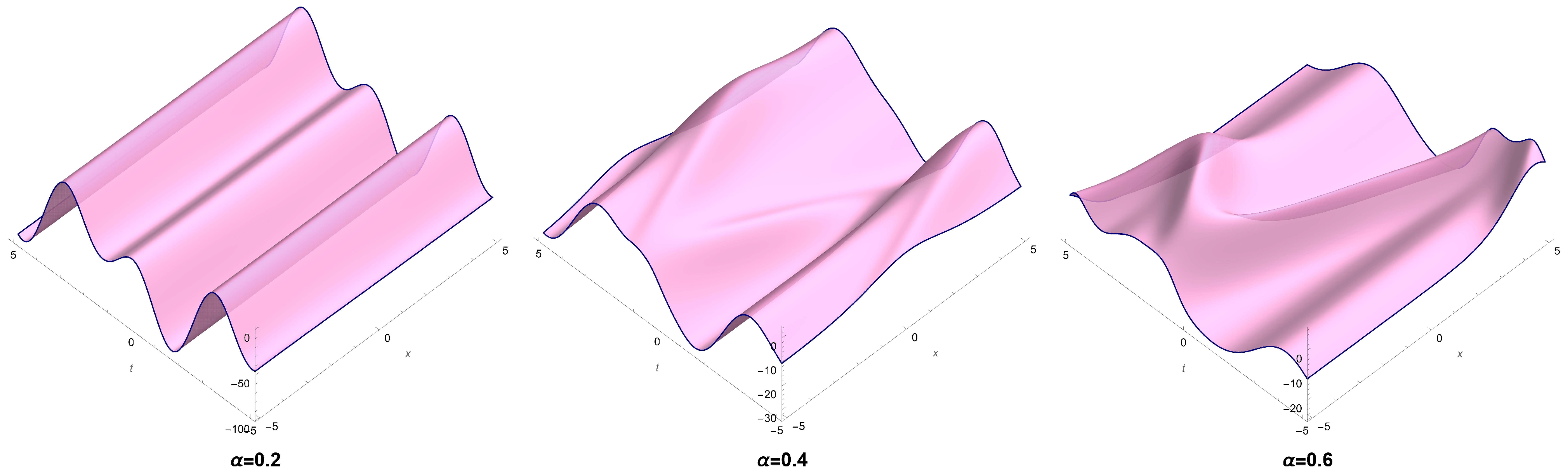
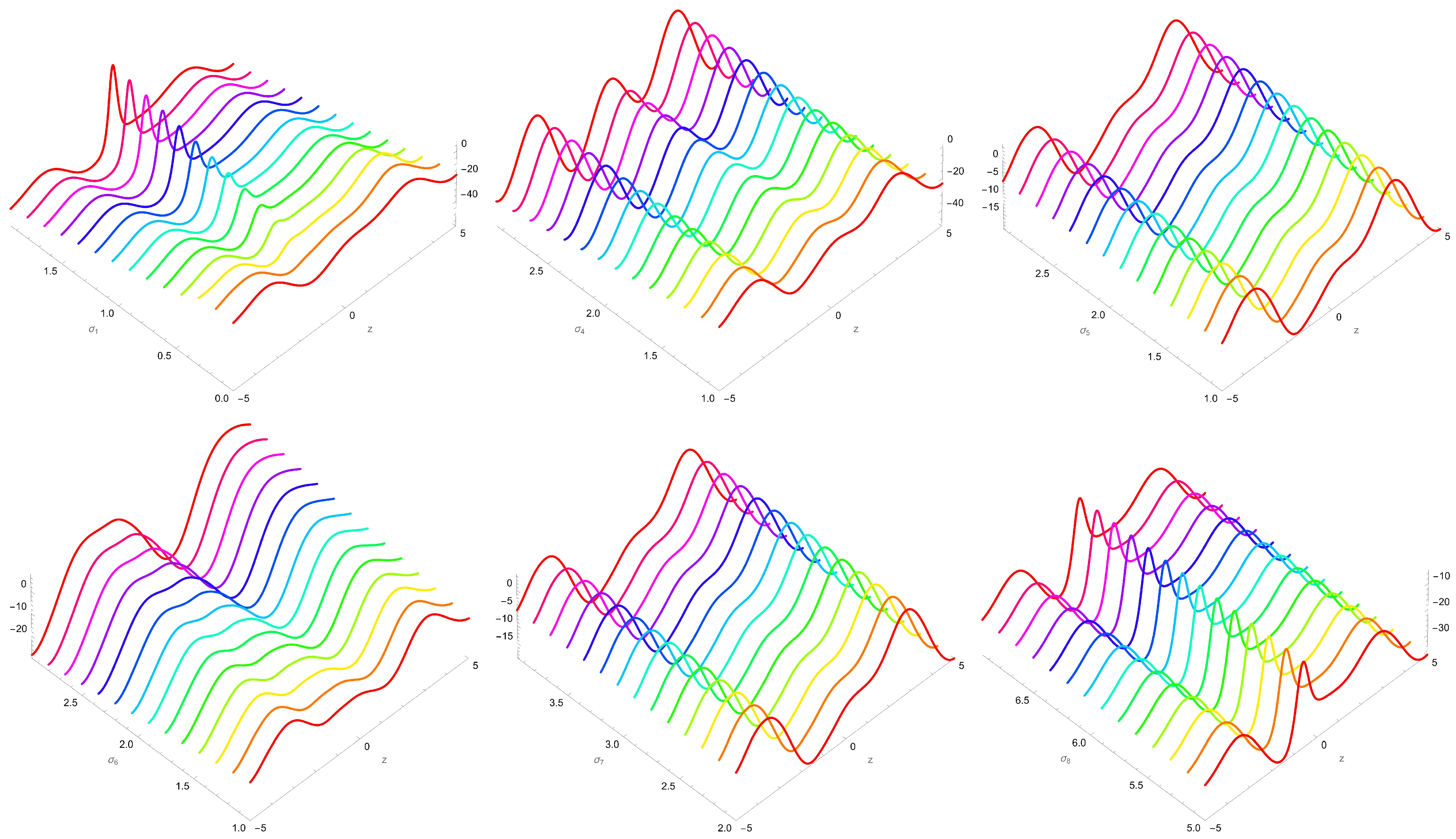
2.2. The Extraction of Soliton Solutions to (18) Using a Logarithm Transformation

In order to derive another analytical solution to Equation (18), we first implement the logarithmic transformation

$$\phi \left(\vartheta \right)={\left(2ln\left(\mathbf{f}\right(\vartheta \left)\right)\right)}_{\vartheta \vartheta }={\displaystyle \frac{2{\mathbf{f}}_{\vartheta \vartheta }\mathbf{f}-2{\mathbf{f}}_{\vartheta }^2}{{\mathbf{f}}^2}},$$

(82)

on Equation (18), and we attain

$$\begin{array}{cc}\hfill -3{\alpha }^3{\kappa }^3{\sigma }_1{\mathbf{f}}_{\vartheta \vartheta }^2{\mathbf{f}}^2& + 12{\alpha }^3{\kappa }^3{\sigma }_1{\mathbf{f}}_{\vartheta \vartheta }{\mathbf{f}}_{\vartheta }^2\mathbf{f}+{\alpha }^3{\kappa }^3{\sigma }_1{\mathbf{f}}_{\vartheta \vartheta \vartheta \vartheta }{\mathbf{f}}^3-4{\alpha }^3{\kappa }^3{\sigma }_1{\mathbf{f}}_{\vartheta }{\mathbf{f}}_{\vartheta \vartheta \vartheta }{\mathbf{f}}^2\hfill \\ & - 6{\alpha }^3{\kappa }^3{\sigma }_1{\mathbf{f}}_{\vartheta }^4+\alpha \kappa {\sigma }_2{\mathbf{f}}_{\vartheta \vartheta }^2{\mathbf{f}}^2-2\alpha \kappa {\sigma }_2{\mathbf{f}}_{\vartheta \vartheta }{\mathbf{f}}_{\vartheta }^2\mathbf{f}+\alpha \kappa {\sigma }_2{\mathbf{f}}_{\vartheta }^4+\omega {\mathbf{f}}_{\vartheta \vartheta }{\mathbf{f}}^3-\omega {\mathbf{f}}_{\vartheta }^2{\mathbf{f}}^2=0.\hfill \end{array}$$

(83)

Now, we examine special structures of $\mathbf{f}\left(\vartheta \right)$ which satisfy Equation (83) as

$$\begin{array}{cc}\hfill \mathbf{f}\left(\vartheta \right)={\lambda }_0& +{\displaystyle \frac{{\lambda }_1{\mathrm{e}}^{{\tau }_1\vartheta }+{\lambda }_2{\mathrm{e}}^{{\tau }_2\vartheta }}{{\lambda }_3{\mathrm{e}}^{{\tau }_3\vartheta }+{\lambda }_4{\mathrm{e}}^{{\tau }_4\vartheta }}},\hfill \end{array}$$

(84)

where ${\lambda }_0,{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4$ and ${\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4$ are disposal parameters.

After inserting (84) in (83) and solving the resulting equation, the unknown parameters are obtained as

$$\begin{array}{c}\hfill \kappa ={\displaystyle \frac{\sqrt{{\sigma }_2}}{\alpha \sqrt{6{\sigma }_1}}},\omega =-{\displaystyle \frac{{\sigma }_2{({\lambda }_1-{\lambda }_4)}^2\sqrt{{\sigma }_2}}{6\sqrt{6{\sigma }_1}}},k_2=0,k_3=0.\end{array}$$

(85)

Inserting these values in (84), we get

$$\mathbf{f}\left(\vartheta \right)=k_0+{\displaystyle \frac{k_1{\mathrm{e}}^{{\lambda }_1\vartheta }}{k_4{\mathrm{e}}^{{\lambda }_4\vartheta }}}.$$

(86)

Moreover, by inserting (86) in (82), one gets

$$\phi \left(\vartheta \right)={\displaystyle \frac{2k_1{k}_4{k}_0{({\lambda }_1-{\lambda }_4)}^2{\mathrm{e}}^{({\lambda }_1-{\lambda }_4)\vartheta }}{{\left(k_0{k}_4+k_1{\mathrm{e}}^{({\lambda }_1-{\lambda }_4)\vartheta }\right)}^2}}.$$

(87)

Combining this solution with Equation (16), the wave solution for Equation (18) is expressed as

$${\psi }_{15}\left(\xi ,t\right)={\displaystyle \frac{2k_1{k}_4{k}_0{({\lambda }_1-{\lambda }_4)}^2{\mathrm{e}}^{-({\lambda }_1+{\lambda }_4)\sqrt{\frac{{\sigma }_1{\sigma }_2}{6}}\left(\frac{{\sigma }_2{({\lambda }_1-{\lambda }_4)}^{2}t}{6{\sigma }_1}-\frac{\xi }{\alpha {\sigma }_1}\right)}}{{\left(k_0{k}_4{\mathrm{e}}^{-{\lambda }_4\sqrt{\frac{{\sigma }_1{\sigma }_2}{6}}\left(\frac{{\sigma }_2{({\lambda }_1-{\lambda }_4)}^{2}t}{6{\sigma }_1}-\frac{\xi }{\alpha {\sigma }_1}\right)}+k_1{\mathrm{e}}^{-{\lambda }_1\sqrt{\frac{{\sigma }_1{\sigma }_2}{6}}\left(\frac{{\sigma }_2{({\lambda }_1-{\lambda }_4)}^{2}t}{6{\sigma }_1}-\frac{\xi }{\alpha {\sigma }_1}\right)}\right)}^2}}.$$

(88)

Therefore, from Equations (5) and (88), we derive a non-soliton solution for Equation (1) as follows:

$$\begin{array}{c}\hfill u_{15}(x,y,z,t)={\psi }_{15}\left(\alpha x+\Theta (y,z,t),t\right)-{\displaystyle \frac{{\sigma }_4{\Theta }_y^2+{\sigma }_8{\Theta }_y{\Theta }_z+\alpha {\sigma }_6{\Theta }_y+{\sigma }_5{\Theta }_z^2+\alpha {\sigma }_7{\Theta }_z+\alpha {\Theta }_t+{\alpha }^2{\sigma }_3}{{\alpha }^2{\sigma }_2}}.\end{array}$$

(89)

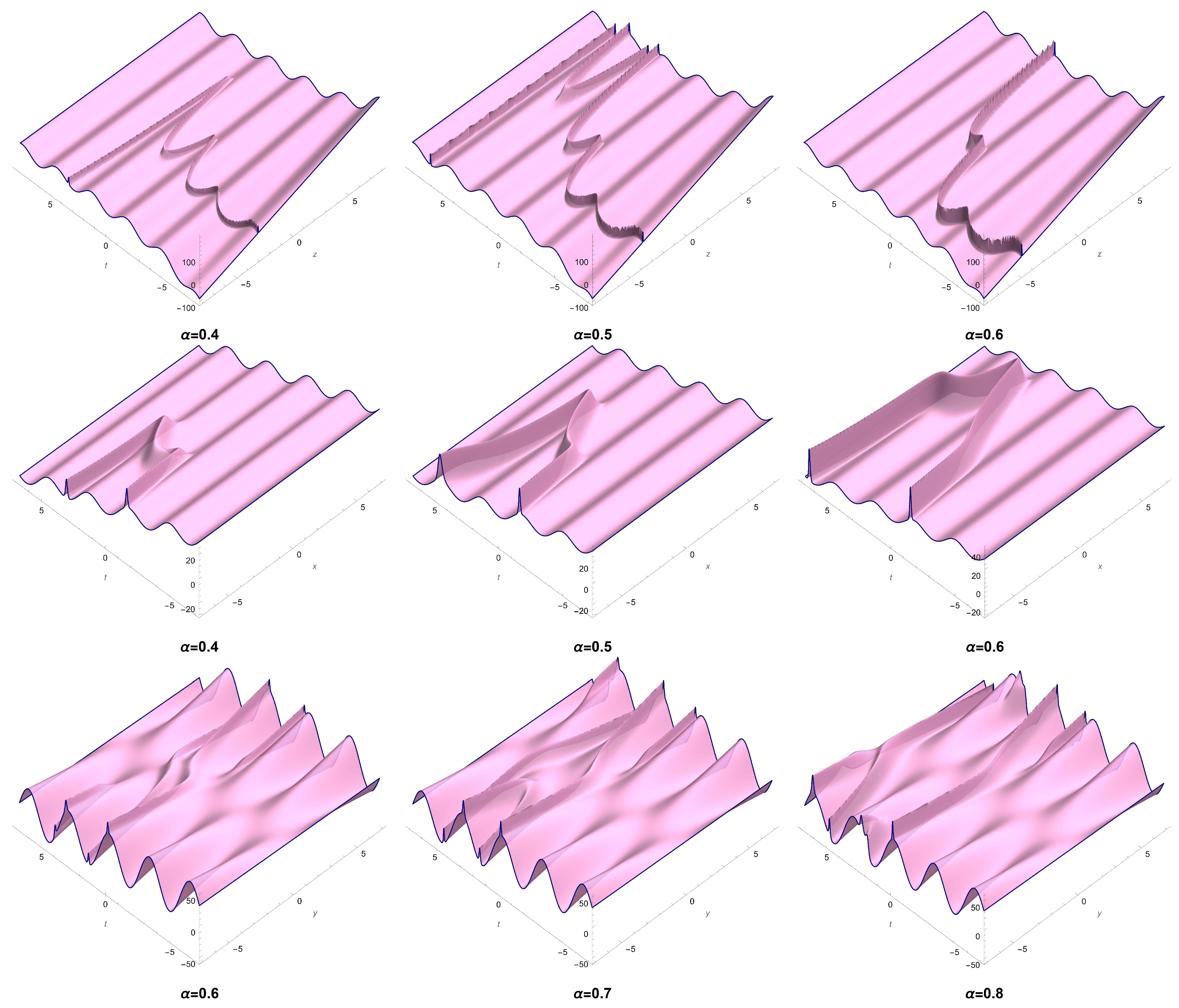
3. The Second Reduction Procedure for Equation (1)

In this section, we investigate a generalized method for variable separation that enables the derivation of non-traveling exact solutions to Equation (1) within the following specified framework.

Theorem 2.

By utilizing the transformation defined as

$$u(x,y,z,t)=\phi (\xi ,\rho ),$$

(90)

where $\xi =\alpha x+\theta (y,z,t)$ and $\rho =\beta y+\eta (z,t)$, with the functions η and θ given by

$$\begin{array}{cc}\hfill & \eta (z,t)={\displaystyle \frac{(-2\beta (\sqrt{{\sigma }_8^2-4{\sigma }_4{\sigma }_5}{c}_2+\alpha {\sigma }_6+2c_1{\sigma }_4)t+2c_4\alpha ){\sigma }_5-\beta (-{\sigma }_8+\sqrt{{\sigma }_8^2-4{\sigma }_4{\sigma }_5})({\sigma }_8{c}_{1}t+({\sigma }_{7}t-z)\alpha )}{2\alpha {\sigma }_5}},\hfill \\ \hfill & \theta (y,z,t)=c_{1}y+c_{2}z-\left({\displaystyle \frac{{\alpha }^2{\sigma }_3+\alpha c_1{\sigma }_6+\alpha c_2{\sigma }_7+c_1^2{\sigma }_4+c_1{c}_2{\sigma }_8+c_2^2{\sigma }_5}{\alpha }}\right)t+c_3,\hfill \end{array}$$

(91)

the original Equation (1) is transformed into the following form:

$$2{\alpha }^2{\sigma }_1{\phi }_{\xi \xi }(\xi ,\rho )+{\sigma }_2{\phi }^2(\xi ,\rho )=0.$$

(92)

Proof. 

First, by inserting the symbolic structure Equation (90) into Equation (1), it is simplified as

$$\begin{array}{c}\hfill {\varrho }_1{\phi }_{\xi \xi }+{\varrho }_2{\phi }_{\rho \rho }+{\varrho }_3{\phi }_{\xi \rho }+{\varrho }_4{\phi }_{\xi }+{\varrho }_5{\phi }_{\rho }+{\alpha }^4{\sigma }_1{\phi }_{\xi \xi \xi \xi }+{\alpha }^2{\sigma }_2\left(\phi {\phi }_{\xi \xi }+{\phi }_{\xi }^2\right)=0,\end{array}$$

(93)

where

$$\begin{array}{cc}\hfill {\varrho }_1& ={\sigma }_4{\theta }_y^2+{\sigma }_8{\theta }_z{\theta }_y+\alpha {\sigma }_6{\theta }_y+{\sigma }_5{\theta }_z^2+\alpha {\sigma }_7{\theta }_z+{\alpha }^2{\sigma }_3+\alpha {\theta }_t,\hfill \\ \hfill {\varrho }_2& ={\sigma }_5{\eta }_z^2+\beta {\sigma }_8{\eta }_z+{\sigma }_4{\beta }^2,\hfill \\ \hfill {\varrho }_3& ={\sigma }_8{\eta }_z{\theta }_y+2{\sigma }_5{\eta }_z{\theta }_z+\alpha {\sigma }_7{\eta }_z+2{\sigma }_4\beta {\theta }_y+{\sigma }_8\beta {\theta }_z+\alpha {\eta }_t+\alpha \beta {\sigma }_6,\hfill \\ \hfill {\varrho }_4& ={\sigma }_5{\theta }_{z,z}+{\sigma }_8{\theta }_{y,z}+{\sigma }_4{\theta }_{y,y},\hfill \\ \hfill {\varrho }_5& ={\sigma }_5{\eta }_{zz}.\hfill \end{array}$$

(94)

At this point, we are seeking the criteria that would transform Equation (93) into a more straightforward and solvable form. To achieve this, we examine the case where all coefficients vanish (${\varrho }_1={\varrho }_2={\varrho }_3={\varrho }_4={\varrho }_5=0$) in Equation (94). By solving the coupled system of partial differential equations for $\theta (y,z,t)$ and $\eta (z,t)$ simultaneously using Maple, we obtain the following solution:

$$\begin{array}{cc}\hfill & \eta \left(z,t\right)={\displaystyle \frac{\left(-2\beta \left(\sqrt{{\sigma }_8^2-4{\sigma }_4{\sigma }_5}{c}_2+\alpha {\sigma }_6+2c_1{\sigma }_4\right)t+2c_4\alpha \right){\sigma }_5-\beta \left(-{\sigma }_8+\sqrt{{\sigma }_8^2-4{\sigma }_4{\sigma }_5}\right)\left({\sigma }_8{c}_{1}t+\left({\sigma }_{7}t-z\right)\alpha \right)}{2\alpha {\sigma }_5}},\hfill \\ & \theta \left(y,z,t\right)=c_{1}y+c_{2}z-\left({\displaystyle \frac{{\alpha }^2{\sigma }_3+\alpha c_1{\sigma }_6+\alpha c_2{\sigma }_7+c_1^2{\sigma }_4+c_1{c}_2{\sigma }_8+c_2^2{\sigma }_5}{\alpha }}\right)t+c_3.\hfill \end{array}$$

(95)

Taking these results into account in Equation (93), one gets

$${\alpha }^2{\sigma }_1{\phi }_{\xi \xi \xi \xi }+{\sigma }_2\left(\phi {\phi }_{\xi \xi }+{\phi }_{\xi }^2\right)=0.$$

(96)

The double integration of Equation (96) over $\xi$, followed by the elimination of integration constants yields

$$2{\alpha }^2{\sigma }_1{\phi }_{\xi \xi }\left(\xi ,\rho \right)+{\sigma }_2{\phi }^2\left(\xi ,\rho \right)=0.$$

(97)

□

The transformation delineated in Theorem 2 demonstrates the process of reducing the original equation to a more simplified form utilizing the newly defined variables $\xi$ and $\rho$. This equation can be solved explicitly using Maple as follows:

$$\phi \left(\xi ,\rho \right)=-{\displaystyle \frac{12{\alpha }^2{\sigma }_1}{{\sigma }_2}}\wp \left(\xi +{\mathbf{f}}_1\left(\rho \right),0,{\mathbf{f}}_2\left(\rho \right)\right),$$

(98)

where is $\wp (\xi ,g_1,g_2)$ the Weierstrass elliptic function with respect to the argument of $\xi$, and $g_1,g_2$ are two algebraic invariants. Moreover, ${\mathbf{f}}_1,{\mathbf{f}}_2$ are two arbitrary functions.

So, from Equations (5) and (25), we can derive a non-soliton solution for Equation (1) as

$$u_{16}=-{\displaystyle \frac{12{\alpha }^2{\sigma }_1}{{\sigma }_2}}\wp \left(\alpha x+\theta (y,z,t)+{\mathbf{f}}_1\left(\beta y+\eta (z,t)\right),0,{\mathbf{f}}_2\left(\beta y+\eta (z,t)\right)\right),$$

(99)

where $\theta ,\eta$ are defined in (95).

Remark 1.

All proposed solutions presented in this work have been rigorously validated through symbolic computation in Maple by direct substitution into the original equation.

4. Conclusions

Using the extended generalized variable separation method combined with symbolic computation, this paper constructed explicit non-traveling wave solutions for a generalized version of the KP equation. This important equation describes many complex problems in fluid dynamics, plasma physics, optics, and engineering. By employing an innovative transformation and conducting a thorough analytical treatment, the original equation is transformed into a more solvable form. The key to our approach lies in the introduction of the auxiliary function $\Theta (y,z,t)$, which offers flexibility in constructing diverse solutions. We presented two distinct forms for $\Theta$, expressed in terms of arbitrary functions, thereby significantly broadening the scope of possible solutions. Applying the mGERFM technique, we obtained a variety of explicit solutions, expressed in terms of exponential functions, trigonometric functions, and Jacobi elliptic functions. In addition to deriving exact non-traveling wave solutions, several illustrative figures have been included in this study to provide a deeper physical interpretation of the obtained solutions. These graphical representations highlight the dynamic behavior of the solutions under varying parameters, offering valuable insight into the underlying wave phenomena described by the considered model. Furthermore, the method employed in this paper can also be applied to other nonlinear evolution equations, making it a valuable tool for investigating complex physical phenomena. The obtained solutions provide new insights into wave propagation dynamics, particularly for long-wave hydrodynamics, and small-amplitude surface waves with weak nonlinearity effects. The stability analysis, as well as the investigation of interaction properties, long-term dynamical behavior, and physical validation of the proposed solutions through experimental data, is recommended as a promising direction for future research on the considered equation.