A Comprehensive Study on the Different Approaches of the Symmetric Difference in Nilpotent Fuzzy Systems

Abstract

This paper comprehensively examines symmetric difference operators within logical systems generated by nilpotent t-norms and t-conorms, specifically addressing their behavior and applicability in bounded and Łukasiewicz fuzzy logic systems. We identify two distinct symmetric difference operators and analyze their fundamental properties, revealing their inherent non-associativity. Recognizing the limitations posed by non-associative behavior in practical multi-step logical operations, we introduce a novel aggregated symmetric difference operator constructed through the arithmetic mean of the previously defined operators. The primary theoretical contribution of our research is establishing the associativity of this new aggregated operator, significantly enhancing its effectiveness for consistent multi-stage computations. Moreover, this operator retains critical properties including symmetry, neutrality, antitonicity, and invariance under negation, thus making it particularly valuable for various computational and applied domains such as image processing, pattern recognition, fuzzy neural networks, cryptographic schemes, and medical data analysis. The demonstrated theoretical robustness and practical versatility of our associative operator provide a clear improvement over existing methodologies, laying a solid foundation for future research in fuzzy logic and interdisciplinary applications. Our broader aim is to derive and study symmetric difference operators in both bounded and Łukasiewicz systems, as this represents a new direction of research.

1. Introduction

Ever since Zadeh’s pioneering work on fuzzy sets [1], researchers have been keenly interested in extending traditional Boolean logic operations to fuzzy systems. These extensions include implications [2], equivalences [3], and differences [4], including the symmetric difference operator, which stands as a fundamental yet notably significant operation in set theory [5,6,7].

This paper extends the foundational work of [8], which introduced a unified framework integrating continuous-valued logic and multi-criteria decision tools for modeling human reasoning by incorporating the concept of the symmetric difference within nilpotent fuzzy systems. Our previous studies [2,3,8,9] demonstrated that the combination of deep neural networks with structured logical rules and decision-making tools improves interpretability, transparency, and safety in neural computation. The incorporation of the symmetric difference operator refines and extends this framework, yielding a more comprehensive and adaptable toolkit for applications. This addition strengthens the theoretical consistency of our approach and further bridges the gap between logical reasoning and neural computation, enabling more nuanced and interpretable decision-making processes in artificial intelligence.

While existing studies, such as [8], have introduced several logical operators within nilpotent systems, the symmetric difference operator has not yet been addressed in this context. This motivates the current research. Our broader aim is to systematically derive and study symmetric difference operators in both Łukasiewicz and bounded systems, thereby contributing to the development of this novel and previously unexplored area of fuzzy logic.

The symmetric difference operator plays a crucial role in introducing metrics that are essential for measuring similarity. Such measurements find application in various domains, such as information retrieval [10,11,12], image processing [13,14,15,16], natural language processing [17,18,19], recommendation systems [20,21,22], pattern recognition [23,24,25], deep learning and neural networks [26,27], data mining [28,29], fuzzy control systems [30,31], and bioinformatics and computational biology [32,33]. Fuzzy similarity measurements are particularly useful in scenarios where items exhibit slight variations rather than exact matches. For example, in the case of images, it can be variations in lighting or angle or in the case of texts, it can be semantic similarity rather than precise matching.

The symmetric difference operator on the power set $2^X$ of a set X is a binary function ${▵}^{*}:2^X\times 2^X\to 2^X$ defined as follows:

$$A{▵}^{*}B=\left\{x\right|x\in A\mathrm{but}x\notin B\mathrm{or}x\in B\mathrm{but}x\notin A\}.$$

(1)

In a Boolean algebra ($P\left(x\right),\cup ,\cap {,}^c$), the symmetric difference operator can be represented by several formulas, but two of the most commonly applied are

$$A{▵}_1^{*}B=(A\cap B^c)\cup (A^c\cap B)$$

(2)

and

$$A{▵}_2^{*}B=(A\cup B)\cap {(A\cap B)}^c,$$

(3)

While Equations (2) and (3) are equivalent in traditional logic, this equivalence does not always hold in fuzzy logic.

In Boolean logic, the symmetric difference operator has the following properties:

• Commutativity: $A{▵}^{*}B=B{▵}^{*}A$;
• Neutral element: $\varnothing {▵}^{*}A=A{▵}^{*}\varnothing =A$;
• Strong negation: $X{▵}^{*}A=A{▵}^{*}X=X\setminus A$;
• Associativity: $\left(A{▵}^{*}B\right){▵}^{*}C=A{▵}^{*}\left(B{▵}^{*}C\right)$;
• Inverse element: $A{▵}^{*}A=\varnothing$;
• Complementarity: $A{▵}^{*}(X\setminus A)=X$;
  for all $A,B,C\subseteq X$.

These identities can also be represented in fuzzy logic. Let $s:[0,1]\times [0,1]\to [0,1]$ be a continuous operator with the boundary conditions $s(0,0)=s(1,1)=0$ and $s(0,1)=s(1,0)=1$ and the following properties, if n is a continuous negation operator:

• Symmetry: $s(x,y)=s(y,x)$;
• Neutrality property: $s(0,x)=s(x,0)=x$;
• Strong negation principle: $s(1,x)=s(x,1)=n\left(x\right)$;
• Exchange principle: $s\left(s\right(x,y),z)=s(x,s(y,z\left)\right)$;
• Reflexivity: $s(x,x)=0$;
• Negation dissimilarity property: $s(x,n(x\left)\right)=1$;
  for all $x,y,z\in [0,1]$.

Although these properties can be extended to fuzzy settings, no single function s satisfies all the conditions outlined above [34].

In nilpotent fuzzy systems, we use nilpotent t-norms and t-conorms defined via generator functions. Due to the behavior of these generators, standard symmetric difference properties (e.g., associativity, reflexivity, etc.) may not hold or they may hold in unexpected ways. Thus, new definitions are required to preserve or approximate these properties in a fuzzy setting. Since consistent connective systems generated by nilpotent t-norms and t-conorms are not necessarily isomorphic to Łukasiewicz systems, results from Łukasiewicz logic cannot be directly transferred. This necessitates the independent development and analysis of symmetric difference operators within bounded systems, where the interplay between multiple generator functions and naturally derived negations introduces new structural behaviors. Bounded systems with multiple generator functions and three negation operators introduce additional complexity; however, this complexity allows for greater expressiveness and flexibility in modeling nuanced logical behavior.

This paper introduces two forms of the symmetric difference operator based on nilpotent t-norms and t-conorms, employing different approaches. In the first formula, the emphasis is placed on ensuring that the symmetric difference of two variables yields 0 when they are equal. In contrast, the second formula prioritizes identifying the values where the symmetric difference is equal to 1, that is, when the variables are definitively unequal. Although it can be proven that neither of these formulas is associative, their arithmetic mean exhibits this property, thus justifying further investigation.

The structure of the paper is as follows: Section 2 introduces the symmetric difference operators in systems generated by nilpotent t-norms and t-conorms. Following this, Section 3 discusses the properties of the previously introduced symmetric difference operator and its dual operator. In Section 4, the aggregated symmetric difference operator is defined, and its associativity is demonstrated. Section 5 emphasizes the relevance of the symmetric difference in various fields of application with a particular focus on the advantages of associativity in real-world fuzzy systems and a worked example in fuzzy image comparison. Finally, Section 6 concludes with a summary of the key findings.

2. Symmetric Difference Operator in Nilpotent Systems

In fuzzy logic, the law of contradiction (that $x\&\neg x$ is always false) and the law of excluded middle (that $x\vee \neg x$ is always true) generally do not hold. However, their intuitive appeal makes it reasonable to explore fuzzy logic systems in which these laws (together, they are called the classification property) apply. The subsequent discussion adheres to the definitions and properties as presented in [9,35].

2.1. Nilpotent Connective Systems

In this paper, the symmetric difference operator is studied in systems, where the conjunction and disjunction operators are continuous Archimedean nilpotent t-norms and t-conorms. Such t-norms and t-conorms will be denoted by $c(x,y):=T(x,y)$ and $d(x,y):=S(x,y)$.

A continuous Archimedean nilpotent t-norm c and t-conorm d can be characterized by unique and normalized continuous additive generator functions $f_c, f_c:[0,1]\to [0,\infty ]$, respectively, where $f_c$ is strictly decreasing with $f_c\left(1\right)=0$ and $f_d$ is strictly increasing with $s\left(0\right)=0$, such that

$$c(x,y)=f_c^{-1}[f_c\left(x\right)+f_c\left(y\right)]$$

(4)

and

$$d(x,y)=f_d^{-1}[f_d\left(x\right)+f_d\left(y\right)],$$

(5)

where $\left[\right]$ is the cutting function for the interval $[0,1]$.

Apart from the given negation operator in a connective system, which also has a generator function $n\left(x\right)=f_n^{-1}(1-f_n\left(x\right))$, there exist two special negations generated by the normalized additive generator functions of the conjunction and disjunction operators:

$$n_c\left(x\right)=f_c^{-1}(1-f_c\left(x\right))$$

(6)

and

$$n_d\left(x\right)=f_d^{-1}(1-f_d\left(x\right)).$$

(7)

A connective system $(c,d,n)$ is nilpotent if the conjunction c is a nilpotent t-norm and the disjunction d is a nilpotent t-conorm. In a connective system, the classification property holds if and only if $n_d\left(x\right)\le n\left(x\right)\le n_c\left(x\right)$. A nilpotent connective system can be classified as either a bounded system or a Łukasiewicz system, depending on the number of distinct negations. If all negations coincide, i.e., $n_c\left(x\right)=n_d\left(x\right)$, the system is referred to as a Łukasiewicz system. Conversely, if the negations differ, i.e., $n_d\left(x\right)<n\left(x\right)<n_c\left(x\right)$, it is classified as a bounded system. In a Łukasiewicz system, $f_c\left(x\right)+f_d\left(x\right)=1$, while in a bounded system, $f_c\left(x\right)+f_d\left(x\right)>1$.

In a connective system, the De Morgan identity signifies that for any $x,y\in [0,1]$:

$$c\left(n\right(x),n(y\left)\right)=n\left(d\right(x,y\left)\right)$$

or

$$d\left(n\right(x),n(y\left)\right)=n\left(c\right(x,y\left)\right).$$

2.2. Symmetric Difference Operator in Bounded Systems

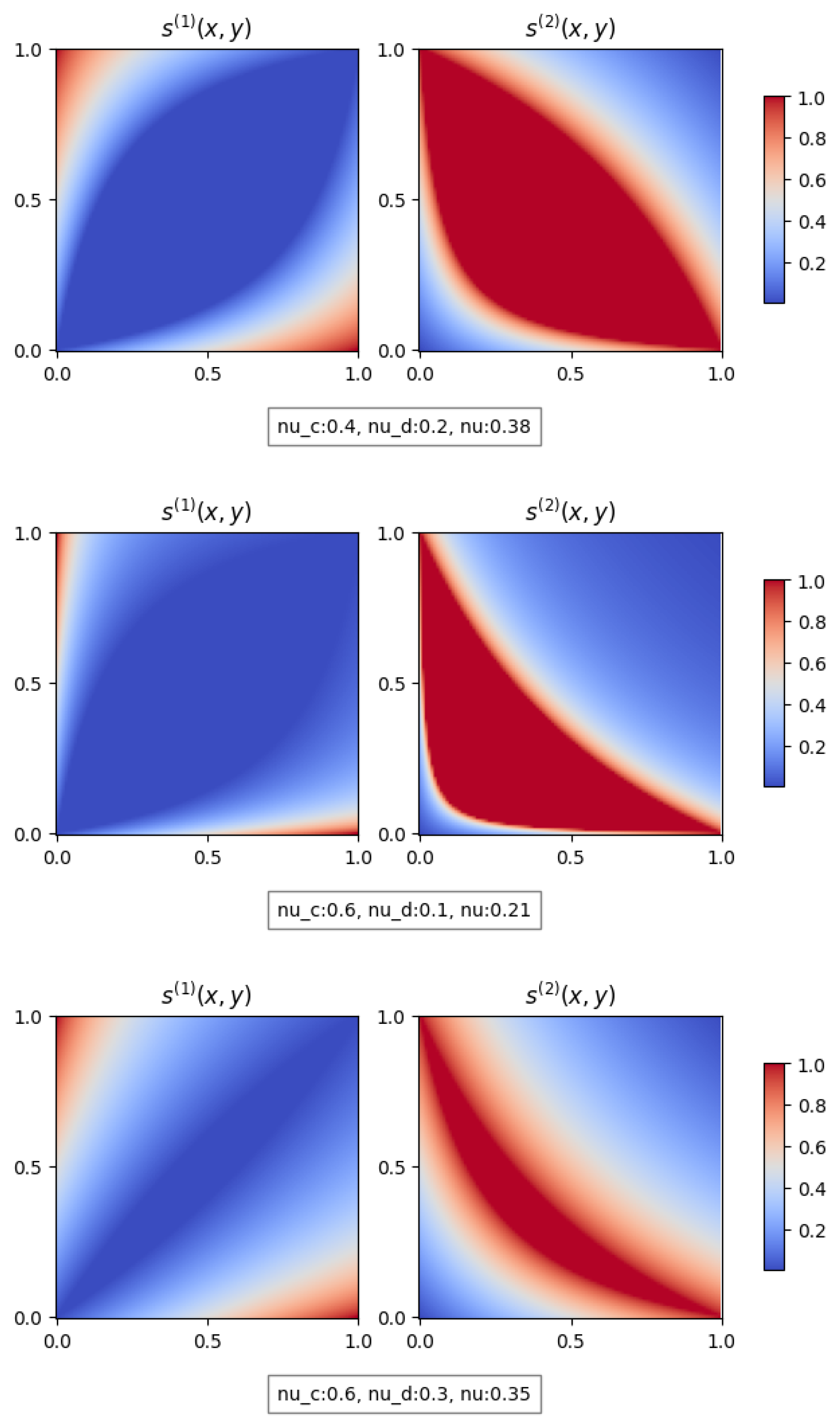
The novelty of the symmetric difference operator in nilpotent systems is the adjustable parameters, which define a threshold with a semantic meaning, either denoting the region of complete similarity or denoting the region of total dissimilarity. If $f_c\left(x\right)+f_d\left(x\right)\ne 1$, then there exist three different negations, $n\left(x\right)$, $n_c\left(x\right)$, and $n_d\left(x\right)$, which increases the flexibility of the symmetric difference operator.

Definition 1

([36]). Let $(c,d,n)$ be a nilpotent connective system. The nilpotent symmetric difference operators $s^{\left(1\right)}$, $s^{\left(2\right)}:[0,1]\times [0,1]\to [0,1]$ are

$$s^{\left(1\right)}(x,y)=d(c(x,n\left(y\right)),c(y,n\left(x\right)))$$

(8)

and

$$s^{\left(2\right)}(x,y)=c(d(x,y),n\left(c(x,y)\right)).$$

(9)

Remark 1.

Let the $(c,d,n)$ nilpotent connective system be bounded and let $f_c$ and $f_d$ denote the normalized generator functions of c and d, respectively. Using the normalized generator functions, the operators in a bounded system can be formulated as

$$s^{\left(1\right)}(x,y)=f_d^{-1}(f_d\left(f_c^{-1}(f_c\left(x\right)+f_c\left(n\left(y\right)\right))\right)+f_d\left(f_c^{-1}(f_c\left(y\right)+f_c\left(n\left(x\right)\right))\right)$$

(10)

and

$$s^{\left(2\right)}(x,y)=f_c^{-1}(f_c\left(f_d^{-1}(f_d\left(x\right)+f_d\left(y\right))\right)+f_c\left(n\left(f_c^{-1}(f_c\left(x\right)+f_c\left(y\right))\right)\right).$$

(11)

To visualize the nilpotent symmetric difference operators, the rational family of the normalized generator functions are considered [37].

Definition 2

([37]). The rational family of the normalized generator functions is

$$f_n\left(x\right)={\displaystyle \frac{1}{1+\frac{\nu }{1-\nu }\frac{1-x}{x}}},f_n\left(0\right)=0,$$

$$f_c\left(x\right)={\displaystyle \frac{1}{1+\frac{{\nu }_c}{1-{\nu }_c}\frac{x}{1-x}}},f_c\left(1\right)=0,$$

$$f_d\left(x\right)={\displaystyle \frac{1}{1+\frac{{\nu }_d}{1-{\nu }_d}\frac{1-x}{x}}},f_d\left(0\right)=0,$$

where $\nu ,{\nu }_c,{\nu }_d\in (0,1)$.

The De Morgan law holds in the connective system generated by the rational family of the normalized generator functions $f_n$, $f_c$, and $f_d$, if and only if

$${\left({\displaystyle \frac{1-\nu }{\nu }}\right)}^2={\displaystyle \frac{{\nu }_c}{1-{\nu }_c}}{\displaystyle \frac{1-{\nu }_d}{{\nu }_d}}$$

(12)

holds for the parameters ${\nu }_d$, ${\nu }_c$, and $\nu$.

Remark 2.

The fixpoints of the negation operators n, $n_c$, and $n_d$ are ν, $1-{\nu }_c$, and ${\nu }_d$ respectively. If $f_c\left(x\right)+f_d\left(x\right)=1$, then for the fixpoints of the negation operators, ${\nu }_c+{\nu }_d=1$. Moreover, if $f_c\left(x\right)+f_d\left(x\right)=1$ and the De Morgan property holds, then $\nu ={\nu }_d$.

Using the rational family of the normalized generator functions and the fact that in a bounded system $f_c\left(x\right)+f_d\left(x\right)>1$, which is equivalent to ${\nu }_c+{\nu }_d<1$, the nilpotent symmetric difference operator from Equations (8) and (9) can be observed in Figure 1. For visualizations, the parameter $\nu$ was calculated using Formula (12), so in this case, the De Morgan property holds.

In the next definition, the concept of duality will be formulated for the symmetric difference operator.

Definition 3.

Let s be a symmetric difference operator in a nilpotent connective system and let n be a strong negation. Then $\overline{s}(x,y)=n\left(s(x,n\left(y\right))\right)$ is called the dual operator of s.

Proposition 1.

The above-defined $s^{\left(2\right)}$ is the dual operator of $s^{\left(1\right)}$ if the De Morgan property holds.

Proof. 

Using the De Morgan identity,

$$\begin{array}{cc}\hfill {\overline{s}}^{\left(1\right)}(x,y)& =n\left(s^{\left(1\right)}(x,n\left(y\right))\right)=n\left(d(c(x,n\left(n\left(y\right)\right)),c(n\left(y\right),n\left(x\right)))\right)\hfill \\ \hfill & =n(d\left(c(x,y)\right),n\left(d(x,y)\right))=c(n\left(c(x,y)\right),n\left(n\left(d(x,y)\right)\right))=s^{\left(2\right)}(x,y).\hfill \end{array}$$

 □

Remark 3.

In a Łukasiewicz system, the De Morgan property holds; therefore, if $f_c\left(x\right)+f_d\left(x\right)=1$, then $s^{\left(2\right)}$ is the dual operator of $s^{\left(1\right)}$.

In a bounded system, the tolerance for total similarity or dissimilarity can be adjusted using the symmetric difference operator. In the rational family of normalized generator functions, the configurable parameters are $\nu$, ${\nu }_c$, and ${\nu }_d$. With these variables, the threshold can be set to determine the degree of similarity in which two elements are considered identical or totally different, as shown in Figure 2.

2.3. Symmetric Difference Operator in Łukasiewicz Systems

Using Equations (8) and (9), the symmetric difference operator in a Łukasiewicz system is as follows:

Proposition 2.

In a Łukasiewicz system,

$$s_l^{\left(1\right)}(x,y)=f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(y\right)\left|\right)$$

(13)

and

$$s_l^{\left(2\right)}(x,y)=f_c^{-1}\left(\right|f_c\left(x\right)+f_c\left(y\right)-1\left|\right).$$

(14)

Proof. 

Let $(c,d,n)$ be a Łukasiewicz consistent system and let $f_c$ and $f_d$ be the generator functions of the logical connectives c and d, respectively. Then $f_c:[0,1]\to [0,1]$ is continuous and strictly decreasing, while $f_d:[0,1]\to [0,1]$ is continuous and strictly increasing.

Also, in a Łukasiewicz system, $f_c\left(x\right)+f_d\left(x\right)=1$ holds for the generator functions and, equivalently, $n_c\left(x\right)=n_d\left(x\right)$; hence,

• $n_c\left(x\right)=f_c^{-1}(1-f_c\left(x\right))$, $f_c\left(n_c\left(x\right)\right)=1-f_c\left(x\right)$ and $f_c\left(n_c\left(x\right)\right)=f_d\left(x\right)$ or
• $n_d\left(x\right)=f_d^{-1}(1-f_d\left(x\right))$, $f_d\left(n_d\left(x\right)\right)=1-f_d\left(x\right)$, $f_d\left(n_d\left(x\right)\right)=f_c\left(x\right)$ and $n_d\left(x\right)=f_d^{-1}\left(f_c\left(x\right)\right)$.

Therefore, the symmetric difference operator can be written as

$$\begin{array}{cc}\hfill s_l^{\left(1\right)}(x,y)=& d(c(x,n_c\left(y\right)),c(y,n_c\left(x\right)))\hfill \\ \hfill =& d(f_c^{-1}(f_c\left(x\right)+f_c\left(n_c\left(y\right)\right)),f_c^{-1}(f_c\left(y\right)+f_c\left(n_c\left(x\right)\right)))\hfill \\ \hfill =& f_d^{-1}(f_d\left(f_c^{-1}(f_c\left(x\right)+f_d\left(y\right))\right)+f_d\left(f_c^{-1}(f_c\left(y\right)+f_d\left(x\right))\right)))\hfill \\ \hfill =& f_d^{-1}([1-f_c\left(f_c^{-1}(f_c\left(x\right)+f_d\left(y\right))\right)]+[1-f_c\left(f_c^{-1}(f_c\left(y\right)+f_d\left(x\right))\right)])\hfill \\ \hfill =& f_d^{-1}([1-(1-f_d\left(x\right)-f_d\left(y\right))]+[1-(1-f_d\left(y\right))-f_d\left(x\right)])\hfill \\ \hfill =& f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(y\right)\left|\right),\hfill \end{array}$$

because $x,y\in [0,1]$ implies $f_d\left(x\right),f_d\left(y\right)\in [0,1]$.

If $f_d\left(x\right)=f_d\left(y\right)$, then the right-hand side is equal to 0.

If $f_d\left(x\right)\ne f_d\left(y\right)$, then either $f_d\left(x\right)<f_d\left(y\right)$, that is, $f_d\left(x\right)-f_d\left(y\right)<0$; thus, $[f_d\left(x\right)-f_d\left(y\right)]=0$, or $f_d\left(y\right)<f_d\left(x\right)$, i.e., $f_d\left(y\right)-f_d\left(x\right)<0$; thus, $[f_d\left(y\right)-f_d\left(x\right)]=0$. Hence, the cutting function can be omitted in the last formula.

For the other formula,

$$\begin{array}{cc}\hfill s_l^{\left(2\right)}(x,y)=& c(d(x,y),n_c\left(c(x,y)\right))\hfill \\ \hfill =& c(f_d^{-1}(f_d\left(x\right)+f_d\left(y\right)),n_c\left(f_c^{-1}(f_c\left(x\right)+f_c\left(y\right))\right))\hfill \\ \hfill =& f_c^{-1}(f_c\left(f_d^{-1}(f_d\left(x\right)+f_d\left(y\right))\right)+f_c\left(f_d^{-1}(f_c\left(x\right)+f_c\left(y\right))\right))\hfill \\ \hfill =& f_c^{-1}([1-f_d\left(f_d^{-1}(f_d\left(x\right)+f_d\left(y\right))\right)]+[1-f_d\left(f_d^{-1}(f_c\left(x\right)+f_c\left(y\right))\right)])\hfill \\ \hfill =& f_c^{-1}([1-(1-f_c\left(x\right)+1-f_c\left(y\right))]+[1-(f_c\left(x\right)+f_c\left(y\right))])\hfill \\ \hfill =& f_c^{-1}\left(\right|f_c\left(x\right)+f_c\left(y\right)-1\left|\right).\hfill \end{array}$$

The last equality holds because either $0\le f_c\left(x\right)+f_c\left(y\right)<1$, in which case $[f_c\left(x\right)+f_c\left(y\right)-1]=0$ and $[1-(f_c\left(x\right)+f_c\left(y\right))]=1-(f_c\left(x\right)+f_c\left(y\right))$, or $1\le f_c\left(x\right)+f_c\left(y\right)\le 2$, in which case $[f_c\left(x\right)+f_c\left(y\right)-1]=f_c\left(x\right)+f_c\left(y\right)-1$ and $[1-(f_c\left(x\right)+f_c\left(y\right))]=0$. □

3. Properties of Symmetric Difference Operator in Nilpotent Systems

In this section, the main properties of $s^{\left(1\right)}$ and $s^{\left(2\right)}$ are examined, as well as their connection to the equivalence operators in nilpotent systems.

3.1. Properties in Bounded Systems

First, the properties of the symmetric difference operators in bounded systems are discussed.

Proposition 3.

The following properties hold for the $s^{\left(1\right)}(x,y)=d(c(x,n\left(y\right)),c(y,n\left(x\right)))$ symmetric difference operator in a bounded system:

1. 

Boundary conditions: $s^{\left(1\right)}(0,0)=s^{\left(1\right)}(1,1)=0$ and $s^{\left(1\right)}(0,1)=s^{\left(1\right)}(1,0)=1$;

2. 

Symmetry: $s^{\left(1\right)}(x,y)=s^{\left(1\right)}(y,x)$;

3. 

Neutrality property: $s^{\left(1\right)}(0,x)=s^{\left(1\right)}(x,0)=x$;

4. 

Strong negation principle: $s^{\left(1\right)}(1,x)=s^{\left(1\right)}(x,1)=n\left(x\right)$;

5. 

Reflexivity with respect to $n_c$: $s^{\left(1\right)}(x,x)=0$;

for all $x,y\in [0,1]$, where n is a continuous, strong negation operator.

Proof. 

• The boundary conditions hold because of the boundary conditions of n, c, and d.
• The symmetry holds trivially.
• The property holds because $c(0,z)=0$, $c(1,z)=z$, and $d(0,z)=z$ for any $z\in [0,1]$.
• Same as above.
• $c(x,n_c\left(x\right))=0$ and $d(0,0)=0$; hence, the equation holds.

 □

Proposition 4.

The following properties hold for the $s^{\left(2\right)}(x,y)=c(d(x,y),n\left(c(x,y)\right))$ symmetric difference operator in a bounded system:

1. 

Boundary conditions: $s^{\left(2\right)}(0,0)=s^{\left(2\right)}(1,1)=0$ and $s^{\left(2\right)}(0,1)=s^{\left(2\right)}(1,0)=1$;

2. 

Symmetry: $s^{\left(2\right)}(x,y)=s^{\left(2\right)}(y,x)$;

3. 

Neutrality property: $s^{\left(2\right)}(0,x)=s^{\left(2\right)}(x,0)=x$;

4. 

Strong negation principle: $s^{\left(2\right)}(1,x)=s^{\left(2\right)}(x,1)=n\left(x\right)$;

for all $x,y\in [0,1]$, where n is a continuous, strong negation operator.

Proof. 

This proof is similar to the proof of the properties of $s^{\left(1\right)}.$ □

Remark 4.

In both cases, reflexivity with respect to the negation n or the negation dissimilarity property may not generally hold, as there is no closed-form relationship between $f_c$ and $f_d$, or equivalently, between $n_c$ and $n_d$, even though both generator functions appear in the formulas.

Proposition 5.

In a bounded system, the antitonicity property, i.e., if $x\le x^{\prime }\le y^{\prime }\le y$, then $s(x^{\prime },y^{\prime })\le s(x,y)$ does not hold for $s^{\left(1\right)}$ or $s^{\left(2\right)}$.

Proof. 

The generator function $f_c$ is strictly decreasing and $f_d$ is strictly increasing. In the case of $s^{\left(1\right)}$, if $y^{\prime }\le y$, then $n\left(y^{\prime }\right)\ge n\left(y\right)$; hence, $f_c\left(n\left(y^{\prime }\right)\right)\le f_c\left(n\left(y\right)\right)$. Also, if $x^{\prime }\ge x$, then $f_c\left(x^{\prime }\right)\le f_c\left(x\right)$. Summing the inequalities yields $f_c\left(n\left(y^{\prime }\right)\right)+f_c\left(x^{\prime }\right)\le f_c\left(n\left(y\right)\right)+f_c\left(x\right)$. From this follows that $f_d\left(f_c^{-1}(f_c\left(n\left(y^{\prime }\right)\right)+f_c\left(x^{\prime }\right))\right)\ge f_d\left(f_c^{-1}(f_c\left(n\left(y\right)\right)+f_c\left(x\right))\right)$. Similarly, $f_d\left(f_c^{-1}(f_c\left(y^{\prime }\right)+f_c\left(n\left(x^{\prime }\right)\right))\right)\le f_d\left(f_c^{-1}(f_c\left(y\right)+f_c\left(n\left(x\right)\right))\right)$. Since one part decreases and the other increases, their combined effect does not guarantee a consistent order, which is required for antitonicity.

In the case of $s^{\left(2\right)}$, if x increases and y decreases, then $f_d\left(x\right)$ also increases, while $f_d\left(y\right)$ also decreases. This also prevents a consistent ordering for $f_d\left(x\right)+f_d\left(y\right)$. □

Proposition 6.

In a bounded system, the operator $s^{\left(1\right)}$ is invariant with respect to n, where n is a strong negation, i.e., $s^{\left(1\right)}(x,y)=s^{\left(1\right)}(n\left(x\right),n\left(y\right))$. However, the operator $s^{\left(2\right)}$ is only invariant with respect to the strong negation n if the De Morgan identity holds.

Proof. 

• $s^{\left(1\right)}(n\left(x\right),n\left(y\right))=d(c(n\left(x\right),n\left(n\left(y\right)\right))$, $c(n\left(y\right),n\left(n\left(x\right)\right)))=s^{\left(1\right)}(x,y).$
• The proof easily follows from the De Morgan identity.

 □

In a bounded system, without an explicit relationship between the generator functions $f_c$ and $f_d$, it is not possible to prove inequalities for the symmetric difference operators using the fixpoints ${\nu }_c$ and ${\nu }_d$ of $f_c$ and $f_d$, respectively, since both formulas involve compositions of both generator functions.

3.2. Properties in Łukasiewicz Systems

In this section, the properties of the symmetric difference operators in a Łukasiewicz system will be discussed; therefore, the closed formulas (see Proposition 2) and the fact that $f_c\left(x\right)+f_d\left(x\right)=1$ will be used.

Proposition 7.

Let $s_l^{\left(1\right)}(x,y)=f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(y\right)\left|\right)$ be a form of the symmetric difference operator in a Łukasiewicz system, where $f_d:[0,1]\to [0,1]$ is a continuous and strictly increasing generator function. Then, the boundary conditions $s_l^{\left(1\right)}(0,0)=s_l^{\left(1\right)}(1,1)=0$ and $s_l^{\left(1\right)}(0,1)=s_l^{\left(1\right)}(1,0)=1$ and the following properties hold, if $n_d$ is the negation operator generated by $f_d$:

1. 

Symmetry: $s_l^{\left(1\right)}(x,y)=s_l^{\left(1\right)}(y,x)$;

2. 

Neutrality property: $s_l^{\left(1\right)}(0,x)=s_l^{\left(1\right)}(x,0)=x$;

3. 

Strong negation principle: $s_l^{\left(1\right)}(1,x)=s_l^{\left(1\right)}(x,1)=n_d\left(x\right)$;

4. 

Reflexivity: $s_l^{\left(1\right)}(x,x)=0$;

for all $x,y\in [0,1]$.

Proof. 

The boundary conditions hold because $s_l^{\left(1\right)}(0,0)=f_d^{-1}\left(\right|f_d\left(0\right)-f_d\left(0\right)\left|\right)=0$, $s_l^{\left(1\right)}(1,1)=f_d^{-1}\left(\right|f_d\left(1\right)-f_d\left(1\right)\left|\right)=0$, $s_l^{\left(1\right)}(0,1)=f_d^{-1}\left(\right|f_d\left(0\right)-f_d\left(1\right)\left|\right)=1$, and $s_l^{\left(1\right)}(1,0)=f_d^{-1}\left(\right|f_d\left(1\right)-f_d\left(0\right)\left|\right)=1$.

Let n be a continuous negation operator and $x,y\in [0,1]$; hence, $f_d\left(x\right),f_d\left(y\right)\in [0,1]$. Then

• $s_l^{\left(1\right)}(x,y)=f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(y\right)\left|\right)=f_d^{-1}\left(\right|f_d\left(y\right)-f_d\left(x\right)\left|\right)=s_l^{\left(1\right)}(y,x)$.
• $s_l^{\left(1\right)}(0,x)=s_l^{\left(1\right)}(x,0)=f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(0\right)\left|\right)=f_d^{-1}\left(\right|f_d\left(x\right)\left|\right)=x$.
• $s_l^{\left(1\right)}(1,x)=s_l^{\left(1\right)}(x,1)=f_d^{-1}\left(\right|f_d\left(1\right)-f_d\left(x\right)\left|\right)=f_d^{-1}(1-f_d\left(x\right))=n_d\left(x\right)$.
• $s_l^{\left(1\right)}(x,x)=f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(x\right)\left|\right)=0$.

 □

Remark 5.

Of all $1-6$ properties of the symmetric difference operator in Boolean logic (listed in the Introduction Section), the exchange principle or associativity and the negation dissimilarity property do not hold for the $s_l^{\left(1\right)}$ operator.

Let $f_d$ be the identity function; then

• $s_l^{\left(1\right)}(s_l^{\left(1\right)}(x,y),z)\ne s_l^{\left(1\right)}(x,s_l^{\left(1\right)}(y,z))$, i.e., $\left|\right|x-y|-z|\ne |x-|y-z\left|\right|$, if $x,y,z\in [0,1]$. The counterexample values can be, e.g., $x=0.3$, $y=0.5$, and $z=0.7$.
• $s_l^{\left(1\right)}(x,n\left(x\right))=|x-(1-x)|=|2x-1|\ne 1$ if $x\in [0,1]$. The counterexample value can be, e.g., $x=0.6$.

Proposition 8.

Let $s_l^{\left(2\right)}(x,y)=f_c^{-1}\left(\right|f_c\left(x\right)+f_c\left(y\right)-1\left|\right)$ be a form of the symmetric difference operator in a Łukasiewicz system, where $f_c:[0,1]\to [0,1]$ is a continuous and strictly decreasing generator function. Then, the boundary conditions $s_l^{\left(2\right)}(0,0)=s(1,1)=0$ and $s_l^{\left(2\right)}(0,1)=s(1,0)=1$ and the following properties hold, if $n_c$ is the negation operator generated by $f_c$:

1. 

Symmetry: $s_l^{\left(2\right)}(x,y)=s_l^{\left(2\right)}(y,x)$;

2. 

Neutrality property: $s_l^{\left(2\right)}(0,x)=s_l^{\left(2\right)}(x,0)=x$;

3. 

Strong negation principle: $s_l^{\left(2\right)}(1,x)=s_l^{\left(2\right)}(x,1)=n_c\left(x\right)$;

4. 

Negation dissimilarity property: $s_l^{\left(2\right)}(x,n_c\left(x\right))=1$,=;

for all $x,y\in [0,1]$.

Proof. 

The boundary conditions hold because $f_c\left(0\right)=1$ and $f_c\left(1\right)=0$; therefore, $s_l^{\left(2\right)}(0,0)=f_c^{-1}\left(\right|f_c\left(0\right)+f_c\left(0\right)-1\left|\right)=0$, $s_l^{\left(2\right)}(1,1)=f_c^{-1}\left(\right|f_c\left(1\right)+f_c\left(1\right)-1\left|\right)=0$, $s_l^{\left(2\right)}(0,1)=f_c^{-1}\left(\right|f_c\left(0\right)+f_c\left(1\right)-1\left|\right)=1$, and $s_l^{\left(2\right)}(1,0)=f_c^{-1}\left(\right|f_c\left(1\right)+f_c\left(0\right)-1\left|\right)=1$.

Let n be a continuous negation operator and $x,y\in [0,1]$; hence, $f_c\left(x\right),f_c\left(y\right)\in [0,1]$. Then

• The symmetry holds trivially.
• The equation holds because $f_c\left(0\right)=1$.
• The equation holds because $f_c\left(1\right)=0$.
• $s_l^{\left(2\right)}(x,n_c\left(x\right))=f_c^{-1}\left(\right|f_c\left(x\right)+f_c\left(n_c\left(x\right)\right)-1\left|\right)=f_c^{-1}\left(\right|f_c\left(x\right)+f_d\left(x\right)-1\left|\right)=f_c^{-1}\left(0\right)=1$.

 □

Remark 6.

Of all $1-6$ properties listed in the Introduction Section for the symmetric difference operator in Boolean logic, two equations do not hold for the $s_l^{\left(2\right)}$ operator, namely the exchange principle or associativity and the reflexivity:

• Let $f_c\left(x\right)=1-x$; then $s_l^{\left(2\right)}(s_l^{\left(2\right)}(x,y),z)\ne s_l^{\left(2\right)}(x,s_l^{\left(2\right)}(y,z))$ is equivalent to $1-\left|\right|1-x-y|-z|\ne 1-\left|\right|1-y-z|-x|$. The counterexample values can be, e.g., $x=0.6$, $y=0.5$, and $z=0.7$.
• $s_l^{\left(2\right)}(x,x)=f_c^{-1}\left(\right|2f_c\left(x\right)-1\left|\right)$, which does not necessarily equal to 0.

Proposition 9.

In a Łukasiewicz system, the antitonicity property, i.e., if $x\le x^{\prime }\le y^{\prime }\le y$, then $s(x^{\prime },y^{\prime })\le s(x,y)$ holds for $s_l^{\left(1\right)}$, but it does not hold for $s_l^{\left(2\right)}$.

Proof. 

If $x\le x^{\prime }\le y^{\prime }\le y$, then $f_d\left(x\right)\le f_d\left(x^{\prime }\right)$ and $f_d\left(y^{\prime }\right)\le f_d\left(y\right)$. Therefore, $s_l^{\left(1\right)}(x^{\prime },y^{\prime })=f_d^{-1}\left(\right|f_d\left(x^{\prime }\right)-f_d\left(y^{\prime }\right)\left|\right)=f_d^{-1}(f_d\left(y^{\prime }\right)-f_d\left(x^{\prime }\right))\le f_d^{-1}\left(\right|f_d\left(y\right)-f_d\left(x\right)\left|\right)=s_l^{\left(1\right)}(x,y).$ In the case of $s_l^{\left(2\right)}$, the property cannot hold due to its formula. □

The next proposition describes the invariance property for the symmetric difference operators.

Proposition 10.

In a Łukasiewicz system, the operator $s_l^{\left(1\right)}$ is invariant with respect to $n_d$, i.e., $s_l^{\left(1\right)}(x,y)=s_l^{\left(1\right)}(n_d\left(x\right),n_d\left(y\right))$, and the operator $s_l^{\left(2\right)}$ is invariant with respect to $n_c$, i.e., $s_l^{\left(2\right)}(x,y)=s_l^{\left(2\right)}(n_c\left(x\right),n_c\left(y\right))$.

Proof. 

• $s_l^{\left(1\right)}(n_d\left(x\right),n_d\left(y\right))=f_d^{-1}\left(\right|f_d\left(f_d^{-1}(1-f_d\left(x\right))\right)-f_d\left(f_d^{-1}(1-f_d\left(y\right))\right)\left|\right)=f_d^{-1}\left(\right|1-f_d\left(x\right)-(1-f_d\left(y\right))\left|\right)=f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(y\right)\left|\right)=s_l^{\left(1\right)}(x,y).$
• $s_l^{\left(2\right)}(n_c\left(x\right),n_c\left(y\right))=f_c^{-1}\left(\right|f_c\left(f_c^{-1}(1-f_c\left(x\right))\right)+f_c\left(f_c^{-1}(1-f_c\left(y\right))\right)-1\left|\right)=f_c^{-1}\left(\right|1-f_c\left(x\right)+1-f_c\left(y\right)-1\left|\right)=f_c^{-1}\left(\right|1-(f_c\left(x\right)+f_c\left(y\right))\left|\right)=s_l^{\left(2\right)}(x,y).$

 □

In the following, the relationship between the symmetric difference operators and the fixpoints of the normalized generator functions are examined:

Proposition 11.

For the fixpoints ${\nu }_c$ and ${\nu }_d$ of the functions $f_c$ and $f_d$,

1. 

$s_l^{\left(1\right)}(x,{\nu }_d)\le {\nu }_d$ and

2. 

$s_l^{\left(2\right)}(x,{\nu }_c)\ge {\nu }_c$.

Proof. 

• Using the fact that $f_d\left({\nu }_d\right)=\frac{1}{2}$ and that $f_d\left(x\right)$ is continuous and strictly increasing, it follows $0\le \left[\right|f_d\left(x\right)-\frac{1}{2}\left|\right]\le \frac{1}{2}$ and $0\le f_d^{-1}\left(\right[|f_d\left(x\right)-\frac{1}{2}\left|\right])\le {\nu }_d$.
• Using the fact that $f_c\left({\nu }_c\right)=\frac{1}{2}$ and that $f_c\left(x\right)$ is continuous and strictly decreasing, it follows $0\le \left[\right|f_c\left(x\right)-\frac{1}{2}\left|\right]\le \frac{1}{2}$ and $1\ge f_c^{-1}\left(\right[|f_c\left(x\right)-\frac{1}{2}\left|\right])\ge {\nu }_d$.

 □

Proposition 12.

If ${\nu }_d<x,y<1$ or $0<x,y<{\nu }_d$, then $s_l^{\left(1\right)}(x,y)<{\nu }_d$. For its dual operator, if $0<x<{\nu }_c<y<1$ or $0<y<{\nu }_c<x<1$, then ${\nu }_c<s_l^{\left(2\right)}(x,y)$.

Proof. 

• If ${\nu }_d<x,y<1$, then $\frac{1}{2}<f_d\left(x\right),f_d\left(y\right)<1$. If $0<x,y<{\nu }_d$, then $0<f_d\left(x\right),f_d\left(y\right)<\frac{1}{2}$. In both cases, $|f_d\left(x\right)-f_d\left(y\right)|<\frac{1}{2}$; hence, $f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(y\right)\left|\right)<{\nu }_d$.
• If either $0<x<{\nu }_c<y<1$ or $0<y<{\nu }_c<x<1$, $\frac{1}{2}<f_c\left(x\right)+f_c\left(y\right)<1$, from which $0<|f_c\left(x\right)+f_c\left(y\right)-1|<\frac{1}{2}$ follows, then $f_c^{-1}\left(\right|f_c\left(x\right)+f_c\left(y\right)-1\left|\right)>{\nu }_d$.

 □

3.3. Relationship to Equivalence Operator

In traditional logic, the equivalence operator corresponds to the negation of the symmetric difference operator. Hence, it is reasonable to investigate whether a similar relationship exists between these two operators in bounded or Łukasiewicz systems.

Definition 4

([3]). The conjunctive and disjunctive equivalence operators in a bounded system are defined by the equalities $e_c(x,y)=f_c^{-1}\left[\right|f_c\left(x\right)-f_c\left(y\right)\left|\right]$ and $e_d(x,y)=f_d^{-1}[1-|f_d\left(x\right)-f_d\left(y\right)\left|\right]$.

In a bounded system, let $f_c$ and $f_d$ be the generator functions of the logical connectives c and d, and let $n_c=f_c^{-1}(1-f_c\left(x\right))$ and $n_d=f_d^{-1}(1-f_d\left(x\right))$ be the natural negations generated by $f_c$ and $f_d$, respectively. Then, the negation of the equivalence operators, using the negation operators with the corresponding generator functions, can be written as

$$n_c\left(e_c(x,y)\right)=f_c^{-1}(1-|f_c\left(x\right)-f_c\left(y\right)\left|\right)$$

(15)

and

$$n_d\left(e_d(x,y)\right)=f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(y\right)\left|\right).$$

(16)

Proposition 13.

In a bounded system, $n_c\left(e_c(x,y)\right)=n_d\left(e_d(x,y)\right)$ if $f_c\left(x\right)+f_d\left(x\right)=1$, i.e., it agrees with a Łukasiewicz system.

Proof. 

If $f_c\left(x\right)+f_d\left(x\right)=1$, then $n_c\left(x\right)=n_d\left(x\right)$. Also, $e_c(x,y)=e_d(x,y)$ only holds in a Łukasiewicz system [3]. □

Proposition 14.

In a bounded system, $s^{\left(1\right)}(x,y)=n_d\left(e_d(x,y)\right)$ implies $f_c\left(x\right)+f_d\left(x\right)=1$.

Proof. 

In a bounded system, $n_d\left(e_d(x,y)\right)=f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(y\right)\left|\right)$ but $s^{\left(1\right)}(x,y)=f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(y\right)\left|\right)$ if and only if $f_c\left(x\right)+f_d\left(x\right)=1$ holds. □

Remark 7.

In [8], it is proven that the above-defined equivalences $e_c$ and $e_d$ are not associative, which implies that $s^{\left(1\right)}$ also cannot be associative.

4. Aggregated Symmetric Difference Operator

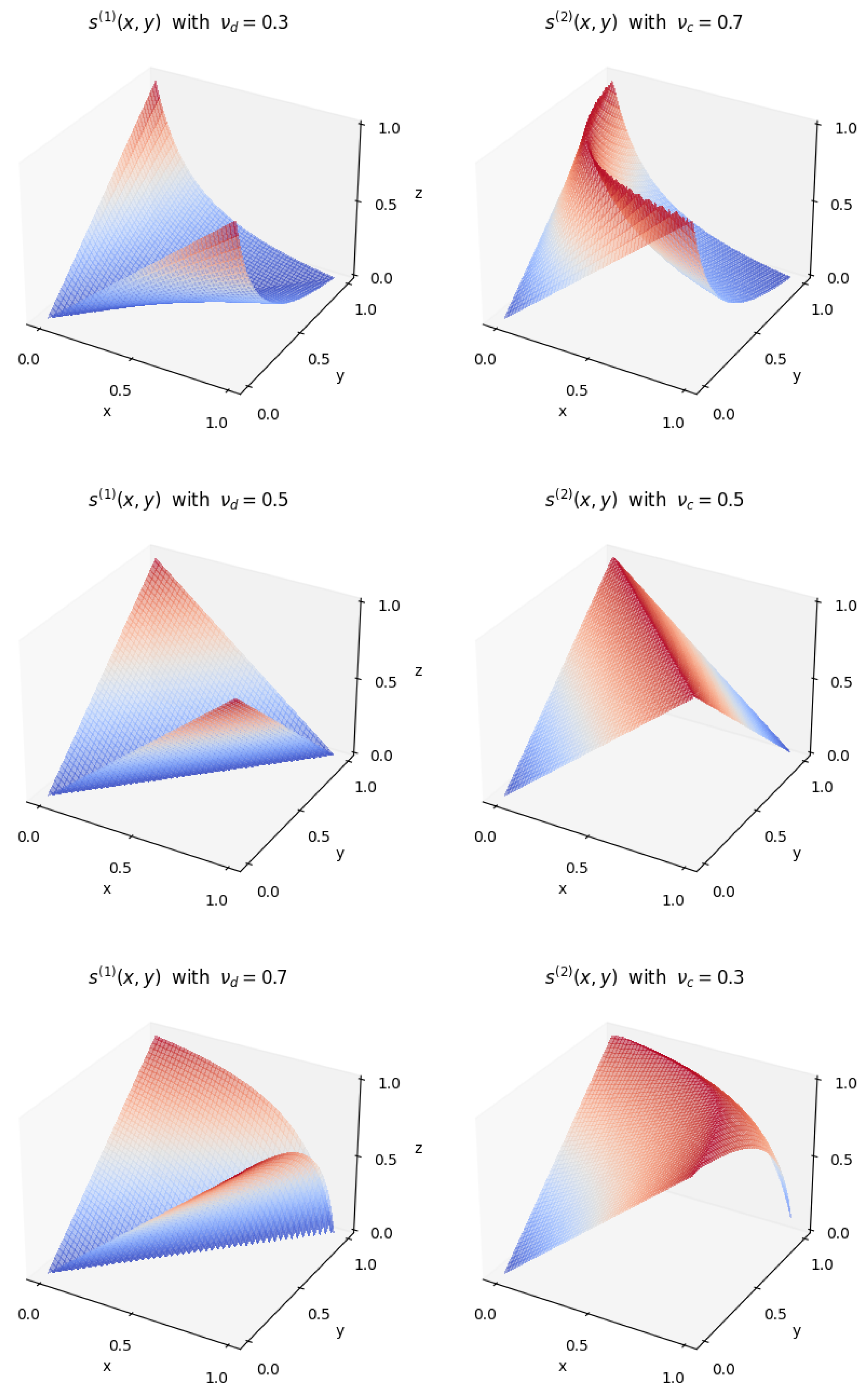
Based on the visualizations of the two formulas of the symmetric difference operator in nilpotent logical systems, as depicted in Figure 3, we can discern the main distinction between them. Specifically, the formula $s_l^{\left(1\right)}$ emphasizes that the result should be 0 on the main diagonal, signifying a symmetric difference of 0. Conversely, for $s_l^{\left(2\right)}$, the focus lies in ensuring that the result on the other diagonal is 1, indicating a symmetric difference of 1. However, when $x=y=0.5$, implying complete uncertainty, their symmetric difference should also be uncertain, i.e., $0.5$. Hence, investigating the arithmetic mean of the two formulas as a nilpotent symmetric difference operator is also reasonable.

Definition 5

([38]). The weighted arithmetic mean operators generated by the normalized generator functions of the conjunction and disjunction operators $f_c$ and $f_d$ are

• $m_c^{\left(\alpha \right)}(x,y)=f_c^{-1}[\alpha f_c\left(x\right)+(1-\alpha )f_c\left(y\right)]$ and
• $m_d^{\left(\alpha \right)}(x,y)=f_d^{-1}[\alpha f_d\left(x\right)+(1-\alpha )f_d\left(y\right)]$,
  where the parameter $\alpha \in (0,1)$.

Proposition 15

([38]). The weighted arithmetic mean operators $m_c^{\left(\alpha \right)}$ and $m_d^{\left(\alpha \right)}$ satisfy the self-De Morgan property with respect to $n_c$ and $n_d$ respectively, i.e.,

• $n_c\left(m_c^{\left(\alpha \right)}(x,y)\right)=m_c^{\left(\alpha \right)}(n_c\left(x\right),n_c\left(y\right))$ and
• $n_d\left(m_d^{\left(\alpha \right)}(x,y)\right)=m_d^{\left(\alpha \right)}(n_d\left(x\right),n_d\left(y\right))$.

The aggregation parameter is fixed at $\alpha =1/2$. This means that both symmetric difference operators need to take part equally in the aggregation. This way, in the case of total uncertainty ($x=y=0.5$), the arithmetic mean of the two operators yields the value of uncertainty, since $s_l^{\left(1\right)}(0.5,0.5)=0$, $s_l^{\left(2\right)}(0.5,0.5)=1$ and the result of the aggregation is $(1+0)/2=0.5$.

Definition 6.

In a nilpotent system, the aggregated symmetric difference operators with the aggregation parameter $\alpha =1/2$ are defined as

$$s_c^{*}(x,y)=m_c^{\left(\frac{1}{2}\right)}(s_l^{\left(1\right)}(x,y),s_l^{\left(2\right)}(x,y))$$

(17)

and

$$s_d^{*}(x,y)=m_d^{\left(\frac{1}{2}\right)}(s_l^{\left(1\right)}(x,y),s_l^{\left(2\right)}(x,y)),$$

(18)

where $s_l^{\left(2\right)}(x,y)={\overline{s}}_l^{\left(1\right)}(x,y)$.

In a Łukasiewicz system, $f_c\left(x\right)+f_d\left(x\right)=1$, which implies $s_c^{*}(x,y)=s_d^{*}(x,y)$. Since the two functions coincide, the notation $s^{*}$ will be used for both $s_c^{*}$ and $s_d^{*}$ in a Łukasiewicz system. To prove this equality, it is enough to substitute $f_c\left(x\right)=1-f_d\left(x\right)$ and $f_c^{-1}\left(x\right)=f_d^{-1}(1-x)$ into $m_c^{\left(\alpha \right)}(x,y)=f_c^{-1}[\alpha f_c\left(x\right)+(1-\alpha )f_c\left(y\right)]$, which yields $f_d^{-1}[\alpha f_d\left(x\right)+(1-\alpha )f_d\left(y\right)]=m_d^{\left(\alpha \right)}(x,y)$.

Proposition 16.

In a Łukasiewicz system, the closed formula of the aggregated symmetric difference operator with $\alpha =1/2$ is

$$s^{*}(x,y)=f_c^{-1}\left[\frac{1}{2}(1-|f_c\left(x\right)-f_c\left(y\right)\left|\right)+\frac{1}{2}\left[\right|f_c\left(x\right)+f_c\left(y\right)-1\left|\right]\right],$$

(19)

where $s^{*}(x,y)=s_c^{*}(x,y)=s_d^{*}(x,y)$.

Proof. 

The result follows from a direct calculation using the previously defined formulas. □

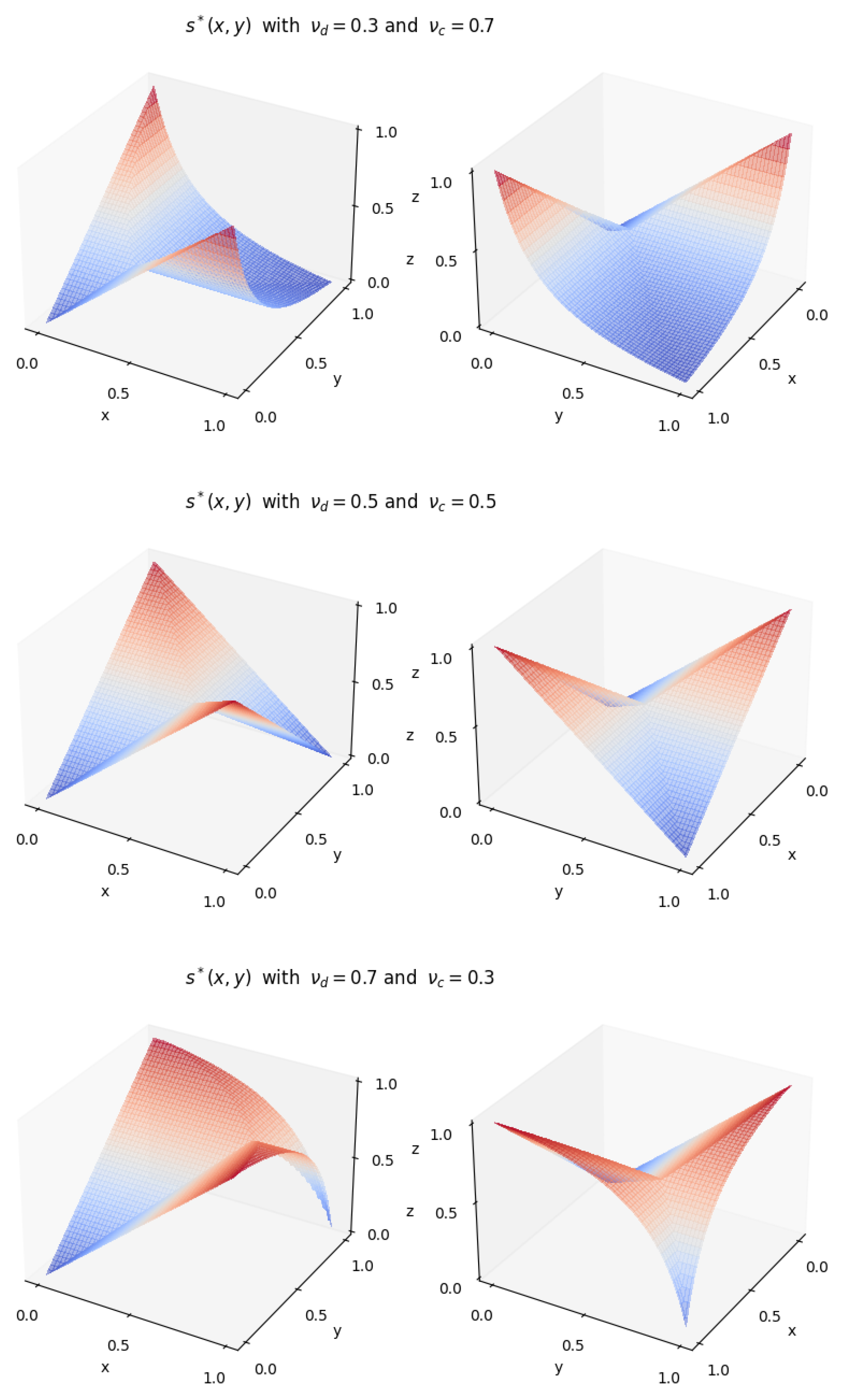
The aggregated symmetric difference operator exhibits an interesting property: its formula simplifies significantly by partitioning the space $[0,1]\times [0,1]$ into four distinct regions, as shown in Figure 4.

Proposition 17.

The aggregated symmetric difference operator has the following property:

$$s^{*}(x,y)=\left\{\begin{array}{cc}y,\hfill & \mathit{if}x\le y\mathit{and}x\le n_c\left(y\right)\hfill \\ n_c\left(x\right),\hfill & \mathit{if}{n}_c\left(y\right)\le x\le y\hfill \\ x,\hfill & \mathit{if}y\le x\le n_c\left(y\right)\hfill \\ n_c\left(y\right),\hfill & \mathit{if}y\le x\mathit{and}{n}_c\left(y\right)\le x.\hfill \end{array}\right.$$

(20)

Note that due to the monotonicity of $f_c$ and the formula of $n_c$, the inequalities $x\le n_c\left(y\right)$ and $y\le n_c\left(x\right)$ are equivalent.

Proof. 

The proof uses the monotonicity of $f_c$ and the equation $n_c\left(x\right)=f_c^{-1}(1-f_c\left(x\right))$.

• If $x\le y$, then $f_c\left(x\right)-f_c\left(y\right)\ge 0$. Also, if $y\le n_c\left(x\right)$, then $f_c\left(x\right)+f_c\left(y\right)\ge 1$, which implies that $s^{*}(x,y)=y$.
• If $n_c\left(y\right)\le x\le y$, then $f_c\left(x\right)-f_c\left(y\right)\ge 0$ and $f_c\left(x\right)+f_c\left(y\right)\le 1$, which implies that $s^{*}(x,y)=n_c\left(x\right)$.
• If $y\le x\le n_c\left(y\right)$, then $f_c\left(x\right)-f_c\left(y\right)\le 0$ and $f_c\left(x\right)+f_c\left(y\right)\ge 1$, which implies that $s^{*}(x,y)=x$.
• If $y\le x$ and $n_c\left(y\right)\le x$, then $f_c\left(x\right)-f_c\left(y\right)\le 0$ and $f_c\left(x\right)+f_c\left(y\right)\le 1$, which implies that $s^{*}(x,y)=n_c\left(y\right)$ (Figure 4).

 □

Proposition 18.

The aggregated symmetric difference operator $s^{*}$ has the following properties:

1. 

Boundary conditions: $s^{*}(0,0)=s^{*}(1,1)=0$ and $s^{*}(0,1)=s^{*}(1,0)=1$.

2. 

Symmetry: $s^{*}(x,y)=s^{*}(y,x)$.

3. 

Neutrality property: $s^{*}(0,x)=s^{*}(x,0)=x$.

4. 

Strong negation principle: $s^{*}(1,x)=s^{*}(x,1)=n_c\left(x\right)$.

5. 

The reflexivity property does not hold, but $s^{*}({\nu }_c,{\nu }_c)={\nu }_c$ for ${\nu }_c$ being the fixpoint of $f_c$. Moreover,

$$s^{*}(x,x)=\left\{\begin{array}{cc}x,\hfill & \mathit{if}x<{\nu }_c\hfill \\ n_c\left(x\right),\hfill & \mathit{if}x>{\nu }_c.\hfill \end{array}\right.$$

6. 

Antitonicity property: if $x\le x^{\prime }\le y^{\prime }\le y$, then $s^{*}(x^{\prime },y^{\prime })\le s^{*}(x,y)$.

7. 

Invariance with respect to $n_c$: $s^{*}(n_c\left(x\right),n_c\left(y\right))=s^{*}(x,y).$

8. 

$s^{*}(x,{\nu }_c)={\nu }_c$.

Proof. 

• Follows from a direct calculation.
• The proof is trivial.
• The equation holds because $f_c\left(0\right)=1.$
• The equation holds because $f_c\left(1\right)=0.$
• The statement follows from Proposition 17 and the fact that $f_c\left({\nu }_c\right)=\frac{1}{2}$ and $f_c^{-1}\left(\frac{1}{2}\right)={\nu }_c$.
• If $x<x^{\prime }<y^{\prime }<y$, then by Proposition 17, there are two cases. If $x<n_c\left(y\right)$, then $s^{*}(x,y)=y$. Again, there are two cases: either $x^{\prime }<n_c\left(y^{\prime }\right)$, in which case $s^{*}(x^{\prime },y^{\prime })=y^{\prime }<y$ or $n_c\left(y^{\prime }\right)<x^{\prime }$; then $s^{*}(x^{\prime },y^{\prime })=n_c\left(x^{\prime }\right)$. Since $n_c\left(y^{\prime }\right)<x^{\prime }$ implies $n_c\left(x^{\prime }\right)<y^{\prime }$ and $y^{\prime }<y$, $s^{*}(x^{\prime },y^{\prime })=n_c\left(x^{\prime }\right)<y$ follows. Otherwise, if $n_c\left(y\right)<x$, then $s^{*}(x,y)=n_c\left(x\right)$. In this case, either $x^{\prime }<n_c\left(y^{\prime }\right)$; therefore, $s^{*}(x^{\prime },y^{\prime })=y^{\prime }<n_c\left(x^{\prime }\right)<n_c\left(x\right)=s^{*}(x,y)$ or $n_c\left(y^{\prime }\right)<x^{\prime }$, in which case $s^{*}(x^{\prime },y^{\prime })=n_c\left(x^{\prime }\right)<n_c\left(x\right)=s^{*}(x,y)$.
• First, see that $f_c\left(n_c\left(x\right)\right)=f_c\left(f_c^{-1}(1-f_c\left(x\right))\right)=1-f_c\left(x\right)$ and, similarly, $f_c\left(n_c\left(y\right)\right)=1-f_c\left(y\right)$. Then

  $$\begin{array}{cc}\hfill s^{*}(n_c\left(x\right),& n_c\left(y\right))=f_c^{-1}\left[{\displaystyle \frac{1}{2}}(1-|1-f_c\left(x\right)-(1-f_c\left(y\right))|+{\displaystyle \frac{1}{2}}\left(\right|1-f_c\left(x\right)+1-f_c\left(y\right)-1\left|\right)\right]\hfill \\ \hfill =& f_c^{-1}\left[{\displaystyle \frac{1}{2}}(1-|f_c\left(y\right)-f_c\left(x\right)\left|\right)+{\displaystyle \frac{1}{2}}\left(\right|1-f_c\left(x\right)-f_c\left(y\right)\left|\right)\right]=s^{*}(x,y).\hfill \end{array}$$
• $s^{*}(x,{\nu }_c)=f_c^{-1}\left[\frac{1}{2}(1-|f_c\left(x\right)-\frac{1}{2}|+|f_c\left(x\right)-\frac{1}{2}\left|\right)\right]=f_c^{-1}\left(\frac{1}{2}\right)={\nu }_c.$

 □

Remark 8.

The negation dissimilarity property does not hold for the aggregated symmetric difference operator. It can be shown similarly to the case of $s_l^{\left(1\right)}$ in Remark 5.

In the following proposition, we establish the associativity of the aggregated symmetric difference operator, rendering the formula more attractive for various applications due to its behavior being more akin to traditional logic operators.

Proposition 19.

The aggregated symmetric difference operator $s^{*}$ is associative.

Proof. 

First, the case of $f_c\left(x\right)=1-x$ is considered. Then, let

$$\begin{array}{cc}\hfill L(x,y):=& s^{*}(x,y)=1-\left[{\displaystyle \frac{1}{2}}(1-|1-x-(1-y)\left|\right)+{\displaystyle \frac{1}{2}}\left(\right|1-x+1-y-1\left|\right)\right]\hfill \\ \hfill =& 1-\left[{\displaystyle \frac{1}{2}}(1-|y-x\left|\right)+{\displaystyle \frac{1}{2}}\left(\right|1-x-y\left|\right)\right]={\displaystyle \frac{1}{2}}(2-(1-|x-y|+|x+y-1|\left)\right)\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}(1+|x-y|-|x+y-1\left|\right).\hfill \end{array}$$

Considering the cases in (20), the following equation holds:

$$L(x,y)=\max \left(\min \right(x,1-y),\min (y,1-x\left)\right),$$

where the right-hand side is associative, because $L(x,L(y,z\left)\right)=\max \left(\min \right(x,y,z),\min (x,1-y,1-z),\min (1-x,y,1-z),\min (1-x,1-y,z\left)\right)=L\left(L\right(x,y),z).$ For an arbitrary generator function $f_c$,

$$f_c^{-1}(L(f_c\left(x\right),L(f_c\left(y\right),f_c\left(z\right)))=f_c^{-1}\left(L(L(f_c\left(x\right),f_c\left(y\right)),f_c\left(z\right))\right)$$

also holds. Since

$$s^{*}(x,y)=f_c^{-1}\left[{\displaystyle \frac{1}{2}}(1-|f_c\left(x\right)-f_c\left(y\right)\left|\right)+{\displaystyle \frac{1}{2}}|f_c\left(x\right)+f_c\left(y\right)-1|\right]=f_c^{-1}\left(L(f_c\left(x\right),f_c\left(y\right))\right)$$

and $s^{*}$ is associative. □

In Figure 5, the aggregated symmetric difference operator with $\alpha =1/2$ can be seen for different parameters ${\nu }_c$ and ${\nu }_d$ such that ${\nu }_c+{\nu }_d=1$. The left-hand figure is a rotation of the right-hand side for better observability.

Table 1. Summary of symmetric difference operators in nilpotent systems.

Name	Formula	Logic System
${▵}_1^{*}:2^X\times 2^X\to 2^X$	$A{▵}_1^{*}B=(A\cap B^c)\cup (A^c\cap B)$	Classical Boolean logic
${▵}_2^{*}:2^X\times 2^X\to 2^X$	$A{▵}_2^{*}B=(A\cup B)\cap {(A\cap B)}^c$	Classical Boolean logic
$s^{\left(1\right)}:[0,1]\times [0,1]\to [0,1]$	$d\left(c\right(x,n\left(y\right)),c(y,n\left(x\right)\left)\right)$	Bounded nilpotent system
$s^{\left(2\right)}:[0,1]\times [0,1]\to [0,1]$	$c\left(d\right(x,y),n(c(x,y)\left)\right)$	Bounded nilpotent system
$s_l^{\left(1\right)}:[0,1]\times [0,1]\to [0,1]$	$f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(y\right)\left|\right)$	Łukasiewicz system
$s_l^{\left(2\right)}:[0,1]\times [0,1]\to [0,1]$	$f_c^{-1}\left(\right|f_c\left(x\right)+f_c\left(y\right)-1\left|\right)$	Łukasiewicz system
$s^{*}:[0,1]\times [0,1]\to [0,1]$	${\displaystyle \frac{1}{2}}(s_l^{\left(1\right)}+s_l^{\left(2\right)})$	Aggregation in Łukasiewicz system

provides a summary of all defined operators with their names, formulas, and the corresponding logic systems. In

Table 2. Properties of the symmetric difference operators. The ✓ indicates that the property holds; ✗ indicates that it does not. Subscripts n, $n_c$, and $n_d$ denote the specific negation with respect to which the invariance is satisfied.

Operator	Symmetry	Neutrality	Strong Negation	Associativity	Reflexivity w.r.t. ${\mathit{n}}_{\mathit{c}}$	Negation Dissimilarity	Antitonicity	Invariance
$s^{\left(1\right)}(x,y)$	✓	✓	✓	✗	✓	✗	✗	✓n
$s^{\left(2\right)}(x,y)$	✓	✓	✓	✗	✗	✗	✗	✗
$s_l^{\left(1\right)}(x,y)$	✓	✓	✓	✗	✓	✗	✓	✓$n_d$
$s_l^{\left(2\right)}(x,y)$	✓	✓	✓	✗	✗	✓	✗	✓$n_c$
$s^{*}(x,y)$	✓	✓	✓	✓	✗	✗	✓	✓$n_c$

, the main properties of the various symmetric different operators are gathered for bounded and Łukasiewicz systems and for the aggregated formula.

5. Relevance and Application of Symmetric Difference Operators

The symmetric difference operator plays a crucial role in fuzzy logic systems, particularly in handling uncertainty, decision-making, and pattern recognition [39,40,41]. One of the most significant properties of this operator is its associativity, which provides multiple advantages across various domains. Associativity allows the symmetric difference operator to be expanded beyond two variables without the need for explicit grouping. In set theory, this means that operations involving multiple sets can be executed without considering parentheses, simplifying computations and improving clarity.

This property is particularly beneficial when dealing with large-scale fuzzy systems where multiple elements interact, ensuring consistency in results without recalculating intermediate steps. In computational applications, the symmetric difference operator finds extensive use in error detection and correction, particularly in coding theory [42,43]. Associativity ensures that sequences of operations can be computed efficiently, enabling a faster identification and rectification of inconsistencies in error-correcting codes and cryptographic protocols [44]. Moreover, in secret sharing schemes, associativity ensures that splitting and reconstructing secret data remains consistent and secure across multiple steps [45].

A key computational advantage of an associative symmetric difference operator is its role in XOR-based operations. Many programming tasks rely on XOR for bitwise manipulations, parity checking, and encryption [46]. When the operator is associative, computations can be reordered or parallelized, reducing execution time and improving algorithmic efficiency [47]. This is particularly valuable in high-performance computing and large-scale data processing tasks.

In graph theory, the symmetric difference operator is used to identify differences in the edge sets of graphs. Associativity ensures that this comparison remains independent of the order in which graphs are processed, making it easier to detect structural variations in networks, analyze connectivity, and solve optimization problems efficiently [48]. In the medical field, analyzing differences between datasets, such as genetic sequences, DNA mutations, and medical records, relies on robust set operations. Associativity simplifies the comparison process, enabling the seamless integration of multiple datasets to identify anomalies [49].

In medical imaging, it facilitates multi-step change detection in scans, helping track tumor growth, birthmarks, or other diagnostic markers over time without ambiguity caused by ordering effects. When working with large-scale data, ensuring consistency and reliability is essential. Associativity in symmetric difference operations simplifies the detection of inconsistencies across multiple sources, making it easier to identify discrepancies in datasets, validate integrity in databases, and enhance decision-making in fuzzy logic-based expert systems. The associativity of the symmetric difference operator is a fundamental property that enhances flexibility, efficiency, and reliability across various disciplines. From theoretical foundations in set theory to practical applications in computing, cryptography, medicine, and graph analysis, this property ensures that operations remain structured, scalable, and computationally efficient. Its role in simplifying multi-element comparisons and enabling seamless information processing makes it an indispensable component of fuzzy logic systems and beyond.

To further illustrate this relevance, we present a real-world application in fuzzy image comparison. In many practical settings, such as low-quality surveillance, thermal imaging, or noisy diagnostics, image differences must be evaluated gradually rather than with strict pixel-by-pixel matching. This is where fuzzy symmetric difference operators excel.

We used the grayscale version of the standard astronaut image and introduced Gaussian noise to create a perturbed version, as shown in Figure 6. Each pixel, normalized in $[0,1]$, is treated as a fuzzy value. We then applied three symmetric difference operators:

$$\begin{array}{cc}\hfill s_l^{\left(1\right)}(x,y)& =f_d^{-1}\left(\right|f_d\left(x\right)-f_d\left(y\right)\left|\right),\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill s_l^{\left(2\right)}(x,y)& =f_c^{-1}\left(\right|f_c\left(x\right)+f_c\left(y\right)-1\left|\right),\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill s^{*}(x,y)& =f_c^{-1}\left[{\displaystyle \frac{1}{2}}(1-|f_c\left(x\right)-f_c\left(y\right)\left|\right)+{\displaystyle \frac{1}{2}}|f_c\left(x\right)+f_c\left(y\right)-1|\right],\hfill \end{array}$$

(23)

where $f_d$ and $f_c$ are generator functions with ${\nu }_d=0.7$ and ${\nu }_c=0.3$, respectively.

Figure 7 compares the outputs:

• $s_l^{\left(1\right)}$ emphasizes absolute differences, detecting small intensity changes.
• $s_l^{\left(2\right)}$ is sensitive to deviations from complementarity, interpreting symmetry around 0.5.
• $s^{*}$, the associative operator, provides a balanced result that smooths the contrast while preserving essential difference features.

While associativity is not required in fuzzy systems, unlike classical logic, it becomes a valuable property in compositional and recursive environments. It ensures that the grouping of comparisons does not affect outcomes, which is essential in systems with hierarchical or iterative operations. However, it comes at the cost of increased complexity. As shown, the associative formula $s^{*}$ is an aggregated combination of the two non-associative symmetric differences, capturing complementary strengths of both.

Therefore, although more intricate, the associative symmetric difference offers a practical and theoretical advantage in applications that demand robust, consistent, and scalable similarity measures within nilpotent fuzzy logic frameworks.

6. Conclusions

This paper comprehensively investigates symmetric difference operators within logical systems generated by nilpotent t-norms and t-conorms, with particular attention to bounded and Łukasiewicz systems. While classical logic presents two equivalent forms of the symmetric difference operator, in nilpotent fuzzy logic, these forms, denoted as $s^{\left(1\right)}$ and $s^{\left(2\right)}$, exhibit distinct behaviors, especially with respect to associativity. We showed that neither operator is associative, despite each satisfying several desirable properties such as symmetry, neutrality, antitonicity, and invariance under negation. This non-associativity limits their utility in recursive or modular fuzzy reasoning systems.

To address this limitation, we proposed a novel symmetric difference operator, $s^{*}$, formed by aggregating $s^{\left(1\right)}$ and $s^{\left(2\right)}$ through their arithmetic mean. A key theoretical contribution of this work is the proof that $s^{*}$ is associative (Proposition 19), enabling consistent multi-element comparisons and simplifying multi-step computations in fuzzy systems. Though this operator is more complex, it retains crucial logical properties and provides smoother and more stable behavior.

In fuzzy logic systems, symmetric difference operators serve as natural measures of contrast or imbalance between fuzzy truth values, making them useful in real-world reasoning scenarios such as decision-making or risk assessment. For example, in evaluating fire risk based on temperature and humidity, a high temperature ($0.9$) and low humidity ($0.2$) reflect strong contrast, which should indicate elevated risk. In a nilpotent fuzzy logic framework, the symmetric difference operators capture this well, with $s^{\left(1\right)}(0.9,0.2)\approx 0.84$, $s^{\left(2\right)}(0.9,0.2)\approx 0.78$, and the aggregated operator $s^{*}(0.9,0.2)\approx 0.62$. All three reflect high contrast but differ in sensitivity, especially when the inputs are closer. For instance, with values $x=0.6$ and $y=0.3$, we get $s^{\left(1\right)}(0.6,0.3)\approx 0.41$, while $s^{\left(2\right)}(0.6,0.3)\approx 0.65$, showing how the two operators behave differently. This arises because $s^{\left(1\right)}$ depends on the difference between generator values, while $s^{\left(2\right)}$ measures how their sum deviates from 1. In such cases, each operator may suggest a different level of opposition, which can affect downstream reasoning in fuzzy systems.

In fuzzy systems such as fuzzy clustering, conflict detection, or information fusion, symmetric difference operators are frequently used to model dissimilarity; however, they are often not associative, meaning the result may vary based on the grouping of terms. While associativity is not a required property in fuzzy logic, where reasoning is inherently graded and context-sensitive, it is a desirable feature that enables more predictable and reliable behavior in larger, modular, or recursive systems. The proposed aggregated operator $s^{*}$ offers a balanced and associative alternative that enhances both theoretical consistency and practical applicability. Its benefits are particularly evident in domains such as image processing, fuzzy neural networks, cryptographic algorithms, and medical data analysis, where interpretable and efficient similarity measures are essential.

This work complements the framework established in [8], which introduced a variety of logical operators in nilpotent systems but did not address symmetric differences. By filling this gap, our broader aim is to systematically derive and study symmetric difference operators in both bounded and Łukasiewicz systems, as this represents a novel direction of research in fuzzy logic. We hope that this contribution not only extends the theoretical foundations of explainable fuzzy systems but also supports future applications in interpretable artificial intelligence and decision-making models.