Abstract
Background: With COVID-19 having a significant impact on economic activity, it has become difficult for the existing dynamic factor models (nowcasting models) to forecast macroeconomics with high accuracy. The real-time monitoring of macroeconomics has become an important research problem faced by banks, governments, and corporations. Subjects and Methods: This paper proposes an adaptive evolutionary causal dynamic factor model (AcNowcasting) for macroeconomic forecasting. Unlike the classical nowcasting models, the AcNowcasting algorithm has the ability to perform feature selection. The criteria for feature selection are based on causality strength rather than being based on the quality of the prediction results. In addition, the factors in the AcNowcasting algorithm have the capacity for adaptive differential evolution, which can generate the best factors. These two abilities are not possessed by classical nowcasting models. Results: The experimental results show that the AcNowcasting algorithm can extract common factors that reflect macroeconomic fluctuations better, and the prediction accuracy of the AcNowcasting algorithm is more accurate than that of traditional nowcasting models. Contributions: The AcNowcasting algorithm provides a new prediction theory and a means for the real-time monitoring of macroeconomics, which has good theoretical and practical value.
Keywords:
Fourier domain transfer entropy; mixed-frequency dynamic factor model; adaptive differential evolution; nowcasting model MSC:
68T05; 68Q10; 68W40; 68W05
1. Introduction
In the era of big data, real-time macroeconomic condition monitoring has become an important task for banks, governments, and corporations. With respect to the economic crises that have occurred in the past 100 years, each crisis has caused serious damage to the macroeconomy. As a result, scholars have paid increasing attention to predictions of the macroeconomic aspects. For example, the worldwide economic crisis from 1929 to 1933 directly gave birth to macroeconomic forecasting research. In the late 1930s, Burns and Mitchell first analyzed economic fluctuations and reviewed hundreds of economic variables to find patterns and rules [1]. These large and complex data were screened to extract relevant information for evaluating the health of the economy.
It is widely known that the financial crisis of 2008 was second only to the global economic crisis of 1929–1933. After the 2008 financial crisis, utilizing traditional cycle theory, many scholars predicted that the depression caused by this crisis would last for up to five years. However, the crisis lasted for nine years, and this prediction completely fell through. It is difficult to explain this phenomenon based on traditional economics. In addition, due to the different release times and frequencies of high-dimensional economic data, missing values often occur. Since most economic analyses require complete data as their input variables, these missing values must be estimated. In view of this issue, in 2008, Giannone et al. [2] proposed the first dynamic factor model that combined big data and filtering technology. In 2014, Bańbura and Modugno [3] improved the expectation maximization (EM) algorithm to estimate the parameters of the dynamic factor model for any dataset with missing data patterns. In 2016, the famous economist Paul M. Romer noted in his article “The Trouble with Macroeconomics” is that no progress has been made with respect to handling identification problems, and it has not progressed since the early 1970s. In 2018, Bok et al. [4] proposed a macroeconomic dynamic factor model (nowcasting model) for forecasting Gross Domestic Products (GDPs) using big data from the Federal Reserve Bank of New York. Since then, nowcasting models have been utilized in a wide range of applications in fields such as economics and finance.
Unfortunately, great stagnation was caused by Coronavirus Disease 2019 (COVID-19) in 2020. The outbreak of the COVID-19 pandemic has led to a deeper and more sustained decline in the global economy than that observed in 2008. Many economic variables have undergone extraordinary changes, and traditional economics also struggles to explain these phenomena. With the significant impact of COVID-19 on economic activity, the existing nowcasting models have difficulty forecasting with high accuracy [5]. In 2022, Nakazawa attempted to improve the accuracy of GDP nowcasting models by using alternative data [5]. However, at present, interdisciplinary methods for macroeconomic prediction research are lacking. The current dynamic factor models cannot choose variables or perform adaptive evolution.
Given the aforementioned problems regarding macroeconomic models, the forecasting accuracy of macroeconomic models is improved in this paper with the help of relevant theories in the computer domain. The desired pattern recognition method that Burns and Mitchell sought in the late 1930s, i.e., feature selection, was detailed decades later in the field of computers. Feature selection is an effective method for reducing redundant features [6], but it easily falls into local optima. To solve the above problem with feature selection, many evolutionary computation methods have been developed. For example, Storn and Price [7] proposed the differential evolution (DE) algorithm in 1997, which evolved the global solution through population mutation, crossover, and selection. Most of the existing methods neglect to consider the selection of high-dimensional features, resulting in issues of stagnation in local optima and numerical instability. In 2022, Wang et al. [8] proposed a self-adaptive weighted DE algorithm to address large-scale feature selection problems.
On the basis of the above model and algorithm, an adaptive evolutionary causal dynamic factor model (AcNowcasting) is proposed in this paper to evaluate macroeconomic health. First, a variable pool is formed by calculating the transfer entropy in the Fourier domain to select the variables that affect macroeconomic fluctuations. The EM algorithm and the Kalman smoother are subsequently used to extract different types of dynamic factors for each economic variable contained in the variable pool. Finally, these dynamic factors generate the optimal factors through a self-adaptive weighted DE algorithm. Therefore, the most suitable potential dynamic factor is generated to improve the accuracy of real-time macroeconomic monitoring.
2. Literature Review
The goal of this paper is to improve some of the shortcomings possessed by the current macroeconomic prediction models in high-dimensional space using relevant algorithms in the computer field, such as the DE algorithm. This topic belongs to the interdisciplinary fields of economics and computer science. Therefore, the relevant references are summarized from the perspectives of economics and computer science as follows.
From the perspective of economic theory, causality has been studied for a long time. Granger [9] proposed the linear Granger causality test in 1969. Marinazzo et al. [10] extended the Granger causality test to nonlinear situations. Dhamala et al. [11] used Fourier and wavelet transformations to propose nonlinear Granger causality. From the perspective of information theory, Schreiber [12] proposed the transfer entropy method to test for causality. Staniek and Lehnertz [13] proved that transfer entropy is a robust and fast causality testing method. Lobier et al. [14] used a coupled neuron model to evaluate the characteristics of transfer entropy. Wollstadt et al. [15] reported that transfer entropy is suitable for use with nonstationary time series. Porfiri et al. [16] determined the causal effect between dynamic systems with the help of transfer entropy. Restrepo et al. [17] proposed a method for determining transfer entropy between two systems. Silini and Masoller [18] proposed the use of pseudotransfer entropy to measure causality. Tian et al. [19] reported that Fourier domain transfer entropy can effectively address nonstationary processes in high-dimensional environments in 2021. At present, the causal models in the economic field, such as the Granger causality test [9,10,11] and transfer entropy [12,13,14,15,16,17,18,19], do not have predictive capabilities and cannot predict the future. They can analyze only historical data for causal analysis purposes.
From the perspective of computer theory, the selected mutation strategy and control parameters have great impacts on the adaptability of DE algorithms [20]. Mohamed and Suganthan [21] proposed an enhanced adaptive DE algorithm to solve global value optimization problems in continuous spaces. Sun et al. [22] introduced a series of combined strategies for implementing DE. Chen [23] proposed dual population self-adaptive DE to solve large-scale nonconvex DE problems. Tarkhaneh et al. [24] proposed an improved DE-based feature selection method using a mutation strategy. Wang et al. [25] proposed an adaptive DE algorithm based on parameter evolution. Meng and Yang [26] proposed a two-stage DE algorithm with parameter control, which is used to globally optimize a single parameter. Wang et al. [27] proposed an adaptive DE algorithm with a neighborhood crossing strategy. Currently, the DE algorithms in the field of computer science, such as adaptive DE algorithms [20,21,22,23,24,25,26,27], do not have causal analysis capabilities and cannot perform causal analyses on the features of models. They are more focused on conducting adaptive DE on model parameters than on implementing adaptive DE for model features.
From the perspective of mixed data models (that is, models that can simultaneously process data with different frequencies), three types of mixed data models exist. The first is mixed data sampling regression (MIDAS). Ghysels et al. [28] proposed the MIDAS model, which handles different time-frequency sequences. Ghysels et al. [29] proposed a variety of expanded MIDAS models. Miller [30] introduced the cointegration MIDAS model, which possesses a common random trend in the predicted model. Gong et al. [31] proposed the Copula-MIDAS model to describe asymmetric returns and liquidity dependence. Ghysels and Qian [32] employed MIDAS to estimate the slope and intercept parameters of regression equations. Liu and Lee [33] used the dynamic correlation coefficient-based MIDAS model to identify dynamic correlations. The second method is the mixed-frequency vector autoregressive (MF-VAR) mode. Mariano and Murasawa [34] proposed the MF-VAR model. Eraker et al. [35] employed a Bayesian approach to estimate the parameters of the MF-VAR model. Foroni et al. [36] integrated the status switching parameters into the MF-VAR model. Schorfheide and Song [37] developed a mixed-frequency Bayesian vector autoregressive (BVAR) model. Knotek and Zaman [38] used the BVAR model and MIDAS model to predict macroeconomic variables. The third type of model includes mixed-frequency dynamic factor models (MF-DFMs), which are dynamic factor models that use state-space expressions to process mixed data. Giannone et al. [2] proposed an MF-DFM model to predict macroeconomic conditions in real time. Jungbacker et al. [39] estimated the parameters of a high-dimensional MF-DFM model via the maximum likelihood method. Forni et al. [40] obtained a unilateral representation of the generalized MF-DFM. Fiorentini et al. [41] effectively estimated the MF-DFM with the help of EM algorithms and ARMA models. Glocker and Kaniovski [42] proposed an MF-DFM based on a set of small-scale factor models. Martínez-Hernández et al. [43] studied the time-related MF-DFM and its associated nonparameter estimation approach. To our knowledge, mixed-frequency models such as MIDAS [28,29,30,31,32,33], MF-VAR models [34,35,36,37,38], and MF-DFMs [39,40,41,42,43] can handle data with different frequencies. However, they do not have the ability to conduct causal analyses on the features of models. They also lack adaptive DE capabilities.
The above literature shows that the existing causal test models and adaptive evolution algorithms are aimed at analyzing data with the same frequency, and have difficulty analyzing mixed-frequency data. The existing mixed data models have a great advantage in terms of processing mixed data, but no causal selection criteria are available for the model variables, and these models show no adaptive evolution capabilities for determining the model parameters in macroeconomic prediction tasks. In view of this, the innovation of this paper is reflected in the attempt to improve the MF-DFM in several ways. An adaptive evolutionary causal dynamic factor (AcNowcasting) model is proposed in this paper, and it has several notable advantages.
First, traditional nowcasting models (such as those of Giannone et al. [2] and Bok et al. [4]) cannot perform feature selection. However, the AcNowcasting algorithm has the ability to perform feature selection. This is because it uses Fourier domain transfer entropy to calculate the statistical significance of causalities for feature selection purposes. The feature selection criteria employed in this paper are based on causal strength. This is different from the feature selection criteria that are used in the computer field, such as those of Tarkhaneh et al. [24], which are usually based on the quality of prediction or classification results.
Second, the factors contained in the traditional nowcasting models (such as those of Bańbura and Modugno [3] and Bok et al. [4]) cannot undergo adaptive evolution. However, the factors included in the AcNowcasting algorithm have adaptive DE capabilities because this model uses a self-adaptive weighted DE algorithm. In addition, the self-adaptive weighted DE algorithm employed in this paper is also different from those in the traditional computer science field, such as that of Wang [8]. That is, our algorithm does not undergo large-scale feature selection, but instead generates the optimal potential factors. These potential factors in the AcNowcasting algorithm, improved by Fourier domain transfer entropy, can be adaptively evolved through the self-adaptive weighted DE algorithm. Regarding the stability of the results, additional limitations are imposed on factor-adaptive DE during the experiments.
Third, in 2022, Nakazawa reported that with COVID-19 having a significant impact on economic activity, the existing nowcasting model has difficulty forecasting with high accuracy [5]. The experimental results in this paper show that the AcNowcasting algorithm can extract common factors that better reflect macroeconomic fluctuations. Compared with that of the traditional nowcasting model, the prediction accuracy of the AcNowcasting algorithm is improved, thus further improving the accuracy of real-time macroeconomic monitoring tasks.
3. Adaptive Evolutionary Causal Dynamic Factor Model
The problem to be solved in this paper is that with COVID-19 having a significant impact on economic activity, the existing dynamic factor models (nowcasting) have difficulty forecasting macroeconomics with high accuracy. That is, the traditional nowcasting model has two defects. First, this model [2,3,4] cannot perform feature selection. Second, the factors contained in the model [2,3,4] cannot undergo adaptive evolution.
To address the aforementioned shortcomings of the traditional nowcasting model, the main idea of the macroeconomic forecasting algorithm (AcNowcasting) proposed in this paper is to utilize relevant algorithms in the computer science field, such as the self-adaptive weighted DE algorithm [8], and causal analysis methods from the economics field, such as Fourier domain transfer entropy [19]. Specifically, to address the first defect, Fourier domain transfer entropy is used to calculate the statistical significance of causality for feature selection purposes. The feature selection criteria employed in this paper are based on causality strength rather than on the quality of the prediction or classification results. To address the second defect, the factors contained in the AcNowcasting algorithm have the ability to undergo adaptive DE because the self-adaptive weighted DE algorithm is utilized. Therefore, the AcNowcasting algorithm can extract common factors that better reflect macroeconomic fluctuations, and the prediction accuracy of the AcNowcasting algorithm is greater than that of the traditional nowcasting model. Table 1 shows the symbols used in the model and explains their roles.

Table 1.
Symbols of model.
The greatest advantages of the proposed approach are that it targets prediction problems in the economic field, selects the advantages of the relevant models in the computer science and mathematical fields to improve the specific shortcomings of economic models, and has interdisciplinary characteristics. The flowchart of the AcNowcasting algorithm is shown in Figure 1. Specifically, Stage 1 involves performing feature selection on the basis of causality to establish a variable pool. The traditional nowcasting model cannot perform feature selection, whereas the AcNowcasting algorithm can do so because it utilizes Fourier domain transfer entropy [19] to calculate the statistical significance of causalities. The feature selection criteria are based on causal strength rather than the quality of the prediction results. The economic variables that affect economic fluctuations are selected, and then a variable pool is established. Stage 2 involves extracting dynamic factors from the economic variable pool. Different types of potential factors are extracted for each variable in the variable pool; this is accomplished by the EM algorithm and a Kalman filter [3]. Stage 3 consists of applying adaptive DE to the dynamic factors. The factors contained in the traditional nowcasting model cannot undergo adaptive evolution. However, these potential factors in the AcNowcasting algorithm can be adaptively evolved to improve the accuracy of macroeconomic predictions through the self-adaptive weighted DE algorithm [8]. Stage 4 involves monitoring the macroeconomy in real time.
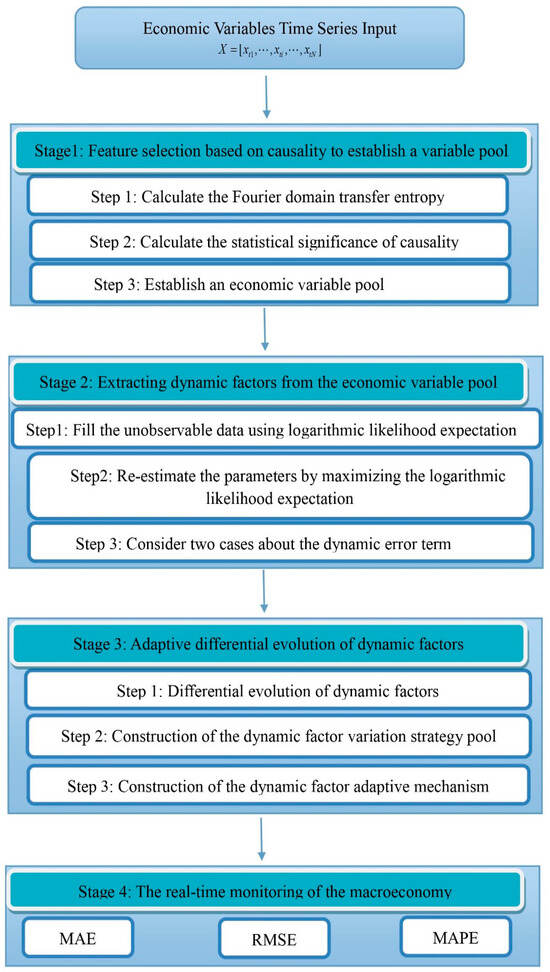
Figure 1.
The flowchart of the AcNowcasting algorithm.
3.1. Performing Feature Selection Based on Causality to Establish an Economic Variable Pool
Burns and Mitchell suggested that the generality of fluctuations in different economic sectors means that they have strong cross-sectional correlations, which indicates that most fluctuations are basically driven by several common sources [2]. Therefore, finding economic variables that cause macroeconomic fluctuations is highly valuable for improving the accuracy of macroeconomic prediction.
One of the differences between the proposed approach and the traditional macroeconomic nowcasting model is that the existing methods, such as that of Giannone et al. [2], cannot perform feature selection. The AcNowcasting model proposed in this paper uses Fourier domain transfer entropy to calculate the statistical significance of causalities for feature selection purposes. Therefore, the AcNowcasting algorithm has the ability to perform feature selection.
Moreover, the difference between the feature selection methods employed in this paper and those used in the traditional computer-based literature is that their feature selection criteria are different. The feature selection criteria in the computer field, such as those of Tarkhaneh et al. [24], are usually based on the quality of the prediction or classification results. However, the feature selection criteria employed in this paper are based on causal strength rather than on the quality of the obtained prediction or classification results. The specific implementation steps are as follows.
Step 1: Calculate the Fourier domain transfer entropy.
Suppose that a variable is the causal factor of an observable variable , which can be expressed as
where represents the associated probability. is a time lag unit, and is the maximum lag. represents the historical information of the economic variables contained in a time interval . For a continuous wavelet (WT) spectrum, the Fourier domain can be expressed as
where indicates the Morlet wavelet function and * denotes the complex conjugate. The parameters and τ represent scale and time translation, respectively. The scale represents frequency localization, which is used to control the scaling of wavelet functions to capture signal changes at different time scales. The function is a bijective mapping from the frequency ω to the scale .
The function represents the Fourier domain of variable S. In addition to and , . Therefore, a two-dimensional symbol scheme with a time order of λ and a frequency order of θ can be obtained:
Equation (3) is mapped to a two-dimensional coordinate . The first coordinate component changes with time, whereas the second coordinate component changes with the frequency. The Fourier domain transfer entropy spectrum is calculated using Equation (4),
Equations (5)–(7) indicate the changes exhibited by the Fourier domain transfer entropy spectrum with time, frequency, and all possibilities, respectively.
The Fourier domain transfer entropy is added along the time t-axis to obtain Equation (5).
The Fourier domain transfer entropy is added along the frequency w-axis to obtain Equation (6).
By adding all the values of Fourier domain transfer entropy values, we obtain Equation (7).
Similarly, we can obtain
Note that is always a negative number. Combined with Equations (5)–(7), the asymmetric properties of the Fourier domain transfer entropy spectrum are obtained to quantify the direction information between S and V, that is, the causal direction.
Thus, the change in transfer entropy can be used to measure the causal direction. That is, when , the information of reduces the uncertainty of , so is the cause of . When the information obtained from increases the uncertainty of , so has a decoupling effect (correlation reduction) on .
Step 2: Calculate the statistical significance of the causality
A set of surrogates is generated, and is calculated for each surrogate . A permutation test is carried out on the mean difference between and , and the statistical significance and the effect size are calculated. In practice, the weakest conditions are and . These thresholds are based on the effect size. If the Fourier domain transfer entropy spectrum is statistically significant, , , and correspond to weakly, neutral and strong significance, respectively.
Step 3: Establish an economic variable pool
On the basis of the above calculation results, the economic variables that have statistically significant causalities with macroeconomic fluctuations are selected in this paper, and a variable pool is constructed.
3.2. Extracting the Dynamic Factors from the Economic Variable Pool
With the help of the dynamic factor model, an observable variable in the variable pool is represented by the unobservable dynamic factor vector and the unobservable error term . n represents the dimensionality of the observable variable. We assume that the observable variable obeys the factor model representation
where is normally distributed, the cross-section is uncorrelated, and is independent of . The matrix is the factor load. The specific steps are as follows.
Step1: Fill the unobservable data using the logarithmic likelihood expectation.
Suppose that the dynamic factor follows a p-order stationary VAR process,
where matrix is the autoregressive coefficient. 0 is the mean. is the covariance matrix. Since is unobservable, the EM algorithm is used in this paper to address such data. represents the joint log likelihood of and , where the parameters in Equations (9) and (10) are collected in the parameter . indicates the available data, which include and .
The expected values of the log likelihood based on the data are calculated using the estimated value of the previous iteration,
Step 2: Re-estimate the parameters by maximizing the logarithmic likelihood expectation with respect to ,
Step 3: Consider two cases involving the dynamic error term .
In the first case, the error term is uncorrelated.
where is a diagonal matrix of the error term. The maximization of and Equation (12) results in the following expressions for and :
The iteration covariance matrix in iteration is calculated as the expected value of the sum of the squares of the residuals, provided that the updated estimates of and are as follows:
When does not contain missing data, we have
The conditional moments and of the dynamic factor can be expressed by the Kalman filter as follows:
Here, contains missing data and is a diagonal matrix of size n. If is missing, the ith diagonal element is equal to 0; otherwise, it is equal to 1. can be obtained as shown below,
where is used as a selection matrix, so only available data are used in the calculation. Similarly, Equation (14) becomes
Then, only the available data estimates are updated. Among nonparametric methods based on principal components, one of the advantages of the maximum likelihood method is that it allows constraints to be imposed on parameters in a relatively direct manner. The restrictions are applied to the models given in Equations (9) and (10), and their expressions are directly adapted to the situation where data are missing, which leads to the restricted estimates given in the following.
where is the unrestricted estimate defined in Equation (11). The parameters contained in the transition equation can be restricted in a similar way (see [3]).
In the second case, the error term follows the AR (1) process.
Assume that in Equation (1) can be decomposed into the following:
Here, and are uncorrelated cross-sections and is a very small number. A new state-space representation is obtained by combining Equations (9), (10) and (20),
where . and are fixed diagonal matrices with on the diagonal. Therefore, the equations for and are the same as the equations mentioned above, whereas the equation for needs to be modified as follows:
In addition, the th iteration of the autoregressive parameter of the error term is given by the following equation:
The conditional moments involving can be obtained from the Kalman filter in the augmented state space given by Equation (21).
3.3. Adaptive Differential Evolution of Dynamic Factors
Another difference between the proposed approach and the traditional macroeconomic nowcasting model is that the factors contained in the traditional nowcasting model literature, such as those used by Bańbura and Modugno [3], are fixed and cannot undergo adaptive evolution. Dynamic factors are extracted by the above method and can be subdivided into global factors, soft factors, real factors and labor factors. However, the factors included in the AcNowcasting algorithm proposed in this paper dynamically change because the self-adaptive weighted DE algorithm is applied to the factors, which can generate the best factors. Therefore, the potential factors in the AcNowcasting algorithm have the ability to undergo adaptive DE. These potential factors can further improve the accuracy of macroeconomic forecasting.
In addition, the self-adaptive weighted DE algorithm employed in this paper is also different from the traditional computer science methods, such as that of Wang [8]. That is, it does not undergo large-scale feature selection, but instead generates the optimal potential factors. These potential factors in the nowcasting model, improved by Fourier domain transfer entropy, can be adaptively differentially evolved through the self-adaptive weighted DE algorithm. The specific implementation steps are as follows.
Step 1: Differential evolution of dynamic factors.
Initially, each candidate factor can be expressed as , where denotes the data dimensions. is randomly initialized as follows,
where is algebraic and . Rand (0,1) represents random numbers in the interval [0,1]. The candidate factors then achieve individual mutations through a differential mutation strategy. Taking the mutation strategy ‘DE/best/1’ as an example, the newly generated mutation factors are as follows:
Here, and are two mutually exclusive random numbers within the range of [1, N]. is the best individual factor in generation G, and F is a scaling parameter that is used to scale the difference vector. The factor individuals are then randomly selected by a cross operation, and the trajectory vector is generated as follows:
Here, is the crossover probability. Then, the selection operation is applied to choose the best factor individuals, as shown below:
Here, represents the objective function. In this paper, a multipopulation mechanism is used to increase the diversity of the factor population. The original factor population is divided into five subpopulations of the same size. Each subpopulation applies a specific solution generation strategy through an adaptive mechanism. The evolution process of each subpopulation is carried out independently, and each subpopulation is searched once. In addition, to maintain the diversity of each subgroup, its individual factors change dynamically in each generation. To use individuals to represent features, C can be defined as an N-dimensional vector as follows:
The threshold is used to convert each element of factor individual into a binary string. If the value of the jth dimension of factor individual is greater than , we set to 1. Otherwise, the jth dimension of is set to 0. No special method is available for identifying the threshold value. In the subsequent program implementation step, the threshold value is set in advance on the basis of experimental experience. We can observe that the value of is 0 or 1. A value of 1 indicates that the jth feature is selected, whereas 0 indicates that the jth feature is not selected. This setting can be described as follows:
The factor population C randomly and dynamically generates subpopulations with equal sizes. To maintain the diversity of the factor population without increasing the complexity of the algorithm, each iteration involves generating five random subpopulations , as follows:
We use N as the population size of the parent factor population, and as the sizes of the subpopulations , respectively. Each subgroup has the same size.
Next, each subgroup is optimized independently in each generation. During the evolution process, subpopulations choose their own strategies through adaptive mechanisms, and then evaluate and evolve the individuals in each subspace. Since each subpopulation uses an adaptive mechanism to select specific strategies, different subpopulations can adopt different strategies. In addition, the sizes of the subpopulations do not change in each generation. Factor individuals can dynamically evolve in each generation, maintain the diversity of subpopulations, and avoid falling into a local optima.
Step 2: Construction of the dynamic factor variation strategy pool.
Due to factor evolution differences, specific mutation strategies have different performances. Therefore, we choose multiple strategies to increase the convergence speed of the developed algorithm by establishing a strategy pool. Eight typical mutation operators representing the current evolutionary DE are selected, and eight candidate mutation strategies are constructed. That is, eight candidate mutation strategies are shown in Equations (31)–(38). During the evolutionary process, DE generates a mutation vector for each individual in generation G. The indices are random integers, which are mutually exclusive within the range [1, N]. represents the best factor individual contained in the current population.
- (1)
- “DE/current to best/1”
- (2)
- “DE/current to rand/1”
- (3)
- “DE/rand/3”
- (4)
- “DE/best/1”
- (5)
- “DE/rand to best/1”
- (6)
- “DE/rand/2”
- (7)
- “DE/best/2”
- (8)
- “DE/best/3”
These strategies are tested on various datasets, and the top five candidate mutation strategies are selected to form a strategy pool.
Step 3: Construction of the dynamic factor adaptation mechanism.
The scaling parameter F and the cross-probability parameter are used to construct an adaptive mechanism according to the characteristics of the given dataset. First, the adaptive selection mechanism randomly selects the appropriate mechanism in the first half of the iterative process to maintain a fair competition. Thereafter, the number of mechanisms is used to record the number of mechanisms selected each time. Furthermore, the change exhibited by each mechanism of the factor individuals in the successfully improved population is recorded as the increased accuracy, which can be defined as follows:
Here, indicates that the accuracy of the successful individuals has increased. After every 20 generations, the mechanism with the best performance receives a reward according to its previous performance . is defined as the maximum ratio of the increased accuracy to the consumed fitness evaluations . The reward received by each mechanism is as follows:
On this basis, the selection mechanisms are established in a global-to-local manner. Specifically, a substrategy pool that is half the size of the original strategy pool is built, and the strategy search scheme is updated from global to local. The performance of each strategy mechanism is calculated before each evaluation, and the top five mechanisms with the highest proportions of the total awards and total selections are selected to build the substrategy pool for further searching. Then, a mechanism is selected from the mechanism pool to ensure that the appropriate mechanism is selected.
To evaluate the importance of each factor, a weighted model is used to calculate the weights of the factors during the evolution procedure. The weighted model has two main processes. The first process records and evaluates the importance of each successive factor in each generation. The second process involves searching the factor subset of the solution. The first process consists of two stages, each of which has different evaluation methods for determining important factors. The first stage (CF) is the evolutionary stage, and it stores the new factors of individuals with better performance during the evolutionary process. The second stage directly records the best 20% of the factor individuals (AFs) at the end of the mechanism during the ranking stage. These two stages can be described as follows:
The purpose of this scheme is to rank the importance levels of the factors and then reduce the search space to effectively find a good solution. In the second process, considering the first process, the solution is searched every 20 generations. First, according to their rankings in the corresponding weight evaluation matrix, factors are selected based on their two different weights in the first process, and then each factor subset is evaluated in each stage. The best factor individual is compared with the worst factor individual in the parent group. If the selected best factor individual performs better, it is used to replace the existing factor individual.
4. Experimental Data
We select 114 economic variables from the Wind database. These 114 economic variables form the maximum number of variables that we can currently find in the Wind database; please refer to Table A1 in the Appendix A for specific economic indicators. Affected by the impact of COVID-19 and the subsequent economic recovery, the GDP growth rate fluctuated sharply from the first quarter of 2020 (2020Q1) to the second quarter of 2021 (2021Q2), and began to gradually recover and stabilize in the third quarter of 2021 (2021Q3). Anomalous data often contain rich information, so we choose the period with obvious fluctuations for variable selection and parameter evolution purposes. To avoid program operation difficulties and abnormal results caused by the use of too few samples, the selected period is extended forward by one year; that is, the final selected period is from 2019Q1 to 2021Q2 and includes 10 quarters in total for variable selection and parameter evolution purposes. On this basis, the GDP growth rate in the three quarters from 2021Q3 to 2022Q1 is predicted.
5. Experimental Results
5.1. Construction of the Variable Pool
Unlike the traditional nowcasting model, which cannot perform feature selection, the AcNowcasting algorithm proposed in this paper can do so. This is because it uses Fourier domain transfer entropy to calculate the statistical significance of causalities. Therefore, the feature selection criteria employed in this paper are based on causality strength rather than on the quality of the prediction or classification results. These are extremely rare feature selection criteria in the computer science field. The specific criteria used for feature selection are as follows.
Economic variable selection criteria: the transfer entropy ΔT >= 0, the p-value <= 0.01, and Δ >= 0.2. The experimental results are shown in Table 2. If the last column in Table 1 is TRUE, then a significant causal relationship between the corresponding economic variable and GDP growth is present, which will be included in the variable pool. If the result is FALSE, the economic variable is not selected. After completing the calculations, 21 economic variables are selected from the 114 economic variables. The number of economic variables used in the experiment is fixed as the initial setting of the algorithm.

Table 2.
Results of causality identification.
These 21 economic variables all satisfy the set selection criteria—transfer entropy ΔT >= 0, p-value <= 0.01, and Δ >= 0.2. This means that significant causal relationships are present between the 21 economic variables and GDP growth. This result means that not all economic variables have direct effects on GDP growth. Therefore, the AcNowcasting algorithm proposed in this paper can perform feature selection, which can greatly reduce the computational complexity of the algorithm and improve its computational efficiency.
5.2. Factor-Adaptive Differential Evolution
Unlike the factors contained in the traditional nowcasting model, which cannot undergo adaptive evolution, the factors in the AcNowcasting algorithm have the ability to undergo adaptive DE through the self-adaptive weighted DE algorithm. In the experiment, some restrictions are imposed on the factor-adaptive DE process, which makes the results more robust. After several tests, the additional constraints are as follows:
- (1)
- All variables have at least 1 factor in addition to a global factor (i.e., each row has at least two values of 1);
- (2)
- At least one-third of the selected economic variables have the same factor (i.e., each column has at least N/3 1 values).
The above restrictions are imposed on the factors as the initialization settings for the algorithm. The results of factor-adaptive DE are shown in Table 3.

Table 3.
Results of factor-adaptive differential evolution.
Four factors are included in Table 3. They are Block1-Global, Block2-Soft, Block3-Real, and Block4-Labor. The number “1” indicates that adaptive evolution is successfully achieved for this factor. The number “0” represents that nonadaptive evolution is applied to this factor. The experimental results listed in Table 2 indicate that the economic variables contained in the AcNowcasting algorithm have the ability to undergo adaptive DE through the self-adaptive weighted DE algorithm, which is a capability that the classic economic forecasting methods do not possess. Each economic variable can adaptively evolve into the optimal factor.
5.3. GDP Growth Rate Prediction Results
It is widely known that great stagnation was caused by the COVID-19 pandemic in 2020. The outbreak of the COVID-19 pandemic led to a deeper and more sustained decline in the global economy than that observed in 2008. In 2022, Nakazawa reported that with COVID-19 having a significant impact on economic activity, the existing GDP nowcasting model has difficulty forecasting with high accuracy [5]. Therefore, we examine whether the common factors generated by the AcNowcasting algorithm developed in this paper can capture the macroeconomic fluctuations observed during these periods.
Figure 2 shows a comparison between the common factors and the GDP growth rate in China. The fluctuation trends of the common factors and the GDP growth rate are almost the same. When the GDP fluctuates more obviously, the common factors can also capture these fluctuations. For example, in 2009, a common factor decreased to a local minimum and then steadily rebounded, reaching a local maximum in 2010. In the first quarter of 2020, the common factors affected by COVID-19 reached their lowest values in recent years. Later, due to rapid economic recovery, the common factors increased to reach a local peak in the second quarter of 2021. Therefore, the AcNowcasting algorithm can extract common factors that better reflect China’s macroeconomic fluctuations.
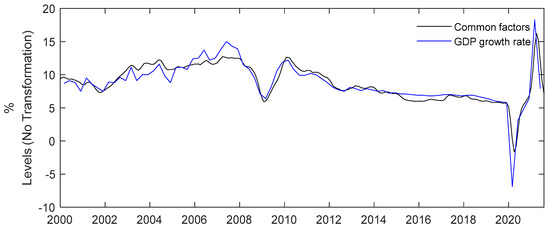
Figure 2.
Comparison between the common factors and GDP growth rate.
China’s GDP growth rate is forecasted in two dimensions. First, the period is divided into three situations—30 days ahead of a GDP announcement, 15 days ahead of a GDP announcement and 1 day ahead of a GDP announcement. Second, the prediction model is divided into three cases. The first case is the traditional mixed dynamic factor model, namely, the nowcasting model. The second model is a preliminarily improved model based on the nowcasting model. That is, the ability to choose economic variables is added to the nowcasting model, and the resulting model is called the CNowcasting model. The third approach is an improved version of the second model, and this model has factor-adaptive evolution capabilities and is called the AcNowcasting algorithm (the model proposed in this paper). We consider three evaluation criteria that have been commonly used in the previous literature [44,45,46], i.e., the mean absolute error (MAE), mean absolute percentage error (MAPE) and root mean square error (RMSE), to compare the predictive accuracies of the models. Table 4 shows the forecasted GDP growth rate results.

Table 4.
Results of GDP growth rate prediction.
When the GDP growth rate is predicted 30 days in advance, the prediction process is divided into three time points: predicting the GDP growth rate for 18 October 2021 on 16 September 2021, predicting the GDP growth rate for 18 January 2022 on 16 December 2021, and predicting the GDP growth rate for 18 April 2022 on 16 March 2022. The experimental MAE, RMSE, and MAPE results indicate that the prediction accuracy of the AcNowcasting algorithm is greater than those of both the nowcasting model and the CNowcasting model. Similarly, the experimental results obtained 15 days in advance and 1 day in advance also show that the prediction accuracy of the AcNowcasting algorithm is higher than those of both the nowcasting model and the CNowcasting model. Therefore, the experimental results in Table 4 show that, compared with that of the traditional mixed dynamic factor model (nowcasting), the prediction accuracy of the AcNowcasting model proposed in this paper is improved.
The AcNowcasting algorithm does not consider mode-shifting analysis approaches, state-of-the-art (SOTA) DE variants such as the winners of relevant recent CEC competitions, or SOTA variants of metaheuristics such as particle swarm optimization (PSO), the genetic algorithm (GA), etc. This is mainly based on the following two considerations.
First, the research problem of this paper is that with COVID-19 having had a significant impact on economic activity, the existing nowcasting model has difficulty forecasting with high accuracy. Therefore, the experimental part involves comparing the prediction accuracy of the AcNowcasting algorithm with that of the classic nowcasting model in different periods. Compared with that of the traditional nowcasting model, the prediction accuracy of the AcNowcasting algorithm is improved because of the introduction of Fourier domain transfer entropy and the self-adaptive weighted DE algorithm. The research objective of this paper has been achieved.
Second, we make appropriate improvements to the Fourier domain transfer entropy and the self-adaptive weighted DE algorithm based on the research problem of this paper, and the experimental results show that this scheme is very effective. Therefore, the AcNowcasting algorithm does not consider mode shifting analysis approaches, SOTA DE variants or SOTA variants. However, this idea can serve as a direction for further research in the future.
6. Conclusions
Macroeconomic forecasting itself is extremely complex. As the famous economist Paul M. Romer noted, in the last three decades, the treatment of identification in macroeconomic models has become no more credible than that in the first-generation large Keynesian models, and has actually become worse because it is far more opaque. At present, interdisciplinary methods for macroeconomic prediction research are lacking. Therefore, the macroeconomic nowcasting model is improved with the help of advanced algorithms from the computer science field to enhance the accuracy of macroeconomic predictions. For real-time macroeconomy monitoring, an AcNowcasting algorithm is proposed in this paper. The AcNowcasting algorithm provides a new prediction theory and a real-time monitoring method for macroeconomics, so it has good theoretical and practical value. This method has several notable advantages.
First, the AcNowcasting algorithm has the ability to perform feature selection, whereas the traditional macroeconomic nowcasting models, such as that of Giannone et al. [2], cannot do so. The reason for this finding is that the AcNowcasting algorithm uses Fourier domain transfer entropy to calculate the statistical significance of causalities for feature selection purposes. Therefore, the AcNowcasting algorithm has the ability to perform feature selection. Moreover, the feature selection criteria employed in the computer science field, such as those of Tarkhaneh et al. [24], are usually based on the quality of the obtained prediction or classification results. However, the feature selection criteria utilized in this paper are based on causal strength rather than on the quality of the prediction or classification results. These are extremely rare feature selection criteria in the computer science field.
Second, the factors included in the AcNowcasting algorithm have the ability to undergo adaptive DE. However, the factors contained in the traditional macroeconomic nowcasting models, such as that of Bańbura and Modugno [3], cannot undergo adaptive evolution. This is because the factors in the AcNowcasting algorithm utilize the self-adaptive weighted DE algorithm to generate the optimal factors. Thus, the factors in the AcNowcasting algorithm have the ability to undergo adaptive DE. In addition, the self-adaptive weighted DE algorithm developed in this paper is also different from traditional computer science methods, such as that of Wang [8]. That is, it does not undergo large-scale feature selection but instead generates the optimal potential factors. To maximize the stability of the results, additional limitations are imposed on the factor-adaptive DE process in the experiment.
Third, the AcNowcasting algorithm can extract common factors that better reflect macroeconomic fluctuations and has higher prediction accuracy than the traditional nowcasting model does. In 2022, Nakazawa reported that with COVID-19 having a significant impact on economic activity, the existing nowcasting model has difficulty forecasting with high accuracy [5]. However, the experimental results presented in this paper show that the AcNowcasting algorithm can extract common factors that better reflect the macroeconomic fluctuations exhibited by China during these periods. Compared with that of the traditional nowcasting model, the prediction accuracy of the AcNowcasting algorithm is improved. The proposed approach can select the economic variables that have causality with respect to GDP fluctuations from a historical dataset and generate the most appropriate potential dynamic factors, thus further improving the accuracy of real-time macroeconomic monitoring.
As with all methods, the AcNowcasting algorithm also has limitations. Because of its strong application background in macroeconomic forecasting, it is limited to macroeconomic forecasting and cannot be applied in the classification or other tasks.
Author Contributions
Conceptualization, Q.W. and H.-G.Z.; methodology, H.-G.Z.; software, H.-G.Z.; validation, Q.W. and H.-G.Z.; formal analysis, H.-G.Z.; investigation, H.-G.Z.; resources, H.-G.Z.; data curation, H.-G.Z.; writing—original draft preparation, H.-G.Z.; writing—review and editing, H.-G.Z.; visualization, H.-G.Z.; supervision, H.-G.Z.; project administration, H.-G.Z.; funding acquisition, H.-G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This paper is supported by The Fundamental Research Funds of Shandong University (2020GN009) and Foundation for University Key Teacher by China Scholarship Council (202406220274).
Data Availability Statement
The corresponding author will provide data according to the reader’s request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Experimental data.
Table A1.
Experimental data.
| Series ID | Series Name |
|---|---|
| M0000612 | Consumer price index (CPI) |
| M0001385 | Money supply |
| M0017126 | Purchase Management Index(PMI) |
| M0001227 | Producer price index (PPI) |
| M0001383 | Money supply |
| M0000545 | Industrial production added |
| S0029657 | Completed Investment in Real Estate Development |
| M0001428 | Total Retail Sales of Consumer Goods |
| M0000273 | Fixed assets investment (FAI) |
| M0000607 | Value of Exports: year |
| M5440435 | Infrastructure Investment |
| M0000357 | FAI: manufacturing |
| M0017128 | PMI: New Orders |
| M0001384 | Broad Money (M2) |
| M0017129 | PMI: New Export Orders |
| M0017127 | PMI: Production |
| M0000606 | Value of Exports |
| M0017131 | PMI: Finished Product Inventory |
| M0000609 | Value of Imports: year |
| M0000616 | CPI: Food |
| M0000561 | Industrial Enterprises: Finished Products |
| M0001427 | Total Retail Sales of Consumer Goods |
| M0009970 | Financial institutions: total loans |
| M0009969 | Financial intermediaries: total loans |
| M0017135 | PMI: Inventory of Raw Materials |
| M0000138 | Non-official China PMI |
| M0001382 | Narrow Money (M1) |
| M0010049 | Foreign Exchange Reserves |
| M0000613 | CPI: Non-food |
| M0017134 | PMI: Prices of Purchased Materials |
| M0000608 | Value of Imports |
| M0043418 | Financial institutions: medium and long-term loans |
| M0012303 | Consumer Confidence Index |
| M5207464 | Industrial Enterprises: Total Profit |
| M0000449 | Real Estate |
| M0048236 | Non-manufacturing PMI |
| M0017136 | PMI: Employment |
| M0017137 | PMI: Speed of Supplier Deliveries |
| S0027013 | Electricity Production: year |
| M0017130 | PMI: Backlog of Orders |
| M0001467 | Retail Sales: Vehicle |
| M0001381 | Cash in circulation |
| M0017133 | PMI: Imports |
| M0001380 | M0 |
| M0024054 | Government Revenue |
| M0000556 | Industrial Enterprises: Total Profit |
| M5207831 | Non-manufacturing PMI: Construction |
| M5207838 | Non-manufacturing PMI: Service |
| M0024055 | Government Expenditure |
| M5206740 | PMI: Small Enterprises |
| M0017132 | PMI: Quantity of Purchases |
| M5525764 | Stock Aggregate Financing to the Real Economy: RMB Loans |
| M0000729 | CPI: YTD |
| M5206738 | PMI: Large Enterprises |
| S0027012 | Electricity Production |
| M5206739 | PMI: Medium-sized Enterprises |
| M5530000 | EPMI |
| M0000605 | Value of Imports and Exports |
| M0001689 | Monetary Authority: Total Assets |
| M0009940 | Financial intermediaries: total deposits |
| M0001232 | PPI: Consumer Goods |
| M0096879 | National Government-managed Fund Revenue |
| S0027374 | Crude Steels |
| M0000615 | CPI: Services |
| M0024063 | Government Revenue |
| M5786898 | Bulk Commodity Index |
| M0001699 | Monetary Authority: Deposits of Government |
| M0043411 | Financial intermediaries: fiscal deposits |
| M0010039 | Average Exchange Rate: USD/CNY |
| M0001461 | Retail Sales: Household Electrics and Video Appliances |
| M0010131 | Money Multiplier |
| M0000604 | Value of Imports and Exports |
| M0043829 | Export Price Index (HS2): Total Index |
| M0096212 | Value-added of Industry: Manufacturing |
| M0024064 | Government Expenditure |
| M0001364 | Producer Purchase Price Index |
| M0000560 | Industrial Enterprises: Finished Products |
| M0000614 | CPI: Consumer Goods |
| M0000650 | CPI: Residence |
| M5480389 | No. of New Employed Population in Urban Areas |
| M0043413 | Financial intermediaries: savings deposits |
| M0000429 | FAI: Transport, Storage and Post Service |
| M0096211 | Value-added of Industry: Mining |
| M0001690 | Monetary Authority: Reserve Money (Monetary Base) |
| M0096883 | National Government-managed Fund Revenue |
| M0041340 | Macro-economic Climate Index: Coincident Index |
| M6096116 | No. of New Employed Population in Urban Areas |
| M0012304 | Consumer Satisfaction Index |
| M0089119 | Central Government Fiscal Revenue |
| GDP | GDP: Constant Prices:year |
| M5567889 | GDP: Constant Prices |
| M6404533 | Leverage Rate of Household Sector |
| M0000001 | GDP: Current Prices |
| M6404532 | Leverage Rate of Non-Financial Sector |
| M0012989 | Per Capita Disposable Income of Urban Households |
| M5567903 | GDP: Constant Prices: Tertiary Industry |
| M6404534 | Leverage Rate of Non-financial Corporations Sector |
| M6347627 | GDP: Current Prices |
| M6404535 | Leverage Rate of General Government Sector |
| M5567901 | GDP: Constant Prices: Primary Industry |
| M5567902 | GDP: Constant Prices: Secondary Industry |
| M0058002 | Average CNY Loan Rates of Financial Institutions |
| M0010096 | Excess Deposit Reserve Ratio: Financial Institutions |
| M0011456 | Loan Demand Climate Index |
| M5792266 | Industrial Capacity Utilization |
| M0007446 | The Proportion of “More Savings” |
| M0012988 | Per Capita Disposable Income of Urban Households |
| M0002004 | Non-performing Loan Ratio |
| M5481759 | National Per Capita Disposable Income |
| M0007438 | Index of Future Income Confidence |
| M6404537 | Leverage Rate of Local Government Sector |
| M5481772 | National Per Capita Consumption Expenditure |
| M0024136 | Urban Registered Unemployment Rate |
| M5207466 | Future Employment Expectations Index |
References
- Shaw, E.S. Burns and Mitchell on Business Cycles. J. Political Econ. 1947, 55, 281–298. [Google Scholar] [CrossRef]
- Giannone, D.; Reichlin, L.; Small, D. Nowcasting: The real-time informational content of macroeconomic data. J. Monet. Econ. 2008, 55, 665–676. [Google Scholar] [CrossRef]
- Bańbura, M.; Modugno, M. Maximum likelihood estimation of factor models on datasets with arbitrary pattern of missing data. J. Appl. Econom. 2014, 29, 133–160. [Google Scholar] [CrossRef]
- Bok, B.; Caratelli, D.; Giannone, D.; Sbordone, A.M.; Tambalotti, A. Macroeconomic nowcasting and forecasting with big data. Annu. Rev. Econ. 2018, 10, 615–643. [Google Scholar] [CrossRef]
- Nakazawa, T. Constructing GDP Nowcasting Models Using Alternative Data (No. 22-E-9); Bank of Japan: Tokyo, Japan, 2022; pp. 1–39. [Google Scholar]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Wong, K.C.; Li, X. A self-adaptive weighted differential evolution approach for large-scale feature selection. Knowl.-Based Syst. 2022, 235, 107633. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Marinazzo, D.; Pellicoro, M.; Stramaglia, S. Kernel method for nonlinear Granger causality. Phys. Rev. Lett. 2008, 100, 144103. [Google Scholar] [CrossRef]
- Dhamala, M.; Rangarajan, G.; Ding, M. Estimating Granger causality from Fourier and wavelet transforms of time series data. Phys. Rev. Lett. 2008, 100, 018701. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [PubMed]
- Staniek, M.; Lehnertz, K. Symbolic transfer entropy. Phys. Rev. Lett. 2008, 100, 158101. [Google Scholar] [CrossRef] [PubMed]
- Lobier, M.; Siebenhühner, F.; Palva, S.; Palva, J.M. Phase transfer entropy: A novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions. Neuroimage 2014, 85, 853–872. [Google Scholar] [CrossRef]
- Wollstadt, P.; Martínez-Zarzuela, M.; Vicente, R.; Díaz-Pernas, F.J.; Wibral, M. Efficient Transfer Entropy Analysis of Non-Stationary Neural Time Series. PLoS ONE 2014, 9, e102833. [Google Scholar] [CrossRef]
- Porfiri, M.; Ruiz Marín, M. Transfer entropy on symbolic recurrences. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 063123. [Google Scholar] [CrossRef] [PubMed]
- Restrepo, J.F.; Mateos, D.M.; Schlotthauer, G. Transfer entropy rate through Lempel-Ziv complexity. Phys. Rev. E 2020, 101, 052117. [Google Scholar] [CrossRef]
- Silini, R.; Masoller, C. Fast and effective pseudo transfer entropy for bivariate data-driven causal inference. Sci. Rep. 2021, 11, 8423. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Y.; Zhang, Z.; Sun, P. Fourier-domain transfer entropy spectrum. Phys. Rev. Res. 2021, 3, L042040. [Google Scholar] [CrossRef]
- Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar]
- Mohamed, A.W.; Suganthan, P.N. Real-parameter unconstrained optimization based on enhanced fitness-adaptive differential evolution algorithm with novel mutation. Soft Comput. 2018, 22, 3215–3235. [Google Scholar] [CrossRef]
- Sun, G.; Yang, B.; Yang, Z.; Xu, G. An adaptive differential evolution with combined strategy for global numerical optimization. Soft Comput. 2020, 24, 6277–6296. [Google Scholar] [CrossRef]
- Chen, X. Novel dual-population adaptive differential evolution algorithm for large-scale multi-fuel economic dispatch with valve-point effects. Energy 2020, 203, 117874. [Google Scholar] [CrossRef]
- Tarkhaneh, O.; Nguyen, T.T.; Mazaheri, S. A novel wrapper-based feature subset selection method using modified binary differential evolution algorithm. Inf. Sci. 2021, 565, 278–305. [Google Scholar] [CrossRef]
- Wang, M.; Ma, Y.; Wang, P. Parameter and strategy adaptive differential evolution algorithm based on accompanying evolution. Inf. Sci. 2022, 607, 1136–1157. [Google Scholar] [CrossRef]
- Meng, Z.; Yang, C. Two-stage differential evolution with novel parameter control. Inf. Sci. 2022, 596, 321–342. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Z.; Wang, Z.; Wei, J.; Chen, X.; Li, Q.; Zheng, Y.; Sheng, W. Adaptive memetic differential evolution with multi-niche sampling and neighborhood crossover strategies for global optimization. Inf. Sci. 2022, 583, 121–136. [Google Scholar] [CrossRef]
- Ghysels, E.; Santa-Clara, P.; Valkanov, R. There is a risk-return trade-off after all. J. Financ. Econ. 2005, 76, 509–548. [Google Scholar] [CrossRef]
- Ghysels, E.; Sinko, A.; Valkanov, R. MIDAS regressions: Further results and new directions. Econom. Rev. 2007, 26, 53–90. [Google Scholar] [CrossRef]
- Miller, J.I. Mixed-frequency cointegrating regressions with parsimonious distributed lag structures. J. Financ. Econom. 2014, 12, 584–614. [Google Scholar] [CrossRef]
- Gong, Y.; Chen, Q.; Liang, J. A mixed data sampling copula model for the return-liquidity dependence in stock index futures markets. Econ. Model. 2018, 68, 586–598. [Google Scholar] [CrossRef]
- Ghysels, E.; Qian, H. Estimating MIDAS regressions via OLS with polynomial parameter profiling. Econom. Stat. 2019, 9, 1–16. [Google Scholar] [CrossRef]
- Liu, M.; Lee, C.C. Is gold a long-run hedge, diversifier, or safe haven for oil? Empirical evidence based on DCC-MIDAS. Resour. Policy 2022, 76, 102703. [Google Scholar] [CrossRef]
- Mariano, R.S.; Murasawa, Y. A coincident index, common factors, and monthly real GDP. Oxf. Bull. Econ. Stat. 2010, 72, 27–46. [Google Scholar] [CrossRef]
- Eraker, B.; Chiu, C.W.; Foerster, A.T.; Kim, T.B.; Seoane, H.D. Bayesian mixed frequency VARs. J. Financ. Econom. 2014, 13, 698–721. [Google Scholar] [CrossRef]
- Foroni, C.; Guérin, P.; Marcellino, M. Markov-switching mixed-frequency VAR models. Int. J. Forecast. 2015, 31, 692–711. [Google Scholar] [CrossRef]
- Schorfheide, F.; Song, D. Real-time forecasting with a mixed-frequency VAR. J. Bus. Econ. Stat. 2015, 33, 366–380. [Google Scholar] [CrossRef]
- Knotek, E.S., II; Zaman, S. Financial nowcasts and their usefulness in macroeconomic forecasting. Int. J. Forecast. 2019, 35, 1708–1724. [Google Scholar] [CrossRef]
- Jungbacker, B.; Koopman, S.J.; Van der Wel, M. Maximum likelihood estimation for dynamic factor models with missing data. J. Econ. Dyn. Control. 2011, 35, 1358–1368. [Google Scholar] [CrossRef]
- Forni, M.; Hallin, M.; Lippi, M.; Zaffaroni, P. Dynamic factor models with infinite-dimensional factor spaces: One-sided representations. J. Econom. 2015, 185, 359–371. [Google Scholar] [CrossRef]
- Fiorentini, G.; Galesi, A.; Sentana, E. A spectral EM algorithm for dynamic factor models. J. Econom. 2018, 205, 249–279. [Google Scholar] [CrossRef]
- Glocker, C.; Kaniovski, S. Macroeconometric forecasting using a cluster of dynamic factor models. Empir. Econ. 2022, 63, 43–91. [Google Scholar] [CrossRef]
- Martínez-Hernández, I.; Gonzalo, J.; González-Farías, G. Nonparametric estimation of functional dynamic factor model. J. Nonparametr. Stat. 2022, 34, 895–916. [Google Scholar] [CrossRef]
- Zhang, H.G.; Su, C.W.; Song, Y.; Qiu, S.; Xiao, R.; Su, F. Calculating Value-at-Risk for high-dimensional time series using a nonlinear random mapping model. Econ. Model. 2017, 67, 355–367. [Google Scholar] [CrossRef]
- Zhang, H.G.; Li, T. News-driven bubbles in futures markets. J. Energy Mark. 2023, 16, 55–78. [Google Scholar] [CrossRef]
- Zhang, H.G.; Wu, L.; Song, Y.; Su, C.W.; Wang, Q.; Su, F. An online sequential learning non-parametric value-at-risk model for high-dimensional time series. Cogn. Comput. 2018, 10, 187–200. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
