An Inductive Logical Model with Exceptional Information for Error Detection and Correction in Large Knowledge Bases
Abstract
1. Introduction
- The inductive logical programming algorithm with exceptional information (EILP) is proposed to detect errors in KBs by considering both negative statements and abnormal information;
- The inductive logical correction method with exceptional features (EILC) is proposed to correct errors, in which a new rule refining algorithm is applied to revise correction rules.
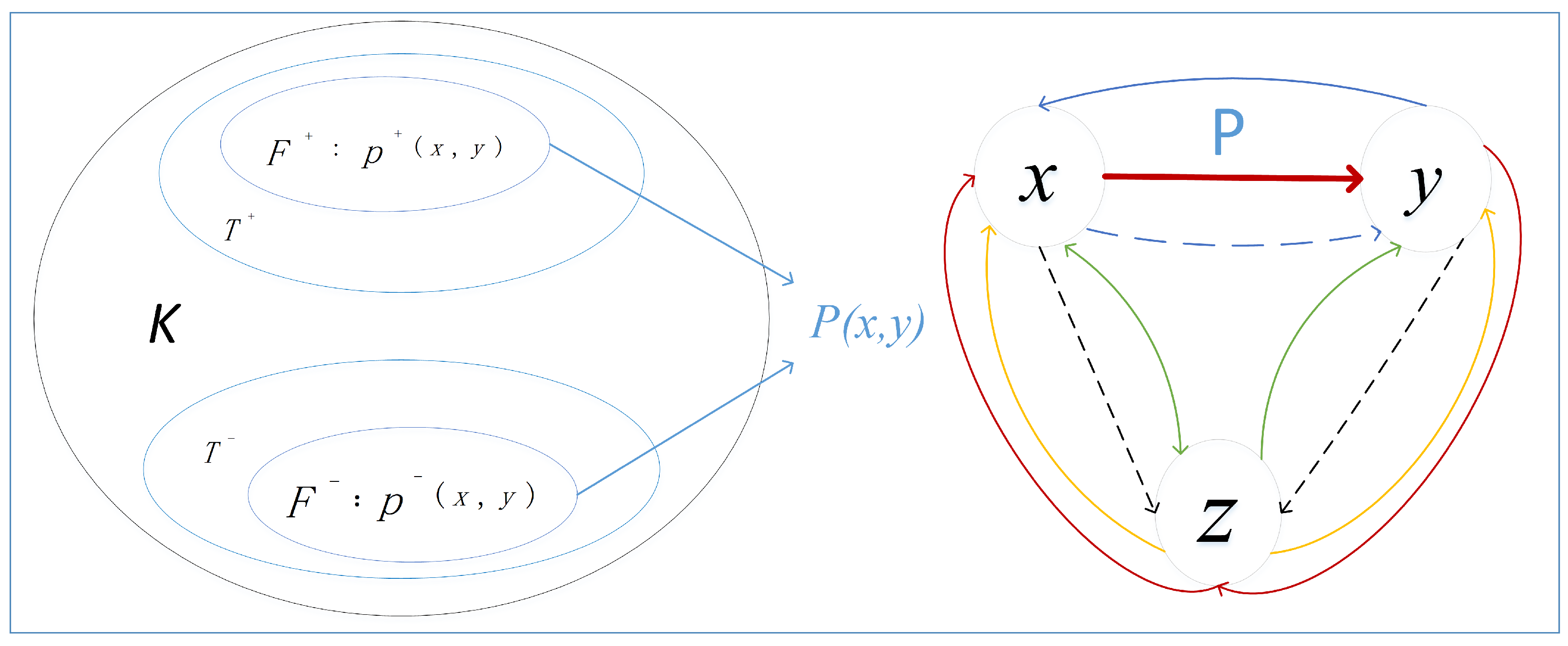
2. Preliminaries
2.1. Problem Statement
2.2. Search Space of Feedback
2.3. Quality Measures
3. Proposed Methods
3.1. Overview of Inductive Logical Model
3.2. EILP
| Algorithm 1 EILP |
| Require: := Ø; := Ø; := ; := Ensure:
|
3.3. EILC
| Algorithm 2 EILC |
| Require: EILP() Ensure:
|
| Algorithm 3 Refine Rules |
| Require: (positive/negative rules), x is variable; y, z are variables or constants; Ensure: : union of conjunctive rewriting queries;
|
3.4. Complexity Analysis
4. Experiments
4.1. General Setup
4.2. Error Detection
4.3. Knowledge Correction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bai, Y.; Ying, Z.; Ren, H.; Leskovec, J. Modeling Heterogeneous Hierarchies with Relation-specific Hyperbolic Cones. Adv. Neural Inf. Process. Syst. 2021, 34, 12316–12327. [Google Scholar]
- Hao, Y.; Zhang, Y.; Liu, K.; He, S.; Liu, Z.; Wu, H.; Zhao, J. An end-to-end model for question answering over knowledge base with cross-attention combining global knowledge. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, Vancouver, BC, Canada, 30 July–4 August 2017; Volume 1: Long Papers. pp. 221–231. [Google Scholar]
- Xiong, C.; Power, R.; Callan, J. Explicit semantic ranking for academic search via knowledge graph embedding. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 1271–1279. [Google Scholar]
- Suchanek, F.M.; Kasneci, G.; Weikum, G. Yago: A core of semantic knowledge. In Proceedings of the 16th International Conference on World Wide Web, Banff, AB, Canada, 8–12 May2007; pp. 697–706. [Google Scholar]
- Bizer, C.; Lehmann, J.; Kobilarov, G.; Auer, S.; Becker, C.; Cyganiak, R.; Hellmann, S. Dbpedia-a crystallization point for the web of data. J. Web Semant. 2009, 7, 154–165. [Google Scholar] [CrossRef]
- Vrandečić, D.; Krötzsch, M. Wikidata: A free collaborative knowledgebase. Commun. Acm 2014, 57, 78–85. [Google Scholar] [CrossRef]
- Fensel, D.; Şimşek, U.; Angele, K.; Huaman, E.; Kärle, E.; Panasiuk, O.; Toma, I.; Umbrich, J.; Wahler, A. Introduction: What is a knowledge graph? In Knowledge Graphs: Methodology, Tools and Selected Use Cases; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–10. [Google Scholar] [CrossRef]
- Bakshi, G.; Shukla, R.; Yadav, V.; Dahiya, A.; Anand, R.; Sindhwani, N.; Singh, H. An optimized approach for feature extraction in multi-relational statistical learning. J. Sci. Ind. Res. 2021, 80, 537–542. [Google Scholar]
- Tekli, G. A survey on semi-structured web data manipulations by non-expert users. Comput. Sci. Rev. 2021, 40, 100367. [Google Scholar] [CrossRef]
- Legast, M.; Legay, A. Rule-Based Expert System for Energy Optimization: Detection and Identification of Relationships Between Rules in Knowledge Base. Master’s Thesis, UCLouvain, Louvain-la-Neuve, Belgium, 2021. [Google Scholar]
- Hangloo, S.; Arora, B. Fake News Detection Tools and Methods—A Review. arXiv 2021, arXiv:2112.11185. [Google Scholar]
- Ahmed, M.; Ansar, K.; Muckley, C.B.; Khan, A.; Anjum, A.; Talha, M. A semantic rule based digital fraud detection. Peerj Comput. Sci. 2021, 7, e649. [Google Scholar] [CrossRef]
- Ko, H.; Witherell, P.; Lu, Y.; Kim, S.; Rosen, D.W. Machine learning and knowledge graph based design rule construction for additive manufacturing. Addit. Manuf. 2021, 37, 101620. [Google Scholar] [CrossRef]
- Tiddi, I.; Schlobach, S. Knowledge graphs as tools for explainable machine learning: A survey. Artif. Intell. 2022, 302, 103627. [Google Scholar] [CrossRef]
- Fan, W.; Geerts, F. Foundations of Data Quality Management; Synthesis Lectures on Data Management; Springer: Berlin/Heidelberg, Germany, 2012; Volume 4, pp. 1–217. [Google Scholar]
- Michelangelo Diligenti, D.; Francesco Giannini, D.; Marco Gori, D.; Marco Maggini, D.; Marra, G. A Constraint-Based Approach to Learning and Reasoning. Neuro-Symb. Artif. Intell. State Art 2022, 342, 192. [Google Scholar]
- Cropper, A.; Dumančić, S. Inductive logic programming at 30: A new introduction. arXiv 2020, arXiv:2008.07912. [Google Scholar] [CrossRef]
- Picado, J.; Termehchy, A.; Fern, A.; Pathak, S.; Ilango, P.; Davis, J. Scalable and usable relational learning with automatic language bias. In Proceedings of the 2021 International Conference on Management of Data, Xi’an, China, 20–25 June 2021; pp. 1440–1451. [Google Scholar]
- Srinivasan, A.; Faruquie, T.A.; Joshi, S. Data and task parallelism in ILP using MapReduce. Mach. Learn. 2012, 86, 141–168. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, J.; Haxhidauti, P.; Venugopal, V.E.; Theobald, M. Guided Inductive Logic Programming: Cleaning Knowledge Bases with Iterative User Feedback. Epic. Ser. Comput. 2020, 72, 92–106. [Google Scholar]
- Gad-Elrab, M.H.; Stepanova, D.; Urbani, J.; Weikum, G. Exception-enriched rule learning from knowledge graphs. In Proceedings of the International Semantic Web Conference, Kobe, Japan, 17–21 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 234–251. [Google Scholar]
- Xue, B.; Zou, L. Knowledge Graph Quality Management: A Comprehensive Survey. IEEE Trans. Knowl. Data Eng. 2022, 35, 4969–4988. [Google Scholar] [CrossRef]
- Dylla, M.; Sozio, M.; Theobald, M. Resolving temporal conflicts in inconsistent RDF knowledge bases. In Datenbanksysteme für Business, Technologie und Web (BTW); Gesellschaft für Informatik e.V.: Bonn, Germany, 2011. [Google Scholar]
- Yakout, M.; Berti-Équille, L.; Elmagarmid, A.K. Don’t be scared: Use scalable automatic repairing with maximal likelihood and bounded changes. In Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 22–27 June 2013; pp. 553–564. [Google Scholar]
- Rekatsinas, T.; Chu, X.; Ilyas, I.F.; Ré, C. Holoclean: Holistic data repairs with probabilistic inference. arXiv 2017, arXiv:1702.00820. [Google Scholar] [CrossRef]
- Lertvittayakumjorn, P.; Kertkeidkachorn, N.; Ichise, R. Correcting Range Violation Errors in DBpedia. In Proceedings of the International Semantic Web Conference (Posters, Demos & Industry Tracks), Vienna, Austria, 23–25 October 2017. [Google Scholar]
- Ortona, S.; Meduri, V.V.; Papotti, P. Robust discovery of positive and negative rules in knowledge bases. In Proceedings of the 2018 IEEE 34th International Conference on Data Engineering (ICDE), Paris, France, 16–19 April 2018; pp. 1168–1179. [Google Scholar]
- Mahdavi, M.; Abedjan, Z. Baran: Effective error correction via a unified context representation and transfer learning. Proc. Vldb Endow. 2020, 13, 1948–1961. [Google Scholar] [CrossRef]
- Abedini, F.; Keyvanpour, M.R.; Menhaj, M.B. Correction Tower: A general embedding method of the error recognition for the knowledge graph correction. Int. J. Pattern Recognit. Artif. Intell. 2020, 34, 2059034. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Z.; Wang, G. Correcting large knowledge bases using guided inductive logic learning rules. In Proceedings of the PRICAI 2021: Trends in Artificial Intelligence: 18th Pacific Rim International Conference on Artificial Intelligence, PRICAI 2021, Hanoi, Vietnam, 8–12 November 2021; Proceedings, Part I 18. Springer: Berlin/Heidelberg, Germany, 2021; pp. 556–571. [Google Scholar]
- Wu, Y.; Zhang, Z. Refining large knowledge bases using co-occurring information in associated KBs. Front. Phys. 2023, 11, 1140733. [Google Scholar] [CrossRef]
- Pellissier-Tanon, T. Knowledge Base Curation Using Constraints. Ph.D. Thesis, Institut Polytechnique de Paris, Palaiseau, France, 2020. [Google Scholar]
- Zaveri, A.; Kontokostas, D.; Sherif, M.A.; Bühmann, L.; Morsey, M.; Auer, S.; Lehmann, J. User-driven quality evaluation of dbpedia. In Proceedings of the 9th International Conference on Semantic Systems, Graz, Austria, 4–6 September 2013; pp. 97–104. [Google Scholar]
- Zhang, L.; Wang, W.; Zhang, Y. Privacy preserving association rule mining: Taxonomy, techniques, and metrics. IEEE Access 2019, 7, 45032–45047. [Google Scholar] [CrossRef]
- Galárraga, L.; Teflioudi, C.; Hose, K.; Suchanek, F.M. Fast rule mining in ontological knowledge bases with AMIE+. Vldb J. 2015, 24, 707–730. [Google Scholar] [CrossRef]
- Hogan, A.; Hogan, A. Resource description framework. In The Web of Data; Springer: Berlin/Heidelberg, Germany, 2020; pp. 59–109. [Google Scholar]
- Picado, J.; Davis, J.; Termehchy, A.; Lee, G.Y. Learning Over Dirty Data Without Cleaning. In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data, Portland, OR, USA, 14–19 June 2020; pp. 1301–1316. [Google Scholar]
- Richardson, M.; Domingos, P. Markov logic networks. Mach. Learn. 2006, 62, 107–136. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, J.; Wang, W. Efficient approximate entity matching using jaro-winkler distance. In Proceedings of the International Conference on Web Information Systems Engineering, Puschino, Russia, 7–11 October 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 231–239. [Google Scholar]
- Islam, A.; Inkpen, D. Semantic text similarity using corpus-based word similarity and string similarity. Acm Trans. Knowl. Discov. Data (TKDD) 2008, 2, 10. [Google Scholar] [CrossRef]
- Lifschitz, V. Foundations of logic programming. Princ. Knowl. Represent. 1996, 3, 69–127. [Google Scholar]
- Lisi, F.A.; Weikum, G. Towards Nonmonotonic Relational Learning from Knowledge Graphs. In Proceedings of the Inductive Logic Programming: 26th International Conference, ILP 2016, London, UK, 4–6 September 2016; Revised Selected Papers. Springer: Berlin/Heidelberg, Germany, 2017; Volume 10326, p. 94. [Google Scholar]
- Bienvenu, M.; Hansen, P.; Lutz, C.; Wolter, F. First order-rewritability and containment of conjunctive queries in Horn description logics. arXiv 2020, arXiv:2011.09836. [Google Scholar]
- Lajus, J.; Galárraga, L.; Suchanek, F. Fast and Exact Rule Mining with AMIE 3. In Proceedings of the European Semantic Web Conference, Crete, Greece, 31 May–4 June 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 36–52. [Google Scholar]











| Aspect | EILP | Generic SPARQL Based Models |
|---|---|---|
| Time Complexity | PSPACE complete (unrestricted) | |
| Space Complexity | (intermediate results) | |
| Scalability | Linear in (optimized) | Limited by PSPACE constraints |
| Positive rules: head: nationality |
| Negative rules: |
| Positive rules: head: nationality(a, b) |
| Negative rules: |
| Positive rules: head: nationality |
| Negative rules: |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Lin, X.; Lian, H.; Zhang, Z. An Inductive Logical Model with Exceptional Information for Error Detection and Correction in Large Knowledge Bases. Mathematics 2025, 13, 1877. https://doi.org/10.3390/math13111877
Wu Y, Lin X, Lian H, Zhang Z. An Inductive Logical Model with Exceptional Information for Error Detection and Correction in Large Knowledge Bases. Mathematics. 2025; 13(11):1877. https://doi.org/10.3390/math13111877
Chicago/Turabian StyleWu, Yan, Xiao Lin, Haojie Lian, and Zili Zhang. 2025. "An Inductive Logical Model with Exceptional Information for Error Detection and Correction in Large Knowledge Bases" Mathematics 13, no. 11: 1877. https://doi.org/10.3390/math13111877
APA StyleWu, Y., Lin, X., Lian, H., & Zhang, Z. (2025). An Inductive Logical Model with Exceptional Information for Error Detection and Correction in Large Knowledge Bases. Mathematics, 13(11), 1877. https://doi.org/10.3390/math13111877







