Common Neighborhood Energy of the Non-Commuting Graphs and Commuting Graphs Associated with Dihedral and Generalized Quaternion Groups

Abstract

This paper explores the common neighborhood energy ($E_{CN}\left(\mathsf{\Gamma }\right)$) of graphs derived from the dihedral group $D_{2n}$ and generalized quaternion group $Q_{4n}$, specifically the non-commuting graph (NCM-graph) and the commuting graph (CM-graph). Studying graphs associated with groups offers a powerful approach to translating algebraic properties into combinatorial structures, enabling the application of graph-theoretic tools to understand group behavior. The common neighborhood energy, defined as the sum of the absolute values of the eigenvalues of the common neighborhood (CN) matrix, i.e., ${\sum }_{i=1}^p\left|{\zeta }_i\right|$, where ${\left\{{\zeta }_i\right\}}_{i=1}^p$ are the CN eigenvalues, provides insights into the structural properties of these graphs. We derive explicit formulas for the CN characteristic polynomials and corresponding CN eigenvalues for both the NCM-graph and CM-graph as functions of n. Consequently, we establish closed-form expressions for the $E_{CN}$ of these graphs, which are parameterized by n. The validity of our theoretical results is confirmed through computational examples. This study contributes to the spectral analysis of algebraic graphs, demonstrating a direct connection between the group-theoretic structure of $D_{2n}$ and $Q_{4n}$, as well as the combinatorial energy of their associated graphs, thus furthering the understanding of group properties through spectral graph theory.

1. Introduction

Let $\mathsf{\Gamma }=(V,E)$ be a graph. The order and the size of $\mathsf{\Gamma }$ are denoted, respectively, by $\left|V\right(\mathsf{\Gamma }\left)\right|$ and $\left|E\right(\mathsf{\Gamma }\left)\right|$. As usual, the complete graph and null graph with p vertices are denoted in this paper by $K_p$ and $\overline{K_p}$, respectively.

The join ${\mathsf{\Gamma }}_1\vee {\mathsf{\Gamma }}_2$ of two graphs ${\mathsf{\Gamma }}_1$ and ${\mathsf{\Gamma }}_2$ with disjoint vertex sets $|V\left({\mathsf{\Gamma }}_1\right)|=p_1$ and $|V\left({\mathsf{\Gamma }}_2\right)|=p_2$ is the graph obtained by connecting each vertex of ${\mathsf{\Gamma }}_1$ to each vertex of ${\mathsf{\Gamma }}_2$ while keeping all edges of both graphs.

In graph theory, the study of energy of graphs has been studied widely because of its connection with various topics of science. The energy of a graph $\mathsf{\Gamma }$, $\epsilon \left(\mathsf{\Gamma }\right)$, has been introduced by Gutman [1] as ${\displaystyle \epsilon \left(\mathsf{\Gamma }\right)=\sum _{i=1}^p\left|{\lambda }_i\right|}$, where ${\lambda }_i$, $\forall i=1,2,\cdots ,p$ are the eigenvalues of the adjacency matrix of $\mathsf{\Gamma }$ [2]. The definition of the energy of a graph is stated in the following.

Definition 1

([3] Energy of Graph). Let Γ be a simple graph, A be its adjacency matrix, and ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_p$ be the eigenvalues of A. The energy of Γ is defined as

$${\displaystyle \epsilon \left(\mathsf{\Gamma }\right)=\sum _{i=1}^p|{\lambda }_i|.}$$

Based on that, Alwardi et al. [4] have introduced the CN matrix and the CN energy of the graph as follows.

Definition 2

([4] CN Matrix and CN Energy of Graph). Let Γ be a graph with a set of vertices $V\left(\mathsf{\Gamma }\right)=\{u_1,u_2,\dots ,u_p\}$. The CN neighborhood $\eta (u_i,u_j)$ of two vertices $u_i$ and $u_j$, with $i\ne j$, is the set of vertices of Γ which are adjacent to both $u_i$ and $u_j$, except for $u_i$ and $u_j$.

The CN matrix of Γ is $CN\left(\mathsf{\Gamma }\right)=\left|\right|b_{ij}\left|\right|$, where

$$b_{ij}=\left\{\begin{array}{cc}\left|\eta \right(u_i,u_j\left)\right|\hfill & \mathit{if}i\ne j;\hfill \\ 0\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

The CN characteristic polynomial of the CN matrix of Γ, $CN\left(\mathsf{\Gamma }\right)$, is defined by

$$\begin{array}{c}\hfill \varphi (\mathsf{\Gamma };\zeta )=det(\zeta I-CN\left(\mathsf{\Gamma }\right))={\zeta }^p+c_1{\zeta }^{p-1}+c_2{\zeta }^{p-2}+\cdots +c_p.\end{array}$$

where I is the unit matrix of order p. The roots ${\zeta }_1,{\zeta }_2,\dots ,{\zeta }_p$ of $\varphi (\mathsf{\Gamma };\zeta )=0$ are the CN eigenvalues of Γ. The CN energy of Γ is given as ${\displaystyle E_{CN}\left(\mathsf{\Gamma }\right)=\sum _{i=1}^p\left|{\zeta }_i\right|}$.

In the following, some results are used in this paper.

Theorem 1

([4]). For the complete graph $K_p$ on p vertices, the CN energy is given by $E_{CN}\left(K_p\right)=2(p-1)(p-2)$.

Proposition 1

([4]). If the graph Γ consists of (connected) components ${\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,\dots ,{\mathsf{\Gamma }}_m$, then

$$E_{CN}\left(\mathsf{\Gamma }\right)=E_{CN}\left({\mathsf{\Gamma }}_1\right)+E_{CN}\left({\mathsf{\Gamma }}_2\right)+\cdots +E_{CN}\left({\mathsf{\Gamma }}_m\right).$$

Proposition 2

([4]). $E_{CN}\left(\mathsf{\Gamma }\right)=0$ if and only if all the components of Γ contain less than three vertices.

Proposition 3

([5]). Let a, b, c, and d be real numbers, $I_p$ be the $p\times p$ identity matrix, and $J_p$ be the $p\times p$ matrix in which all its entries are equal to 1. Then, the determinant of the $(p_1+p_2)\times (p_1+p_2)$ matrix of the form

$$\begin{array}{c}\hfill \left|\begin{array}{ccc}(\lambda +a)I_{p_1}-a{J}_{p_1}& & -b{J}_{p_1\times p_2}\\ & & \\ -c{J}_{p_2\times p_1}& & (\lambda +d)I_{p_2}-d{J}_{p_1}\end{array}\right|\end{array}$$

can be simplified in an expression as

$${\left(\lambda +a\right)}^{p_1-1}{\left(\lambda +d\right)}^{p_2-1}\left(\left(\lambda -a(p_1-1)\right)\left(\lambda -d(p_2-1)\right)-p_1{p}_{2}cb\right).$$

Proposition 4

([6]). If a square matrix $M=\left[\begin{array}{cc}W& X\\ Y& Z\end{array}\right]$ can be partitioned into four blocks W, X, Y, and Z, where $\left|W\right|\ne 0$, then

$$\left|M\right|=\left|\begin{array}{cc}W& X\\ 0& Z-Y{W}^{-1}X\end{array}\right|=\left|W\right||Z-Y{W}^{-1}X|.$$

The dihedral group $D_{2n}$, representing symmetries of regular $n–$gons, and the generalized quaternion group $Q_{4n}$, a non-abelian Hamiltonian group, are pivotal in algebraic and applied studies due to their structural richness and broad applicability. $D_{2n}$ serves as a foundational model for discrete symmetry, with applications in crystallography (classifying crystal lattices), cryptography (group-based encryption), and spectral graph theory (Cayley graphs), while $Q_{4n}$, extending Hamilton’s quaternions, plays a critical role in topology (manifold classification), quantum mechanics, and error-correcting codes; see [7,8,9]. For further details on the applications of groups, graph representations, and their various energies in computer science, we refer the reader to [10,11,12,13,14].

The integration of graph-theoretic methods into the study of algebraic structures has emerged as a significant area of interdisciplinary research, owing to its profound implications for establishing explicit connections between graph theory and algebraic systems. A prominent focus within this domain involves the investigation of graphs of groups, where combinatorial representations elucidate structural properties of algebraic entities. Among these, the CM-graph (commuting graph) and NCM-graph (non-commuting graph) associated with finite groups have garnered considerable attention. For instance, CM-graphs have been extensively investigated in the context of specific group families: seminal contributions include the analyses by Vahidi and Talebi [15], Segev and Seitz [16], Raza and Faizi [17], and Parker [18]. In contrast, NCM-graphs have been the subject of comprehensive studies by Abdollahi et al. [19], Moradipour et al. [20], and Ahanjideh and Iranmanesh [21], demonstrating their utility in characterizing non-commutative group behaviors. These frameworks not only bridge discrete mathematics and abstract algebra but also serve as powerful tools for analyzing group-theoretic properties through combinatorial invariants.

In this research, we aim to determine general formulas for the CN energy of the NCM-graph and the CM-graph associated with two types of non-abelian groups, which are the dihedral group, $D_{2n}$, and the generalized quaternion group, $Q_{4n}$.

In the following, the definition of $D_{2n}$ and some of its properties are presented.

Definition 3

([22] $D_{2n}$). The dihedral group, denoted by $D_{2n}$, is a group of symmetries of a regular polygon, which include rotations and reflections, and its order is $2n$, where n is an integer at least 3. The dihedral groups can be presented in the form of generators and relations given as follows:

$$D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉.$$

The following proposition presents some properties of $D_{2n}$.

Proposition 5

([22]). Let G be a dihedral group of order $2n$, i.e.,

$$D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉.$$

Then, $D_{2n}$ has the following properties:

1. 

For odd n,

(a) 

The center $Z\left(D_{2n}\right)=\left\{e\right\}$.

(b) 

The elements of the form $a^i$, where $i=1,2,\dots ,n-1$, commute with each other, and $a^i$ does not commute with the elements of the form $a^{j}b$, where $j=0,1,2,\dots ,n-1$.

(c) 

The elements of the form $a^{j}b$, where $j=0,1,2,\dots ,n-1$, commute with any element in $D_{2n}$ except the identity element.

2. 

For even n,

(a) 

The center $Z\left(D_{2n}\right)=\{e,a^{{\displaystyle \frac{n}{2}}}\}$,

(b) 

The non-central elements of the form $a^i$, i.e., $i=1,2,\dots ,n-1$ and $i\ne {\displaystyle \frac{n}{2}}$, commute with each other, and $a^i$ does not commute with the elements of the form $a^{j}b$, where $j=0,1,2,\dots ,n-1$.

(c) 

Each element of the form $a^{j}b$, where $j=0,1,2,\dots ,n-1$ do not commute with any element in $D_{2n}$ except the identity element and the element of the form $a^{{\displaystyle \frac{n}{2}}+j}b$.

Next, the definition of the generalized quaternion group, $Q_{4n}$, and some of its properties are provided.

Definition 4

([23] Generalized Quaternion Group $Q_{4n}$). The generalized quaternion group, $Q_{4n}$, is a non-abelian group of order $4n$, where n is an integer and $n\ge 2$, with the group presentation

$$Q_{4n}\cong 〈a,b:a^n=b^2,a^{2n}=b^4=e,b^{-1}a=a^{-1}{b}^{-1}〉.$$

Proposition 6 presents some properties of $Q_{4n}$.

Proposition 6

([23]). Let G be a generalized quaternion group of order $4n$, with $n\ge 2$, i.e.,

$$Q_{4n}\cong 〈a,b:a^n=b^2,a^{2n}=b^4=e,b^{-1}a=a^{-1}{b}^{-1}〉,n\ge 2.$$

Then, $Q_{4n}$ has the following properties:

1. 

The center $Z\left(Q_{4n}\right)=\{e,a^n\}$.

2. 

The non-central elements of the form $a^i$, i.e., $i=1,2,\dots ,2n-1$, commute with each other, and $a^i$ does not commute with the elements of the form $a^{j}b$, where $j=0,1,2,\dots ,2n-1$.

3. 

Each element of the form $a^{j}b$, where $j=0,1,2,\dots ,2n-1$, does not commute with any element in $Q_{4n}$ except the identity element and the element of the form $a^{n+j}b$.

4. 

$Q_{4n}$ has a unique involution $a^n=b^2$.

Next, the definitions of the NCM-graph and CM-graph related to a non-abelian finite group G are provided.

Definitio 5

([19] The NCM-Graph). Suppose that G is a non-abelian finite group and $Z\left(G\right)$ is its center. An NCM-graph of G, ${\mathsf{\Gamma }}_G^{ncm}$, is a graph with a set of vertices corresponding to the non-central elements of G, i.e., $G-Z\left(G\right)$, and the two vertices $u_1$ and $u_2$ are adjacent if $u_1{u}_2\ne u_2{u}_1$.

Definition 6

([15] The CM-Graph). Suppose that G is a non-abelian finite group and $Z\left(G\right)$ is its center. A CM-graph of G, ${\mathsf{\Gamma }}_G^{cm}$, is a graph with a set of vertices corresponding to $G-Z\left(G\right)$, and the two vertices $u_1$ and $u_2$ are adjacent if $u_1{u}_2=u_2{u}_1$.

Next, the general form of the NCM-graph related to $D_{2n}$ is provided in Proposition 7.

Proposition 7

([24]). Let $D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉$ be a dihedral group of order $2n$. Then, the NCM-graph of $D_{2n}$, ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$, is one of the following forms:

$${\mathsf{\Gamma }}_{D_{2n}}^{ncm}=\left\{\begin{array}{cc}{K}_n\vee \overline{K_{n-1}},\hfill & \mathit{if}n\mathit{is}\mathit{odd};\hfill \\ \\ U_n\vee \overline{K_{n-2}},\hfill & \mathit{if}n\mathit{is}\mathit{even},\hfill \end{array}\right.$$

where $U_n$ is an $(n-2)$-regular graph with n vertices.

In the following section, the CN energy of the NCM-graph associated with dihedral groups, $D_{2n}$, is found in terms of n and illustrated by some examples.

2. CN Energy of the NCM-Graph of D_2n

Here, the general formula of the CN characteristic polynomial and the CN eigenvalues for the NCM-graph of $D_{2n}$, ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$, are presented. In addition, the general formula of the CN energy of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ is determined in terms of n. Moreover, two examples are given to illustrate the results based on the parity of n.

In the following, Lemma 1 gives the general formula of the CN characteristic polynomial and the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ in the case of n being an odd integer.

Lemma 1.

Let $G=D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉$, with $n\ge 3$ being an odd integer and ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ being its NCM-graph. Then, the characteristic polynomial of the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ is given as follows:

$$\varphi ({\mathsf{\Gamma }}_{D_{2n}}^{ncm};\zeta )={\left(\zeta +n\right)}^{n-2}{\left(\zeta +(2n-3)\right)}^{n-1}({\zeta }^2-(3n^2-7n+3)\zeta +n(n-1)(n^2-5n+5)),$$

and hence, the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ are ${\zeta }_1=-n$ with multiplicity $(n-2)$, ${\zeta }_2=-(2n-3)$ with multiplicity $(n-1)$, and

$${\zeta }_{3,4}={\displaystyle \frac{(3n^2-7n+3)\pm \sqrt{5n^4-18n^3+27n^2-22n+9}}{2}}.$$

Proof. 

Let $G=D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉$, with $n\ge 3$ being an odd integer. Then, by Definition 5 and Proposition 5,

$$V\left({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\right)=\{b,a,ab,a^2,a^{2}b,a^3,a^{3}b,\cdots ,a^{n-1},a^{n-1}b\},$$

which means $p=\left|V\right({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\left)\right|=2n-1$. Thus, the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ is a square matrix of order $(2n-1)$.

By Proposition 7, ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}=\overline{K_{n-1}}\vee K_n$, where the vertices of $\overline{K_{n-1}}$ are the elements of form $a^i$, $i=1,2,\cdots ,n-1$, and the vertices of $K_n$ are the elements of form $a^{j}b$, where $j=0,1,2,\cdots ,n-1$. Therefore, there exist three cases to determine the number common neighborhoods between the vertices of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$.

Case 1. The number of common neighborhoods between the vertices of $\overline{K_{n-1}}$ (which are the vertices of form $a^i$). By Proposition 5 and Definition 5, every vertex of form $a^i$ is adjacent only to all the vertices of form $a^{j}b$, $\forall i,j$ (recall that $a^{j}b$ are the vertices of $K_n$). Therefore, $\left|\eta \right(a^k,a^l\left)\right|=n$, $\forall k\ne l$, where $\{k,l\}\subseteq \{1,\cdots ,n-1\}$.

Case 2. The number of common neighborhoods between the vertices of $K_n$ (which are the vertices of form $a^{j}b$). By Proposition 5 and Definition 5, these vertices are adjacent to themselves, and each of them is adjacent also to all the vertices of form $a^i$. Hence, $\left|\eta \right(a^{k}b,a^{l}b\left)\right|=n-1+n-2=2n-3$, $\forall k\ne l$, where $\{k,l\}\subseteq \{0,1,\cdots ,n-1\}$.

Case 3. Consider the value $\left|\eta \right(a^i,a^{j}b\left)\right|$ for all $i,j$. Since vertices of the form $a^i$ are adjacent only to vertices of the form $a^{j}b$ (for all $i,j$), it follows that $\left|\eta \right(a^i,a^{j}b\left)\right|=n-1$ for all $i,j$.

Hence, the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ is given by

$$\begin{array}{cc}\hfill CN\left({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\right)& =\left[\begin{array}{cccccccc}0& n& \cdots & n& n-1& \cdots & \cdots & n-1\\ n& 0& \ddots & ⋮& ⋮& \ddots & \ddots & ⋮\\ ⋮& & \ddots & n& ⋮& ⋮& \ddots & ⋮\\ n& \cdots & n& 0& n-1& \cdots & \cdots & n-1\\ n-1& \cdots & \cdots & n-1& 0& 2n-3& \cdots & 2n-3\\ ⋮& \ddots & \ddots & ⋮& 2n-3& \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & ⋮& ⋮& \ddots & \ddots & 2n-3\\ n-1& \cdots & \cdots & n-1& 2n-3& \cdots & 2n-3& 0\end{array}\right]\hfill \\ & =\left[\begin{array}{ccc}n{J}_{n-1}-n{I}_{n-1}& & (n-1)J_{(n-1)\times n}\\ & & \\ (n-1)J_{n\times (n-1)}& & (2n-3)J_n-(2n-3)I_n\end{array}\right].\hfill \end{array}$$

Therefore, the CN characteristic polynomial of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ is found as follows:

$$\begin{array}{cc}\hfill \varphi ({\mathsf{\Gamma }}_{D_{2n}}^{ncm};\zeta )=& det\left(I\zeta -CN\left({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\right)\right)=\left|\begin{array}{ccc}(\zeta +n)I_{n-1}-n{J}_{n-1}& & -(n-1)J_{(n-1)\times n}\\ & & \\ -(n-1)J_{n\times (n-1)}& & \left(\zeta +(2n-3)\right)I_n-(2n-3)J_n\end{array}\right|.\hfill \end{array}$$

Thus, by Proposition 3 (with $a=n$, $b=c=n-1$, and $d=2n-3$), $\varphi ({\mathsf{\Gamma }}_{D_{2n}}^{ncm};\zeta )$ is given as follows:

$$\begin{array}{cc}\hfill \varphi ({\mathsf{\Gamma }}_{D_{2n}}^{ncm};\zeta )=& {\left(\zeta +n\right)}^{n-2}{\left(\zeta +(2n-3)\right)}^{n-1}[\left(\zeta -(n-2)n\right)\left(\zeta -(n-1)(2n-3)\right)\hfill \\ & -(n-1)n{(n-1)}^2]\hfill \\ \hfill =& {\left(\zeta +n\right)}^{n-2}{\left(\zeta +(2n-3)\right)}^{n-1}\left({\zeta }^2-(3n^2-7n+3)\zeta +n(n-1)(n^2-5n+5)\right).\hfill \end{array}$$

Hence, the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ are ${\zeta }_1=-n$ with multiplicity $(n-2)$, ${\zeta }_2=-(2n-3)$ with multiplicity $(n-1)$, and

$$\begin{array}{cc}\hfill {\zeta }_{3,4}& ={\displaystyle \frac{(3n^2-7n+3)\pm \sqrt{{(3n^2-7n+3)}^2-4n(n-1)(n^2-5n+5)}}{2}}\hfill \\ & ={\displaystyle \frac{(3n^2-7n+3)\pm \sqrt{5n^4-18n^3+27n^2-22n+9}}{2}}.\square \hfill \end{array}$$

Next, the CN characteristic polynomial and the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ when n is an even integer are provided in Lemma 2.

Lemma 2.

Let $G=D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉$, with $n\ge 3$ being an even integer, and ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ be its NCM-graph. Then the characteristic polynomial of the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ is given as follows:

$$\begin{array}{cc}\hfill \varphi ({\mathsf{\Gamma }}_{D_{2n}}^{ncm};\zeta )=& {\left(\zeta +n\right)}^{n-3}{\left(\zeta +2(n-4)\right)}^{{\displaystyle \frac{n-2}{2}}}{\left(\zeta +2(n-2)\right)}^{{\displaystyle \frac{n}{2}}}({\zeta }^2-(n-1)(3n-8)\zeta \hfill \\ & +n{(n-2)}^2(n-4)),\hfill \end{array}$$

and hence, the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ are ${\zeta }_1=-n$ with multiplicity $(n-3)$, ${\zeta }_2=-2(n-4)$ with multiplicity $\left({\displaystyle \frac{n-2}{2}}\right)$, ${\zeta }_3=-2(n-2)$ with multiplicity $\left({\displaystyle \frac{n}{2}}\right)$, and

$${\zeta }_{4,5}={\displaystyle \frac{(n-1)(3n-8)\pm \sqrt{5n^4-34n^3+89n^2-112n+64}}{2}}.$$

Proof. 

Suppose $G=D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉$, with $n\ge 3$ being an even integer. Then, by Definition 5 and Proposition 5,

$$V\left({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\right)=\{a,\dots ,a^{{\displaystyle \frac{n}{2}}-1},a^{{\displaystyle \frac{n}{2}}+1},\cdots ,a^{n-1},b,ab,a^{2}b,\dots ,a^{n-1}b\},$$

which means $p=\left|V\right({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\left)\right|=2n-2$. Thus, the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ is a square matrix of order $(2n-2)$.

By Proposition 7, ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}=\overline{K_{n-2}}\vee U_n$, where the vertices of $\overline{K_{n-2}}$ are the elements of form $a^i$, $i=1,2,\cdots ,n-1$, with $i\ne {\displaystyle \frac{n}{2}}$ (recall that $Z\left(D_{2n}\right)=\{e,a^{{\displaystyle \frac{n}{2}}}\}$), and the vertices of $U_n$ are the elements of form $a^{j}b$, where $j=0,1,2,\cdots ,n-1$. Therefore, the entries of the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ are obtained in four cases:

Case 1. The number of common neighborhoods between the vertices of form $a^i$. By Definition 5 and Proposition 5, every vertex of form $a^i$ is only adjacent to the vertices $a^{j}b$$\forall i,j$. Therefore, $\left|\eta \right(a^k,a^l\left)\right|=n$, $\forall k\ne l$, where $\{k,l\}\subseteq \{1,\cdots ,n-1\}$.

Case 2. The number of common neighborhoods between the vertices of form $a^{j}b$ and $a^{{\displaystyle \frac{n}{2}}+j}b$ (i.e., $|\eta (a^{j}b,a^{{\displaystyle \frac{n}{2}}+j}b)|$). By Proposition 5, these two elements commute, thus as vertices of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$, they are pairwise non-adjacent but adjacent to all other vertices of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$. Therefore,

$$|\eta (a^{j}b,a^{{\displaystyle \frac{n}{2}}+j}b)|=2n-2-2=2n-4,\forall j=0,1,\cdots ,n-1.$$

Case 3. The number of common neighborhoods between the vertices of form $a^{k}b$ and $a^{l}b$ with $l\ne {\displaystyle \frac{n}{2}}+k$ (i.e., $\left|\eta \right(a^{k}b,a^{l}b\left)\right|$). By Definition 5 and Proposition 5, the vertex $a^{k}b$ is adjacent to all the vertices of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ except the vertex $a^{{\displaystyle \frac{n}{2}}+k}b$, and the vertex $a^{l}b$ is adjacent to all the vertices of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ except the vertex $a^{{\displaystyle \frac{n}{2}}+l}b$. Therefore,

$$\left|\eta \right(a^{k}b,a^{l}b\left)\right|=2n-2-2-2=2n-6.$$

Case 4. It remains now to calculate $\left|\eta \right(a^i,a^{j}b\left)\right|$, $\forall i,j$. By Definition 5 and Proposition 5, the vertices of form $a^i$ are adjacent only to the vertices of form $a^{j}b$, $\forall i,j$. Therefore,

$$\left|\eta \right(a^i,a^{j}b\left)\right|=n-2,\forall i,j.$$

Hence, the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ is of the form:

$$\begin{array}{cc}\hfill CN\left({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\right)& =\left[\begin{array}{ccccc}n\left(J_{n-2}-I_{n-2}\right)& & (n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}}& & (n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}}\\ & & \\ (n-2)J_{{\displaystyle \frac{n}{2}}\times (n-2)}& & (2n-6)(J_{{\displaystyle \frac{n}{2}}}-I_{{\displaystyle \frac{n}{2}}})& & (2n-6)J_{{\displaystyle \frac{n}{2}}}+2I_{{\displaystyle \frac{n}{2}}}\\ & & \\ (n-2)J_{{\displaystyle \frac{n}{2}}\times (n-2)}& & (2n-6)J_{{\displaystyle \frac{n}{2}}}+2I_{{\displaystyle \frac{n}{2}}}& & (2n-6)(J_{{\displaystyle \frac{n}{2}}}-I_{{\displaystyle \frac{n}{2}}})\end{array}\right].\hfill \end{array}$$

Therefore, the CN characteristic polynomial of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ is given by

$$\begin{array}{cc}\hfill \varphi & ({\mathsf{\Gamma }}_{D_{2n}}^{ncm};\zeta )=|\zeta I-CN\left({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\right)|\hfill \\ \hfill & =\left|\begin{array}{ccc}(\zeta +n)I_{n-2}-n{J}_{n-2}& -(n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}}& -(n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}}\\ & & \\ -(n-2)J_{{\displaystyle \frac{n}{2}}\times (n-2)}& (\zeta +2n-6)I_{{\displaystyle \frac{n}{2}}}-(2n-6)J_{{\displaystyle \frac{n}{2}}}& -(2n-6)J_{{\displaystyle \frac{n}{2}}}-2I_{{\displaystyle \frac{n}{2}}}\\ & & \\ -(n-2)J_{{\displaystyle \frac{n}{2}}\times (n-2)}& -(2n-6)J_{{\displaystyle \frac{n}{2}}}-2I_{{\displaystyle \frac{n}{2}}}& (\zeta +2n-6)I_{{\displaystyle \frac{n}{2}}}-(2n-6)J_{{\displaystyle \frac{n}{2}}}\end{array}\right|.\hfill \end{array}$$

(1)

The symbol $O_{a\times b}$ is employed to denote the zero matrix of dimensions $a\times b$, where a and b correspond to the number of rows and columns, respectively.

In order to obtain $\varphi ({\mathsf{\Gamma }}_{D_{2n}}^{ncm};\zeta )$, the determinant in Equation (1) needs some elementary rows and columns operations as follows:

• Replace $R_{n-2+{\displaystyle \frac{n}{2}}+i}$ by the operation $R_{n-2+{\displaystyle \frac{n}{2}}+i}^{\prime }=R_{n-2+{\displaystyle \frac{n}{2}}+i}-R_{n-2+i}$ for all $1\le i\le {\displaystyle \frac{n}{2}}$; then, the determinant becomes

  $$\left|\begin{array}{ccc}(\zeta +n)I_{n-2}-n{J}_{n-2}& -(n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}}& -(n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}}\\ & & \\ -(n-2)J_{{\displaystyle \frac{n}{2}}\times (n-2)}& (\zeta +2n-6)I_{{\displaystyle \frac{n}{2}}}-(2n-6)J_{{\displaystyle \frac{n}{2}}}& -(2n-6)J_{{\displaystyle \frac{n}{2}}}-2I_{{\displaystyle \frac{n}{2}}}\\ & & \\ O_{{\displaystyle \frac{n}{2}}\times (n-2)}& -(\zeta +2n-4)I_{{\displaystyle \frac{n}{2}}}& (\zeta +2n-4)I_{{\displaystyle \frac{n}{2}}}\end{array}\right|.$$
• Replace $C_{n-2+i}$ by the operation $C_{n-2+i}^{\prime }=C_{n-2+{\displaystyle \frac{n}{2}}+i}+C_{n-2+i}$ for all $1\le i\le {\displaystyle \frac{n}{2}}$; then, the determinant becomes

  $$\begin{array}{cc}& \left|\begin{array}{ccc}(\zeta +n)I_{n-2}-n{J}_{n-2}& -2(n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}}& -(n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}}\\ & & \\ -(n-2)J_{{\displaystyle \frac{n}{2}}\times (n-2)}& (\zeta +2n-8)I_{{\displaystyle \frac{n}{2}}}-2(2n-6)J_{{\displaystyle \frac{n}{2}}}& -(2n-6)J_{{\displaystyle \frac{n}{2}}}-2I_{{\displaystyle \frac{n}{2}}}\\ & & \\ O_{{\displaystyle \frac{n}{2}}\times (n-2)}& O_{{\displaystyle \frac{n}{2}}\times {\displaystyle \frac{n}{2}}}& (\zeta +2n-4)I_{{\displaystyle \frac{n}{2}}}\end{array}\right|\hfill \\ & =\left|\begin{array}{ccc}W& & X\\ Y& & Z\end{array}\right|,\hfill \end{array}$$

  where

  $$\left|W\right|=\left|\begin{array}{cc}(\zeta +n)I_{n-2}-n{J}_{n-2}& -2(n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}}\\ -(n-2)J_{{\displaystyle \frac{n}{2}}\times (n-2)}& (\zeta +2n-8)I_{{\displaystyle \frac{n}{2}}}-2(2n-6)J_{{\displaystyle \frac{n}{2}}}\end{array}\right|,$$
  $\left|X\right|=\left|\begin{array}{c}-(n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}}\\ -(2n-6)J_{{\displaystyle \frac{n}{2}}}-2I_{{\displaystyle \frac{n}{2}}}\end{array}\right|$, $\left|Y\right|=\left|\begin{array}{c}{O}_{{\displaystyle \frac{n}{2}}\times (n-2+{\displaystyle \frac{n}{2}})}\end{array}\right|$, and $\left|Z\right|=\left|\begin{array}{c}(\zeta +2n-4)I_{{\displaystyle \frac{n}{2}}}\end{array}\right|$

Therefore, by Proposition 4,

$$\varphi ({\mathsf{\Gamma }}_{D_{2n}}^{ncm};\zeta )=\left|\begin{array}{ccc}W& & X\\ Y& & Z\end{array}\right|=\left|W\right|\left|Z\right|.$$

It can be seen that $\left|Z\right|={\left(\zeta +2(n-2)\right)}^{{\displaystyle \frac{n}{2}}}$. Thus, we need to calculate $\left|W\right|$. First, $\left|W\right|$ can be written as

$$\left|W\right|=\left|\begin{array}{ccc}(\zeta +n)I_{n-2}-n{J}_{n-2}& -2(n-2)J_{(n-2)\times 1}& -2(n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}-1}\\ -(n-2)J_{1\times (n-2)}& \zeta -(2n-4)& -2(2n-6)J_{1\times {\displaystyle \frac{n}{2}}-1}\\ -(n-2)J_{{\displaystyle \frac{n}{2}}-1\times (n-2)}& -2(2n-6)J_{{\displaystyle \frac{n}{2}}-1\times 1}& (\zeta +2n-8)I_{{\displaystyle \frac{n}{2}}-1}-2(2n-6)J_{{\displaystyle \frac{n}{2}}-1}\end{array}\right|.$$

Next, $\left|W\right|$ is calculated by placing the following operation:

• Replace $R_{n-1+i}^{\prime }=R_{n-1+i}-R_{n-1}$ for all $1\le i\le {\displaystyle \frac{n}{2}}-1$; then, $\left|W\right|$ becomes

  $$\left|\begin{array}{ccc}(\zeta +n)I_{n-2}-n{J}_{n-2}& -2(n-2)J_{(n-2)\times 1}& -2(n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}-1}\\ -(n-2)J_{1\times (n-2)}& \zeta -(2n-4)& -2(2n-6)J_{1\times {\displaystyle \frac{n}{2}}-1}\\ O_{{\displaystyle \frac{n}{2}}-1\times (n-2)}& -(\zeta +2n-8)J_{{\displaystyle \frac{n}{2}}-1\times 1}& (\zeta +2n-8)I_{{\displaystyle \frac{n}{2}}-1}\end{array}\right|.$$
• Replace $C_{n-1}^{\prime }=C_{n-1}+C_n+C_{n+1}+\dots +C_{n-2+{\displaystyle \frac{n}{2}}}$; then,

  $$\left|\begin{array}{ccc}(\zeta +n)I_{n-2}-n{J}_{n-2}& -n(n-2)J_{(n-2)\times 1}& -2(n-2)J_{(n-2)\times {\displaystyle \frac{n}{2}}-1}\\ -(n-2)J_{1\times (n-2)}& \zeta -(n-2)(2n-4)& -2(2n-6)J_{1\times {\displaystyle \frac{n}{2}}-1}\\ O_{{\displaystyle \frac{n}{2}}-1\times (n-2)}& O_{{\displaystyle \frac{n}{2}}-1\times 1}& (\zeta +2n-8)I_{{\displaystyle \frac{n}{2}}-1}\end{array}\right|.$$
  Therefore, by Proposition 4,

  $$\left|W\right|=\left|\begin{array}{cc}D& E\\ F& H\end{array}\right|=\left|D\right|\left|H\right|,$$

  where $\left|H\right|=\left|\begin{array}{c}(\zeta +2n-8)I_{{\displaystyle \frac{n}{2}}-1}\end{array}\right|={\left(\zeta +2(n-4)\right)}^{{\displaystyle \frac{n-2}{2}}}$ and

  $$\begin{array}{cc}\hfill \left|D\right|=& \left|\begin{array}{cc}(\zeta +n)I_{n-2}-n{J}_{n-2}& -n(n-2)J_{(n-2)\times 1}\\ -(n-2)J_{1\times (n-2)}& \zeta -2{(n-2)}^2\end{array}\right|\hfill \\ \hfill =& \left|\begin{array}{ccc}(\zeta +n)I_{n-3}-n{J}_{n-3}& -n{J}_{(n-3)\times 1}& -n(n-2)J_{(n-3)\times 1}\\ -n{J}_{1\times (n-3)}& \zeta & -n(n-2)\\ -(n-2)J_{1\times (n-3)}& -(n-2)& \zeta -2{(n-2)}^2\end{array}\right|.\hfill \end{array}$$

Finally, $\left|D\right|$ is calculated by placing the following operations:

• Replace $C_i^{\prime }=C_i-C_{n-2}$ for all $1\le i\le n-3$; then,

  $$\left|D\right|=\left|\begin{array}{ccc}(\zeta +n)I_{n-3}& -n{J}_{(n-3)\times 1}& -n(n-2)J_{(n-3)\times 1}\\ -(\zeta +n)J_{1\times (n-3)}& \zeta & -n(n-2)\\ O_{1\times (n-3)}& -(n-2)& \zeta -2{(n-2)}^2\end{array}\right|.$$
• Replace $R_{n-2}^{\prime }=R_{n-2}+R_1+R_2+\cdots +R_{n-3}$; then,

  $$\begin{array}{cc}\hfill \left|D\right|=& \left|\begin{array}{ccc}(\zeta +n)I_{n-3}& -n{J}_{(n-3)\times 1}& -n(n-2)J_{(n-3)\times 1}\\ O_{1\times (n-3)}& \zeta -n(n-3)& -n{(n-2)}^2\\ O_{1\times (n-3)}& -(n-2)& \zeta -2{(n-2)}^2\end{array}\right|\hfill \\ \hfill =& |(\zeta +n)I_{n-3}|(\left(\zeta -n(n-3)\right)\left(\zeta -2{(n-2)}^2\right)-n{(n-2)}^3)\hfill \\ \hfill =& {(\zeta +n)}^{n-3}\left({\zeta }^2-(n-1)(3n-8)\zeta +n{(n-2)}^2(n-4)\right)\hfill \end{array}$$

Hence, Equation (1) is obtained as

$$\begin{array}{cc}\hfill \varphi ({\mathsf{\Gamma }}_{D_{2n}}^{ncm};\zeta )=& \left|W\right|\left|Z\right|=\left|D\right|\left|H\right|\left|Z\right|\hfill \\ \hfill =& {\left(\zeta +n\right)}^{n-3}{\left(\zeta +2(n-4)\right)}^{{\displaystyle \frac{n-2}{2}}}{\left(\zeta +2(n-2)\right)}^{{\displaystyle \frac{n}{2}}}({\zeta }^2-(n-1)(3n-8)\zeta \hfill \\ & +n{(n-2)}^2(n-4)),\hfill \end{array}$$

and hence, the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ are ${\zeta }_1=-n$ with multiplicity $(n-3)$, ${\zeta }_2=-2(n-4)$ with multiplicity $\left({\displaystyle \frac{n-2}{2}}\right)$, ${\zeta }_3=-2(n-2)$ with multiplicity $\left({\displaystyle \frac{n}{2}}\right)$, and

$$\begin{array}{cc}\hfill {\zeta }_{4,5}& ={\displaystyle \frac{(n-1)(3n-8)\pm \sqrt{{(n-1)}^2{(3n-8)}^2-4n{(n-2)}^2(n-4)}}{2}}\hfill \\ & ={\displaystyle \frac{(n-1)(3n-8)\pm \sqrt{5n^4-34n^3+89n^2-112n+64}}{2}}.\hfill \end{array}$$

□

Based on Lemmas 1 and 2, the general formula of the CN energy of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ is found as follows.

Theorem 2.

Let $G=D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉$, with $n\ge 3$ being an integer and ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ being its NCM-graph. Then, the CN energy of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$, $E_{CN}\left({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\right)$, is given by

$$E_{CN}\left({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\right)=\left\{\begin{array}{cc}2(3n^2-7n+3),\hfill & \mathit{if}n\mathit{is}\mathit{odd};\hfill \\ \\ 2(n-1)(3n-8),\hfill & \mathit{if}n\mathit{is}\mathit{even}.\hfill \end{array}\right.$$

Proof. 

Based on the value of n to be odd or even, the proof contains two cases.

Case 1. Assume that n is odd. Then, by Lemma 1, the CN eigenvalues of the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ of the dihedral groups $D_{2n}$ with $n\ge 3$ are ${\zeta }_1=-n$ with multiplicity $(n-2)$, ${\zeta }_2=-(2n-3)$ with multiplicity $(n-1)$, and

$${\zeta }_{3,4}={\displaystyle \frac{(3n^2-7n+3)\pm \sqrt{5n^4-18n^3+27n^2-22n+9}}{2}}.$$

Therefore, by Definition 2, the CN energy of the ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ when n is an odd integer is

$$\begin{array}{cc}\hfill E_{CN}\left({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\right)& =(n-2)|-n|+(n-1)|-(2n-3)|\hfill \\ & +\left|{\displaystyle \frac{(3n^2-7n+3)\pm \sqrt{5n^4-18n^3+27n^2-22n+9}}{2}}\right|\hfill \\ & =n(n-2)+(n-1)(2n-3)+3n^2-7n+3\hfill \\ & =6n^2-14n+6.\hfill \end{array}$$

Case 2. Assume that n is even. Then, by Lemma 2, the CN eigenvalues of the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ of the dihedral groups $D_{2n}$ with $n\ge 3$ are ${\zeta }_1=-n$ with multiplicity $(n-3)$, ${\zeta }_2=-2(n-4)$ with multiplicity $\left({\displaystyle \frac{n-2}{2}}\right)$, ${\zeta }_3=-2(n-2)$ with multiplicity $\left({\displaystyle \frac{n}{2}}\right)$, and

$${\zeta }_{4,5}={\displaystyle \frac{(n-1)(3n-8)\pm \sqrt{5n^4-34n^3+89n^2-112n+64}}{2}}.$$

Therefore, by Definition 2, the CN energy of the ${\mathsf{\Gamma }}_{D_{2n}}^{ncm}$ when n is an even integer is

$$\begin{array}{cc}\hfill E_{CN}\left({\mathsf{\Gamma }}_{D_{2n}}^{ncm}\right)& =(n-3)|-n|+{\displaystyle \frac{n-2}{2}}|-2(n-4)|+{\displaystyle \frac{n}{2}}|-2(n-2)|\hfill \\ & +\left|{\displaystyle \frac{(n-1)(3n-8)\pm \sqrt{5n^4-34n^3+89n^2-112n+64}}{2}}\right|\hfill \\ & =n(n-3)+(n-2)(n-4)+n(n-2)+(n-1)(3n-8)\hfill \\ & =2(n-1)(3n-8)\hfill \end{array}$$

□

Next, the following two examples illustrate the results in Theorem 2. First, Example 1 illustrates the result of the case of n is odd.

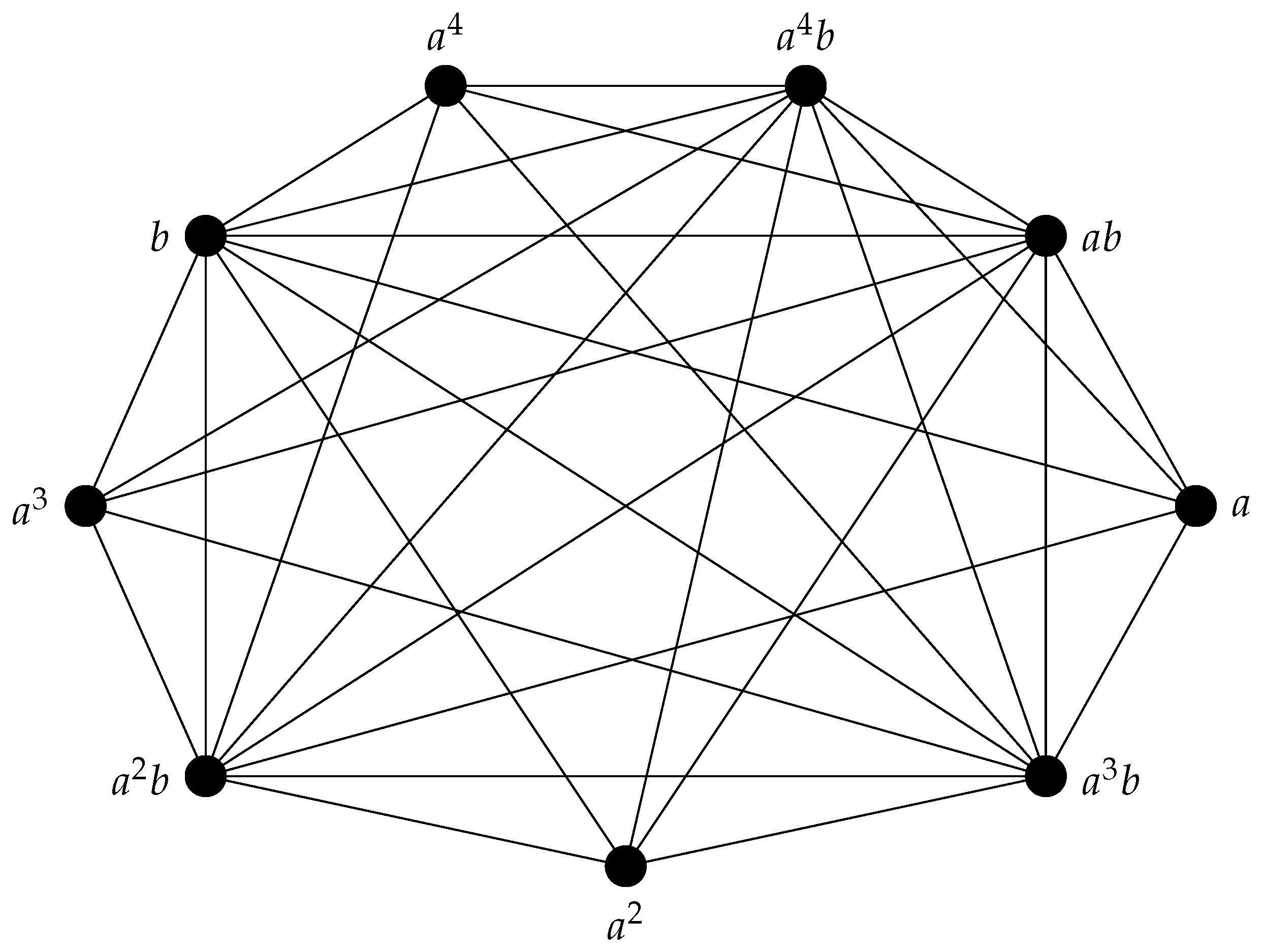
Example 1.

Let $G=D_{10}$, where $D_{10}=\{e,a,a^2,a^3,a^4,b,ab,a^{2}b,a^{3}b,a^{4}b\}$.

By applying Definition 5 and the properties of the dihedral group $D_{2n}$ established in Proposition 5 to the case of $D_{10}$, we conclude that the set of vertices of ${\mathsf{\Gamma }}_{D_{10}}^{ncm}$ is

$$V\left({\mathsf{\Gamma }}_{D_{10}}^{ncm}\right)=\{a,a^2,a^3,a^4,b,ab,a^{2}b,a^{3}b,a^{4}b\}.$$

Also, the edge set of the graph ${\mathsf{\Gamma }}_{D_{10}}^{ncm}$ is obtained as follows:

$$\begin{array}{cc}\hfill E\left({\mathsf{\Gamma }}_{D_{10}}^{ncm}\right)=& \{\{b,a\},\{b,a^2\},\{b,a^3\},\{b,a^4\},\{b,ab\},\{b,a^{2}b\},\{b,a^{3}b\},\{b,a^{4}b\},\hfill \\ \hfill \{ab& ,a\},\{ab,a^2\},\{ab,a^3\},\{ab,a^4\},\{ab,a^{2}b\},\{ab,a^{3}b\},\{ab,a^{4}b\},\{a^{2}b,a\},\hfill \\ \hfill \{a^{2}b& ,a^2\},\{a^{2}b,a^3\},\{a^{2}b,a^4\},\{a^{2}b,a^{3}b\},\{a^{2}b,a^{4}b\},\{a^{3}b,a\},\{a^{3}b,a^2\},\hfill \\ \hfill \{a^{3}b& ,a^3\},\{a^{3}b,a^4\},\{a^{3}b,a^{4}b\},\{a^{4}b,a\},\{a^{4}b,a^2\},\{a^{4}b,a^3\},\{a^{4}b,a^4\}\}.\hfill \end{array}$$

Figure 1 shows the graph ${\mathsf{\Gamma }}_{D_{10}}^{ncm}$.

Therefore, the CN matrix of ${\mathsf{\Gamma }}_{D_{10}}^{ncm}$ is

$$\begin{array}{cc}\hfill CN\left({\mathsf{\Gamma }}_{D_{10}}^{ncm}\right)& =\left[\begin{array}{ccccccccc}0& 5& 5& 5& 4& 4& 4& 4& 4\\ 5& 0& 5& 5& 4& 4& 4& 4& 4\\ 5& 5& 0& 5& 4& 4& 4& 4& 4\\ 5& 5& 5& 0& 4& 4& 4& 4& 4\\ 4& 4& 4& 4& 0& 7& 7& 7& 7\\ 4& 4& 4& 4& 7& 0& 7& 7& 7\\ 4& 4& 4& 4& 7& 7& 0& 7& 7\\ 4& 4& 4& 4& 7& 7& 7& 0& 7\\ 4& 4& 4& 4& 7& 7& 7& 7& 0\end{array}\right].\hfill \end{array}$$

Now, the CN characteristic polynomial of the CN matrix of ${\mathsf{\Gamma }}_{D_{10}}^{ncm}$, where $\varphi ({\mathsf{\Gamma }}_{D_{10}}^{ncm};\zeta )$, is obtained as

$$\begin{array}{cc}\hfill \varphi ({\mathsf{\Gamma }}_{D_{10}}^{ncm};\zeta )& =det\left(\zeta I-CN\left({\mathsf{\Gamma }}_{D_{10}}^{ncm}\right)\right)\hfill \\ & =\left|\begin{array}{ccccccccc}\zeta & -5& -5& -5& -4& -4& -4& -4& -4\\ -5& \zeta & -5& -5& -4& -4& -4& -4& -4\\ -5& -5& \zeta & -5& -4& -4& -4& -4& -4\\ -5& -5& -5& \zeta & -4& -4& -4& -4& -4\\ -4& -4& -4& -4& \zeta & -7& -7& -7& -7\\ -4& -4& -4& -4& -7& \zeta & -7& -7& -7\\ -4& -4& -4& -4& -7& -7& \zeta & -7& -7\\ -4& -4& -4& -4& -7& -7& -7& \zeta & -7\\ -4& -4& -4& -4& -7& -7& -7& -7& \zeta \end{array}\right|.\hfill \end{array}$$

Assisted by Matlab Version 9.14 (R2023a) software [25], the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{10}}^{ncm}$ are ${\zeta }_1=-5$ with multiplicity 3, ${\zeta }_2=-7$ with multiplicity 4, and ${\zeta }_{3,4}={\displaystyle \frac{43\pm 3\sqrt{161}}{2}}$. Hence, the CN energy of ${\mathsf{\Gamma }}_{D_{10}}^{ncm}$ is

$$E_{CN}\left({\mathsf{\Gamma }}_{D_{10}}^{ncm}\right)=3|-5|+4|-7|+\left|{\displaystyle \frac{43\pm 3\sqrt{161}}{2}}\right|=15+28+43=86.$$

Now, by Theorem 2, the CN energy of ${\mathsf{\Gamma }}_{D_{10}}^{ncm}$ is given as

$$E_{CN}\left({\mathsf{\Gamma }}_{D_{10}}^{ncm}\right)=2\left(3{\left(5\right)}^2-7\left(5\right)+3\right)=86,$$

which is the same result.

Next, this example illustrates the result of the case where n is even.

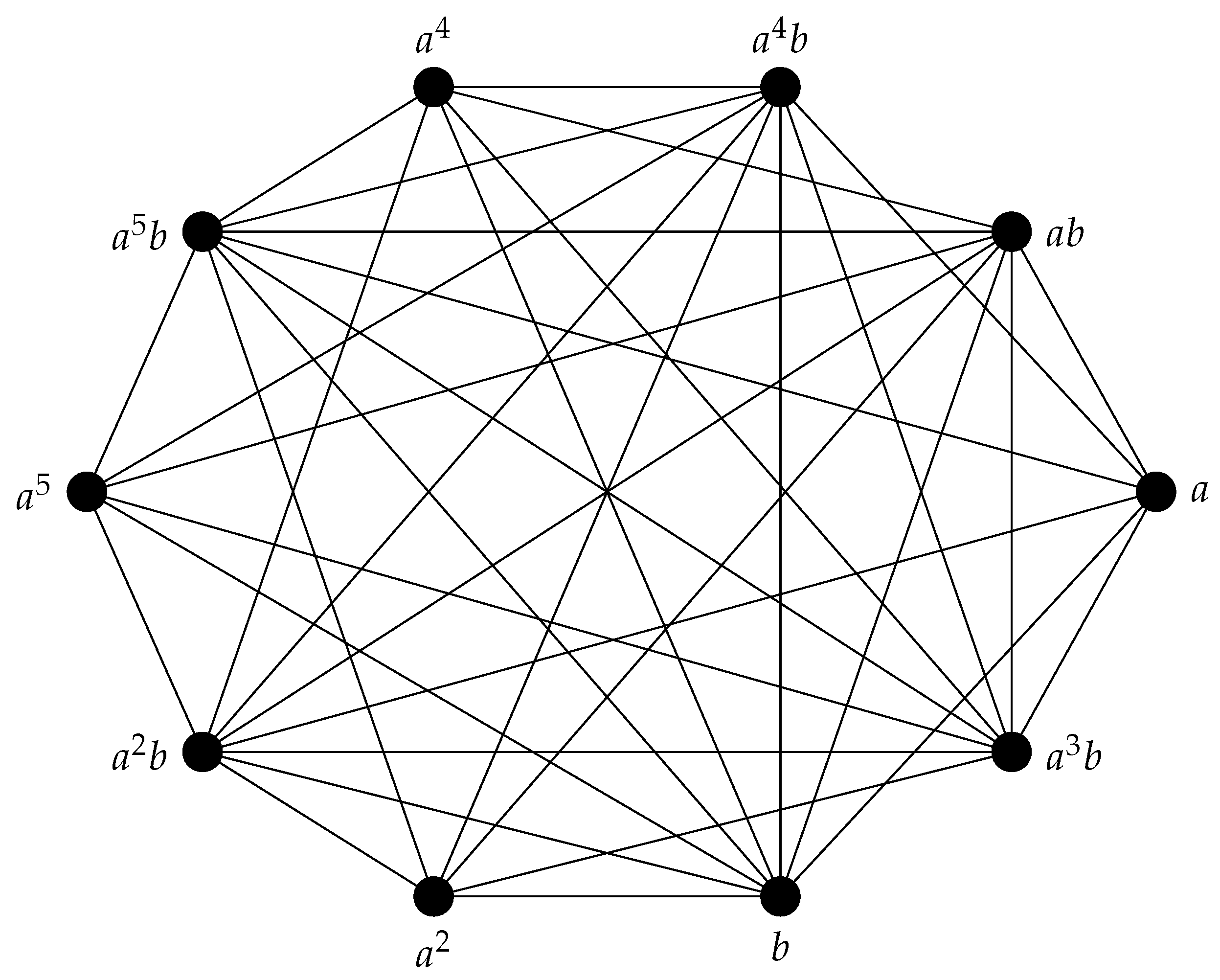
Example 2.

Let $G=D_{12}$, where $D_{12}=\{e,a,a^2,a^3,a^4,a^5,b,ab,a^{2}b,a^{3}b,a^{4}b,a^{5}b\}$.

By applying Definition 5 and the properties of the dihedral group $D_{2n}$ established in Proposition 5 to the case of $D_{12}$, we conclude that the set of vertices of ${\mathsf{\Gamma }}_{D_{12}}^{ncm}$ is

$$V\left({\mathsf{\Gamma }}_{D_{12}}^{ncm}\right)=\{a,a^2,a^4,a^5,b,ab,a^{2}b,a^{3}b,a^{4}b,a^{5}b\}.$$

Also, the edge set of the graph ${\mathsf{\Gamma }}_{D_{12}}^{ncm}$ is obtained as follows:

$$\begin{array}{cc}\hfill E\left({\mathsf{\Gamma }}_{D_{12}}^{ncm}\right)=& \left\{\right\{b,a\},\{b,a^2\},\{b,a^4\},\{b,a^5\},\{b,ab\},\{b,a^{2}b\},\{b,a^{4}b\},\{b,a^{5}b\}\hfill \\ \hfill \{ab& ,a\},\{ab,a^2\},\{ab,a^4\},\{ab,a^5\},\{ab,a^{2}b\},\{ab,a^{3}b\},\{ab,a^{5}b\},\{a^{2}b,a\},\hfill \\ \hfill \{a^{2}b& ,a^2\},\{a^{2}b,a^4\},\{a^{2}b,a^5\},\{a^{2}b,a^{3}b\},\{a^{2}b,a^{4}b\},\{a^{3}b,a\},\{a^{3}b,a^2\},\hfill \\ \hfill \{a^{3}b& ,a^4\},\{a^{3}b,a^5\},\{a^{3}b,a^{4}b\},\{a^{3}b,a^{5}b\},\{a^{4}b,a\},\{a^{4}b,a^2\},\{a^{4}b,a^4\},\{a^{4}b,a^5\},\hfill \\ \hfill \{a^{4}b& ,a^{5}b\},\{a^{5}b,a\},\{a^{5}b,a^2\},\{a^{5}b,a^4\},\{a^{5}b,a^5\}\}.\hfill \end{array}$$

Figure 2 shows the graph ${\mathsf{\Gamma }}_{D_{12}}^{ncm}$.

Therefore, the CN matrix of ${\mathsf{\Gamma }}_{D_{12}}^{ncm}$ is

$$\begin{array}{cc}\hfill CN\left({\mathsf{\Gamma }}_{D_{12}}^{ncm}\right)& =\left[\begin{array}{cccccccccc}0& 6& 6& 6& 4& 4& 4& 4& 4& 4\\ 6& 0& 6& 6& 4& 4& 4& 4& 4& 4\\ 6& 6& 0& 6& 4& 4& 4& 4& 4& 4\\ 6& 6& 6& 0& 4& 4& 4& 4& 4& 4\\ 4& 4& 4& 4& 0& 6& 6& 8& 6& 6\\ 4& 4& 4& 4& 6& 0& 6& 6& 8& 6\\ 4& 4& 4& 4& 6& 6& 0& 6& 6& 8\\ 4& 4& 4& 4& 8& 6& 6& 0& 6& 6\\ 4& 4& 4& 4& 6& 8& 6& 6& 0& 6\\ 4& 4& 4& 4& 6& 6& 8& 6& 6& 0\end{array}\right].\hfill \end{array}$$

Now, the CN characteristic polynomial of ${\mathsf{\Gamma }}_{D_{12}}^{ncm}$, where $\varphi ({\mathsf{\Gamma }}_{D_{12}}^{ncm};\zeta )$, is given as

$$\begin{array}{cc}\hfill \varphi ({\mathsf{\Gamma }}_{D_{12}}^{ncm};\zeta )& =det\left(\zeta I-CN\left({\mathsf{\Gamma }}_{D_{12}}^{ncm}\right)\right)\hfill \\ & =\left|\begin{array}{cccccccccc}\zeta & -6& -6& -6& -4& -4& -4& -4& -4& -4\\ -6& \zeta & -6& -6& -4& -4& -4& -4& -4& -4\\ -6& -6& \zeta & -6& -4& -4& -4& -4& -4& -4\\ -6& -6& -6& \zeta & -4& -4& -4& -4& -4& -4\\ -4& -4& -4& -4& \zeta & -6& -6& -8& -6& -6\\ -4& -4& -4& -4& -6& \zeta & -6& -6& -8& -6\\ -4& -4& -4& -4& -6& -6& \zeta & -6& -6& -8\\ -4& -4& -4& -4& -8& -6& -6& \zeta & -6& -6\\ -4& -4& -4& -4& -6& -8& -6& -6& \zeta & -6\\ -4& -4& -4& -4& -6& -6& -8& -6& -6& \zeta \end{array}\right|.\hfill \end{array}$$

Assisted by Matlab software [25], the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{12}}^{ncm}$ are ${\zeta }_1=-6$ with multiplicity 3, ${\zeta }_2=-4$ with multiplicity 2, ${\zeta }_3=-8$ with multiplicity 3, and ${\zeta }_{4,5}=25\pm \sqrt{433}$. Hence, the CN energy of ${\mathsf{\Gamma }}_{D_{12}}^{ncm}$ is obtained as

$$E_{CN}\left({\mathsf{\Gamma }}_{D_{12}}^{ncm}\right)=3|-6|+2|-4|+3|-8|+|25\pm \sqrt{433}|=18+8+24+50=100,$$

and by Theorem 2,

$$E_{CN}\left({\mathsf{\Gamma }}_{D_{12}}^{ncm}\right)=2(6-1)\left(3\left(6\right)-8\right)=10\times 10=100,$$

which is the same result.

Next, the CN energy of the CM-graph associated with dihedral groups, $D_{2n}$, is obtained in terms of n, and the results are illustrated by some examples.

3. CN Energy of the CM-Graph of D_2n

In this part, the general formula of the CN energy of the CM-graph of $D_{2n}$ is determined in terms of n.

First, in two lemmas (based on the value of n as either odd or even) the CN characteristic polynomials of the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ are provided along with their CN eigenvalues.

Next, based on the two lemmas, Theorem 3 determines the general formula of the CN energy of the CM-graph of $D_{2n}$ in terms of n. Moreover, two examples are presented to illustrate the results of Theorem 3.

The following two lemmas are necessary to determine the CN energy of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$. First, Lemma 3 obtains the CN characteristic polynomial and the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ in the case where n is an odd integer.

Lemma 3.

Let $G=D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉$, with $n\ge 3$ being an odd integer and ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ being its CM-graph. Then, the characteristic polynomial of the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ is given as follows:

$$\varphi ({\mathsf{\Gamma }}_{D_{2n}}^{cm};\zeta )={\zeta }^n{\left(\zeta +(n-3)\right)}^{n-2}\left(\zeta -(n-2)(n-3)\right),$$

and hence, the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ are ${\zeta }_1=0$ with multiplicity n, ${\zeta }_2=-(n-3)$ with multiplicity $(n-2)$, and ${\zeta }_3=(n-2)(n-3)$.

Proof. 

Suppose that $G=D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉$, where $n\ge 3$ is an odd integer, and ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ is its CM-graph. Then, by Definition 6 and Proposition 5, the number of vertices of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ is in this case $p=2n-1$ (recall that $Z\left(D_{2n}\right)=\left\{e\right\}$). Because the elements of the form $a^i$ commute each other and the elements of the form $a^{i}b$ do not commute with each other and also commute with the elements $a^i$, then there exists three situations of CN neighborhoods of the vertices of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$, which are the following:

• $\left|\eta \right(a^k,a^l\left)\right|=n-3$, $\forall k\ne l$, where $\{k,l\}\subseteq \{1,\cdots ,n-1\}$.
• $\left|\eta \right(a^{k}b,a^{l}b\left)\right|=0$, $\forall k\ne l$, where $\{k,l\}\subseteq \{0,1,\cdots ,n-1\}$.
• $\left|\eta \right(a^i,a^{j}b\left)\right|=0$, $\forall i,j$.

Thus, the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$, $CN\left({\mathsf{\Gamma }}_{D_{2n}}^{cm}\right)$, is given by

$$\begin{array}{cc}\hfill CN\left({\mathsf{\Gamma }}_{D_{2n}}^{cm}\right)& =\left[\begin{array}{cccccccc}0& n-3& \cdots & n-3& 0& \cdots & \cdots & 0\\ n-3& 0& \ddots & ⋮& ⋮& \ddots & \ddots & ⋮\\ ⋮& & \ddots & n-3& ⋮& ⋮& \ddots & ⋮\\ n-3& \cdots & n-3& 0& 0& \cdots & \cdots & 0\\ 0& \cdots & \cdots & 0& 0& 0& \cdots & 0\\ ⋮& \ddots & \ddots & ⋮& 0& \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & ⋮& ⋮& \ddots & \ddots & 0\\ 0& \cdots & \cdots & 0& 0& \cdots & 0& 0\end{array}\right]\hfill \\ & =\left[\begin{array}{cc}(n-3)J_{n-1}-(n-3)I_{n-1}& O_{(n-1)\times n}\\ & \\ O_{n\times (n-1)}& O_{n\times n}\end{array}\right].\hfill \end{array}$$

Therefore, the CN characteristic polynomial of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ is found as follows:

$$\begin{array}{cc}\hfill \varphi ({\mathsf{\Gamma }}_{D_{2n}}^{cm};\zeta )=& det\left(I\zeta -CN\left({\mathsf{\Gamma }}_{D_{2n}}^{cm}\right)\right)=\left|\begin{array}{cc}(\zeta +n-3)I_{n-1}-(n-3)J_{n-1}& O_{(n-1)\times n}\\ & \\ O_{n\times (n-1)}& \zeta I_n\end{array}\right|.\hfill \end{array}$$

Then, by Proposition 4,

$$\varphi ({\mathsf{\Gamma }}_{D_{2n}}^{cm};\zeta )=|(\zeta +n-3)I_{n-1}-(n-3)J_{n-1}\left|\right|\zeta I_n|.$$

Now, by Proposition 3—with $p_1=n-1$, $p_2=n$, $a=n-3$, and $b=c=d=0$—$\varphi ({\mathsf{\Gamma }}_{D_{2n}}^{cm};\zeta )$ is found as

$$\varphi ({\mathsf{\Gamma }}_{D_{2n}}^{cm};\zeta )={\zeta }^n{\left(\zeta +(n-3)\right)}^{n-2}\left(\zeta -(n-2)(n-3)\right),$$

and hence, the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ are ${\zeta }_1=0$ with multiplicity n, ${\zeta }_2=-(n-3)$ with multiplicity $(n-2)$, and ${\zeta }_3=(n-2)(n-3)$. □

Next, the CN characteristic polynomial and the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ when n is an even integer are provided in Lemma 4.

Lemma 4.

Let $G=D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉$, where $n\ge 3$ is an even integer, and ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ is its CM-graph. Then, the characteristic polynomial of the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ is given as follows:

$$\varphi ({\mathsf{\Gamma }}_{D_{2n}}^{cm};\zeta )={\zeta }^n{\left(\zeta +(n-4)\right)}^{n-3}\left(\zeta -(n-3)(n-4)\right),$$

and hence, the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ are ${\zeta }_1=0$ with multiplicity n, ${\zeta }_2=-(n-4)$ with multiplicity $(n-3)$, and ${\zeta }_3=(n-3)(n-4)$.

Proof. 

Suppose $G=D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉$, where $n\ge 3$ is an even integer, and ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ is its CM-graph. Then, by Definition 6 and Proposition 5, the number of vertices of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ is in this case $p=2n-2$ (recall that $Z\left(D_{2n}\right)=\{e,a^{{\displaystyle \frac{n}{2}}}\}$). Because the elements of the form $a^i$ commute with each other and any element of the form $a^{i}b$ commutes only with the element $a^{i+{\displaystyle \frac{n}{2}}}b$, then there exist three cases of the CN neighborhoods between the vertices of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ which are the following:

• $\left|\eta \right(a^k,a^l\left)\right|=n-4$, $\forall k\ne l$, where $\{k,l\}\subseteq \{1,\cdots ,n-1\}$.
• $\left|\eta \right(a^i,a^{j}b\left)\right|=0$, $\forall i,j$.
• $\left|\eta \right(a^{k}b,a^{l}b\left)\right|=0$, $\forall k\ne l$, where $\{k,l\}\subseteq \{0,1,\cdots ,n-1\}$.

Thus, the CN matrix of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$, where $CN\left({\mathsf{\Gamma }}_{D_{2n}}^{cm}\right)$, is given by

$$CN\left({\mathsf{\Gamma }}_{D_{2n}}^{cm}\right)=\left[\begin{array}{cc}(n-4)J_{n-2}-(n-4)I_{n-2}& O_{(n-2)\times n}\\ & \\ O_{n\times (n-2)}& O_{n\times n}\end{array}\right].$$

By the same argument of Lemma 3,

$$\varphi ({\mathsf{\Gamma }}_{D_{2n}}^{cm};\zeta )={\zeta }^n{\left(\zeta +(n-4)\right)}^{n-3}\left(\zeta -(n-3)(n-4)\right),$$

and hence, the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ are ${\zeta }_1=0$ with multiplicity n, ${\zeta }_2=-(n-4)$ with multiplicity $(n-3)$, and ${\zeta }_3=(n-3)(n-4)$. □

Now, Theorem 3 gives the general formula of $E_{CN}\left({\mathsf{\Gamma }}_{D_{2n}}^{cm}\right)$ as follows.

Theorem 3.

Let $G=D_{2n}\cong 〈a,b:a^n=b^2=e,ba=a^{-1}b〉$, with $n\ge 3$, and ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ be its CM-graph. Then, the CN energy of ${\mathsf{\Gamma }}_{D_{2n}}^{cm}$ is given by

$$E_{CN}\left({\mathsf{\Gamma }}_{D_{2n}}^{cm}\right)=\left\{\begin{array}{cc}2(n-2)(n-3),\hfill & \mathit{if}n\mathit{is}\mathit{odd};\hfill \\ \\ 2(n-3)(n-4),\hfill & \mathit{if}n\mathit{is}\mathit{even}.\hfill \end{array}\right.$$

Proof. 

The result follows directly from Lemma 4. □

Next, two examples are provided to illustrate the results in Theorem 3. The first example illustrates the case when n is odd, and the second example illustrates the case when n is even.

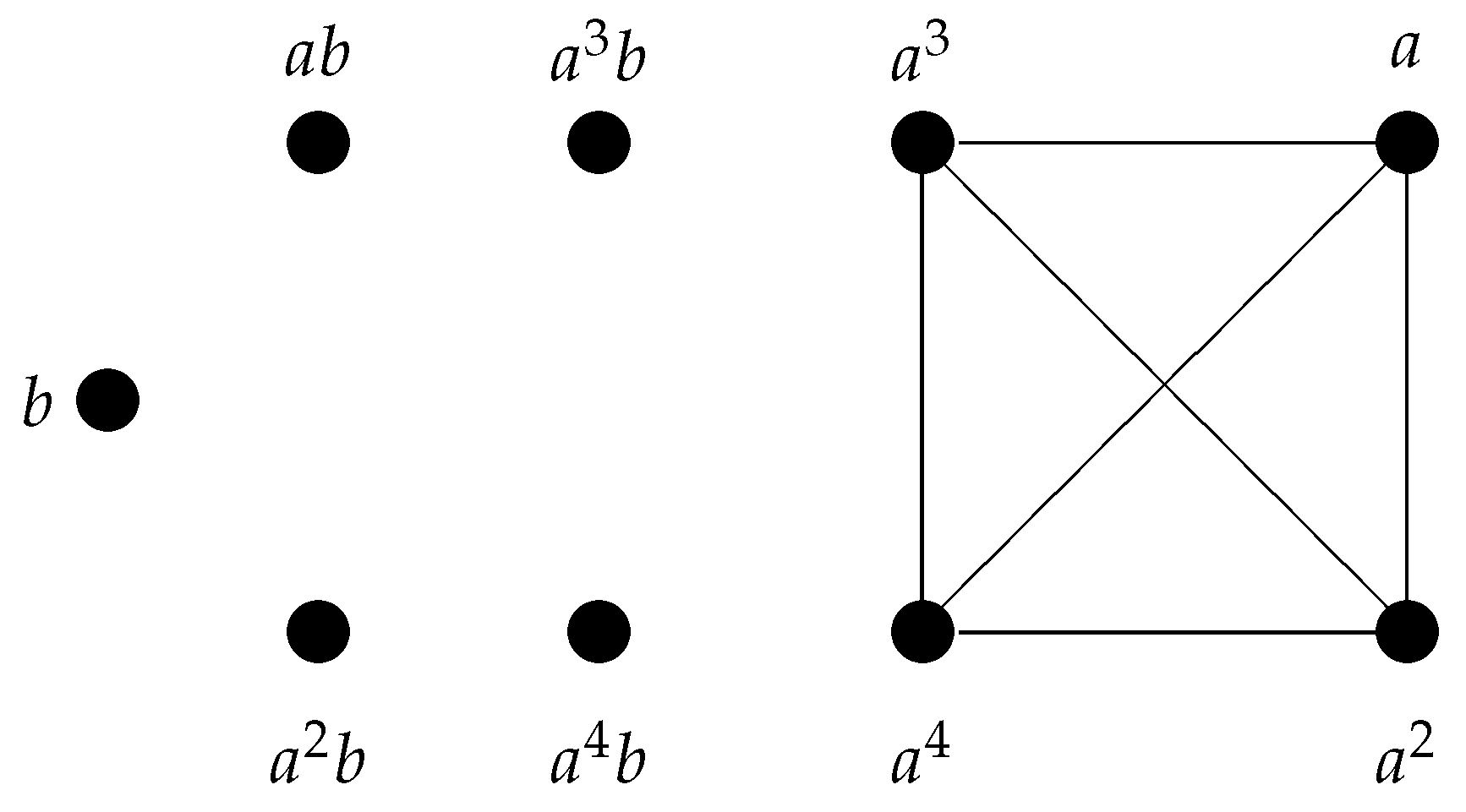
Example 3.

Let $G=D_{10}$, where $D_{10}=\{e,a,a^2,a^3,a^4,b,ab,a^{2}b,a^{3}b,a^{4}b\}$.

By utilizing the Definition 6 and the properties of the dihedral group $D_{2n}$ established in Proposition 5 to the case of $D_{10}$, we conclude that $Z\left(D_{10}\right)=\left\{e\right\}$ and the set of vertices of ${\mathsf{\Gamma }}_{D_{10}}^{cm}$ is

$$V\left({\mathsf{\Gamma }}_{D_{10}}^{cm}\right)=\{a,a^2,a^3,a^4,b,ab,a^{2}b,a^{3}b,a^{4}b\}.$$

Also, the set of edges of ${\mathsf{\Gamma }}_{D_{10}}^{cm}$ is presented as

$$E\left({\mathsf{\Gamma }}_{D_{10}}^{cm}\right)=\left\{\{a,a^2\},\{a,a^3\},\{a,a^4\},\{a^2,a^3\},\{a^2,a^4\},\{a^3,a^4\}\right\}.$$

Figure 3 shows the graph ${\mathsf{\Gamma }}_{D_{10}}^{cm}$.

Therefore, the CN matrix of ${\mathsf{\Gamma }}_{D_{10}}^{cm}$ is

$$\begin{array}{cc}& CN\left({\mathsf{\Gamma }}_{D_{10}}^{cm}\right)=\left[\begin{array}{ccccccccc}0& 2& 2& 2& 0& 0& 0& 0& 0\\ 2& 0& 2& 2& 0& 0& 0& 0& 0\\ 2& 2& 0& 2& 0& 0& 0& 0& 0\\ 2& 2& 2& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right].\hfill \end{array}$$

The characteristic polynomial of $CN\left({\mathsf{\Gamma }}_{D_{10}}^{cm}\right)$ is

$$\begin{array}{cc}\hfill \varphi ({\mathsf{\Gamma }}_{D_{10}}^{cm};\zeta )& =det\left(\zeta I-CN\left({\mathsf{\Gamma }}_{D_{10}}^{cm}\right)\right)=\left|\begin{array}{ccccccccc}\zeta & -2& -2& -2& 0& 0& 0& 0& 0\\ -2& \zeta & -2& -2& 0& 0& 0& 0& 0\\ -2& -2& \zeta & -2& 0& 0& 0& 0& 0\\ -2& -2& -2& \zeta & 0& 0& 0& 0& 0\\ 0& 0& 0& 0& \zeta & 0& 0& 0& 0\\ 0& 0& 0& 0& 0& \zeta & 0& 0& 0\\ 0& 0& 0& 0& 0& 0& \zeta & 0& 0\\ 0& 0& 0& 0& 0& 0& 0& \zeta & 0\\ 0& 0& 0& 0& 0& 0& 0& 0& \zeta \end{array}\right|\hfill \\ & ={\zeta }^5{(\zeta +2)}^3(\zeta -6).\hfill \end{array}$$

Thus, the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{10}}^{cm}$ are ${\zeta }_1=0$ with multiplicity 5, ${\zeta }_2=-2$ with multiplicity 3, and ${\zeta }_3=6$. Hence, the CN energy of ${\mathsf{\Gamma }}_{D_{10}}^{cm}$ is

$$E_{CN}\left({\mathsf{\Gamma }}_{D_{10}}^{cm}\right)=5\left|0\right|+3|-2|+\left|6\right|=12,$$

and by Theorem 3, the CN energy of ${\mathsf{\Gamma }}_{D_{10}}^{cm}$ is given by

$$E_{CN}\left({\mathsf{\Gamma }}_{D_{10}}^{cm}\right)=2(5-2)(5-3)=12,$$

which is the same result.

Now, Example 4 illustrates the case where n is even.

Example 4.

Consider $G=D_{12}$, where $D_{12}=\{e,a,a^2,a^3,a^4,a^5,b,ab,a^{2}b,a^{3}b,a^{4}b,a^{5}b\}$.

By utilizing Definition 6 and the properties of the dihedral group $D_{2n}$ established in Proposition 5 to the specific case of $D_{12}$, we conclude that $Z\left(D_{12}\right)=\{e,a^3\}$, and then the set of vertices of ${\mathsf{\Gamma }}_{D_{12}}^{cm}$ is

$$V\left({\mathsf{\Gamma }}_{D_{12}}^{cm}\right)=\{a,a^2,a^4,a^5,b,ab,a^{2}b,a^{3}b,a^{4}b,a^{5}b\}.$$

Also, the set of edges is

$$\begin{array}{c}\hfill E\left({\mathsf{\Gamma }}_{D_{12}}^{cm}\right)=\left\{\{a,a^2\},\{a,a^4\},\{a,a^5\},\{a^2,a^4\},\{a^2,a^5\},\{a^4,a^5\},\{b,a^{3}b\},\{ab,a^{4}b\},\{a^{2}b,a^{5}b\}\right\}.\end{array}$$

Figure 4 shows the graph ${\mathsf{\Gamma }}_{D_{12}}^{cm}$.

Thus, the CN matrix of ${\mathsf{\Gamma }}_{D_{12}}^{cm}$ is

$$\begin{array}{cc}& CN\left({\mathsf{\Gamma }}_{D_{12}}^{cm}\right)=\left[\begin{array}{cccccccccc}0& 2& 2& 2& 0& 0& 0& 0& 0& 0\\ 2& 0& 2& 2& 0& 0& 0& 0& 0& 0\\ 2& 2& 0& 2& 0& 0& 0& 0& 0& 0\\ 2& 2& 2& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right].\hfill \end{array}$$

The characteristic polynomial of $CN\left({\mathsf{\Gamma }}_{D_{12}}^{cm}\right)$ is

$$\begin{array}{cc}\hfill \varphi ({\mathsf{\Gamma }}_{D_{12}}^{cm};\zeta )& =det\left(\zeta I-CN\left({\mathsf{\Gamma }}_{D_{12}}^{cm}\right)\right)=\left|\begin{array}{cccccccccc}\zeta & -2& -2& -2& 0& 0& 0& 0& 0& 0\\ -2& \zeta & -2& -2& 0& 0& 0& 0& 0& 0\\ -2& -2& \zeta & -2& 0& 0& 0& 0& 0& 0\\ -2& -2& -2& \zeta & 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& \zeta & 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& \zeta & 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& \zeta & 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& \zeta & 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& \zeta & 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& \zeta \end{array}\right|\hfill \\ & ={\zeta }^6{(\zeta +2)}^3(\zeta -6).\hfill \end{array}$$

Therefore, the CN eigenvalues of ${\mathsf{\Gamma }}_{D_{12}}^{cm}$ are ${\zeta }_1=0$ with multiplicity 6, ${\zeta }_2=-2$ with multiplicity 3, and ${\zeta }_3=6$. Hence, the CN energy of ${\mathsf{\Gamma }}_{D_{12}}^{cm}$ is

$$E_{CN}\left({\mathsf{\Gamma }}_{D_{12}}^{cm}\right)=6\left|0\right|+3|-2|+\left|6\right|=12,$$

and by using Theorem 3,

$$E_{CN}\left({\mathsf{\Gamma }}_{D_{12}}^{cm}\right)=2(6-3)(6-4)=12,$$

which is the same result.

In the following section, general formulas for the CN energy of the CM- and NCM-graphs associated to the generalized quaternion group, $Q_{4n}$, are provided.

4. CN Energy of the CM- and NCM- Graphs of Q_4n

In this section, based on Proposition 1 (which determines the CN energy of the complete graph on p vertices, $K_p$) and Proposition 1 (which determines the CN energy of disconnected graphs), a general formula of the CN energy of the CM-graph for $Q_{4n}$ is obtained in terms of n. In addition, the CN characteristic polynomial, CN eigenvalues, and a general formula of the CN energy of the NCM-graph of $Q_{4n}$ are provided.

First, Theorem 4 presents a general formula of $E_{CN}$ of the CM-graph associated with $Q_{4n}$.

Theorem 4.

Let $G=Q_{4n}\cong 〈a,b:a^n=b^2,a^{2n}=b^4=e,b^{-1}a=a^{-1}{b}^{-1}〉$, with $n\ge 2$, and ${\mathsf{\Gamma }}_{Q_{4n}}^{cm}$ be its CM-graph. Then, the CN energy of ${\mathsf{\Gamma }}_{Q_{4n}}^{cm}$ is given by

$$E_{CN}\left({\mathsf{\Gamma }}_{Q_{4n}}^{cm}\right)=4(n-2)(2n-3).$$

Proof. 

Suppose that $G=Q_{4n}\cong 〈a,b:a^n=b^2,a^{2n}=b^4=e,b^{-1}a=a^{-1}{b}^{-1}〉$, with $n\ge 2$, and ${\mathsf{\Gamma }}_{Q_{4n}}^{cm}$ be its CM-graph. Then, by Definition 6 and Proposition 6, the number of vertices of ${\mathsf{\Gamma }}_{Q_{4n}}^{cm}$ in this case is $(4n-2)$ (recall that $Z\left(Q_{4n}\right)=\{e,a^n\}$). Because the elements of the form $a^i$, where $i\in \{1,2,\dots ,2n-1\}$ and $i\ne n$, commute with each other, they form a complete graph $K_{2n-2}$. Furthermore, any element of the form $a^{j}b$, where $j\in \{0,1,2,\dots ,2n-1\}$, only commutes with the element $a^{j+n}b$. Consequently, these vertices form n connected components, each isomorphic to the complete graph $K_2$.

$${\mathsf{\Gamma }}_{Q_{4n}}^{cm}=K_{2n-2}\cup n{K}_2.$$

(2)

Therefore, by Proposition 1,

$$E_{CN}\left({\mathsf{\Gamma }}_{Q_{4n}}^{cm}\right)=E_{CN}\left(K_{2n-2}\right)+n{E}_{CN}\left(K_2\right).$$

Now, by Proposition 1 and Proposition 2, the CN energy of ${\mathsf{\Gamma }}_{Q_{4n}}^{cm}$ is given by

$$E_{CN}\left({\mathsf{\Gamma }}_{Q_{4n}}^{cm}\right)=2(2n-2-1)(2n-2-2)=4(n-2)(2n-3).$$

□

Next, a general formula of $E_{CN}$ of the NCM-graph associated with $Q_{4n}$, ${\mathsf{\Gamma }}_{Q_{4n}}^{ncm}$, is found in Theorem 5.

Theorem 5.

Let $G=Q_{4n}\cong 〈a,b:a^n=b^2,a^{2n}=b^4=e,b^{-1}a=a^{-1}{b}^{-1}〉$, with $n\ge 2$, and ${\mathsf{\Gamma }}_{Q_{4n}}^{ncm}$ be its NCM-graph. Then, the CN energy of ${\mathsf{\Gamma }}_{Q_{4n}}^{ncm}$ is given by

$$E_{CN}\left({\mathsf{\Gamma }}_{Q_{4n}}^{ncm}\right)=4(2n-1)(3n-4).$$

Proof. 

Suppose that $G=Q_{4n}\cong 〈a,b:a^n=b^2,a^{2n}=b^4=e,b^{-1}a=a^{-1}{b}^{-1}〉$, with $n\ge 2$, and let ${\mathsf{\Gamma }}_{Q_{4n}}^{ncm}$ be its NCM-graph. Then, by Definition 5 and Proposition 6, the number of vertices of ${\mathsf{\Gamma }}_{Q_{4n}}^{ncm}$ in this case is $(4n-2)$ (recall that $Z\left(Q_{4n}\right)=\{e,a^n\}$).

It can be seen from Definition 5 and Definition 6 that ${\mathsf{\Gamma }}_G^{ncm}=\overline{{\mathsf{\Gamma }}_G^{cm}}$, where G is a group. Therefore, by Equation (2),

$${\mathsf{\Gamma }}_{Q_{4n}}^{ncm}=\overline{{\mathsf{\Gamma }}_{Q_{4n}}^{cm}}=\overline{K_{2n-2}\cup n{K}_2}=K_{\underset{ntimes}{\underbrace{2,2,\cdots ,2}},2n-2}.$$

Again, by Proposition 6, there exist four situations of common neighborhoods of the vertices of ${\mathsf{\Gamma }}_{Q_{4n}}^{ncm}$, which are clarified as follows:

• $\left|\eta \right(a^k,a^l\left)\right|=2n$, $\forall k\ne l$, where $\{k,l\}\subseteq \{1,\cdots ,2n-1\}-\left\{n\right\}$.
• $\left|\eta \right(a^i,a^{j}b\left)\right|=2n-2$, $\forall i,j$.
• $\left|\eta \right(a^{k}b,a^{l}b\left)\right|=4n-4$, $\forall l=k+n$, where $\{k,l\}\subseteq \{0,1,\cdots ,2n-1\}$.
• $\left|\eta \right(a^{k}b,a^{l}b\left)\right|=4n-6$, $\forall l\ne k+n$, where $\{k,l\}\subseteq \{0,1,\cdots ,2n-1\}$.

Then, the CN matrix of ${\mathsf{\Gamma }}_{Q_{4n}}^{ncm}$ is written as

$$\begin{array}{cc}\hfill CN\left({\mathsf{\Gamma }}_{Q_{4n}}^{ncm}\right)& =\left[\begin{array}{ccccc}2n\left(J_{2n-2}-I_{2n-2}\right)& & (2n-2)J_{(2n-2)\times n}& & (2n-2)J_{(2n-2)\times n}\\ & & \\ (2n-2)J_{n\times (2n-2)}& & (4n-6)\left(J_n-I_n\right)& & (4n-6)J_n+2I_n\\ & & \\ (2n-2)J_{n\times (2n-2)}& & (4n-6)J_n+2I_n& & (4n-6)\left(J_n-I_n\right)\end{array}\right].\hfill \end{array}$$

Thus, the CN characteristic polynomial of ${\mathsf{\Gamma }}_{Q_{4n}}^{ncm}$ is given by

$$\begin{array}{cc}& \varphi ({\mathsf{\Gamma }}_{Q_{4n}}^{ncm};\zeta )=|\zeta I-CN\left({\mathsf{\Gamma }}_{Q_{4n}}^{ncm}\right)|\hfill \\ \hfill & =\left|\begin{array}{ccc}(\zeta +2n)I_{2n-2}-2n{J}_{2n-2}& -(2n-2)J_{(2n-2)\times n}& -(2n-2)J_{(2n-2)\times n}\\ & & \\ -(2n-2)J_{n\times (2n-2)}& (\zeta +4n-6)I_n-(4n-6)J_n& -(4n-6)J_n-2I_n\\ & & \\ -(2n-2)J_{n\times (2n-2)}& -(4n-6)J_n-2I_n& (\zeta +4n-6)I_n-(4n-6)J_n\end{array}\right|.\hfill \end{array}$$

(3)

Now, to obtain $\varphi ({\mathsf{\Gamma }}_{Q_{4n}}^{ncm};\zeta )$, the determinant in Equation (3) needs some elementary operations for its rows and columns, which are defined as follows:

• Replace $R_{3n-2+i}$ by the operation $R_{3n-2+i}^{\prime }=R_{3n-2+i}-R_{2n-2+i}$ for all $1\le i\le n$; then, the determinant becomes

  $$\left|\begin{array}{ccc}(\zeta +2n)I_{2n-2}-2n{J}_{2n-2}& -(2n-2)J_{(2n-2)\times n}& -(2n-2)J_{(2n-2)\times n}\\ & & \\ -(2n-2)J_{n\times (2n-2)}& (\zeta +4n-6)I_n-(4n-6)J_n& -(4n-6)J_n-2I_n\\ & & \\ O_{n\times (2n-2)}& -(\zeta +4n-4)I_n& (\zeta +4n-4)I_n\end{array}\right|.$$
• Replace $C_{2n-2+i}$ by the operation $C_{2n-2+i}^{\prime }=C_{3n-2+i}+C_{2n-2+i}$ for all $1\le i\le n$; then the determinant becomes

  $$\begin{array}{cc}& \left|\begin{array}{ccc}(\zeta +2n)I_{2n-2}-2n{J}_{2n-2}& -(4n-4)J_{(2n-2)\times n}& -(2n-2)J_{(2n-2)\times n}\\ & & \\ -(2n-2)J_{n\times (2n-2)}& (\zeta +4n-8)I_n-2(4n-6)J_n& -(4n-6)J_n-2I_n\\ & & \\ O_{n\times (2n-2)}& O_{n\times n}& (\zeta +4n-4)I_n\end{array}\right|\hfill \\ & =\left|\begin{array}{ccc}W& & X\\ Y& & Z\end{array}\right|,\hfill \end{array}$$

  where

  $$\left|W\right|=\left|\begin{array}{cc}(\zeta +2n)I_{2n-2}-2n{J}_{2n-2}& -2(2n-2)J_{(2n-2)\times n}\\ -(2n-2)J_{n\times (2n-2)}& (\zeta +4n-8)I_n-2(4n-6)J_n\end{array}\right|,$$
  $\left|X\right|=\left|\begin{array}{c}-(2n-2)J_{(2n-2)\times n}\\ -(4n-6)J_n-2I_n\end{array}\right|$, $\left|Y\right|=\left|\begin{array}{c}{O}_{n\times (3n-2)}\end{array}\right|$, and $\left|Z\right|=\left|\begin{array}{c}(\zeta +4n-4)I_n\end{array}\right|$

Therefore, by Proposition 4,

$$\varphi ({\mathsf{\Gamma }}_{Q_{4n}}^{ncm};\zeta )=\left|\begin{array}{ccc}W& & X\\ Y& & Z\end{array}\right|=\left|W\right|\left|Z\right|.$$

It can be seen that $\left|Z\right|={\left(\zeta +4(n-1)\right)}^n$. Thus, we need to calculate $\left|W\right|$. First, $\left|W\right|$ can be written as

$$\left|W\right|=\left|\begin{array}{ccc}(\zeta +2n)I_{2n-2}-2n{J}_{2n-2}& -2(2n-2)J_{(2n-2)\times 1}& -2(2n-2)J_{(2n-2)\times n-1}\\ -(2n-2)J_{1\times (2n-2)}& \zeta -(4n-4)& -2(4n-6)J_{1\times n-1}\\ -(2n-2)J_{n-1\times (2n-2)}& -2(4n-6)J_{n-1\times 1}& (\zeta +4n-8)I_{n-1}-2(4n-6)J_{n-1}\end{array}\right|.$$

Next, $\left|W\right|$ has been calculated by placing the following operation:

• Replace $R_{2n-1+i}^{\prime }=R_{2n-1+i}-R_{2n-1}$ for all $1\le i\le n-1$; then $\left|W\right|$ becomes

  $$\left|\begin{array}{ccc}(\zeta +2n)I_{2n-2}-2n{J}_{2n-2}& -2(2n-2)J_{(2n-2)\times 1}& -2(2n-2)J_{(2n-2)\times n-1}\\ -(2n-2)J_{1\times (2n-2)}& \zeta -(4n-4)& -2(4n-6)J_{1\times n-1}\\ O_{n-1\times (2n-2)}& -(\zeta +4n-8)J_{n-1\times 1}& (\zeta +4n-8)I_{n-1}\end{array}\right|.$$
• Replace $C_{2n-1}^{\prime }=C_{2n-1}+C_{2n}+C_{2n+1}+\cdots +C_{3n-2}$, then

  $$\left|\begin{array}{ccc}(\zeta +2n)I_{2n-2}-2n{J}_{2n-2}& -2n(2n-2)J_{(2n-2)\times 1}& -2(2n-2)J_{(2n-2)\times n-1}\\ -(2n-2)J_{1\times (2n-2)}& \zeta -(2n-2)(4n-4)& -2(4n-6)J_{1\times n-1}\\ O_{n-1\times (2n-2)}& O_{n-1\times 1}& (\zeta +4n-8)I_{n-1}\end{array}\right|.$$
  Therefore, by Proposition 4,

  $$\left|W\right|=\left|\begin{array}{cc}D& E\\ F& H\end{array}\right|=\left|D\right|\left|H\right|,$$

  where $\left|H\right|=\left|\begin{array}{c}(\zeta +4n-8)I_{n-1}\end{array}\right|={\left(\zeta +4(n-2)\right)}^{n-1}$ and

  $$\begin{array}{cc}\hfill \left|D\right|=& \left|\begin{array}{cc}(\zeta +2n)I_{2n-2}-2n{J}_{2n-2}& -2n(2n-2)J_{(2n-2)\times 1}\\ -(2n-2)J_{1\times (2n-2)}& \zeta -8{(n-1)}^2\end{array}\right|\hfill \\ \hfill =& \left|\begin{array}{ccc}(\zeta +2n)I_{2n-3}-2n{J}_{2n-3}& -2n{J}_{(2n-3)\times 1}& -2n(2n-2)J_{(2n-3)\times 1}\\ -2n{J}_{1\times (2n-3)}& \zeta & -2n(2n-2)\\ -(2n-2)J_{1\times (2n-3)}& -(2n-2)& \zeta -8{(n-1)}^2\end{array}\right|.\hfill \end{array}$$

Finally, $\left|D\right|$ is calculated by placing the following operations:

• Replace $C_i^{\prime }=C_i-C_{2n-2}$ for all $1\le i\le 2n-3$; then,

  $$\left|D\right|=\left|\begin{array}{ccc}(\zeta +2n)I_{2n-3}& -2n{J}_{(2n-3)\times 1}& -2n(2n-2)J_{(2n-3)\times 1}\\ -(\zeta +2n)J_{1\times (2n-3)}& \zeta & -2n(2n-2)\\ O_{1\times (2n-3)}& -(2n-2)& \zeta -8{(n-1)}^2\end{array}\right|.$$
• Replace $R_{2n-2}^{\prime }=R_{2n-2}+R_1+R_2+\cdots +R_{2n-3}$, then

  $$\begin{array}{cc}\hfill \left|D\right|=& \left|\begin{array}{ccc}(\zeta +2n)I_{2n-3}& -2n{J}_{(2n-3)\times 1}& -4n(n-1)J_{(2n-3)\times 1}\\ O_{1\times (2n-3)}& \zeta -2n(2n-3)& -8n{(n-1)}^2\\ O_{1\times (2n-3)}& -2(n-1)& \zeta -8{(n-1)}^2\end{array}\right|\hfill \\ \hfill =& |(\zeta +2n)I_{2n-3}|(\left(\zeta -2n(2n-3)\right)\left(\zeta -8{(n-1)}^2\right)-16n{(n-1)}^3)\hfill \\ \hfill =& {(\zeta +2n)}^{2n-3}\left({\zeta }^2-2(2n-1)(3n-4)\zeta +16n{(n-1)}^2(n-2)\right)\hfill \end{array}$$

Hence, Equation (3) is obtained as

$$\begin{array}{cc}\hfill \varphi ({\mathsf{\Gamma }}_{Q_{4n}}^{ncm};\zeta )=& \left|W\right|\left|Z\right|=\left|D\right|\left|H\right|\left|Z\right|\hfill \\ \hfill =& {\left(\zeta +2n\right)}^{2n-3}{\left(\zeta +4(n-2)\right)}^{n-1}{\left(\zeta +4(n-1)\right)}^n({\zeta }^2-2(2n-1)(3n-4)\zeta \hfill \\ & +16n{(n-1)}^2(n-2)),\hfill \end{array}$$

and hence, the CN eigenvalues of ${\mathsf{\Gamma }}_{Q_{4n}}^{ncm}$ are ${\zeta }_1=-2n$ with multiplicity $(2n-3)$, ${\zeta }_2=-4(n-2)$ with multiplicity $(n-1)$, ${\zeta }_3=-4(n-1)$ with multiplicity $\left(n\right)$, and

$$\begin{array}{cc}\hfill {\zeta }_{4,5}& ={\displaystyle \frac{2(2n-1)(3n-4)\pm \sqrt{4{(2n-1)}^2{(3n-4)}^2-64n{(n-1)}^2(n-2)}}{2}}\hfill \\ & =(2n-1)(3n-4)\pm \sqrt{{(2n-1)}^2{(3n-4)}^2-16n{(n-1)}^2(n-2)}\hfill \\ & =(2n-1)(3n-4)\pm \sqrt{20n^4-68n^3+89n^2-56n+16}.\hfill \end{array}$$

Hence, by Definition 2, the CN energy of ${\mathsf{\Gamma }}_{Q_{4n}}^{ncm}$ is given by

$$\begin{array}{cc}\hfill E_{CN}\left({\mathsf{\Gamma }}_{Q_{4n}}^{ncm}\right)=& (2n-3)|-2n|+(n-1)|-4(n-2\left)\right|+n|-4(n-1\left)\right|\hfill \\ & +|(2n-1)(3n-4)\pm \sqrt{20n^4-68n^3+89n^2-56n+16}|\hfill \\ \hfill =& 2n(2n-3)+4(n-1)(n-2)+4n(n-1)+2(2n-1)(3n-4)\hfill \\ \hfill =& 4(2n-1)(3n-4)\hfill \end{array}$$

□

5. Conclusions

Motivated by the interplay between algebraic graph theory and spectral analysis, particularly in applications to mathematical chemistry and symmetric network design, this paper systematically investigates the CN spectral properties of non-commuting (NCM) and commuting (CM) graphs derived from the dihedral group $D_{2n}$ and the generalized quaternion group $Q_{4n}$. These groups, renowned for their rich symmetries, provide a natural framework for studying graph invariants, yet their CN energy and spectral structures remain undercharacterized in the literature.

We first construct the CN matrix for NCM- and CM- graphs of $D_{2n}$ and $Q_{4n}$, explicitly defining their entries as functions of the parameter n. From this foundation, we derive closed form expressions for the CN characteristic polynomial and rigorously compute the CN eigenvalues, revealing spectral patterns intrinsic to the groups’ algebraic structure. Subsequently, we establish general formulas for the CN energy of these graphs in terms of n, unifying their energetic behavior.

The theoretical results are validated through illustrative examples, confirming the consistency of the derived formulas with direct computational methods. This work not only advances the spectral theory of group based graphs but also provides tools for quantifying energetic properties in chemical and physical networks modeled by such structures.

This study opens several directions for further research:

• Extending the methodology to other non-abelian groups, such as symmetric groups $S_n$ or polyhedral groups, to identify universal spectral invariants.
• Implementing the closed form CN energy formulas in computational frameworks for large-scale network analysis or quantum chemical simulations.
• Investigating the relationship between the CN energy of graphs associated with groups and the inherent properties of those groups.
• Investigating links between CN energy and physical properties, such as molecular stability in chemical graph models or robustness in engineering networks.
• Comparative studies of CN energy with other graph energies (e.g., adjacency, Laplacian) to uncover deeper connections in spectral graph theory.

These efforts would further bridge algebraic structures, spectral analysis, and interdisciplinary applications, enriching both theoretical and applied graph theory.