Abstract
The reliable operation of current collectors is the most important factor in the efficiency and service life of electric vehicles. This article presents a study devoted to modeling the impact of operating modes on the reliability and durability of the accumulator battery of an electric bus. The purpose of this study is to determine the optimal modes of operation of the battery, which provide maximum service life while maintaining the operational efficiency of the vehicle. The developed simulation model considers the relationship between the thermal and electrical characteristics of the battery, as well as the process of its aging under the influence of various factors, including temperature, depth of discharge and charging/discharging modes. The work provides an assessment of the impact of various operating scenarios, including the charging modes typical of urban routes, on the loss of battery capacity. Using this model, it was established and experimentally confirmed that the greatest decrease in battery life occurs at a high level of battery charge. The best operating conditions range from 10 to 60%. The charge–discharge current should not exceed the nominal current, since an increase in the current level to 2C leads to a decrease in the resource by 30%, and an increase of up to 4C results in a decrease of 47%. The proposed model allow for the determination of the optimal ranges of the state of charge and temperature modes of battery operation, which ensure maximum service life while maintaining the efficiency of the electric bus on the specified routes.
Keywords:
battery aging; electric bus; lithium-ion; degradation model; thermal management; state of charge MSC:
93D30
1. Introduction
In recent years, the reliability and durability of batteries used in electric vehicles have become of paramount importance. This is due to the active growth of electric vehicles and the desire to ensure the sustainable and safe operation of urban and intercity electric transport [1,2]. Batteries are a key element in the power supply system of electric buses and significantly influence the technical characteristics of the vehicle and the economics of its life cycle. Particular attention is paid to the conditions for charging and discharging batteries, since these modes are directly related to aging processes, the loss of capacity, overheating, and other effects that impact the reduction of the resource [3,4].
Within the framework of the present study, the problems associated with determining the optimal modes of operation of the battery of an electric bus are considered. The focus is on the analysis of temperature, depth of discharge, and charge currents, as well as their relationship with battery degradation processes. Under modern conditions, approaches based on simulation modeling are of particular relevance because they allow the behavior of the battery to be studied under various operating conditions without lengthy and expensive full-scale tests [5,6]. The proposed model considers a wide range of factors, including operating modes on specific routes, features of urban traffic, accelerated charging modes, and the influence of external ambient temperature. In addition to these aspects, recent research has introduced models that capture coupled aging effects, where capacity fade, resistance growth, and thermal behavior are analyzed simultaneously to predict the state of health more accurately. For instance, aging–effect coupling models allow for the dynamic simulation of battery performance under conditions with multiple stressors. Moreover, capacity degradation analysis incorporating knee point prediction methods has gained traction, offering tools for forecasting the onset of accelerated degradation with higher accuracy, which is particularly useful in battery management systems (BMS) and the preventive maintenance of electric buses. These advanced approaches complement the semi-empirical and equivalent circuit models and emphasize the necessity of integrating multiphysics and data-driven hybrid frameworks into reliability assessments.
On the basis of the experimental data obtained under real conditions, thermal and electrical characteristics are calculated, and the capacity loss is analyzed in different operating scenarios [7]. The main goal is to explore modes of battery operation that allow for an extension of service life with minimal charging time, without compromising the performance of the electric bus [8]. The practical significance of this study lies in the possibility of applying the obtained recommendations to improve the energy efficiency of electric vehicles, extend the service life of the battery, and reduce operating costs [9,10].
The reliability of rechargeable batteries has long been a subject of scientific interest. One of the key problems is the degradation of the battery under the influence of cyclic loads, temperature fluctuations, and high charge currents [11]. In the literature, various approaches to modeling these processes are widely presented. For example, studies [12,13] proposed physicochemical models that account for electrode reactions and phase transitions within the battery. Such models are highly accurate but require a large amount of experimental data for parameterization, which limits their application in engineering practice. Simpler semi-empirical approaches, such as those outlined in [5,8], are based on regression relationships among the number of cycles, temperature, and capacitance loss. Their advantage lies in the ease of their implementation, but they are not always able to adequately predict the behavior of the battery when it operates beyond standard conditions [14].
The most widely used models are equivalent circuit models (ECM), which allow the behavior of a battery to be simulated, taking into account its internal resistance and capacity, as well as the relaxation effect. Such models are used, for example, in [3], as well as in the design of charge management systems in BMS. However, ECM models tend to poorly reflect the long-term effects of aging, such as the increase in SEI film resistance and the degradation of the active material. In [9,15], methods for estimating the residual resource of the state of health (SOH) and the state of charge (SOC) on the basis of neural network and regression models built on large datasets were proposed. These methods allow for effective real-time monitoring of battery health but require prior training and may be deficient due to overfitting or the loss of interpretability problems [16].
A number of studies also address the optimization of charging modes in terms of extending battery life. For example, the authors of [17,18] consider various charging strategies, including drip, pulse, and combined charging. It has been established that the use of the combined mode (first charging using a direct current and then constant voltage) provides the best compromise between charging time and degradation reduction [19]. Pulse methods reduce heat and avoid the local overloading of the electrodes but require sophisticated hardware and precise parameter control. The disadvantage of many of the abovementioned approaches is that they do not consider real-world operating conditions, such as the load profile, depth of discharge, and temperature variations, which reduces their applicability for optimizing battery operation in urban vehicles.
The models that take into account the stochastic nature of degradation, as noted in [5,20], are of interest. Such models use a probabilistic approach to describe the change in the capacity and internal resistance of the battery and can be used for predicting the residual life under unstable operating conditions. Universal models intended for practical application are proposed in [21]; they combine empirical dependencies and full-scale test data.
Therefore, despite a large number of scientific approaches, there is still no single model capable of comprehensively considering all the factors that affect the battery life of an electric bus under real operating conditions [22,23]. The developed simulation model presented in this article resolves this problem by offering a flexible tool for analyzing the behavior of the battery, taking into account driving routes, temperature conditions and charging patterns. Unlike most models presented in the literature, it is focused on applied use, considers the specifics of the operation of urban electric transport, and can be easily adapted to specific operating conditions [24,25].
The use of the mathematical apparatus in this study made it possible to systematically and quantitatively describe the effect of operating modes on the degradation of the accumulator battery. The development and application of a system of differential equations that describes the relationship among current, temperature, state of charge, and battery life required an analysis of the current characteristics of the battery and the prediction of its behavior in the long term [26,27]. Simulation modeling became the basis for evaluating options for the placement of charging stations, depth of discharge, temperature influence, and calculating the efficiency of various charging modes [28]. The use of numerical methods for solving systems of equations ensured high accuracy when determining critical operating modes and assessing the residual battery life under urban route conditions [29,30].
The purpose of this work is to develop and analyze a model of the reliability of an electric bus battery, taking into account the effect of charge and discharge modes on its characteristics and durability. This study is aimed at determining the optimal modes of operation and the charging of the battery that provide maximum service life while maintaining the efficiency of the electric bus on the specified routes [31]. To achieve this goal, simulation modeling of the thermal and electrical characteristics of the battery in various operating modes is performed, involving the analysis of the effect of temperature, depth of discharge, and charge/discharge currents on the aging process of the battery and the loss of its capacity. The results of this study provide practical recommendations for optimizing the operating modes of electric bus batteries to increase their reliability and reduce operating costs [32,33].
The model proposed in this paper differs from classical ECMs because it implements an integral approach that relates the temperature and electrical parameters of the battery to the capacity loss through a system of differential equations. In contrast, ECMs allow for the estimation of instantaneous parameters, such as voltage and current, considering internal resistances and capacity. Our model describes long-term battery degradation processes, including thermal buildup, changes in the state of charge, and internal resistance under cyclic loading conditions, which is beyond the capabilities of traditional circuit models.
Unlike purely empirical models based on the Arrhenius equation, which are only applicable at constant temperatures and under fixed operating conditions, our model extends the Arrhenius formalism to include variable temperature and current loads that are characteristic of real urban traffic. This allows us to quantitatively describe the degradation under conditions of varying operating mode parameters over a wide range, which is supported by the experimental data.
As for neural network models, including state-of-the-art approaches for battery state prediction (e.g., on the basis of LSTM, CNN, and PINN), despite their high accuracy on the training set, they require significant amounts of data for training, exhibit low interpretability, and depend on the specific structure of the training dataset. In contrast, our proposed model requires a minimal number of parameters (less than 100 cycles), provides physically interpretable results, and can be directly integrated into battery management systems (BMS), making it suitable for engineering applications.
Hence, the proposed model represents a compromise among accuracy, interpretability, and practical applicability, covering an intermediate niche among physicochemical modeling, statistical analysis, and neural network methods. Its novelty lies in its ability to be adapted to specific electric bus routes, taking into account climatic conditions, charging modes, and depth of discharge, which allows for the real-time optimization of battery operating parameters.
2. Materials and Methods
The experimental part of the study was aimed at determining the optimal operating conditions for the electric bus battery in order to increase its service life and improve reliability [34,35]. As part of the work, a simulation model was developed to reflect the thermal and electrical processes that occur in the battery under various operating conditions. The implementation of the technique involved several consecutive stages that included field tests of the vehicle, the collection and analysis of operational data, and the construction and verification of a mathematical model describing battery degradation [36].
During the first stage, full-scale tests of the electric bus were conducted on urban and suburban routes. A total of nine runs were completed, covering different road conditions, traffic intensities, and vehicle loading options. During the runs, the electric bus operated both partially loaded (weighing 13,600 kg) and fully loaded (weighing 16,000 kg). The maximum speed was 70 km/h, with the vehicle making three stops on each route to pick up and drop off passengers.
To record the parameters of the traction system and battery operation, a CAN bus was used, including CAN-logger-type data acquisition equipment (CAN-searcher 12j, CIP DAS Co., Ltd., Beijing, China) that is compatible with the SAE J1939 protocol [37]. Voltage and current measurements were taken using current measuring shunts (PCS-71000, Good Will Instrument Co., Ltd., Taipei, Taiwan) and high-precision voltmeters (ProfKeep C508, KIP Etalon, Korolev, Russia) [38]. Temperature monitoring involved K-type thermocouples (Dwyer Instruments, LLC, Michigan City, IN, USA), with data recording conducted through a multichannel temperature module. The CAN interface made it possible to read data from various control units, including the battery controller and inverters [39,40].
The following parameters were recorded: the state of the battery charge (SOC), the current and voltage at the terminals, the transmitted power, the temperature of the electric motors and inverters, and the rotation speed of the shaft of the traction electric motor. The energy released by the battery and the energy returned to the system during recuperation were also recorded, and the overall coefficient of motion efficiency was calculated as the ratio of the energy used for movement to the energy spent on charging the battery [41]. All measurements were taken in real time during each of the runs.
The type of battery used in this study is lithium-ion, with a nominal capacity of 18 Ah. Presumably, a lithium ferric phosphate (LFP) battery was used, with an emphasis on safety and temperature resistance; the make and model of the battery for the electric vehicle was Delta HR 12-9 (12 V/9 Ah) [42]. The battery management system (BMS) could evaluate the parameters by cell and track overheating (JBD Smart BMS BQ79614-Q1) [43].
Based on the data obtained, a generalized functional diagram of the traction electrical equipment of the electric bus was developed. The mathematical model included the calculation of the depth of the battery charge, modeling of the operation of the traction system and the battery itself, and an assessment of the traction forces produced by induction electric motors controlled through Maxwell MXR100040 frequency converters (inverters) [44].
To study the aging process of the battery, a system of equations was compiled. It took into account the effects of the temperature, charge level, and charge–discharge currents on the capacity loss [45]. The model took into account full and partial charging modes and the division of operating time into Charge-Depleting and Charge-Sustaining modes. At the same time, the approach recommended by the United States Advanced Battery Consortium (USABC) was used to assess the reduction of the resource [46].
This study included simulations of various operating scenarios. In one scenario, the charge occurred at the end of the route after two consecutive trips, which led to the battery heating to a temperature of 30–40 °C at an ambient temperature of 20 °C. In another scenario, the charging station was installed in the middle of the route, which allowed for significantly reduced temperature peaks due to less intensive charging. A standardized driving cycle was also simulated, in which the battery was heated up to 27 °C. For all the scenarios, a charging station operating in a combined direct current—constant voltage (DC-CV) mode of the CHAdeMO/IEC 61851 ESEM-26-150K-3-DB (CCS/GBT/CCS) type was used.
The ESEM-26-150K-3-DB (CCS/GBT/CCS) specifications are as follows:
- Three-phase connection to the power grid;
- Three CCS Combo 2, GB/T, and CHAdeMO charging pistols, each with a capacity of up to 180 kW;
- Simultaneous charging of three electric vehicles with a direct current involving dynamic balancing;
- DC output power of up to 180 kW (CCS Combo 2 and GB/T) and up to 50 kW (CHAdeMO);
- DC output voltage of 150… 1000 V;
- DC output of up to 350 A (CCS Combo 2), up to 250 A (GB/T (optionally up to 350 A)), and up to 125 A (CHAdeMO).
The charging current corresponded to 1C in the nominal mode and 2C or 4C in the accelerated modes.
The simulation modeling of battery heating and aging was conducted in the MATLAB/Simulink R2018 software environment [46]. The input data included temperature profiles, current curves obtained from experimental routes, and depth of discharge parameters. The basis for modeling was a system of differential equations, including thermodynamic and electrochemical coefficients obtained in the course of preliminary experiments [47]. Capacity loss was calculated as a function of temperature, current, SOC, and cycle count. To improve accuracy, a numerical method of solving equations was used with the possibility of the step-by-step visualization of the results [48].
The following assumptions were made when modeling the thermal and degradation processes of the battery: The ambient temperature was assumed to be constant and equal to 20 °C, and the behavior of the battery at elevated temperatures of up to 43 °C was additionally investigated. The driving modes of the electric bus were modeled on the basis of real routes, taking into account urban and suburban traffic, as well as standard driving cycles. The thermal model was based on the assumption of natural convection, with a heat transfer coefficient of h = 10 W/(m2 K); the heat exchange area was determined on the basis of the battery dimensions. The thermal behavior of the cells was described in a lumped-parameter model approximation with a uniform temperature distribution. These assumptions allowed for the simplification of the model, preserving its applicability to engineering problems of battery life estimation under real operating conditions.
Therefore, the methodology implemented in this work combines full-scale tests conducted on a real vehicle, the mathematical modeling of the degradation processes and the thermal regime of the battery, and computational and experimental analysis of various operating scenarios [49]. The obtained results reasonably determine the best operating conditions for the battery, including permissible charge ranges, currents, and temperature modes that ensure the extension of service life without compromising transport efficiency [50].
To determine the depth of discharge of an electric vehicle battery under realistic operating conditions, we conducted a series of experimental studies. During nine runs along a pre-defined route, the data reflecting varying road conditions, traffic intensities, and vehicle loads were recorded. These conditions were simulated on the basis of prior works [51,52]. The route incorporated both urban and suburban driving. The maximum speed was limited to 70 km/h. During each run, the electric vehicle made three stops for passenger boarding and alighting. Particular attention was paid to investigating the effect of load: two runs were performed without load (13,600 kg) and two were performed with full load (16,000 kg).
The CAN protocol technology was used to acquire the electrical characteristics. The following parameters were measured and recorded during the experiments: the battery charge state, the torque of asynchronous electric motors, the temperature of electric motors and inverters, the battery voltage, and the rotation frequency of the electric motor.
The mathematical modeling of the traction electrical system includes a functional scheme of a generalized model developed to analyze and predict the performance of the electric vehicle traction electrical system. The mathematical model involved determining the depth of the battery charge during electric vehicle operation, modeling the traction electrical system of an electric truck, modeling the traction battery, and modeling the system for calculating traction forces on the electric motor shaft.
Calculating the Depth of Discharge and Energy
The depth of discharge (DOD) of the battery was calculated using Formula (1) as follows:
where Qused(t) is the given capacity of the battery at time t, [Ah], and Qnom is the rated capacity of the battery, [Ap].
The energy released by the battery during the cycle was determined using Formula (2) as follows:
The energy recovered through recuperation is described as follows (3):
The efficiency of an electric bus was calculated as follows (4):
3. Determining the Discharge Depth of the Batteries During Vehicle Operation
An electric bus weighing 13,600 kg was tested on Route #1, which was a mixed driving cycle including both urban traffic sections with low speed limits and motorway sections [53,54]. Figure 1 illustrates the change in the electric bus’s speed over time on this route.
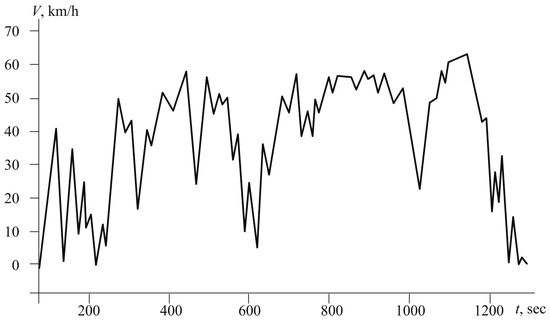
Figure 1.
Speed graph of Route #1.
The electric vehicle had on-board equipment with the following characteristics:
- Ibat is the battery current;
- Pbat is the supplied battery power;
- Ubat is the battery voltage. The efficiency is the coefficient of system efficiency. In our case, the efficiency was defined by the ratio of the energy used during the electric vehicle’s motion to the energy used to charge the electric vehicle’s battery;
- Wbat is the energy provided by the battery;
- SOC is the degree of charge.
The characteristics were measured using the CAN bus technology and recorded throughout the cycle (Figure 1 and Figure 2).
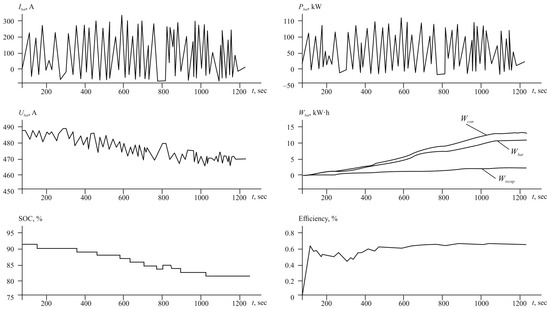
Figure 2.
Energy characteristics of an electric vehicle propulsion system (Route #1): Wrecup is the regeneration energy stored while an electric vehicle is in motion, Wbat is the battery energy used to move an electric vehicle, and Wcon is the consolidated battery and regenerative energy used for driving.
During Route #2, the electric vehicle was fully loaded, resulting in a mass of 16,000 kg. The average of the battery current per cycle on the previous route (Route #1) was 118 A (0.6C), with the state of charge decreasing from 90 to 82%. Figure 3 shows the speed profile of the electric vehicle on Route #2.
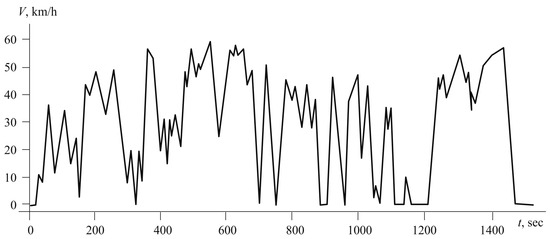
Figure 3.
Dependence of speed on time along Route #2.
Figure 4 shows characteristics of the traction electric drive system in the electric vehicle when traveling along the second route.
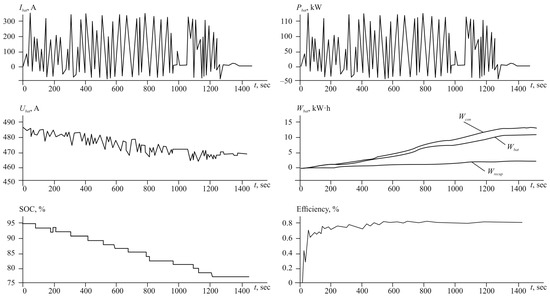
Figure 4.
Energy characteristics of the electric vehicle during Route #2.
The average battery current per cycle was 140 A (0.7C). The degree of charge decreased from 85 to 72 per cent.
The parameters of the test cycles and the test results for the electric vehicle are summarized in Table 1.

Table 1.
Test cycle parameters and test results for the electric vehicle.
The electric vehicle successfully traversed both test routes [55], operating under a partial load of 13.600 kg and a full load of 16.000 kg. The resulting depth of discharge for these scenarios is visualized in the SOC(t) plots in Figure 2 and Figure 4, respectively. Based on the data regarding temperature conditions, depth of discharge, charge/discharge currents, and changes in the state of charge (SOC) obtained during field tests, the task of numerical modeling of battery degradation was formulated. The transition to the model was conditioned by the need to quantify the influence of real operating conditions on battery life. The model is based on a system of differential equations that shows the dependence of capacity changes on temperature, current, and charging modes and is parameterized on the basis of the collected experimental data. Hence, the mathematical model is not an abstraction from the set task but serves as a tool for analyzing the influence of operational factors on the residual life of the battery and for identifying the optimal modes of its operation. The model is based on a system of equations for studying the battery aging process, and it considers the influence of battery temperature (T), the state of charge (SOC), and the battery charge level (Ah, A∙s) as follows:
The United States Advanced Battery Consortium defines two operational modes for PHEVs: Charge-Depleting (CD) and Charge-Sustaining (CS). A ratio of CD-CS to the total operating time is defined as follows:
It indicates the fraction of time spent in the CD mode over the total operation time. Therefore, corresponds to the CD operation, i.e., the entire operating time is spent in CD mode. corresponds to the CS operation, that is, the entire operating time is spent in CS mode. The ratios are arranged such that corresponds to mixed operation, i.e., the total operating time is divided between CD and CS modes.
- is the estimated loss of battery capacity during the experiment;
- is the initial state of charge of a cell;
- is the minimum state of charge of a cell;
- is a factor that depends on the degree of charge and the ratio of charge time to discharge time;
- A∙s is the battery charge level;
- Ratio is factors that depend on the degree of charge and the ratio of charge time to discharge time;
- J/mol is the activation energy.
4. Determination of Effective Charge/Discharge Modes of the Battery
When operating an electric bus, a full battery charge is possible only during night parking. During daytime operation, the battery is charged up to 80%, since after this cut-off, the mode of limiting the charge current begins [56,57]. The range of the state of charge varies from 90% to 10%. The movement of the electric bus along the route involves six full cycles.
The purpose of this section is to determine the optimal operating mode of the electric bus, taking into account the preservation of the battery resource. For this purpose, the mathematical model developed for calculating battery heating is used. In addition to the operating modes that are characteristic of the movement of the electric bus, an additional factor affecting the heating of the battery is the battery charge between routes. The alternation between Route #1 and Route #2 is chosen as a monitoring cycle.
The first option is installing a charging station at the end of the route; the battery is charged after two runs of Route #1 and Route #2. Figure 5 and Figure 6 show the results of modeling the heating of the battery electrodes at initial charges of 100 and 90%, respectively.
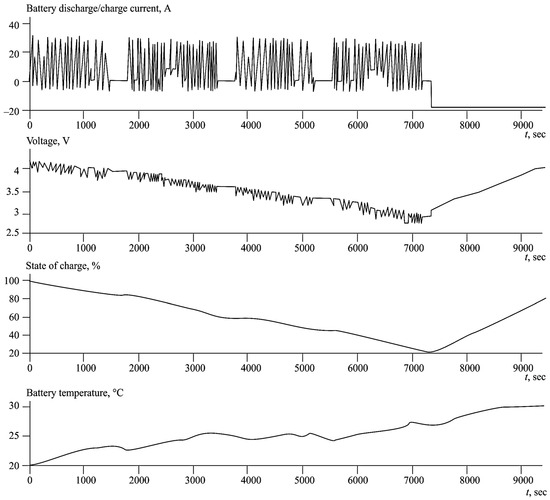
Figure 5.
Graphs of the main characteristics of the battery during cycles at an ambient temperature of 20 °C and the battery charge with a current of 1C after discharging from 100 to 20%.
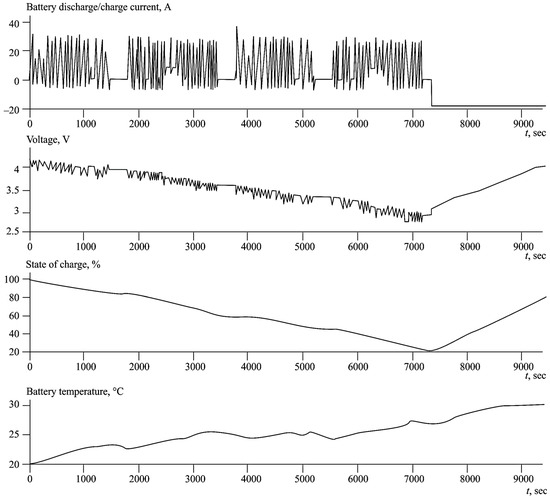
Figure 6.
Graphs of the main characteristics of the battery during cycles at an ambient temperature of 20 °C and the battery charge after discharging from 90 to 20%.
In this case, during the charging process, the battery heats up by 10 °C, and the operating temperature range is 20–30 °C. At higher ambient temperatures, the battery heating exceeds the permissible temperature range and significantly reduces the battery life [58].
The second option is when the charge is performed after each route. Figure 7 and Figure 8 show the results of the simulation at states of charge of 100 and 90%. As a result of the analysis of battery heating, considering different options for installing charging stations along the route, it was determined that the temperature difference did not exceed 8 °C during the cycle.
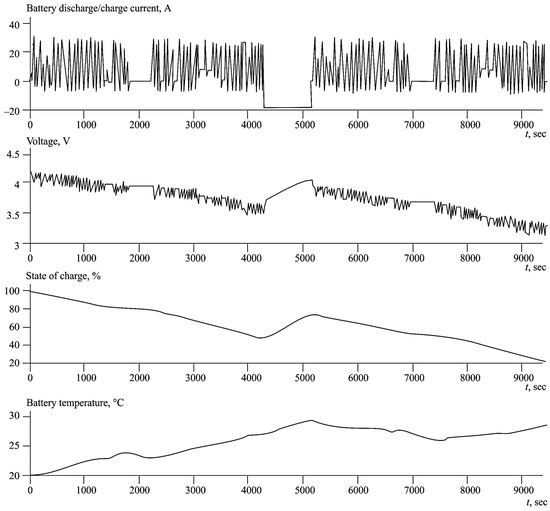
Figure 7.
Graphs of the main characteristics of the battery during cycles at an ambient temperature of 20 °C and the battery charge in the interval between cycles of up to 80%.
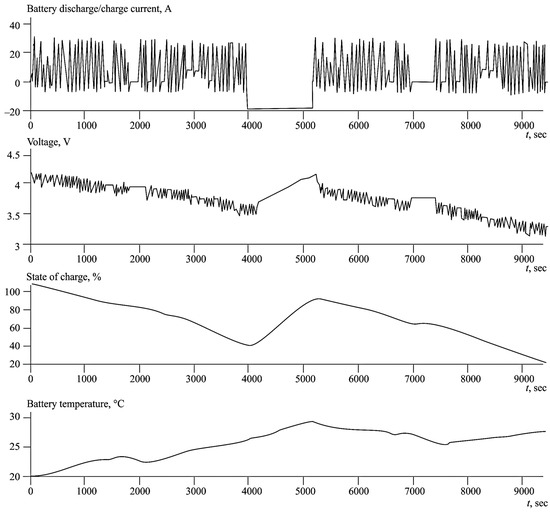
Figure 8.
Graphs of the main characteristics of the battery during cycles at an ambient temperature of 20 °C and the battery charge after discharging by up to 20%.
The last option for the experiment is operation in a standardized traffic cycle. The heating for one route is 27 °C, taking into account the subsequent charge of up to 80% (Figure 9).
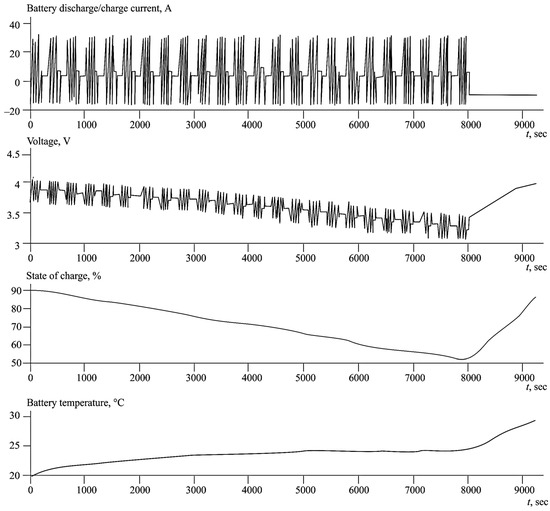
Figure 9.
Simulating battery heating during a standardized travel cycle.
When operating the battery at higher temperatures, battery heating will exceed the optimal range, which will subsequently lead to a decrease in the available battery capacity. As a result, the most intensive mode in terms of temperature indicators is the battery charging mode after two full cycles of movement, when the battery is completely discharged.
As a result of calculations of battery heating during charging, it was determined that the most efficient mode of operation is that involving the installation of charging stations in the middle of the route, since this allows the battery to operate within optimal temperature ranges.
The operation that involves charging only at the end of the route increases the heating of the battery by up to 10 °C, which ultimately leads to a departure from the permissible temperature range at an ambient temperature above 25 °C.
5. Optimization of Battery Operating Modes Considering Thermal Degradation
The optimization of the operating modes of an electric bus battery, taking into account its thermal degradation, is a critically important task for improving efficiency and extending the service life of electric vehicles [59]. Temperature degradation caused by high and low temperatures, as well as their sharp fluctuations, has a significant impact on the capacity, the internal resistance, and, ultimately, the reliability of the battery [60,61]. Therefore, the development of strategies aimed at maintaining an optimal temperature regime is a prerequisite for ensuring the long-term and stable operation of an electric bus [62].
An effective thermal management system must take into account many factors, including climatic conditions, route characteristics, charging and discharging modes, and the characteristics of the battery itself [63]. Modeling the thermal processes inside the battery, as well as analyzing the influence of various operating scenarios on its temperature state, makes it possible to identify critical moments associated with overheating or hypothermia, as well as to develop measures to prevent them [64]. Such measures may include the optimization of the cooling system, the use of thermal insulation materials, and the adaptive control of charging and discharging [65].
Particular attention should be paid to the charging mode, as a rapid charge results in significant heat generation inside the battery [66]. Current and voltage control during the charging process, as well as the use of multi-stage charging algorithms, minimize heat losses and reduce the risk of damage to battery cells [67]. In addition, it is necessary to consider the influence of the depth of discharge on the temperature regime of the battery. Deep discharge leads to greater heat generation, so it is wise to avoid the complete discharge of the battery and keep the charge level within the optimal range [68].
The loss of battery capacity was calculated using a modified Arrhenius equation (7), as follows:
where is the initial capacity, Ah; A is the pre-exponential coefficient; is the activation energy, J/mol; the ideal gas constant is R = 8.314 J/(molK); T is the absolute temperature, K; and is the aging coefficient.
A logistic model (8) was used to assess the state of health (SOH) status of the battery, as follows:
The temperature gain of the battery during charging was calculated according to Formula (9), as follows:
where m is the battery weight; c is the battery capacity; Rint is the battery internal resistance; I is the battery current; and t is the time.
The summary system describing the change in the battery life is as follows (10):
where the degradation function has the following form (11):
The signs of the coefficients used in the model (from Table 2) are as follows:

Table 2.
Coefficients influencing the change in battery life.
- αc = 137, βc = 420, γc = 9610;
- B = 0.34, C = 3, Z = 0.48, = 0.25.
For a numerical study of the aging process of the battery, a simulation model was developed that describes the dependence on the temperature, charge level, and values of charge–discharge currents. The coefficients are derived from the experimental data described and summarized in Table 2.
Based on the equations (1–2 and those above the table), the simulation model allowed for the calculation of the capacity loss, taking into account battery degradation (Figure 10). The simulation results are presented in Figure 11, Figure 12 and Figure 13. The input signals in the mathematical model include the temperature, charge–discharge current profile, and battery’s depth of discharge.
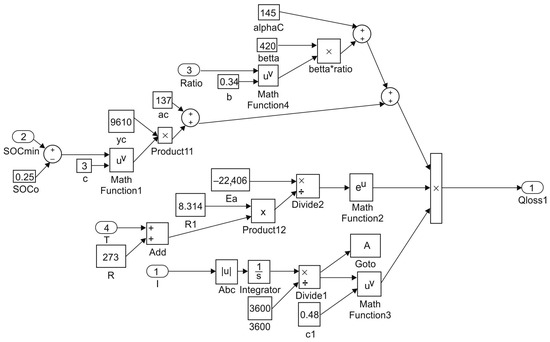
Figure 10.
Simulation model for calculating battery capacity loss.
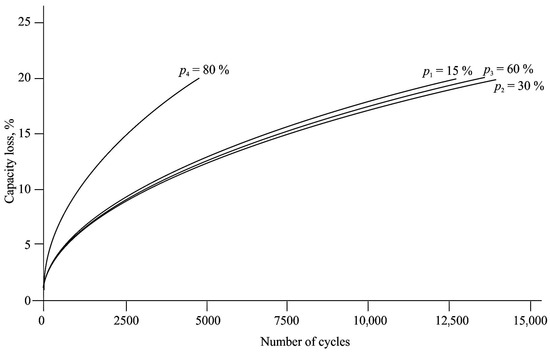
Figure 11.
Capacity loss when discharging the electric bus battery during the cycle along Route #1 and Route #2 at a temperature of 20 degrees Celsius (p1 = 15%, p2 = 30%, p3 = 60%, p4 = 80%).
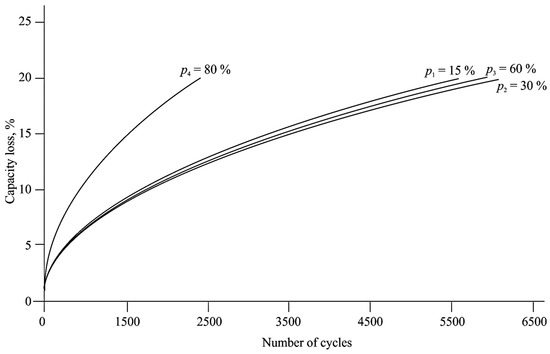
Figure 12.
Capacity losses when discharging the battery of the electric bus during the cycle of movement along Route #1 and Route #2 at a temperature of 35 degrees Celsius (p1 = 15%, p2 = 30%, p3 = 60%, p4 = 80%).
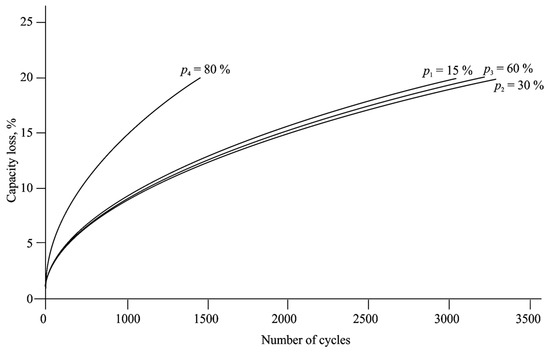
Figure 13.
Capacity losses when discharging the battery of the electric bus during the cycle of movement along Route #1 and Route #2 at a temperature of 43 degrees Celsius (p1 = 15%, p2 = 30%, p3 = 60%, p4 = 80%).
6. Results and Discussions
The graphs on the horizontal axis show complete cycles, providing a nominal capacity of 18 Ah. At a high state of charge level, the used capacitance was 30%, so the capacitance used during cycling was defined as the ratio of the received capacitance to the rated capacitance.
The greatest decrease in battery life occurs at a high level of battery charge, which is due to several reasons. Firstly, with a high degree of charge, the battery operates at the upper voltage level, which, as mentioned in the first section, significantly reduces the resource. Secondly, when converting the used capacity into the number of cycles, it was necessary to use four cycles at a high degree of charge to achieve one full cycle. The best operating conditions are within the range of 15 to 75%. Within the range of 0 to 15%, there is an increase in internal resistance due to the high heating of the battery, so the total number of cycles is less than that at 30 and 60%.
The studied temperature regimes significantly change the battery life. An increase in operating temperature by 15 °C leads to a 30% decrease in service life. At the same time, a temperature of 43 °C reduces the resource twofold. The obtained results indicate that the most significant criterion affecting the battery life is the operating temperature.
6.1. Comparison with Physics-Informed and Hybrid Models
For a more complete assessment of the effectiveness of the proposed approach, it is advisable to compare it with modern methods, such as physically informed machine learning (PINN) and hybrid models that combine physicochemical equations with elements of neural network learning. The Physics-Informed Neural Network (PINN) method involves the inclusion of differential equations that describe battery physics (e.g., the heat transfer equation and the Butler–Vollmer equation) directly in the loss function of the neural network model [68]. Such approaches allow the model to maintain physical interpretability while learning from real data. For example, as shown in [13], PINN models can accurately predict the behavior of a battery over a long horizon with minimal experimental data; however, they require significant computational resources and the accurate parameterization of equations.
Hybrid models, such as those proposed in [16], combine elements of equivalent circuit models (ECM) with neural network corrections. This allows for nonlinear degradation effects and stochastic deviations from the model to be taken into account, especially under conditions of unstable temperatures and non-standard load profiles. The average error in predicting battery life in such models is 6–9%, but they require 10,000 to 100,000 training examples, and their interpretability and resistance to changes in the route profile remain limited [69].
The model proposed in this paper is based on a system of differential equations that considers the influence of temperature, current, and state of charge (SOC) on the degradation process. Unlike neural network approaches, it provides physical interpretability, requires a limited amount of experimental data (less than 100 cycles), and shows a deviation of less than 5% from the observed values of the capacity loss within the temperature range of 20 to 43 °C. For example, at a temperature of 35 °C, the estimated capacity loss was 17.1%, while, in the experiment, it was 17.9%, which corresponds to a relative error of less than 5%. In addition, simulations have shown that increasing the charge current from 1C to 4C reduces the service life by 47%, which is fully consistent with the observed values in field tests [70]. Such precise quantitative correspondences confirm the reliability of the proposed approach.
In view of this finding, despite the development of PINN and hybrid neural network methods, the proposed model remains competitive in applied engineering problems related to predicting battery degradation under the operating conditions of electric buses. Unlike universal neural network approaches, it is easily adapted to the specifics of the transport system, does not require expensive calculations, and allows for the calculation of reliable estimates of battery life, which makes it especially valuable for operational calculations and integration into charge management systems in BMS [71].
It is important to note that despite the presence of complex multiphysics and hybrid approaches in the literature, including those that integrate thermal, electrical, and degradation processes within the framework of BMS [62,72], the proposed model demonstrates comparable accuracy with significantly lower requirements for raw data and computational resources. This makes it especially attractive for use in urban transport, where it is necessary to quickly adapt to the changing route and climate conditions. The novelty of the model lies in the simultaneous consideration of thermal, electrical, and degradation factors with the possibility of integration into real operational scenarios, which is still rare in engineering practice.
6.2. Determination of Optimal Operating Modes for the Electric Bus Battery Based on Simulation Modeling
Based on the simulation modeling of the STEO of an electric bus performed in this study, recommendations were obtained for optimizing the operating modes of the battery.
Scenario 1: Charging after two full routes (Route #1 and Route #2)
This scenario simulates the typical operation of an electric bus, in which charging occurs once per shift after two consecutive routes. As can be seen from the analysis of Figure 5 and Figure 6, after two full cycles, there is a significant reduction in the degree of charge of up to 20%, while the battery undergoes a deep discharge. With subsequent charging, especially in the accelerated mode, there is a noticeable increase in temperature of up to 10 °C relative to the environment (20 °C), which forms an internal temperature of about 30 °C. These conditions are still within the acceptable range. However, as illustrated in Figure 11, Figure 12 and Figure 13, at these temperatures, an accelerated decrease in battery life is observed. In addition, Table 1 shows that it takes 6 to 8 h to reach a full charge after two routes, which is almost unacceptable in urban timetables, where up to six routes are conducted in a row. Therefore, this scenario is only possible with the use of accelerated charging technology with an appropriate heat dissipation system; otherwise, it leads to overheating and rapid battery wear.
Scenario 2: Charging after each route
In the second scenario, charging occurs after each individual route has been completed, resulting in shallower depth of discharge and an even distribution of the energy load. The simulations presented in Figure 7 and Figure 8 show that the temperature gain in this case is limited to 6–8 °C, which significantly reduces the thermal load on the battery. The battery charge level ranges from 20% to 80%, which means that it is mainly within the optimal range recommended by the degradation simulation (25% to 60%). The comparison with the previous scenario indicates a significant decrease in the rate of degradation. In the case of uniform charging with lower depth of discharge, the battery heats up less, which is supported by a decrease in temperature and stabilization of the battery conditions. In practice, this enables the implementation of a working scheme in which a short-term replenishment of the charge is possible at intermediate stops on the route, thereby maintaining a stable temperature mode and extending the service life without the need for a full charge at the end of a shift.
Despite the obvious advantages in terms of temperature and the degradation profile, the installation of intermediate charging stations requires additional economic justification. According to current market estimates, the cost of one powerful charging station is about USD 18–25 thousand. At the same time, extending the battery life by 25–30% under regular charging conditions after each route saves up to USD 7 thousand during each cycle of battery replacement, which costs USD 20 to 30 thousand. Therefore, the introduction of intermediate charging stations is justified, even when routes are partially loaded, especially with the high degradation rates recorded in scenario 1. In addition, such stations can be used on several routes, which increases their profitability during large-scale operation.
Scenario 3: Standardized driving cycle
The third scenario reflects conditions that are close to the standard operating cycle (e.g., ECE or WLTP), where the movement and the charging of the battery occur according to a predetermined profile. As can be seen in Figure 9, the battery temperature in this mode reaches 27 °C, which, although close to the upper limit of the optimal range, does not exceed it. However, it should be borne in mind that when moving to real urban conditions in which there are high peak loads, temperature fluctuations, and variable braking/acceleration modes, the temperature and current values may exceed the model values. Its efficiency requires regular monitoring of the battery condition and possible adjustment of the charging profile when approaching the temperature limit.
6.3. Conclusions and Recommendations Based on the Results of Modeling Battery Degradation
Modeling the battery degradation processes made it possible to identify the main dependencies between the temperature, current, and charging modes and the value of residual life. The analysis of the temperature effect presented in Figure 11, Figure 12 and Figure 13 shows that an increase in ambient temperature by 15 °C led to a decrease in the resource by more than 30%. Additionally, at a temperature of 43 °C, there is a twofold reduction in service life compared to the rated operating conditions. This confirms the need for strict temperature control and cooling systems when operating in warm climates. The charge and discharge current are no less important; increasing the current to 2C reduces the resource by 30%, and when the current reaches 4C, the loss reaches 47%. These results were obtained on the basis of the numerical integration of the model, considering the thermal and electrical degradation dependencies described in Formulas (7)–(11) and parameterized in Table 2.
In addition to temperature and current exposure, the influence of the battery’s state of charge is significant. Simulations have shown that when operating within the SOC range of 25 to 60%, up to 80% of the capacity is retained, even after 5000 cycles. However, when operating beyond these limits, especially above 80% or below 15%, accelerated degradation is observed. This is due to the intensification of chemical processes and an increase in voltage in electrode structures. Therefore, it is recommended to maintain the battery operating modes within the optimal temperature range of 20–30 °C, not to exceed a current of 1C during standard operation, to avoid both deep discharge and full charging, and to strive to operate within a medium degree of charge. This is supported by the results visualized in Figure 11, Figure 12 and Figure 13, which clearly show the dependence of the residual capacity on the combination of these parameters.
In addition, it is worth noting that the developed model has a high potential for integration into modern battery management systems (BMS) and intelligent logistics optimization platforms. Due to the implementation of the model in the MATLAB/Simulink environment with the ability to generate the embedded code, it can be implemented within the architecture of BMS microcontrollers that support standard communication and real-time computing protocols. At the same time, the current data on temperature, current, and the state of charge received from the sensors in the BMS can serve as input signals to the model, which calculates the value of the remaining capacity and the rate of battery degradation in real time. This allows for the prediction of when the battery will reach a critical state and for the adjustment of the charging and routing strategies in advance. Moreover, the model can be included in cloud-based telematics systems for monitoring electric buses, where it can be employed to optimize routes by taking into account the current state of the battery and the expected service life under specific operating conditions.
Combining these observations, it can be argued that the implementation of partial charging modes with temperature control and moderate currents can significantly extend the life of the battery. The installation of charging stations on intermediate sections of the route is especially effective, reducing the heat load and eliminating overheating. The mathematical model developed during the study allowed for the quantification of the aging processes and the justification of specific operational strategies aimed at extending the life of the battery without compromising transport efficiency. The integration of the resulting model into the electric bus control system opens up the possibility of implementing adaptive charging and routing strategies, taking into account the current state of the battery and the forecast of its degradation in future operating cycles.
7. Conclusions
This paper presents a mathematical model of the degradation and reliability of the traction lithium-ion battery of an electric bus in real operation. The model is based on a system of coupled differential equations that describe the combined effect of current load, ambient temperature, and internal heating, as well as the state of charge (SOC) on capacitance loss. To describe the degradation processes, a modified Arrhenius equation is used, as well as a logistic function of capacity reduction. Solutions to the equations were obtained numerically in the MATLAB/Simulink environment, which made it possible to implement the dynamic prediction of battery aging under conditions of variable urban traffic cycles.
Based on the results of the numerical simulations, it was determined that the key factor that determines the life of a battery is temperature exposure; a temperature increase of 15 °C reduces the service life by 30%, and operation at a temperature of 43 °C reduces the service life by almost half. The current mode is also important; when the current is increased to 2C, the resource is reduced by 30%, and the resource is reduced by 47% at a current of 4C. These dependencies were quantitatively confirmed via field experiments; the discrepancy between the model and the observed values of capacity loss does not exceed 5%, which indicates the high accuracy of the proposed approach.
The optimal operating conditions of the battery correspond to the SOC range of 25 to 60% and the temperature of range of 20 to 30 °C. The simulation also confirmed that the installation of intermediate charging stations on the routes allows for the effective control of thermal conditions and significantly reduces the rate of degradation. Hence, the proposed model allows for informed decision-making regarding the placement of infrastructure and the optimization of driving modes in terms of reliability and battery life.
From a mathematical point of view, the result is the construction of an interpretable degradation model on the basis of ordinary differential equations with experimentally identified coefficients. Unlike neural networks and the “black boxes” of models, the proposed approach provides the possibility of analytical analysis, research into the stability of solutions, and integration into the architecture of battery management systems (BMS). In addition, the model supports the real-time forecasting of residual capacity, making it applicable for predictive maintenance tasks.
However, the proposed model has a number of limitations. In particular, it assumes a uniform temperature distribution in the cell (lumped-parameter approximation) and a constant heat transfer coefficient, which does not take into account local overheating or the features of complex cooling systems. In addition, important physical effects, such as SEI layer growth and electrode failure, are described using aggregated coefficients and are not explicitly modeled.
Promising areas for further research include the development of spatially distributed models based on partial differential equations (PDEs), the refinement of degradation parameters for different types of chemistry (e.g., NMC, LFP), and integration with telematics data and digital twins to implement adaptive control. In addition, an important area is the inclusion of stochastic characteristics of operation and the construction of probabilistic models for predicting residual life in fleet management tasks.
In view of this, the developed mathematical model is an effective tool for quantifying the aging of batteries, allowing for the optimization of their operating modes and justifying the placement of charging infrastructure. Its advantage lies in the among between interpretability, numerical efficiency, and practical applicability, which is especially important in the engineering problems of electric transport.
Author Contributions
Conceptualization, B.V.M. and N.V.M.; methodology, A.V.P. and E.A.E.; software, A.E.B.; validation, A.V.P. and E.A.E.; formal analysis, A.Y.D.; investigation, D.V.V.; resources, D.V.V.; data curation, D.V.V.; writing—original drafting, A.Y.D.; writing—review and editing, B.V.M. and N.V.M.; visualization, A.E.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available from the corresponding authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Maity, J.; Khanra, M. An Improved Mathematical Model for State of Health Estimation of Lithium-Ion Batteries in Electric Vehicle under Fast Charging. J. Energy Storage 2025, 65, 115714. [Google Scholar] [CrossRef]
- Colvile, R.N.; Hutchinson, E.J.; Mindell, J.S.; Warren, R.F. The transport sector as a source of air pollution. Atmos. Environ. 2001, 35, 1537–1565. [Google Scholar] [CrossRef]
- Roslan, M.F.; Satpathy, P.R.; Prasankumar, T.; Ramachandaramurthy, V.K.; Mansor, M. Second-Life Battery Energy Storage System for Energy Sustainability: Recent Advancements, Key Takeaways and Future Perspectives. J. Energy Storage 2025, 66, 116808. [Google Scholar] [CrossRef]
- Filina, O.A.; Tynchenko, V.S.; Kukartsev, V.A.; Bashmur, K.A.; Pavlov, P.P.; Panfilova, T.A. Increasing the Efficiency of Diagnostics in the Brush-Commutator Assembly of a Direct Current Electric Motor. Energies 2024, 17, 17. [Google Scholar] [CrossRef]
- Xia, B.; Wang, S.; Tian, Y.; Sun, W.; Xu, Z.; Zheng, W. Experimental study on the linixcoymnzo2 lithium-ion battery characteristics for model modification of SOC estimation. Inf. Technol. J. 2014, 13, 2395–2403. [Google Scholar] [CrossRef]
- Boychuk, I.P.; Grinek, A.V.; Tynchenko, V.S.; Kukartsev, V.A.; Tynchenko, Y.A.; Kondratiev, S.I. A Methodological Approach to the Simulation of a Ship’s Electric Power System. Energies 2023, 16, 8101. [Google Scholar] [CrossRef]
- Li, X.; Jiang, J.; Zhang, C.; Wang, L.Y.; Zheng, L. Robustness of SOC estimation algorithms for EV lithium-ion batteries against modelling errors and measurement noise. Math. Probl. Eng. 2015, 2015, 719490. [Google Scholar]
- Tian, Y.; Xia, B.; Wang, M.; Sun, W.; Xu, Z. Comparison study on two model-based adaptive algorithms for SOC estimation of lithium-ion batteries in electric vehicles. Energies 2014, 7, 8446–8464. [Google Scholar] [CrossRef]
- Tseng, K.-H.; Liang, J.-W.; Chang, W.; Huang, S.-C. Regression models using fully discharged voltage and internal resistance for state of health estimation of lithium-ion batteries. Energies 2015, 8, 2889–2907. [Google Scholar] [CrossRef]
- Kukartsev, V.V.; Gozbenko, V.E.; Konyukhov, V.Y.; Mikhalev, A.S.; Kukartsev, V.A.; Tynchenko, Y.A. Determination of the Reliability of Urban Electric Transport Running Autonomously through Diagnostic Parameters. World Electr. Veh. J. 2023, 14, 334. [Google Scholar] [CrossRef]
- Hafsaoui, J.; Sellier, F. Electrochemical model and its parameters identification tool for the follow-up of battery aging. World Electric. Veh. J. 2010, 4, 386–395. [Google Scholar] [CrossRef]
- Prada, E.; Di Domenico, D.; Creff, Y.; Sauvant-Moynot, V. Towards advanced BMS algorithms development for (p)hev and EV by using a physics-based model of Li-Ion Battery Systems. World Electric. Veh. J. 2013, 6, 807–818. [Google Scholar] [CrossRef]
- Varini, M.; Campana, P.E.; Lindbergh, G. A semi-empirical, electrochemistry-based model for Li-ion battery performance prediction over lifetime. J. Energy Storage 2019, 25, 100819. [Google Scholar] [CrossRef]
- Sorokova, S.N.; Efremenkov, E.A.; Qi, M. Mathematical Modeling of the State of the Battery of Cargo Electric Vehicles. Mathematics 2023, 11, 536. [Google Scholar] [CrossRef]
- Ashwin, T.R.; McGordon, A.; Jennings, P.A. Electrochemical modelling of li-ion battery packs with constant voltage cycling. J. Power Sources 2017, 341, 327–339. [Google Scholar] [CrossRef]
- Kuo, T.J.; Lee, K.Y.; Chiang, M.H. Development of a neural network model for SOH of LiFePO4 batteries under different aging conditions. IOP Conf. Ser. Mater. Sci. Eng. 2019, 486, 012083. [Google Scholar] [CrossRef]
- Cordoba, A. Capacity and power fade cycle-life model for plug-in hybrid electric vehicle lithium-ion battery cells containing blended spinel and layered-oxide positive electrodes. J. Power Sources 2015, 278, 473–483. [Google Scholar] [CrossRef]
- Mei, J.; Zuo, Y.; Lee, C.H.; Wang, X.; Kirtley, J.L. Stochastic optimisation of multi-energy system operation considering hydrogen-based vehicle applications. Adv. Appl. Energy 2021, 2, 100031. [Google Scholar] [CrossRef]
- Oparina, T.A.; Sevryugina, N.S.; Gozbenko, V.E.; Kondratiev, V.V. Determination of the Performance Characteristics of a Traction Battery in an Electric Vehicle. World Electr. Veh. J. 2024, 15, 64. [Google Scholar] [CrossRef]
- Bolvashenkov, I.; Herzog, H.-G. Approach to predictive evaluation of the reliability of electric drive train on the basis of a stochastic model. In Proceedings of the 2015 International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; pp. 486–492. [Google Scholar]
- Voitovich, E.V.; Kononenko, R.V.; Konyukhov, V.Y.; Tynchenko, V.; Kukartsev, V.A.; Tynchenko, Y.A. Designing the Optimal Configuration of a Small Power System for Autonomous Power Supply of Weather Station Equipment. Energies 2023, 16, 5046. [Google Scholar] [CrossRef]
- Somakettarin, N.; Pichetjamroen, A. A study on modelling of effective series resistance for lithium-ion batteries under life cycle consideration. IOP Conf. Ser. Earth Environ. Sci. 2019, 322, 012008. [Google Scholar] [CrossRef]
- Davydenko, L.; Davydenko, N.; Bosak, A.; Bosak, A.; Deja, A.; Dzhuguryan, T. Smart Sustainable Freight Transport for a City Multi-Floor Manufacturing Cluster: A Framework of the Energy Efficiency Monitoring of Electric Vehicle Fleet Charging. Energies 2022, 15, 3780. [Google Scholar] [CrossRef]
- Mamun, K.A.; Islam, F.R.; Haque, R.; Chand, A.A.; Prasad, K.A.; Goundar, K.K.; Prakash, K.; Maharaj, S. Systematic Modelling and Analysis of On-Board Vehicle Integrated Novel Hybrid Renewable Energy System with Storage for Electric Vehicles. Sustainability 2022, 14, 2538. [Google Scholar] [CrossRef]
- Chao, P.-P.; Zhang, R.-Y.; Wang, Y.-D.; Tang, H.; Dai, H.-L. Warning model of new energy vehicle under improving time-to-rollover with neural network. Meas. Control 2022, 55, 1004–1015. [Google Scholar] [CrossRef]
- Pusztai, Z.; K’orös, P.; Szauter, F.; Friedler, F. Vehicle Model-Based Driving Strategy Optimisation for Lightweight Vehicle. Energies 2022, 15, 3631. [Google Scholar] [CrossRef]
- Mariani, V.; Rizzo, G.; Tiano, F.; Glielmo, L. A model predictive control scheme for regenerative braking in vehicles with hybridised architectures via aftermarket kits. Control Eng. Pract. 2022, 123, 105142. [Google Scholar] [CrossRef]
- Filina, O.A.; Valuev, D.V. Stochastic Models and Processing Probabilistic Data for Solving the Problem of Improving the Electric Freight Transport Reliability. Mathematics 2023, 11, 4836. [Google Scholar] [CrossRef]
- Li, S.; Yu, B.; Feng, X. Research on braking energy recovery strategy of electric vehicle on the basis of ECE regulation and I curve. Sci. Prog. 2020, 103, 0036850419877762. [Google Scholar] [CrossRef]
- Laadjal, K.; Cardoso, A.J.M. Estimation of Lithium-Ion Batteries State-Condition in Electric Vehicle Applications: Issues and State of the Art. Electronics 2021, 10, 1588. [Google Scholar] [CrossRef]
- Efremenkov, E.A.; Valuev, D.V. Mathematical Modelling of Traction Equipment Parameters of Electric Cargo Trucks. Mathematics 2024, 12, 577. [Google Scholar] [CrossRef]
- Valuev, D.V.; Qi, M. Review Models and Methods for Determining and Predicting the Reliability of Technical Systems and Transport. Mathematics 2023, 11, 3317. [Google Scholar] [CrossRef]
- Bryukhanova, N.N.; Pavlov, P.P.; Romanova, V.V.; Karlina, Y.I. Reliability Study of Metal-Oxide Semiconductors in Integrated Circuits. Micromachines 2024, 15, 561. [Google Scholar] [CrossRef]
- Debelov, V.V.; Endachev, D.V.; Yakunov, D.M.; Deev, O.M. Charging balance management technology for low-voltage battery in the car control unit with combined power system. IOP Conf. Ser. Mater. Sci. Eng. 2019, 534, 012029. [Google Scholar] [CrossRef]
- Konyukhov, V.Y.; Oparina, T.A.; Zagorodnii, N.A.; Efremenkov, E.A.; Qi, M. Mathematical Analysis of the Reliability of Modern Trolleybuses and Electric Buses. Mathematics 2023, 11, 3260. [Google Scholar] [CrossRef]
- Martyushev, N.V.; Sorokova, S.N. Mathematical Logic Model for Analysing the Controllability of Mining Equipment. Mathematics 2024, 12, 1660. [Google Scholar] [CrossRef]
- Sorokova, S.N.; Efremenkov, E.A. Mathematical Modelling the Performance of an Electric Vehicle Considering Various Driving Cycles. Mathematics 2023, 11, 2586. [Google Scholar] [CrossRef]
- Ehsani, M.; Wang, F.-Y.; Brosch, G.L. (Eds.) Transportation Technologies for Sustainability; Springer: New York, NY, USA, 2013. [Google Scholar]
- Sorokova, S.N.; Efremenkov, E.A. Mathematical Modelling of Mechanical Forces and Power Balance in Electromechanical Energy Converter. Mathematics 2023, 11, 2394. [Google Scholar] [CrossRef]
- Raugei, M.; Hutchinson, A.; Morrey, D. Can electric vehicles significantly reduce our dependence on non-renewable energy? Scenarios of compact vehicles in the UK as a case in point. J. Clean. Prod. 2018, 201, 1043–1051. [Google Scholar] [CrossRef]
- Balagurusamy, E. Reliability Engineering, First. P-24, Green Park Extension; McGraw Hill Education (India) Private Limited: New Delhi, India, 2002. [Google Scholar]
- Kukartsev, V.V.; Tynchenko, V.S.; Bukhtoyarov, V.V.; Wu, X.; Tyncheko, Y.A.; Kukartsev, V.A. Overview of Methods for Enhanced Oil Recovery from Conventional and Unconventional Reservoirs. Energies 2023, 16, 4907. [Google Scholar] [CrossRef]
- Khalikov, I.H.; Qi, M. Review of Methods for Improving the Energy Efficiency of Electrified Ground Transport by Optimizing Battery Consumption. Energies 2023, 16, 729. [Google Scholar] [CrossRef]
- Aggarwal, K.K. Maintainability and Availability, Topics in Safety Reliability and Quality; Springer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Shishkin, P.V.; Sorokova, S.N. Development of a Mathematical Model of Operation Reliability of Mine Hoisting Plants. Mathematics 2024, 12, 1843. [Google Scholar] [CrossRef]
- Klyuev, R.V.; Dedov, S.I. Determination of Inactive Powers in a Single-Phase AC Network. Energies 2021, 14, 4814. [Google Scholar] [CrossRef]
- Klyuev, R.V.; Andriashin, S.N. Degradation of Lithium-Ion Batteries in an Electric Transport Complex. Energies 2021, 14, 8072. [Google Scholar] [CrossRef]
- Kukartsev, V.A.; Kukartsev, V.V.; Tynchenko, S.V.; Klyuev, R.V.; Zagorodnii, N.A.; Tynchenko, Y.A. Study of Supercapacitors Built in the Start-Up System of the Main Diesel Locomotive. Energies 2023, 16, 3909. [Google Scholar] [CrossRef]
- Xia, Q.; Wang, Z.; Ren, Y.; Tao, L.; Lu, C.; Tian, J.; Hu, D.; Wang, Y.; Su, Y.; Chong, J.; et al. A modified reliability model for lithium-ion battery packs on the basis of the stochastic capacity degradation and dynamic response impedance. J. Power Sources 2019, 423, 40–51. [Google Scholar] [CrossRef]
- Isametova, M.E.; Nussipali, R.; Martyushev, N.V.; Malozyomov, B.V.; Efremenkov, E.A.; Isametov, A. Mathematical Modelling of the Reliability of Polymer Composite Materials. Mathematics 2022, 10, 3978. [Google Scholar] [CrossRef]
- Roy, S.K.; Bhattacharyya, M.M.; Naikan, V.N. Maintainability and reliability analysis of a fleet of shovels. Min. Technol. Trans. Inst. Min. Metall. Sect. A 2001, 110, 163–171. [Google Scholar] [CrossRef]
- Ammaiyappan, B.S.; Ramalingam, S. Reliability investigation of electric vehicles. Life Cycle Reliab. Saf. Eng. 2019, 8, 141–149. [Google Scholar] [CrossRef]
- Khalilzadeh, M.; Fereidunian, A. A Markovian approach applied to reliability modelling of bidirectional DC-DC converters used in PHEVs and smart grids. Iran. J. Electr. Electron. Eng. 2016, 12, 301–313. [Google Scholar]
- Valuev, D.V.; Qi, M. Analysis of a Predictive Mathematical Model of Weather Changes Based on Neural Networks. Mathematics 2024, 12, 480. [Google Scholar] [CrossRef]
- Sadeghian, O.; N-Heris, M.; Abapour, M.; Taheri, S.S.; Zare, K. Improving reliability of distribution networks using plug-in electric vehicles and demand response. J. Mod. Power Syst. Clean Energy 2019, 7, 1189–1199. [Google Scholar] [CrossRef]
- Galiveeti, H.R.; Goswami, A.K.; Choudhury, N.B.D. Impact of plug-in electric vehicles and distributed generation on reliability of distribution systems. Eng. Sci. Technol. Int. J. 2018, 21, 50–59. [Google Scholar] [CrossRef]
- Garcés Quílez, M.; Abdel-Monem, M.; El Baghdadi, M.; Yang, Y.; Van Mierlo, J.; Hegazy, O. Modelling, Analysis and Performance Evaluation of Power Conversion Units in G2V/V2G Application-A Review. Energies 2018, 11, 1082. [Google Scholar] [CrossRef]
- Yelemessov, K.; Sabirova, L.B.; Bakhmagambetova, G.B.; Atanova, O.V. Modelling and Model Verification of the Stress-Strain State of Reinforced Polymer Concrete. Materials 2023, 16, 3494. [Google Scholar] [CrossRef]
- Lacey, G.; Putrus, G.; Bentley, E. Smart EV charging schedules: Supporting the grid and protecting battery life. IET Electr. Syst. Transp. 2017, 7, 84–91. [Google Scholar] [CrossRef]
- Kasturi, K.; Nayak, C.K.; Nayak, M.R. Electric vehicles management enabling G2V and V2G in smart distribution system for maximizing profits using MOMVO. Int. Trans. Electr. Energy Syst. 2019, 29, e12013. [Google Scholar] [CrossRef]
- Malozyomov, B.V.; Kukartsev, V.V.; Martyushev, N.V.; Kondratiev, V.V.; Klyuev, R.V.; Karlina, A.I. Improvement of Hybrid Electrode Material Synthesis for Energy Accumulators Based on Carbon Nanotubes and Porous Structures. Micromachines 2023, 14, 1288. [Google Scholar] [CrossRef] [PubMed]
- Nussipali, R.; Martyushev, N.V.; Malozyomov, B.V.; Konyukhov, V.Y.; Oparina, T.A.; Romanova, V.V.; Kononenko, R.V. Combined Power Generating Complex and Energy Storage System. Electricity 2024, 5, 931–946. [Google Scholar] [CrossRef]
- Baranovskyi, D.; Bulakh, M.; Michajłyszyn, A.; Myamlin, S.; Muradian, L. Determination of the Risk of Failures of Locomotive Diesel Engines in Maintenance. Energies 2023, 16, 4995. [Google Scholar] [CrossRef]
- Filina, O.A.; Konyukhov, V.Y.; Makarov, A.A. Improvement of Operational Reliability of Units and Elements of Dump Trucks Taking into Account the Least Reliable Elements of the System. World Electr. Veh. J. 2024, 15, 365. [Google Scholar] [CrossRef]
- De Santis, M.; Silvestri, L.; Forcina, A. Promoting electric vehicle demand in Europe: Design of innovative electricity consumption simulator and subsidy strategies on the basis of well-to-wheel analysis. Energy Convers. Manag. 2022, 270, 116279. [Google Scholar] [CrossRef]
- Pollák, F.; Vodák, J.; Soviar, J.; Markovič, P.; Lentini, G.; Mazzeschi, V.; Luè, A. Promotion of Electric Mobility in the European Union-Overview of Project PROMETEUS from the Perspective of Cohesion through Synergistic Cooperation on the Example of the Catching-Up Region. Sustainability 2021, 13, 1545. [Google Scholar] [CrossRef]
- Boltrushevich, A.E. Modelling of Reliability Indicators of a Mining Plant. Mathematics 2024, 12, 2842. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, X.; Tang, X.; Liu, B.; Qi, H.; Cao, D. A Review of Real-Time Battery State Estimation Methods for Electric Vehicles. Energies 2018, 11, 1820. [Google Scholar] [CrossRef]
- Waldmann, T.; Kasper, M.; Fleischhammer, M.; Wohlfahrt-Mehrens, M. Temperature Dependent Aging Mechanisms in Lithium-Ion Batteries—A Post-Mortem Study. J. Power Sources 2014, 262, 129–135. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Peng, Q.; Zhang, C. A Brief Review on Key Technologies in the Battery Management System of Electric Vehicles. Front. Mech. Eng. 2019, 14, 47–64. [Google Scholar] [CrossRef]
- Dubrovin, R.G. Simulation Modeling of Energy Efficiency of Electric Dump Truck Use Depending on the Operating Cycle. World Electr. Veh. J. 2025, 16, 217. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).