Learning Parameter Dependence for Fourier-Based Option Pricing with Tensor Trains
Abstract
1. Introduction
2. Tensor Train
2.1. Compression Techniques
2.1.1. Tensor Cross Interpolation
2.1.2. Singular Value Decomposition
3. Fourier Transform-Based Option Pricing Aided by Tensor Cross Interpolation
3.1. Fourier Transform-Based Option Pricing
3.2. Fourier Transform-Based Option Pricing with Tensor Trains
3.3. Monte Carlo-Based Option Pricing
4. Learning Parameter Dependence with Tensor Trains
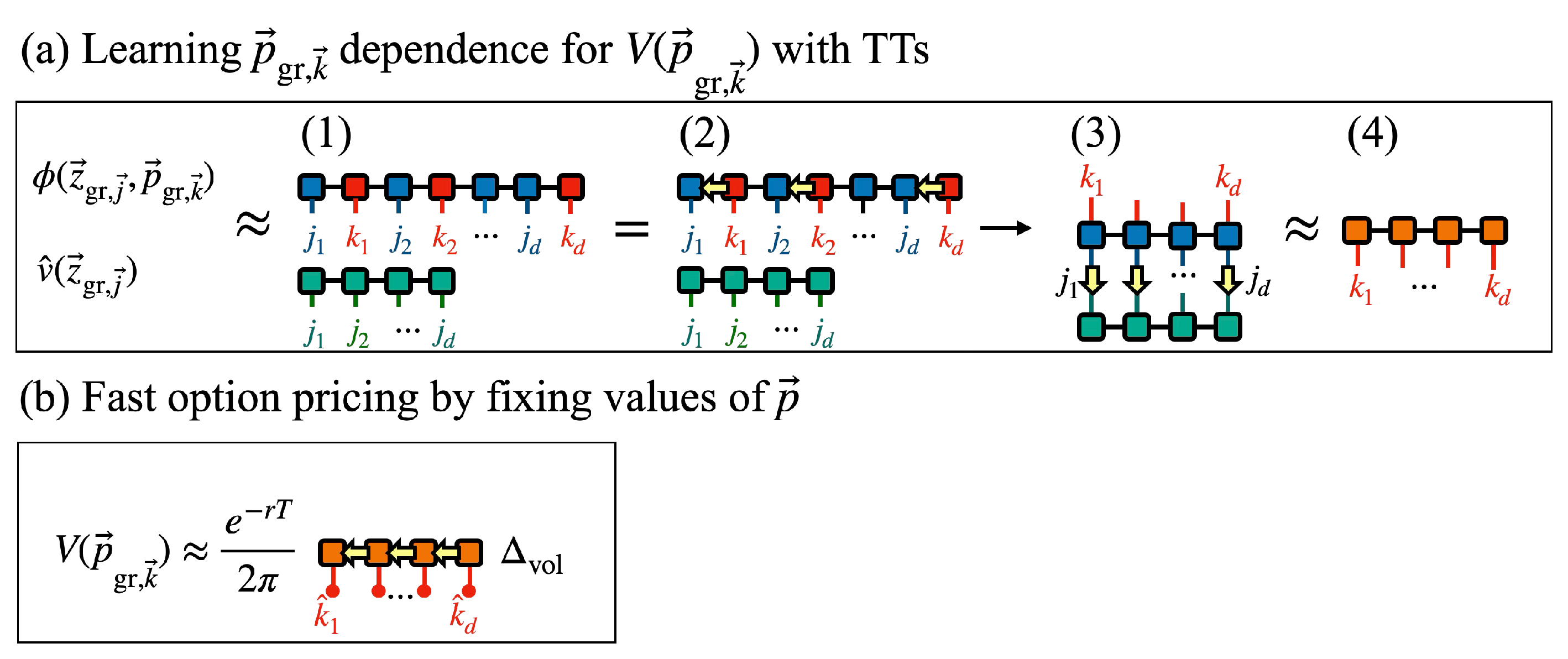
4.1. Outline
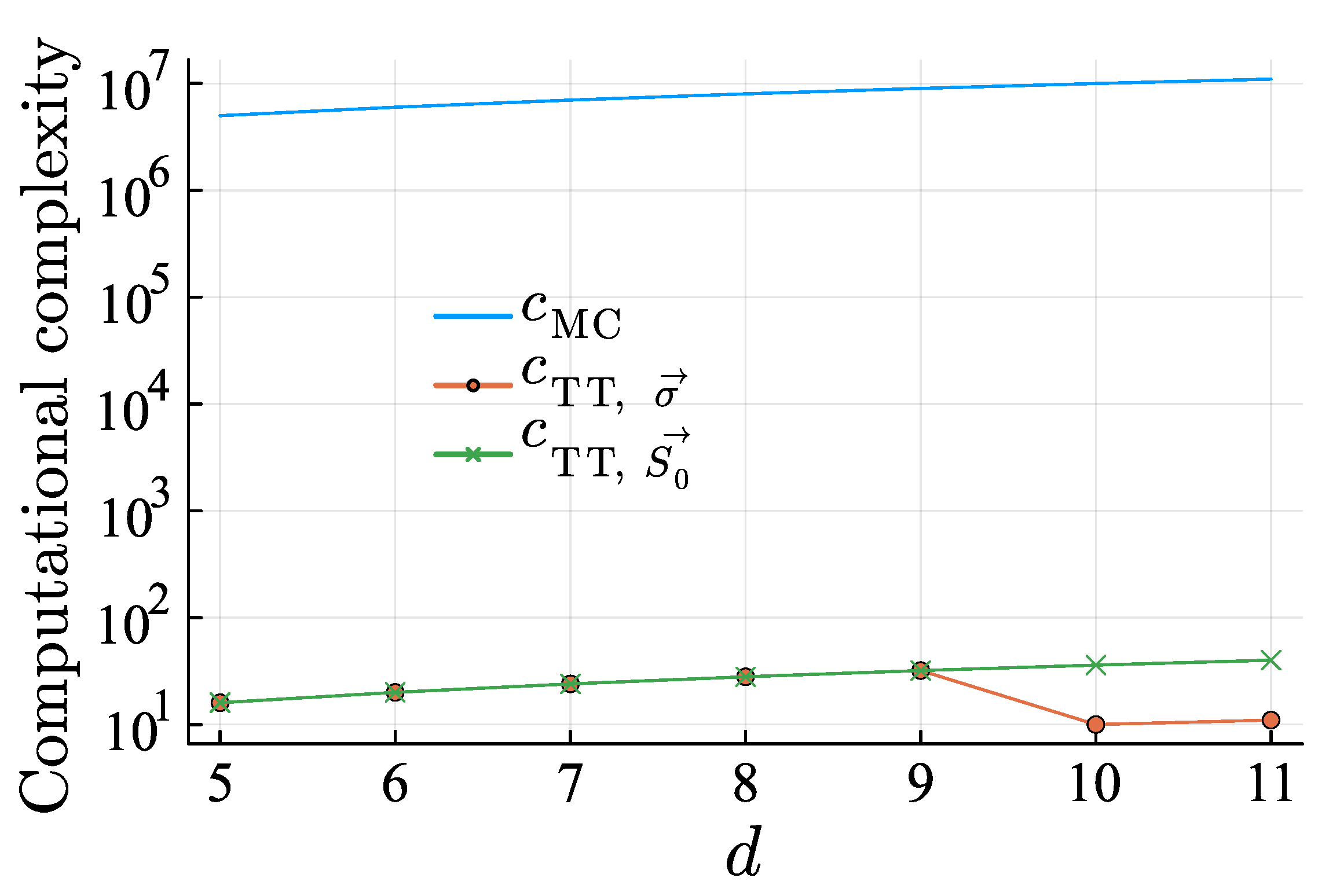
4.2. Computational Complexity
5. Numerical Demonstration
5.1. Details
5.1.1. Ranges of Volatility and Initial Stock Price
5.1.2. Other Parameters
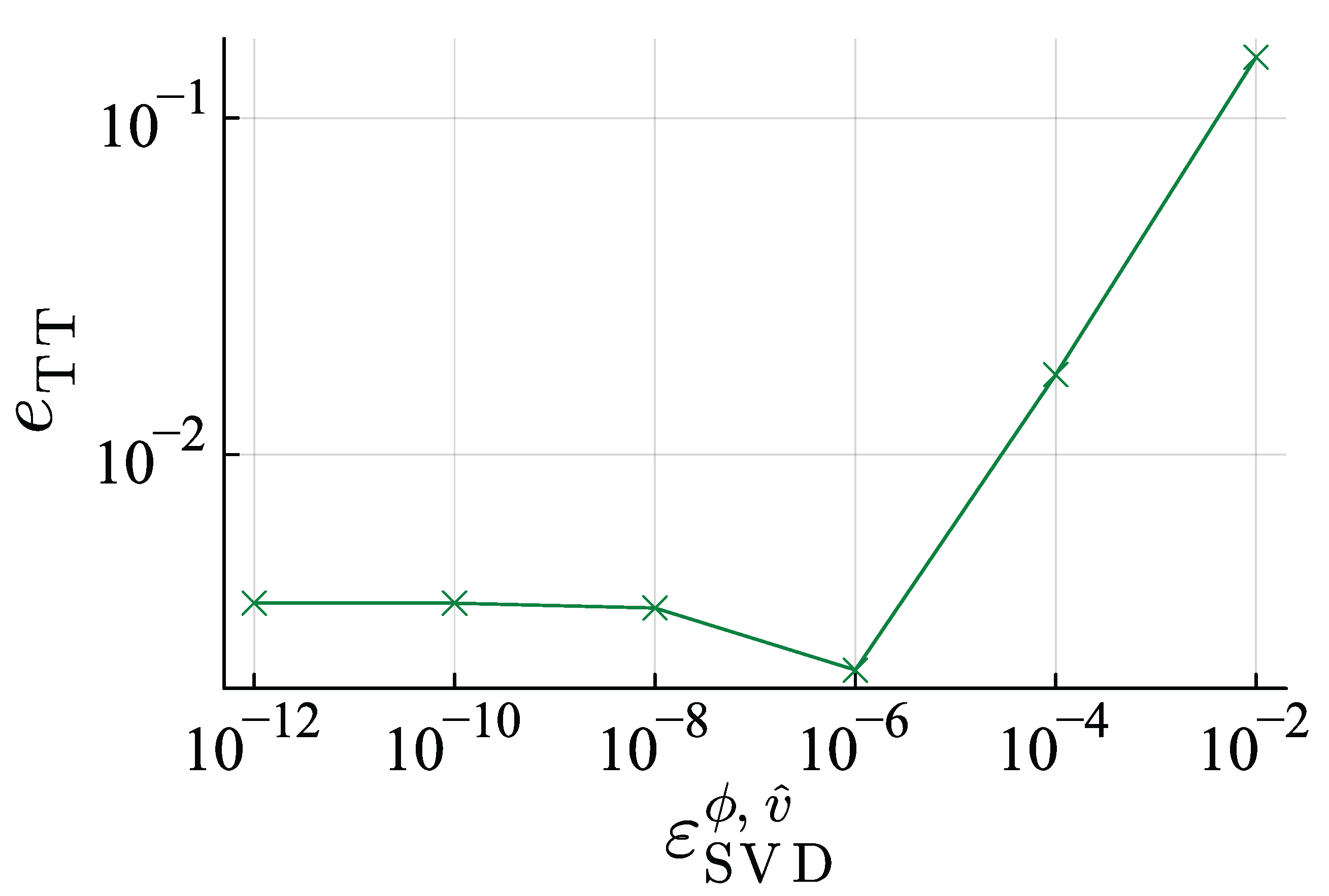
5.1.3. Error Evaluation
5.1.4. Software and Hardware Used in This Study
5.2. Results
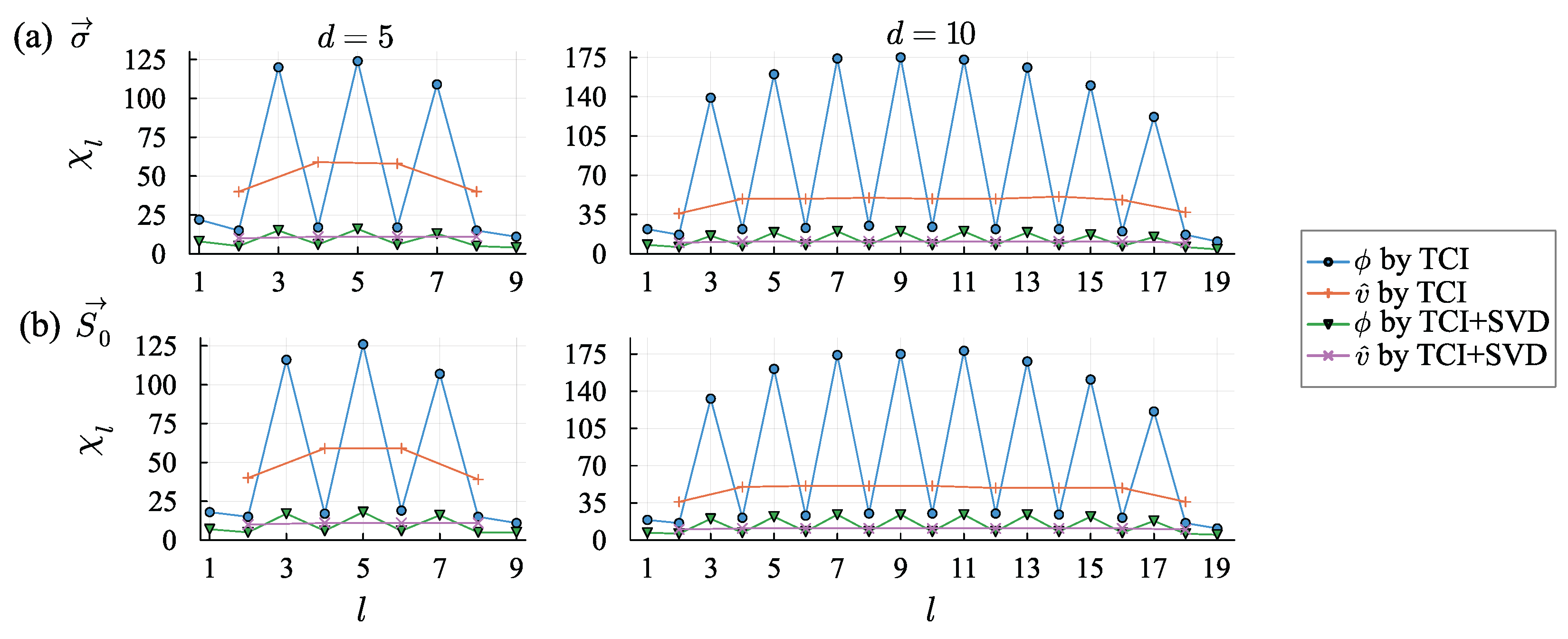
5.2.1. The Case of Varying Volatilities
5.2.2. The Case of Varying Initial Stock Prices
5.2.3. Randomness in Learning the TTs
5.2.4. Total Computational Time for Obtaining the TTs
6. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Hull, J.C. Options Futures and Other Derivatives; Pearson: London, UK, 2003. [Google Scholar]
- Shreve, S.E. Stochastic Calculus for Finance I & II; Springer: New York, NY, USA, 2004. [Google Scholar]
- Stulz, R. Options on the minimum or the maximum of two risky assets: Analysis and applications. J. Financ. Econ. 1982, 10, 161–185. [Google Scholar] [CrossRef]
- Johnson, H. Options on the maximum or the minimum of several assets. J. Financ. Quant. Anal. 1987, 22, 277–283. [Google Scholar] [CrossRef]
- Duffy, D.J. Finite Difference Methods in Financial Engineering: A Partial Differential Equation Approach; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Clewlow, L.; Strickland, C. Implementing Derivative Models; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Bayer, C.; Siebenmorgen, M.; Tempone, R. Smoothing the payoff for efficient computation of Basket option prices. Quant. Financ. 2018, 18, 491–505. [Google Scholar] [CrossRef]
- Liu, S.; Owen, A.B. Preintegration via Active Subspace. SIAM J. Numer. Anal. 2023, 61, 495–514. [Google Scholar] [CrossRef]
- Bayer, C.; Hammouda, C.B.; Papapantoleon, A.; Samet, M.; Tempone, R. Quasi-Monte Carlo for Efficient Fourier Pricing of Multi-Asset Options. arXiv 2024, arXiv:2403.02832. [Google Scholar]
- Herman, D.; Googin, C.; Liu, X.; Sun, Y.; Galda, A.; Safro, I.; Pistoia, M.; Alexeev, Y. Quantum computing for finance. Nat. Rev. Phys. 2023, 5, 450–465. [Google Scholar] [CrossRef]
- Montanaro, A. Quantum speedup of Monte Carlo methods. Proc. R. Soc. A 2015, 471, 20150301. [Google Scholar] [CrossRef]
- Glau, K.; Kressner, D.; Statti, F. Low-Rank Tensor Approximation for Chebyshev Interpolation in Parametric Option Pricing. SIAM J. Financ. Math. 2020, 11, 897–927. [Google Scholar] [CrossRef]
- Kastoryano, M.; Pancotti, N. A highly efficient tensor network algorithm for multi-asset Fourier options pricing. arXiv 2022, arXiv:2203.02804. [Google Scholar]
- Patel, R.; Hsing, C.W.; Sahin, S.; Jahromi, S.S.; Palmer, S.; Sharma, S.; Michel, C.; Porte, V.; Abid, M.; Aubert, S.; et al. Quantum-Inspired Tensor Neural Networks for Partial Differential Equations. arXiv 2022, arXiv:2208.02235. [Google Scholar]
- Bayer, C.; Eigel, M.; Sallandt, L.; Trunschke, P. Pricing High-Dimensional Bermudan Options with Hierarchical Tensor Formats. SIAM J. Financ. Math. 2023, 14, 383–406. [Google Scholar] [CrossRef]
- Oseledets, I.V. Tensor-Train Decomposition. SIAM J. Sci. Comput. 2011, 33, 2295–2317. [Google Scholar] [CrossRef]
- Carr, P.; Madan, D. Option valuation using the fast Fourier transform. J. Comput. Financ. 1999, 2, 61–73. [Google Scholar] [CrossRef]
- Lewis, A.L. A Simple Option Formula for General Jump-Diffusion and Other Exponential Lévy Processes. 2001. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=282110 (accessed on 22 May 2025).
- Orús, R. A practical introduction to tensor networks: Matrix product states and projected entangled pair states. Ann. Phys. 2014, 349, 117–158. [Google Scholar] [CrossRef]
- Okunishi, K.; Nishino, T.; Ueda, H. Developments in the Tensor Network—From Statistical Mechanics to Quantum Entanglement. J. Phys. Soc. Jpn. 2022, 91, 062001. [Google Scholar] [CrossRef]
- Stoudenmire, E.; Schwab, D.J. Supervised Learning with Tensor Networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Lee, D., Sugiyama, M., Luxburg, U., Guyon, I., Garnett, R., Eds.; Curran Associates, Inc.: Sydney, Australia, 2016; Volume 29. [Google Scholar]
- Novikov, A.; Trofimov, M.; Oseledets, I. Exponential machines. arXiv 2016, arXiv:1605.03795. [Google Scholar] [CrossRef]
- Sozykin, K.; Chertkov, A.; Schutski, R.; Phan, A.H.; Cichocki, A.; Oseledets, I. TTOpt: A Maximum Volume Quantized Tensor Train-based Optimization and its Application to Reinforcement Learning. arXiv 2022, arXiv:2205.00293. [Google Scholar]
- Shinaoka, H.; Wallerberger, M.; Murakami, Y.; Nogaki, K.; Sakurai, R.; Werner, P.; Kauch, A. Multiscale Space-Time Ansatz for Correlation Functions of Quantum Systems Based on Quantics Tensor Trains. Phys. Rev. X 2023, 13, 021015. [Google Scholar] [CrossRef]
- Núñez Fernández, Y.; Jeannin, M.; Dumitrescu, P.T.; Kloss, T.; Kaye, J.; Parcollet, O.; Waintal, X. Learning Feynman Diagrams with Tensor Trains. Phys. Rev. X 2022, 12, 041018. [Google Scholar] [CrossRef]
- Takahashi, H.; Sakurai, R.; Shinaoka, H. Compactness of quantics tensor train representations of local imaginary-time propagators. arXiv 2024, arXiv:2403.09161. [Google Scholar] [CrossRef]
- Ye, E.; Loureiro, N.F.G. Quantum-inspired method for solving the Vlasov-Poisson equations. Phys. Rev. E 2022, 106, 035208. [Google Scholar] [CrossRef] [PubMed]
- Kornev, E.; Dolgov, S.; Pinto, K.; Pflitsch, M.; Perelshtein, M.; Melnikov, A. Numerical solution of the incompressible Navier–Stokes equations for chemical mixers via quantum-inspired Tensor Train Finite Element Method. arXiv 2023, arXiv:2305.10784. [Google Scholar]
- Gourianov, N.; Lubasch, M.; Dolgov, S.; van den Berg, Q.Y.; Babaee, H.; Givi, P.; Kiffner, M.; Jaksch, D. A quantum-inspired approach to exploit turbulence structures. Nat. Comput. Sci. 2022, 2, 30–37. [Google Scholar] [CrossRef] [PubMed]
- Oseledets, I.; Tyrtyshnikov, E. TT-cross approximation for multidimensional arrays. Linear Algebra Appl. 2010, 432, 70–88. [Google Scholar] [CrossRef]
- Dolgov, S.; Savostyanov, D. Parallel cross interpolation for high-precision calculation of high-dimensional integrals. Comput. Phys. Commun. 2020, 246, 106869. [Google Scholar] [CrossRef]
- Ritter, M.K.; Núñez Fernández, Y.; Wallerberger, M.; von Delft, J.; Shinaoka, H.; Waintal, X. Quantics Tensor Cross Interpolation for High-Resolution Parsimonious Representations of Multivariate Functions. Phys. Rev. Lett. 2024, 132, 056501. [Google Scholar] [CrossRef]
- Bayer, C.; Ben Hammouda, C.; Papapantoleon, A.; Samet, M.; Tempone, R. Optimal damping with a hierarchical adaptive quadrature for efficient Fourier pricing of multi-asset options in Lévy models. J. Comput. Financ. 2023, 27, 43–86. [Google Scholar] [CrossRef]
- Shashua, A.; Levin, A. Linear image coding for regression and classification using the tensor-rank principle. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2001, Kauai, HI, USA, 8–14 December 2001; Volume 1, p. I-I. [Google Scholar] [CrossRef]
- Vasilescu, M.A.O.; Terzopoulos, D. Multilinear Analysis of Image Ensembles: TensorFaces. In Computer Vision—ECCV 2002: Proceedings of the 7th European Conference on Computer Vision Copenhagen, Denmark, 28–31 May 2002; Heyden, A., Sparr, G., Nielsen, M., Johansen, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 447–460. [Google Scholar]
- Ion, I.G.; Wildner, C.; Loukrezis, D.; Koeppl, H.; De Gersem, H. Tensor-train approximation of the chemical master equation and its application for parameter inference. J. Chem. Phys. 2021, 155, 034102. [Google Scholar] [CrossRef]
- Ballani, J.; Grasedyck, L. Hierarchical Tensor Approximation of Output Quantities of Parameter-Dependent PDEs. SIAM/ASA J. Uncertain. Quantif. 2015, 3, 852–872. [Google Scholar] [CrossRef][Green Version]
- Schollwock, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96–192. [Google Scholar] [CrossRef]
- Ernst Eberlein, K.G.; Papapantoleon, A. Analysis of Fourier Transform Valuation Formulas and Applications. Appl. Math. Financ. 2010, 17, 211–240. [Google Scholar] [CrossRef]
- Glasserman, P. Monte Carlo Methods in Financial Engineering; Springer: New York, NY, USA, 2004; Volume 53. [Google Scholar]
- Available online: https://indexes.nikkei.co.jp/en/nkave/index/profile?idx=nk225vi (accessed on 29 December 2024).
- Fernández, Y.N.; Ritter, M.K.; Jeannin, M.; Li, J.W.; Kloss, T.; Louvet, T.; Terasaki, S.; Parcollet, O.; von Delft, J.; Shinaoka, H.; et al. Learning tensor networks with tensor cross interpolation: New algorithms and libraries. arXiv 2024, arXiv:2407.02454. [Google Scholar] [CrossRef]
- Google. tf-Quant-Finance. 2023. Available online: https://github.com/google/tf-quant-finance (accessed on 29 December 2024).
- Dupire, B. Pricing with a smile. Risk 1994, 7, 18–20. [Google Scholar]
- Heston, S.L. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef]
- Hagan, P.S.; Kumar, D.; Lesniewski, A.S.; Woodward, D.E. Managing Smile Risk. Wilmott Mag. 2002, 1, 84–108. [Google Scholar]
- Madan, D.B.; Seneta, E. The Variance Gamma (V.G.) Model for Share Market Returns. J. Bus. 1990, 63, 511–524. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O. Processes of normal inverse Gaussian type. Financ. Stoch. 1997, 2, 41–68. [Google Scholar] [CrossRef]
| T | r | K | |||||
|---|---|---|---|---|---|---|---|
| 1 | 100 | 100 |
| (a) | |||||||||
| d | [s] | [s] | |||||||
| 5 | 0.00178 | 0.00606 | 16 | 16 | 11 | 2 | |||
| 6 | 0.00154 | 0.00503 | 20 | 16 | 11 | 2 | |||
| 7 | 0.00134 | 0.00428 | 24 | 17 | 11 | 2 | |||
| 8 | 0.00136 | 0.00372 | 28 | 18 | 11 | 2 | |||
| 9 | 0.000867 | 0.00329 | 32 | 20 | 11 | 2 | |||
| 10 | 0.00229 | 0.00294 | 10 | 20 | 11 | 1 | |||
| 11 | 0.000554 | 0.00265 | 11 | 20 | 11 | 1 | |||
| (b) | |||||||||
| d | [s] | [s] | |||||||
| 5 | 0.00151 | 0.00773 | 16 | 18 | 11 | 2 | |||
| 6 | 0.00122 | 0.00640 | 20 | 19 | 11 | 2 | |||
| 7 | 0.00112 | 0.00547 | 24 | 21 | 10 | 2 | |||
| 8 | 0.000973 | 0.00477 | 28 | 23 | 11 | 2 | |||
| 9 | 0.000686 | 0.00424 | 32 | 24 | 11 | 2 | |||
| 10 | 0.000662 | 0.00377 | 36 | 24 | 11 | 2 | |||
| 11 | 0.00114 | 0.00339 | 40 | 25 | 13 | 2 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakurai, R.; Takahashi, H.; Miyamoto, K. Learning Parameter Dependence for Fourier-Based Option Pricing with Tensor Trains. Mathematics 2025, 13, 1828. https://doi.org/10.3390/math13111828
Sakurai R, Takahashi H, Miyamoto K. Learning Parameter Dependence for Fourier-Based Option Pricing with Tensor Trains. Mathematics. 2025; 13(11):1828. https://doi.org/10.3390/math13111828
Chicago/Turabian StyleSakurai, Rihito, Haruto Takahashi, and Koichi Miyamoto. 2025. "Learning Parameter Dependence for Fourier-Based Option Pricing with Tensor Trains" Mathematics 13, no. 11: 1828. https://doi.org/10.3390/math13111828
APA StyleSakurai, R., Takahashi, H., & Miyamoto, K. (2025). Learning Parameter Dependence for Fourier-Based Option Pricing with Tensor Trains. Mathematics, 13(11), 1828. https://doi.org/10.3390/math13111828







