Commutators of Pre-Lie n-Algebras and PL∞-Algebras
Abstract
1. Introduction
- Theorem 2, which states that the -algebra structure on V can be extended as a nilpotent coderivation of degree on coalgebra .
- Theorem 3, which provides the relation of homotopy algebras, along with Corollary 2 providing the relation of n-ary algebras.
2. Preliminaries
- an -algebra, if
- a -algebra, if
- an -algebra, if
- an -algebra, if
- a -algebra, if
- an -algebra, if
- is a partially associative n-algebra if and only if is an -algebra.
- is a pre-Lie n-algebra if and only if is a -algebra.
- is a Lie n-algebra if and only if is an -algebra.
3. Coalgebras, Coderivations, and Homotopy Algebras
3.1. Coalgebras and Coalgebra Maps Between Them
- is a graded vector space equipped with a comultiplication map
- The comultiplication of is provided by
- The n-part of is denoted by and its comultiplication is defined by
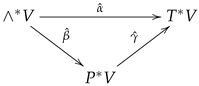
3.2. Equivalent Definitions of Homotopy Algebras
3.3. Proof of Theorem 2
4. Relation Among n-Ary Algebras and Homotopy Algebras
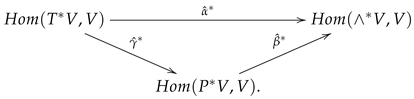
- Suppose that is an -algebra; then, is a -algebra.
- For a -algebra , the collection defines an -algebra structure on V.
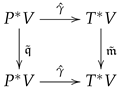
- Suppose that is an -algebra; then, is a -algebra.
- For a -algebra , the collection defines an -algebra structure on V.

- Every partially associative n-algebra carries a pre-Lie n-algebra structure defined by
- Every pre-Lie n-algebra carries a Lie n-algebra structure defined by
- The associated -algebra structure on V is provided by for any , , and is zero except
- The associated -algebra structure on V is provided by for any and is zero except
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cayley, A. On the Theory of Analytic Forms Called Trees; Collected Mathematical Papers of Arthur Cayley; Cambridge University Press: Cambridge, UK, 1890; Volume 3, pp. 242–246. [Google Scholar]
- Vinberg, E.B. Convex homogeneous cones. Transl. Moscow Math. Soc. 1963, 12, 340–403. [Google Scholar]
- Koszul, J.-L. Domaines borńes homogènes et orbites de groupes de transformations affines. Bull. Soc. Math. Fr. 1961, 89, 515–533. [Google Scholar] [CrossRef]
- Chapoton, F.; Livernet, M. Pre-Lie algebras and the rooted trees operad. Internat. Math. Res. Notices 2001, 8, 395–408. [Google Scholar] [CrossRef]
- Pei, J.; Bai, C.; Guo, L. Splitting of operads and Rota-Baxter operators on operads. Appl. Categ. Struct. 2017, 25, 505–538. [Google Scholar] [CrossRef]
- Goze, M.; Goze, N.; Remm, E. n-Lie algebras. Afr. J. Math. Phys. 2010, 8, 17–28. [Google Scholar]
- Lada, T.; Stasheff, J. Introduction to sh Lie algebras for physicists. Int. J. Theor. Phys. 1993, 32, 1087–1103. [Google Scholar] [CrossRef]
- Stasheff, J. Homotopy associativity of H-spaces I. Trans. Am. Math. Soc. 1963, 108, 275–292. [Google Scholar]
- Stasheff, J. Homotopy Associativity of H-spaces II. Trans. Am. Math. Soc. 1963, 108, 293–312. [Google Scholar] [CrossRef]
- Lada, T. Commutators of A∞ structures. In Higher Homotopy Structures in Topology and Mathematical Physics; Publishing House: Providence, RI, USA, 1999; pp. 227–233. [Google Scholar]
- Yanagida, S. Derived gluing construction of chiral algebras. Lett. Math. Phys. 2021, 111, 51. [Google Scholar] [CrossRef]
- Markl, M. A cohomology theory for A(m)-algebras and applications. J. Pure Appl. Algebra 1992, 83, 141–175. [Google Scholar] [CrossRef]
- Loday, J.-L.; Vallette, B. Algebraic operads, Volume 346 of Grundlehren der Mathematischen Wissenschaften; Springer: Cham, Switzerland, 2012. [Google Scholar]
- Burde, D. Left-symmetric algebras, or pre-Lie algebras in geometry and physics. Cent. Eur. J. Math. 2006, 4, 323–357. [Google Scholar] [CrossRef]
- Wang, Q.; Sheng, Y.; Bai, C.; Liu, J. Nijenhuis operators on pre-Lie algebras. Commun. Contemp. Math. 2019, 21, 1850050. [Google Scholar] [CrossRef]
- Tang, R.; Hou, S.; Sheng, Y. Lie 3-algebras and deformations of relative Rota-Baxter operators on 3-Lie algebras. J. Algebra 2021, 567, 37–62. [Google Scholar] [CrossRef]
- Hanlon, P.; Wachs, M. On Lie k-algebras. Adv. Math. 1995, 113, 206–236. [Google Scholar] [CrossRef]
- Lada, T.; Markl, M. Strongly homotopy Lie algebras. Comm. Algebra 1995, 23, 2147–2161. [Google Scholar] [CrossRef]
- Keller, B. Introduction to A-infinity algebras and modules. Homol. Homotopy Appl. 2001, 3, 1–35. [Google Scholar] [CrossRef]
- Lazarev, A.; Sheng, Y.; Tang, R. Deformations and Homotopy Theory of Relative Rota-Baxter Lie Algebras. Commun. Math. Phys. 2021, 383, 595–631. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Wu, Z. Commutators of Pre-Lie n-Algebras and PL∞-Algebras. Mathematics 2025, 13, 1792. https://doi.org/10.3390/math13111792
Wang M, Wu Z. Commutators of Pre-Lie n-Algebras and PL∞-Algebras. Mathematics. 2025; 13(11):1792. https://doi.org/10.3390/math13111792
Chicago/Turabian StyleWang, Mengjun, and Zhixiang Wu. 2025. "Commutators of Pre-Lie n-Algebras and PL∞-Algebras" Mathematics 13, no. 11: 1792. https://doi.org/10.3390/math13111792
APA StyleWang, M., & Wu, Z. (2025). Commutators of Pre-Lie n-Algebras and PL∞-Algebras. Mathematics, 13(11), 1792. https://doi.org/10.3390/math13111792





