Abstract
Amid accelerating population aging and the rapid evolution of digital technologies, the digital transformation of rural elderly care services has become a pivotal strategy for restructuring the rural elderly care system. This study identified the local government, rural elderly care service centers, and the elderly population as the principal stakeholders, and developed a tripartite evolutionary game-theory model to examine the dynamic strategic interactions among these actors under the influence of digital technologies. The model further investigated the evolutionary trajectories and equilibrium conditions of their behavioral strategies. Numerical simulations conducted via MATLAB were employed to validate and visualize the model outcomes. The findings revealed the following. (1) The evolutionary equilibrium of digital elderly care service development in rural areas is jointly determined by the strategic choices of the three parties, with its stability shaped by a complex interplay of cost structures, incentive mechanisms, and utility outcomes. (2) Cost factors exhibit heterogeneous effects across stakeholders. Specifically, excessive regulatory costs diminish the performance incentives of local governments, digital infrastructure and operational expenditures influence service centers’ capacity for precision-oriented service delivery, and the participation of the elderly is constrained by affordability thresholds. (3) Local government behavior demonstrates a pronounced sensitivity to incentives. In particular, rewards and social reputation conferred by higher-level governmental bodies exert a significantly stronger influence than punitive measures. (4) Government subsidies for digital transformation enhance cross-stakeholder synergy through dual transmission channels. Nonetheless, excessive subsidies may escalate fiscal risk, while moderately calibrated penalty mechanisms effectively curb moral hazard within service centers. This study advances theoretical understanding of multi-stakeholder coordination in the context of digitally enabled rural elderly care and provides actionable insights for policymakers aiming to formulate interest-aligned strategies and construct resilient, intelligent governance systems for elderly care.
Keywords:
digital transformation; rural elderly services; smart senior care; evolutionary game; simulation analysis MSC:
91A22; 91A80; 65C99
1. Introduction
Population aging is a pressing global issue in the 21st century. According to World Population Prospects 2024 released by the United Nations, the number of people aged 65 and over is projected to reach 2.2 billion by the late 2070s, posing significant socio-economic challenges worldwide [1,2]. China is experiencing one of the most rapid and extensive aging processes globally [3], with rural areas facing a particularly severe situation due to a higher proportion of elderly residents and relatively weaker infrastructure and social support systems [4,5].
In these rural regions, economic constraints, inadequate medical resources, and the outmigration of younger generations have led to a growing number of “left-behind elderly”, exacerbating the difficulties in providing adequate care and support. Addressing this issue has become a national priority. In June 2024, the Chinese government issued its Guiding Opinions on Accelerating the Development of Rural Elderly Care Services policy, highlighting the need to enhance rural elderly care capacity and service quality.
In response to the aging challenge, “smart elderly care” 26 has emerged as a strategic solution. Supported by successive policies at various governmental levels, smart elderly care integrates advanced technologies such as the Internet of Things (IoT), cloud computing, and big data into traditional care systems [6,7,8]. This model aims to provide intelligent and personalized services—including health monitoring, home safety, and psychological support—through smart devices and platforms. For instance, Jingu County in Yunnan Province has implemented a three-tier rural service network that includes a “15 min elderly care service circle” and eight village-level health stations. These initiatives, coupled with digital platforms and wearable technologies such as smart wristbands, represent a growing trend of technologically empowered care solutions in rural China. This marks the industry’s shift from the exploratory stage to a more mature development phase, with increasing demand projected in the near future [9,10].
Despite these developments, the implementation of smart home-based elderly care in rural areas remains in its early stages. Major challenges persist, including underdeveloped information platforms, uneven service quality, and fragmented resource integration [11]. Studies have yet to fully examine how different stakeholders—government bodies, technology providers, service organizations, and families—interact within this emerging ecosystem. Therefore, this study sought to explore the interaction mechanisms among key actors involved in rural smart elderly care services, identify the factors influencing cooperation and efficiency, and offer insights into how these systems can be optimized. By addressing these gaps, we aimed to contribute to the sustainable development of smart elderly care models and improve the quality of life for the rural elderly population.
Digitally empowered smart elderly care services have emerged as a critical strategy to address the challenges posed by population aging, garnering increasing attention from both academic research and practical applications. In Western countries, where internet infrastructure and smart device technologies are well established, the development of smart home-based elderly care systems is relatively advanced. Moreover, due to smaller urban–rural economic disparities and well-developed rural mutual elderly care systems, the service coverage gap between urban and rural areas is minimal. Typically, these systems manifest as retirement communities, embodying a community-based elderly care model tailored for rural seniors [12]. Building upon this model, scholars have demonstrated the promising prospects of smart home-based elderly care in applications such as home monitoring, disease surveillance, and medical support [13,14,15]. These functions effectively alleviate seniors’ anxieties about aging in place. For instance, Jo’s research confirms that elderly users generally hold positive attitudes toward smart elderly care systems, recognizing their potential to enhance quality of life [16].
However, extant research predominantly emphasizes the technological underpinnings and subjective benefits of these systems, often overlooking the lived experiences and challenges faced by certain elderly individuals [17]. Zhu and colleagues highlight the dual-edged nature of smart home-based elderly care, cautioning against neglecting privacy and security concerns [18]. Complementing this perspective, Pirzada et al. argue that smart elderly care services should adhere to four essential principles: personalization, dignity and independence preservation, user autonomy, and social inclusivity [19]. Addressing potential technological barriers encountered by the elderly, Bhalotia et al. explore the interaction among individuals, activities, technologies, and environments, underscoring the importance of inclusiveness and humanistic care in smart elderly services [20].
In China, the rapidly aging population has created an urgent impetus for transforming the elderly care sector. Smart elderly care, a cornerstone of this digital transformation, drives industrial upgrading through multidimensional integration and innovation. Furthermore, effective rural aging management is integral to the broader shift from smallholder farming to sustainable agricultural practices [21]. Current studies propose that industrializing smart elderly care necessitates a five-dimensional integration framework encompassing enterprise collaboration, value distribution, technological support, product innovation, and spatial layout optimization [22]. The deep application of artificial intelligence offers new opportunities to reshape home-based elderly care, although this advancement requires balancing technological risks with humanistic concerns [23]. At the macro level, digital infrastructure and human capital emerge as critical drivers of the elderly care industry’s development [24]. Research focused on rural elderly care highlights the necessity of government-led, multi-stakeholder community care networks and the empowering role of emerging information technologies [25]. Empirical studies reveal that medical and nursing services remain the most demanded by rural elderly populations, and participation in smart elderly care is significantly influenced by digital feedback mechanisms [26,27]. Collectively, these findings underscore the importance of establishing collaborative governance frameworks involving government, families, and society to promote digitally empowered rural elderly care.
While most existing research centers on service models, practical frameworks, and technical pathways for smart home-based and rural elderly care, the core challenge lies in the interplay between technology and management models, particularly through the lens of multi-stakeholder interactions and transformation dynamics [28]. A growing number of scholars have employed evolutionary game theory to investigate elderly care service regulation. For example, Ma et al. [29] and Yao et al. [30] introduced stable equilibrium strategies to analyze the dynamic evolution of participants and the impact of uncertainties on strategic choices. Yue et al. modeled elderly user feedback’s effectiveness in quality control using evolutionary games [31]. Chen et al. incorporated service ecosystem theory to highlight the government’s regulatory role [32]. He et al. examined the decision-making evolution among private investors, consumers, and the government, analyzing the effects of static and dynamic subsidies [33]. Mao et al. utilized system dynamics to simulate evolutionary game paths among governments, communities, providers, and households, facilitating the transition from traditional to smart community elderly care [10]. Xiao and Liu emphasized proactive government management as vital for smart platform operation through a game theory model involving governments, platforms, and enterprises [34].
Despite the growing body of literature on smart elderly care, particularly in rural contexts, several theoretical and practical limitations remain insufficiently addressed. First, existing studies tend to emphasize service models and technological innovations while paying insufficient attention to the complex dynamics among stakeholders, especially the strategic interactions and interest alignments among local governments, service providers, and rural elderly. The lack of a game-theory perspective limits our understanding of how these actors adapt and evolve within a multi-agent system. Second, much of the literature assumes a relatively even distribution of digital resources, yet in rural China, significant disparities in digital infrastructure and literacy persist. This rural digital divide not only impedes the implementation of smart technologies but also raises concerns about equity and inclusivity in policy design and service access. Third, while subjective acceptance of smart technologies by the elderly is frequently documented, there is limited discussion of their bounded rationality: their cognitive limitations, habitual resistance to change, and dependence on others for digital engagement. These factors may lead to low actual usage rates despite positive attitudinal indicators, signaling a gap between intention and behavior.
Therefore, this study moved beyond descriptive summaries to critically engage with these gaps by employing evolutionary game theory to model stakeholder interactions and exploring how digital inequality and behavioral constraints influence the sustainability of rural smart home-based elderly care systems. In doing so, it contributes to both the theoretical refinement and practical optimization of digitally empowered rural aging solutions.
2. Model Assumptions and Construction
2.1. Analysis of the Subject of the Game
The construction of a rural digital elderly care service system necessitates the collaborative involvement of three key stakeholders: local governments, rural elderly care service centers (RECS centers), and rural elderly. The strategic and functional relationships among these actors are illustrated in Figure 1.
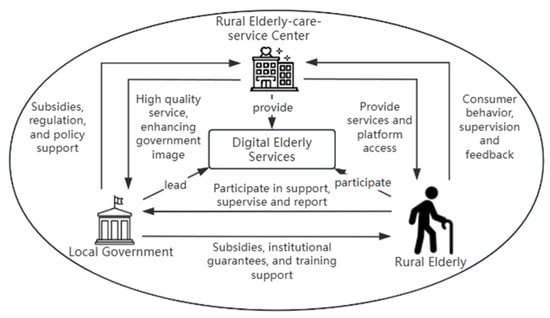
Figure 1.
Logical relationship diagram of the three-party evolutionary game.
As policymakers and resource allocators, local governments play a guiding and regulatory role in the system. They delegate the operation of RECS centers, formulate supportive policies, and offer financial subsidies to ensure effective service delivery. Simultaneously, they implement oversight mechanisms to encourage RECS centers to enhance the quality of smart elderly care services. Moreover, local governments help foster trust in RECS centers among elderly consumers, thereby promoting their active participation in digital services.
RECS centers, entrusted by the government, are responsible for platform-based operation and concrete service implementation. They leverage existing infrastructure—such as rural nursing homes—for functional transformation and upgrading. Their services include centralized care for individuals in extreme hardship, socialized elderly care, and home-based nursing services for nearby residents. These centers monitor the conditions of elderly clients through the smart service platform and provide partially paid services in response to their needs.
Elderly individuals, as service recipients, not only consume services but also engage in active participation, particularly by purchasing and utilizing smart devices and associated care services. Furthermore, they hold supervisory rights: in cases of misconduct or rights infringement, they may report RECS centers to relevant local government departments for redress.
2.2. Model Assumptions
Hypothesis 1.
Local governments, RECS centers, and the elderly are modeled as boundedly rational actors operating under conditions of incomplete or limited information. In line with the evolutionary game theory framework, it is assumed that stakeholders do not possess perfect knowledge of all contextual variables or the utility functions of other actors. Instead, strategies evolve over time through repeated interactions, learning, and imitation. Each stakeholder seeks to maximize its own benefits while minimizing associated costs within the constraints of their limited cognitive capacity and available information. Specifically, local governments adopt the strategy of “positive construction” with probability and “negative construction” with probability . The RECS center selects “positive transformation” with probability and “negative transformation” with probability , while the elderly engage in “active participation” with probability and “passive participation” with probability .
Hypothesis 2.
This hypothesis centers on the strategic options available to local governments, namely positive construction versus negative construction. When local governments adopt a positive construction strategy, they provide subsidies to RECS centers that undergo positive transformation, thereby incentivizing the improvement of service quality. To deter RECS centers from exploiting policy support to fraudulently obtain subsidies, local governments enforce strict regulatory measures and imposes fines on negatively transformed centers, incurring regulatory costs . If RECS centers are positively transformed and conscientiously comply with quality standards for elderly care, they deliver high-quality services, which in turn earn the local government rewards from higher-level authorities and enhance its social reputation . Conversely, if local governments adopt a negative construction approach—failing to regulate, reward, or sanction the strategic behaviors of service centers and the elderly—and the service centers are negatively transformed, service violations may occur. Due to ineffective supervision and failure to address low-quality service in a timely manner, public dissatisfaction arises, leading to accountability penalties and social reputation losses imposed on local governments by higher authorities.
Hypothesis 3.
This hypothesis pertains to the strategic decisions of RECS centers, which can either positively or negatively transform. A positively transformed service center, beyond incurring baseline fixed costs, invests additional resources to enhance the quality and level of smart elderly care services through measures such as caregiver training and digital infrastructure upgrades, resulting in higher digital operation and construction costs . Consequently, it receives government subsidies and attains greater economic benefits . In contrast, a negatively transformed center invests lower human and material resources, bearing lower digital operation and construction costs , and correspondingly obtains lower economic returns .
Hypothesis 4.
This hypothesis addresses the strategic choices of rural elderly, who may engage in either positive or negative participation. Positive participation entails not only purchasing smart elderly care services but also dedicating time and effort to learning how to operate smart devices and platforms, as well as supervising service centers to identify irregularities, incurring a total cost . Under scenarios of positive and negative transformation of service centers, the elderly derive utility values and respectively, with evidently. To encourage positive participation and enhance elderly supervision motivation, the government provides subsidies to the elderly when it is positively constructing the service centers.
2.3. Model Construction
2.3.1. Parameter Setting
The symbols and corresponding definitions of the parameters involved in the tripartite evolutionary game among the local government, RECS centers, and rural elderly are presented in Table 1.

Table 1.
Parameter symbols and definitions.
2.3.2. Payment Matrix
The corresponding payoff matrix is presented in Table 2. In this matrix, , , and represent the respective payoffs of local governments, RECS centers, and rural elderly.

Table 2.
Payment matrix of the three-party evolutionary game.
3. Model Analysis
3.1. Calculation of Dynamic Replication Equations
Based on the foregoing analysis and assumptions, the average expected payoff for each participant is calculated following the principles of dynamic equations. Subsequently, replicator dynamic equations are derived to identify the equilibrium points of the evolutionary game. Specifically, from Table 2, the expected payoffs of local governments under positive and negative construction strategies are denoted and , respectively.
The average expected payoff for local governments is given by:
The replicator dynamic equation for local governments’ positive construction strategy, denoted , is expressed as:
Similarly, the expected payoffs for RECS centers when choosing the positive and negative transformation strategies are denoted and , respectively.
The average expected payoff for RECS centers is given by:
The replicator dynamic equation for the RECS centers’ positive transformation strategy, denoted , is given by:
The expected payoffs for the elderly adopting positive participation and negative participation strategies are denoted and , respectively.
The average expected payoff for the elderly is given by:
The replicator dynamic equation for the elderly’s positive participation strategy, denoted , is expressed as:
In the constructed evolutionary game model, variables such as subsidies, penalties, regulatory costs, and active participation costs influence the strategic choices of each actor. Accordingly, the derivation of Equations (1)–(3) yields:
3.2. Asymptotic Stability Analysis of Game Subjects
3.2.1. Asymptotic Stability Analysis of Local Governments
According to the stability theorem of differential equations, for local governments’ strategy choice to reach an evolutionarily stable state, the following conditions must be satisfied: and . When , it holds that , indicating that the system remains in a stable state, regardless of the value of . In other words, local governments’ strategy will not change over time, no matter which strategy is chosen. However, when , the two equilibrium points satisfying are and . Substituting these values into Equation (4) yields:
When , by analyzing Equations (7) and (8), it follows that , , indicating that is the stable strategy. This corresponds to local governments adopting a negative construction strategy. When , from Equations (7) and (8), we have , , which implies that is the stable strategy. This corresponds to local governments adopting a positive construction strategy.
3.2.2. Analysis of the Progressive Stability of RECS Centers for the Elderly
For RECS centers to reach an evolutionarily stable strategy, the following conditions must be met: and . When , it holds that , indicating that the system is in a stable state and the RECS centers’ strategy will not change over time. However, when , the two equilibrium points satisfying are and . Substituting these values into Equation (5) yields:
When , by analyzing Equations (9) and (10), it follows that , , indicating that is the stable strategy, meaning RECS centers adopt a positive transformation. Conversely, when , from Equations (9) and (10), we have , , which implies that is the stable strategy, corresponding to RECS centers adopting a negative transformation.
3.2.3. Analysis of the Progressive Stability of the Rural Elderly
For the rural elderly’s strategy choice to reach an evolutionarily stable state, the conditions and must be satisfied. When , it holds that , indicating the system is in a steady state and the elderly’s strategy will not change over time. However, when , the two equilibrium points satisfying are and . Substituting these values into Equation (6) yields:
When , based on Equations (11) and (12), it follows that , , indicating that z = 0 is the stable strategy, meaning the elderly choose negative participation. Conversely, when , from Equations (11) and (12), we have and . which implies that is the stable strategy, indicating that the elderly actively participate.
3.3. Equilibrium Points and Evolutionarily Stable Strategies in Tripartite Evolutionary Games
3.3.1. Evolutionary Game Equilibrium
Within the evolutionary game framework of rural smart senior care service systems, where all stakeholders exhibit bounded rationality, local governments, RECS centers, and the elderly are initially unable to determine optimal strategies or equilibrium points. Through iterative learning and repeated trial-and-error processes, the game participants gradually converge to a stable state, which corresponds to an effective Nash equilibrium. To facilitate the identification of this equilibrium point, the following parameters are defined:
From the above equations, the eight equilibrium points of the evolutionary game can be identified as follows: , , , , , , , .
These points delineate the boundary of the solution space for the tripartite dynamic evolutionary game in the rural smart home-based elderly care service system, expressed as .
3.3.2. Evolutionary Stabilization Strategies
According to Lyapunov’s stability theory, the stability of an equilibrium point can be assessed by examining the sign properties of the Jacobian matrix [35]. Specifically, if all eigenvalues of the Jacobian matrix possess negative real parts, the equilibrium point is asymptotically stable. As presented in Equation (14), the Jacobian matrix is constructed by computing the first-order partial derivatives of the replicator dynamic equations corresponding to the three parties in the rural smart home-based elderly care service system evolutionary game.
To determine whether the equilibrium point can serve as an evolutionarily stable strategy (ESS) and to establish its formation conditions, we analyze its Jacobian matrix, as shown in Equation (15). The eigenvalues of the Jacobian matrix at are: , , .
Therefore, the equilibrium point is evolutionarily stable if the following conditions hold simultaneously: , , and .
By substituting the remaining equilibrium points into the Jacobian matrix, we compute the corresponding eigenvalues and analyze their signs to determine the stability of each equilibrium point, as summarized in Table 3 and Table 4.

Table 3.
Eigenvalues of equilibrium points and evolutionary stability.

Table 4.
Asymptotic stability analysis of equilibrium points under different scenarios.
Scenario 1: , ,
When local governments adopt a proactive construction strategy, the net benefits derived from higher-level governmental rewards and enhanced social reputation—after accounting for the subsidies provided to RECS centers and elderly individuals—exceed the regulatory cost savings associated with a passive construction strategy. This indicates that the proactive approach yields superior overall economic returns. Similarly, under a positive transformation strategy, RECS centers’ net benefits, augmented by government subsidies, surpass those achieved under a negative transformation strategy, which are diminished by incurred penalties. This suggests that pursuing a positive transformation is economically more advantageous for RECS centers.
Furthermore, elderly individuals who actively participate in smart home-based elderly care services not only receive subsidies and benefits sufficient to offset their associated costs but also realize additional economic gains. This underscores the economic rationality and incentive compatibility of active engagement from the elderly population.
As shown in Table 4, all eigenvalues of the Jacobian matrix at the equilibrium point are negative, indicating that the strategic combination of proactive construction by the government, positive transformation by RECS centers, and active participation by the elderly constitutes an evolutionarily stable strategy (ESS) within the system. This finding provides theoretical support for the formulation and implementation of policies that encourage coordinated and proactive participation among all stakeholders.
Scenario 2: , ,
When local governments adopt a negative construction strategy, the resulting regulatory cost savings exceed the net benefits derived from higher-level government rewards and social reputation incentives after deducting the subsidies allocated to RECS centers and elderly individuals. This indicates that from local governments’ perspective, a passive construction strategy offers greater cost-effectiveness.
Nevertheless, RECS centers’ net benefits, when combined with subsidies under a positive transformation strategy, remain higher than the net benefits obtained under a negative transformation strategy, which are reduced by penalty costs. This demonstrates that even under a passive governmental stance, positive transformation remains economically advantageous for RECS centers.
Moreover, elderly individuals who actively participate in smart home-based elderly care services continue to receive subsidies and benefits that not only offset their expenditures but also yield surplus gains. This reaffirms the economic rationality and sustained attractiveness of active participation from the perspective of elderly users.
As presented in Table 4, all eigenvalues of the Jacobian matrix at the equilibrium point are negative, confirming that under Scenario 2, the strategic combination of negative construction by local governments, positive transformation by RECS centers, and active participation by elderly individuals constitutes an evolutionarily stable strategy (ESS). This finding suggests that system stability can be achieved even in the presence of passive government engagement, provided that other stakeholders maintain proactive strategic behaviors.
Scenario 3: , ,
When local governments adopt a proactive construction strategy, the net difference between the penalties imposed on RECS centers and the subsidies granted to elderly individuals exceeds the net savings derived from regulatory cost reductions under a negative construction strategy after deducting the penalties from higher-level governments and losses in social reputation. This indicates that from the local governments’ perspective, the proactive strategy incurs higher net costs than would be saved through a passive regulatory approach.
In parallel, RECS centers achieve higher net benefits under a negative transformation strategy, even after accounting for penalties, compared to the combined net benefits and subsidies available under a positive transformation strategy. This implies that within this scenario, the negative transformation strategy is economically preferable for RECS centers.
At the same time, elderly individuals who actively participate in smart home-based elderly care services continue to receive subsidies and benefits that exceed their participation costs, demonstrating the sustained economic appeal of positive engagement from their standpoint.
As indicated in Table 4, the eigenvalues of the Jacobian matrix at the equilibrium point are all negative, confirming that the strategic configuration involving proactive construction by local governments, negative transformation by RECS centers, and active participation by the elderly constitutes an evolutionarily stable strategy (ESS). This outcome highlights the potential for system stability even under strategic asymmetries among stakeholders.
Scenario 4: , ,
When local governments adopt a proactive construction strategy, the net benefits derived from higher-level government incentives and enhanced social reputation—after deducting the subsidies provided to RECS centers—exceed the regulatory cost savings attainable under a negative construction strategy. This reflects the overall economic advantage of an active governmental approach.
Simultaneously, the subsidies received by RECS centers outweigh the marginal gains from operational cost savings under a negative transformation strategy after accounting for penalties. This reinforces the economic rationale for RECS centers to pursue a positive transformation strategy.
In contrast, elderly individuals who opt not to participate in smart home-based elderly care services avoid participation costs that would surpass the total value of subsidies and benefits otherwise received. Under this scenario, non-participation emerges as the economically rational choice for the elderly.
As shown in Table 4, the Jacobian matrix at the equilibrium point exhibits exclusively negative eigenvalues, confirming that the strategic combination of proactive construction by local governments, positive transformation by RECS centers, and non-participation by elderly individuals constitutes an evolutionarily stable strategy (ESS) for the system. This result underscores the dynamic stability of this strategic configuration, even in the presence of divergent stakeholder incentives.
4. Simulation Analysis
To verify the validity and rationality of the evolutionary game model for the rural smart elderly care service system, we drew upon relevant literature [29,30,31,32] and incorporates empirical cases and data related to rural elderly care services to inform parameter assignments. Numerical simulations were then conducted using MATLAB 2020b under various scenarios to analyze the influence of key parameter values on the evolutionary dynamics of stakeholders’ behavioral strategies.
4.1. Impact of Changes on Evolutionary Stability of Initial Strategy
4.1.1. Scenario 1: Numerical Simulation
Assigning Parameter Set 1 values of , , , , , , , , , , and , , satisfies the conditions specified in Scenario 1. The evolutionary process was simulated over 50 iterations, with the results depicted in Figure 2, illustrating the dynamic evolution of strategy selection over time. Furthermore, under this parameter configuration, the initial willingness levels of the three stakeholders were systematically varied. Each initial willingness variable was iterated from 0.1 to 0.9 with increments of 0.2. This parameter sweep facilitated an in-depth analysis of the evolutionary trajectories of the tripartite game strategies under varying initial willingness combinations. The resulting evolutionary strategy graphs reveal how different initial conditions affect the strategic evolution of all participants over time.
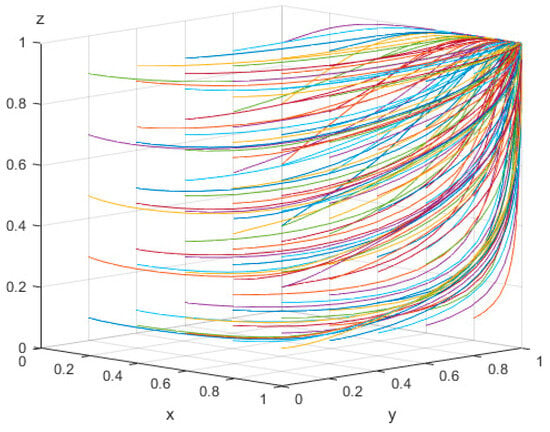
Figure 2.
Results of 50 iterations of evolution with Parameter Set 1.
As illustrated in Figure 3, the point represent the evolutionary equilibrium, signifying the existence of an evolutionarily stable strategy (ESS) characterized by the strategic combination of proactive construction by local governments, positive transformation by RECS centers, and active participation by elderly individuals.
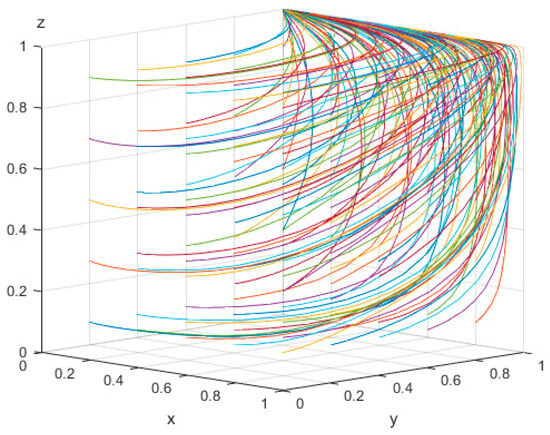
Figure 3.
Results of 50 iterations of evolution with Parameter Set 2.
This outcome indicates that when the payoffs for all three stakeholders exceed their respective costs, each actor is incentivized to adopt a proactive or positive strategy. Specifically, local governments are motivated to support and invest in smart elderly care infrastructure, RECS centers are encouraged to enhance service quality through positive transformation, and the elderly are willing to engage actively with the service model.
4.1.2. Scenario 2: Numerical Simulation
Assigning Parameter Set 2 values of , , , , , , , , , , , , satisfies the conditions of Scenario 2, the evolutionary process that was simulated over 50 iterations. The resulting dynamics of strategy selection are presented in Figure 3, illustrating the temporal evolution of the strategic behaviors of all stakeholders. The parameters , , and each vary within the range of 0.1 to 0.9, with incremental steps of 0.2.
As illustrated in Figure 4, under the conditions specified by Parameter Set 2, the system converges to an evolutionary equilibrium at point . This equilibrium corresponds to an evolutionarily stable strategy (ESS) characterized by negative construction by local governments, positive transformation by RECS centers, and active participation by elderly individuals, consistent with the findings of Scenario 2.
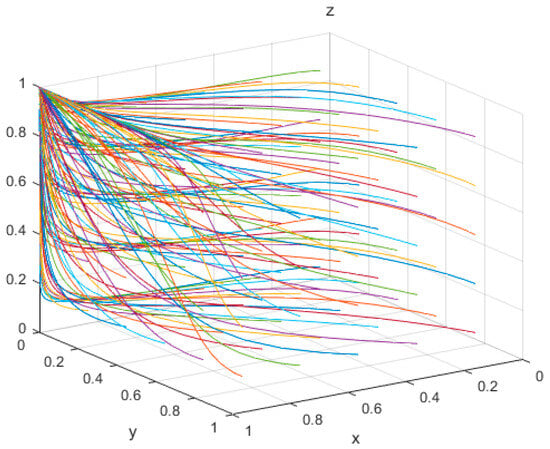
Figure 4.
Results of 50 iterations of evolution with Parameter Set 3.
This result highlights the critical role of higher-level governments and public stakeholders in adopting a forward-looking perspective and implementing targeted support measures to reinforce local governments’ engagement in promoting the development of rural smart home-based elderly care systems. By providing adequate recognition, performance-based rewards, and institutional incentives, it is possible to stimulate innovation, enhance governance effectiveness, and sustain the long-term motivation of local governments in this essential public welfare endeavor.
4.1.3. Scenario 3: Numerical Simulation
Assigning Parameter Set 3 values of , , , , , , , , , , , , satisfies the conditions of Scenario 3. Numerical simulations conducted over 50 iterations are presented in Figure 4, which depicts the dynamic evolution of strategy selection among the stakeholders over time. The parameters , , and each vary within the range of 0.1 to 0.9, with incremental steps of 0.2.
As illustrated in Figure 4, under the conditions specified by Parameter Set 3, the system converges to an evolutionary equilibrium at point . This equilibrium reflects an evolutionarily stable strategy (ESS) wherein local governments adopt a proactive construction strategy, RECS centers choose a negative transformation strategy, and the elderly actively participate in smart home-based elderly care services.
This outcome suggests that when the cost savings associated with a negative transformation exceed the penalties incurred and surpass the subsidies provided for positive transformation, RECS centers are economically motivated to adopt a negative transformation strategy to maximize their own utility.
Therefore, to shift RECS centers’ strategic choice, increasing the rewards for high-quality service delivery and intensifying penalties for substandard or non-compliant service behaviors may reshape the cost–benefit calculus. Such policy adjustments could reduce the relative attractiveness of negative transformation and promote a transition toward more desirable service outcomes.
4.1.4. Scenario 4: Numerical Simulation
Assigning Parameter Set 4 values of , , , , , , , , , , , , satisfies the conditions of Scenario 4. The evolutionary process was simulated over 50 iterations, and the results are presented in Figure 5, depicting the dynamic evolution of strategy selection among the stakeholders over time. The parameters , , and each vary within the range of 0.1 to 0.9, with incremental steps of 0.2.
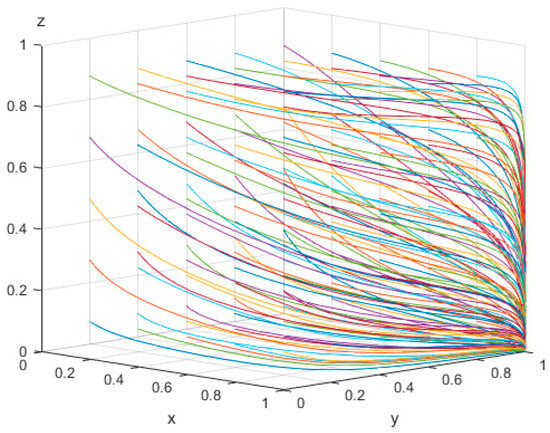
Figure 5.
Results of 50 iterations of evolution with Parameter Set 4.
As shown in Figure 5, under the conditions defined by Parameter Set 4, the system converges to an evolutionary equilibrium at point . This equilibrium corresponds to an evolutionarily stable strategy (ESS) characterized by proactive construction by local governments, positive transformation by RECS centers, and non-participation by rural elderly.
This outcome indicates that when the costs incurred by the elderly exceed the total value of benefits and subsidies received, their willingness to actively participate in smart home-based elderly care services declines. The economic disincentive discourages engagement, even in the presence of institutional and technological improvements on the supply side.
To address this challenge, it is essential for local governments to strengthen policy support and enhance financial incentives aimed directly at the elderly population. Additionally, efforts should be made to improve service transparency and credibility, thereby fostering greater consumer trust and broader acceptance of the smart elderly care service model.
4.2. Influence of the Values of the Main Parameters on the Evolution of Subjects’ Behavior
In the three-party evolutionary game, the decision-making behavior of each participant is influenced and constrained by multiple factors, including the strategic choices of other players. Based on Parameter Set 1, further sensitivity analysis is conducted to examine the impact of key parameters—, , , , , , , , , —on the evolutionary dynamics and outcomes. When isolating the effect of any specific parameter, all other parameters are held constant to ensure an unbiased assessment of its influence.
To investigate the impact of regulatory costs borne by local governments during positive construction, simulations were performed with values set at 0, 1.5, and 3. The resulting evolutionary trajectories of the replicator dynamic equations are depicted in Figure 6. The simulation results demonstrate that an increase in regulatory costs reduces the likelihood that the local government will opt for positive development. Concurrently, the pace at which RECS centers and elderly individuals reach evolutionary equilibrium is significantly accelerated.
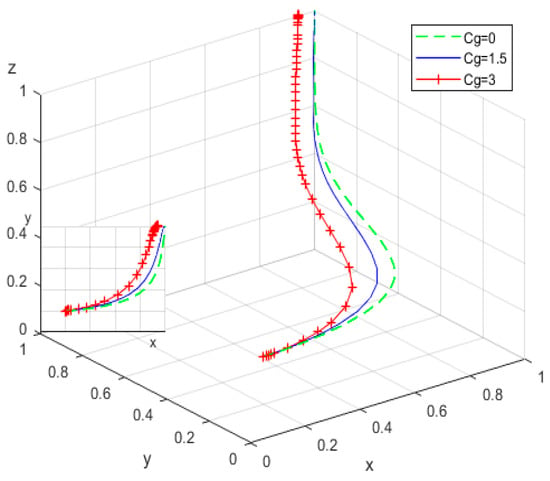
Figure 6.
Influence of regulatory costs on local government input.
This phenomenon can be explained from two perspectives, as follows.
(a) Resource allocation trade-off: Elevated regulatory costs may constrain the government’s budget for other public services, potentially undermining the overall efficiency and quality of public service delivery. This fiscal pressure compels the government to adopt more rational and selective strategies regarding its commitment to rural smart elderly care services.
(b) Signaling and trust enhancement: Higher regulatory expenditure can function as both a tangible demonstration of commitment and a positive signal to external stakeholders. Such signaling reduces risks and uncertainties associated with service implementation, fostering greater societal confidence. This in turn promotes increased investment by RECS centers and greater participation willingness among the elderly.
Therefore, local governments should establish robust regulatory frameworks, enhance oversight efficiency, and manage regulatory costs prudently. Such measures will prevent resource wastage, ensure the sustainable development of rural smart elderly care services, and ultimately improve the well-being and satisfaction of the elderly population.
To explore the impact of rewards and reputational incentives () received by local governments due to the positive transformation of RECS centers, simulations were conducted by assigning . Additionally, to examine the effect of penalties and reputational losses () incurred by local governments when RECS centers adopt negative transformation, was set to 0, 5, and 10. The evolutionary trajectories of the replicator dynamic equations were analyzed, with the results illustrated in Figure 7 and Figure 8.
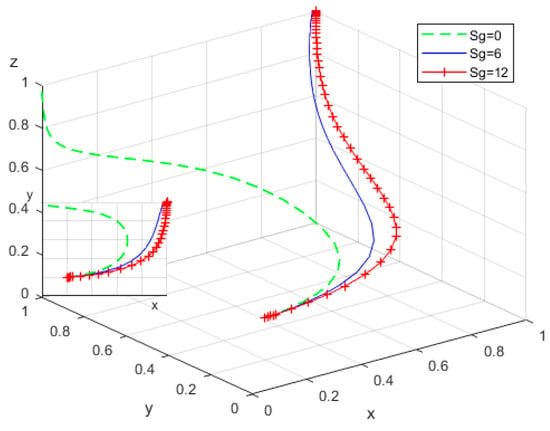
Figure 7.
Influence of rewards received by the government.
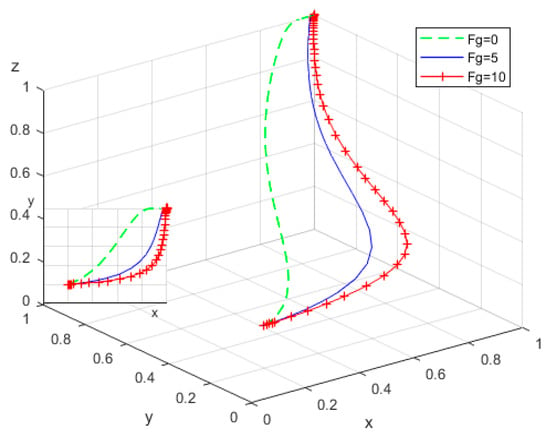
Figure 8.
Influence of penalties borne by the government.
The findings indicate that as both and increase, the probability of local governments choosing the positive construction strategy approaches 1 more rapidly. Notably, the convergence speed under increased is significantly faster than that under increased . This suggests that both rewards and penalties from higher authorities and public opinion incentivize local governments to actively promote smart home-based elderly care systems and strengthen their oversight of RECS centers. However, compared to penalties and reputational losses, rewards and reputational incentives from higher authorities exert a greater influence on local government decision-making. This disparity stems from the fact that penalties and reputational losses tend to produce negative psychological effects, whereas rewards enhance motivation and proactiveness, fostering policy sustainability and collaboration among multiple stakeholders.
It is important to note that when , the probability of local governments opting for positive construction sharply declines to zero. In the initial phase, local governments may engage in positive construction driven by motivations such as improving public welfare, complying with national policies, and enhancing local reputation. However, if these efforts do not garner sufficient public recognition or generate significant social benefits, local governments may adjust their strategies and redirect resources elsewhere.
To mitigate this issue, higher authorities should implement scientifically designed incentive mechanisms, such as establishing dedicated reward funds and performance-linked reputational evaluation systems. A positive incentive framework should be employed to encourage local governments’ active participation. Furthermore, rather than emphasizing short-term investments, priority should be given to long-term social benefits to stimulate intrinsic motivation, accelerate the comprehensive development of rural smart elderly care systems, and promote their continuous optimization.
To investigate the impact of increasing the cost differential in digital operation () between positive and negative transformation strategies of RECS centers on the evolution of participant behaviors, was held constant while was assigned values of 2, 3, and 4. The evolutionary trajectories of the replicator dynamic equations under these conditions are presented in Figure 9.
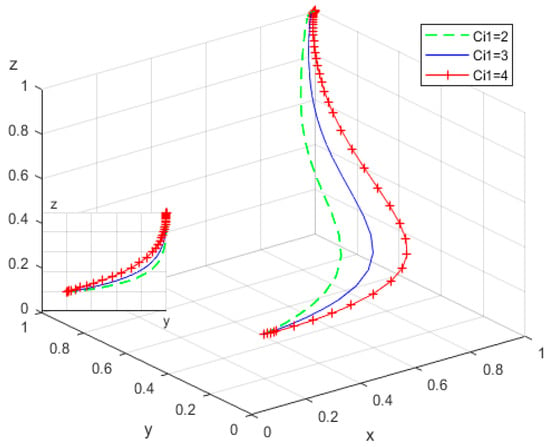
Figure 9.
Influence of differences in the construction costs of digital operation invested by RECS centers.
As shown in Figure 9, when , the probability of RECS centers adopting a positive transformation strategy increases at the slowest rate. This suggests that as the operational costs associated with providing smart elderly care services rise, the willingness of RECS centers to collaborate with local governments on service transformation diminishes. Conversely, with an increase in , the probability that both local governments and elderly individuals select positive strategies rises more rapidly.
Generally, the operational costs of RECS centers—particularly expenditures on human and material resources—constitute the foundation for enhancing service quality and standards. Substantial investment in operational costs often corresponds with improved service management and the adoption of innovative technologies, which significantly elevate service quality and efficiency, thereby increasing the appeal to elderly consumers. Therefore, RECS centers must balance the control of operational costs with continuous exploration of innovative service models. By delivering high-quality services, they can stimulate the elderly care market, promote greater consumer engagement, and ultimately achieve sustainable development alongside improved well-being for the elderly population.
To examine the impact of subsidies () received by RECS centers during positive transformation under active government construction, simulations were conducted by assigning . The resulting evolutionary trajectories of the replicator dynamic equations are depicted in Figure 10.
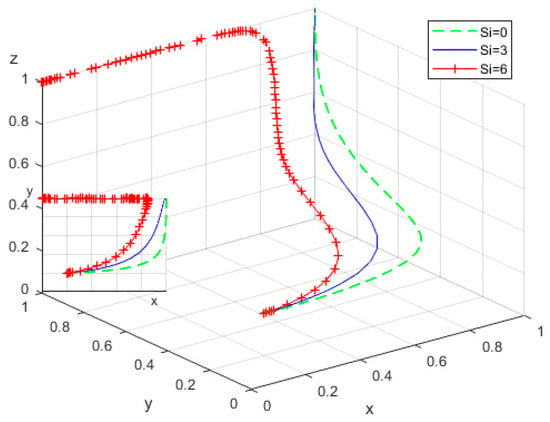
Figure 10.
Influence of subsidies received by RECS centers.
As increases, the probability of local governments choosing positive construction decreases, while the evolutionary rate of RECS centers toward positive transformation accelerates. When , despite the absence of direct financial subsidies, the government’s active construction fosters favorable conditions for RECS centers’ transformation through policy guidance, infrastructure development, and the cultivation of a supportive environment. Consequently, RECS centers opt for positive transformation by considering long-term development, balancing social responsibility with economic benefits.
When , local governments initially tend toward a positive construction strategy (approaching 1), but subsequently sharply shift toward a negative strategy (approaching 0). This phenomenon suggests that while increased subsidies provide substantial financial support to enhance RECS centers’ willingness and capacity to transform, they simultaneously impose greater fiscal pressure on the government. If the subsidy policy sufficiently incentivizes transformation or if the transformation outcomes fail to meet expectations, the government may consider reducing subsidy levels or adjusting the subsidy approach. Such policy shifts can indirectly affect local governments’ propensity to pursue positive construction.
Therefore, it is crucial for the government to establish a flexible subsidy adjustment mechanism aligned with RECS centers’ transformation progress and local fiscal conditions. This mechanism would ensure that subsidy funds are allocated efficiently, promoting the effective construction and operation of smart elderly care services and thereby enhancing fund utilization efficiency while preventing resource waste and misuse.
To investigate the impact of penalties () imposed on RECS centers for negative transformation during active government construction, simulations were performed by assigning . The evolutionary trajectories of the replicator dynamic equations under these conditions are presented in Figure 11.
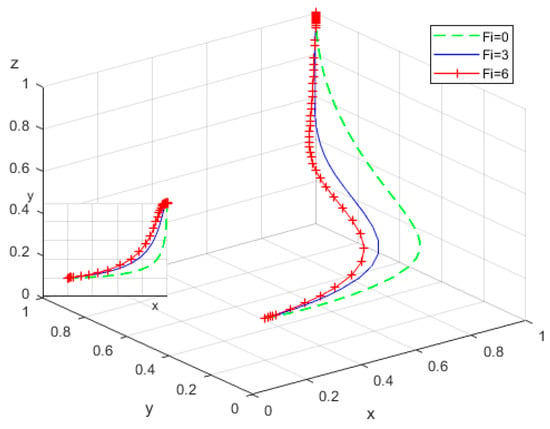
Figure 11.
Influence of penalties borne by RECS centers.
The increase in penalties functions as a negative incentive, compelling RECS centers to carefully weigh the costs and benefits associated with transformation. Consequently, the evolutionary convergence rate of RECS centers’ strategy accelerates. In this context, elderly individuals also demonstrate increased engagement in supervising and providing feedback on the services, actively voicing their opinions and needs through complaints, evaluations, and other communication channels. This participatory behavior further motivates RECS centers to prioritize the demands and feedback of the elderly, thereby promoting a more rapid shift toward positive transformation.
Therefore, it is imperative for local governments to strengthen policy enforcement and transparency, establish comprehensive and diversified supervision and feedback mechanisms, and prevent RECS centers from exploiting policy loopholes for rent-seeking. Such measures will encourage RECS centers to explore and implement smart elderly care service models and solutions that are tailored to the specific needs of its local community.
To investigate the impact of participation costs () incurred by rural elderly in actively engaging with smart home-based elderly care services, simulations were conducted by assigning . The evolutionary trajectories of the replicator dynamic equations under these conditions are depicted in Figure 12.
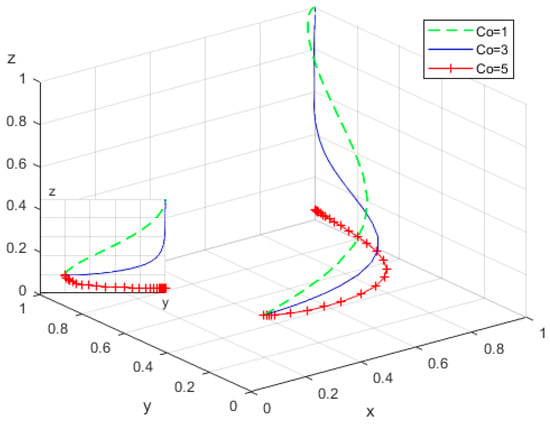
Figure 12.
Influence of the cost of positive participation of the elderly.
As increases, the evolutionary rate of elderly individuals’ active participation gradually declines. When the cost reaches a certain threshold, elderly individuals are more likely to adopt a negative participation strategy. For economically disadvantaged elderly groups, the financial burden of service costs may exceed their capacity, prompting withdrawal from participation. Furthermore, rural elderly generally exhibit weaker learning and adaptation abilities: increased time and cognitive costs associated with learning new technologies may lead to feelings of being overwhelmed and a negative attitude toward participation.
Consequently, it is essential for local governments to implement targeted subsidy policies that enhance the economic purchasing power of elderly individuals, thereby ensuring their demand for smart home-based elderly care services is effectively met. Simultaneously, RECS centers should adopt scientifically grounded and reasonable pricing strategies that balance service value with the economic affordability of the elderly population. Moreover, organizing specialized training programs aimed at reducing learning barriers and costs will facilitate elderly individuals’ mastery of smart elderly care technologies. These measures will promote widespread adoption and integration of technology within elderly care services, contributing to the sustainable development of the rural smart elderly care system.
To examine the impact of the utility difference () gained by elderly individuals from actively participating in smart home-based elderly care services during RECS centers’ active and passive transformation phases, simulations were conducted by fixing Eo2 and assigning values of . The evolutionary trajectories of the replicator dynamic equations under these conditions are illustrated in Figure 13.
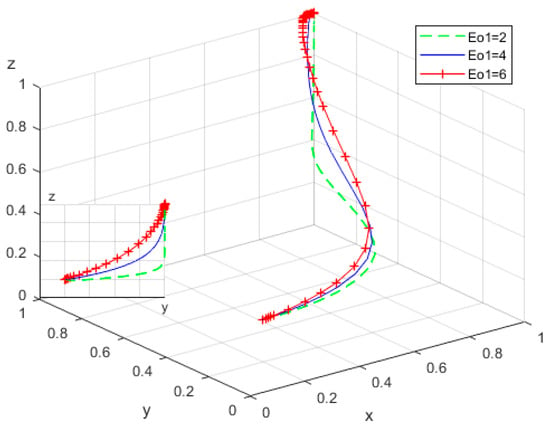
Figure 13.
Influence of poor utility received by the elderly.
Given the bounded rationality of elderly individuals, a larger utility difference () corresponds to a faster convergence to a stable participation state. When the utility difference is small, the evolutionary rate initially progresses slowly, but accelerates sharply thereafter. This pattern arises because a significant utility difference allows elderly individuals to distinctly perceive the convenience, efficiency, and personalized benefits of smart elderly care services, thereby markedly improving their quality of life. This pronounced contrast effect enhances their willingness to actively participate in the services.
Conversely, when the utility difference is minimal, elderly individuals may not fully recognize the advantages of smart elderly care services due to factors such as information asymmetry or cognitive inertia. As RECS centers continue to transform and gain wider visibility, elderly individuals gradually experience and acknowledge the benefits of these services, leading to shifts in their initial perceptions and behavior patterns.
Accordingly, local governments should designate actively transforming rural elderly care service centers as demonstration models, showcasing the advantages of smart elderly care services through practical case studies to encourage elderly participation. Furthermore, attention should be paid to the needs and feedback of elderly individuals, enhancing service experience and satisfaction by integrating technological empowerment with humanistic care.
To investigate the impact of subsidies () received by rural elderly for actively participating in smart home-based elderly care services under conditions of positive government construction promotion, simulations were conducted by assigning values of . The resulting evolutionary trajectories of the replicator dynamic equations are depicted in Figure 14.
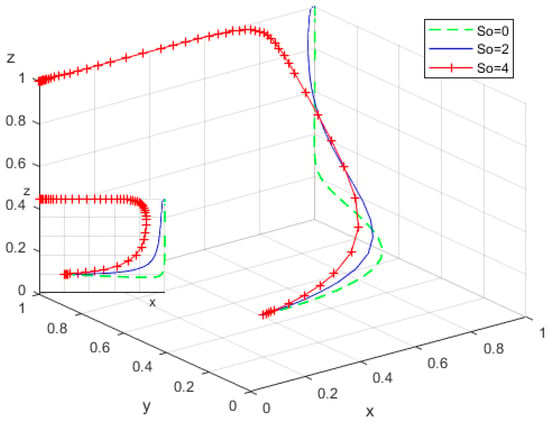
Figure 14.
Influence of subsidies received by the elderly.
When the subsidy level is relatively low, the willingness of local governments to actively engage in construction gradually increases. However, at a higher subsidy level (), local governments tend to adopt a negative construction strategy, indicating that excessive subsidy growth exacerbates fiscal pressure on local governments. Additionally, increased subsidies significantly enhance elderly individuals’ willingness to participate. In the absence of subsidies, the probability of elderly individuals’ active participation markedly declines. Nonetheless, once the government strategy stabilizes, elderly individuals rapidly shift toward active participation.
These findings highlight the direct role of economic incentives in alleviating the burden of elderly care. As government efforts deepen and service quality improves, elderly individuals experience the convenience and effectiveness of smart elderly care services firsthand. This positive experience fosters trust and reliance on such services, encouraging active participation even in the absence of subsidies.
Therefore, local governments should develop long-term, rational, and sustainable subsidy mechanisms that prevent overreliance on financial incentives. Additionally, policies should promote mutual assistance among rural elderly populations to strengthen social identity and belonging, thereby cultivating a supportive social environment conducive to the widespread adoption of smart elderly care services.
5. Conclusions and Recommendation
In response to the intensifying challenge of rural population aging in China, this study constructed an evolutionary game model involving local governments, RECS centers, and rural elderly to examine the dynamic behavioral interactions among these key stakeholders. Through theoretical modeling and simulation analysis, we identified the theoretically optimal evolutionary outcome as a coordinated scenario in which local governments actively promote construction, RECS centers pursue proactive transformation, and elderly individuals engage positively in smart home-based elderly care services. The stability of this equilibrium is found to be influenced by a variety of factors, including the costs of digital infrastructure, the scale and structure of subsidies, the design of incentive and penalty mechanisms, and stakeholders’ perceived utility from participation.
(1) Local governments: The strategy choices of local governments are highly sensitive to incentive mechanisms. Compared with punitive measures and reputational losses, reward mechanisms—especially those offered by higher-level authorities—are more effective in encouraging proactive government engagement. In the early stages, governments may initiate construction efforts due to social responsibility or policy directives. However, sustained and effective promotion relies on public support and the realization of social value. While the regulatory burden may reduce the probability of proactive participation, it also strengthens the implicit governance effects by fostering trust between RECS centers and the elderly. Therefore, local governments must play a guiding role through supportive policy tools that stimulate the transformation efforts of RECS centers and cultivate trust among the elderly. Financial subsidies should be balanced to prevent excessive fiscal stress, and penalty mechanisms should be strategically implemented to reduce rent-seeking behaviors and improve service quality.
(2) RECS centers: The strategic behavior of RECS centers reflects a dual influence of operational cost constraints and transformation responsiveness. When facing initiatives from local governments, RECS centers tend to act passively unless operational costs remain within manageable limits. Investment in digital operations not only reflects a demand for refined service provision but also serves as a key factor in attracting elderly participation. Although government subsidies enhance the willingness of RECS centers to collaborate, overreliance on these incentives may erode their intrinsic motivation for independent innovation. The extent and depth of transformation—particularly when driven by technological empowerment and service innovation—serve as mediating forces that influence elderly individuals’ perceptions and decisions, thereby reinforcing behavioral shifts toward active participation.
(3) Rural elderly: The decision-making processes of elderly individuals are shaped by multidimensional constraints related to participation costs and utility perceptions. Due to age-related functional decline, economic disparities, and educational limitations, elderly individuals often exhibit high sensitivity to cost-related barriers. Excessive financial or cognitive burdens may lead to passive or non-participatory behavior. Government subsidies play a critical role in reducing economic barriers, while improvements in service quality and perceived benefits are key to fostering sustained engagement. Furthermore, as regulatory and feedback mechanisms improve, elderly individuals evolve from passive recipients to active participants in monitoring and co-governance, which in turn influences system-wide stability.
Based on the above conclusions, the following policy recommendations are proposed to advance the development of rural digital elderly care services.
(1) At the local government level: Local authorities should reinforce their leadership roles by establishing a collaborative governance framework that involves multiple stakeholders. A tripartite coordination mechanism among governments, RECS centers, and the elderly should be developed, incorporating regular joint meetings and transparent information-sharing platforms to improve communication efficiency, policy clarity, and mutual trust. Incentive and constraint systems should be optimized by complementing fiscal and tax incentives with symbolic rewards (e.g., honorary titles) and establishing rigorous accountability mechanisms to handle service failures. Administrative processes should be streamlined and digital oversight systems strengthened to reduce regulatory costs. Additionally, targeted and performance-based subsidies should be provided to RECS centers that demonstrate transformation progress, thereby fostering innovation while minimizing dependency.
(2) At the RECS center level: RECS centers should establish a cost–benefit balancing framework and develop a robust service innovation system. Regarding cost management, centers must assess the affordability of rural elderly, implementing tiered pricing and diversified service packages to ensure accessibility and financial sustainability. In terms of innovation, smart technologies should be adopted to optimize service delivery, with new models such as “internet + healthcare” and “smart nursing” explored. To address digital literacy gaps, RECS centers should design elderly-friendly digital interfaces and provide targeted digital literacy training. Furthermore, internal service quality assurance systems—including regular audits, data transparency, and external supervision—should be institutionalized to ensure continuous improvement and accountability.
(3) At the elderly level: Given the physiological and cognitive diversity of the rural elderly population, both governmental and societal efforts are necessary to promote inclusive digital access. This includes the development of age-adapted user interfaces, hands-on training programs, and public education campaigns to reduce cognitive barriers and promote digital acceptance. A responsive feedback system with multiple reporting channels should be established to empower elderly individuals as active contributors to service oversight. For those in remote or economically disadvantaged regions, a bottom-line guarantee mechanism must be implemented to ensure equitable access to digital care services. These measures will facilitate a more inclusive sharing of digital dividends and contribute to the long-term goals of rural revitalization and social equity.
This study innovatively applied evolutionary game theory within a multi-agent collaborative governance framework for rural smart elderly care services, focusing on the dynamic interactions among local governments, rural elderly care centers, and elderly individuals. It broadens the research scope beyond the traditional emphasis on urban elderly care or single-agent behaviors, addressing a significant gap in multi-agent game studies in the context of rural smart elderly care. Methodologically, the study developed an evolutionary game model specifically tailored to rural settings, overcoming the limitations inherent in conventional qualitative approaches by elucidating the evolutionary trajectories and stability of agents’ strategies. This enhances both the theoretical rigor and empirical robustness of the framework. By incorporating assumptions such as bounded rationality, multiple game interactions, and adaptive learning, the research deepens the application of evolutionary game theory in public service domains, rendering the model more reflective of the complex realities of smart elderly care systems. Furthermore, based on the game outcomes, the study proposes digital empowerment optimization pathways, offering theoretical foundations and policy recommendations to support the sustainable development of rural smart elderly care.
This study has several limitations that should be addressed in future research. Firstly, the model assumes homogeneity within each stakeholder group, which simplifies the complex realities where significant heterogeneity exists—for example, differences in economic status and digital literacy among the elderly, as well as varying capacities and resources across RECS centers. Incorporating such intragroup differences would enhance the model’s realism and explanatory power. Secondly, future research could incorporate the impact of dynamic subsidy mechanisms on system evolution.
Author Contributions
Z.W.: methodology, software, writing—original draft preparation. M.M.: resources, validation, writing—review and editing. J.X.: data curation, investigation, methodology, validation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Scientific Research Fund of the Hunan Provincial Education Department of China (Excellent Young Program, grant 24B1106).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviation is used in this manuscript:
| RECS | rural elderly care service |
References
- Guillemot, J.R.; Zhang, X.; Warner, M.E. Population Aging and Decline Will Happen Sooner than We Think. Soc. Sci. 2024, 13, 190. [Google Scholar] [CrossRef]
- United Nations. World Population Prospects 2024. Available online: https://www.un.org/development/desa/pd/world-population-prospects-2024 (accessed on 11 March 2024).
- Wang, Y.; Zeng, H.; Lv, F.; Wang, J. Analysis of Demand and Influencing Factors for Smart Senior Care among Older Adults in Underdeveloped Regions of Western China: A Case Study of Lanzhou. Front. Public. Health 2024, 12, 1337584. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Hao, Y.; Ma, J. Family Income Level, Income Structure, and Dietary Imbalance of Elderly Households in Rural China. Foods 2024, 13, 190. [Google Scholar] [CrossRef] [PubMed]
- Morais Campos, H.L.; De Leon, E.B.; Merllin Batista De Souza, I.; Quialheiro, A.; Araújo de Oliveira, E.R. Cognition, Physical Function, and Life Purpose in the Rural Elderly Population: A Systematic Review Protocol. PLoS ONE 2024, 19, e0291699. [Google Scholar] [CrossRef]
- Edwards, K.J.; Jones, R.B.; Shenton, D.; Page, T.; Maramba, I.; Warren, A.; Fraser, F.; Križaj, T.; Coombe, T.; Cowls, H.; et al. The Use of Smart Speakers in Care Home Residents: Implementation Study. J. Med. Internet Res. 2021, 23, e26767. [Google Scholar] [CrossRef]
- Jeong, H.N.; Chang, S.J.; Kim, S. Associations with Smartphone Usage and Life Satisfaction among Older Adults: Mediating Roles of Depressive Symptoms and Cognitive Function. Geriatr. Nurs. 2024, 55, 168–175. [Google Scholar] [CrossRef]
- Huang, Q.; Li, Y.; Wu, X.; Ge, S.; Qu, Z.; Wang, A.; Tang, X. The Willingness and Influencing Factors to Choose Smart Senior Care among Old Adults in China. BMC Geriatr. 2022, 22, 967. [Google Scholar] [CrossRef]
- Kong, D.; Liu, S.; Hong, Y.; Chen, K.; Luo, Y. Perspectives on the Popularization of Smart Senior Care to Meet the Demands of Older Adults Living Alone in Communities of Southwest China: A Qualitative Study. Front. Public. Health 2023, 11, 1094745. [Google Scholar] [CrossRef]
- Mao, Q.; Mao, Y.; Sun, Q.; Xu, L. Smart Transition Pathways and Development Incentive Mechanism of China’s Smart Community Elderly Care Industry under Market Dominance: Considering a Multi-Subjective Behavior Game. PLoS ONE 2024, 19, e0297696. [Google Scholar] [CrossRef]
- Chen, H.; Hagedorn, A.; An, N. The Development of Smart Eldercare in China. Lancet Reg. Health—West. Pac. 2023, 35, 100547. [Google Scholar] [CrossRef]
- Cohen, S.A.; Greaney, M.L. Aging in Rural Communities. Curr. Epidemiol. Rep. 2022, 10, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Boobalan, J.; Malleswaran, M. A Novel and Customizable Framework for IoT Based Smart Home Nursing for Elderly Care. In Emerging Trends in Computing and Expert Technology; Hemanth, D.J., Kumar, V.D.A., Malathi, S., Castillo, O., Patrut, B., Eds.; Lecture Notes on Data Engineering and Communications Technologies; Springer International Publishing: Cham, Switzerland, 2020; Volume 35, pp. 27–38. ISBN 978-3-030-32149-9. [Google Scholar]
- Hu, R.; Linner, T.; Trummer, J.; Güttler, J.; Kabouteh, A.; Langosch, K.; Bock, T. Developing a Smart Home Solution Based on Personalized Intelligent Interior Units to Promote Activity and Customized Healthcare for Aging Society. Popul. Ageing 2020, 13, 257–280. [Google Scholar] [CrossRef]
- Hong, S.; Jang, E.; Cho, J.; Lee, J.; Rhee, J.H.; Lee, H.; Lee, M.; Cha, S.H.; Koo, C.; Baik, O.M. A Living Lab to Develop Smart Home Services for the Residential Welfare of Older Adults. Technol. Soc. 2024, 77, 102577. [Google Scholar] [CrossRef]
- Jo, T.H.; Ma, J.H.; Cha, S.H. Elderly Perception on the Internet of Things-Based Integrated Smart-Home System. Sensors 2021, 21, 1284. [Google Scholar] [CrossRef]
- Creaney, R.; Reid, L.; Currie, M. The Contribution of Healthcare Smart Homes to Older Peoples’ Wellbeing: A New Conceptual Framework. Wellbeing. Space Soc. 2021, 2, 100031. [Google Scholar] [CrossRef]
- Zhu, J.; Shi, K.; Yang, C.; Niu, Y.; Zeng, Y.; Zhang, N.; Liu, T.; Chu, C.H. Ethical Issues of Smart Home-Based Elderly Care: A Scoping Review. J. Nurs. Manag. 2022, 30, 3686–3699. [Google Scholar] [CrossRef] [PubMed]
- Pirzada, P.; Wilde, A.; Doherty, G.H.; Harris-Birtill, D. Ethics and Acceptance of Smart Homes for Older Adults. Inform. Health Soc. Care 2022, 47, 10–37. [Google Scholar] [CrossRef]
- Bhalotia, N.; Kumar, M.; Alameen, A.; Mohapatra, H.; Kolhar, M. A Helping Hand to the Elderly: Securing Their Freedom through the HAIE Framework. Appl. Sci. 2023, 13, 6797. [Google Scholar] [CrossRef]
- Liao, X.; Li, Y.; Li, Y. Research on the Optimization Path of Smart Endowment Industry Based on Industry Chain Integration Theory. China Soft Sci. 2019, 4, 50–56. [Google Scholar]
- Sui, D.; Liu, X. The Problem and Paths of Home Pension Based on Artificial Intelligence Technology. J. Xi’an Univ. Financ. Econ. 2020, 33, 27–36. [Google Scholar]
- Liu, X.; Xu, Y. Research on the Growth Path of the Elderly Care Industry Enabled by Digital Economy. Popul. Econ. 2024, 4, 45–58. [Google Scholar]
- Li, R. Path exploration for solving rural elderly care problems in the new era. People’s Trib. 2022, 5, 36–39. [Google Scholar]
- Yin, Q. Investigation and Research on Media Literacy of Rural Elderly Groups under the Background of Intelligent Pension. Health Vocat. Educ. 2023, 41, 118–121. [Google Scholar]
- Li, Q.; Meng, R. The intrinsic mechanism and micro-evidence of digital backfeeding driving the participation of rural elderly in smart home-based elderly care. Electron. Gov. 2024, 3, 105–116. [Google Scholar]
- Ren, C.; Zhou, X.; Wang, C.; Guo, Y.; Diao, Y.; Shen, S.; Reis, S.; Li, W.; Xu, J.; Gu, B. Ageing Threatens Sustainability of Smallholder Farming in China. Nature 2023, 616, 96–103. [Google Scholar] [CrossRef]
- Han, J.; Li, S.; Wang, J. Research on the Long-term Mechanism of Responsible Innovation from the Perspective of Multi-agent Behavior Evolution. Manag. Rev. 2024, 36, 155–167. [Google Scholar]
- Ma, Y.; Wen, Z.; Yi, D. Research on Elderly Care Service Supervision based on System Dynamics from the Perspective of Multi-agent. Northwest Popul. J. 2020, 41, 88–101. [Google Scholar]
- Yao, C.; Luo, Z.; Yang, Y.; Ping, Y. Analysis on the Evolution Game of Rural Pension Mechanism in Beijing-Tianjin-Hebei Region. J. Syst. Sci. 2020, 28, 100–104. [Google Scholar]
- Yue, X.; Lin, Y. The Effectiveness of the Feedback from Elderly Users in Elderly Care Services: An Evolutionary Game Analysis. J. Jiangxi Univ. Financ. Econ. 2022, 04, 71–82. [Google Scholar]
- Chen, J.; Huang, M.; Lü, Q. Evolutionary Game Analysis of Smart Elderly Service Ecosystems in a Digital Context. Complex Systems and Complexity Science. Available online: http://kns.cnki.net/kcms/detail/37.1402.N.20240130.1756.004.html (accessed on 30 January 2024).
- He, J.; Luo, X.; Zhang, Z.; Yu, Y. Strategic Analysis of Participants in the Provision of Elderly Care Services-an Evolutionary Game Perspective. Int. J. Environ. Res. Public. Health 2021, 18, 8595. [Google Scholar] [CrossRef]
- Xiao, M.; Liu, H. The Impact Mechanism of Government Regulation on the Operation of Smart Health Senior Care Service Platform: A Perspective from Evolutionary Game Theory. Int. J. Health Policy Manag. 2025, 14, 8646. [Google Scholar] [CrossRef]
- Lyapunov, A.M. The general problem of the stability of motion. Int. J. Control. 1992, 55, 531–534. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).