Robustness Measurement of Comprehensive Evaluation Model Based on the Intraclass Correlation Coefficient
Abstract
1. Introduction
- Error-based metrics: These metrics directly reflect the degree of deviation between the model’s predicted values and the true values [8], but they are sensitive to outliers. A commonly used metric in this category is the Root Mean Square Error (RMSE).
- Ranking consistency metrics: These metrics are effective in assessing the consistency of ranking results, but they are limited in their ability to capture changes in the actual numerical scores. A widely used method in this category is Kendall’s W [9].
- Result consistency metrics: These metrics evaluate whether the model’s overall scores remain stable under different conditions—such as variable substitution [10] or sample adjustments [11]. However, they are often influenced by the subjectivity of perturbation settings and lack universality and comparability.
2. Methods
2.1. Traditional Robustness Indicators
2.2. ICC(3,1) and Its Application in Comprehensive Evaluation Models
- Evaluated object: The sample in the original dataset.
- Rater: The comprehensive scores produced by the evaluation model under each perturbation group.
- Observed value: The standardized comprehensive score matrix, where the number of rows corresponds to the sample size and the number of columns corresponds to the number of perturbation groups.
- Rating consistency: This refers to the stability of the model’s scoring structure for the same sample across different perturbations.
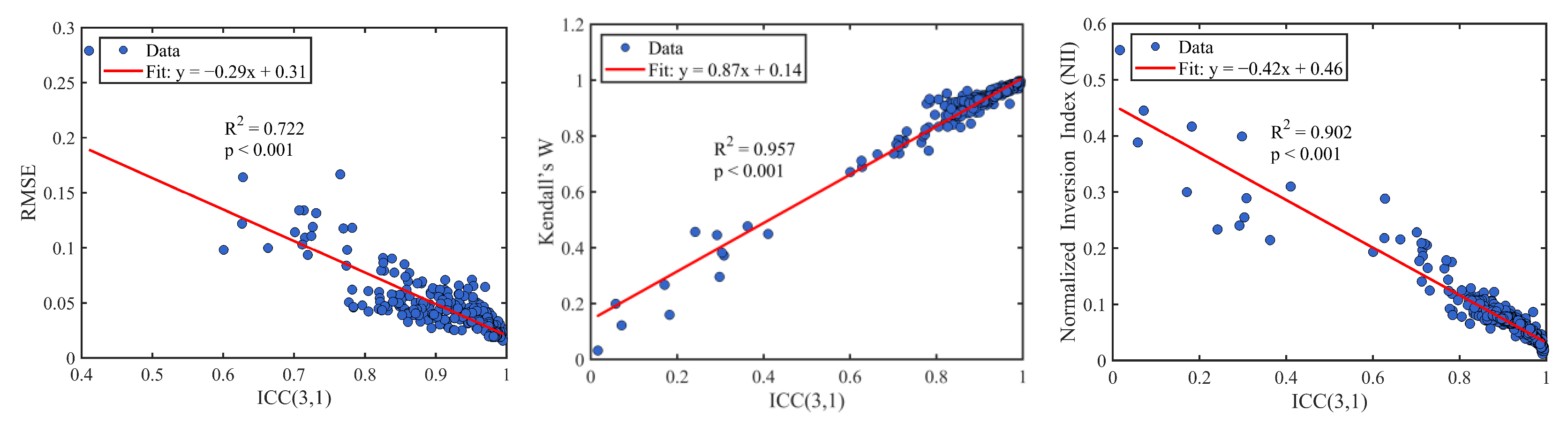
- Property 1 demonstrates that ICC(3,1) effectively reflects the robustness of a model under perturbation. A higher ICC value indicates greater robustness.
- Property 2 confirms that ICC(3,1) is invariant to positive linear transformations, ensuring the comparability and scale independence of evaluation results.
- Property 3 further shows that ICC(3,1) captures both the degree of numerical deviation and the consistency of ranking after perturbation, thus incorporating both absolute and relative aspects of robustness.
2.3. Robustness Measurement Framework of ICC(3,1)
3. Experimental Design
3.1. Datasets and Models
- Normal Distribution: As one of the most classical and widely used distributions in statistical analysis, the normal distribution is characterized by symmetry, zero skewness, and light tails. It serves as a benchmark for evaluating model robustness under ideal and balanced data conditions, helping to understand the model’s baseline behavior.
- Uniform Distribution: This distribution represents a completely non-concentrated data scenario where all values have equal probability. It is used to test the adaptability and stability of the comprehensive evaluation model when faced with data containing minimal concentration of information.
- Exponential Distribution: Characterized by right skewness and a light tail, the exponential distribution is commonly used to model natural phenomena such as waiting times and failure intervals. Its inclusion allows for assessing the model’s robustness and bias resistance under skewed data conditions.
- Log-Normal Distribution: This asymmetric distribution features a long right tail and is widely used in domains such as economics, finance, and environmental studies. Incorporating this distribution brings the study closer to practical application and allows examination of model performance under asymmetric and complex data structures.
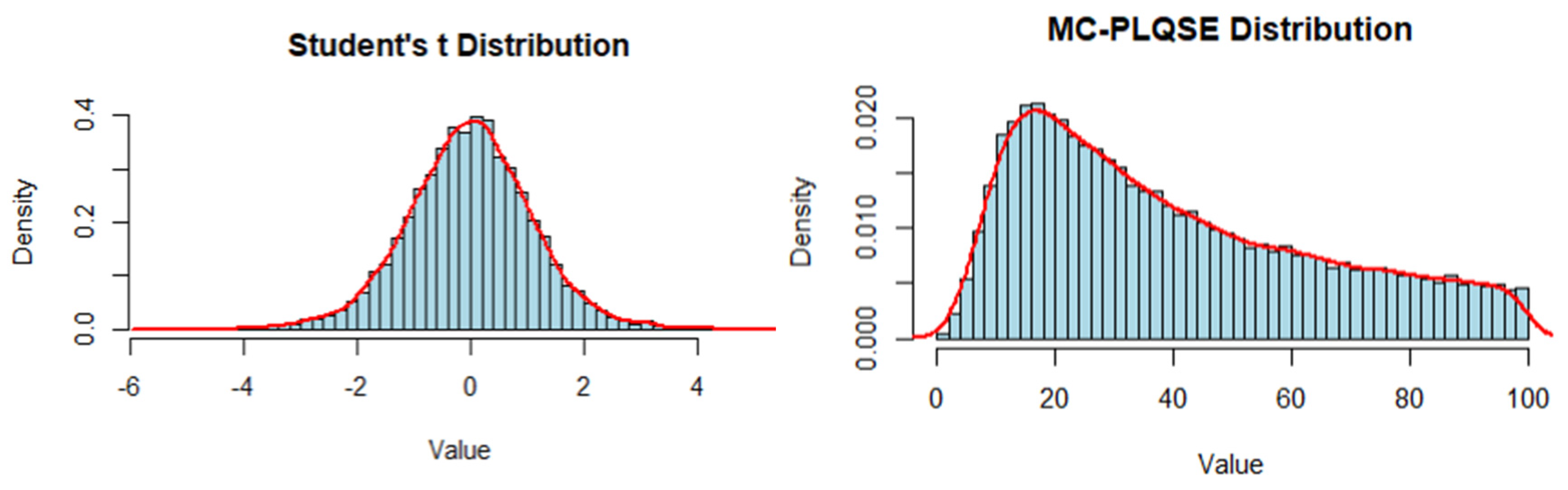
- Student’s t Distribution: Known for its heavy tails, the t-distribution can simulate extreme values or sharp fluctuations in data. It is widely applied in fields sensitive to tail risks, such as finance and medicine. Using this distribution helps evaluate the model’s robustness under highly volatile data conditions.
- Multiplicative Combination of a Power Law and q-Stretched Exponential Distribution [21] (MC-PLQSE): This hybrid distribution combines power law behavior with q-stretched exponential features and is capable of capturing complex system signals, such as those seen in EEG signals. In this study, it is used to simulate indicator distributions under strong nonlinearity and complex coupling mechanisms, thereby testing the model’s robustness in highly complex environments.
- Coverage of varying orders of magnitude: The selected sample sizes span from very small (n < 30) to very large (n ≥ 10,000), allowing for an examination of model robustness under varying levels of data sparsity and density. Extremely small samples (e.g., n = 25) reflect scenarios with limited resources or difficult data access, whereas large-scale samples (e.g., n = 50,000, 100,000) simulate the model’s stability limits under massive data environments.
- Reference to critical thresholds in statistical analysis: The sample sizes align with key benchmarks commonly used in statistical practice. For example:
- n = 25: Approximates the minimum effective sample size, useful for testing model stability under high uncertainty.
- n = 100 and 200: Represent small to medium samples, widely used in actual questionnaire surveys, experimental designs, etc.
- n = 500 to 3000: Considered medium-sized, typical in most empirical research and modeling contexts.
- n ≥ 5000: Marks the transition to large samples, suitable for simulating conditions with higher stability and reduced variance.
- n = 50,000 and 100,000: Represent massive datasets, designed to test whether the model converges or exhibits new robustness behaviors under big data scenarios.
- Stepwise growth design: The sample sizes are arranged in a non-uniform, incremental fashion (e.g., from 1000 to 3000 to 5000). This stepwise increase allows for the detection of potential performance shifts or threshold effects as the sample grows, particularly during transitions from small to medium scales. Larger intervals in the upper range (e.g., above 10,000) help to balance comprehensiveness with computational feasibility.
- Alignment with real-world data scales: The selected sample sizes reflect common application domains, including questionnaire surveys (tens to hundreds of responses), social network analysis (thousands to tens of thousands of nodes), and internet log analysis (tens of thousands or more). This ensures that the simulation results remain practical, relevant, and generalizable.
3.2. Data Perturbation Processing
4. Results
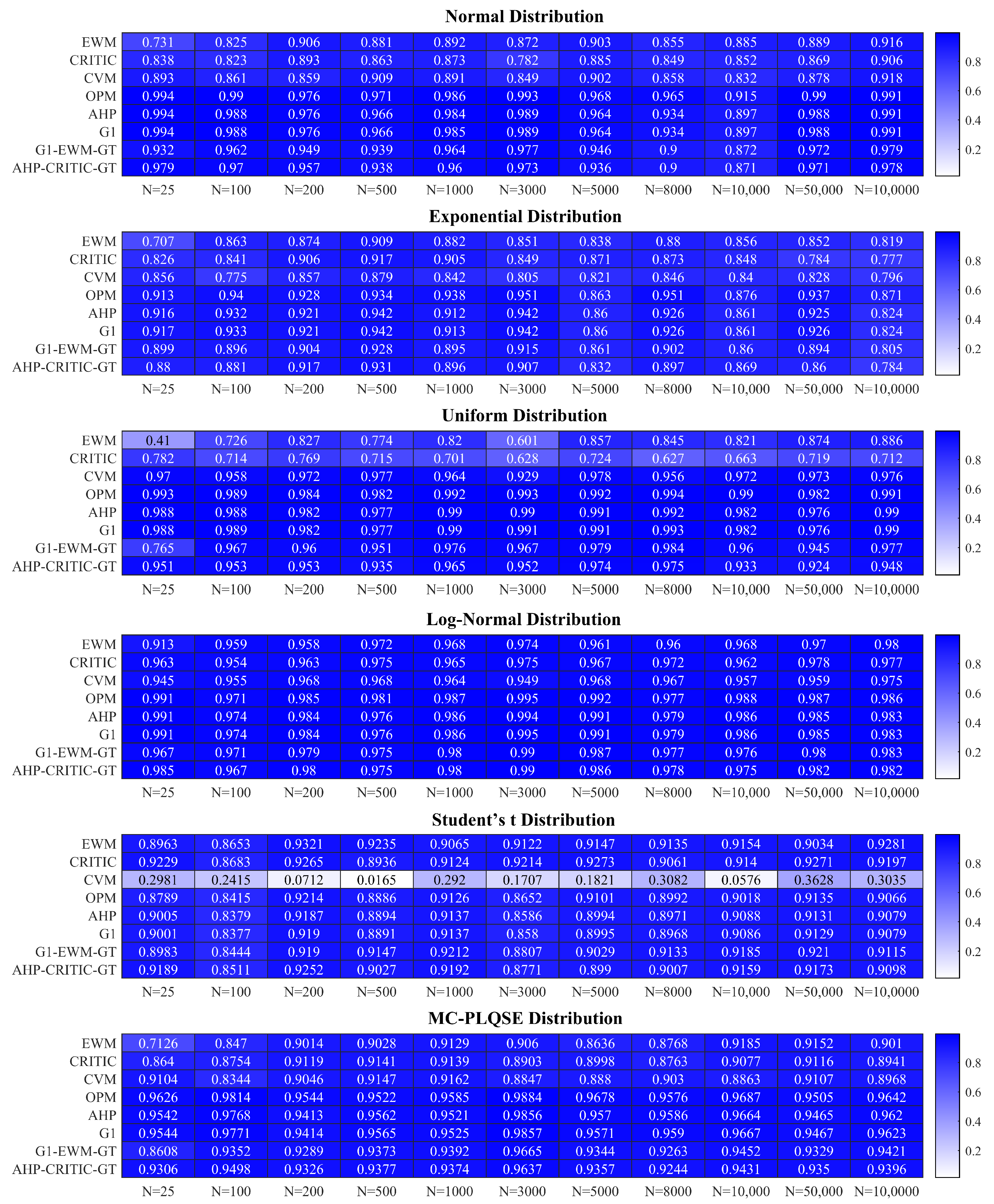
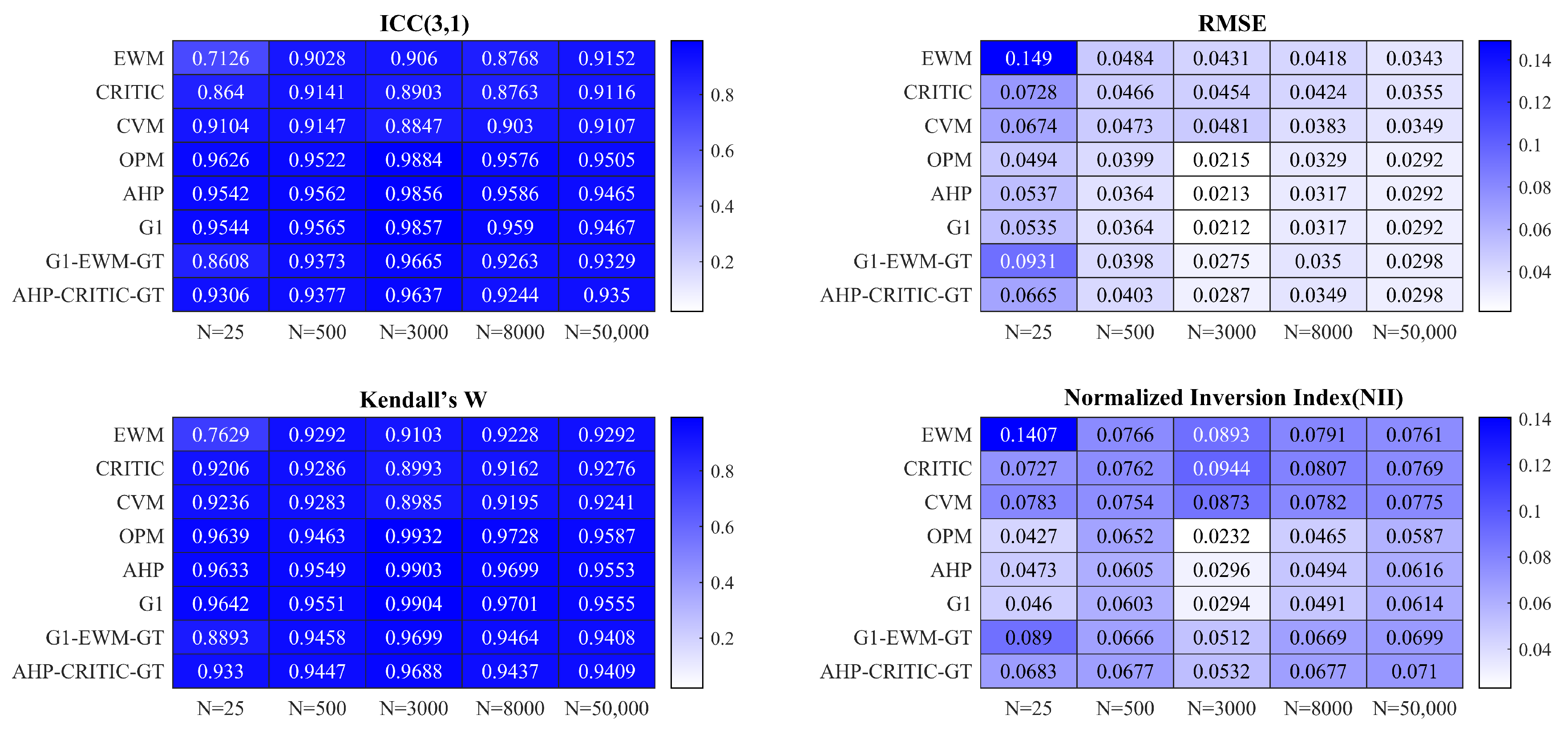
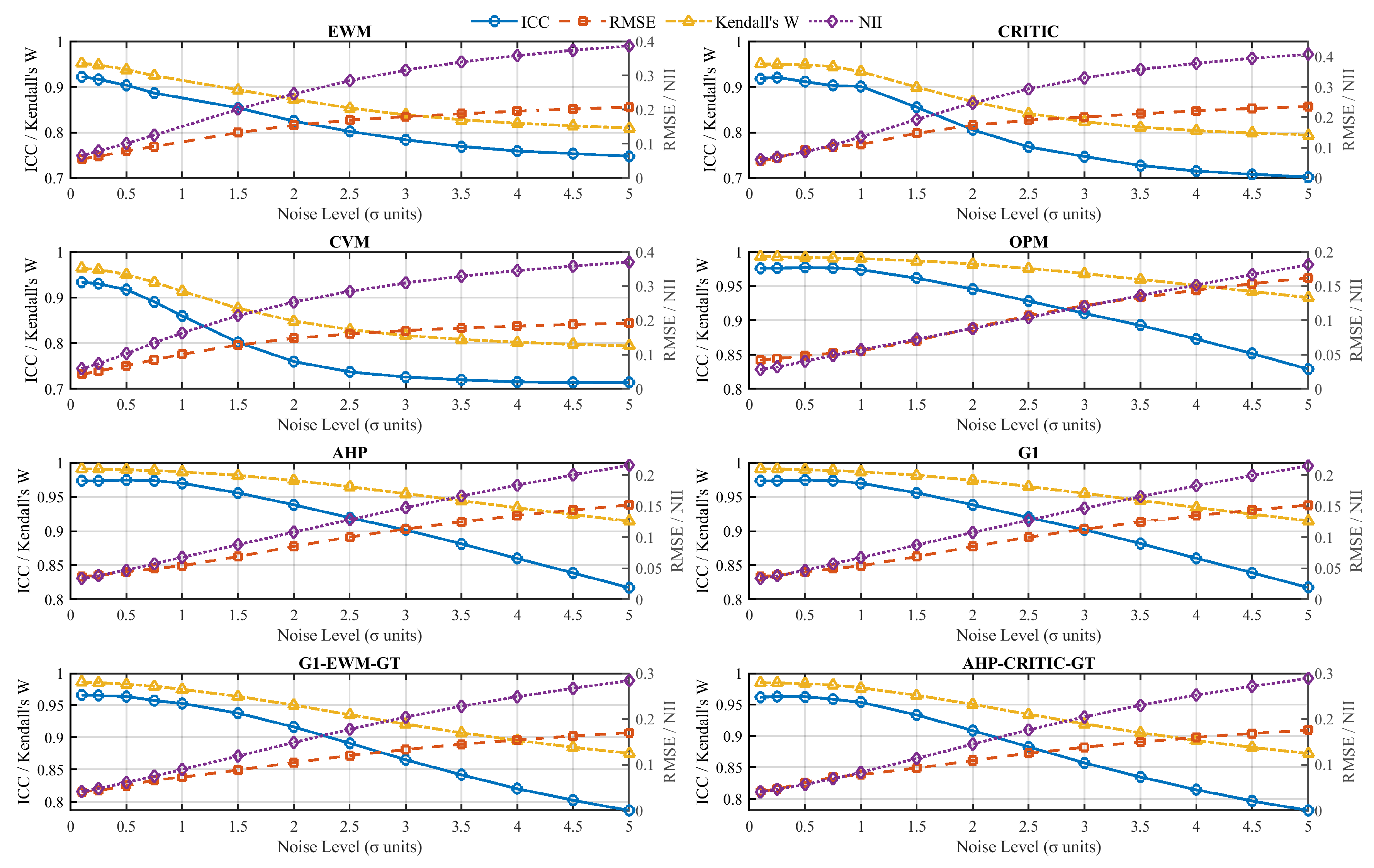
4.1. Evaluation of ICC(3,1) as a Robustness Measurement Tool
4.2. Comprehensive Comparative Advantages of ICC(3,1)
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, Y.; Liu, J.; Li, J.; Jiang, Z.; Ma, B.; Chu, C.; Geng, Z. Novel risk assessment model of food quality and safety considering physical-chemical and pollutant indexes based on coefficient of variance integrating entropy weight. Sci. Total Environ. 2023, 877, 162730. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, X. A three-dimensional sampling design based on the coefficient of variation method for soil environmental damage investigation. Environ. Monit. Assess. 2024, 196, 1–15. [Google Scholar] [CrossRef]
- Saisana, M.; Saltelli, A.; Tarantola, S. Uncertainty and sensitivity analysis techniques as tools for the quality assessment of composite indicators. J. R. Stat. Soc. Ser. A Stat. Soc. 2005, 168, 307–323. [Google Scholar] [CrossRef]
- Foster, J.; McGillivray, M.; Seth, S. Rank Robustness of Composite Indices: Dominance and Ambiguity; Queen Elizabeth House, University of Oxford: Oxford, UK, 2012. [Google Scholar]
- Paruolo, P.; Saisana, M.; Saltelli, A. Ratings and rankings: Voodoo or science? J. R. Stat. Soc. Ser. A Stat. Soc. 2013, 176, 609–634. [Google Scholar] [CrossRef]
- Doumpos, M. Robustness Analysis in Decision Aiding, Optimization, and Analytics; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Greco, S.; Ishizaka, A.; Tasiou, M.; Torrisi, G. On the methodological framework of composite indices: A review of the issues of weighting, aggregation, and robustness. Soc. Indic. Res. 2019, 141, 61–94. [Google Scholar] [CrossRef]
- Taraji, M.; Haddad, P.R.; Amos, R.I.J.; Talebi, M.; Szucs, R.; Dolan, J.W.; Pohl, C.A. Error measures in quantitative structure-retention relationships studies. J. Chromatogr. A 2017, 1524, 298–302. [Google Scholar] [CrossRef] [PubMed]
- Matuszny, M.; Strączek, J. Approaches of the concordance coefficient in assessing the degree of subjectivity of expert assessments in technology selection. Pol. Tech. Rev. 2024. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Zhang, W.T.; Li, T. Research on the impact of digital technology application on corporate environmental performance: Empirical evidence from A-share listed companies. Macroecon. Res. 2023, 67–84. [Google Scholar] [CrossRef]
- Chen, J.; Lü, Y.Q.; Zhao, B. The impact of digital inclusive financial development on residents’ social welfare performance. Stat. Decis. 2024, 40, 138–143. [Google Scholar]
- Shrout, P.E.; Fleiss, J.L. Intraclass correlations: Uses in assessing rater reliability. Psychol. Bull. 1979, 86, 420. [Google Scholar] [CrossRef] [PubMed]
- Surov, A.; Eger, K.I.; Potratz, J.; Gottschling, S.; Wienke, A.; Jechorek, D. Apparent diffusion coefficient correlates with different histopathological features in several intrahepatic tumors. Eur. Radiol. 2023, 33, 5955–5964. [Google Scholar] [CrossRef] [PubMed]
- Senthil Kumar, V.S.; Shahraz, S. Intraclass correlation for reliability assessment: The introduction of a validated program in SAS (ICC6). Health Serv. Outcomes Res. Methodol. 2024, 24, 1–13. [Google Scholar] [CrossRef]
- Yardim, Y.; Cüvitoğlu, G.; Aydin, B. The Intraclass Correlation Coefficient as a Measure of Educational Inequality: An Empirical Study with Data from PISA 2018. Res. Sq. 2024. [Google Scholar] [CrossRef]
- Van Hooren, B.; Bongers, B.C.; Rogers, B.; Gronwald, T. The between-day reliability of correlation properties of heart rate variability during running. Appl. Psychophysiol. Biofeedback 2023, 48, 453–460. [Google Scholar] [CrossRef] [PubMed]
- Marcinkiewicz, E. Pension systems similarity assessment: An application of Kendall’s W to statistical multivariate analysis. Contemp. Econ. 2017, 11, 303–314. [Google Scholar]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
- McGraw, K.O.; Wong, S.P. Forming inferences about some intraclass correlation coefficients. Psychol. Methods 1996, 1, 30. [Google Scholar] [CrossRef]
- Chen, G.; Taylor, P.A.; Haller, S.P.; Kircanski, K.; Stoddard, J.; Pine, D.S.; Leibenluft, E.; Brotman, M.A.; Cox, R.W. Intraclass correlation: Improved modeling approaches and applications for neuroimaging. Hum. Brain Mapp. 2018, 39, 1187–1206. [Google Scholar] [CrossRef] [PubMed]
- Abramov, D.M.; Lima, H.S.; Lazarev, V.; Galhanone, P.R.; Tsallis, C. Identifying attention-deficit/hyperactivity disorder through the electroencephalogram complexity. Phys. A Stat. Mech. Its Appl. 2024, 653, 130093. [Google Scholar] [CrossRef]

| Notation | Description |
|---|---|
| The score of the i-th method for the j-th evaluation object (sample) | |
| The benchmark score of the j-th sample | |
| The sum of the rankings given by all experts to the i-th sample | |
| Number of discordant pairs index | |
| NII | Normalized inversion index |
| Variance between samples | |
| Variance of error | |
| MSR | Mean Square Between Row/Raters, which represents the mean square error between samples (i.e., the systematic differences between samples identified by the model) |
| MSE | Mean Square Error (i.e., non-systematic rating differences caused by perturbations) |
| Changes in ICC(3,1) before and after model improvement | |
| AR | The decay rate of ICC(3,1) after injecting data perturbation |
| The ratio of error variance to total variance | |
| Robustness score of model M | |
| The ratio of noise to system variance, i.e., |
| McGraw and Wong (1996) [19] | Shrout and Fleiss (1979) [12] | ICC Calculation Formula | ||
|---|---|---|---|---|
| Model | Rater | Consistency | ||
| One-way random effects | Single | Absolute | ICC(1,1) | |
| One-way random effects | Multiple | Absolute | - | |
| Two-way random effects | Single | Relatively | ICC(2,1) | |
| Two-way random effects | Multiple | Relatively | ICC(3,1) | |
| Two-way random effects | Single | Absolute | - | |
| Two-way random effects | Multiple | Absolute | ICC(1,k) | |
| Two-way mixing effect | Single | Relatively | - | |
| Two-way mixing effect | Multiple | Relatively | ICC(2,k) | |
| Two-way mixing effect | Single | Absolute | ICC(3,k) | |
| Two-way mixing effect | Multiple | Absolute | - | |
| Group | Disturbance Level | Noise | Bias | Zoom |
|---|---|---|---|---|
| D1 | Mild noise | 0.10 | ||
| D2 | Low noise | 0.20 | ||
| D3 | Medium Noise | 0.35 | ||
| D4 | High noise | 0.6 | ||
| D5 | Overall bias | |||
| D6 | Bias + Light Noise | 0.20 | ||
| D7 | Slight zoom | |||
| D8 | Random Scaling of Variables | |||
| D9 | Random Scaling + Bias | |||
| D10 | Combined perturbations | 0.3 | ||
| D11 | No disturbance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xian, S.; Zhang, L. Robustness Measurement of Comprehensive Evaluation Model Based on the Intraclass Correlation Coefficient. Mathematics 2025, 13, 1748. https://doi.org/10.3390/math13111748
Xian S, Zhang L. Robustness Measurement of Comprehensive Evaluation Model Based on the Intraclass Correlation Coefficient. Mathematics. 2025; 13(11):1748. https://doi.org/10.3390/math13111748
Chicago/Turabian StyleXian, Shilai, and Li Zhang. 2025. "Robustness Measurement of Comprehensive Evaluation Model Based on the Intraclass Correlation Coefficient" Mathematics 13, no. 11: 1748. https://doi.org/10.3390/math13111748
APA StyleXian, S., & Zhang, L. (2025). Robustness Measurement of Comprehensive Evaluation Model Based on the Intraclass Correlation Coefficient. Mathematics, 13(11), 1748. https://doi.org/10.3390/math13111748






