Exploring the Crossing Numbers of Three Join Products of 6-Vertex Graphs with Discrete Graphs

Abstract

The significance of searching for edge crossings in graph theory lies inter alia in enhancing the clarity and readability of graph representations, which is essential for various applications such as network visualization, circuit design, and data representation. This paper focuses on exploring the crossing number of the join product $G^{*}+D_n$, where $G^{*}$ is a graph isomorphic to the path on four vertices $P_4$ with an additional two vertices adjacent to two inner vertices of $P_4$, and $D_n$ is a discrete graph composed of n isolated vertices. The proof is based on exact crossing-number values for join products involving particular subgraphs $H_k$ of $G^{*}$ with discrete graphs $D_n$ combined with the symmetrical properties of graphs. This approach could also be adapted to determine the unknown crossing numbers of two other 6-vertices graphs obtained by adding one or two additional edges to the graph $G^{*}$.

1. Introduction

The crossing number in graph theory is the minimum number of edge intersections required when drawing a graph on a plane. This concept is crucial for creating clear and effective visualizations of complex networks [1,2], such as those found in social, technological, or logistical systems. By reducing the crossing number, the underlying structure of a graph becomes more apparent, aiding in the identification of critical nodes and connections [3]. For example, in social network analysis [4], reducing crossings can more clearly reveal key influencers or tightly connected groups. In circuit design, minimizing crossings reduces potential signal interference and simplifies the layout of wires [5]. In transportation networks [6], a lower crossing number helps highlight critical hubs, such as major train stations or highway junctions. The crossing number also optimizes the layout of communication networks, ensuring efficient visualization of data flows. However, computing the exact crossing number for large or complex graphs is often computationally intensive, leading to the use of heuristic algorithms. Research into crossing numbers continues to advance graph drawing techniques, improving their practical applications [7,8].

Examining the count of edge crossings in simple graphs remains a challenging and enduring problem. Garey and Johnson [9] proved that determining the crossing number $\mathrm{cr}\left(G\right)$ for a graph G falls into the category of NP-complete problems. Reference [10] provides a comprehensive survey of exact crossing numbers for specific graph classes. This survey seeks to compile published results on crossing numbers, provide relevant citations, and acknowledge the original researchers who contributed these results.

Let $D_n$ represent the discrete graph on n isolated vertices, and let $G+D_n$ denote the join product of the two graphs G and $D_n$. The precise crossing-number values for $G+D_n$ pertaining to all graphs with at most four vertices are provided by Klešč and Schrötter [11]. Furthermore, for certain connected graphs G with five and six vertices, the values are detailed in additional studies [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. It is important to highlight that $\mathrm{cr}(G+D_n)$ values are known only for specific disconnected graphs [21,28,29].

The aim of this paper is to expand upon existing findings related to the crossing numbers of graphs by applying them to new graph structures. This paper investigates the crossing number of the join product $G^{*}+D_n$. Here, $G^{*}$ is a graph isomorphic to the path on four vertices $P_4$ with two additional vertices adjacent to the two inner vertices of $P_4$. To determine the crossing number $\mathrm{cr}(G^{*}+D_n)$ we examine the drawings for all eight possible non-isomorphic good drawings of $G^{*}$. For the six vertices of $G^{*}$, all potential rotations of adjacent edges are outlined, and the associated cyclic permutations of six elements are described. Then, fixing edges in subgraphs allows us to determine $\mathrm{cr}(G^{*}+D_n)$. Finally, two new graphs $G_1$ and $G_2$ are investigated by adding one or two additional edges that do not induce crossings to the graph $G^{*}$. For them, $\mathrm{cr}(G_1+D_n)$ and $\mathrm{cr}(G_2+D_n)$ are determined.

The crossing number $\mathrm{cr}\left(G\right)$ of a graph G is defined as the minimum possible number of edge crossings through all possible good drawings of G in the plane. Clearly, a drawing with the minimal number of crossings, termed an optimal drawing, is always considered a good drawing. In such a drawing, no edge crosses itself, no two edges intersect more than once, and edges sharing a common vertex do not intersect. This paper investigates the crossing number $\mathrm{cr}\left(G\right)$ of a composite graph G formed by the join product of two graphs $G_i$ and $G_j$, denoted as $G=G_i+G_j$. This structure comprises distinct copies of $G_i$ and $G_j$ with no shared vertices, connected by all possible edges between their vertex sets $V\left(G_i\right)$ and $V\left(G_j\right)$. When $\left|V\right(G_i\left)\right|=m$ and $\left|V\right(G_j\left)\right|=n$, the edge set of G includes the non-overlapping edge sets $E\left(G_i\right)$, $E\left(G_j\right)$, and the complete bipartite graph $K_{m,n}$. Consequently, portions of the proofs rely on Kleitmanś findings [30] regarding the crossing numbers of specific $K_{m,n}$. Kleitman [30] demonstrated that

$$\mathrm{cr}\left(K_{m,n}\right)=⌊{\displaystyle \frac{m}{2}}⌋⌊{\displaystyle \frac{m-1}{2}}⌋⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋,\mathrm{if}min\{m,n\}\le 6.$$

(1)

For a subgraph $G_i$ of the graph G, define $D\left(G_i\right)$ as the subdrawing of $G_i$ that is induced by the drawing D. For two subgraphs $G_i$ and $G_j$ of G that share no common edges, let ${\mathrm{cr}}_D(G_i,G_j)$ represent the count of edge crossings between $G_i$ and $G_j$ in D, and let ${\mathrm{cr}}_D\left(G_i\right)$ denote the number of crossings among the edges within $G_i$ in D. It is straightforward to observe that for any trio of mutually edge-disjoint subgraphs $G_i$, $G_j$, and $G_k$, the following relationships are satisfied:

$${\mathrm{cr}}_D(G_i\cup G_j)={\mathrm{cr}}_D\left(G_i\right)+{\mathrm{cr}}_D\left(G_j\right)+{\mathrm{cr}}_D(G_i,G_j),$$

$${\mathrm{cr}}_D(G_i\cup G_j,G_k)={\mathrm{cr}}_D(G_i,G_k)+{\mathrm{cr}}_D(G_j,G_k).$$

2. Cyclic Permutations and Possible Drawings of $G^{*}$

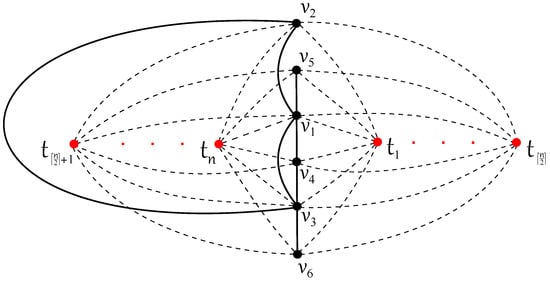
The join product $G^{*}+D_n$ (occasionally denoted as $G^{*}+n{K}_1$) comprises a single instance of the graph $G^{*}$ and n vertices $t_1,\dots ,t_n$, where each vertex $t_i$ is connected to all vertices of $G^{*}$. The subgraph formed by the six edges incident to a specific vertex $t_i$ is denoted as $T^i$, which implies that

$$G^{*}+D_n=G^{*}\cup \left(\bigcup _{i=1}^n{T}^i\right).$$

(2)

In a good drawing D of $G^{*}+D_n$, the rotation ${\mathrm{rot}}_D\left(t_i\right)$ of a vertex $t_i$ in the drawing D is defined as the cyclic permutation capturing the counter-clockwise (cyclic) order in which the edges emanate from $t_i$, as established by Hernández-Vélez et al. [31] and Woodall [32]. We use the notation $\left(123456\right)$ if the counter-clockwise order of the edges incident with the vertex $t_i$ is $t_i{v}_1$, $t_i{v}_2$, $t_i{v}_3$, $t_i{v}_4$, $t_i{v}_5$, and $t_i{v}_6$. We have to emphasize that rotation is a cyclic permutation. Let ${\overline{\mathrm{rot}}}_D\left(t_i\right)$ denote the inverse permutation of ${\mathrm{rot}}_D\left(t_i\right)$. In the specified drawing D, it is advantageous to partition the n subgraphs $T^i$ into four disjoint groups based on the number of times the edges of $G^{*}$ are intersected by $T^i$ in D. We designate $R_D$, $S_D$, and $T_D$ as the sets of subgraphs where ${\mathrm{cr}}_D(G^{*},T^i)=0$, ${\mathrm{cr}}_D(G^{*},T^i)=1$, and ${\mathrm{cr}}_D(G^{*},T^i)=2$, respectively. Each remaining subgraph $T^i$ has its edges crossing those of $G^{*}$ at least three times in D. Furthermore, let $F^i$ denote the subgraph $G^{*}\cup T^i$ for $T^i\in R_D$, where $i\in 1,\dots ,n$. Consequently, for a given subdrawing of $G^{*}$ in D, each subgraph $F^i$ is precisely characterized by ${\mathrm{rot}}_D\left(t_i\right)$.

First, note that if D is a good drawing of $G^{*}+D_n$ with the empty set $R_D\cup S_D$, then ${\sum }_{i=1}^n{\mathrm{cr}}_D(G^{*},T^i)\ge 2n$, resulting in more than $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ edge crossings in D provided by

$${\mathrm{cr}}_D(G^{*}+D_n)={\mathrm{cr}}_D\left(K_{6,n}\right)+{\mathrm{cr}}_D(G^{*},K_{6,n})+{\mathrm{cr}}_D\left(G^{*}\right)$$

$$\ge 6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+2n>6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋.$$

As per the anticipated outcome of the main Theorem 3, this necessitates that the set $R_D\cup S_D$ is non-empty in all optimal drawings of $G^{*}+D_n$.

We now explore all possible drawings of $G^{*}$ induced by D, characterized by the degree sequence $(1, 1, 2, 2, 4, 4)$. The graph $G^{*}$ includes a cycle $C_4$ as a subgraph, formed by four vertices with degrees 4, 2, 4, and 2 (denoted as $C_4\left(G^{*}\right)$ for conciseness). Let $v_1$, $v_2$, $v_3$, and $v_4$ represent these vertices in the cyclic order of $C_4\left(G^{*}\right)$. Throughout the paper, we assume that ${deg}_{G^{*}}\left(v_5\right)=1$ and ${deg}_{G^{*}}\left(v_6\right)=1$, provided $v_1{v}_5, v_3{v}_6\in E\left(G^{*}\right)$. As illustrated in Figure 1, we can adjust a crossing between two edges incident to distinct leaves to produce a new drawing of $G^{*}$ induced by D (with vertices labeled in a different order), achieving fewer edge crossings. Consequently, in any optimal drawing of $G^{*}+D_n$, the edges $v_1{v}_5$ and $v_3{v}_6$ of $G^{*}$ do not intersect.

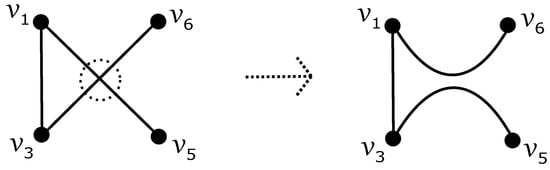
Figure 1. Elimination of a crossing on edges of $G^{*}$.

Let $H_1$ denote the graph $K_{1,5}\setminus e$, formed by deleting a single edge from the complete bipartite graph $K_{1,5}$. Let $H_2$ be the graph comprising two leaves connected to two opposite vertices of a 4-cycle. Their drawings are also depicted in Figure 2. The crossing numbers for the join products of $H_1$ and $H_2$ with the discrete graphs $D_n$ are well established, as determined by Su and Huang [33] for $H_1$ and by Berežný and Staš [13] for $H_2$.

Figure 2. Planar drawings of two graphs $H_1$ and $H_2$.

Theorem 1

([33], Theorem 4.1). $\mathrm{cr}(H_1+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋$ for $n\ge 1$.

Lemma 1.

For $n\ge 1$, let D be a good drawing of $G^{*}+D_n$. If there are at least $⌊\frac{n}{2}⌋$ crossings on the edges $v_1{v}_2, v_1{v}_4, v_1{v}_5$ or $v_3{v}_2, v_3{v}_4, v_3{v}_6$ of $G^{*}$, then D has at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings.

Proof. 

Consider any good drawing D of $G^{*}+D_n$ that has at least $⌊\frac{n}{2}⌋$ crossings on the edges $v_1{v}_2$, $v_1{v}_4$, and $v_1{v}_5$. By excluding these three edges from $G^{*}$, we derive a subgraph isomorphic to the graph $H_1$. Theorem 1 provides the precise crossing number for $H_1+D_n$, indicating that D contains at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings. Due to the symmetry of the graph $G^{*}$, the proof proceeds in the same way for the second three edges, $v_3{v}_2$, $v_3{v}_4$, and $v_3{v}_6$, of $G^{*}$. □

Theorem 2

([13], Theorem 3.1). $\mathrm{cr}(H_2+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋$ for $n\ge 1$.

As Theorem 2 allows the same reasoning for removing the edge $v_1{v}_3$ from $G^{*}$ to be applied to all possible subdrawings of $G^{*}$ induced by D, the proof of Lemma 2 can be skipped.

Lemma 2.

For $n\ge 1$, let D be a good drawing of $G^{*}+D_n$. If the edge $v_1{v}_3$ of $G^{*}$ is crossed at least $⌊\frac{n}{2}⌋$ times, then there are at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings in D.

Corollary 1.

For $n\ge 1$, let D be a good drawing of $G^{*}+D_n$ with the empty set $R_D$. If each subgraph $T^i$ crosses some edge of $G^{*}\setminus \left\{v_1{v}_3\right\}$, then there are at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings in D.

Proof. 

Assume a good drawing D of $G^{*}+D_n$ with the empty set $R_D$. If any subgraph $T^i$ crosses some edge of $G^{*}\setminus \left\{v_1{v}_3\right\}$, then at least one edge of $v_1{v}_2, v_1{v}_4, v_1{v}_5$, or $v_3{v}_2, v_3{v}_4, v_3{v}_6$ is crossed in D. All such subgraphs $T^i$ enforce at least $⌊\frac{n}{2}⌋$ crossings on the edges $v_1{v}_2, v_1{v}_4, v_1{v}_5$, or $v_3{v}_2, v_3{v}_4, v_3{v}_6$ of $G^{*}$, and therefore we obtain at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings in D due to Lemma 1. □

To achieve fewer than $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings in D, if we consider a subdrawing $D\left(G^{*}\right)$ with five vertices of $G^{*}$ on its boundary, then there is a subgraph $T^i$ by which only the edge $v_1{v}_3$ of $G^{*}$ can be crossed using Corollary 1. In this case, we obtain only one such possible drawing of $G^{*}$, in such a way as shown in Figure 3a. Assuming a subdrawing $D\left(G^{*}\right)$ where all six vertices of $G^{*}$ lie on its boundary and the edges of $C_4\left(G^{*}\right)$ do not intersect, we derive three distinct drawings, as shown in Figure 3b–d. Conversely, if the edges of $C_4\left(G^{*}\right)$ intersect, four additional configurations arise, as depicted in Figure 3e–h.

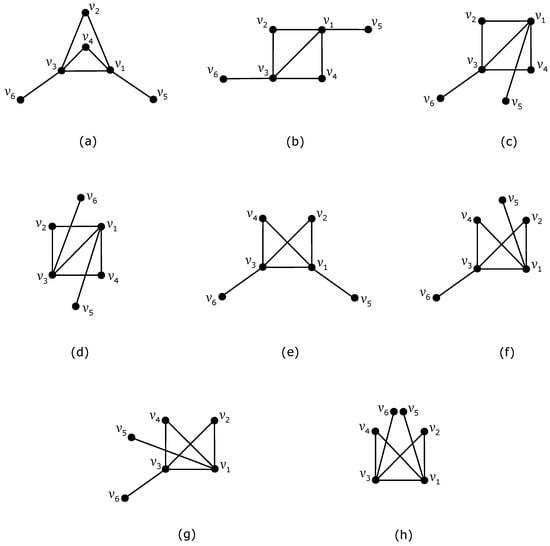
Figure 3. Eight possible non-isomorphic drawings of the graph $G^{*}$: (a) the planar drawing of $G^{*}$ with one triangular face; (b) the planar drawing of $G^{*}$ with two triangular faces; (c) the drawing of $G^{*}$ with ${\mathrm{cr}}_D\left(G^{*}\right)=1$ and no crossing among edges of $C_4\left(G^{*}\right)$; (d) the drawing of $G^{*}$ with ${\mathrm{cr}}_D\left(G^{*}\right)=2$ and no crossing among edges of $C_4\left(G^{*}\right)$; (e) the drawing of $G^{*}$ with ${\mathrm{cr}}_D\left(G^{*}\right)=1$ and one crossing among edges of $C_4\left(G^{*}\right)$; (f) the drawing of $G^{*}$ with ${\mathrm{cr}}_D\left(G^{*}\right)=2$ and one crossing among edges of $C_4\left(G^{*}\right)$; (g) the drawing of $G^{*}$ with ${\mathrm{cr}}_D\left(G^{*}\right)=3$ and four triangular faces; (h) the drawing of $G^{*}$ with ${\mathrm{cr}}_D\left(G^{*}\right)=3$ and five triangular faces.

Note that a drawing D of $G^{*}+D_n$ with less than $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings with the empty set $R_D$ enforces at least $⌈\frac{n}{2}⌉$ subgraphs whose edges cross $G^{*}$ exactly once, but the edge $v_1{v}_3$ of $G^{*}$ can be crossed less than $⌊\frac{n}{2}⌋$ times according to Lemma 2. More details are described also in the proof of Theorem 3.

Suppose there exists a good drawing D of the join product $G^{*}+D_n$ where the edges of $G^{*}$ do not intersect. To explore this, we consider the planar drawing of $G^{*}$ depicted in Figure 3b. For subgraphs $T^i\in R_D$, we identify all possible rotations ${\mathrm{rot}}_D\left(t_i\right)$ that may occur in the drawing D. Evidently, there is only one subdrawing of $F^i\setminus v_1,v_3$, which can be described by the subrotation $\left(2546\right)$. Depending on the placement of edges $t_i{v}_1$ and $t_i{v}_3$ in one of two regions, we obtain four distinct subdrawings of $F^i=G^{*}\cup T^i$. These $2\times 2=4$ cases, labeled as ${\mathcal{A}}_p$ for $p=1,2,3,4$, are referred to as the configurations of the corresponding subdrawings of the subgraph $G^{*}\cup T^i$ in D. Their illustrations are provided in Figure 4, as the choice of the unbounded region in $D(G^{*}\cup T^i)$ is topologically irrelevant. We connect the vertex $t_i$ to the vertex $v_1$, and gradually add five remaining edges to vertices $v_2,\dots ,v_6$, preserving the rotation ${\mathrm{rot}}_D\left(t_i\right)$ and without any crossing on edges of the graph $G^{*}$.

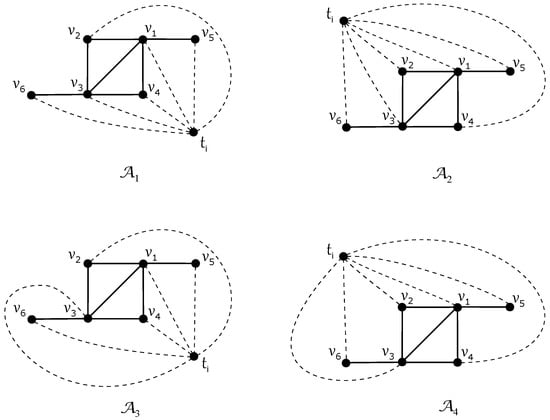
Figure 4. Drawings of four possible configurations ${\mathcal{A}}_p$ of subgraph $F^i$ for $T^i\in R_D$.

Throughout the remainder of the paper, we denote a cyclic permutation by placing 1 in the first position. Accordingly, the configurations ${\mathcal{A}}_1$, ${\mathcal{A}}_2$, ${\mathcal{A}}_3$, and ${\mathcal{A}}_4$ correspond to the cyclic permutations $\left(143625\right)$, $\left(154632\right)$, $\left(146325\right)$, and $\left(154362\right)$, respectively. Clearly, in a fixed drawing of the graph $G^{*}+D_n$, some configurations from $\mathcal{M}=\{{\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3,{\mathcal{A}}_4\}$ need not appear. We define ${\mathcal{M}}_D$ as the set of configurations from $\mathcal{M}$ that appear in the drawing D.

Our objective now is to determine the smallest possible number of edge crossings between two distinct subgraphs $F^i$ and $F^j$ by leveraging the concept of the aforementioned configurations. For any two configurations $\mathcal{X}$ and $\mathcal{Y}$ in ${\mathcal{M}}_D$ (which may be identical), let ${\mathrm{cr}}_D(\mathcal{X},\mathcal{Y})$ represent the number of edge crossings in $D(T^i\cup T^j)$ for two distinct subgraphs $T^i,T^j\in R_D$, where $F^i$ and $F^j$ correspond to configurations $\mathcal{X}$ and $\mathcal{Y}$, respectively. We define $\mathrm{cr}(\mathcal{X},\mathcal{Y})$ as the minimum value of ${\mathrm{cr}}_D(\mathcal{X},\mathcal{Y})$ across all pairs $\mathcal{X},\mathcal{Y}\in \mathcal{M}$ in all good drawings D of the join product $G^{*}+D_n$. Moving forward, we aim to establish lower bounds for $\mathrm{cr}(\mathcal{X},\mathcal{Y})$ for every possible pair $\mathcal{X},\mathcal{Y}\in \mathcal{M}$. Specifically, the configurations ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ are denoted by the cyclic permutations $\left(143625\right)$ and $\left(154632\right)$, respectively. Each subgraph $T^j$ with $\mathrm{conf}\left(F^j\right)={\mathcal{A}}_2$ intersects the edges of each $T^i$ with $\mathrm{conf}\left(F^i\right)={\mathcal{A}}_1$ at least four times, as the minimum number of adjacent element swaps needed to transform $\left(143625\right)$ into the inverse of $\left(154632\right)$, i.e., $\left(123645\right)$, is four, implying $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_2)\ge 4$. For more details, see also Woodall [32]. The same reason gives $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_3)\ge 5$, $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_4)\ge 5$, $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_3)\ge 5$, $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_4)\ge 5$, and $\mathrm{cr}({\mathcal{A}}_3,{\mathcal{A}}_4)\ge 4$. Clearly, also $\mathrm{cr}({\mathcal{A}}_p,{\mathcal{A}}_p)\ge 6$ for any $p=1,2,3,4$. Moreover, by a discussion of possible subdrawings, we can verify that $\mathrm{cr}({\mathcal{A}}_3,{\mathcal{A}}_4)\ge 5$. For any $T^i\in R_D$ with $\mathrm{conf}\left(F^i\right)={\mathcal{A}}_3$, the edges $t_i{v}_1$, $t_i{v}_3$, or $t_i{v}_2$, $t_i{v}_4$ together with edges of $G^{*}$ separate four vertices of $G^{*}$ into two pairs. So, any different subgraph $T^j\in R_D$ enforces at least four crossings on the four edges $t_i{v}_1$, $t_i{v}_2$, $t_i{v}_3$, and $t_i{v}_4$. The edges $t_i{v}_5$, $t_i{v}_6$ together with edges of $G^{*}$ also separate the vertices $v_2$ and $v_4$, and therefore at least one of them must be crossed by the subgraph $T^j$.

Consider a nonplanar subdrawing of the graph $G^{*}$ induced by a drawing D of $G^{*}+D_n$, as illustrated in Figure 3e. For each $T^i\in R_D$, there are precisely four possible subdrawings of $G^{*}\cup T^i$, determined by the placement of edges $t_i{v}_1$ and $t_i{v}_3$ in one of two regions. These four configurations are labeled as ${\mathcal{B}}_p$ for $p=1,2,3,4$, with their drawings depicted in Figure 5.

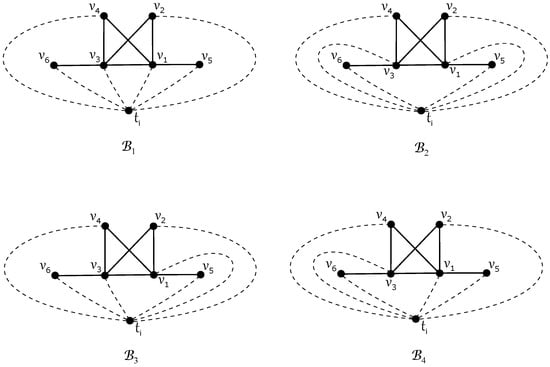
Figure 5. Drawings of four possible configurations ${\mathcal{B}}_p$ of subgraph $F^i$ for $T^i\in R_D$.

The configurations ${\mathcal{B}}_1$, ${\mathcal{B}}_2$, ${\mathcal{B}}_3$, and ${\mathcal{B}}_4$ are represented by the cyclic permutations $\left(136425\right)$, $\left(156342\right)$, $\left(153642\right)$, and $\left(163425\right)$, respectively. Since not all configurations from the set $\mathcal{N}={\mathcal{B}}_1,{\mathcal{B}}_2,{\mathcal{B}}_3,{\mathcal{B}}_4$ may be present in a given drawing of $G^{*}+D_n$, we define ${\mathcal{N}}_D$ as the subset of $\mathcal{N}$ containing only those configurations that appear in the drawing D. The process of establishing lower bounds for the number of crossings between pairs of configurations in $\mathcal{N}$ follows the same approach as described previously. Consequently, all lower bounds for crossings between pairs of configurations from both $\mathcal{M}$ and $\mathcal{N}$ are compiled in a shared symmetry (Table 1). The presented bounds are heavily used in the proof of the main Theorem 3 of this paper in order to reach a contradiction for two possible induced drawings of the graph $G^{*}$ shown in Figure 3b,e.

Table 1. The minimum number of edge crossings between $T^i$ and $T^j$ for two configurations ${\mathcal{X}}_p$ and ${\mathcal{X}}_q$ of subgraphs $F^i=G^{*}\cup T^i$ and $F^j=G^{*}\cup T^j$, where $\mathcal{X}$ represents $\mathcal{A}$ for configurations in $\mathcal{M}$ and $\mathcal{B}$ for configurations in $\mathcal{N}$.

−	${\mathcal{X}}_1$	${\mathcal{X}}_2$	${\mathcal{X}}_3$	${\mathcal{X}}_4$
${\mathcal{X}}_1$	6	4	5	5
${\mathcal{X}}_2$	4	6	5	5
${\mathcal{X}}_3$	5	5	6	5
${\mathcal{X}}_4$	5	5	5	6

In the proof of Theorem 3, the following statement is required regarding some restricted subdrawings of the graph $G^{*}+D_n$.

Lemma 3.

$\mathrm{cr}(G^{*}+D_1)=0$ and $\mathrm{cr}(G^{*}+D_2)=3$.

Proof. 

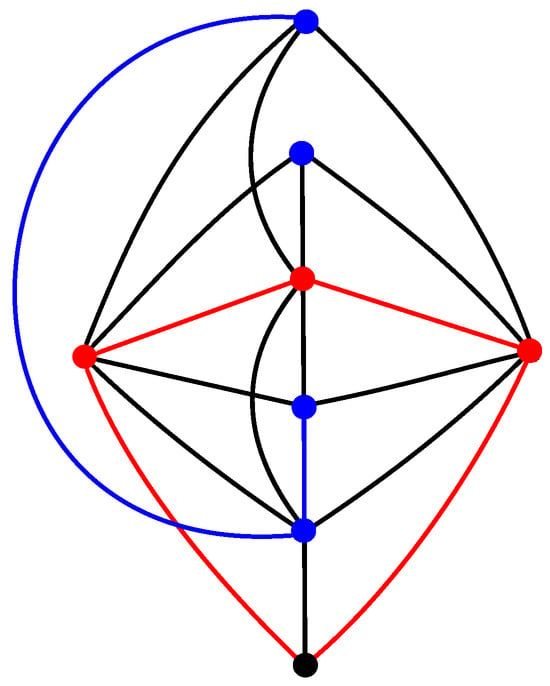
$\mathrm{cr}(G^{*}+D_1)=0$ because the graph $G^{*}+D_1$ is planar. Figure 6 offers the drawing of $G^{*}+D_2$ with three crossings, and so $\mathrm{cr}(G^{*}+D_2)\le 3$.

Figure 6. The good drawing of $G^{*}+D_2$ with three crossings.

The graph $G^{*}+D_2$ contains a subgraph isomorphic to the join product of the cycle $C_3$, with $K_{1,3}\setminus e$ obtained by removing one edge from $K_{1,3}$, and it has been shown by Klešč [34] that $\mathrm{cr}(K_{1,3}\setminus e+C_n)=2⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+1$. As $\mathrm{cr}(G^{*}+D_2)\ge \mathrm{cr}(K_{1,3}\setminus e+C_3)=3$, the proof of Lemma 3 is complete. □

Theorem 3.

$\mathrm{cr}(G^{*}+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ for all integers $n\ge 1$.

Proof. 

The result is true for both $n=1$ and $n=2$ thanks to Lemma 3. In Figure 7, the edges of $K_{6,n}$ cross each other

$$6\left({\displaystyle \genfrac{}{}{0pt}{}{\lceil \frac{n}{2}\rceil }{2}}\right)+6\left({\displaystyle \genfrac{}{}{0pt}{}{\lfloor \frac{n}{2}\rfloor }{2}}\right)=6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋$$

times; each subgraph $T^i$, $i=1,\dots ,⌈\frac{n}{2}⌉$ on the right-hand side does not cross edges of $G^{*}$ and each subgraph $T^i$, $i=⌈\frac{n}{2}⌉+1,\dots ,n$ on the left-hand side crosses edges of $G^{*}$ exactly three times. Thus, $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings appear among edges of the graph $G^{*}+D_n$ in this drawing. To prove the reverse inequality by induction on n, suppose now that there is an optimal drawing D of $G^{*}+D_n$ with

$${\mathrm{cr}}_D(G^{*}+D_n)<6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋\text{for}\text{some}n\ge 3,$$

(3)

and let also

$$\mathrm{cr}(G^{*}+D_m)=6⌊{\displaystyle \frac{m}{2}}⌋⌊{\displaystyle \frac{m-1}{2}}⌋+3⌊{\displaystyle \frac{m}{2}}⌋\text{for}\text{each}\text{positive}\text{integer}m<n.$$

(4)

In the following, let $r=|R_D|$ and $s=|S_D|$. Assumption (3), together with ${\mathrm{cr}}_D\left(K_{6,n}\right)\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$ using (1), implies the following dependence of the number of crossings on edges of $G^{*}$ by possible subgraphs $T^i$ in D:

$${\mathrm{cr}}_D\left(G^{*}\right)+\sum _{T^i\in R_D}{\mathrm{cr}}_D(G^{*},T^i)+\sum _{T^i\in S_D}{\mathrm{cr}}_D(G^{*},T^i)+\sum _{T^i\notin R_D\cup S_D}{\mathrm{cr}}_D(G^{*},T^i)<3⌊{\displaystyle \frac{n}{2}}⌋,$$

i.e.,

$${\mathrm{cr}}_D\left(G^{*}\right)+0r+1s+2(n-r-s)<3⌊{\displaystyle \frac{n}{2}}⌋.$$

(5)

The obtained inequality (5) forces $2r+s\ge \lceil \frac{n}{2}\rceil +1$, and above all $s\ge \lceil \frac{n}{2}\rceil +1$ if $r=0$. Based on this consideration of the existence of a subgraph $T^i$ by which edges of $G^{*}$ are crossed at most once in D, a contradiction with assumption (3) will be obtained in all the discussed subcases.

Figure 7. The good drawing of $G^{*}+D_n$ with $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings.

Case 1: ${\mathrm{cr}}_D\left(G^{*}\right)=0$. There are two non-isomorphic planar drawings of the graph $G^{*}$ and in both of them, by using Lemma 2 or Corollary 1, we can obtain a more detailed description of an existing subgraph $T^i\in R_D\cup S_D$ that helps us to bound the number of crossings in the drawing D. Let us first consider the subdrawing of $G^{*}$ induced by D given in Figure 3a. The set $R_D$ is empty and therefore there are at least $\lceil \frac{n}{2}\rceil +1$ subgraphs $T^i\in S_D$ using inequality (5). For some $T^i\in S_D$, the edge $t_i{v}_4$ can cross just one of the edges $v_1{v}_2$, $v_1{v}_3$, and $v_2{v}_3$ of the graph $G^{*}$. The result of Lemma 2 allows less than $\lfloor \frac{n}{2}\rfloor$ crossings on the edge $v_1{v}_3$, which yields that there is at least one subgraph $T^i\in S_D$ by which one of the edges $v_1{v}_2$ or $v_2{v}_3$ is crossed in D. Due to the symmetry of the graph $G^{*}$, let $v_1{v}_2$ of $G^{*}$ be crossed by $T^i\in S_D$. This offers four ways of obtaining the subdrawing of $G^{*}\cup T^i$ depending on which region of $D(G^{*}\cup T^i\setminus \{v_1,v_3\})$ the edges $t_i{v}_1$ and $t_i{v}_3$ are placed in.

(a)

Let the subgraph $G^{*}\cup T^i$ be described by either the rotation $\left(163245\right)$ or $\left(153624\right)$, as shown in Figure 8. The edges of $G^{*}\cup T^i$ could be crossed four times only by a subgraph $T^j$ that crosses the edge $v_1{v}_3$ of $G^{*}$.

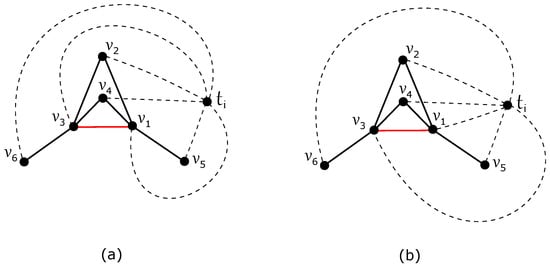Figure 8. One possible subdrawing of $G^{*}\cup T^i$ with ${\mathrm{cr}}_D(G^{*},T^i)=1$: (a) ${\mathrm{rot}}_D\left(t_i\right)=\left(163245\right)$; (b) ${\mathrm{rot}}_D\left(t_i\right)=\left(153624\right)$.

Let $\alpha$ be the number of subgraphs $T^j$ by which $v_1{v}_3$ of $G^{*}$ is crossed in D, and note that $\alpha <\lfloor \frac{n}{2}\rfloor$, again by Lemma 2. By fixing $G^{*}\cup T^i$, we obtain

$${\mathrm{cr}}_D(G^{*}+D_n)={\mathrm{cr}}_D\left(K_{6,n-1}\right)+{\mathrm{cr}}_D(K_{6,n-1},G^{*}\cup T^i)+{\mathrm{cr}}_D(G^{*}\cup T^i)$$

$$\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5(n-\alpha -1)+4\alpha +1$$

$$=6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n-\alpha -4\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n+1-⌊{\displaystyle \frac{n}{2}}⌋-4$$

$$\ge 6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋.$$

(b)

Let $G^{*}\cup T^i$ be described by the rotation $\left(156324\right)$ and let $\alpha$ be the number of subgraphs $T^j$ by which the edge $v_1{v}_3$ of $G^{*}$ is crossed in D. Also, by fixing $G^{*}\cup T^i$ we have

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+6(n-\alpha -1)+3\alpha +1$$

$$=6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+6n-3\alpha -5\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+6n+3\left(1-⌊{\displaystyle \frac{n}{2}}⌋\right)-5$$

$$\ge 6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋.$$

(c)

Let $G^{*}\cup T^i$ be described by the rotation $\left(136245\right)$ and let $\beta$ be the number of subgraphs $T^j$ by which $v_2{v}_3$ of $G^{*}$ is crossed in D. In this subcase, $\beta <\lfloor \frac{n}{2}\rfloor$ using Lemma 1. Again, by fixing $G^{*}\cup T^i$ we obtain

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5(n-\beta -1)+4\beta +1$$

$$=6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n-\beta -4\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n+1-⌊{\displaystyle \frac{n}{2}}⌋-4$$

$$\ge 6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋.$$

All three subcases contradict assumption (3) in D. Now, let us turn to the subdrawing of $G^{*}$ induced by D given in Figure 3b. By Corollary 1, the set $R_D$ cannot be empty because any subgraph $T^i\notin R_D$ crosses at least one edge of $G^{*}\setminus \left\{v_1{v}_3\right\}$. Thus, we deal with the possible configurations ${\mathcal{A}}_p$ from ${\mathcal{M}}_D$. Now, we discuss two main subcases:

(a)

${\mathcal{A}}_p\in {\mathcal{M}}_D$ for some $p\in \{3,4\}$. In the rest of the proof, assume that $T^i\in R_D$ with the configuration ${\mathcal{A}}_p$ of $F^i$. Let $\alpha$ be the number of subgraphs $T^j$ by which the edge $v_1{v}_3$ of $G^{*}$ is crossed in D. By fixing $G^{*}\cup T^i$, we obtain

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5(n-\alpha -1)+4\alpha +0$$

$$=6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n-\alpha -5\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n+1-⌊{\displaystyle \frac{n}{2}}⌋-5$$

$$\ge 6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋.$$

(b)

${\mathcal{A}}_p\notin {\mathcal{M}}_D$ for $p=3,4$, that is, ${\mathcal{A}}_q\in {\mathcal{M}}_D$ for some $q\in \{1,2\}$. Without loss of generality, let us also consider that the number of all subgraphs with the configuration ${\mathcal{A}}_1$ is at least as great as the number of all subgraphs with the configuration ${\mathcal{A}}_2$, and let $T^i\in R_D$ be such a subgraph with the configuration ${\mathcal{A}}_1$ of $F^i$. It is easy to verify (thanks to the knowledge of the drawing) that edges of $T^i$ are crossed by any $T^j\in S_D$ at least three times. So, let us denote $S_D\left(T^i\right)=\{T^j\in S_D:{\mathrm{cr}}_D(T^i,T^j)=3\}$. If $T^j$ is a subgraph from the non-empty set $S_D\left(T^i\right)$, then we can check over all possible regions of $D(G^{*}\cup T^i\cup T^j)$ that the edges of $G^{*}\cup T^i\cup T^j$ are crossed at least 9, 8, and 7 times by each subgraph $T^k\in R_D$, $k\ne i$, $T^k\in S_D$, $k\ne j$, and $T^k\in T_D$, respectively. By fixing $G^{*}\cup T^i\cup T^j$, we obtain

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊{\displaystyle \frac{n-2}{2}}⌋⌊{\displaystyle \frac{n-3}{2}}⌋+9(r-1)+8(s-1)+7t+6(n-r-s-t)+4$$

$$=6⌊{\displaystyle \frac{n-2}{2}}⌋⌊{\displaystyle \frac{n-3}{2}}⌋+6n+(3r+2s+t)-13\ge 6⌊{\displaystyle \frac{n-2}{2}}⌋⌊{\displaystyle \frac{n-3}{2}}⌋$$

$$+6n+3⌈{\displaystyle \frac{n}{2}}⌉+1-13\ge 6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋,$$

where ${\mathrm{cr}}_D(G^{*}\cup T^i\cup T^j)=4$ and the modified inequality (5), for $1s+2t+3(n-r-s-t)<3\lfloor \frac{n}{2}\rfloor$, forces $3r+2s+t>3\lceil \frac{n}{2}\rceil$ if $t=|T_D|$. This also contradicts assumption (3). Therefore, assuming $S_D\left(T^i\right)=\varnothing$, the edges of $G^{*}\cup T^i$ are crossed by each $T^j\in S_D$ more than four times.

If there is a subgraph $T^j\notin R_D\cup S_D$ such that ${\mathrm{cr}}_D(G^{*}\cup T^i,T^j)<4$, then the vertex $t_j$ must be placed in the triangular region of subdrawing $D\left(G^{*}\right)$ with three vertices $v_1$, $v_2$, and $v_3$ of $G^{*}$ on its boundary, and ${\mathrm{cr}}_D(G^{*}\cup T^i,T^j)=3$ enforces ${\mathrm{cr}}_D(T^i,T^j)=0$. Thus, by fixing $T^i\cup T^j$ we obtain

$${\mathrm{cr}}_D(G^{*}+D_{n-2})+{\mathrm{cr}}_D(T^i\cup T^j)+{\mathrm{cr}}_D(K_{6,n-2},T^i\cup T^j)+{\mathrm{cr}}_D(G^{*},T^i\cup T^j)$$

$$\ge 6⌊{\displaystyle \frac{n-2}{2}}⌋⌊{\displaystyle \frac{n-3}{2}}⌋+3⌊{\displaystyle \frac{n-2}{2}}⌋+0+6(n-2)+3=6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋,$$

because the edges of $T^i\cup T^j$ must be crossed by each other $T^k$ at least six times using ${\mathrm{cr}}_D\left(K_{6,3}\right)\ge 6$, again due to (1). The obtained crossing number also forces a contradiction with (3) in D and confirms that each $T^j\notin R_D\cup S_D$ must cross edges of $G^{*}\cup T^i$ at least four times.

Let $\gamma$ be the number of subgraphs $T^j$ by which edges of $G^{*}\cup T^i$ are crossed just four times in D. If $\gamma \ge ⌊\frac{n}{2}⌋$, Lemma 1 contradicts assumption (3) in D. Finally, in the case of $\gamma <⌊\frac{n}{2}⌋$, by fixing $G^{*}\cup T^i$ we obtain

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5(r-1)-1+5s+4\gamma +5(n-r-s-\gamma )$$

$$=6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n-\gamma -6\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n+1-⌊{\displaystyle \frac{n}{2}}⌋-6$$

$$\ge 6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋.$$

Case 2: ${\mathrm{cr}}_D\left(G^{*}\right)\ge 1$. Let us first consider the subdrawing of $G^{*}$ induced by D given in Figure 3c or Figure 3d. For both subdrawings, Corollary 1 again enforces the non-empty set $R_D$. Let $\delta$ be the number of subgraphs $T^j$ by which the edge $v_3{v}_4$ of $G^{*}$ is crossed in D, and note that $\delta <\lfloor \frac{n}{2}\rfloor$ using Lemma 1. By fixing $G^{*}\cup T^i$ for some $T^i\in R_D$, we obtain

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5(n-\delta -1)+4\delta +1$$

$$=6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n-\delta -4\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n+1-⌊{\displaystyle \frac{n}{2}}⌋-4$$

$$\ge 6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋.$$

Now, let us turn to the subdrawing of $G^{*}$ induced by D, given in Figure 3e. In the following, we must discuss two main subcases with respect to either the non-empty or empty set $R_D$.

(a)

The set $R_D$ is non-empty, that is, we deal with the possible configurations ${\mathcal{B}}_p$ from ${\mathcal{N}}_D$. We are able to use a similar discussion technique as in case 1 for configurations ${\mathcal{A}}_p\in {\mathcal{M}}_D$. If there is a subgraph $T^i\in R_D$ with the configuration ${\mathcal{B}}_p\in {\mathcal{N}}_D$ of $F^i$ for some $p\in \{3,4\}$, then edges of $G^{*}\cup T^i$ are crossed at least five times by each other subgraph $T^j$. By fixing $G^{*}\cup T^i$, we have

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5(n-1)+1\ge 6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋.$$

If ${\mathcal{B}}_q\in {\mathcal{N}}_D$ only for some $q\in \{1,2\}$, we choose $T^i\in R_D$ with the configuration ${\mathcal{B}}_q$ of $F^i$ (again with more frequent occurrences in D). We define the set $S_D\left(T^i\right)$ in the same way as above with the same discussion with respect to whether $S_D\left(T^i\right)$ is empty or not. Since there is no subgraph $T^j\notin R_D\cup S_D$ with exactly three crossings on edges of $G^{*}\cup T^i$, we also define $\gamma$ as the number of subgraphs $T^j$ such that ${\mathrm{cr}}_D(G^{*}\cup T^i,T^j)=4$. Consequently, both considered subcases with respect to $\gamma$ force a contradiction with (3) in D.

(b)

The set $R_D$ is empty. Again by Corollary 1, there is a subgraph $T^i\notin R_D$ whose edges cross only the edge $v_1{v}_3$ of $G^{*}$. In this case, the vertex $t_i$ is placed in the triangular region of subdrawing $D\left(G^{*}\right)$ with two vertices $v_1$ and $v_3$ of $G^{*}$ on its boundary, and ${\mathrm{cr}}_D(G^{*}\setminus \left\{v_1{v}_3\right\},T^i)=0$ enforces four crossings on the edge $v_1{v}_3$ of $G^{*}$ in $D(G^{*}\cup T^i)$. The edges of $G^{*}\cup T^i$ could be crossed four times only by a subgraph $T^j\in T_D$ that crosses both edges $v_1{v}_4$ and $v_2{v}_3$ of $G^{*}$, or by a subgraph $T^j\in S_D$ that crosses exactly one of them. For all three possibilities, we can verify over all possible regions of $D(G^{*}\cup T^i\cup T^j)$ that edges of $G^{*}\cup T^i\cup T^j$ are crossed at least eight times by each other $T^k$. Thus, by fixing $G^{*}\cup T^i\cup T^j$ we obtain

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊{\displaystyle \frac{n-2}{2}}⌋⌊{\displaystyle \frac{n-3}{2}}⌋+8(n-2)+9\ge 6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋.$$

Finally, let us assume the subdrawing of $G^{*}$ induced by D given in Figure 3f, Figure 3g, or Figure 3h. In all three subdrawings, we define $\epsilon$ as the number of subgraphs $T^j$ by which the edge $v_2{v}_3$ of $G^{*}$ is crossed in D if the set $R_D$ is non-empty. By fixing $G^{*}\cup T^i$ for some $T^i\in R_D$, we obtain

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5(n-\epsilon -1)+4\epsilon +2$$

$$=6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n-\epsilon -3\ge 6⌊{\displaystyle \frac{n-1}{2}}⌋⌊{\displaystyle \frac{n-2}{2}}⌋+5n+1-⌊{\displaystyle \frac{n}{2}}⌋-3$$

$$\ge 6⌊{\displaystyle \frac{n}{2}}⌋⌊{\displaystyle \frac{n-1}{2}}⌋+3⌊{\displaystyle \frac{n}{2}}⌋.$$

We have shown, in all cases, that there is no optimal drawing D of $G^{*}+D_n$ with less than $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings, and the proof of Theorem 3 is complete. □

3. Two Other Graphs

Finally, into the drawing in Figure 7, we can include both edges $v_2{v}_5$ and $v_2{v}_6$ to the graph $G^{*}$ with no new crossing, and we obtain two new graphs $G_1$ and $G_2$, represented in Figure 9. Therefore, the drawings of $G_1+D_n$ and $G_2+D_n$ with exactly $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings are obtained; see Figure 10. On the other hand, $G^{*}+D_n$ is a subgraph of $G_1+D_n$ that is a subgraph of $G_2+D_n$, and therefore $\mathrm{cr}(G_2+D_n)\ge \mathrm{cr}(G_1+D_n)\ge \mathrm{cr}(G^{*}+D_n)$. Thus, the next results are obvious.

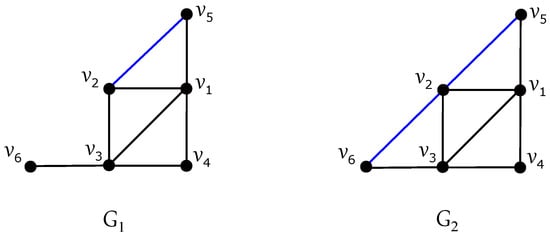
Figure 9. Two graphs $G_1$ and $G_2$ by adding new edges to the graph $G^{*}$.

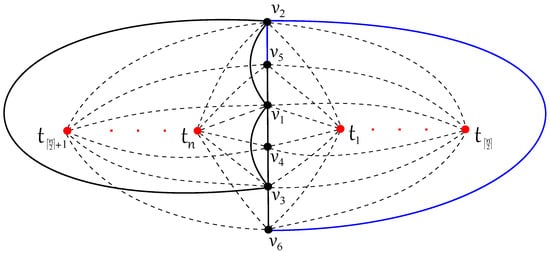
Figure 10. The good drawing of $G_2+D_n$ with $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ crossings.

Corollary 2.

$\mathrm{cr}(G_1+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ for $n\ge 1$.

Corollary 3.

$\mathrm{cr}(G_2+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3⌊\frac{n}{2}⌋$ for $n\ge 1$.

It is well known that adding edges increases the number of possible non-isomorphic drawings of the resulting graph. If we sought to prove the crossing numbers of the graphs $G_1+D_n$ or $G_2+D_n$ without knowing the crossing number of $G^{*}+D_n$, their determination would be significantly more challenging due to the increased number of subcases.

4. Conclusions

In the presented paper, we focused on establishing the same crossing numbers for the three join products of connected 6-vertex graphs with the discrete graph $D_n$. We began by clarifying the crossing number of the join product $G^{*}+D_n$, where $G^{*}$ is a graph isomorphic to the path $P_4$ with two additional vertices adjacent to two inner vertices of $P_4$. Here, the upper bound on the number of crossings of the join product $G^{*}+D_n$ arises from its demonstrated good drawing. The lower bounds on the crossing number of $G^{*}+D_n$ were derived for all eight possible non-isomorphic good drawings of the graph $G^{*}$. Some drawings of the graph $G^{*}$ were excluded from the investigation due to their failure to occur in optimal drawings. In this context, cyclic rotations, subgraphs with fixed edges, and exact crossing number values for join products involving two particular subgraphs $H_k$ of the graph $G^{*}$ with $D_n$ were utilized. As a result, the exact value $\mathrm{cr}(G^{*}+D_n)$ was obtained. Finally, two new graphs $G_1$ and $G_2$ were investigated by adding one or two additional edges that do not induce crossings to the graph $G^{*}$. For them, $\mathrm{cr}(G_1+D_n)$ and $\mathrm{cr}(G_2+D_n)$ were determined.

The main theorem presented in this paper is utilized to determine the crossing number of the join product of a specific type of graph on six vertices with the discrete graphs. We also hypothesize that the presented techniques, with slight modification, can be used to derive an unknown crossing number of other graphs that have six vertices but more edges. This approach is equally applicable to graphs that include $G^{*}$ as a subgraph. These discussions encompass some integration of graphs with discrete graphs, but also with paths and cycles.