Incentive Mechanism for Cloud Service Offloading in Edge–Cloud Computing Environment
Abstract
1. Introduction
2. Related Work
2.1. Service Offloading in Mobile Cloud Computing
2.2. Edge Computing
2.3. Incentive Mechanism in Edge Computing
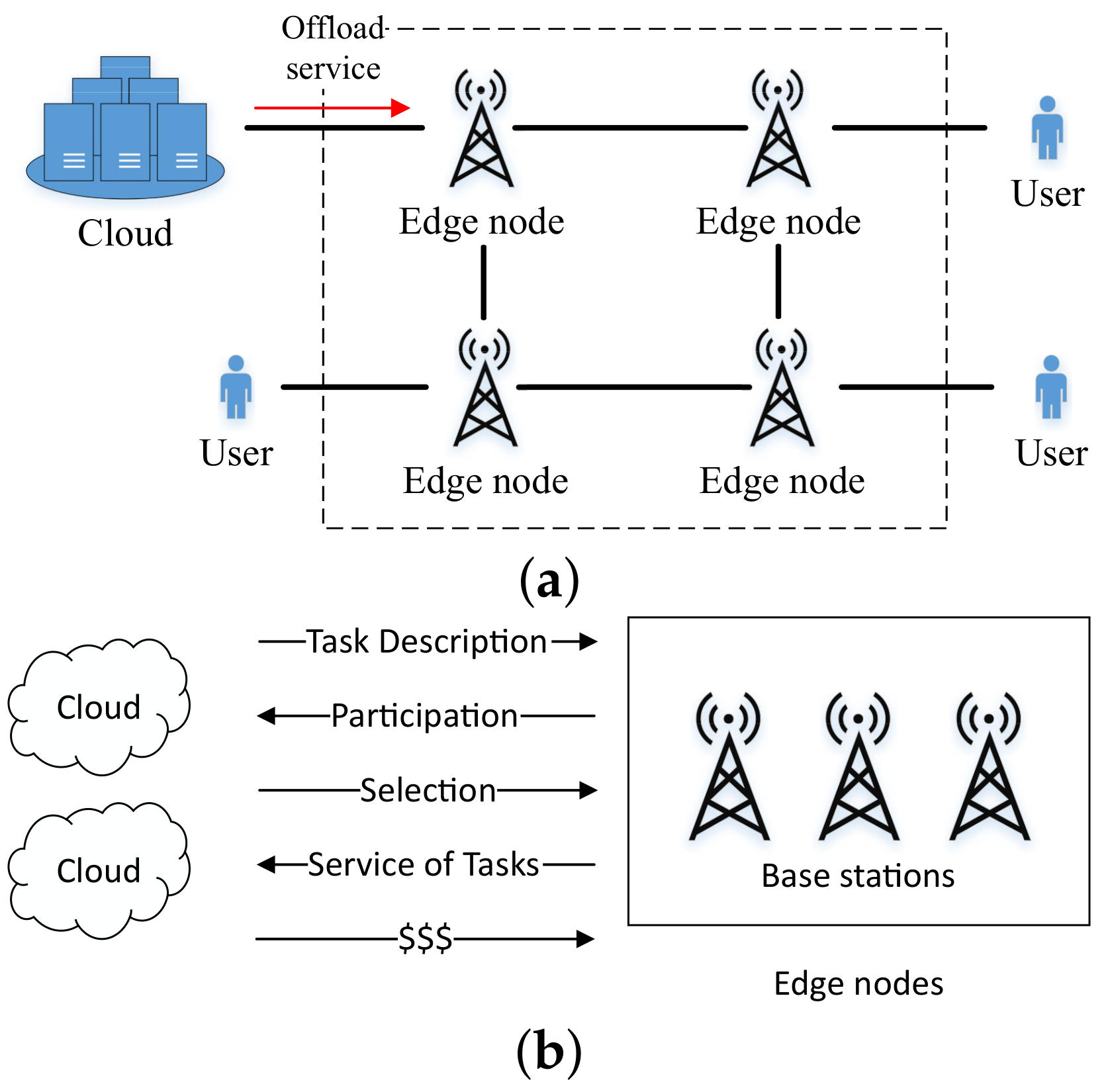
3. System Model and Problem Formulation
3.1. Problem Description
3.2. Model of Offloaded Cloud Task
3.3. Challenges and Overview of the Solving Process
4. Stackelberg Game-Based Incentive Mechanism
4.1. Stackelberg Equilibrium
4.2. Optimal Resource Strategy
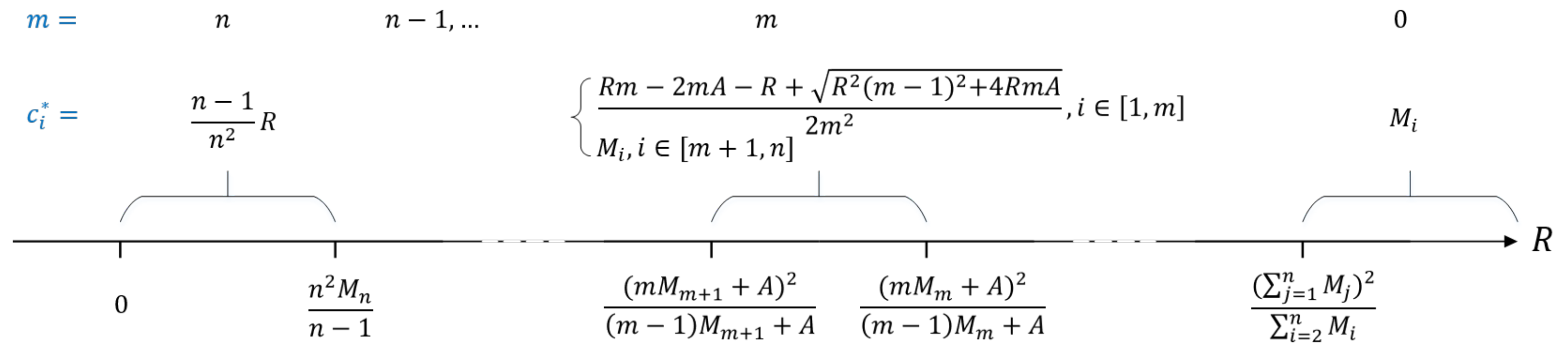
4.3. Optimal Reward Strategy
- If , we have , and .
- If , we have , and . Since , the situation is infeasible.
- If , it follows that . Then, we obtain , where .
- If , it follows that . Then, we obtain .
5. Efficient Algorithm for Solving the Optimal Strategy
| Algorithm 1: Computation of the SE. |
Require: Sort of all edge nodes in the descent order. Ensure: 1: 2: - 3: 4: 5: return |
| Algorithm 2:- |
Require: in a descent order Ensure: 1: if then 2: 3: else if then 4: 5: else 6: - 7: 8: 9: end if 10: return |
| Algorithm 3:- |
Require: in a descent order Ensure: m 1: for each do 2: 3: if then 4: 5: end if 6: end for 7: return m |
6. Rethinking Our Incentive Mechanism in Dynamic Edge–Cloud Computing Environment
7. Performance Evaluation
7.1. Settings of Evaluation
7.2. Performance Evaluation Results
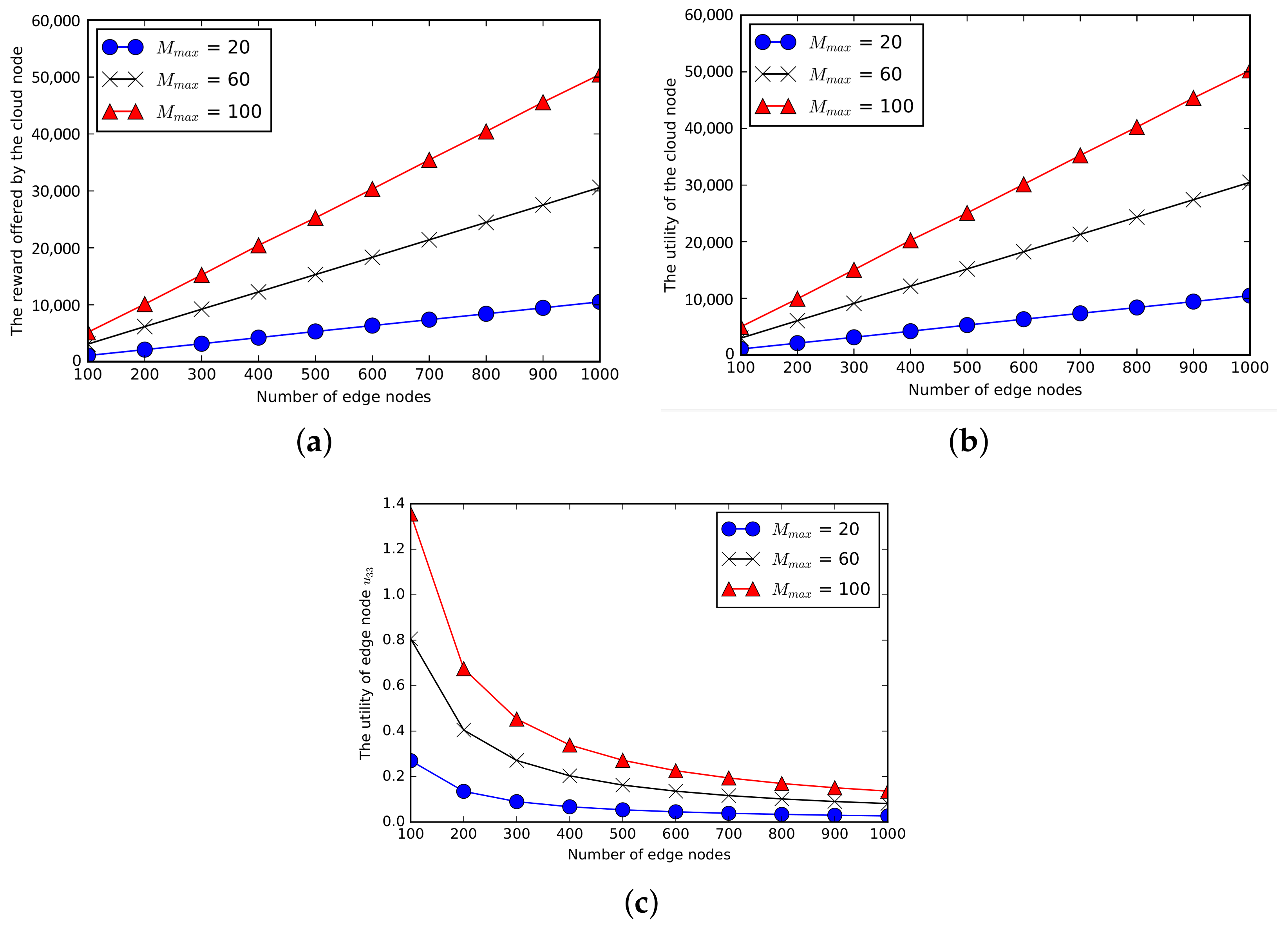
7.2.1. The Reward and Utility of the Cloud Node
7.2.2. The Resource Cost and Utility of Edge Nodes
7.2.3. Impact of the Resource Cost Budget of Edge Nodes on Utilities
7.3. Comparison with the Benchmarks
- Random assignment (Ran.). In the random assignment, the cloud node assigns the offloaded cloud task to edge nodes randomly. The resource cost edge node i pays for the offloaded cloud task is random but cannot exceed its cost budget . The total reward the cloud node provides R is random as well.
- Proportional assignment (Prop.). In the proportional assignment, each edge node is assigned a portion of the offloaded cloud task. The total reward the cloud node provides is .
- Social welfare maximization (SWM). In the social welfare maximization scheme, the objective is to maximize the system-level utility . The respective utility of the cloud node or the edge node is not considered.
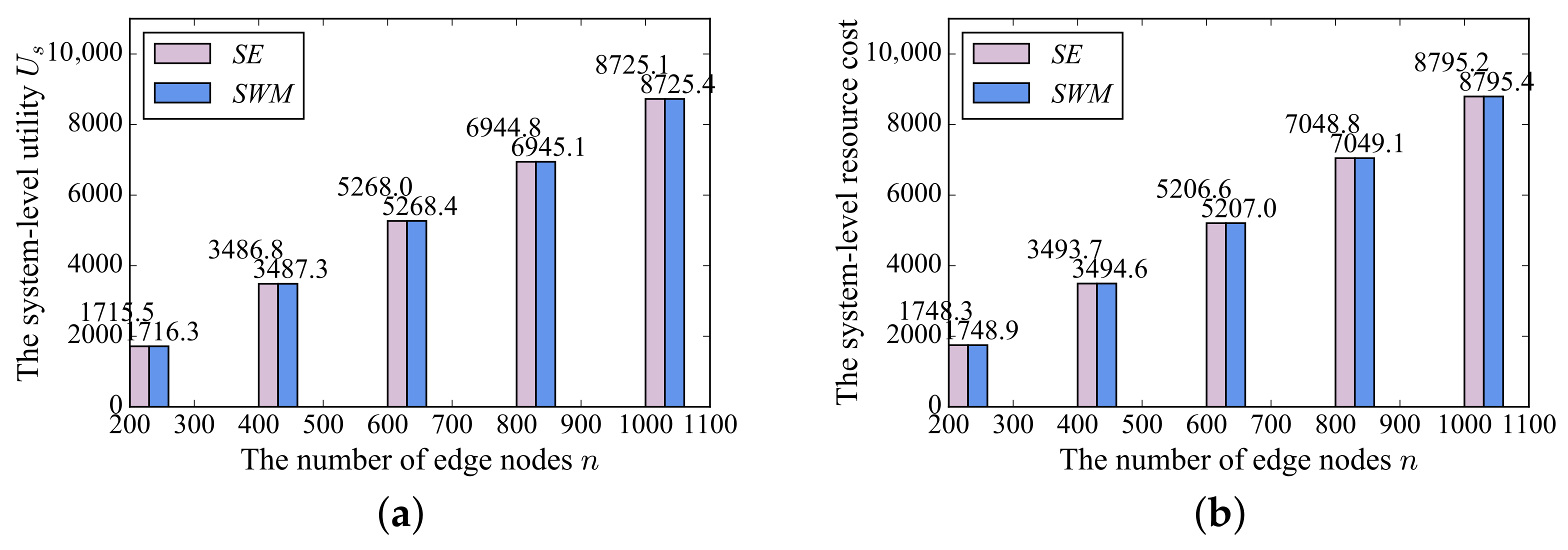
7.4. Comparison on the System-Level Utility with SWM Scheme
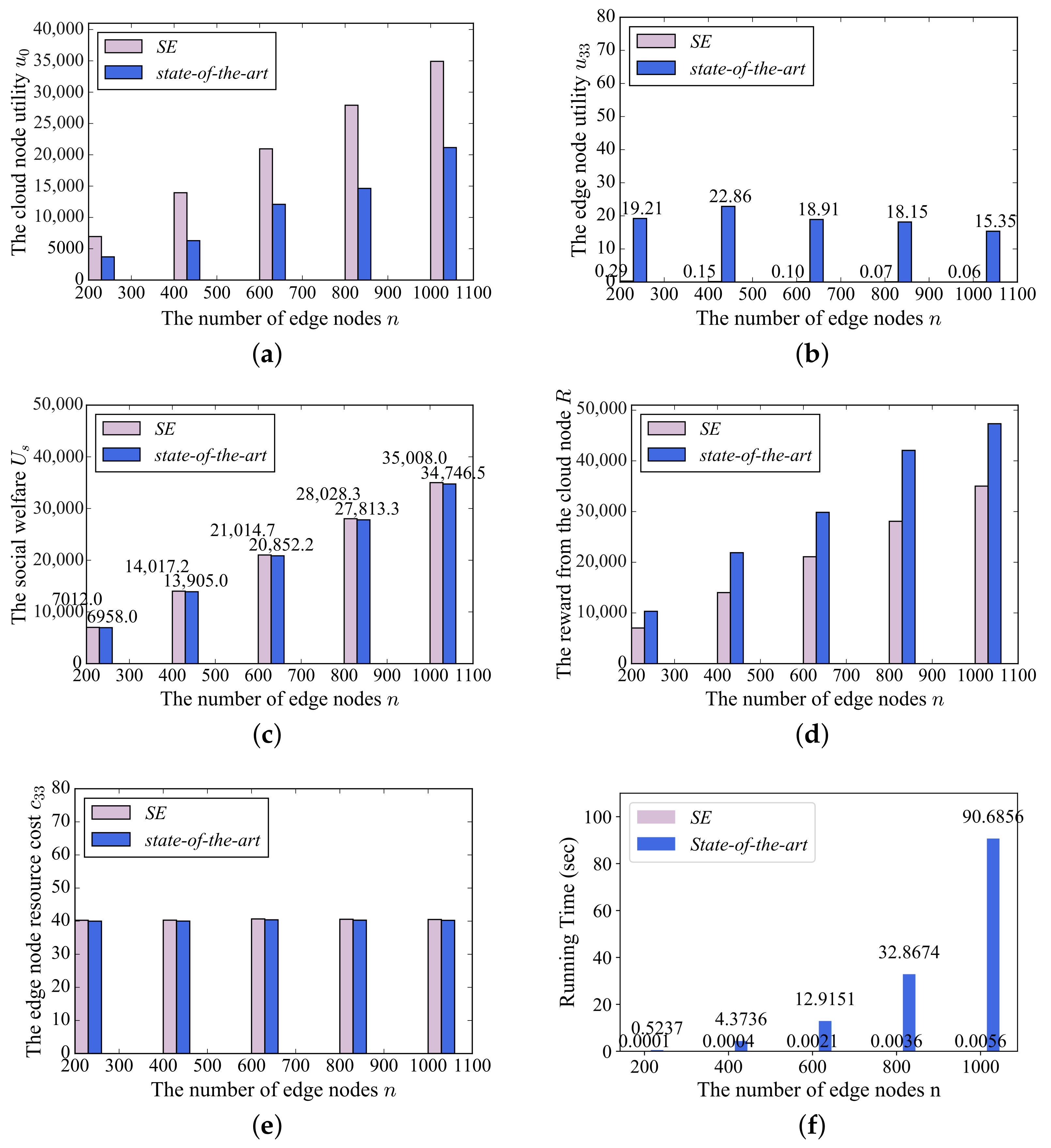
7.5. Comparison with the State-of-the-Art Mechanism
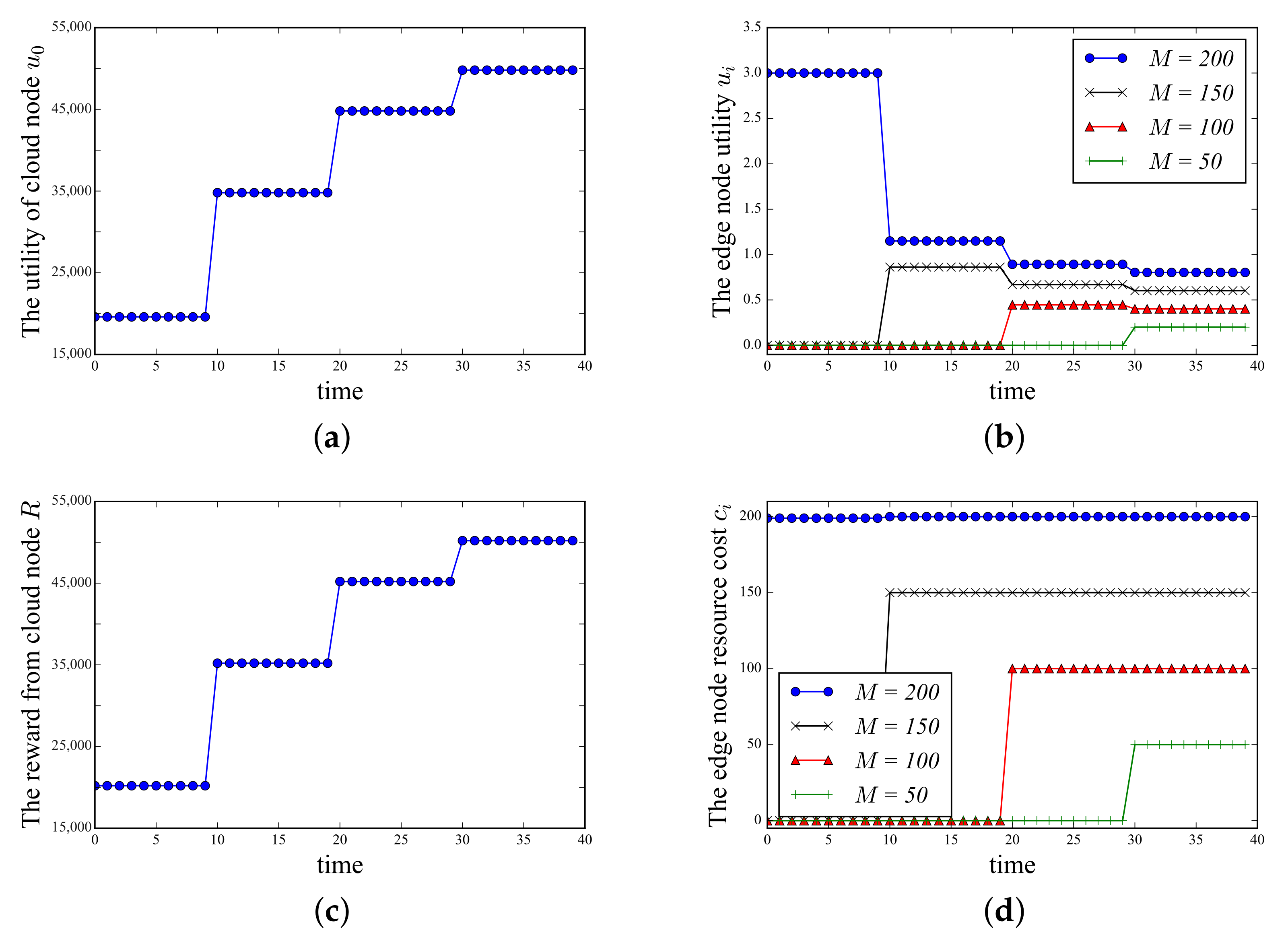
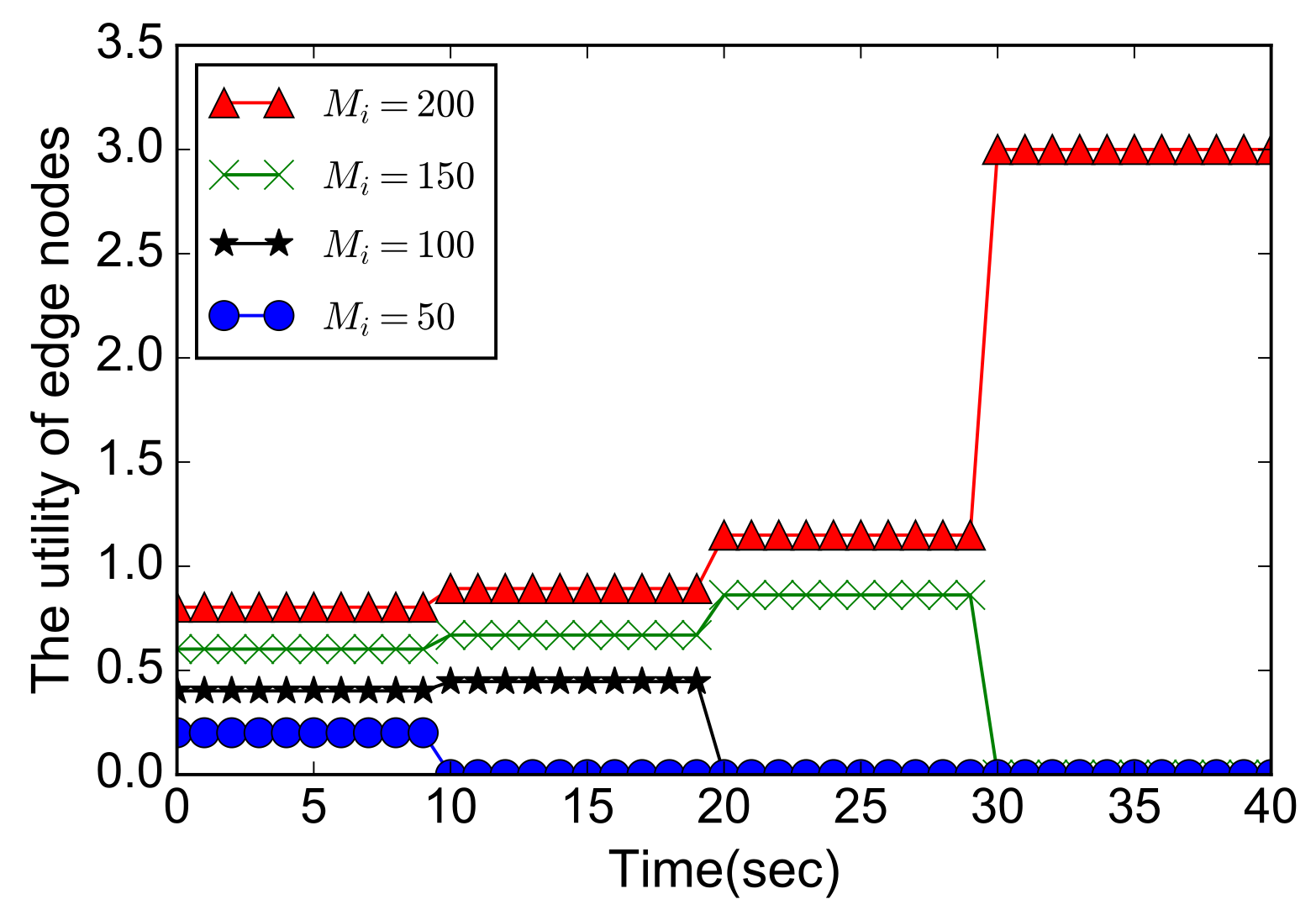
7.6. Performance Analysis in the Dynamic Scenarios
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mahmud, R.; Buyya, R. Fog Computing: A Taxonomy, Survey and Future Directions; Springer: Berlin/Heidelberg, Germany, 2016; pp. 103–139. [Google Scholar]
- Mach, P.; Becvar, Z. Mobile Edge Computing: A Survey on Architecture and Computation Offloading. IEEE Commun. Surv. Tutor. 2017, 19, 1628–1656. [Google Scholar] [CrossRef]
- Arif, A.; Ahmed, E. A Survey on Mobile Edge Computing. In Proceedings of the 10th International Conference on Intelligent Systems and Control (ISCO), Vietri sul Mare, Italy, 16–18 May 2016; pp. 1–8. [Google Scholar]
- Bonomi, F.; Milito, R.A.; Zhu, J.; Addepalli, S. Fog computing and its role in the internet of things. In Proceedings of the Military Communications and Information Systems Conference (MCC), Oeiras, Portugal, 8–9 October 2012; pp. 13–16. [Google Scholar]
- Mohan, N.; Kangasharju, J. Edge-Fog cloud: A distributed cloud for Internet of Things computations. In Proceedings of the Cloudification of the Internet of Things (CIoT), Paris, France, 23–25 November 2016; pp. 1–6. [Google Scholar]
- Yang, B.; Chai, W.K.; Xu, Z.; Katsaros, K.V.; Pavlou, G. Cost-Efficient NFV-Enabled Mobile Edge-Cloud for Low Latency Mobile Applications. IEEE Trans. Netw. Serv. Manag. 2018, 15, 475–488. [Google Scholar] [CrossRef]
- Wang, S.; Urgaonkar, R.; Zafer, M.; He, T.; Chan, K.S.; Leung, K.K. Dynamic service migration in mobile edge-clouds. In Proceedings of the 2015 12th Working IEEE/IFIP Conference on Software Architecture, Washington, DC, USA, 4–8 May 2015; pp. 1–9. [Google Scholar]
- He, T.; Khamfroush, H.; Wang, S.; Porta, T.L.; Stein, S. It’s Hard to Share: Joint Service Placement and Request Scheduling in Edge Clouds with Sharable and Non-Sharable Resources. In Proceedings of the 2018 IEEE 38th International Conference on Distributed Computing Systems (ICDCS), Vienna, Austria, 2–5 July 2018; pp. 365–375. [Google Scholar]
- Pasteris, S.; Wang, S.; Herbster, M.; He, T. Service Placement with Provable Guarantees in Heterogeneous Edge Computing Systems. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 514–522. [Google Scholar]
- Poularakis, K.; Llorca, J.; Tulino, A.M.; Taylor, I.; Tassiulas, L. Joint Service Placement and Request Routing in Multi-cell Mobile Edge Computing Networks. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 10–18. [Google Scholar]
- Chun, B.G.; Ihm, S.; Maniatis, P.; Naik, M.; Patti, A. Clonecloud: Elastic execution between mobile device and cloud. In Proceedings of the Sixth Conference on Computer Systems, Salzburg, Austria, 10 April 2011; ACM: New York, NY, USA, 2011; pp. 301–314. [Google Scholar]
- Yang, L.; Cao, J.; Cheng, H.; Ji, Y. Multi-user computation partitioning for latency sensitive mobile cloud applications. IEEE Trans. Comput. 2014, 64, 2253–2266. [Google Scholar] [CrossRef]
- Farhadi, V.; Mehmeti, F.; He, T.; Porta, T.L.; Khamfroush, H.; Wang, S.; Chan, K.S. Service Placement and Request Scheduling for Data-intensive Applications in Edge Clouds. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 1279–1287. [Google Scholar]
- Josilo, S.; Dán, G. Wireless and Computing Resource Allocation for Selfish Computation Offloading in Edge Computing. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 2467–2475. [Google Scholar]
- Zhang, W.; Li, S.; Liu, L.; Jia, Z.; Zhang, Y.; Raychaudhuri, D. Hetero-Edge: Orchestration of Real-time Vision Applications on Heterogeneous Edge Clouds. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 1270–1278. [Google Scholar]
- Ouyang, T.; Li, R.; Chen, X.; Zhou, Z.; Tang, X. Adaptive User-managed Service Placement for Mobile Edge Computing: An Online Learning Approach. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 1468–1476. [Google Scholar]
- Mohan, N.; Zavodovski, A.; Zhou, P.; Kangasharju, J. Anveshak: Placing Edge Servers In The Wild. In Proceedings of the 2018 Workshop on Mobile Edge Communications, SIGCOMM, Budapest, Hungary, 20 August 2018; pp. 7–12. [Google Scholar]
- Silva, P.; Pérez, C.; Desprez, F. Efficient Heuristics for Placing Large-Scale Distributed Applications on Multiple Clouds. In Proceedings of the 2016 16th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGrid), Cartagena, Colombia, 16–19 May 2016; pp. 483–492. [Google Scholar]
- Sahoo, J.; Salahuddin, M.A.; Glitho, R.H.; Elbiaze, H.; Ajib, W. A Survey on Replica Server Placement Algorithms for Content Delivery Networks. IEEE Commun. Surv. Tutor. 2017, 19, 1002–1026. [Google Scholar] [CrossRef]
- Huang, Y.; Song, X.; Ye, F.; Yang, Y.; Li, X. Fair Caching Algorithms for Peer Data Sharing in Pervasive Edge Computing Environments. In Proceedings of the 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 June 2017; pp. 605–614. [Google Scholar]
- Bernardini, C.; Silverston, T.; Festor, O. MPC: Popularity-based caching strategy for content centric networks. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 3619–3623. [Google Scholar]
- Xie, J.; Qian, C.; Guo, D.; Wang, M.; Shi, S.; Chen, H. Efficient Indexing Mechanism for Unstructured Data Sharing Systems in Edge Computing. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 820–828. [Google Scholar]
- Zhang, H.; Zeng, K. Pairwise Markov Chain: A Task Scheduling Strategy for Privacy-Preserving SIFT on Edge. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 1432–1440. [Google Scholar]
- Myerson, R.B. Game Theory; Harvard University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Fernando, N.; Loke, S.W.; Rahayu, W. Mobile cloud computing: A survey. Future Gener. Comput. Syst. 2013, 29, 84–106. [Google Scholar] [CrossRef]
- Dinh, H.T.; Lee, C.; Niyato, D.; Wang, P. A survey of mobile cloud computing: Architecture, applications, and approaches. Wirel. Commun. Mob. Comput. 2013, 13, 1587–1611. [Google Scholar] [CrossRef]
- Chen, X. Decentralized computation offloading game for mobile cloud computing. IEEE Trans. Parallel Distrib. Syst. 2014, 26, 974–983. [Google Scholar] [CrossRef]
- Liu, Y.; Lee, M.J.; Zheng, Y. Adaptive multi-resource allocation for cloudlet-based mobile cloud computing system. IEEE Trans. Mob. Comput. 2015, 15, 2398–2410. [Google Scholar] [CrossRef]
- Zhou, B.; Dastjerdi, A.V.; Calheiros, R.N.; Srirama, S.N.; Buyya, R. mCloud: A context-aware offloading framework for heterogeneous mobile cloud. IEEE Trans. Serv. Comput. 2015, 10, 797–810. [Google Scholar] [CrossRef]
- Shih, C.S.; Wang, Y.H.; Chang, N. Multi-tier elastic computation framework for mobile cloud computing. In Proceedings of the 2015 3rd IEEE International Conference on Mobile Cloud Computing, Services, and Engineering, San Francisco, CA, USA, 30 March–3 April 2015; IEEE: Piscataway, NJ, USA; pp. 223–232. [Google Scholar]
- Gao, B.; Zhou, Z.; Liu, F.; Xu, F. Winning at the starting line: Joint network selection and service placement for mobile edge computing. In Proceedings of the IEEE INFOCOM 2019-IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1459–1467. [Google Scholar]
- Meng, J.; Tan, H.; Xu, C.; Cao, W.; Liu, L.; Li, B. Dedas: Online Task Dispatching and Scheduling with Bandwidth Constraint in Edge Computing. In Proceedings of the IEEE INFOCOM 2019-IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2287–2295. [Google Scholar]
- Chen, S.; Jiao, L.; Wang, L.; Liu, F. An online market mechanism for edge emergency demand response via cloudlet control. In Proceedings of the IEEE INFOCOM 2019-IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2566–2574. [Google Scholar]
- Zhou, Z.; Liao, H.; Gu, B.; Huq, K.M.S.; Mumtaz, S.; Rodriguez, J. Robust mobile crowd sensing: When deep learning meets edge computing. IEEE Netw. 2018, 32, 54–60. [Google Scholar] [CrossRef]
- Shen, F.; Zhang, G.; Zhang, C.; Yang, Y.; Yang, R. An incentive framework for resource sensing in fog computing networks. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Zheng, Z.; Song, L.; Han, Z.; Li, G.Y.; Poor, H.V. A Stackelberg game approach to proactive caching in large-scale mobile edge networks. IEEE Trans. Wirel. Commun. 2018, 17, 5198–5211. [Google Scholar] [CrossRef]
- Zeng, M.; Li, Y.; Zhang, K.; Waqas, M.; Jin, D. Incentive mechanism design for computation offloading in heterogeneous fog computing: A contract-based approach. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Liu, Y.; Xu, C.; Zhan, Y.; Liu, Z.; Guan, J.; Zhang, H. Incentive mechanism for computation offloading using edge computing: A Stackelberg game approach. Comput. Netw. 2017, 129, 399–409. [Google Scholar] [CrossRef]
- Kang, X.; Wu, Y. Incentive Mechanism Design for Heterogeneous Peer-to-Peer Networks: A Stackelberg Game Approach. arXiv 2014, arXiv:1408.0727. [Google Scholar]
- Yang, D.; Xue, G.; Fang, X.; Tang, J. Crowdsourcing to smartphones: Incentive mechanism design for mobile phone sensing. In Proceedings of the 18th Annual International Conference on Mobile Computing and Networking, Istanbul, Turkey, 22–26 August 2012; pp. 173–184. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press, Inc.: Cambridge, UK, 2004; pp. 215–231. [Google Scholar]
- Kang, X.; Zhang, R.; Liang, Y.; Garg, H.K. Optimal Power Allocation Strategies for Fading Cognitive Radio Channels with Primary User Outage Constraint. IEEE J. Sel. Areas Commun. 2011, 29, 374–383. [Google Scholar] [CrossRef]
- Reniers, V.; Van Landuyt, D.; Viviani, P.; Lagaisse, B.; Lombardi, R.; Joosen, W. Analysis of architectural variants for auditable blockchain-based private data sharing. In Proceedings of the 34th ACM/SIGAPP Symposium on Applied Computing, Limassol, Cyprus, 8–12 April 2019; pp. 346–354. [Google Scholar]
- Shi, P.; Wang, H.; Yang, S.; Chen, C.; Yang, W. Blockchain-based trusted data sharing among trusted stakeholders in IoT. Softw. Pract. Exp. 2021, 51, 2051–2064. [Google Scholar] [CrossRef]
- Huang, Y.; Zeng, Y.; Ye, F.; Yang, Y. Fair and protected profit sharing for data trading in pervasive edge computing environments. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1718–1727. [Google Scholar]

| Notation | Description |
|---|---|
| N | the set of edge nodes |
| S | the set of selected edge nodes |
| n | the number of selected edge nodes |
| R | the reward offered by a cloud node |
| the utility of edge node i | |
| the utility of a cloud node | |
| the weight of the resource cost in | |
| the resource cost of edge node i | |
| the resource cost budget of edge node i | |
| the upper bound of resource cost budget among edge nodes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, C.; Xie, J.; Liu, Z. Incentive Mechanism for Cloud Service Offloading in Edge–Cloud Computing Environment. Mathematics 2025, 13, 1685. https://doi.org/10.3390/math13101685
Yao C, Xie J, Liu Z. Incentive Mechanism for Cloud Service Offloading in Edge–Cloud Computing Environment. Mathematics. 2025; 13(10):1685. https://doi.org/10.3390/math13101685
Chicago/Turabian StyleYao, Chendie, Junjie Xie, and Zhong Liu. 2025. "Incentive Mechanism for Cloud Service Offloading in Edge–Cloud Computing Environment" Mathematics 13, no. 10: 1685. https://doi.org/10.3390/math13101685
APA StyleYao, C., Xie, J., & Liu, Z. (2025). Incentive Mechanism for Cloud Service Offloading in Edge–Cloud Computing Environment. Mathematics, 13(10), 1685. https://doi.org/10.3390/math13101685






