Parametric Analysis of Auxetic Honeycombs
Abstract
1. Introduction
2. Modelling: Analytical and Numerical Formulations
2.1. Theoretical Background
2.2. Finite Elements Model
3. Results
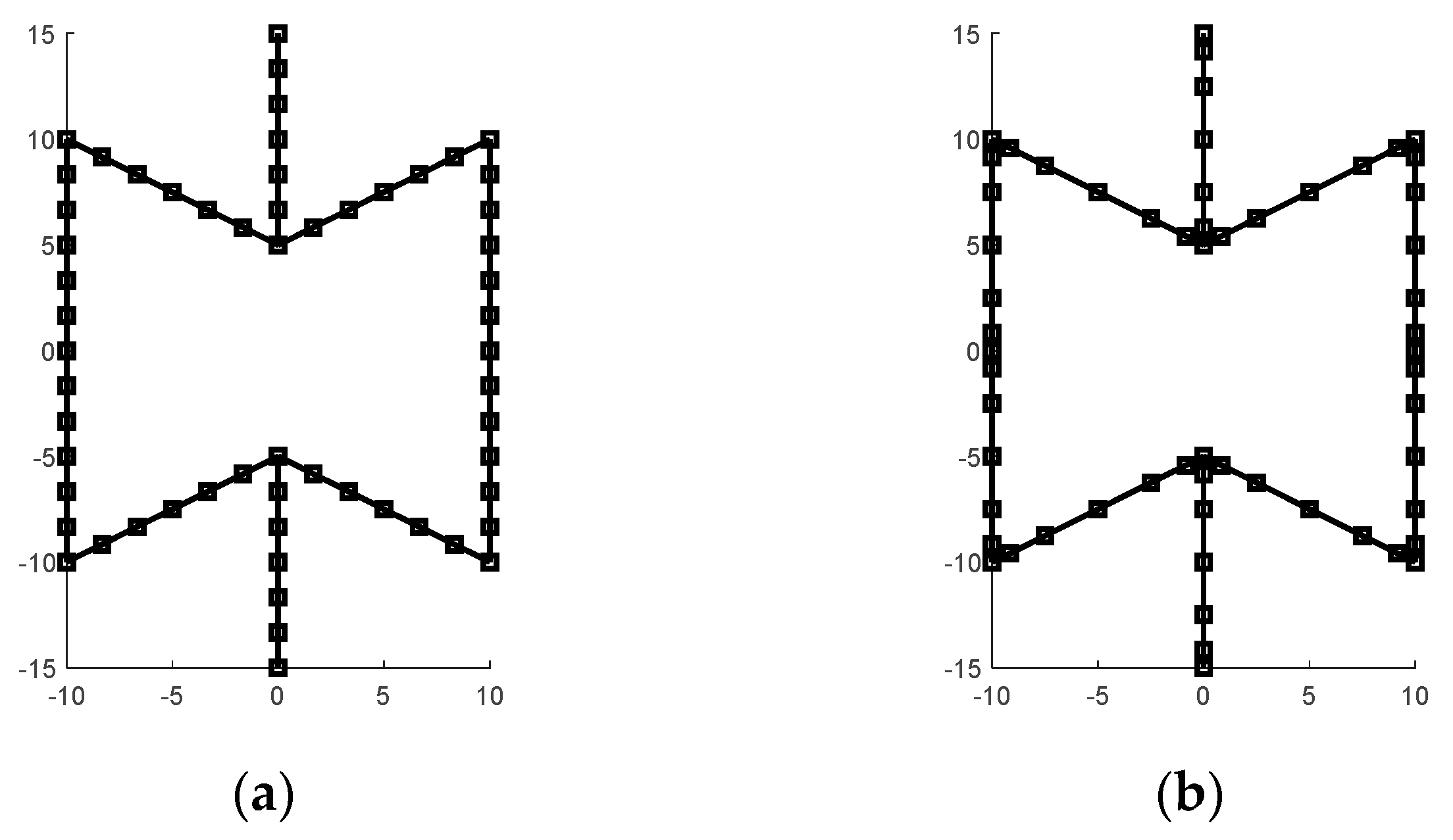
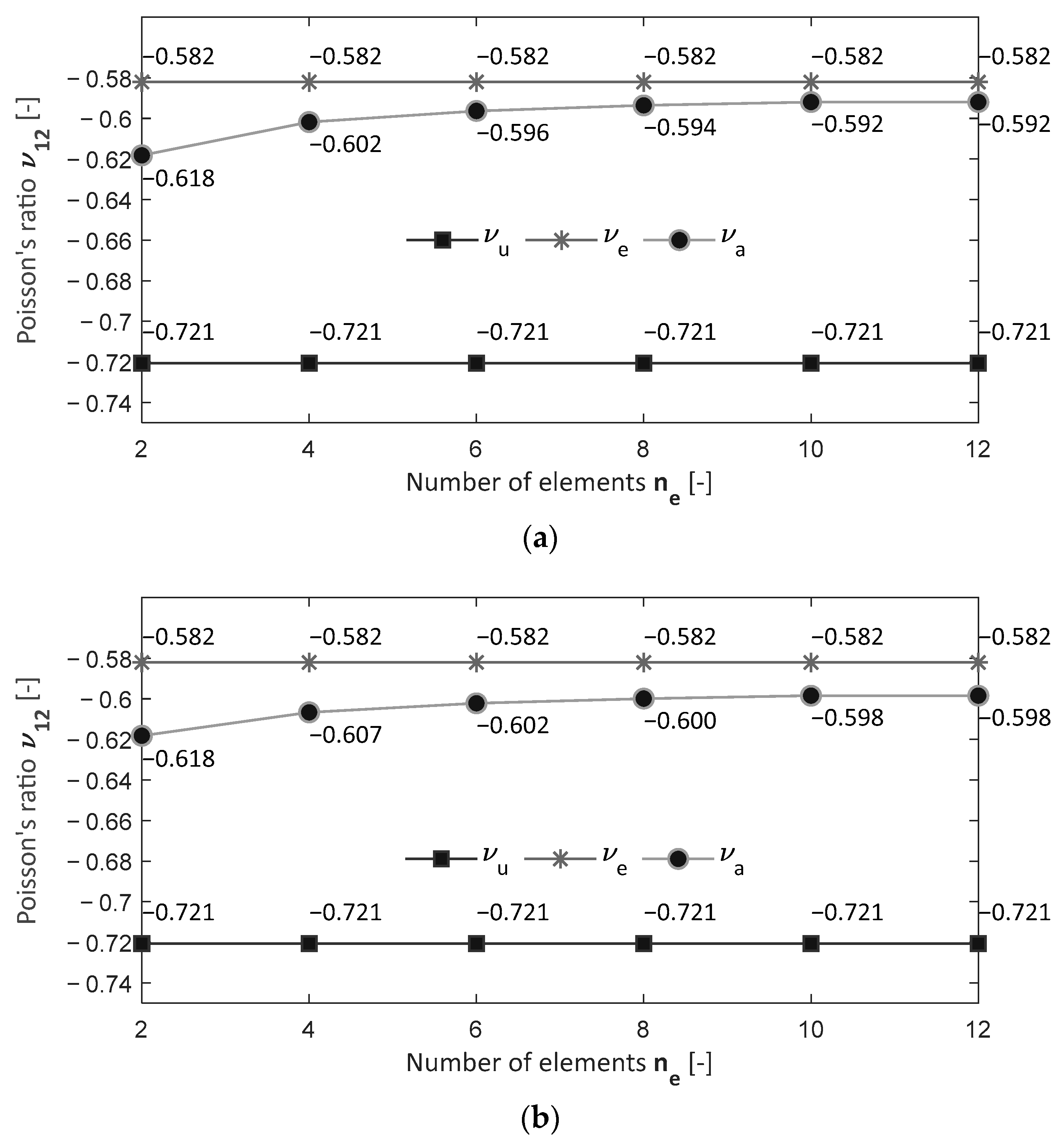
3.1. Validation of the Numerical Model—Convergence Analysis
- cell level : for the central feature, two pairs of nodes are identified: the first one is located at the midpoint of the vertical ligaments, while the second pair is located at the convergence of the horizontal (or inclined) ligaments (Figure 2f);
- structure level—maximum displacement : two pairs of nodes are defined: the first pair is defined by the nodes located on the left and right side at the middle of the structure, while the second pair is defined by points located on top and bottom of the structure (Figure 2f);
- structure level—average displacement . The averaged displacements [20] of the nodes located on the left and right sides are evaluated to define the first pair of coordinates. The second dimension is defined by nodes located on the top and bottom of the structure.
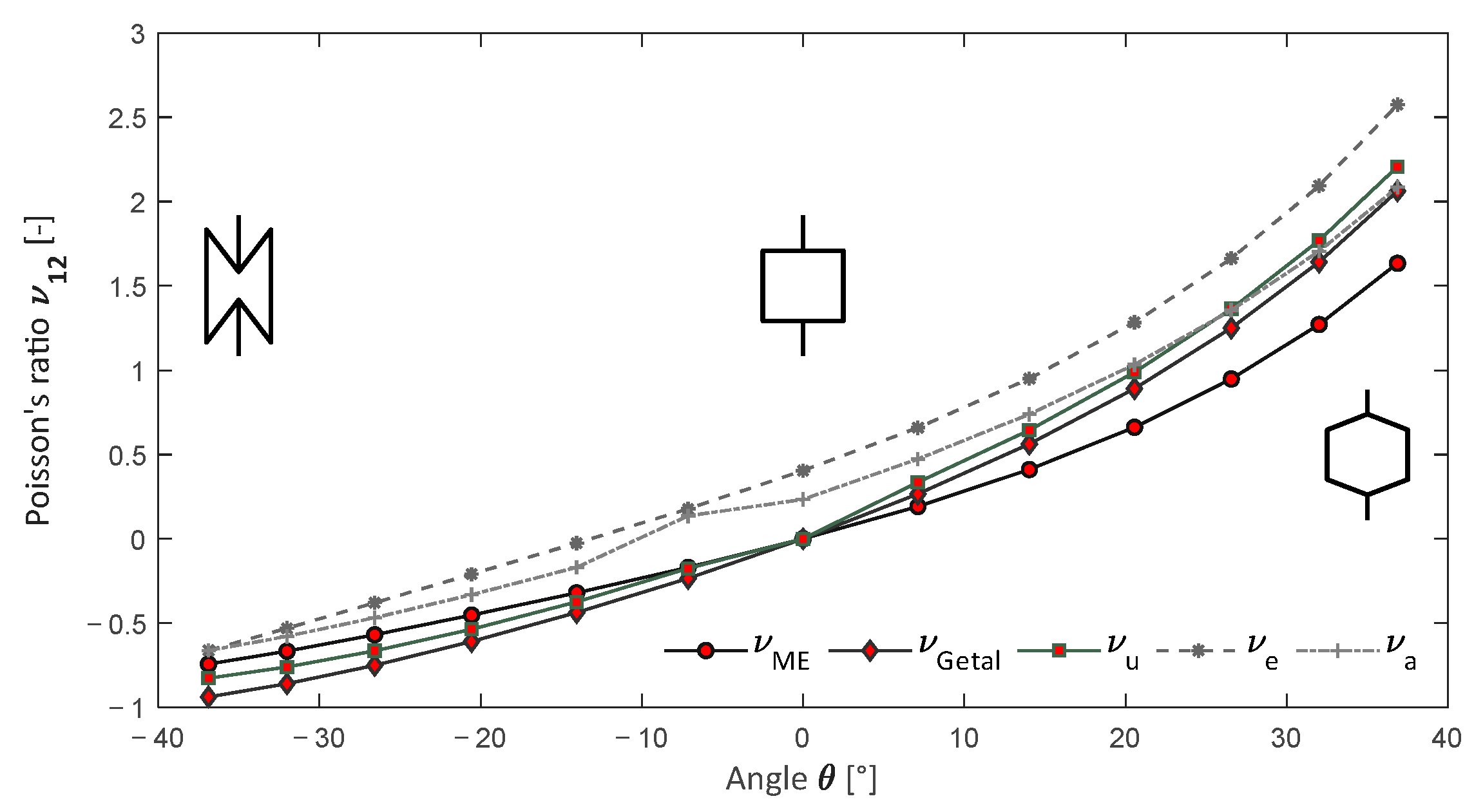
3.2. Analytical vs. Numerical Solution
3.3. Experimental Work
4. Discussion
4.1. Configuration of the Structure
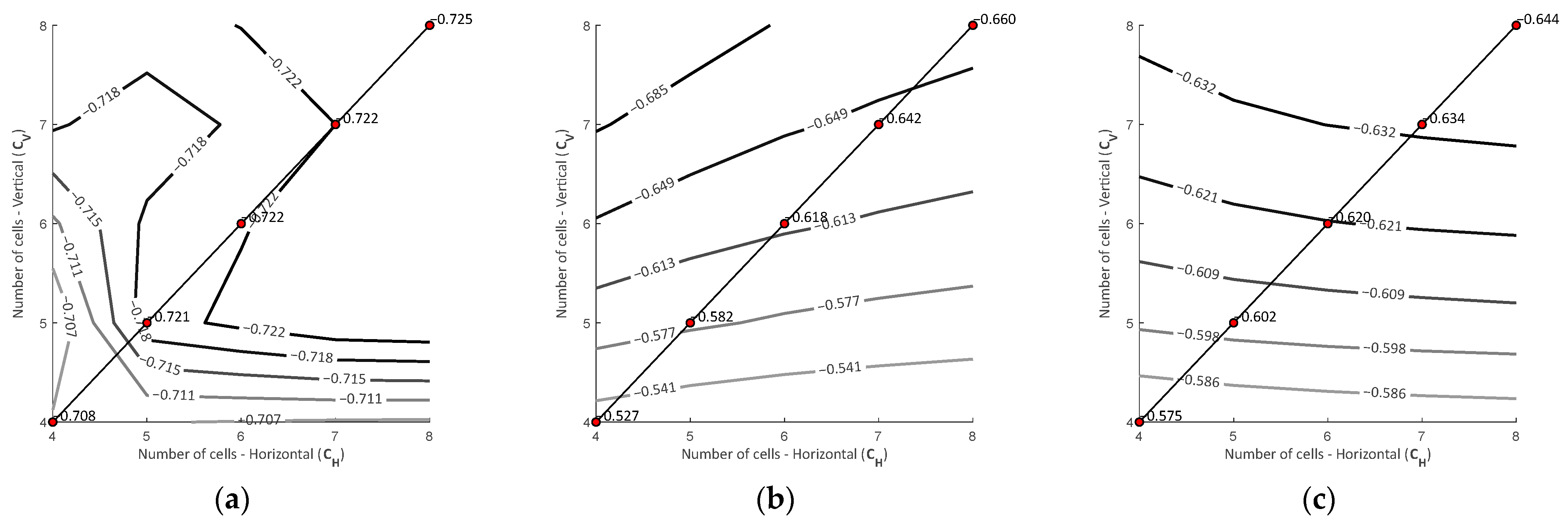
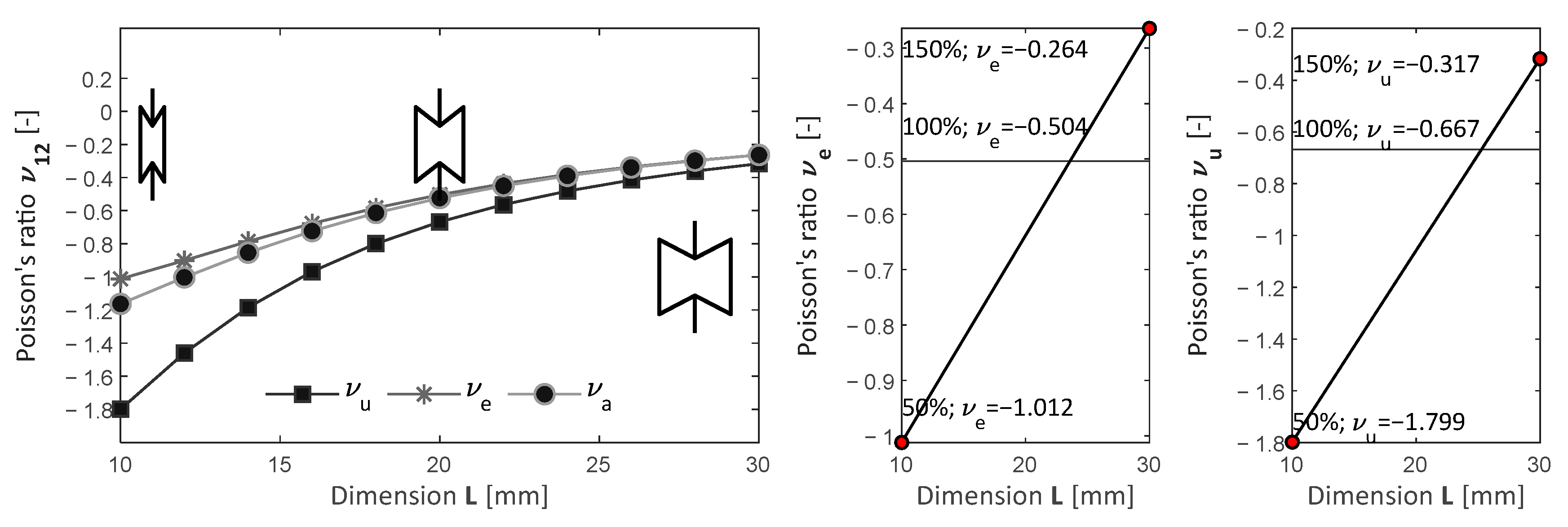
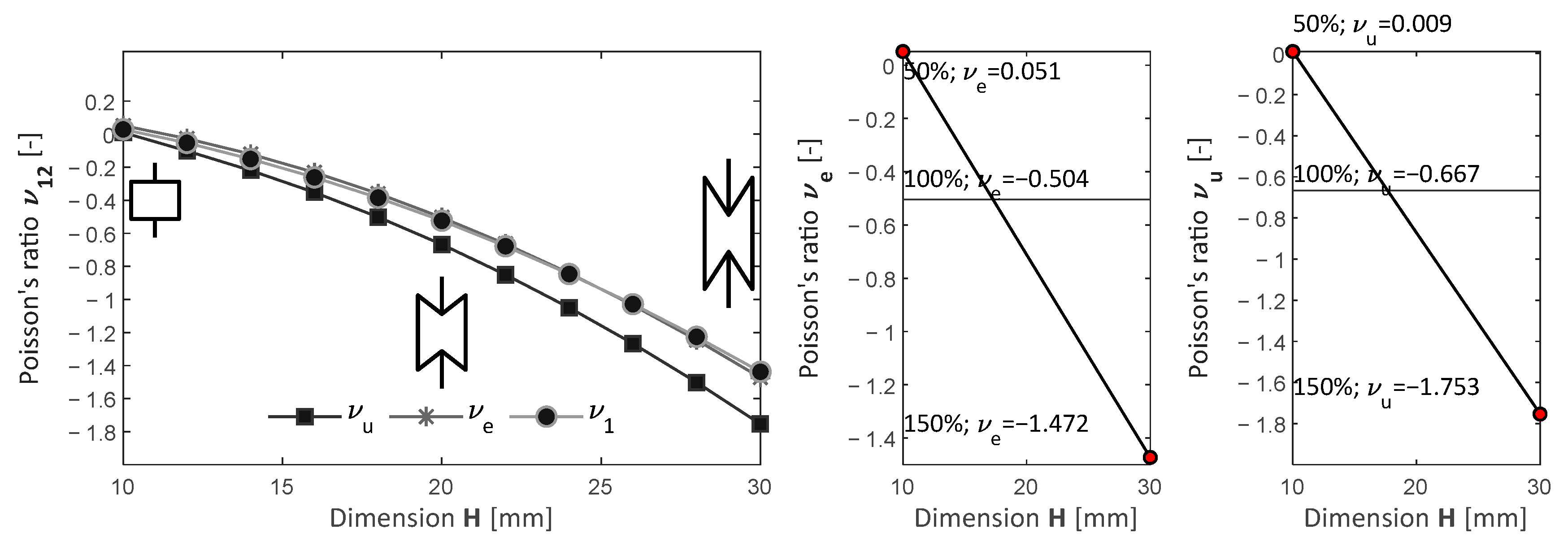
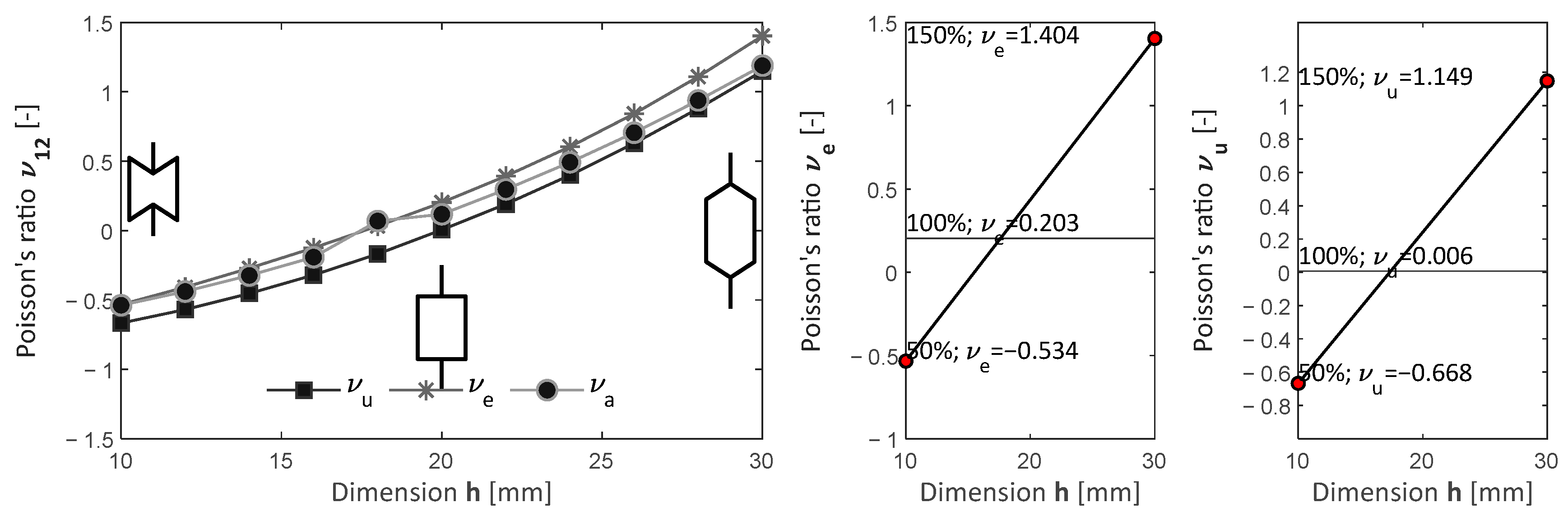
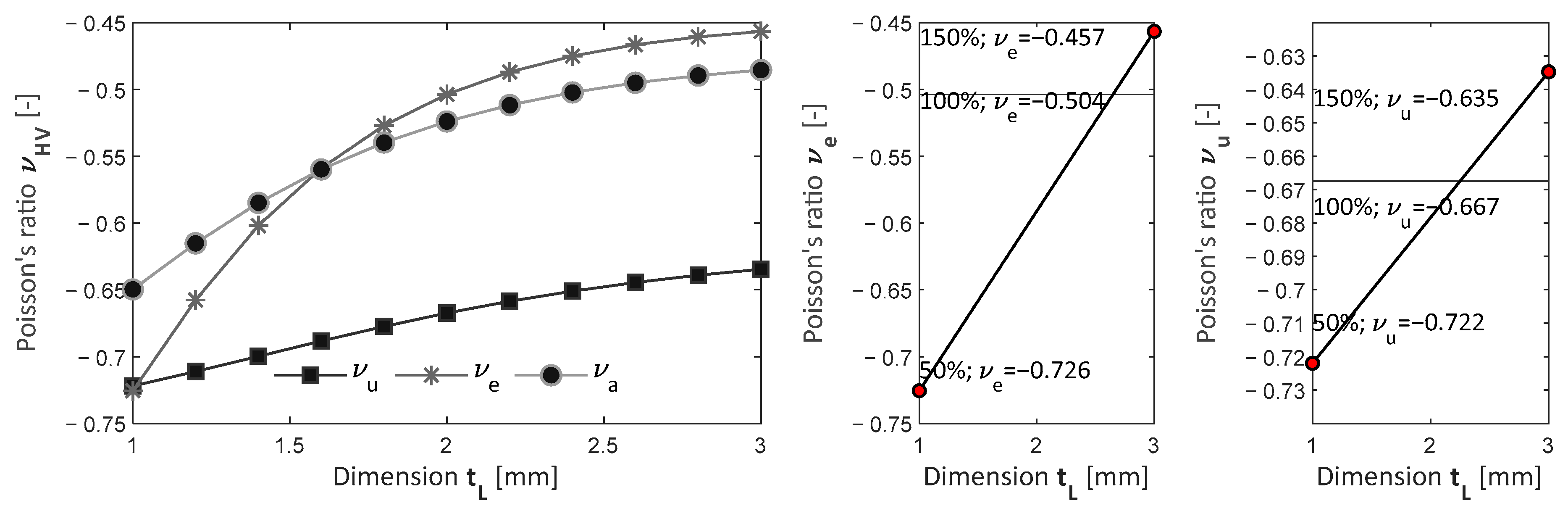
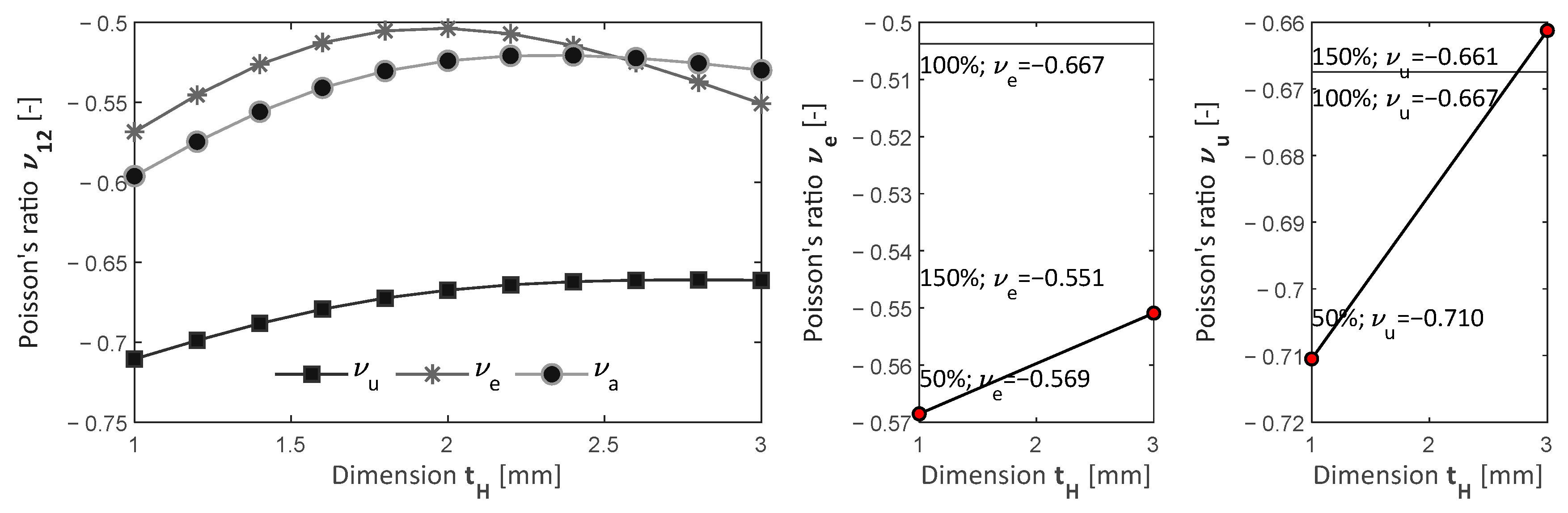
4.2. Parametric Analysis
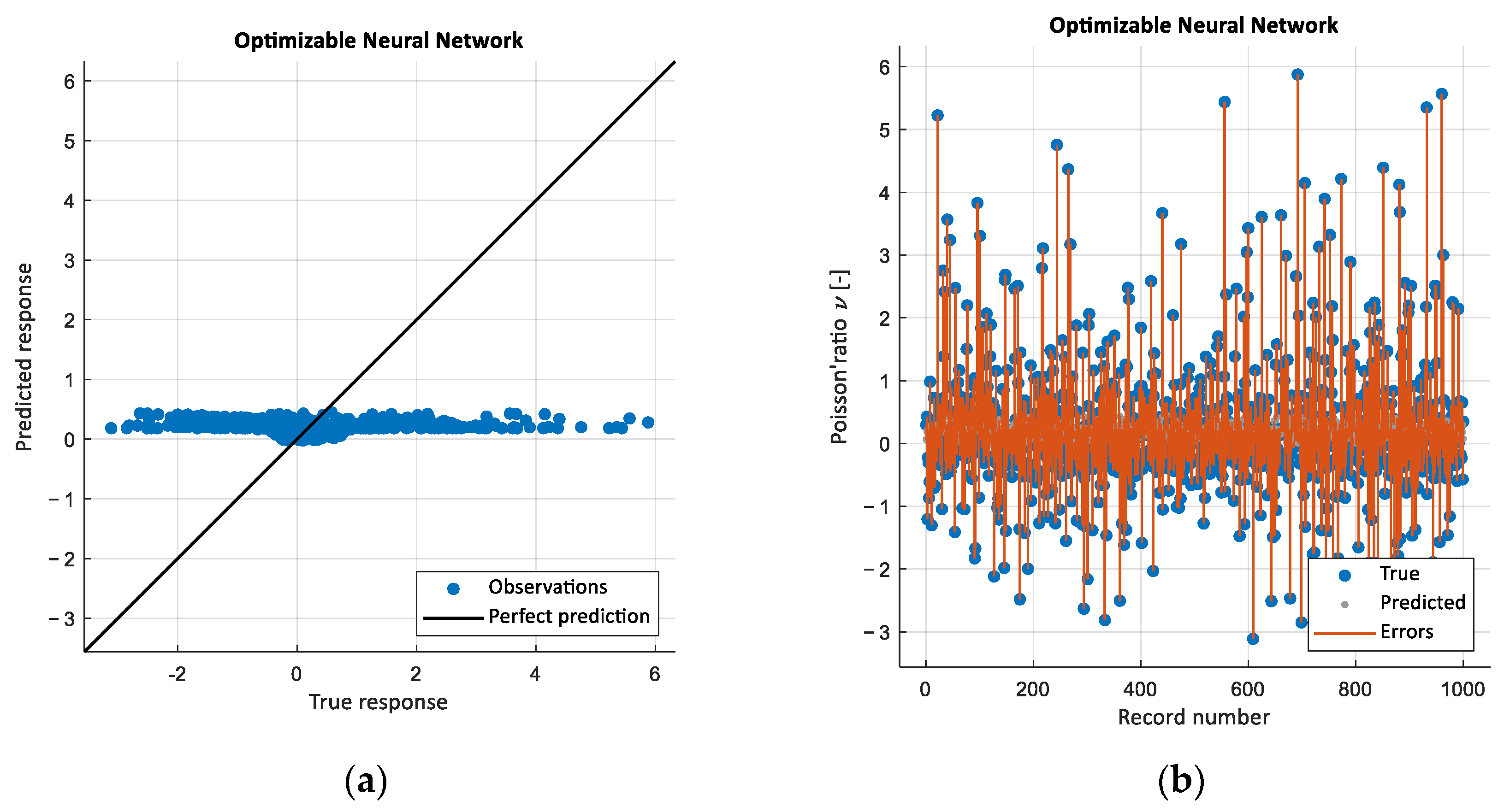
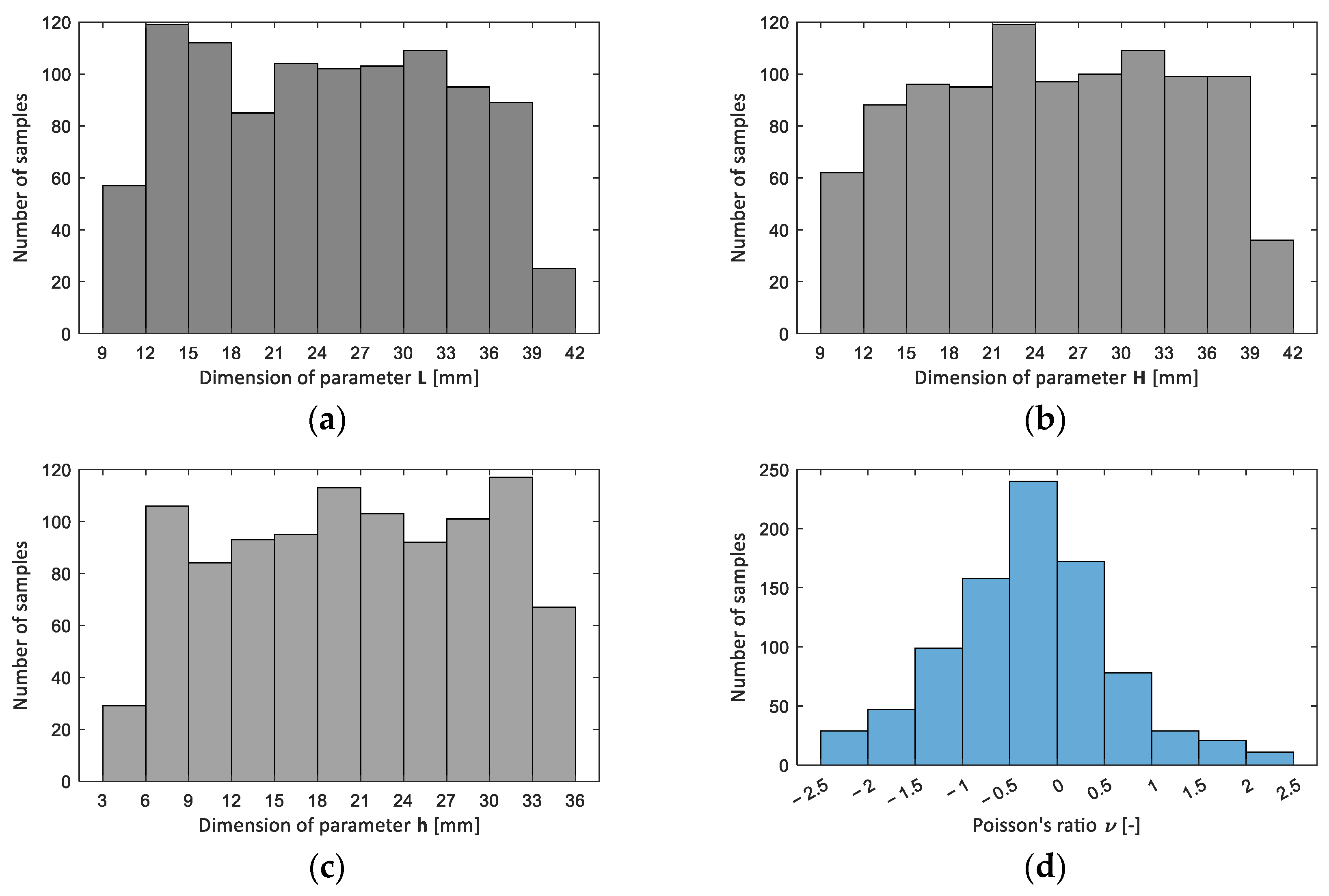
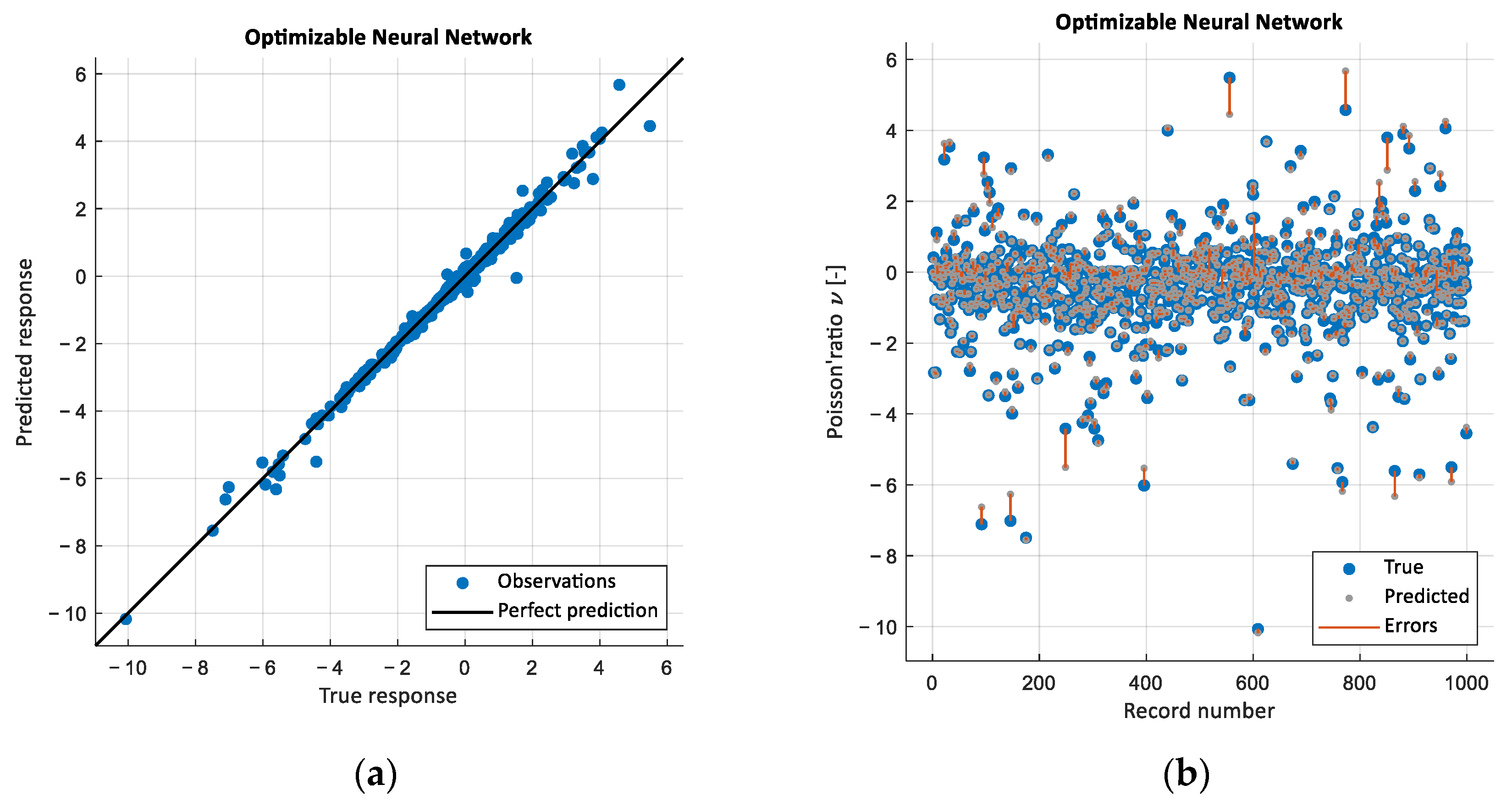
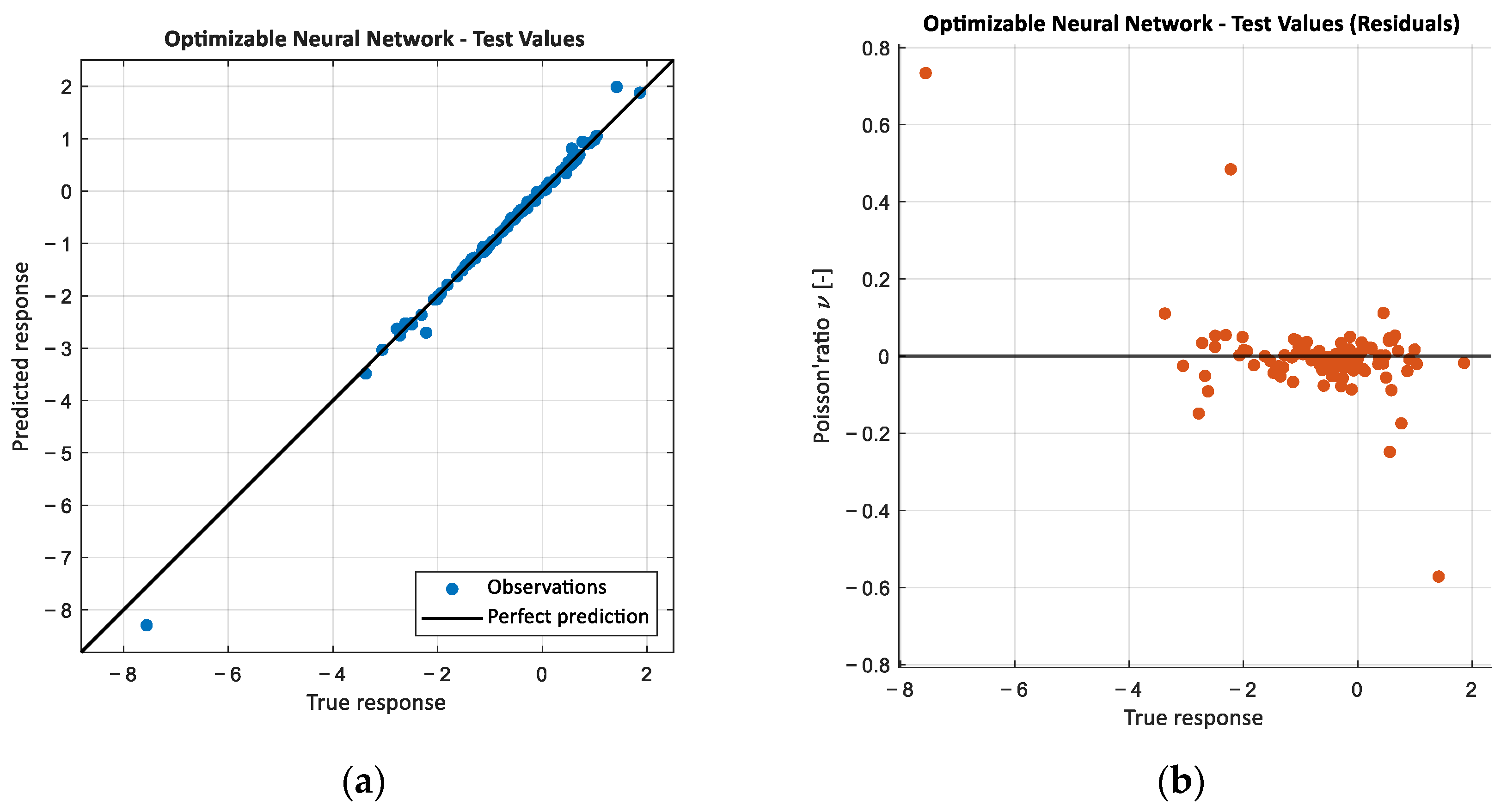
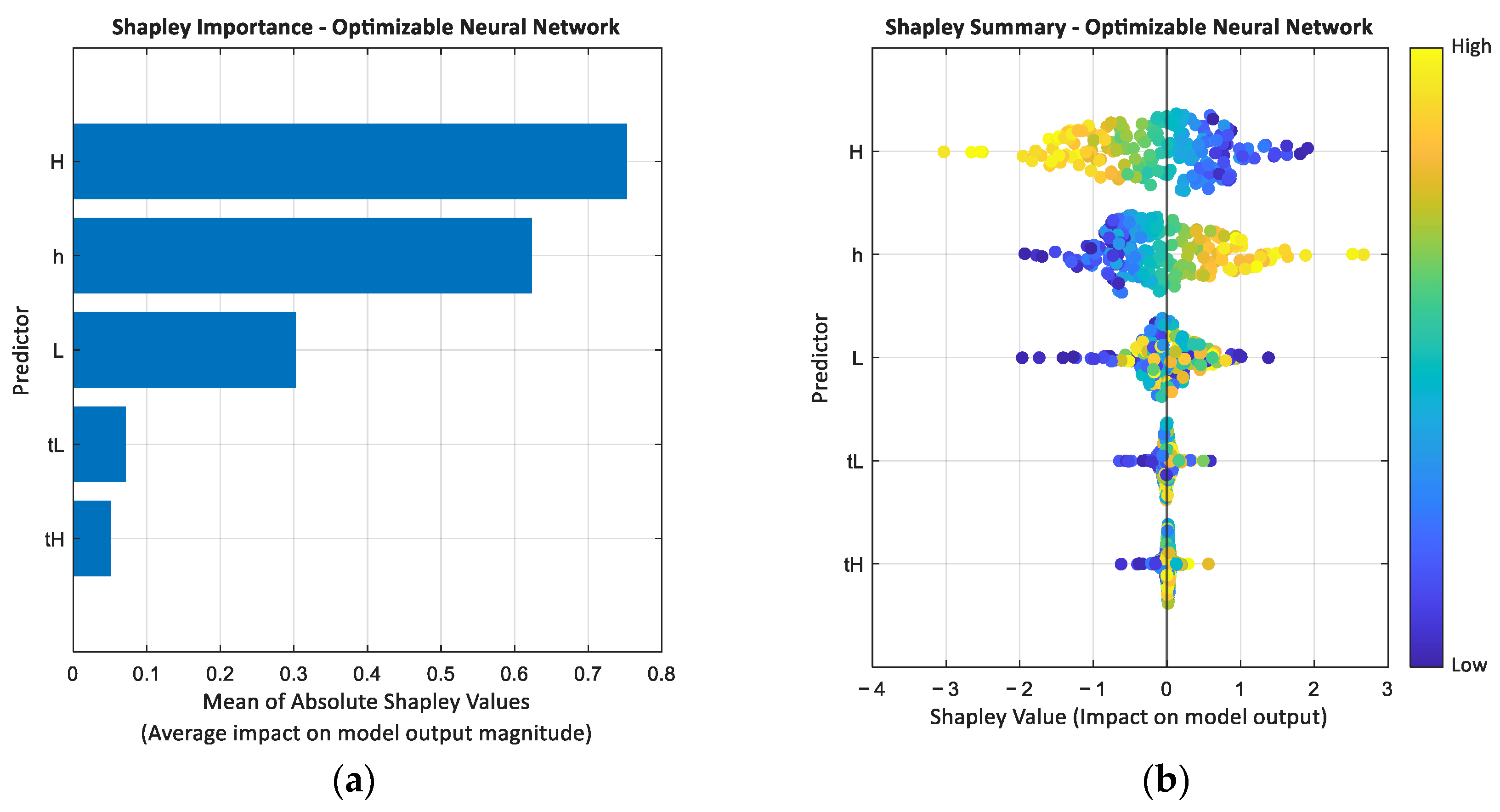
4.3. Machine Learning—Regression Learner
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xue, X.; Lin, C.; Wu, F.; Li, Z.; Liao, J. Lattice Structures with Negative Poisson’s Ratio: A Review. Mater. Today Commun. 2023, 34, 105132. [Google Scholar] [CrossRef]
- Gibson, L.J.; Schajer, M.F.; Schajerj, J.G.S. The Mechanics of Two-Dimensional Cellular Materials. R. Soc. 1982, 382, 25–42. [Google Scholar]
- Stronge, W.J.; Shim, P.-W. Dynamic Crushing of a Ductile Cellular Array. Int. J. Mech. Sci. 1987, 29, 381–406. [Google Scholar] [CrossRef]
- Banhart, J. Manufacture, Characterisation and Application of Cellular Metals and Metal Foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Lakes, R. Cellular Solid Structures with Unbounded Thermal Expansion. J. Mater. Sci. Lett. 1996, 15, 477. [Google Scholar] [CrossRef]
- Jiao, P. Mechanical Energy Metamaterials in Interstellar Travel. Prog. Mater. Sci. 2023, 137, 101132. [Google Scholar] [CrossRef]
- Li, X.; Peng, W.; Wu, W.; Xiong, J.; Lu, Y. Auxetic Mechanical Metamaterials: From Soft to Stiff. Int. J. Extrem. Manuf. 2023, 5, 042003. [Google Scholar] [CrossRef]
- Sanami, M.; Ravirala, N.; Alderson, K.; Alderson, A. Auxetic Materials for Sports Applications. In Proceedings of the Procedia Engineering; Elsevier Ltd.: Amsterdam, The Netherlands, 2014; Volume 72, pp. 453–458. [Google Scholar]
- Tan, X.; Chen, X. Parameters Affecting Energy Absorption and Deformation in Textile Composite Cellular Structures. Mater. Des. 2005, 26, 424–438. [Google Scholar] [CrossRef]
- Kier, Z.T.; Salvi, A.; Theis, G.; Waas, A.M.; Shahwan, K. Estimating Mechanical Properties of 2D Triaxially Braided Textile Composites Based on Microstructure Properties. Compos. Part B Eng. 2015, 68, 288–299. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Wang, C.; Qiu, J. The Application of Negative Poisson’s Ratio Metamaterials in the Optimization of a Variable Area Wing. Aerospace 2025, 12, 125. [Google Scholar] [CrossRef]
- Thompson, M.K.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, R.I.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for Additive Manufacturing: Trends, Opportunities, Considerations, and Constraints. CIRP Ann. Manuf. Technol. 2016, 65, 737–760. [Google Scholar] [CrossRef]
- Rao, R.V.; Rai, D.P. Optimization of Fused Deposition Modeling Process Using Teaching-Learning-Based Optimization Algorithm. Eng. Sci. Technol. Int. J. 2016, 19, 587–603. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Mechanical Performance of Additively Manufactured Meta-Biomaterials. Acta Biomater. 2019, 85, 41–59. [Google Scholar] [CrossRef] [PubMed]
- du Plessis, A.; Razavi, S.M.J.; Benedetti, M.; Murchio, S.; Leary, M.; Watson, M.; Bhate, D.; Berto, F. Properties and Applications of Additively Manufactured Metallic Cellular Materials: A Review. Prog. Mater. Sci. 2022, 125, 100918. [Google Scholar] [CrossRef]
- Kelkar, P.U.; Kim, H.S.; Cho, K.H.; Kwak, J.Y.; Kang, C.Y.; Song, H.C. Cellular Auxetic Structures for Mechanical Metamaterials: A Review. Sensors 2020, 20, 3132. [Google Scholar] [CrossRef]
- Dong, H.; Wang, H.; Hazell, P.J.; Sun, N.; Dura, H.B.; Escobedo-Diaz, J.P. Effects of Printing Parameters on the Quasi-Static and Dynamic Compression Behaviour of 3D-Printed Re-Entrant Auxetic Structures. Thin-Walled Struct. 2025, 210, 113000. [Google Scholar] [CrossRef]
- Tian, Z.; Shi, S.; Liao, Y.; Wang, W.; Zhang, L.; Xiao, Y. Energy Absorption Mechanisms of Riveted and Assembled Double-Trapezoidal Auxetic Honeycomb Core Structures Under Quasi-Static Loading. J. Compos. Sci. 2025, 9, 89. [Google Scholar] [CrossRef]
- Széles, L.; Horváth, R.; Cveticanin, L. Research on Auxetic Lattice Structure for Impact Absorption in Machines and Mechanisms. Mathematics 2024, 12, 1983. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, X.; Xie, Y.M.; Wang, Z.; Zhou, S. Re-Entrant Auxetic Lattices with Enhanced Stiffness: A Numerical Study. Int. J. Mech. Sci. 2020, 178, 105619. [Google Scholar] [CrossRef]
- Panowicz, R.; Jeschke, A.; Durejko, T.; Zachman, M.; Konarzewski, M. The Mechanical Properties and Energy Absorption of AuxHex Structures. Materials 2024, 17, 6073. [Google Scholar] [CrossRef]
- Peng, X.; Zhou, K.; Han, Y.; Jia, W.; Li, J.; Jiang, S. Compression Performance Analysis of Hexagonal and Re-Entrant Hybrid Honeycomb Structures. Polym. Test. 2025, 145, 108745. [Google Scholar] [CrossRef]
- Zhang, X.; An, C.; Shen, Z.; Wu, H.; Yang, W.; Bai, J. Dynamic Crushing Responses of Bio-Inspired Re-Entrant Auxetic Honeycombs under in-Plane Impact Loading. Mater. Today Commun. 2020, 23, 100918. [Google Scholar] [CrossRef]
- Liu, Y.; Schaedler, T.A.; Jacobsen, A.J.; Chen, X. Quasi-Static Energy Absorption of Hollow Microlattice Structures. Compos. Part B Eng. 2014, 67, 39–49. [Google Scholar] [CrossRef]
- Mohsenizadeh, S.; Alipour, R.; Shokri Rad, M.; Farokhi Nejad, A.; Ahmad, Z. Crashworthiness Assessment of Auxetic Foam-Filled Tube under Quasi-Static Axial Loading. Mater. Des. 2015, 88, 258–268. [Google Scholar] [CrossRef]
- Hong, S.T.; Pan, J.; Tyan, T.; Prasad, P. Quasi-Static Crush Behavior of Aluminum Honeycomb Specimens under Compression Dominant Combined Loads. Int. J. Plast. 2006, 22, 73–109. [Google Scholar] [CrossRef]
- Qi, C.; Jiang, F.; Yang, S.; Remennikov, A. Multi-Scale Characterization of Novel Re-Entrant Circular Auxetic Honeycombs under Quasi-Static Crushing. Thin-Walled Struct. 2021, 169, 108314. [Google Scholar] [CrossRef]
- Lu, H.; Wang, X.; Chen, T. In-Plane Dynamics Crushing of a Combined Auxetic Honeycomb with Negative Poisson’s Ratio and Enhanced Energy Absorption. Thin-Walled Struct. 2021, 160, 107366. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Q.M. Dynamic Compressive Behaviour of Cellular Materials: A Review of Phenomenon, Mechanism and Modelling. Int. J. Impact Eng. 2018, 112, 74–115. [Google Scholar] [CrossRef]
- Ma, Q.; Zhang, J. Nonlinear Constitutive and Mechanical Properties of an Auxetic Honeycomb Structure. Mathematics 2023, 11, 2062. [Google Scholar] [CrossRef]
- Ai, L.; Gao, X.L. An Analytical Model for Star-Shaped Re-Entrant Lattice Structures with the Orthotropic Symmetry and Negative Poisson’s Ratios. Int. J. Mech. Sci. 2018, 145, 158–170. [Google Scholar] [CrossRef]
- Jiang, F.; Yang, S.; Qi, C. Quasi-Static Crushing Response of a Novel 3D Re-Entrant Circular Auxetic Metamaterial. Compos. Struct. 2022, 300, 116066. [Google Scholar] [CrossRef]
- Luo, H.; Gao, Q.; Zhou, J.; Zhang, Y.; Bao, F.; Chen, J.; Cui, Y.; Wang, L.; Wang, X. Hybrid Honeycombs with Re-Entrant Auxetic and Face-Centered Cubic Cells: Design and Mechanical Characteristics. Eng. Struct. 2025, 328, 119731. [Google Scholar] [CrossRef]
- Bora, K.M.; Varshney, S.K.; Kumar, C.S. Rounded Corner Thicken Strut Re-Entrant Auxetic Honeycomb: Analytical and Numerical Modeling. Mech. Res. Commun. 2024, 136, 104246. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, S.; Scarpa, F.; Wang, J.; Sun, R. In-Plane Mechanical Behavior of Novel Auxetic Hybrid Metamaterials. Thin-Walled Struct. 2021, 159, 107191. [Google Scholar] [CrossRef]
- Jiang, Y.; Rudra, B.; Shim, J.; Li, Y. Limiting Strain for Auxeticity under Large Compressive Deformation: Chiral vs. Re-Entrant Cellular Solids. Int. J. Solids Struct. 2019, 162, 87–95. [Google Scholar] [CrossRef]
- Schürger, B.; Pástor, M.; Frankovský, P.; Lengvarský, P. Photoelasticity as a Tool for Stress Analysis of Re-Entrant Auxetic Structures. Appl. Sci. 2025, 15, 1250. [Google Scholar] [CrossRef]
- Liu, X.; Shapiro, V. Homogenization of Material Properties in Additively Manufactured Structures. Comput.-Aided Des. 2016, 78, 71–82. [Google Scholar] [CrossRef]
- Wang, T.; Wang, L.; Ma, Z.; Hulbert, G.M. Elastic Analysis of Auxetic Cellular Structure Consisting of Re-Entrant Hexagonal Cells Using a Strain-Based Expansion Homogenization Method. Mater. Des. 2018, 160, 284–293. [Google Scholar] [CrossRef]
- Gunaydin, K.; Gülcan, O.; Tamer, A. Application of Homogenization Method in Free Vibration of Multi-Material Auxetic Metamaterials. Vibration 2025, 8, 2. [Google Scholar] [CrossRef]
- Gongora, A.E.; Snapp, K.L.; Pang, R.; Tiano, T.M.; Reyes, K.G.; Whiting, E.; Lawton, T.J.; Morgan, E.F.; Brown, K.A. Designing Lattices for Impact Protection Using Transfer Learning. Matter 2022, 5, 2829–2846. [Google Scholar] [CrossRef]
- Hasanzadeh, R. A New Polymeric Hybrid Auxetic Structure Additively Manufactured by Fused Filament Fabrication 3D Printing: Machine Learning-Based Energy Absorption Prediction and Optimization. Polymers 2024, 16, 3565. [Google Scholar] [CrossRef] [PubMed]
- Al-Rifaie, H.; Movahedi, N.; Lim, T.C. Development of Novel Auxetic-Nonauxetic Hybrid Metamaterial. Eng. Fail. Anal. 2025, 175, 109559. [Google Scholar] [CrossRef]
- Masters, I.G.; Evans, K.E. Models for the Elastic Deformation of Honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Grima, J.N.; Attard, D.; Ellul, B.; Gatt, R. An Improved Analytical Model for the Elastic Constants of Auxetic and Conventional Hexagonal Honeycombs. Cell. Polym. 2011, 30, 287–310. [Google Scholar] [CrossRef]
- Tabacu, S.; Negrea, R.F.; Negrea, D. Experimental, Numerical and Analytical Investigation of 2D Tetra-Anti-Chiral Structure under Compressive Loads. Thin-Walled Struct. 2020, 155, 106929. [Google Scholar] [CrossRef]
- Rao, S.S. The Finite Element Method in Engineering; Elsevier Butterworth-Heinmann: Oxford, UK, 2005; ISBN 0-7506-7828-3. [Google Scholar]
- Wang, G.; Qi, Z.; Xu, J. A High-Precision Co-Rotational Formulation of 3D Beam Elements for Dynamic Analysis of Flexible Multibody Systems. Comput. Methods Appl. Mech. Eng. 2020, 360, 112701. [Google Scholar] [CrossRef]
- Khakalo, S.; Balobanov, V.; Niiranen, J. Modelling Size-Dependent Bending, Buckling and Vibrations of 2D Triangular Lattices by Strain Gradient Elasticity Models: Applications to Sandwich Beams and Auxetics. Int. J. Eng. Sci. 2018, 127, 33–52. [Google Scholar] [CrossRef]
- Günaydın, K.; Rea, C.; Kazancı, Z. Energy Absorption Enhancement of Additively Manufactured Hexagonal and Re-Entrant (Auxetic) Lattice Structures by Using Multi-Material Reinforcements. Addit. Manuf. 2022, 59, 103076. [Google Scholar] [CrossRef]
- Surjadi, J.U.; Gao, L.; Du, H.; Li, X.; Xiong, X.; Fang, N.X.; Lu, Y. Mechanical Metamaterials and Their Engineering Applications. Adv. Eng. Mater. 2019, 21, 1800864. [Google Scholar] [CrossRef]
- Yang, J.; Bhattacharya, K. Augmented Lagrangian Digital Image Correlation. Exp. Mech. 2019, 59, 187–205. [Google Scholar] [CrossRef]
- Popławski, A.; Bogusz, P.; Grudnik, M. Digital Image Correlation and Numerical Analysis of Mechanical Behavior in Photopolymer Resin Lattice Structures. Materials 2025, 18, 384. [Google Scholar] [CrossRef] [PubMed]
- Tabacu, S.; Predoiu, P.; Negrea, R. A Theoretical Model for the Estimate of Plateau Force for the Crushing Process of 3D Auxetic Anti-Tetra Chiral Structures. Int. J. Mech. Sci. 2021, 199, 106405. [Google Scholar] [CrossRef]
- Zhang, X.G.; Ren, X.; Jiang, W.; Zhang, X.Y.; Luo, C.; Zhang, Y.; Xie, Y.M. A Novel Auxetic Chiral Lattice Composite: Experimental and Numerical Study. Compos. Struct. 2022, 282, 115043. [Google Scholar] [CrossRef]
- Sinha, P.; Mukhopadhyay, T. Programmable Multi-Physical Mechanics of Mechanical Metamaterials. Mater. Sci. Eng. R Rep. 2023, 155, 100745. [Google Scholar] [CrossRef]









| Specification | Data |
|---|---|
| Density | |
| Flexural modulus | |
| Flexural strength | |
| Tensile strength | |
| Elongation at break |
| 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|
| 0.722 | 0.722 | 0.722 | 0.722 | 0.722 | |
| 0.575 | 0.602 | 0.620 | 0.634 | 0.644 | |
| 0.652 | 0.591 | 0.611 | 0.626 | 0.637 | |
| −2.21 | −1.81 | −1.42 | −1.28 | −1.06 | |
| 0.408 | 0.408 | 0.408 | 0.408 | 0.408 | |
| 0.329 | 0.344 | 0.353 | 0.362 | 0.367 | |
| 0.318 | 0.334 | 0.345 | 0.354 | 0.360 | |
| −3.42 | −2.89 | −2.16 | −2.29 | −1.89 | |
| Model (p) | ||
|---|---|---|
| 2 | 1.0769 | 0.006 |
| 2 + 1 | 0.0427 | 0.9984 |
| 3 | 0.0642 | 0.9987 |
| 5 | 0.1300 | 0.9902 |
| 5-2 | 0.3867 | 0.9135 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabacu, S.; Badea, A.-G.; Aparaschivei, A.-I.; Anghel, D.-C. Parametric Analysis of Auxetic Honeycombs. Mathematics 2025, 13, 1676. https://doi.org/10.3390/math13101676
Tabacu S, Badea A-G, Aparaschivei A-I, Anghel D-C. Parametric Analysis of Auxetic Honeycombs. Mathematics. 2025; 13(10):1676. https://doi.org/10.3390/math13101676
Chicago/Turabian StyleTabacu, Stefan, Ana-Gabriela Badea, Alina-Ionela Aparaschivei, and Daniel-Constantin Anghel. 2025. "Parametric Analysis of Auxetic Honeycombs" Mathematics 13, no. 10: 1676. https://doi.org/10.3390/math13101676
APA StyleTabacu, S., Badea, A.-G., Aparaschivei, A.-I., & Anghel, D.-C. (2025). Parametric Analysis of Auxetic Honeycombs. Mathematics, 13(10), 1676. https://doi.org/10.3390/math13101676









