N00N State Generation by Floquet Engineering
Abstract
1. Introduction
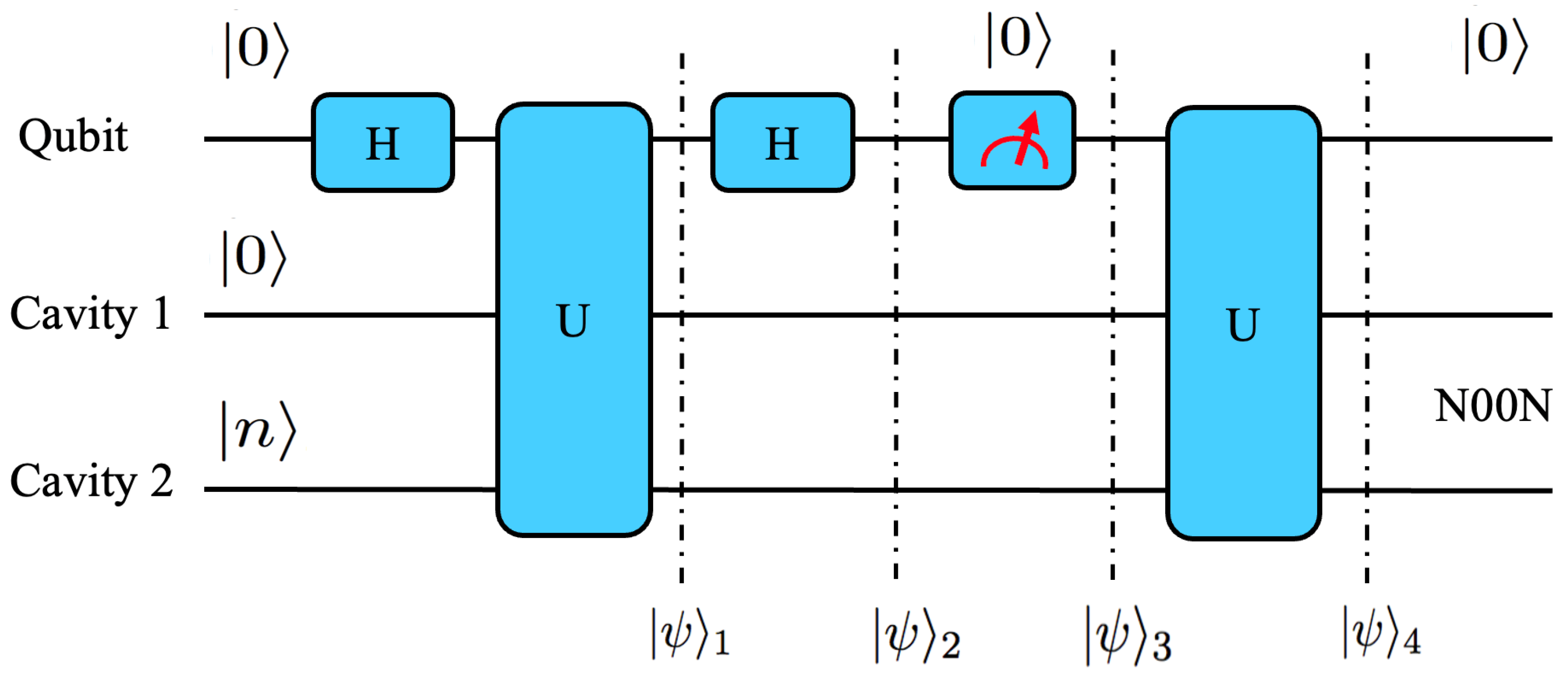
2. Quantum Circuit for N00N State Generation
3. N00N State Generation in Different Systems
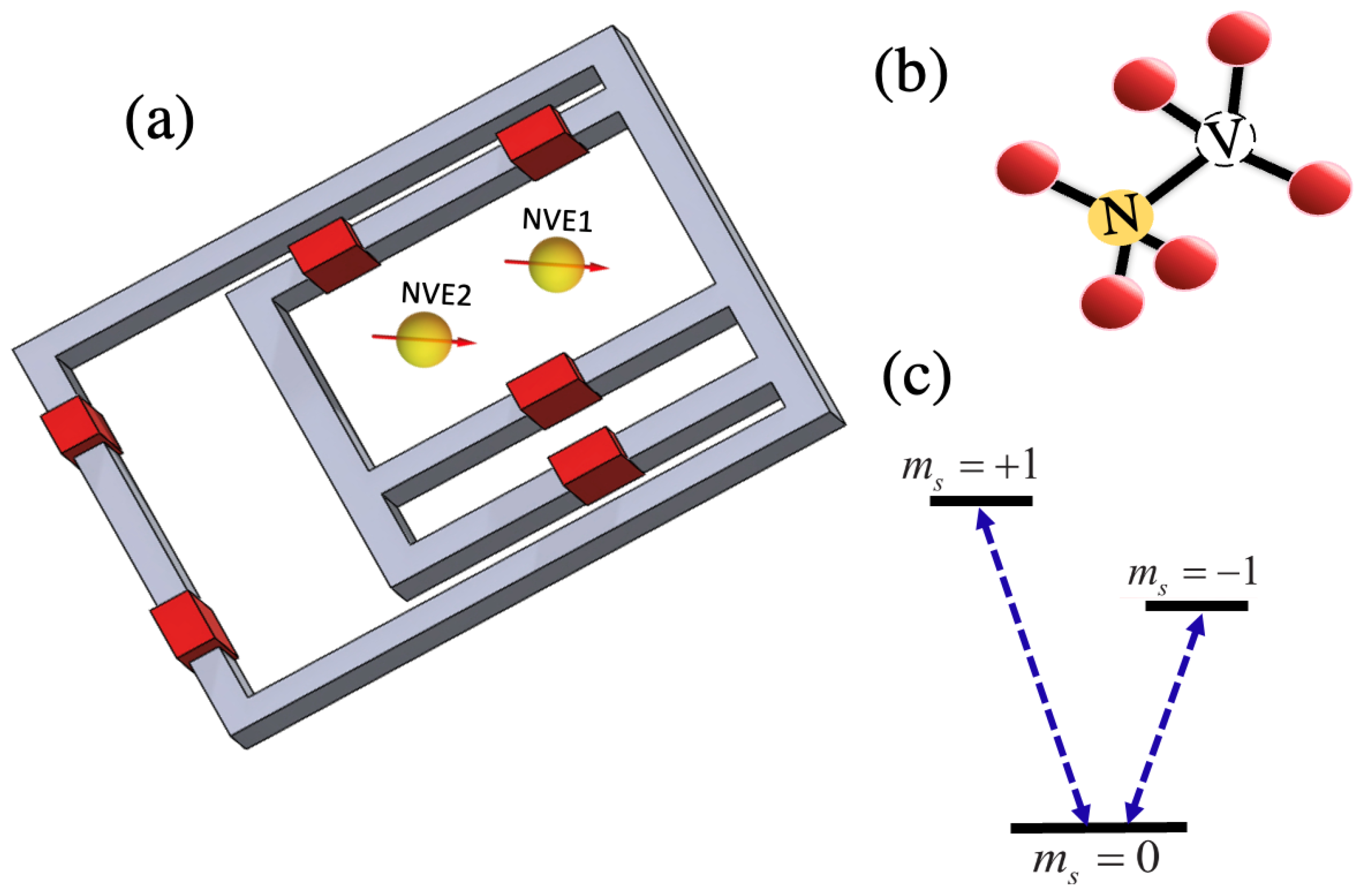
3.1. N00N State in Nitrogen-Vacancy Centers in Diamond
3.2. N00N State as a Superposition of Light and Motion
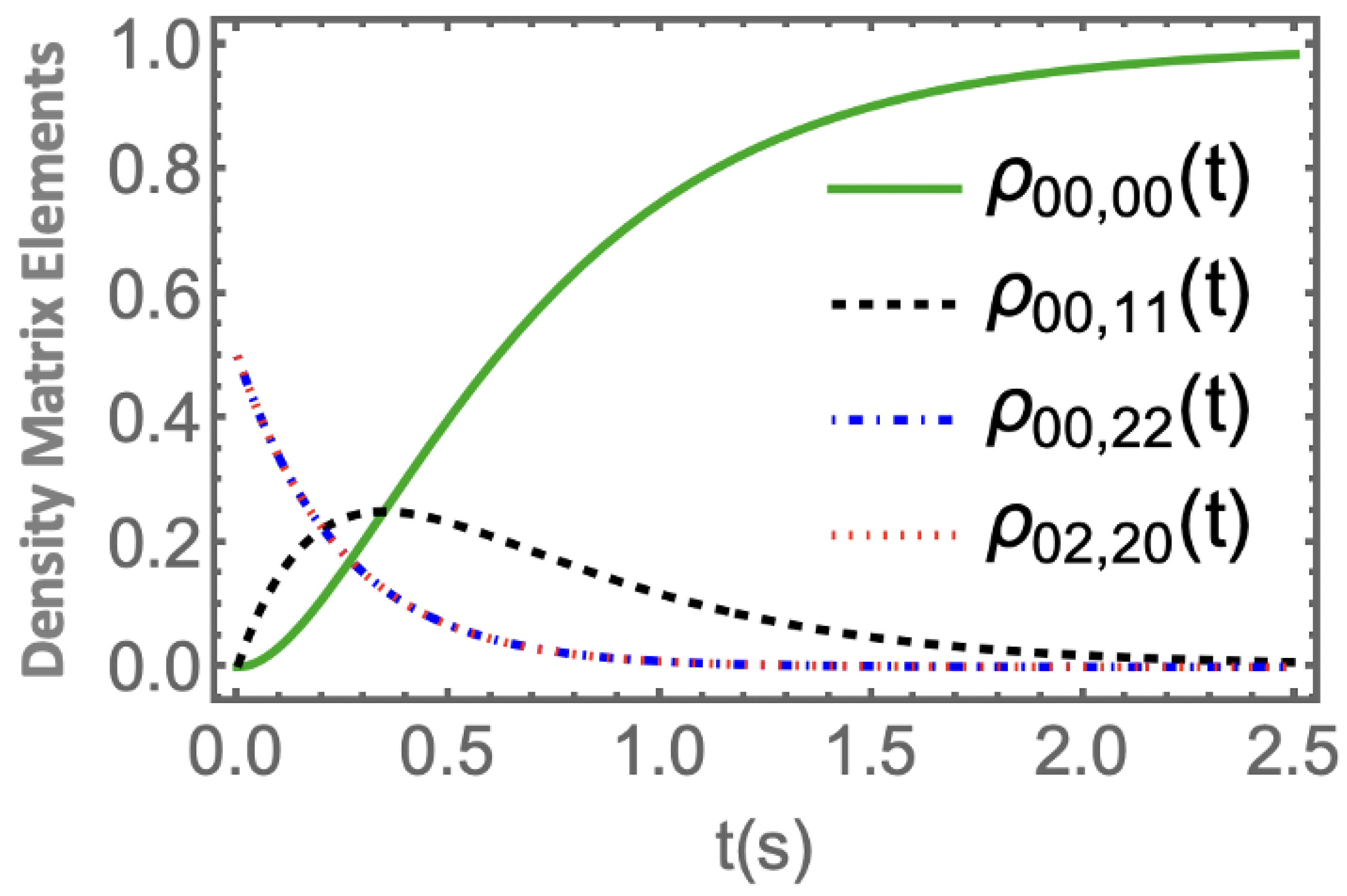
3.3. Impact of Decoherence on the N00N State
4. Entangled State Generations Beyond the N00N State
5. Eantangled State Generation Beyond the Two-Mode States
6. Heisenberg Limit Metrology Beyond N00N States
7. Conclusions
Funding
Conflicts of Interest
Appendix A. Derivation of the Effective Hamiltonian
Appendix A.1. Modulating the Coupling Between the Qubit and the Resonators
Appendix A.2. Modulating the Frequencies of the Resonators
Appendix B. Spin Algebra
References
- Helstrom, C.W. Quantum Detection and Estimation Theory; Springer: New York, NY, USA, 1976. [Google Scholar]
- Holevo, A.S. Probabilistic and Statistical Aspects of Quantum Theory; Springer Science & Business Media: Berlin, Germany, 2011; Volume 1. [Google Scholar]
- Caves, C.M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439. [Google Scholar] [CrossRef] [PubMed]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Khashami, F. Fundamentals of NMR and MRI: From Quantum Principles to Medical Applications; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Komar, P.; Kessler, E.M.; Bishof, M.; Jiang, L.; Sørensen, A.S.; Ye, J.; Lukin, M.D. A quantum network of clocks. Nat. Phys. 2014, 10, 582–587. [Google Scholar] [CrossRef]
- Lewis-Swan, R.J.; Castro, J.Z.; Barberena, D.; Rey, A.M. Exploiting nonclassical motion of a trapped ion crystal for quantum-enhanced metrology of global and differential spin rotations. Phys. Rev. Lett. 2024, 132, 163601. [Google Scholar] [CrossRef]
- DeMille, D.; Hutzler, N.R.; Rey, A.M.; Zelevinsky, T. Quantum sensing and metrology for fundamental physics with molecules. Nat. Phys. 2024, 20, 741–749. [Google Scholar] [CrossRef]
- Albarelli, F.; Barbieri, M.; Genoni, M.G.; Gianani, I. A perspective on multiparameter quantum metrology: From theoretical tools to applications in quantum imaging. Phys. Lett. A 2020, 384, 126311. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Maleki, Y.; Zubairy, M.S. Distributed phase estimation and networked quantum sensors with W-type quantum probes. Phys. Rev. A 2022, 105, 032428. [Google Scholar] [CrossRef]
- Bevington, P.R.; Robinson, D.K. Data Reduction and Error Analysis for the Physical Sciences; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Sanders, B.C. Quantum dynamics of the nonlinear rotator and the effects of continual spin measurement. Phys. Rev. A 1989, 40, 2417. [Google Scholar] [CrossRef] [PubMed]
- Boto, A.N.; Kok, P.; Abrams, D.S.; Braunstein, S.L.; Williams, C.P.; Dowling, J.P. Quantum interferometric optical lithography: Exploiting entanglement to beat the diffraction limit. Phys. Rev. Lett. 2000, 85, 2733. [Google Scholar] [CrossRef]
- Maleki, Y.; Zubairy, M.S. Universal criteria for entanglement-assisted dynamical speed enhancement. Phys. Rev. A 2024, 110, 052415. [Google Scholar] [CrossRef]
- Taylor, M.A.; Bowen, W.P. Quantum metrology and its application in biology. Phys. Rep. 2016, 615, 1–59. [Google Scholar] [CrossRef]
- Aslam, N.; Zhou, H.; Urbach, E.K.; Turner, M.J.; Walsworth, R.L.; Lukin, M.D.; Park, H. Quantum sensors for biomedical applications. Nat. Rev. Phys. 2023, 5, 157–169. [Google Scholar] [CrossRef]
- Lee, H.; Kok, P.; Dowling, J.P. A quantum Rosetta stone for interferometry. J. Mod. Opt. 2002, 49, 2325–2338. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzański, R.; Górecki, W.; Guţă, M. Multi-parameter estimation beyond quantum Fisher information. J. Phys. A Math. Theor. 2020, 53, 363001. [Google Scholar] [CrossRef]
- Pezze, L.; Smerzi, A.; Oberthaler, M.K.; Schmied, R.; Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 2018, 90, 035005. [Google Scholar] [CrossRef]
- Ono, T.; Okamoto, R.; Takeuchi, S. An entanglement-enhanced microscope. Nat. Commun. 2013, 4, 2426. [Google Scholar] [CrossRef]
- Dowling, J.P. Quantum optical metrology–the lowdown on high-N00N states. Contemp. Phys. 2008, 49, 125–143. [Google Scholar] [CrossRef]
- Cappellaro, P.; Emerson, J.; Boulant, N.; Ramanathan, C.; Lloyd, S.; Cory, D.G. Entanglement assisted metrology. Phys. Rev. Lett. 2005, 94, 020502. [Google Scholar] [CrossRef]
- Suzuki, J.; Yang, Y.; Hayashi, M. Quantum state estimation with nuisance parameters. J. Phys. A Math. Theor. 2020, 53, 453001. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, H.; Lu, X.-M.; Wang, X. Quantum Fisher information matrix and multiparameter estimation. J. Phys. A Math. Theor. 2020, 53, 023001. [Google Scholar] [CrossRef]
- Conlon, L.O.; Suzuki, J.; Lam, P.K.; Assad, S.M. Efficient computation of the Nagaoka–Hayashi bound for multiparameter estimation with separable measurements. npj Quantum Inf. 2021, 7, 110. [Google Scholar] [CrossRef]
- Hayashi, M.; Ouyang, Y. Tight Cramér-Rao type bounds for multiparameter quantum metrology through conic programming. Quantum 2023, 7, 1094. [Google Scholar] [CrossRef]
- Sidhu, J.S.; Ouyang, Y.; Campbell, E.T.; Kok, P. Tight bounds on the simultaneous estimation of incompatible parameters. Phys. Rev. X 2021, 11, 011028. [Google Scholar] [CrossRef]
- Maleki, Y.; Ahansaz, B.; Maleki, A. Speed limit of quantum metrology. Sci. Rep. 2023, 13, 12031. [Google Scholar] [CrossRef]
- Afek, I.; Ambar, O.; Silberberg, Y. High-NOON states by mixing quantum and classical light. Science 2010, 328, 879–881. [Google Scholar] [CrossRef]
- Maleki, Y. Quantum phase estimations with spin coherent states superposition. Eur. Phys. J. Plus 2021, 136, 1028. [Google Scholar] [CrossRef]
- Maleki, Y.; Scully, M.O.; Zheltikov, A.M. Quantum metrology with superposition spin coherent states: Insights from Fisher information. Phys. Rev. A 2021, 104, 053712. [Google Scholar] [CrossRef]
- Holl, M.J.; Burnett, K. Interferometric detection of optical phase shifts at the Heisenberg limit. Phys. Rev. Lett. 1993, 71, 1355–1358. [Google Scholar]
- Zhou, S.; Zhang, M.; Preskill, J.; Jiang, L. Achieving the Heisenberg limit in quantum metrology using quantum error correction. Nat. Commun. 2018, 9, 78. [Google Scholar] [CrossRef]
- Xiang, G.Y.; Higgins, B.L.; Berry, D.W.; Wiseman, H.M.; Pryde, G.J. Entanglement-enhanced measurement of a completely unknown optical phase. Nat. Photonics 2011, 5, 43–47. [Google Scholar] [CrossRef]
- Grün, D.S.; Wittmann, W.K.; Ymai, L.H.; Links, J.; Foerster, A. Protocol designs for NOON states. Commun. Phys. 2022, 5, 36. [Google Scholar] [CrossRef]
- Matthews, J.C.; Politi, A.; Bonneau, D.; O’Brien, J.L. Heralded entanglement for quantum enhanced measurement with photons. Phys. Rev. Lett. 2011, 107, 163602. [Google Scholar] [CrossRef]
- Rozema, L.A.; Bateman, J.D.; Mahler, D.H.; Okamoto, R.; Feizpour, A.; Hayat, A.; Steinberg, A.M. Scalable spatial superresolution using entangled photons. Phys. Rev. Lett. 2014, 112, 223602. [Google Scholar] [CrossRef]
- Chen, Y.-A.; Bao, X.-H.; Yuan, Z.-S.; Chen, S.; Zhao, B.; Pan, J.-W. Heralded generation of an atomic NOON state. Phys. Rev. Lett. 2010, 104, 043601. [Google Scholar] [CrossRef]
- Birrittella, R.J.; Alsing, P.M.; Gerry, C.C. The parity operator: Applications in quantum metrology. AVS Quantum Sci. 2021, 3, 014701. [Google Scholar] [CrossRef]
- Nimbe, P.; Weyori, B.A.; Adekoya, A.F. Models in quantum computing: A systematic review. Quantum Inf. Process. 2021, 20, 80. [Google Scholar] [CrossRef]
- Motta, M.; Rice, J.E. Emerging quantum computing algorithms for quantum chemistry. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1580. [Google Scholar] [CrossRef]
- Chen, J. Review on quantum communication and quantum computation. J. Phys. Conf. Ser. 2021, 1865, 022008. [Google Scholar] [CrossRef]
- Yang, Z.; Zolanvari, M.; Jain, R. A survey of important issues in quantum computing and communications. IEEE Commun. Surv. Tutor. 2023, 25, 1059–1094. [Google Scholar] [CrossRef]
- Hu, X.M.; Guo, Y.; Liu, B.H.; Li, C.F.; Guo, G.C. Progress in quantum teleportation. Nat. Rev. Phys. 2023, 5, 339–353. [Google Scholar] [CrossRef]
- Israel, Y.; Rosen, S.; Silberberg, Y. Supersensitive polarization microscopy using NOON states of light. Phys. Rev. Lett. 2014, 112, 103604. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Um, M.; Lv, D.; Zhang, J.N.; Duan, L.M.; Kim, K. NOON states of nine quantized vibrations in two radial modes of a trapped ion. Phys. Rev. Lett. 2018, 121, 160502. [Google Scholar] [CrossRef]
- Dengis, S.; Wimberger, S.; Schlagheck, P. Accelerated creation of NOON states with ultracold atoms via counterdiabatic driving. Phys. Rev. A 2025, 111, L031301. [Google Scholar] [CrossRef]
- Qi, S.F.; Jing, J. Generating entangled states from coherent states in circuit QED. Phys. Rev. A 2023, 107, 042412. [Google Scholar] [CrossRef]
- Nikoghosyan, G.; Hartmann, M.J.; Plenio, M.B. Generation of mesoscopic entangled states in a cavity coupled to an atomic ensemble. Phys. Rev. Lett. 2012, 108, 123603. [Google Scholar] [CrossRef]
- Lidar, D.A.; Chuang, I.L.; Whaley, K.B. Decoherence-free subspaces for quantum computation. Phys. Rev. Lett. 1998, 81, 2594. [Google Scholar] [CrossRef]
- Lidar, D.A.; Bacon, D.; Whaley, K.B. Concatenating decoherence-free subspaces with quantum error correcting codes. Phys. Rev. Lett. 1999, 82, 4556. [Google Scholar] [CrossRef]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Linear entropy of multiqutrit nonorthogonal states. Opt. Express 2019, 27, 8291–8307. [Google Scholar] [CrossRef]
- Maniscalco, S.; Francica, F.; Zaffino, R.L.; Lo Gullo, N.; Plastina, F. Protecting entanglement via the quantum Zeno effect. Phys. Rev. Lett. 2008, 100, 090503. [Google Scholar] [CrossRef]
- Basit, A.; Badshah, F.; Ali, H.; Ge, G.-Q. Protecting quantum coherence and discord from decoherence of depolarizing noise via weak measurement and measurement reversal. Europhys. Lett. 2017, 118, 30002. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Generating maximally-path-entangled number states in two spin ensembles coupled to a superconducting flux qubit. Phys. Rev. A 2018, 97, 012312. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. A high-N00N output of harmonically driven cavity QED. Sci. Rep. 2019, 9, 16780. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Perfect swap and transfer of arbitrary quantum states. Opt. Commun. 2021, 496, 126870. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Wang, H.; Mariantoni, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; O’Connell, A.D.; Sank, D.; Weides, M.; Wenner, J.; et al. Deterministic entanglement of photons in two superconducting microwave resonators. Phys. Rev. Lett. 2011, 106, 060401. [Google Scholar] [CrossRef]
- Su, Q.-P.; Yang, C.-P.; Zheng, S.-B. Fast and simple scheme for generating NOON states of photons in circuit QED. Sci. Rep. 2014, 4, 3898. [Google Scholar] [CrossRef]
- Kubo, Y.; Ong, F.R.; Bertet, P.; Vion, D.; Jacques, V.; Zheng, D.; Dréau, A.; Roch, J.-F.; Auffeves, A.; Jelezko, F.; et al. Strong coupling of a spin ensemble to a superconducting resonator. Phys. Rev. Lett. 2010, 105, 140502. [Google Scholar] [CrossRef] [PubMed]
- Niemczyk, T.; Deppe, F.; Huebl, H.; Menzel, E.P.; Hocke, F.; Schwarz, M.J.; Garcia-Ripoll, J.J.; Zueco, D.; Hümmer, T.; Solano, E.; et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat. Phys. 2010, 6, 772–776. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; Lisenfeld, J.; Marcos, D.; Garcia-Ripoll, J.J.; Solano, E.; Harmans, C.J.P.M.; Mooij, J.E. Observation of the Bloch-Siegert Shift in a Qubit-Oscillator System in the Ultrastrong Coupling Regime. Phys. Rev. Lett. 2010, 105, 237001. [Google Scholar] [CrossRef] [PubMed]
- Song, W.L.; Yin, Z.Q.; Yang, W.L.; Zhu, X.B.; Zhou, F.; Feng, M. One-step generation of multipartite entanglement among nitrogen-vacancy center ensembles. Sci. Rep. 2015, 5, 7755. [Google Scholar] [CrossRef] [PubMed]
- Marcos, D.; Wubs, M.; Taylor, J.M.; Aguado, R.; Lukin, M.D.; Sørensen, A.S. Coupling nitrogen-vacancy centers in diamond to superconducting flux qubits. Phys. Rev. Lett. 2010, 105, 210501. [Google Scholar] [CrossRef]
- Childress, L.; Gurudev Dutt, M.V.; Taylor, J.M.; Zibrov, A.S.; Jelezko, F.; Wrachtrup, J.; Hemmer, P.R.; Lukin, M.D. Coherent dynamics of coupled electron and nuclear spin qubits in diamond. Science 2006, 314, 281–285. [Google Scholar] [CrossRef]
- Dutt, M.G.; Childress, L.; Jiang, L.; Togan, E.; Maze, J.; Jelezko, F.; Zibrov, A.S.; Hemmer, P.R.; Lukin, M.D. Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 2007, 316, 1312–1316. [Google Scholar] [CrossRef]
- Liu, T.; Su, Q.-P.; Xiong, S.-J.; Liu, J.-M.; Yang, C.-P.; Nori, F. Generation of a macroscopic entangled coherent state using quantum memories in circuit QED. Sci. Rep. 2016, 6, 32004. [Google Scholar] [CrossRef]
- Ranjan, V.; de Lange, G.; Schutjens, R.; Debelhoir, T.; Groen, J.P.; Szombati, D.; Thoen, D.J.; Klapwijk, T.M.; Hanson, R.; DiCarlo, L. Probing dynamics of an electron-spin ensemble via a superconducting resonator. Phys. Rev. Lett. 2013, 110, 067004. [Google Scholar] [CrossRef]
- Reagor, M.; Pfaff, W.; Axline, C.; Heeres, R.W.; Ofek, N.; Sliwa, K.; Holland, E.; Wang, C.; Blumoff, J.; Chou, K.; et al. Quantum memory with millisecond coherence in circuit QED. Phys. Rev. B 2016, 94, 014506. [Google Scholar] [CrossRef]
- Bar-Gill, N.; Pham, L.M.; Jarmola, A.; Budker, D.; Walsworth, R.L. Solid-state electronic spin coherence time approaching one second. Nat. Commun. 2013, 4, 1743. [Google Scholar] [CrossRef]
- Xiang, Z.L.; Ashhab, S.; You, J.Q.; Nori, F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 2013, 85, 623–653. [Google Scholar] [CrossRef]
- Xiang, Z.-L.; Lu, X.-Y.; Li, T.F.; You, J.Q.; Nori, F. Hybrid quantum circuit consisting of a superconducting flux qubit coupled to a spin ensemble and a transmission-line resonator. Phys. Rev. B 2013, 87, 144516. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Witnessing quantum entanglement in ensembles of nitrogen–vacancy centers coupled to a superconducting resonator. Opt. Express 2018, 26, 17849–17858. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Macroscopic tripartite entanglement of nitrogen-vacancy centers in diamond coupled to a superconducting resonator. J. Opt. Soc. Am. B 2019, 36, 443–450. [Google Scholar] [CrossRef]
- Hammerer, K.; Sørensen, A.S.; Polzik, E.S. Quantum interface between light and atomic ensembles. Rev. Mod. Phys. 2010, 82, 1041–1093. [Google Scholar] [CrossRef]
- Raizen, M.G.; Thompson, R.J.; Brecha, R.J.; Kimble, H.J.; Carmichael, H.J. Normal-mode splitting and linewidth averaging for two-state atoms in an optical cavity. Phys. Rev. Lett. 1989, 63, 240. [Google Scholar] [CrossRef]
- Zhu, X.; Saito, S.; Kemp, A.; Kakuyanagi, K.; Karimoto, S.; Nakano, H.; Munro, W.J.; Tokura, Y.; Everitt, M.S.; Nemoto, K.; et al. Coherent coupling of a superconducting flux qubit to an electron spin ensemble in diamond. Nature 2011, 478, 221–224. [Google Scholar] [CrossRef]
- Lü, X.-Y.; Xiang, Z.-L.; Cui, W.; You, J.Q.; Nori, F. Quantum memory using a hybrid circuit with flux qubits and nitrogen-vacancy centers. Phys. Rev. A 2013, 88, 012329. [Google Scholar] [CrossRef]
- Yang, W.L.; Hu, Y.; Yin, Z.Q.; Deng, Z.J.; Feng, M. Entanglement of nitrogen-vacancy-center ensembles using transmission line resonators and a superconducting phase qubit. Phys. Rev. A 2011, 83, 022302. [Google Scholar] [CrossRef]
- Parkins, A.S.; Larsabal, E. Preparation and light-mediated distribution of motional state entanglement. Phys. Rev. A 2000, 63, 012304. [Google Scholar] [CrossRef]
- Parkins, A.S.; Kimble, H.J. Quantum state transfer between motion and light. J. Opt. B Quantum Semiclassical Opt. 1999, 1, 496–504. [Google Scholar] [CrossRef]
- Maleki, Y.; Maleki, A. Entangled multimode spin coherent states of trapped ions. J. Opt. Soc. Am. B 2018, 35, 1211–1217. [Google Scholar] [CrossRef]
- Agarwal, G.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; OUP: Oxford, UK, 2002. [Google Scholar]
- Maleki, Y.; Ahansaz, B. Quantum correlations in qutrit-like superposition of spin coherent states. Laser Phys. Lett. 2019, 16, 075205. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Joo, J.; Munro, W.J.; Spiller, T.P. Quantum metrology with entangled coherent states. Phys. Rev. Lett. 2011, 107, 083601. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar] [CrossRef]
- Su, Q.P.; Zhu, H.H.; Yu, L.; Zhang, Y.; Xiong, S.J.; Liu, J.M.; Yang, C.P. Generating double NOON states of photons in circuit QED. Phys. Rev. A 2017, 95, 022339. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Spin cat-state family for Heisenberg-limit metrology. J. Opt. Soc. Am. B 2020, 37, 1021–1026. [Google Scholar] [CrossRef]
- Sanders, B.C.; Gerry, C.C. Connection between the NOON state and a superposition of SU(2) coherent states. Phys. Rev. A 2014, 90, 045804. [Google Scholar] [CrossRef]
- Arecchi, F.T.; Courtens, E.; Gilmore, R.; Thomas, H. Atomic coherent states in quantum optics. Phys. Rev. A 1972, 6, 2211. [Google Scholar] [CrossRef]
- Perelomov, A.M. Coherent states for arbitrary Lie group. Commun. Math. Phys. 1972, 26, 222–236. [Google Scholar] [CrossRef]
- Wang, D.-W.; Song, C.; Feng, W.; Cai, H.; Xu, D.; Deng, H.; Li, H.; Zheng, D.; Zhu, X.; Wang, H.; et al. Synthesis of antisymmetric spin exchange interaction and chiral spin clusters in superconducting circuits. Nat. Phys. 2019, 15, 382–386. [Google Scholar] [CrossRef]
- Wang, D.W.; Cai, H.; Liu, R.B.; Scully, M.O. Mesoscopic superposition states generated by synthetic spin-orbit interaction in Fock-state lattices. Phys. Rev. Lett. 2016, 116, 220502. [Google Scholar] [CrossRef] [PubMed]
- Roushan, P.; Neill, C.; Megrant, A.; Chen, Y.; Babbush, R.; Barends, R.; Campbell, B.; Chen, Z.; Chiaro, B.; Dunsworth, A.; et al. Chiral ground-state currents of interacting photons in a synthetic magnetic field. Nat. Phys. 2017, 13, 146–151. [Google Scholar] [CrossRef]
- Wang, D.-W.; Cai, H.; Yuan, L.; Zhu, S.-Y.; Liu, R.-B. Topological phase transitions in superradiance lattices. Optica 2015, 2, 712–715. [Google Scholar] [CrossRef]
- Goldman, N.; Dalibard, J. Periodically driven quantum systems: Effective Hamiltonians and engineered gauge fields. Phys. Rev. X 2014, 4, 031027. [Google Scholar] [CrossRef]
- Jotzu, G.; Messer, M.; Desbuquois, R.; Lebrat, M.; Uehlinger, T.; Greif, D.; Esslinger, T. Experimental realization of the topological Haldane model with ultracold fermions. Nature 2014, 515, 237–240. [Google Scholar] [CrossRef]
- Maleki, Y.; Zhou, C.; Zubairy, M.S. Time-reversal-symmetry breaking in a scalable cavity QED lattice. Phys. Rev. A 2023, 108, 063709. [Google Scholar] [CrossRef]
- Maleki, Y.; Zhou, C.; Zubairy, M.S. Time-reversal-symmetry breaking and chiral quantum state manipulation in plasmonic nanorings. Phys. Rev. A 2022, 105, 042422. [Google Scholar] [CrossRef]
- Koch, J.; Houck, A.A.; Hur, K.L.; Girvin, S.M. Time-reversal-symmetry breaking in circuit-QED-based photon lattices. Phys. Rev. A 2010, 82, 043811. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photonics 2012, 6, 782–787. [Google Scholar] [CrossRef]
- Huang, J.; Zhuang, M.; Lu, B.; Ke, Y.; Lee, C. Achieving Heisenberg-limited metrology with spin cat states via interaction-based readout. Phys. Rev. A 2018, 98, 012129. [Google Scholar] [CrossRef]
- Huang, J.; Qin, X.; Zhong, H.; Ke, Y.; Lee, C. Quantum metrology with spin cat states under dissipation. Sci. Rep. 2015, 5, 17894. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Sanders, B.C.; Pan, S.H. Entangled coherent states for systems with SU(2) and SU(1, 1) symmetries. J. Phys. A Math. Gen. 2000, 33, 7451. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maleki, Y. N00N State Generation by Floquet Engineering. Mathematics 2025, 13, 1667. https://doi.org/10.3390/math13101667
Maleki Y. N00N State Generation by Floquet Engineering. Mathematics. 2025; 13(10):1667. https://doi.org/10.3390/math13101667
Chicago/Turabian StyleMaleki, Yusef. 2025. "N00N State Generation by Floquet Engineering" Mathematics 13, no. 10: 1667. https://doi.org/10.3390/math13101667
APA StyleMaleki, Y. (2025). N00N State Generation by Floquet Engineering. Mathematics, 13(10), 1667. https://doi.org/10.3390/math13101667





