Abstract
We review quantum architectures for engineering the N00N state, a bipartite maximally entangled state essential in quantum metrology. These schemes transform the initial state into the N00N state, where and are Fock states with N and 0 excitations, respectively. We demonstrate that this state can be generated through superpositions of quantum light modes, hybrid light–matter interactions, or spin ensembles. Our approach also enables the creation of mesoscopic and macroscopic entangled states, including entangled coherent and squeezed states. Furthermore, we show that a broad class of maximally entangled states can be realized within this framework. Extensions to multi-mode state engineering are also explored.
Keywords:
quantum metrology; quantum phase estimation; N00N state; entanglement; Heisenberg-limit metrology MSC:
81P45
1. Introduction
The estimation of unknown parameters is a fundamental challenge across various scientific fields, underpinning both technological progress and scientific breakthroughs [1,2,3,4,5,6,7,8,9,10,11]. Achieving the highest precision in parameter estimation is a central goal in metrology [12,13,14,15,16,17,18,19,20]. A widely adopted approach to improving estimation accuracy involves repeating experiments and gathering more information about the parameter of interest. When employing N independent resources to estimate a parameter , the achievable precision leads to an uncertainty scaling of . This regime is commonly known as the shot-noise limit or standard quantum limit [21,22,23].
Quantum physics offers a remarkable advantage in parameter estimation, surpassing the limits imposed by classical methodologies [24,25,26]. By harnessing quantum resources, it is possible to achieve measurement precision beyond what is attainable within classical frameworks [27,28,29,30,31]. This quantum-enhanced precision paves the way for unprecedented accuracy, transforming scientific and technological domains where ultra-precise measurements are essential [32,33,34,35,36,37]. The investigation of quantum-enhanced estimation has emerged as a key research area, with the potential to redefine the fundamental limits of measurement precision.
Therefore, quantum resources enable a significant enhancement in precision, exceeding classical limits and approaching the fundamental bounds set by quantum mechanics. In particular, quantum-enhanced estimation can surpass the classical shot-noise limit and reach the Heisenberg limit (HL), where the estimation error scales as for a given resource count N [38]. A notable quantum state capable of achieving this precision is the N00N state, expressed as Renowned for its potential to attain Heisenberg-limited precision, the N00N state is a key resource in quantum metrology [38,39,40,41,42].
The quantum advantage provided by the N00N state stems from its intrinsic quantum entanglement [43]. Entanglement underpins the unique properties of quantum systems and serves as a fundamental resource for a wide range of quantum applications, including quantum computing, quantum communication, and beyond [44,45,46,47,48]. In recent years, significant efforts have been devoted to harnessing entangled states for quantum sensing and metrology, aiming to push the boundaries of measurement precision.
Despite their potential, N00N states are notoriously difficult to realize due to the complexities involved in their generation and their high sensitivity to decoherence [49,50,51,52,53]. These challenges are not exclusive to N00N states; rather, they reflect broader obstacles that challenge quantum technologies more generally [54,55,56,57,58,59]. The generation of N00N states remains a central challenge in the field. Achieving and preserving such entanglement under realistic conditions is difficult, highlighting the fundamental limitations in controlling quantum systems for practical use in metrology. Overcoming these limitations is essential for advancing quantum-enhanced technologies, particularly in the context of high-precision parameter estimation.
This review examines quantum architectures aimed at engineering entangled states, with a particular emphasis on generating N00N states. We present strategies for producing these states via superpositions involving quantum light modes, hybrid light–matter interactions, and coupled spin ensembles. The approaches outlined here are capable of generating both mesoscopic and macroscopic entangled states, such as entangled coherent states and squeezed states. As a result, we demonstrate that a wide variety of maximally entangled states can be realized using these architectural schemes. Furthermore, we extend this discussion to encompass multi-mode scenarios, providing a comprehensive analysis of the techniques used to engineer complex entangled states across multiple degrees of freedom.
This review is organized as follows. In Section 2, we introduce a quantum circuit for N00N state generation, with detailed consideration of cavity-QED systems. In Section 3, we discuss N00N state generation as a superposition of spin ensembles and as a superposition of light and motion. Section 4 explores entangled state generation beyond the N00N state, identifying the creation of a broader class of entangled states. In Section 5, we extend the discussion to entangled state generation beyond two-mode systems, considering multimode state generation. Section 6 focuses on Heisenberg-limit metrology beyond N00N states, where a wide range of states achieving Heisenberg-limit precision in phase estimation are identified. Finally, we briefly conclude this review in Section 7.
2. Quantum Circuit for N00N State Generation
To facilitate the generation of the N00N state, we consider an interaction Hamiltonian interaction describing two cavity modes coupled to a two-level qubit, expressed as follows [60,61,62].
in which the bosonic annihilation and creation operators for the first and second modes are denoted by and , respectively. These operators can correspond to any harmonic oscillator system, such as the quantized electromagnetic field modes in a cavity. The qubit operators are given by , and , representing the standard Pauli operators that generate the Lie algebra. Moreover, is the effective coupling strength between the two bosonic modes mediated by the qubit. It determines the rate at which excitations are coherently transferred between the two modes.
Hence, the system effectively describes a two-level qubit interacting with two bosonic modes, such as two distinct modes of the cavity field [62].
A key element in our approach to high-N00N state generation is the derivation of the effective Hamiltonian presented in Equation (1). A detailed derivation of the effective Hamiltonian is presented in Appendix A. For conceptual clarity, let us consider a setup where two cavity modes interact with a single qubit, as illustrated in Figure 1. It is insightful to explore how the above Hamiltonian can lead to the generation of a N00N state, beginning with an initial configuration of N photons in one of the cavities. Specifically, we demonstrate that this interaction can result in a N00N state shared between the two cavity modes. To proceed, we initialize the qubit in a logical superposition state, while the first and second cavity modes are prepared in the Fock states and , respectively. Thus, the initial state of the combined system—comprising the qubit and the two cavities—can be expressed as
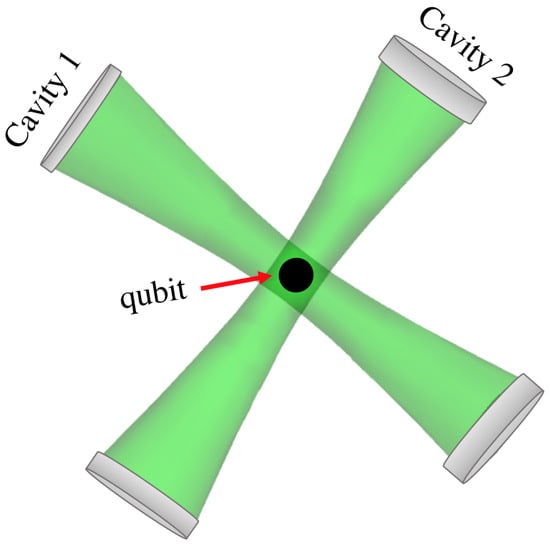
Figure 1.
Schematic illustration of the N00N state generation setup. The system includes two cavities coupled to a qubit, which interacts dispersively with both cavities to facilitate the creation of entangled states.
Starting from this initial state, we analyze the time evolution of the entire system governed by the effective Hamiltonian introduced earlier. The dynamics are dictated by the unitary time evolution operator
Applying this operator to the initial state, , allows us to study how the interaction leads to the formation of a N00N state in the two cavity modes.
We allow the system to evolve over a time interval . Under this evolution, the state of the system transforms into
In this state, the two cavity modes become entangled with the qubit, resulting in a tripartite entangled system. A measurement on the first resonator projecting it into the Fock state effectively collapses the qubit into a superposition state that depends on the parity of k. Specifically, if k is even, the qubit is projected onto the symmetric state , while for odd k, it collapses into the antisymmetric state . These two states form an orthogonal basis in the qubit’s Hilbert space. Conversely, a measurement performed on the qubit in the basis provides information about the parity of k in the first mode. A similar analysis applies to measurements on the second cavity mode, owing to the symmetric structure of the state.
Next, we apply the Hadamard gate to the qubit. The Hadamard operation is represented by a unitary matrix acting on the Hilbert space of a single qubit, defined as [63]
This gate performs a rotation in the qubit’s computational basis, mapping the states as follows: and Applying the Hadamard transformation to the qubit in the previously evolved state induces a local change of basis. After this operation, we allow the system to evolve again under the same effective Hamiltonian for another time interval .
Following this second round of evolution, the quantum state of the system becomes
This state explicitly separates the contributions of even and odd photon number states due to the parity-dependent coefficients . The terms corresponding to even k contribute to the component with the qubit in state , while odd k terms contribute to the component with the qubit in state .
Subsequently, we perform a projective measurement on the qubit in the computational basis. This measurement collapses the total wavefunction, projecting the two cavity modes into a superposition of number states depending on the measurement outcome. If the qubit is found in the state , the total state of the system collapses into
It is evident from this expression that the qubit is now disentangled from the cavity modes due to the measurement-induced collapse of the wavefunction. The remaining state of the field modes is a parity-filtered superposition, containing only contributions from even values of k.
Alternatively, if the qubit measurement yields the outcome , the total wavefunction collapses into
As in the previous case, the qubit becomes disentangled from the field modes due to the projective measurement. The resulting state is a superposition of number states that includes only contributions from odd values of k.
Following the qubit measurement, regardless of the specific outcome, we proceed by applying the unitary time evolution operator once more to the post-measurement state. Suppose, first, that the outcome of the measurement is . In this case, evolving the system for an additional time interval leads to the formation of a N00N state of the form
Alternatively, if the qubit is found in the state , the system must evolve for a longer duration, specifically , in order to reach the N00N state given by
It is worth noting that, regardless of what the outcome of the measurement of the qubit state is, the N00N state can be obtained at the final step of this protocol. Therefore, the N00N state generated with this protocol is deterministic.
It is noteworthy that, once the initial Fock state is prepared, the number of steps required to generate the corresponding N00N state remains independent of the photon number N. In contrast, many conventional N00N state generation protocols begin with a single-photon () N00N state and increase the photon number systematically [64,65]. In such approaches, the number of operations typically scales with N, making them more vulnerable to decoherence and operational errors. However, in the architecture presented here, the N00N state can be achieved through a fixed number of well-defined steps, regardless of the value of N. This feature is particularly advantageous in minimizing the exposure to decoherence, as it reduces the number of required operations and the time the system spends in vulnerable intermediate states. Notably, once a high-fidelity Fock state is prepared in one of the cavity modes—without entangling it initially with other parts of the system—it can be efficiently converted into a N00N state using a small number of coherent operations. This simplicity enhances the scheme’s practicality, as it requires only a single qubit coupled to two cavity modes. Unlike many alternative proposals, the present scheme avoids complex multi-qubit operations or ancillary systems. The full architecture of this setup is illustrated schematically in Figure 2.
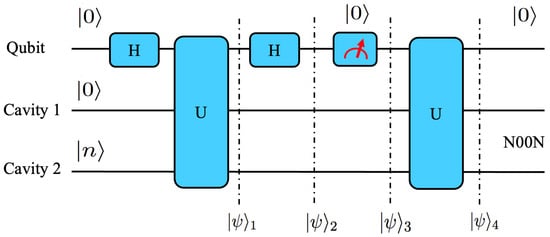
Figure 2.
Schematics of the N00N state generation circuit. The operator U denotes the unitary time evolution governed by the effective Hamiltonian . The Hadamard gate acts locally on the qubit, transforming its basis. Starting from the initial state, the system evolves under U for a time interval , reaching the intermediate state . Application of the Hadamard gate results in the state . A subsequent projective measurement on the qubit collapses the total wavefunction to . Finally, a second time evolution under U transforms the system into the target N00N state.
3. N00N State Generation in Different Systems
The effective Hamiltonian discussed above can be implemented across various quantum platforms. One particularly promising approach involves coupling two superconducting resonators to a common qubit [60,61]. In such systems, the coupling strength between the resonators and the qubit can reach the order of tens of MHz [66,67,68], allowing the system to operate well within the strong-coupling regime. This facilitates the realization of the effective Hamiltonian and enables the generation of N00N states shared between the two resonators, following the quantum circuit protocol described in detail in Figure 2.
Along the same direction, we show that the same effective Hamiltonian can be realized in spin-based systems. In particular, we focus on nitrogen-vacancy (NV) centers in diamond as a candidate for implementing this scheme. NV ensembles (NVEs) offer several key advantages, including long coherence times, which help mitigate one of the main challenges associated with N00N states—decoherence. Moreover, NVEs are excellent candidates for quantum memory applications. Thus, generating and storing N00N states in such systems could be of great importance, enabling long-term preservation of entangled states for quantum technologies.
Furthermore, we demonstrate that the desired effective Hamiltonian can be realized in a trapped ion system, where an atomic transition between two electronic states is coupled to a cavity mode and driven by an external classical laser field. This configuration enables the generation of a N00N state as a superposition of light and motion, effectively entangling the cavity field with the motional degree of freedom of the ion.
3.1. N00N State in Nitrogen-Vacancy Centers in Diamond
Following the developments in Ref. [60], we now demonstrate that N00N states can also be generated in ensembles of nitrogen-vacancy centers (NVEs) in diamond. The overall N00N state generation strategy follows the same circuit protocol described previously. Here, we outline a scenario in which a similar effective Hamiltonian can be engineered for NVEs interacting with a common qubit. In this architecture, we consider a hybrid quantum system composed of two spatially separated, non-interacting NVEs embedded in diamond, both coupled to the same superconducting flux qubit. Specifically, we assume a large, gap-tunable flux qubit (Figure 3a) as the central coupling element [69,70].
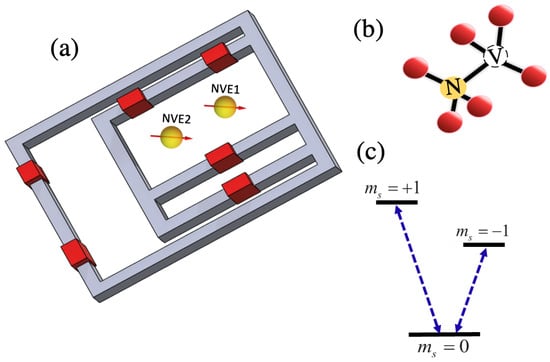
Figure 3.
(a) Schematic of two ensembles of nitrogen-vacancy (NV) centers in diamond coupled to a superconducting flux qubit. The flux qubit consists of four Josephson junctions arranged in a main loop and an additional -loop for tunability. (b) Crystal lattice structure of an NV center in diamond. (c) Energy level diagram of the NV center showing the ground and excited spin states.
This hybrid scheme has several advantages: the long coherence times associated with NV spins, the ability to manipulate NV centers via both microwave and optical fields [71,72], the frequency tunability and circuit scalability offered by superconducting devices, and their compatibility with advanced nanofabrication techniques [64,69,70,73,74].
Although superconducting resonators provide a powerful platform for N00N state generation—thanks to their strong interactions and fast gate times—the coherence times of microwave photons in these resonators typically remain on the order of milliseconds [75]. In contrast, NV centers in diamond can exhibit coherence times approaching one second, even at relatively high temperatures [76]. Therefore, integrating NVEs with superconducting qubits in a single architecture offers a compelling pathway toward high-fidelity quantum state preparation, combining fast gate operations with long-term coherence and quantum memory capabilities.
We now describe the quantum characteristics of the flux qubit. To this end, we note that the flux bias applied to the main loop of the qubit must be chosen close to half of the magnetic flux quantum, . Under this condition, the flux qubit can be effectively modeled as a two-level system described by a Hamiltonian in a two-dimensional Hilbert space. The effective Hamiltonian for the flux qubit takes the form [69]
where and are the standard Pauli operators in the flux qubit basis. The term represents the energy bias between the two persistent current states and depends on the external magnetic flux threading the main loop. The term denotes the tunneling amplitude between these states, which can be controlled via the external flux through the -loop.
When a static magnetic field corresponding to half of the flux quantum is applied perpendicularly to the main loop, the clockwise and counterclockwise persistent current states become nearly degenerate [77,78]. These two states can be used to define the logical basis states and , representing the clockwise and counterclockwise circulating currents, respectively.
Importantly, and are independently tunable via external magnetic fluxes applied to the main and auxiliary loops. Setting places the qubit at its optimal working point, where the system exhibits maximum coherence and symmetric energy levels. With the qubit initialized in either of the computational basis states or , arbitrary single-qubit operations can be implemented using the Hamiltonian above.
In the following, we demonstrate how such a flux qubit can be integrated with nitrogen-vacancy ensembles (NVEs) in diamond to form a hybrid quantum architecture suitable for both quantum information processing and entangled state generation.
For the nitrogen-vacancy (NV) centers in diamond, we focus exclusively on their ground-state manifold. Notably, the ground state of an NV center forms a spin-triplet configuration, with a zero-field splitting of approximately GHz between the sublevel and the degenerate sublevels (Figure 3b,c). To lift the degeneracy of the states, we apply an external static magnetic field along the [100] crystallographic axis of the diamond. This induces a Zeeman splitting between the and levels, allowing us to isolate the two-level subspace spanned by and (Figure 3c).
This two-level subspace enables a natural definition of a computational basis for quantum information processing, effectively reducing the Hilbert space of each NV center to a qubit. Within this reduced space, we can express the spin operators for the jth NV center using Pauli-like operators
To generalize this for an ensemble containing NV centers, we define collective spin operators by summing over individual spins
Qubits based on NV centers, operated under external magnetic fields that induce Zeeman splitting between the states, have been studied extensively (see, e.g., [77,78,79,80]). However, the approach we consider here introduces an additional element, where we apply time-dependent magnetic fields to the NV ensembles, along with the static field , in order to periodically modulate the energy splitting between the and levels. This time-periodic modulation plays a central role in enabling the generation of N00N states, which is the primary goal of this work.
To derive the desired effective Hamiltonian, we employ the Holstein–Primakoff (HP) transformation [81], which allows us to map the collective spin degrees of freedom of the NV ensemble onto bosonic modes. Applying the HP transformation to the periodically modulated two-level system formed by the and states leads to a closed-form Hamiltonian suitable for N00N state generation.
To apply the HP transformation, we restrict our analysis to the weak excitation regime, where the number of excitations is much smaller than the total number of NV centers, . Under this condition, the collective spin operators of each ensemble can be approximated as follows
where labels the two NV ensembles, and the bosonic operators satisfy .
An important feature of this collective spin representation is the enhancement of the coupling strength by a factor of compared to a single spin [82], allowing the system to reach the strong coupling regime more easily. The weak-excitation condition ensures the validity of the HP approximation. In practice, values of have been realized [83], allowing for N00N states with photon numbers .
The total Hamiltonian of the hybrid NVE–flux-qubit system is given by
where
Here, is the Landé g-factor, is the Bohr magneton, is the effective field from the applied and the flux qubit, and g is the coupling strength between the NVE and the flux qubit.
We assume that the NVEs are sufficiently small that spatial inhomogeneities of the qubit-generated magnetic field can be neglected. The external magnetic fields are chosen such that
with the sinusoidal modulation controlled by the AC magnetic fields . For and large , we apply the rotating-wave approximation and move to the flux qubit eigenbasis to obtain the interaction Hamiltonian
This Hamiltonian can be mapped to a Floquet form. Setting (so that ) and ), we obtain the effective interaction Hamiltonian
where is a tunable coupling coefficient determined by the modulation phase difference, acting as an effective interaction rate between two collective modes, mediated by a common qubit. For example, with and , we obtain MHz. Such coupling strengths have been demonstrated experimentally for flux qubits interacting with NVEs containing centers [83].
Assuming decay rates of Hz for NVEs [76] and MHz for the flux qubit [84], the strong coupling condition is clearly satisfied.
An important feature of the proposed N00N-state generation protocol is that it only requires local operations on the flux qubit during the second and third steps, where the state evolves into . As a result, the operation times and reduce to typical single-qubit operation times, approximately ∼1 ns [78]. This allows the total time for N00N state preparation, , to remain very short—minimizing decoherence effects. Given MHz, the interaction time ns. Therefore, the N00N-state preparation time can be determined by considering ns if the measurement outcome is and ns if the outcome is . In both cases, the generation time is significantly shorter than the coherence times of the flux qubit (∼1 s [84]) and the NVEs (∼350 s [85]), ensuring that high-fidelity N00N states can be prepared within this hybrid platform.
3.2. N00N State as a Superposition of Light and Motion
The desired effective Hamiltonian can be realized in a trapped ion system, where an ion is coupled to a cavity mode and driven by an external classical field. This configuration enables the generation of a N00N state as a superposition of light and motion.
To show this, we consider a trapped ion system characterized by an atomic transition between two electronic states, denoted by and , with transition frequency . The ion is coupled to a cavity mode of frequency and is driven externally by a classical laser field with frequency . In the rotating frame defined by the laser frequency , the system’s Hamiltonian can be written as [86,87]
Here, a and are the annihilation and creation operators for the cavity field, while b and correspond to the quantized vibrational (phonon) modes of the trapped ion. The Pauli operators are defined as , , and . The parameter denotes the Lamb–Dicke parameter, quantifying the extent of coupling between the ion’s motion and the light field.
The detuning parameters are defined as and , while encodes the complex amplitude of the driving laser. The coupling strength describes the interaction between the ion, the cavity photon, and the standing-wave pattern of the cavity field.
In the Lamb–Dicke regime (), the sine term can be linearized as which simplifies the Hamiltonian. Assuming resonant atomic driving () and setting , we move to the interaction picture and apply the rotating wave approximation (RWA), yielding the simplified interaction Hamiltonian
We then apply a unitary transformation to move into a rotated basis
which transforms the Hamiltonian to . Under the condition , and after adiabatically eliminating the fast-oscillating terms via RWA, we redefine the phase as . The resulting effective interaction Hamiltonian takes the form [88]
where the effective coupling strength is given by .
This effective Hamiltonian describes a controllable excitation exchange between the cavity field and the ion’s motional mode, with the interaction modulated by the relative phase and governed by the internal state of the ion.
3.3. Impact of Decoherence on the N00N State
Now, we consider the effect of decoherence on the N00N state. Without loss of generality, we use the parameters of NVE systems; however, a similar analysis can be developed for the other systems as well.
To model our scheme, we solve the evolution equation governing the density operator , given by [89,90].
where , and denotes the decoherence rate of the j-th nitrogen-vacancy ensemble (NVE). Here, is the thermal excitation number at temperature T and frequency . After generating the desired state, the magnetic field is switched off, setting .
For our analysis, we set and fix the temperature at . At this temperature, the coherence time is approximately , which is attainable for NV centers. Figure 4 shows the time evolution of the density matrix elements , with the initial condition corresponding to an N00N state shared between the two ensembles at . Decoherence builds up over a timescale of hundreds of milliseconds.
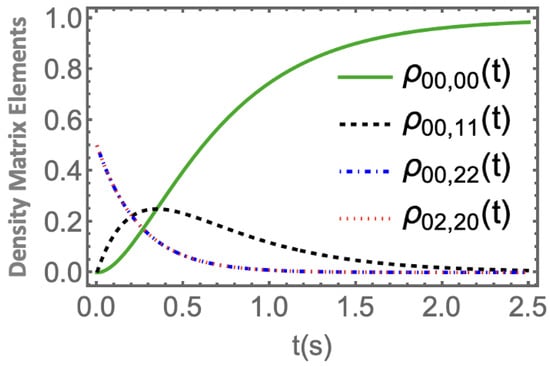
Figure 4.
The time evolution of the density matrix elements corresponding to an N00N state, illustrating the dynamics of coherence and decoherence in the system.
At , the mean thermal excitation number is . With modern cooling techniques, achieving temperatures below is feasible, where . Therefore, thermal excitation effects can be safely neglected. Assuming , the master equation for the N00N state admits an exact solution. Ignoring thermal excitations, the time evolution of the N00N state density matrix can be expressed as
From this solution, the ultimate precision limit of a phase measurement, , is found to satisfy
indicating that decoherence introduces an exponential degradation in the sensitivity of phase estimation as time evolves.
This allows for evaluating the fidelity of the N00N state, defined as the overlap between the evolved state and the initial N00N state
The fidelity F of the N00N state under decoherence can be calculated as
Thus, the fidelity decays exponentially over time, highlighting the fragility of highly entangled states against environmental noise. In fact, this analysis reveals the fundamental challenge associated with generating entangled states and highlights how decoherence poses a significant obstacle to the realization of quantum computing and quantum technologies.
Since the decoherence rate is inversely proportional to the system’s coherence time, , platforms with longer coherence times offer significant advantages. In particular, nitrogen-vacancy ensembles (NVEs) benefit from exceptionally long coherence times, providing an exponential improvement in robustness compared to many other proposed physical systems.
For a fixed photon number N, the fidelity drops to approximately when , signaling that the state has largely decohered. Therefore, maintaining coherence over timescales satisfying is crucial for preserving the quantum advantage offered by N00N states.
4. Entangled State Generations Beyond the N00N State
Now, we explore the generation of entangled states beyond the N00N state. These more general entangled states are valuable resources for a wide range of quantum information processing applications [91]. Following the approach in [61], we demonstrate that a broad class of entangled states, including various maximally entangled configurations, can be engineered using the same underlying framework.
We begin with the effective Hamiltonian introduced earlier in Equation (1), where two cavity modes interact with a common qubit. From this Hamiltonian, we derive the Heisenberg equations of motion for the field operators
Solving these equations yields the time evolution of the cavity operators
At the specific interaction time , these evolve into
Next, the photon fields are passed through a beam splitter, described by the unitary operation
This transformation yields the field operator relations
Combining both the qubit-dependent dynamics and the beam splitter transformation, the effective photon operators become
These transformations are conditional on the state of the qubit and form the foundation of a powerful entanglement generation protocol. They can map initial states into entangled superpositions of field and qubit states, which can be utilized for quantum state engineering tasks. To illustrate this mechanism, consider the following input state
where the first and second terms denote the photon number states in the two cavity modes, and the third term is the superposition state of the qubit.
Applying the above transformations to this input yields the entangled output state
By applying an external pulse (Hadamard gate) to the atom, the system evolves into the state
Thus, a projective measurement on the atom yields different N00N states depending on the measurement outcome. Detecting the atom in the excited state produces the N00N state
while detection in the ground state yields
Despite the relative sign difference, both states are equivalent in applications such as phase estimation and represent genuine N00N states.
The overall protocol is summarized schematically in Figure 5. The input state first interacts with the resonators–qubit system for a duration of , then passes through a beam splitter, and finally, a Hadamard operation and measurement on the qubit complete the N00N state preparation.
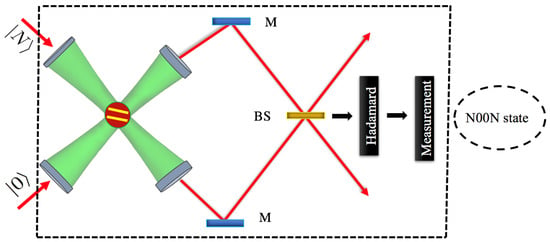
Figure 5.
Architecture for entangled state generation. The input state first evolves under the interaction between two resonators and a common qubit for a duration corresponding to . The photons from the resonators are then directed through a beam splitter. Finally, by applying a Hadamard gate and performing a projective measurement on the qubit, a N00N state is obtained.
As previously mentioned, the capabilities of our setup extend beyond N00N state generation. For instance, consider an initial coherent state [92]
where is a complex amplitude. Preparing the system in the initial state
the protocol results in the entangled state
This constitutes a micro–macro entangled state, where a shared coherent state is entangled with the atomic qubit. After measuring the atomic state, we obtain states of the form
where the + (−) corresponds to a symmetric (antisymmetric) superposition. The symmetric state is shown to be particularly useful for quantum metrology tasks [93].
Moreover, the scheme allows for the generation of a wide range of entangled states. Starting with general input states
the initial system is prepared in
Following the interaction and measurement, detection of the atom in the excited (ground) state produces the symmetric (antisymmetric) entangled states
As an example, if the initial states are coherent states, one can generate entangled states, such as
Also, superposition of two squeezed states
or hybrid entangled states
can be generated using this setup. Such entangled states are crucial for surpassing the shot-noise limit in quantum metrology and have broad applications in quantum information science.
To quantify the entanglement of the generated states , we employ the concurrence as an entanglement measure [94], defined by
where is the Pauli-y matrix and denotes the complex conjugate of .
A straightforward calculation yields
where the plus (minus) sign corresponds to the concurrence of (). Interestingly, the antisymmetric state is maximally entangled for any input states. In contrast, the symmetric state becomes maximally entangled only when the input states are orthogonal, i.e., .
Starting with the input states , the protocol generates maximally entangled states
which reduces to a N00N state when .
Given the ability to generate a large class of maximally entangled states, this platform holds significant promise for various quantum protocols. The versatility and robustness of the scheme make it a powerful tool for quantum information processing and quantum metrology applications.
5. Eantangled State Generation Beyond the Two-Mode States
As demonstrated earlier, the architecture we proposed allows for the generation of a wide variety of entangled states, including N00N states and entangled coherent states. It is therefore natural to consider extending the scheme to a multimode scenario. Generating entangled states involving more than two modes is highly valuable for many applications in quantum information science and quantum metrology. However, the creation of multimode entangled states remains a significant experimental challenge. Thus, the extension presented here could find broad utility across quantum disciplines.
We now describe how the previously introduced scheme can be generalized to generate multimode entangled states. We consider an array of resonators, where each pair of cavities interacts with a common qubit, as shown in Figure 6. The initial state of the full system is prepared as
where each pair of resonators starts with N photons in the first mode and vacuum in the second mode.
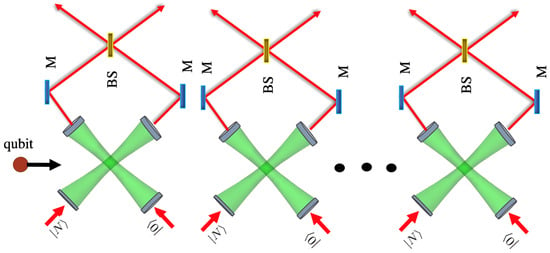
Figure 6.
Network architecture for multi-N00N state generation. A single qubit sequentially interacts with each resonator pair in the array. After the interaction, the photons within each resonator pair are passed through a beam splitter.
The protocol proceeds by sequentially sending the qubit through the network, allowing it to interact for a duration with each resonator pair. After interaction, the photons in each pair are directed through beam splitters. As a result, the system evolves into the entangled state
Applying a pulse (Hadamard gate) on the qubit followed by a projective measurement yields the multi-N00N state
where the sign depends on the measurement outcome.
An important feature of this scheme is the scaling of the phase resolution. For an array of M resonator pairs, the phase uncertainty scales as
which improves linearly with the number of resonator pairs M and the number of photons N. Achieving a similar phase resolution using a traditional N00N state would require increasing the photon number to in a single mode, which becomes extremely challenging for large M and N.
A scheme for generating double-N00N states was proposed in Ref. [95]. To highlight the advantages of our approach, consider the case , and directly compare it with the scheme introduced in Ref. [95]. Their approach requires operational steps to produce a double N00N state, while our system achieves N00N state generation in only a few steps, regardless of the photon number. This operational simplicity constitutes a major strength of our method. Furthermore, our architecture naturally extends to the generation of multi-N00N states, offering valuable advantages for quantum phase estimation.
6. Heisenberg Limit Metrology Beyond N00N States
As discussed earlier, N00N states possess the special capability of achieving the Heisenberg limit (HL) in phase estimation sensitivity. Here, we revisit the Heisenberg-limited sensitivity in the algebra framework and explore its generalization. In particular, we demonstrate that a broader class of Fock state superpositions can also achieve HL sensitivity. To formulate this more generally, we analyze the connection between the N00N state and spin coherent state superpositions, following Ref. [96].
A detailed consideration of spin algebra is given in Appendix B. Based on the formulation of the algebra in Appendix B, for N photons in one of the two modes of the system, we can write
Thus, the N00N state can be expressed in the Dicke basis as [97]
This corresponds to a coherent superposition of the north and south poles on the Bloch sphere in the z-basis. It is important to note that general superpositions of other states, such as
lead to Fock basis states of the form
which do not, in general, achieve Heisenberg-limited sensitivity.
However, if we consider superpositions involving extreme points along other axes, such as the x-axis, interesting possibilities arise. In the x-basis, the Dicke states are related to the z-basis states through
where is the binomial coefficient.
Thus, a normalized superposition of the two extremal states along x is given by
Now, applying a unitary rotation about the x-axis, , to this state yields
The phase uncertainty for this state is found to be indicating Heisenberg-limited sensitivity, identical to that of the N00N state. Similar results hold for superpositions of the two extreme points along the y-axis, involving the states . These considerations were investigated in detail in Ref. [97].
It is natural to ask whether other superposition states, beyond the N00N state, can achieve Heisenberg-limited sensitivity, or whether the three classes discussed so far (along x, y, and z axes) are the only possibilities. If other states exist, what are their properties? Additionally, how can such superposition states be generated, especially in the x, y, and z directions? We address these questions in the following.
Notably, in all these cat-like superposition states, the two constituent states are antipodal points on the Bloch sphere. In general, any point on the Bloch sphere can be obtained by applying a suitable rotation to a reference state, such as . This rotation can be expressed using the generators of the algebra. The most general form of the rotation operator is [96]
In the z-basis, the term introduces only a phase factor, which does not affect phase sensitivity. Indeed, the state
has the same precision sensitivity as the standard N00N state (the inclusion of this phase factor was previously discussed in Ref. [97] to facilitate N00N state generation).
The first exponential term in the rotation operator displaces the ground Dicke state into a spin coherent state, given by [98,99]
where .
The overlap between two spin coherent states and is
Now, consider the superposition of two antipodal spin coherent states
To investigate the phase sensitivity associated with this state, we define the Hermitian operator
This operator allows the construction of a unitary phase shift operator .
Applying the phase shift yields
Thus, the phase uncertainty is reaching the Heisenberg limit.
This result shows that the Heisenberg-limited phase sensitivity is not exclusive to N00N states. A broad class of quantum states, including superpositions of antipodal spin coherent states on the Bloch sphere, can achieve HL precision. Such generalized states provide a wider landscape of useful resources for quantum metrology.
As a natural question, one may ask if it is possible to achieve Heisenberg-limited sensitivity using the superposition of two non-orthogonal spin coherent states that are not antipodal points? Or is this property restricted to antipodal, orthogonal superpositions? To gain better insight, we explore the relation between N00N states and such superposition states. First, observe that the two extreme points along the x-axis are related to the z-axis spin coherent states via a rotation around the y-axis
where is the rotation operator. This relation is illustrated in Figure 7. Thus, by rotating the x-axis cat state about the y-axis and recalling that and one generates the N00N state
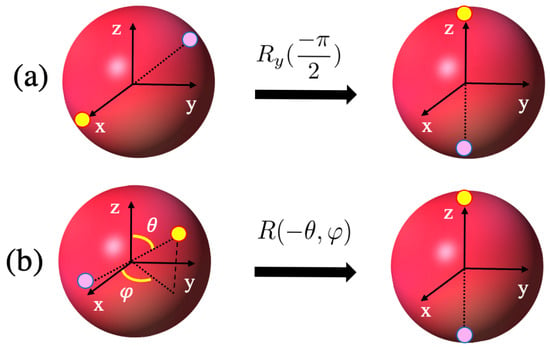
Figure 7.
(a) Rotation of the superposition state around the y-axis on the Bloch sphere. (b) Rotation of an arbitrary antipodal superposition state to achieve N00N state under appropriate evolution.
This shows that a N00N state is a particular case of a spin cat state [97]. More generally, a spin coherent state can be expressed as the action of a rotation operator on the ground state The antipodal point of this coherent state is then
Applying the inverse rotation maps the antipodal spin coherent states into a N00N state. However, such transformations generally change the structure of the states significantly.
Now, consider the superposition of two arbitrary spin coherent states Applying yields
This condition can be fulfilled if where we note that .
The composition of two rotation operators satisfies
where
with and To recover a N00N-like state, the condition
must be satisfied, where is some phase determined by the initial parameters. Thus, and must correspond to antipodal points.
If this condition is not met, the superposition will not transform into a N00N state under a global unitary operation, and the corresponding state will have a different structure. In the Fock basis, such a general two-mode superposition state reads
where n is the total number of photons. Although this state is structurally different from a N00N state, it still achieves Heisenberg-limited phase sensitivity. Therefore, it offers a more general path to HL precision.
To consider the generation of such states, we start with the interaction Hamiltonian between the two-mode field, and a two-level atom reads
where is the coupling strength.
Suppose the atom is initially prepared in the superposition state while the two-mode field is prepared such that mode-a is in the vacuum and mode-b is in the Fock state . Then, the initial state reads
Defining , the evolved state becomes
where denotes a spin coherent state.
This describes a micro–macro entangled state between the atomic and photonic degrees of freedom. Applying a pulse on the atomic state, and subsequently performing a projective measurement on the atomic ground state collapses the system to which is a spin cat state.
Thus, a large class of spin cat states can achieve Heisenberg-limited metrology, providing new routes toward practical realization of quantum-enhanced precision measurements.
7. Conclusions
In this review, we presented a comprehensive framework for the generation of N00N states—a bipartite maximally entangled state crucial for quantum metrology applications. This was achieved by employing Floquet-engineered interactions across a variety of physical platforms, including superconducting resonators, nitrogen-vacancy ensembles, and hybrid light–motion systems. Our approach significantly reduces the operational complexity typically associated with N00N state generation by requiring a fixed number of steps independent of the photon number N, thus minimizing exposure to decoherence.
Despite the advantages demonstrated, several limitations remain. The most important limitation is the vulnerability of N00N states to decoherence, which leads to a decrease in fidelity over time and imposes significant requirements on the coherence times of the physical systems involved. Although our proposed architectures—particularly those based on NV ensembles—benefit from long intrinsic coherence times, practical implementations may still face challenges due to fabrication imperfections, control errors, and thermal noise. Possible improvements could involve the integration of quantum error correction techniques or decoherence-free subspace encoding to enhance robustness.
This study not only advances practical strategies for N00N state generation, but also broadens the landscape of states capable of achieving Heisenberg-limited sensitivity. By extending the methods to more general spin coherent state superpositions, we lay a foundation for future investigations into more resilient and scalable quantum-enhanced technologies.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Derivation of the Effective Hamiltonian
Appendix A.1. Modulating the Coupling Between the Qubit and the Resonators
We consider a system consisting of two resonators coupled to a common two-level atom (qubit), described by a Hamiltonian composed of a free and an interaction part
as introduced in [61]. The coupling between the qubit and the cavity fields is assumed to be periodically modulated. The free Hamiltonian is given by
where is the energy splitting of the qubit, and and are the resonance frequencies of the first and second cavities, respectively. The interaction Hamiltonian takes the form [100,101,102]
where denotes the qubit–cavity coupling strength, while and represent the modulation frequency and phase for cavity mode . For simplicity, we work in the resonant regime, where , and set .
To extract the effective Hamiltonian responsible for N00N state generation, we move into the rotating frame defined by the unitary operator
In this frame, the interaction Hamiltonian becomes
Evaluating this expression yields [101,102,103,104,105]
where is the detuning between the qubit and the cavity modes. Using the exponential representation of the cosine function, we rewrite the Hamiltonian as
To simplify the expression, we define the operator [101,102,103,104,105]
which allows us to compactly write the interaction Hamiltonian as
This time-periodic Hamiltonian corresponds to a Floquet system [101,102,103,104,105,106,107,108,109], enabling the application of Floquet theory to derive an effective time-independent Hamiltonian. This effective Hamiltonian will be central to the generation of the N00N state discussed previously.
Without loss of generality, we assume identical modulation frequencies for both resonators, i.e., . Additionally, it is useful to note that each operator commutes with its Hermitian conjugate, such that . Under these conditions, the time-averaged (effective) Hamiltonian simplifies to [61,106]
The interaction strength in this Hamiltonian can be controlled through the modulation phase difference between the two cavities. To maximize the effective coupling, we set and define the effective coupling constant as This allows the Hamiltonian to be expressed as
In the resonant case where , the effective Hamiltonian takes the final simplified form [61]
It is notable that the modulation phase difference governs the strength of the interaction. When , the sine term vanishes, eliminating the effective interaction term entirely. This highlights the importance of precise phase control in experimental implementations of the scheme.
Although is large when is small, care must be taken to ensure that the system remains in the strong-coupling regime. Since Floquet theory generally assumes a high-frequency modulation, must still be significantly larger than . However, choosing to be too large diminishes . For instance, selecting yields a moderate coupling strength of This trade-off between frequency and coupling strength must be carefully balanced in practice to ensure effective dynamics.
Appendix A.2. Modulating the Frequencies of the Resonators
We demonstrated that the effective Hamiltonian of our system can be engineered by modulating the qubit–cavity coupling in a setup involving two resonators interacting with a common qubit. Here, we present an alternative scheme to realize the same effective Hamiltonian through a different type of modulation. In this approach, we again consider two resonators coupled to the same qubit, but instead of modulating the coupling strength, we modulate the resonance frequencies of the cavities themselves. The time-dependent frequencies are given by [101,103]
where is the central frequency, is the modulation amplitude, is the modulation frequency, and is the modulation phase of resonator .
In this configuration, the qubit frequency remains constant, and no modulation is applied to it. Consequently, the Hamiltonian of the system takes the form
where is the (constant) coupling strength between the qubit and the cavity modes.
This alternative modulation scheme, involving dynamic control of the cavity frequencies with phase-offset sinusoidal drives, will be shown to yield an effective Hamiltonian similar in form to the one previously derived using coupling modulation.
Here, denotes the constant coupling strength between the qubit and the cavity modes. The quantities and represent the time-dependent resonator frequencies modulated, as described previously. Starting from the full Hamiltonian, one can derive the interaction Hamiltonian by moving to an appropriate rotating frame. Under the rotating wave approximation (RWA), and assuming the resonant condition , the total Hamiltonian simplifies to the following interaction form
where is the modulation index.
This form explicitly captures the time-dependent phase modulation induced by the sinusoidal frequency drives on the resonators. The interaction terms now feature exponential functions of cosine arguments, which naturally lend themselves to expansion in terms of Bessel functions for further simplification. This Hamiltonian can be recast as a Floquet Hamiltonian using the identity [101,107]
where denotes the nth-order Bessel function of the first kind. Substituting this expansion into the interaction Hamiltonian allows us to express it in the standard Floquet form
where is the time-independent part of the Hamiltonian, corresponding to the component
The time-dependent terms in the Floquet expansion are captured by
According to Floquet theory [101,102,103,104,105,106,107,108,109], the effective Hamiltonian can be derived by averaging over the fast modulation, yielding
This leads to the effective Hamiltonian
where the effective coupling coefficient is defined as and the modulation-dependent parameter is given by
It is evident that the modulation phase difference plays a crucial role in the emergence of the desired Hamiltonian. If the phases are equal, i.e., , the parameter vanishes, thereby suppressing the effective interaction term. To enhance the coupling strength of the system, one can optimize the value of , which provides a direct and tunable strategy for controlling the interaction via modulation phase engineering.
We specifically choose () and to derive the effective Hamiltonian [60,61]
To maximize the effective coupling coefficient of the Hamiltonian , one can maximize by controlling the phase difference . If we choose , we will obtain .
Appendix B. Spin Algebra
We introduce the Schwinger realization of the algebra in terms of two-mode bosonic field operators [110,111,112]
Here, and are the raising and lowering operators, and is the z-component of the angular momentum operator.
These operators satisfy the standard commutation relations
By defining
we can map the Fock basis onto the Dicke state basis
This provides a direct connection between the two-mode Fock space and the angular momentum space. Two important cases are
The action of the spin operators on the Dicke basis is given by
The set of states form the eigenbasis of the Hilbert space of the spin system.
References
- Helstrom, C.W. Quantum Detection and Estimation Theory; Springer: New York, NY, USA, 1976. [Google Scholar]
- Holevo, A.S. Probabilistic and Statistical Aspects of Quantum Theory; Springer Science & Business Media: Berlin, Germany, 2011; Volume 1. [Google Scholar]
- Caves, C.M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439. [Google Scholar] [CrossRef] [PubMed]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Khashami, F. Fundamentals of NMR and MRI: From Quantum Principles to Medical Applications; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Komar, P.; Kessler, E.M.; Bishof, M.; Jiang, L.; Sørensen, A.S.; Ye, J.; Lukin, M.D. A quantum network of clocks. Nat. Phys. 2014, 10, 582–587. [Google Scholar] [CrossRef]
- Lewis-Swan, R.J.; Castro, J.Z.; Barberena, D.; Rey, A.M. Exploiting nonclassical motion of a trapped ion crystal for quantum-enhanced metrology of global and differential spin rotations. Phys. Rev. Lett. 2024, 132, 163601. [Google Scholar] [CrossRef]
- DeMille, D.; Hutzler, N.R.; Rey, A.M.; Zelevinsky, T. Quantum sensing and metrology for fundamental physics with molecules. Nat. Phys. 2024, 20, 741–749. [Google Scholar] [CrossRef]
- Albarelli, F.; Barbieri, M.; Genoni, M.G.; Gianani, I. A perspective on multiparameter quantum metrology: From theoretical tools to applications in quantum imaging. Phys. Lett. A 2020, 384, 126311. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Maleki, Y.; Zubairy, M.S. Distributed phase estimation and networked quantum sensors with W-type quantum probes. Phys. Rev. A 2022, 105, 032428. [Google Scholar] [CrossRef]
- Bevington, P.R.; Robinson, D.K. Data Reduction and Error Analysis for the Physical Sciences; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Sanders, B.C. Quantum dynamics of the nonlinear rotator and the effects of continual spin measurement. Phys. Rev. A 1989, 40, 2417. [Google Scholar] [CrossRef] [PubMed]
- Boto, A.N.; Kok, P.; Abrams, D.S.; Braunstein, S.L.; Williams, C.P.; Dowling, J.P. Quantum interferometric optical lithography: Exploiting entanglement to beat the diffraction limit. Phys. Rev. Lett. 2000, 85, 2733. [Google Scholar] [CrossRef]
- Maleki, Y.; Zubairy, M.S. Universal criteria for entanglement-assisted dynamical speed enhancement. Phys. Rev. A 2024, 110, 052415. [Google Scholar] [CrossRef]
- Taylor, M.A.; Bowen, W.P. Quantum metrology and its application in biology. Phys. Rep. 2016, 615, 1–59. [Google Scholar] [CrossRef]
- Aslam, N.; Zhou, H.; Urbach, E.K.; Turner, M.J.; Walsworth, R.L.; Lukin, M.D.; Park, H. Quantum sensors for biomedical applications. Nat. Rev. Phys. 2023, 5, 157–169. [Google Scholar] [CrossRef]
- Lee, H.; Kok, P.; Dowling, J.P. A quantum Rosetta stone for interferometry. J. Mod. Opt. 2002, 49, 2325–2338. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzański, R.; Górecki, W.; Guţă, M. Multi-parameter estimation beyond quantum Fisher information. J. Phys. A Math. Theor. 2020, 53, 363001. [Google Scholar] [CrossRef]
- Pezze, L.; Smerzi, A.; Oberthaler, M.K.; Schmied, R.; Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 2018, 90, 035005. [Google Scholar] [CrossRef]
- Ono, T.; Okamoto, R.; Takeuchi, S. An entanglement-enhanced microscope. Nat. Commun. 2013, 4, 2426. [Google Scholar] [CrossRef]
- Dowling, J.P. Quantum optical metrology–the lowdown on high-N00N states. Contemp. Phys. 2008, 49, 125–143. [Google Scholar] [CrossRef]
- Cappellaro, P.; Emerson, J.; Boulant, N.; Ramanathan, C.; Lloyd, S.; Cory, D.G. Entanglement assisted metrology. Phys. Rev. Lett. 2005, 94, 020502. [Google Scholar] [CrossRef]
- Suzuki, J.; Yang, Y.; Hayashi, M. Quantum state estimation with nuisance parameters. J. Phys. A Math. Theor. 2020, 53, 453001. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, H.; Lu, X.-M.; Wang, X. Quantum Fisher information matrix and multiparameter estimation. J. Phys. A Math. Theor. 2020, 53, 023001. [Google Scholar] [CrossRef]
- Conlon, L.O.; Suzuki, J.; Lam, P.K.; Assad, S.M. Efficient computation of the Nagaoka–Hayashi bound for multiparameter estimation with separable measurements. npj Quantum Inf. 2021, 7, 110. [Google Scholar] [CrossRef]
- Hayashi, M.; Ouyang, Y. Tight Cramér-Rao type bounds for multiparameter quantum metrology through conic programming. Quantum 2023, 7, 1094. [Google Scholar] [CrossRef]
- Sidhu, J.S.; Ouyang, Y.; Campbell, E.T.; Kok, P. Tight bounds on the simultaneous estimation of incompatible parameters. Phys. Rev. X 2021, 11, 011028. [Google Scholar] [CrossRef]
- Maleki, Y.; Ahansaz, B.; Maleki, A. Speed limit of quantum metrology. Sci. Rep. 2023, 13, 12031. [Google Scholar] [CrossRef]
- Afek, I.; Ambar, O.; Silberberg, Y. High-NOON states by mixing quantum and classical light. Science 2010, 328, 879–881. [Google Scholar] [CrossRef]
- Maleki, Y. Quantum phase estimations with spin coherent states superposition. Eur. Phys. J. Plus 2021, 136, 1028. [Google Scholar] [CrossRef]
- Maleki, Y.; Scully, M.O.; Zheltikov, A.M. Quantum metrology with superposition spin coherent states: Insights from Fisher information. Phys. Rev. A 2021, 104, 053712. [Google Scholar] [CrossRef]
- Holl, M.J.; Burnett, K. Interferometric detection of optical phase shifts at the Heisenberg limit. Phys. Rev. Lett. 1993, 71, 1355–1358. [Google Scholar]
- Zhou, S.; Zhang, M.; Preskill, J.; Jiang, L. Achieving the Heisenberg limit in quantum metrology using quantum error correction. Nat. Commun. 2018, 9, 78. [Google Scholar] [CrossRef]
- Xiang, G.Y.; Higgins, B.L.; Berry, D.W.; Wiseman, H.M.; Pryde, G.J. Entanglement-enhanced measurement of a completely unknown optical phase. Nat. Photonics 2011, 5, 43–47. [Google Scholar] [CrossRef]
- Grün, D.S.; Wittmann, W.K.; Ymai, L.H.; Links, J.; Foerster, A. Protocol designs for NOON states. Commun. Phys. 2022, 5, 36. [Google Scholar] [CrossRef]
- Matthews, J.C.; Politi, A.; Bonneau, D.; O’Brien, J.L. Heralded entanglement for quantum enhanced measurement with photons. Phys. Rev. Lett. 2011, 107, 163602. [Google Scholar] [CrossRef]
- Rozema, L.A.; Bateman, J.D.; Mahler, D.H.; Okamoto, R.; Feizpour, A.; Hayat, A.; Steinberg, A.M. Scalable spatial superresolution using entangled photons. Phys. Rev. Lett. 2014, 112, 223602. [Google Scholar] [CrossRef]
- Chen, Y.-A.; Bao, X.-H.; Yuan, Z.-S.; Chen, S.; Zhao, B.; Pan, J.-W. Heralded generation of an atomic NOON state. Phys. Rev. Lett. 2010, 104, 043601. [Google Scholar] [CrossRef]
- Birrittella, R.J.; Alsing, P.M.; Gerry, C.C. The parity operator: Applications in quantum metrology. AVS Quantum Sci. 2021, 3, 014701. [Google Scholar] [CrossRef]
- Nimbe, P.; Weyori, B.A.; Adekoya, A.F. Models in quantum computing: A systematic review. Quantum Inf. Process. 2021, 20, 80. [Google Scholar] [CrossRef]
- Motta, M.; Rice, J.E. Emerging quantum computing algorithms for quantum chemistry. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1580. [Google Scholar] [CrossRef]
- Chen, J. Review on quantum communication and quantum computation. J. Phys. Conf. Ser. 2021, 1865, 022008. [Google Scholar] [CrossRef]
- Yang, Z.; Zolanvari, M.; Jain, R. A survey of important issues in quantum computing and communications. IEEE Commun. Surv. Tutor. 2023, 25, 1059–1094. [Google Scholar] [CrossRef]
- Hu, X.M.; Guo, Y.; Liu, B.H.; Li, C.F.; Guo, G.C. Progress in quantum teleportation. Nat. Rev. Phys. 2023, 5, 339–353. [Google Scholar] [CrossRef]
- Israel, Y.; Rosen, S.; Silberberg, Y. Supersensitive polarization microscopy using NOON states of light. Phys. Rev. Lett. 2014, 112, 103604. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Um, M.; Lv, D.; Zhang, J.N.; Duan, L.M.; Kim, K. NOON states of nine quantized vibrations in two radial modes of a trapped ion. Phys. Rev. Lett. 2018, 121, 160502. [Google Scholar] [CrossRef]
- Dengis, S.; Wimberger, S.; Schlagheck, P. Accelerated creation of NOON states with ultracold atoms via counterdiabatic driving. Phys. Rev. A 2025, 111, L031301. [Google Scholar] [CrossRef]
- Qi, S.F.; Jing, J. Generating entangled states from coherent states in circuit QED. Phys. Rev. A 2023, 107, 042412. [Google Scholar] [CrossRef]
- Nikoghosyan, G.; Hartmann, M.J.; Plenio, M.B. Generation of mesoscopic entangled states in a cavity coupled to an atomic ensemble. Phys. Rev. Lett. 2012, 108, 123603. [Google Scholar] [CrossRef]
- Lidar, D.A.; Chuang, I.L.; Whaley, K.B. Decoherence-free subspaces for quantum computation. Phys. Rev. Lett. 1998, 81, 2594. [Google Scholar] [CrossRef]
- Lidar, D.A.; Bacon, D.; Whaley, K.B. Concatenating decoherence-free subspaces with quantum error correcting codes. Phys. Rev. Lett. 1999, 82, 4556. [Google Scholar] [CrossRef]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Linear entropy of multiqutrit nonorthogonal states. Opt. Express 2019, 27, 8291–8307. [Google Scholar] [CrossRef]
- Maniscalco, S.; Francica, F.; Zaffino, R.L.; Lo Gullo, N.; Plastina, F. Protecting entanglement via the quantum Zeno effect. Phys. Rev. Lett. 2008, 100, 090503. [Google Scholar] [CrossRef]
- Basit, A.; Badshah, F.; Ali, H.; Ge, G.-Q. Protecting quantum coherence and discord from decoherence of depolarizing noise via weak measurement and measurement reversal. Europhys. Lett. 2017, 118, 30002. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Generating maximally-path-entangled number states in two spin ensembles coupled to a superconducting flux qubit. Phys. Rev. A 2018, 97, 012312. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. A high-N00N output of harmonically driven cavity QED. Sci. Rep. 2019, 9, 16780. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Perfect swap and transfer of arbitrary quantum states. Opt. Commun. 2021, 496, 126870. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Wang, H.; Mariantoni, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; O’Connell, A.D.; Sank, D.; Weides, M.; Wenner, J.; et al. Deterministic entanglement of photons in two superconducting microwave resonators. Phys. Rev. Lett. 2011, 106, 060401. [Google Scholar] [CrossRef]
- Su, Q.-P.; Yang, C.-P.; Zheng, S.-B. Fast and simple scheme for generating NOON states of photons in circuit QED. Sci. Rep. 2014, 4, 3898. [Google Scholar] [CrossRef]
- Kubo, Y.; Ong, F.R.; Bertet, P.; Vion, D.; Jacques, V.; Zheng, D.; Dréau, A.; Roch, J.-F.; Auffeves, A.; Jelezko, F.; et al. Strong coupling of a spin ensemble to a superconducting resonator. Phys. Rev. Lett. 2010, 105, 140502. [Google Scholar] [CrossRef] [PubMed]
- Niemczyk, T.; Deppe, F.; Huebl, H.; Menzel, E.P.; Hocke, F.; Schwarz, M.J.; Garcia-Ripoll, J.J.; Zueco, D.; Hümmer, T.; Solano, E.; et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat. Phys. 2010, 6, 772–776. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; Lisenfeld, J.; Marcos, D.; Garcia-Ripoll, J.J.; Solano, E.; Harmans, C.J.P.M.; Mooij, J.E. Observation of the Bloch-Siegert Shift in a Qubit-Oscillator System in the Ultrastrong Coupling Regime. Phys. Rev. Lett. 2010, 105, 237001. [Google Scholar] [CrossRef] [PubMed]
- Song, W.L.; Yin, Z.Q.; Yang, W.L.; Zhu, X.B.; Zhou, F.; Feng, M. One-step generation of multipartite entanglement among nitrogen-vacancy center ensembles. Sci. Rep. 2015, 5, 7755. [Google Scholar] [CrossRef] [PubMed]
- Marcos, D.; Wubs, M.; Taylor, J.M.; Aguado, R.; Lukin, M.D.; Sørensen, A.S. Coupling nitrogen-vacancy centers in diamond to superconducting flux qubits. Phys. Rev. Lett. 2010, 105, 210501. [Google Scholar] [CrossRef]
- Childress, L.; Gurudev Dutt, M.V.; Taylor, J.M.; Zibrov, A.S.; Jelezko, F.; Wrachtrup, J.; Hemmer, P.R.; Lukin, M.D. Coherent dynamics of coupled electron and nuclear spin qubits in diamond. Science 2006, 314, 281–285. [Google Scholar] [CrossRef]
- Dutt, M.G.; Childress, L.; Jiang, L.; Togan, E.; Maze, J.; Jelezko, F.; Zibrov, A.S.; Hemmer, P.R.; Lukin, M.D. Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 2007, 316, 1312–1316. [Google Scholar] [CrossRef]
- Liu, T.; Su, Q.-P.; Xiong, S.-J.; Liu, J.-M.; Yang, C.-P.; Nori, F. Generation of a macroscopic entangled coherent state using quantum memories in circuit QED. Sci. Rep. 2016, 6, 32004. [Google Scholar] [CrossRef]
- Ranjan, V.; de Lange, G.; Schutjens, R.; Debelhoir, T.; Groen, J.P.; Szombati, D.; Thoen, D.J.; Klapwijk, T.M.; Hanson, R.; DiCarlo, L. Probing dynamics of an electron-spin ensemble via a superconducting resonator. Phys. Rev. Lett. 2013, 110, 067004. [Google Scholar] [CrossRef]
- Reagor, M.; Pfaff, W.; Axline, C.; Heeres, R.W.; Ofek, N.; Sliwa, K.; Holland, E.; Wang, C.; Blumoff, J.; Chou, K.; et al. Quantum memory with millisecond coherence in circuit QED. Phys. Rev. B 2016, 94, 014506. [Google Scholar] [CrossRef]
- Bar-Gill, N.; Pham, L.M.; Jarmola, A.; Budker, D.; Walsworth, R.L. Solid-state electronic spin coherence time approaching one second. Nat. Commun. 2013, 4, 1743. [Google Scholar] [CrossRef]
- Xiang, Z.L.; Ashhab, S.; You, J.Q.; Nori, F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 2013, 85, 623–653. [Google Scholar] [CrossRef]
- Xiang, Z.-L.; Lu, X.-Y.; Li, T.F.; You, J.Q.; Nori, F. Hybrid quantum circuit consisting of a superconducting flux qubit coupled to a spin ensemble and a transmission-line resonator. Phys. Rev. B 2013, 87, 144516. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Witnessing quantum entanglement in ensembles of nitrogen–vacancy centers coupled to a superconducting resonator. Opt. Express 2018, 26, 17849–17858. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Macroscopic tripartite entanglement of nitrogen-vacancy centers in diamond coupled to a superconducting resonator. J. Opt. Soc. Am. B 2019, 36, 443–450. [Google Scholar] [CrossRef]
- Hammerer, K.; Sørensen, A.S.; Polzik, E.S. Quantum interface between light and atomic ensembles. Rev. Mod. Phys. 2010, 82, 1041–1093. [Google Scholar] [CrossRef]
- Raizen, M.G.; Thompson, R.J.; Brecha, R.J.; Kimble, H.J.; Carmichael, H.J. Normal-mode splitting and linewidth averaging for two-state atoms in an optical cavity. Phys. Rev. Lett. 1989, 63, 240. [Google Scholar] [CrossRef]
- Zhu, X.; Saito, S.; Kemp, A.; Kakuyanagi, K.; Karimoto, S.; Nakano, H.; Munro, W.J.; Tokura, Y.; Everitt, M.S.; Nemoto, K.; et al. Coherent coupling of a superconducting flux qubit to an electron spin ensemble in diamond. Nature 2011, 478, 221–224. [Google Scholar] [CrossRef]
- Lü, X.-Y.; Xiang, Z.-L.; Cui, W.; You, J.Q.; Nori, F. Quantum memory using a hybrid circuit with flux qubits and nitrogen-vacancy centers. Phys. Rev. A 2013, 88, 012329. [Google Scholar] [CrossRef]
- Yang, W.L.; Hu, Y.; Yin, Z.Q.; Deng, Z.J.; Feng, M. Entanglement of nitrogen-vacancy-center ensembles using transmission line resonators and a superconducting phase qubit. Phys. Rev. A 2011, 83, 022302. [Google Scholar] [CrossRef]
- Parkins, A.S.; Larsabal, E. Preparation and light-mediated distribution of motional state entanglement. Phys. Rev. A 2000, 63, 012304. [Google Scholar] [CrossRef]
- Parkins, A.S.; Kimble, H.J. Quantum state transfer between motion and light. J. Opt. B Quantum Semiclassical Opt. 1999, 1, 496–504. [Google Scholar] [CrossRef]
- Maleki, Y.; Maleki, A. Entangled multimode spin coherent states of trapped ions. J. Opt. Soc. Am. B 2018, 35, 1211–1217. [Google Scholar] [CrossRef]
- Agarwal, G.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; OUP: Oxford, UK, 2002. [Google Scholar]
- Maleki, Y.; Ahansaz, B. Quantum correlations in qutrit-like superposition of spin coherent states. Laser Phys. Lett. 2019, 16, 075205. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Joo, J.; Munro, W.J.; Spiller, T.P. Quantum metrology with entangled coherent states. Phys. Rev. Lett. 2011, 107, 083601. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar] [CrossRef]
- Su, Q.P.; Zhu, H.H.; Yu, L.; Zhang, Y.; Xiong, S.J.; Liu, J.M.; Yang, C.P. Generating double NOON states of photons in circuit QED. Phys. Rev. A 2017, 95, 022339. [Google Scholar] [CrossRef]
- Maleki, Y.; Zheltikov, A.M. Spin cat-state family for Heisenberg-limit metrology. J. Opt. Soc. Am. B 2020, 37, 1021–1026. [Google Scholar] [CrossRef]
- Sanders, B.C.; Gerry, C.C. Connection between the NOON state and a superposition of SU(2) coherent states. Phys. Rev. A 2014, 90, 045804. [Google Scholar] [CrossRef]
- Arecchi, F.T.; Courtens, E.; Gilmore, R.; Thomas, H. Atomic coherent states in quantum optics. Phys. Rev. A 1972, 6, 2211. [Google Scholar] [CrossRef]
- Perelomov, A.M. Coherent states for arbitrary Lie group. Commun. Math. Phys. 1972, 26, 222–236. [Google Scholar] [CrossRef]
- Wang, D.-W.; Song, C.; Feng, W.; Cai, H.; Xu, D.; Deng, H.; Li, H.; Zheng, D.; Zhu, X.; Wang, H.; et al. Synthesis of antisymmetric spin exchange interaction and chiral spin clusters in superconducting circuits. Nat. Phys. 2019, 15, 382–386. [Google Scholar] [CrossRef]
- Wang, D.W.; Cai, H.; Liu, R.B.; Scully, M.O. Mesoscopic superposition states generated by synthetic spin-orbit interaction in Fock-state lattices. Phys. Rev. Lett. 2016, 116, 220502. [Google Scholar] [CrossRef] [PubMed]
- Roushan, P.; Neill, C.; Megrant, A.; Chen, Y.; Babbush, R.; Barends, R.; Campbell, B.; Chen, Z.; Chiaro, B.; Dunsworth, A.; et al. Chiral ground-state currents of interacting photons in a synthetic magnetic field. Nat. Phys. 2017, 13, 146–151. [Google Scholar] [CrossRef]
- Wang, D.-W.; Cai, H.; Yuan, L.; Zhu, S.-Y.; Liu, R.-B. Topological phase transitions in superradiance lattices. Optica 2015, 2, 712–715. [Google Scholar] [CrossRef]
- Goldman, N.; Dalibard, J. Periodically driven quantum systems: Effective Hamiltonians and engineered gauge fields. Phys. Rev. X 2014, 4, 031027. [Google Scholar] [CrossRef]
- Jotzu, G.; Messer, M.; Desbuquois, R.; Lebrat, M.; Uehlinger, T.; Greif, D.; Esslinger, T. Experimental realization of the topological Haldane model with ultracold fermions. Nature 2014, 515, 237–240. [Google Scholar] [CrossRef]
- Maleki, Y.; Zhou, C.; Zubairy, M.S. Time-reversal-symmetry breaking in a scalable cavity QED lattice. Phys. Rev. A 2023, 108, 063709. [Google Scholar] [CrossRef]
- Maleki, Y.; Zhou, C.; Zubairy, M.S. Time-reversal-symmetry breaking and chiral quantum state manipulation in plasmonic nanorings. Phys. Rev. A 2022, 105, 042422. [Google Scholar] [CrossRef]
- Koch, J.; Houck, A.A.; Hur, K.L.; Girvin, S.M. Time-reversal-symmetry breaking in circuit-QED-based photon lattices. Phys. Rev. A 2010, 82, 043811. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photonics 2012, 6, 782–787. [Google Scholar] [CrossRef]
- Huang, J.; Zhuang, M.; Lu, B.; Ke, Y.; Lee, C. Achieving Heisenberg-limited metrology with spin cat states via interaction-based readout. Phys. Rev. A 2018, 98, 012129. [Google Scholar] [CrossRef]
- Huang, J.; Qin, X.; Zhong, H.; Ke, Y.; Lee, C. Quantum metrology with spin cat states under dissipation. Sci. Rep. 2015, 5, 17894. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Sanders, B.C.; Pan, S.H. Entangled coherent states for systems with SU(2) and SU(1, 1) symmetries. J. Phys. A Math. Gen. 2000, 33, 7451. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).