Conformable Lagrangian Mechanics of Actuated Pendulum

Abstract

In this paper, we construct the conformable actuated pendulum model in the conformable Lagrangian formalism. We solve the equations of motion in the absence of force and in the case of a specific force resulting from torques, which generalizes a well known mechanical model. Our study shows that the conformable model captures essential information about the physical system encoded in the parameters which depend on the conformability factor $\alpha$. This dependence can describe internal variations such as viscous friction, transmission, or environmental effects. We solve the equations of motion analytically for $\alpha =1/2$ and using Frobenius’ method for $\alpha \ne 1/2$.

1. Introduction

The conformable derivative was proposed in [1] as an alternative to fractional derivatives that satisfy the Leibniz rule [2]. Soon after, several fundamental mathematical properties were proved in [3,4,5,6,7]. A generalization of the conformable derivative with an exponential scale factor was proposed in [8] and studied in [9], and its extension to an arbitrary time scale was given in [10]. However, it was shown in [11] that the fractional derivatives break the Leibniz rule, particularly for non-integer orders. Subsequently, two criteria for fractional derivatives were formulated in [12]. This analysis led to the conclusion that the conformable derivative is not a proper fractional derivative [13,14]. Despite not being a fractional calculus according to these criteria, conformable calculus has recently attracted attention due to its analytical properties. In mathematics, it has been generalized to Hermite polynomials [15], arbitrary time scales [16], formal diffusion equation [17], Banach spaces [18], several variables [19,20], q-deformed derivative [21], soliton solutions for fractional evolution equations [22], mathematical aspects of conformable differential equations with damping terms [23,24], theory of distributions [25], and the effect of the conformable derivative on differential equations [26]. In physics, attempts to interpret the conformable derivative were made in [27,28,29]. The conformable Newtonian mechanics was given in [30], while the Lagrangian formalism was formulated in [31]. In quantum mechanics, several conformable systems were analyzed in [6,32,33,34,35,36,37,38,39,40,41,42]. Important hints of the nature of the conformable derivative as a fractal were given in [5,43,44]. More recently, it was argued that the conformable derivative is suitable for describing fractal media and fractal distributions of matter in continuum models with fractal density of states in [45]. For a recent review of the applications of conformable calculus in physics, see [46].

Despite the large number of studies on the applications of conformable calculus in physics, there are still unanswered questions about the physical information that can be encoded in a conformable model. In particular, a crucial problem concerns the generalization of Lagrangian mechanics and the physical effects that can be described by such a system. The variational principle of conformable systems was studied previously in [31,47,48], with emphasis on establishing formal results. In particular, Ref. [31] gives a detailed construction of Lagrangian and Hamiltonian formalism for conformable systems that include frictional forces.

In this paper, we address the problem of the physical effects described by conformable calculus in the Lagrangian formulation from the point of view of the relationship between the model’s physical quantities and parameters and its physical content in the case of a simple mechanical system. This problem allows us to understand if the conformable calculus is applicable to a more abstract or complex system, or whether there are simple mechanical systems which could be described by conformable mechanical models. We focus our attention on the actuated pendulum, which is a model with many applications in physics and engineering. We construct the conformable actuated pendulum using the Lagrangian formalism, in which the main physical observable, defined in terms of the conformable time derivative, is the kinetic energy, which is quadratic in the conformable derivatives of the position variable. The consistency of the action functional with the conformable calculus requires us to define it, in terms of conformable integrals [31]. From the very definition of the conformable Lagrangian functional, the conformable kinetic energy acquires a factor which is a noninteger power of the time variable.. This immediately implies a redefinition of the mass parameter as well as the interpretation of the conformable model in terms of the non-standard damping effect (damping that is not simply proportional to velocity), which is not present in the standard model. Other time-dependent effects are also captured in the conformable formalism, such as decreasing inertia and memory-effect simulation. This suggests that the conformable calculus is suitable for analyzing certain mechanical systems, particularly those with internal friction or complex microstructures (such as viscoelastic materials or materials containing microcracks), where energy dissipation cannot be accurately modeled using standard potential terms or external damping forces: see [49,50,51]. By mimicking memory effects, the conformable calculus could model materials whose dynamic behavior depends explicitly on coefficients that vary with time, while the introduction of non-standard damping allows the conformable calculus to describe phenomena in which the damping characteristics vary with time (similar descriptions of damping phenomena were given in [52]).

By modifying the kinetic energy rather than introducing additional potential terms or non-conservative forces, we can describe complex dissipative behaviors while maintaining the elegance and consistency of the Lagrangian formalism. Let us detail some important consequences of this form of expressing dissipation:

• Since, in general, dissipation described by non-conservative forces breaks the variational structure of classical mechanics, modifying the kinetic term with conformable derivatives preserves the action principle, which allows us to construct models with various symmetries, conserved charges, and phenomenological rich generalizations. This is crucial for maintaining compatibility with Noether’s theorem, symplectic structure, canonical quantization, and important tools of theoretical physics.
• Since the conformable derivative encodes scale-dependent time dynamics and breaks time-reversal symmetry when $\alpha <1$, embedding the irreversible behavior in the kinetic term itself can be viewed as geometrizing dissipation, similar to how general relativity encodes forces into the curvature of spacetime.
• Traditional damping models require inserting terms like $-b\dot{x}$, with arbitrary coefficients b. These models break energy conservation and lack universality. The conformable kinetic term replaces such ad hoc additions with a single parameter $\alpha$, offering a principled and systematic generalization of classical mechanics, which is important for theoretical construction. In phenomenological applications, $\alpha$ should be related to physical parameters.
• Quantum systems with classical damping are notoriously hard to formulate. The conformable approach, with its modified kinetic term, allows the direct application of canonical quantization [9,33,34,37,38]:

  $${\widehat{p}}^{\left(\alpha \right)}=-i{\hslash }_{\alpha }^{\alpha }{D}_x^{\alpha }$$

  (1)

  where ${\widehat{p}}^{\left(\alpha \right)}$ is the canonical momentum associated to the conformable coordinate operator ${\widehat{x}}^{\alpha }$, ${\hslash }_{\alpha }^{\alpha }$ is the Planck constant in the conformable quantum mechanics, and $D_x^{\alpha }$ is the conformable derivative for variable x. The conformable setting preserves Hermiticity and inner product structure on a properly defined Hilbert space. The energy spectrum and eigenfunctions can be derived as usual, providing a connection between dissipation and quantum theory.
• The dissipation is obtained in the conformable approach with a minimal and elegant modification, replacing $\dot{x}$ with $D_t^{\alpha }x$. No external functions or potentials are introduced. The resulting models connect naturally to memory effects, anomalous diffusion, and non-Markovian behavior.

Moreover, the conformable formalism introduces other time-dependent terms that represent physical effects. This aspect becomes more relevant in the analysis of systems in which damping or inertia vary over time, as these coefficients are related to the physical characteristics and structural properties of the system.

It is important to note that a comprehensive discussion of the Lagrangian equations of motion for a damped pendulum was previously presented in [31]. Our study introduces significant advancements by providing an in-depth analysis of this type of system. Firstly, we present a model that is closer to practical applications, as previously mentioned, by explicitly incorporating parameters associated with physical components, such as viscosity. This model incorporates fractional characteristics within these parameters, thereby supporting various experimental and numerical studies in the literature that indicate this possibility. Secondly, our mathematical analysis of the equations of motion generates detailed solutions, either in analytic form or as power series, which are further illustrated through some simple examples.

This paper is organized as follows. In Section 2, we briefly review the basic concepts of conformable calculus. We also briefly present the relationship between conformable, fractal [53,54], and Jackson derivatives [55]. In Section 3, we give the basic relations of the conformable Lagrangian formalism for point particle mechanics and derive the Euler–Lagrange equations from it. We argue here that non-standard damping effects can be modeled by the conformable kinetic energy. In Section 4, we construct the conformable pendulum and derive its equations of motion in the absence of force. Moreover, we derive the general analytic solution of the equation of motion for $\alpha =1/2$ and the power series solution for $\alpha \ne 1/2$. In Section 5, we construct the conformable actuated pendulum under the influence of a non-conservative generalized force. This model generalizes an arm pendulum connected through a shaft to a mechanical source of torque. We derive the general solutions of the equations of motion for $\alpha =1/2$, which can be analytically obtained in terms of Bessel functions. Also, we obtain the power series solution for $\alpha \ne 1/2$ using Frobenius’ method. Section 6 contains a simple numerical study of the general conformable actuated pendulum. In Section 7, we discuss our results and suggest some future research. In Appendix A, Appendix B, Appendix C, Appendix D and Appendix E, we collect several lengthy derivations of the main mathematical results.

2. Fundamentals of Conformable Calculus

In this section, we review the definitions of the conformable derivative and integral and their basic properties, whose applications will be discussed throughout this paper. We also revisit an important relationship between the conformable and fractal derivatives, which allows us to interpret conformable models. Although it does not meet all the criteria to be classified as a classical fractional derivative, the conformable derivative proves to be very useful and convenient for many practical applications. For more details, we suggest consulting [1,4,5] and the references therein.

2.1. Conformable Derivative and Integral

Let $f:{\mathbb{R}}^{+}\to \mathbb{R}$ be a real continuous function in its domain. The conformable derivative of order $\alpha \in (0,1]$, denoted by $D_x^{\alpha }f\left(x\right)$ at $x\in \mathbb{R}$, is defined, in case that the convergence holds, by the following relation:

$$D_x^{\alpha }f\left(x\right):=\underset{ϵ\to 0}{lim}{\displaystyle \frac{f\left(x+ϵx^{1-\alpha }\right)-f\left(x\right)}{ϵ}}.$$

(2)

If the definition can be extended to all $x>0$, then we say that the function f is $\alpha$-differentiable on ${\mathbb{R}}^{+}$.

The conformable integral of the order $\alpha$ is defined as

$$I_x^{\alpha }f\left(x\right):={\int }_0^x{\xi }^{\alpha -1}f\left(\xi \right)d\xi .$$

(3)

The definitions of $D_x^{\alpha }$ and $I_x^{\alpha }$ establish these two operators as inverse to each other in the following sense:

$$D_x^{\alpha }{I}_x^{\alpha }f\left(x\right)=f\left(x\right),$$

(4)

$$I_x^{\alpha }{D}_x^{\alpha }f\left(x\right)=f\left(x\right)-f\left(0\right).$$

(5)

The conformable derivative has the following basic properties for all f and g and all $a,b\in \mathbb{R}$ constants:

$$D_x^{\alpha }(af\left(x\right)+bg\left(x\right))=a{D}_x^{\alpha }f\left(x\right)+b{D}_x^{\alpha }g\left(x\right)$$

(6)

$$D_x^{\alpha }\left(f\left(x\right)g\left(x\right)\right)=\left(D_x^{\alpha }f\left(x\right)\right)g\left(x\right)+f\left(x\right)D_x^{\alpha }g\left(x\right)$$

(7)

$$D_x^{\alpha }f\left(g\left(x\right)\right)=\left(D_{g\left(x\right)}^{\alpha }f\left(g\left(x\right)\right)\right)\left(D_x^{\alpha }g\left(x\right)\right)g{\left(x\right)}^{\alpha -1}$$

(8)

Some important properties involve the conformable fractional derivatives of monomials, which are used to represent functions in power series of the function quotients and of the constant functions. Here, we list these properties, which can easily be proven based on their definitions:

$$D_x^{\alpha }\left(x^p\right)=p{x}^{p-\alpha }$$

(9)

$$D_x^{\alpha }\left({\displaystyle \frac{f\left(x\right)}{g\left(x\right)}}\right)={\displaystyle \frac{g\left(x\right)D_x^{\alpha }f\left(x\right)-f\left(x\right)D_x^{\alpha }g\left(x\right)}{g^2\left(x\right)}}$$

(10)

$$D_x^{\alpha }\left(c\right)=0$$

(11)

where p and c are real constants. The above properties are similar to the ones of derivatives in standard calculus. In what follows, we are interested in systems with conformable time derivatives.

2.2. Conformable, Fractal, and Jackson Derivatives

The algebra of the conformable derivatives is similar to that of standard derivatives, as shown above. In fact, the conformable derivative is related to the fractional and the generalized Jackson derivatives, even at the level of their definitions, as shown below.

Consider the fractal derivative of a function f in a space, with fractal dimension $\beta$ defined as [53,54]

$$F_{\alpha }^{\beta }f\left(t_0\right)={\displaystyle \frac{{\partial }^{\beta }f\left(t_0\right)}{\partial t^{\alpha }}}=\underset{t\to t_0}{lim}{\displaystyle \frac{f^{\beta }\left(t\right)-f^{\beta }\left(t_0\right)}{t^{\alpha }-t_0^{\alpha }}}$$

(12)

if the convergence exists, where $\alpha$ is the fractal dimension of $t\in {\mathbb{R}}^{+}$ variable. One can easily show that if the variable has a fractal structure, then

$$F_{\alpha }f\left(t_0\right)={\displaystyle \frac{\partial f\left(t_0\right)}{\partial t^{\alpha }}}=\underset{t\to t_0}{lim}{\displaystyle \frac{f\left(t\right)-f\left(t_0\right)}{t^{\alpha }-t_0^{\alpha }}}={\displaystyle \frac{t^{1-\alpha }}{\alpha }}{\displaystyle \frac{df\left(t_0\right)}{dt}}$$

(13)

for all $\alpha >0$. On the other hand, from the definition (2), results

$$D_t^{\alpha }f\left(t\right)=t^{1-\alpha }{\displaystyle \frac{df\left(t\right)}{dt}}.$$

(14)

Then, from Equations (13) and (14), we obtain the relation between the conformable and fractal derivatives:

$$F_{\alpha }f\left(t\right)={\displaystyle \frac{1}{\alpha }}{D}_t^{\alpha }f\left(t\right).$$

(15)

Equation (15) shows that the fractal and conformable derivatives are formally equal up to a constant. However, they have different interpretations as they belong to different mathematical structures. The concept of fractal derivatives originates from fractal geometry and they are associated with systems or functions that exhibit fractal (self-similar) properties, meaning they often describe processes occurring on irregular, non-integer-dimensional spaces [56]. On the other hand, the conformable derivatives generalize classical derivatives and retain many of the fundamental properties of standard derivatives, such as the product rule and chain rule, while extending differentiation to non-integer orders, their interpretation being more straightforward and generally associated with continuous systems.

The conformable derivative is also related to the generalized Jackson derivative, and is defined by [55]

$$D_{q,\alpha }f\left(t\right)=\underset{q\to 1}{lim}{\left({\displaystyle \frac{d}{dt}}\right)}_{q}f\left(t\right)={\displaystyle \frac{f\left(qt\right)-f\left(t\right)}{q{t}^{\alpha }-t^{\alpha }}}$$

(16)

if the convergence holds and $q>0$. This can be seen by making the substitution $q=1+\epsilon t^{-\alpha }$ and taking the limits $\epsilon \to 0$ and $q\to 1$ to obtain [5]

$$D_{\alpha }f\left(t\right)=\underset{q\to 1}{lim}{D}_{q,\alpha }f\left(t\right).$$

(17)

The relations among these derivatives show that the conformable derivative can be applied to the same range of problems as the fractal and Jackson derivatives. The relation (14) suggests that the algebra of conformable derivatives is obtained by extending themvia a tensor product of the standard derivative algebra with fractional powers of the variable. Therefore, this structure exhibits a certain degree of triviality in the function’s space over $\mathbb{R}$, as previously analyzed in the literature mentioned in the Introduction.

It is worth noting that the apparent triviality of the conformable derivative does not imply that it lacks physical significance. Rather, its proportional relationship to the classical derivative allows for an effective re-scaling of dynamics. This scaling encodes the effects of dissipative processes or time-dependent media without violating the structure of classical Lagrangian or Hamiltonian formalisms. For example, in modeling dissipation, the conformable derivative allows us to represent the dissipative behavior via a modified kinetic term. Although the derivative itself is not fundamentally different from the classical derivative, its scaling by $x^{1-\alpha }$ or $t^{1-\alpha }$ introduces a non-uniform response that depends on the independent variable, effectively simulating position- or time-dependent inertia. Another consequence is that, since the conformable derivative preserves the linearity and product rule of standard derivatives, it can be directly incorporated into a variational formulation without requiring external, non-conservative forces. This maintains the symmetry properties and conservation laws associated with Noether’s theorem in a modified form. The proportionality to the standard derivative facilitates analytical calculations. This is particularly useful when deriving energy spectra, expectation values, or transition amplitudes in conformable quantum mechanics. In many practical applications, the conformable derivative serves as an approximation of more complex memory-dependent systems. This makes it interesting for simulation when full non-local fractional derivatives are computationally prohibitive.

Classical calculus assumes constant parameters and simple friction or damping laws, which cannot accurately describe complex mechanical systems characterized by internal properties that vary over time. The conformable calculus formalism was chosen because it effectively extends the concept of classical derivatives, offering a more accurate representation of time-dependent properties such as variable inertia, friction, or damping in real pendulum systems.

3. Conformable Lagrangian Mechanics of Point Particle

In this section, we present the conformable generalization of Lagrangian mechanics. The basic principle in generalizing standard mechanical models to fractional or conformable systems is to substitute the standard derivatives for the modified ones. However, a different approach, which may or may not lead to the same equations of motion, is to construct an action functional by replacing standard derivatives with fractional or conformable derivatives and reinterpreting function spaces. In this approach, physical quantities such as kinetic energy, potential energy, and action are modified from the beginning, incorporating the features encoded within fractional or conformable calculus. Then, extending the variational principle to the new functional space provides the equations of motion. Other classical mechanical constructs, such as non-holonomic forces, can be incorporated into the formalism with corresponding interpretations. In the following, we apply these principles to construct the action functional of a conformable classical particle. Our main objective is to examine how conformable calculus contributes to the mathematical and physical insights of these models.

3.1. Conformable Lagrangian Formalism

Consider a conformable particle in ${\mathbb{R}}^d$ whose instantaneous position is denoted by $q\left(t\right)=\left\{q^i\left(t\right)\right\}$, where $i,j,\dots =1,2,\dots ,d$. In order to describe the particle’s dynamics, we construct a conformable Lagrangian functional for a particle $L^{\alpha }\left[q\left(t\right),D_t^{\alpha }q\left(t\right)\right]$ by applying the general principle that requires that standard derivatives be replaced by the conformable ones. If the particle moves under the influence of a general external potential $V\left[q\left(t\right)\right]$, then the Lagrangian is defined by

$$L^{\alpha }\left[q\left(t\right),D_t^{\alpha }q\left(t\right)\right]={\displaystyle \frac{M_{\alpha }}{2}}\sum _{i=1}^d{D}_t^{\alpha }{q}^i\left(t\right)D_t^{\alpha }{q}^i\left(t\right)-V^{\alpha }\left[q\left(t\right)\right]$$

(18)

where $V^{\alpha }\left[q\left(t\right)\right]$ is a potential functional of dimension $E{T}^{1-\alpha }$. The parameter $M_{\alpha }$ plays the role of a conformable mass. By dimensional analysis, we can see that $\langle M_{\alpha }\rangle =E{T}^{1+\alpha }{L}^{-2}$, which is natural units $c=1$ is $\langle M_{\alpha }\rangle =E{T}^{\alpha -1}$. In the classical mechanics limit $\alpha \to 1$, the conformal mass becomes the standard mass, as expected:

$$\underset{\alpha \to 1}{lim}{M}_{\alpha }=m.$$

(19)

As in classical mechanics, we want to interpret the particle’s trajectory as the extrema of the action corresponding to $L^{\alpha }\left[q\left(t\right),D_t^{\alpha }q\left(t\right)\right]$ in the time interval $[0,T]$. For reasons that will become apparent shortly, we define the action functional using the conformable integral by the relation

$$S^{\alpha }\left[q\right]=\underset{0}{\overset{T}{\int }}{L}^{\alpha }\left[q\left(t\right),D_t^{\alpha }q\left(t\right)\right]d{\mu }_t^{\alpha },$$

(20)

where $d{\mu }_t^{\alpha }=t^{\alpha -1}dt$ is the integration measure of conformable integral. For a simple numerical example of the effect of the integration measure, see Appendix A.

To derive the Euler–Lagrange equations, we consider variations $\delta q^i\left(t\right)$ of the functions $q^i\left(t\right)$ that vanish at the boundary of the time interval $[0,T]$. The variation of the action functional is given by

$$\delta S^{\alpha }=\underset{0}{\overset{T}{\int }}\left[{\displaystyle \frac{\partial L^{\alpha }}{\partial q^i}}\delta q^i+{\displaystyle \frac{\partial L^{\alpha }}{\partial \left(D_t^{\alpha }{q}^i\right)}}\delta \left(D_t^{\alpha }{q}^i\right)\right]t^{\alpha -1}dt.$$

(21)

We recall that the variation $\delta$ commutes with the multiplication by $t^{1-\alpha }$ because $t^{1-\alpha }$ is a function of the independent variable t and does not depend on the varied quantity $q\left(t\right)$. As a result, the conformable derivative has the following property:

$$\delta \left(D_t^{\alpha }{q}^i\right)=D_t^{\alpha }\left(\delta q^i\right).$$

(22)

By using the relation (22) and integrating by parts the second term, we obtain

$$\underset{0}{\overset{T}{\int }}{\displaystyle \frac{\partial L^{\alpha }}{\partial \left(D_t^{\alpha }{q}^i\right)}}{D}_t^{\alpha }\left(\delta q^i\right)t^{\alpha -1}dt={\left.{\displaystyle \frac{\partial L^{\alpha }}{\partial \left(D_t^{\alpha }{q}^i\right)}}\delta q^i{t}^{\alpha -1}\right|}_0^T-\underset{0}{\overset{T}{\int }}{D}_t^{\alpha }\left({\displaystyle \frac{\partial L^{\alpha }}{\partial \left(D_t^{\alpha }{q}^i\right)}}{t}^{\alpha -1}\right)\delta q^{i}dt$$

(23)

Since $\delta q^i$ vanishes at the endpoints, the boundary term is zero, and we are left with

$$\underset{0}{\overset{T}{\int }}{\displaystyle \frac{\partial L^{\alpha }}{\partial \left(D_t^{\alpha }{q}^i\right)}}{D}_t^{\alpha }\left(\delta q^i\right)t^{\alpha -1}dt=-\underset{0}{\overset{T}{\int }}{D}_t^{\alpha }\left({\displaystyle \frac{\partial L^{\alpha }}{\partial \left(D_t^{\alpha }{q}^i\right)}}{t}^{\alpha -1}\right)\delta q^{i}dt.$$

(24)

Substituting Equation (24) back into (21), the variation of the action becomes

$$\delta S^{\alpha }=\underset{0}{\overset{T}{\int }}\left[{\displaystyle \frac{\partial L^{\alpha }}{\partial q^i}}-D_t^{\alpha }\left({\displaystyle \frac{\partial L^{\alpha }}{\partial \left(D_t^{\alpha }{q}^i\right)}}{t}^{\alpha -1}\right)\right]\delta q^i{t}^{\alpha -1}dt.$$

(25)

For the action to be stationary ($\delta S^{\alpha }=0$) for arbitrary variations $\delta q^i$, the integrand must vanish. This yields the conformable Euler–Lagrange equations

$${\displaystyle \frac{\partial L^{\alpha }}{\partial q^i}}-D_t^{\alpha }\left({\displaystyle \frac{\partial L^{\alpha }}{\partial \left(D_t^{\alpha }{q}^i\right)}}{t}^{\alpha -1}\right)=0.$$

(26)

For the Lagrangian functional from (18), we obtain the following equations of motion:

$$M_{\alpha }{\left(D_t^{\alpha }\right)}^2{q}^i\left(t\right)-{\displaystyle \frac{\partial V^{\alpha }\left[q\left(t\right)\right]}{\partial q^i\left(t\right)}}=0,$$

(27)

where we adopt the notation

$${\left(D_t^{\alpha }\right)}^2{q}^i\left(t\right)=D_t^{\alpha }\left[D_t^{\alpha }{q}^i\left(t\right)\right].$$

(28)

Using the property (14), the Equation (27) can be expressed as a differential equation in standard derivatives:

$$M_{\alpha }{t}^{2-2\alpha }{\displaystyle \frac{d^2{q}^i\left(t\right)}{d{t}^2}}+(1-\alpha )M_{\alpha }{t}^{1-2\alpha }{\displaystyle \frac{d{q}^i\left(t\right)}{dt}}-{\displaystyle \frac{\partial V^{\alpha }}{\partial q^i\left(t\right)}}=0.$$

(29)

This shows a time-dependent damping term proportional to ${\displaystyle \frac{d{q}^i\left(t\right)}{dt}}$, with coefficient $(1-\alpha )M_{\alpha }{t}^{1-2\alpha }$, and a time-dependent “mass” term $M_{\alpha }\left(t\right)=M_{\alpha }{t}^{2(1-\alpha )}$ multiplying the standard acceleration.

By analogy with classical mechanics, we define the conformable linear momentum by

$$p_{\alpha }^i\left(t\right):={\displaystyle \frac{\partial L}{\partial D_t^{\alpha }{q}^i\left(t\right)}},p_{\alpha }^i\left(t\right)=M_{\alpha }{D}_t^{\alpha }{q}^i\left(t\right).$$

(30)

Then, the conformable force can be defined as

$$F_{\alpha }^i\left(t\right):=D_t^{\alpha }{p}_{\alpha }^i\left(t\right),$$

(31)

which allows us to interpret the equations of motion (27) as the conformable version of Newton’s second law:

$$M_{\alpha }{\left(D_t^{\alpha }\right)}^2{q}^i\left(t\right)=F_{\alpha }^i\left(t\right).$$

(32)

The conformable derivative, due to its mathematical properties, allows us to construct a conformable classical mechanics similar to the standard one. For example, we define the Hamiltonian functional by analogy with classical mechanics:

$$H^{\alpha }\left[q\left(t\right),p_{\alpha }\left(t\right)\right]:=\sum _{i=1}^n{p}_{\alpha }^i\left(t\right)D_t^{\alpha }{q}^i\left(t\right)-L^{\alpha }\left[q\left(t\right),D_t^{\alpha }q\left(t\right)\right].$$

(33)

Then, it is easy to check that $H^{\alpha }\left[q\left(t\right),p_{\alpha }\left(t\right)\right]$ takes the familiar form

$$H^{\alpha }\left[q\left(t\right),p_{\alpha }\left(t\right)\right]:=\sum _{i=1}^n{\displaystyle \frac{p_{\alpha }^2}{2M_{\alpha }}}+V^{\alpha }\left[q\left(t\right)\right].$$

(34)

Similarly, we define the conformable velocity and acceleration of the conformable particle as

$$v_{\alpha }^i\left(t\right):=D_t^{\alpha }{q}^i\left(t\right)$$

(35)

$$a_{\alpha }^i\left(t\right):=D_t^{\alpha }{v}_{\alpha }^i\left(t\right)={\left(D_t^{\alpha }\right)}^2{q}^i\left(t\right).$$

(36)

These definitions allow us to interpret conformable dynamics in terms of known concepts.

It now seems necessary to provide further comments here. Due to the mathematical properties of the conformable Lagrangian, primarily the property of linearity and the Leibniz rule, we can develop a conformable mechanics of point particles, which can be generalized to more complex systems based on concepts. Similarly to fractional systems, the conformable parameter $\alpha \in (0,1]$ defines a family of distinct conformable systems, meaning that not only do the physical quantities, such as conformable mass and potential energy, have different dimensionalities, but the corresponding dynamical equations also belong to different classes of differential equations. Nevertheless, the formulation of conformable mechanics obeys a correspondence principle in the limit $\alpha \to 1$, where the standard classical mechanics is recovered. Moreover, classical mechanics belongs to the family of conformable mechanics, since $\alpha =1$ is an allowed value for the conformable parameter.

From a physical point of view, the conformable Lagrangian mechanics describes a non-standard damping effect and time-dependent mass terms $M_{\alpha }\left(t\right)$, as shown in Equation (29). Furthermore, while the conformable derivative is local, the $t^{\alpha -1}$ measure in the action assigns weight to past configurations, introducing a memory-like weighting in the action. The time-dependent coefficients in the equation of motion cause the system’s response to depend on accumulated temporal effects, resembling a memory effect.

The equations of motion obtained above are local, while the memory effects are, in general, non-local properties of dissipative systems. Therefore, it is interesting to ask whether the formalism can be used to express non-local forces. One possible avenue to explore is noting that a force term of the following form

$$F_{\mathrm{mem}}\left(t\right)={\displaystyle \frac{\alpha -1}{t}}{\displaystyle \frac{\partial L}{\left(\partial D_t^{\alpha }q\left(t\right)\right)}}$$

(37)

can be written as non-local in time convolution if we use the following identity:

$${\displaystyle \frac{1}{t}}={\int }_0^t{\displaystyle \frac{d}{ds}}\left(ln(t-s)\right)ds.$$

(38)

Then, we can write

$$F_{\mathrm{mem}}\left(t\right)=(\alpha -1){\int }_0^{t}K(t-s){\displaystyle \frac{\partial L}{\left(\partial D_s^{\alpha }q\left(s\right)\right)}}ds,K\left(u\right)={\displaystyle \frac{1}{u}}$$

(39)

which clearly exhibits memory of the past trajectory $q\left(s\right)$. The term $F_{\mathrm{mem}}\left(t\right)$ in (39) acts like a viscoelastic or hereditary force, since it depends on the entire history of the momentum $\partial L/\partial \left(\partial D_s^{\alpha }q\left(s\right)\right)$ before time $s<t$, and can lead to forces which are analogous to fractional damping in viscoelastic models. Thus, we see that the conformable measure does not just rescale inertia, but can also generate a non-local damping force with kernel $K\left(u\right)=1/u$, encoding a long-term memory of past motion.

Observe that, in numerical integration, one must account for the history integral (39), leading to $O\left(N^2\right)$ complexity in naive implementations. For the numerical analysis, fast convolution algorithms or memory-truncation schemes may be employed. Physically, such non-local forces explain the anomalous relaxation and power-law decay of oscillations, which are consistent with observations in complex materials.

3.2. Brief Discussion of Generalized Integration Measures

In this subsection, we are going to briefly discuss more general integration measures. In the conformable calculus framework, the integration measure

$$d{\mu }_t^{\alpha }=t^{\alpha -1}dt$$

(40)

induces memory effects by weighting early times more heavily when $\alpha <1$ [1]. One may ask whether other weighting functions $h\left(t\right)$ can be used in place of $t^{\alpha -1}$, and what criteria guide their selection. A generalized weighted integral can be written as

$${\int }_0^{T}f\left(t\right)h\left(t\right)dt.$$

(41)

Here, $h\left(t\right)$ is a non-negative weight or density function. The choice of $h\left(t\right)$ determines how past history influences the present dynamics. To preserve a well-defined variational principle and ensure the self-adjointness of the kinetic operator, the weight $h\left(t\right)$ should satisfy the following requirements:

• Positivity: $h\left(t\right)>0$ for $t\in (0,T]$ to define a bona fide measure.
• Regularity: $h\left(t\right)$ should be sufficiently smooth, e.g., continuous or piecewise continuous, so that integration by parts holds

  $${\int }_0^T{u}^{\prime }\left(t\right)v\left(t\right)h\left(t\right)dt={\left[u\left(t\right)v\left(t\right)h\left(t\right)\right]}_0^T-{\int }_0^{T}u\left(t\right){\displaystyle \frac{d}{dt}}\left[h\left(t\right)v\left(t\right)\right]dt.$$

  (42)
• Normalization (optional): For probability or thermodynamic interpretations, one may require that

  $${\int }_0^{T}h\left(t\right)dt=1.$$

  (43)

From a physical point of view, the family of general weights $h\left(t\right)$ should contain the memory kernels. If $h\left(t\right)$ decays rapidly, the system has short memory; if it decays slowly, e.g., by power laws, the system exhibits long-term memory [57]. Time-dependent weights can model aging media, where the response changes as the system evolves [58]. The support of $h\left(t\right)$ should respect causality; typically, $h\left(t\right)=0$ for $t<0$ in physical applications.

From this analysis, we can conclude that, by replacing the conformable measure with a general $h\left(t\right)$, some properties of the model can be affected. First, the Euler–Lagrange equation obtains additional terms from $\dot{h}\left(t\right)$, leading to generalized friction or aging terms [59]. Second, the form of energy decay or growth depends sensitively on the tail behavior of $h\left(t\right)$. Third, in quantized models, the inner product weight changes to $h\left(\theta \right)d\theta$, which modifies the orthogonality and completeness relations of the eigenfunctions.

The following are some examples of general weights that could be employed:

• Exponential Decay: $h\left(t\right)=\lambda e^{-\lambda t}$ models a memory kernel with finite memory timescale ${\lambda }^{-1}$ [57].
• Stretched Exponential: $h\left(t\right)={\displaystyle \frac{\beta }{\tau }}{\left({\displaystyle \frac{t}{\tau }}\right)}^{\beta -1}{e}^{-{(t/\tau )}^{\beta }}$ captures a broad distribution of memory times.
• Power-Law: $h\left(t\right)=C{t}^{-\gamma }$$(0<\gamma <1)$ yields a long-memory kernel like in fractional integrals.

To conclude this subsection, generalizing the integration measure to an arbitrary weight $h\left(t\right)$ allows one to express more complex memory and dissipation properties of the system. Mathematical consistency (positivity, regularity) and physical considerations (memory depth, causality) should guide the choice of $h\left(t\right)$, which in turn shapes the dynamics and its quantization. However, it is important to note that the conformable integral is defined as the inverse of conformable derivative, which means that more general definitions of the latter should also be used in formulating extended conformable systems.

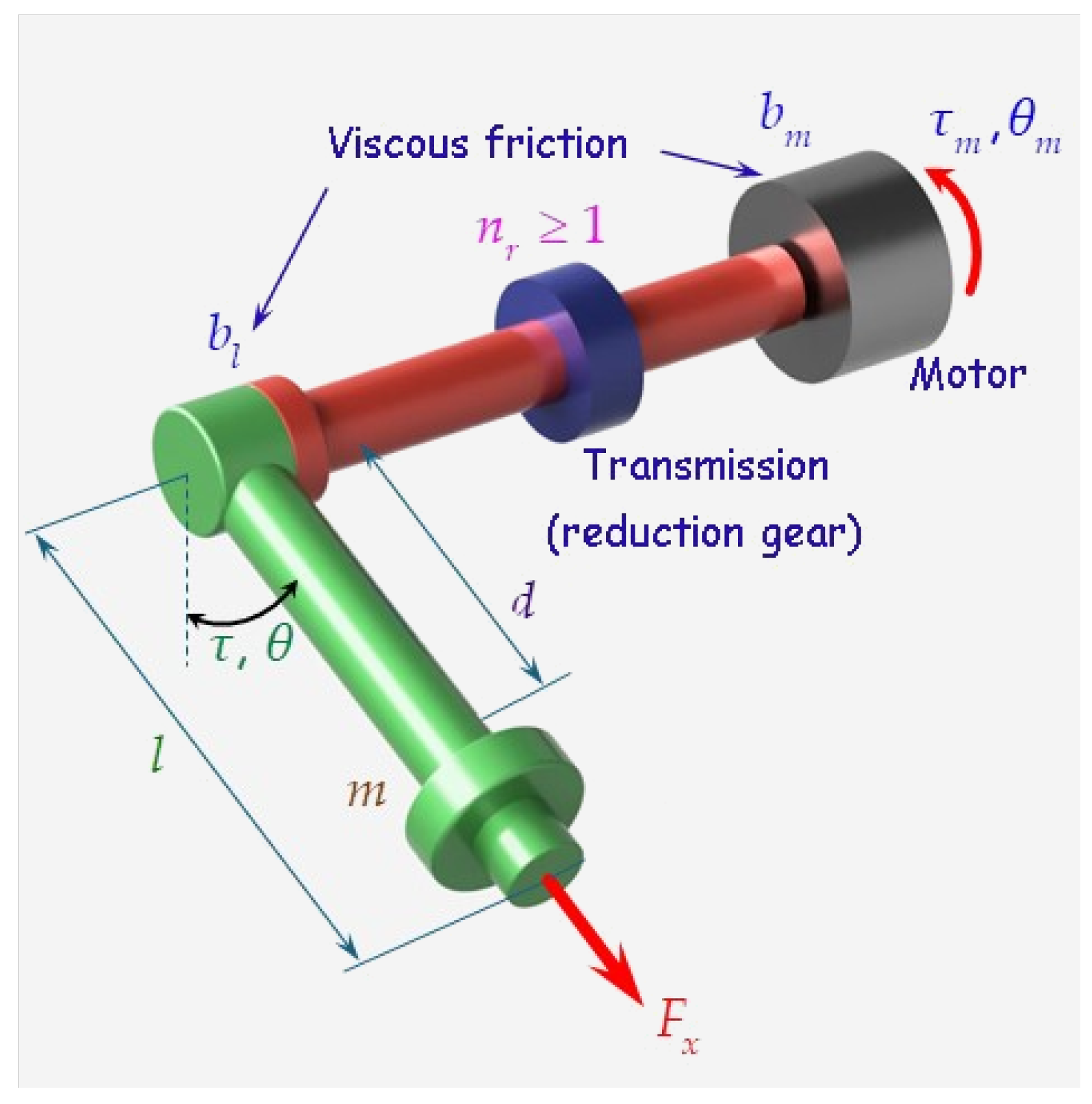
4. Conformable Actuated Pendulum

The standard actuated pendulum model describes a physical system in which a pendulum is influenced by both kinetic and potential energy. An illustration of a possible schematics for this system is presented in Figure 1. The kinetic energy is dependent on the moment of inertia and the square of the angular velocity. The potential energy is influenced by gravity, the mass of the pendulum bob, and the angular position. This model is useful for understanding the dynamics of pendulums in various physical situations and has many applications, including analysis of simple harmonic motion in pendulums, as studied in physics and mechanics, and the design and control of robotic arms, pendulum-based systems, and the study of oscillatory systems in mechanical and civil engineering [60,61].

4.1. Classical Actuated Pendulum

In classical mechanics, the actuated pendulum Lagrangian is given by

$$L_{standard}\left[\theta ,\dot{\theta }\right]={\displaystyle \frac{1}{2}}I{\left({\displaystyle \frac{d\theta }{dt}}\right)}^2-V\left[\theta \right],$$

(44)

$$V\left[\theta \right]=V_0-mgdcos\theta ,$$

(45)

where I is the moment of inertia, $\theta$ is the angular displacement and the degree of freedom of the pendulum, ${\displaystyle \frac{d\theta }{dt}}$ is the angular velocity, V is the potential energy of the system with $V_0$ a constant reference potential energy, m is the mass of the pendulum bob (pendulum’s arm center of mass), g is the acceleration due to gravity, d is the distance from the pivot point to the center of mass of the pendulum bob, and $cos\theta$ is the cosine of the angular displacement. By applying the variational principle to the action constructed for $L_{standard}$, we obtain the well-known equation of motion

$$I\ddot{\theta }+mgdsin\theta =0.$$

(46)

In many applications, it is important to introduce non-conservative generalized forces $u^i$ to perform work on the degree of freedom $q^i$. These forces are external or dissipative, and represent interactions with the environment. In what follows, we consider a simple force that acts on pendulum-based systems, also used in describing the control of robotic arms. The modified equation of motion (46) has the following form:

$$I\ddot{\theta }+mgdsin\theta =n_r{\tau }_m-\left(b_l+b_m{n}_r^2\right)\dot{\theta }+lcos\theta ·F_x.$$

(47)

Here, ${\tau }_m$ and $b_m\dot{\theta }$ are the applied or dissipated torques that are multiplied by a transmission factor $n_r\ge 1$. These terms can be used, for example, to model motors in a robotic arm. The factors $b_l$ and $b_m$ are important, as they describe viscous friction at the end points of the physical axis connecting the motor and the pendulum arm. If this axis is oriented along the horizontal z axis and the vertical position is along the y axis, then the torque of the horizontal force $F_x$ is given by the last term on the right-hand side of the above equation $lcos\theta ·F_x$. Equations (46) and (47) are non-linear, due to the presence of $\theta \left(t\right)$ in the arguments of the harmonic functions.

4.2. Conformable Dynamics with No Force

In order to describe the conformable actuated pendulum dynamics, we apply the conformable Lagrangian formalism developed in Section 3. The conformable Lagrangian is obtained from the standard Lagrangian in Equation (45) by applying the general principle of replacing the standard derivatives with conformable derivatives:

$$L^{\left(\alpha \right)}\left[\theta ,D_t^{\alpha }\theta \right]:={\displaystyle \frac{1}{2}}{I}^{\left(\alpha \right)}{\left(D_t^{\alpha }\theta \right)}^2+m^{\left(\alpha \right)}gdcos\theta -V_0^{\left(\alpha \right)}.$$

(48)

The conformable action functional is obtained from Equation (20) by replacing the general Lagrangian with the one from Equation (48), above. The result is given by

$$S^{\left(\alpha \right)}\left[\theta \right]=\underset{0}{\overset{T}{\int }}\left[{\displaystyle \frac{1}{2}}{I}^{\left(\alpha \right)}{\left(D_t^{\alpha }\theta \right)}^2+m^{\left(\alpha \right)}gdcos\theta -V_0^{\left(\alpha \right)}\right]d{\mu }_t^{\alpha }$$

(49)

In the International System of Units, $\langle I^{\left(\alpha \right)}\rangle =E{T}^{1+\alpha }$ and $\langle m^{\left(\alpha \right)}\rangle =M^{-1}{T}^{\alpha -1}$. The equations of motion are obtained either by applying the variational principle to the action $S^{\left(\alpha \right)}\left[\theta \right]$ or from Equation (26), and the result is

$$I^{\left(\alpha \right)}{D}_t^{\alpha }\left(D_t^{\alpha }\theta \right)+m^{\left(\alpha \right)}gdsin\theta =0.$$

(50)

The conformable force, the conformable linear momentum of mass blob, and the conformable angular momentum can be identified as previously defined, and are given by

$$F_{\alpha }=-m^{\left(\alpha \right)}gdsin\theta ,p_{\alpha }=m^{\left(\alpha \right)}{D}_t^{\alpha }\theta ,P_{\alpha }=I^{\left(\alpha \right)}{D}_t^{\alpha }\theta .$$

(51)

It is evident that the standard equation of motion and physical quantities are obtained from conformable Equation (50) and quantities defined by relations (51) in the limit $\alpha \to 1$, as expected.

To better interpret Equation (50), it is useful to express it in the form of a standard differential equation:

$$I^{\left(\alpha \right)}·t^{2-2\alpha }\ddot{\theta }+(1-\alpha )I^{\left(\alpha \right)}{t}^{1-2\alpha }\dot{\theta }+m^{\left(\alpha \right)}gdsin\left(\theta \right)=0.$$

(52)

Unlike the classical pendulum Equation (46), the modified Equation (50) introduces time-dependent scaling factors. The factor $t^{2-2\alpha }$ multiplying the angular acceleration $\ddot{\theta }$ results in a time-dependent system inertia. For $\alpha <1$, the term $t^{2-2\alpha }$ varies over time, modifying the effective “mass” that resists angular acceleration. The term $(1-\alpha )I{t}^{1-2\alpha }\dot{\theta }$ acts as an effective damping term whose magnitude depends both on the conformable parameter $\alpha$ and on time t. For $\alpha =1$, this damping term disappears, restoring the classical undamped dynamics of the pendulum. Thus, the parameter $\alpha$ controls the degree of time-scaling in both inertia and damping contributions. From a physical perspective, such modifications may result from a non-standard time reparameterization or from modeling physical phenomena such as energy dissipation or effective mass variation, which evolve according to a power law in time.

It is interesting to analyze the type of differential equation from the family described by Equation (50) for various $\alpha$. The nature of the differential Equation (50) depends on the value of $\alpha$.

• Case 1: $\alpha =1$.

When $\alpha =1$, we have

$$t^{2-2\alpha }=t^0=1\mathrm{and}(1-\alpha )=0$$

(53)

so that (50) reduces to

$$I\ddot{\theta }+mgdsin\left(\theta \right)=0.$$

(54)

This corresponds to the classical nonlinear pendulum equation, where $I^{\left(1\right)}=I$ and $m^{\left(1\right)}=m$. Its linearization is obtained by assuming $sin\theta \approx \theta$ for small angles, which leads to the well-known simple harmonic oscillator equation.

• Case 2: $\alpha ={\displaystyle \frac{1}{2}}$.

For $\alpha ={\displaystyle \frac{1}{2}}$, the time factors become

$$t^{2-2\alpha }=t^{2-1}=t,\mathrm{and}{t}^{1-2\alpha }=t^{1-1}=1.$$

(55)

Then, (50) becomes

$$I^{\left({\displaystyle \frac{1}{2}}\right)}t\ddot{\theta }+\frac{1}{2}{I}^{\left(\frac{1}{2}\right)}\dot{\theta }+m^{\left(\frac{1}{2}\right)}gdsin\left(\theta \right)=0.$$

(56)

This non-autonomous ODE has a linearly time-dependent inertia term and a constant-coefficient damping term. In the linearized regime, an appropriate change of variables can transform the equation in a form related to Bessel’s equation.

• Case 3: $\alpha \in (0,1)$ with $\alpha \ne \frac{1}{2}$.

For other values of $\alpha$ in $(0,1)$, the equation remains a non-autonomous second-order ODE with power-law time-dependent coefficients:

$$I^{\left(\alpha \right)}{t}^{2-2\alpha }\ddot{\theta }+(1-\alpha )I^{\left(\alpha \right)}{t}^{1-2\alpha }\dot{\theta }+m^{\left(\alpha \right)}gdsin\left(\theta \right)=0.$$

(57)

When linearized, the equation takes the form

$$t^{2-2\alpha }\ddot{\theta }+(1-\alpha )t^{1-2\alpha }\dot{\theta }+{\lambda }^{\left(\alpha \right)}\theta =0,\mathrm{with}{\lambda }^{\left(\alpha \right)}={\displaystyle \frac{m^{\left(\alpha \right)}gd}{I^{\left(\alpha \right)}}}.$$

(58)

Unlike the classical Euler–Cauchy or equidimensional equations, which have the form

$$t^2\ddot{y}+at\dot{y}+by=0,$$

(59)

the exponents from Equation (58) do not generally match the Euler–Cauchy structure unless $\alpha$ takes the excluded value $\alpha =0$. Hence, for the general $\alpha \ne 1$, these equations belong to a class of time-dependent ODEs whose solutions may involve special functions or require numerical methods for a complete description.

In the following, we derive the general solution of (54), which is obtained analytically. For other values of $\alpha$, the solution is expressed as a power series.

4.3. General Solution for $\alpha =\frac{1}{2}$

For $\alpha =\frac{1}{2}$, the modified linearized pendulum equation, obtained by replacing $sin\theta$ with $\theta$ for small oscillations, takes the form of Equation (54), which is repeated here for convenience:

$$It\ddot{\theta }\left(t\right)+{\displaystyle \frac{I}{2}}\dot{\theta }\left(t\right)+mgd\theta \left(t\right)=0.$$

(60)

In Appendix B, we obtain the solution for $\theta \left(t\right)$:

$${\theta }^{\left(\frac{1}{2}\right)}\left(t\right)=Acos\left(2\sqrt{{\displaystyle \frac{m^{\left(\frac{1}{2}\right)}gd}{I^{\left(\frac{1}{2}\right)}}}t}\right)+Bsin\left(2\sqrt{{\displaystyle \frac{m^{\left(\frac{1}{2}\right)}gd}{I^{\left(\frac{1}{2}\right)}}}t}\right).$$

(61)

As expected, the solution given in Equation (61) describes a harmonic oscillator whose behavior is determined by the conformable mass, gravitational force, and conformable moment of inertia.

4.4. Power Series Solution of the Linearized Equation for $\alpha \ne 1/2$

In this section, we present the power series solution for the linearized homogeneous equation corresponding to $\alpha \ne 1/2$, which is obtained from Equation (57) and has the following form:

$$t^{2-2\alpha }\ddot{\theta }\left(t\right)+(1-\alpha )t^{1-2\alpha }\dot{\theta }\left(t\right)+\mu \theta \left(t\right)=0$$

(62)

where

$$\mu ={\displaystyle \frac{mgd}{I}}.$$

(63)

The details of the derivation are given in Appendix C, in which it is found that for $\alpha \in (0,1)$ with $\alpha \ne {\displaystyle \frac{1}{2}}$, corresponding to the choice $s=\alpha$, we have

$${\theta }^{\left(\alpha \right)}\left(t\right)=t^{\alpha }\sum _{m=0}^{\infty }{a}_m^{\left(\alpha \right)}{t}^{2\alpha m}.$$

(64)

The recurrence relation (A35) is used to determine the coefficients of the series.

5. Conformable Actuated Pendulum with a Non-Conservative Force

In most applications from physics and engineering, the actuated pendulum interacts with non-conservative generalized forces. In this section, we consider a model that is widely used in theoretical mechanics and which describes the action of a pendulum constrained in the vertical $(x,g)$ plane and is subject to a force $F_x$ directed along the x axis, acting at the tip of a pendulum arm of length l. The pendulum is articulated at the origin of the Cartesian coordinate system $(x,y,z)$, where it is connected to a horizontal shaft. At the opposite end, the shaft is attached to a second mechanical component which enables its rotation. The articulation and the mechanical component are characterized by viscous friction coefficients $b_l$ and $b_m$, respectively. The torque applied at one end of the mechanical component is multiplied by a rotational coefficient $n_r\ge 1$ (for example, this configuration can represent a robotic arm of length l driven by a motor m with a reduction gear r). Under these conditions, the conformable Euler–Lagrange Equation (50) becomes

$$I^{\left(\alpha \right)}{D}_t^{\alpha }\left(D_t^{\alpha }\theta \right)+m^{\left(\alpha \right)}gdsin\theta =n_r^{\left(\alpha \right)}{\tau }_m^{\left(\alpha \right)}-\left(b_l^{\left(\alpha \right)}+b_m^{\left(\alpha \right)}{n_r^{\left(\alpha \right)}}^2\right)\dot{\theta }+lcos\theta F_x^{\left(\alpha \right)}$$

(65)

where all superscripted quantities, e.g., $I^{\left(\alpha \right)}$, $m^{\left(\alpha \right)}$, $b_l^{\left(\alpha \right)}$, etc., indicate that the physical parameters may depend on the conformable parameter $\alpha$. We note that the parameters describing the generalized force now depend on $\alpha$ as well, and have different units from the non-conformable case resulting from dimensional analysis. In terms of the standard derivative, Equation (65) represents the conformable modification of Equation (52), and takes the form

$$I^{\left(\alpha \right)}·t^{2-2\alpha }\ddot{\theta }+\left[(1-\alpha )I^{\left(\alpha \right)}{t}^{1-2\alpha }+b_l^{\left(\alpha \right)}+b_m^{\left(\alpha \right)}{n_r^{\left(\alpha \right)}}^2\right]\dot{\theta }+m^{\left(\alpha \right)}gdsin\left(\theta \right)=n_r^{\left(\alpha \right)}{\tau }_m^{\left(\alpha \right)}+lcos\theta F_x^{\left(\alpha \right)}.$$

(66)

The physical interpretation of the model proposed in this work is related to the physical content of these parameters.

5.1. Physical Interpretation of Parameters

The conformable parameters $m^{\left(\alpha \right)}$, $I^{\left(\alpha \right)}$, $b_l^{\left(\alpha \right)}$, and $b_m^{\left(\alpha \right)}$ were initially introduced as formal generalizations of classical parameters. However, these parameters are not only mathematical objects; they may also represent effective or apparent physical quantities, reflecting changes in the physical properties of real systems. More precisely, variations in apparent mass $m^{\left(\alpha \right)}$ and moment of inertia $I^{\left(\alpha \right)}$ can describe physical phenomena such as viscoelasticity or the presence of microcracks in the structure of materials. Such effects modify the mass distribution, stiffness, or damping characteristics, influencing inertia and dissipative behaviors. For this reason, conformable parameters provide a practical mathematical framework for modeling this type of complex, time-dependent physical behavior in materials with intricate internal structures such as viscoelastic materials, composites, or microcracked structures. Hence, such complex systems can be effectively modeled using a conformable formalism, with parameters explicitly depending on $\alpha$. This approach allows for direct or indirect experimental validation through measurements and numerical simulations. In particular, since $b_l^{\left(\alpha \right)}$ and $b_m^{\alpha }$ characterize viscous friction in the articulations between the shaft, the arm, and the generator of mechanical force, a fractional variation in these friction components makes the system suitable for the application of this model. This can be observed in Equation (50), where the friction terms $b_l^{\left(\alpha \right)}$ and $b_m^{\left(\alpha \right)}{n_r^{\left(\alpha \right)}}^2$ represent the viscous friction at the endpoints of the physical shaft connecting, for example, a motor to the pendulum arm. Their presence in the coefficient of $\dot{\theta }\left(t\right)$ indicates that, in addition to the time-varying friction term, $(1-\alpha )I^{\left(\alpha \right)}{t}^{1-2\alpha }$, there are also constant friction contributions that depend on $\alpha$. Regarding the physical origin of these terms, one can consider that viscous friction may vary due to internal changes in viscosity at the articulations in a closed system, or due to environmental factors in systems with open articulations. Similarly, the parameter $n_r^{\left(\alpha \right)}$ can be interpreted as a variable transmission coefficient that depends on $\alpha$ as a consequence of internal modifications or interactions with the environment. The same reasoning can be applied to the conformable force $F_x^{\left(\alpha \right)}$.

In support of the above interpretation, we could cite several studies in the literature which have applied fractional or conformable derivatives to pendulum dynamics and observed that the effective damping (friction) depends on the fractional order parameter. In [62], a fractional-derivative model was fitted to high-resolution, long-time video data of a free physical pendulum. It was found that the best fit occurs for a fractional order $\alpha \approx 0.94$ and that the effective damping coefficient $b_{\mathrm{eff}}$ emerges from the fit rather than being prescribed. In [63], a double pendulum with a non-singular fractional kernel was simulated and it was observed that for $\alpha <1$, the phase diagrams exhibit energy dissipation. The additional damping factor scales with the fractional order, illustrating how $b\left(\alpha \right)$ increases as $\alpha$ decreases. Also, in [64], an adaptive observer was used to identify static, dynamic, and viscous friction parameters in a tilted Furuta pendulum. Although not conformable, the results from this work show that friction parameters depend on modeling choices, suggesting that a conformable-order dependence $b\left(\alpha \right)$ could be similarly estimated experimentally.

5.2. Numerical Validation Example

To illustrate how $b_{\mathrm{eff}}$ varies with $\alpha$, consider the linearized conformable oscillator (see also [65]):

$$D_t^{\alpha }x\left(t\right)+{\omega }_0^{2}x\left(t\right)=0,x\left(0\right)=1,D_t^{\alpha }x\left(0\right)=0,$$

(67)

whose solution is the Mittag–Leffler function

$$x\left(t\right)=E_{\alpha }\left(-{\omega }_0^2{t}^{\alpha }\right).$$

(68)

For ${\omega }_0=1$, we numerically extract the envelope decay constant by fitting

$$x\left(t\right)\approx Aexp\left(-b_{\mathrm{eff}}\left(\alpha \right)t\right).$$

(69)

We represent the data in the following table (

Table 1. Effective damping coefficient $b_{\mathrm{eff}}$ extracted by fitting the Mittag–Leffler decay (68) to an exponential (69).

$\mathit{\alpha }$	${\mathit{b}}_{\mathbf{eff}}\mathbf{\left(}\mathit{\alpha }\mathbf{\right)}$	Relative Increase vs. $\mathit{\alpha }=1$
1.00	0.00	0%
0.90	0.10	+10%
0.75	0.25	+25%
0.50	0.50	+50%
0.25	0.75	+75%

).

Our numerical example shows that, for a conformable-order oscillator, the envelope decay rate $b_{\mathrm{eff}}\left(\alpha \right)$ rises nearly linearly as $\alpha$ decreases from 1 to 0.25.

These results collectively support the interpretation that in conformable pendulum models, the friction parameters b, joint transmission factors n, and effective torque offsets $\tau$ should be treated as functions of the conformable order $\alpha$.

From a physical perspective, the conformable actuated pendulum could model non-standard damping effects. Observe that the conformable action functional simulates memory effects through the integration kernel. However, these effects are not genuine physical phenomena, since the theory remains local. In both the free and forced cases, if the effective inertia $I^{\left(\alpha \right)}$ or the friction coefficients $b_l^{\left(\alpha \right)}$ and $b_m^{\left(\alpha \right)}$ are influenced by scaling laws, these factors capture that behavior. Moreover, the friction terms $b_l^{\left(\alpha \right)}$ and $b_m^{\left(\alpha \right)}{n_r^{\left(\alpha \right)}}^2$ describe viscous friction at the end-points of the physical shaft, which connects, for example, a motor to the pendulum arm. Their presence in the coefficient of $\dot{\theta }\left(t\right)$ suggests that, in addition to the time-varying friction term $(1-\alpha )I^{\left(\alpha \right)}{t}^{1-2\alpha }$, there are also constant friction contributions that depend on $\alpha$.

The term $m^{\left(\alpha \right)}gdsin\theta \left(t\right)$ is the conformable gravitational restoring torque, which differs from the classical case due to the dependence of the mass parameter on $\alpha$. Its presence ensures that, in the absence of friction and external forces, the system exhibits oscillatory (or pendulum-like) behavior. A new physical effects arises from the external actuation and forcing terms on the right-hand side of Equation (66). These terms describe the actuation and external perturbations influencing the pendulum system in different regimes characterized by the values of $\alpha$.

This leads to an analysis of the mathematical nature of the fractional differential equations obtained from this model.

5.3. Families of Conformable Equations

As in the case of a conformable pendulum without force, discussed in the previous section, the physical interpretation of the modified actuated pendulum equation, which includes a non-conservative generalized force, can be inferred from Equation (66). The time-dependent factors $t^{2-2\alpha }$ and $t^{1-2\alpha }$ affect the inertial and damping terms, respectively, resulting in a power-law dependence on time of these effects. Physically, this can be interpreted as a time reparameterization or an adjustment of the inertia and damping of the conformable actuated pendulum as the system evolves. This interpretation remains valid in the free case, as it results from the contribution of the conformable kinetic term to the equations of motion.

As in the free case, the classification of the equations of motion for the conformable actuated pendulum with non-holonomic generalized forces depends on the value of the conformable parameter. The general form of Equation (66) corresponds to a second-order, non-autonomous ordinary differential equation (ODE) with time-dependent coefficients. The properties of this ODE depend on $\alpha$ and are detailed below.

• Case 1: $\alpha =1$.

When $\alpha =1$, the time-scaling factors simplify:

$$t^{2-2\alpha }=t^0=1,t^{1-2\alpha }=t^{-1}.$$

(70)

Thus, (66) becomes

$$I^{\left(1\right)}\ddot{\theta }\left(t\right)+\left[b_l^{\left(1\right)}+b_m^{\left(1\right)}{n_r^{\left(1\right)}}^2\right]\dot{\theta }\left(t\right)+m^{\left(1\right)}gdsin\theta \left(t\right)=n_r^{\left(1\right)}{\tau }_m^{\left(1\right)}+lcos\theta \left(t\right)F_x^{\left(1\right)}.$$

(71)

This corresponds to the classical actuated pendulum equation with constant coefficients, apart from the inherent nonlinearity in $sin\theta$ and $cos\theta$. When linearized for small angles (i.e., $sin\theta \approx \theta$ and $cos\theta \approx 1$), it reduces to a linear second-order ODE with constant coefficients. This equation is a standard result and belongs to the class of autonomous ODEs.

• Case 2: $\alpha ={\displaystyle \frac{1}{2}}$.

For $\alpha ={\displaystyle \frac{1}{2}}$, the time factors become

$$t^{2-2\alpha }=t^{2-1}=t,t^{1-2\alpha }=t^{1-1}=1.$$

(72)

Then, Equation (66) reads

$$\begin{array}{cc}\hfill I^{(1/2)}t\ddot{\theta }\left(t\right)& +\left[{\displaystyle \frac{1}{2}}{I}^{(1/2)}+b_l^{(1/2)}+b_m^{(1/2)}{n_r^{(1/2)}}^2\right]\dot{\theta }\left(t\right)+m^{(1/2)}gdsin\theta \left(t\right)\hfill \\ \hfill & =n_r^{(1/2)}{\tau }_m^{(1/2)}+lcos\theta \left(t\right)F_x^{(1/2)}.\hfill \end{array}$$

(73)

In the linearized regime, this non-autonomous ODE has a time-dependent inertial term proportional to t, while the damping term remains constant. Through an appropriate transformation, the linear part can be rewritten in a form related to Bessel’s equation or a Euler-type equation. Thus, for $\alpha ={\displaystyle \frac{1}{2}}$ the equation belongs to a class of ODEs that can be solved using known techniques involving special functions.

• Case 3: $\alpha \in (0,1)$ with $\alpha \ne {\displaystyle \frac{1}{2}}$.

For general $\alpha$ in the interval $(0,1)$ (with $\alpha \ne {\displaystyle \frac{1}{2}}$), the equation

$$\begin{array}{cc}\hfill I^{\left(\alpha \right)}{t}^{2-2\alpha }\ddot{\theta }\left(t\right)& +\left[(1-\alpha )I^{\left(\alpha \right)}{t}^{1-2\alpha }+b_l^{\left(\alpha \right)}+b_m^{\left(\alpha \right)}{n_r^{\left(\alpha \right)}}^2\right]\dot{\theta }\left(t\right)+m^{\left(\alpha \right)}gdsin\theta \left(t\right)\hfill \\ \hfill & =n_r^{\left(\alpha \right)}{\tau }_m^{\left(\alpha \right)}+lcos\theta \left(t\right)F_x^{\left(\alpha \right)},\hfill \end{array}$$

(74)

has power-law time-dependent coefficients in both the inertial and damping terms. In the linearized form, one obtains a non-autonomous ODE of the form

$$t^{2-2\alpha }\ddot{\theta }\left(t\right)+\left[(1-\alpha )t^{1-2\alpha }+C\right]\dot{\theta }\left(t\right)+\mu \theta \left(t\right)=\mathrm{forcing},$$

(75)

with constants C and $\mu$ defined in terms of the physical parameters. As noted earlier, in general, such an ODE does not belong to the classical Euler–Cauchy (also known as equidimensional equation) form unless the exponents match the ones in the Euler–Cauchy equation. Only for specific values of $\alpha$ ($\alpha =1$ and $\alpha ={\displaystyle \frac{1}{2}}$) does the equation reduce to forms for which the solutions can be obtained by well-known methods. For other values of $\alpha$, one typically needs to apply power series methods (such as the Frobenius method), as illustrated in previous derivations, and numerical methods or specialized transformations to relate the equation to known special functions.

In the next subsections, we discuss the solutions to Equation (66) in the linearized limit.

5.4. General Solution for $\alpha =1/2$

We consider the linearized equation

$$\begin{array}{cc}\hfill I^{(1/2)}t\ddot{\theta }\left(t\right)& +\left[{\displaystyle \frac{1}{2}}{I}^{(1/2)}+b_l^{(1/2)}+b_m^{(1/2)}{\left(n_r^{(1/2)}\right)}^2\right]\dot{\theta }\left(t\right)\hfill \\ \hfill & +m^{(1/2)}gd\theta \left(t\right)=n_r^{(1/2)}{\tau }_m^{(1/2)}+l{F}_x^{(1/2)},\hfill \end{array}$$

(76)

where the trigonometric functions have been linearized by approximating

$$sin\theta \approx \theta ,cos\theta \approx 1.$$

(77)

For simplicity, we redefine the quantities in Equation (76) and omit the index $1/2$:

$$I_0\equiv I^{(1/2)},$$

(78)

$$D\equiv \frac{1}{2}{I}^{(1/2)}+b_l^{(1/2)}+b_m^{(1/2)}{\left(n_r^{(1/2)}\right)}^2,$$

(79)

$$\mu \equiv m^{(1/2)}gd,$$

(80)

$$F\equiv n_r^{(1/2)}{\tau }_m^{(1/2)}+l{F}_x^{(1/2)}.$$

(81)

Also, we divide (76) by $I_0$ to obtain the standard form

$$t\ddot{\theta }\left(t\right)+p\dot{\theta }\left(t\right)+q\theta \left(t\right)=f,$$

(82)

with

$$p={\displaystyle \frac{D}{I_0}},q={\displaystyle \frac{\mu }{I_0}},f={\displaystyle \frac{F}{I_0}}.$$

(83)

Since the derivation of the solution is somewhat lengthy, yet follows standard methods, we leave it to Appendix D. The general solution of the linearized Equation (76) is given by (A69). It consists of a steady-state (particular) solution and a homogeneous solution expressed in terms of Bessel functions of order $1-p$, where the parameter p is defined in (83), and, in the original notation, in Equation (A70). The general solution has the form

$$\begin{array}{cc}\hfill {\theta }^{(1/2)}\left(t\right)& ={\displaystyle \frac{n_r^{(1/2)}{\tau }_m^{(1/2)}+l{F}_x^{(1/2)}}{m^{(1/2)}gd}}\hfill \\ \hfill & +{\left[2\sqrt{{\displaystyle \frac{m^{(1/2)}gd}{I^{(1/2)}}}t}\right]}^{1-p}\left\{A{J}_{1-p}\left(2\sqrt{{\displaystyle \frac{m^{(1/2)}gd}{I^{(1/2)}}}t}\right)+B{Y}_{1-p}\left(2\sqrt{{\displaystyle \frac{m^{(1/2)}gd}{I^{(1/2)}}}t}\right)\right\}\hfill \end{array}$$

(84)

where

$$p={\displaystyle \frac{D}{I^{(1/2)}}},\mathrm{with}D={\displaystyle \frac{1}{2}}{I}^{(1/2)}+b_l^{(1/2)}+b_m^{(1/2)}{\left(n_r^{(1/2)}\right)}^2$$

(85)

and A and B are constants determined by the initial conditions. For small values of t, the solution (85) takes the form

$${\theta }^{(1/2)}\left(X\left(t\right)\right)\simeq {\displaystyle \frac{n_r^{(1/2)}{\tau }_m^{(1/2)}+l{F}_x^{(1/2)}}{m^{(1/2)}gd}}+X{\left(t\right)}^{1-p}\left[{\displaystyle \frac{A}{\Gamma (p+1)}}{\left({\displaystyle \frac{1}{2}}X\left(t\right)\right)}^p-{\displaystyle \frac{B\Gamma \left(p\right)}{\pi }}{\left({\displaystyle \frac{1}{2}}X\left(t\right)\right)}^{-p}\right]$$

(86)

where

$$X\left(t\right)=2\sqrt{{\displaystyle \frac{m^{(1/2)}gd}{I^{(1/2)}}}t}.$$

(87)

It is important to note that, in addition to the solution given in Equation (84), another general solution can be obtained for discrete values of the parameter p. Namely, if

$$p_n={\displaystyle \frac{1}{2}}+{\displaystyle \frac{b_l^{(1/2)}+b_m^{(1/2)}{\left(n_r^{(1/2)}\right)}^2}{I^{(1/2)}}}={\displaystyle \frac{1}{2}}(2n+1),n=0,1,2,\dots$$

(88)

then the general solution of Equation (76) is given by

$${\theta }_n^{(1/2)}\left(t\right)=\left\{\begin{array}{c}{A}_1{\displaystyle \frac{d^n}{d{t}^n}}cos{\left[4\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{b_l^{(1/2)}+b_m^{(1/2)}{\left(n_r^{(1/2)}\right)}^2}{I^{(1/2)}}}\right)t\right]}^{1/2}\hfill \\ +B_1{\displaystyle \frac{d^n}{d{t}^n}}sin{\left[4\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{b_l^{(1/2)}+b_m^{(1/2)}{\left(n_r^{(1/2)}\right)}^2}{I^{(1/2)}}}\right)t\right]}^{1/2},\mathrm{if}:\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{b_l^{(1/2)}+b_m^{(1/2)}{\left(n_r^{(1/2)}\right)}^2}{I^{(1/2)}}}\right)t>0\hfill \\ A_2{\displaystyle \frac{d^n}{d{t}^n}}cosh{\left[4\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{b_l^{(1/2)}+b_m^{(1/2)}{\left(n_r^{(1/2)}\right)}^2}{I^{(1/2)}}}\right)t\right]}^{1/2}\hfill \\ +B_2{\displaystyle \frac{d^n}{d{t}^n}}sinh{\left[4\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{b_l^{(1/2)}+b_m^{(1/2)}{\left(n_r^{(1/2)}\right)}^2}{I^{(1/2)}}}\right)t\right]}^{1/2},\mathrm{if}\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{b_l^{(1/2)}+b_m^{(1/2)}{\left(n_r^{(1/2)}\right)}^2}{I^{(1/2)}}}\right)t<0\hfill \end{array}\right.$$

(89)

Here, $A_1$, $B_1$, $A_2$, and $B_2$ are integration constants. We note that under the assumption made in the previous section and for $n=0$, the harmonic solution (A17) of the conformable free pendulum is obtained as a particular case of (89).

The above discussion raises the question of the existence of a critical $\alpha$ for oscillations. The oscillatory behavior results from the Bessel functions $J_{1-p}\left(X\right)$ and $Y_{1-p}\left(X\right)$ and can be better seen at large values of arguments. For example, at large values, $J_{1-p}\left(X\right)$ takes the form

$$J_{1-p}\left(X\right)\sim \sqrt{{\displaystyle \frac{2}{\pi X}}}cos\left(X-{\displaystyle \frac{(1-p)\pi }{2}}-{\displaystyle \frac{\pi }{4}}\right).$$

(90)

The above equation is oscillatory for all real orders $1-p$. Since $X\left(t\right)\propto t^{1/2}$ grows for $t>0$, the oscillations persist for any p, hence any $\alpha \in (0,1]$. There is no finite critical α that extinguishes oscillations, only their envelope decay rate changes.

From the large-X asymptotic phase $\Phi \left(X\right)=X-(1-p)\pi /2-\pi /4$, the instantaneous argument evolves at rate

$${\omega }_{\mathrm{inst}}\left(t\right)={\displaystyle \frac{d}{dt}}\left[X\left(t\right)\right]={\displaystyle \frac{d}{dt}}\left(2\sqrt{\frac{m^{(1/2)}gd}{I^{(1/2)}}t}\right)=\sqrt{{\displaystyle \frac{m^{(1/2)}gd}{I^{(1/2)}}}}{t}^{-\frac{1}{2}}.$$

(91)

Thus, the solution is approximately

$${\theta }^{(1/2)}\left(t\right)\approx {\Theta }_{\mathrm{env}}\left(t\right)cos\left(\Phi \left(X\left(t\right)\right)\right),{\Theta }_{\mathrm{env}}\left(t\right)\propto t^{{\displaystyle \frac{1-p}{2}}}$$

(92)

with a time-decaying frequency ${\omega }_{\mathrm{inst}}\left(t\right)\propto t^{-1/2}$.

We can easily see that the oscillation envelope decays as

$${\Theta }_{\mathrm{env}}\left(t\right)\propto t^{{\displaystyle \frac{1-p}{2}}}.$$

(93)

To quantify a dissipation time $\tau \left(\alpha \right)$, we define $t_{1/e}$ by

$${\Theta }_{\mathrm{env}}\left(t_{1/e}\right)={\displaystyle \frac{1}{e}}{\Theta }_{\mathrm{env}}\left(1\right)⟹t_{1/e}^{\frac{1-p}{2}}=e^{-1}.$$

(94)

It follows that

$$\tau \left(\alpha \right)=t_{1/e}=e^{{\displaystyle \frac{2}{p\left(\alpha \right)-1}}}.$$

(95)

Since $p\left(\alpha \right)>1$ for typical friction parameters, $\tau \left(\alpha \right)$ is finite and increases rapidly as $p\to 1^{+}$, i.e., as $\alpha \to 1$. This provides a direct measure of how dissipation accelerates when $\alpha$ decreases.

Thus, we conclude that no finite $\alpha <1$ eliminates oscillations which persist through the Bessel oscillatory kernel. The instantaneous oscillation frequency decays as ${\omega }_{\mathrm{inst}}\left(t\right)\propto t^{-1/2}$, according to (91). A characteristic dissipation time can be defined by (95), capturing the power-law envelope decay in a single parameter.

5.5. Power Series Solution of Linearized Forced Equation for $\alpha \ne 1/2$

The linearized equation for the conformable forced actuated pendulum (74) is given by

$$\begin{array}{cc}\hfill I^{\left(\alpha \right)}{t}^{2-2\alpha }\ddot{\theta }\left(t\right)& +\left[(1-\alpha )I^{\left(\alpha \right)}{t}^{1-2\alpha }+b_l^{\left(\alpha \right)}+b_m^{\left(\alpha \right)}{n_r^{\left(\alpha \right)}}^2\right]\dot{\theta }\left(t\right)+m^{\left(\alpha \right)}gd\theta \left(t\right)\hfill \\ \hfill & =n_r^{\left(\alpha \right)}{\tau }_m^{\left(\alpha \right)}+l{F}_x^{\left(\alpha \right)},\hfill \end{array}$$

(96)

where the $\alpha \ne 1/2$ and we have adopted the linearization $sin\theta \approx \theta$ and $cos\theta \approx 1$. Since the derivation is quite lengthy, we present it in Appendix E. The final result is given in Equation (A101) which is

$$\theta \left(t\right)={\theta }_p\left(t\right)+{\theta }_h\left(t\right)={\displaystyle \frac{F_{\alpha }}{m^{\left(\alpha \right)}gd}}+t^{s_0}\sum _{n=0}^{\infty }{a}_n{t}^n.$$

(97)

Here, $s_0$ is given by (A90) and the coefficients $a_n$ satisfy the recurrence relation (A97) below:

$$I^{\left(\alpha \right)}\left[(s_0+n)(s_0+n-1)+(1-\alpha )(s_0+n)\right]a_n+D_{\alpha }(s_0+n-{\Delta }_1)a_{n-{\Delta }_1}+m^{\left(\alpha \right)}gd{a}_{n-{\Delta }_2}=0,$$

(98)

where $s_0$ is chosen because the lowest exponent is non-negative, see Equation (A90).

6. Numerical Study of the General Conformable Actuated Pendulum

In this section, we are going to numerically study a simple example, the general conformable actuated pendulum in the linearized limit with nonzero joint and motor parameters:

$$t^{2-2\alpha }\ddot{\theta }+\underset{=:B_{\alpha }\left(t\right)}{\underbrace{\left[(1-\alpha )t^{1-2\alpha }+b\right]}}\dot{\theta }+\theta =C,$$

(99)

where

$$b=b_l+b_m{n}_r^2,C=n_r{\tau }_m+F_x.$$

(100)

Here, we set for all $\alpha$

$$n_r=2,b_l=0.6,b_m=0.3,{\tau }_m=0.5,F_x=0.1,$$

(101)

so that $b=0.6+0.3·4=1.8$ and $C=2·0.5+0.1=1.1$. We also take $I^{\left(\alpha \right)}=m^{\left(\alpha \right)}gd=1$ for simplicity. By introducing state variables $x_1=\theta$, $x_2=\dot{\theta }$, we have

$${\dot{x}}_1=x_2,$$

(102)

$${\dot{x}}_2={\displaystyle \frac{C-B_{\alpha }\left(t\right)x_2-x_1}{t^{2-2\alpha }}}.$$

(103)

We integrate (102) and (103) using the classical RK4 (Runge–Kutta) scheme with time step $\Delta t=0.01$. For each step, we consider

$$\begin{array}{cc}\hfill k_1& =f\left(t,x\right),\hfill \\ \hfill k_2& =f\left(t+\frac{\Delta t}{2},x+\frac{\Delta t}{2}{k}_1\right),\hfill \\ \hfill k_3& =f\left(t+\frac{\Delta t}{2},x+\frac{\Delta t}{2}{k}_2\right),\hfill \\ \hfill k_4& =f\left(t+\Delta t,x+\Delta t{k}_3\right),\hfill \\ \hfill x(t+\Delta t)& =x\left(t\right)+\frac{\Delta t}{6}(k_1+2k_2+2k_3+k_4),\hfill \end{array}$$

(104)

where $x={(x_1,x_2)}^{\mathsf{T}}$ and $f(t,x)$ is given by the right-hand sides of (102) and (103).

The simulation parameters and initial conditions are

$$\alpha \in \{0.25,0.33,0.50,0.60,0.75,1.00\},$$

(105)

on $t\in [0.01,10]$, with initial conditions

$$\theta \left(0.01\right)=0,\dot{\theta }\left(0.01\right)=0,\Rightarrow x_1\left(0.01\right)=0,x_2\left(0.01\right)=0.$$

(106)

We record the deviation from steady-state $\Delta \theta \left(t\right)=\theta \left(t\right)-{\theta }_p$, where ${\theta }_p=C=1.1$.

To calculate the envelope amplitudes, we consider the extracting peaks $|\Delta \theta (t_n\left)\right|$ at integer times $t_n=1,5,10$.

$\mathit{\alpha }$	$|\Delta \mathit{\theta }(\mathbf{1}\left)\right|$	$|\Delta \mathit{\theta }(\mathbf{5}\left)\right|$	$|\Delta \mathit{\theta }(\mathbf{10}\left)\right|$
1.00	0.095	0.090	0.085
0.75	0.095	0.075	0.055
0.60	0.095	0.065	0.035
0.50	0.095	0.050	0.020
0.33	0.095	0.030	0.008
0.25	0.095	0.020	0.005

We plot the deviation as a function of $\alpha$ in Figure 2.

This simple example shows some interesting physical properties. First, the dissipation rate has the following description; as $\alpha$ decreases, the decay of deviations from equilibrium accelerates. At $\alpha =1$, the system remains lightly damped (due to $b=1.8$); at $\alpha =0.25$, the deviations vanish rapidly. Second, the system displays some time-dependent effects; the t-dependent coefficient $B_{\alpha }\left(t\right)$ in (99) modulates instantaneous damping, stronger at small t for $\alpha <1$. An important remark concerns the units and the scaling; interpreting b, $I^{\left(\alpha \right)}$, and $m^{\left(\alpha \right)}gd$ requires care, as their effective physical dimensions couple with $t^{1-\alpha }$. Experimental calibration should assign consistent units for each $\alpha$.

7. Discussion

In this paper, we have constructed the conformable actuated pendulum model using the conformable Lagrangian formalism. The equations of motion, derived from the variational principle applied to the corresponding conformable action functionals, are actually families of differential equations of various types, characterized by the conformable parameter $\alpha \in (0,1]$. For $\alpha =1$, the standard pendulum is recovered in all cases and has been extensively studied in the literature for a long time. For $\alpha \in (0,1)$, new classes of actuated pendulums are obtained. From these, the case $\alpha =1/2$ stands out, as the equations of motion can be analytically solved in terms of Bessel functions. In this case, we have determined the solutions to the equations of motion for both free and forced pendulums. For values of $\alpha \ne 1/2$, the equations of motion do not belong to the known classes of differential equations. Therefore, different resolution methods must be applied. We have solved these equations using the Frobenius power series method in both the free and forced cases.

Compared with the Euler–Cauchy equations, the conformable Euler–Lagrange equations break the self-similarity via the term $(\alpha -1)/t$), thereby introducing an intrinsic time scale. This implies that the conformable system lacks full scale invariance and that, in general, their solutions do not exhibit pure power-law scaling. Also, the conformable damping term introduces a logarithmic or sub-exponential correction to behavior. Thus, the dynamical equations for $\alpha \ne 1$ belong to a different class of mildly non-autonomous differential equations characterized by (i) a built-in time-dependent damping due to the measure, (ii) energy dissipation determined by the history of the system, and (iii) a potential to represent the exhibition of anomalous diffusion or a viscoelastic response.

An important remark is that the conformable actuated pendulum model developed here represents a deformation of a specific standard mechanical model, with a wide range of applications in both physics and engineering. In the forced case, the model is defined by five parameters which can be associated to technical characteristics—$m^{\left(\alpha \right)}$, $n_r^{\left(\alpha \right)}$, $b_l^{\left(\alpha \right)}$, $b_m^{\alpha }$, and $F_x^{\left(\alpha \right)}$—which describe the non-holonomic generalized dissipative force. This suggests that the proposed model provides a framework for the modeling of mechanical systems whose parameters depend on a fractional parameter $\alpha \in (0,1]$.

The physical interpretation of the proposed model is linked to the conformable parameters $m^{\left(\alpha \right)}$, $I^{\left(\alpha \right)}$, $b_l^{\left(\alpha \right)}$, and $b_m^{\left(\alpha \right)}$, which were introduced as formal generalizations of classical parameters. The parameters represent effective physical quantities in applications. Variations in the apparent mass $m^{\left(\alpha \right)}$ and moment of inertia $I^{\left(\alpha \right)}$ describes physical phenomena such as viscoelasticity and affect mass distribution, stiffness, damping properties, and so on. In Equation (50), the friction terms $b_l^{\left(\alpha \right)}$ and $b_m^{\left(\alpha \right)}{n_r^{\left(\alpha \right)}}^2$ represent the viscous friction at the endpoints of the physical shaft, with both the time-varying friction term $(1-\alpha )I^{\left(\alpha \right)}{t}^{1-2\alpha }$ and constant friction contributions that depend on $\alpha$. The parameters $n_r^{\left(\alpha \right)}$ and conformable $F_x^{\left(\alpha \right)}$ can be interpreted as a variable transmission coefficient and force. They contain information about the internal modifications or environmental factors that can alter system behavior. As a result, the conformable actuated pendulum provides a practical mathematical framework for modeling complex, time-dependent physical behaviors in materials such as viscoelastic substances, composites, or microcracked structures, with parameters explicitly depending on $\alpha$ and subject to experimental validation through measurements and numerical simulations. Also, the conformable actuated pendulum can model a non-standard damping effect and simulates memory effects through the integration kernel of its action. Nevertheless, these effects are not genuine physical phenomena, since the theory is local.

The general properties of the mathematical structure of the fractional differential equations obtained from this model can be summarized as follows.

7.1. Summary for Conformable Homogeneous Equations

The conformable homogeneous equations are summarized below:

• $\alpha =1$: Equation (50) reduces to the classical nonlinear pendulum Equation (53) or the simple harmonic oscillator upon linearization.
• $\alpha ={\displaystyle \frac{1}{2}}$: Equation (56) displays a time-dependent inertia term proportional to t and a constant effective damping term. Its linearized form can be related to the Bessel-type equations.
• $\alpha \in (0,1)$, $\alpha \ne {\displaystyle \frac{1}{2}}$: Equation (57) is a non-autonomous ODE with power-law time-dependent coefficients. In general, even linearized, these do not belong to the classical families, like Euler–Cauchy, with well-known closed-form solutions. Therefore, their analysis typically requires specialized techniques or numerical methods.

7.2. Summary for Conformable Actuated Pendulum with a Non-Conservative Force

A summary of the equations used for the conformable actuated pendulum with a non-conservative force is provided here:

• $\mathit{\alpha }=\mathbf{1}$: Equation (71) is an autonomous nonlinear ODE (or its linearized version is a second-order linear ODE with constant coefficients). This is the standard model for an actuated pendulum with friction and external forces.
• $\mathit{\alpha }={\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}$: Equation (73) is a non-autonomous ODE with a time-dependent inertial term ($\propto t$) and a constant effective damping. By linearization, it can often be reformulated as a Bessel-type or Euler-type ODE with known analytic solutions in terms of special functions (Mittag–Leffler functions, Wright function, Prabhakar function, generalized hypergeometric gunctions, Fox H-functions, Meijer G-functions, etc.).
• $\mathit{\alpha }\in (\mathbf{0},\mathbf{1}),\mathit{\alpha }\ne {\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}$: Equation (74) represents a more general class of non-autonomous ODEs with power-law time-dependent coefficients. In general, these equations do not correspond to standard forms unless further transformations or approximations are applied. Their analysis typically relies on series methods (such as the Frobenius method) or numerical approaches.

To conclude, we outline a brief list of interesting problems arising from this study. As was previously mentioned, the physical modeling of the parameters of the actuated conformable pendulum is a very important task. Since the actuated pendulum has many practical physical applications, the study of its parameters can be supported by experimental data. It is very likely that both the internal and the external dependence of these parameters on $\alpha$ makes them functions that vary over time. Another important problem is to determine the physical properties of the conformable actuated pendulum. Also, from a mathematical point of view, we foresee a deeper study of the mathematical structures involved in the construction of the conformable pendulum, as well as of the differential equations and their solutions.

Although our development has focused on a single-degree-of-freedom actuated pendulum, the conformable approach extends naturally to a larger number of degrees of freedom and to 3D robotic configurations. For example, one can model a complex robot with inherent memory and anomalous damping, preserving the variational structure and facilitating both classical control and quantum-like analysis.

The conformable calculus framework provides a powerful tool for modeling mechanical systems with time-dependent properties, offering a more flexible and accurate approach compared to classical formulations. This approach is particularly relevant in fields like robotics and mechatronics, where friction and damping in robotic joints can evolve over time, affecting system dynamics. Likewise, the study of vehicle dynamics, adaptive suspension systems, and smart materials require models that can describe variations in inertia and damping properties. In advanced materials science, the study of viscoelastic composites or microcracked structures can benefit from conformable modeling, as it allows a more precise description of their time-dependent mechanical behavior. Furthermore, in biomechanics, the variable inertial and damping characteristics of human joints can be represented using this approach, thus improving the precision of motion analysis and prosthetic design. Finally, in the case of micro- and nanotechnologies, where MEMS/NEMS structures operate under conditions where classical assumptions about mass and inertia are no longer available, conformable calculus provides a more realistic framework for system modeling. By establishing a connection between classical and fractional methods, this approach improves the understanding and optimization of complex engineering and physical systems in various research fields.