Numerical Determination of a Time-Dependent Source in a Modified Benjamin–Bona–Mahony Equation

Abstract

In this paper, we consider a modified Benjamin–Bona–Mahony (BBM) equation, which, for example, arises in shallow-water models. We discuss the well-posedness of the Dirichlet initial-boundary-value problem for the BBM equation. Our focus is on identifying a time-dependent source based on integral observation. First, we reformulate this inverse problem as an equivalent direct (forward) problem for a nonlinear loaded pseudoparabolic equation. Next, we develop and implement two efficient numerical methods for solving the resulting loaded equation problem. Finally, we analyze and discuss computational test examples.

1. Introduction

The Benjamin–Bona–Mahony (BBM) equation is a fundamental model in nonlinear wave theory, particularly for describing long waves in dispersive media. It was originally introduced as an improvement to the Korteweg–de Vries equation [1], offering better well-posedness properties while still capturing essential wave dynamics, such as surface waves in shallow water and internal waves in stratified fluids [2]. Beyond fluid dynamics, the BBM equation is also applied in plasma physics and nonlinear acoustics, where it models wave propagation in dispersive media with greater stability [3].

The BBM equation belongs to the class of nonlinear pseudoparabolic equations of the Sobolev type. This equation and its various modifications have been extensively studied by numerous authors. For example, the decay of solutions of the generalized BBM equation is investigated in [4], while the unique continuation for a linearized BBM equation is defined and analyzed in [5]. The authors of [6] apply Rothe’s fixed point theorem to establish the interior approximate controllability of a BBM-type equation with impulses and delay. The approximate controllability of the impulsive functional BBM equation with a nonlinear term involving a spatial derivative is proven in [7]. Properties related to control and energy dissipation for the BBM equation are discussed in [8].

Many numerical methods have been developed for solving both 1D and 2D BBM-type equations [9,10,11,12,13]. The finite volume-difference method is constructed in [9]. A fully discrete finite difference scheme with efficient convolution-based artificial boundary conditions for solving the Cauchy problem for the 1D linearized BBM equation is derived and theoretically analyzed in [13]. High-order accurate finite difference approximation, for a modified BBM equation is constructed in [11]. The approach is based on the use of high-order accurate summation-by-parts finite difference operators for the spatial discretization and explicit fourth-order accurate Runge–Kutta method in time. In [12], an explicit asymmetric three-layer second-order difference scheme is proposed for solving the BBM problem. A three-level conservative finite difference scheme is constructed and analyzed in [10] for solving a generalized BBM equation. A fully discrete finite difference scheme with efficient convolution-based artificial boundary conditions for solving the Cauchy problem associated with the 1D linearized BBM equation is derived and theoretically analyzed in [13]. High-order finite difference approximation for a modified BBM equation is constructed in [11]. In [12], an explicit asymmetric three-layer second-order difference scheme is proposed for solving the BBM problem. A three-level conservative finite difference scheme is constructed and analyzed in [10] for solving a generalized BBM equation.

One of the well-studied modifications of the BBM equation is the Benjamin–Bona–Mahony–Burgers (BBMB) equation, which incorporates viscous dissipation. Numerical methods are presented to solve the BBMB equation, for instance, in [14,15,16]. The authors of [14] develop a three-layer fourth-order implicit finite difference scheme that preserves energy dissipation for solving the 2D BBMB. In [15], a Crank–Nicolson-type finite difference scheme is constructed for the 1D BBMB equation. In [16], a second-order linearized finite difference scheme is developed to solve the 1D BBMB equation. The authors of [17] develop a spectral scheme, applying the transformed generalized Jacobi polynomial combined with the explicit fourth-order Runge–Kutta method for time integration.

Problems for differential equations in which both the solution and certain unknown parameters of the mathematical model must be determined are known as inverse problems; see, e.g., [18,19,20,21,22,23]. In this study, the unknown parameter is a time-dependent source in a modified BBM equation. Similar problems, though for linear or nonlinear parabolic, elliptic, or hyperbolic equations, have been extensively investigated; see, e.g., [18,19,20,21,22,23,24]. Notably, a considerable number of studies have focused on inverse problems for parabolic equations using an integral condition as additional information; see, e.g., [21,24,25,26,27]. The integral condition can represent total energy, average temperature, total mass of impurities, total flux, moments, and other physical quantities.

Currently, there are no known publications specifically addressing the solution of inverse source problems with integral observation for the BBM-type equation. Our goal in this paper is to partially fill this gap. However, there are studies on similar inverse problems for pseudoparabolic equations, which are closely related to the BBM equation. For instance, in [28], the authors discuss recovering the time-dependent source coefficient in a semilinear pseudoparabolic equation with a Neumann boundary condition from integral measurements. Using Rothe’s method, they prove the existence and uniqueness of a weak solution and construct a numerical time-discrete scheme, which is also analyzed. In [29], the inverse problem for determining an unknown time-dependent potential coefficient in a linear pseudoparabolic equation from nonlocal overdetermination conditions is considered. The authors establish uniqueness and the Lipschitz conditional stability of the inverse problem and develop an iterative algorithm for its solution. In [30], the authors investigate an inverse source pseudoparabolic problem with a p-Laplacian and integral observation. They prove the global and local in-time existence of solutions using the Galerkin method. Sufficient conditions for blow-up of the local solutions are derived, and the asymptotic behavior of the solutions to the inverse problem is explored.

In our previous papers [31,32], numerical methods are proposed for recovering a time-dependent boundary function in a two-dimensional linear pseudoparabolic equation using integral observations. In [32], the integral observation is imposed only on the part of the domain boundary. The well-posedness of both direct and inverse problems is also discussed.

Existence and uniqueness results for the direct and inverse time-dependent source problems for a time-fractional pseudo-parabolic equation with final time data are presented in [33]. The solvability of the inverse problem for the identification of a space-dependent source in a linear pseudoparabolic equation with final time measurements is studied in [34]. The authors of [35] investigate the well-posedness of an inverse space-dependent source problem for linear pseudoparabolic equations with a memory term and additional measurements at the final time. The problem is solved numerically by applying extended cubic B-spline functions and formulating it as a nonlinear least-squares minimization with Tikhonov regularization.

The paper [36] focuses on the identification of unknown parameters in a quasi-linear pseudoparabolic equation with periodic boundary conditions. The authors prove the existence and uniqueness of the solution and construct an implicit finite difference scheme.

The main contributions of this paper are as follows:

-

Proving the well-posedness of the Dirichlet initial-boundary-value problem for a modified BBM equation.

-

Formulating the inverse problem for identifying a time-dependent source based on integral measurements and establishing its well-posedness.

-

Reformulating the inverse source problem as a direct Dirichlet initial-boundary-value problem for a nonlinear loaded pseudoparabolic equation.

-

Developing and comparing two numerical methods for solving the inverse source problem.

Our motivation for the present study arises from both the practical applicability of the considered model and the mathematical challenge it poses—both theoretically and numerically.

The remainder of this paper is organized as follows. In the next section, we introduce the direct problem for the BBM equation and study its well-posedness. Section 3 formulates the source identification inverse problem and discusses its solution by reducing it to the direct problem. In Section 4, we develop two numerical methods for solving the inverse problem. The numerical results from test examples are presented in Section 5. Finally, the paper concludes with remarks and future research directions.

2. The BBM Model

In this section, we introduce the model problem and establish its well-posedness.

2.1. Problem Formulation

We consider the modified BBM equation [2,37].

$${\displaystyle \frac{\partial u}{\partial t}}+{\displaystyle \frac{\partial }{\partial x}}\left(u+{\displaystyle \frac{1}{2}}{u}^2\right)-b{\displaystyle \frac{{\partial }^{3}u}{\partial t\partial x^2}}=f\left(x\right)g\left(t\right),(x,t)\in Q_T=\mathsf{\Omega }\times (0,T),$$

(1)

with the initial condition

$$u(x,0)=u^0\left(x\right),x\in \mathsf{\Omega }=(0,1),$$

(2)

and the boundary conditions

$$u(0,t)=g_0\left(t\right),u(1,t)=g_1\left(t\right),t\in (0,T].$$

(3)

The BBM equation appears in various physical models and plays a significant role in the theory and applications of long waves in nonlinear dispersive processes. It describes various physical phenomena, including long-wavelength surface oscillations in liquids, wave propagation in cold plasma environments (hydromagnetic waves), compressible fluid dynamics involving acoustic-gravity modes, and lattice vibrations (acoustic waves) in idealized harmonic crystal structures [38].

When the constant $b>0$ is known and the functions $f\left(x\right)$, $g\left(t\right)$, $u^0\left(x\right)$, $g_0\left(t\right)$, and $g_1\left(t\right)$ are given, the problem (1)–(3) is well defined; see, e.g., [18,20,21,22].

This initial-boundary-value problem, referred to as the direct (or forward) problem, has been extensively studied in the literature. For instance, the existence of solutions for the modified BBM equation has been established in [3,39,40,41].

2.2. Well-Posedness

In this subsection, we discuss the existence and uniqueness of regular solutions to the problem (1)–(3). We apply the Galerkin method following the investigations in [39] and the results presented in [3] (Chapter 4).

Let $H^s(0,1)$ denote the Sobolev space of order s, where s is a non-negative integer. In particular, $H^0(0,1)$ corresponds to the standard $L^2(0,1)$ space, equipped with the inner product $(·,·)$ and the norm $\parallel ·\parallel$.

Furthermore, we define $L^p(0,T;B)$ as the Banach space of integrable functions $v:(0,T)\to B$, such that ${\parallel v\left(t\right)\parallel }_B$ belongs to $L^p(0,T)$, with the norm

$${\parallel v\parallel }_{L(0,T;B)}^p={\int }_0^T{\parallel v\left(t\right)\parallel }_B^{p}dtfor1\le p<+\infty ,$$

and

$${\parallel v\parallel }_{L^{\infty }(0,T;B)}\underset{0<t<T}{\mathrm{ess}}{\parallel v\left(t\right)\parallel }_B,B\mathrm{is} a \mathrm{Banach} \mathrm{space}.$$

For later use, we require the following inequality: [3,18]

$${\parallel v\parallel }_{\infty }=\underset{0\le x\le 1}{sup}\left|v\left(x\right)\right|\le {C\parallel v\parallel }^{1/2}{\left(\parallel v\parallel +∥{\displaystyle \frac{\partial v}{\partial x}}∥\right)}^{1/2},$$

(4)

where $v\in H^1(0,1)$, $\parallel ·\parallel$ denotes the usual $L_2$ norm in $\mathsf{\Omega }$, and the constant C is independent of v.

Additionally, we require the Agmon inequality

$${\parallel v\parallel }_{\infty }={C\parallel v\parallel }^{1/2}.{\parallel v\parallel }_{H^1\left(\mathsf{\Omega }\right)}^{1/2}.$$

(5)

We now apply the Galerkin method to establish the existence and uniqueness of a solution to (1)–(3).

Theorem 1. 

Let $g\left(t\right),g_0\left(t\right),g_l\left(t\right)\in L^{\infty }(0,T)$, $f\left(x\right)\in L^2\left(\mathsf{\Omega }\right)$ and $u_0\left(x\right)\in H^1\left(\mathsf{\Omega }\right)$. Then, there exists a unique solution to (1)–(3), satisfying $u\in L^{\infty }(0,T;H^1\left(\mathsf{\Omega }\right)),{\displaystyle \frac{\partial u}{\partial t}}\in L^{\infty }(0,T;H^1\left(\mathsf{\Omega }\right)).$

Proof. 

We adopt the proof of Theorem 1.1 from [39], where the Cauchy problem with compact support is studied.

First, we consider the case of homogeneous Dirichlet boundary conditions, i.e., $g_0\left(t\right)=g_1\left(t\right)=0$. We seek an approximate solution to Equation (1) in the form outlined in Step (i) of [39]:

$$u^m(x,t)={\displaystyle \sum _{\rho =1}^m}{g}_{\rho m}\left(t\right)v_{\rho }\left(x\right),m\in N,v_s\in H^1\left(\mathsf{\Omega }\right),$$

(6)

where we assume that $v_1,v_2,\dots ,v_m$ are linearly independent and that their finite linear combinations are dense in $H^1\left(\mathsf{\Omega }\right)$.

The functions $g_{\rho m}\left(t\right)$ are determined from the system of ordinary differential equations (ODEs)

$$\left({\displaystyle \frac{\partial u^m}{\partial t}},v_s\right)+ba\left({\displaystyle \frac{\partial u^m}{\partial t}},v_s\right)+\left({\left(u+{\displaystyle \frac{1}{2}}{u}^2\right)}_x,v_s\right)=g\left(t\right)(f\left(x\right),v_s),s=1,\dots ,m,$$

(7)

where

$$a(u,v)\equiv {\int }_0^1{\displaystyle \frac{\partial u}{\partial x}}{\displaystyle \frac{\partial v}{\partial x}}dx.$$

The ODE system (7), solved with the initial conditions $u^m\left(0\right)=u_{0m}={\sum }_{\rho =1}^m{c}_{\rho m}{v}_m$ converges to $u_0$ strongly in $H^1\left(\mathsf{\Omega }\right)$ as m goes to infinity, and $\left\{c_{\rho m}\right\}$ are constants.

Since the coefficient matrix of $g_{\rho m}^{\prime }$ is invertible, we can prove the local existence and uniqueness of the ODE system (7) in the same manner as in [39]. Step (ii) provides a priori estimates, which guarantee the global solution on $[0,T]$.

To derive a priori estimates for the problem (1)–(3), it is convenient to rewrite them with zero boundary conditions:

$$u(x,t)=w(x,t)+g^{\ast }(x,t),g^{\ast }(x,t)=x{g}_1\left(t\right)+(1-x)g_0\left(t\right),$$

(8)

$${\displaystyle \frac{\partial w}{\partial t}}+{\displaystyle \frac{\partial }{\partial x}}\left(w+{\displaystyle \frac{1}{2}}{w}^2\right)+g^{\ast }(x,t){\displaystyle \frac{\partial w}{\partial x}}+g_{-}\left(t\right)w-b{\displaystyle \frac{{\partial }^{3}w}{\partial t\partial x^2}}=f\left(x\right)g\left(t\right)-Q(x,t),$$

where

$$g_{-}\left(t\right)=g_1\left(t\right)-g_0\left(t\right),Q(x,t)=x{g}_{-}^{\prime }\left(t\right)-g_{-}\left(t\right)g^{\ast }(x,t).$$

We solve this equation with the initial condition

$$w(x,0)=u^0\left(x\right)-g^{\ast }(x,0),$$

and the boundary conditions

$$w(0,t)=w(1,t)=0.$$

The approximate solution for $w(x,t)$ is then found using (6) and (8)

$$w^m(x,t)={\displaystyle \sum _{\rho =1}^m}{g}_{\rho m}\left(t\right)v_{\rho }\left(x\right)-g^{\ast }(x,t),m\in \mathbb{N},v_s\in H_0^1\left(\mathsf{\Omega }\right).$$

The unknown functions $g_{\rho m}\left(t\right)$ are the same as in (6) and can be determined from the system ODEs

$$\begin{array}{c}\hfill \left({\displaystyle \frac{\partial w^m}{\partial t}},v_s\right)+ba\left({\displaystyle \frac{\partial w^m}{\partial t}},v_s\right)+\left({\displaystyle \frac{\partial }{\partial x}}\left(w^m+{\displaystyle \frac{1}{2}}{\left(w^m\right)}^2\right),v_s\right)+\left(g^{\ast }(x,t){\displaystyle \frac{\partial w^m}{\partial x}},v_s\right)\\ \hfill +g_{-}\left(t\right)\left(w^m,v_s\right)=g\left(t\right)\left(f\left(x\right),v_s\right)-\left(Q(x,t),v_s\right),s=1,2,\dots ,m.\end{array}$$

Now, as an a priory estimate in [39] (Step (ii)), we derive the estimate

$$\parallel w^m{\parallel }_{H_0^1\left(\mathsf{\Omega }\right)}\le C=\mathrm{const}.,\mathrm{independent}\mathrm{of}m,t\in [0,T].$$

Finally, following [39] (Step (iii)), we use (4) and (5) to obtain the estimate

$${∥u^m+{\displaystyle \frac{1}{2}}{\left(u^m\right)}^2∥}_{H_0^1\left(\mathsf{\Omega }\right)}\le C=\mathrm{const}.,\mathrm{independent}\mathrm{of}m,t\in [0,T].$$

Further, we proceed as in [39] to prove convergence of the approximate solution $w^m(x,t)$ (respectively, $u^m(x,t)$) and, consequently, the existence and uniqueness of the solution to the problem (1)–(3). □

3. The Inverse Problem

In this section, we discuss the solution to the time-dependent source identification inverse problem. We consider Equation (1), assuming that the function $g\left(t\right),t\in (0,T]$ is unknown, and the integral observation is given by

$${\int }_0^{1}u(x,t)dx=m\left(t\right),t\in [0,T].$$

(9)

3.1. Reformulation of the Inverse Problem to a Direct One

We reduce the the inverse problem (1)–(3), (9) into a direct problem, assuming the existence of all necessary continuous derivatives. We differentiate Equation (9) with respect to t and use (1) to express ${\displaystyle \frac{\partial u}{\partial t}}$ in the resulting equation. This leads to the following expression:

$$g\left(t\right)={\displaystyle \frac{-b\left(\frac{{\partial }^{2}u(1,t)}{\partial t\partial x}-\frac{{\partial }^{2}u(0,t)}{\partial t\partial x}\right)}{{\int }_0^{1}f\left(x\right)dx}}+{\displaystyle \frac{(g_1\left(t\right)-g_0\left(t\right))\left[1+\frac{1}{2}\left(g_1\left(t\right)+g_0\left(t\right)\right)\right]+m^{\prime }\left(t\right)}{{\int }_0^{1}f\left(x\right)dx}}.$$

(10)

Now, we replace $g\left(t\right)$ on the right-hand side of (1) with formula (10) to obtain the new equation for the unknown function $u(x,t)$.

$$\begin{array}{c}\hfill \begin{array}{cc}& {\displaystyle \frac{\partial u}{\partial t}}+{\displaystyle \frac{\partial }{\partial x}}\left(u+{\displaystyle \frac{1}{2}}{u}^2\right)-b{\displaystyle \frac{{\partial }^{3}u}{\partial t\partial x^2}}+{\displaystyle \frac{bf\left(x\right)}{{\int }_0^{1}f\left(x\right)dx}}\left({\displaystyle \frac{{\partial }^{2}u(1,t)}{\partial t\partial x}}-{\displaystyle \frac{{\partial }^{2}u(0,t)}{\partial t\partial x}}\right)\hfill \\ & ={\displaystyle \frac{f\left(x\right)}{{\int }_0^{1}f\left(x\right)dx}}\left[(g_1\left(t\right)-g_0\left(t\right))\left(1+{\displaystyle \frac{1}{2}}\left(g_1\left(t\right)+g_0\left(t\right)\right)\right)+m^{\prime }\left(t\right)\right]=f\left(x\right)G\left(t\right).\hfill \end{array}\end{array}$$

(11)

So, we transform the inverse problem (1)–(3) and (9) to the loaded nonlinear pseudoparabolic Equation (11), subject the initial conditions (2) and boundary conditions (3).

In contrast to various studies on linear loaded parabolic and pseudoparabolic equations (see, e.g., [20,21,23,25,42,43,44,45,46,47]), the differential operator incorporates internal or boundary values of the solution or its first derivatives, while Equation (11) includes a mixed second-order derivative. Specifically, in [25,42,43,45,46,47] the linear loaded operator involves the solution values at the interior points of the domain, while in [44], both the solution and the temporal derivative of the solution are involved in the differential operator.

The work [28] examines a semilinear pseudoparabolic problem (including the BBM equation), where the differential operator involves an integral of the solution.

The loaded Equation (11) differs from those studied in the existing literature.

3.2. The Well-Posedness of the Reduced Problem

In this subsection, we study the existence, uniqueness, and regularity of the solution to (11), subject to the initial conditions (2) and the boundary conditions (3), using the Galerkin method. The following assertion holds.

Theorem 2. 

Let the conditions of Theorem 1 be fulfilled and ${\displaystyle \underset{0}{\overset{1}{\int }}}f\left(x\right)dx\ne 0$. Then, there exists a unique solution $u\in H^1\left(\mathsf{\Omega }\right)$ to the problem (1)–(3) and (9).

Proof. 

The proof follows the line of reasoning in [39]. We seek a solution to (11), that satisfies the following system of ODEs:

$$\begin{array}{ccc}& & \left({\displaystyle \frac{\partial u^m}{\partial t}},v_s\right)+ba\left({\displaystyle \frac{\partial u^m}{\partial t}},v_s\right)+\left({\displaystyle \frac{\partial }{\partial x}}\left(u+{\displaystyle \frac{1}{2}}{\left(u^m\right)}^2\right),v_s\right)\hfill \\ & & +{\displaystyle \frac{b}{{\int }_0^{1}f\left(x\right)dx}}\left(f\left(x\right),v_s\right){\displaystyle \sum _{\rho =1}^m}{g}_{\rho m}^{\prime }\left(t\right)(v_{\rho }^{\prime }\left(1\right)-v_{\rho }^{\prime }\left(0\right))=G\left(t\right)(f\left(x\right),v_s),s=1,2,\dots ,m.\hfill \end{array}$$

Now, we choose the system $\left\{v_s\right\}$, $s\in \mathbb{N}$ in such a way that the coefficient matrix of $\left\{g_{\rho m}^{\prime }\right\}$ is invertible. We then proceed as in Theorem 1, following the approach outlined in [39]. □

4. Numerical Solution to the Direct Problem

In this section, we develop second-order-in-space-and-time finite difference schemes for solving (1)–(3) assuming that the differential problem solution is sufficiently smooth for performing the corresponding operations.

We consider the uniform spatial and temporal meshes

$$\begin{array}{ccc}& & {\overline{w}}_h=\left\{x=x_i,x_i=ih,i=0,1,\dots I,h={\displaystyle \frac{1}{I}}\right\},\hfill \\ & & {\overline{w}}_{\tau }=\left\{t=t_n,t_n=n\tau ,n=0,1,\dots N,\tau ={\displaystyle \frac{T}{N}}\right\},\hfill \end{array}$$

and denote $u_i=u_i\left(t\right)=u(x_i,t)$ and $u_i^n=u(x_i,t_n)$.

Let $W=\{v=(v_0,v_1,\dots ,v_I\in R^{I+1};v_0=v_I=0$}. We use the inner product and norm

$${(v,w)}_h=h{\displaystyle \sum _{i=1}^{I-1}}{v}_i{w}_i,{\parallel v\parallel }_h={(v,w)}_h^{1/2},u,w\in W.$$

Further, we introduce the difference approximation [48] of continuously differential functions $v(x,t)$ up to the second order

$$\begin{array}{cc}& {\displaystyle v_{\overline{x},i}=\frac{v_i-v_{i-1}}{h}=\frac{dv}{dx}\left(x_i\right)+O\left(h\right),v_{x,i}=\frac{v_{i+1}-v_i}{h}=\frac{dv}{dx}\left(x_i\right)+O\left(h\right),}\\ & {\displaystyle v_{\mathring{x},i}=\frac{v_{i+1}-v_{i-1}}{2h}=\frac{dv}{dx}\left(x_i\right)+O\left(h^2\right),v_{\overline{x}x,i}={\left(v_x\right)}_{\overline{x},i},}\\ & {\displaystyle v_{t,i}^{n+1}=\frac{v_i^{n+1}-v_i^n}{\tau }=\frac{d{v}_i}{dt}\left(t_n\right)+O\left(\tau \right),}\end{array}$$

the discrete $H^1$ seminorm and norm ${|·|}_{1,h}$, ${\parallel ·\parallel }_{1,h}$, and $L^{\infty }$-norm ${\parallel ·\parallel }_{\infty ,h}$

$${\left|v\right|}_{1,h}={\left(h{\displaystyle \sum _{i=0}^{I-1}}{v}_{x,i}\right)}^{1/2}{,\parallel v\parallel }_{1,h}={\left({\parallel v\left|\right|}_h^2+{\left|v\right|}_{1,h}^2\right)}^{1/2}{,\parallel v\parallel }_{\infty ,h}=\underset{1\le i\le I}{sup}\left|v_i\right|.$$

Let ${\left(\phi (·,·)\right)}_i$ be the bilinear form

$${\left(\phi (v,w)\right)}_i={\displaystyle \frac{u_{\mathring{x},i}}{3}}\left(u_{i-1}+u_i+u_{i+1}\right).$$

We approximate the nonlinear term ${\displaystyle u\frac{\partial u}{\partial x}}$ in (1) on the basis of the representation

$$u{\displaystyle \frac{\partial u}{\partial x}}{|}_{x=x_i}={\displaystyle \frac{1}{3}}\left(u{\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{\partial u^2}{\partial x}}\right){|}_{x=x_i}\simeq {\displaystyle \frac{1}{3}}\left(u_i^{n+1/2}{u}_{\mathring{x},i}^{n+1/2}+{\left({\left(u^{n+1/2}\right)}^2\right)}_{\mathring{x},i}\right),$$

(12)

where $u_i^{n+1/2}=(u_i^n+u_i^{n+1})/2$.

Thus, using (12), the initial-boundary-value problem (1)–(3) is discretized with the Crank–Nicolson finite difference scheme

$$\begin{array}{c}\hfill \begin{array}{cc}& u_{t,i}^{n+1}-b{u}_{\overline{x}xt,i}^{n+1}+u_{\mathring{x},i}^{n+1/2}+{\displaystyle \frac{1}{6h}}\left(u_{i-1}^{n+1/2}+u_i^{n+1/2}+u_{i+1}^{n+1/2}\right)\left(u_{i+1}^{n+1/2}-u_{i-1}^{n+1/2}\right)\hfill \\ & =f\left(x_i\right)g^{n+1/2},i=1,2,\dots ,I-1,\hfill \\ & u_i^0=u^0\left(x_i\right),i=0,1,\dots ,I,\hfill \\ & u_0^{n+1}=g_0\left(t_{n+1}\right),u_I^{n+1}=g_1\left(t_{n+1}\right),n=1,2,\dots ,N.\hfill \end{array}\end{array}$$

(13)

Here, $g^{n+1/2}=g\left(t_{n+1/2}\right)$, where $t_{n+1/2}=t_n+\tau /2$.

We use some results from [15] to prove the following assertion.

Theorem 3. 

Assume that the solution $u(x,t)$ of (1)–(3) is sufficiently smooth. Then, for small τ, there exists a unique solution to the difference scheme (13).

Proof. 

For simplicity, without loss of generality, we take zero boundary conditions for (13). Next, fixing n, we express Equation (13) in the following form:

$$2(u_i^{n+1/2}-u_i^n)-2b{(u^{n+1/2}-u^n)}_{\overline{x}x,i}+\tau u_{\mathring{x},i}^{n+1/2}+\tau \phi (u_i^{n+1/2},u_i^{n+1/2})=\tau f\left(x_i\right)g^{n+1/2},$$

(14)

which requires the continuous mapping $q:W\to W$:

$$q\left(U\right)=2(U-u^n)-2b{(U-u^n)}_{\overline{x}x}+\tau U_{\mathring{x},i}+\tau \phi (U,U)-\tau f\left(x\right)g^{n+1/2}.$$

We perform the inner product of Equation (14) with U and use Lemma 1 in [15] to find

$${(q\left(U\right),U)}_h={2\parallel U\parallel }_h^2-2b{\left(u^n,U\right)}_h+2{\left|U\right|}_{1,h}^2-2h{\displaystyle \sum _{i=1}^{I-1}}{u}_{x,i}^n{U}_{x,i}-\tau g^{n+1/2}{\displaystyle \sum _{i=1}^{I-1}}f\left(x_i\right)U_i.$$

Applying the Cauchy inequality to the last term, we obtain

$$\begin{array}{ccc}\hfill {(q\left(U\right),U)}_h& \ge & {2\parallel U\parallel }_h^2-b\left(\parallel u^n{\parallel }_h^2+{\parallel U\parallel }_h^2\right)+{2\left|U\right|}_{1,h}^2-\left(|u^n{|}_{1,h}^2+{\left|U\right|}_{1,h}^2\right)-\tau C{\parallel U\parallel }_{1,h}^2,\hfill \\ \hfill {(q\left(U\right),U)}_h& \ge & {\parallel U\parallel }_{1,h}^2-\parallel u^n{\parallel }_{1,h}^2-\tau C{\parallel U\parallel }_{1,h}^2,\hfill \end{array}$$

where C is a generic constant depending on $f\left(x\right)$ and $g\left(t\right)$.

Furthermore, using a discrete Sobolev embedding inequality, we find

$${(q\left(U\right),U)}_h\ge {(1-C\tau )\parallel U\parallel }_{1,h}^2-{\parallel u^n\parallel }_{1,h}^2.$$

Therefore, for

$${\parallel U\parallel }_{1,h}={\displaystyle \frac{1}{1-C\tau }}{\parallel u^n\parallel }_{1,h}+1,$$

we have ${(q\left(U\right),U)}_h>0$, and from Lemma 2 in [15] follows the existence of an approximate solution $u^n$ to the scheme (13).

Next, we take the inner product of (13) with $u^{n+1/2}$ and use Lemma 2 in [15] to derive

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{\parallel u^{n+1}{\parallel }_h^2-{\parallel u^n\parallel }_h^2}{\tau }}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{|u^{n+1}{|}_h^2-{\left|u^n\right|}_h^2}{\tau }}-g^{n+1/2}{\displaystyle \sum _{i=1}^{I-1}}f\left(x_i\right)u_i^n=0.$$

Now, applying the Cauchy inequality and then the Sobolev embedding discrete inequality to the last term, we obtain

$${\displaystyle \frac{1}{\tau }}\left((1-C\tau )\parallel u^{n+1}{\parallel }_{1,h}^2-{\parallel u^n\parallel }_{1,h}^2\right)\le 0.$$

Then, as in [15], the discrete Gronwall inequality and the discrete Sobolev inequality give the global boundness of the discrete solution

$$\parallel u^n{\parallel }_{\infty ,h}\le C_0,$$

(15)

where $C_0$ is a constant that may depend only on the input data.

Further, as in Theorem 4 in [15], using (15), one can prove the uniqueness of the approximate solution $u^n$ to the scheme (13). □

In order to solve the nonlinear system of difference Equation (13), avoiding the iteration process, we use the quasi-linearization

$$v^{n+1}{w}^{n+1}=v^{n+1}{w}^n+v^n{w}^{n+1}-v^n{w}^n+O\left({\tau }^2\right).$$

Therefore, the linearized difference scheme (13) becomes

$$\begin{array}{c}\hfill \begin{array}{cc}& {\alpha }_i^n{u}_{i-1}^{n+1}+{\beta }_i^n{u}_i^{n+1}+{\gamma }_i^n{u}_{i+1}^{n+1}=F_i^n+f\left(x_i\right)g^{n+1/2},i=1,2,\dots ,I-1,\hfill \\ & u_i^0=u^0\left(x_i\right),i=0,1,\dots ,I,\hfill \\ & u_0^{n+1}=g_0\left(t_{n+1}\right),u_I^{n+1}=g_1\left(t_{n+1}\right),n=1,2,\dots ,N.\hfill \end{array}\end{array}$$

(16)

where

$$\begin{array}{cc}& {\displaystyle {\alpha }_i^n=-\frac{b}{\tau h^2}-\frac{1}{4h}-u_{\tilde{x},i}^n+\frac{1}{6}{u}_{\mathring{x},i}^n=-\frac{b}{\tau h^2}-\frac{1}{4h}-\frac{u_i^n+2u_{i-1}^n}{12h},}\\ & {\displaystyle {\beta }_i^n=\frac{1}{\tau }+\frac{2b}{\tau h^2}+\frac{1}{6}{u}_{\mathring{x},i}^n,{\gamma }_i^n=-\frac{b}{\tau h^2}+\frac{1}{4h}+u_{\tilde{x},i}^n+\frac{1}{6}{u}_{\mathring{x},i}^n=-\frac{b}{\tau h^2}+\frac{1}{4h}+\frac{2u_{i+1}^n+u_i^n}{12h},}\\ & {\displaystyle u_{\tilde{x},i}^n=\frac{u_{i-1}^n+u_i^n+u_{i+1}^n}{12h},F_i^n=\frac{u_i^n}{\tau }-\frac{b}{\tau }{u}_{\overline{x}x,i}^n-\frac{1}{2}{u}_{\mathring{x},i}^n.}\end{array}$$

5. Numerical Solution to the Inverse Problem

In this section, we develop two algorithms for solving the inverse problem (1)–(3), (9). Both methods are based on second-order linearized discretization (16). The first algorithm employs an iterative procedure for g, which is common for solving non-local problems. The second approach is an iteration-free approach.

First, we approximate $g\left(t\right)$ in (10) at $t_{n+1/2}$. Applying second-order discretizations for the derivatives, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill g^{n+1/2}=& {\displaystyle \frac{-b\left(u_{\overleftarrow{x},I}^{n+1}-u_{\overleftarrow{x},I}^n-u_{\overrightarrow{x},0}^{n+1}+u_{\overrightarrow{x},0}^n\right)+\tau m^{\prime }\left(t_{n+1/2}\right)}{\tau I_f}}+G^{n+1/2}+O\left({\tau }^2\right),\hfill \end{array}\end{array}$$

(17)

where

$$\begin{array}{ccc}& & G^{n+1/2}={\displaystyle \frac{\left(g_1\left(t_{n+1/2}\right)-g_0\left(t_{n+1/2}\right)\right)\left[1+\frac{1}{2}\left(g_1\left(t_{n+1/2}\right)+g_0\left(t_{n+1/2}\right)\right)\right]}{I_f}},\hfill \\ & & u_{\overrightarrow{x},0}^n={\displaystyle \frac{-3u_0^n+4u_1^n-u_2^n}{2h}},u_{\overleftarrow{x},I}^n={\displaystyle \frac{3u_I^n-4u_{I-1}^n+u_{I-2}^n}{2h}},\hfill \end{array}$$

and the quantity $I_f$ is obtained exactly or numerically, depending on the function $f\left(x\right)$:

$$\begin{array}{c}\hfill I_f={\int }_0^{1}f\left(x\right)dx,\mathrm{or}{I}_f={\displaystyle \frac{h}{2}}\left(u_0+2{\displaystyle \sum _{i=1}^{I-1}}{u}_i+u_I\right).\end{array}$$

Numerical method 1 (NM1). At each time layer, we solve (16) for $g^{n+1/2}$, obtained from (17) at the corresponding iteration k. Specifically, we determine $g^{n+1/2}$ iteratively, starting with an initial guess $g^{\left(0\right)}$. Assume that $u^{(k+1)}=u^{n+1,(k+1)}$. At each time layer, for $k=0,1,\dots$, we compute

$$\begin{array}{c}\hfill \begin{array}{cc}& {\alpha }_i^n{u}_{i-1}^{(k+1)}+{\beta }_i^n{u}_i^{(k+1)}+{\gamma }_i^n{u}_{i+1}^{(k+1)}=F_i^n+f\left(x_i\right)g^{\left(k\right)},i=1,2,\dots ,I-1,\hfill \\ & u_i^0=u^0\left(x_i\right),i=0,1,\dots ,I,\hfill \\ & u_0^{(k+1)}=g_0\left(t_{n+1}\right),u_I^{(k+1)}=g_1\left(t_{n+1}\right),n=1,2,\dots ,N.\hfill \end{array}\end{array}$$

(18)

Then, we update the value of g at time layer $n+1/2$

$$\begin{array}{ccc}\hfill & & g^{(k+1)}={\displaystyle \frac{-b\left(u_{\overleftarrow{x},I}^{(k+1)}-u_{\overleftarrow{x},I}^n-u_{\overrightarrow{x},0}^{(k+1)}+u_{\overrightarrow{x},0}^n\right)+\tau m^{\prime }\left(t_{n+1/2}\right)}{\tau I_f}}+G^{n+1/2}.\hfill \end{array}$$

For $n>0$, we set $g^{\left(0\right)}:=g^{n-1/2}$. The iteration process continues until the desired accuracy $ϵ$ is achieved, i.e.,

$$\parallel g^{(k+1)}-g^{\left(k\right)}\parallel \le ϵ,\parallel v\parallel =\underset{0\le i\le I}{max}\left|v_i\right|.$$

Note that if an iterative procedure is used to solve the nonlinear system of difference Equation (13), such as Newton’s or Picard’s method, then solving the corresponding system (18) will involve two nested iterations—an outer and an inner loop.

Proposition 1. 

Under the restriction

$$\tau \le min\left\{{\displaystyle \frac{4b}{h(1+\parallel u^n\parallel )}},{\displaystyle \frac{2h}{\parallel u^n\parallel }}\right\},$$

(19)

the inverse problem (18) is uniquely solvable.

Proof. 

The coefficient matrix of (18) is the same as that of the direct problem (16). Under restriction (19), it is a tridiagonal, diagonally dominant matrix. Indeed, let $v^{+}=max\{0,v\}$ and $v^{-}=max\{0,-v\}$. Then, we have

$$\begin{array}{ccc}\hfill |{\beta }_i^n|-|{\alpha }_i^n|-|{\gamma }_i^n|& =& \left|{\displaystyle \frac{1}{\tau }}+{\displaystyle \frac{2b}{\tau h^2}}+{\displaystyle \frac{1}{6}}({(u_{\mathring{x},i}^n)}^{+}-(u_{\mathring{x},i}^n{)}^{-})\right|\hfill \\ & & -\left|{\displaystyle \frac{b}{\tau h^2}}+{\displaystyle \frac{1}{4h}}+{(u_{\tilde{x},i}^n)}^{+}-{(u_{\tilde{x},i}^n)}^{-}+{\displaystyle \frac{1}{6}}({(u_{\mathring{x},i}^n)}^{-}-{(u_{\mathring{x},i}^n)}^{+})\right|\hfill \\ & & -\left|{\displaystyle \frac{b}{\tau h^2}}-{\displaystyle \frac{1}{4h}}+{(u_{\tilde{x},i}^n)}^{-}-{(u_{\tilde{x},i}^n)}^{+}+{\displaystyle \frac{1}{6}}({(u_{\mathring{x},i}^n)}^{-}-{(u_{\mathring{x},i}^n)}^{+})\right|\hfill \\ & \ge & {\displaystyle \frac{1}{\tau }}-{\displaystyle \frac{∥{(u_{\mathring{x}}^n)}^{-}∥}{2}}\ge {\displaystyle \frac{1}{\tau }}-{\displaystyle \frac{\parallel u^n\parallel }{2h}}\ge 0,i=1,2,\dots ,I.\hfill \end{array}$$

Taking into account (15) and the boundary conditions, we conclude that the coefficient matrix of (18) is a diagonally dominant matrix and, therefore, invertible. This ensures the solvability of the inverse problem using MN1. □

• Numerical method 2 (NM2). This approach is based on the discretization of (11). We approximate this differential equation in the same way as (16), avoiding an iterative procedure, and apply discretization (17) to approximate $g^{n+1/2}$. The resulting finite difference scheme is

  $$\begin{array}{c}\hfill \begin{array}{cc}& -4{\eta }_i{u}_1^{n+1}+{\eta }_i{u}_2^{n+1}+{\alpha }_i^n{u}_{i-1}^{n+1}+{\beta }_i^n{u}_i^{n+1}+{\gamma }_i^n{u}_{i+1}^{n+1}+{\eta }_i{u}_{I-2}^{n+1}-4{\eta }_i{u}_{I-1}^{n+1}\hfill \\ & =-3\eta (g_0\left(t_{n+1}\right)+g_1\left(t_{n+1}\right))+F_i^n+f\left(x_i\right){\tilde{G}}^{n+1/2},i=1,2,\dots ,I-1,\hfill \\ & u_i^0=u^0\left(x_i\right),i=0,1,\dots ,I,\hfill \\ & u_0^{n+1}=g_0\left(t_{n+1}\right),u_I^{n+1}=g_1\left(t_{n+1}\right),n=1,2,\dots ,N,\hfill \end{array}\end{array}$$

  (20)

  where

  $${\eta }_i={\displaystyle \frac{bf\left(x_i\right)}{2\tau h{I}_f}},{\tilde{G}}^{n+1/2}={\displaystyle \frac{b\left(u_{\overleftarrow{x},I}^n-u_{\overrightarrow{x},0}^n\right)+\tau m^{\prime }\left(t_{n+1/2}\right)}{\tau I_f}}+G^{n+1/2}.$$

  The coefficient matrix of (21) is sparse, but not tridiagonal; see Figure 1. Moreover, the diagonal domination cannot be guaranteed only for a large-space step size $h>5b∥f\left(x\right)/I_f∥$. For example, for $i=4,5,\dots ,I-4$, we have

  $$|{\beta }_i^n|-|{\alpha }_i^n|-|{\gamma }_i^n|-10|{\eta }_i|\ge {\displaystyle \frac{1}{\tau }}\left(1-{\displaystyle \frac{5b}{h}}∥{\displaystyle \frac{f\left(x\right)}{I_f}}∥\right)-{\displaystyle \frac{\parallel u^n\parallel }{2h}}.$$

In order to overcome this computational disadvantage, we apply the decomposition technique [43]. We rewrite the system (21) in the form

$$\begin{array}{c}\hfill \begin{array}{cc}& {\alpha }_i^n{u}_{i-1}^{n+1}+{\beta }_i^n{u}_i^{n+1}+{\gamma }_i^n{u}_{i+1}^{n+1}+P^{n+1}\hfill \\ & =-3\eta (g_0\left(t_{n+1}\right)+g_1\left(t_{n+1}\right))+F_i^n+f\left(x_i\right){\tilde{G}}^{n+1/2},i=1,2,\dots ,I-1,\hfill \\ & u_i^0=u^0\left(x_i\right),i=0,1,\dots ,I,\hfill \\ & u_0^{n+1}=g_0\left(t_{n+1}\right),u_I^{n+1}=g_1\left(t_{n+1}\right),n=1,2,\dots ,N,\hfill \end{array}\end{array}$$

(21)

where

$$P^{n+1}={\eta }_i(-4u_1^{n+1}+u_2^{n+1}+u_{I-2}^{n+1}-4u_{I-1}^{n+1})=\sum _{j=1,2,I-1,I-2}{s}_j{u}_j^{n+1}.$$

(22)

Next, we represent the solution $u_i^{n+1}$ in the form

$$u_i^{n+1}=U_i^{n+1}-{\lambda }_i{P}^{n+1}.$$

(23)

Thus, from (21) and (23), we obtain two systems:

$$\begin{array}{c}\hfill \begin{array}{cc}& {\alpha }_i^n{U}_{i-1}^{n+1}+{\beta }_i^n{U}_i^{n+1}+{\gamma }_i^n{U}_{i+1}^{n+1}\hfill \\ & =-3\eta (g_0\left(t_{n+1}\right)+g_1\left(t_{n+1}\right))+F_i^n+f\left(x_i\right){\tilde{G}}^{n+1/2},i=1,2,\dots ,I-1,\hfill \\ & U_i^0=u^0\left(x_i\right),i=0,1,\dots ,I,\hfill \\ & U_0^{n+1}=g_0\left(t_{n+1}\right),U_I^{n+1}=g_1\left(t_{n+1}\right),n=1,2,\dots ,N,\hfill \end{array}\end{array}$$

(24)

and

$$\begin{array}{c}\hfill \begin{array}{cc}& {\alpha }_i^n{\lambda }_{i-1}+{\beta }_i^n{\lambda }_i+{\gamma }_i^n{\lambda }_{i+1}=1,i=1,2,\dots ,I-1,\hfill \\ & {\lambda }_0=0,{\lambda }_I=0.\hfill \end{array}\end{array}$$

(25)

Further, from (22) and (23), we obtain

$$P^{n+1}=\sum _{j=1,2,I-1,I-2}{s}_j(U_j^{n+1}-{\lambda }_j{P}^{n+1}),$$

and finally, we determine

$$P^{n+1}=\sum _{j=1,2,I-1,I-2}{s}_j{U}_j^{n+1}{\left(1+\sum _{j=1,2,I-1,I-2}{s}_j{\lambda }_j\right)}^{-1}.$$

We compute the solution $u^{n+1}$ from (21) for an already known quantity $P^{n+1}$.

The coefficient matrices of systems (24), (25), and (21) for a given $P^{n+1}$ are identical to those of systems (18) and (16). Consequently, the solvability of the inverse problem (1)–(3), (9) using NM2 is ensured under condition (19).

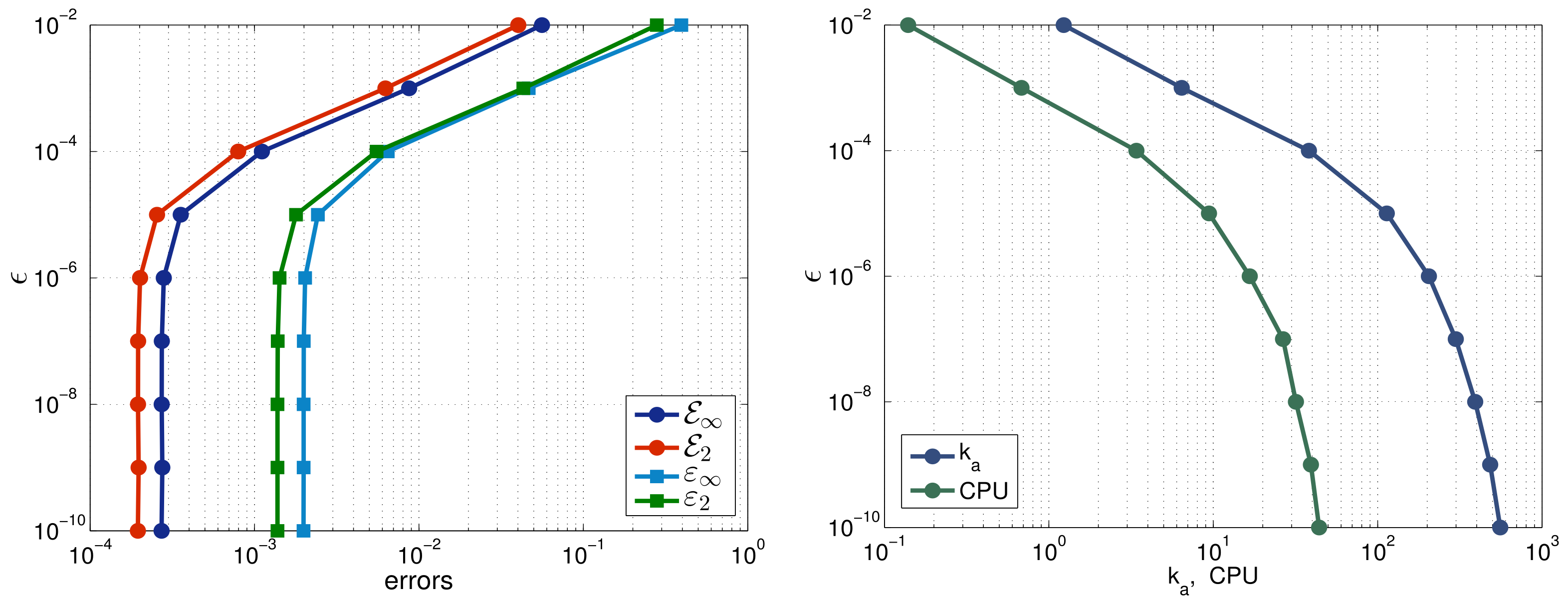
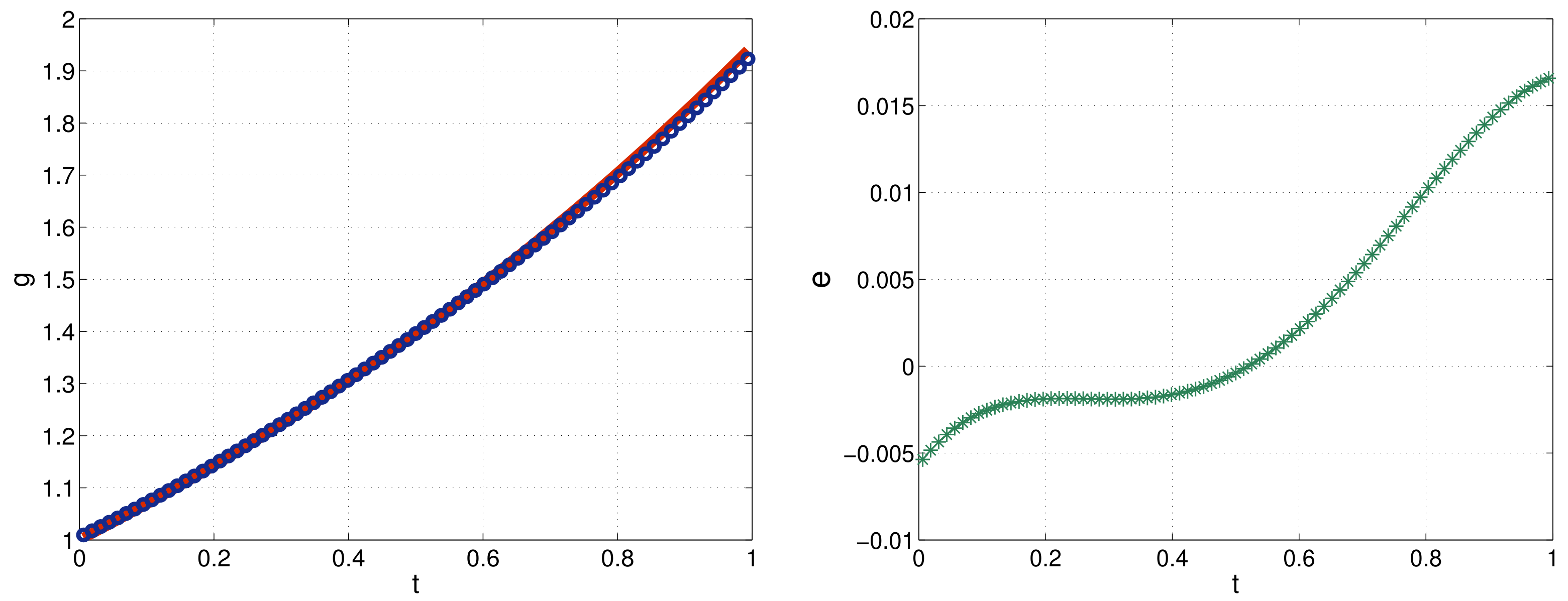
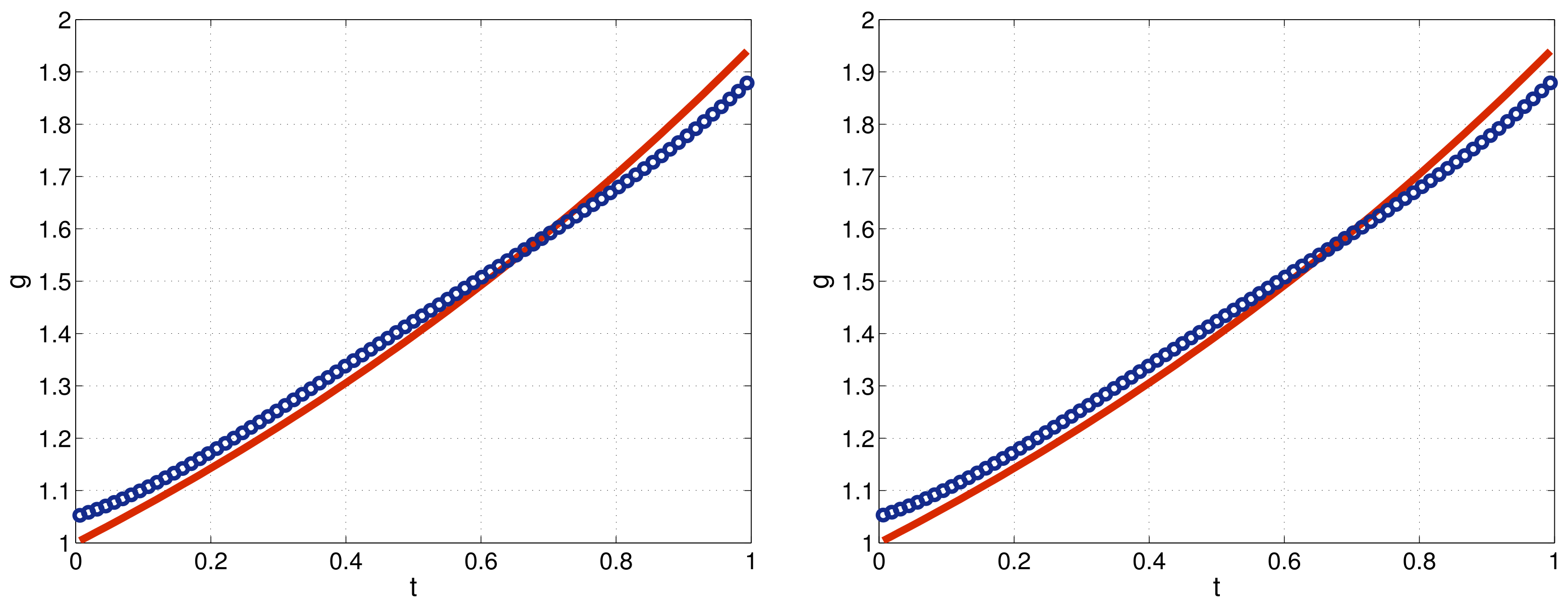
6. Computational Results

In this section, we assess the accuracy and efficiency of both numerical methods, NM1 and NM2, for solving the inverse problem (1)–(3), (9). We provide the results for exact and noisy measurements (9). For comparison, we also present the computational results for the direct problem (1)–(3), solved by the finite difference scheme (16).

Let

$$b={\displaystyle \frac{76}{25}},f\left(x\right)={\displaystyle \frac{5}{4}}{e}^{5x/2},g_0=e^{t/3},g_1=e^{t/3+5/4},T=1.$$

In this case, the exact solution to the problem (1)–(3) is given by $u(x,t)=e^{t/3+5x/4}$ for $g\left(t\right)=e^{2t/3}$.

The errors and order of convergence are presented in maximum and $L_2$ discrete norms:

$$\begin{array}{c}\hfill \begin{array}{cc}& {\displaystyle E_i=u_i^N-u(x_i,T),e^n=g^n-g\left(t_n\right),}\hfill \\ & {\displaystyle {\mathcal{E}}_{\infty }={\mathcal{E}}_{\infty }^I=\underset{0\le i\le I}{max}\left|E_i\right|,{\mathcal{E}}_2={\mathcal{E}}_2^I=\sqrt{h{\displaystyle \sum _{i=0}^I}{\left(E_i\right)}^2},}\hfill \\ & {\displaystyle {\epsilon }_{\infty }=e_{\infty }^N=\underset{1\le n\le N}{max}\left|e^n\right|,{\epsilon }_2={\epsilon }_2^N=\sqrt{\tau {\displaystyle \sum _{i=0}^N}{\left(e^n\right)}^2},}\hfill \\ & {\displaystyle C{R}_{\infty }={log}_2\frac{{\mathcal{E}}_{\infty }^I}{{\mathcal{E}}_{\infty }^{2I}},C{R}_2={log}_2\frac{{\mathcal{E}}_2^I}{{\mathcal{E}}_2^{2I}},c{r}_{\infty }={log}_2\frac{{ϵ}_{\infty }^N}{{ϵ}_{\infty }^{2N}},c{r}_2={log}_2\frac{{ϵ}_2^N}{{ϵ}_2^{2N}}.}\hfill \end{array}\end{array}$$

All computations are performed for a fixed ratio $\tau =h$, i.e., $N=I$, and for the stopping criteria of the iteration process in NM1, we set $ϵ={10}^{-7}$.

Example 1 (Direct problem).

In this example, we present the computational results for the direct problem (1)–(3), as they will serve as a benchmark for evaluating the numerical accuracy of the inverse problem solution.

Table 1. Errors and convergence rates of solution u, direct problem, Example 1.

I	${\mathcal{E}}_{\mathit{\infty }}$	${\mathit{CR}}_{\mathit{\infty }}$	${\mathcal{E}}_2$	${\mathit{CR}}_2$
20	5.783$\times {10}^{-4}$		4.161$\times {10}^{-4}$
40	1.448$\times {10}^{-4}$	1.997	1.040$\times {10}^{-4}$	2.000
80	3.621$\times {10}^{-5}$	2.000	2.600$\times {10}^{-5}$	2.000
160	9.051$\times {10}^{-6}$	2.000	6.501$\times {10}^{-6}$	2.000
320	2.263$\times {10}^{-6}$	2.000	1.625$\times {10}^{-6}$	2.000

displays the errors and corresponding orders of convergence. The numerical experiments confirm that the accuracy of the finite difference scheme (16) is $O({\tau }^2+h^2)$.

Example 2 (Inverse problem problem: exact data).

In the numerical experiments, the measured function $g\left(t\right)$ in (9) is derived directly from the exact solution. The results presented in Table 1 and

Table 2. Errors and convergence rates of the recovered function g and solution u, NM1, Example 2.

N	${\mathcal{E}}_{\mathit{\infty }}$	${\mathit{CR}}_{\mathit{\infty }}$	${\mathcal{E}}_2$	${\mathit{CR}}_2$	${\mathit{e}}_{\mathit{\infty }}$	${\mathit{cr}}_{\mathit{\infty }}$	${\mathit{e}}_2$	${\mathit{cr}}_2$	${\mathit{k}}_{\mathit{a}}$	CPU
20	1.341$\times {10}^{-2}$		9.648$\times {10}^{-3}$		8.880$\times {10}^{-2}$		6.629$\times {10}^{-2}$		316.105	0.512
40	4.099$\times {10}^{-3}$	1.710	2.419$\times {10}^{-3}$	1.713	2.876$\times {10}^{-2}$	1.626	2.047$\times {10}^{-2}$	1.695	338.897	1.950
80	1.086$\times {10}^{-3}$	1.916	7.794$\times {10}^{-4}$	1.916	7.795$\times {10}^{-3}$	1.884	5.446$\times {10}^{-3}$	1.911	324.278	6.946
160	2.758$\times {10}^{-4}$	1.977	1.979$\times {10}^{-4}$	1.977	1.994$\times {10}^{-3}$	1.967	1.384$\times {10}^{-3}$	1.976	298.547	24.282
320	6.974$\times {10}^{-5}$	1.983	5.005$\times {10}^{-5}$	1.983	5.044$\times {10}^{-4}$	1.983	3.500$\times {10}^{-4}$	1.984	270.429	87.645

show both the accuracy and convergence rates for the reconstructed data $g^n$ and the computed solution u, obtained using MN1 and NM2, respectively.

Additionally, we provide the CPU time and the average number of iterations ($k_a$) required by NM1 to achieve the desired accuracy $ϵ$. The results indicate that the recovered source $g^n$ and the solution u exhibit second-order accuracy in both time and space, in both the maximum and $L_2$ norms. The precision of the restored $g^n$ and solution u is comparable for both methods; however, NM1 requires significantly more CPU time than NM2 due to the iterative process.

Figure 2 illustrates the accuracy of the recovered source and the solution u in the maximum and $L_2$ norms (left), as well as the average number of iterations and the corresponding CPU time (right) for different values of $ϵ$, NM1, and $I=160$. Although the number of iterations is relatively high, it decreases as the mesh is refined or when the required accuracy $ϵ$ is reduced. For this example, if $ϵ$ is approximately greater than ${10}^{-7}$, the accuracy improves insignificantly, and similarly, the increase in the number of iterations and CPU time becomes negligible.

The numerical experiments demonstrate that NM2 is significantly more efficient than NM1. Comparing the results in Table 1 with those in Table 1 and

Table 3. Errors and convergence rates of the recovered function g and solution u, NM2, Example 2.

N	${\mathcal{E}}_{\mathit{\infty }}$	${\mathit{CR}}_{\mathit{\infty }}$	${\mathcal{E}}_2$	${\mathit{CR}}_2$	${\mathit{e}}_{\mathit{\infty }}$	${\mathit{cr}}_{\mathit{\infty }}$	${\mathit{e}}_2$	${\mathit{cr}}_2$	CPU
20	1.341$\times {10}^{-2}$		9.647$\times {10}^{-3}$		8.880$\times {10}^{-2}$		6.628$\times {10}^{-2}$		0.019
40	4.099$\times {10}^{-3}$	1.710	2.941$\times {10}^{-3}$	1.714	2.876$\times {10}^{-2}$	1.627	2.047$\times {10}^{-2}$	1.695	0.083
80	1.085$\times {10}^{-3}$	1.917	7.788$\times {10}^{-4}$	1.917	7.790$\times {10}^{-3}$	1.884	5.442$\times {10}^{-3}$	1.911	0.242
160	2.749$\times {10}^{-4}$	1.981	1.973$\times {10}^{-4}$	1.981	1.989$\times {10}^{-3}$	1.969	1.380$\times {10}^{-3}$	1.979	0.886
320	6.889$\times {10}^{-5}$	1.997	4.944$\times {10}^{-5}$	1.997	4.999$\times {10}^{-4}$	1.993	3.459$\times {10}^{-4}$	1.996	3.355

, we can conclude that, as expected, the numerical solution obtained by solving the direct problem with the exact $g\left(t\right)$ is more accurate than the one computed by solving the inverse problem for the reconstructed source $g^n$. Nevertheless, the accuracy achieved through the inverse problem remains sufficiently high, and the convergence rate $O({\tau }^2+h^2)$ is preserved.

Example 3. 

(Inverse problem: noisy data) In these tests, we deal with noisy measurements

$$\begin{array}{c}\hfill m^n=m\left(t_n\right)+2\rho ({\sigma }^n-0.5),\end{array}$$

where ρ is the noise level and ${\sigma }^n$ represents random values, uniformly distributed on the interval $[0,1]$. To generate the values of $m^{\prime }\left(t_n\right)$, we approximate $m^{\prime }$ using central finite difference approximation in time for $n=1,2,\dots ,M-1$, and left and right second-order approximations similar to those in (17). We apply polynomial curve fitting of degree 5 to smooth the data.

In

Table 4. Errors of the numerically recovered source g and solution u, NM1, Example 3.

$\mathit{\rho }$	${\mathcal{E}}_{\mathit{\infty }}$	${\mathcal{E}}_2$	${\mathit{\epsilon }}_{\mathit{\infty }}$	${\mathit{\epsilon }}_2$	${\mathit{k}}_{\mathit{a}}$
0.003	9.053$\times {10}^{-4}$	6.516$\times {10}^{-4}$	1.349$\times {10}^{-2}$	6.142$\times {10}^{-3}$	139.886
0.005	7.308$\times {10}^{-4}$	5.274$\times {10}^{-4}$	1.701$\times {10}^{-2}$	7.295$\times {10}^{-3}$	141.532
0.01	3.034$\times {10}^{-4}$	2.186$\times {10}^{-4}$	2.580$\times {10}^{-2}$	1.174$\times {10}^{-2}$	142.321
0.03	1.487$\times {10}^{-3}$	1.033$\times {10}^{-3}$	6.094$\times {10}^{-2}$	3.365$\times {10}^{-2}$	144.514

and

Table 5. Errors of the numerically recovered source g and solution u, NM2, Example 3.

$\mathit{\rho }$	${\mathcal{E}}_{\mathit{\infty }}$	${\mathcal{E}}_2$	${\mathit{\epsilon }}_{\mathit{\infty }}$	${\mathit{\epsilon }}_2$
0.003	8.225$\times {10}^{-4}$	5.922$\times {10}^{-4}$	1.306$\times {10}^{-2}$	5.854$\times {10}^{-3}$
0.005	6.481$\times {10}^{-4}$	4.680$\times {10}^{-4}$	1.658$\times {10}^{-2}$	7.106$\times {10}^{-3}$
0.01	2.249$\times {10}^{-4}$	1.603$\times {10}^{-4}$	2.536$\times {10}^{-2}$	1.170$\times {10}^{-2}$
0.03	1.569$\times {10}^{-3}$	1.093$\times {10}^{-3}$	6.051$\times {10}^{-2}$	3.374$\times {10}^{-2}$

, we present the accuracy of the recovered source and solution u for different levels of noise, obtained using NM1, with $ϵ={10}^{-5}$, and NM2, with $I=80$ for both methods. As in Example 1, the accuracy achieved by both methods is similar, but NM1 operates more slowly due to the iterative process. We observe that the restoration achieves satisfactory precision even with perturbed data. The numerically recovered time-dependent source is sufficiently accurate to ensure that the solution u achieves optimal accuracy.

In Figure 3 and Figure 4, we present the exact function g and its recovered counterpart obtained using NM2, along with the corresponding errors for $\rho =0.005$ and $\rho =0.01$, respectively. Figure 5 illustrates the exact and recovered functions g for $\rho =0.03$, computed using NM1 and NM2. In Figure 6, the solution u recovered by NM2 and the corresponding error across the entire computational domain are depicted.

7. Conclusions

In this work, we considered the initial-boundary-value problem for the Benjamin–Bona–Mahony equation and established the existence and uniqueness of its solution. We formulated and investigated an inverse problem for identifying the time-dependent source in the BBM equation. The inverse problem was reformulated as a direct problem for a loaded equation, and its well-posedness was discussed and justified. Based on this reformulation, we developed and compared two numerical methods for solving the problem. The computational results demonstrated that the proposed methods achieve second-order accuracy in both space and time for exact measurements. For noisy data, the recovery remains sufficiently precise. The numerically reconstructed time-dependent source is accurate enough to ensure the solution attains optimal accuracy.

Following the nature of the considered mathematical model for the BBM equation, our future work will continue with studying inverse coefficient and source problems for the Benjamin–Bona–Mahony–Burgers equation.