Numerical Determination of a Time-Dependent Source in a Modified Benjamin–Bona–Mahony Equation
Abstract
1. Introduction
- -
- Proving the well-posedness of the Dirichlet initial-boundary-value problem for a modified BBM equation.
- -
- Formulating the inverse problem for identifying a time-dependent source based on integral measurements and establishing its well-posedness.
- -
- Reformulating the inverse source problem as a direct Dirichlet initial-boundary-value problem for a nonlinear loaded pseudoparabolic equation.
- -
- Developing and comparing two numerical methods for solving the inverse source problem.
2. The BBM Model
2.1. Problem Formulation
2.2. Well-Posedness
3. The Inverse Problem
3.1. Reformulation of the Inverse Problem to a Direct One
3.2. The Well-Posedness of the Reduced Problem
4. Numerical Solution to the Direct Problem
5. Numerical Solution to the Inverse Problem
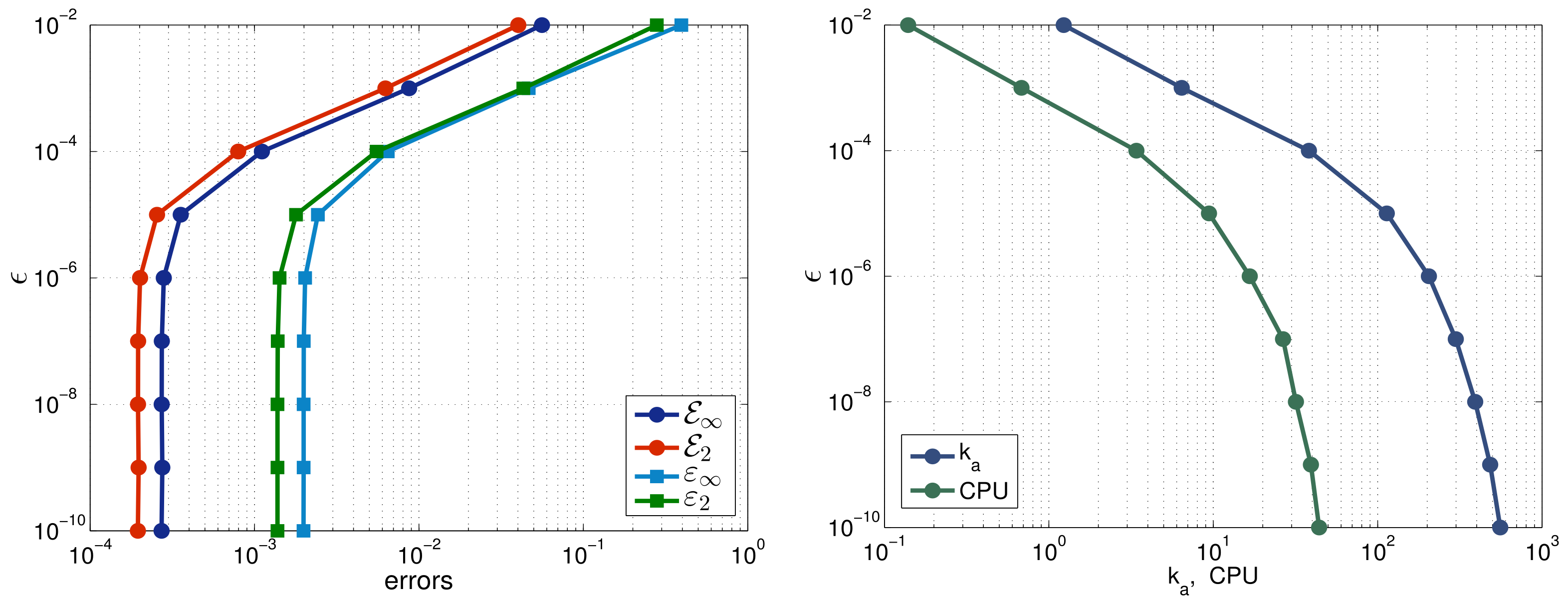
- Numerical method 2 (NM2). This approach is based on the discretization of (11). We approximate this differential equation in the same way as (16), avoiding an iterative procedure, and apply discretization (17) to approximate . The resulting finite difference scheme iswhereThe coefficient matrix of (21) is sparse, but not tridiagonal; see Figure 1. Moreover, the diagonal domination cannot be guaranteed only for a large-space step size . For example, for , we have
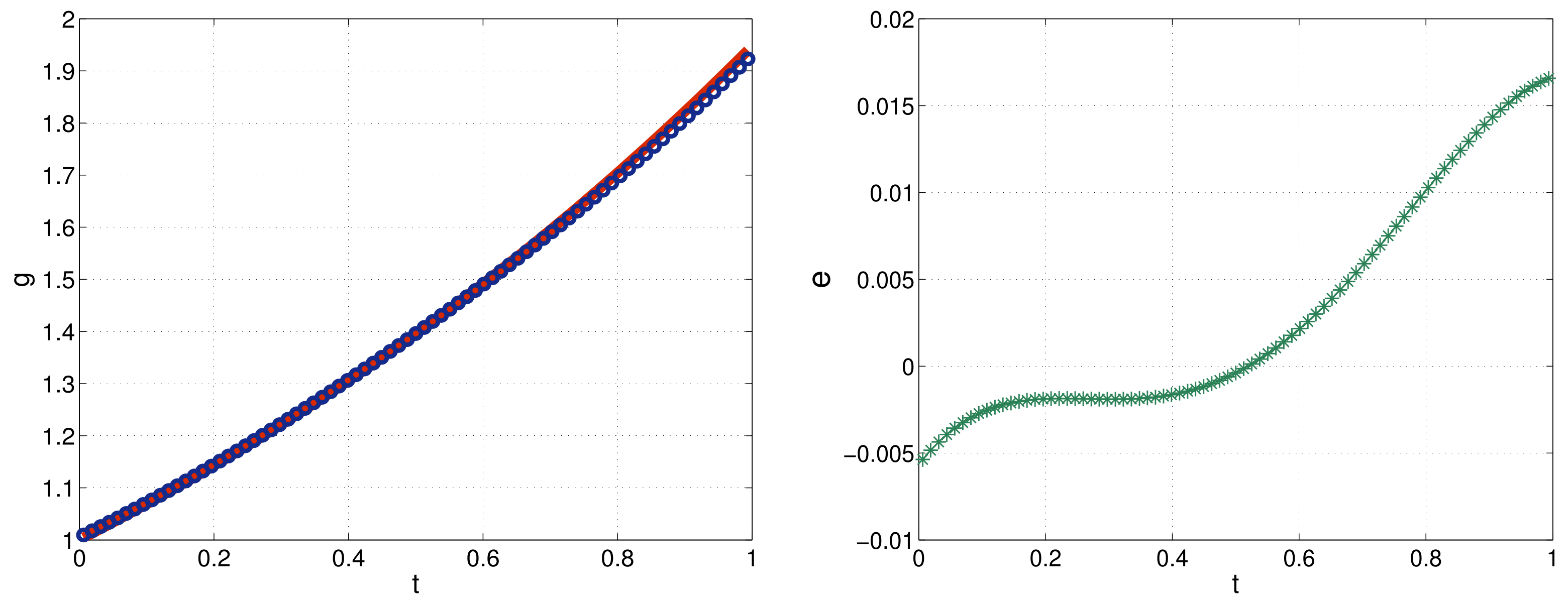
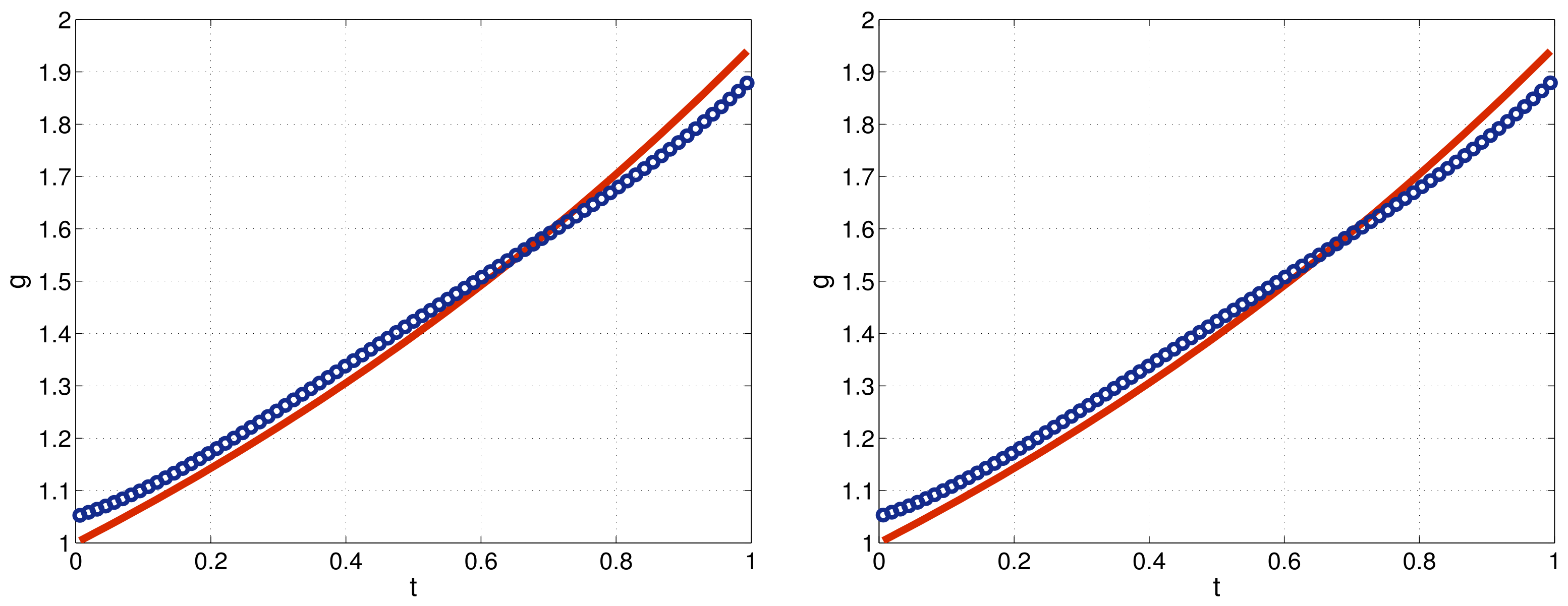
6. Computational Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bona, J.L.; Smith, R. The initial value problem for the Korteweg-de Vries equation. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1975, 278, 555–604. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Bona, J.L.; Mahony, J.J. Model equations for long waves in nonlinear dispersive systems. Philos. Trans. Roy. Soc. Lond. Ser. A 1972, 272, 47. [Google Scholar]
- Larkin, N.A.; Novikov, V.A.; Ianenko, N.N. Nonlinear Equations of ‘Variable Type’; Izdatel’stvo Nauka: Novosibirsk, Russia, 1983; 272p. (In Russian) [Google Scholar]
- Albert, J. On the decay of solutions of the generalized Benjamin-Bona-Mahony equation. J. Math. Anal. Allps. 1989, 141, 527–537. [Google Scholar] [CrossRef]
- Zhang, X.; Zuazua, E. Unique continuation for the linearized Benjamin-Bona-Mahony equation with space-dependent potential. Math. Ann. 2003, 325, 543–582. [Google Scholar] [CrossRef][Green Version]
- Leiva, H.; Sanchez, J.L. Rothe’s fixed point theorem and the controllability of the Benjamin-Bona-Mahony equation with impulses and delay. Appl. Math. 2016, 7, 1748–1764. [Google Scholar] [CrossRef]
- Leiva, H. Controllability of the impulsive functional BBM equation with nonlinear term involving spatial derivative. Syst. Control. Lett. 2017, 109, 12–16. [Google Scholar] [CrossRef]
- Rosier, L.; Zhang, B.-Y. Unique continuation property and control for the Benjamin-Bona-Mahony equation on a periodic domain. J. Differ. Equ. 2013, 254, 141–178. [Google Scholar] [CrossRef]
- Amiraliev, G.M. Difference schemes for problems in the theory of dispersive waves. Dokl. Math. 1991, 42, 235–238. [Google Scholar]
- Berikelashvili, G.; Miranashvili, M. On the convergence of difference schemes for generalized Benjamin-Bona-Mahony equation. Numer. Methods Partial. Differ. Equ. 2013, 30, 301–320. [Google Scholar] [CrossRef]
- Kjelldahl, V.; Mattsson, K. Numerical simulation of the generalized modified Benjamin-Bona-Mahony equation using SBP-SAT in time. J. Comput. Appl. Math. 2025, 459, 116377. [Google Scholar] [CrossRef]
- Saul’ev, V.K.; Chernikov, A.A. A solution by the finite difference method of a nonlinear regularized equation of shallow water. Differ. Uravn. 1983, 19, 1818–1820. [Google Scholar]
- Zheng, Z.; Pang, G.; Ehrhardt, M.; Liu, B. A fast second-order absorbing boundary condition for the linearized Benjamin-Bona-Mahony equation. Numer. Algorithms 2025, 98, 2037–2080. [Google Scholar] [CrossRef]
- Cheng, H.; Wang, X. A high-order linearized difference scheme preserving dissipation property for the 2D Benjamin-Bona-Mahony-Burgers equation. J. Math. Anal. Appl. 2021, 500, 125182. [Google Scholar] [CrossRef]
- Omrani, K.; Ayadi, M. Finite difference discretization of the Benjamin-Bona-Mahony-Burgers equation. Numer. Methods Partial. Differ. Equ. 2008, 24, 239–248. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, L.; Zhang, J. The numerical analysis of two linearized difference schemes for Benjamin-Bona-Mahony-Burgers equation. Numer. Methods Partial. Differ. Equ. 2020, 26, 1790–1810. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiao, J. Spectral method for one dimensional Benjamin-Bona-Mahony-Burgers equation using the transformed generalized Jacobi polynomial. Math. Model. Anal. 2024, 29, 509–524. [Google Scholar] [CrossRef]
- Hasanov, A.H.; Romanov, V.G. Introduction to Inverse Problems for Differential Equations, 1st ed.; Springer: Cham, Switzerland, 2017; 261p. [Google Scholar]
- Isakov, V. Inverse Problems for Partial Differential Equations, 3rd ed.; Springer: Cham, Switzerland, 2017; p. 406. [Google Scholar]
- Kabanikhin, S.I. Inverse and Ill-Posed Problems; DeGruyer: Berlin, Germany, 2011. [Google Scholar]
- Lesnic, D. Inverse Problems with Applications in Science and Engineering; CRC Press: Abingdon, UK, 2021; p. 349. [Google Scholar]
- Prilepko, A.I.; Orlovsky, D.G.; Vasin, I.A. Methods for Solving Inverse Problems in Mathematical Physics; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Samarskii, A.A.; Vabishchevich, P.N. Numerical Methods for Solving Inverse Problems of Mathematical Physics; Walter de Gruyter: Berlin, Germany, 2007; 452p. [Google Scholar]
- Prilepko, A.I.; Kamynin, V.L.; Kostin, A.B. Inverse source problem for parabolic equation with the condition of integral observation in time. J. Inverse Ill-Posed Probl. 2018, 26, 523–539. [Google Scholar] [CrossRef]
- Cannon, J.R.; Lin, Y.; Wang, S. Determination of a control parameter in a parabolic partial differential equation. J. Aust. Math. Soc. Ser. B Appl. Math. 1991, 33, 149–163. [Google Scholar] [CrossRef]
- Cannon, J.R. The solution of the heat equation subject to the specification of energy. Quart. Appl. Math. 1963, 21, 155–160. [Google Scholar] [CrossRef]
- Vasin, I.A.; Kamynin, V.L. Asymptotic behaviour of the solutions of inverse problems for parabolic equations with irregular coefficients. Sb. Math. 1997, 188, 371–387. [Google Scholar] [CrossRef]
- Van Bockstal, K.; Khompysh, K. A time-dependent inverse source problem for a semilinear pseudo-parabolic equation with Neumann boundary condition. arXiv 2025, arXiv:2502.04821. [Google Scholar]
- Fu, J.-L.; Liu, J. Recovery of a potential coefficient in a pseudoparabolic system from nonlocal observation. Appl. Numer. Math. 2023, 184, 121–136. [Google Scholar] [CrossRef]
- Khompysh, K.; Huntul, M.J.; Shazyndayeva, M.K.; Iqbal, M.K. An inverse problem for pseudoparabolic equation: Existence, uniqueness, stability, and numerical analysis. Quaest. Math. 2024, 47, 1979–2001. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Numerical determination of a time-dependent boundary condition for a pseudoparabolic equation from integral observation. Computation 2024, 12, 243. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. The numerical solution of an inverse pseudoparabolic problem with a boundary integral observation. Mathematics 2025, 13, 908. [Google Scholar] [CrossRef]
- Ruzhansky, M.; Serikbaev, D.; Torebek, B.T.; Tokmagambetov, N. Direct and inverse problems for time-fractional pseudo-parabolic equations. Quaest. Math. 2021, 45, 1071–1089. [Google Scholar] [CrossRef]
- Nikolaev, O.Y. Solvability of the linear inverse problem for the pseudoparabolic equation. Math. Notes NEFU 2023, 30, 58–66. [Google Scholar]
- Huntul, M.J.; Khompysh, K.; Shazyndayeva, M.K.; Iqbal, M.K. An inverse source problem for a pseudoparabolic equation with memory. AIMS Math. 2024, 9, 14186–14212. [Google Scholar] [CrossRef]
- Baglan, I.; Kanca, F.; Mishra, V.N. Fourier method for an existence of quasilinear inverse pseudo-parabolic equation. Iran. J. Math. Sci. Inform. 2024, 19, 193–209. [Google Scholar] [CrossRef]
- Bona, J.L.; Tzvetkov, N. Sharp well-posedness for the BBM equation. Discret. Contin. Dyn. Syst. 2009, 23, 1241–1252. [Google Scholar] [CrossRef]
- Belobo, D.B.; Das, T. Solitary and Jacobi elliptic wave solutions of the generalized Benjamin-Bona-Mahony equation. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 270–277. [Google Scholar] [CrossRef]
- Medeiros, L.A.; Miranda, M.M. Weak solutions for a nonlinear dispersive equation. J. Math. Anal. Appl. 1977, 59, 432–441. [Google Scholar] [CrossRef]
- Medeiros, L.A.; Miranda, M.M.; Medeiros, L.A.; Perla Menzala, G. On global solutions of a nonlinear dispersive equation of Sobolev type. Bol. Soc. Bras. Mat 1978, 9, 49–59. [Google Scholar] [CrossRef]
- Medeiros, L.A.; Perla Menzala, G. Existence and uniqueness for periodic solutions of the Benjamin-Bona-Mahony equation. SIAM J. Math. Anal. 1977, 8, 792–799. [Google Scholar] [CrossRef]
- Abdullayev, V.M.; Aida-zade, K.R. Finite-difference methods for solving loaded parabolic equations. Comput. Math. Math. Phys 2016, 56, 93–105. [Google Scholar] [CrossRef]
- Bondarev, E.A.; Voevodin, A.F. A finite difference method for solving initial-boundary value problems for loaded differential and integro-differential equations. Differ. Equ. 2000, 36, 1711–1714. [Google Scholar] [CrossRef]
- Kandilarov, J.D.; Valkov, R.L. A numerical approach for the American call option pricing model. In Numerical Methods and Applications; Dimov, I., Dimova, S., Kolkovska, N., Eds.; NMA 2010. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6046, pp. 453–460. [Google Scholar]
- Koleva, M.N.; Vulkov, L.G. Reconstruction of time-dependent right-hand side in parabolic equations on disjoint domains. J. Phys. Conf. Ser. 2023, 2675, 012025. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Reconstruction of the time-dependent diffusion coefficient in a space-fractional parabolic equation. In New Trends in the Applications of Differential Equations in Sciences; Slavova, A., Ed.; NTADES 2023. Springer Proceedings in Mathematics & Statistics; Springer: Cham, Switzerland, 2024; Volume 449. [Google Scholar]
- Nakhusher, A.M. Loaded Equations and Applications; Nauka: Moscow, Russia, 2012. (In Russian) [Google Scholar]
- Samarskii, A.A. The Theory of Difference Schemes; Nauka: Moscow, Russia; Marcel Dekker, Inc.: New York, NY, USA; Basel, Switzerland, 2001. (In Russian) [Google Scholar]



| I | ||||
|---|---|---|---|---|
| 20 | 5.783 | 4.161 | ||
| 40 | 1.448 | 1.997 | 1.040 | 2.000 |
| 80 | 3.621 | 2.000 | 2.600 | 2.000 |
| 160 | 9.051 | 2.000 | 6.501 | 2.000 |
| 320 | 2.263 | 2.000 | 1.625 | 2.000 |
| N | CPU | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 1.341 | 9.648 | 8.880 | 6.629 | 316.105 | 0.512 | ||||
| 40 | 4.099 | 1.710 | 2.419 | 1.713 | 2.876 | 1.626 | 2.047 | 1.695 | 338.897 | 1.950 |
| 80 | 1.086 | 1.916 | 7.794 | 1.916 | 7.795 | 1.884 | 5.446 | 1.911 | 324.278 | 6.946 |
| 160 | 2.758 | 1.977 | 1.979 | 1.977 | 1.994 | 1.967 | 1.384 | 1.976 | 298.547 | 24.282 |
| 320 | 6.974 | 1.983 | 5.005 | 1.983 | 5.044 | 1.983 | 3.500 | 1.984 | 270.429 | 87.645 |
| N | CPU | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 20 | 1.341 | 9.647 | 8.880 | 6.628 | 0.019 | ||||
| 40 | 4.099 | 1.710 | 2.941 | 1.714 | 2.876 | 1.627 | 2.047 | 1.695 | 0.083 |
| 80 | 1.085 | 1.917 | 7.788 | 1.917 | 7.790 | 1.884 | 5.442 | 1.911 | 0.242 |
| 160 | 2.749 | 1.981 | 1.973 | 1.981 | 1.989 | 1.969 | 1.380 | 1.979 | 0.886 |
| 320 | 6.889 | 1.997 | 4.944 | 1.997 | 4.999 | 1.993 | 3.459 | 1.996 | 3.355 |
| 0.003 | 9.053 | 6.516 | 1.349 | 6.142 | 139.886 |
| 0.005 | 7.308 | 5.274 | 1.701 | 7.295 | 141.532 |
| 0.01 | 3.034 | 2.186 | 2.580 | 1.174 | 142.321 |
| 0.03 | 1.487 | 1.033 | 6.094 | 3.365 | 144.514 |
| 0.003 | 8.225 | 5.922 | 1.306 | 5.854 |
| 0.005 | 6.481 | 4.680 | 1.658 | 7.106 |
| 0.01 | 2.249 | 1.603 | 2.536 | 1.170 |
| 0.03 | 1.569 | 1.093 | 6.051 | 3.374 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koleva, M.N.; Vulkov, L.G. Numerical Determination of a Time-Dependent Source in a Modified Benjamin–Bona–Mahony Equation. Mathematics 2025, 13, 1618. https://doi.org/10.3390/math13101618
Koleva MN, Vulkov LG. Numerical Determination of a Time-Dependent Source in a Modified Benjamin–Bona–Mahony Equation. Mathematics. 2025; 13(10):1618. https://doi.org/10.3390/math13101618
Chicago/Turabian StyleKoleva, Miglena N., and Lubin G. Vulkov. 2025. "Numerical Determination of a Time-Dependent Source in a Modified Benjamin–Bona–Mahony Equation" Mathematics 13, no. 10: 1618. https://doi.org/10.3390/math13101618
APA StyleKoleva, M. N., & Vulkov, L. G. (2025). Numerical Determination of a Time-Dependent Source in a Modified Benjamin–Bona–Mahony Equation. Mathematics, 13(10), 1618. https://doi.org/10.3390/math13101618






