1. Introduction
The Battle of Sexes is a classical model in the game theory literature. In its standard form, this game provides a coordination problem between two players who have conflicting preferences. Players must choose between two alternatives (often represented as “going to the opera” vs. “going to the boxing match”), each preferring one to the other but both desiring coordination to avoid a complete loss of payoffs. The game has a key characteristic: it has multiple equilibria and (as the Battle of Sexes is a generic game) all the equilibria are stable with respect to perturbations so that no refinement concept can be effective. Precisely, we refer to the classical refinements based on properties of stability with respect to perturbations, such as trembling hand perfection [
1] or properness [
2]; see also [
3] for an extensive survey on Nash equilibrium refinements. As the multiplicity of equilibria makes coordination challenging, different approaches have been proposed as selection mechanisms, such as pre-play communication, cheap talk, and the focal point theory.
From another perspective, an interesting issue considered in the literature is the impact of the psychological traits of players on the interaction described by the Battle of Sexes game. In [
4], the Battle of Sexes game was used to model and test behaviors in individuals with personality disorders. The test concerns dominant (i.e., prioritizing personal status) and submissive (i.e., prioritizing the relationship above their own individual desires) behaviors in individuals with narcissistic and dependent traits. It emerged that participants’ behavior was affected by personal traits. The behavior may be influenced by an increase in basic individuals’ fears or in the accuracy of underlying beliefs. In [
5], weighted Rawlsian preferences were used and applied to the Battle of Sexes game in order to accommodate concerns that players may have about the payoff of the opponent. It emerged that the Nash equilibria are strongly affected by these kinds of player concerns. When one of the players is pro-social, the Nash equilibrium in mixed strategies of the original Battle of Sexes game is not an equilibrium anymore, regardless of the other player’s attitude.
The present paper aims to provide an alternative insight into the influence of feelings on the Battle of Sexes game by considering the consequences of the sentiment of guilt aversion. This psychological trait arises when agents’ utility is negatively affected by harming other individuals, and seems to be particularly suited for the Battle of Sexes, as players in this game have incentives to coordinate their choices with their opponents. In particular, we refer to the formal model of guilt aversion by [
6,
7,
8], in which a guilt-averse agent (say Bob) has a disutility if he believes that his opponent (say Ann) is disappointed by his play, as she receives a lower payoff than the one she originally expected given her beliefs. The approach described previously is one of the possible models in which players’ utilities may be affected by a psychological term (see [
8,
9,
10,
11,
12]). Standard game theory models cannot be exploited to cover this type of situation, as highlighted in the pioneering paper by [
13]. Indeed, a wide range of phenomena can be better explained by letting the payoff functions depend explicitly on hierarchies of belief; that is, the utilities depend not only on what every player does, but also on what that player thinks every other player believes as well as on what they think every other player believes the others believe, and so forth. Therefore, psychological game theory must be taken into account, meaning that the classical Nash equilibrium concept must be replaced by the psychological Nash equilibrium. Different theoretical frameworks have been examined in the literature, including both static and dynamic psychological games ([
7,
8,
13,
14,
15,
16]) as well as specific models for different kinds of feelings ([
6,
17,
18,
19], to mention just a few).
In this work, we construct a psychological Battle of Sexes game in which a player is sensitive to guilt aversion. We then characterize the psychological Nash equilibria of the game. Additionally, we investigate whether the results are robust when beliefs are allowed to be ambiguous. So-called strategic ambiguity arises in classical games when players have ambiguous (first-order) beliefs about their opponents’ play, and consistently affects players’ behavior and equilibria. The effects of strategic ambiguity in games are well-established both theoretically ([
20,
21,
22,
23,
24,
25]) and empirically ([
26,
27,
28,
29,
30]). Several papers have already investigated the effects of strategic ambiguity in the Battle of Sexes game (see [
22,
25,
29]); more details are provided in
Section 5. The paper by De Marco et al. [
31] constitutes a first step in which ambiguity theory and psychological game theory have been merged into a unique model. Here, we look at ambiguity in the associated psychological Battle of Sexes game with guilt aversion and apply the general tools from [
31], with the psychological Nash equilibrium concept generalized to cases in which the entire hierarchy of beliefs might be ambiguous. In particular, in the present paper we characterize psychological Nash equilibria under ambiguity in the Battle of Sexes game in the case where players have an optimistic attitude towards ambiguity (corresponding to max–max preferences) as well as in the pessimistic case corresponding to max–min preferences; by contrast, [
31] only considered max–min preferences.
The results from both the non-ambiguous and ambiguous models confirm that the equilibria of the Battle of Sexes game are extremely robust in the case of guilt aversion. In particular, the two pure strategy equilibria are not affected at all by the presence of a guilt-averse player, while in the mixed strategy equilibrium only the strategy of the player that has no psychological utility (the non-psychological player, Ann) is affected by guilt aversion. In the non-ambiguous case, the equilibrium strategy of the non-psychological player prescribes that she will play the less preferred strategy with a higher probability than without any psychological effect. Moreover, the former probability increases as the sensitivity to guilt of the psychological player (Bob) increases; in other words, Ann is willing to accept a lower expected utility in order to compensate for Bob’s disutility due to guilt aversion. Nevertheless, in equilibrium, the non-psychological player (Ann) will always play her most preferred strategy with a higher probability than the less-preferred strategy. The presence of ambiguity only affects the mixed strategy equilibrium. With a pessimistic attitude on the part of Bob, Ann will play the less preferred strategy with a higher probability than she would have without ambiguity, regardless of Bob’s sensitivity to guilt. Moreover, Ann will play her most preferred strategy with a lower probability than the less-preferred one if Bob’s sensitivity to guilt is sufficiently high. With an optimistic attitude on the part of Bob, the mixed strategy equilibrium is destroyed by the ambiguity, as Bob’s optimal strategy can only be pure.
Our main results can be summarized as follows:
- -
We construct a psychological version of the Battle of Sexes game with guilt aversion.
- -
We characterize the equilibria of the psychological game.
- -
We introduce ambiguity and characterize the equilibria in cases with max–min and max–max preferences, comparing the set of solutions in the different cases.
- -
We show the changes in the proposed model when introducing classical strategic ambiguity.
- -
In the appendix, we present complementary results concerning (A) an analysis of equilibria in a game in which both players are guilt averse, and (B) a characterization of the equilibria in the case of max–min preferences in a simplified model.
The paper is organized as follows:
Section 2 illustrates the main concepts of equilibrium in psychological games that are useful for our analysis; in
Section 3, the Battle of Sexes game under guilt aversion is introduced and the characterization of equilibria is presented;
Section 4 is devoted to ambiguity and equilibria;
Section 5 discusses the differences between our proposed formulation and classical strategic ambiguity;
Section 6 concludes the paper;
Appendix A presents the case in which both players are guilt-averse; finally,
Appendix B examines the issue of
max–min preferences.
2. Preliminaries
In order to include psychological aspects and ambiguity in the Battle of Sexes game, we take into account the model for static ambiguous psychological games introduced in [
31]. Consider a finite set of players
. For each player
,
denotes the finite set of pure strategies of player
i. Following the standard notation,
represents the set of strategy profiles and
represents the set of strategy profiles of
i’s opponents. The set
denotes the set of mixed strategies of player
i, while
and
respectively denote the set of mixed strategy profiles and the set of mixed strategies of
i’s opponents. We often use the notation
with
and
to indicate the mixed strategies profile
.
2.1. Beliefs Structure
The hierarchical structure of beliefs is constructed in the following way: given a set
X,
denotes the set of probability measures on
X; then,
and so on, where
for every player
i and for every
.
Therefore, the
k-th order beliefs of player
i are represented by a probability measure over other players’ mixed strategies and beliefs up to order
. In the end, the set of hierarchies of beliefs for player
i is
the elements of which are infinite hierarchies of beliefs
Hence, player
i’s beliefs represent (via probability measures) what strategy player
i believes the others will play, what player
i thinks the other players believe their opponents will play, and so on. Because
is compact for every
and can be metrized as a separable metric space, the set
is in turn, metrizable and separable. Moreover, it turns out to be compact under the topology induced by this metric; see [
31] for further details.
We restrict our attention to the subset of collectively coherent beliefs
, which is the set of beliefs of player
i about which he is sure (i.e., with probability equal to 1) that it is common knowledge that the beliefs are coherent. Specifically, a belief
is said to be coherent if the following holds for every
:
The set
is compact as well (the detailed construction of the set of collectively coherent beliefs can be found in [
13], and the proof of its compactness in [
31]); therefore, a standard psychological game is described by
, where for every
the utility functions
have the form
([
13]).
In the present work, we follow the more general model of [
31] in which ambiguity of beliefs is allowed, i.e., the belief of player
i is represented by a compact subset
. This choice enables us to cover the case in which agents have ambiguous beliefs about other players’ actions and beliefs, e.g., agent
i does not have a precise belief
, as in [
13], but rather knows that the belief can be any
. In order to compare ambiguous alternatives, we take into account two classical approaches: first, in line with [
31], max–min preferences are considered, which correspond to a pessimistic attitude towards ambiguity. In particular, each agent
i is endowed with a utility function
defined by
where
denotes the set of all compact subsets of
. Consequently, a pessimistic psychological game under ambiguity is described by
The second approach covers optimistic behavior with respect to ambiguity, exploiting the max–max preferences. In this case, each agent
i is endowed with a utility function
defined by
An optimistic psychological game under ambiguity is then described by
This latter model is actually included in the work [
32], where the more general structure of Hurwicz preferences was considered.
2.2. Equilibrium Notions
The notion of psychological Nash equilibrium introduced in [
13] is based on the idea that the entire hierarchy of beliefs must be correct in equilibrium. More precisely, each player is equipped with a function
which, for every
, selects the hierarchy of beliefs
in which player
i believes (with probability 1) that his opponents follow the mixed strategy profile
, that each opponent
believes that his opponents follow
, that each opponent
believes that his opponents believe that the others follow the mixed strategy profile
, and so on. Then, a psychological Nash equilibrium is defined as a pair
where
with
and
such that for every player
i,
- (i)
, and
-
(ii)
for every .
We can also say that is a psychological Nash equilibrium of the game .
In the case of ambiguity, the function
that maps strategy profiles to correct beliefs is replaced by a set-valued map (called ambiguous belief correspondence) that maps strategy profiles to the subsets of those beliefs that player
i perceives to be consistent with the corresponding strategy profile. In detail, each agent
i is now endowed with a set-valued map
such that each set
is not empty and compact, i.e., for every
,
Each subset provides the set of beliefs that player i perceives to be consistent given the strategy profile .
A psychological Nash equilibrium under ambiguity (henceforth, PNEUA [
31]) of game
with belief correspondences
is a pair
where
with
and
such that for every player
i,
- (i)
, and
-
(ii)
for every .
In this case, we can also say that is a psychological Nash equilibrium under ambiguity. Note also that the concept of psychological Nash equilibrium under ambiguity is -dependent in the sense that same games with different correspondences may have different equilibria.
Similarly, an optimistic psychological Nash equilibrium under ambiguity (henceforth, OPNEUA; see [
32] for the general case of
max–min preferences) of game
is analogously defined; it is sufficient to substitute
for the pessimistic utility function
in condition (ii).
2.3. Summary Utility Functions and Best Replies
PNEUA and OPNEUA can be characterized as classical Nash equilibria via the functions
, called summary utility functions, which are defined by
Indeed, as shown in Lemma 2.8 in [
31],
is a psychological Nash equilibrium under ambiguity if and only if for every
it is the case that
or equivalently, if and only if for every
it is the case that
with
Analogously, as shown in Lemma 1 in [
32] for
,
is an optimistic psychological Nash equilibrium under ambiguity if and only if for every
it is the case that
or, equivalently, if and only if for every
it is the case that
with
A similar formulation was first obtained by Geanakoplos et al. [
13] for standard psychological Nash equilibria; in that case, the summary utility functions are defined as follows:
Then,
is a psychological Nash equilibrium if and only if for every
it is the case that
or equivalently,
with
Finally, note that in the case with no ambiguity and correct beliefs, i.e., when reduces to , the correspondences and coincide with . If in addition there are no psychological terms in the utility function of player i (which then coincides with the classical expected utility), and reduce to the classical best reply correspondence.
3. Battle of Sexes Game with Guilt Aversion
In this section, we analyze the Battle of Sexes game while introducing the sentiment of guilt in the payoff of Player 2 (Bob), who feels guilty about letting Player 1 (Ann) down. Our results shed light on the fact that the sentiment of guilt generated by disappointing the other player’s expectation has a significant impact on the completely mixed equilibrium strategy of the standard game, while the two pure strategy equilibria are robust with respect to this kind of preference’s perturbation. Moreover, it turns out that in the former case the equilibrium mixed strategy played by Ann (whose payoff is not affected by any psychological aspect) actually depends on Bob’s sensitivity to guilt.
3.1. The Standard Game
The Battle of Sexes game in its standard form consists of the following: Player 1 (Ann) and Player 2 (Bob) have to choose which event to attend for the evening, going to the opera or to a boxing match. Thus, the strategy sets are
. Bob prefers the boxing match, while Ann prefers the opera, although they both prefer to go out together. The matrix form is shown below.
| Player 2 | | |
| Player 1 | |
| | |
| | |
A generic mixed strategy for Player 1 (Ann) is , where as usual (with an abuse of notation), and . Similarly, a generic mixed strategy for Player 2 (Bob) is , where (with an abuse of notation) and . Therefore, denotes a generic strategy profile. Note that the set of mixed strategies reduces to and . The term (resp. ) denotes the classical expected payoff of Player 1 (resp. Player 2) for every . For the sake of simplicity, we denote with the generic pure strategy of Ann, where means that Ann plays and means that Ann plays . Similarly, we denote with the generic pure strategy of Bob, where means that Bob plays and means that Bob plays .
In this form, the game has three equilibria:
: Both players choose the boxing match.
: Both players choose the opera.
: Both players choose at random.
3.2. Modeling Guilt Aversion
Guilt aversion arises when harming others, and can be explained by many reasons; however, it is often a consequence of letting others down. This is the perspective mainly considered in the theoretical papers devoted to this issue. We refer to the models in [
6,
7,
8], in which it is said that player
j is let down if their actual material payoff
received after playing is lower than the initial expected payoff
. Therefore, the disappointment of player
j is provided by
Given the strategy profile
, player
i’s beliefs
, and player
i’s guilt sensitivity parameter
, the guilt-dependent utility of player
i can be constructed as follows:
where
represents player
i’s expectation of player
j’s disappointment. In particular,
represents what player
i believes is the payoff that player
j initially expects to receive, while
is what player
j actually receives.
We build on this guilt aversion model and consider a variation of the Battle of Sexes game in which Bob feels guilty about letting Ann down. On the other hand, Ann is not affected by psychological factors. Let denote the mixed strategy of the players; then, is the expectation of Ann’s first-order beliefs about Bob’s strategy choice q and is the expectation of Bob’s second-order beliefs about the first-order beliefs of Ann . The term denotes Bob’s sensitivity to guilt.
Now, recall that
are the classical expected utility functions. If a pure strategy profile is played, say
with
, then Bob believes that Ann’s initial expected payoff is
, which corresponds to Ann choosing
and Bob choosing randomly with probabilities
and
; more precisely,
Then, for every pure strategy profile
, Bob’s utility is
which leads to the psychological game shown below.
| Player 2 |
Boxing
|
Opera
|
| Player 1 | |
|
Boxing
| | |
|
Opera
| | |
3.3. Psychological Nash Equilibria
We now analyze the psychological Nash equilibria of the game introduced above. Ann’s expected utility does not depend on any psychological term; thus, her best reply correspondence coincides with that of the standard game:
On the other hand, Bob’s expected utility is computed from the psychological game, as follows:
A precise condition for Bob’s correct belief would require many more details that are irrelevant for the present model. The idea is that Bob’s hierarchy of belief belonging to
should include a second-order belief for which the expectation
corresponds to
q. As the expectation
is the unique psychological term that affects Bob’s utility, there is no need for us to characterize Bob’s entire hierarchy of beliefs. For our purposes, given a mixed strategy profile
, the correct belief function
requires that the corresponding second-order belief
of Bob must coincide with
q, i.e.,
. It follows that the summary utility function defined in (
8) is
for all
.
Therefore, Bob’s best reply, constructed as in (
10), takes the form of the correspondence
defined by
The next proposition characterizes Bob’s best reply and the psychological Nash equilibria of the game.
Proposition 1. For every , Bob’s best reply correspondence is provided by the following:whereand the function is strictly decreasing with Therefore, the Battle of Sexes game with guilt aversion has the following PNE:
- (i)
,
- (ii)
,
- (iii)
.
Proof. From Equation (
13), we know that Bob’s expected utility given any mixed strategy
p of Player 1 (Ann) is as follows:
Equation (
15) ensures that
if and only if
Consequently, we need to maximize with respect to y under the condition that must be consistent with the maximum point.
First, we observe the following:
- (1)
If
then
is strictly increasing; therefore, it is maximized only by
. The consistency condition with the maximum for correct beliefs implies that
; thus, it follows that (
18) becomes
Hence, when
,
and
.
In this case, there cannot be any other best reply.
- (2)
If
then
is strictly decreasing and is maximized only by
. In this case, the consistency condition with the maximum for correct beliefs implies that
; thus, it follows that (
19) becomes
Hence, for
, it follows that
and
.
In this case, there cannot be any other best reply.
- (3)
If
then
; therefore, every
maximizes
. However, (
20) implies that
Thus, in this case
is Bob’s unique best reply provided that
. It can be easily checked that
that (
17) holds, and that
is strictly decreasing in the interval
and attains only the values in
.
Summarizing, for
,
and
.
In this case, there cannot be any other best reply.
From the previous arguments, the characterization of
provided in (
16) follows directly.
Finally, from Ann’s best reply as described in (
12), it follows that
and
are PNE. Moreover, only one other equilibrium exists in completely mixed strategies. In this equilibrium, Bob must play
as the best reply to Ann’s mixed strategy
. We find
as follows:
Hence, the third equilibrium is . □
3.4. Equilibrium Analysis
Previous results substantially confirm that the equilibria of this game are stable with respect to perturbations. It is well known that the Battle of Sexes is a generic game; as such, all of the equilibria are stable with respect to classical perturbations and no refinement concept (such as trembling hand perfection [
1] or properness [
2]; see also [
3] for an extensive survey on Nash equilibrium refinements) can be effective. Moreover, joint deviations are not Pareto-improving, regardless of the equilibrium. In our case, the presence of guilt aversion does not affect the two pure strategy equilibria of the standard game, while the completely mixed strategy equilibrium
of the standard game is the limit point of the equilibrium
of the game when guilt aversion vanishes (that is,
converges to 0).
Nevertheless, there are interesting insights arising from the mixed strategy equilibrium. First of all, Bob’s sensitivity to guilt affects only the equilibrium strategy of Ann. While this result might seem surprising, it is consistent with the previous literature; the paper by [
8] analyzed a sequential trust game with guilt aversion, finding that
affects only the equilibrium strategy of the player with no guilty feelings. Moreover, as the function
is strictly increasing, in equilibrium Ann will play Boxing with a higher probability regarding the case with
, meaning that she has lower expected utility to compensate for Bob’s disutility due to guilty feelings. However,
increases to 1/2 when
, meaning that Ann will never play Boxing with a probability greater then that of Opera.
4. Equilibria Under Ambiguity
In this section, we consider the case in which Bob has ambiguous second-order beliefs, then analyze the corresponding effect on equilibria. In particular, we consider the impact of full ignorance, i.e., Bob completely ignores what Ann believes his choice will be. From the mathematical point of view, Bob is endowed with a belief correspondence that does not impose any restriction on his second-order beliefs, meaning that can be any element in the interval .
4.1. Pessimistic Attitude
In the first instance, we analyze the consequences of Bob’s pessimistic attitude towards ambiguous beliefs. In this case, the summary utility function of Bob as defined in (
2) takes the following form:
for all
.
Bob’s best reply, defined in (
5), takes the form of the correspondence
, where for every
it is the case that
The next proposition provides the characterization of Bob’s pessimistic best reply correspondence and the corresponding equilibria in the case of ambiguity.
Proposition 2. Bob’s best reply correspondence is provided by the following: Therefore, the Battle of Sexes game with guilt aversion provides the following PNEUA:
- -
If :
- (i)
,
- (ii)
,
- (iii)
.
- -
If :
- (i)
,
- (ii)
,
- (iii)
.
Proof. From the characterization (
22) of the summary utility functions along with the formula of Bob’s expected utility function (
13), we have
Then, for every
, we get:
Consequently, for every
we have
To compute the best reply
, recall that
Now:
- (1)
Therefore:
- -
for , that is, , the function is strictly increasing in .
- -
for , that is, , the function is strictly decreasing in .
- -
for , that is, , the function is constant in .
- (2)
Therefore:
- -
for , that is, , the function is strictly increasing in .
- -
for , that is, , the function is strictly decreasing in .
- -
for , that is, , the function is constant in .
Recall that (
21) holds, that is,
It follows that:
- (a)
If
, then the function
is strictly decreasing in the interval
and attains its maximum in
. Therefore,
- (b)
If
, then the function
is constant and equal to
in the interval
and strictly decreasing in the interval
. Then, every
is a maximum point; thus, for every
, we have
- (c)
If
, then the function
is strictly increasing in
and strictly decreasing in
. Hence, the unique maximum point is attained at
. Therefore,
- (d)
If
, then the function
is increasing for
while it is constant and equal to
in the interval
. This means that every
is a maximum point. Thus, for every
,
- (e)
If
, then the function
is strictly increasing for
and attains its maximum in
. Therefore,
The previous arguments immediately imply that the best reply
satisfies (
24).
Next, we look at the equilibria of the game from the previous characterization of
and from the characterization of
provided in (
12). It immediately follows that
and
are PNEUA. Moreover, there are no other equilibria in which one of the two players chooses a pure strategy, as
and
are both singletons.
Here, we show that there is another equilibrium in completely mixed strategies. In this kind of equilibrium, Bob’s strategy can only be , as it consists of Bob’s unique completely mixed strategy contained in Ann’s best reply set. Note also that every mixed strategy for Ann is a best reply to . Thus, we only need to find some strategy for Ann where Bob’s best reply contains . Now,
- (i)
and , because in these cases and , respectively, and cannot be a best reply to .
- (ii)
, because in this case , while for every ; thus, cannot be a best reply to .
- (iii)
If
, then (
24) implies that
is a best reply to
if and only if
, which is equivalent to
. However,
thus,
is PNEUA if and only if
- (iv)
If
, then
is a best reply to
if and only if
However,
hence,
is PNEUA if and only if
From the previous arguments, the assertion immediately follows. □
4.2. Equilibrium Analysis
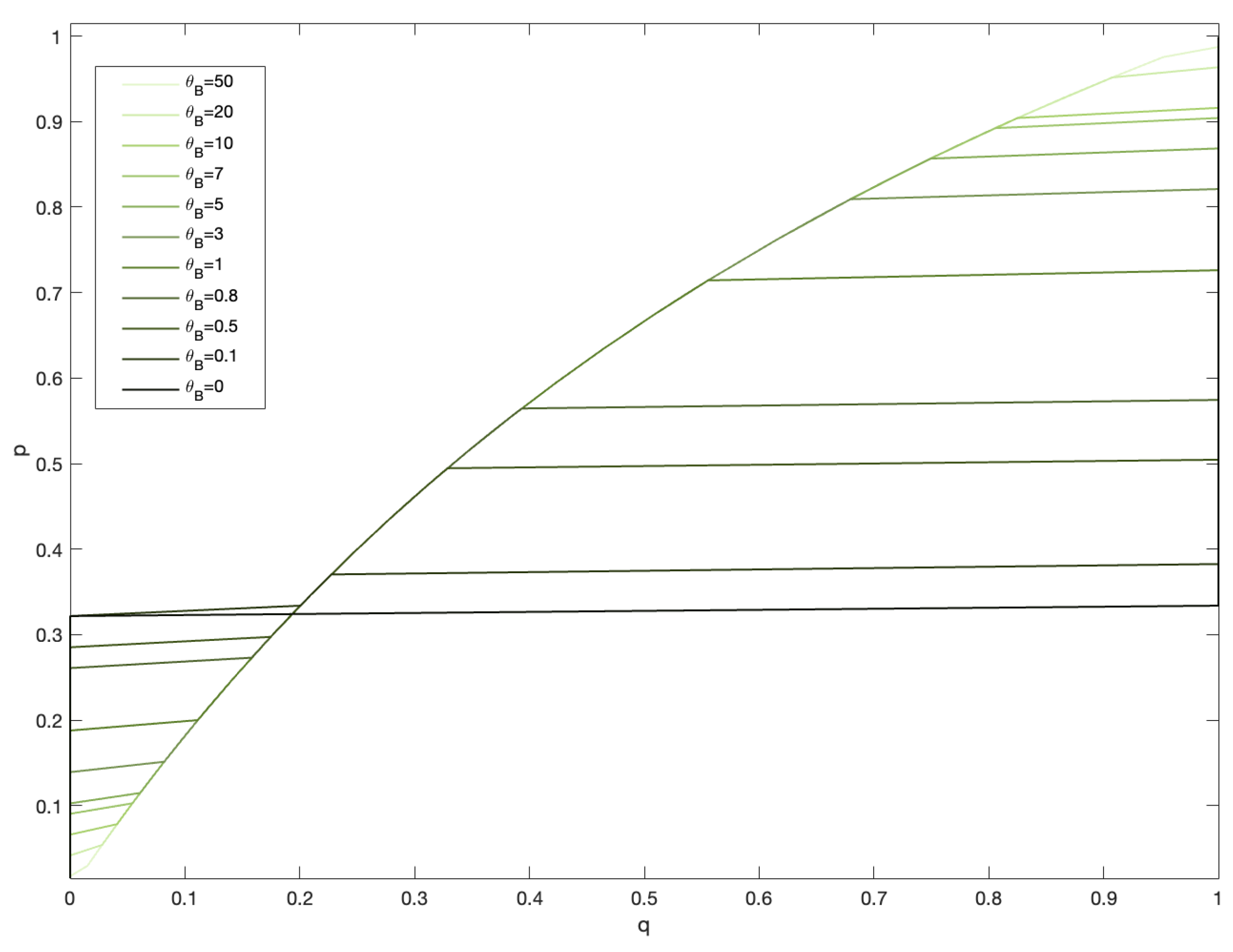
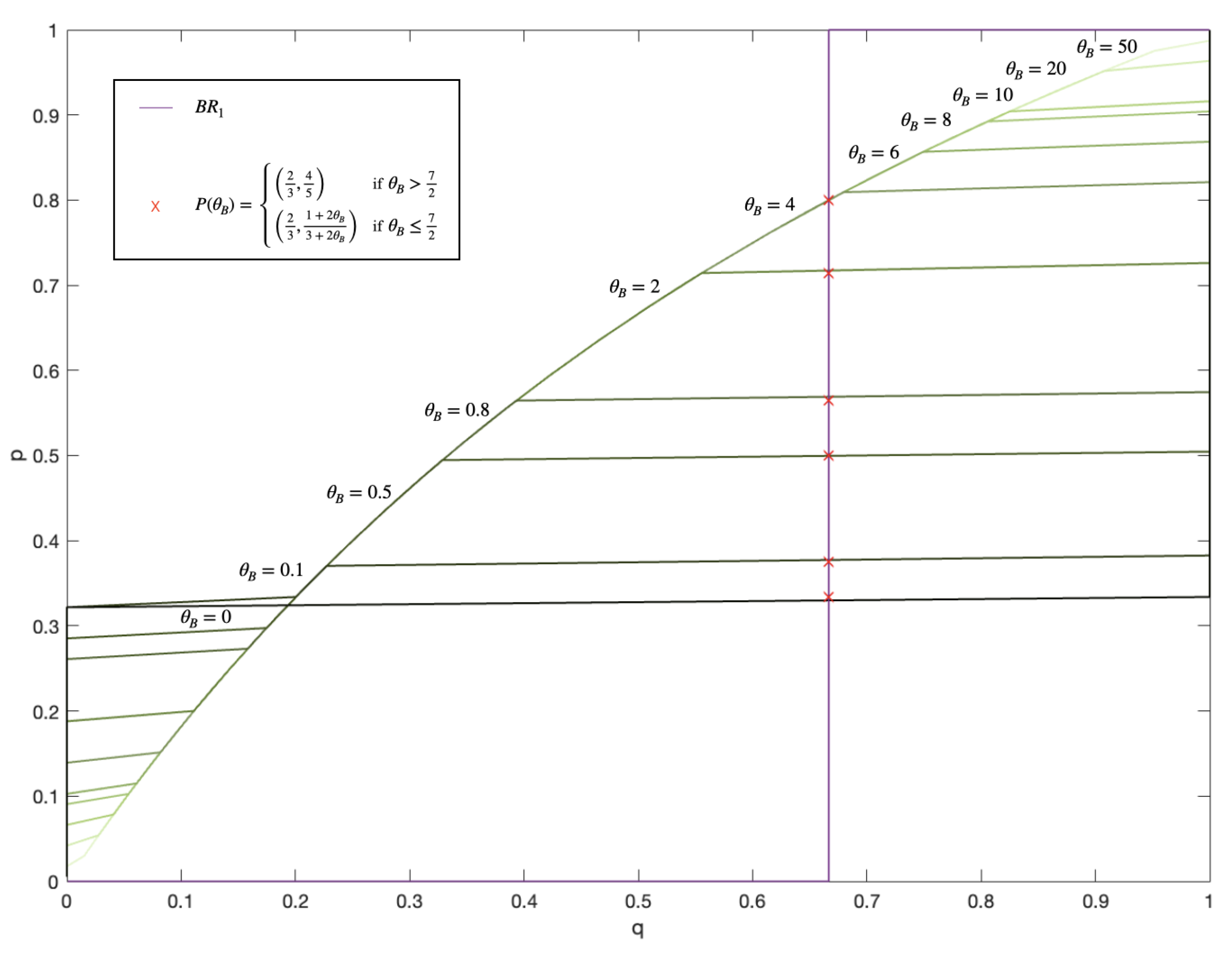
Figure 1 shows how Bob’s best reply correspondence varies depending on the parameter
. In particular, the previous proposition shows that ambiguity does not affect the two pure strategy equilibria. However, it can be easily checked that
for every
. This implies that in the mixed strategy equilibrium Ann must play her less-preferred alternative (Boxing) with a probability that is larger than in the non-ambiguous case; it follows that ambiguity requires Ann to reduce her expected utility more, as Bob’s disutility from guilt is larger in the ambiguous case. Moreover, in the non-ambiguous case Ann will never play Boxing with a probability larger than that of Opera; however, in the ambiguous case Ann will play Boxing with a probability larger than 1/2 when
. This probability is strictly increasing in
until
reaches value 7/2, after which it becomes constant and equal to 4/5, as illustrated in
Figure 2. This implies that Ann will always have an expected utility that is larger than she receives by playing Boxing with probability 1. In summary, just as for the non-ambiguous case, the equilibria of the Battle of Sexes game are rather robust with respect to the effects of guilt aversion. Nevertheless, the equilibrium in mixed strategy games is substantially perturbed when
is sufficiently large, and the perturbation is always greater than the corresponding one in the non-ambiguous case.
4.3. Optimistic Attitude
In this section, we analyze the consequences of Bob’s optimistic attitude towards ambiguous beliefs. Given Bob’s optimistic behavior, the summary utility function of Bob is defined in (
3), and takes the form
for all
.
In this case, Bob’s best reply, as defined in (
5), takes the form of the correspondence
, where for every
we have
The next proposition provides the characterization of Bob’s optimistic best reply correspondence and the corresponding equilibria in the case with ambiguity.
Proposition 3. Bob’s optimistic best reply correspondence is provided by the following: Therefore, the Battle of Sexes game with guilt aversion provides the following OPNEUA:
- (i)
,
- (ii)
.
Proof. From the characterization (
26) of the summary utility functions and the formula of Bob’s expected utility function (
13), we obtain
Then, for every
, we obtain
Consequently, for every
, we have
To compute the best reply
, recall that
Now:
- (1)
Therefore:
- -
for , that is, , the function is strictly increasing in .
- -
for , that is, , the function is strictly decreasing in .
- -
for , that is, , the function is constant in .
- (2)
Therefore:
- -
for , that is, , the function is strictly increasing in .
- -
for , that is, , the function is strictly decreasing in .
- -
for , that is, , the function is constant in .
Recall that (
21) holds and that it can be easily checked that
It follows that:
- (a)
If
, then the function
is strictly decreasing in the interval
and attains its maximum in
. Therefore,
- (b)
If , then the function is strictly decreasing in the interval and constant and equal to in the interval . Then, the unique maximum point is again attained in .
- (c)
If
, then the function
is strictly decreasing in
and strictly increasing in
. Then,
and
are the only possible best replies. For every
,
then,
It immediately follows that
If
, then
If
, then
- (d)
If
, then the function
is constant in the interval
, while it is strictly increasing in the interval
. This means that
is the unique maximum point; thus,
- (e)
If
, then the function
is strictly increasing for
and attains its maximum in
. Therefore,
The previous arguments immediately imply that the best reply
satisfies (
28).
Now, we can look at the equilibria of the game. From the previous characterization of
and the characterization of
provided in (
12), it immediately follows that
and
are OPNEUA. Moreover there are no other equilibria, as
and
are both singletons.
From the previous arguments, the assertion of Proposition 3 immediately follows. □
4.4. Equilibrium Analysis
An optimistic attitude on the part of the psychological player (Bob) significantly alters the scenario. Regardless of Bob’s sensitivity parameter
, his best reply correspondence
does not contain any mixed strategy regardless of Ann’s strategy; in other words, guilt aversion means that it is never optimal for Bob to choose randomly. As a consequence, the mixed strategy equilibrium is destroyed by the presence of ambiguity. From the mathematical point of view, it turns out that the max operator used in the definition of optimistic preferences makes the utility function convex but not quasi-concave in general; thus, the best reply correspondence is not necessarily convex-valued (see also Remark 1 below for a more general perspective). Lack of convexity in the images of the best reply correspondence is the reason for the equilibrium in mixed strategies being destroyed in this model. However, in [
32] it was shown that optimistic preferences do not always restrict the set of equilibria, as in some cases they simply provide different equilibria with respect to pessimistic preferences. More generally, the literature on strategic ambiguity (without psychological utilities) shows that optimistic preferences might enlarge the set of equilibria with respect to the non-ambiguous or pessimistic cases.
Finally, the previous proposition also highlights the fact that the mixed strategy equilibrium of the original game cannot be approached by a sequence of equilibria in the psychological games, as the sensitivity converges to 0 when the psychological player is optimistic. This is an example of the lack of lower semi-continuity of psychological equilibrium correspondence in the case of ambiguity, which could not be observed in the non-ambiguous or pessimistic cases.
Remark 1. The previous analysis shows that the existence of a mixed equilibrium in the Battle of Sexes game with guilt aversion might be lost when deviating from the classical pessimistic preferences (max–min). The literature shows that intermediate attitudes towards ambiguity can be modeled by considering α-MEU preferences (defined in [32]). In α-MEU preferences, each ambiguous alternative is evaluated by a convex combination of the worst-case (with weight α) and best-case (with weight ) scenarios. Hence, the parameter characterizes the players’ respective attitudes towards ambiguity. In Appendix B, we provide a simplified model (in the case with ) and show that the value acts as a threshold level for the survival of the mixed strategy equilibrium. Indeed, when , the mixed strategies equilibrium exists, while when it does not. The reason for this is that the best reply correspondence for is not convex valued, which is a consequence of the preferences’ lack of convexity. We point out that, for the same reason, we can obtain a complete lack of existence on the part of psychological Nash equilibria under ambiguity, as shown in [32]. 4.5. On the Definition of Guilt Aversion
In the literature dealing with guilt aversion, extensive-form games are usually considered; in that framework, two concepts of guilt aversion arise ([
6]), each involving a different order of beliefs. A player
i (Bob) is said to be affected by simple guilt towards player
j (Ann) if he is concerned about letting her down, while Bob is instead said to be affected by guilt from blame if he dislikes being blamed by Ann. In the first case, Bob is worried about the consequences of his actions on the payoff of Ann, and feels guilty about letting her down; in the second case, Bob’s preferences are affected by what he believes she will believe about his intention to let her down, meaning that his guilty sentiment is a consequence of Ann’s belief regarding his behavior. As shown in [
6], the notions of simple guilt and guilt from blame coincide in static games such as the Battle of Sexes; thus, the difference between these two concepts is not effective in our model. In the Battle of Sexes game, we can interpret Bob’s sentiment of guilt as a consequence of making Ann disappointed because of miscoordination. Indeed, Bob continues to feel guilty as far as the occurrence of miscoordination has positive probability, while his guilt disappears when both players coordinate with probability one (we thank an anonymous referee for shedding light on this aspect).
A different perspective related to guilt aversion may be found in [
33], where the authors analyzed the impact of co-players’ vulnerability (in terms of payoff vulnerability and endowment vulnerability) on guilt for new variations of a three-player trust game.
5. A Remark on Strategic Ambiguity
The literature on strategic ambiguity looks at games in which players have ambiguous beliefs about their opponents’ behavior. From the perspective of this work, the issue of strategic ambiguity can be regarded as a problem of ambiguous first-order beliefs in players’ utilities with no psychological terms. Several papers have already considered the impact of strategic ambiguity on the classical Battle of Sexes model (with no psychological utilities): in [
22], the author highlighted that players’ ambiguous beliefs may appear as a consequence of differences in common culture or history. In that work, a parametric approach was used, leading to the introduction of ambiguous games where non-additive probabilities are exploited as a tool to manage ambiguity. In the context of Ellsberg games, again with the use of capacities, [
29] analyzed a modified version of the Battle of Sexes game from an experimental point of view. Applying the concept of equilibrium under ambiguity (EUA) previously introduced by [
34], they concluded that aversion to ambiguity strongly influences the behavior of the players. This is because individuals tend to choose an ambiguity-safe option, which results in other options being taken off the table when applying the standard Nash equilibrium concept. In [
25], the Battle of Sexes game was studied as a special case of
coordination games. The authors applied the concept of Ellsberg equilibrium (based on an imprecise probabilistic approach) and computed the Ellsberg equilibria in a general
coordination game. The set of equilibria turns out to be given by intervals of probability distributions such that the Nash equilibria and max–min strategies provide the boundaries of the largest set.
In this section, we look at strategic ambiguity in our simple framework in which ambiguous beliefs are represented by sets of probabilistic beliefs. In particular, we do not consider psychological utilities or higher-order beliefs; rather, ambiguity is provided by a set of first-order (imprecise) beliefs. This approach allows us to showcase a substantial difference with respect to the guilt aversion case. In fact, in the pessimistic case, all of the classical equilibria are destroyed and a new equilibrium emerges in which Ann plays her preferred pure strategy while Bob randomizes by choosing his preferred strategy with probability 1/3. In the optimistic case, the unique equilibrium is the one in which both players play Boxing with probability 1. Details are provided below.
Example 1. Recall that Bob’s expected utility for the standard game is Consider the case in which Bob has full ignorance about Ann’s strategy choice. In the case where Bob is pessimistic, his utility is It immediately follows that is the unique maximum point regardless of p; thus, the best reply is This leads to the unique equilibrium Example 2. In the case where Bob is optimistic, his utility is It immediately follows that is the unique maximum point regardless of p; thus, the best reply is This leads to the unique equilibrium 6. Conclusions
The Battle of Sexes is a very simple game that turns out to have many natural applications. Moreover, it is characterized by its multiplicity of equilibria and by the fact that it is a generic game, meaning that coordination on a single equilibrium is challenging on the basis of classical game theory. For all of these reasons, this model has always attracted the attention of new research.
In this paper, we provide a different perspective by investigating the Battle of Sexes game under the effect of guilt aversion and studying the corresponding psychological game. It turns out that the pure strategy equilibria are confirmed to be extremely robust with respect to perturbations of agents’ preferences, while the mixed strategy equilibrium is sensitive in such a way that a non-psychological (or material) player is willing to accept a lower expected utility in order to compensate others’ disutility from guilt. In the (pessimistic) ambiguous case, the sensitivity is more effective, as it is higher than the disutility from guilt. In both cases, the mixed strategy equilibrium remains stable, converging to the classical one when guilt aversion vanishes. The present paper shows that guilt aversion and a pessimistic attitude towards ambiguity do not break the structure of the equilibria; however, they do have a clear effect, for which the interpretation is rather natural but not especially obvious. This paper contributes to the line of research concerning the issue of ambiguous higher-order beliefs in psychological games, showing that such issues can be relevant even in simple and classical games. Obtaining a general result for the class of coordination games, which includes the Stag Hunt game and the Hawk–Dove game, constitutes a goal for future work. Another aspect that is worth considering in future research concerns extensive-form psychological games under ambiguity with guilt aversion. Such games could be investigated in relation to the way that equilibria behave under two different notions of guilt, namely, guilt from blame and simple guilt.