Vibration Reduction of Permanent Magnet Synchronous Motors by Four-Layer Winding: Mathematical Modeling and Experimental Validation
Abstract
1. Introduction
2. Concerns Regarding FSCW PMSMs
2.1. Sub-Harmonics in Airgap Magnetic Flux Density of FSCW PMSM
2.2. Vibration Order in Radial Electromagnetic Force of FSCW PMSM
3. Proposed Four-Layer Winding for Vibration Reduction
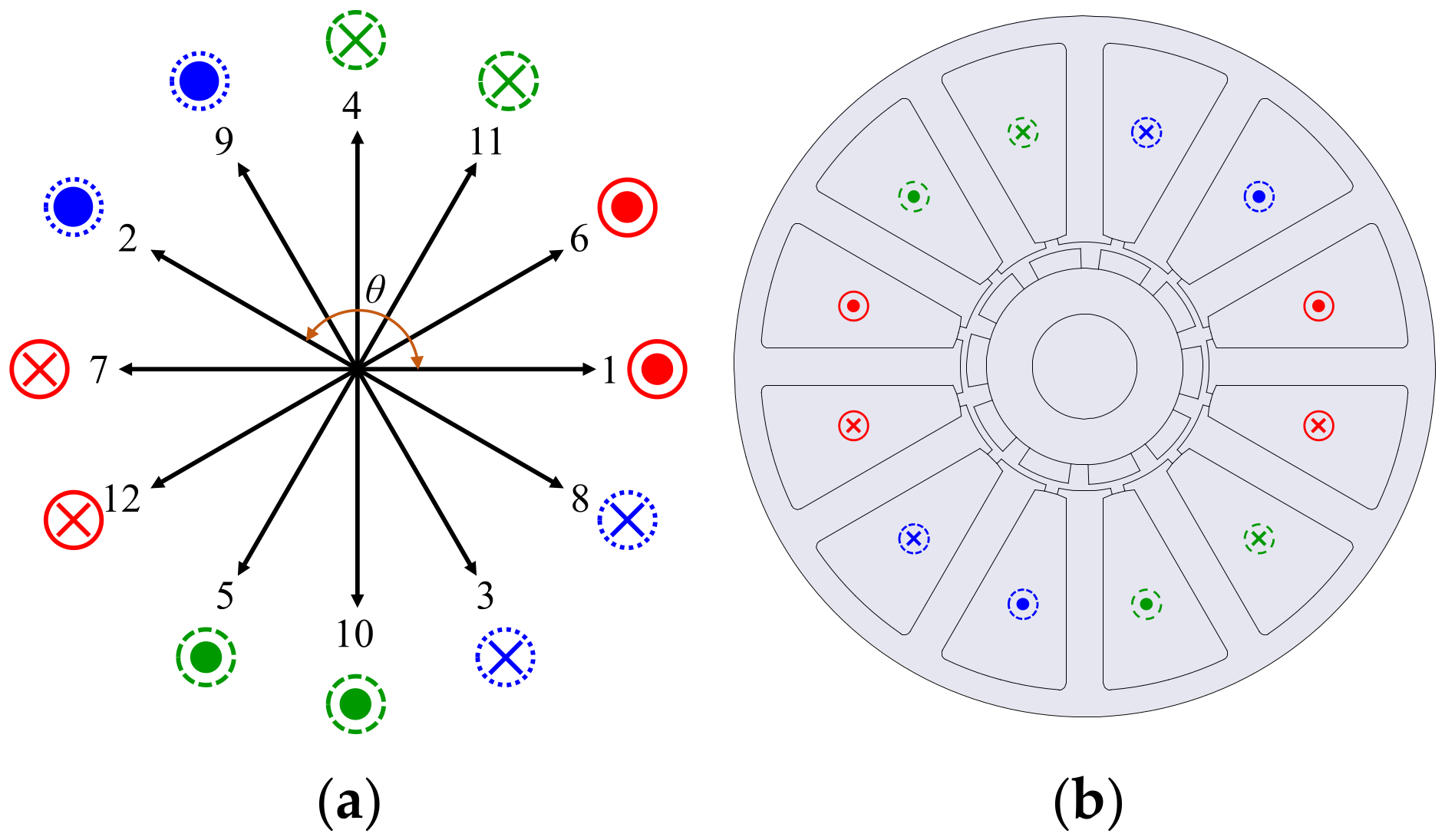
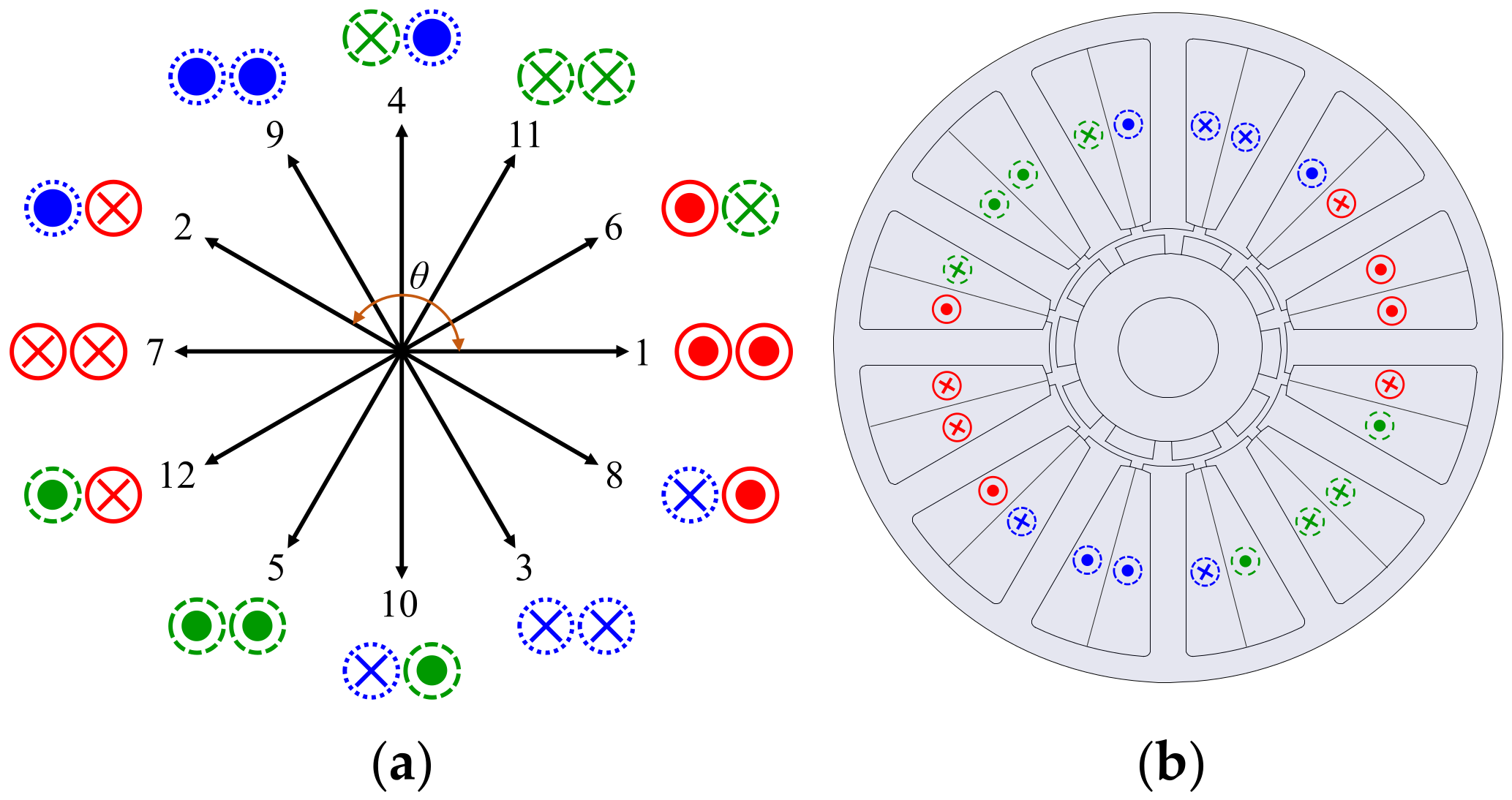
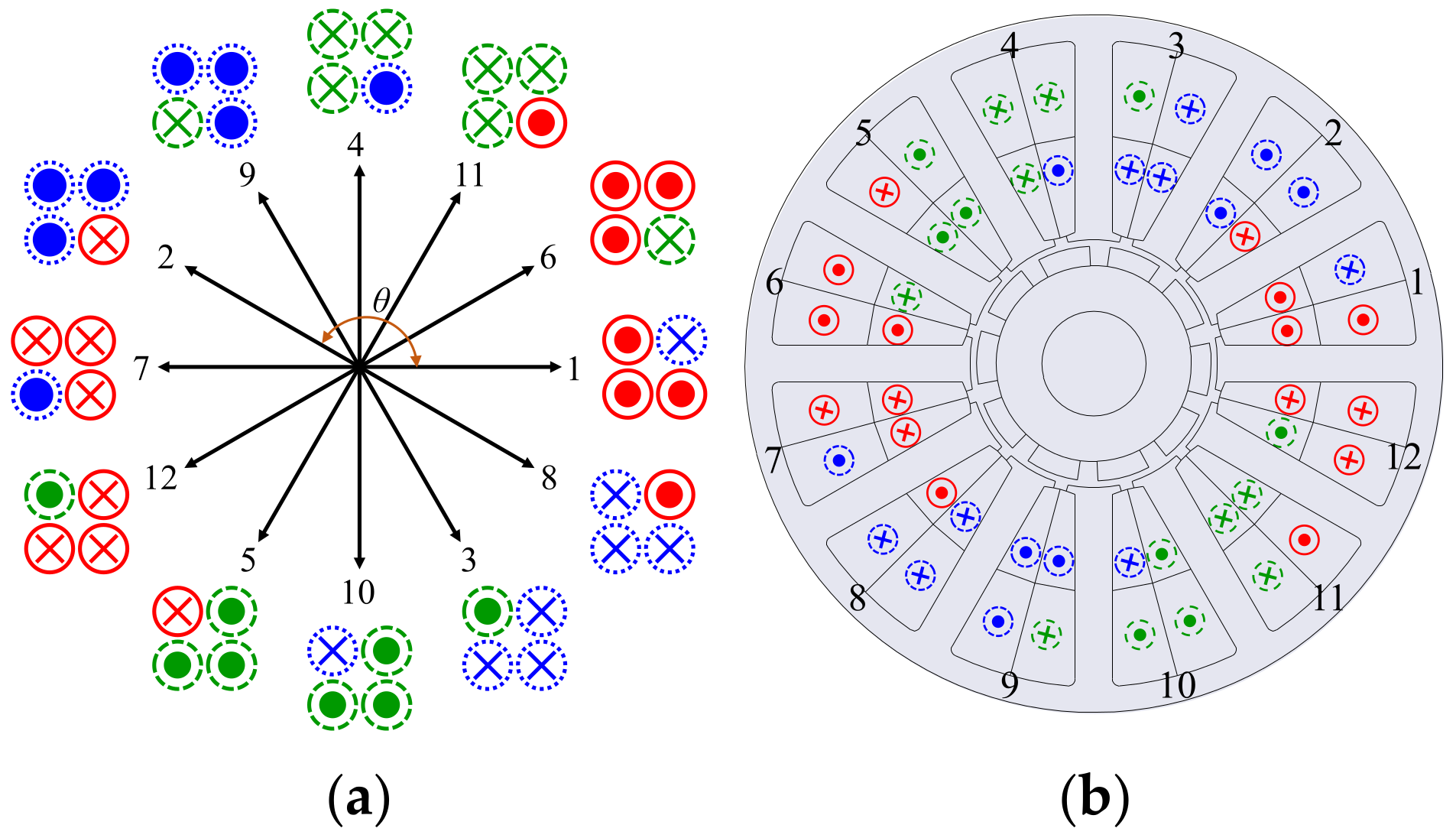
3.1. Winding Layout by Winding Methods
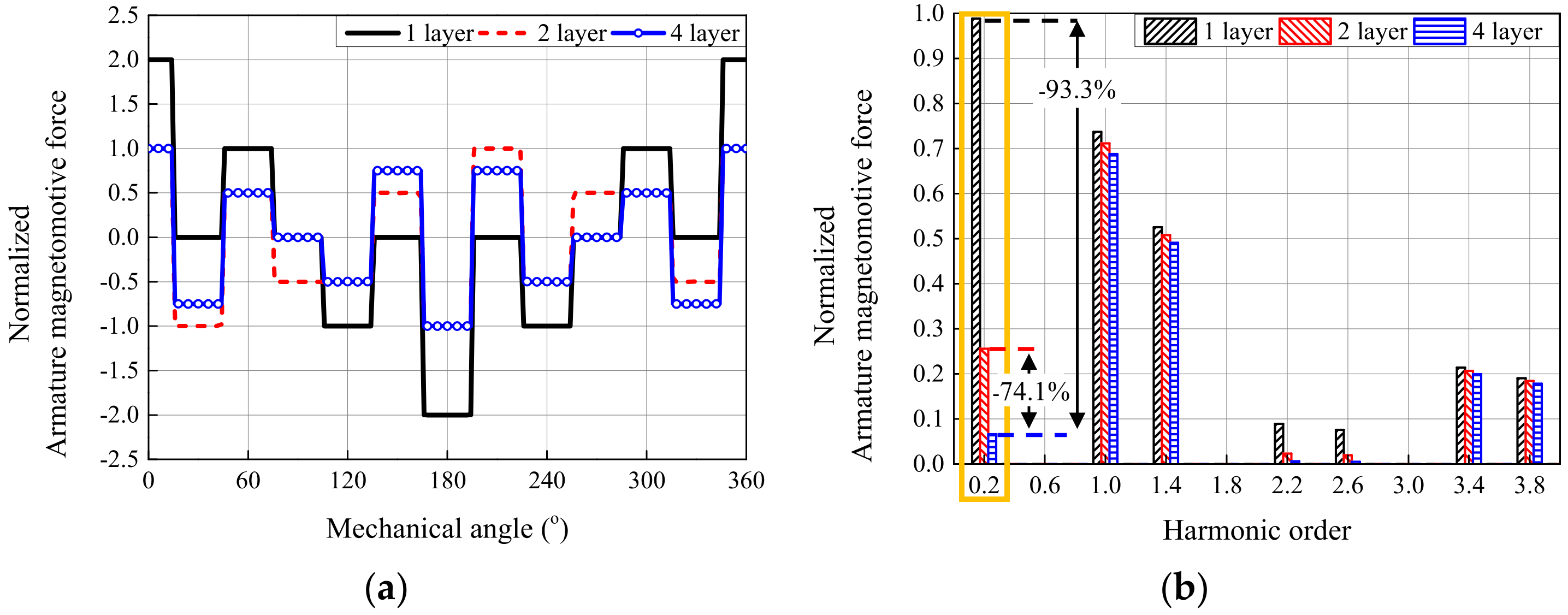
3.2. Analysis of Armature Magnetomotive Force by Winding Methods
3.3. Winding Factor by Winding Methods
3.4. Applicability of Four-Layer Winding
4. FEA-Based Comparison of Electromagnetic and Vibration Characteristics
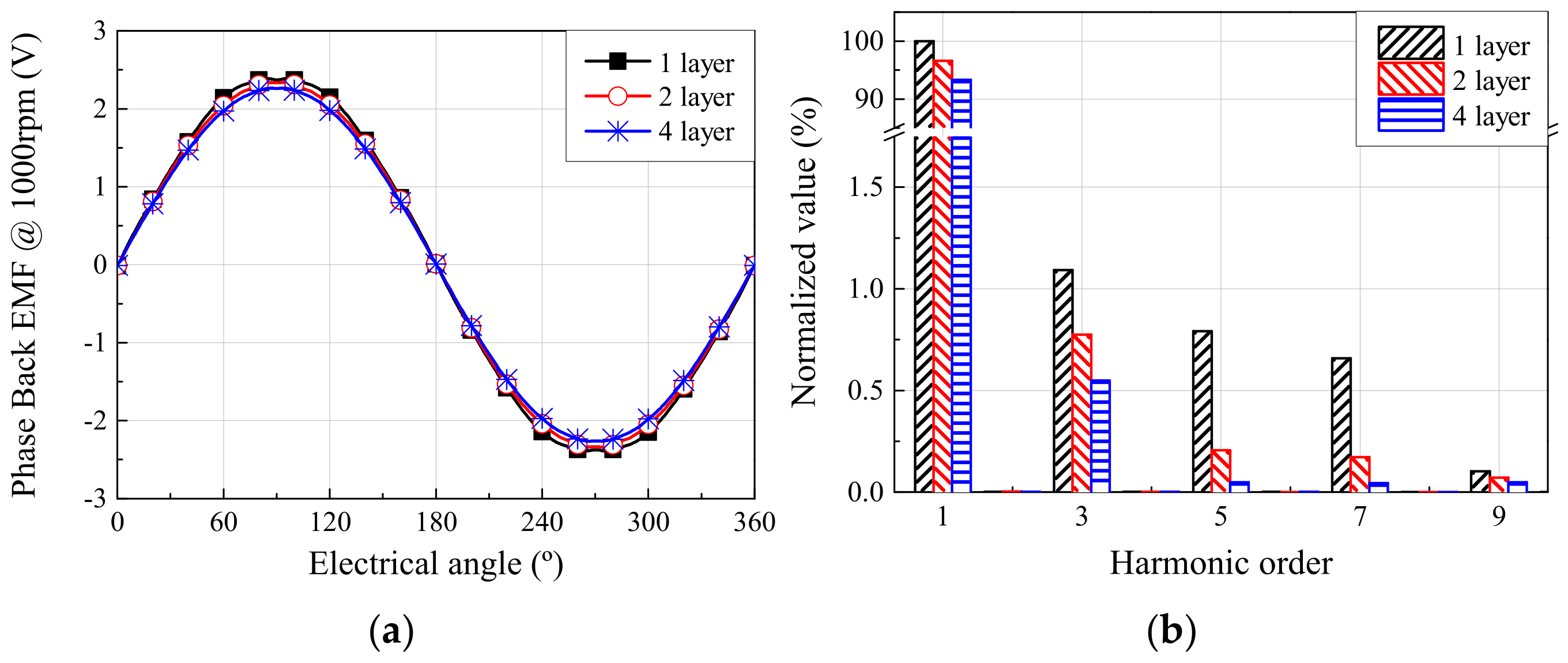
4.1. Back-EMF and Torque Characteristics via FEA
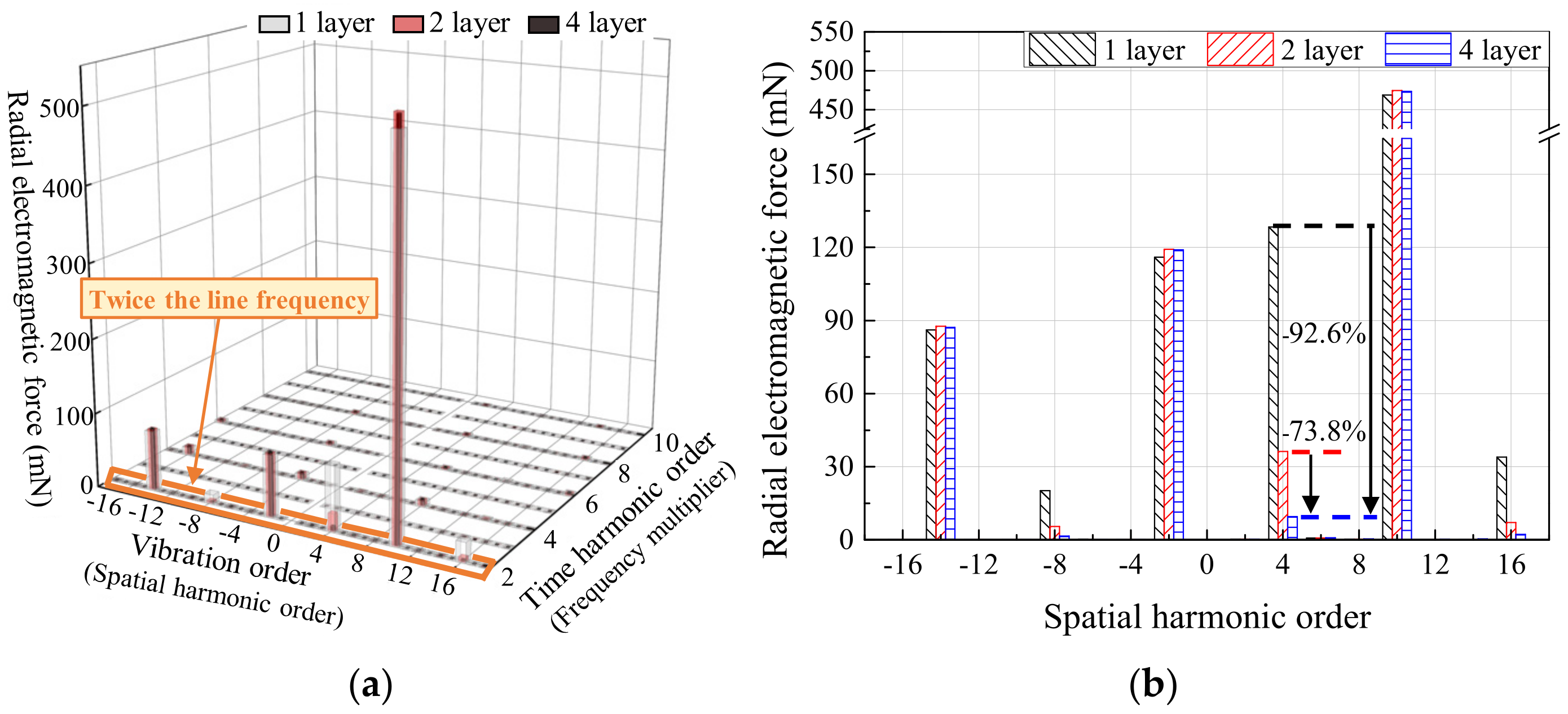
4.2. Vibration Characteristics Based on FEA
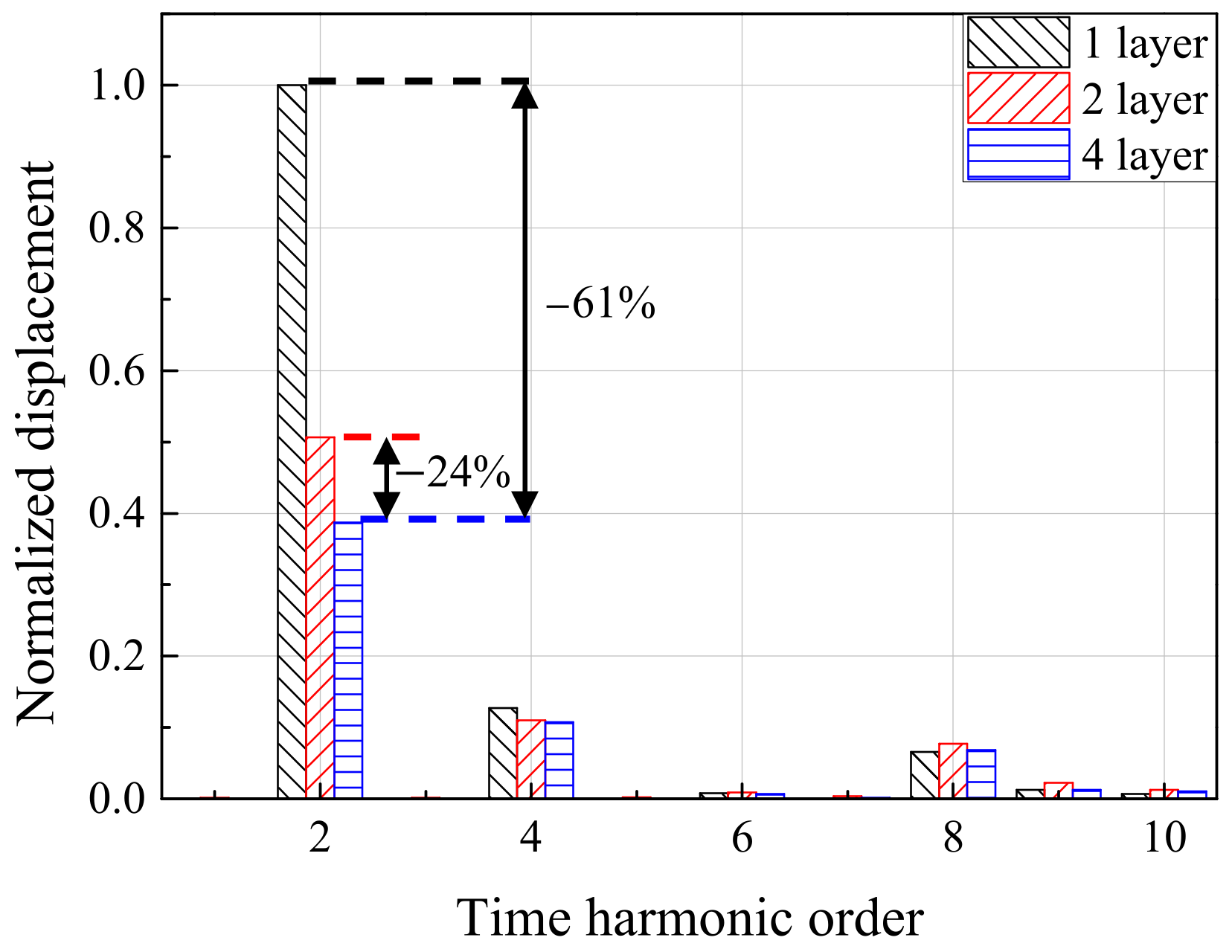
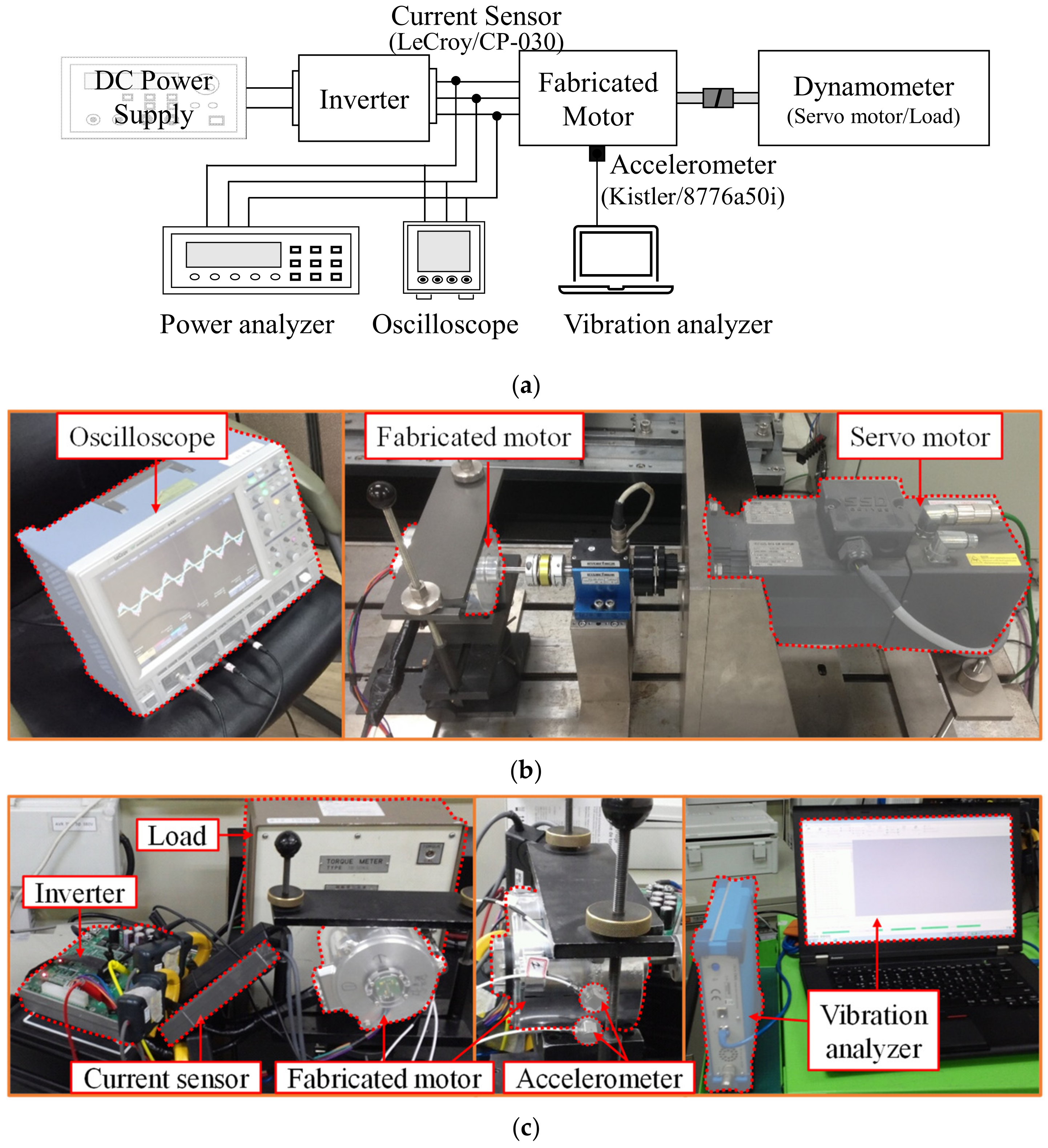
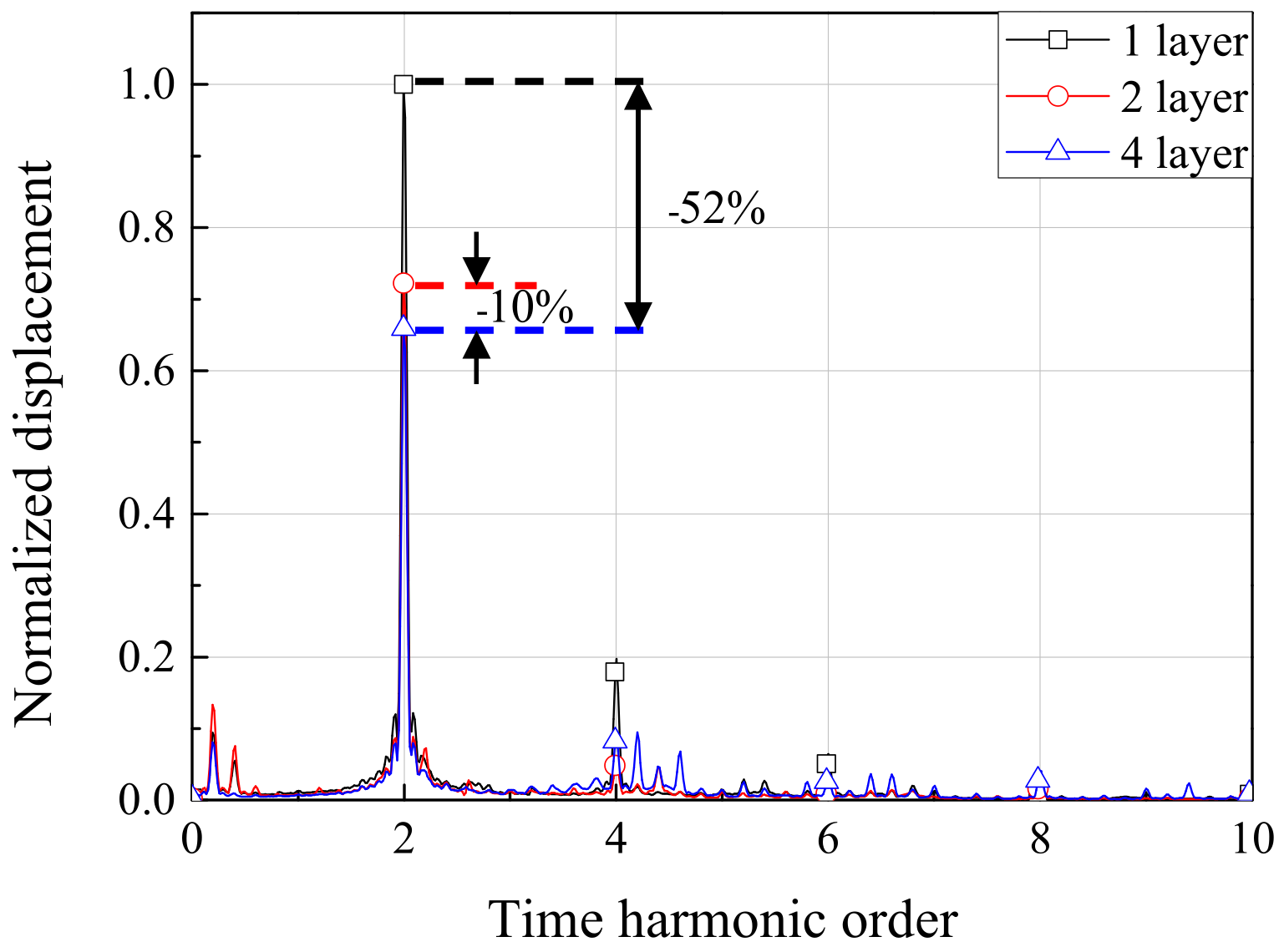
5. Experimental Validation of Vibration Reduction with Four-Layer Winding
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, X.; Zhang, B.; Qu, R.; Li, D.; Li, J.; Huo, J. Comparative Thermal Analysis of IPMSMs with Integral-Slot Distributed-Winding (ISDW) and Fractional-Slot Concentrated-Winding (FSCW) for Electric Vehicle Application. IEEE Trans. Ind. Appl. 2019, 55, 3577–3588. [Google Scholar] [CrossRef]
- Chen, H.; Qu, R.; Li, J.; Li, D. Demagnetization Performance of a 7MW Interior Permanent Magnet Wind Generator with Fractional-Slot Concentrated Windings. IEEE Trans. Magn. 2015, 51, 8205804. [Google Scholar] [CrossRef]
- EL-Refaie, A.M. Fractional-Slot Concentrated-Windings Synchronous Permanent Magnet Machines: Opportunities and Challenges. IEEE Trans. Ind. Electron. 2010, 57, 107–121. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Ahmed, S.; Massoud, A. Low Space Harmonics Cancelation in Double-Layer Fractional Slot Winding Using Dual Multiphase Winding. IEEE Trans. Magn. 2015, 51, 8104710. [Google Scholar] [CrossRef]
- Dutta, R.; Chong, L.; Rahman, M.F. Design and Experimental Verification of an 18-Slot/14-pole Fractional-Slot Concentrated Winding Interior Permanent Magnet Machine. IEEE Trans. Energy Convers. 2013, 28, 181–190. [Google Scholar] [CrossRef]
- Wang, J.; Atallah, K.; Zhu, Z.Q.; Howe, D. Modular Three-Phase Permanent-Magnet Brushless Machines for In-Wheel Applications. IEEE Trans. Veh. Technol. 2008, 57, 2714–2720. [Google Scholar] [CrossRef]
- Zhou, C.; Huang, X.; Li, Z.; Cao, W. Design Consideration of Fractional Slot Concentrated Winding Interior Permanent Magnet Synchronous Motor for EV and HEV Applictaions. IEEE Access 2021, 9, 64116–64126. [Google Scholar] [CrossRef]
- Ahsanullah, K.; Dutta, R.; Rahman, M.F. Analysis of Low-Speed IPMMs with Distributed and Fractional Slot Concentrated Windings for Wind Energy Applications. IEEE Trans. Magn. 2017, 53, 3101710. [Google Scholar] [CrossRef]
- Kim, H.-J.; Kim, D.-J.; Hong, J.-P. Characteristic Analysis for Concentrated Multiple-Layer Winding Machine with Optimum Turn Ratio. IEEE Trans. Magn. 2014, 50, 7019504. [Google Scholar] [CrossRef]
- Farshadnia, M.; Cheema, M.A.M.; Dutta, R.; Fletcher, J.E. Analytical Modeling of Armature MMF Airgap flux density Considering the Non-Homogeneously Saturated Rotor in a Fractional-Slot Concentrated-Wound IPM Machine. IEEE Trans. Magn. 2017, 53, 8200412. [Google Scholar] [CrossRef]
- Farshadnia, M.; Cheema, M.A.M.; Dutta, R.; Fletcher, J.E.; Rahman, M.F. Detailed Analytical Modeling of Fractional-Slot Concentrated-Wound Interior Permanent Magnet Machines for Prediction of Torque Ripple. IEEE Trans. Ind. Appl. 2017, 53, 5272–5283. [Google Scholar] [CrossRef]
- Dutta, R.; Rahman, M.F.; Chong, L. Winding Inductances of an Interior Permanent Magnet (IPM) Machine with Fractional Slot Concentrated Winding. IEEE Trans. Magn. 2012, 48, 4842–4849. [Google Scholar] [CrossRef]
- Carraro, E.; Bianchi, N.; Zhang, S.; Koch, M. Design and Performance Comparison of Fractional Slot Concentrated Winding Spoke Type Synchronous Motors with Different Slot-Pole Combinations. IEEE Trans. Ind. Appl. 2018, 54, 2276–2284. [Google Scholar] [CrossRef]
- Dutta, R.; Pouramin, A.; Rahman, M.F. A Novel Rotor Topology for High-Performance Fractional Slot Concentrated Winding Interior Permanent Magnet Machine. IEEE Trans. Energy Convers. 2021, 36, 658–670. [Google Scholar] [CrossRef]
- Chung, S.; Kim, J.; Koo, D.; Woo, B.; Hong, D.; Lee, J. Fractional Slot Concentrated Winding Permanent Magnet Synchronous Machine with Consequent Pole Rotor for Low Speed Direct Drive. IEEE Trans. Magn. 2012, 48, 2965–2968. [Google Scholar] [CrossRef]
- Yang, J.; Liu, G.; Zhao, W.; Chen, Q.; Jiang, Y.; Sun, L.; Zhu, X. Quantitative Comparison for Fractional-Slot Concentrated-Winding Configurations of Permanent-Magnet Vernier Machines. IEEE Trans. Magn. 2013, 49, 3826–3829. [Google Scholar] [CrossRef]
- Toda, H.; Xia, Z.; Wang, J.; Atallah, K.; Howe, D. Rotor eddy-current loss in permanent magnet brushless machines. IEEE Trans. Magn. 2004, 40, 2104–2106. [Google Scholar] [CrossRef]
- Wu, L.; Qu, R.; Li, D. Reduction of Rotor Eddy-Current Losses for Surface PM Machines with Fractional Slot Concentrated Windings and Retaining Sleeve. IEEE Trans. Magn. 2014, 50, 8205704. [Google Scholar] [CrossRef]
- Choi, G.; Jahns, T.M. Reduction of Eddy-Current Losses in Fractional-Slot Concentrated-Winding Synchronous PM Machines. IEEE Trans. Magn. 2016, 52, 8105904. [Google Scholar] [CrossRef]
- Chaithongsuk, S.; Takorabet, N.; Kreuawan, S. Reduction of Eddy-Current Losses in Fractional-Slot Concentrated-Winding Synchronous PM Motors. IEEE Trans. Magn. 2015, 51, 8102204. [Google Scholar] [CrossRef]
- Wang, J.; Patel, V.I.; Wang, W. Fractional-Slot Permanent Magnet Brushless Machines with Low Space Harmonic Contents. IEEE Trans. Magn. 2014, 50, 8200209. [Google Scholar] [CrossRef]
- Islam, M.S.; Kabir, M.A.; Mikail, R.; Husain, I. Space-Shifted Wye–Delta Winding to Minimize Space Harmonics of Fractional-Slot Winding. IEEE Trans. Ind. Appl. 2020, 56, 2520–2530. [Google Scholar] [CrossRef]
- Alberti, L.; Bianchi, N. Theory and Design of Fractional-Slot Multilayer Windings. IEEE Trans. Ind. Appl. 2013, 49, 841–849. [Google Scholar] [CrossRef]
- Alberti, L.; Barcaro, M.; Bianchi, N. Design of a Low-Torque-Ripple Fractional-Slot Interior Permanent-Magnet Motor. IEEE Trans. Ind. Appl. 2014, 50, 1801–1808. [Google Scholar] [CrossRef]
- Sun, A.; Li, J.; Qu, R.; Li, D. Effect of Multilayer Windings on Rotor Losses of Interior Permanent Magnet Generator with Fractional-Slot Concentrated-Windings. IEEE Trans. Magn. 2014, 50, 8105404. [Google Scholar] [CrossRef]
- Bianchi, N.; Alberti, L.; Barcaro, M. Design and Tests of a Four-Layer Fractional-Slot Interior Permanent-Magnet Motor. IEEE Trans. Ind. Appl. 2016, 52, 2234–2240. [Google Scholar] [CrossRef]
- Liu, G.; Zhai, F.; Chen, Q.; Xu, G. Torque Pulsation Reduction in Fractional-Slot Concentrated-Windings IPM Motors by Lowering Sub-Harmonics. IEEE Trans. Energy Convers. 2019, 34, 2084–2095. [Google Scholar] [CrossRef]
- Gieras, J.F.; Wang, C.; Lai, J.C. Magnetic fields and radial forces in polyphase motors fed with sinusoidal currents. In Noise of Polyphase Electric Motors, 1st ed.; CRC Press: Boca Raton, FL, USA, 2006; Chapter 2; pp. 21–64. [Google Scholar]
- Kim, D.-Y.; Park, M.-R.; Sim, J.-H.; Hong, J.-P. Advanced Method of Selecting Number of Poles and Slots for Low-Frequency Vibration Reduction of Traction Motor for Elevator. IEEE/ASME Trans. Mechatron. 2017, 22, 1554–1562. [Google Scholar] [CrossRef]
- Jung, Y.; Park, M.; Lim, M. Asymmetric Rotor Design of IPMSM for Vibration Reduction Under Certain Load Condition. IEEE Trans. Energy Convers. 2020, 35, 928–937. [Google Scholar] [CrossRef]
- Lu, W.; Gui, Z.; Ni, J.; Xu, S. Influence of asymmetric-paths winding on electromagnetic force of variable speed pump storage generator-motor. Results Eng. 2024, 21, 101813. [Google Scholar] [CrossRef]







| Poles | Slots | j | Space-Harmonic Order |
|---|---|---|---|
| 8 | 9 | 8 | 1/4, 2/4, 1, 5/4, 7/4, 2, 10/4, … |
| 12 | 2 | 1, 2, 4, 5, 7, 8, 10, … | |
| 18 | 4 | 1/2, 1, 2, 5/2, 7/2, 4, 5, … | |
| 48 | 1 | 1, 5, 7, 11, 13, 17, 19, … | |
| 10 | 12 | 5 | 1/5, 1, 7/5, 11/5, 13/5, 17/5, 19/5, … |
| 15 | 2 | 1, 2, 4, 5, 7, 8, 10, … | |
| 60 | 1 | 1, 5, 7, 11, 13, 17, 19, … | |
| 12 | 18 | 2 | 1, 2, 4, 5, 7, 8, 10, … |
| 27 | 4 | 1/2, 1, 2, 5/2, 7/2, 4, 5, … | |
| 72 | 1 | 1, 5, 7, 11, 13, 17, 19, … | |
| 14 | 12 | 7 | 1/7, 5/7, 1, 11/7, 13/7, 17/7, 19/7, … |
| 18 | 7 | 1/7, 5/7, 1, 11/7, 13/7, 17/7, 19/7, … | |
| 21 | 2 | 1, 2, 4, 5, 7, 8, 10, … | |
| 16 | 18 | 8 | 1/4, 2/4, 1, 5/4, 7/4, 2, 10/4, … |
| 24 | 2 | 1, 2, 4, 5, 7, 8, 10, … | |
| 36 | 4 | 1/2, 1, 2, 5/2, 7/2, 4, 5, … |
| Contents | Frequency | Vibration Order |
|---|---|---|
| Self of PM | (μ1 ± μ2)f | p(μ1 ± μ2) |
| Self of armature MMF | (n1 ± n2)f | p(ν1 ± ν2) |
| Mutual of the PM and armature MMF | (μ ± n)f | p(μ ± ν) |
| Mutual of the PM and stator slot | (μ1 ± μ2)f | p(μ1 ± μ2) ± kS or p(μ1 ± μ2) ± (k1 ± k2)S |
| Mutual of the armature MMF and stator slot | (n1 ± n2)f | p(ν1 ± ν2) ± kS or p(ν1 ± ν2) ± (k1 ± k2)S |
| Poles | Slots | Vibration Order |
|---|---|---|
| 8 | 9 | 1, 2, 4, 5, 7, 8, 10, … |
| 12 | 4, 8, 16, 20, 28, 32, 40, … | |
| 18 | 2, 4, 8, 10, 14, 16, 20, … | |
| 48 | 8, 16, 32, 40, 56, 64, 80, … | |
| 10 | 12 | 2, 4, 8, 10, 14, 16, 20, … |
| 15 | 5, 10, 20, 25, 35, 40, 50, … | |
| 60 | 10, 20, 40, 50, 70, 80, 100, … | |
| 12 | 18 | 6, 12, 24, 30, 42, 48, 60, … |
| 27 | 3, 6, 12, 15, 21, 24, 30, … | |
| 72 | 12, 24, 48, 60, 84, 96, 120, … | |
| 14 | 12 | 2, 4, 8, 10, 14, 16, 20, … |
| 18 | 2, 4, 8, 10, 14, 16, 20, … | |
| 21 | 7, 14, 28, 35, 49, 56, 70, … | |
| 16 | 18 | 2, 4, 8, 10, 14, 16, 20, … |
| 24 | 8, 16, 32, 40, 56, 64, 80, … | |
| 36 | 4, 8, 16, 20, 28, 32, 40, … |
| Item | Harmonic Order | One-Layer | Two-Layer | Four-Layer |
|---|---|---|---|---|
| kpν | ν | |||
| kdν | ν | 1 | ||
| kwν | 0.2 | 0.259 | 0.067 | 0.017 |
| 1 | 0.966 | 0.933 | 0.901 | |
| 1.4 | 0.966 | 0.933 | 0.901 | |
| 2.2 | 0.259 | 0.067 | 0.017 | |
| 2.6 | −0.259 | 0.067 | −0.017 | |
| 3.4 | −0.966 | 0.933 | −0.901 | |
| 3.8 | −0.966 | 0.933 | −0.901 |
| Content | Unit | Value |
|---|---|---|
| Motor type | - | SPMSM |
| Pole/slot number | - | 10/12 |
| Rotor outer diameter | mm | 36 |
| Stator outer diameter | mm | 107 |
| Stack length | mm | 44 |
| Core material | - | 50PN470 |
| Residual induction | T | 1.29 |
| Rated speed | rpm | 2500 |
| Rated torque | Nm | 2.0 |
| Rated Power | W | 524 |
| Drive method | - | id = 0 control |
| Content | Unit | One-Layer | Two-Layer | Four-Layer |
|---|---|---|---|---|
| Fundamental component of back EMF | Vrms | 1.67 | 1.61 | 1.56 |
| THD of back EMF | % | 1.5 | 0.8 | 0.6 |
| Average torque | Nm | 2.0 | 2.0 | 2.0 |
| Torque ripple | % | 3.8 | 0.5 | 0.4 |
| Line-to-line voltage | Vrms | 9.6 | 8.6 | 8.1 |
| Line current | Arms | 43.8 | 45.2 | 46.8 |
| Power factor | % | 80.1 | 86.1 | 87.8 |
| Efficiency | % | 89.7 | 90.6 | 90.3 |
| Copper loss | W | 23.3 | 24.8 | 26.6 |
| Iron loss | W | 21.6 | 14.2 | 14.2 |
| Mechanical loss | W | 15.2 | 15.2 | 15.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, Y.-H.; Kim, D.-M.; Cha, K.-S.; Park, S.-H.; Park, M.-R. Vibration Reduction of Permanent Magnet Synchronous Motors by Four-Layer Winding: Mathematical Modeling and Experimental Validation. Mathematics 2025, 13, 1603. https://doi.org/10.3390/math13101603
Jung Y-H, Kim D-M, Cha K-S, Park S-H, Park M-R. Vibration Reduction of Permanent Magnet Synchronous Motors by Four-Layer Winding: Mathematical Modeling and Experimental Validation. Mathematics. 2025; 13(10):1603. https://doi.org/10.3390/math13101603
Chicago/Turabian StyleJung, Young-Hoon, Dong-Min Kim, Kyoung-Soo Cha, Soo-Hwan Park, and Min-Ro Park. 2025. "Vibration Reduction of Permanent Magnet Synchronous Motors by Four-Layer Winding: Mathematical Modeling and Experimental Validation" Mathematics 13, no. 10: 1603. https://doi.org/10.3390/math13101603
APA StyleJung, Y.-H., Kim, D.-M., Cha, K.-S., Park, S.-H., & Park, M.-R. (2025). Vibration Reduction of Permanent Magnet Synchronous Motors by Four-Layer Winding: Mathematical Modeling and Experimental Validation. Mathematics, 13(10), 1603. https://doi.org/10.3390/math13101603







