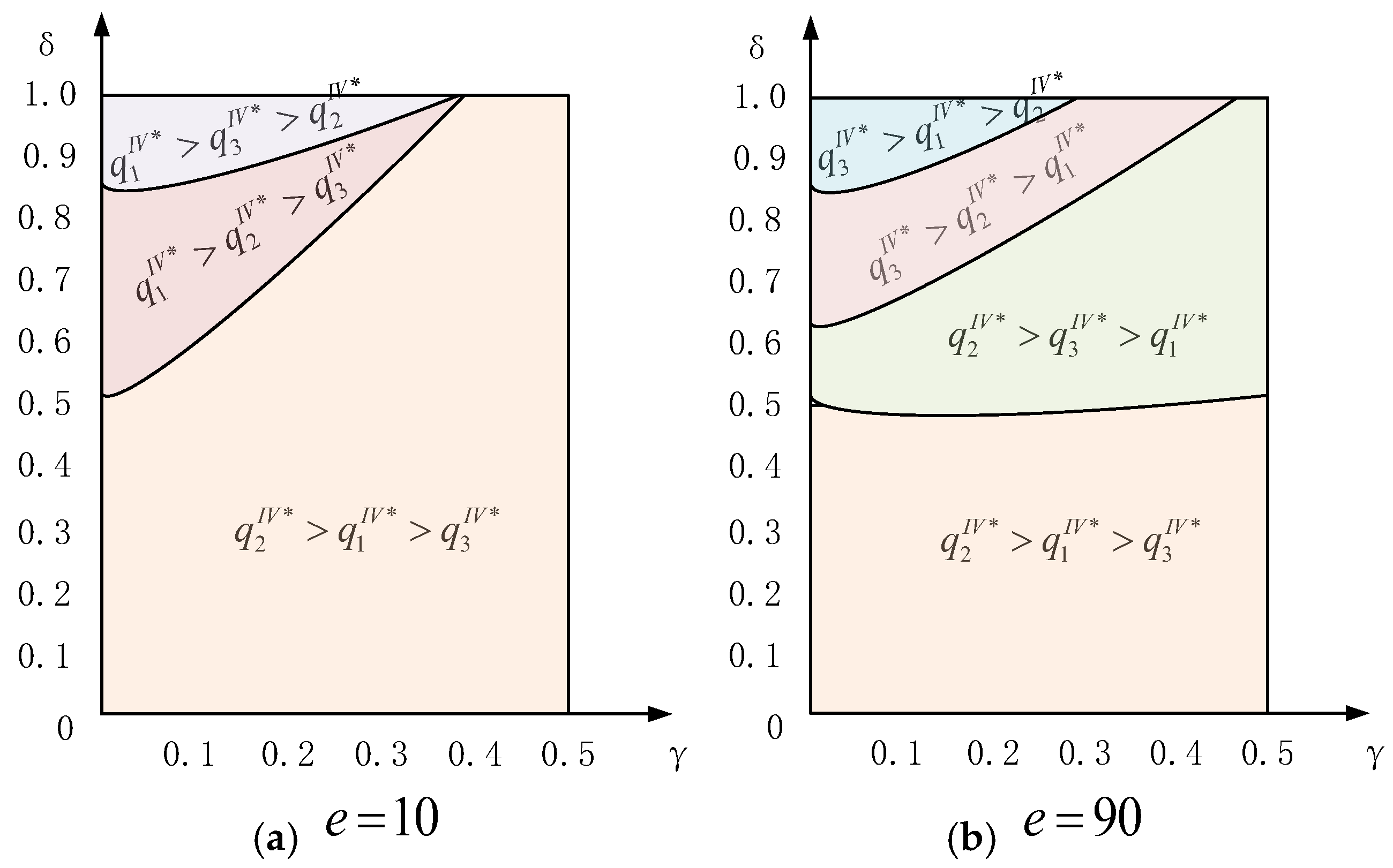The Strategic Adoption of Platform Schemes and Its Impacts on Traditional Distributors: A Case Study of Gree

Abstract

This article is motivated by the challenge of the increasing power of e-commerce compared to traditional commerce. An online retail platform can provide both agency selling and reselling schemes, while the supplier can adopt one scheme or both. For a case study of Gree, we formulate four cases based on the channel structures to investigate the adoption strategies of platform schemes and their impacts on a traditional distributor, Jinghai. Firstly, we discuss the impacts of the slotting fee, the revenue-sharing proportion earned by the supplier, and the market competition intensity on the profits and decisions of members. A more intense market and a higher revenue-sharing proportion for the supplier will lead to a lower price in the traditional distribution channel. Secondly, we study how a supplier should employ the platform schemes with a traditional distributor. Particularly, the extremely low extra market demand driven by the online platform and the sufficiently low market intensity may not lead to a motivation for suppliers to adopt the agency scheme. Finally, Gree’s introduction of an agency scheme does not always spell disaster for traditional distributors, and it may not be such a bad thing for Jinghai to agree to Gree adding the online reselling scheme.

1. Introduction

The issue of online retailing has received a lot of attention during the last decade. The transaction volume of the online retail market was valued at RMB 15.42 trillion, accounting for 27.6% of the total retail sales of social consumer goods in 2023, according to the National Bureau of Statistics of China. Online retailing provides a convenient transaction platform for not only enterprises but also consumers [1]. Online platforms contribute to economic efficiency by shrinking distances and timescales, lowering distribution and transaction costs, speeding up product development, providing more information to buyers and sellers and increasing customer choice and supplier reach [2]. Generally, online platforms can provide suppliers with an agency selling scheme and a reselling scheme, depending on whether the suppliers have direct access to consumers. For example, www.amazon.com, the largest integrated online retailer in the U.S., has attracted many brand owners and provided businesses with access to consumers [3]. Amazon not only serves as an online platform but also functions as a traditional merchant, in that it buys goods from suppliers and resells them to consumers [4]. Meanwhile, in China, prominent online retail platforms, such as www.Taobao.com and www.JD.com [5], are available for businesses that seek to develop multi-channel online sales to further enlarge the influence of brands and products.

Normally, in the home appliance industry, online platforms are used for display and communication, offering consumers services related to consultation, distribution, after/pre-sales service and others. The 2022 Gfk survey on the home appliances market in China reported that by the end of 2022, online retail channels for home appliances will account for more than 50%. More and more consumers choose to buy home appliances online. Driven by the potential market demand from online platforms, suppliers will pay fees in exchange for the opportunity to market their products to more customers. Based on which selling scheme the supplier chooses, a slotting fee or a portion of their sales revenue is required by the platform. For example, Gome adopts a platform retailer business model, where it rents space within the store to manufacturers, followed by a slotting fee to cover real estate, advertisement, and overhead costs [6].

In addition, no matter how the supplier chooses to enter the online market, it will inevitably have an impact on traditional offline channels, which precede e-commerce channels. For example, Gree’s live-streaming sales on the JD platform result in considerable benefits, but they hurt the interests of offline dealers to some degree. Moreover, offline retailers have inevitably lost customers since IKEA has paid more attention to its online business to address its declining performance. Consumers are more sensitive to Internet content than to offline demand. However, especially for the market of consumer electronics and appliances, these offline outlets are indispensable because they can offer customers face-to-face and experiential service. Thus, the supplier has to consider the impact of offline channels when choosing the online selling scheme. The above observations motivate our research, which aims to address the following general questions.

Under the reselling scheme, we consider that selling through an online platform can attract more consumers to suppliers. However, suppliers seldom pay for the selling effort (or service) of their retailers. In order to alleviate the free-riding problem [7], for example, Alibaba (an online platform) holds 25.25% of shares in Haier, and Jinghai (one of the top four dealers of Gree) purchases part of Gree’s shares [8]. Therefore, the slotting fee and the revenue-sharing proportion are useful in encouraging or discouraging the adoption of the online channel strategy by suppliers. This paper aims to investigate the optimal decision-making strategies for the above-defined platform schemes. The key research questions are summarized as follows:

• Which online platform scheme would be preferred by suppliers in such a multifarious market environment?
• How should products sold online be priced under different platform schemes?
• How do the slotting fee, the revenue-sharing proportion, and the market intensity affect the profits of participants in the supply chain?
• How does the supplier’s choice have an impact on the traditional distributor’s profit, and how does the channel behavior of traditional distributors affect suppliers’ choice of platform scheme?

The key findings can be summarized as follows. (1) When the supplier adopts only the agency selling scheme in addition to the traditional distribution, their profitability is not always greater than that without any platform schemes. It depends on not only the market intensity but also on the extra market demand provided by the online platform. (2) When the supplier adopts only the online reselling scheme in addition to the traditional distribution, it may happen that the wholesale price in the traditional distribution channel is less than that in the online reselling channel. (3) When the supplier adopts both agency selling and online reselling schemes in addition to the traditional distribution, the extremely intense market may result in more profits for the supplier. This study hints that the intense market has more influence on decisions and profitability than any other factors. Furthermore, (4) the motivation of suppliers to sell through an online reseller could outweigh that to employ an agency selling strategy, while market competition is relatively intense. For example, some brands, such as Nestle Coffee and HP, are more motivated to employ a reselling scheme to enter into the local market [9]. Our research also suggests that the traditional distributor does not always oppose the supplier adopting platform schemes.

2. Literature Review

Our work builds upon contributions regarding online platform retailing, strategic choice of supplier, and the impact of online platform schemes. Also, our paper expands the study of online retailing platforms to competitive supply chains. We hereby review these papers that are most relevant to our work.

Prior work on Internet retailing has primarily focused on the interaction between online and offline consumer purchasing [10,11,12]. For example, Estee Lauder, one of the world’s largest skincare companies, plans to sell its flagship Clinique brand directly via the Internet, which puts it squarely in competition with the department stores whose cosmetics counters show its products. However, the magnitude of consumers between online and brick-and-mortar retailing stores is different. Chu et al. [13] find that consumers prefer to shop online, and people who are loyal to offline brick-and-mortar stores sometimes purchase corresponding brands’ commodities online. From the survey results of Ipthorp in 2013, more and more people always act in accordance with the following rule: “first, look for goods online; second, go to the corresponding brick-and-mortar store to experience it; third, place an order online”. This may imply the future development trend that brick-and-mortar stores are mainly for experiential customers, while online retailing stores are always for transactional buyer. Firms have taken advantage of online retailing, which provides a channel through which to better promote and distribute their products. Moreover, as a matter of fact, some suppliers are looking for an online expansion strategy, relying on retail platforms in addition to their preexisting offline channels.

Online retailing platform has provided all sorts of channels for suppliers to sell their products. They serve as an intermediary, matching buyers with sellers, whereas control of the product is left to the seller [14]. A supplier who offers substitutable products through multiple online channels definitely results in competition between channels. Yan et al. found that selling through a new channel would impact manufacturers’ sales in the traditional channel because of the presence of spillover between channels [15]. However, the addition of a direct channel alongside a reseller channel in the e-commerce age is not necessarily detrimental to the reseller. Actually, both parties could benefit from the associated adjustment in the manufacturer’s pricing [16]. Furthermore, Shen et al. [17] studied how a manufacturer should engage with an online platform retailer and a traditional reseller, and they derived the condition of the equilibrium channel. Abhishek et al. used a stylized theoretical model to answer a key question that e-tailers are facing [18]: when should an agency selling format be used instead of the more conventional reselling format? They found that an online platform used to directly connect sellers with buyers is more efficient than reselling and leads to lower retail prices. In fact, if a supplier sells products through a traditional reseller, the supplier is regarded as a leader, while the traditional reseller is taken as a follower of the Stackelberg game. Meanwhile, if a supplier sells through an online platform reseller, we regard the online platform as outsourcing their supply to a supplier in which the platform is a leader, while the supplier is a follower. Classically, Atkins and Liang [19] presented a more general explanation for why the decentralization (distribution) mode may be preferred for the fierce market environment. Moreover, they found that there is no qualitative difference when either the supplier or the retailer is modeled as the channel leader and makes the distribution decisions.

Lastly, this research can be linked to the literature that explores the service fee from online retailing platforms. To fulfill an online order, firms take on the cost of storage and hiring staff, which are viewed as fixed. From the perspective of suppliers, they should pay the fixed order fulfillment costs when they sell products directly to consumers through the online platform [20]. On the other hand, online retailers play a role of third partner in online commodity transactions. For example, Amazon can sell products directly as an intermediary connecting consumers and suppliers, or they can create access to suppliers to offer products, and suppliers will charge them a service fee, including advertising promotion, product exposure, platform licensing (slotting fee), and so on. Ryan et al. also indicated that although selling the product through the online platform expands the market of available consumers for the retailer, it generally comes at some expense to the retailer, e.g., a fixed participation fee or a revenue-sharing requirement. Shen et al. found that the slotting fee is neither always beneficial to the platform retailer nor always harmful to the supplier, and it depends on the demand substitution effect between the two retail channels. In other words, when the market competition is fierce, the supplier may benefit from the requirements of the slotting fee. For example, a publisher can sell e-books on its website or Amazon, who should operate as an online marketplace because of low order-fulfillment costs; meanwhile, the publisher sells print books with high order-fulfillment costs on Amazon, who should function as a reseller.

Table 1. Comparison of studies.

Article	Equilibrium Analysis	The Demand Functions from Three Channels	Channel Competition	Strategic Effect
Yan et al. [15]	√		√	√
Shen et al. [17]	√		√
Shi et al. [21]	√	√	√	√
Zhang et al. [22]	√		√
Zhang et al. [23]	√		√
Our study	√	√	√	√

contrasts this study with the extant works. It helps to understand how we bridge research gaps.

The distinctiveness of our research:

The most noticeable argument in our study is that the online promotion service cost (a slotting fee or a revenue-sharing proportion) is an exogenous factor that impacts the channel strategies of the supplier. The inspiration mainly comes from the processing method of service cost [24,25]. Compared with the existing literature, our model is innovative in the following aspects. First, we extend the competitive supply chain to the setting of multiple channels’ strategies with extra market potential stimulated by online platforms, and we investigate supply chain competition issues under different channel structures. Second, we consider the factors of participants’ profits maximization in chain-to-chain competition and build on the existing literature in channels strategy of online retailing, with a focus on the magnitude of slotting fee (or revenue-sharing proportion), the substitution effect between the both products (or the intensity of price competition), and the growth rate of demand and channel performance of the members of a given channel. Third, our paper contributes to the channel strategy literature by investigating the effects of channel structures on the profits of participants. In addition, a game-theoretic approach is considered, and the equilibrium solutions are calculated under different channel structures. Meanwhile, some meaningful management implications are offered to participants in the supply chain.

3. Problem Description and Basic Assumptions

3.1. Problem Description

We consider a supply chain consisting of a monopoly supplier (Gree) and a traditional distributor (Jinghai). The supplier sells a single product through the distributor’s brick-and-mortar channel. Moreover, the supplier is driven to decide whether to adopt one/two platform scheme(s) because of the dividends of e-commerce. In view of the platform scheme, if a supplier adopts the agency selling scheme (i.e., Gree sets up a direct-sales store on Tmall), the platform will provide online access for the supplier directly to consumers and charge an exogenous slotting fee and a commission rate. Otherwise, the supplier adopts the reselling scheme (i.e., Gree sells their products through an online reseller, and JD is a self-employed store), where the platform (i.e., JD) functions as a reseller. Hence, we design four different channel structures: (I) the supplier does not adopt either of the two schemes; (II) the supplier adopts the agency selling scheme; (III) the supplier adopts the reselling scheme; and (IV) the supplier adopts both schemes. The channel structures are illustrated by Figure 1.

The timeline of the game is as follows. Stage 1: the supplier chooses whether to adopt the platform scheme, which results in four potential supply chain channel structures. Stage 2: the supplier acting as a leader sets the wholesale price $w_1$ in the traditional distribution channel. If an agency selling scheme is adopted, the platform offers the supplier a marketplace to sell products by charging a commission rate $\lambda$ and an exogenous slotting fee $F$. If a reselling scheme is adopted, the supplier sets the wholesale price $w_2$($w_3$) for the platform reseller. Stage 3: the supplier determines the retail price $p_2$ under an agency selling scheme, while the platform reseller decides the retail price $p_3$ under a reselling scheme.

3.2. Market Demand

The initial total market size is expressed as $2a$. If the supplier does not adopt the platform scheme, the demand from the traditional market follows a linear function:

$$q^I=2a-p^I,$$

(1)

If the supplier adopts one of the platform schemes, the traditional channel and the platform channel will engage in price competition. The demand functions in both channels can be given by

$$q_1^{\mathrm{\Phi }}=a-p_1^{\mathrm{\Phi }}+\gamma p_2^{\mathrm{\Phi }},$$

(2)

$$q_2^{\mathrm{\Phi }}=a+e-p_2^{\mathrm{\Phi }}+\gamma p_1^{\mathrm{\Phi }},$$

(3)

where a is the base market size in each channel and $\gamma \in (0,1)$ measures the degree of substitution (or the competitive coefficient) between the two channels. The parameter e captures the extra market potential driven by the promotion service (or selling effort) and provided by the platform. Herein, we assume $a>e$. For notational convenience, we define $\mathrm{\Phi }=\{II,III\}$. Specifically, when an agency selling scheme is adopted, $\mathrm{\Phi }=II$. When a reselling scheme is adopted, $\mathrm{\Phi }=III$.

If the supplier adopts both platform schemes, the demand functions are as follows:

$$q_1^{IV}=a-p_1^{IV}+\gamma (p_2^{IV}+p_3^{IV}),$$

(4)

$$q_2^{IV}=(1-\delta )(a+e)-p_2^{IV}+\gamma (p_1^{IV}+p_3^{IV}),$$

(5)

$$q_3^{IV}=\delta (a+e)-p_3^{IV}+\gamma (p_1^{IV}+p_2^{IV}),$$

(6)

where $\delta \in (0,1)$ measures the market share of the reselling scheme and $(1-\delta )$ measures the market share of the agency selling scheme. Similar assumptions can be drawn from the previous literature [21,26]. As a matter of fact, the main reason why a supplier generates some incentive to employ the platform schemes to sell their products is that the platform may effectively promote the benefits of the supplier (Ryan et al. [14]). For example, the platform (JD, Tmall, or Amazon) can provide the advertising, pre-sales consulting, display, detailed product presentation, and logistics to facilitate transactions (Jiang et al. [11]). When $e=0$, it may imply that consumers are indifferent to advertisement promotion from the online retail platform. In contrast, it is very likely for consumers to place an order under the influence of promotion activity from the online retail platform. This statement is consistent with conventional wisdom.

4. Equilibrium Analysis

In this section, we examine the equilibrium decisions and profits for the four modes, and relevant proofs are provided in the Appendix A.

4.1. Mode I

Under this setting, the supplier sells products only through the traditional distributor. In order to maximize their profit function ${\pi }_S^I=\theta w^I{q}^I$, the supplier first sets the wholesale price $w^I$. Then, the distributor responds by determining the retail price $p^I$ to maximize their profit function ${\pi }_R^I=(p^I-w^I)q^I+(1-\theta )w^I{q}^I$. These profit functions imply that the traditional distributor holds $(1-\theta )$ shares of their upstream supplier (e.g., Gree and Jinghai). In order to guarantee the decision-making independence of both participants, $\theta$ should be smaller than 0.5; otherwise (i.e., $\theta >0.5$), the supplier will lose their decision power and become a subsidiary firm of the platform retailer (Ren et al. [7]). In addition, when $\theta =1$, it denotes that the relationship between the two participants becomes traditional and relatively independent. Given the Stackelberg game, the equilibrium results can be solved backwards and then given as follows.

In mode I, the optimal pricing and demand decisions are, respectively,

$$w^{I*}={\displaystyle \frac{a}{\theta }}, p^{I*}={\displaystyle \frac{3a}{2}} \mathrm{and} q^{I*}={\displaystyle \frac{a}{2}}.$$

The corresponding equilibrium profits are

$${\pi }_S^{I*}={\displaystyle \frac{a^2}{2}} \mathit{and} {\pi }_R^{I*}={\displaystyle \frac{a^2}{4}}.$$

Accordingly, the necessary condition for $\theta$ is more than 2/3, which is derived from $w^{I*}<p^{I*}$. This means that the traditional distributor should be restricted to holding no more than one third of the supplier’s shares.

4.2. Mode II

In this mode, the supplier sells their products through both the traditional distribution channel and the online agency selling channel. First, the supplier simultaneously decides the wholesale price $w_1^{II}$ and the retail price $p_2^{II}$ in the online channel. Then, the brick-and-mortar distributor decides the retail price $p_1^{II}$. The profit functions of the supplier, platform, and distributor are ${\pi }_S^{II}=\theta w_1^{II}{q}_1^{II}+\lambda p_2^{II}{q}_2^{II}-F$, ${\pi }_E^{II}=(1-\lambda )p_2^{II}{q}_2^{II}+F$ and ${\pi }_R^{II}=(p_1^{II}-w_1^{II})q_1^{II}+(1-\theta )w_1^{II}{q}_1^{II}$, respectively. As a matter of fact, the exogenous commission rate $1-\lambda$ charged by the platform is predetermined for different product categories. For example, Amazon offers a commission rate ranging from 6% to 25% for all suppliers. JD offers a commission rate which is normally lower than 10% [22,23]. Specifically, for the household appliance industry, JD sets a commission rate of 4.5% for the air conditioner and asks for a platform licensing fee of RMB 1000 “https://zhaoshang.jd.com/index/qualificate (accessed on 26 April 2024)”. Herein, we assume $\lambda \in (0.7,1]$ and define $A_1={\lambda }^2{\gamma }^2+6\lambda {\gamma }^2+{\gamma }^2-8\lambda$.

The optimal pricing and demand decisions are given by

$$w_1^{II*}={\displaystyle \frac{({\gamma }^2-\lambda {\gamma }^2-2\gamma -2\lambda \gamma -4)\lambda a-2(1+\lambda )\lambda \gamma e}{\theta A_1}},$$

$$p_1^{II*}={\displaystyle \frac{(2{\gamma }^2-3\gamma -\lambda \gamma -6)\lambda a-(3+\lambda )\lambda \gamma e}{A_1}}, p_2^{II*}={\displaystyle \frac{(-\gamma -3\lambda \gamma -4\lambda )a-4\lambda e}{A_1}},$$

$$q_1^{II*}={\displaystyle \frac{({\gamma }^2+\lambda {\gamma }^2-\gamma +\lambda \gamma -2)\lambda a-(1-\lambda )\lambda \gamma e}{A_1}},$$

and

$$q_2^{II*}={\displaystyle \frac{(2\lambda {\gamma }^3+{\gamma }^2+3\lambda {\gamma }^2+\gamma -3\lambda \gamma -4\lambda )a+({\gamma }^2+3\lambda {\gamma }^2-4\lambda )e}{A_1}}$$

The corresponding equilibrium profits are

$${\pi }_S^{II*}=-\lambda {\displaystyle \frac{(\lambda {\gamma }^2+\gamma +3\lambda \gamma +2\lambda +1)a^2+2\lambda e^2+(\gamma +3\lambda \gamma +4\lambda )ae}{A_1}}-F,$$

and

$${\pi }_R^{II*}={\left[{\displaystyle \frac{({\gamma }^2+\lambda {\gamma }^2-\gamma +\lambda \gamma -2)\lambda a-(1-\lambda )\lambda \gamma e}{A_1}}\right]}^2.$$

In order to make sure that the prices are non-negative and then guarantee the feasibility of this mode, we define $\gamma \le {\gamma }^{II}$, where ${\gamma }^{II}=\sqrt{8\lambda /{\lambda }^2+6\lambda +1}$. To better compare the equilibrium results and thus obtain the analytical solutions, we first study the case of $\lambda =1$, and further discussion about the case of $\lambda \ne 1$ can be found in Proposition 2 and Corollary 1. When $\lambda =1$, the supplier is only required to pay a slotting fee $F$ to enter the online platform.

Lemma 1.

The $\theta$ shares hold by supplier should satisfy ${\displaystyle \frac{2}{3}}<{\theta }^{II}<\theta <1$, where $k={\displaystyle \frac{a}{e}}>1$ and ${\theta }^{II}={\displaystyle \frac{2k(\gamma +1)+2\gamma }{k(3+2\gamma -{\gamma }^2)+2\gamma }}$.

This condition ensures that the equilibrium wholesale price $w_1^{II*}$ is less than the equilibrium retail price $p_1^{II*}$ in the traditional distribution channel. Compared with the case where the supplier adopts neither of the platform schemes, we find that the supplier adopting the agency selling scheme should hold more shares to ensure the maximization of their profit. On the other hand, if the supplier decides to adopt the agency selling scheme, it will harm the shareholding of the traditional distributor (i.e., $(1-\theta )<{\displaystyle \frac{1}{3}}$).

Lemma 2.

When $F<F^{II}$, the supplier will have the incentive to adopt the agency selling scheme, where $F^{II}={\displaystyle \frac{\gamma ae}{8(1-{\gamma }^2)}}$.

The condition that the slotting fee charged by the platform should satisfy is induced by ${\pi }_S^{II*}(e,F)>{\pi }_S^{II*}(0,0)$. Obviously, the slotting fee increases with the extra market potential $e$ driven by the agency selling scheme and the degree of substitution between the two channels.

Moreover, in the case with $\lambda =1$, we compare the equilibrium decisions and profits, and the results are detailed in the following proposition.

Proposition 1.

When the supplier adopts the agency selling scheme (i.e., $F<F^{II}$), we obtain the comparison of equilibrium decisions from both channels,

(1)

$p_1^{II*}>p_2^{II*}$ and  $q_1^{II*}<q_2^{II*}$;

When the supplier adopts the agency selling scheme (i.e., $F<F^{II}$), we obtain the comparison of equilibrium profits from both modes,

(2)

${\pi }_S^{I*}<{\pi }_S^{II*}$ and  ${\pi }_R^{I*}>{\pi }_R^{II*}$.

Part (1) indicates that the products are of high retail price and low order quantity in the traditional distribution channel. On the contrary, the products in the agency selling channel are of low retail price and high order quantity. Analyzing the reason for this from the channel structure side, the supplier selecting an agency selling scheme means they can sell directly to consumers. This has more advantages in terms of retail price and order quantity compared to the traditional distribution mode. On the other hand, we believe that the extra market potential e driven by the promotion service and provided by the platform can stimulate the order quantity from the agency selling channel.

According to part (2), this hints that the supplier has the incentive to adopt the agency scheme, even if they have to pay the slotting fee. Thus, the reasonable channel expansion is beneficial in improving the profitability of supplier. Nevertheless, for the traditional distributor, the adoption of a platform scheme will make their profit tend to decline. The addition of a new sales channel carves up the base market of the traditional distribution channel. It makes the traditional distributor lose the advantages of order quantity. Moreover, because of the characteristics of the agency selling channel, the distributor also does not have a price advantage. As a matter of fact, this also explains why Jinghai would have a negative attitude about Gree’s adoption of an online platform scheme.

When $\lambda \ne 1$, the supplier is allowed to adopt the agency selling scheme by paying a slotting fee $F$ and a revenue-sharing proportion $1-\lambda$ to the platform. How the parameter $\lambda$ affects these decisions and profits in mode II will be explained by the following proposition.

Proposition 2.

In mode II, we have the following assumptions:

(1)

$p_2^{II*}$, $q_1^{II*}$ and ${\pi }_R^{II*}$ are decreasing with $\lambda$;

(2)

$q_2^{II*}$ and ${\pi }_S^{II*}$ are increasing with $\lambda$.

Proposition 2 demonstrates that the retail price (order quantity) of products on the platform decreases (increases) when the revenue-sharing proportion $\lambda$ for the supplier increases. To maximize the supplier’s profit, the lower revenue sharing for the supplier will result in higher retail price. The order quantity will be affected and then decrease. Otherwise, the order quantity in the traditional distribution channel will rise to cope with the supplier’s lower revenue due to the reduction in revenue sharing from the online platform channel.

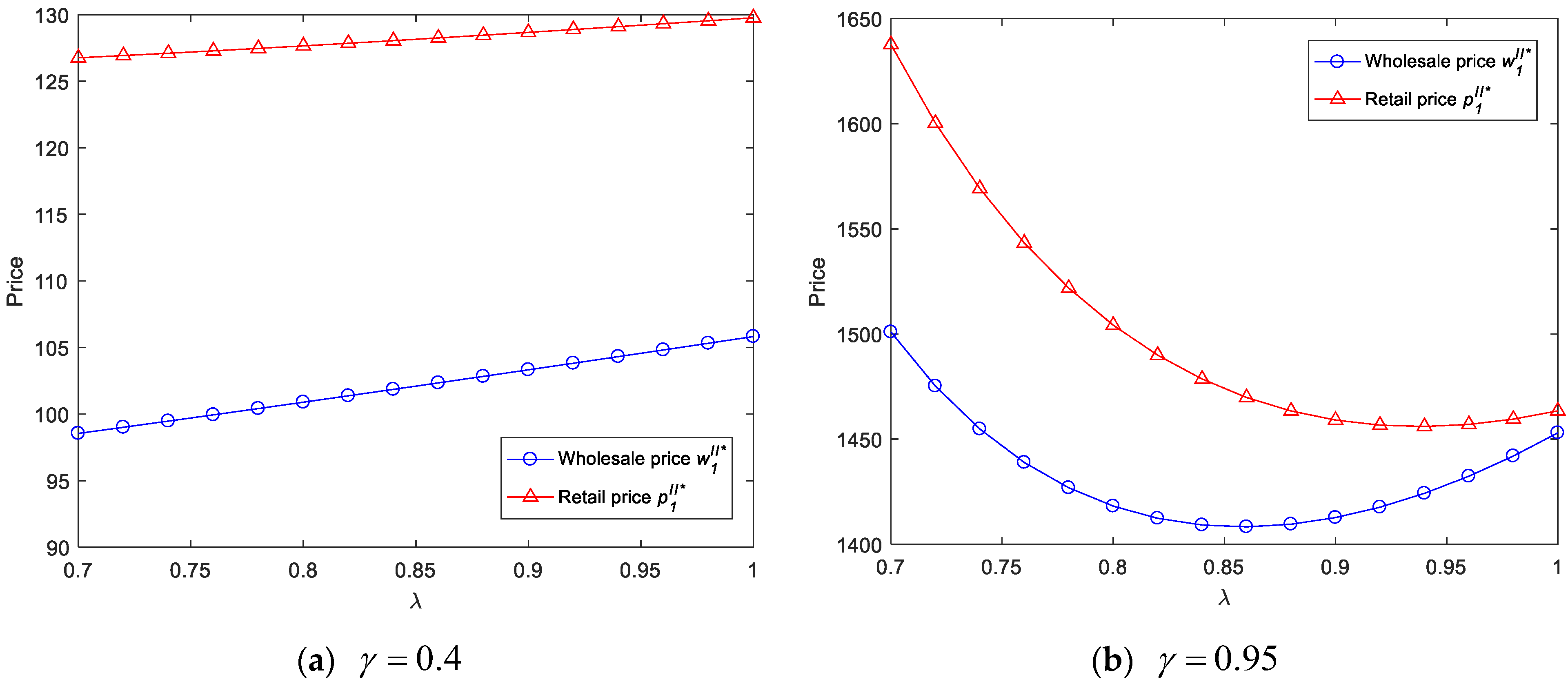
To better illustrate the impact of $\lambda$ on $w_1^{II*}$ and $p_1^{II*}$, Figure 2 shows how the parameter $\lambda$ affects the prices in the traditional distribution channel, where we set $a=100$, $e=90$, and $\theta =0.99$. According to Figure 2a, the retail (wholesale) price in the traditional distribution channel increases with the supplier’s revenue-sharing proportion $\lambda$ if the market competition intensity is relatively low. The main reason behind this is that the order quantity of the traditional distribution channel decreases with the revenue-sharing proportion earned by the supplier (see part (1) in Proposition 2). To ensure profitability, the supplier has to raise prices ($w_1^{II*}$ and $p_1^{II*}$). Significantly, when the market competition level $\gamma$ is very large and the supplier’s revenue-sharing proportion $\lambda$ is relatively high, the prices of the traditional distribution channel will decrease with the supplier’s revenue-sharing proportion. This hints that the intense market has more influence on the prices than the supplier’s revenue-sharing proportion. Therefore, from the perspective of Jinghai, their retail price is affected by not only the market intensity but also the supplier’s revenue-sharing proportion.

From the point of view of profit, we observe that the traditional distributor’s profit decreases when the revenue-sharing proportion $\lambda$ for the supplier increases; instead, the supplier’s profit increases with the revenue sharing for the supplier. This point reflects the influence of introducing the agency scheme on the traditional distributor’s profitability to some extent. As the supplier’s profit gained from one sales channel increases, their profit from the other sales channel will gradually decrease. As a result, the profitability of the traditional distributor is affected and declines.

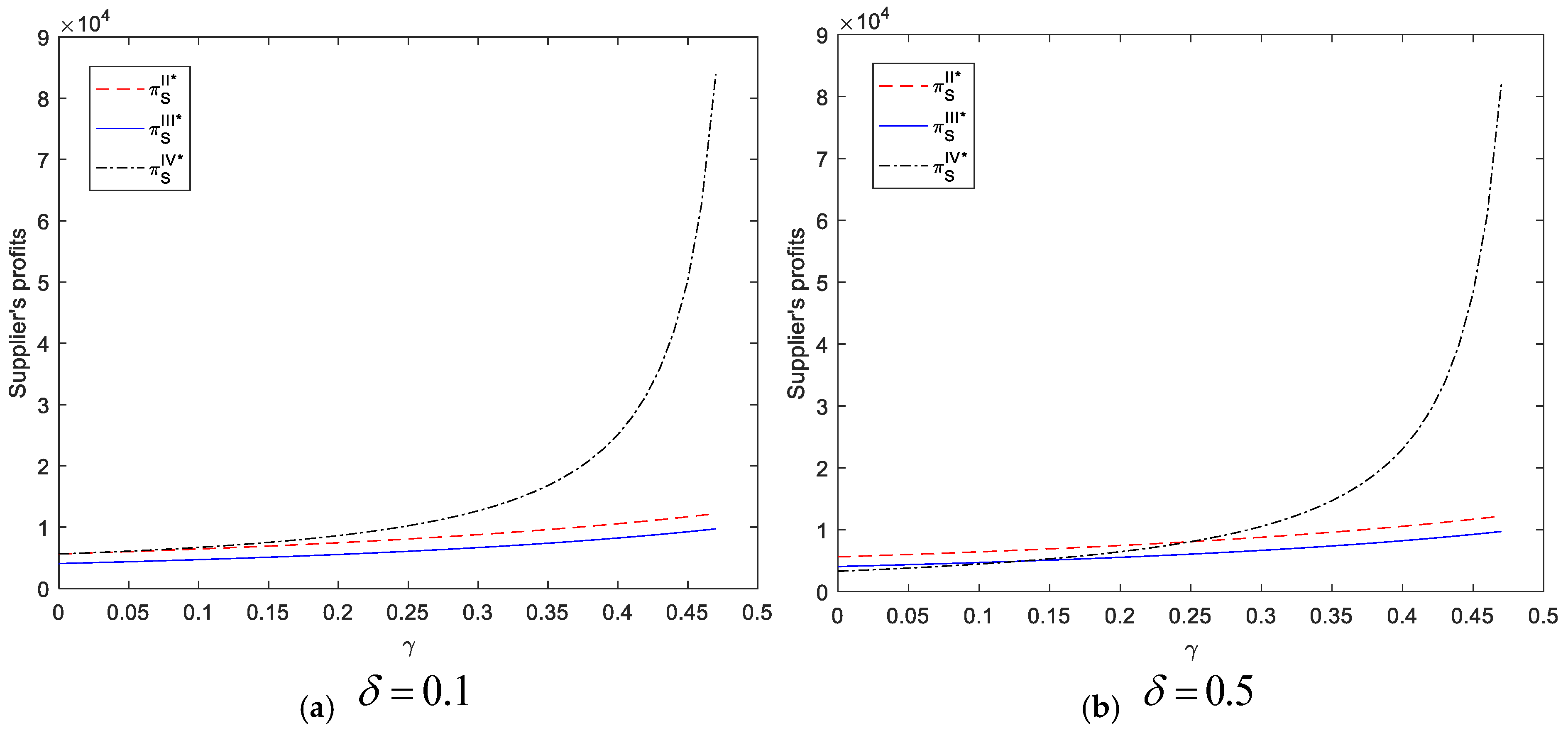
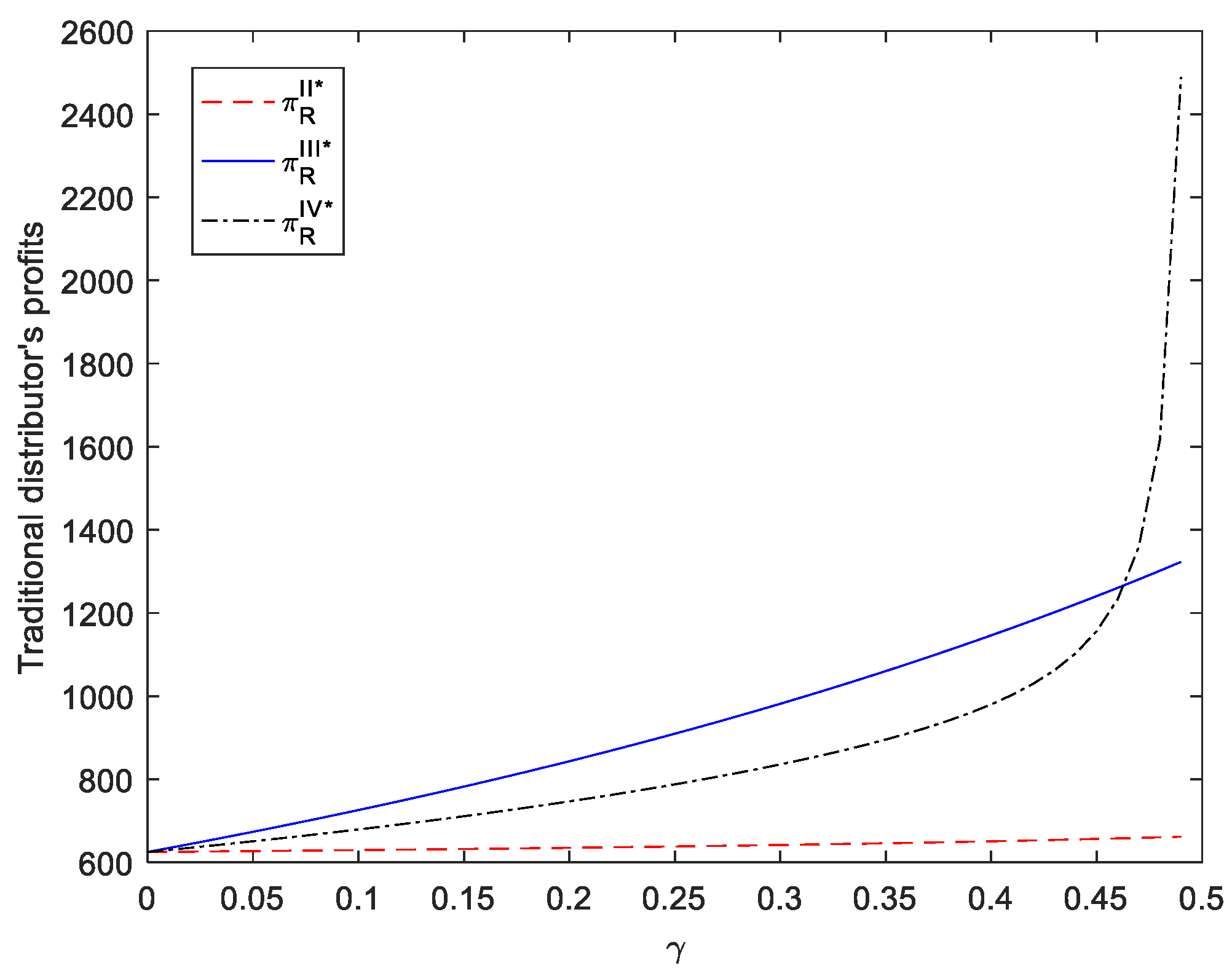
Based on Proposition 2, we further compare the supplier’ (or the traditional distributors’) profits with and without the adoption of an agency scheme. To facilitate comparative analysis, herein, we assume that the slotting fee $F=0$ and that the supplier who adopts an agency selling scheme only needs to pay a revenue-sharing proportion $1-\lambda$ to the platform. This assumption is in line with most realities. For example, TMall, the online platform in China, does not charge merchants a platform licensing fee $F$ but sets a commission rate 2% as a condition of entry.

Corollary 1.

When ${∆}_1<0$, we have ${\pi }_R^{II*}>{\pi }_R^{I*}$; otherwise, ${\pi }_R^{II*}\le {\pi }_R^{I*}$. When ${∆}_2>0$, we have ${\pi }_S^{II*}>{\pi }_S^{I*}$; otherwise, ${\pi }_S^{II*}\le {\pi }_S^{I*}$, where

$$\left\{\begin{array}{l}{∆}_1=(2a+\gamma a+2e)\gamma {\lambda }^2-2(2{\gamma }^{2}a+\gamma a+6a+\gamma e)\lambda -{\gamma }^{2}a\\ {∆}_2=[3(\gamma a+2a^2+2e)\gamma a+4{(a+e)}^2]{\lambda }^2+2[3({\gamma }^2+1)a+(a+e)\gamma ]a\lambda +{\gamma }^2{a}^2.\end{array}\right.$$

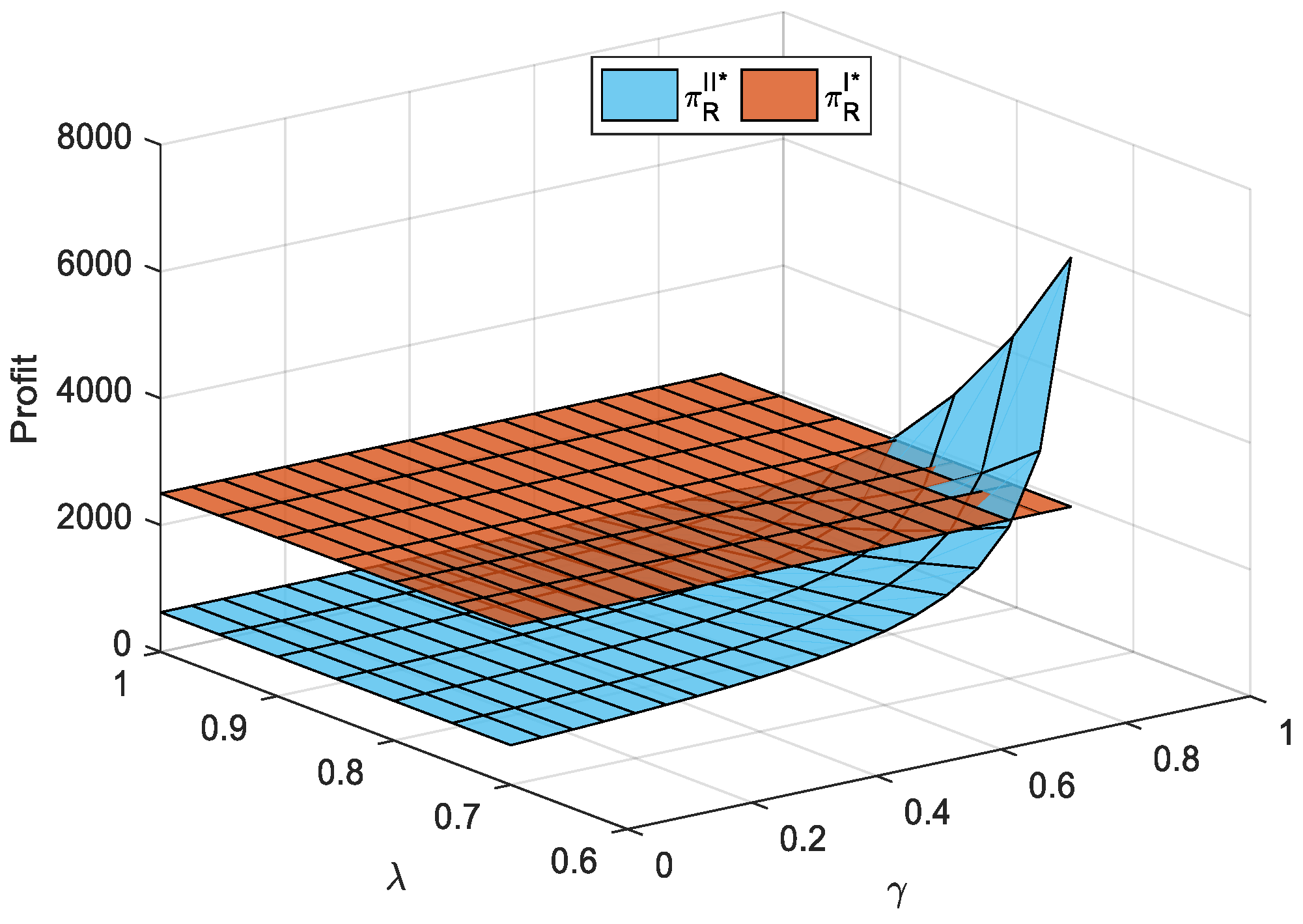
For intuitive analysis and comparison, we take Figure 3 and Figure 4 to illustrate these results. According to Figure 3, when the competition intensity in market is sufficiently fierce and the revenue sharing for the supplier is relatively low, the profit of the traditional distributor with the supplier adopting the agency scheme is higher than that without the supplier adopting such a scheme. As a result, Gree’s opening of new sales channels (i.e., introducing an agency scheme) does not always spell disaster for traditional distributors (i.e., Jinghai). Moreover, as long as the condition $a>e$ is satisfied, this conclusion is still valid regardless of the size of $e$.

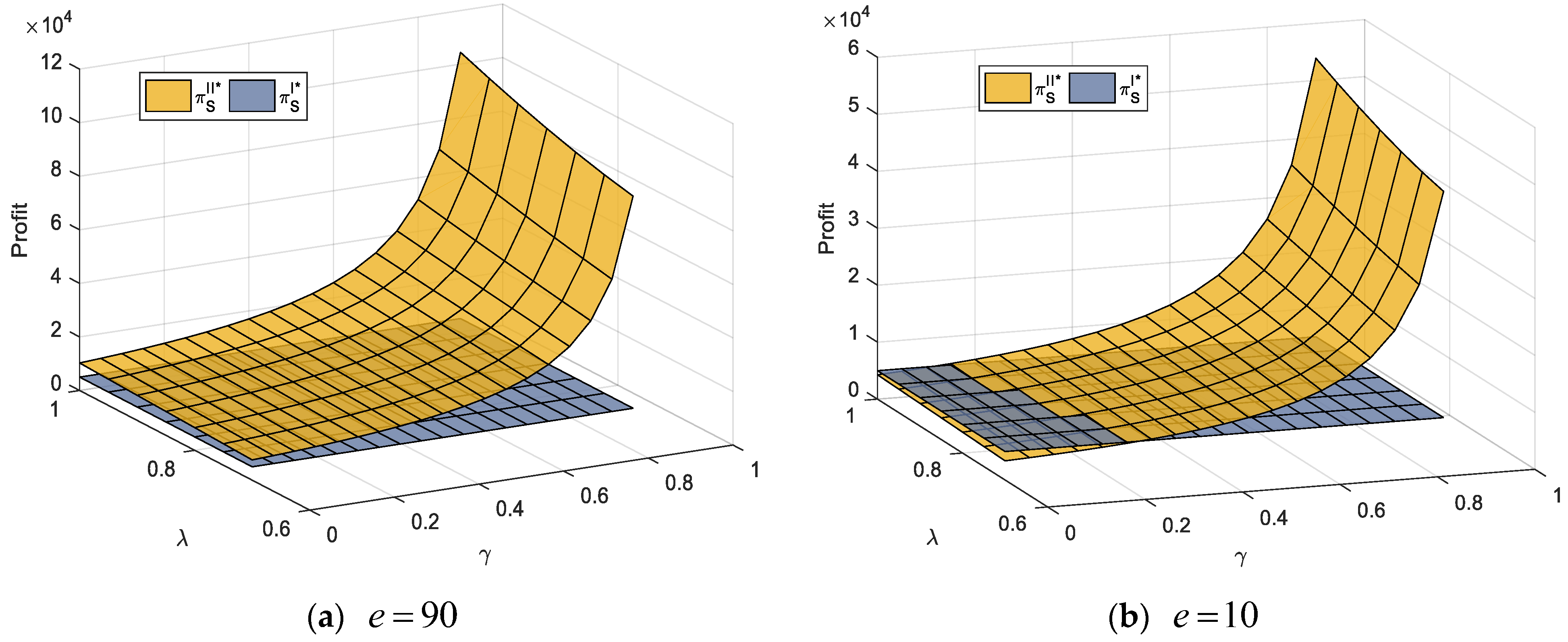
Nevertheless, the suppliers’ profit comparison results depend on the size of $e$, as Figure 4 shows. First, we set $a=100$ and $e=90$. This means that the additional market demand driven by the promotional service provided by the online platform grows closer to the market potential a. At this point, we observe that the profitability of the supplier adopting the agency scheme is always higher than that not adopting. The main reason for this is that the relatively high promotion service provided by the online platform effectively boosts profits. Even if the revenue sharing for the supplier is relatively low, the supplier prefers to engage in selling products through both channels. Separately, when the extra market demand driven by the online platform is much lower than the market potential a (i.e., $a=100$ and $e=10$), the profit of the supplier adopting the agency scheme is lower than that not adopting if the market intensity is sufficiently low. In other words, the low substitutability of products sold through both channels reduces the overall market demand. The supplier has no incentive to introduce an agency selling mode in addition to the traditional distribution.

4.3. Mode III

The supplier sells through both the traditional distribution channel and the online reselling channel in this mode. First, they simultaneously decide the wholesale prices $w_1^{III}$ in the traditional distribution channel and $w_2^{III}$ in the online reselling channel. Second, the brick-and-mortar distributor and the platform reseller determine the retail prices $p_1^{III}$ and $p_2^{III}$, respectively. The profit functions of supplier, platform reseller and distributor are ${\pi }_S^{III}=\theta w_1^{III}{q}_1^{III}+w_2^{III}{q}_2^{III}$, ${\pi }_E^{III}=(p_2^{III}-w_2^{III})q_2^{III}$ and ${\pi }_R^{III}=(p_1^{III}-w_1^{III})q_1^{III}+(1-\theta )$ $w_1^{III}{q}_1^{III}$, respectively. The equilibrium results can be solved backwards and then given as follows.

The optimal pricing and demand decisions are given by

$$w_1^{III*}={\displaystyle \frac{a+\gamma a+\gamma e}{2\theta (1-{\gamma }^2)}}, w_2^{III*}={\displaystyle \frac{a+\gamma a+e}{2(1-{\gamma }^2)}}, p_1^{III*}={\displaystyle \frac{(3-2\gamma )(1+\gamma )(2+\gamma )a+(5-2{\gamma }^2)\gamma e}{2(4-{\gamma }^2)(1-{\gamma }^2)}},$$

$$p_2^{III*}={\displaystyle \frac{(3-2\gamma )(1+\gamma )(2+\gamma )a+3(2-{\gamma }^2)\gamma e}{2(4-{\gamma }^2)(1-{\gamma }^2)}}, q_1^{III*}={\displaystyle \frac{(2+\gamma )a+\gamma e}{2(4-{\gamma }^2)}}, \mathrm{and}$$

$$q_2^{III*}={\displaystyle \frac{(2+\gamma )a+2e}{2(4-{\gamma }^2)}}.$$

The corresponding equilibrium profits are

$$\begin{gathered} {\pi }_S^{III*}={\displaystyle \frac{2(1+\gamma )(2+\gamma )(a+e)a+({\gamma }^2+2)e^2}{4(4-{\gamma }^2)(1-{\gamma }^2)}} \mathrm{and} \\ {\pi }_R^{III*}={\left(q_1^{III*}\right)}^2={\left[{\displaystyle \frac{(2+\gamma )a+\gamma e}{2(4-{\gamma }^2)}}\right]}^2. \end{gathered}$$

To ensure that the equilibrium wholesale price $w_1^{III*}$ is less than the equilibrium retail price $p_1^{III*}$, the feasible range of $\theta$ is defined as the following lemma.

Lemma 3.

The share proportion $\theta$ of the supplier should satisfy ${\displaystyle \frac{2}{3}}<{\theta }^{III}<{\theta }^{II}<\theta <1$, where ${\theta }^{III}={\displaystyle \frac{(4-{\gamma }^2)(1+\gamma )k+(4-{\gamma }^2)\gamma }{(3-2\gamma )(1+\gamma )(2+\gamma )k+(5-2{\gamma }^2)\gamma }}$ and $k={\displaystyle \frac{a}{e}}$.

According to Lemma 3, we find that the supplier adopting the reselling scheme may hold fewer shares than that adopting the agency scheme. In other words, if the supplier decides to introduce the online reselling scheme in addition to traditional distribution, their offline distributor may own the most shares but no more than two thirds of shares. Therefore, in order to ensure the maximum profit, the traditional distributor (i.e., Jinghai) should properly increase their shareholding in Gree, since Gree adopts an online reselling scheme.

Further, we compare the equilibrium decisions and profits as follows.

Proposition 3.

In mode III, we have

(1)

If $k={\displaystyle \frac{a}{e}}>{\displaystyle \frac{(\theta -\gamma )}{(1-\theta )(1+\gamma )}}$, $w_1^{III*}>w_2^{III*}$; otherwise $w_1^{III*}\le w_2^{III*}$;

(2)

$p_1^{III*}<p_2^{III*}$ and $q_1^{III*}<q_2^{III*}$.

From part 1, the middlemen may obtain different purchase prices from the supplier because of the Nash equilibrium. Specifically, when the extra market demand driven by the online promotion service provided by the platform is sufficiently large and the share proportion of the supplier is relatively high, the wholesale price in the traditional distribution channel could be less than that in the online reselling channel. From the perspective of supplier’s equilibrium profit, the high share proportion $\theta$ could result in a low wholesale price in the traditional distribution channel. For Gree, they should have the ability to adjust the wholesale price in both channels and the share proportion of the traditional distributor, according to market performance.

However, in terms of retail price from part 2, the platform reseller’s is larger than the traditional distributor’s. The main reason for this is that the source of traditional distributor’s profits primarily consists of two aspects: their own and upstream shares. Based on the premise of ensuring optimal profitability, their retail price would not be higher than platform reseller’s. Furthermore, the platform reseller’s order quantity is more than the traditional distributor’s due to online promotion efforts.

Next, we discuss whether the supplier is always motivated to develop a new sales channel in addition to the traditional channel.

Proposition 4.

The comparison of equilibrium decision profits from both modes I and III is as follows: $w^{I*}<w_1^{III*}$, $p^{I*}<p_1^{III*}$, $q^{I*}<q_1^{III*}$, ${\pi }_S^{I*}<{\pi }_S^{III*}$ and ${\pi }_R^{I*}<{\pi }_R^{III*}$.

Once the supplier starts to engage in the online reselling scheme, the wholesale and retail prices of the traditional distributor will become higher than before. This phenomenon is primarily caused by the competitive market. In this sense, it is undesirable for customers to add a new sales channel to the supplier. But if the supplier does not, she will be unable to meet consumers’ excessive demand for products. Obviously, the order quantity of the traditional distributor is more than before, on account of the entry of a retail competitor. Similar to Proposition 1 (2), the supplier distinctly benefits from adopting an online reselling scheme in addition to the traditional distribution channel. From the traditional distributor’s point of view, they benefit from the supplier introducing an online reselling scheme and suffer from supplier introducing an agency selling scheme. This conclusion does not align with common sense. It may not be a such bad thing for Jinghai to agree to Gree adding an online reselling scheme.

4.4. Mode IV

In this section, the supplier adopts both the agency selling and reselling schemes in addition to the traditional distribution. The profit functions of supplier, traditional distributor, and platform reseller are ${\pi }_S^{IV}=\theta w_1^{IV}{q}_1^{IV}+\lambda p_2^{IV}{q}_2^{IV}$$+w_3^{IV}{q}_3^{IV}-F$, ${\pi }_R^{IV}=(p_1^{IV}-$ $w_1^{IV})$$q_1^{IV}+(1-\theta )w_1^{IV}{q}_1^{IV}$ and ${\pi }_P^{IV}=(1-\lambda )p_2^{IV}{q}_2^{IV}+(p_3^{IV}-w_3^{IV})q_3^{IV}+F$, respectively. The supplier makes the first decision on the wholesale prices $w_1^{IV}$ in the traditional channel and $w_3^{IV}$ in the online reselling channel, and the retail price $p_2^{IV}$ in the agency selling channel. Then, the brick-and-mortar distributor and the platform reseller as followers of the Stackelberg game determine the retail prices $p_1^{IV}$ and $p_3^{IV}$, respectively. We solve this game backwards to obtain the equilibrium solutions. For the sake of space, the equilibrium results of $\lambda =1$ are presented by the following, and the results of $\lambda \ne 1$ are shown in Appendix A.

The optimal pricing and demand decisions are given by

$$w_1^{IV*}={\displaystyle \frac{a+\gamma e}{2\theta (1-2\gamma )(\gamma +1)}}, w_3^{IV*}={\displaystyle \frac{[2\gamma (1-\delta )+\delta ](a+e)-\gamma e}{2(1-2\gamma )(\gamma +1)}},$$

$$\begin{gathered} p_1^{IV*}={\displaystyle \frac{(2+\delta \gamma )a+2\theta w_1^{IV*}+(2+\gamma )\gamma p_2^{IV*}+\gamma w_3^{IV*}+\delta \gamma e}{4-{\gamma }^2}}, \\ {p}_2^{IV*}={\displaystyle \frac{(1-\delta +2\delta \gamma )(a+e)-\gamma e}{2(1-2\gamma )(\gamma +1)}}, \\ {p}_3^{IV*}={\displaystyle \frac{(2\delta +\gamma )a+\gamma \theta w_1^{IV*}+(2+\gamma )\gamma p_2^{IV*}+2w_3^{IV*}+2\delta e}{4-{\gamma }^2}}, \end{gathered}$$

$$q_1^{IV*}={\displaystyle \frac{2a+\delta \gamma (a+e)}{8-2{\gamma }^2}}, q_2^{IV*}={\displaystyle \frac{(2-2\delta +2\delta \gamma )(a+e)-\gamma e}{2(2-\gamma )}}, \mathrm{and}$$

$$q_3^{IV*}={\displaystyle \frac{\gamma a+2\delta (a+e)}{8-2{\gamma }^2}}.$$

The corresponding equilibrium profits are

$${\pi }_S^{IV*}={\displaystyle \frac{\begin{array}{l}{[2\delta (a+e)-e]}^2{\gamma }^3+[(2{\delta }^2+3\delta -1){(a+e)}^2+(\delta +3)a^2-\delta e^2]{\gamma }^2\hfill \\ +2[(7\delta -7{\delta }^2+1){(a+e)}^2+(\delta -2)ae+(\delta -3)e^2]\gamma \hfill \\ +2(3{\delta }^2-4\delta +3)(a^2+e^2+2)-2(e^2+2)\hfill \end{array}}{4(2{\gamma }^4+{\gamma }^3-9{\gamma }^2-4\gamma +4)}}-F, \mathrm{and}$$

$${\pi }_R^{IV*}={\displaystyle \frac{{[(a+e)\delta \gamma +2a]}^2}{4{(4-{\gamma }^2)}^2}}.$$

In order to guarantee the non-negativity of the prices, there is $\gamma <{\displaystyle \frac{1}{2}}$. First, we study the case of $\lambda =1$ and then discuss the case of $\lambda \ne 1$ in Proposition 6 and Corollary 2. When $\lambda =1$, the supplier is only required to pay a slotting fee $F$ to enter the online platform. Similar to modes II and III, the shares $\theta$ held by the supplier should satisfy ${\displaystyle \frac{2}{3}}<{\theta }^{IV}<1$ to ensure that the equilibrium wholesale price $w_1^{IV*}$ is less than the equilibrium retail price $p_1^{IV*}$, where

$${\theta }^{IV}={\displaystyle \frac{(4-{\gamma }^2)(k+\gamma )}{[6+(\delta -2)\gamma -(\delta +5){\gamma }^2-2\delta {\gamma }^3]k+[2+\delta -\delta \gamma -(2\delta +1){\gamma }^2]\gamma }}.$$

Lemma 4.

When $F<F^{IV}$, the supplier will have the incentive to adopt both the platform schemes, where $F^{IV}={\displaystyle \frac{\begin{array}{l}[(2\delta -1)e+4\delta a](2\delta -1)e{\gamma }^3+[(2{\delta }^2+2\delta -1)(2a+e)+2\delta a]e{\gamma }^2\hfill \\ +2[\delta (8-7\delta )(2a+e)-\delta a-2e]e\gamma +2(3{\delta }^2-4\delta +2)(2+e^2)\hfill \end{array}}{4(2{\gamma }^4+{\gamma }^3-9{\gamma }^2-4\gamma +4)}}$.

The condition of the slotting fee charged by the platform is induced by ${\pi }_S^{IV*}(e,F)>{\pi }_S^{IV*}$ $(0,0)$. Additionally, from $F^{IV}>F^{II}$, we believe that the maximum slotting fee the supplier can afford is more when the supplier adopts both the platform schemes than when she only adopts the agency selling scheme.

Next, we compare the equilibrium decisions and profits in the case of $\lambda =1$. The following conclusions can be made from Figure 5 and Figure 6.

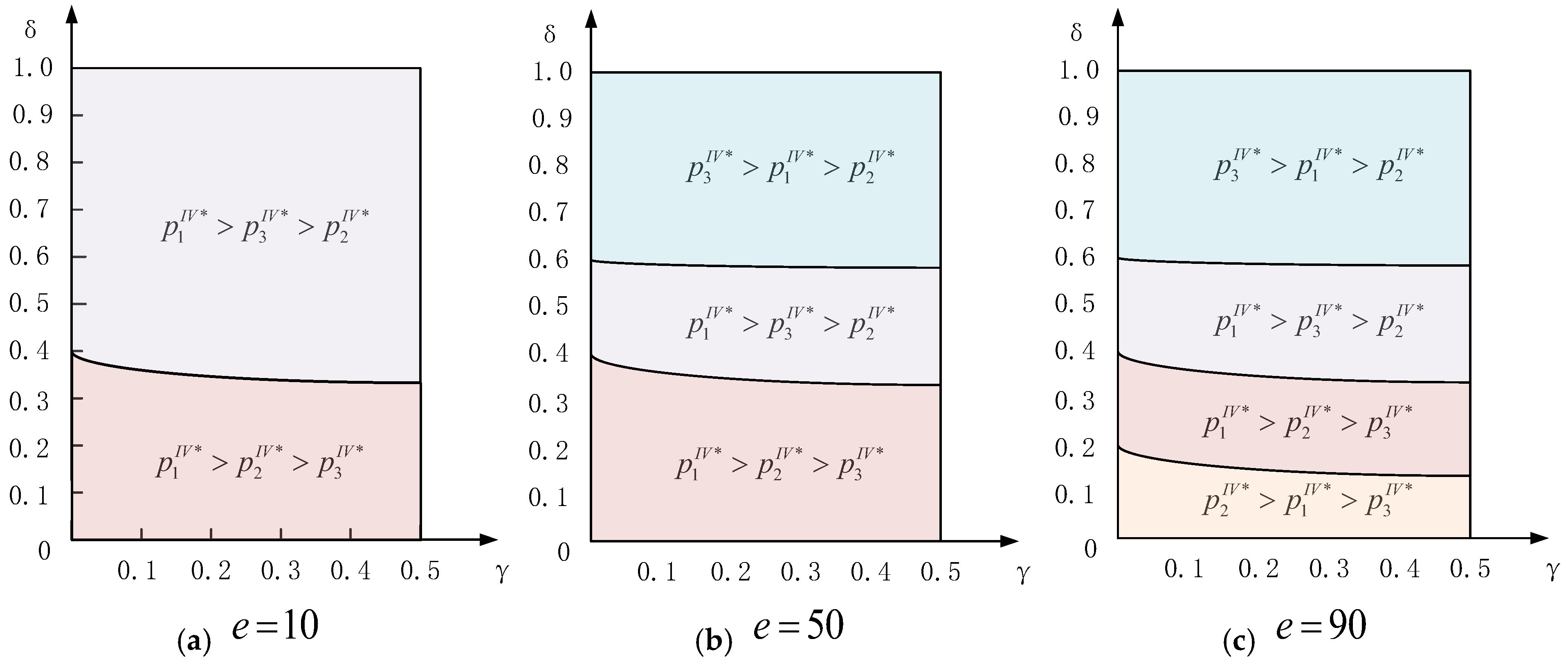
(1) When the market basis a and the extra market demand e driven by the online schemes are 100 and 10, respectively, the relationship of retail prices in these three channels emerges in two forms. Specifically, if the market share of the online reselling scheme $\delta$ is above about $\delta =0.4$, the retail price in the traditional distribution channel is the highest, followed by that in the online reselling channel, and it is the lowest in the online agency selling channel. Otherwise, the retail price in the online reselling channel is the lowest. Because of the low extra market demand e and the shares $1-\theta$ held by the traditional distributor, the wholesale price in the traditional channel is more than that in the online reselling channel. Then, we have $p_1^{IV*}>p_3^{IV*}$ in Figure 5a. Moreover, the higher market share of the agency selling scheme (namely, the lower market share of the online reselling scheme) drives the supplier to pay more costs, which leads to a higher retail price $p_2^{IV*}$. On the contrary, the lower market share of the agency selling scheme will result in a lower retail price $p_2^{IV*}$ as the region above about $\delta =0.4$ shows.

(2) When $a=100$ and $e=50$, we find that the retail price in the traditional distribution channel is lower than that in the online reselling channel since the market share of the online reselling scheme $\delta$ is relatively large. The larger extra market demand and market share of online reselling scheme urge the online reseller to raise the retail price. For this reason, if the market share of the online reselling scheme $\delta$ is sufficiently small and the extra market demand sufficiently large, the retail price in the traditional distribution channel is lower than that in the online agency selling channel. Therefore, on the premise of large extra market demand e, the larger market share of the online reselling scheme will result in the higher retail prices in the online reselling channel, and the larger market share of online agency selling scheme will generate a higher retail price in the agency selling channel. As the extra market demand e increases, the relationship of retail prices in these three channels becomes dynamic and variable.

(3) In terms of order quantity (i.e., Figure 6), when the market share of the online reselling scheme $\delta$ (or the market share of the online agency selling scheme $1-\delta$) is sufficiently small (or large), the order quantity in the online agency selling channel is the highest, followed by that in the traditional distribution channel and the lowest in the online reselling channel, regardless of the size of extra market demand e. The larger market share of the online reselling scheme and the higher extra market demand could result in the highest order quantity in the online reselling channel. By contrast, if the extra market demand at this point is sufficiently lower, the order quantity in the traditional distribution channel would be the highest (Figure 6).

Proposition 5.

In the case of $\lambda =1$, through comparing the profits of mode I and mode IV, we have

(1)

${\pi }_S^{I*}>{\pi }_S^{IV*}$, when ${∆}_3<0$;

(2)

${\pi }_R^{I*}>{\pi }_R^{IV*}$, where ${∆}_3$ is a binary function determined by the independent variables $\gamma$ and $\delta$ and can be seen in Appendix B.

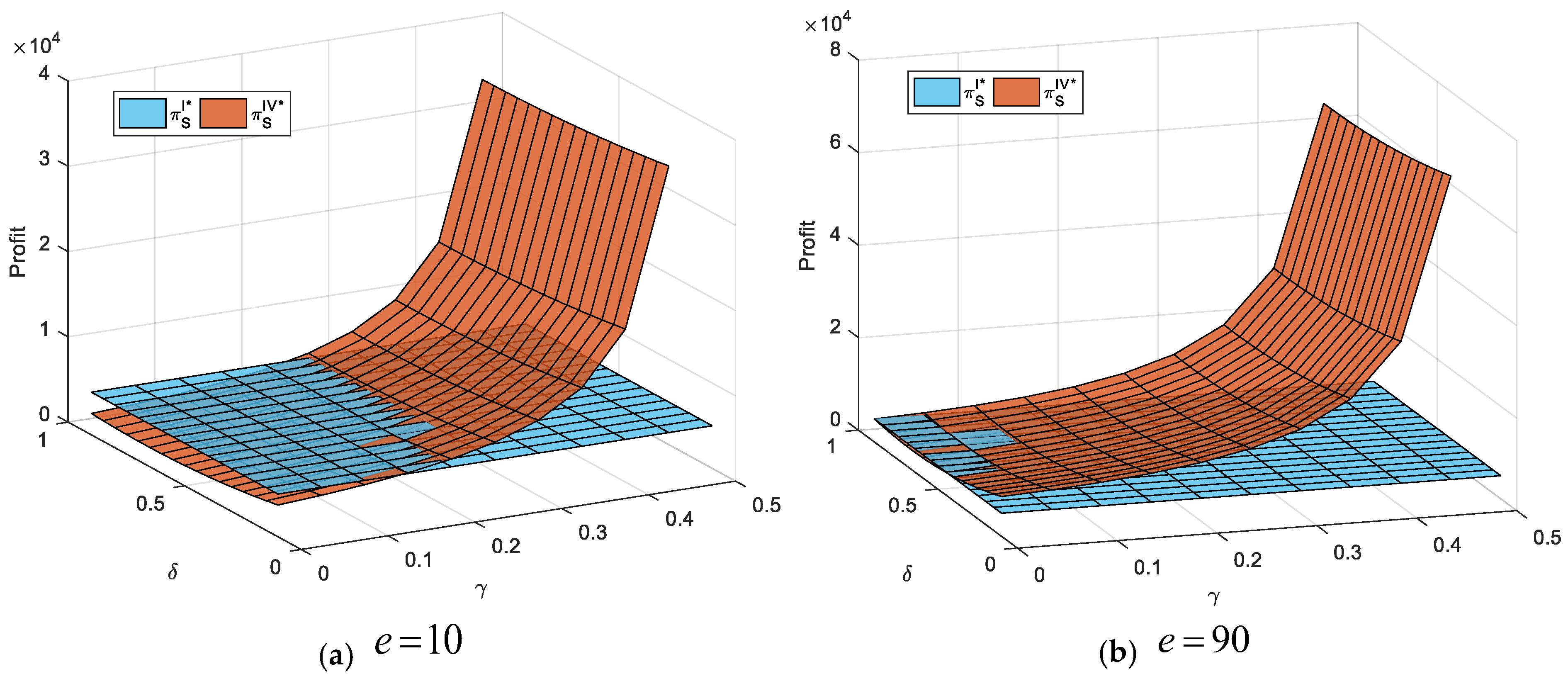
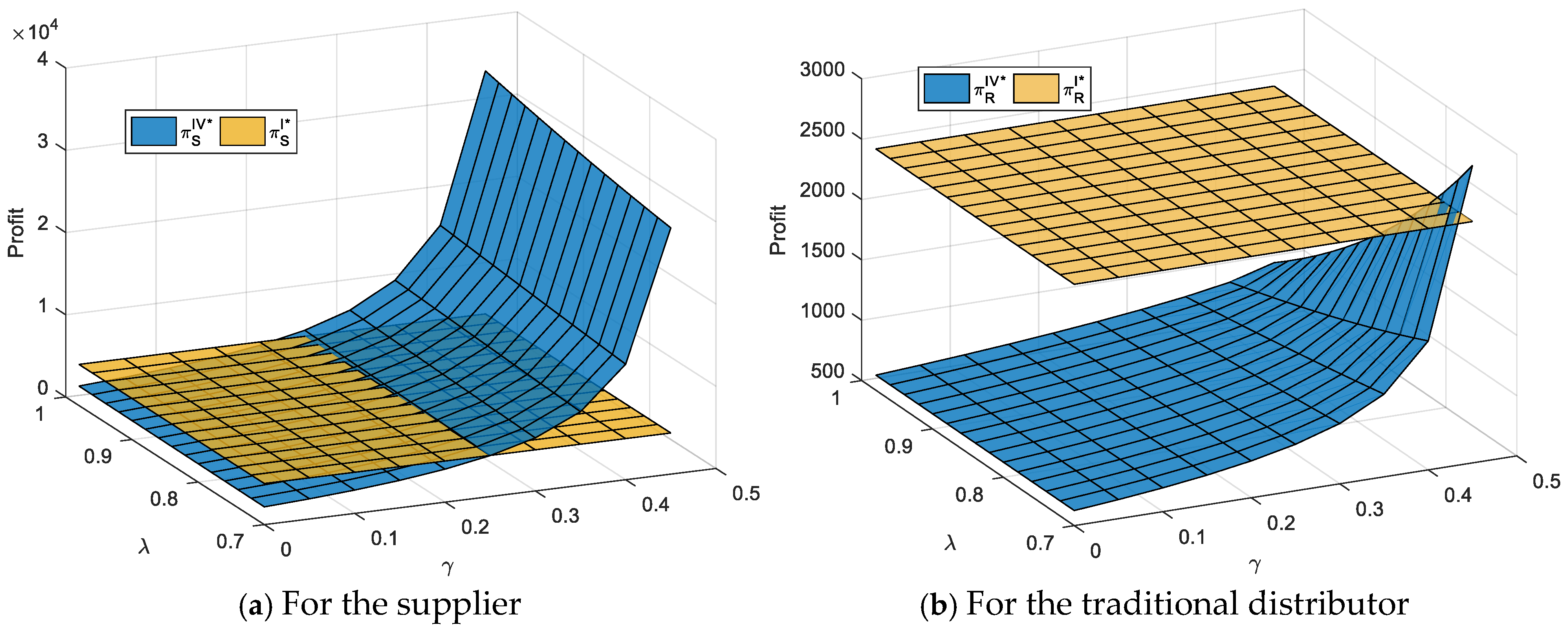
From the perspective of the supplier, we find that the profit of the supplier who adopts both the agency selling and reselling schemes in addition to the traditional distribution is not always more than that only selling through the traditional distributor. To provide a more intuitive description for the relationship between supplier’ profits, we take Figure 7 to illustrate the result. Based on this figure, we can easily find that the profit of the supplier who adopts both the agency selling and reselling schemes in addition to the traditional distribution is less than that only selling through the traditional distributor when the degree of substitution between the three channels is relatively low. Moreover, if the size of extra market demand e is very large (i.e., e = 0.9 in Figure 7b), the supplier does not have the incentive to adopt both schemes due to the relatively high market share of the online reselling scheme $\delta$ and the sufficiently low degree of substitution between the three channels. Therefore, it is not always a good thing for Gree to adopt as many channel schemes as possible. From the perspective of the traditional distributor’s profit, from Proposition 5, we observe that the offline distributor’s profitability is always damaged by the supplier introducing both online schemes. Jinghai are reluctant to accept Gree’s introduction of both the agency selling and reselling schemes in addition to traditional distribution.

When $\lambda \ne 1$, we will explore how the parameter $\lambda$ affects these decisions and profits in mode IV, and the following proposition provides some explanation.

Proposition 6.

In mode IV, we have

(1)

$w_1^{IV*}$, $w_3^{IV*}$ and $q_2^{IV*}$ increase with $\lambda$;

(2)

$p_2^{IV*}$, $q_1^{IV*}$, $q_3^{IV*}$ and ${\pi }_R^{IV*}$ increase with $\lambda$.

Proposition 6 shows that the wholesale prices (order quantities) in the traditional distribution and online reselling channels increase (decrease) with the revenue-sharing proportion $\lambda$ held by the supplier. The increase in $\lambda$ implies that the supplier would gain more profits from the online agency selling channel. Thus, there is a distinct increase in order quantity in this channel. By contrast, it indirectly leads to a decrease in order quantities in the traditional distribution and online reselling channels. To ensure the maximum profit of supplier, they will be pleased to raise the wholesale prices ($w_1^{IV*}$ and $w_3^{IV*}$).

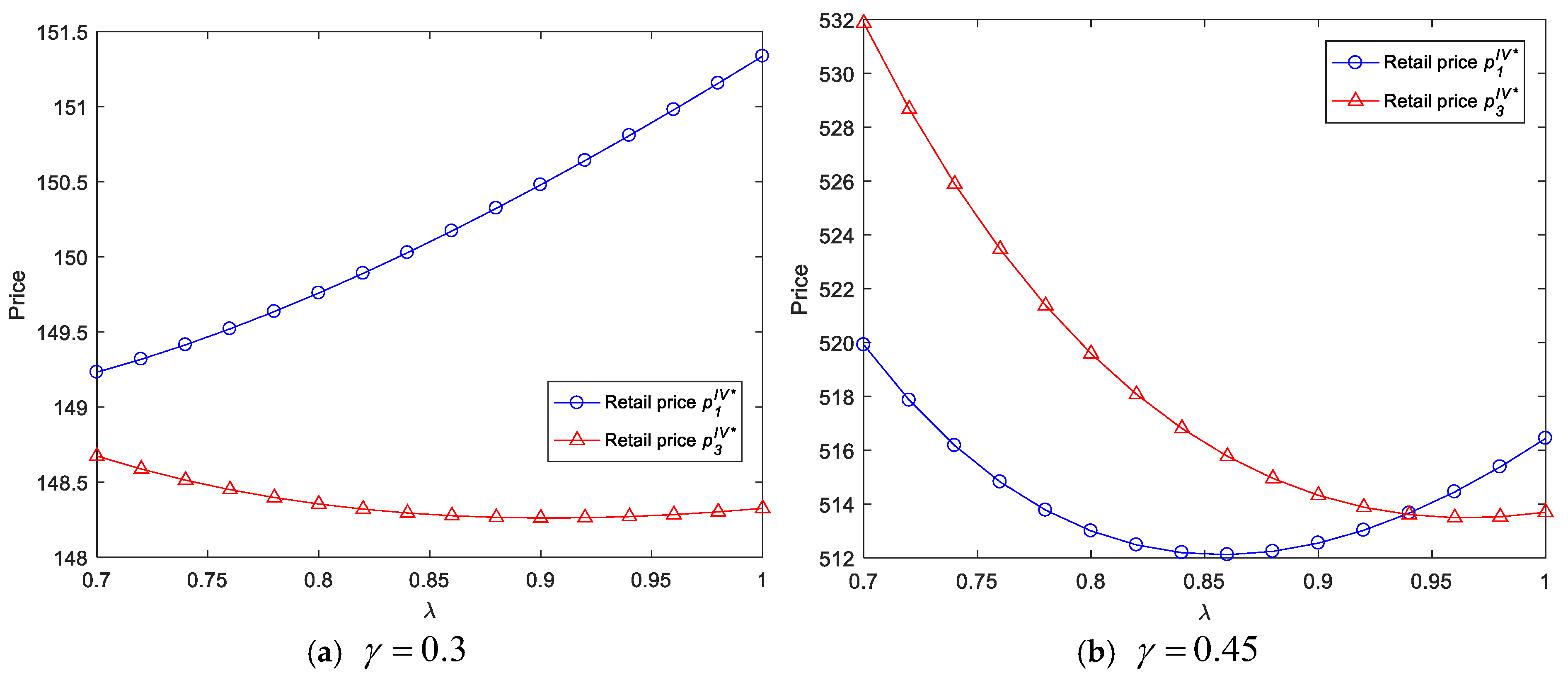
From the perspective of retail price, Figure 8 is used to represent the effect of $\lambda$ on retail prices in the traditional distribution and online reselling channels. Herein, we set $a=100$, $e=90$, $\delta =0.5$ and $\theta =0.99$. According to Figure 8, the retail price in the online reselling channel firstly decreases and then increases with the revenue-sharing proportion $\lambda$ held by the supplier. Moreover, the larger market intensity results in the higher retail prices. Therefore, from the online platform point of view, they should adjust the retail price of products according not only to the market intensity but also to the revenue-sharing proportion $\lambda$ of the supplier. The reason why the retail price in the traditional distribution channel increases with the revenue-sharing proportion $\lambda$ is that the traditional distributor (i.e., Jinghai) seeks to maximize profitability but has a decreasing order quantity. Even so, the profit of Jinghai decreases with the revenue sharing for the supplier in the online agency selling channel.

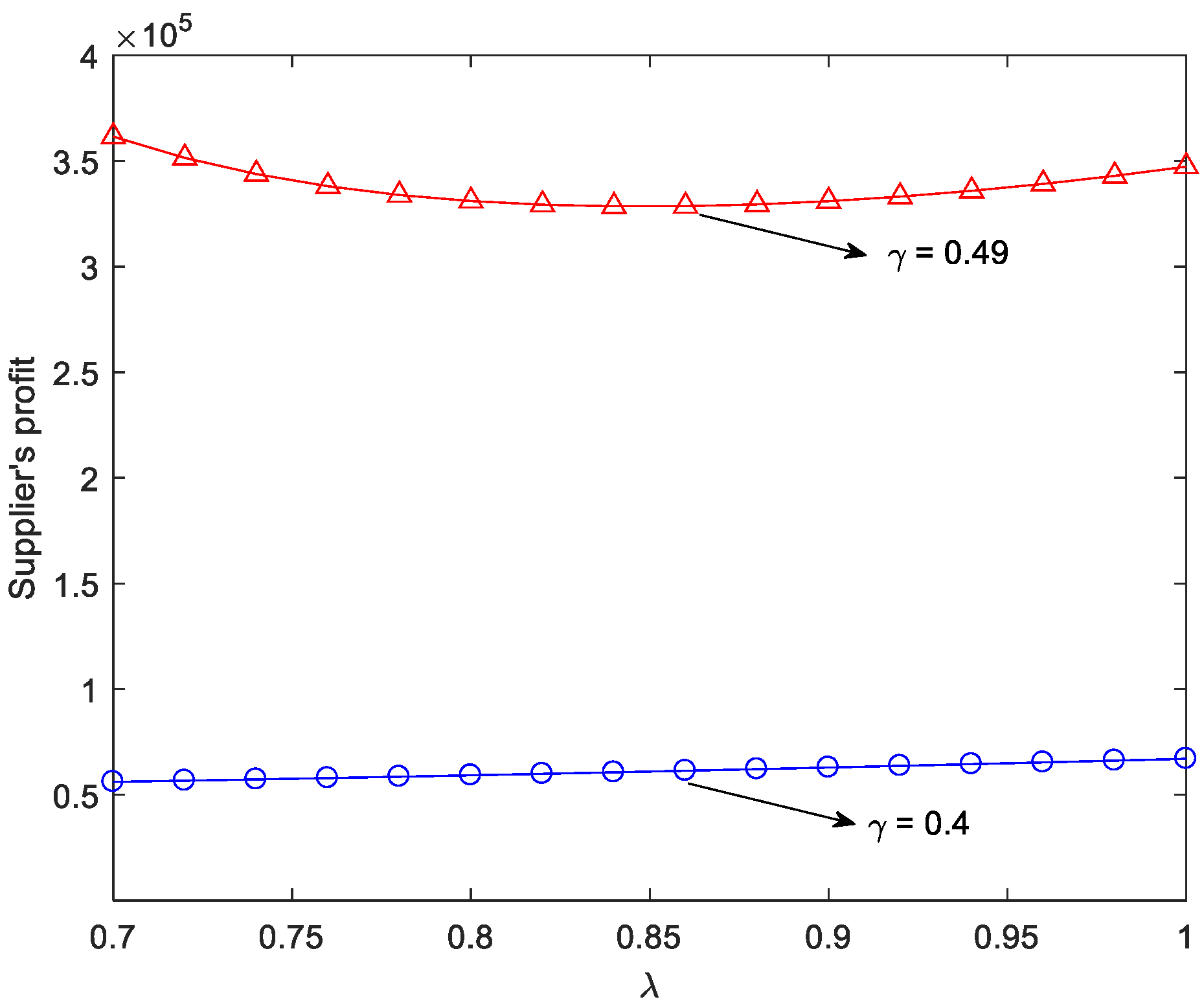
Finally, according to Figure 9 we analyze how the revenue-sharing proportion $\lambda$ held by the supplier affects the supplier’s profit. It is not the truth that the higher the revenue sharing of the supplier in the online agency selling channel, the higher the profit of the supplier. Specifically, if the substitutability between the three channels is extremely high, the profit of the supplier firstly decreases and then increases with the commission rate $\lambda$. Therefore, it is not wise for Gree to maximize their profits by blindly raising the proportion of revenue sharing. They should be induced to pay close attention to the market intensity.

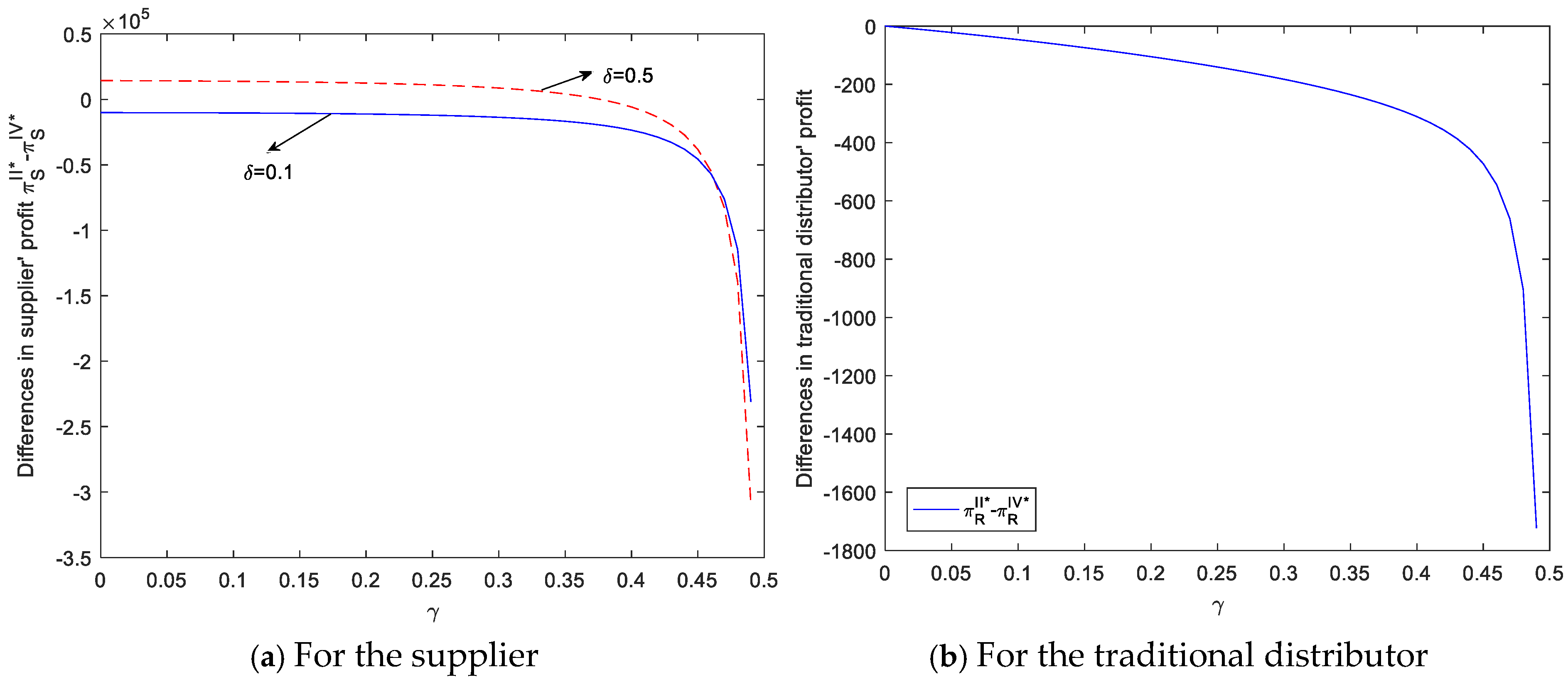
Considering the effect of the revenue-sharing proportion $\lambda$ on the participants’ profit (see Proposition 6), we further compare the supplier’s (or the traditional distributor’s) profits in mode I with those in mode IV to explore the motivation of the supplier’s adoption and the impact of their strategic adoption on the traditional distributor. Similar to Corollary 1, herein, we assume the slotting fee $F=0$, and the supplier who adopts an agency selling scheme only needs to pay a revenue-sharing proportion $1-\lambda$ to the platform.

Corollary 2.

In the case that $\delta =0.5$,

(1)

when ${∆}_4<0$, we have ${\pi }_S^{IV*}<{\pi }_S^{I*}$; otherwise, ${\pi }_S^{IV*}>{\pi }_S^{I*}$;

(2)

when ${∆}_5<0$, we have ${\pi }_R^{IV*}>{\pi }_R^{I*}$; otherwise, ${\pi }_R^{IV*}<{\pi }_R^{I*}$, where ${∆}_4$ and ${∆}_5$ are, respectively, a binary function determined by the independent variables $\gamma$ and $\lambda$, and both can be seen in Appendix B.

Conventional wisdom suggests that instead of only adopting the traditional distribution channel, the supplier could gain more profits from adopting both online schemes. At the same time, the profit of the traditional distributor will be hurt by the supplier’s adoption of both online schemes. Nevertheless, from Part 1, we observe that the supplier could not obtain more profits from introducing both online schemes than only relying on the traditional distribution channel when the intensity of market competition is extremely low. To provide a more intuitive description for the conclusion, we take Figure 10a to illustrate that the market competition level (or the substitutability between channels) plays a more important role in the supplier’s profit. Since the lower substitutability between the three channels causes the online schemes provided by the platform to generate more potential costs, the supplier will have no incentive to introduce these online schemes. Conversely, the higher the substitutability between the three channels is, the more likely it is that the supplier will benefit from adopting these online schemes.

Based on Figure 10b, when the market intensity is comparatively higher and the revenue-sharing proportion earned by the supplier is relatively lower, the traditional distributor will benefit from the supplier’s adoption of both online schemes. The reason for this is that the intense market stimulates demand for products, and the lower revenue sharing drives the supplier to give the middlemen in other channels more order quantities. Therefore, it is not always a bad thing for Jinghai to encourage Gree to adopt both the agency selling and reselling schemes in addition to the traditional distribution channel.

5. Impacts of Different Adoption Strategies on the Supplier and Traditional Distributor: A Case Study of Gree

In this section, we compare the supplier’s (or the traditional distributor’s) profits under the supplier’s different adoption strategies and explore the optimal adoption strategy of the supplier and the effect of it on traditional distributor’s profitability. As a matter of fact, JD sets a commission rate of 4.5% for an air conditioner and asks for a platform licensing fee of RMB 1000. Thus, we set $\lambda =0.955$ and $F=1000$.

Proposition 7.

Through comparing the supplier’s (or the traditional distributor’s) profits in mode II and mode III, we have

(1)

when $\gamma >{\gamma }_1$, ${\pi }_S^{II*}<{\pi }_S^{III*}$; otherwise, ${\pi }_S^{II*}>{\pi }_S^{III*}$;

(2)

when $\gamma >{\gamma }_2$, ${\pi }_R^{II*}>{\pi }_R^{III*}$; otherwise, ${\pi }_R^{II*}<{\pi }_R^{III*}$, where ${\gamma }_1$ and ${\gamma }_2$ are uniquely determined by the equations $f_1({\gamma }_1)=0$ and $f_2({\gamma }_2)=0$, as seen in Appendix B.

Part 1 indicates that Gree’s strategic adoption of platform schemes depends on the market competition level (or the substitutability between channels). Specifically, if the market intensity is extremely high (for example, the market intensity is more than 0.94 as Figure 11 shows), Gree is likely to choose the online reselling scheme. It not only avoids paying an extra platform licensing fee but also increases the order quantity of the product. Otherwise, we will suggest that Gree opens an online flagship store on JD for selling directly to consumers.

In addition, from Part 2, we can observe that when the market intensity is extremely high (for example, when the market intensity is more than 0.98, as Figure 11 shows), Jinghai would benefit more from Gree’s adoption of the online agency selling scheme relative to the online reselling scheme. The higher market intensity directly stimulates demand for products, especially in the distribution channel. In other words, if Gree adopts the agency selling scheme in addition to the traditional distribution channel, the higher market intensity will drive order quantitities in the traditional distribution channel to a larger extent. Otherwise, Jinghai would tend to encourage Gree to adopt the online reselling scheme.

Proposition 8.

Through comparing the supplier’s (or the traditional distributor’s) profits in mode II and mode IV, we have

(1)

in the case that $\delta =0.5$, if $\gamma <{\gamma }_3$, ${\pi }_S^{II*}>{\pi }_S^{IV*}$; otherwise ${\pi }_S^{II*}<{\pi }_S^{IV*}$;

(2)

in the case that $\delta =0.1$, ${\pi }_S^{II*}<{\pi }_S^{IV*}$;

(3)

${\pi }_R^{II*}<{\pi }_R^{IV*}$, where ${\gamma }_3$ is uniquely determined by the equation $f_3({\gamma }_3)=0$ seen in Appendix B.

In this proposition, we first find that the strategic adoption of Gree depends on not only the market intensity but also the market share of the online reselling scheme. Specifically, if the market share of the online reselling scheme $\delta$ is small (i.e., $\delta =0.1$), Gree will always benefit more from introducing both online schemes than from only adopting the agency selling scheme. This implies that the small market share allocated to the reselling channel would bring Gree better benefits than that allocated to the agency selling channel. However, when the market share of the online reselling scheme $\delta$ is moderate, Gree’s profitability will be determined by the market intensity. In general, Gree prefers to adopt the agency selling scheme, for example, by opening a flagship store in JD. Whereas, if the market competition is relatively intense (i.e., $\gamma >0.45$, as Figure 12a shows), Gree is inclined to introduce both the agency selling and the reselling schemes. This is in line with the reality, that is, the fiercer the market competition, the more diverse the product sales channels. From Part 3, it is straightforward to imply that Jinghai always benefits more from Gree’s adoption of both online selling schemes than that of only the online agency selling scheme, as Figure 12b shows. Obviously, the online market share all allocated to the agency selling channel is bound to have a negative impact on the traditional distributor.

Proposition 9.

Through comparing the supplier’s (or the traditional distributor’s) profits in mode III and mode IV, we have

(1)

in the case that $\delta =0.5$, if $\gamma <{\gamma }_4$, ${\pi }_S^{III*}>{\pi }_S^{IV*}$; otherwise, ${\pi }_S^{III*}<{\pi }_S^{IV*}$;

(2)

in the case that $\delta =0.1$, ${\pi }_S^{III*}<{\pi }_S^{IV*}$;

(3)

if $\gamma >{\gamma }_5$, ${\pi }_R^{III*}<{\pi }_R^{IV*}$; otherwise, ${\pi }_R^{III*}>{\pi }_R^{IV*}$, where ${\gamma }_4$ and ${\gamma }_5$ are uniquely determined by the equations $f_4({\gamma }_4)=0$ and $f_5({\gamma }_5)=0$ seen in Appendix B.

Proposition 9 shows that Gree does not always benefit more from adopting both the online platform schemes than from only introducing the online reselling scheme. Particularly, if the market share of the online reselling scheme $\delta$ is moderate and the market intensity $\gamma$ is relatively lower, Gree tends to adopt only the online reselling scheme. The reason for this is consistent with the content of proposition 8. Similarly, we present Figure 13 to visually demonstrate the comparison results.

In terms of the traditional distributor’s profit, from Figure 13b, we believe that when the market intensity is higher than 0.45, the traditional distributor will benefit more from Gree’s adoption of both online platform schemes than only the online reselling scheme. The first main reason for this phenomenon is that the higher market intensity stimulates the product demand, especially in the distribution channel. Secondly, in this market situation, the online agency selling scheme has a more positive effect on the traditional distributor’s profitability than the online reselling scheme. Moreover, as a result of the lower market intensity (i.e., $\gamma =0.45$), Jinghai would like to encourage Gree to adopt only the online reselling scheme.

Thereafter, we set the extra market potential e driven by the online platform scheme to 50 and explore how the market intensity $\gamma$ and the market share of the online reselling scheme $\delta$ affect Gree’s strategic adoption of online platform schemes. Moreover, we focus on the influence of these parameters and Gree’s adoption of platform schemes on Jinghai’s profitability.

According to Figure 14, we find that Gree’s adoption of both online platform schemes could yield the most profits when the market intensity is relatively higher. Nevertheless, if the market intensity is sufficiently lower, the optimal adoption strategy of Gree may also be influenced by the market share of the online reselling scheme. Specifically, when the market share of the online reselling scheme is relatively higher (i.e., $\delta =0.5$, as Figure 14b shows), the lower market intensity will cause Gree to have the incentive to adopt only the online agency selling scheme. The reasons for this are twofold. On the one hand, the advantage of agency selling outweighs that of reselling in the low market. On the other hand, more market share is allocated to the online reselling channel.

However, from the perspective of the traditional distributor (i.e., Jinghai), we can draw a different conclusion from the above. First, Jinghai is not willing to yield to Gree’s adoption of only the agency selling scheme, regardless of the market intensity and the market share. It could hurt their profitability the most, as the bottom line of Figure 15 shows. As a matter of fact, Gree’s introduction of an online platform scheme prompts resistance from Jinghai. Interestingly, when the market intensity or the substitutability between channels is relatively higher, they can achieve agreement on the fact that introducing both the online platform schemes is the optimal strategy. As a result, Gree’s expansion of online channels has not always had a negative impact on Jinghai in the long term.

6. Conclusions and Future Research

In our paper, we have studied Gree’s channel selection issues, depending on the role of the online platform, versus an offline traditional distributor (Jinghai). The online retail platform offers two options to Gree. They can act as an “online marketplace”, where Gree operates as an independent supplier to sell products directly to consumers on this platform. Also, they can act as a reseller, where products are bought from Gree and resold to consumers. Therefore, we have formulated four models to explore the impact of these factors on decisions and profits, such as the magnitude of slotting fee (or revenue-sharing proportion), the substitution effect between the both products (or the intensity of market competition), and the growth rate of demand and channel performance of members. When the market intensity (or the substitutability between products/channels) is relatively higher, the supplier has an incentive to adopt the agency selling or the online reselling schemes in most cases. Of course, if the extra market demand stimulated by the platform schemes is sufficiently low, the supplier would be reluctant to introduce the agency selling scheme in addition to the traditional distribution scheme. In particular, it would be wise to advise the supplier to adopt both agency selling and reselling schemes while the market intensity is extremely high.

From the perspective of the traditional distributor, generally, the agency selling (reselling) scheme adopted by the supplier will have a negative (positive) impact on the profitability of the traditional distributor. However, when the market competition is sufficiently intense and the revenue-sharing proportion earned by the supplier is relatively lower, the traditional distributor would benefit from supplier introducing both online platform schemes. As a matter of fact, it is not always a bad thing for Jinghai to support Gree in adding online platform schemes.

Extensions of our work may capture other factors on suppliers’ channel strategies, such as complementary markets, consumers’ channel preferences, and economies of scale. Another possible avenue may be to convert this present demand function into a stochastic demand function.