Cubic Shaping of Lattice Constellations from Multi-Level Constructions from Codes ^†

Abstract

Lattice codes play an important role in wireless communication and are closely related to linear codes. Multi-level constructions of complex lattices from codes are known to produce lattice codes with desirable parameters and efficient encoding and decoding of information bits. However, their constellation usually involves superfluous elements that need to be mapped to a representative within the same coset to reduce average transmission power. One such elegant shaping function is a componentwise modulo, which is known to produce a cubic shaping for Barnes–Wall lattices. In this paper, we generalize this result to lattices over quadratic rings of integers, thus encompassing constructions from p-ary codes, where p is a prime number. We identify all bases that permit cubic modulo shaping. This provides useful insights into practical encoding and decoding of lattice codes from multi-level constructions.

1. Introduction

Coding theory is essential in reliable digital communications because it can mitigate noise and interference through error detection and correction. Lattice codes provide a suitable method of communication over Additive White Gaussian Noise (AWGN) channels [1]. Furthermore, they have promising applications in post-quantum cryptography [2,3,4]. Lattice codes are typically constructed from linear codes, using their structure in a finite field to form a well-defined lattice in the Euclidean space. For example, Construction A produces a lattice from one single linear code through natural embedding. The properties of the resulting lattice, such as density and minimum distance, are directly obtained from the parameters of the underlying linear codes [5].

It is unsurprising that multi-level lattice constructions offer several advantages over straightforward single-level ones [6], including improved shaping gain [7], greater flexibility in density and minimum distance [8], and better performance with multi-stage decoding [9]. A well-known example is the Barnes–Wall lattices, which can be obtained from Reed–Muller codes through Construction C [5]. Alternatively, Forney [10] proposed a complex lattice construction from binary codes that uses a Gaussian integer of squared norm 2, namely, $1+i$, as the scaling factor of the partition chain. This is known as the Code Formula and corresponds to the real lattice constructed from binary codes, which uses 2 as the scaling factor.

At the same time, codes over ${\mathbb{F}}_p$ where p is a prime have been the subject of numerous research studies and offer rich connections with several branches of algebra [11]. Reed–Solomon codes, for example, are a class of powerful error-correcting codes widely used in data transmission and storage [12,13,14]. Lattices from nonbinary codes with promising properties have been extensively studied. At the foundation, $\mathbb{Z}\left[\omega \right]$ is a better lattice than $\mathbb{Z}\left[i\right]$ in terms of density, kissing number, and coding gain, but it is only compatible with ternary codes. Algebraic lattices over quadratic rings of integers are discovered to be particularly useful for the fading channel [15,16,17]. Meanwhile, lattices can also be constructed from codes on ${\mathbb{Z}}_q$ (as opposed to ${\mathbb{F}}_q$) where q is a power of a prime [18,19]. In this work, we consider lattices over complex quadratic rings of integers, thus allowing us to consider complex lattice construction from p-ary codes and diversify the scaling factors.

Lattice shaping is a common technique used in digital communication to improve the efficiency of signal constellation [20,21]. In 2013, Harshan et al. [22] showed that the complex Barnes–Wall lattice has a cubic shaping property, which results in lower average transmission energy consumption. This is due to the fact that complex Construction C and Construction D from binary codes use $1+i$ as the scaling factor. Their novel shaping function simply treats the real and imaginary parts separately and applies an isolated modulo in each component. An interesting consequence is the question of whether there exist bases other than $1+i$ in the Gaussian integers (or any other quadratic rings of integers) that would permit the same property. In 2017, Pooksombat et al. [23] discovered more bases with this property, which is then called the tileable property or tileability. In this paper, we provide a complete answer to this question. That is, we enumerate all bases that permit cubic shaping of an even-level constellation from a multi-level construction.

2. Preliminary Information

This section introduces some terminology that we use throughout. It also explores the fundamentals of lattice constructions over a quadratic ring of integers from codes over a finite field with prime cardinality. The definition of tileability and some examples are given.

2.1. Quadratic Ring of Integers

We denote $i=\sqrt{-1}$ and $\omega =-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{\sqrt{-3}}{2}}$. The conjugate of $z=x+yi$ is $\overline{z}=x-yi$ where x and y are real numbers. We give the standard definition for the ring of integers next.

Definition 1. 

Let $D<0$ be a square-free integer. The ring of integers of $\mathbb{Q}\left(\sqrt{D}\right)$ is $\mathbb{Z}\left[\theta \right]$, where

$$\theta =\left\{\begin{array}{cc}\sqrt{D},\hfill & \mathrm{if}D\equiv 2,3(mod4),\hfill \\ {\displaystyle \frac{-1+\sqrt{D}}{2}},\hfill & \mathrm{if}D\equiv 1(mod4).\hfill \end{array}\right.$$

Moreover, θ can be identified by its minimal polynomial ${\theta }^2+A\theta +B=0$, where

$$(A,B)=\left\{\begin{array}{cc}(0,-D),\hfill & \mathrm{if}D\equiv 2,3(mod4),\hfill \\ \left(1,{\displaystyle \frac{1-D}{4}}\right),\hfill & \mathrm{if}D\equiv 1(mod4).\hfill \end{array}\right.$$

Here, we use the notation $(A,B)$ to refer to D. Since our focus is primarily on the elements of $\mathbb{Z}\left[\theta \right]$, we abuse the terminology and refer to the real and imaginary parts relative to $\theta$.

Definition 2. 

For an element $z=x+y\theta \in \mathbb{Z}\left[\theta \right]$, where $x,y\in \mathbb{Z}$, we call $\mathcal{R}\left(z\right)=x$ the real part and $\mathcal{I}\left(z\right)=y$ the imaginary part.

We state the following standard results from algebraic number theory, which will be helpful in the embedding of p-ary codes into the Euclidean space. We note here that A and B are coefficients of the minimal polynomial for $\theta$ as given in Definition 1.

Lemma 1. 

For an element $\alpha =x+y\theta \in \mathbb{Z}\left[\theta \right]$ where $x,y\in \mathbb{Z}$, its squared Euclidean norm is given by ${\left|\alpha \right|}^2=x^2-Axy+B{y}^2$.

Lemma 2. 

Let $\alpha =x+y\theta \in \mathbb{Z}\left[\theta \right]$. If ${\left|\alpha \right|}^2=p$ is a prime, then the following statements hold.

• Either $\alpha =\pm \theta$ and B is prime or $x,y,p$ are pairwisely coprime.
• $y\ne 0$.
• $\mathbb{Z}\left[\theta \right]/\alpha \mathbb{Z}\left[\theta \right]\simeq {\mathbb{F}}_p$.

The first lemma follows from the fact that $\theta$ and $\overline{\theta }$ are the solutions to $X^2+AX+B=0$, and so ${\left|\alpha \right|}^2=(x+y\theta )(x+y\overline{\theta })=x^2+xy(\theta +\overline{\theta })+y^2(\theta ·\overline{\theta })=x^2-Axy+B{y}^2$.

2.2. Constructions of Lattices from Linear Codes

We start this subsection with a definition for p-ary codes and lattices.

Definition 3. 

A p-ary code of length n is a set $C\subseteq {\mathbb{F}}_p^n$. If C is a subspace of ${\mathbb{F}}_p^n$, then C is said to be linear, and the dimension of the code is the dimension of the subspace, denoted by $dimC$.

Definition 4. 

A lattice Λ is a finitely generated $\mathbb{Z}$- or $\mathbb{Z}\left[i\right]$-module or equivalently a discrete additive subgroup of ${\mathbb{R}}^n$ or ${\mathbb{C}}^n$.

The elements of ${\mathbb{F}}_p$ will be mapped into the Euclidean space via the following natural embedding. This will be helpful in the construction and representation of lattices (or their constellations) from codes.

Definition 5. 

For a prime number p, the function $\psi :{\mathbb{F}}_p\to \mathbb{C}$ is the natural embedding function. Here, under the usual representation ${\mathbb{F}}_p=\{0,1,\dots ,p-1\}$, $\psi \left(n\right)=n$ for all $n=0,1,\dots ,p-1$.

For example, we can represent ${\mathbb{F}}_3$ by the cosets of $\mathbb{Z}/3\mathbb{Z}$ since 3 is a prime number. Therefore, ${\mathbb{F}}_3=\{3\mathbb{Z}+0,3\mathbb{Z}+1,3\mathbb{Z}+2\}$. The natural embedding function is $\psi :{\mathbb{F}}_3\to \mathbb{C}$, defined as $\psi (3\mathbb{Z}+n)=n$ for $n=0,1,2$.

We now describe constructions of complex lattices from codes, followed by an example. While the constructions originally only produce real lattices, the generalization to quadratic rings of integers is analogous to the real case and is considered, for example, in [10,22]. Technically speaking, multi-level constructions take a chain of nested codes as an ingredient, and each code in the chain is scaled by an increasing power of the scaling factor, thereby creating so-called levels. In our general setting, this scaling factor is referred to as “base” so that the terminology is consistent with the p-ary decomposition that we introduce later. Here and throughout, we use boldface letters to represent vectors.

Definition 6 

(Complex Construction by Code Formula). Let $C_0\subseteq C_1\subseteq \dots \subseteq C_{m-1}\subseteq C_m={\mathbb{F}}_p^n$ be nested p-ary linear codes of length n. The set ${\Gamma }_{\mathrm{CF}}\subseteq \mathbb{Z}{\left[\theta \right]}^n$ constructed from the codes via Construction by Code Formula with the base α, ${\left|\alpha \right|}^2=p$, is defined as ${\Gamma }_{\mathrm{CF}}={\mathcal{C}}_{\mathrm{CF}}+{\alpha }^m\mathbb{Z}{\left[\theta \right]}^n$, where

$${\mathcal{C}}_{\mathrm{CF}}=\psi \left(C_0\right)+\alpha \psi \left(C_1\right)+{\alpha }^2\psi \left(C_2\right)+\cdots +{\alpha }^{m-1}\psi \left(C_{m-1}\right).$$

Definition 7 

(Complex Construction D). Let $C_0\subseteq C_1\subseteq \dots \subseteq C_{m-1}\subseteq C_m={\mathbb{F}}_p^n$ be nested p-ary linear codes of length n. Let $k_j=dim\left(C_j\right)$ and $\{{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_n\}$ be a basis of ${\mathbb{F}}_p^n$ such that ${\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_{k_j}$ span $C_j$. The set ${\Lambda }_{\mathrm{D}}\subseteq \mathbb{Z}{\left[\theta \right]}^n$ constructed from the codes via scaled Construction D with the base α, ${\left|\alpha \right|}^2=p$, is defined as ${\Lambda }_{\mathrm{D}}={\mathcal{C}}_{\mathrm{D}}+{\alpha }^m\mathbb{Z}{\left[\theta \right]}^n$, where

$${\mathcal{C}}_{\mathrm{D}}=\left\{\sum _{j=0}^{m-1}{\alpha }^j\sum _{l=1}^{k_j}{c}_{j,l}\psi \left({\mathbf{v}}_l\right)|c_{j,l}\in \psi \left({\mathbb{F}}_p\right)\right\}.$$

A classical example of these constructions is the Barnes–Wall lattices. For $p=2$, $\alpha =2$ or $1+i$, and $RM(r,m)$, the Reed–Muller codes of order r and length $n=2^m$, ${\Gamma }_{\mathrm{CF}}$ and ${\Lambda }_{\mathrm{D}}$ coincide and yield the Barnes–Wall lattices [22]. We note here that relationships between the two constructions for real lattices are outlined, for example, in [19,24]. However, the general comparison for the complex constructions is yet to be explored. As we will see, our work applies to a superset of ${\mathcal{C}}_{\mathrm{CF}}$ and ${\mathcal{C}}_{\mathrm{D}}$ and is independent of the underlying codes or whether they produce a lattice under the constructions. We now proceed with an example.

Example 1. 

Let $C_0\subseteq C_1\subseteq {\mathbb{F}}_3^3$ be nested ternary codes of length 4, defined as

$$\begin{array}{c}{C}_0={span}_{{\mathbb{F}}_3}\left\{(1,1,0)\right\},\hfill \\ C_1={span}_{{\mathbb{F}}_3}\{(1,1,0),(1,0,2)\}.\hfill \end{array}$$

By using the ring of integers $\mathbb{Z}\left[\omega \right]$ with the base of expansion $\alpha =2+\omega$ whose norm is ${\left|\alpha \right|}^2=3$, we have the following sets:

• (Code Formula) ${\Gamma }_{\mathrm{CF}}\in \mathbb{Z}{\left[\omega \right]}^3$ is defined as ${\Gamma }_{\mathrm{CF}}={\mathcal{C}}_{\mathrm{CF}}+{\alpha }^2\mathbb{Z}{\left[\omega \right]}^3$, where

  $${\mathcal{C}}_{\mathrm{CF}}=\psi \left(C_0\right)+\alpha \psi \left(C_1\right).$$
• (Construction D) ${\Lambda }_{\mathrm{D}}\in \mathbb{Z}{\left[\omega \right]}^3$ is defined as ${\Lambda }_{\mathrm{D}}={\mathcal{C}}_{\mathrm{D}}+{\alpha }^2\mathbb{Z}{\left[\omega \right]}^3$, where

  $${\mathcal{C}}_{\mathrm{D}}=\left\{c_{0,1}(1,1,0)+c_{1,1}\alpha (1,1,0)+c_{1,2}\alpha (1,0,2)|c_{j,l}\in \{0,1,2\}\right\}.$$

Direct calculation shows that the constellations ${\mathcal{C}}_{\mathrm{CF}}$ and ${\mathcal{C}}_{\mathrm{D}}$ are as follows:

$$\begin{array}{cc}\hfill {\mathcal{C}}_{\mathrm{CF}}& =\left\{\begin{array}{ccc}(0,0,0),\hfill & (1,1,0),\hfill & (2,2,0),\hfill \\ (\alpha ,\alpha ,0),\hfill & (1+\alpha ,1+\alpha ,0),\hfill & (2+\alpha ,2+\alpha ,0),\hfill \\ (2\alpha ,2\alpha ,0),\hfill & (1+2\alpha ,1+2\alpha ,0),\hfill & (2+2\alpha ,2+2\alpha ,0),\hfill \\ (\alpha ,0,2\alpha ),\hfill & (1+\alpha ,1,2\alpha ),\hfill & (2+\alpha ,2,2\alpha ),\hfill \\ (2\alpha ,\alpha ,2\alpha ),\hfill & (1+2\alpha ,1+\alpha ,2\alpha ),\hfill & (2+2\alpha ,2+\alpha ,2\alpha ),\hfill \\ (0,2\alpha ,2\alpha ),\hfill & (1,1+2\alpha ,2\alpha ),\hfill & (2,2+2\alpha ,2\alpha ),\hfill \\ (2\alpha ,0,\alpha ),\hfill & (1+2\alpha ,1,\alpha ),\hfill & (2+2\alpha ,2,\alpha ),\hfill \\ (0,\alpha ,\alpha ),\hfill & (1,1+\alpha ,\alpha ),\hfill & (2,2+\alpha ,\alpha ),\hfill \\ (\alpha ,2\alpha ,\alpha ),\hfill & (1+\alpha ,1+2\alpha ,\alpha ),\hfill & (2+\alpha ,2+2\alpha ,\alpha )\hfill \end{array}\right\},\hfill \\ \hfill {\mathcal{C}}_{\mathrm{D}}& =\left\{\begin{array}{ccc}(0,0,0),\hfill & (1,1,0),\hfill & (2,2,0),\hfill \\ (\alpha ,\alpha ,0),\hfill & (1+\alpha ,1+\alpha ,0),\hfill & (2+\alpha ,2+\alpha ,0),\hfill \\ (2\alpha ,2\alpha ,0),\hfill & (1+2\alpha ,1+2\alpha ,0),\hfill & (2+2\alpha ,2+2\alpha ,0),\hfill \\ (\alpha ,0,2\alpha ),\hfill & (1+\alpha ,1,2\alpha ),\hfill & (2+\alpha ,2,2\alpha ),\hfill \\ (2\alpha ,\alpha ,2\alpha ),\hfill & (1+2\alpha ,1+\alpha ,2\alpha ),\hfill & (2+2\alpha ,2+\alpha ,2\alpha ),\hfill \\ (3\alpha ,2\alpha ,2\alpha ),\hfill & (1+3\alpha ,1+2\alpha ,2\alpha ),\hfill & (2+3\alpha ,2+2\alpha ,2\alpha ),\hfill \\ (2\alpha ,0,4\alpha ),\hfill & (1+2\alpha ,1,4\alpha ),\hfill & (2+2\alpha ,2,4\alpha ),\hfill \\ (3\alpha ,\alpha ,4\alpha ),\hfill & (1+3\alpha ,1+\alpha ,4\alpha ),\hfill & (2+3\alpha ,2+\alpha ,4\alpha ),\hfill \\ (4\alpha ,2\alpha ,4\alpha ),\hfill & (1+4\alpha ,1+2\alpha ,4\alpha ),\hfill & (2+4\alpha ,2+2\alpha ,4\alpha ),\hfill \end{array}\right\}.\hfill \end{array}$$

Although ${\mathcal{C}}_{\mathrm{CF}}\ne {\mathcal{C}}_{\mathrm{D}}$, they produce the same lattice once they are used together with ${\alpha }^2\mathbb{Z}{\left[\omega \right]}^3=3\mathbb{Z}{\left[\omega \right]}^3$ to tile the complex plane. In other words, ${\Gamma }_{\mathrm{CF}}={\mathcal{C}}_{\mathrm{CF}}+{\alpha }^2\mathbb{Z}{\left[\omega \right]}^3$ from Code Formula is the same as ${\Lambda }_{\mathrm{D}}={\mathcal{C}}_{\mathrm{D}}+{\alpha }^2\mathbb{Z}{\left[\omega \right]}^3$ from Construction D. This is not so surprising, since ${\mathcal{C}}_{\mathrm{D}}$ can be reduced in modulo 3 in the real and imaginary parts to ${\mathcal{C}}_{\mathrm{CF}}$.

As we can see in the above example, there might be different ways to represent the constellation of a set or a lattice. This inspires us to use p-ary decomposition to represent elements of $\mathbb{Z}\left[\theta \right]$, which can be performed uniquely.

Lemma 3 

(p-ary decomposition). Let $\alpha =x+y\theta \in \mathbb{Z}\left[\theta \right]$ be a base with ${\left|\alpha \right|}^2=p$ prime. For a fixed exponent $m\ge 1$, any vector of $\mathbb{Z}{\left[\theta \right]}^n$ can be uniquely written as

$$\sum _{j=0}^{m-1}{\mathbf{a}}_j{\alpha }^j+\mathbf{z}{\alpha }^m,$$

where ${\mathbf{a}}_j\in \psi {\left({\mathbb{F}}_p\right)}^n$ and $\mathbf{z}\in \mathbb{Z}{\left[\theta \right]}^n$.

Proof. 

Suppose that ${\left|\alpha \right|}^2=p$ is prime, so we have $\mathbb{Z}\left[\theta \right]/\alpha \mathbb{Z}\left[\theta \right]\simeq {\mathbb{F}}_p$. This means that any element $z_0\in \mathbb{Z}\left[\theta \right]$ can be uniquely represented as $a_0+z_1\alpha$, where $a_0\in \psi \left({\mathbb{F}}_p\right)$ and $z_1\in \mathbb{Z}\left[\theta \right]$. To show that this representation is unique, we suppose that $a_0+z_1\alpha =a_0^{\prime }+z_1^{\prime }\alpha$ for some $a_0,a_0^{\prime }\in \psi \left({\mathbb{F}}_p\right)$ and $z_1,z_1^{\prime }\in \mathbb{Z}\left[\theta \right]$. Since they are equal, they are in the same coset of $\mathbb{Z}/\alpha \mathbb{Z}$. This implies that $a_0$ and $a_0^{\prime }$ are equal in $\psi \left({\mathbb{F}}_p\right)$, and thus $z_1=z_1^{\prime }$.

We iterate this process to obtain $z_j=a_j+z_{j+1}\alpha$ for $j=1,2,\dots ,m-1$ and let $z_m=z$. Finally, we have a representation of $z_0$ as

$$z_0=a_0+a_1\alpha +a_2{\alpha }^2+\cdots +a_{m-1}{\alpha }^{m-1}+z{\alpha }^m.$$

To extend to vectors in $\mathbb{Z}{\left[\theta \right]}^n$, we apply this process to all of the entries. □

Example 2. 

On $\mathbb{Z}\left[\omega \right]$, by using $\alpha =-1+\omega$ as the base, we can decompose $6-2\omega$ into $m=3$ levels as $1+\alpha +2{\alpha }^2+(-\omega ){\alpha }^3$.

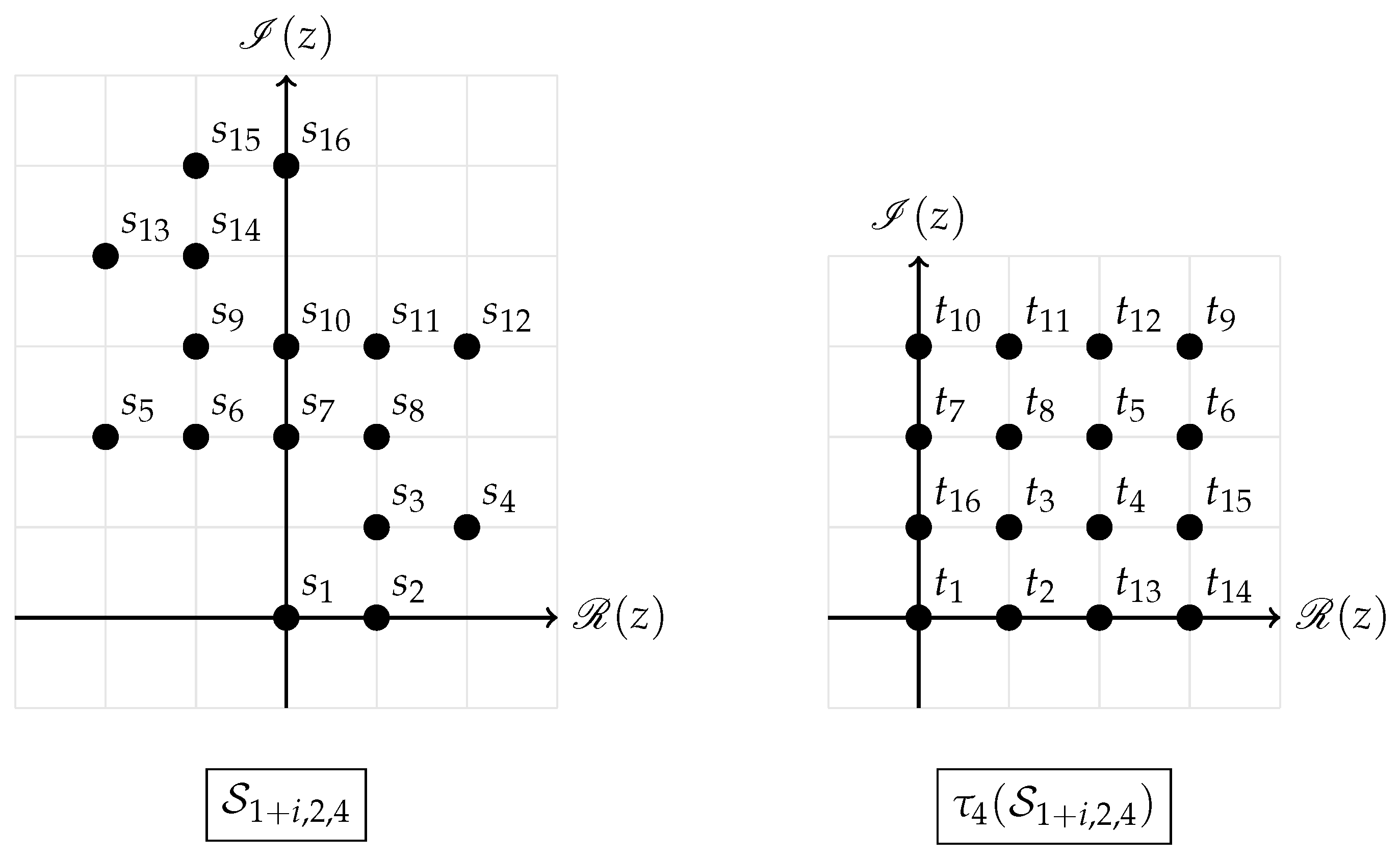
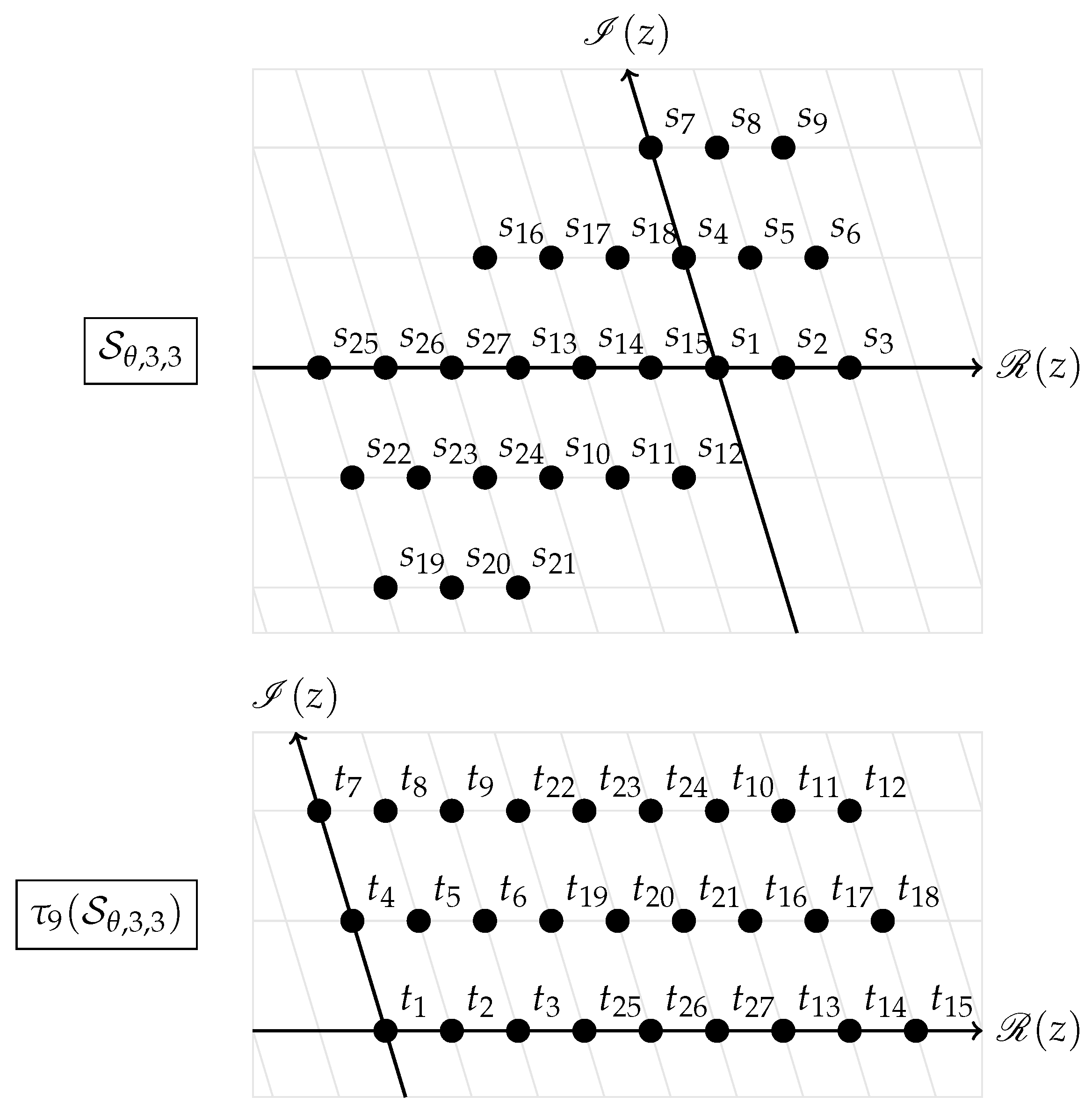
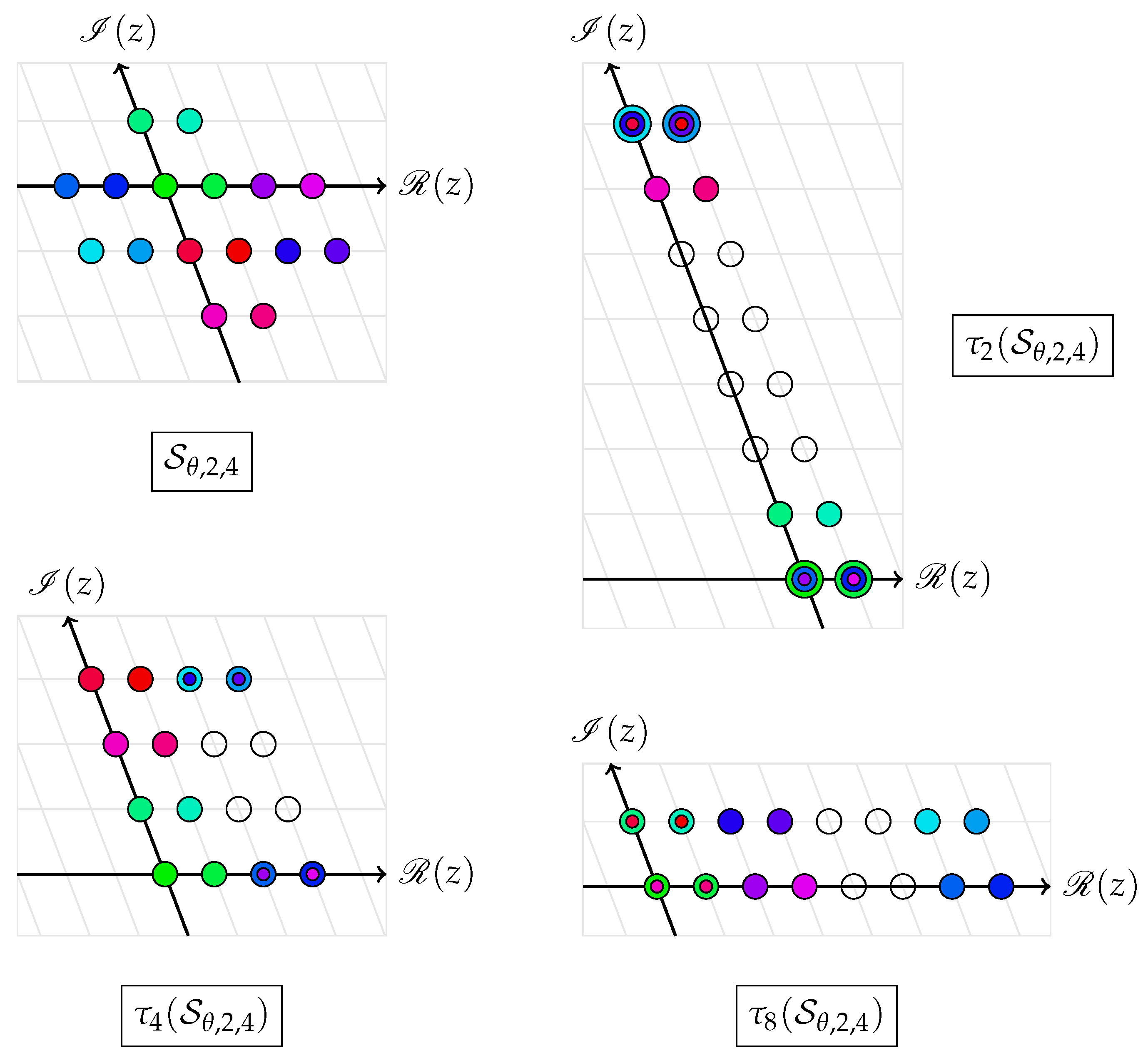
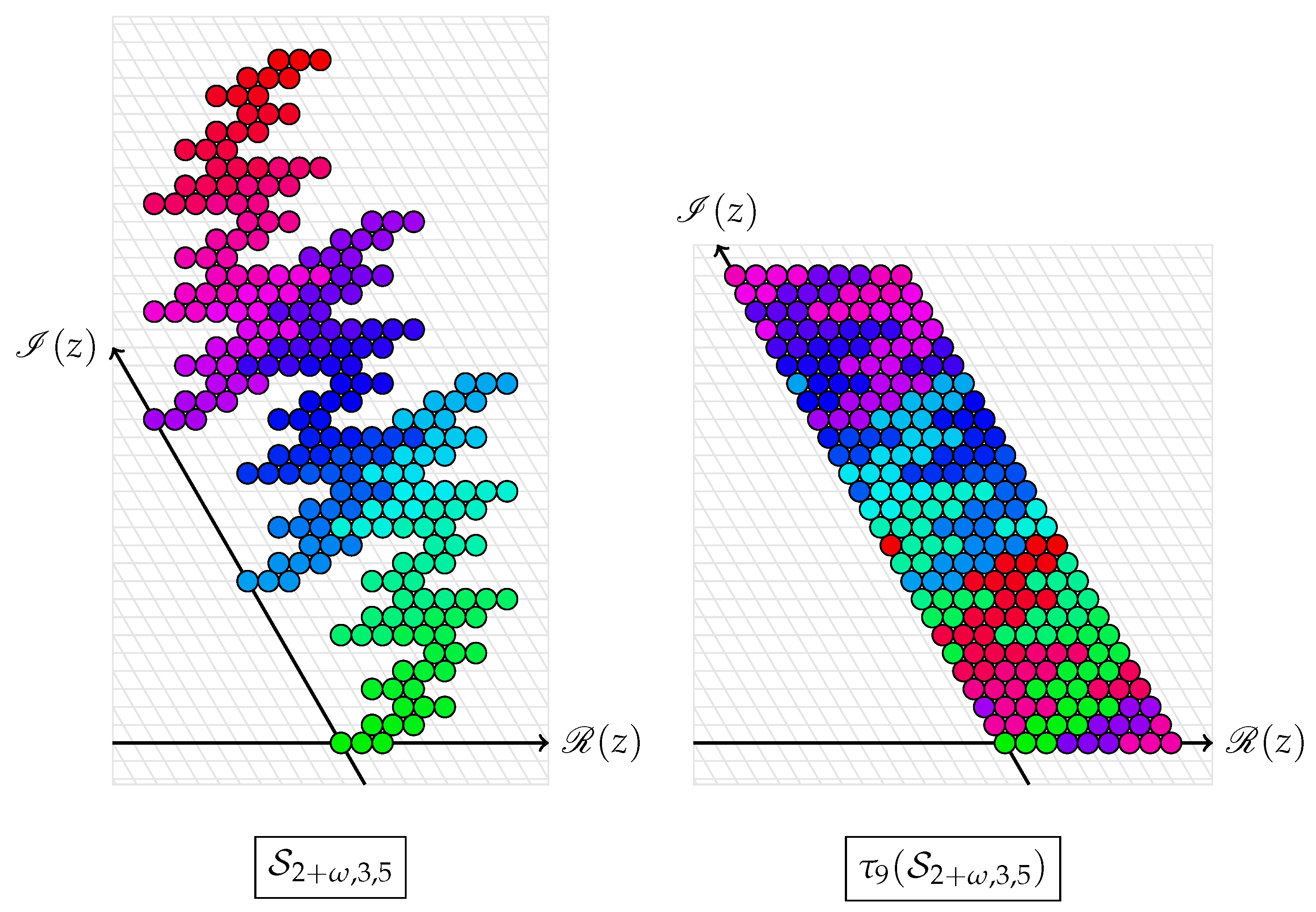
2.3. Tileability

As we have seen in the previous subsection, the outputs of multi-level complex constructions are always of the form $\mathcal{C}+{\alpha }^m\mathbb{Z}{\left[\theta \right]}^n$. Furthermore, $\mathcal{C}$ can be seen as a residue with ${\alpha }^m\mathbb{Z}{\left[\theta \right]}^n$ as a modulation that tessellates $\mathcal{C}$ to the whole plane. According to the decomposition base $\alpha$ on $\mathbb{Z}\left[\theta \right]$, one can write each entry of an element in the constellation $\mathcal{C}$ as $a_0+a_1\alpha +a_2{\alpha }^2+\cdots +a_{m-1}{\alpha }^{m-1}$ taking modulo ${\alpha }^m$, where $a_j\in \psi \left({\mathbb{F}}_p\right)$. As a result, we are interested in numbers of this form.

Definition 8. 

The set ${\mathcal{S}}_{\alpha ,p,m}$, where $p={\left|\alpha \right|}^2$, is defined as

$${\mathcal{S}}_{\alpha ,p,m}=\left\{a_0+a_1\alpha +a_2{\alpha }^2+\cdots +a_{m-1}{\alpha }^{m-1}|a_j\in \psi \left({\mathbb{F}}_p\right)\right\}.$$

The set ${\mathcal{S}}_{\alpha ,p,m}$ given here acts as the set that contains all possible elements obtained from multi-level lattice constructions from codes. We now define an auxiliary notation which will be used to formally describe cubic shaping.

Definition 9. 

For integers $w,w^{†}>1$, the set ${\mathbb{Z}}_{w,w^{†}}\left[\theta \right]$ is defined as

$${\mathbb{Z}}_w\oplus \theta {\mathbb{Z}}_{w^{†}}=\left\{x+y\theta |x\in {\mathbb{Z}}_w\mathrm{and}y\in {\mathbb{Z}}_{w^{†}}\right\},$$

where w and $w^{†}$ are called width and height, respectively.

Despite the term “cubic”, we note that, geometrically speaking, cubic shaping rearranges a lattice constellation into a multi-dimensional cube or parallelepiped. Because of the uniqueness of the decomposition, there are exactly $p^m$ elements in ${\mathcal{S}}_{\alpha ,p,m}$. Moreover, the number of elements in ${\mathbb{Z}}_{w,w^{†}}\left[\theta \right]$ is $w·w^{†}$. In the following definition, we define a map between ${\mathcal{S}}_{\alpha ,p,m}$ and ${\mathbb{Z}}_{w,w^{†}}\left[\theta \right]$. With the assumption that $p^m=w·w^{†}$, the sets ${\mathcal{S}}_{\alpha ,p,m}$ and ${\mathbb{Z}}_{w,w^{†}}\left[\theta \right]$ are of the same size. Note that if $p^m>w·w^{†}$, the map would not be injective and thus could not preserve the structure of the lattice. On the other hand, if $p^m<w·w^{†}$, then the resulting image would not be maximally compact from the geometric perspective. This leads to a higher average norm of the elements in the constellation. Therefore, for our purposes, we aim to fixate $w·w^{†}=p^m$. Since p is a prime number and $w,w^{†}>1$ are positive integers, for a base $\alpha$ with norm ${\left|\alpha \right|}^2=p$ and exponent m, we choose a proper width w such that $w\mid p^m$, and the height is set to be $w^{†}={\displaystyle \frac{p^m}{w}}$ automatically.

Definition 10. 

For the base α with norm ${\left|\alpha \right|}^2=p$ and exponent m, the tiling map of width w, where $w\mid p^m$ and $1<w<p^m$, is defined as ${\tau }_w:{\mathcal{S}}_{\alpha ,p,m}\to {\mathbb{Z}}_{w,w^{†}}\left[\theta \right]$ given by

$${\tau }_w(a+b\theta )=(amodw)+(bmod{w}^{†})\theta ,$$

where $w^{†}={\displaystyle \frac{p^m}{w}}$.

This tiling map can be thought of as componentwise modulo on the real and imaginary parts, since they are mapped individually through modulo w and $w^{†}$, respectively.

Definition 11. 

The set ${\mathcal{S}}_{\alpha ,p,m}$ is said to be tileable if there exists a width w that makes the tiling map ${\tau }_w$ a bijection. Such a width w is called the tiling width.

We note here that the tiling width may not be unique. Moreover, since ${\mathcal{S}}_{\alpha ,p,m}$ and ${\mathbb{Z}}_{w,w^{†}}\left[\theta \right]$ are of the same size, provided that $w^{†}={\displaystyle \frac{p^m}{w}}$, bijectivity, injectivity, and surjectivity of ${\tau }_w$ are equivalent. Therefore, it suffices to prove or disprove bijectivity through either injectivity or surjectivity.

Example 3. 

On the ring $\mathbb{Z}\left[i\right]$, the set ${\mathcal{S}}_{1+i,2,4}$ is tileable with tiling width $w=4$.

Consider the ring of Gaussian integers $\mathbb{Z}\left[i\right]$, the base $\alpha =1+i$ with norm $p=2$ and exponent $m=4$. The set ${\mathcal{S}}_{1+i,2,4}$ is defined as

$$\begin{array}{cc}\hfill {\mathcal{S}}_{1+i,2,4}& =\left\{a_0+a_1(1+i)+a_2{(1+i)}^2+a_3{(1+i)}^3|a_j\in \psi \left({\mathbb{F}}_2\right)\right\}.\hfill \end{array}$$

The set is illustrated in Figure 1 (left).

In this example, the set ${\mathcal{S}}_{1+i,2,4}$ has $p^m=16$ elements, and we use tiling width $w=4$. As a result, the corresponding height is $w^{†}={\displaystyle \frac{16}{4}}=4$. The tiling map ${\tau }_4:{\mathcal{S}}_{1+i,2,4}\to {\mathbb{Z}}_{4,4}\left[i\right]$, defined below, is bijective

$${\tau }_4(a+bi)=(amod4)+(bmod4)i$$

as illustrated by Figure 1 (right). In particular, ${\tau }_4\left(s_j\right)=t_j$ for all $j=1,2,\dots ,16$.

In fact, Harshan [22] and Pooksombat [23] have proved that the set ${\mathcal{S}}_{1+i,2,m}$ is tileable for all $m\ge 2$.

Example 4. 

On the ring $\mathbb{Z}\left[\theta \right]$, where $\theta ={\displaystyle \frac{-1+\sqrt{-11}}{2}}$, the set ${\mathcal{S}}_{-1-\theta ,3,3}$ is not tileable.

In this example, the ring $\mathbb{Z}\left[\theta \right]$ is equipped with $\theta ={\displaystyle \frac{-1+\sqrt{-11}}{2}}$, whose minimal polynomial is ${\theta }^2+\theta +3=0$. The base $\alpha =-1-\theta$ is of norm $p=3$, and the exponent is $m=3$. Therefore, the set ${\mathcal{S}}_{-1-\theta ,3,3}$ is defined as

$$\begin{array}{cc}\hfill {\mathcal{S}}_{-1-\theta ,3,3}& =\left\{a_0+a_1(-1-\theta )+a_2{(-1-\theta )}^2|a_j\in \psi \left({\mathbb{F}}_3\right)\right\}.\hfill \end{array}$$

The possible widths are $w=3$ and $w=9$, but neither ${\tau }_3$ nor ${\tau }_9$ is bijective. Concrete examples here are ${\tau }_3\left(0\right)={\tau }_3(\alpha +{\alpha }^2)$ and ${\tau }_9\left(2\alpha \right)={\tau }_9\left({\alpha }^2\right)$.

Since we are interested in multi-level constructions of lattices, we consider the case where ${\mathcal{S}}_{\alpha ,p,m}$ is tileable for any number of levels. An element $\alpha$ with this property is given a name in the following definition.

Definition 12. 

A base α is said to be totally tiling if ${\mathcal{S}}_{\alpha ,p,m}$ is tileable for all $m\ge 2$.

3. Cubic Shaping of ${\mathcal{S}}_{\mathit{\alpha },\mathit{p},\mathit{m}}$

This section provides the statement and the proof for the main results of this paper. Section 3.1 establishes supporting theorems that assist us in Section 3.2, where we enumerate all totally tiling bases. All other cases are given counterexamples in Section 3.3.

3.1. Introductory Theorems in Tileability

Firstly, we show that constellations with exponent 2 are always tileable. We also provide some trivial cases for exponent 3.

Proposition 1. 

On a ring $\mathbb{Z}\left[\theta \right]$, for any base $\alpha =x+y\theta \in \mathbb{Z}\left[\theta \right]$ with norm $p={\left|\alpha \right|}^2$ prime, the set ${\mathcal{S}}_{\alpha ,p,2}$ is tileable with tiling width $w=p$.

Proof. 

Here, width and height are both equal to p, namely, $w=w^{†}=p$, and the tiling map is componentwise modulo p on both the real and imaginary parts. We will show that ${\tau }_w$ is surjective.

Consider a fixed element $z_0+z_1\theta \in {\mathbb{Z}}_{p,p}\left[\theta \right]$. Since $gcd(y,p)=1$, $a_1=z_1{y}^{-1}modp$ is well-defined. Next, we take $a_0=z_0-a_{1}xmodp$. Notice that $a_0,a_1\in \psi \left({\mathbb{F}}_p\right)$. Therefore, $a_0+a_1\alpha \in {\mathcal{S}}_{\alpha ,p,2}$. We are left to check that ${\tau }_w(a_0+a_1\alpha )=z_0+z_1\theta$. Indeed,

$$\begin{array}{cc}\hfill {\tau }_w(a_0+a_1\alpha )& ={\tau }_w((a_0+a_{1}x)+\left(a_{1}y\right)\theta )\hfill \\ \hfill & =(a_0+a_{1}xmodp)+(a_{1}ymodp)\theta \hfill \\ \hfill & =z_0+z_1\theta ,\hfill \end{array}$$

which implies that ${\tau }_w$ is surjective, or equivalently bijective. □

Proposition 2. 

On a ring $\mathbb{Z}\left[\theta \right]$ where B is prime, for the base $\alpha =\pm \theta$ with norm $p=B$, the set ${\mathcal{S}}_{\alpha ,p,3}$ is tileable with tiling width $w=p^2$.

Proof. 

We only prove the base $\alpha =\theta$ since the case $\alpha =-\theta$ can be handled similarly.

Here, the norm is $p=B$, and we use width $w=p^2$ and height $w^{†}=p$. The tiling map ${\tau }_{p^2}$ is componentwise modulo $p^2$ on the real part and p on the imaginary part. We will show that ${\tau }_w$ is surjective.

For a fixed element $z_0+z_1\theta \in {\mathbb{Z}}_{p^2,p}\left[\theta \right]$, $z_0\in {\mathbb{Z}}_{p^2}$ and $z_1\in {\mathbb{Z}}_p$, choose $a_0=z_{0}modp$, $a_2={\displaystyle \frac{a_0-z_0}{p}}modp$, and $a_1=z_1+A{a}_{2}modp$. By the choice of $a_0$, we have that $a_2$ and $a_1$ are well-defined. Moreover, $a_0,a_1,a_2\in \psi \left({\mathbb{F}}_p\right)$. Therefore, $a_0+a_1\alpha +a_2{\alpha }^2\in {\mathcal{S}}_{\alpha ,p,3}$ and

$$\begin{array}{cc}\hfill {\tau }_w(a_0+a_1\alpha +a_2{\alpha }^2)& ={\tau }_w((a_0-p{a}_2)+(a_1-A{a}_2)\theta )\hfill \\ \hfill & =(a_0-p{a}_{2}mod{p}^2)+(a_1-A{a}_{2}modp)\theta \hfill \\ \hfill & =z_0+z_1\theta .\hfill \end{array}$$

The proof is complete. □

Example 5. 

On the ring $\mathbb{Z}\left[\theta \right]$, where $\theta ={\displaystyle \frac{-1+\sqrt{-11}}{2}}$, the set ${\mathcal{S}}_{\theta ,3,3}$ is tileable with tiling width $w=9$.

The ring is generated from $\theta ={\displaystyle \frac{-1+\sqrt{-11}}{2}}$, whose minimal polynomial is ${\theta }^2+\theta +3=0$, meaning that $A=1$ and $B=3$. Since $B=3$ is prime and the base is $\alpha =\theta$, the result is a direct consequence from Proposition 2. Here, the norm is $p=3$. Therefore, ${\mathcal{S}}_{\theta ,3,3}$ is tileable with tiling width $p^2=9$. The tileability through ${\tau }_9$ is shown in Figure 2.

The next result will be helpful in finding counterexamples when the set is not tileable.

Proposition 3. 

The tiling map ${\tau }_w$ is bijective if and only if there is no element of the form $d=d_0+d_1\alpha +\cdots +d_{m-1}{\alpha }^{m-1}$, where $d_j$’s are integers, not all zero and $\left|d_j\right|<p$ such that $w\mid \mathcal{R}\left(d\right)$ and $w^{†}\mid \mathcal{I}\left(d\right)$.

Proof. 

We prove by contraposition in both directions.

• Suppose that ${\tau }_w$ is not bijective. This means that there exist two distinct elements $a,b\in {\mathcal{S}}_{\alpha ,p,m}$ such that ${\tau }_w\left(a\right)={\tau }_w\left(b\right)$. Suppose that a and b are with coefficients $a_j,b_j\in \psi \left({\mathbb{F}}_p\right)$, respectively. We define $d=a-b$, which will have coefficients $d_j=a_j-b_j$ where $|d_j|<p$. Since a and b are distinct, it follows that $d_j$’s are not all zero.
  However, we have ${\tau }_w\left(a\right)={\tau }_w\left(b\right)$. By considering the real and imaginary parts of the equation, which are under modulo w and $w^{†}$, respectively, together with the fact that $d=a-b$, one obtains $w\mid \mathcal{R}\left(d\right)$ and $w^{†}\mid \mathcal{I}\left(d\right)$ as desired.
• Suppose that there exists an element d with coefficients $d_j$, where $d_j$’s are not all zero and $|d_j|<p$ such that $w\mid \mathcal{R}\left(d\right)$ and $w^{†}\mid \mathcal{I}\left(d\right)$. Next, we separate the coefficients of d into positive and negative ones and use them to construct such a and b. Define

  $$a=\sum _{\begin{array}{c}0\le j<m,\\ d_j>0\end{array}}{d}_j{\alpha }^j\mathrm{and}b=\sum _{\begin{array}{c}0\le j<m,\\ d_j<0\end{array}}-d_j{\alpha }^j.$$
  Since the coefficients of a and b are in $\psi \left({\mathbb{F}}_p\right)$, $a,b\in {\mathcal{S}}_{\alpha ,p,m}$. It is obvious that $a\ne b$, and from the fact that $d=a-b$ together with the property that $w\mid \mathcal{R}\left(d\right)$ and $w^{†}\mid \mathcal{I}\left(d\right)$, one may combine the real and imaginary parts into one equation, namely, ${\tau }_w\left(a\right)={\tau }_w\left(b\right)$. This concludes that ${\tau }_w$ is not bijective.

  □

In the next theorem, we abuse the notation slightly by using ${\tau }_w$ on different sets. Nevertheless, the sets are from the same family of bases with the same norm and same exponent. The definition and range of ${\tau }_w$ is technically unaffected.

Theorem 1. 

On a ring $\mathbb{Z}\left[\theta \right]$, let $\alpha \in \mathbb{Z}\left[\theta \right]$ be a base with norm $p={\left|\alpha \right|}^2$ prime and m be an exponent.

1.

For any w, the bijectivity of ${\tau }_w$ for ${\mathcal{S}}_{\alpha ,p,m}$ and ${\mathcal{S}}_{-\alpha ,p,m}$ is the same.

2.

If m is even, the bijectivity of ${\tau }_{p^{\frac{m}{2}}}$ for ${\mathcal{S}}_{\alpha ,p,m}$, ${\mathcal{S}}_{-\alpha ,p,m}$, ${\mathcal{S}}_{\overline{\alpha },p,m}$, and ${\mathcal{S}}_{-\overline{\alpha },p,m}$ is the same.

Proof. 

We shall prove each part separately through contraposition.

• Suppose that ${\tau }_w$ for ${\mathcal{S}}_{\alpha ,p,m}$ is not bijective. According to Proposition 3, there exists an element d with coefficients $d_0,d_1,\dots ,d_{m-1}$, where $d_j$’s are not all zero and $|d_j|<p$ such that $w\mid \mathcal{R}\left(d\right)$ and $w^{†}\mid \mathcal{I}\left(d\right)$.
  We construct a counterexample for ${\mathcal{S}}_{-\alpha ,p,m}$ by introducing an element $d^{\prime }$ with coefficients $d_j^{\prime }={(-1)}^j{d}_j$ for all $j=0,1,\dots ,m-1$. From the definition, we can see that $d_j^{\prime }$’s are not all zero with $|d_j^{\prime }|<p$. Furthermore,

  $$d^{\prime }=\sum _{j=0}^{m-1}{d}_j^{\prime }{(-\alpha )}^j=\sum _{j=0}^{m-1}{(-1)}^j{d}_j{(-\alpha )}^j=\sum _{j=0}^{m-1}{d}_j{\alpha }^j=d.$$
  Therefore, $w\mid \mathcal{R}\left(d^{\prime }\right)$ and $w^{†}\mid \mathcal{I}\left(d^{\prime }\right)$ as well. From Proposition 3, it implies that ${\tau }_w$ is not bijective for ${\mathcal{S}}_{-\alpha ,p,m}$.
• Suppose that m is even. It now suffices to show that the bijectivity of ${\tau }_w$ for ${\mathcal{S}}_{\alpha ,p,m}$ and ${\mathcal{S}}_{\overline{\alpha },p,m}$ coincides.
  Suppose that ${\tau }_{p^{\frac{m}{2}}}$ is not bijective for ${\mathcal{S}}_{\alpha ,p,m}$. From Proposition 3, there exists an element d with coefficients $d_j$, where $d_j$’s are not all zero and $|d_j|<p$ such that $\mathcal{R}\left(d\right)$ and $\mathcal{I}\left(d\right)$ are both divisible by $p^{\frac{m}{2}}$.
  We construct a counterexample again, this time with $d^{\prime }\in {\mathcal{S}}_{\overline{\alpha },p,m}$ employing the same coefficients. In other words, $d^{\prime }=d_0+d_1\overline{\alpha }+\cdots +d_{m-1}{\overline{\alpha }}^{m-1}$, implying that $d^{\prime }=\overline{d}$. Nonetheless, it follows from ${\theta }^2+A\theta +B=0$ that $\overline{\theta }=-A-\theta$. As a result,

  $$\begin{array}{cc}\hfill \mathcal{R}\left(d^{\prime }\right)& =\mathcal{R}\left(d\right)-A·\mathcal{I}\left(d\right),\hfill \\ \hfill \mathcal{I}\left(d^{\prime }\right)& =-\mathcal{I}\left(d\right).\hfill \end{array}$$
  Since $\mathcal{R}\left(d\right)$ and $\mathcal{I}\left(d\right)$ are divisible by $p^{\frac{m}{2}}$, so are $\mathcal{R}\left(d^{\prime }\right)$ and $\mathcal{I}\left(d^{\prime }\right)$.

The proof is now complete. □

Note that the second part of the above theorem only works when m is even and the tiling map is cubic, meaning $w=w^{†}$. When m is odd, the result varies depending on the base and exponent. Since Theorem 1 now allows us to deduce the tileability of $-\alpha$ and $\pm \overline{\alpha }$ from that of $\alpha$, we say that they are in the same family.

Note also that the bases from Examples 4 and 5 are conjugates of each other. However, the set ${\mathcal{S}}_{\theta ,3,3}$ is tileable, whereas ${\mathcal{S}}_{\overline{\theta },3,3}$ is not. This is further explored in Section 3.2.

3.2. Totally Tiling Bases

This subsection identifies all totally tiling bases. Theorems 2 and 3 cover the trivial cases where bases are of the form $\sqrt{-p}$, while Theorems 4–6 cover all other bases, which happen to be Gaussian and Eisenstein integers. The proof that there is no other element with this property is given in the next subsection.

We have seen from Proposition 2 that ${\mathcal{S}}_{\alpha ,p,3}$ is tileable on $\mathbb{Z}\left[\theta \right]$, where $\alpha =\pm \theta$ with norm $p=B$ when B is prime. This is true regardless of whether $A=0$ or $A=1$. However, once we change the exponent to $m=4$, the same statement no longer holds. The next theorem shows that $\alpha =\pm \theta$ is a totally tiling base if and only if $A=0$.

Theorem 2. 

On a ring $\mathbb{Z}\left[\theta \right]$ where B is prime, the base $\alpha =\pm \theta$ with norm $p=B$ is totally tiling if and only if $A=0$. Under such a case, the tiling width is

$$w=\left\{\begin{array}{cc}{p}^{\frac{m}{2}}\hfill & \mathrm{if}m\mathrm{is}\mathrm{even},\hfill \\ p^{\frac{m+1}{2}}\hfill & \mathrm{if}m\mathrm{is}\mathrm{odd}.\hfill \end{array}\right.$$

Proof. 

According to Theorem 1, it suffices to only show the case $\alpha =\theta$.

First, we prove that $\alpha =\theta$, where $A=0$ and B is prime, is totally tiling. In particular, $\alpha =\theta =\sqrt{-B}=\sqrt{-p}$ with norm $p=B$. We divide the proof into two subparts by the parity of m. For an element $s\in {\mathcal{S}}_{\theta ,p,m}$, we let $a_j\in \psi \left({\mathbb{F}}_p\right)$ be its coefficients. In other words, $s=a_0+a_1\theta +\cdots +a_{m-1}{\theta }^{m-1}$.

• For m even, we use $w=w^{†}=p^{\frac{m}{2}}$. Since ${\tau }_w$ is the componentwise modulo $p^{\frac{m}{2}}$ on the real and imaginary parts, for any $s\in {\mathcal{S}}_{\theta ,p,m}$, ${\tau }_w\left(s\right)=s+r{p}^{\frac{m}{2}}=s+r^{\prime }{\theta }^m$ for some $r,r^{\prime }\in \mathbb{Z}\left[\theta \right]$. Therefore,

  $${\tau }_w\left(s\right)=\sum _{j=0}^{m-1}{a}_j{\theta }^j+r^{\prime }{\theta }^m.$$
  The equation shows that ${\tau }_w$ is the p-ary decomposition through base $\theta$, which is unique.
• For m odd, we use $w=p^{\frac{m+1}{2}}$ and $w^{†}=p^{\frac{m-1}{2}}$. Similarly, for any $s\in {\mathcal{S}}_{\theta ,p,m}$,

  $${\tau }_w\left(s\right)=s+\left(r_1{p}^{\frac{m+1}{2}}+r_2{p}^{\frac{m-1}{2}}\theta \right)=s+{\theta }^{m-1}\left(r_1^{\prime }p+r_2^{\prime }\theta \right)$$

  for some $r_1,r_2,r_1^{\prime },r_2^{\prime }\in \mathbb{Z}$. As a result,

  $${\tau }_w\left(s\right)=\sum _{j=0}^{m-2}{a}_j{\theta }^j+\left(a_{m-1}+r_1^{\prime }p+r_2^{\prime }\theta \right){\theta }^{m-1}.$$
  This p-ary decomposition base $\theta$ is unique as long as $r^{\prime }=(a_{m-1}+r_1^{\prime }p)+\left(r_2^{\prime }\right)\theta$ is also uniquely represented. Here, its real and imaginary parts are $\mathcal{R}\left(r^{\prime }\right)=a_{m-1}+r_1^{\prime }p$ and $\mathcal{I}\left(r^{\prime }\right)=r_2^{\prime }$, which are then both uniquely represented, since $a_{m-1}\in \psi \left({\mathbb{F}}_p\right)$ and $r_1^{\prime },r_2^{\prime }\in \mathbb{Z}$.

Next, we demonstrate counterexamples with $m=4$ that $\alpha =\theta$, where $A=1$ and B is prime, is not totally tiling. In this case, $\alpha =\theta ={\displaystyle \frac{-1+\sqrt{1-4B}}{2}}$ with norm $p=B$. Since the exponent is $m=4$, there are three possible widths. Explicit counterexamples are shown as follows:

• For $w=p$, we have ${\tau }_w\left(0\right)={\tau }_w(\alpha +{\alpha }^2)$.
• For $w=p^2$, we have ${\tau }_w\left((p-1){\alpha }^2\right)={\tau }_w\left({\alpha }^3\right)$.
• For $w=p^3$, we have ${\tau }_w\left(0\right)={\tau }_w({\alpha }^2+{\alpha }^3)$.

We conclude that on the ring $\mathbb{Z}\left[\theta \right]$ where B is prime, the base $\alpha =\pm \theta$ is totally tiling if and only if $A=0$. □

We illustrate the second part of Theorem 2 in the next example.

Example 6. 

On the ring $\mathbb{Z}\left[\theta \right]$ where $\theta ={\displaystyle \frac{-1+\sqrt{-7}}{2}}$, the set ${\mathcal{S}}_{\theta ,2,4}$ is not tileable.

Here, $A=1$ and $B=2$. The base $\alpha =\theta$ is of norm $p=2$. Figure 3 shows that none of the tiling maps ${\tau }_2,{\tau }_4,{\tau }_8$ are bijective.

Although the base $\alpha =\pm \theta$ is not totally tiling when $A=1$, the base $\alpha =\pm (1+2\theta )$ with norm $p=4B-1$ is, under the assumption that $4B-1$ is prime. This is stated as the next theorem.

Theorem 3. 

On a ring $\mathbb{Z}\left[\theta \right]$, where $A=1$ and $4B-1$ is prime, the base $\alpha =\pm (1+2\theta )$ with norm $p=4B-1$ is totally tiling with tiling width

$$w=\left\{\begin{array}{cc}{p}^{\frac{m}{2}}\hfill & \mathrm{if}m\equiv 0(mod2),\hfill \\ p^{\frac{m+1}{2}}\hfill & \mathrm{if}m\equiv 1(mod2).\hfill \end{array}\right.$$

We omit the proof of this theorem since $\alpha =\pm \sqrt{1-4B}=\pm \sqrt{-p}$, and the result can be obtain in a similar fashion to that of Theorem 2.

Example 7. 

On the ring $\mathbb{Z}\left[\omega \right]$, the set ${\mathcal{S}}_{1+2\omega ,3,4}$ is tileable with tiling width $w=9$.

In this example, we have $A=1$ and $B=1$, with $4B-1=3$ prime. According to Theorem 3, the base $\alpha =1+2\omega$ with norm $p=3$ is totally tiling.

Now that we have handled the general yet trivial cases, we move on to the special cases for the Gaussian integers $\mathbb{Z}\left[i\right]$ and the Eisenstein integers $\mathbb{Z}\left[\omega \right]$. Of all possible bases, only those of norm $p=2$ in $\mathbb{Z}\left[i\right]$ and norm $p=3$ in $\mathbb{Z}\left[\omega \right]$ are totally tiling.

Theorem 4. 

On the ring $\mathbb{Z}\left[i\right]$, the base $\alpha =\pm (1+i),\pm (1-i)$ with norm $p=2$ is totally tiling with tiling width

$$w=\left\{\begin{array}{cc}{2}^{\frac{m}{2}}\hfill & \mathrm{if}m\equiv 0(mod2),\hfill \\ 2^{\frac{m+1}{2}}\hfill & \mathrm{if}m\equiv 1(mod4),\hfill \\ 2^{\frac{m-1}{2}}\hfill & \mathrm{if}m\equiv 3(mod4).\hfill \end{array}\right.$$

Proof. 

We show only the case $\alpha =1+i$, since other bases can be performed similarly or deduced from Theorem 1. We divide the proof into three parts according to the case of exponent m as stated in the theorem. We write an element $s\in {\mathcal{S}}_{\alpha ,2,m}$ as $s=a_0+a_1\alpha +\cdots +a_{m-1}{\alpha }^{m-1}$ where $a_j\in \psi \left({\mathbb{F}}_2\right)$.

• For $m\equiv 0(mod2)$, we use $w=w^{†}=2^{\frac{m}{2}}$. Because ${\tau }_w$ is componentwise modulo $p^{\frac{m}{2}}$ on both real and imaginary parts, for any $s\in {\mathcal{S}}_{\alpha ,2,m}$, ${\tau }_w\left(s\right)=s+r·2^{\frac{m}{2}}=s+r^{\prime }{\alpha }^m$ for some $r,r^{\prime }\in \mathbb{Z}\left[i\right]$. Consequently,

  $${\tau }_w\left(s\right)=\sum _{j=0}^{m-1}{a}_j{\alpha }^j+r^{\prime }{\alpha }^m,$$

  which is the binary decomposition base $\alpha$, and is unique.
• For $m\equiv 1(mod4)$, we use $w=2^{\frac{m+1}{2}}$ and $w^{†}=2^{\frac{m-1}{2}}$. Therefore, for any $s\in {\mathcal{S}}_{\alpha ,2,m}$,

  $${\tau }_w\left(s\right)=s+\left(r_1·2^{\frac{m+1}{2}}+r_2·2^{\frac{m-1}{2}}i\right)=s+\left(r_1^{\prime }·2+r_2^{\prime }i\right){\alpha }^{m-1}$$

  for some $r_1,r_2,r_1^{\prime },r_2^{\prime }\in \mathbb{Z}\left[i\right]$. As a result,

  $${\tau }_w\left(s\right)=\sum _{j=0}^{m-2}{a}_j{\alpha }^j+\left(a_{m-1}+r_1^{\prime }·2+r_2^{\prime }i\right){\alpha }^{m-1}.$$
  From the uniqueness property of binary decomposition base $\alpha$, it is left to show that the term $r^{\prime }=(a_{m-1}+r_1^{\prime }·2)+\left(r_2^{\prime }\right)i$ is uniquely represented. Here, its real and imaginary parts are $\mathcal{R}\left(r^{\prime }\right)=a_{m-1}+r_1^{\prime }·2$ and $\mathcal{I}\left(r^{\prime }\right)=r_2^{\prime }$, and so the uniqueness of the expressions ensues from the fact that $a_{m-1}\in \psi \left({\mathbb{F}}_2\right)$ and $r_1^{\prime },r_2^{\prime }\in \mathbb{Z}\left[i\right]$.
• For $m\equiv 3(mod4)$, we use $w=2^{\frac{m-1}{2}}$ and $w^{†}=2^{\frac{m+1}{2}}$. For any $s\in {\mathcal{S}}_{\alpha ,2,m}$, we can write the tiling map as

  $${\tau }_w\left(s\right)=s+\left(r_1·2^{\frac{m-1}{2}}+r_2·2^{\frac{m+1}{2}}i\right)=s+\left(r_2^{\prime }·2+r_1^{\prime }i\right){\alpha }^{m-1}$$

  for some $r_1,r_2,r_1^{\prime },r_2^{\prime }\in \mathbb{Z}\left[i\right]$. This implies that

  $${\tau }_w\left(s\right)=\sum _{j=0}^{m-2}{a}_j{\alpha }^j+\left(a_{m-1}+r_2^{\prime }·2+r_1^{\prime }i\right){\alpha }^{m-1}.$$
  By applying the same technique as in the previous case, we conclude that it is uniquely represented.

In conclusion, the base $\alpha =1+i$ is totally tiling. □

Next, we consider the case of Eisenstein integers.

Theorem 5. 

On the ring $\mathbb{Z}\left[\omega \right]$, the base $\alpha =\pm (2+\omega )$ with norm $p=3$ is totally tiling with tiling width

$$w=\left\{\begin{array}{cc}{3}^{\frac{m}{2}}\hfill & \mathrm{if}m\equiv 0(mod2),\hfill \\ 3^{\frac{m+1}{2}}\hfill & \mathrm{if}m\equiv 1(mod6),\hfill \\ 3^{\frac{m\pm 1}{2}}\hfill & \mathrm{if}m\equiv 3(mod6),\hfill \\ 3^{\frac{m-1}{2}}\hfill & \mathrm{if}m\equiv 5(mod6).\hfill \end{array}\right.$$

Proof. 

We give the proof for $\alpha =2+\omega$, which is divided into five separate parts. Again, we write $s\in {\mathcal{S}}_{\alpha ,3,m}$ as $s=a_0+a_1\alpha +\cdots +a_{m-1}{\alpha }^{m-1}$ where $a_j\in \psi \left({\mathbb{F}}_3\right)$.

• For $m\equiv 0(mod2)$, we use $w=w^{†}=3^{\frac{m}{2}}$. Hence, for any element $s\in {\mathcal{S}}_{\alpha ,3,m}$, we have ${\tau }_w\left(s\right)=s+r·3^{\frac{m}{2}}=s+r^{\prime }{\alpha }^m$ for some $r,r^{\prime }\in \mathbb{Z}\left[\omega \right]$. It can be rewritten as

  $${\tau }_w\left(s\right)=\sum _{j=0}^{m-1}{a}_j{\alpha }^j+r^{\prime }{\alpha }^m,$$

  which is a ternary decomposition base $\alpha$ and is unique.
• For $m\equiv 1(mod6)$, we use $w=3^{\frac{m+1}{2}}$ and $w^{†}=3^{\frac{m-1}{2}}$. For any element $s\in {\mathcal{S}}_{\alpha ,3,m}$, we have ${\tau }_w\left(s\right)=s+\left(r_1·3^{\frac{m+1}{2}}+r_2·3^{\frac{m-1}{2}}\omega \right)=s+\left(r_1^{\prime }·3+r_2^{\prime }\omega \right){\alpha }^{m-1}$ for some $r_1,r_2,r_1^{\prime },r_2^{\prime }\in \mathbb{Z}\left[\omega \right]$. Therefore,

  $${\tau }_w\left(s\right)=\sum _{j=0}^{m-2}{a}_j{\alpha }^j+\left(a_{m-1}+r_1^{\prime }·3+r_2^{\prime }\omega \right){\alpha }^{m-1}.$$
  We invoke unique decomposition base $\alpha$, and it remains to be shown that $r^{\prime }=a_{m-1}+r_1^{\prime }·3+r_2^{\prime }\omega$ is uniquely represented. By considering its real part, we have $\mathcal{R}\left(r^{\prime }\right)=a_{m-1}+r_1^{\prime }·3$, which is uniquely represented via division modulo $\alpha$ and that $a_{m-1}\in \psi \left({\mathbb{F}}_3\right)$. Furthermore, its imaginary part is $\mathcal{I}\left(r^{\prime }\right)=r_2^{\prime }$, which is uniquely represented.
• For $m\equiv 3(mod6)$, the first possibility is $w=3^{\frac{m+1}{2}}$ and $w^{†}=3^{\frac{m-1}{2}}$. For $s\in {\mathcal{S}}_{\alpha ,3,m}$, we have ${\tau }_w\left(s\right)=s+\left(r_1·3^{\frac{m+1}{2}}+r_2·3^{\frac{m-1}{2}}\omega \right)=s+\left(r_2^{\prime }+(r_1^{\prime }·3+r_2^{\prime })\omega \right){\alpha }^{m-1}$ for some $r_1,r_2,r_1^{\prime },r_2^{\prime }\in \mathbb{Z}\left[\omega \right]$. Therefore,

  $${\tau }_w\left(s\right)=\sum _{j=0}^{m-2}{a}_j{\alpha }^j+\left(a_{m-1}+r_2^{\prime }+(r_1^{\prime }·3+r_2^{\prime })\omega \right){\alpha }^{m-1}.$$
  Again, it is only left to show that the term $r^{\prime }=(a_{m-1}+r_2^{\prime })+(r_1^{\prime }·3+r_2^{\prime })\omega$ is uniquely represented. Notice that

  $$r^{\prime }=(a_{m-1}-r_1^{\prime }·3)+(r_1^{\prime }·3+r_2^{\prime })(1+\omega ).$$
  Since $\mathbb{Z}\left[\omega \right]$ is a free $\mathbb{Z}$-module which can be generated by 1 and $1+\omega$, we have that the expressions $(a_{m-1}-r_1^{\prime }·3)$ and $(r_1^{\prime }·3+r_2^{\prime })$ are uniquely represented. However, the first term is uniquely represented by $a_{m-1}$ and $r_1^{\prime }$, since $a_{m-1}\in \psi \left({\mathbb{F}}_3\right)$ and $r_1^{\prime }\in \mathbb{Z}\left[\omega \right]$. As a result, $r_2^{\prime }\in \mathbb{Z}\left[\omega \right]$ must be unique as well.
• For $m\equiv 3(mod6)$, the second possibility is $w=3^{\frac{m-1}{2}}$ and $w^{†}=3^{\frac{m+1}{2}}$. For any $s\in {\mathcal{S}}_{\alpha ,3,m}$, ${\tau }_w\left(s\right)=s+\left(r_1·3^{\frac{m-1}{2}}+r_2·3^{\frac{m+1}{2}}\omega \right)=s+\left(r_2^{\prime }·3+(r_1^{\prime }+r_2^{\prime }·3)\omega \right){\alpha }^{m-1}$ for some $r_1,r_2,r_1^{\prime },r_2^{\prime }\in \mathbb{Z}\left[\omega \right]$. Then,

  $${\tau }_w\left(s\right)=\sum _{j=0}^{m-2}{a}_j{\alpha }^j+\left(a_{m-1}+r_2^{\prime }·3+(r_1^{\prime }+r_2^{\prime }·3)\omega \right){\alpha }^{m-1}.$$
  In this case, we are left to show that $r^{\prime }=(a_{m-1}+r_2^{\prime }·3)+(r_1^{\prime }+r_2^{\prime }·3)\omega$ is uniquely represented. Since its real part is $\mathcal{R}\left(r^{\prime }\right)=a_{m-1}+r_2^{\prime }·3$, where $a_{m-1}\in \psi \left({\mathbb{F}}_3\right)$ and $r_2^{\prime }\in \mathbb{Z}\left[\omega \right]$, it is uniquely represented by $a_{m-1}$ and $r_2^{\prime }$. From the uniqueness of $r_2^{\prime }\in \mathbb{Z}\left[\omega \right]$, it follows that $r_1^{\prime }\in \mathbb{Z}\left[\omega \right]$ must be unique, in order to make $\mathcal{I}\left(r^{\prime }\right)=r_1^{\prime }+r_2^{\prime }·3$ unique.
• For $m\equiv 5(mod6)$, we use $w=3^{\frac{m-1}{2}}$ and $w^{†}=3^{\frac{m+1}{2}}$. For any element $s\in {\mathcal{S}}_{\alpha ,3,m}$, ${\tau }_w\left(s\right)=s+\left(r_1·3^{\frac{m-1}{2}}+r_2·3^{\frac{m+1}{2}}\omega \right)=s+\left(r_1^{\prime }+(r_1^{\prime }+r_2^{\prime }·3)\omega \right){\alpha }^{m-1}$ for some $r_1,r_2,r_1^{\prime },r_2^{\prime }\in \mathbb{Z}\left[\omega \right]$. Hence,

  $${\tau }_w\left(s\right)=\sum _{j=0}^{m-2}{a}_j{\alpha }^j+\left(a_{m-1}+r_1^{\prime }+(r_1^{\prime }+r_2^{\prime }·3)\omega \right){\alpha }^{m-1}.$$
  Lastly, it is left to show that $r^{\prime }=(a_{m-1}+r_1^{\prime })+(r_1^{\prime }+r_2^{\prime }·3)\omega$ is uniquely represented by $a_{m-1}\in \psi \left({\mathbb{F}}_3\right)$ and $r_1^{\prime },r_2^{\prime }\in \mathbb{Z}\left[\omega \right]$. Notice that

  $$r^{\prime }=(a_{m-1}-r_2^{\prime }·3)+(r_1^{\prime }+r_2^{\prime }·3)(1+\omega ).$$
  We once again use the fact that $\mathbb{Z}\left[\omega \right]$ is a free $\mathbb{Z}$-module generated by 1 and $1+\omega$ to conclude that the expressions $(a_{m-1}-r_2^{\prime }·3)$ and $(r_1^{\prime }+r_2^{\prime }·3)$ are unique. Since $a_{m-1}\in \psi \left({\mathbb{F}}_3\right)$ and $r_2^{\prime }\in \mathbb{Z}\left[\omega \right]$, the first term is uniquely represented by $a_{m-1}$ and $r_2^{\prime }$. Consequently, $r_1^{\prime }$ is unique as well.

  □

Example 8 below illustrates the result of the previous theorem.

Example 8. 

On the ring $\mathbb{Z}\left[\omega \right]$, the set ${\mathcal{S}}_{2+\omega ,3,5}$ is tileable with tiling width $w=9$.

From Theorem 5, on $\mathbb{Z}\left[\omega \right]$, the set generated by $\alpha =2+\omega$ with norm $p=3$ and exponent $m=5$ is tileable with tiling width $w=9$. Figure 4 shows the bijectivity of the tiling map ${\tau }_9$.

Alternatively, the base $\alpha =\pm (-1+\omega )$ is also totally tiling for the Eisenstein integers. The proof for the next theorem is omitted since it is similar to that of Theorem 5.

Theorem 6. 

On the ring $\mathbb{Z}\left[\omega \right]$, the base $\alpha =\pm (-1+\omega )$ with norm $p=3$ is totally tiling with tiling width

$$w=\left\{\begin{array}{cc}{3}^{\frac{m}{2}}\hfill & \mathrm{if}m\equiv 0(mod2),\hfill \\ 3^{\frac{m+1}{2}}\hfill & \mathrm{if}m\equiv 1(mod6),\hfill \\ 3^{\frac{m-1}{2}}\hfill & \mathrm{if}m\equiv 3(mod6),\hfill \\ 3^{\frac{m\pm 1}{2}}\hfill & \mathrm{if}m\equiv 5(mod6).\hfill \end{array}\right.$$

Example 9. 

On the ring $\mathbb{Z}\left[\omega \right]$, the set ${\mathcal{S}}_{-1+\omega ,3,5}$ is tileable with tiling width $w=9$ or $w=27$.

According to Theorem 6, the set ${\mathcal{S}}_{-1+\omega ,3,5}$ on $\mathbb{Z}\left[\omega \right]$ is tileable with tiling width $w=9$ or $w=27$. Figure 5 shows the bijectivity of both ${\tau }_9$ and ${\tau }_{27}$.

3.3. Counterexamples for the Remaining Cases

To prove that a base is not totally tiling, it suffices to find an exponent m and exhaust all possible tiling widths. As it turns out, counterexamples for bases other than those we mentioned in the previous subsection can be found for $m=4$. Here, there are 3 possible tiling maps: ${\tau }_p,{\tau }_{p^2},{\tau }_{p^3}$. Our next two theorems will rule out the tileability of ${\tau }_p$ and ${\tau }_{p^3}$.

Theorem 7. 

For ${\mathcal{S}}_{\alpha ,p,4}$ on $\mathbb{Z}\left[\theta \right]$ with $p={\left|\alpha \right|}^2$ prime, the tiling map ${\tau }_p$ is not bijective.

Proof. 

Let $\alpha =x+y\theta$ and $p={\left|\alpha \right|}^2=x^2-Axy+B{y}^2$. According to Proposition 3, we show that for any base $\alpha$, there exists $d=d_0+d_1\alpha +d_2{\alpha }^2+d_3{\alpha }^3$, where $|d_j|<p$ such that $p\mid \mathcal{R}\left(d\right)$ and $p^3\mid \mathcal{I}\left(d\right)$.

First, we show counterexamples for some particular bases, which are $\pm (1+i)$, $\pm (1-i)$, $\pm (2+i),\pm (2-i)$ in $\mathbb{Z}\left[i\right]$ and $\pm (2+\omega ),\pm (-1+\omega )$ in $\mathbb{Z}\left[\omega \right]$.

• On $\mathbb{Z}\left[i\right]$, for $\alpha =1\pm i$ with norm $p=2$, we have $d={\alpha }^2-{\alpha }^3=2$.
• On $\mathbb{Z}\left[i\right]$, for $\alpha =2\pm i$ with norm $p=5$, we have $d=3\alpha +2{\alpha }^2-{\alpha }^3=10$.
• On $\mathbb{Z}\left[\omega \right]$, for $\alpha =2+\omega ,-1+\omega$ with norm $p=3$, we have $d=2{\alpha }^2-{\alpha }^3=3$.

For other bases, we construct d with coefficients $d_0=0$, $d_1=2x-Ay$, $d_2=-1$, and $d_3=0$. Direct computation shows that $d=p$, which serves as a counterexample. It is left to show that the coefficients we picked satisfy the criterion $|d_j|<p$.

• For $d_0=0$, $d_2=-1$, and $d_3=0$, it is obvious that they obey $|d_j|<p$.
• For $d_1=2x-Ay$, suppose on the contrary that $|2x-Ay|\ge x^2-Axy+B{y}^2$. The inequality can be written as a polynomial inequality in x as

  $$x^2-(Ay\pm 2)x+(B{y}^2\pm Ay)\le 0$$

  whose discriminant is $(A^2-4B)y^2+4$. The inequality holds if and only if the discriminant is non-negative, which means that $y^2\le {\displaystyle \frac{4}{4B-A^2}}$. Since $y\ne 0$, we can conclude that $B=1$. As for the next step, we consider whether $A=0$ or $A=1$.

  –

  When $A=0$, we have the ring $\mathbb{Z}\left[i\right]$. The inequality of discriminant is $y^2\le 1$. Therefore, $y=\pm 1$, and thus $x=\pm 1,\pm 2$. The only possible bases are $\alpha =\pm (1+i)$, $\pm (1-i),\pm (2+i)\pm (2-i)$, which have already been given a counterexample.

  –

  When $A=1$, we have the ring $\mathbb{Z}\left[\omega \right]$. The inequality of discriminant is $y^2\le {\displaystyle \frac{4}{3}}$. As a result, we have $y=1$ and $x=\pm 1,2$ or $y=-1$ and $x=\pm 1,-2$. The resulting bases are $\alpha =\pm (1+\omega ),\pm (1-\omega ),\pm (2+\omega )$. However, each of them either has norm $p<2$ or has been given a counterexample previously.

Therefore, ${\tau }_p$ is not bijective in any case. □

Theorem 8. 

For ${\mathcal{S}}_{\alpha ,p,4}$ on $\mathbb{Z}\left[\theta \right]$ with $p={\left|\alpha \right|}^2$ prime, the tiling map ${\tau }_{p^3}$ is not bijective.

Proof. 

Let $\alpha =x+y\theta$ and $p={\left|\alpha \right|}^2=x^2-Axy+B{y}^2$. Our goal is to find a counterexample $d=d_0+d_1\alpha +d_2{\alpha }^2+d_3{\alpha }^3$, where $|d_j|<p$ such that $p^3\mid \mathcal{R}\left(d\right)$ and $p\mid \mathcal{I}\left(d\right)$. The proof is divided into two main parts depending on whether $A=0$ or $A=1$.

For $A=0$, we have $p=x^2+B{y}^2$. We give a counterexample to a special case of $\alpha$, followed by its general case.

• For $\alpha =\pm \theta$ with norm $p=B$, we use $d={\alpha }^3=\mp p\theta$ as a counterexample.
• For other bases, we take $d_0=0$, $d_1=B{y}^2-x^2$, $d_2=x$, and $d_3=0$, which gives us $d=yp\theta$. Again, we have yet to verify that the coefficients obey $|d_j|<p$.

  –

  It is clear that $d_0=0$ and $d_3=0$ satisfy $|d_j|<p$.

  –

  For $d_1=B{y}^2-x^2$, we have $|d_1|\le |B{y}^2|+|-x^2|=x^2+B{y}^2=p$. The only case of equality is when $x=0$. This would imply $y=\pm 1$ where a counterexample has already been constructed.

  –

  For $d_2=x$, we have $|d_2|=|x|\le x^2<x^2+B{y}^2=p$ as desired.

For $A=1$, we have $p=x^2-xy+B{y}^2$. We divide the proof into a special case of $\alpha$ and then three cases for $\left|x\right|=\sqrt{B}\left|y\right|$, $\left|x\right|>\sqrt{B}\left|y\right|$ and $\left|x\right|<\sqrt{B}\left|y\right|$ as follows.

• For $B=2$ and the base $\alpha =\pm (1+\theta )$ with norm $p=2$, we use $d=\alpha \pm {\alpha }^2=\pm 2\theta$ as a counterexample.
• Suppose that $\left|x\right|=\sqrt{B}\left|y\right|$. According to Lemma 2, either $(x,y)=(0,\pm 1)$ or $gcd(x,y)=1$. Therefore, the only possible value for b is 1, and thus $\left|x\right|=\left|y\right|$. This leads to the bases $\alpha =\pm (-1+\omega )$ with norm $p=3$ in $\mathbb{Z}\left[\omega \right]$. For the base $\alpha =-1+\omega$, we choose $d={\alpha }^2=-3\omega$ as a counterexample.
• Suppose that $\left|x\right|>\sqrt{B}\left|y\right|$. We choose $d_0=0$, $d_1=2B{y}^2-xy$, $d_2=y-x$, and $d_3=1$, which yields $d=yp\theta$. It is left to show that the coefficients satisfy $|d_j|<p$.

  –

  It is clear that $d_0=0$ and $d_3=1$ follow $|d_j|<p$.

  –

  The inequality $|d_1|<p$ is equivalent to either $\left|x\right|>\sqrt{B}\left|y\right|$, which is true by the assumption, or ${(x-y)}^2+(3B-1)y^2>0$, which is always true for all $x,y\in \mathbb{Z}$ and $B\ge 1$. Hence, $|d_1|<p$.

  –

  For $d_2=y-x$, we suppose on the contrary that $|d_2|\ge p$, which is equivalent to a polynomial inequality in x as follows:

  $$x^2-(y\pm 1)x+(B{y}^2\pm y)\le 0.$$

  The inequality has a solution if and only if the discriminant of the polynomial is non-negative, meaning that $|y\mp 1|\ge \sqrt{B}\left|2y\right|$. The only solutions to this inequality where $B\ge 1$ are $y=0,\pm 1$. Here, $y=0$ contradicts Lemma 2 and $y=\pm 1$ implies $\alpha =\pm \omega$ with norm $p=1$ in $\mathbb{Z}\left[\omega \right]$, both of which are not in consideration.

• Suppose that $\left|x\right|<\sqrt{B}\left|y\right|$. We choose $d_0=0$, $d_1=xy-2x^2$, $d_2=3x-y$, and $d_3=-1$, which gives $d=yp\theta$. Again, we show next that $|d_j|<p$ for all $d_j$’s.

  –

  The statement is clear for $d_0=0$ and $d_3=-1$.

  –

  For $d_1=xy-2x^2$, the inequality $|d_1|<p$ is equivalent to either ${(3x-y)}^2+(3B-1)y^2>0$, which is always the case for all $x,y\in \mathbb{Z}$ and $B\ge 1$, or $\left|x\right|<\sqrt{B}\left|y\right|$, which is true from the assumption. Thus, $|d_1|<p$.

  –

  For $d_2=3x-y$, we suppose on the contrary that $|d_2|\ge p$, which can be written as a polynomial inequality in x as

  $$x^2-(y\pm 3)x+(B{y}^2\pm y)\le 0.$$

  Similar to the previous case, the discriminant is non-negative when ${(y\pm 1)}^2+8\ge 4B{y}^2$. For $B\ge 1$ to satisfy the inequality, the only solutions are $y=0,\pm 1,\pm 2$. Once again, $y=0$ contradicts Lemma 2. The solutions $y=\pm 1$ give the following bases.

  –

  For $B=1$, $\alpha =\pm (-2+\omega ),\pm (-1+\omega ),\pm \omega ,\pm (1+\omega ),\pm (2+\omega ),\pm (3+\omega )$ in $\mathbb{Z}\left[\omega \right]$. Each of them either fails $\left|x\right|<\sqrt{B}\left|y\right|$ or $p>1$.

  –

  For $B=2$, $\alpha =\pm (1-\theta ),\pm (1+\theta ),\pm (2+\theta ),\pm (3+\theta )$ in $\mathbb{Z}\left[\theta \right]$, where $\theta ={\displaystyle \frac{-1+\sqrt{-7}}{2}}$. Each of them either fails $\left|x\right|<\sqrt{B}\left|y\right|$ or $p>1$ or has already been given a counterexample.

  –

  For $B=3$, $\alpha =\pm (2+\theta )$ in $\mathbb{Z}\left[\theta \right]$ where $\theta ={\displaystyle \frac{-1+\sqrt{-11}}{2}}$. They both fail the assumption $\left|x\right|<\sqrt{B}\left|y\right|$.

  Lastly, the solutions $y=\pm 2$ give bases $\alpha =\pm (2+2\omega ),\pm (3+2\omega )$ in $\mathbb{Z}\left[\omega \right]$, and they all fail to satisfy $\left|x\right|<\sqrt{B}\left|y\right|$. We conclude that $|d_2|<p$.

We have exhausted all cases and we conclude that ${\tau }_{p^3}$ is not bijective. □

We are now left to rule out the case of the cubic tiling map ${\tau }_{p^2}$, where $w=w^{†}=p^2$. Recall that all known totally tiling bases require $w=p^2$ as the tiling width when $m=4$. Our strategy here is to consider separately the cases of $A=0$ and $A=1$. Although the proof for these two cases are different, they both make use of the following lemma, which assists in finding counterexample d.

Lemma 4. 

On a ring $\mathbb{Z}\left[\theta \right]$, for a base $\alpha =x+y\theta$ with norm $p={\left|\alpha \right|}^2>0$, there exist integers $d_2$ and $d_3$ that are not both zero, $|d_2|,|d_3|\le p$, and $d_2{\alpha }^2+d_3{\alpha }^3=p^2(s+yt\theta )$ for some integers s and t that are not both zero.

Proof. 

Consider a lattice $L\subseteq {\mathbb{R}}^2$ with a generator matrix G, defined as

$$G=\left[\begin{array}{cc}3x^2-3Axy+(A^2-B)y^2& -x^3+3Bx{y}^2-AB{y}^3\\ -2x+Ay& x^2-B{y}^2\end{array}\right].$$

The fundamental region is of volume $|det\left(G\right)|={(x^2-Axy+B{y}^2)}^2=p^2$. With the fact that $p>0$, the lattice L is well-defined and of full-rank.

Let $C\subseteq {\mathbb{R}}^2$ be the set of all points within a square centered at the origin and of length $2(p+\epsilon )$, where $0<\epsilon <1$ is a fixed constant. More precisely, ${(c_1,c_2)}^T\in C$ if and only if $|c_1|,|c_2|<p+\epsilon$. It is not hard to see that the volume of C is $vol\left(C\right)=4{(p+\epsilon )}^2$, and C is convex and symmetric with respect to the origin.

According to Minkowski’s Convex Body Theorem for ${\mathbb{R}}^2$, there exists a nonzero point in the lattice, say $G{(s,t)}^T\in L$, where $s,t$ are integers and are not both zero, which lies in the region of C. As a result, we can find a lattice point in the region C other than the origin. We denote by ${(d_2,d_3)}^T=G{(s,t)}^T$ this particular lattice point, i.e.,

$$\left[\begin{array}{c}{d}_2\\ d_3\end{array}\right]=\left[\begin{array}{cc}3x^2-3Axy+(A^2-B)y^2& -x^3+3Bx{y}^2-AB{y}^3\\ -2x+Ay& x^2-B{y}^2\end{array}\right]\left[\begin{array}{c}s\\ t\end{array}\right].$$

(1)

The fact that ${(s,t)}^T\ne 0$ implies ${(d_2,d_3)}^T\ne 0$. Furthermore, ${(d_2,d_3)}^T\in C$ implies that $|d_2|,|d_3|<p+\epsilon$. Because $x,y,A,B,s,t$ are all integers, so must be $d_2$ and $d_3$. Since $\epsilon <1$, we can hence additionally conclude that $|d_2|,|d_3|\le p$.

Equation (1) can also be rewritten as

$$\left[\begin{array}{c}s\\ t\end{array}\right]={\displaystyle \frac{1}{p^2}}\left[\begin{array}{cc}{x}^2-B{y}^2& x^3-3Bx{y}^2+AB{y}^3\\ 2x-Ay& 3x^2-3Axy+(A^2-B)y^2\end{array}\right]\left[\begin{array}{c}{d}_2\\ d_3\end{array}\right].$$

Direct computation shows that $p^2(s+yt\theta )=d_2{\alpha }^2+d_3{\alpha }^3$, as desired. □

By applying this lemma, it ensures the existence of a counterexample $d=d_2{\alpha }^2+d_3{\alpha }^3$ such that $p^2\mid \mathcal{R}\left(d\right)$ and $p^2\mid \mathcal{I}\left(d\right)$. However, it comes with bounds $|d_2|\le p$ and $|d_3|\le p$. We must exclude the cases $|d_2|=p$ and $|d_3|=p$ separately whenever Lemma 4 is utilized. Now we provide all scenarios where ${\tau }_{p^2}$ is bijective when $A=0$.

Theorem 9. 

For ${\mathcal{S}}_{\alpha ,p,4}$ on $\mathbb{Z}\left[\theta \right]$ where $\theta =\sqrt{-B}$ and $p={\left|\alpha \right|}^2$ is a prime, the tiling map ${\tau }_{p^2}$ is bijective if and only if α is from the family of $1+i$ in $\mathbb{Z}\left[i\right]$ or the family of $\sqrt{-B}$ in $\mathbb{Z}\left[\sqrt{-B}\right]$, where B is prime.

Proof. 

Note that $A=0$ implies $\theta =\sqrt{-B}$, and the necessity part of the theorem has been proved. Let $\alpha =x+y\theta$ and $p={\left|\alpha \right|}^2=x^2+B{y}^2$. Suppose that ${\tau }_{p^2}$ is bijective and $\alpha$ is neither from the family of $1+i$ in $\mathbb{Z}\left[i\right]$ nor the family of $\sqrt{-B}$ in $\mathbb{Z}\left[\sqrt{-B}\right]$, where B is prime. We provide a counterexample d.

If $x=0$, then $y=\pm 1$ and $p=B$ is prime. However, this leads to $\alpha =\pm \theta$, which is the family of $\sqrt{-B}$ in $\mathbb{Z}\left[\sqrt{-B}\right]$, where B is prime. Moreover, the only possible $\alpha$ in which $p=2$ are from the family of $1+i$ in $\mathbb{Z}\left[i\right]$ or the family of $\sqrt{-2}$ in $\mathbb{Z}\left[\sqrt{-2}\right]$. Therefore, from this point onwards, we assume that $x\ne 0$ and $p>2$.

According to Lemma 4, there exist $d_2$ and $d_3$ such that $(d_2,d_3)\ne 0$, $|d_2|,|d_3|\le p$, and $d_2{\alpha }^2+d_3{\alpha }^3=p^2(s+yt\theta )$ for some integers $s,t$ such that $(s,t)\ne (0,0)$. In particular,

$$\left[\begin{array}{c}s\\ t\end{array}\right]={\displaystyle \frac{1}{p^2}}\left[\begin{array}{cc}{x}^2-B{y}^2& x^3-3Bx{y}^2\\ 2x& 3x^2-B{y}^2\end{array}\right]\left[\begin{array}{c}{d}_2\\ d_3\end{array}\right].$$

Now that the setup is completed, we prove that neither $|d_2|=p$ nor $|d_3|=p$ is possible. We divide the rest of the proof into two parts as follows.

• First, we show that $|d_2|=p$ implies $|d_3|=0$ or $|d_3|=p$, and that $|d_3|=p$ implies $|d_2|=0$ or $|d_2|=p$.

  –

  Suppose that $|d_2|=p$. Since t is an integer, $(3x^2-B{y}^2)d_3$ must be divisible by p. However, $p=x^2+B{y}^2$, and so we have $(3x^2-B{y}^2)d_3\equiv 4x^2{d}_3(modp)$. As a result, $4x^2{d}_3\equiv 0(modp)$. Because $p\nmid 2$ and $p\nmid x$, it follows that $d_3\equiv 0(modp)$, which eventually implies that $|d_3|=0$ or p.

  –

  Suppose that $|d_3|=p$. Because t is an integer, $\left(2x\right)d_2$ must be divisible by p. Due to the fact that $p\nmid 2$ and $p\nmid x$, we obtain $d_2\equiv 0(modp)$, and thus $|d_2|=0$ or p.

  Therefore, if $|d_2|$ or $|d_3|$ is equal to p, the other one must be either 0 or p. This takes us to the next step of the proof.
• We show that $\left(\right|d_2|,|d_3\left|\right)=(p,0),(0,p),(p,p)$ are all impossible.

  –

  Suppose that $|d_2|=p$ and $|d_3|=0$. It follows that $\left|t\right|=\left|{\displaystyle \frac{2x}{p}}\right|$. Unfortunately, $p\nmid 2$ and $p\nmid x$, meaning that t is not an integer, which is a contradiction.

  –

  Suppose that $|d_2|=0$ and $|d_3|=p$. It follows that $\left|t\right|=\left|{\displaystyle \frac{4x^2}{p}}-1\right|$. Again, $p\nmid 2$ and $p\nmid x$, and so t is not an integer, which is a contradiction.

  –

  Suppose that $|d_2|=|d_3|=p$. It follows that $\left|t\right|=\left|{\displaystyle \frac{\left(2x\right)(2x\pm 1)}{p}}-1\right|$. Because $p\nmid 2$ and $p\nmid x$, $\left|t\right|$ is an integer if and only if $2x\pm 1$ is divisible by p. Since $2x\pm 1\ne 0$, it implies $|2x\pm 1|\ge p$, or equivalently $|2x\pm 1|\ge x^2+B{y}^2$. The only solutions here are $(x,y,B)=(1,\pm 1,1),(-1,\pm 1,1),(2,\pm 1,1),(-2,\pm 1,1),(1,\pm 1,2),(-1,\pm 1,2)$. Excluding those from the family of known tiling bases, we are left with the following bases, for which we now provide a counterexample.

  –

  For $\alpha =2\pm i$ in $\mathbb{Z}\left[i\right]$ with norm $p=5$, we have $d=-2{\alpha }^2+3{\alpha }^3=\pm 25i$.

  –

  For $\alpha =1\pm \sqrt{-2}$ in $\mathbb{Z}\left[\sqrt{-2}\right]$ with norm $p=3$, we have $d={\alpha }^2-2{\alpha }^3=9$.

  We have shown that $|d_2|<p$ and $|d_3|<p$, thus guaranteeing the existence of a counterexample, and the proof is now complete.

  □

The next step is to consider the case when $A=1$. We begin with two auxiliary lemmas showing that $p\mid 4B-1$ or $y\equiv 2x\pm 1(modp)$ leads to ${\tau }_{p^2}$ not being bijective. Then, the final theorem is presented.

Lemma 5. 

For ${\mathcal{S}}_{\alpha ,p,4}$ on $\mathbb{Z}\left[\theta \right]$ where $p={\left|\alpha \right|}^2$ is a prime, $\theta ={\displaystyle \frac{-1+\sqrt{1-4B}}{2}}$, and $4B-1>0$ is square-free; if $\alpha \ne \pm (1+2\theta )$ and $p>3$, then $p\nmid 4B-1$.

Proof. 

Suppose that $A=1$ and thus $\theta ={\displaystyle \frac{-1+\sqrt{1-4B}}{2}}$, where $4B-1>0$ is square-free. Let $\alpha =x+y\theta$ and $p={\left|\alpha \right|}^2=x^2-xy+B{y}^2$. By contraposition, suppose that $p\mid 4B-1$. We show that $\alpha =\pm (1+2\theta )$ or $p={\left|\alpha \right|}^2\le 3$.

The divisibility $p\mid 4B-1$ is equivalent to $x^2-xy+B{y}^2\mid 4B-1$. Hence,

$${(2x-y)}^2+(4B-1)y^2\mid 4(4B-1).$$

Since $4(4B-1)\ne 0$, this divisibility implies that ${(2x-y)}^2+(4B-1)y^2\le 4(4B-1)$. It follows that $\left|y\right|\le 2$, and since $y\ne 0$, we consider the following two cases:

• If $y=\pm 1$, we have $p=x^2\mp x+B$, or equivalently $4p={(2x\mp 1)}^2+(4B-1)$. However, $p\mid 4B-1$, and so $p\mid {(2x\mp 1)}^2$. Since p is a prime, $p\mid 2x\mp 1$. Because $2x\mp 1\ne 0$, we have $p\le |2x\mp 1|$, or $x^2\mp x+B\le |2x\mp 1|$. The existence of solutions occurs when $B=1$, and they are $(x,y)=(\pm 1,1),(\pm 2,1),(\pm 1,-1),(-1\pm 1,-1)$. These solutions only produce bases of norms $p=1$ or $p=3$.
• If $y=\pm 2$, the inequality implies that $2x-y=0$, and thus $\alpha =\pm (1+2\theta )$.

To summarize, if $p\mid 4B-1$, then $\alpha =\pm (1+2\theta )$ or $p={\left|\alpha \right|}^2\le 3$, as desired. □

Lemma 6. 

For ${\mathcal{S}}_{\alpha ,p,4}$ on $\mathbb{Z}\left[\theta \right]$, where $p={\left|\alpha \right|}^2$ is a prime, $\theta ={\displaystyle \frac{-1+\sqrt{1-4B}}{2}}$ and $4B-1>0$ is square-free, if ${\tau }_{p^2}$ is bijective and $p>3$, then $y\not\equiv 2x\pm 1(modp)$.

Proof. 

Suppose that $A=1$ and thus $\theta ={\displaystyle \frac{-1+\sqrt{1-4B}}{2}}$, where $4B-1>0$ is square-free. Let $\alpha =x+y\theta$ and $p={\left|\alpha \right|}^2=x^2-xy+B{y}^2$. By contraposition, suppose that $y\equiv 2x\pm 1(modp)$, and we show that ${\tau }_{p^2}$ is not bijective or $p={\left|\alpha \right|}^2\le 3$.

We consider the two cases where $y-(2x\pm 1)=0$ and $y-(2x\pm 1)\ne 0$ separately.

• Suppose that $y-(2x\pm 1)=0$, or $y=2x\pm 1$. Notice that $x+(2x+1)\theta =-\left(\right(-x)+(2(-x)-1\left)\theta \right)$. According to Theorem 1, it is sufficient to show the case $\alpha =x+(2x-1)\theta$, whose norm is $p=(4B-1)x^2-(4B-1)x+B$. Here, we choose $d=(p-1){\alpha }^2+{\alpha }^3=-p^2$ as a counterexample, which implies that ${\tau }_{p^2}$ is not bijective.
• Suppose that $y-(2x\pm 1)\ne 0$. Since $p\mid y-(2x\pm 1)$ and $p=x^2-xy+B{y}^2$,

  $$x^2-xy+B{y}^2\le |y-(2x\pm 1)|.$$
  This inequality simplifies to either $x^2-xy+B{y}^2\le y-2x\pm 1$ or $x^2-xy+B{y}^2\le -y+2x\mp 1$. When x is considered a variable, the discriminant of these inequalities is either $8-(4B-1)y^2$ or $-(4B-1)y^2$. We can omit the case $-(4B-1)y^2$ since an inequality with a negative discriminant cannot have a real solution. On the other hand, if $8-(4B-1)y^2\ge 0$, then a solution exists only when $B=2$, and they are $(x,y)=(1,1),(-1,-1)$. These solutions give bases of norm $p=2$.

This completes our proof by contraposition. □

We are now ready to prove the last result of this section.

Theorem 10. 

For ${\mathcal{S}}_{\alpha ,p,4}$ on $\mathbb{Z}\left[\theta \right]$, where $p={\left|\alpha \right|}^2$ is a prime, $\theta ={\displaystyle \frac{-1+\sqrt{1-4B}}{2}}$ and $4B-1>0$ is square-free, the tiling map ${\tau }_{p^2}$ is bijective if and only if α is from the family of $2+\omega$ in $\mathbb{Z}\left[\omega \right]$ or the family of $1+2\theta$ in $\mathbb{Z}\left[\theta \right]$.

Proof. 

In this theorem, $A=1$, and thus $\theta ={\displaystyle \frac{-1+\sqrt{1-4B}}{2}}$ where $4B-1>0$ is square-free. Let $\alpha =x+y\theta$ and $p=x^2-xy+B{y}^2$. The necessity of the statement is already proven. Suppose now that ${\tau }_{p^2}$ is bijective and $\alpha$ is neither from the family $2+\omega$ in $\mathbb{Z}\left[\omega \right]$ nor the family of $1+2\theta$ in $\mathbb{Z}\left[\theta \right]$.

If $p=2$, the only bases with this norm are of family $\theta$ in $\mathbb{Z}\left[\theta \right]$, where $\theta ={\displaystyle \frac{-1+\sqrt{-7}}{2}}$. However, this base does not provide a tileable set according to Proposition 2.

If $p=3$, the only bases with this norm are of family $2+\omega$ or $1+2\omega$ in $\mathbb{Z}\left[\omega \right]$, or $\theta$ in $\mathbb{Z}\left[\theta \right]$ where $\theta ={\displaystyle \frac{-1+\sqrt{-11}}{2}}$. The first two families are omitted from the assumption, while the last family does not produce a tileable set according to Proposition 2.

For the case $p>3$, we apply Lemmas 5 and 6. It follows that $p\nmid 4B-1$ and $y\not\equiv 2x\pm 1(modp)$. We also utilize Lemma 4, and so there exist integers $d_2$ and $d_3$ such that $(d_2,d_3)\ne (0,0)$, $|d_2|,|d_3|\le p$, and $d_2{\alpha }^2+d_3{\alpha }^3=p^2(s+t\theta )$, where

$$\left[\begin{array}{c}s\\ t\end{array}\right]={\displaystyle \frac{1}{p^2}}\left[\begin{array}{cc}{x}^2-B{y}^2& x^3-3Bx{y}^2+B{y}^3\\ 2x-y& 3x^2-3xy+(1-B)y^2\end{array}\right]\left[\begin{array}{c}{d}_2\\ d_3\end{array}\right].$$

We show that it is impossible for $|d_2|$ and $|d_3|$ to be equal to p. The elimination process is divided into two parts as follows:

• We show that $|d_2|=p$ implies $|d_3|=0$ or $|d_3|=p$, and that $|d_3|=p$ implies $|d_2|=0$ or $|d_2|=p$

  –

  Suppose that $|d_2|=p$. Since t is an integer, $(3x^2-3xy+(1-B)y^2)d_3$ is divisible by p. However, by the fact that $p=x^2-xy+B{y}^2$, we have that $(3x^2-3xy+(1-B)y^2)d_3\equiv (1-4B)y^2{d}_3(modp)$. As a result, $(1-4B)y^2{d}_3\equiv 0(modp)$. From $p\nmid 4B-1$ and $gcd(y,p)=1$, we have $d_3\equiv 0(modp)$, which means that $|d_3|=0$ or p.

  –

  Suppose that $|d_3|=p$. Since s and t are integers, $(x^2-B{y}^2)d_2$ and $(2x-y)d_2$ are divisible by p. Hence, $y(x-2By)d_2=(xy-2B{y}^2)d_2=2(x^2-B{y}^2)d_2-x(2x-y)d_2$ is divisible by p. Since $gcd(y,p)=1$, $(x-2By)d_2$ must then be divisible by p. This, however, makes $(4B-1)y{d}_2=(2x-y)d_2-2(x-2By)d_2$ divisible by p. Since $p\nmid 4B-1$ and $gcd(y,p)=1$, we conclude that $d_2\equiv 0(modp)$, implying $|d_2|=0$ or p.

• We show that $\left(\right|d_2|,|d_3\left|\right)=(p,0),(0,p),(p,p)$ are impossible.

  –

  Suppose that $|d_2|=p$ and $|d_3|=0$. It follows that $\left|s\right|=\left|1+{\displaystyle \frac{(x-2By)y}{p}}\right|$ and $\left|t\right|=\left|{\displaystyle \frac{2x-y}{p}}\right|$. Because s and t are integers and $gcd(y,p)=1$, $x-2By$ and $2x-y$ must both be divisible by p. This implies that p divides $(4B-1)y$, contradicting the fact that $p\nmid 4B-1$ and $gcd(y,p)=1$.

  –

  Suppose that $d_2=0$ and $|d_3|=p$. It follows that $\left|t\right|=\left|3-{\displaystyle \frac{(4B-1)y^2}{p}}\right|$. Since $p\nmid 4B-1$ and $gcd(y,p)=1$, it contradicts the fact that t is an integer.

  –

  Suppose that $|d_2|=|d_3|=p$. It follows that

  $$\begin{array}{cc}\hfill \left|s\right|& =\left|\pm 1+x+y+{\displaystyle \frac{(\pm (x-2By)+(1-4B\left)xy\right)y}{p}}\right|\mathrm{and}\hfill \\ \hfill \left|t\right|& =\left|3+{\displaystyle \frac{\pm (2x-y)+(1-4B)y^2}{p}}\right|.\hfill \end{array}$$

  Because $s,t$ are integers and $gcd(y,p)=1$, we have

  $$\begin{array}{cc}\hfill \pm (x-2By)+(1-4B)xy& \equiv 0(modp)\mathrm{and}\hfill \\ \hfill \pm (2x-y)+(1-4B)y^2& \equiv 0(modp).\hfill \end{array}$$

  From these equations, we obtain $(4B-1)(\pm y+2xy-y^2)\equiv 0(modp)$. Since $p\nmid 4B-1$ and $gcd(y,p)=1$, we have $y\equiv 2x\pm 1(modp)$, which is a contradiction. This finishes the last piece of the theorem.

  □

4. Summary and Application

We showed in the last section that $\alpha$ is totally tiling if and only if $\alpha$ is one of the following:

• The trivial $\alpha =\pm \theta =\pm \sqrt{-B}$ in $\mathbb{Z}\left[\theta \right]$ where $\theta =\sqrt{-B}$ and B is prime,
• The trivial $\alpha =\pm (1+2\theta )=\pm \sqrt{1-4B}$ in $\mathbb{Z}\left[\theta \right]$, where $\theta ={\displaystyle \frac{-1+\sqrt{1-4B}}{2}}$ and $4B-1$ is prime,
• $\pm (1+i),\pm (1-i)$ in $\mathbb{Z}\left[i\right]$,
• $\pm (2+\omega ),\pm (-1+\omega )$ in $\mathbb{Z}\left[\omega \right]$.

In this section, we apply this result on shaping to constellations built from complex multi-level constructions and give some concrete examples demonstrating how the theorems can be applied. We are particularly interested in the case of even exponent m since it permits natural cubic shaping. The tiling width here is $w=p^{\frac{m}{2}}$ where $p={\left|\alpha \right|}^2$ is the norm of the base. First, we lay out a supporting lemma.

Lemma 7. 

Let α be a totally tiling base on $\mathbb{Z}\left[\theta \right]$. If m is even, there exists a unit $u\in \mathbb{Z}\left[\theta \right]$ such that ${\alpha }^m=u{\left|\alpha \right|}^m$.

Proof. 

It suffices to show that there exists a unit element $u\in \mathbb{Z}\left[\theta \right]$ such that ${\alpha }^2=u{\left|\alpha \right|}^2$. We simply check each of the four cases as follows:

• For $\alpha =\pm \theta \in \mathbb{Z}\left[\theta \right]$ where $\theta =\sqrt{-B}$ and B is prime, the norm is ${\left|\alpha \right|}^2=B$, and ${\alpha }^2=-B=-1·{\left|\alpha \right|}^2$.
• For $\alpha =\pm (1+2\theta )\in \mathbb{Z}\left[\theta \right]$ where $\theta ={\displaystyle \frac{-1+\sqrt{1-4B}}{2}}$ and $4B-1$ is prime, the norm is ${\left|\alpha \right|}^2=4B-1$, and ${\alpha }^2=1-4B=-1·{\left|\alpha \right|}^2$.
• For $\alpha =\pm (1+i),\pm (1-i)\in \mathbb{Z}\left[i\right]$, the norm is ${\left|\alpha \right|}^2=2$. Here, if $\alpha =\pm (1+i)$, then ${\alpha }^2=2i=i·{\left|\alpha \right|}^2$, and if $\alpha =\pm (1-i)$, then ${\alpha }^2=-2i=-i·{\left|\alpha \right|}^2$.
• For $\alpha =\pm (2+\omega ),\pm (-1+\omega )\in \mathbb{Z}\left[\omega \right]$, the norm is ${\left|\alpha \right|}^2=3$. If $\alpha =\pm (2+\omega )$, then ${\alpha }^2=3+3\omega =(1+\omega )·{\left|\alpha \right|}^2$, and if $\alpha =\pm (-1+\omega )$, then ${\alpha }^2=-3\omega =-\omega ·{\left|\alpha \right|}^2$.

  □

Given that $\alpha$ is totally tiling, the map ${\tau }_w:{\mathcal{S}}_{\alpha ,p,m}\to {\mathbb{Z}}_{w,w^{†}}\left[\theta \right]$ is bijective. Consequently, one can see ${\mathbb{Z}}_{w,w^{†}}\left[\theta \right]$ as a new representation of ${\mathcal{S}}_{\alpha ,p,m}$ where the shaping function ${\tau }_w$ is used to map information bits. The implication of this theorem is that the shaped constellation ${\tau }_w\left(\mathcal{C}\right)$ preserves the underlying lattice structure. Thus, it is a practical candidate and an efficient alternative to the constellation $\mathcal{C}$ obtained directly from lattice constructions.

Theorem 11. 

Let $\alpha \in \mathbb{Z}\left[\theta \right]$ be a totally tiling base with norm $p={\left|\alpha \right|}^2$ prime, $m\ge 2$ be an even exponent, and τ be the tiling map of ${\mathcal{S}}_{\alpha ,p,m}$. Let $\Gamma =\mathcal{C}+{\alpha }^m\mathbb{Z}{\left[\theta \right]}^n$ be a set constructed from a multi-level construction using codes over ${\mathbb{F}}_p$ with m levels. Then, $\Gamma =\tau \left(\mathcal{C}\right)+{\alpha }^m\mathbb{Z}{\left[\theta \right]}^n$.

Proof. 

Note that the width and height of the tiling map $\tau$ is $w=w^{†}=p^{\frac{m}{2}}$. Therefore, for an element $s\in {\mathcal{S}}_{\alpha ,p,m}$, $\tau \left(s\right)=s+r{p}^{\frac{m}{2}}$ for some $r\in \mathbb{Z}\left[\theta \right]$. Furthermore, Lemma 7 allows us to rewrite $p^{\frac{m}{2}}={\left|\alpha \right|}^m$ as $u^{-1}{\alpha }^m$, where $u\in \mathbb{Z}\left[\theta \right]$ is a unit. As a result, $\tau \left(s\right)=s+r^{\prime }{\alpha }^m$, where $r^{\prime }=u^{-1}r\in \mathbb{Z}\left[\theta \right]$.

It is not hard to see that $\tau \left(\mathcal{C}\right)$ is well-defined since $\mathcal{C}\subseteq {\mathcal{S}}_{\alpha ,p,m}^n$ according to the p-ary decomposition base $\alpha$. It follows that $\tau \left(\mathcal{C}\right)=\mathcal{C}+{\alpha }^m\mathbf{r}$ for some $\mathbf{r}\in \mathbb{Z}{\left[\theta \right]}^n$. Consequently,

$$\Gamma =\mathcal{C}+{\alpha }^m\mathbb{Z}{\left[\theta \right]}^n=\tau \left(\mathcal{C}\right)-{\alpha }^m\mathbf{r}+{\alpha }^m\mathbb{Z}{\left[\theta \right]}^n=\tau \left(\mathcal{C}\right)+{\alpha }^m\mathbb{Z}{\left[\theta \right]}^n$$

as desired. □

Example 10. 

Let $C_0\subseteq C_1\subseteq {\mathbb{F}}_3^3$ be nested ternary linear codes defined as follows:

$$\begin{array}{cc}\hfill C_0& ={span}_{{\mathbb{F}}_3}\left\{(1,0,0)\right\},\hfill \\ \hfill C_1& ={span}_{{\mathbb{F}}_3}\{(1,0,0),(0,1,2)\}.\hfill \end{array}$$

The lattice ${\Lambda }_{\mathrm{D}}$ constructed from this family of codes via Construction D using the base $\alpha =2+\omega$ on $\mathbb{Z}\left[\omega \right]$ is ${\Lambda }_{\mathrm{D}}={\mathcal{C}}_{\mathrm{D}}+{\alpha }^2\mathbb{Z}{\left[\omega \right]}^3$, where

$${\mathcal{C}}_{\mathrm{D}}=\left\{c_{0,1}(1,0,0)+c_{1,1}\alpha (1,0,0)+c_{1,2}\alpha (0,1,2)|c_{j,l}\in \{0,1,2\}\right\},$$

which is

$$\left\{\begin{array}{ccc}(0,0,0),\hfill & (1,0,0),\hfill & (2,0,0),\hfill \\ (2+\omega ,0,0),\hfill & (3+\omega ,0,0),\hfill & (4+\omega ,0,0),\hfill \\ (4+2\omega ,0,0),\hfill & (5+2\omega ,0,0),\hfill & (6+2\omega ,0,0),\hfill \\ (0,2+\omega ,4+2\omega ),\hfill & (1,2+\omega ,4+2\omega ),\hfill & (2,2+\omega ,4+2\omega ),\hfill \\ (2+\omega ,2+\omega ,4+2\omega ),\hfill & (3+\omega ,2+\omega ,4+2\omega ),\hfill & (4+\omega ,2+\omega ,4+2\omega ),\hfill \\ (4+2\omega ,2+\omega ,4+2\omega ),\hfill & (5+2\omega ,2+\omega ,4+2\omega ),\hfill & (6+2\omega ,2+\omega ,4+2\omega ),\hfill \\ (0,4+2\omega ,8+4\omega ),\hfill & (1,4+2\omega ,8+4\omega ),\hfill & (2,4+2\omega ,8+4\omega ),\hfill \\ (2+\omega ,4+2\omega ,8+4\omega ),\hfill & (3+\omega ,4+2\omega ,8+4\omega ),\hfill & (4+\omega ,4+2\omega ,8+4\omega ),\hfill \\ (4+2\omega ,4+2\omega ,8+4\omega ),\hfill & (5+2\omega ,4+2\omega ,8+4\omega ),\hfill & (6+2\omega ,4+2\omega ,8+4\omega )\hfill \end{array}\right\}.$$

Since $m=2$ and $p={\left|\alpha \right|}^2=3$, we use $w=w^{†}=3$, i.e.,

$${\tau }_3(a+b\omega )=(amod3)+(bmod3)\omega .$$

Now, ${\tau }_3\left({\mathcal{C}}_{\mathrm{D}}\right)$ is

$$\left\{\begin{array}{ccc}(0,0,0),\hfill & (1,0,0),\hfill & (2,0,0),\hfill \\ (2+\omega ,0,0),\hfill & (\omega ,0,0),\hfill & (1+\omega ,0,0),\hfill \\ (1+2\omega ,0,0),\hfill & (2+2\omega ,0,0),\hfill & (2\omega ,0,0),\hfill \\ (0,2+\omega ,1+2\omega ),\hfill & (1,2+\omega ,1+2\omega ),\hfill & (2,2+\omega ,1+2\omega ),\hfill \\ (2+\omega ,2+\omega ,1+2\omega ),\hfill & (\omega ,2+\omega ,1+2\omega ),\hfill & (1+\omega ,2+\omega ,1+2\omega ),\hfill \\ (1+2\omega ,2+\omega ,1+2\omega ),\hfill & (2+2\omega ,2+\omega ,1+2\omega ),\hfill & (2\omega ,2+\omega ,1+2\omega ),\hfill \\ (0,1+2\omega ,2+1\omega ),\hfill & (1,1+2\omega ,2+1\omega ),\hfill & (2,1+2\omega ,2+1\omega ),\hfill \\ (2+\omega ,1+2\omega ,2+1\omega ),\hfill & (\omega ,1+2\omega ,2+1\omega ),\hfill & (1+\omega ,1+2\omega ,2+1\omega ),\hfill \\ (1+2\omega ,1+2\omega ,2+1\omega ),\hfill & (2+2\omega ,1+2\omega ,2+1\omega ),\hfill & (2\omega ,1+2\omega ,2+1\omega )\hfill \end{array}\right\},$$

and ${\Lambda }_{\mathrm{D}}={\tau }_3\left({\mathcal{C}}_{\mathrm{D}}\right)+{\alpha }^2\mathbb{Z}{\left[\omega \right]}^3$. Here, ${\tau }_3$ provides a cubic shaping, and it is clear that the elements of ${\tau }_3\left({\mathcal{C}}_{\mathrm{D}}\right)$ have less norm and thus consume less transmission energy in comparison to ${\mathcal{C}}_{\mathrm{D}}$. This constellation can easily be shifted to have its center located at the origin.

While the proposed tiling maps retain the lattice structure and exhibit low computational complexity, the resulting constellation may not be minimal in terms of the average norm of the elements. The explicit minimal representation for bases in Gaussian integers and, generally, quadratic rings of integers were proposed by Jordan et al. [25] and Tadee et al. [26], respectively. However, no algorithm for finding such a representation was provided. Consequently, future research remains to find maps with low computational complexity that provide minimal constellations. Lastly, we note that since the tiling map alters the Euclidean distance between constellation points, the receiver needs to be equipped with a proper decoder. This is performed, for example, in [22].