Quantitative Controllability Metric for Disturbance Rejection in Linear Unstable Systems
Abstract
1. Introduction
- Applicable to unstable systems.
- Computed by solving only algebraic equations, allowing for straightforward calculations without numerical issues.
- Independent of final time considerations.
2. Preliminaries
2.1. Definition and Closed-Form Solution
2.2. Steady-State Solution for Asymptotically Stable Systems
3. Proposed Metric to Quantify Disturbance Rejection Capabilities of Unstable Systems
3.1. Properties of Gramian Matrices in Unstable Systems
3.2. Steady-State Solution for Unstable Systems
4. Numerical Examples
4.1. Inverted Pendulum–Cart System
4.2. Multi-Link Inverted Pendulum System
4.3. Discussion
5. Conclusions
- Robust control system design for multi-input systems: By leveraging the metric’s independence from the controller design, it is possible to evaluate the disturbance rejection performance prior to designing the controller and incorporate the results into the system design. This can be particularly useful in applications such as the optimal input allocation for over-actuated vehicles [45] or multi-rotor aerial vehicles [31,32,33], as well as in fault-tolerant control system design [46,47].
- Extension to nonlinear systems: Similar to how conventional Gramian-based DoC metrics have been extended from linear to nonlinear systems [9,10,11,12], the main theorems derived in this study can be utilized to adapt the proposed metric for nonlinear systems. Such an extension would allow for its application in the control system design of representative nonlinear systems, such as walking robots [34,35,36].
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paige, C. Properties of numerical algorithms related to computing controllability. IEEE Trans. Autom. Control 1981, 26, 130–138. [Google Scholar] [CrossRef]
- Hughes, P.; Skelton, R. Controllability and observability of linear matrix-second-order systems. J. Appl. Mech. 1980, 47, 415–420. [Google Scholar] [CrossRef]
- Hamdan, A.; Nayfeh, A. Measures of modal controllability and observability for first-and second-order linear systems. J. Guid. Control. Dyn. 1989, 12, 421–428. [Google Scholar] [CrossRef]
- Tarokh, M. Measures for controllability, observability and fixed modes. IEEE Trans. Autom. Control 1992, 37, 1268–1273. [Google Scholar] [CrossRef]
- Viswanathan, C.; Longman, R.; Likins, P. A degree of controllability definition-fundamental concepts and application to modal systems. J. Guid. Control. Dyn. 1984, 7, 222–230. [Google Scholar] [CrossRef]
- Müller, P.; Weber, H. Analysis and optimization of certain qualities of controllability and observability for linear dynamical systems. Automatica 1972, 8, 237–246. [Google Scholar] [CrossRef]
- Marx, B.; Koenig, D.; Georges, D. Optimal sensor/actuator location for descriptor systems using Lyapunov-like equations. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; Volume 4, pp. 4541–4542. [Google Scholar]
- Marx, B.; Koenig, D.; Georges, D. Optimal sensor and actuator location for descriptor systems using generalized gramians and balanced realizations. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 3, pp. 2729–2734. [Google Scholar]
- Singh, A.K.; Hahn, J. Determining optimal sensor locations for state and parameter estimation for stable nonlinear systems. Ind. Eng. Chem. Res. 2005, 44, 5645–5659. [Google Scholar] [CrossRef]
- Singh, A.K.; Hahn, J. Sensor location for stable nonlinear dynamic systems: Multiple sensor case. Ind. Eng. Chem. Res. 2006, 45, 3615–3623. [Google Scholar] [CrossRef]
- Shaker, H.R.; Stoustrup, J. An interaction measure for control configuration selection for multivariable bilinear systems. Nonlinear Dyn. 2013, 72, 165–174. [Google Scholar] [CrossRef]
- Tahavori, M. Model reduction via truncated cross-gramian for bilinear systems. In Proceedings of the 2021 International Conference on Recent Advances in Mathematics and Informatics (ICRAMI), Tebessa, Algeria, 21–22 September 2021; pp. 1–5. [Google Scholar]
- Zhao, S.; Pasqualetti, F. Networks with diagonal controllability Gramian: Analysis, graphical conditions, and design algorithms. Automatica 2019, 102, 10–18. [Google Scholar] [CrossRef]
- Babazadeh, M. Gramian-based vulnerability analysis of dynamic networks. IET Control Theory Appl. 2022, 16, 625–637. [Google Scholar] [CrossRef]
- Hać, A.; Liu, L. Sensor and actuator location in motion control of flexible structures. J. Sound Vib. 1993, 167, 239–261. [Google Scholar] [CrossRef]
- Roh, H.S.; Park, Y. Actuator and exciter placement for flexible structures. J. Guid. Control. Dyn. 1997, 20, 850–856. [Google Scholar] [CrossRef]
- Shaker, H.R.; Tahavori, M. Optimal sensor and actuator location for unstable systems. J. Vib. Control 2013, 19, 1915–1920. [Google Scholar] [CrossRef]
- Seyed Sakha, M.; Shaker, H.R.; Tahavori, M. Optimal sensors and actuators placement for large-scale switched systems. Int. J. Dyn. Control 2019, 7, 147–156. [Google Scholar] [CrossRef]
- Hovd, M.; Skogestad, S. Simple frequency-dependent tools for control system analysis, structure selection and design. Automatica 1992, 28, 989–996. [Google Scholar] [CrossRef]
- Cao, Y.; Rossiter, D.; Owens, D. Input selection for disturbance rejection under manipulated variable constraints. Comput. Chem. Eng. 1997, 21, S403–S408. [Google Scholar] [CrossRef]
- Mirza, M.A.; Van Niekerk, J.L. Optimal actuator placement for active vibration control with known disturbances. J. Vib. Control 1999, 5, 709–724. [Google Scholar] [CrossRef]
- Kang, O.; Park, Y.; Park, Y.; Suh, M. New measure representing degree of controllability for disturbance rejection. J. Guid. Control. Dyn. 2009, 32, 1658–1661. [Google Scholar] [CrossRef]
- Lee, H.; Park, Y. Degree of disturbance rejection capability for linear anti-stable systems. In Proceedings of the 2014 14th International Conference on Control, Automation and Systems (ICCAS 2014), Seoul, Republic of Korea, 22–25 October 2014; pp. 154–156. [Google Scholar]
- Lee, H.; Park, Y. Degree of disturbance rejection capability for linear marginally stable systems. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (ICCAS), Busan, Republic of Korea, 13–16 October 2015; pp. 307–310. [Google Scholar]
- Xia, Y.; Yin, M.; Cai, C.; Zhang, B.; Zou, Y. A new measure of the degree of controllability for linear system with external disturbance and its application to wind turbines. J. Vib. Control 2018, 24, 739–759. [Google Scholar] [CrossRef]
- Xia, Y.; Yin, M.; Li, R.; Liu, D.; Zou, Y. Integrated structure and maximum power point tracking control design for wind turbines based on degree of controllability. J. Vib. Control 2019, 25, 397–407. [Google Scholar] [CrossRef]
- Xia, Y.; Li, R.; Yin, M.; Zou, Y. A quantitative measure of the degree of output controllability for output regulation control systems: Concept, approach, and applications. J. Vib. Control 2022, 28, 2803–2815. [Google Scholar] [CrossRef]
- Jeong, I.; Park, Y. Input energy minimization with acoustic potential energy constraint for active noise control system. J. Vib. Control 2024, 2024, 10775463241227477. [Google Scholar] [CrossRef]
- Zhou, K.; Salomon, G.; Wu, E. Balanced realization and model reduction for unstable systems. Int. J. Robust Nonlinear Control. IFAC-Affil. J. 1999, 9, 183–198. [Google Scholar] [CrossRef]
- Lee, H.; Park, Y. Degree of controllability for linear unstable systems. J. Vib. Control 2016, 22, 1928–1934. [Google Scholar] [CrossRef]
- Chang, X.; Jin, C.; Cheng, Y. Dynamics and advanced active disturbance rejection control of tethered UAV. Appl. Math. Model. 2024, 135, 640–665. [Google Scholar] [CrossRef]
- Khadraoui, S.; Fareh, R.; Baziyad, M.; Elbeltagy, M.B.; Bettayeb, M. A Comprehensive Review and Applications of Active Disturbance Rejection Control for Unmanned Aerial Vehicles. IEEE Access 2024, 12, 185851–185868. [Google Scholar] [CrossRef]
- Le, W.; Xie, P.; Chen, J. Disturbance rejection control of the agricultural quadrotor based on adaptive neural network. Inf. Process. Agric. 2024. In Press. [Google Scholar] [CrossRef]
- Espinosa-Espejel, K.I.; Rosales-Luengas, Y.; Salazar, S.; Lopéz-Gutiérrez, R.; Lozano, R. Active Disturbance Rejection Control via Neural Networks for a Lower-Limb Exoskeleton. Sensors 2024, 24, 6546. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.; Kim, H.b.; Ham, B.I.; Kim, K.S. External Force Adaptive Control in Legged Robots Through Footstep Optimization and Disturbance Feedback. IEEE Access 2024, 12, 157531–157539. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Y.; Hou, H.; Yue, Y.; Meng, K.; Yang, Z. Active Disturbance Rejection Control With Backstepping for Decoupling Control of Hydraulic Driven Lower Limb Exoskeleton Robot. IEEE Trans. Ind. Electron. 2024, 72, 714–723. [Google Scholar] [CrossRef]
- Shen, M.; Gu, Y.; Zhu, S.; Zong, G.; Zhao, X. Mismatched quantized H∞ output-feedback control of fuzzy Markov jump systems with a dynamic guaranteed cost triggering scheme. IEEE Trans. Fuzzy Syst. 2023, 32, 1681–1692. [Google Scholar] [CrossRef]
- Lee, H. Controllability measure for disturbance rejection capabilities of control systems with undamped flexible structures. J. Frankl. Inst. 2024, 361, 107320. [Google Scholar] [CrossRef]
- Bandyopadhyay, B.; Deepak, F.; Kim, K.S. Sliding Mode Control Using Novel Sliding Surfaces; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 392. [Google Scholar]
- Tao, G. Adaptive Control Design and Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 37. [Google Scholar]
- Chen, B.M.; Lin, Z.; Shamash, Y. Linear Systems Theory: A Structural Decomposition Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Colobert, B.; Crétual, A.; Allard, P.; Delamarche, P. Force-plate based computation of ankle and hip strategies from double-inverted pendulum model. Clin. Biomech. 2006, 21, 427–434. [Google Scholar] [CrossRef]
- Günther, M.; Grimmer, S.; Siebert, T.; Blickhan, R. All leg joints contribute to quiet human stance: A mechanical analysis. J. Biomech. 2009, 42, 2739–2746. [Google Scholar] [CrossRef]
- Bowden, C.; Holderbaum, W.; Becerra, V. Actuator placement in the multi-link inverted pendulum. In Proceedings of the UKACC International Conference on Control 2010, Coventry, UK, 7–10 September 2010; pp. 1–6. [Google Scholar]
- Park, J.; Park, Y. Optimal input design for fault identification of overactuated electric ground vehicles. IEEE Trans. Veh. Technol. 2015, 65, 1912–1923. [Google Scholar] [CrossRef]
- Park, J.; Park, Y. Experimental Verification of Fault Identification for Overactuated System With a Scaled-Down Electric Vehicle. Int. J. Automot. Technol. 2020, 21, 1037–1045. [Google Scholar] [CrossRef]
- Park, J.; Park, Y. Multiple-Actuator Fault Isolation Using a Minimal ℓ1-Norm Solution with Applications in Overactuated Electric Vehicles. Sensors 2022, 22, 2144. [Google Scholar] [CrossRef] [PubMed]
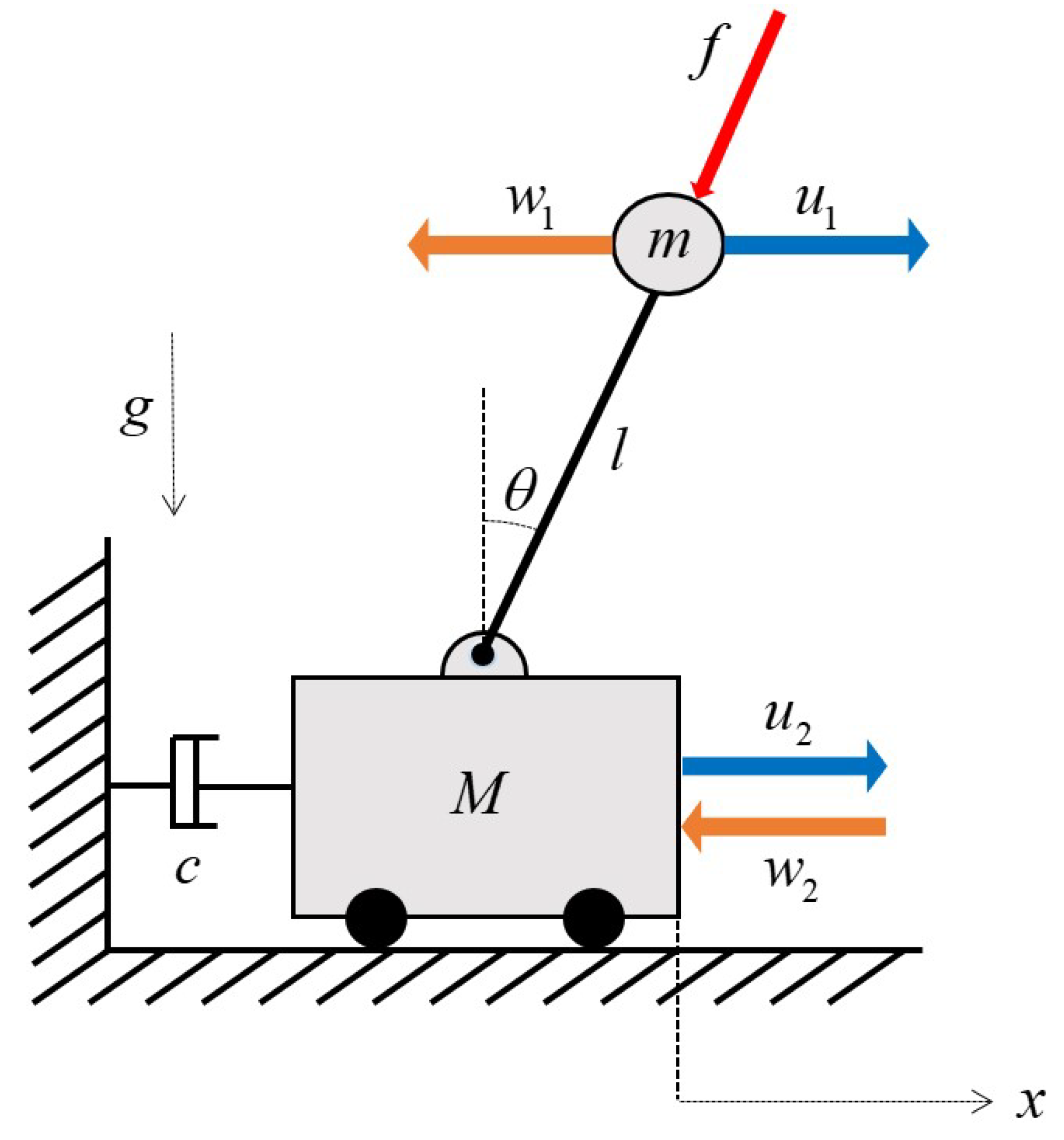
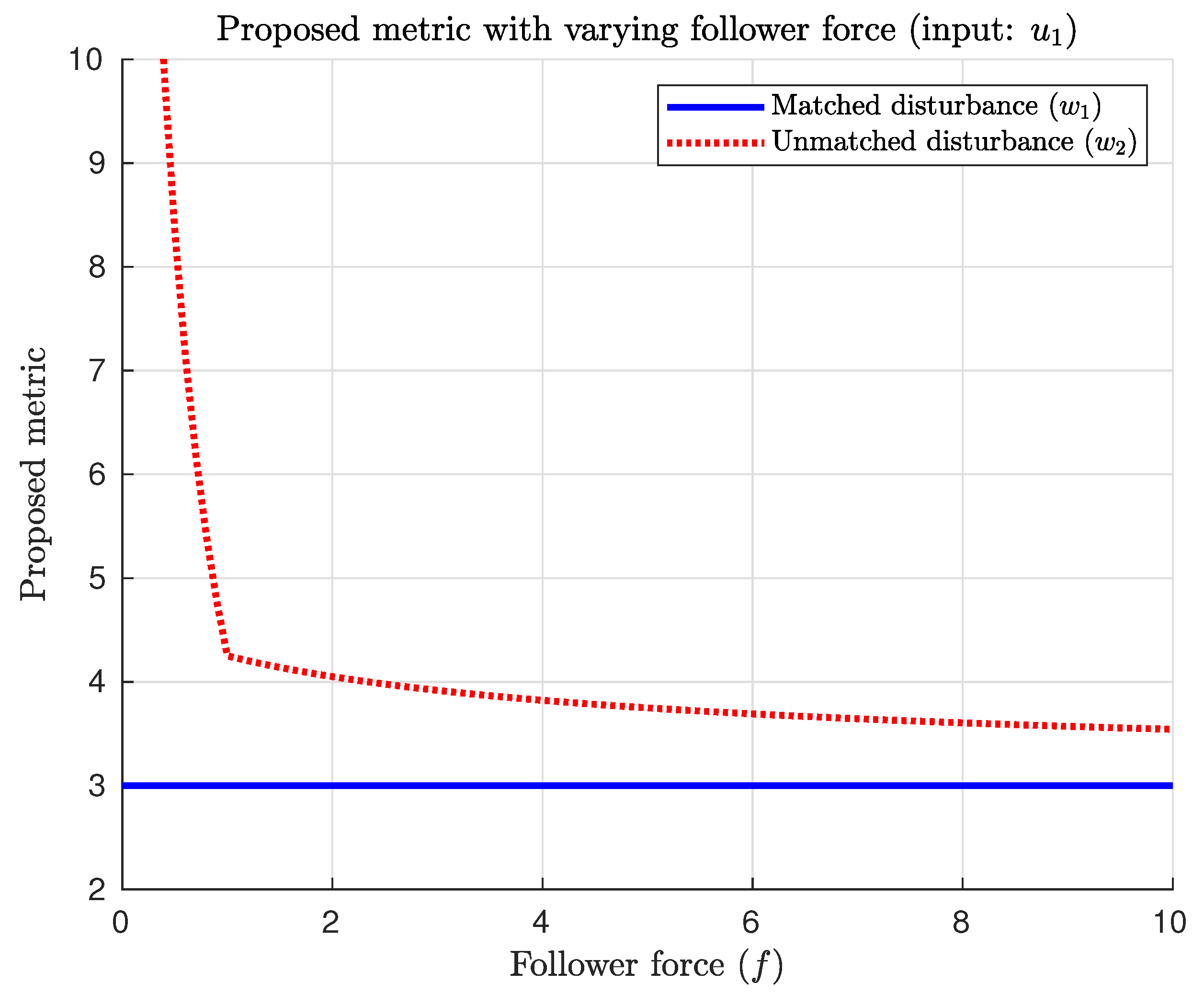
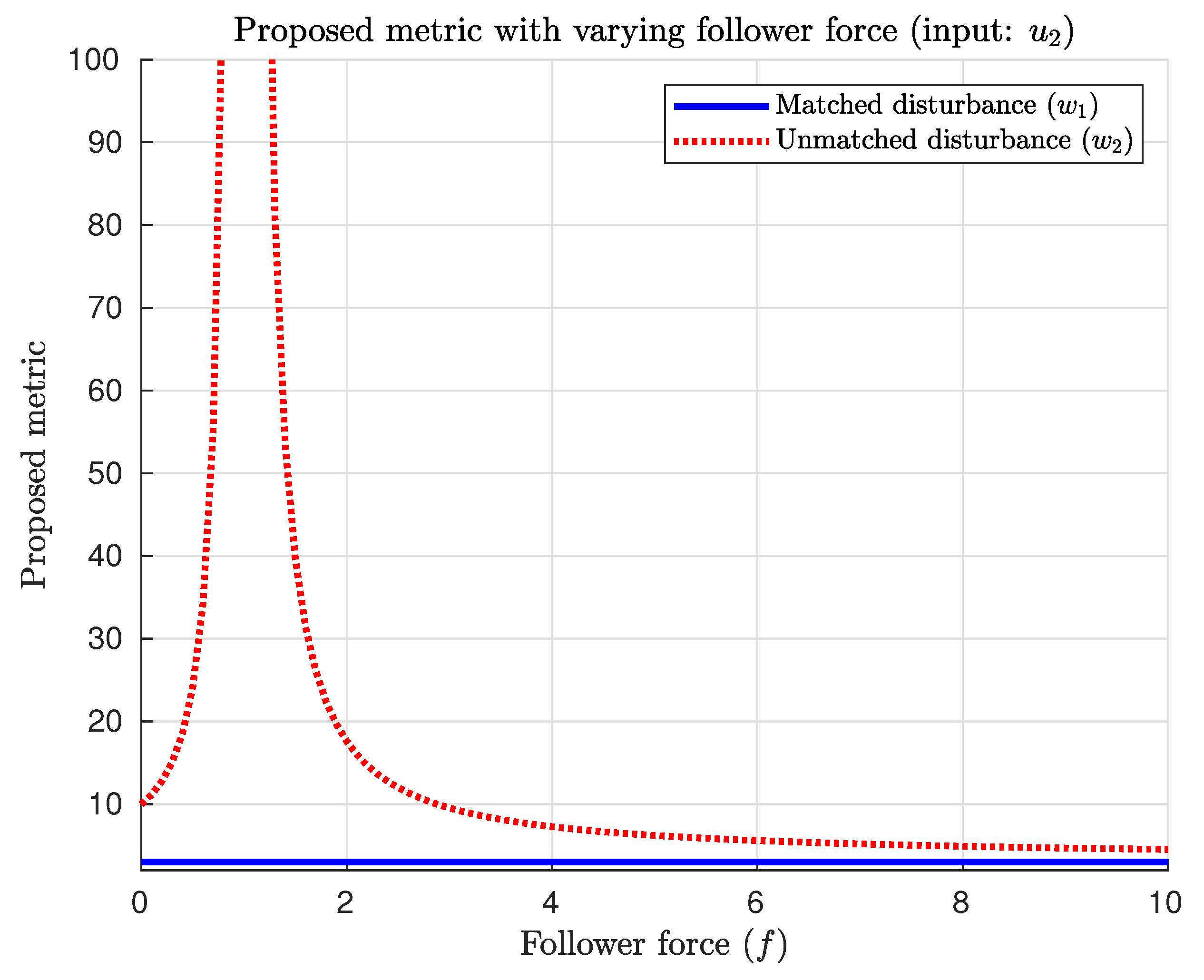
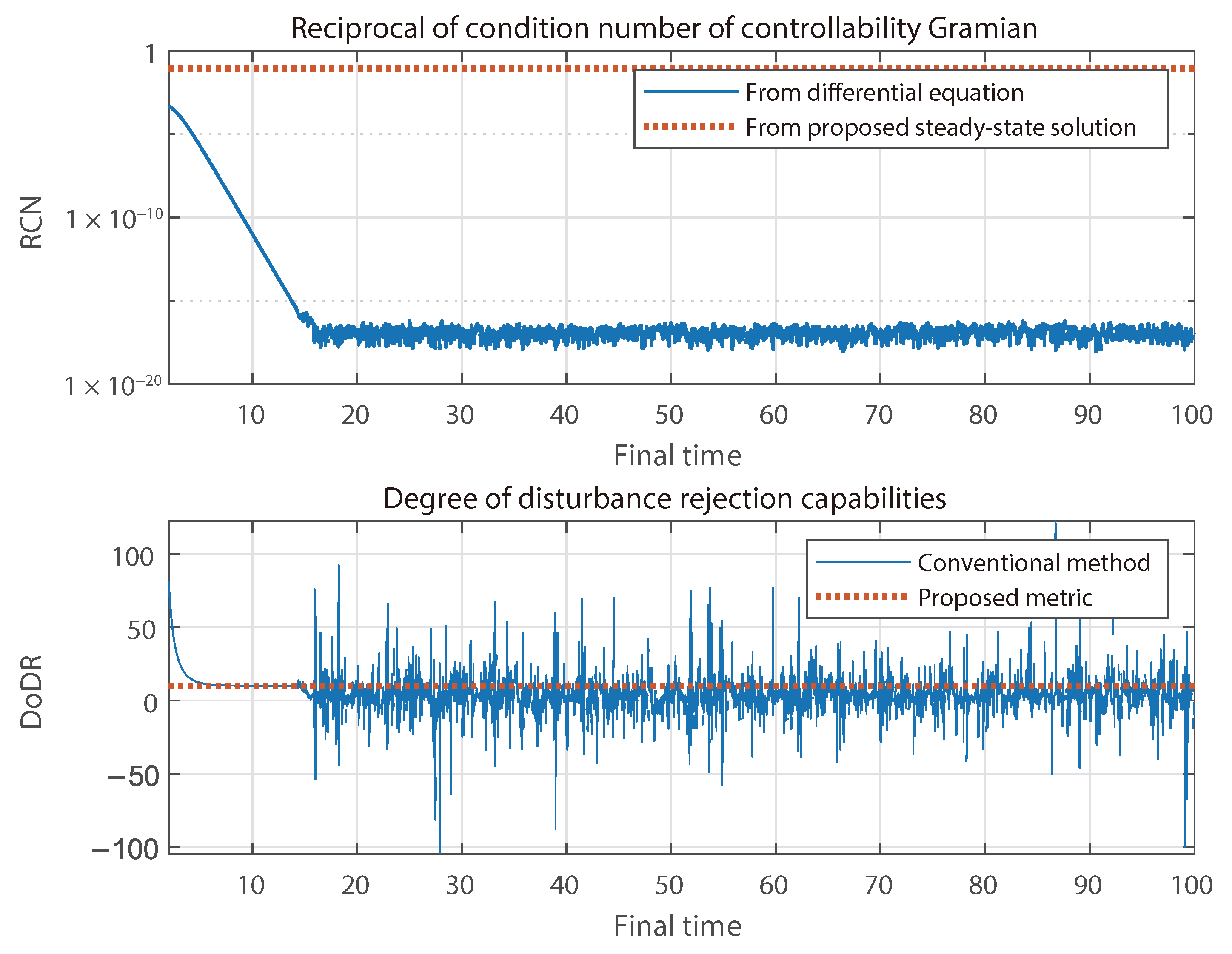
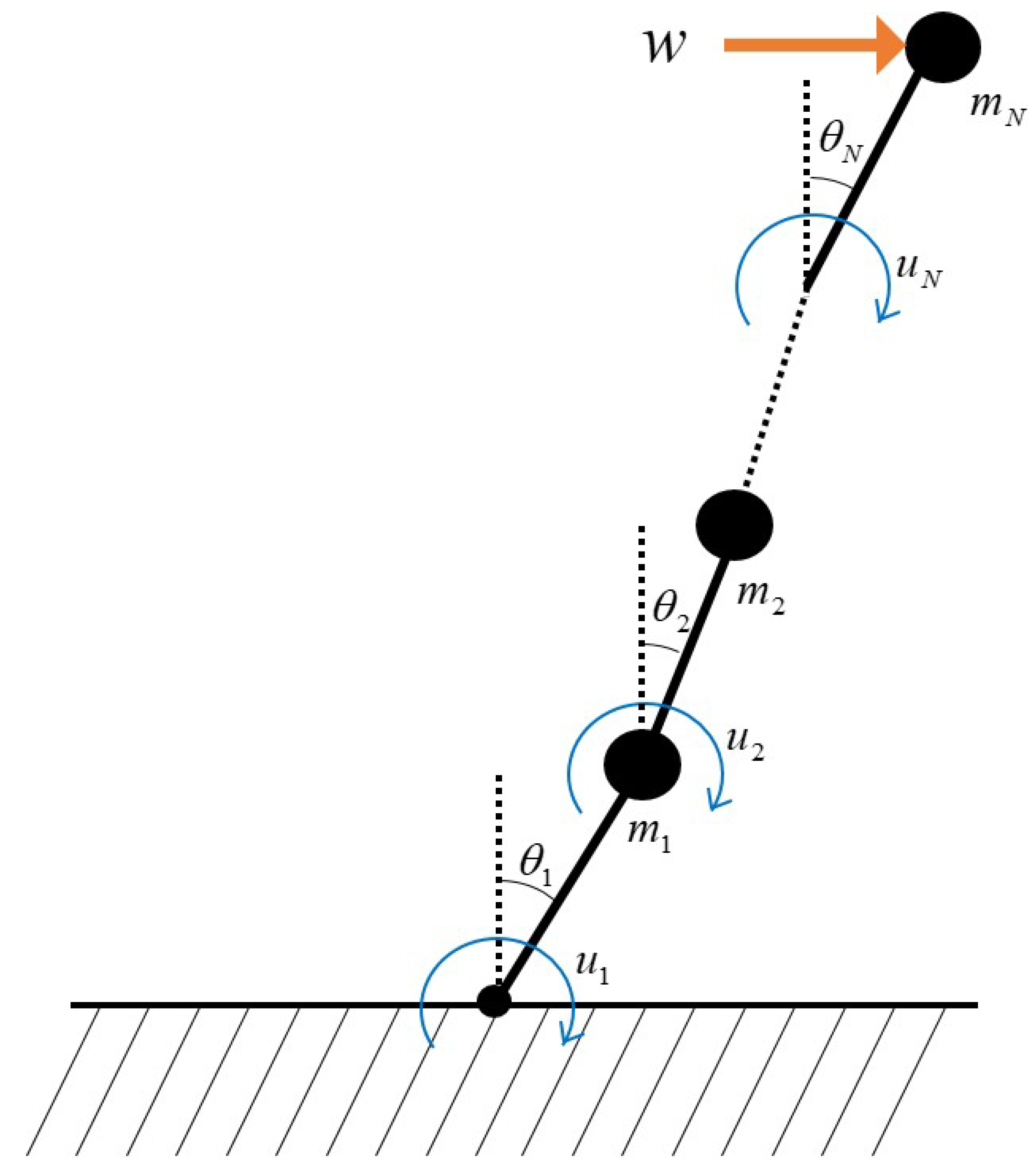
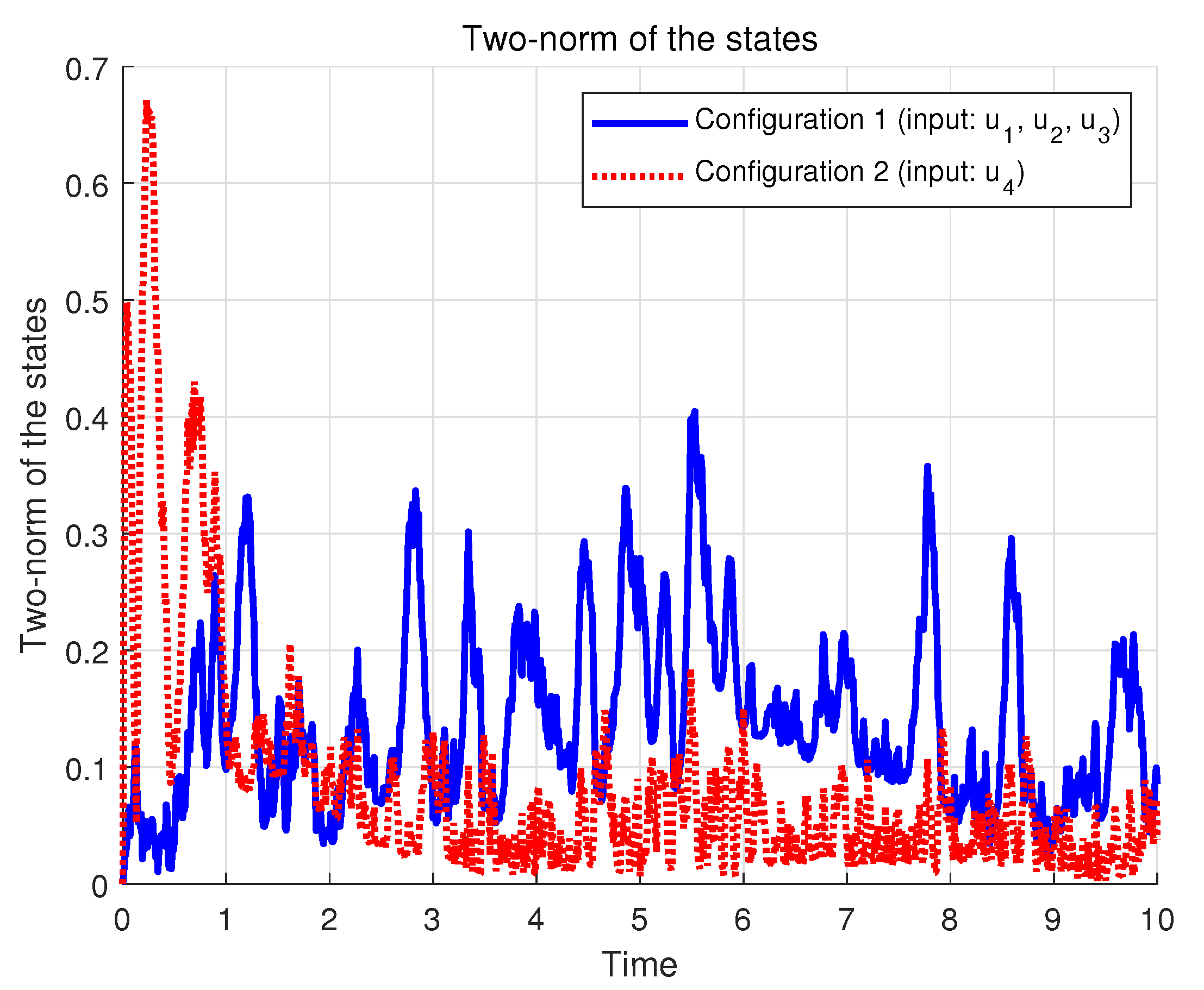
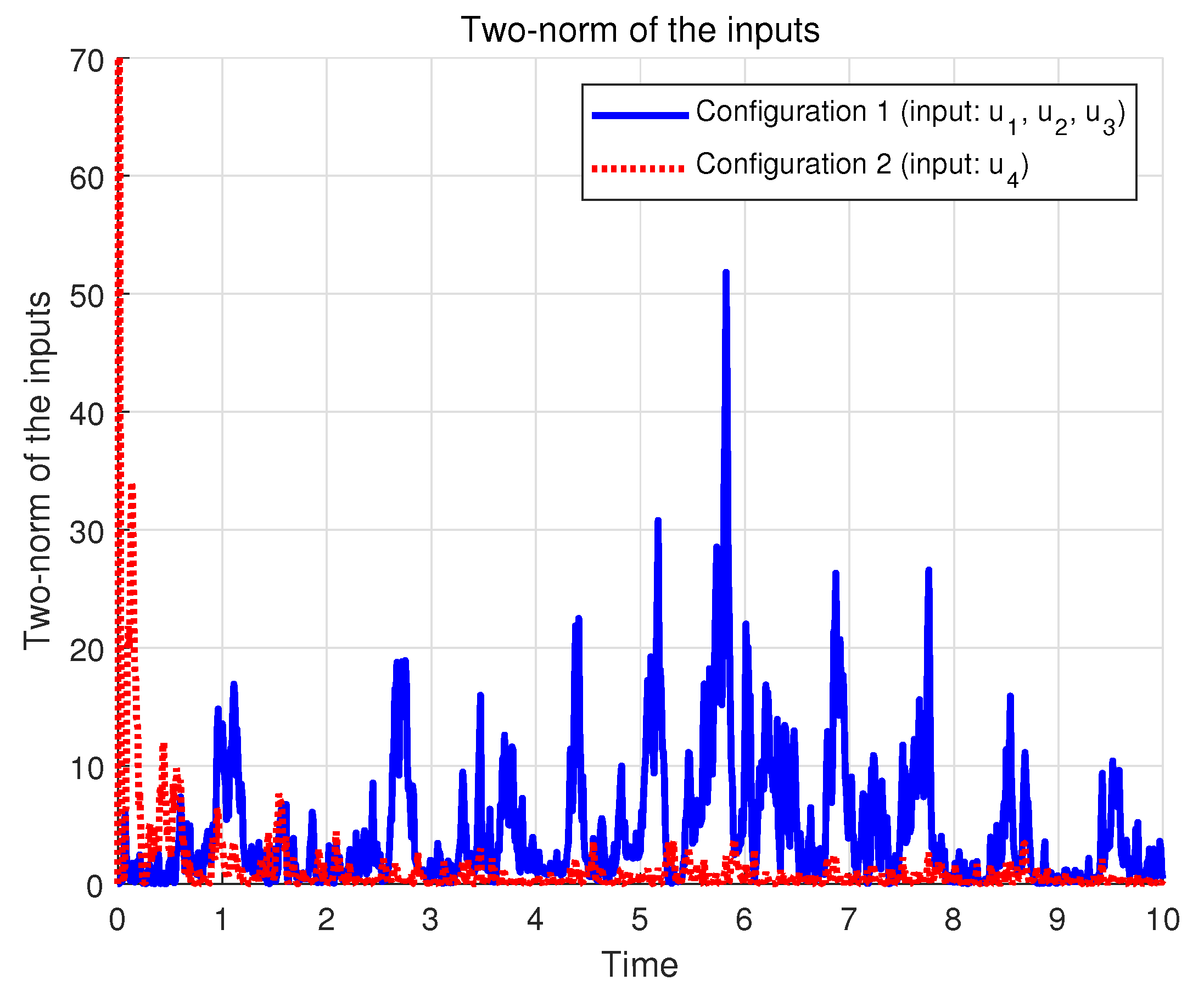

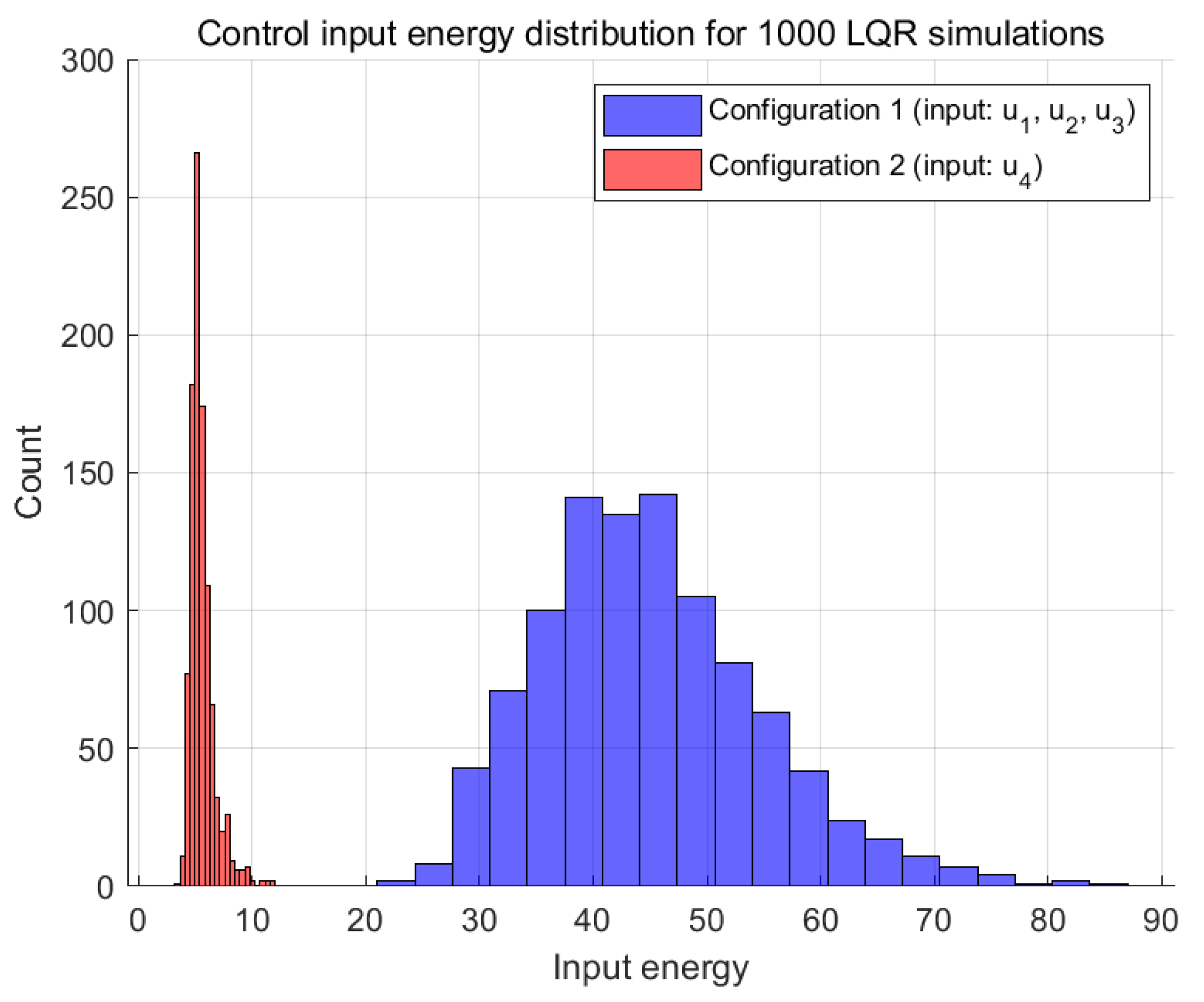
| Inputs | ||
|---|---|---|
| 3.00 | 22.20 | |
| 9.99 | 3.00 |
| # of Actuators | Input Selected | Proposed Metric | |||
|---|---|---|---|---|---|
| 1 | O | 5.49 × | |||
| O | 1.55 × | ||||
| O | 1.07 × | ||||
| O | 8.00 × | ||||
| 2 | O | O | 2.56 × | ||
| O | O | 4.25 × | |||
| O | O | 4.14 × | |||
| O | O | 2.47 × | |||
| O | O | 4.19 × | |||
| O | O | 2.95 × | |||
| 3 | O | O | O | 1.14 × | |
| O | O | O | 3.28 × | ||
| O | O | O | 2.43 × | ||
| O | O | O | 2.34 × | ||
| 4 | O | O | O | O | 2.15 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Park, J. Quantitative Controllability Metric for Disturbance Rejection in Linear Unstable Systems. Mathematics 2025, 13, 6. https://doi.org/10.3390/math13010006
Lee H, Park J. Quantitative Controllability Metric for Disturbance Rejection in Linear Unstable Systems. Mathematics. 2025; 13(1):6. https://doi.org/10.3390/math13010006
Chicago/Turabian StyleLee, Haemin, and Jinseong Park. 2025. "Quantitative Controllability Metric for Disturbance Rejection in Linear Unstable Systems" Mathematics 13, no. 1: 6. https://doi.org/10.3390/math13010006
APA StyleLee, H., & Park, J. (2025). Quantitative Controllability Metric for Disturbance Rejection in Linear Unstable Systems. Mathematics, 13(1), 6. https://doi.org/10.3390/math13010006






