Trust Region Policy Learning for Adaptive Drug Infusion with Communication Networks in Hypertensive Patients

Abstract

In the field of biomedical engineering, the issue of drug delivery constitutes a multifaceted and demanding endeavor for healthcare professionals. The intravenous administration of pharmacological agents to patients and the normalization of average arterial blood pressure (AABP) to desired thresholds represents a prevalent approach employed within clinical settings. The automated closed-loop infusion of vasoactive drugs for the purpose of modulating blood pressure (BP) in patients suffering from acute hypertension has been the focus of rigorous investigation in recent years. In previous works where model-based and fuzzy controllers are used to control AABP, model-based controllers rely on the precise mathematical model, while fuzzy controllers entail complexity due to rule sets. To overcome these challenges, this paper presents an adaptive closed-loop drug delivery system to control AABP by adjusting the infusion rate, as well as a communication time delay (CTD) for analyzing the wireless connectivity and interruption in transferring feedback data as a new insight. Firstly, a nonlinear backstepping controller (NBC) is developed to control AABP by continuously adjusting vasoactive drugs using real-time feedback. Secondly, a model-free deep reinforcement learning (MF-DRL) algorithm is integrated into the NBC to adjust dynamically the coefficients of the controller. Besides the various analyses such as normal condition (without CTD strategy), stability, and hybrid noise, a CTD analysis is implemented to illustrate the functionality of the system in a wireless manner and interruption in real-time feedback data.

1. Introduction

Patients undergoing major surgery (especially cardiovascular surgery) may experience episodes of acute blood pressure elevation during the intra- and postoperative periods. Such episodes may last between a few minutes and several hours and involve a heightened risk of complications for the patient, such as cardiovascular or cerebrovascular accidents. Careful management of acute hypertension is therefore required and is generally achieved by infusion of suitable vasoactive drugs by clinical operators [1,2,3,4].

Due to significant variability in pharmacological sensitivity among patients and even within the same individual over temporal spans, the appropriate infusion rate cannot be established a priori, necessitating the process of dose titration. This undertaking is labor-intensive and time-consuming for clinical practitioners, and manual titration may lack precision. In this framework, the advancement of a closed-loop system capable of autonomously modulating the drug infusion rate to sustain a patient’s average arterial blood pressure (AABP) within a designated range would constitute a noteworthy enhancement to medical technology [5,6]. The advantages of such a system would encompass an elevation in patient outcomes by diminishing the probability of complications, eliminating the risk of human error, and enabling the reallocation of human resources towards more critical responsibilities. This study addresses the challenge associated with the automatic closed-loop regulation of sodium nitroprusside (SNP) infusion. SNP is a potent and rapidly acting vasodilatory agent that facilitates a reduction in blood pressure by inducing a decrease in both arterial and venous resistance. Patients exhibiting elevated blood pressure subsequent to surgical procedures have conventionally received treatment with this particular medication [7,8,9].

The complexities associated with the response of the SNP medication paradigm, encompassing time-dependent uncertainties, modeling discrepancies, and temporal delays, render the automation of the control of a patient’s AABP a formidable challenge. In prior scholarly investigations, researchers have devised an array of systems intended for the modulation of AABP through the utilization of SNP. For example, earlier studies [10,11] presented an optimal Interval Type-2 Fuzzy Logic Control (IT2-FLC) framework alongside a two-layer Fractional Order Fuzzy Logic Control, wherein the optimization of controller parameters was conducted via the Grey Wolf Optimization (GWO) algorithm. Reference [12] executed an IT2-FLC system with the optimization of controller parameters being realized through the Cuckoo Search algorithm. Furthermore, in an alternative investigation, a Model Predictive Control (MPC) strategy employed Particle Swarm Optimization (PSO) for the calibration of the controller’s coefficients [13]. Additionally, a Fractional Order Proportional Integrative (FO-PI) controller was conceived to govern MABP. In another distinct study, the Q-learning algorithm, a variant of reinforcement learning, and the active disturbance rejection control (ADRC) utilizing deep deterministic policy gradient (DDPG) for the tuning of ADRC coefficients were implemented as a modern control approach for MABP regulation [14,15]. In addition to these methodologies, other techniques such as the development and assessment of a simple adaptive PI controller for MAP regulation [16], robust multi-model adaptive control [17], and embedded PI controller [18] have been devised for the management of BP.

In prior research, significant advancements have been made in regulating AABP using various control methodologies; however, several notable deficiencies persist. Firstly, most studies rely on ideal connection assumptions, neglecting the complexities of real-world implementations that often depend on wireless connectivity, which can introduce signal delays, and communication variability, adversely affecting control efficacy. Secondly, many controllers, such as MPC and PID, depend heavily on mathematical models that may not accurately represent the system dynamics, resulting in performance declines when actual conditions deviate from these models. Thirdly, while IT2-FLC does not require exact models, it faces challenges related to rule complexity, tuning difficulties, and interpretability [19,20]. Additionally, metaheuristic optimization algorithms like GWO and PSO can struggle with local optima convergence and parameter sensitivity, while DRL methods, such as Q-learning, suffer from sample inefficiency and exploration–exploitation trade-offs. Although the implementation of these strategies may result in favorable outcomes for a finite period, it is imperative to acknowledge that they do not ensure either optimal or locally optimal solutions. The related constraints encompass limited generalization abilities, lack of learning ability, convergence to local optima, and an increased susceptibility to variations in parameter configurations [21,22]. To address these issues, this study introduces a novel data-driven NBC optimized using TRPO. This approach reduces reliance on precise mathematical models, incorporates communication time delays to enhance robustness in wireless scenarios, and effectively manages model uncertainties. The TRPO algorithm improves parameter tuning, ensuring better exploration–exploitation balance and real-time adaptability, thereby enhancing the controller’s performance in dynamic environments where system parameters may vary. The structure of the closed-loop AABP strategy is presented in Figure 1.

The backstepping controller has conventionally been conceived as a model-based control strategy, distinguished by its methodical design process that utilizes mathematical models of the system to guarantee stability and performance. This methodology entails the iterative formulation of control laws predicated on the system’s dynamics, facilitating accurate tracking and regulation of intended outputs. Nonetheless, in this manuscript, we present an innovative model-free backstepping controller that considerably augments flexibility and adaptability. In contrast to its model-based analogue, this model-free variant is not contingent upon precise mathematical characterizations of the system, thereby empowering it to proficiently manage uncertainties and nonlinearities in real-time applications. Through the application of a data-driven approach, the model-free backstepping controller is capable of continuously assimilating insights from the system’s behavior, enabling real-time modifications and enhanced performance across diverse operating conditions. This progression not only alleviates the constraints associated with model inaccuracies but also bolsters the controller’s resilience in dynamic environments.

The complex attributes of physiological dynamic systems present a considerable challenge in the formulation of controllers for previously unexamined systems. Additionally, fluctuations in the output may elicit significant alterations in the system’s behavior. The nonlinear backstepping control (NBC) methodology guarantees the global asymptotic stability of stringent feedback systems by creating a linkage between the selection of a control Lyapunov function and the development of a feedback controller [23,24]. By integrating parameter estimations for unidentified variables within the control framework, the adaptive NBC approach emerges as a refined iteration of the backstepping control paradigm, appropriate for a variety of applications. In contexts characterized by uncertainties, the NBC strategy is recognized as an invaluable instrument. Notably, NBC has exhibited exceptional effectiveness in governing nonlinear systems with fixed models in the presence of external disturbances [25]. Furthermore, the implementation of integral action functions to mitigate steady-state discrepancies is significant. It is crucial to underscore that NBC operates in a recursive fashion [26]. Despite the numerous advantages offered by the NBC relative to both Conventional Controllers and modern techniques, it is pertinent to acknowledge that this specific controller is constrained by the lack of online functionality and automatic parameter adjustment. This limitation represents a considerable barrier when employing the NBC in complex dynamic systems and biological simulations. The absence of online adaptability and automated parameter modifications may hinder the controller’s capacity to adeptly navigate the inherent complexities, practical implementation issues, and time-sensitive characteristics of such systems. To enable online updates for the developed strategy, a model-free deep reinforcement learning (MF-DRL) framework, specifically the Trust Region Policy Optimization (TRPO) algorithm, has been designed and incorporated into the NBC as an on-policy approach [27].

TRPO represents a resilient algorithm within the domain of reinforcement learning (RL) that has attracted significant scholarly attention within the field of artificial intelligence (AI) [28]. A pivotal aspect of TRPO lies in its ability to provide consistent and incremental improvements to the policy during the optimization process [29]. Unlike other policy-based methodologies that may face instability and oscillations, TRPO incorporates a trust region constraint to ensure that the newly modified policy remains sufficiently close to its predecessor, thus preventing drastic declines in performance. This feature makes TRPO particularly advantageous for tasks that involve large state and action spaces, where navigating the policy landscape can be particularly challenging. The core principle supporting TRPO centers on optimizing the policy by maximizing the expected return within a defined trust region, with this limitation characterized by the Kullback–Leibler (KL) divergence between the existing and updated policies. This approach enables TRPO to identify the most effective policy adjustment while ensuring that changes in the policy distribution remain within a manageable range, thereby promoting stable learning outcomes and enhanced sample efficiency [30,31]. In the current investigation, an advanced methodology utilizing the NBC in conjunction with the TRPO algorithm has been formulated to rectify the shortcomings identified in previous research endeavors. Furthermore, a novel perspective has been introduced by incorporating a communication time delay into the established framework, intended to illustrate the operational capabilities of closed-loop AABP within a wireless context. The contributions of the present manuscript are encapsulated as follows:

(1)

The formulation of a data-driven nonlinear backstepping controller (NBC) is intended to concurrently modulate the average arterial blood pressure (AABP) via vasoactive drugs, thereby facilitating a more precise and efficient regulation of the system in comparison to traditional controllers that rely on static, predetermined configurations.

(2)

The implementation of the MF-DRL methodology serves to augment the effectiveness of the NBC strategy through the adjustment of parameters. This technique enhances the controller’s performance and permits timely modifications, thereby ensuring the system’s capacity to adaptively respond to fluctuating conditions and continuously improve its operational capabilities.

(3)

The implementation of the communication time delay (CTD) approach allows for an in-depth analysis of how transfer delay signals impact the system’s dynamics. This framework facilitates a comprehensive evaluation of its effectiveness and efficiency in managing and mitigating these delays, which is crucial for real-world applications. As a result, it offers valuable insights into the system’s robustness and applicability across various latency scenarios.

(4)

The performance of the established system when faced with a variety of patients is analyzed, in addition to assessing the system’s robustness against variations in critical parameters and exposure to hybrid noise disturbances.

The organization of this paper is as follows. The problem of average arterial blood pressure (AABP) is mathematically formulated in Section 2. Moreover, the control methodology is presented in this section. The next section, Section 3, is devoted to the design of the controller using the TRPO algorithm. The simulation examinations are provided in Section 4. The results of the proposed methodology are concluded in Section 5.

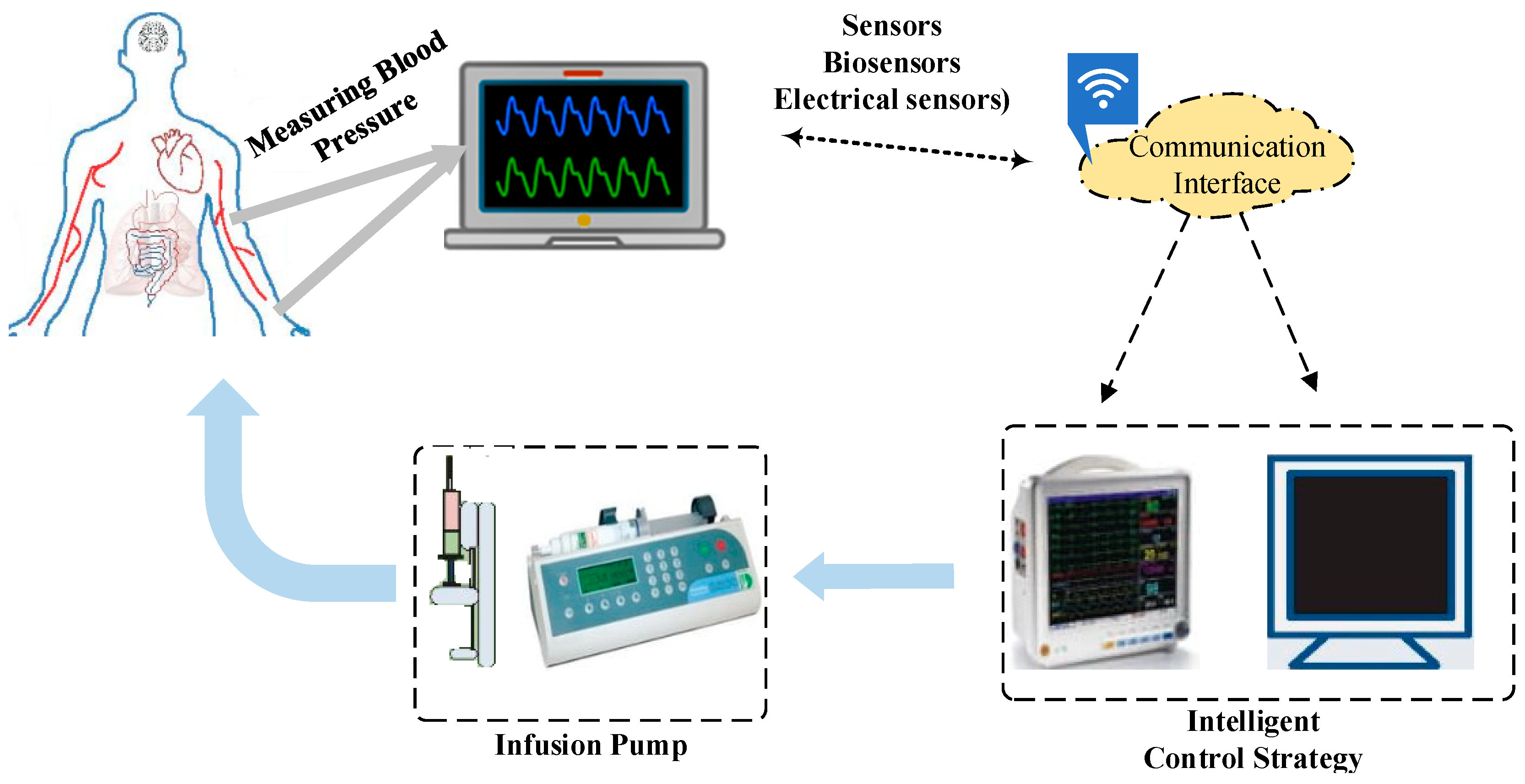
2. Problem Formulation and Methodology

2.1. AABP Dynamic Model

This section delineates the dynamic patient model utilized for the continuous monitoring of average arterial blood pressure (AABP) during the administration of the sodium nitroprusside (SNP) pharmacological agent, aimed at achieving the patients’ targeted AABP. Furthermore, the ensuing discourse encompasses the limitations inherent in the control objectives of the previously mentioned model. The dynamic model under examination elucidates the relationship between the infusion rates of the SNP therapeutic agent and the subsequent alterations in mean AABP as a consequence of the drug administration. The dynamic model elucidates how fluctuations in BP influence the velocity at which the pharmacological agent is administered. The representation of the dynamic model is articulated as follows [16,32]:

$${\mathcal{G}}_{patient}\left(\mathcal{s}\right)={\displaystyle \frac{{\mathcal{y}}_{patient}\left(\mathcal{s}\right)}{{\mathcal{I}}_{patient}\left(\mathcal{s}\right)}}=\left({\displaystyle \frac{{\psi }_{patient}\left(1+{{\rm X}}_{i3}\mathcal{s}\right)e^{-\left({\Omega }_{patient}\right)\mathcal{s}}}{[\left(1+X_{i3}\mathcal{s}\right)\left(1+X_{i2}\mathcal{s}\right)-{\varpi }_{patient}]}}\right)\times \left({\displaystyle \frac{1}{1+{{\rm X}}_{i1}\mathcal{s}}}\right)$$

(1)

The patient’s blood pressure change, represented by ${\mathcal{y}}_{patient}\left(\mathcal{s}\right)$, is the controlled variable, while the rate of drug infusion, ${\mathcal{I}}_{patient}\left(\mathcal{s}\right)$, is the control input. The temporal constants ${\mathsf{{\rm X}}}_{i1}\mathcal{s}$, ${\mathsf{{\rm X}}}_{i2}\mathcal{s}$, and ${\mathsf{{\rm X}}}_{i3}\mathcal{s}$ dictate the rate at which the SNP medication is assimilated and takes effect in the patient’s physiological system for different individuals. The parameter ${\mathsf{\varpi }}_{patient}$ represents the proportion of recirculated SNP medication that contributes to the overall therapeutic effect, while ${\mathsf{\Omega }}_{patient}$ captures the time delay between the initiation of medication administration and its impact on the patient’s blood pressure. The parameter ${\psi }_{patient}$ illustrates the patient’s sensitivity to the pharmacological intervention and its subsequent effect on their blood pressure. The closed-loop structure allows the system to continuously monitor the patient’s blood pressure and adjust the drug infusion rate accordingly to maintain the desired AABP level, with the nonlinear transfer functions capturing the complex dynamics involved in the drug administration and its impact on the patient’s physiology. Consequently, the output of the AABP can be articulated as follows:

$$AABP\left(t\right)=S_s+AABP\left(0\right)$$

(2)

The initial BP denoted as $AABP\left(0\right)$. The comprehensive structure of the studied model is shown visually in Figure 2a.

As previously articulated, the primary objective of this study is to regulate AABP through meticulous administration of the medication SNP. Within the framework of this research, the reference input value, as depicted in Figure 2b, necessitates effective control via the appropriate dosage of SNP medication to achieve an AABP that remains within the acceptable threshold of 100 mmHg. Given the deviation from the initial elevated AABP value of 150 mmHg, the constraints associated with the SNP drug infusion rate must be judiciously considered.

2.2. Mechanism of Nonlinear Backstepping Controller (NBC)

The NBC’s structure is depicted in Figure 2a, and the controller’s specifics are provided below. The NBC approach and system stability will be discussed next. The following model is used to demonstrate the BP dynamics:

$$n^{\left(x\right)}=\beta \left(n\right)+\kappa u$$

(3)

where $\beta \left(n\right)$ and $u$, respectively, indicate the BP and input system’s dynamics.

$$n^{\left(x\right)}=\beta \left(n\right)+{\beta }_e\left(·\right)+\widehat{\kappa }u$$

(4)

Where $\widehat{\kappa }$ is the estimate of the unknown gain of the parameter $M$, and ${\beta }_e\left(·\right)$ is the unmodeled and uncertain dynamics of BP. Thus, ${\beta }_e\left(·\right)$ can be written as follows: ${\beta }_e\left(·\right)=\mathsf{\Lambda }+(\kappa -\widehat{\kappa })u$. The model uncertainties are represented by $\mathsf{\Lambda }$. An observer can be used for the known and projected nonlinear dynamics of BP, which can reduce the error of some state variables [33].

$$n^{\left(x\right)}=\beta \left(n\right)+F+\widehat{\kappa }u$$

(5)

$${F=n}^{\left(x\right)}-f\left(n\right)-\widehat{\kappa }u$$

(6)

$$u={\displaystyle \frac{F-n_d^{\left(x\right)}-u_c}{\widehat{\kappa }}}$$

(7)

$$n^{\left(x\right)}=\beta \left(n\right)+n_d^{\left(x\right)}+u_c$$

(8)

The AABP model’s state variable can be represented as follows:

$$n_1=AABP$$

(9)

$$n_2={\dot{n}}_1$$

(10)

Nevertheless, in fact, the desired and actual values of the state variable ($n_1$) differ; this difference is expressed by the formula $E_1=n_1-n_1^d=n_1-n_d$. The NBC theory can be used to force position-tracking and amplitude-tracking error to converge to a single variable. The Lyapunov function is selected in order to ensure the convergence stability of the nonlinear BP model. The Lyapunov function $L\left({\mathsf{{\rm M}}}_1\right)$ can be expressed as follows and will be positive definite around the state variable:

$$L_1\left({\mathsf{{\rm M}}}_1\right)={\displaystyle \frac{1}{2}}{\mathsf{{\rm M}}}_1^2$$

(11)

The derivative of Equation (11) can be written as follows:

$${\dot{L}}_1\left({\mathsf{{\rm M}}}_1\right)={\mathsf{{\rm M}}}_1{\dot{\mathsf{{\rm M}}}}_1={\mathsf{{\rm M}}}_1(n_2-{\dot{n}}_d)$$

(12)

A dynamic disparity occurs between a variable and its intended value because we are not able to regulate the variable. As a result, the amplitude-tracking error can be used to offset the dynamic error.

$${\mathsf{{\rm M}}}_2=n_2-n_2^d$$

(13)

In the event that a semi-negative Lyapunov function is selected, the error will approach zero. The following is one way to express the implicit input:

$$n_2^d={\dot{\mathrm{n}}}_d-w_1{\mathsf{{\rm M}}}_1$$

(14)

$${\mathsf{{\rm M}}}_2=n_2-{\dot{\mathrm{n}}}_d+w_1{E}_1$$

(15)

Errors and uncertainties in the model lead to steady-state inaccuracy. This problem can be resolved by applying the integral term to the system as described below [34].

$$n_2={\dot{\mathrm{n}}}_d-w_1{\mathsf{{\rm M}}}_1-w_3\int {\mathsf{{\rm M}}}_1$$

(16)

$${\mathsf{{\rm M}}}_2=n_2-{\dot{\mathrm{n}}}_d+w_1{\mathsf{{\rm M}}}_1+w_3\int {\mathsf{{\rm M}}}_1$$

(17)

Therefore, the following information describes the derivative for both amplitude and position tracking.

$${\dot{\mathsf{{\rm M}}}}_1={\dot{\mathrm{n}}}_1-{\dot{\mathrm{n}}}_d={\mathsf{{\rm M}}}_2+n^{*}-{\dot{\mathrm{n}}}_d={\mathsf{{\rm M}}}_2-w_1{\mathsf{{\rm M}}}_1-w_3\int {\mathsf{{\rm M}}}_1$$

(18)

$${\dot{\mathsf{{\rm M}}}}_2={\dot{n}}_2-{\ddot{n}}_d+w_1{\dot{\mathsf{{\rm M}}}}_1-w_{3}e{\mathsf{{\rm M}}}_1={\dot{n}}_2-{\ddot{n}}_d+w_1{\mathsf{{\rm M}}}_2-w_1^2{\mathsf{{\rm M}}}_1-w_1{w}_3\int E_1-w_3{\mathsf{{\rm M}}}_1$$

(19)

The Lyapunov functions $L_1\left({\mathsf{{\rm M}}}_1.\int {\mathsf{{\rm M}}}_1\right)$ and $L_2\left({\mathsf{{\rm M}}}_1.{\mathsf{{\rm M}}}_2.\int {\mathsf{{\rm M}}}_1\right)$ are defined for the position- and amplitude-tracking error and are expressed as follows [35]:

$$L_1\left({\mathsf{{\rm M}}}_1.\int {\mathsf{{\rm M}}}_1\right)={\displaystyle \frac{1}{2}}{\mathsf{{\rm M}}}_1^2+{\displaystyle \frac{w_3}{2}}{(\int {\mathsf{{\rm M}}}_1)}^2$$

(20)

$${\dot{L}}_1\left({\mathsf{{\rm M}}}_1.\int {\mathsf{{\rm M}}}_1\right)={\mathsf{{\rm M}}}_1{\dot{\mathsf{{\rm M}}}}_1+w_3{\mathsf{{\rm M}}}_1\int {\mathsf{{\rm M}}}_1={\mathsf{{\rm M}}}_1{\mathsf{{\rm M}}}_2-w_1{{\mathsf{{\rm M}}}_1}^2$$

(21)

$$L_2\left({\mathsf{{\rm M}}}_1.{\mathsf{{\rm M}}}_2.\int {\mathsf{{\rm M}}}_1\right)={\displaystyle \frac{1}{2}}{\mathsf{{\rm M}}}_1^2+{\displaystyle \frac{1}{2}}{\mathsf{{\rm M}}}_2^2+{\displaystyle \frac{w_3}{2}}{(\int {\mathsf{{\rm M}}}_1)}^2$$

(22)

$$\begin{array}{ll}{\dot{L}}_2\left({\mathsf{{\rm M}}}_1.{\mathsf{{\rm M}}}_2.\int {\mathsf{{\rm M}}}_1\right)& ={\mathsf{{\rm M}}}_1{\dot{\mathsf{{\rm M}}}}_1+{\mathsf{{\rm M}}}_2{\dot{\mathsf{{\rm M}}}}_2+w_3{\mathsf{{\rm M}}}_1\int {\mathsf{{\rm M}}}_1\\ & ={\mathsf{{\rm M}}}_1{\mathsf{{\rm M}}}_2-w_1{{\mathsf{{\rm M}}}_1}^2+{\mathsf{{\rm M}}}_2({\dot{n}}_2-{\ddot{n}}_d+w_1{\mathsf{{\rm M}}}_2-w_1^2{\mathsf{{\rm M}}}_1-w_1{w}_3\int {\mathsf{{\rm M}}}_1-w_3{\mathsf{{\rm M}}}_1)\end{array}$$

(23)

In order to ensure that the $E_2$ will eventually approach zero, the ${\dot{L}}_2\left({\mathsf{{\rm M}}}_1.{\mathsf{{\rm M}}}_2.\int {\mathsf{{\rm M}}}_1\right)$ must be semi-negative definite. The solution to this is to select Equation (24).

$${\mathsf{{\rm M}}}_1{\mathsf{{\rm M}}}_2+{\mathsf{{\rm M}}}_2\left({\dot{n}}_2-{\ddot{n}}_d+w_1{\mathsf{{\rm M}}}_2-w_1^2{\mathsf{{\rm M}}}_1-w_1{w}_3\int {\mathsf{{\rm M}}}_1-w_3{\mathsf{{\rm M}}}_1\right)=-w_2{{\mathsf{{\rm M}}}_2}^2$$

(24)

Thus, ${\dot{n}}_2$ can be expressed as follows:

$${\dot{n}}_2={f\left(x\right)+\ddot{n}}_d+u_c={\ddot{n}}_d+\left(w_1^2+w_3-1\right){\mathsf{{\rm M}}}_1-\left(w_1+w_2\right){\mathsf{{\rm M}}}_2+w_1{w}_3\int {\mathsf{{\rm M}}}_1$$

(25)

$$u=\left[({w_1^2+w}_3-1){\mathsf{{\rm M}}}_1-\left(w_1+w_2\right){\mathsf{{\rm M}}}_2+w_1{w}_3\int {\mathsf{{\rm M}}}_1\right]-\beta \left(x\right)$$

(26)

Remark 1.

The performance of the backstepping controller relies heavily on the careful selection and precise tuning of its coefficients. This tuning is crucial for enhancing the controller’s effectiveness and stability, allowing it to optimally respond to varying system dynamics. Therefore, thorough adjustment of these coefficients is essential for achieving desired control objectives and ensuring robustness in practical applications.

Remark 2.

Traditional methods for tuning NBC coefficients, such as heuristic and fuzzy approaches, have notable weaknesses. Heuristic methods often rely on trial and error, leading to time-consuming processes without guaranteed optimal solutions. Fuzzy Logic tuning can become complex and difficult to manage, especially with multiple input variables, resulting in challenges related to rule complexity and interpretability. To address these issues, we have developed the TRPO method, which offers a systematic and data-driven approach for tuning NBC coefficients. TRPO enhances the tuning process by ensuring stable learning and convergence to optimal solutions, ultimately improving the performance and robustness of the backstepping controller.

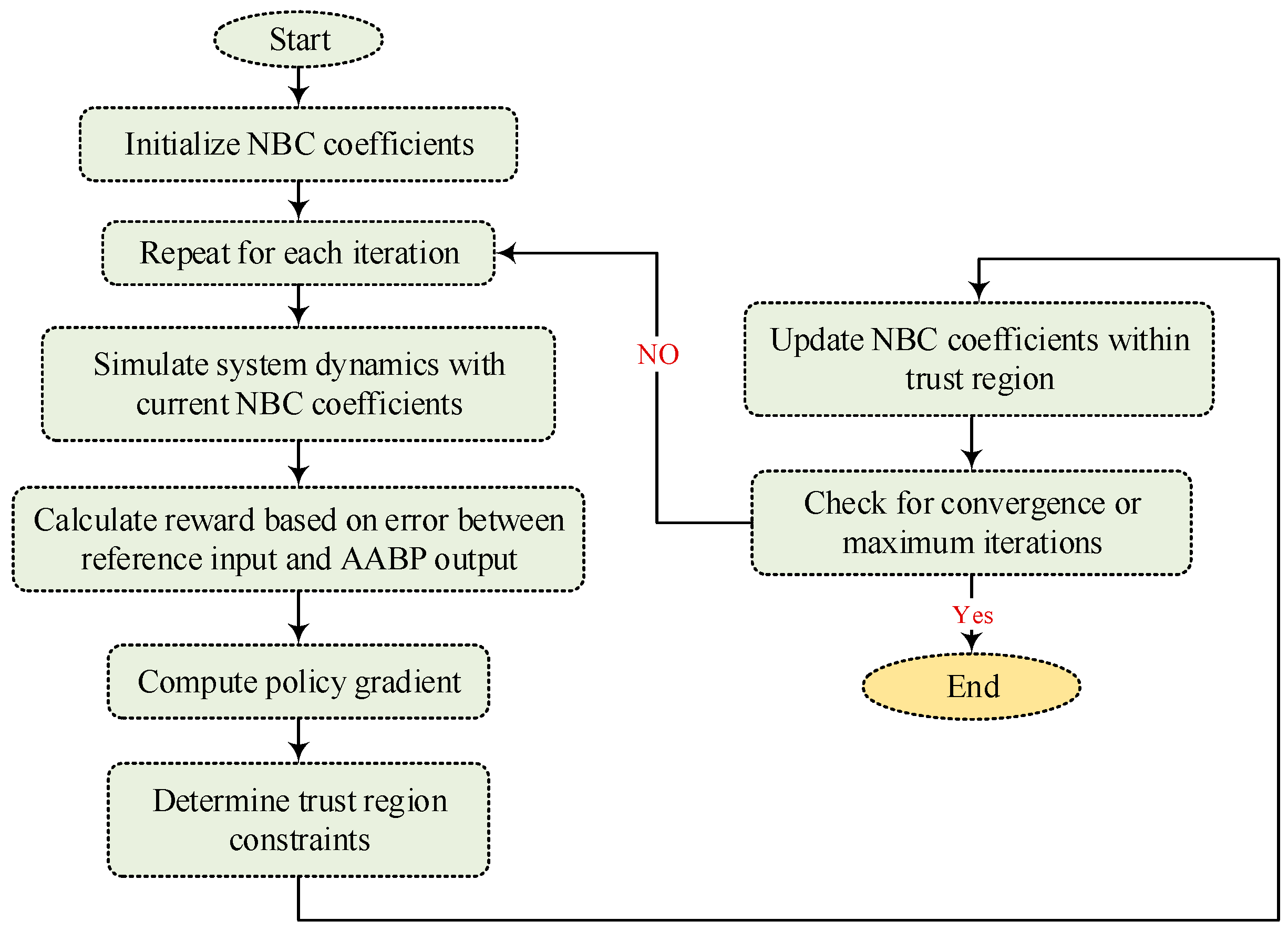
3. The Design of the NBC Based on Trust Region Policy Optimization DRL

The Trust Region Policy Optimization (TRPO) algorithm is a model-free strategy that represents a prominent technique within the domains of artificial intelligence (AI) and machine learning (ML). This algorithm is meticulously crafted to augment the policy of an agent by incrementally improving its operational efficacy in a stable and effective fashion [36]. A fundamental characteristic of TRPO is its focus on ensuring that only minor adjustments to the policy occur during each iteration, which functions to maintain stability and avert significant modifications that could detrimentally impact the learning trajectory [37]. This technique aspires to derive an efficient behavioral policy through iterative trial-and-error interactions with an opaque environment. The primary aim is to optimize an agent’s behavioral policy concerning the overarching expected discounted reward. MF-DRL algorithms do not formulate a model of the environment. This algorithm is generally adaptable, requires relatively minimal modifications, and is capable of seamlessly integrating powerful function approximators such as deep neural networks (DNNs). The topology of the policy network and value network of the TRPO algorithm is illustrated in Figure 3.

TRPO is categorized as an on-policy algorithm. On-policy approaches confer a multitude of advantages, including the ability to evaluate each resultant policy [38,39]. Furthermore, in the context of on-policy optimization, traditional policy gradient algorithms experience sporadic updates characterized by substantial step sizes, resulting in the acquisition of inferior samples. To mitigate this instability, this methodology constrains the Kullback–Leibler (KL) divergence between successive policies to facilitate significantly more stable updates [40].

3.1. The Fundamental of TRPO Algorithm

The expected return from the start state is represented by the policy performance objective $\xi \left(\pi \right)=E_{s0,a0}\left[{Rew}_0\right]$, and the goal of RL is to maximize it. This objective is stated as follows:

$$\xi \left(\pi \right)=E_{s0,a0,\dots }\left[\sum _0^{\infty }{\lambda }^{t}r(X_t,a_{kt})\right]$$

(27)

$$X_0~{\delta }_0~a_t~\pi \left(0,X_t\right),X_{t+1}~\mathsf{{\rm Y}}(0,X_t,a_t)$$

(28)

where the state and action spaces are denoted, respectively, by $X$ and $a$. Furthermore, $r$ denotes the reward term, $\delta$ represents the initial state distribution, $\mathsf{{\rm Y}}$ represents the dynamic distribution, and $\lambda$ determines the discount factor [41]. The advantage over $\pi$, accumulated over time, can be utilized to predict the expected return on investment for an additional policy $\widehat{\pi }$:

$$\xi \left(\widehat{\pi }\right)=\xi \left(\pi \right)+E_{s0,a0,\dots ~\widehat{\pi }}\left[\sum _0^{\infty }{\lambda }^t{A}_{\pi }\left(X_t,a_{kt}\right)\right]$$

(29)

$$=\xi \left(\pi \right)+{\sum }_X{\delta }_{\widehat{\pi }}\left(X\right){\sum }_a\widehat{\pi }\left(a\right|X\left)A_{\pi }\right(X,a)$$

(30)

It is crucial to recognize that any policy update $\pi \to \widehat{\pi }$ that satisfies Equation (31) guarantees the improvement of policy $\xi$. The guarantee of policy improvement is difficult because $\widehat{\pi }$ influences ${\delta }_{\widehat{\pi }}\left(X\right)$. This leads to complexity. To reduce such interdependence, a possible solution is provided by a local estimation of ${\delta }_{\widehat{\pi }}$, where ${\delta }_{\pi }$ is substituted for the visiting frequency $\xi \left(\widehat{\pi }\right)$ [42].

$${\sum }_X{\delta }_{\widehat{\pi }}\left(X\right){\sum }_a\widehat{\pi }\left(a\right|X\left)A_{\pi }\right(X,a)\ge 0$$

(31)

$${\mathsf{{\rm T}}}_{\pi }\left(\widehat{\pi }\right)=\xi \left(\pi \right)+{\sum }_X{\delta }_{\pi }\left(X\right){\sum }_a\widehat{\pi }\left(a\right|X\left)A_{\pi }\right(X,a)$$

(32)

Improvements to ${\mathsf{{\rm T}}}_{\pi }$ will result in improvements to $\xi$ if the perturbation $\pi \to \widehat{\pi }$ is negligibly large. However, this small correction places a limit on the possible growth of $\xi$.

The TRPO algorithm is suggested as a workaround for this restriction, driven by the ideas of conservative policy iteration [43]. TRPO introduces a surrogate objective function and shows how improving this function improves policy performance by placing a more relaxed constraint on policy performance. In particular, TRPO provides the following lower bound:

$$\xi \left({\pi }_{new}\right)\ge {\mathsf{{\rm T}}}_{{\pi }_{old}}\left({\pi }_{new}\right)-{\displaystyle \frac{4\in \lambda }{{\left(1-\lambda \right)}^2}}{d}_{KL}^{max}({\pi }_{old},{\pi }_{new})$$

(33)

where $\in ={max}_{X,a}\left|A_{{\pi }_{old}}\left(X,a\right)\right|$. The existing policies, identified as ${\pi }_{old}$ and ${\pi }_{new}$, are separated by a measure called $d_{KL}^{max}({\pi }_{old},{\pi }_{new})$, which is determined by the KL divergence:

$$d_{KL}^{max}\left({\pi }_{old},{\pi }_{new}\right)={max}_X{d}_{KL}\left({\pi }_{old}\right(0\left|X\right)|\left|{\pi }_{new}\left(0|X\right)\right)$$

(34)

As shown by $\xi$, Equation (34) shows that improving the surrogate objective function on the right-hand side may enhance policy performance. The surrogate objective function in ${\mathsf{{\rm T}}}_{{\pi }_{old}}\left({\pi }_{new}\right)$ is dependent on a particular behavior policy, namely, the present policy π_old, for the frequency of visits ${\delta }_{{\pi }_{old}}$. The process of the functionality of the TRPO strategy is illustrated in Figure 4.

3.2. The Functionality of the TRPO Algorithm in Tuning NBC’s Coefficients

The efficacy of the policy methodology can be deduced from the magnitude of the reward associated with the agent’s state–action pair. As elucidated in Section 2.1, a relationship exists between the values of both variables (AABP and SNP); hence, both variables can be incorporated into the reward function. For this purpose, as illustrated in Figure 5, the error between the reference input and AABP output is considered as a reward function for the specifically designed controller. Consequently, the final objective is to ascertain that the algorithm endeavors to modulate the NBC coefficients by actions ($A_1$, $A_2$, $A_3$) and to manage the level of AABP produced. The prevailing policy (i.e., the existing configuration of controller parameters) is systematically assessed by simulating the system dynamics and quantifying the reward, subsequently enhancing the policy utilizing the TRPO algorithm. This methodology is applied to each of the three NBC parameters. To preserve stability, the TRPO algorithm computes the policy gradient, which elucidates the optimal direction for updating the policy parameters to optimize reward. It subsequently imposes constraints on the updated step size to ensure that the new policy remains sufficiently aligned with the preceding version. Subsequently, while adhering to the trust region constraints, the policy parameters are modified in accordance with the predicted policy gradient. Through the iterative execution of this protocol, the TRPO algorithm is capable of identifying, from the simulated dynamic model, the optimal controller parameters that manage AABP while concurrently considering SNP dose control.

$$\mathbb{R}={\displaystyle \frac{1}{{(Ref-AABP)}^2}}$$

(35)

From Figure 5, it can be seen that the fundamental component of the proposed framework is the NBC strategy, which is tasked with the generation of regulatory actions that are subsequently administered to the patient. This NBC assimilates the reference input (Ref) alongside the current states of the system, subsequently yielding the requisite control signal to be implemented for the patient. Upon the generation of the control signal by the NBC, it is subsequently administered to the patient, precipitating alterations in the patient’s dynamics and the comprehensive state of the system. The modified state of the system is then monitored by the observer block, which accumulates pertinent information regarding the system, notably the AABP signal emanating from the environment. The acquired state information of the observed system is then reintroduced into the TRPO component. The TRPO algorithm employs this state information to refine both the policy network and the value network, which constitute the principal elements of the TRPO algorithm. The policy network is tasked with the mapping of system states to the optimal actions, specifically the regulatory actions produced by the NBC. Conversely, the value network is designed to estimate the anticipated long-term reward (or value) associated with being in a given state while executing a specific action. The TRPO algorithm subsequently utilizes these policy and value networks to engage in policy optimization. This is accomplished by modifying the weights and biases of the networks through techniques based on gradient optimization, while concurrently ensuring that the policy updates remain within acceptable limits relative to the existing policy, adhering to the “trust region” constraint. Through the iterative refinement of the policy and value networks, the TRPO algorithm seeks to ascertain the optimal policy capable of effectively managing the patient’s condition, considering the intricate dynamics involving the patient, their environment, and the interactions therein.

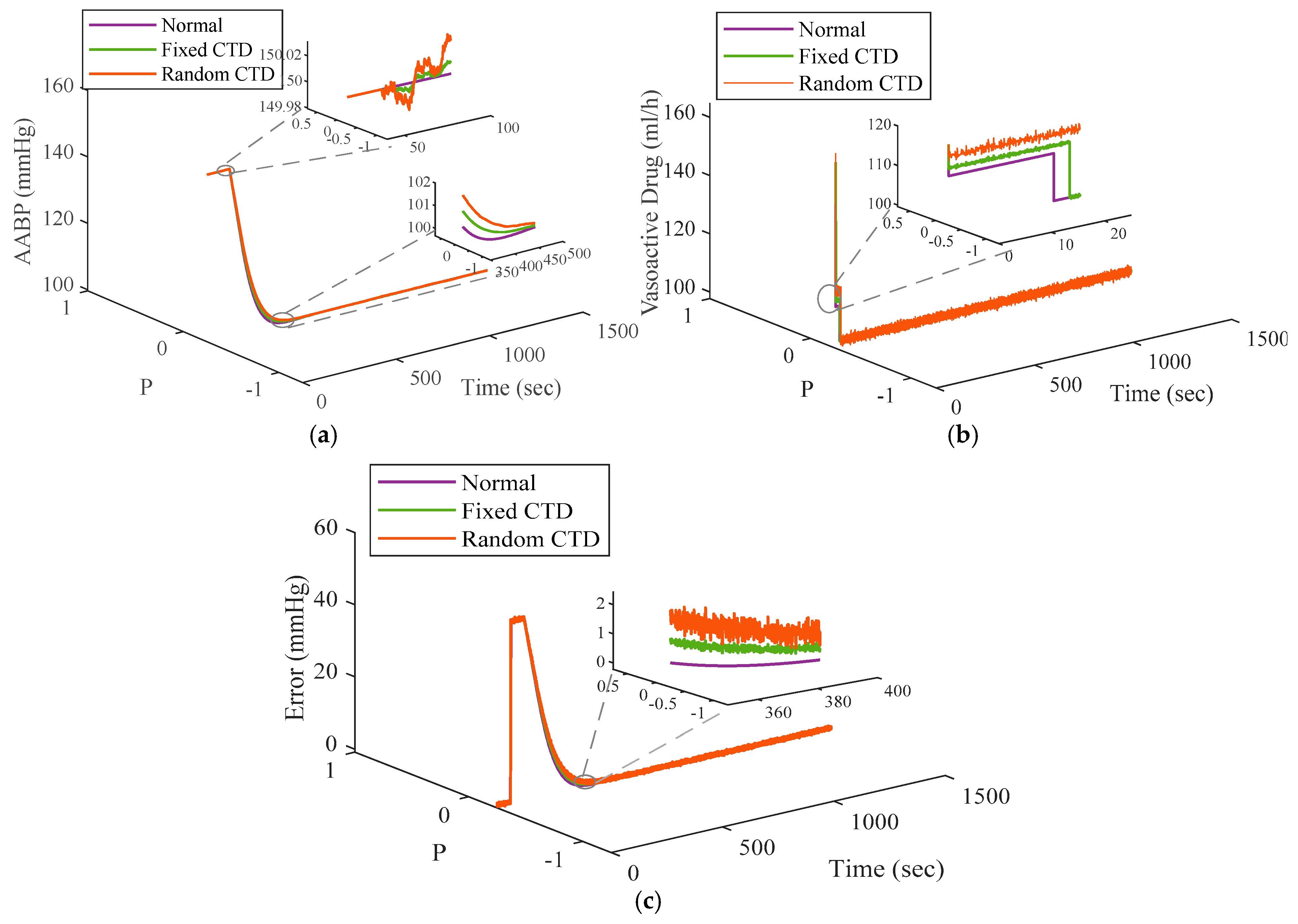
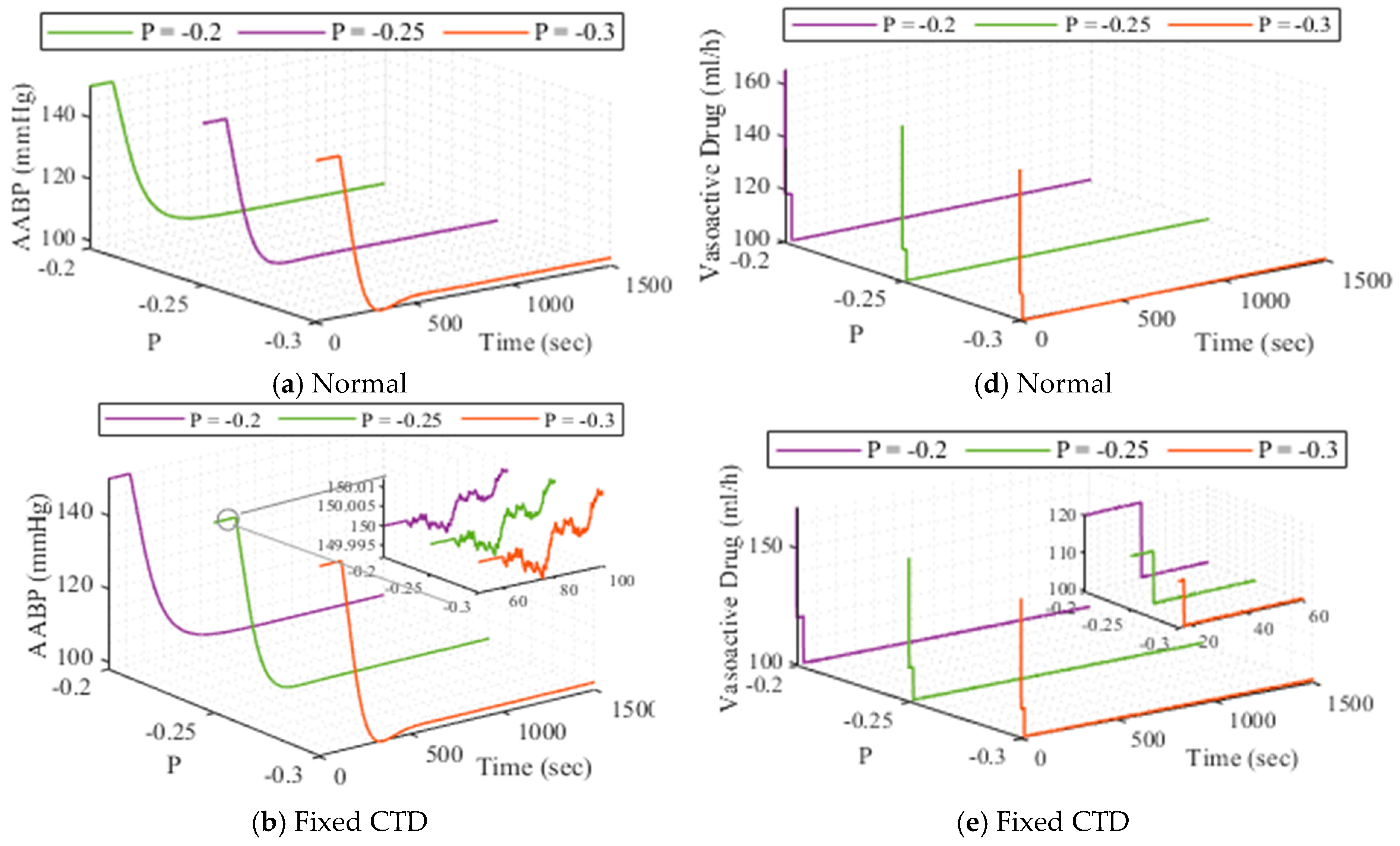
4. Simulation Verifications and Statistical Analysis

This section provides a detailed examination of the efficacy of the TRPO-based NBC methodology within the dynamic framework of the AABP test system, aiming to handle BP by adjusting SNP dosage under normal conditions (without CTD) as well as in wireless interactions among individuals diagnosed with high BP. The nominal value of the AABP system and hyperparameters of the TRPO algorithm have been adjusted according to

Table 1. Quantities and variables of the AABP system and TRPO hyperparameters.

Variables	Quantities	Variables	Quantities
Systematic circulation	${\mathsf{{\rm X}}}_{i2}=30\mathrm{s}$	Drug fraction recirculated	$\mathsf{\Phi }=0.5$
Drug action	${\mathsf{{\rm X}}}_{i1}=50\mathrm{s}$	Delay	$\left(\mathsf{\Omega }\right)\mathrm{s}=60\mathrm{s}$
Pulmonary Circulation	${\mathsf{{\rm X}}}_{i3}=10\mathrm{s}$	Sensitivity	$P=-0.25 \mathrm{m}\mathrm{m}\mathrm{H}\mathrm{g}$
TRPO Hyperparameters
Number of hidden layers	2	Activation function	ReLU
Learning rate	$0.01$	Discount factor	$0.99$
KL divergence constraint		$0.01$

.

To achieve the most advantageous outcome, it is imperative to acknowledge the limitations imposed by the administration of SNP medications [12,14]. The subsequent constraints are enumerated:

Constraint 1.

The definitive closed-loop control mechanism must not exhibit oscillatory behavior at any point in time (oscillations within the system governing (AABP) possess the potential to induce instability and adverse consequences for the patient. The preservation of stability is imperative to ensure an uninterrupted and secure regulation of AABP).

Constraint 2.

The proposed sensor should achieve stabilization within a time frame of less than ten to fifteen minutes, respectively (the attainment of rapid stabilization of the AABP control system is vital for promptly reaching the designated AABP target value and minimizing the duration of suboptimal AABP encountered during the transient response phase).

Constraint 3.

The optimal AABP should be maintained within the range of [70, 120] mmHg subsequent to stabilization (the AABP range of 70 to 120 mmHg is universally recognized in clinical practice as an appropriate target for cardiac patients in the postoperative recovery phase, considering its congruence with safety parameters and physiological standards that facilitate patient rehabilitation).

Constraint 4.

It is imperative to ensure that the patient’s AABP does not fall below the critical threshold of 70 mmHg (maintaining AABP levels above 70 mmHg is crucial to ensure adequate perfusion and oxygenation to vital organs, thereby preventing the emergence of potential complications such as organ dysfunction or insufficient perfusion [44]).

Constraint 5.

In order to attain the desired AABP of 100 mmHg, it is critical that the ultimate steady-state MABP remains confined within a tolerance of ±5 mmHg (sustaining the AABP within a range of ±5 mmHg from the reference value of 100 mmHg is essential for ensuring precise regulation and mitigating deviations that may adversely affect the patient’s health status).

Constraint 6.

Administering a substantial quantity of sodium nitroprusside (SNP) to a patient undergoing treatment or recuperation from an injury may pose significant risks. Consequently, it is vital that the patient’s medication dosage be constrained between 0 and 180 milliliters per hour. The methodology, along with the testing system, has been systematically implemented into Simulink and MATLAB, respectively, to facilitate the attainment of this goal. The formulated strategy has been subjected to empirical testing across a multitude of conditions and scenarios, which are thoroughly elucidated in the ensuing subsections.

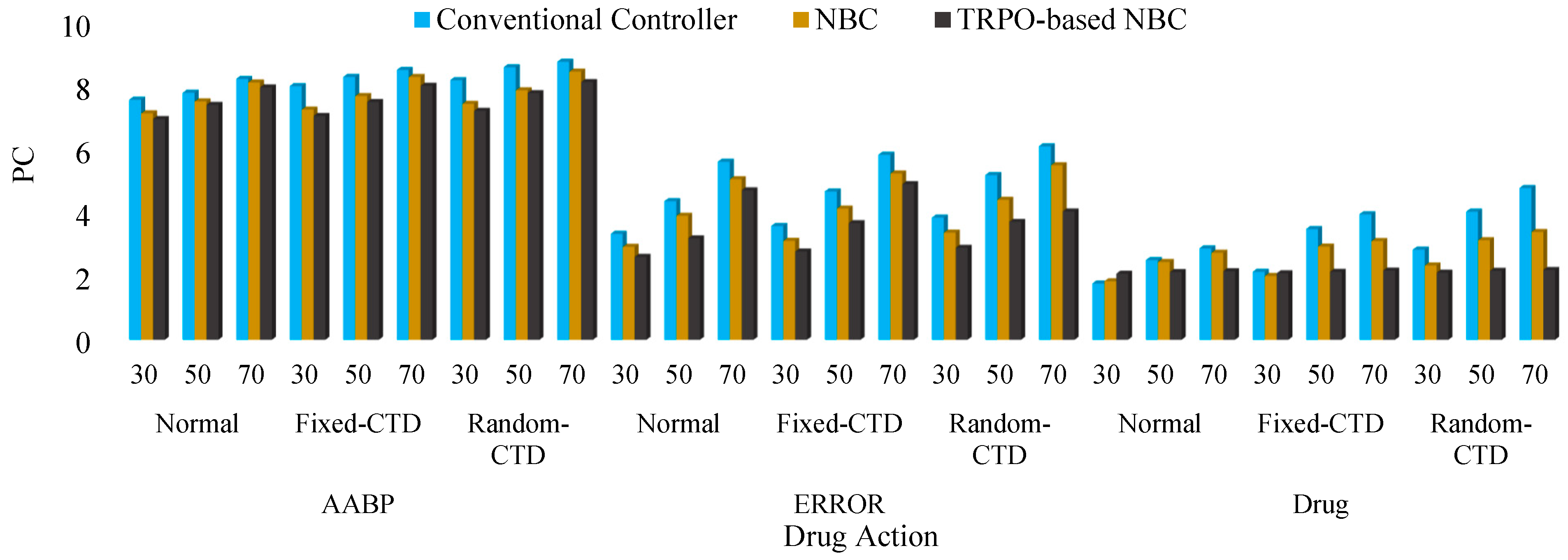
4.1. Scenario 1 (Performance of the TRPO-Based NBC Under Normal Configuration and with CTD)

In order to elucidate the operational properties of the system within a conventional framework frequently represented in the prevailing scholarly literature, the experimental system and methodology are established with the default parameters delineated in Table 1. In recognition of the pivotal role played by the wireless connection in the closed-loop system, a communication time delay (CTD) is integrated to replicate the wireless connectivity. This delay is implemented and calibrated employing both fixed values, [0.005], and stochastic values, [0.006 0.05]. The system’s performance is illustrated under standard conditions (controller without CTD approach), a fixed CTD value, and a stochastic CTD value in Figure 6. From outcomes of Figure 6, one can confirm superior level of performance can be achieved by suggested schemes than other designed controllers.

4.2. Scenario 2 (Performance of the TRPO-Based NBC When Facing Parameters Changing (Different Patients) and Hybrid Noise)

The outcomes of the strategy employed for AABP level, under P variation across various methodologies (normal, fixed CTD, random CTD) are depicted in Figure 7. Also, the outputs of the system for three mentioned agents under drug action (${\mathsf{{\rm X}}}_{i1}$) variation are illustrated in Figure 8. As a final adaptive analysis implemented for the system, the functionality of the closed-loop AABP under reference input changing is pictured in Figure 9.

The simulation results are presented individually for distinct scenarios to illustrate the strategy’s adaptability for various patients and the effect of wireless connectivity on system efficiency. The results indicate that the established framework maintains a consistent performance in managing and mitigating the AABP rate through the modulation of SNP. Notwithstanding the influence of the CTD technique on system operations, the system demonstrates stable performance and effectively diminishes and keeps AABP within an acceptable threshold.

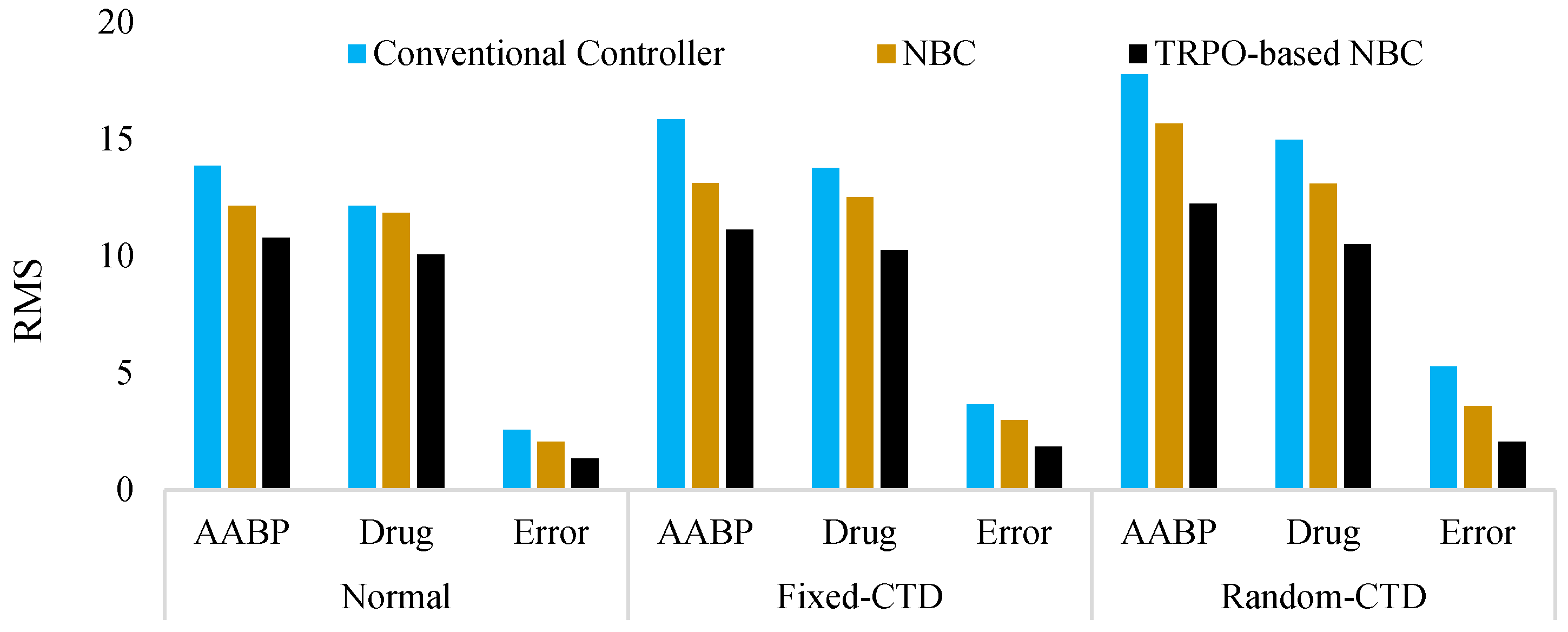
4.3. Scenario 3 (Quantitative Analysis and Comparative Assessment)

Following the demonstration of the superior efficacy of the devised strategy through visual representations, a comprehensive statistical analysis for AABP, drug infusion rate, and error was performed by incorporating various metrics for diverse scenarios and conducting comparative studies in two categories: (i) against state-of-the-art methodologies, (ii) in relation to prior research.

To achieve this objective, two specific metrics were used, namely performance criteria (PC) and root mean square (RMS), which were derived using the following expressions.

$$PC={\int }_0^{\infty }t.{agents}^2.dt$$

(36)

$$RMS=\sqrt{mean\left(Agents\right)}$$

(37)

In the interest of elucidation and to mitigate any potential ambiguity, the alternative models that were devised for the purpose of comparative analysis are delineated as follows: Controller 1: TRPO-based NBC, Controller 2: NBC, Controller 3: Conventional Controller. The PC outcomes for the various controllers under P and $X_{i1}$ variation are illustrated by the bar chart in Figure 10 and Figure 11, respectively. In the subsequent phase, the PC value for the various stages of reference changing was computed and compared across different categories, and is documented in

Table 2. PC results of the controllers under reference input changes.

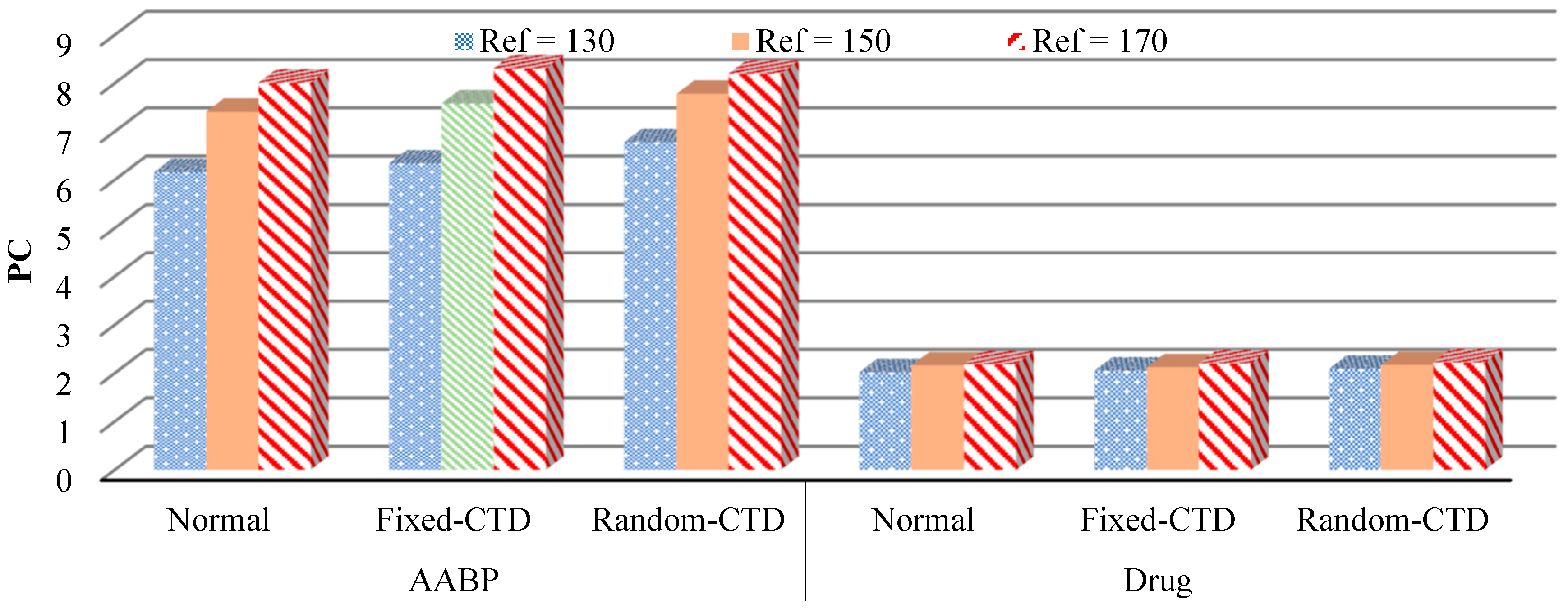
Methods	Agents	Normal			Fixed CTD			Random CTD
		130	150	170	130	150	170	130	150	170
Controller 1	AABP	6.16	7.41	8.01	6.34	7.58	8.31	6.78	7.78	8.2
	Drug	2.02	2.16	2.18	2.05	2.12	2.2	2.09	2.17	2.22
	Error	2.75	3.23	4.15	3.06	3.72	4.68	3.54	3.85	4.98
Controller 2	AABP	6.48	7.56	8.38	6.75	7.76	8.72	6.97	7.93	8.59
	Drug	2.12	2.53	2.85	2.74	2.96	3.15	3.08	3.15	3.61
	Error	3.21	3.95	4.76	3.74	4.18	5.31	4.01	4.53	5.1
Controller 3	AABP	6.89	7.83	8.98	7.12	8.36	9.24	7.58	8.65	8.93
	Drug	2.28	2.56	3.02	2.96	3.52	3.95	3.54	4.05	4.58
	Error	3.72	4.41	5.19	4.23	4.73	5.85	4.65	5.27	5.81

. Subsequently, an evaluation of the efficacy of the newly devised approach under the influence of hybrid noise characterized by a variance of 0.001 was conducted. The RMS results obtained were juxtaposed with alternative control mechanisms and are presented in Figure 12. Also, a comparison with previous studies was conducted and is presented in

Table 3. Comparison of the outcomes of the current research with prior studies.

Control Strategy		Setling Time	Over Shoot	IAE
IT2-FLC-PID-based Cuckoo Search algorithm [8]		350	0	10,450
Interval Type-2 Fuzzy Logic-based Grey Wolf Optimization (GWO) [9]		277	0	8327
Fractional Order two-layer Fuzzy Logic-based GWO [10]		274	0	8331
ADRC-based CPAG [13]		268	0	8307
2 degrees of freedom (DOF)-PI-based dragonfly optimization (DA) [45]		495	0.0951	13,124
Type-1 Fuzzy (IT2F) Logic and teaching–learning-based optimization (TLBO) algorithm [46]		319	0.63	9560
Current strategy	Normal	262	0	8135
	Fixed CTD	271	0	8319
	Random CTD	282	0	8346

as phase 2 of the comparative study. Based on the findings of the statistical and comparative analysis, it is evident that the devised approach demonstrated superior and consistent performance across diverse scenarios. Moreover, a comparison with alternative methodologies in the various aspects revealed the enhanced functionality of the proposed strategy.

As evidenced in the AABP response plot Figure 10a, both the Conventional Controller and the standalone NBC demonstrate a significant deterioration in their capacity to manage the AABP when subjected to variations in sensitivity, particularly in the context of fixed or random CTD scenarios. Their AABP responses are characterized by extended settling times and substantial deviations from the target reference value. Conversely, the TRPO-based NBC successfully preserves its operational efficiency and stability in regulating the AABP, even amidst the challenges posed by communication delays. The AABP response associated with the TRPO-based NBC consistently aligns closely with the desired reference, exhibiting minimal disruption from the fixed or random CTD conditions.

This assertion is further substantiated by the error plot Figure 10b, which reveals that the TRPO-based NBC consistently exhibits the lowest error metrics across all evaluated scenarios, including those involving CTD. In contrast, the alternative controllers encounter a significant escalation in their error measurements when exposed to communication delays.

The drug (SNP) dosage profile plot Figure 10c additionally underscores the TRPO-based NBC’s proficiency in sustaining stable and uniform drug administration, even in the context of CTD. The dosage modifications are maintained within stringent control parameters, thereby ensuring a safer and more comfortable treatment experience for the patient. In sharp contrast, the Conventional Controller and standalone NBC present more erratic and less stable drug dosage profiles under CTD conditions, which may result in suboptimal AABP regulation and raise potential concerns regarding patient safety.

The same behavior is observed from Figure 11, where the functionality of the systems is illustrated under drug action changing.

Moreover, as previously indicated, Figure 12 illustrates the operational characteristics of the controllers in the presence of external uncertainties. It is imperative to note that the system parameters are established as standard, $P=-0.25$ and ${\mathsf{{\rm X}}}_{i1}=50\mathrm{s}$. It is evident that the influence of external noise adversely affects the efficacy of the controllers; however, the proposed controller adeptly addresses these uncertainties, thereby maintaining superior functionality across all agents in comparison to alternative controllers. The RMS results, Figure 12, prove this superiority.

5. Conclusions and Forward-Looking Perspectives

The present research initiative has achieved notable advancements in tackling the critical issue of regulating AABP via the modulation of SNP for individuals suffering from BP-related complications, alongside a novel understanding of wireless connectivity in a closed-loop configuration. By employing a closed-loop platform that amalgamates nonlinear backstepping control (NBC) with Trust Region Policy Optimization (TRPO), the proposed framework exhibits a capacity for real-time dynamic updates of the control system, thereby effectively addressing both AABP and SNP dosage simultaneously. The analysis accentuates the critical role of wireless connectivity in augmenting the operational efficiency of the closed-loop system. The integration of a communication delay network facilitated a comprehensive assessment of the ramifications of wireless connectivity on the system’s performance, emphasizing its essential function in ensuring the efficacy of the proposed therapeutic methodology.

The comprehensive experimentation carried out in this investigation, which includes evaluations across a spectrum of patient demographics (varying sensitivity stages, reference inputs, and drug action) and considers hybrid noise and uncertainties with diverse strategies such as normal (without CTD approach), fixed CTD, and random CTD, further highlights the adaptability and dependability of the closed-loop platform. Moreover, the calculation of various metrics such as PC and RMS for the assorted strategies, in conjunction with a comparative analysis with contemporary controllers and prior studies, serves to exemplify the capabilities and superiority of the developed framework through statistical methodologies. These findings pave the way for more personalized and efficient therapeutic interventions for individuals who must manage BP, while concurrently enhancing the closed-loop AABP system for remote patient control. This study endeavors to bridge a knowledge gap and contribute to the scholarly discourse by offering insights that could fortify complex interdisciplinary frameworks for managing the diverse array of BP-related problems. The outcomes of this research could substantially enhance the quality of life for individuals with BP and may also have broader implications for efforts aimed at improving tailored healthcare interventions. Looking forward, the implemented system presents potential applicability to real-world data and clinical analyses, thereby allowing for an exploration of its functionality under practical circumstances.