A New Approach for Modeling Vertical Dynamics of Motorcycles Based on Graph Theory
Abstract
1. Introduction
2. Graph Theory Formulation
2.1. Method Overview
- To begin, identify the various components of your mechanical system. These may include masses, springs, dampers, rigid bodies, and other relevant elements. Once identified, assign nodes to each component within the graph.
- For each component of the system, create a node. These nodes may represent masses, joints, or other key points. Physical connections between nodes, such as springs or dampers, are represented by edges. The type of connection will determine the edge’s properties.
- Assign properties to the edges that represent physical connections between components. For springs, the edge may have a spring constant (k), while for dampers, it could have a damping coefficient (c). These properties will be used to derive equations later.
- Define a suitable coordinate system for the mechanical system. This involves selecting reference points and directions for displacement and forces. This step is crucial as it determines how the equations will be expressed.
- Assign variables to represent the displacements of nodes in the chosen coordinate system. These variables are typically functions of time (e.g., x(t), y(t), z(t)).
- For each node, apply Newton’s second law to write down the equations of motion based on the forces acting on the node. These forces can include applied forces, spring forces, and damping forces. Express these forces in terms of the node displacements and any known properties.
- Set the equations of motion to zero to find equilibrium positions. Combine the equations of motion from each node to form a system of differential equations. This system of equations will describe the dynamic behavior of the mechanical system.
- Solve these equations analytically or numerically.
- Implement the equations to study the dynamic behavior of your mechanical system.
2.2. Representation and Conception of Graph
3. Physical Modeling of Vertical Dynamics of Motorcycles
3.1. System Description
- −
- Sprung mass (): the weight of all the components of the car that rest on the suspension system (such as the chassis, engine, and transmission).
- −
- Unsprung mass (): the weight of all the components located in the wheel hub, such as the hub itself, brake disk and caliper, axle, tire, wheel rim, etc.
- −
- The suspension system comprises various components that connect the sprung mass to the unsprung mass. It plays a crucial role in ensuring both comfort and handling while driving.
3.2. Hypotheses
- −
- The moment caused by weight overturning has been ignored; no assumptions have been made regarding the height of the pitch center in relation to the ground.
- −
- The vertical dynamics of a motorcycle tire can be effectively modeled as a rigid body under certain conditions.
- −
- Tire deformations are negligible compared to its dimensions, and the tire maintains contact with the ground.
- −
- Tires are commonly known to be rigid, lacking flexibility. As a result, they do not provide much compliance.
- −
- It is assumed that the longitudinal positions of both the springs and the shock absorber are identical.
- −
- There are no aerodynamic forces being taken into consideration.
- −
- The stiffness and damping values pertain to the entire axle and are attributed to a singular spring or shock absorber.
- −
- The mass and moment of inertia are referring to the whole weight of the vehicle’s suspension system.
- −
- The vehicle’s body is considered to be a rigid body.
4. Linear Graph Representation
4.1. Graph Representation of the System
4.2. Constitutive Equations
- Rigid body element
- -
- The inertial element
- -
- The mass elements
- The rigid arm element
- Tire element
- Suspension element
- The external force element
- -
- For the translational domain:
- -
- For the rotational domain:
- Rotation matrix element
5. Motion Equations
5.1. Equation of Dynamics
- Rotational cutset equations
- Translational circuit equations
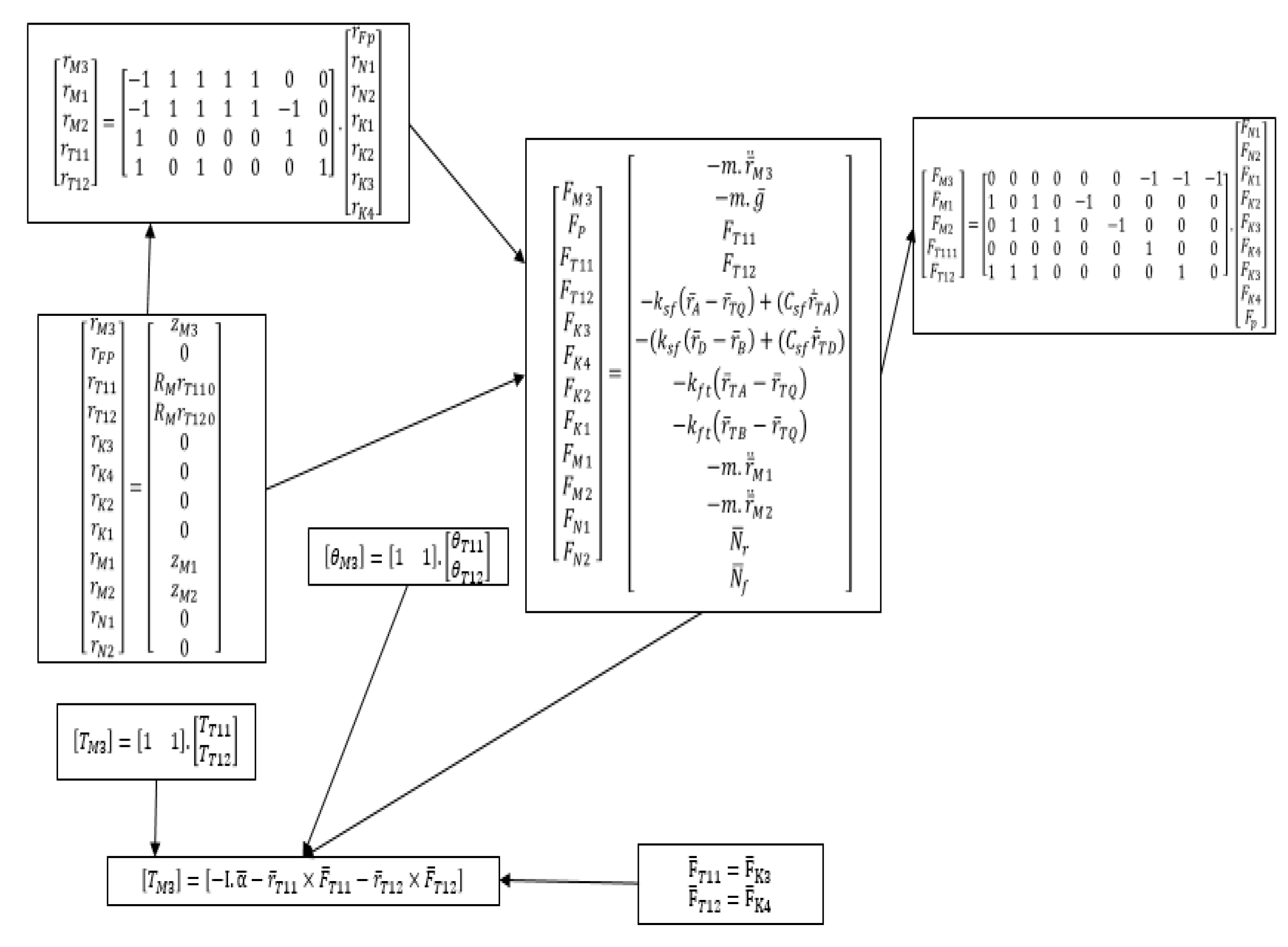
5.2. Formulation Procedure
- -
- The circuit equation
- -
- The cutset equation
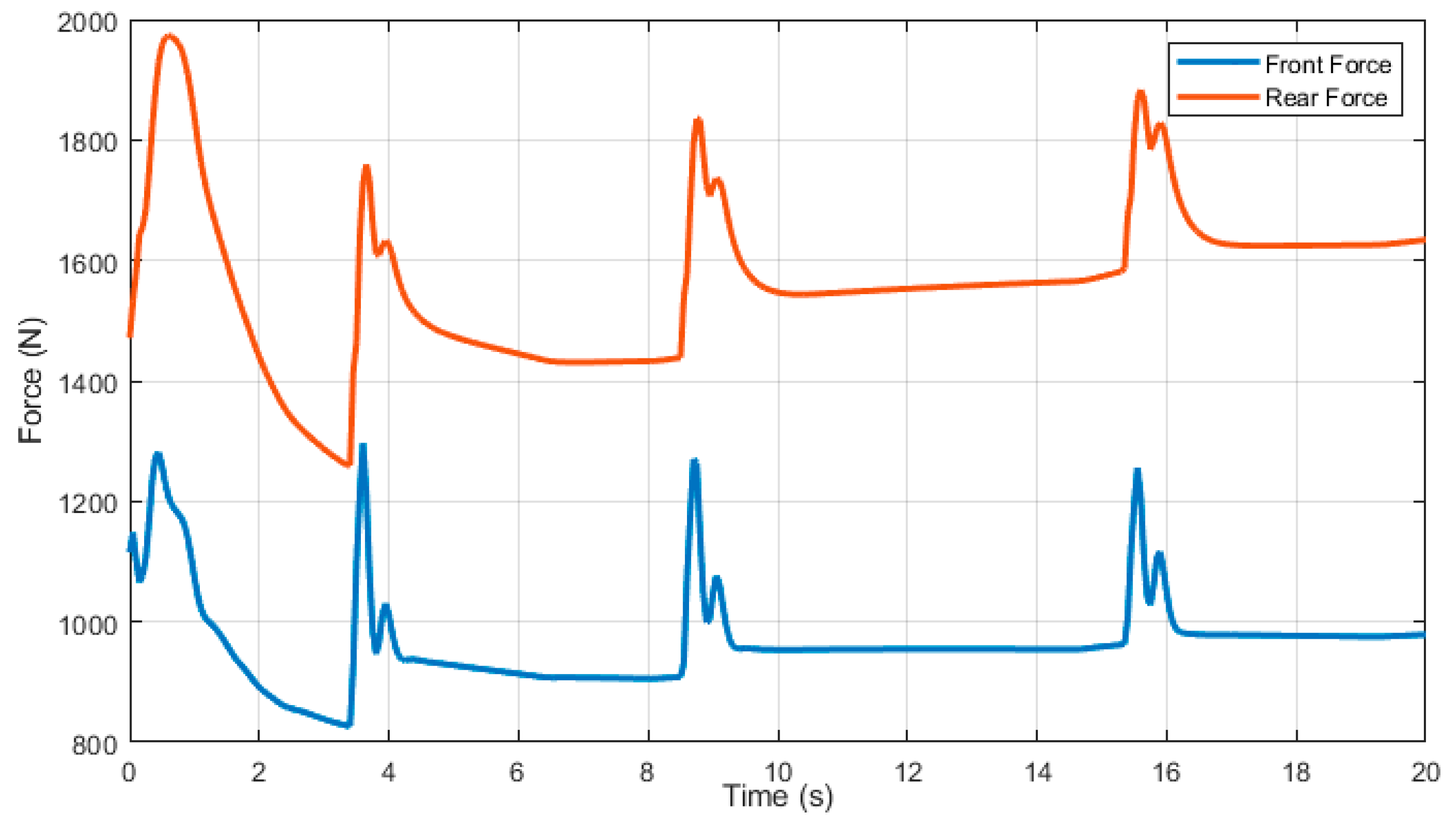
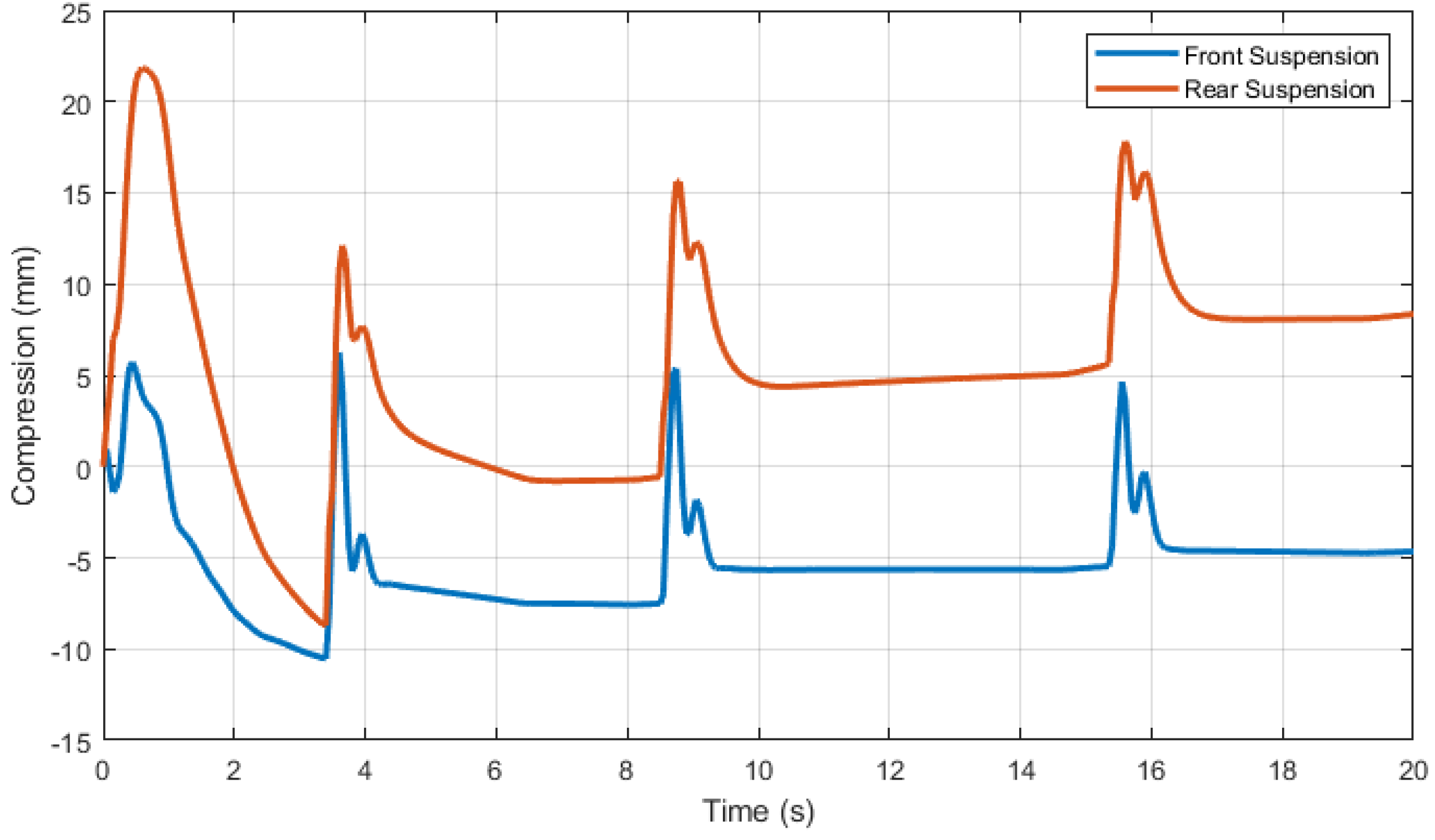
6. Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Nomenclature | Value |
|---|---|---|
| Sprung mass | 12,850 kg | |
| Moment of inertia | I | |
| Front unsprung mass | 1400 kg | |
| 700 kg | ||
| Front wheelbase | a | 1.716 m |
| rear wheelbase | b | 1.271 m |
| Rear suspension stiffness | 55,000 N/m | |
| Front suspension stiffness | 110,000 N/m | |
| Front tire stiffness | 116,000 N/m | |
| Rear tire stiffness | 232,000 N/m | |
| Front suspension damping coefficient | 640 Ns/m | |
| Rear tire suspension coefficient | 320 Ns/m |
References
- Gross, J.L.; Yellen, J. Handbook of Graph Theory; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Morency, K. Automatic Generation of Real-Time Simulation Code for Vehicle Dynamics using Linear Graph Theory and Symbolic Computing. MASc Thesis, Department of Systems Design Engineering, University of Waterloo, Waterloo, ON, Canada, 2007. [Google Scholar]
- Shi, P.; McPhee, J. Dynamics of flexible multibody systems using virtual work and linear graph theory. Multibody Syst. Dyn. 2000, 4, 355–381. [Google Scholar] [CrossRef]
- Garziad, M.; Saka, A. An Overview of the Main Topics and Applications of Graph Theoretic Problems in Multiphysics Engineering. J. Appl. Mech. Eng. 2017, 6, 284. [Google Scholar] [CrossRef]
- Bombardier, W.; McPhee, J.; Schmitke, C. Symbolic Formulation of Multibody Dynamic Equations for Wheeled Vehicle Systems on Three-Dimensional Roads. SAE Int. J. Mater. Manuf. 2010, 3, 454–467. [Google Scholar]
- Schmitke, C.; Morency, K.; McPhee, J. Using graph theory and symbolic computing to generate efficient models for multi-body vehicle dynamics. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2008, 222, 339–352. [Google Scholar] [CrossRef]
- Banerjee, J.M.; McPhee, J.J. Graph-Theoretic Modeling and Dynamic Simulation of an Automotive Torque Converter. In Proceedings of the 7th Vienna International Conference on Mathematical Modelling, Vienna, Austria, 14–17 February 2012; Troch, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Amine, B. Modélisation des Systèmes Multi-Corps Rigid Basée sur la Méthode des Réseaux Virtuels; Université Laval: Quebec City, QC, Canada, 2010. [Google Scholar]
- Schmitke, C.; McPhee, J. Using linear graph theory and the principle of orthogonality to model multibody, multi-domain systems. Adv. Eng. Inform. 2007, 22, 147–160. [Google Scholar] [CrossRef]
- Al-Hakim, L.; Kusiak, A.; Mathew, J. A graph-theoretic approach to conceptual design with functional perspectives. Comput.-Aided Des. 2000, 32, 867–875. [Google Scholar] [CrossRef]
- Vogt, H.S.; Schmitke, C.C.; Jalali, K.; McPhee, J.J. Unified modelling and real-time simulation of an electric vehicle. Int. J. Veh. Auton. Syst. 2008, 6, 288–307. [Google Scholar] [CrossRef]
- Dunlop, J.; Khajepour, A. A new multi-terminal pulley model for use in graph theoretic modelling. Mech. Mach. Theory 2000, 35, 1601–1621. [Google Scholar] [CrossRef]
- Sreeram, T.R. Graph theory based parametric influences applied to torsional vibration analysis. Adv. Eng. Softw. 2005, 36, 209–224. [Google Scholar] [CrossRef]
- McPhee, J.; Redmond, S.M. Modelling multibody systems with indirect coordinates. Comp. Methods Appl. Mech. Eng. 2006, 195, 6942–6957. [Google Scholar] [CrossRef]
- Dao, T.S.; McPhee, J. Dynamic modeling of electrochemical systems using linear graph theory. J. Power Sources 2011, 196, 10442–10454. [Google Scholar] [CrossRef]
- Zawiślak, S.; Rysiński, J. (Eds.) . Graph-Based Modelling in Engineering; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Cheng, D.; Liu, Y.; Qin, D.; Hu, M.; Wan, W.F. Analysis of the efficiency of the power coupling mechanism for tracked vehicle transmission based on the graph theory. In Power Transmissions: Proceedings of the International Conference on Power Transmissions 2016 (ICPT 2016), Chongqing, China, 27–30 October 2016; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Chen, W.K. Applied Graph Theory; Elsevier: Amsterdam, The Netherlands, 2012; Volume 13. [Google Scholar]
- Dörfler, F.; Simpson-Porco, J.W.; Bullo, F. Electrical networks and algebraic graph theory: Models, properties, and applications. Proc. IEEE 2018, 106, 977–1005. [Google Scholar] [CrossRef]
- Huang, T.; Whitehouse, D.J. The use of graph theory to formulate the linear dynamic characteristics of rigid body systems. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1997, 453, 1299–1310. [Google Scholar] [CrossRef]
- Lang, S.Y. Graph-theoretic modelling of epicyclic gear systems. Mech. Mach. Theory 2005, 40, 511–529. [Google Scholar] [CrossRef]
- Mcphee, J.J. A unified graph—Theoretic approach to formulating multibody dynamics equations in absolute or joint coordinates. J. Frankl. Inst. 1997, 334, 431–445. [Google Scholar] [CrossRef]
- Hong, K.-T.; Lang, Y.T. A Graph Theoretic Approach to CAD for the Analysis of Planar Mechanisms, pdf-file. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=b27aa95c76ecc0d2e58db84a79deaf0e5828c919 (accessed on 27 April 2024).
- Cossalter, V.; Lot, R.; Massaro, M. Motorcycle dynamics. In Modelling, Simulation and Control of Two-Wheeled Vehicles; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; pp. 1–42. [Google Scholar]
- McPhee, J.; Schmitke, C.; Redmond, S. Dynamic modelling of mechatronic multibody systems with symbolic computing and linear graph theory. Math. Comput. Model. 2004, 10, 1–23. [Google Scholar] [CrossRef]
- McPhee, J.J. Automatic generation of motion equations for planar mechanical systems using the new set of “branch coordinates”. Mech. Mach. Theory 1998, 33, 805–823. [Google Scholar] [CrossRef]
- Shahriar, A.; Rahman, K.A.; Tanvir, S. Simulation and analysis of half-car passive suspension system. Mech. Eng. Res. J. 2016, 10, 66–70. [Google Scholar]
- Garcia-Pozuelo, D.; Gauchia, A.; Olmeda, E.; Diaz, V. Bump modeling and vehicle vertical dynamics prediction. Adv. Mech. Eng. 2014, 6, 736576. [Google Scholar] [CrossRef]
- Melinte, O.D.; Dumitru, D.N. CARSIM software simulations of half-car vertical 2D dynamics and vehicle suspension behavior. In The Annual Symposium of the Institute of Solid Mechanics SISOM; Acta Technica Napocensis, Series: Applied Mathematics and Mechanics vol. 56, issue iv; November 2013; Available online: https://docplayer.net/44987274-Carsim-software-simulations-of-half-car-vertical-2d-dynamics-and-vehicle-suspension-behavior.html (accessed on 27 April 2024).



| Parameter | Nomenclature |
|---|---|
| Sprung Mass | |
| Moment of inertia of the motorcycle body | |
| Front unsprung mass | |
| Rear unsprung mass | |
| Wheelbase | p |
| Rear wheelbase | b |
| Rear and front suspension stiffness | , |
| Front and rear tire stiffness | , |
| Front and rear suspension damping coefficient | |
| Rear and front tire damping coefficient | |
| Pitch angle | |
| Rear and front vertical coordinate | |
| Rear and front vertical coordinate of unsprung mass |
| Edge | Description |
|---|---|
| , | Masses of front and rear tire |
| Rotational inertia | |
| Rigid arm (define centroidal position on a mass) | |
| , | Rear and front suspension element |
| Front and rear elastic tire | |
| Front and rear reaction force | |
| Weight force |
| Component | Terminal Equations |
|---|---|
| , | |
| , | |
| , | |
| (t) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garziad, M.; Saka, A.; Moustabchir, H.; Scutaru, M.L. A New Approach for Modeling Vertical Dynamics of Motorcycles Based on Graph Theory. Mathematics 2024, 12, 1390. https://doi.org/10.3390/math12091390
Garziad M, Saka A, Moustabchir H, Scutaru ML. A New Approach for Modeling Vertical Dynamics of Motorcycles Based on Graph Theory. Mathematics. 2024; 12(9):1390. https://doi.org/10.3390/math12091390
Chicago/Turabian StyleGarziad, Mouad, Abdelmjid Saka, Hassane Moustabchir, and Maria Luminita Scutaru. 2024. "A New Approach for Modeling Vertical Dynamics of Motorcycles Based on Graph Theory" Mathematics 12, no. 9: 1390. https://doi.org/10.3390/math12091390
APA StyleGarziad, M., Saka, A., Moustabchir, H., & Scutaru, M. L. (2024). A New Approach for Modeling Vertical Dynamics of Motorcycles Based on Graph Theory. Mathematics, 12(9), 1390. https://doi.org/10.3390/math12091390






