Practical Security of Continuous Variable Quantum Key Distribution Ascribable to Imperfect Modulator for Fiber Channel
Abstract
1. Introduction
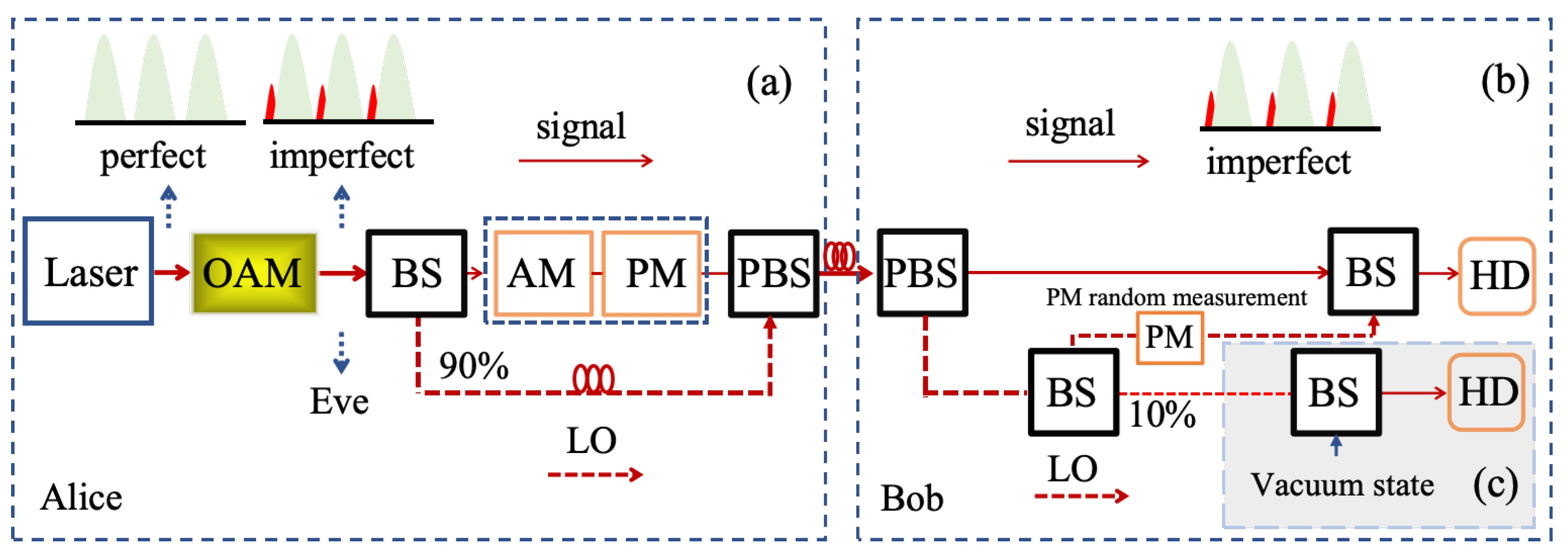
2. AM-Embedded CVQKD
3. Performance Analysis
3.1. Derivation of the Secret Key Rate
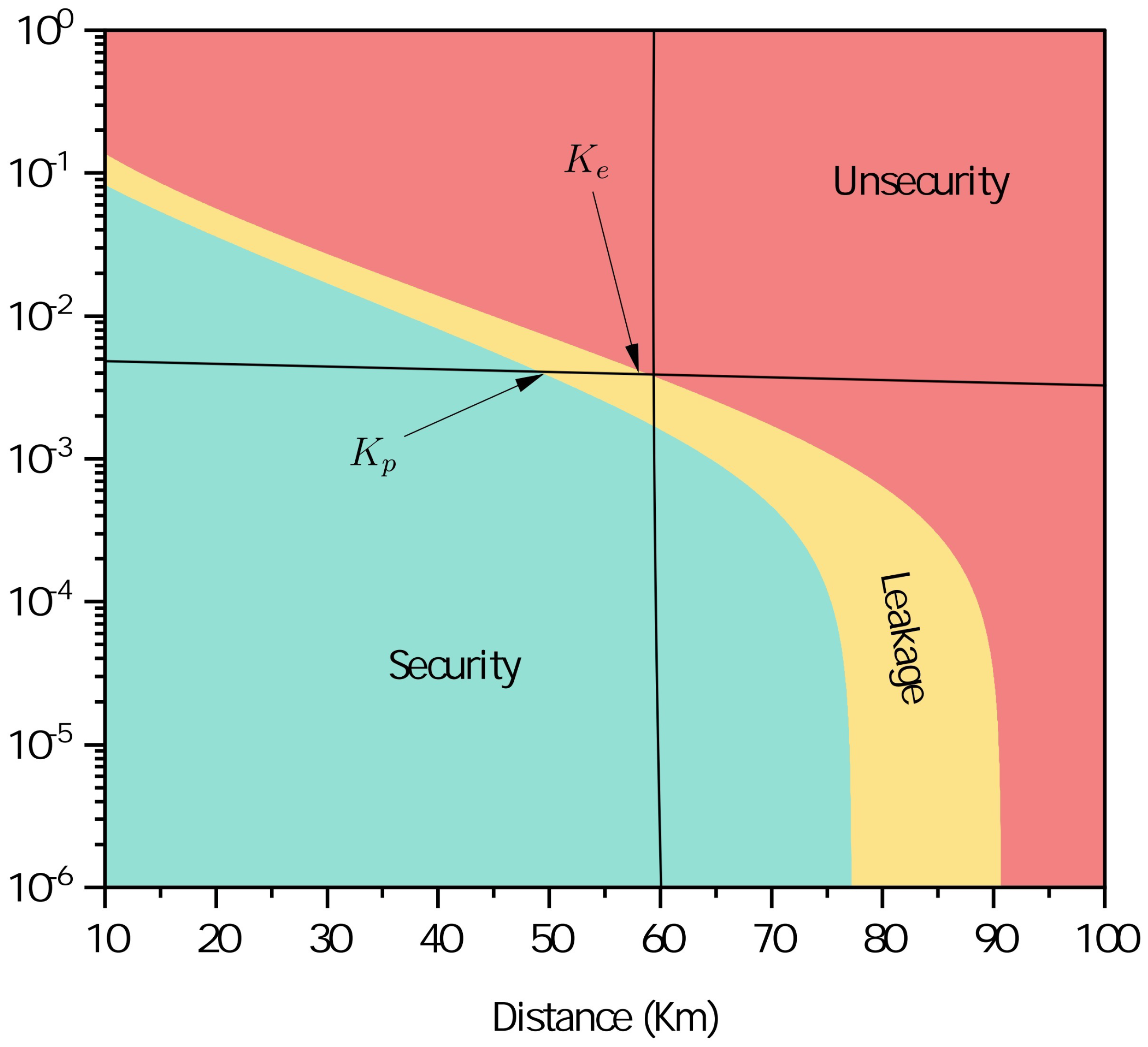
3.2. Numerical Simulations
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A.; Grangier, P.; Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photonics 2013, 7, 378–381. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Hu, L.; Al-Amri, M.; Liao, Z.; Zubairy, M.S. Continuous-variable quantum key distribution with non-Gaussian operations. Phys. Rev. A 2020, 102, 012608. [Google Scholar] [CrossRef]
- Milovančev, D.; Vokić, N.; Laudenbach, F.; Pacher, C.; Hübel, H.; Schrenk, B. High rate CV-QKD secured mobile WDM fronthaul for dense 5G radio networks. J. Light. Technol. 2021, 39, 3445–3457. [Google Scholar] [CrossRef]
- Qin, H.; Kumar, R.; Alléaume, R. Quantum hacking: Saturation attack on practical continuous-variable quantum key distribution. Phys. Rev. 2016, 94, 012325. [Google Scholar] [CrossRef]
- Ferreyrol, F.; Blandino, R.; Barbieri, M.; Tualle-Brouri, R.; Grangier, P. Experimental realization of a nondeterministic optical noiseless amplifier. Phys. Rev. 2011, 83, 063801. [Google Scholar] [CrossRef]
- Beveratos, A.; Brouri, R.; Gacoin, T.; Villing, A.; Poizat, J.-P.; Grangier, P. Single photon quantum cryptography. Phys. Rev. Lett. 2002, 89, 187901. [Google Scholar] [CrossRef] [PubMed]
- Derkach, I.; Usenko, V.C.; Filip, R. Continuous-variable quantum key distribution with a leakage from state preparation. Phys. Rev. 2017, 96, 062309. [Google Scholar] [CrossRef]
- Zheng, Y.; Huang, P.; Huang, A.; Peng, J.; Zeng, G. Security analysis of practical continuous-variable quantum key distribution systems under laser seeding attack. Opt. Express 2019, 27, 27369–27384. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.-Z.; Weedbrook, C.; Yin, Z.-Q.; Wang, S.; Li, H.-W.; Chen, W.; Guo, G.-C.; Han, Z.-F. Quantum hacking of a continuous-variable quantum-key-distribution system using a wavelength attack. Phys. Rev. A 2013, 87, 062329. [Google Scholar] [CrossRef]
- Li, H.-W.; Wang, S.; Huang, J.-Z.; Chen, W.; Yin, Z.-Q.; Li, F.-Y.; Zhou, Z.; Liu, D.; Zhang, Y.; Guo, G.-C.; et al. Attacking a practical quantum-key-distribution system with wavelength-dependent beam-splitter and multiwavelength sources. Phys. Rev. A 2011, 84, 062308. [Google Scholar] [CrossRef]
- Tan, X.; Guo, Y.; Zhang, L.; Huang, J.; Shi, J.; Huang, D. Wavelength attack on atmospheric continuous-variable quantum key distribution. Phys. Rev. A 2021, 103, 012417. [Google Scholar] [CrossRef]
- Mao, Y.; Huang, W.; Zhong, H.; Wang, Y.; Qin, H.; Guo, Y.; Huang, D. Detecting quantum attacks: A machine learning based defense strategy for practical continuous-variable quantum key distribution. New J. Phys. 2020, 22, 083073. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Zhou, Z.; Guo, Y. Practical Security of Continuous Variable Quantum Key Distribution Ascribable to Imperfect Modulator for Fiber Channel. Mathematics 2024, 12, 1356. https://doi.org/10.3390/math12091356
Xu S, Zhou Z, Guo Y. Practical Security of Continuous Variable Quantum Key Distribution Ascribable to Imperfect Modulator for Fiber Channel. Mathematics. 2024; 12(9):1356. https://doi.org/10.3390/math12091356
Chicago/Turabian StyleXu, Shengzhe, Zicheng Zhou, and Ying Guo. 2024. "Practical Security of Continuous Variable Quantum Key Distribution Ascribable to Imperfect Modulator for Fiber Channel" Mathematics 12, no. 9: 1356. https://doi.org/10.3390/math12091356
APA StyleXu, S., Zhou, Z., & Guo, Y. (2024). Practical Security of Continuous Variable Quantum Key Distribution Ascribable to Imperfect Modulator for Fiber Channel. Mathematics, 12(9), 1356. https://doi.org/10.3390/math12091356





