More Numerically Accurate Algorithm for Stiff Matrix Exponential
Abstract
1. Introduction and Related Work
2. The L-EXPM Algorithm
2.1. Algorithm
| Algorithm 1 L-EXPM |
|
2.2. Proof of Soundness and Completeness
3. Numerical Algorithm Evaluation
3.1. Artificial Stiff Matrices Analysis
- Matrices for which the difference between the eigenvalues of the matrix is small but not negligible: we randomly pick a value () and an amplitude () and generate matrices with eigenvalues that are in the range ().
- Matrices for which the eigenvalues are approaching 0: we generate matrices with eigenvalues that satisfy the following formula: .
- Matrices with large diameters: we generate matrices with eigenvalues that satisfy the formula, where a and b are picked randomly such that .
- Matrices that have a large condition number: we generate matrices with eigenvalues that satisfy the formula , such that .
- Matrices that have eigenvalues with significant algebraic multiplicity: we generate matrices with eigenvalues with an algebraic multiplicity of at least two.
- Matrices with a single eigenvalue: we generate matrices with a single eigenvalue picked at random.
- Matrices with complex eigenvalues with a large imaginary part: we generate matrices with eigenvalues that satisfy the formula , where is a random number.
3.2. Control System’s Observability Use Case
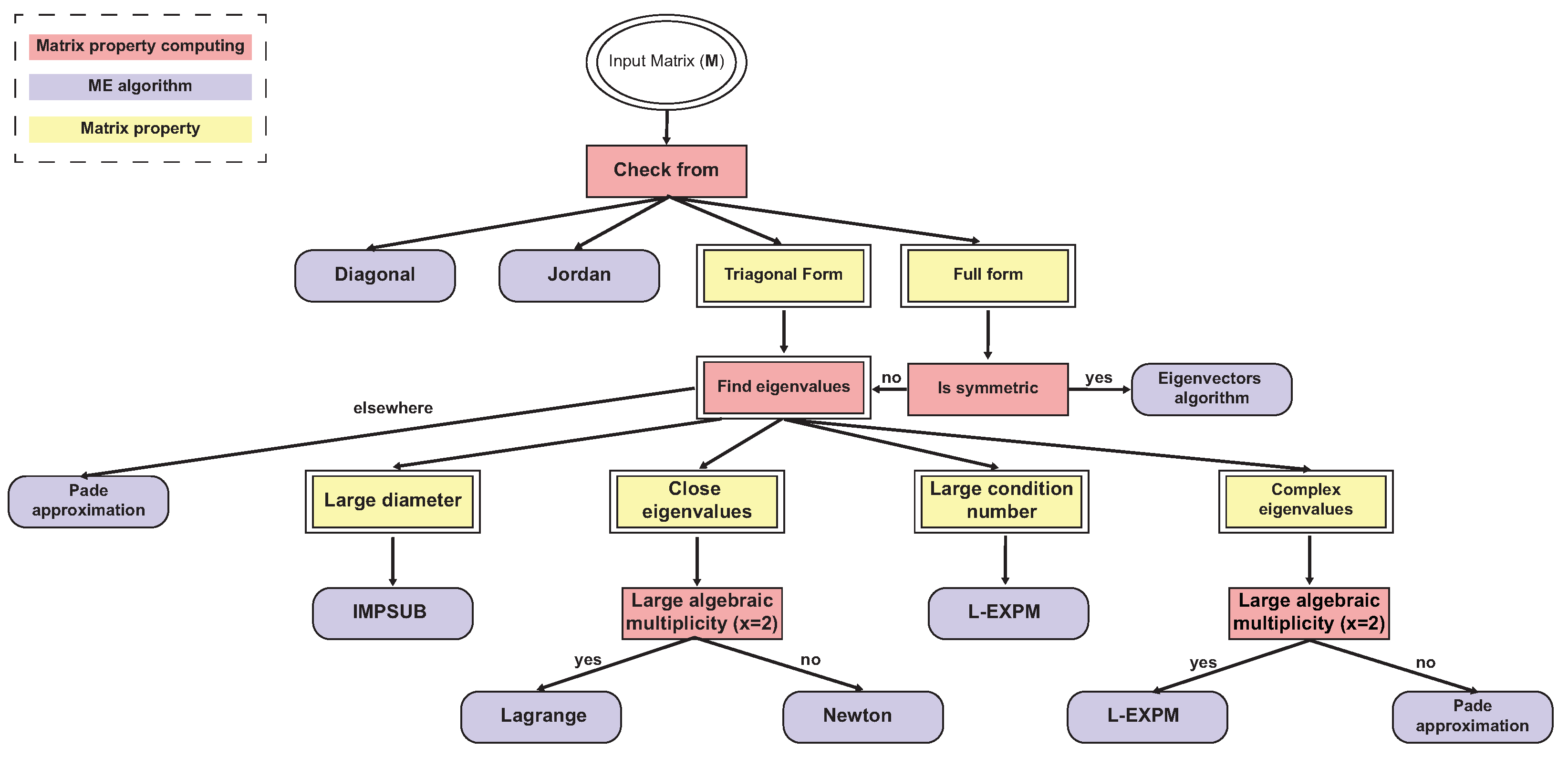
4. Matrix Exponential Decision Tree
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dunn, S.M.; Constantinides, A.; Moghe, P.V. Chapter 7—Dynamic Systems: Ordinary Differential Equations. In Numerical Methods in Biomedical Engineering; Academic Press: Cambridge, MA, USA, 2006; pp. 209–287. [Google Scholar]
- Van Loan, C. Computing integrals involving the matrix exponential. IEEE Trans. Autom. Control 1978, 23, 395–404. [Google Scholar] [CrossRef]
- Al-Mohy, A.H.; Higham, N.J. Computing the Action of the Matrix Exponential, with an Application to Exponential Integrators. SIAM J. Sci. Comput. 2011, 33, 488–511. [Google Scholar] [CrossRef]
- Aboanber, A.E.; Nahla, A.A.; El-Mhlawy, A.M.; Maher, O. An efficient exponential representation for solving the two-energy group point telegraph kinetics model. Ann. Nucl. Energy 2022, 166, 108698. [Google Scholar] [CrossRef]
- Damgaard, P.; Hansen, E.; Plante, L.; Vanhove, P. Classical observables from the exponential representation of the gravitational S-matrix. J. High Energy Phys. 2023, 2023, 183. [Google Scholar] [CrossRef]
- Datta, B.N. Chapter 5—Linear State-Space Models and Solutions of the State Equations. In Numerical Methods for Linear Control Systems: Design and Analysis; Academic Press: Cambridge, MA, USA, 2004; pp. 107–157. [Google Scholar]
- Fadali, M.S.; Visioli, A. State–space representation. In Digital Control Engineering: Analysis and Design; Academic Press: Cambridge, MA, USA, 2020; pp. 253–318. [Google Scholar]
- Moler, C.; Van Loan, C. Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later. SIAM Rev. 2003, 45, 3–49. [Google Scholar] [CrossRef]
- Ward, R.C. Numerical Computation of the Matrix Exponential with Accuracy Estimate. SIAM J. Numer. Anal. 1977, 14, 600–610. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, Z.; Chen, Y.; Xu, J.; Li, R. Benchmark Buckling Solutions of Truncated Conical Shells by Multiplicative Perturbation With Precise Matrix Exponential Computation. J. Appl. Mech. 2022, 89, 081004. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, Y.; Yang, G.; Guo, H. Two-Dimensional Exponential Sparse Discriminant Local Preserving Projections. Mathematics 2023, 11, 1722. [Google Scholar] [CrossRef]
- Najfeld, I.; Havel, T. Derivatives of the Matrix Exponential and Their Computation. Adv. Appl. Math. 1995, 16, 321–375. [Google Scholar] [CrossRef]
- Genocchi, A.; Peano, G. Calcolo Differenziale e Principii di Calcolo Integrale; Fratelli Bocca: Rome, Italy, 1884; Volume 67, pp. XVII–XIX. (In Italian) [Google Scholar]
- Biswas, B.N.; Chatterjee, S.; Mukherjee, S.P.; Pal, S. A Discussion on Euler Method: A Review. Electron. J. Math. Anal. Appl. 2013, 1, 294–317. [Google Scholar]
- Hochbruck, M.; Ostermann, A. Exponential Integrators; Cambridge University Press: Cambridge, UK, 2010; pp. 209–286. [Google Scholar]
- Butcher, J. A history of Runge-Kutta methods. Appl. Numer. Math. 1996, 20, 247–260. [Google Scholar] [CrossRef]
- Wang, H. The Krylov Subspace Methods for the Computation of Matrix Exponentials. Ph.D. Thesis, University of Kentucky, Lexington, KY, USA, 2015. [Google Scholar]
- Dinh, K.N.; Sidje, R.B. Analysis of inexact Krylov subspace methods for approximating the matrix exponential. Math. Comput. Simul. 2017, 1038, 1–13. [Google Scholar] [CrossRef]
- Druskin, V.; Greenbaum, A.; Knizhnerman, L. Using nonorthogonal Lanczos vectors in the computation of matrix functions. SIAM J. Sci. Comput. 1998, 19, 38–54. [Google Scholar] [CrossRef]
- Druskin, V.L.; Knizhnerman, L.A. Krylov subspace approximations of eigenpairs and matrix functions in exact and computer arithemetic. Numer. Linear Algebra Appl. 1995, 2, 205–217. [Google Scholar] [CrossRef]
- Ye, Q. Error bounds for the Lanczos methods for approximating matrix exponentials. SIAM J. Numer. Anal. 2013, 51, 66–87. [Google Scholar] [CrossRef][Green Version]
- Pulungan, R.; Hermanns, H. Transient Analysis of CTMCs: Uniformization or Matrix Exponential. Int. J. Comput. Sci. 2018, 45, 267–274. [Google Scholar]
- Reibman, A.; Trivedi, K. Numerical transient analysis of markov models. Comput. Oper. Res. 1988, 15, 19–36. [Google Scholar] [CrossRef]
- Wu, W.; Li, P.; Fu, X.; Wang, Z.; Wu, J.; Wang, C. GPU-based power converter transient simulation with matrix exponential integration and memory management. Int. J. Electr. Power Energy Syst. 2020, 122, 106186. [Google Scholar] [CrossRef]
- Dogan, O.; Yang, Y.; Taspınar, S. Information criteria for matrix exponential spatial specifications. Spat. Stat. 2023, 57, 100776. [Google Scholar] [CrossRef]
- Wahln, E. Alternative Proof of Putzer’s Algorithm. 2013. Available online: http://www.ctr.maths.lu.se/media11/MATM14/2013vt2013/putzer.pdf (accessed on 17 February 2021).
- Lanczos, C. An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. J. Res. Natl. Bur. Stand. 1950, 45, 225–282. [Google Scholar] [CrossRef]
- Ojalvo, I.U.; Newman, M. Vibration modes of large structures by an automatic matrix-reduction methods. AIAA J. 1970, 8, 1234–1239. [Google Scholar] [CrossRef]
- Barnard, S.T.; Simon, H.D. Fast multilevel implementation of recursive spectral bisection for partitioning unstructured problems. Concurr. Comput. Pract. Exp. 1994, 6, 101–117. [Google Scholar] [CrossRef]
- Liu, R.; Liu, E.; Yang, J.; Li, M.; Wang, F. Optimizing the Hyper-parameters for SVM by Combining Evolution Strategies with a Grid Search. In Intelligent Control and Automation; Springer: Berlin/Heidelberg, Germany, 2006; Volume 344. [Google Scholar]
- Al-mohy, A.H.; Higham, N.J. A New Scaling and Squaring Algorithm for the Matrix Exponential. SIAM J. Matrix Anal. Appl. 2009, 31, 970–989. [Google Scholar] [CrossRef]
- Higham, N.J. The Scaling and Squaring Method for the Matrix Exponential Revisited. SIAM J. Matrix Anal. Appl. 2005, 26, 1179–1193. [Google Scholar] [CrossRef]
- Demmel, J.; Dumitriu, I.; Holtz, O.; Kleinberg, R. Fast matrix multiplication is stable. Numer. Math. 2007, 106, 199–224. [Google Scholar] [CrossRef]
- Poulsen, N.K. The Matrix Exponential, Dynamic Systems and Control; DTU Compute: Kongens Lyngby, Denmark, 2004. [Google Scholar]
- Kailath, T. Linear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 1980. [Google Scholar]
- Farman, M.; Saleem, M.U.; Tabassum, M.F.; Ahmad, A.; Ahmad, M.O. A linear control of composite model for glucose insulin glucagon pump. Ain Shams Eng. J. 2019, 10, 867–872. [Google Scholar] [CrossRef]
- Swain, P.H.; Hauska, H. The decision tree classifier: Design and potential. IEEE Trans. Geosci. Electron. 1977, 15, 142–147. [Google Scholar] [CrossRef]
- Stiglic, G.; Kocbek, S.; Pernek, I.; Kokol, P. Comprehensive Decision Tree Models in Bioinformatics. PLoS ONE 2012, 7, e33812. [Google Scholar] [CrossRef] [PubMed]
- Kohavi, R. A Study of Cross Validation and Bootstrap for Accuracy Estimation and Model Select. In Proceedings of the International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995. [Google Scholar]
- Lu, Y.Y. Exponentials of symmetric matrices through tridiagonal reductions. Linear Algerba Its Appl. 1998, 279, 317–324. [Google Scholar] [CrossRef]
- Koza, J.R.; Poli, R. Genetic Programming. In Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques; Springer: New York, NY, USA, 2005; pp. 127–164. [Google Scholar]
- Alexi, A.; Lazebnik, T.; Shami, L. Microfounded Tax Revenue Forecast Model with Heterogeneous Population and Genetic Algorithm Approach. Comput. Econ. 2023. [Google Scholar] [CrossRef]
- Grabmeier, J.L.; Lambe, L.A. Decision trees for binary classification variables grow equally with the Gini impurity measure and Pearson’s chi-square test. Int. J. Bus. Intell. Data Min. 2007, 2, 213–226. [Google Scholar] [CrossRef]
- Lazebnik, T.; Bahouth, Z.; Bunimovich-Mendrazitsky, S.; Halachmi, S. Predicting acute kidney injury following open partial nephrectomy treatment using SAT-pruned explainable machine learning model. BMC Med. Inform. Decis. Mak. 2022, 22, 133. [Google Scholar] [CrossRef] [PubMed]
- Moore, E.F. The shortest path through a maze. In Proceedings of the International Symposium on the Theory of Switching; Harvard University Press: Cambridge, MA, USA, 1959; pp. 285–292. [Google Scholar]

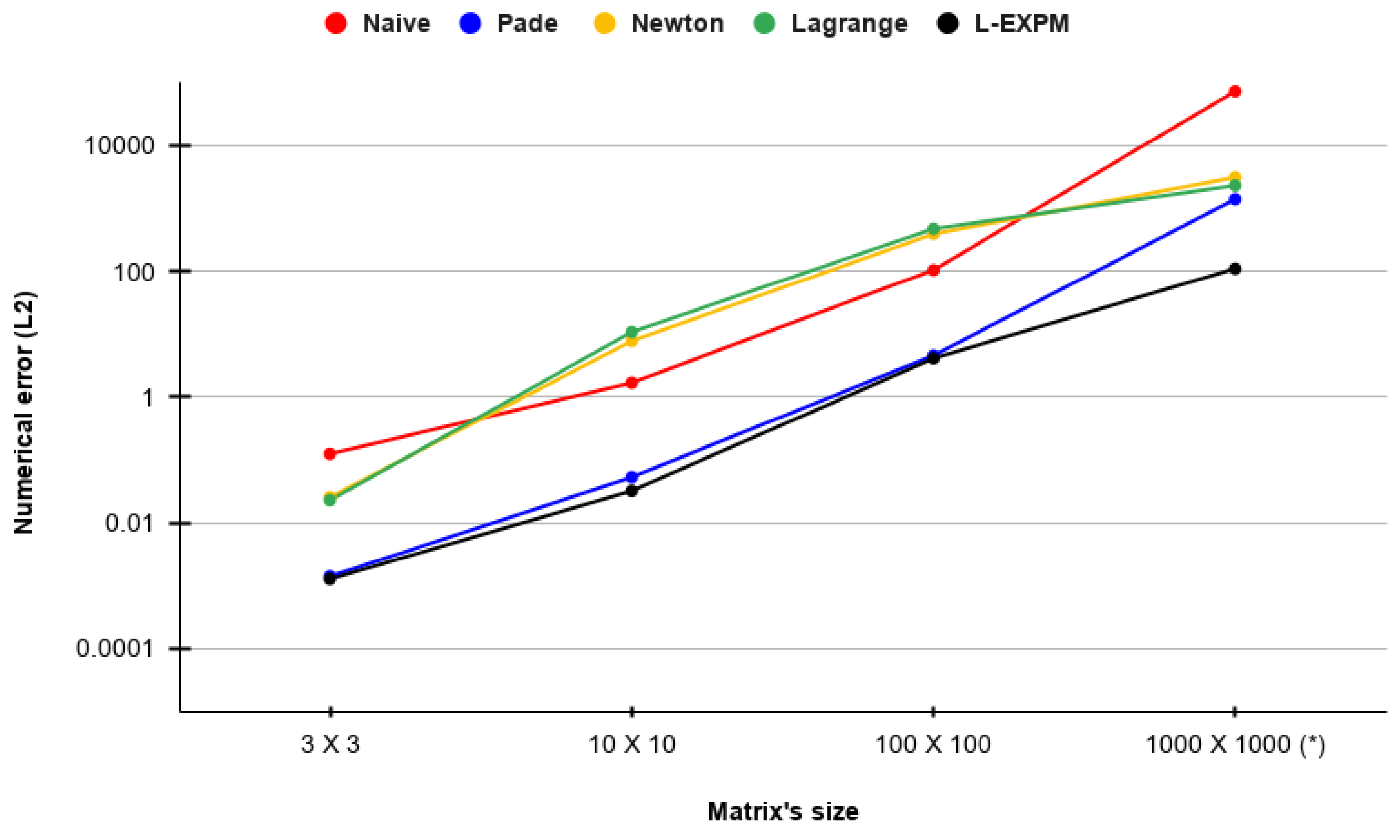
| Matrix Size | Algorithm | Type 1 | Type 2 | Type 3 | Type 4 | Type 5 | Type 6 | Type 7 |
|---|---|---|---|---|---|---|---|---|
| Naive | ||||||||
| Pade | ||||||||
| Newton | ||||||||
| Lagrange | ||||||||
| L-EXPM | ||||||||
| Naive | ||||||||
| Pade | ||||||||
| Newton | ||||||||
| Lagrange | ||||||||
| L-EXPM | ||||||||
| Naive | ||||||||
| Pade | ||||||||
| Newton | ||||||||
| Lagrange | ||||||||
| L-EXPM | ||||||||
| Naive | Err | Err | Err | Err | ||||
| Pade | Err | Err | ||||||
| Newton | Err | Err | Err | Err | ||||
| Lagrange | Err | Err | Err | Err | ||||
| L-EXPM | Err | Err |
| Algorithm | Metric | 3 × 3 | 10 × 10 | 100 × 100 | 1000 × 1000 |
|---|---|---|---|---|---|
| Pade | Error | ||||
| Time | |||||
| L-EXPM | Error | ||||
| Time |
| Index | Component | Description | Worst Case Complexity | Average Relative Numerical Error | Is Leaf Node |
|---|---|---|---|---|---|
| 1 | Check form | The matrix is diagonal, trigonal, Jordan, or full | 0 | No | |
| 2 | Is symmetric | The matrix is symmetric or not | 0 | No | |
| 3 | Large diameter | The diameter of the matrix is larger than some threshold or not | 0 | No | |
| 4 | Large algebraic multiplicity | There are eigenvalues with algebraic multiplicity that are larger than some threshold or not | 0 | No | |
| 5 | Large condition number | The condition number of the matrix is larger than some threshold x or not | 0 | No | |
| 6 | Single eigenvalue | Does the matrix have a single eigenvalue | 0 | No | |
| 7 | Complex eigenvalues | Eigenvalues are complex with a big imaginary part | 0 | No | |
| 8 | Close eigenvalues | Eigenvalues such that | 0 | No | |
| 9 | Diagonal | Diagonal matrix exponential | 0.13 | Yes | |
| 10 | Jordan | Jordan matrix exponential | 21.21 | Yes | |
| 11 | Eigenvector algorithms | TRED2 [40] and TQL2 [8] | 18.89 | Yes | |
| 12 | Ill condition algorithms | IMPSUB [8] | 47.05 | Yes | |
| 13 | L-EXPM | The proposed L-EXPM algorithm | 8.45 | Yes | |
| 14 | Eigenvalue-based approximation | Lagrange algorithm [8] | 54.98 | Yes | |
| 15 | Different eigenvalue approximation | Newton algorithm [8] | 52.73 | Yes | |
| 16 | Power series approximation | Pade approximation algorithm [8] | 11.09 | Yes | |
| 17 | Naive | Naive algorithm | 78.20 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lazebnik, T.; Bunimovich-Mendrazitsky, S. More Numerically Accurate Algorithm for Stiff Matrix Exponential. Mathematics 2024, 12, 1151. https://doi.org/10.3390/math12081151
Lazebnik T, Bunimovich-Mendrazitsky S. More Numerically Accurate Algorithm for Stiff Matrix Exponential. Mathematics. 2024; 12(8):1151. https://doi.org/10.3390/math12081151
Chicago/Turabian StyleLazebnik, Teddy, and Svetlana Bunimovich-Mendrazitsky. 2024. "More Numerically Accurate Algorithm for Stiff Matrix Exponential" Mathematics 12, no. 8: 1151. https://doi.org/10.3390/math12081151
APA StyleLazebnik, T., & Bunimovich-Mendrazitsky, S. (2024). More Numerically Accurate Algorithm for Stiff Matrix Exponential. Mathematics, 12(8), 1151. https://doi.org/10.3390/math12081151







