Optimal Control Applied to Piecewise-Fractional Ebola Model
Abstract
1. Introduction
2. The Fractional Order Model
3. Fractional Optimal Control of the Model
4. Main Results
4.1. Parameter Estimation
| Parameter | Value | Description | Source |
|---|---|---|---|
| 0.03537 | Density-independent part of the birth rate for individuals. | [13] | |
| – | Density-dependent part of the birth rate for individuals. | ||
| 0.14 | Contact rate of infective individuals and susceptible. | [4] | |
| 0.29 | Contact rate of infective individuals and hospitalized. | [4] | |
| 0.40 | Contact rate of infective individuals and dead. | [4] | |
| – | Contact rate of infective individuals and asymptomatic. | ||
| 1/11.4 | Per capita rate at which exposed individuals become infectious. | [4] | |
| 1/10 | Per capita rate of progression of individuals from the infectious class to the asymptomatic class. | [4] | |
| 1/5 | Per capita rate of progression of individuals from the hospitalized class to the asymptomatic class. | [4] | |
| 1/30 | Per capita recovery rate of individuals from the asymptomatic class to the complete recovered class. | [4] | |
| 1/9.6 | Fatality rate. | [4] | |
| 0.2 | Per capita rate of progression of individuals from the infectious class to the hospitalized class. | [4] | |
| incineration rate | [4] | ||
| 0.5 | Per capita rate of progression of individuals from the dead class to the buried class. | [4] | |
| 1/4.6 | Per capita rate of progression of individuals from the hospitalized class to the buried class. | [4] | |
| Density independent part of the death rate for individuals. | [13] | ||
| – | Density dependent part of the death rate for individuals. |
| 31,329 | 3295 | 663 | 1923 | 134 | 295 | 9378 | 2013 |

| RMSD | ||||
|---|---|---|---|---|
| 306.69 | 306.476 | |||
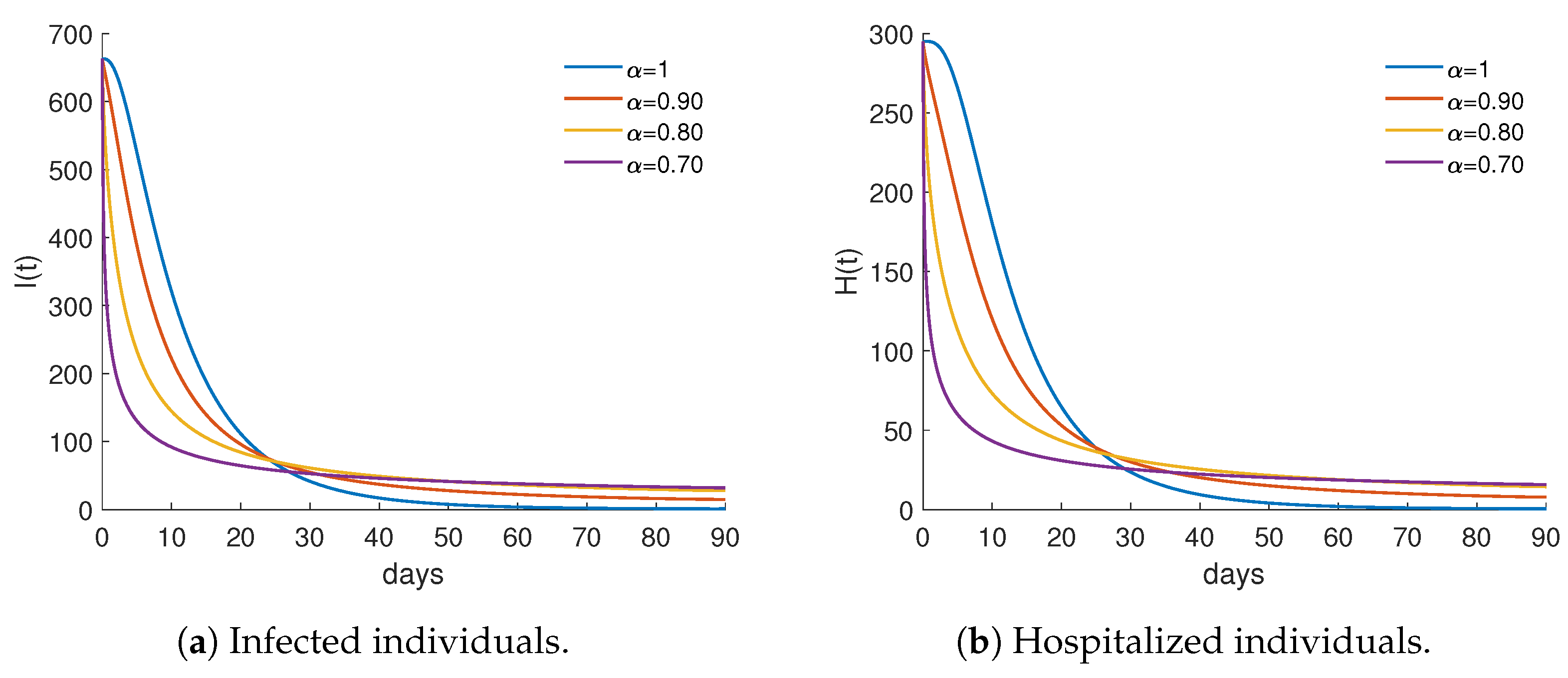
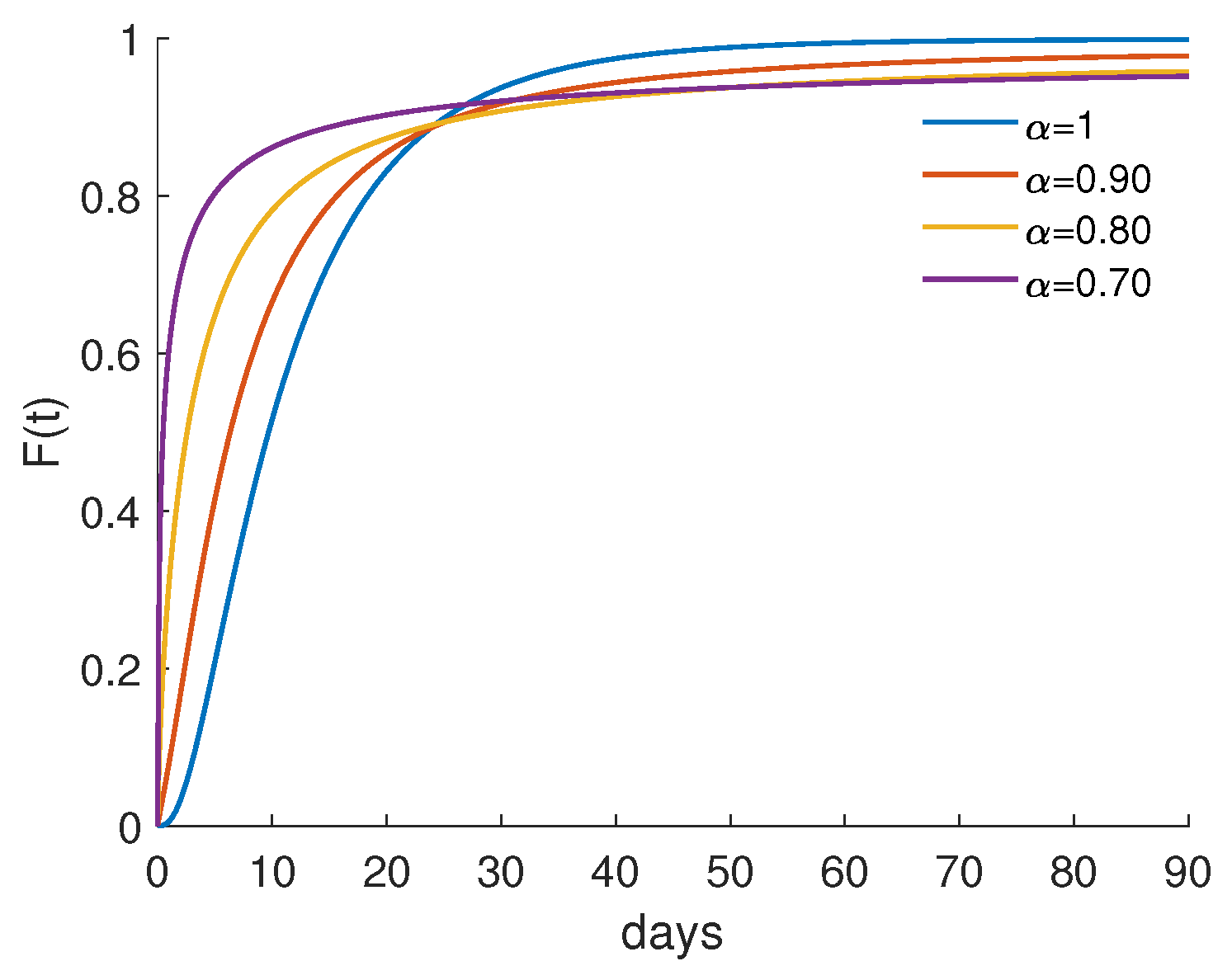
4.2. Numerical Results and Cost-Effectiveness Analysis for the Fractional Optimal Control Problem
| 1.0 | 51,324.6 | 140,210 | 2.73183 | 0.860142 |
| 0.90 | 51,845.6 | 105,735 | 2.03943 | 0.868873 |
| 0.80 | 52,826.6 | 83,674.3 | 1.58394 | 0.885313 |
| 0.70 | 54,376.8 | 50,182.6 | 0.92287 | 0.911292 |
4.3. Piecewise Derivative with Fractional Caputo Derivatives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Ebola Virus Disease. Available online: https://www.who.int/news-room/fact-sheets/detail/ebola-virus-disease (accessed on 6 February 2024).
- Wikipedia. Ebola. Available online: https://en.wikipedia.org/wiki/Ebola (accessed on 16 March 2024).
- Kaufman, J.S.B.; Jones, A. Ebola Virus Disease. Available online: https://wiki.eclipse.org/Ebola_Models (accessed on 21 March 2024).
- Area, I.; Ndaïrou, F.; Nieto, J.J.; Silva, C.J.; Torres, D.F.M. Ebola model and optimal control with vaccination constraints. J. Ind. Manag. Optim. 2018, 14, 427–446. [Google Scholar] [CrossRef]
- Siettos, C.; Anastassopoulou, C.; Russo, L.; Grigoras, C.; Mylonakis, E. Modeling the 2014 ebola virus epidemic–agent-based simulations, temporal analysis and future predictions for liberia and sierra leone. PLoS Curr. 2015, 7. [Google Scholar] [CrossRef]
- Webb, G.; Browne, C.; Huo, X.; Seydi, O.; Seydi, M.; Magal, P. A model of the 2014 Ebola epidemic in West Africa with contact tracing. PLoS Curr. 2015, 7. [Google Scholar] [CrossRef] [PubMed]
- Djiomba Njankou, S.D.; Nyabadza, F. Modelling the Role of Human Behaviour in Ebola Virus Disease (EVD) Transmission Dynamics. Comput. Math. Methods Med. 2022, 2022, 4150043. [Google Scholar] [CrossRef] [PubMed]
- Berge, T.; Lubuma, J.M.S.; Moremedi, G.M.; Morris, N.; Kondera-Shava, R. A simple mathematical model for Ebola in Africa. J. Biol. Dyn. 2017, 11, 42–74. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Wang, K.; Li, C.; Hong, G.; Zhang, X.; Shan, M.; Li, H.; Wang, J. Mathematical models for devising the optimal Ebola virus disease eradication. J. Transl. Med. 2017, 15, 124. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Mhlanga, A. Assessing the impact of optimal health education programs on the control of zoonotic diseases. Comput. Math. Methods Med. 2020, 2020, 6584323. [Google Scholar] [CrossRef] [PubMed]
- Area, I.; Batarfi, H.; Losada, J.; Nieto, J.J.; Shammakh, W.; Torres, A. On a fractional order Ebola epidemic model. Adv. Differ. Equ. 2015, 2015, 278. [Google Scholar] [CrossRef]
- Rachah, A.; Torres, D.F.M. Dynamics and optimal control of Ebola transmission. Math. Comput. Sci. 2016, 10, 331–342. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Khalighi, M.; Lahti, L. Ebola epidemic model with dynamic population and memory. Chaos Solitons Fractals 2023, 170, 113361. [Google Scholar] [CrossRef]
- Rosa, S.; Torres, D.F.M. Optimal control of a fractional order epidemic model with application to human respiratory syncytial virus infection. Chaos Solitons Fractals 2018, 117, 142–149. [Google Scholar] [CrossRef]
- Almeida, R. Analysis of a fractional SEIR model with treatment. Appl. Math. Lett. 2018, 84, 56–62. [Google Scholar] [CrossRef]
- Carvalho, A.R.M.; Pinto, C.M.A. Immune response in HIV epidemics for distinct transmission rates and for saturated CTL response. Math. Model. Nat. Phenom. 2019, 14, 307. [Google Scholar] [CrossRef]
- Bergounioux, M.; Bourdin, L. Pontryagin maximum principle for general Caputo fractional optimal control problems with Bolza cost and terminal constraints. ESAIM Control Optim. Calc. Var. 2020, 26, 35. [Google Scholar] [CrossRef]
- Almeida, R.; Pooseh, S.; Torres, D.F.M. Computational Methods in the Fractional Calculus of Variations; Imperial College Press: London, UK, 2015; pp. xii+266. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D.; Luchko, Y. Algorithms for the fractional calculus: A selection of numerical methods. Comput. Methods Appl. Mech. Eng. 2005, 194, 743–773. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman & Hall/CRC Mathematical and Computational Biology Series; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007; pp. xii+261. [Google Scholar]
- Rodrigues, P.; Silva, C.J.; Torres, D.F. Cost-effectiveness analysis of optimal control measures for tuberculosis. Bull. Math. Biol. 2014, 76, 2627–2645. [Google Scholar] [CrossRef] [PubMed]
- Okosun, K.O.; Rachid, O.; Marcus, N. Optimal control strategies and cost-effectiveness analysis of a malaria model. BioSystems 2013, 111, 83–101. [Google Scholar] [CrossRef] [PubMed]
- Atangana, A.; İğret Araz, S. New concept in calculus: Piecewise differential and integral operators. Chaos Solitons Fractals 2021, 145, 110638. [Google Scholar] [CrossRef]
- Rosa, S.; Torres, D.F.M. Fractional-Order Modelling and Optimal Control of Cholera Transmission. Fractal Fract. 2021, 5, 261. [Google Scholar] [CrossRef]

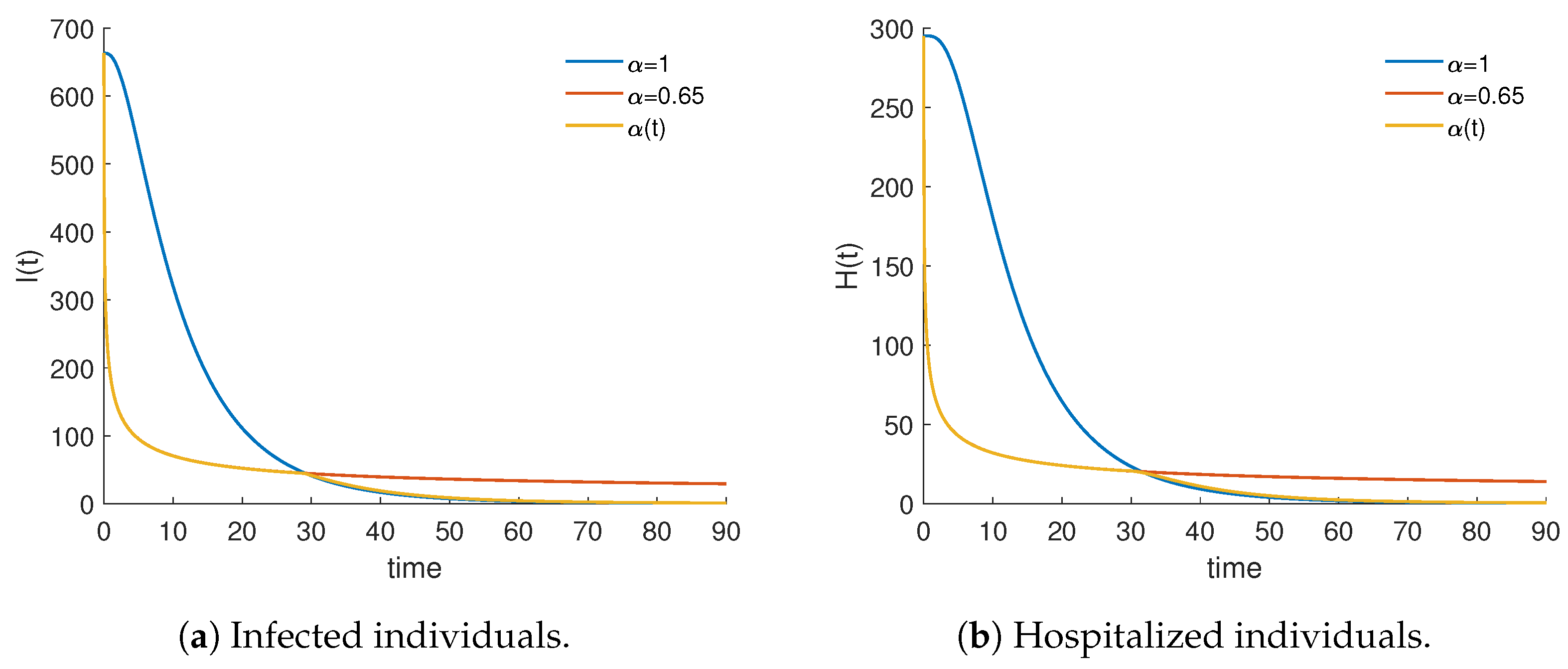
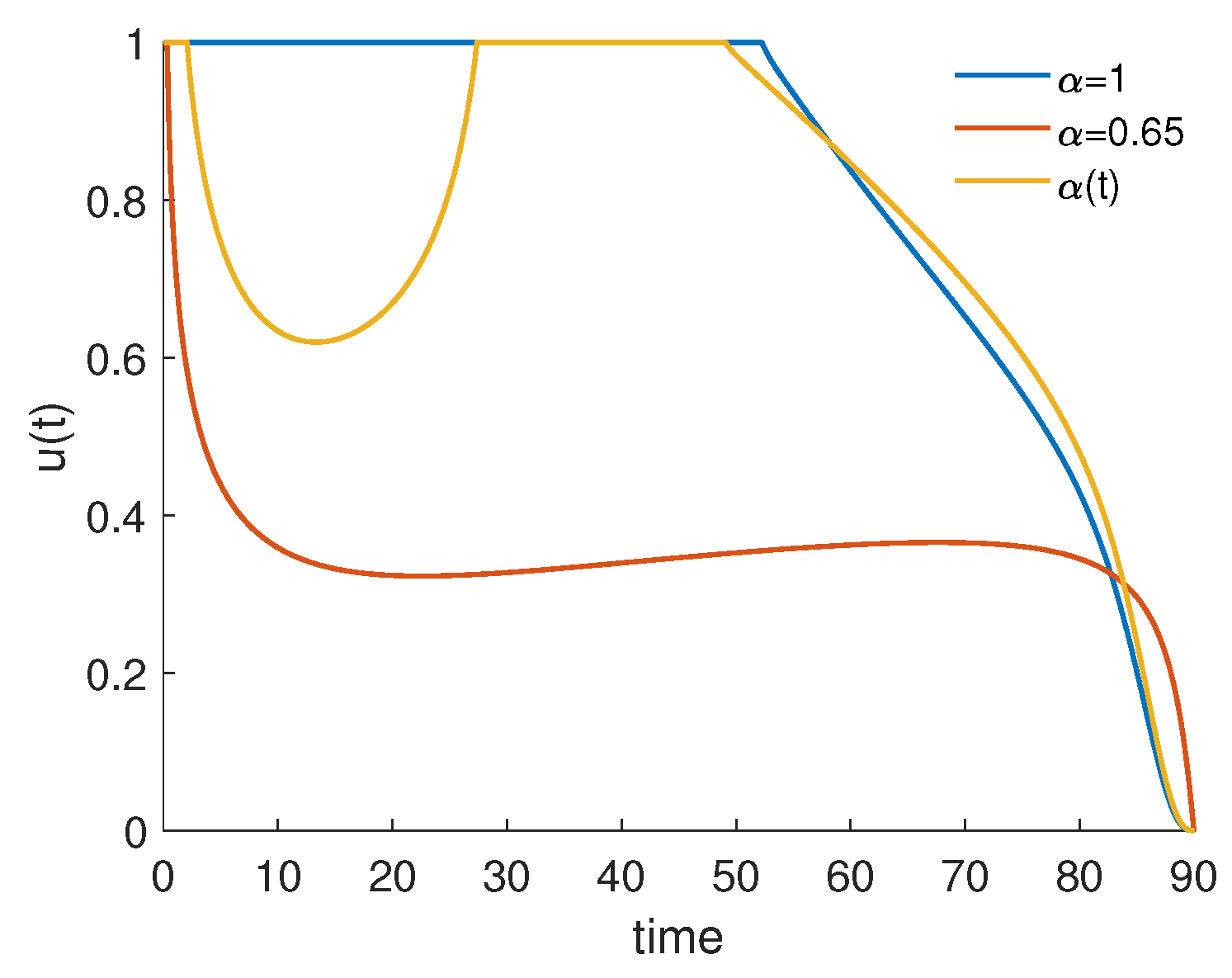
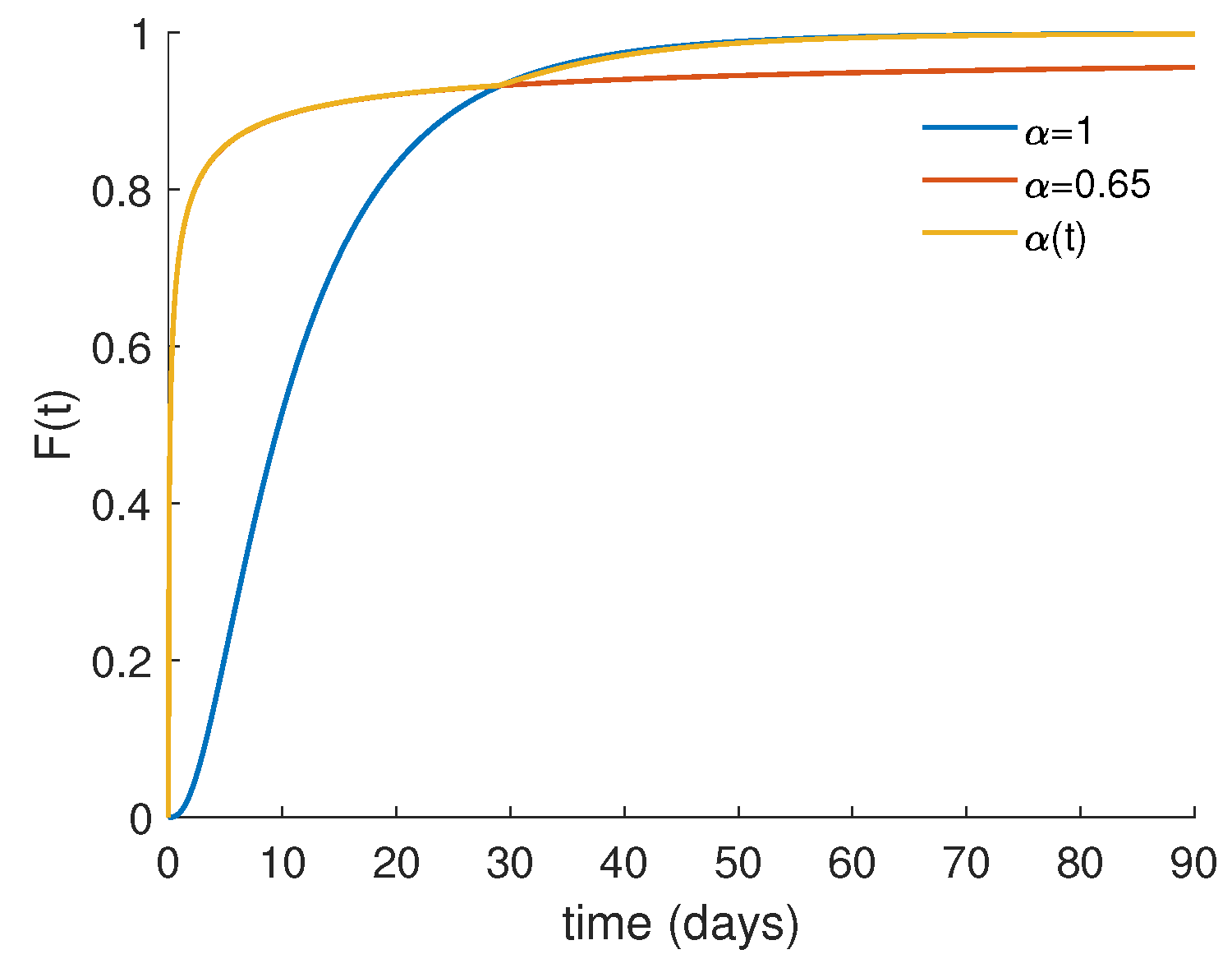
| 56,861.4 | 48,248.8 | 0.848534 | 0.952931 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosa, S.; Ndaïrou, F. Optimal Control Applied to Piecewise-Fractional Ebola Model. Mathematics 2024, 12, 985. https://doi.org/10.3390/math12070985
Rosa S, Ndaïrou F. Optimal Control Applied to Piecewise-Fractional Ebola Model. Mathematics. 2024; 12(7):985. https://doi.org/10.3390/math12070985
Chicago/Turabian StyleRosa, Silvério, and Faïçal Ndaïrou. 2024. "Optimal Control Applied to Piecewise-Fractional Ebola Model" Mathematics 12, no. 7: 985. https://doi.org/10.3390/math12070985
APA StyleRosa, S., & Ndaïrou, F. (2024). Optimal Control Applied to Piecewise-Fractional Ebola Model. Mathematics, 12(7), 985. https://doi.org/10.3390/math12070985