Abstract
Logistics and the supply chain are areas of great importance within organizations. Due to planning gaps, an increase in extra and unnecessary transport costs is usually observed in several companies due to their commercial commitments and need to comply with the delivery time and the batch quantity of products, leading to a negative economic impact. Thus, the objective of this work was to adjust an optimization model to maximize the shipments usually carried out by the companies. To validate the model, an automotive components manufacturer was selected, allowing us to apply the model to a real case study and evaluate the advantages and drawbacks of this tool. It was found that the company to validate the model exports most of its products, and most pallets sent are not fully optimized, generating excessive expense for the company in terms of urgent transport. To solve this problem, two mathematical optimization models were used for the company’s current reality, optimizing the placement of boxes per pallet and customer. With the use of the new tool, it was possible to determine that five pallets should be sent to the customer weekly, which correspond to their needs, and that have the appropriate configurations so that the pallet is sent completely.
Keywords:
optimization; logistics; supply chain; transport management program; randomly sized packages; pallets organization; pallets loading problem MSC:
49K45
1. Introduction
Transport can be considered an element of great importance in terms of logistics costs for organizations [1]. Therefore, it is essential to focus on the efficiency of the logistics operation, aiming for customer satisfaction [2]. On the other hand, process automation is becoming increasingly common in the market, mainly due to its proven contribution to reducing production expenses and efficiency [3].
There are several definitions for the concept of logistics and supply chains. Regarding Ballou [4], the supply chain is a set of functional activities (transport, stock control, etc.) that are repeated countless times along the channel through which raw materials are converted into finished products, which add value to the final consumer product. Concerning Stevenson’s work [5], the area of logistics is part of a supply chain involved in the flow of goods, services, money, and information, and for Rushton et al. [6], logistics is the positioning of the resource at the right time, place, cost, and quality.
When thinking of the supply chain as a global service, there is a consensus among several authors who say that it is the set of stakeholders involved, directly or indirectly, in fulfilling a customer order. Thus, the supply chain includes not only manufacturers and suppliers but also freight forwarders, warehouses, resellers, and customers themselves [7]. From this, it can be said that one of the goals of the supply chain is to achieve a sustainable competitive advantage [8]. For example, Bozart et al. [9] consider the supply chain as a network of manufacturers and service providers that work together to convert and move goods from the raw material state to the final consumer.
Thus, comparing the definitions of logistics and supply chain, it can be said that logistics refers to activities that occur within the limits of a single organization, while the supply chain concerns networks of companies that work and coordinate their actions to deliver a product to the market [10]. In other words, while logistics focuses on the company’s own operations, the supply chain looks from the beginning to the final links in the chain of suppliers and customers [11]. Thus, it can be said that logistics is an area in which the physical movement and the storage of materials are observed. For example, in the work of Anca [12], logistics is defined as the coordination of material and information flows through the integration of the entire company so that a strategic management process can occur in a profitable way. Therefore, according to the author, logistics management can be referred to as part of supply chain management, from the moment supply chain management was placed in the logistics life cycle. Thus, this work is mainly focused on logistics, as these two concepts are also put together in some works.
Since this is a comprehensive area, multiple works have been developed in logistics and supply chain; however, there are a lot of works in the literature when it comes to pallet optimization and mathematical modeling, but many of them are difficult to apply in companies, where time is money. The works found range in topic, from storage and transport, to supply, among others. Therefore, the objective of this work was to improve the transport area of the companies facing the problems of several weekly incomplete shipments to the same customer due to delivery and production restrictions. The problem of urgent transport causes companies to incur extra and unnecessary costs in order to fulfill their commercial commitments to their customers. This type of cost represents around 33% of total transport costs, proving to have a major economic impact. Therefore, this work arises from the need to analyze the transport carried out by the company under study, aiming to reduce costs and organize its shipping planning. To validate the model developed, an example of the characterization of current transport carried out between weeks 22 and 39 of 2023 in an automotive components’ producer was considered, with the determination of the pallets’ occupancy and its optimization. The mathematical model developed in this work is simpler than the models found in the previous literature, which makes its use easier. Furthermore, it is reliable and shows flexibility when it comes to introducing constraints. In addition, it is emphasized that the model can be easily replicated in other areas of the company, as well as being an insight for future work in this field.
2. Literature Review
2.1. Logistics and Operational Research
Since logistics is a very comprehensive area, multiple works have been developed in this field, such as storage, transport, and supply, among other approaches. For example, Freitas et al. [13] applied Lean tools to improve hybrid warehouse efficiency (storage and preparation) to redefine internal logistics’ spaces and flows. The authors observed a reduction in the selection and picking process time, a reduction in employee movement times, and a gain in space in the raw materials’ reception area. In turn, Garza-Reyes et al. [14] carried out an approach for the study of the road transport operations of a manufacturer of paper packaging solutions; using Lean concepts and tools, the authors identified six wastes, and using the indicator OEE (overall equipment effectiveness), an efficiency of 54% of the process was determined.
Another aspect that must be taken into consideration is operational research, which is considered the science of decision-making. However, in the scientific community, several definitions emerge and each one concerns one or another characteristic of operational research, but none of them explains or gives a complete picture of the subject. Blumenfeld [15] considers that this area encompasses various scientific disciplines, such as mathematics, statistics, computing, physics, engineering, economics, and social sciences, which provides a systematic approach to making complex decisions in manufacturing operations, for example. More recently, there is the definition by Rardin [16], who defines operational research as the study of how to form mathematical models from complex engineering and management problems and then analyze them to obtain plausible solutions.
In this way, it can be said that operational research is interconnected with the resolution of decision-making through mathematical models. According to Murthy [17], several steps must be followed for the problem to be solved through operational investigation: problem formulation; identification of variables and restrictions; establishing relationships between variables and restrictions; formulation of a mathematical model consistent with the problem; determination of the relevant solution; evaluation of results; and decision-making.
2.2. Pallet Optimization Problems
Optimization models are a part of mathematical programming models, which in turn allow for determining under what conditions a given objective can be maximized or minimized, given the existence of a set of limitations or restrictions. Thus, the problem to be solved here concerns a linear programming problem, and this type of problem is the simplest and constitutes the fundamental basis of operational research [18]. Furthermore, the wide application of linear programming is due to its practical nature [19], as it allows obtaining results that can be realistically implemented, as long as they are complemented with qualitative information and subjective assessments.
Some applications of operational research can be seen in the literature, namely pallet optimization problems, which are related to the practical problem that will be addressed in this work. Beasley [20] carried out a heuristic study on the exact cut in two dimensions using the “Tree search procedure” method. This study resulted from the need to reduce material waste when cutting raw materials to exact measurements. The author concluded that his optimization model could solve average problems for non-guillotined cutting, where in some numerical tests, it reduced waste by 100%, with the average of all tests being 60%. In turn, Tsai et al. [21] presented a transformation procedure to convert the three-dimensional pallet loading problem into an exact mixed-integer programming model. This made it possible to allocate boxes of different sizes on the same pallet.
Considering MPL (manufacturer’s pallet loading), Morabito et al. [22] presented a simple and effective heuristic to solve the problem of packing the maximum number of boxes on a pallet, without overlapping. With this procedure, the authors were able to find the optimal solution in 99.9% of more than 20 thousand examples analyzed. In turn, Letchford et al. [23] considered the upper limits for the pallet loading problem (PLP—pallet loading problem). It was found that a limit due to Nelissen and a limit obtained from the linear programming relaxation of a packing formulation dominate all others, with the latter being almost always ideal. Wäscher et al. [24] focused on IIPP (identical item packing problem), which consists of optimizing as much as possible the number of small items in a limited number of larger items to minimize the number of necessary transports, reducing costs of transport, and thus obtain a maximum level of efficiency. Another approach was used by Martins et al. [25], who considered new limits, heuristics, and an exact algorithm for the pallet loading problem (PLP), which maximizes the number of boxes placed on a rectangular pallet, with the boxes having similar dimensions. Table 1 shows recent works that fit into the PLP issue, and how the authors achieved the respective results and improvements.

Table 1.
Recent works about PLP and their solutions.
The works listed above show solutions to the pallet optimization problem, leaving as a gap the existence of a model that is simpler to use, that is effectively reliable, and that is as universal as possible. This universality can be easily observed and adjusted by modifying the conditions that govern the model.
For the development of the optimization model, the models that best suit what will be presented in this work are those proposed by Beasley [20] and Tsai et al. [21].
3. Development
3.1. Company Framework
This work considered a sample of the external logistics area of one of the production units of the Ficosa Group to develop and validate the proposed model. The company exports most of its products, which makes transport a fundamental part of its logistics chain. Therefore, it is necessary to determine their efficiency and, supported by operational research, optimize the corresponding shipments. Therefore, the period under analysis was considered from week 22 to week 39 of 2018.
In the first phase of analysis, a study was carried out to verify which countries the company transported most frequently to. Furthermore, transport efficiency was verified in terms of pallet occupancy, with the percentage of occupancy given by the formula presented in Equation (1):
The quantity sent (Qsent) is obtained through the data entered by the MOM (Manufacturing Operations Management) platform, and the quantity per pallet (Qpallete) is given through the packaging instructions for each product reference. In addition, the costs involved in transportation were analyzed due to the pallets not being complete, i.e., the cost paid in excess.
3.2. Optimization Model
It is known that the geometric characteristics of products and packaging units used in their distribution directly affect packaging and handling costs, as well as the efficiency of transport and storage operations. By optimizing pallets sent by normal transport, the cost of urgent transport will be lower. In this sense, a mathematical optimization model was developed, optimizing the placement of packages per pallet and customer.
In order to evaluate the concept, two critical company projects were taken into consideration: A1 (KIEV408XL1) and B1 (23XX520XL1). These projects present specific packaging instructions for each reference. Thus, Table 2 shows the type of packages and pallets used for delivery to the customer. The dimensions shown refer to the length (l), width (w), and height (h) of the packages and the length (L), width (W), and height (H) of the pallets.

Table 2.
Characteristics of packages and pallets.
The truck used for transport must have the following characteristics:
- Typology: 100 m3;
- Payload: 25 tons;
- Capacity: 33 Europallets;
- Inner capacity: 13.6 m long and 2.45 m wide.
Therefore, to formulate the mathematical model, it is necessary to define and restrict the problem based on the following premises, if the mathematical model represented is per pallet, i.e., it is the optimization of the position of the different packages on the pallet:
- The use of mixed pallets is allowed, i.e., pallets with different products and, consequently, with packages of different sizes.
- A package can have six different orientations when placed on a pallet, as it can be rotated around all the X, Y, and Z axes. However, only two are considered due to the type of product transported.
- The maximum pallet volume is 1.152 m3 (maximum truck height of 3 m, overlapping two pallets, a height of 1.5 m per pallet, and includes the height of the euro pallet (0.144 m) with a margin for the handling of the parts inside the truck; a useful height of 1.2 m is assumed).
- A package cannot coincide (overlap) in the same space as another, and each package must be contained entirely within the pallet, with its sides parallel to the sides of the pallet.
- The proportion of the number of packages of a given size to the total number of packages on a complete pallet should be as close as possible to the customer’s specifications (proportion ratio).
- The adopted model only covers the case in which the packages must be placed on the pallet in a single orientation. However, in this case, the packages can rotate, and both orientations should be considered so that it is possible to adopt the model and allow the packages to have different orientations, and therefore be positioned on the pallet with more than one orientation.
- Moreover, it is decided to consider a type of package with a different orientation as a different package. The developed algorithm differs from what is already found in the literature due to its simplicity of use, reliability in application, as well as flexibility in introducing constraints.
3.2.1. Formulation of the Problem According to Beasley [20]
To model the pallet loading problem, the 0–1 integer linear programming model proposed by Beasley [20] has been adopted. Thus, the first step was to define the indices and parameters to be used to formulate the model. Table 3 presents the indices, parameters, and decision variable.

Table 3.
Indices, parameters, and decision variable, according to Beasley [20].
Through a Cartesian coordinate system, L, W, and H can be defined through the following sets:
Therefore, aipqrstu is a function calculated as follows (Equation (5)):
Considering
Therefore, all the conditions for formulating the problem are met, and since the aim is to maximize the total volume of the packages inserted in the pallet, the following is considered as a mathematical model (Equation (9)):
Subject to (Equations (10)–(12))
Therefore, the restriction in Equation (10) prevents packages from overlapping on the pallet, and the restrictions in Equation (11) prevent the number of packages of each type within the pallet from being lower or higher than the stipulated values. In turn, the restrictions imposed in Equation (12) guarantee the proportion of packages according to the ratio of each customer, and define the domain of the decision variables.
3.2.2. Formulation of the Problem According to Tsai et al. [21]
On the other hand, another model can be used for this problem, namely the 0–1 mixed-integer linear programming model presented by Tsai et al. [21], for the three-dimensional pallet loading problem.
A collection of m packages, expressed by set S = {b1, b2, …, bm}, needs to be considered. Each package bi has a length li, width wi, and heigh hi.
Therefore, in this approach, the indices, parameters, and decision variable are presented in Table 4.

Table 4.
Indices, parameters, and decision variable, according to Tsai et al. [21].
Therefore, Equation (13) is used to maximize the total pallet volume occupied by packages to be loaded, according to the model adapted from Tsai et al. [21]:
The previous Equation (13) needs to be parametrized by taking into account the restrictions of the problem. Thus, the restrictions pointed out by Equations (14)–(16) prevent the overlapping of packages that must be linearized and considered. The restrictions pointed out by Equations (17)–(22) prevent the packages from violating the dimensions of the pallet, and Equations (23) and (24) impose restrictions that define the domain of the decision variables:
4. Results and Discussion
4.1. Characterization of Normal Transport
As transport is an area of utmost importance for companies that need to deliver their products to other companies or markets, to define its efficiency, it was necessary to identify the countries through which transport was most frequent. Figure 1 illustrates the analysis with the percentage of usual transport by destination country, in terms of the cost, taking into account the markets served by the company collaborating in this study.
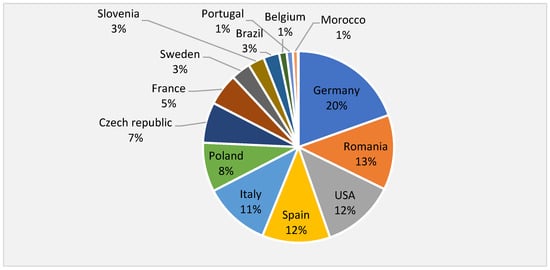
Figure 1.
Percentage of usual transport costs by destination country.
Based on this, it seems that around 80% of transport costs are spent in countries such as Germany, Romania, the United States of America, Spain, Italy, Poland, and the Czech Republic. On the other hand, analyzing transport efficiency in terms of pallet occupancy, it is generally seen that most pallets sent are not fully optimized. This issue can be seen in Figure 2, which illustrates the percentage of complete and incomplete pallets.
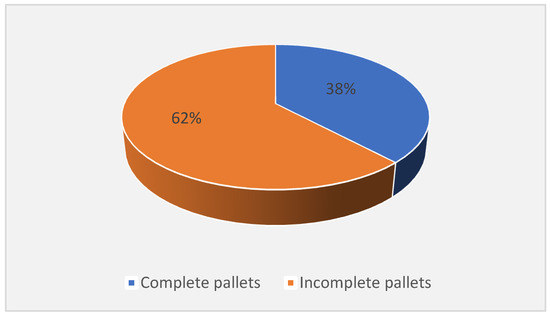
Figure 2.
Percentage of incomplete versus complete pallets.
Thus, it is observed that 62% of pallets are incomplete, which results in excessive costs through urgent transport. In the graph in Figure 3, based on client code, the difference in costs can be observed, in percentage, i.e., the cost paid in excess because the pallets were incomplete. In this analysis, the real cost refers to the actual cost paid for transportation and the optimized cost refers to the cost that should be charged for shipping the components on complete pallets (optimized pallets).
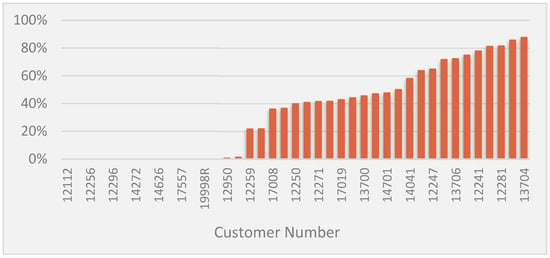
Figure 3.
Difference between current cost and optimized cost per customer (codified to preserve the confidentiality required by the company).
What can be observed is that of the 41 customers for which the company is responsible for transport, only 14 (around 34%) shipped with fully complete pallets. In other words, in terms of costs, if the pallets were sent at full capacity, the company would obtain savings of around EUR 47 thousand during the period in which the study was carried out. Extrapolating to annual values, the savings would reach EUR 338 thousand. Figure 4 illustrates the missing quantity in shipments to the customer, which, in the period, 4,855,094 units remained to be sent. Thus, it appears that 30% of customers receive pallets with less than 50% of the components they were supposed to receive, and 10% of customers receive pallets with a missing quantity percentage greater than 80%. Therefore, an intervention was necessary to improve this process through the optimization of pallets.
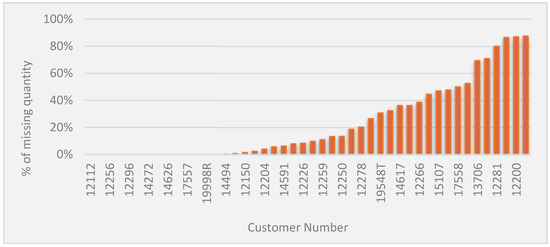
Figure 4.
Missing quantity in shipments.
4.2. Pallet Optimization
As previously mentioned, there is a large inefficiency, where pallets are loaded per customer and order, but in 60% of cases, the pallets remain incomplete. To optimize pallets, reduce costs, and generate greater efficiency, shipments made to customer 14701, from the A1 (KIEV408XL1) product, which is the most complex in terms of diversity of packages and volume of orders, were used. Furthermore, the tool used was the “CLP Spreadsheet Solver”, an open-source tool for representing, solving, and visualizing the results of CLPs (container loading problems) developed by Gunes Erdogan from the University of Bath.
Regarding CLPs, in the work of Alonso et al. [38], the problem of loading pallets on trucks was analyzed and solved using integer linear models. Thus, the authors considered three restrictions for the case: geometric restrictions, weight restrictions, and dynamic stability restrictions. It was observed that the models met the optimization in most cases, with around 44 loading trucks analyzed. Furthermore, Kurpel et al. [39], in their work, analyzed pallet loading problems based on rectangular boxes positioned orthogonally and without overlapping, with an aim in optimization, i.e., maximizing the value of packages or minimizing the number of pallets required. Thus, the authors evaluated mathematical models on five different sets of benchmarks, with the result of the analysis being beneficial in terms of obtaining optimal solutions for the respective problem.
For optimization, the customer’s weekly order was considered to make a single shipment, with only two types of pallets. Currently, the company uses six different types of pallets for this project, with differences essentially related to height, a situation that is corrected by the optimization model. Therefore, Table 5 presents data relating to the type of pallets available, the type of packages, and the weekly demand corresponding to each box. It should be noted that for the pallets accepted by the selected customer, a maximum height for both dimensions of 1200 mm was considered to maximize the volume of the pallets.

Table 5.
Types of pallets and packages used in the mathematical model.
The solution provided by the “CLP Spreadsheet Solver” tool revealed that one pallet of type 1 and four pallets of type 2 were necessary. In Table 6, it is possible to check the distribution of packages across the selected pallets. The problem studied is not a large size problem, so, the computational time of the “CLP Spreadsheet Solver” was small, spanning just a few seconds, depending on the complexity of the problem introduced (the number of different size packages to optimize).

Table 6.
Solution provided by the “CLP Spreadsheet Solver” tool for optimizing pallets with corresponding packages.
Figure 5, Figure 6, Figure 7 and Figure 8 show the distribution of packages in all configurations determined by the “CLP Spreadsheet Solver” tool. Figure 5 illustrates the distribution of packages on the type 1 pallet, which is only used once, whereas Figure 6 shows the distribution of packages on the type 2 pallet, whereby this configuration is used twice and designated as configuration 1. In turn, Figure 7 shows the distribution of packages on the type 2 pallet designated as configuration 2, and Figure 8 illustrates configuration 3 of the type 2 pallet. Therefore, to optimize the problem, in relation to customer 14701, five pallets must be sent weekly, corresponding to their needs. Thus, the software counts the packages that need to be sent, which means that the volume of packages on a pallet is maximized, thus minimizing the number of pallets needed for shipping.

Figure 5.
Singular configuration for type 1 pallet.
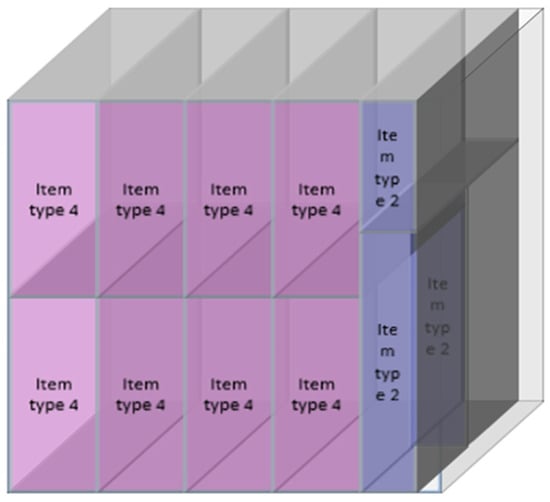
Figure 6.
Configuration 1 of pallet 2.
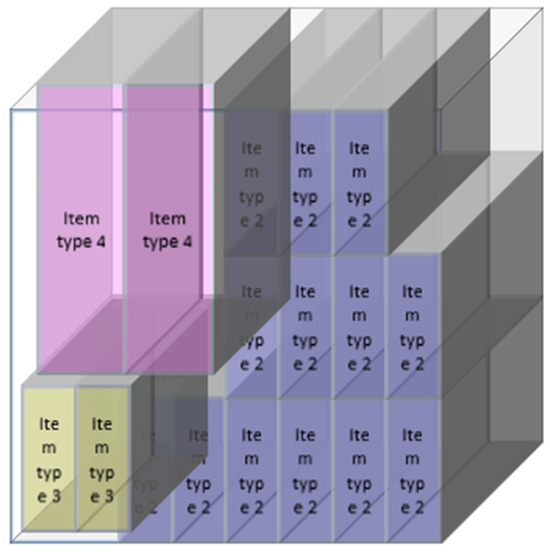
Figure 7.
Configuration 2 of pallet 2.
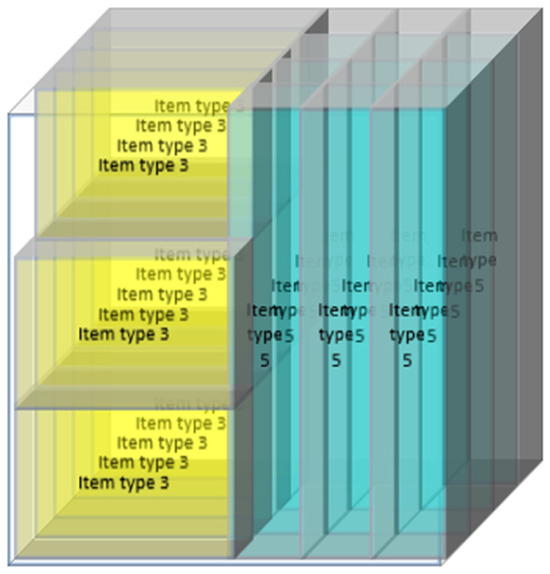
Figure 8.
Configuration 3 of pallet 2.
The results obtained show that it is possible to optimize logistical operations with adequate programming using models that allow the work to be systematized, leading to significant monetary savings without this translating into additional effort for the entity that makes up the pallets, in this case, a manufacturer of components for the automotive industry. In the field of logistics and supply chain, the challenges are enormous in terms of reducing waste as much as possible, not only for economic reasons, which are very important for the economic sustainability of the business, but also for environmental sustainability reasons, as less transport implies a lower volume of emissions, which translates into a benefit for the environment [40]. Given that packaging is responsible for benefits or waste in the way goods are packaged and grouped for subsequent transport, numerous studies have been developed in this area, almost all involving mathematical optimization models of varying complexity. Ronzoni et al.’s research [41], with the main concerns of cost reduction and environmental impact, studied the use of reusable plastic containers in the Food Catering Supply Chain sector using a model capable of virtualizing the logistic and operational costs as well as the transportation and disposal impact of reusable and recyclable plastic containers. To this end, it used a multi-objective optimization model, which is based on two objective functions: cost optimization and optimization of emissions generated by transport. The model was successfully applied in an Italian catering industry, but given its generic scope, it could be applied in another sector, like the one presented as case study in this work.
However, the model is more complex than that one used in this work, leading to the preferable adoption of the latter one. Complexity is quite common in these optimization models, which are commonly carried out in two stages. Resat and Unsal [42] presented a model for supply chain optimization based on two steps: first, they applied the Analytic Hierarchy Process (AHP) to select the suppliers with the best performance, and then they used a mixed-integer linear multi-objective mathematical model to optimize the supply chain, with the main factors of concern in optimization being cost, time, and social factors. Vitale et al. [43] sought to optimize the flow of raw materials in the wood pellet industry. To achieve this, a standard decomposition technique was used, which initially consisted of designing routes, and then, products and raw material flows were computed, solving in this way the optimization problem. Once again, a two-step solution was employed to solve a logistics problem. Sharifi et al. [44] also used a two-step multi-objective model to optimize the soybean supply chain under uncertain conditions. The model combines a multi-criteria decision-making technique with a new multi-objective optimization model. The combination of these techniques also provides good results, but it is a more complex system than the one developed in this work and is not as widely applicable.
However, studies aimed at optimizing the occupancy of containers and pallets have been little studied. Jiao et al. [45] studied the robotic loading of containers, but subject to multiple restrictions, such as load balancing, orientations, stability, and multi-drop, as well as constraints related to pallet continuity and robot position. Given the restrictions that the algorithm would have to overcome, the solution is much more complex than the one presented here.
5. Conclusions
Following the objectives proposed for this work, and using a case study proposed by a company of Ficosa Group, it was possible to characterize the current transport used by that company, as well as visualize existing problems based on incomplete loading of pallets. It was found that most of the company’s products are exported, with most of the pallets being sent incomplete, which generates excessive and unnecessary costs for the company. Because this problem is common to several small and medium enterprises, this study intended to find a cheap and flexible solution to overcome this problem and make the companies more competitive in terms of external logistics costs.
In this context, it was also possible to use two existing mathematical models, allowing for the optimization of the pallets sent, i.e., greater use of the space for each shipment by the company. With the help of the “CLP Spreadsheet Solver V1.60” software (Gunes Erdogan, University of Bath, Bath, UK), it was verified that it is necessary to send five pallets weekly to satisfy the customer’s needs in different configurations that allow the pallets to be sent completely. The constraints used in this work are common to a lot of problems usually faced by several small and medium companies and can be adjusted punctually regarding specific needs.
As a proposal for future work, it is proposed to improve the mathematical models in order to consider the characteristics of the trucks used and analyze the need for urgent transportation, which lead to an increase in freight costs for the company.
Author Contributions
Investigation, N.P.V.S. and A.B.M.M.; Conceptualization, F.J.G.S. and A.M.S.B.; Supervision, F.J.G.S., A.M.S.B., I.M.P. and R.C.M.S.-C.; Data collection, A.B.M.M. and I.M.P.; Formal analysis, N.P.V.S., F.J.G.S., I.M.P., L.P.F. and R.C.M.S.-C.; Methodology, A.B.M.M. and A.M.S.B.; Visualization, N.P.V.S. and R.C.M.S.-C.; Data curation: N.P.V.S., F.J.G.S., I.M.P., L.P.F. and A.M.S.B.; Writing—draft, N.P.V.S. and R.C.M.S.-C.; Writing—reviewing, F.J.G.S., I.M.P. and L.P.F.; Resources, F.J.G.S. and A.M.S.B.; Main research, A.B.M.M. All authors have read and agreed to the published version of the manuscript.
Funding
The work was carried out within the scope of the project “DRIVOLUTION—Transition to the factory of the future”, supported by the European Structural and Investment Funds under “Portugal 2020” (C644913740-00000022).
Data Availability Statement
Data is contained within the article.
Acknowledgments
The authors thank the ISEP, Polytechnic of Porto and FicoCables Lda., for the infrastructure offered for the development of this project.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yingfei, Y.; Mengze, Z.; Zeyu, L.; Ki-Hyung, B.; Andriandafiarisoa Ralison Ny Avotra, A.; Nawaz, A. Green Logistics Performance and Infrastructure on Service Trade and Environment-Measuring Firm’s Performance and Service Quality. J. King Saud Univ. Sci. 2022, 34, 101683. [Google Scholar] [CrossRef]
- Tan, B.Q.; Wang, F.; Liu, J.; Kang, K.; Costa, F. A Blockchain-Based Framework for Green Logistics in Supply Chains. Sustainability 2020, 12, 4656. [Google Scholar] [CrossRef]
- Lowenberg-DeBoer, J.; Huang, I.Y.; Grigoriadis, V.; Blackmore, S. Economics of Robots and Automation in Field Crop Production. Precis. Agric. 2020, 21, 278–299. [Google Scholar] [CrossRef]
- Ballou, R.H. Business Logistics/Supply Chain Management; Bookman: Clifton, NJ, USA, 2006. [Google Scholar]
- Stevenson, W.J. Operations Management, 11th ed.; McGrawHill: New York, NY, USA, 2009. [Google Scholar]
- Rushton, A.; Croucher, P.; Baker, P. The Handbook of Logistics and Distribution Management, 3rd ed.; Kogan Page: London, UK, 2006. [Google Scholar]
- Chopra, S.; Meindl, P. Supply Chain Management: Strategy, Planning, and Operation, 5th ed.; Pearson: London, UK, 2012. [Google Scholar]
- Li, L. Managing Supply Chain and Logistics; World Scientific: Singapore, 2014. [Google Scholar] [CrossRef]
- Bozart, C.C.; Handfield, R.B. Introduction to Operations and Supply Chain Management, 4th ed.; Pearson: Clifton, NJ, USA, 2015. [Google Scholar]
- Hugos, M. Essentials of Supply Chain Management; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Machline, C. Cinco Décadas de Logística Empresarial e Administração Da Cadeia de Suprimentos No Brasil. Rev. Adm. Empresas 2011, 51, 227–231. [Google Scholar] [CrossRef]
- Anca, V. Logistics and Supply Chain Management: An Overview. Stud. Bus. Econ. 2019, 14, 209–215. [Google Scholar] [CrossRef]
- Freitas, A.M.; Silva, F.J.G.; Ferreira, L.P.; Sá, J.C.; Pereira, M.T.; Pereira, J. Improving Efficiency in a Hybrid Warehouse: A Case Study. Procedia Manuf. 2019, 38, 1074–1084. [Google Scholar] [CrossRef]
- Garza-Reyes, J.A.; Forero, J.S.B.; Kumar, V.; Villarreal, B.; Cedillo-Campos, M.G.; Rocha-Lona, L. Improving Road Transport Operations Using Lean Thinking. Procedia Manuf. 2017, 11, 1900–1907. [Google Scholar] [CrossRef]
- Blumenfeld, D. Operations Research Calculations Handbook, 2nd ed.; CRC Press Taylor and Francis Group: New York, NY, USA, 2009. [Google Scholar]
- Rardin, R.L. Optimization in Operations Research, 2nd ed.; Pearson: Clifton, NJ, USA, 2017. [Google Scholar]
- Murthy, P.R. Operations Research, 2nd ed.; New Age International Publishers: New Delhi, India, 2007. [Google Scholar]
- Ramalhete, M.; Guerreiro, J.; Magalhães, A. Programação Linear I; McGrawHill: Lisboa, Portugal, 1995. [Google Scholar]
- Hill, M.M.; dos Santos, M.M. Investigação Operacional—Programação Linear, 3rd ed.; Edições Sílabo: Lisboa, Portugal, 2015. [Google Scholar]
- Beasley, J.E. An Exact Two-Dimensional Non-Guillotine Cutting Tree Search Procedure. Oper. Res. 1985, 33, 49–64. [Google Scholar] [CrossRef]
- Tsai, R.D.; Malstom, E.M.; Kuo, W.A.Y. Three Dimensional Palletization of Mixed Box Sizes. IIE Trans. 1993, 25, 64–75. [Google Scholar] [CrossRef]
- Morabito, R.; Morales, S. A Simple and Effective Recursive Procedure for the Manufacturer’s Pallet Loading Problem. J. Oper. Res. Soc. 1998, 49, 819–828. [Google Scholar] [CrossRef]
- Letchford, A.N.; Amaral, A. Analysis of Upper Bounds for the Pallet Loading Problem. Eur. J. Oper. Res. 2001, 132, 582–593. [Google Scholar] [CrossRef]
- Wäscher, G.; Haußner, H.; Schumann, H. An Improved Typology of Cutting and Packing Problems. Eur. J. Oper. Res. 2007, 183, 1109–1130. [Google Scholar] [CrossRef]
- Martins, G.H.A.; Dell, R.F. Solving the Pallet Loading Problem. Eur. J. Oper. Res. 2008, 184, 429–440. [Google Scholar] [CrossRef]
- Zhu, W.; Fu, Y.; Zhou, Y. 3D Dynamic Heterogeneous Robotic Palletization Problem. Eur. J. Oper. Res. 2024, in press. [CrossRef]
- Alvarez-Valdes, R.; Parreño, F.; Tamarit, J.M. A Branch-and-Cut Algorithm for the Pallet Loading Problem. Comput. Oper. Res. 2005, 32, 3007–3029. [Google Scholar] [CrossRef]
- Lu, Y.; Cha, J. A Fast Algorithm for Identifying Minimum Size Instances of the Equivalence Classes of the Pallet Loading Problem. Eur. J. Oper. Res. 2014, 237, 794–801. [Google Scholar] [CrossRef]
- Sheng, L.; Hongxia, Z.; Xisong, D.; Changjian, C. A Heuristic Algorithm for Container Loading of Pallets with Infill Boxes. Eur. J. Oper. Res. 2016, 252, 728–736. [Google Scholar] [CrossRef]
- Singh, M.; Almasarwah, N.; Süer, G. A Two-Phase Algorithm to Solve a 3-Dimensional Pallet Loading Problem. Procedia Manuf. 2019, 39, 1474–1481. [Google Scholar] [CrossRef]
- Terno, J.; Scheithauer, G.; Sommerweiß, U.; Riehme, J. An Efficient Approach for the Multi-Pallet Loading Problem. Eur. J. Oper. Res. 2000, 123, 372–381. [Google Scholar] [CrossRef]
- Ahn, S.; Park, C.; Yoon, K. An Improved Best-First Branch and Bound Algorithm for the Pallet-Loading Problem Using a Staircase Structure. Expert Syst. Appl. 2015, 42, 7676–7683. [Google Scholar] [CrossRef]
- Chan, F.T.S.; Bhagwat, R.; Kumar, N.; Tiwari, M.K.; Lam, P. Development of a Decision Support System for Air-Cargo Pallets Loading Problem: A Case Study. Expert Syst. Appl. 2006, 31, 472–485. [Google Scholar] [CrossRef]
- Arun Prasad, S.; Krishnakumar, P. Higher Order Block Heuristics for 2D Pallet Loading Problems with Multiple Box Inputs. Mater. Today Proc. 2021, 46, 4625–4633. [Google Scholar] [CrossRef]
- Ribeiro, G.M.; Lorena, L.A.N. Lagrangean Relaxation with Clusters and Column Generation for the Manufacturer’s Pallet Loading Problem. Comput. Oper. Res. 2007, 34, 2695–2708. [Google Scholar] [CrossRef]
- Gzara, F.; Elhedhli, S.; Yildiz, B.C. The Pallet Loading Problem: Three-Dimensional Bin Packing with Practical Constraints. Eur. J. Oper. Res. 2020, 287, 1062–1074. [Google Scholar] [CrossRef]
- Mascarenhas, W.F. Two Aspects of the Pallet Loading Problem. Electron. Notes Discret. Math. 2005, 19, 381–387. [Google Scholar] [CrossRef]
- Alonso, M.T.; Alvarez-Valdes, R.; Iori, M.; Parreño, F. Mathematical Models for Multi Container Loading Problems with Practical Constraints. Comput. Ind. Eng. 2019, 127, 722–733. [Google Scholar] [CrossRef]
- Kurpel, D.V.; Scarpin, C.T.; Pécora Junior, J.E.; Schenekemberg, C.M.; Coelho, L.C. The Exact Solutions of Several Types of Container Loading Problems. Eur. J. Oper. Res. 2020, 284, 87–107. [Google Scholar] [CrossRef]
- Silva, F.G.; Gouveia, R.M. Cleaner Production—Toward a Better Future; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Ronzoni, M.; Accorsi, R.; Guidani, B.; Manzini, R. Economic and Environmental Optimization of Packaging Containers Choice in Food Catering Supply Chain. Transp. Res. Procedia 2022, 67, 163–171. [Google Scholar] [CrossRef]
- Resat, H.G.; Unsal, B. A Novel Multi-Objective Optimization Approach for Sustainable Supply Chain: A Case Study in Packaging Industry. Sustain. Prod. Consum. 2019, 20, 29–39. [Google Scholar] [CrossRef]
- Vitale, I.; Dondo, R.G.; González, M.; Cóccola, M.E. Modelling and Optimization of Material Flows in the Wood Pellet Supply Chain. Appl. Energy 2022, 313, 118776. [Google Scholar] [CrossRef]
- Sharifi, E.; Fang, L.; Amin, S.H. A Novel Two-Stage Multi-Objective Optimization Model for Sustainable Soybean Supply Chain Design under Uncertainty. Sustain. Prod. Consum. 2023, 40, 297–317. [Google Scholar] [CrossRef]
- Jiao, G.; Huang, M.; Song, Y.; Li, H.; Wang, X. Container Loading Problem Based on Robotic Loader System: An Optimization Approach. Expert Syst. Appl. 2024, 236, 121222. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).