Abstract
This paper introduces an application of the dandelion optimization (DO) algorithm in antenna arrays. This is the first time that the DO algorithm has been used for optimizing antenna arrays. For antenna array optimization, sidelobe level (SLL) and deep nulls are key technical indicators. A lower SLL can improve the signal-to-noise ratio and reduce the impact of clutter signals outside the main beam. Deep nulls need to be aligned with the direction of interference to eliminate the influence of interference sources. The combination of the two can effectively improve the anti-interference ability of the entire system. Therefore, antenna arrays with ultra-low sidelobes and ultra-deep nulls are currently hot in the field of antenna array design and are also some of the key technologies needed to achieve modern high-performance radar systems. As a new type of evolutionary algorithm inspired by nature, the DO algorithm is inspired by the wind propagation behavior of dandelions in nature. This algorithm iteratively updates the population from three stages of ascent, descent, and landing, ultimately finding the optimal position. It has good optimization ability in solving complex problems such as those involving nonlinearity, discreteness, and non-convexity, and the antenna array pattern synthesis optimization problem belongs to multivariate nonlinear problems. Therefore, the DO algorithm can be effectively applied in the field of antenna array optimization. In this work, we use the following method to obtain an optimized pattern of a linear array with the lowest sidelobe level (SLL), null placement in particular directions, and a lower notch in particular directions: by controlling the antenna array’s element spacing and leaving the phase unchanged to optimize the current amplitudes and by controlling the excitation current and phase fixation of the antenna array and changing the element spacing. In the first and second examples, different algorithms are used to reduce the SLL of the antenna. In the first example, the DO algorithm reduces the SLL to −33.37 dB, which is 2.67 dB, 2.67 dB, 3.77 dB, 2.74 dB, and 2.52 dB lower than five other algorithms. In the second example, the SLL optimized by the DO algorithm is −42.56 dB, which is 5.04 dB and 1.48 dB lower than two other algorithms. In both examples, the DO algorithm reduces the SLL lower than other algorithms when the main lobe of the antenna is not significantly widened. Examples 3, 4, and 5 use the DO algorithm to optimize the amplitude of the current, generating deep nulls and deep notches in specific directions. In Example 3, the DO algorithm obtains a depth of nulls equal to −187.6 dB, which is 66.7 dB and 44.3 dB lower than that of the flower pollination algorithm (FPA) and the chaotic colony predation algorithm (CCPA), respectively. In Example 4, the deep null obtained by the DO algorithm is as low as −98.69 dB, which is 6.67 dB lower than the deep null obtained by the grey wolf optimization (GWO) algorithm. In Example 5, the deep notch obtained by the DO algorithm is as low as −63.1 dB, which is 6.4 dB and 1.9 dB lower than the spider monkey optimization (SMO) algorithm and the grasshopper optimization algorithm (GOA), respectively. The data prove that the DO algorithm produces deeper nulls and notches than other algorithms. The last two examples involve reducing sidelobe levels and generating deep nulls by optimizing the spacing between elements. In Example 5, the SLL obtained using the DO algorithm is −22.8766 dB, which is 0.1998 dB lower than the lowest SLL of −22.6768 dB among other algorithms. In Example 6, the SLL obtained using the DO algorithm is −20.1012 dB, and the null depth is −125.1 dB, which is 1.592 dB lower than the SLL obtained by the cat swarm optimization (CSO) algorithm and 19.1 dB lower than the deep null obtained by the GWO algorithm, respectively. In summary, the results of six simulation experiments indicate that the DO algorithm has better optimization ability in linear array optimization than other evolutionary algorithms.
Keywords:
dandelion optimization algorithm; antenna array; pattern synthesis; antenna current amplitude; antenna array element spacing MSC:
78-10
1. Introduction
Antennas are an indispensable part of wireless communication systems, and the quality of antenna design determines the quality of wireless communication. Modern antenna system design requirements are often quite strict and must meet the strict performance standards specified in specific application requirements [1,2,3], which usually consider characteristics such as antenna gain [4] and radiation pattern [5]. There are also many design methods for modern antenna systems, such as using swarm intelligence optimization algorithms to optimize antenna models or using electromagnetic (EM) simulation software for modeling and analysis, and so on. Although EM simulation tools have become important tools in contemporary antenna design, the high cost of antenna optimization methods based on EM simulation is a challenge, and a single full-wave simulation may take tens of seconds or several hours, making the time cost of solving design tasks involving multiple EM analyses potentially enormous [6,7,8]. Therefore, in many cases, designers choose to change their thinking and no longer use EM simulation design but instead turn to metaheuristic intelligent optimization algorithms to optimize antenna design, especially when dealing with multiple objectives such as sidelobe level and null depth of antennas. Using metaheuristic intelligent optimization algorithms to solve optimization problems in the antenna field becomes very efficient. In real life, wireless communication systems are mostly used for remote communication. However, for remote communication, a single antenna does not have sufficient gain and may be interfered with by buildings or other nearby obstacles, which seriously reduces its performance. Therefore, it cannot meet the requirements of high quality and efficiency for remote communication. Antenna arrays have advantages that a single antenna does not have, including high directionality, high gain, high anti-interference ability, and beam control ability, which can achieve the above requirements for remote communication. Therefore, the design of antenna arrays is crucial for remote wireless communication systems. An antenna array is a special type of antenna composed of no less than two regular or randomly arranged antenna elements, which obtain predetermined radiation characteristics through appropriate excitation. For antenna arrays, when the main lobe width remains unchanged, the lower the SLL, the deeper the null, and the more concentrated the radiation energy, the better its performance. The performance of antenna arrays varies through different optimization techniques. As is well known, the design optimization or synthesis of antennas and antenna arrays in electromagnetics is a complex nonlinear problem, and traditional methods such as the Chebyshev technique, the Taylor method [9], and gradient-based optimization often find it difficult to achieve ideal results when dealing with such problems. However, with the emergence of more and more metaheuristic intelligent optimization algorithms, they are very effective in solving multi-dimensional nonlinear, discrete, and non-convex problems in engineering applications. Therefore, they have replaced traditional optimization methods and are currently widely used in the field of antenna array optimization. For example, the ant colony optimization (ACO) algorithm [10], particle swarm optimization (PSO) algorithm [11], genetic algorithm (GA) [12], differential evolution (DE) algorithm [13], artificial bee colony (ABC) algorithm [14], ACO algorithm [15], SMO algorithm [16], DE algorithm [17], CSO algorithm [18], fruit fly optimization algorithm (FFOA) [19], and invasive weed optimization (IWO) algorithm [20] have also been effectively used for linear antenna array optimization. In general, each algorithm has its own advantages and disadvantages, and there is no perfect algorithm in the world that can solve all optimization problems [21]. However, in the field of smart antenna optimization, with the increasing demand for anti-interference in information transmission, discovering and researching a new algorithm or innovating based on existing algorithms to achieve better optimization performance has become a hot topic for some researchers recently.
However, this is the first time that the DO algorithm has been used for pattern synthesis of antenna arrays. The DO algorithm is an evolutionary type of algorithm that simulates the growth and reproduction behavior of dandelions in nature; the optimization of the algorithm is divided into a total of four steps, which are as follows: initializing the population, ascending phase evolution, descending phase evolution, and landing phase evolution. The solution space is continuously updated, and the optimal solution is eventually found. Moreover, the DO algorithm has the advantages of fast convergence speed and high convergence accuracy, which can better find the optimal solution. In this paper, the DO algorithm is applied to two types of pattern synthesis problems for linear arrays; one type is an equidistant symmetric array, which obtains the desired directional pattern by optimizing the amplitudes of excitation currents of the array elements while maintaining the phases of the element excitation currents to be zero; the other type is to optimize the spacing of array elements for non-equidistant arrays to obtain the desired directional pattern while maintaining the amplitudes and phases of the excitation currents of the array elements unchanged.
The rest of the paper is organized as follows: The DO algorithm is described in detail in Section 2. Then, in Section 3, various examples of linear array synthesis are presented and the DO algorithm is adopted to optimize the amplitudes of excitation currents for equidistant symmetric arrays and the spacing of array elements for non-equidistant arrays. The results are compared with other natural evolution algorithms to assess the effectiveness of the DO algorithm in synthesizing linear arrays. Finally, in Section 4, a summary is given.
2. Dandelion Optimization Algorithm
This section describes the dandelion optimization algorithm in detail, including inspiration, mathematical models, expressions, time complexity, and pseudocode of the DO algorithm [22]. Among them, the pseudocode of the DO algorithm is provided in Table 1.

Table 1.
Pseudocode for DO algorithm.
2.1. Inspiration
As we all know, dandelions, in Figure 1, are a gift from nature; they are not very common in life. As a plant, dandelion reproduction is carried out with the help of wind; when the wind blows, dandelion seeds spread everywhere, to multiply. The inspiration for the dandelion optimization algorithm is mainly based on the long flight of dandelion seeds scattered in the wind. Wind speed is used to determine whether the dandelion seeds fly long or short distances, and the weather conditions determine the flight of dandelion seeds.

Figure 1.
Dandelion in nature.
An overview of the mathematical representation of the dandelion optimization algorithm is given in the section that follows.
2.2. Mathematical Model
The mathematical model describing the dandelion optimization algorithm has four stages: initialization, ascent process, descent process, and landing process.
2.2.1. Initialization
Each dandelion seed is thought to stand for a potential solution, whose population is represented as
where pop stands for population size and Dim for the variable’s dimension. Between the specified problem’s upper bound (UB) and lower bound (LB), each candidate solution is generated at random. The expression of the ith individual Xi is
where lbi and ubi represent the dimensions of the lower and upper bounds of each population of dandelions; i is an integer between 1 and pop, and rand refers to a number between 0 and 1. LB and UB are expressed as
During initialization, the DO algorithm takes the individual with the best fitness value as the initial optimal body and approximates it as the most suitable location for dandelion seeds to survive and reproduce. Using the minimum number as an illustration, the mathematical expression Xbest of the initial optimal body is
where find () refers to two indexes with the same values.
2.2.2. Rising Process
When dandelions are in the rising process, the impacts of wind speed, air humidity, and other variables vary depending on the weather. Here, the weather is divided into sunny and rainy days, and then dandelion flight behavior in these two conditions is analyzed separately.
In the case of sunny days, wind speeds can be regarded to have a log-normal distribution . Such a distribution allows dandelions to fly farther away. Dandelions are randomly scattered around the search area by the wind. The dandelions fly higher and spread farther with a stronger wind. In this instance, the dandelion evolutionary iteration’s mathematical expression is
where Xt denotes where the dandelion was at the tth iteration. Equation (6) gives the expression for the randomly generated location, and Xs denotes the randomly chosen position in the search space during iteration t.
where lnY denotes a log-normal distribution subject to = 0 and = 1, and its mathematical formula is
In Equation (7), y represents the standard normal distribution N (0, 1). Following a logarithmic normal distribution, dandelions are more distributed on the y axis, which increases the chances of dandelions spreading to distant regions and expands the search domain. The mathematical expression for α, an adaptive parameter used to modify the search step length, is
In Equation (8), α is a random number between [0, 1] and follows the principle of nonlinear reduction. It is determined by the current number of iterations and the maximum number of iterations. It shows a gradually decreasing trend, and the decrease becomes slower and slower. This allows for the use of wind speed in the limited time in the early stage to fly to a farther search interval with a larger step size, in order to find the most suitable location for dandelion growth. The curve of α is shown in Figure 2a. T represents the maximum number of iterations. Dandelions produce vortices during ascent, while vx and vy represent the two components of the force generated by the vortex. We must apply Equation (9) to calculate vx and vy.
where θ is a random number between [−π, π], e represents the natural constant, and r represents the rising vortex distance. r, vx, and vy are all related to the angle θ.
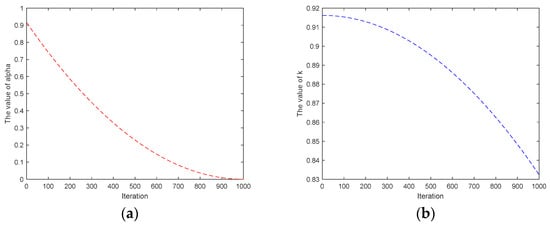
Figure 2.
(a): Step size control parameter α in sunny iteration. (b): Step size control parameter k in rainy day iteration.
In the case of rainy days, a dandelion cannot be carried by the wind to distant areas; it can only spread in a small area in its locality. Thus, the mathematical expression for this stage is
where k controls the dandelion’s local search domain, and the domain is calculated using Equation (11).
The DO algorithm with a lengthy stride in the beginning and a short cloth length later is conducive to the local exploitation of the algorithm. q represents the factor that determines the control step size based on the number of iterations and the maximum number of iterations. k is determined by a random number between 0 and 1 and the value of q. In order to ensure overall convergence to the ideal search agent, k continuously decreases in the later stages of the iteration to achieve a small step exploration and gradually find a suitable location for dandelion growth. The curve of k is shown in Figure 2b.
For both weather conditions mentioned above, the dandelion evolutionary iteration mathematical model is
where randn is a random number that follows the standard normal distribution. We chose the cut-off point of randn to be 1.5 because during the sunny stage, due to the use of wind power, dandelions can fly further, resulting in longer iteration and update times. Therefore, the probability of this stage is higher. During rainy days, dandelions are often hit by rainwater, and they can only iterate and update in a small area around them. The update time is shorter, so the probability of this stage is lower, so the node should be set to the right of the randn function curve in Figure 3. Only when the cut-off point is set to 1.5 can the search for dandelions traverse the entire search space as much as possible in the first stage, providing the correct direction for the iterative optimization in the next stage.
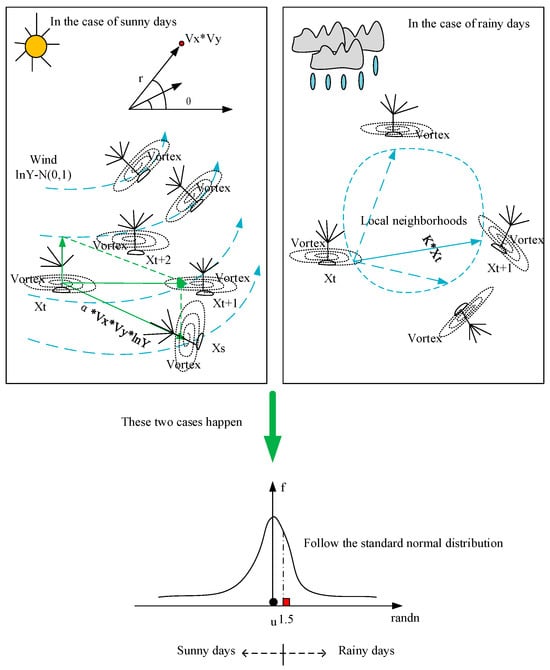
Figure 3.
Movement behavior during the ascent process of dandelions.
Figure 3 shows the flight behavior of dandelions in two weather conditions. In the first instance, dandelions randomly choose location data during the update iteration as they flutter in the wind on a sunny day. In the second instance, dandelions merely reposition themselves in the appropriate tiny neighborhood around themselves when it rains rather than taking to the air with the wind. The cut-off point in both cases is set to 1.5, which is more conducive to the global convergence of the DO algorithm.
2.2.3. Descending Process
In this stage, after the dandelions have risen to a certain height, they begin to decline steadily. During the descent, Brownian motion is used to describe the flight behavior of dandelions. With iterative updates, it is simple for people to go across more search regions since Brownian motion follows a normal distribution with each modification. At the same time, to ensure the stability of dandelion landing, we use the average position data from the ascending phase when detailing the iteration procedure in the descending phase. The mathematical expression corresponding to this stage is
where βt denotes Brownian motion and is a random number from the standard normal distribution [23]. Brownian motion is a continuous random process that is used to iterate the descent stage of dandelions, allowing them to traverse and search for more locations in as limited a time as possible, thus obtaining the updated location of the next generation of dandelions with a greater probability. In addition, the trajectory of Brownian motion is also shown in Figure 4. The mathematical expression for Xmean_t, which stands for the population’s average location, is
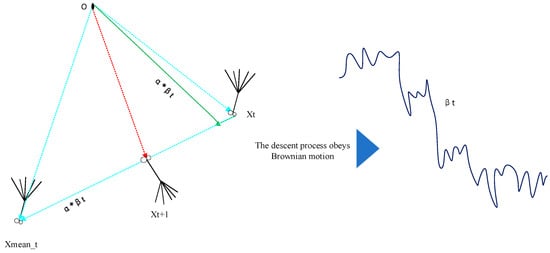
Figure 4.
Movement behavior during the descent process of dandelions.
Figure 4 shows the descent of dandelions. As can be seen, the population’s average position information is crucial in both the rising and falling stages and is crucial for determining the direction of evolution for the iterative updating of individuals. During iterative updates, Brownian motion helps dandelions avoid falling into local extrema, driving populations to settle in areas close to the global optimal solution.
2.2.4. Landing Process
This part is based on the first two stages, in which dandelions are chosen to land randomly. The search agent uses the current optimal body’s position information to iterate in its neighborhoods as the iteration goes on. Finally, the global optimal solution can be found. Therefore, the DO algorithm reaches the global optimal outcome. Equation (15) describes this behavior.
where Xelite represents the optimal position of the dandelions in the ith iteration. Levy () represents the function of Levy flight and is calculated using Equation (16) [24].
The Levy flight function follows the trajectory of a power function to adjust the search step size. Most of the steps in motion are very short, and there are also a small number of long steps, which is more in line with the landing phase and the motion trajectory of dandelions. When a dandelion starts landing, the step size increases first under the adjustment of Levy flight, and the neighborhood of the optimal solution is comprehensively searched within its vicinity. In the middle and late stages of landing, the steps start to become shorter and shorter; only in this way can we avoid crossing the optimal solution due to step length and, thus, constantly approach the optimal solution. The parameter settings in the Levy flight function [22,24,25,26] are learned from the experience of researchers throughout history. In Equation (16), β takes a value of 1.5 in this paper. s is a fixed value of 0.01. w and t are random numbers between [0, 1] [22].
The mathematical expression of is
where β is fixed at 1.5. δ is a function that increases linearly from [0, 2] and its expression is expressed by Equation (18). It is an iterative factor of linear growth used to control the current position of dandelions. As the number of iterations increases, the location range of dandelions expands, increasing the opportunity to find the optimal solution. Figure 5 shows the linear variation of δ.
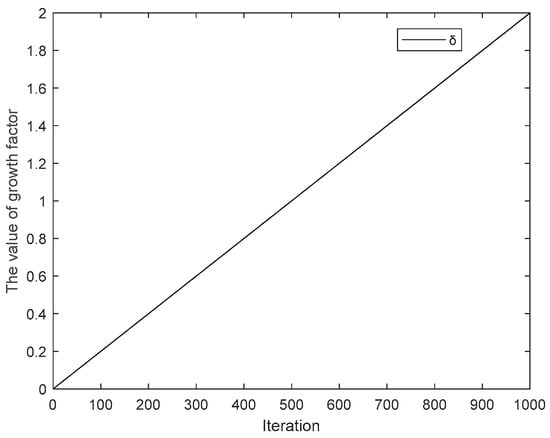
Figure 5.
Linear growth graph of parameter δ.
Figure 6 shows the process of the landing stage. In this process, a linear increasing function is applied to individuals to avoid overexploitation. To model individual movement step length, the Levy flight coefficient was applied. This is because, under the Gaussian distribution, the Levy flight coefficient can allow dandelions to cross to other distant locations with a greater probability. It helps the DO algorithm precisely converge to the global optimal solution.
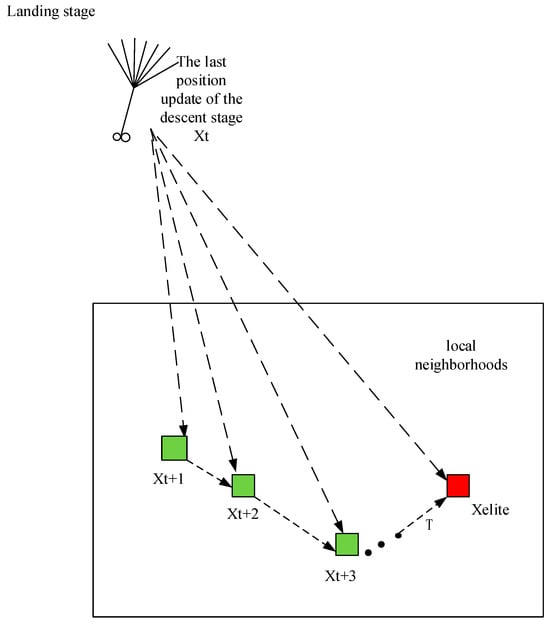
Figure 6.
Movement behavior during the landing process of dandelions.
2.3. Time Complexity
To describe the running time of the algorithm, we can use different mathematical formulas for analysis. However, in the field of computer science, there is a specialized term to characterize the time complexity of algorithms, namely big O notation. Big O notation does not indicate how long the algorithm needs to run; it represents the speed at which the algorithm’s running time increases, that is, the running time of the algorithm increases at different speeds, which is known as the overall time complexity. In big O notation, the formula for time complexity is
where f (n) represents the sum of the number of times each line of code is executed, while O represents a proportional relationship.
The total time complexity of the DO algorithm includes three aspects: population initialization, three iterative update processes, and each individual iteration. When the DO algorithm starts executing, it takes O (pop × Dim) time to initialize the population during the initialization stage. Among them, pop represents the population size, and Dim represents the dimension of the variable. When the initialization stage of dandelion ends and the iterative update process begins, it is necessary to calculate the fitness value of the population, which requires an amount of time equal to O (pop × f). Among them, f is the objective function for defining the problem. Also, because the iterative updating process of dandelions includes three stages, namely the ascending stage, the descending stage, and the landing stage, each stage requires some time until the maximum number of iterations T is completed; therefore, an amount of time equaling O (pop × Dim × T) is required for the three stages. Among them, T represents the maximum number of iterations. Moreover, each iteration in the three stages also requires time, with each iteration taking O (m) to find the optimal solution for the current dandelion, which is the most suitable location for dandelion growth. In summary, the total time complexity of the DO algorithm throughout the entire iteration process is O (m × pop × Dim × f × T).
3. Linear Antenna Array Synthesis
3.1. Geometric Illustration of Linear Antenna Array
A geometric representation of a linear antenna array is shown in Figure 7. As shown in the figure, the linear antenna array consists of 2N array elements arranged symmetrically on a horizontal line. If the array elements are arranged at an equal distance, it is called an equidistant symmetric array. If the distance between the array elements is not equal, it is called a non-equidistant symmetric array. When the DO algorithm is used to optimize the linear antenna array, it is necessary to calculate the array factor. The electric field in the far field of the dipole can be expressed as Equation (20) [27].
where Idl is the excitation amplitude, is the impedance of free space, k is the wave number of free-space waves, , and is the wavelength.
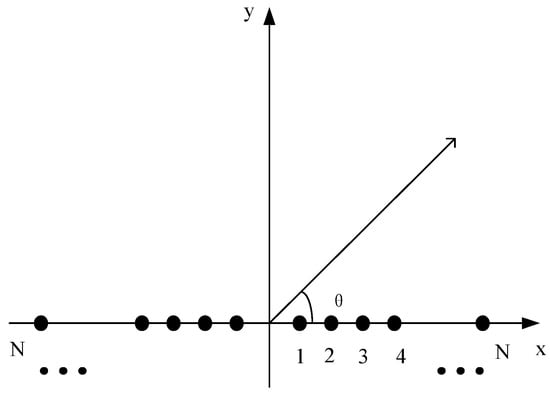
Figure 7.
Geometric illustration of a linear antenna array.
For antenna arrays, the far-field radiation pattern can be represented as the product of element factor EF (θ) (EF (θ) = sin θ for electric dipole and EF (θ) = 1 for isotropic source) and array factor AF (θ), as shown in Equation (21).
In this article, we consider an antenna array composed of isotropic sources, so we can ignore the influence of the far-field expression EF (θ) here, and only the array factor AF (θ) is considered. The array factor AF (θ) of a far-field linear symmetric antenna array is given by [28].
where In and φn are the excitation amplitude and phase in the array, and xn denotes the position of the array element. k is the wave number and is given by and θ is the azimuth angle.
Two types of simulation experiments are conducted on linear arrays to verify the superiority of the DO algorithm. One type is an equidistant linear array, where the amplitude of the array elements is optimized assuming that the excitation phase of the array elements is 0; the other type involves optimizing the spacing of array elements based on the assumption that the excitation amplitude and phase of the array elements remain unchanged, in order to obtain the desired directional pattern.
3.2. Antenna Current Optimization
The DO algorithm is used for pattern synthesis design of linear array antennas to obtain the desired pattern. Examples 1–5 are provided to demonstrate how to optimize the current amplitudes In for the best pattern synthesis. Because the handling phase involves a great deal of complexity, the excitation current phase is set to 0, that is, φn = 0.
The array factor for optimizing antenna current amplitude is changed from Equation (22) to Equation (23):
In an equally spaced antenna array, the positions of antenna elements are fixed as xn = nd, where d is equal to .
3.2.1. Minimizing Peak SLL
As shown in [29,30], the fitness function used to reduce peak SLL is written as follows:
Here, gives the maximum SLL (peak SLL). is the array factor given by Equation (23).
In order to reduce the peak SLL, this section provides two design examples that demonstrate how the DO algorithm can be used to optimize antenna current amplitudes. For both situations, the fitness function provided by Equation (24) is applied. The population (N) of the DO algorithm is set to 40 and the number of iterations is set to 1000.
Design Example 1: We consider a 2N = 16 linear array to achieve the lowest possible SLL in regions θ = [0°, 76°] and θ = [104°, 180°]. We optimize this antenna model using different algorithms, including traditional methods such as the Chebyshev method [31] and the Taylor method [31], as well as popular evolutionary algorithms such as the PSO algorithm [29] and the ant lion optimization (ALO) algorithm [32] and compare them with the DO algorithm. Table 2 shows the peak SLL values obtained by a uniform array, the Chebyshev method [31], Taylor method 1 (Taylor one-parameter distribution) [31], Taylor method 2 (Taylor distribution) [31], and the PSO [29], ALO [32], and DO algorithms as well as their corresponding excitation current amplitude values. According to the optimized excitation current amplitude values in Table 2, the optimized antenna array pattern of the model can be drawn. Moreover, based on the size of the optimized peak SLL, it is possible to visually compare which algorithm has stronger optimization ability in reducing antenna sidelobes. To be more precise, the peak SLL obtained by the DO algorithm is −35.69 dB, which is 22.54 dB lower than the peak SLL of a uniform array, 4.99 dB lower than the array optimized by the Chebyshev method [31], 4.99 dB lower than the array optimized by Taylor method 1 [31], 6.09 dB lower than the array optimized by Taylor method 2 [31], and 5.06 dB lower than the array optimized by the PSO [29] algorithm. The peak SLL decreased from −30.85 dB to −35.69 dB (by 4.84 dB) compared with the ALO [32] algorithm. Figure 8 depicts the pattern obtained by a uniform array and the optimized array patterns of the six methods. Meanwhile, Figure 9 shows the three-dimensional radiation patterns (two-dimensional plane rotates 180° around the z axis) before and after optimization by the DO algorithm.

Table 2.
Peak SLL is minimized with optimal current amplitudes.
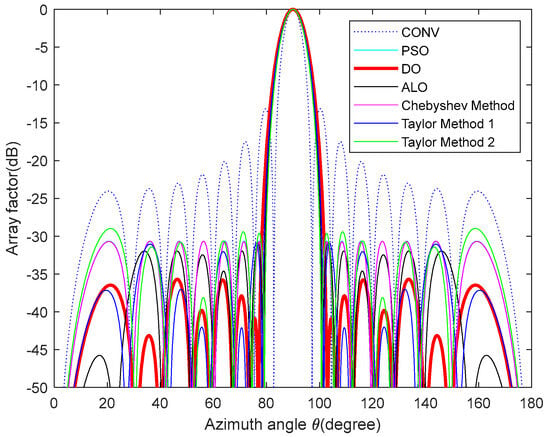
Figure 8.
Array patterns for design Example 1.
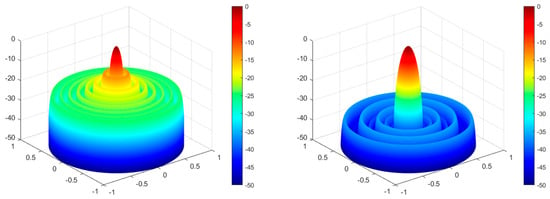
Figure 9.
DO algorithm optimization—3D radiation pattern before and after optimization for design Example 1.
Design Example 2: we present an array with 2N = 24 elements to achieve minimum SLL. Three algorithms, namely the modified spider monkey optimization (MSMO) algorithm [33], the runner-root algorithm (RRA) [34], and the DO algorithm, are used to optimize the excitation current amplitude of the array; the excitation current amplitudes and the results of peak SLL suppression are summarized in Table 3. According to the optimized excitation current amplitude values in Table 3, the optimized antenna array pattern of the model can be drawn. Moreover, based on the size of the optimized peak SLL, it is possible to visually compare which algorithm has stronger optimization ability in reducing antenna sidelobes. It can be seen that the peak SLL values provided by the MSMO [33] algorithm and RRA [34] are −37.52 dB and −41.08 dB; the DO algorithm can reduce the peak SLL value to −42.56 dB, which is equivalent to a decrease of 5.04 dB compared to the MSMO [33] algorithm and 1.48 dB compared to RRA [34], although the DO algorithm causes a slight broadening of the main lobe (FNBW) compared to the other three. Figure 10 shows the original uniform array and the array direction optimized by three algorithms. Figure 11 shows the array pattern and 3D radiation patterns (two-dimensional plane rotates 180° around the z axis) of the 24 elements of the LAA before and after DO algorithm optimization. From the figure, it can be observed that the DO algorithm has better optimization performance in reducing the level of the sidelobes.

Table 3.
Optimized excitation amplitudes: 2N = 24 elements.
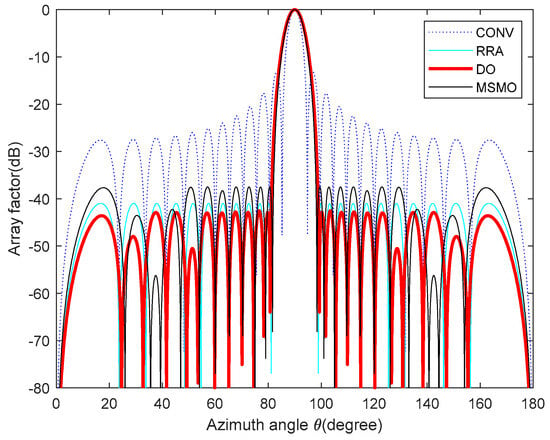
Figure 10.
Array patterns for design Example 2.
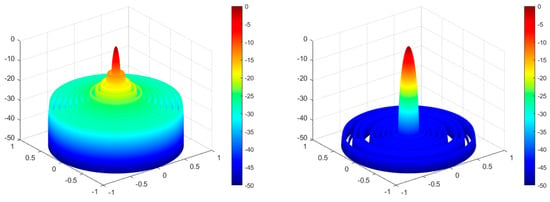
Figure 11.
DO algorithm optimization—3D radiation pattern before and after optimization for design Example 2.
3.2.2. Minimizing Peak SLL and Forming Deep Nulls
In this section, while reducing peak SLL, we need to achieve deep nulls in the specified directions to counteract the impact of strong interference on the performance of the array; the fitness function is shown in Equation (25) [30]:
where θli and θui are the spatial regions in which SLL is suppressed and θi = θui − θli. The null direction is given by θk. The first term of the fitness function in Equation (25) accounts for SLL suppression, and the second term takes into consideration the nulls in the desired directions. is the array factor given by Equation (23). The fitness function used for Example 3, Example 4, and Example 5 are given by Equation (25).
Design Example 3: The DO algorithm is considered to optimize the excitation current amplitude of 20 elements of a linear array to minimize the SLL and form deep nulls. We reduce the SLL in the regions of θ = [0°, 76°] and θ = [104°, 180°] as well as form deep nulls at θ = 76° and θ = 104°. The population size (N) is set to 20 and the maximum number of iterations is set to 500. Figure 12 shows the array patterns optimized by three algorithms. The 3D radiation patterns (two-dimensional plane rotates 180° around the z axis) are shown in Figure 13. The excitation current amplitude values optimized by the DO algorithm are listed in Table 4. From Table 4, the amplitude values of the excitation current for optimizing a 20-element linear array using the DO algorithm can be obtained. Based on these 10 current values, the antenna array pattern optimized by the DO algorithm under this condition can be drawn, providing readers with a clear and intuitive perspective. A comparison of the peak SLL values and null depths are shown in Table 5. From Table 5, we can obtain the peak SLL and null depth of each algorithm after optimizing the antenna array model. The smaller the peak SLL and null depth, the stronger the optimization ability of this algorithm compared to other algorithms.
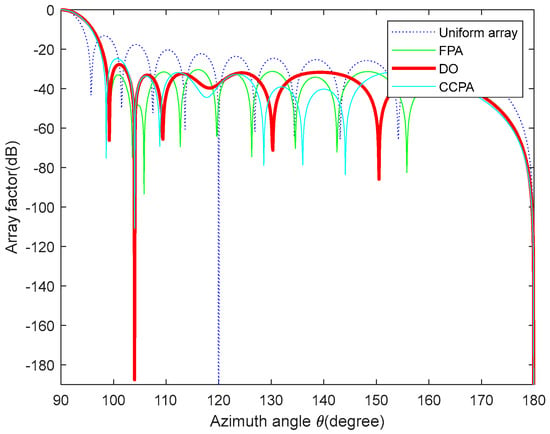
Figure 12.
Array patterns for design Example 3.
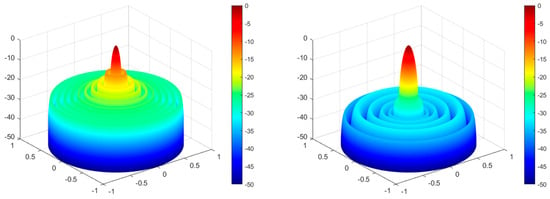
Figure 13.
DO algorithm optimization—3D radiation pattern before and after optimization for design Example 3.

Table 4.
The optimal excitation current amplitudes obtained using the DO algorithm.

Table 5.
Comparison of 20-element linear array results optimized by different algorithms.
As shown in Table 5, the DO algorithm obtains better results than FPA [35] and CCPA [36]. For the maximum SLL, the maximum SLL value obtained by the DO algorithm is −31.72 dB, which is 0.41 dB and 0.15 dB lower than the maximum SLL optimized by FPA [35] and CCPA [36], respectively. Meanwhile, for the depth of nulls, the DO algorithm obtains a depth of nulls equaling −187.6 dB, which is 66.7 dB and 44.3 dB lower than that of FPA [35] and CCPA [36], respectively. This shows that the DO algorithm has a better performance in optimizing linear antenna arrays.
Design Example 4: A 20-element linear array is considered, with the design objective of forming low sidelobes in the regions θ = [0°, 82°] and θ = [98°, 180°] and deep nulls at θ = 64°, 76°, 104°, and 116°. The GWO [37] algorithm and the DO algorithm are used to optimize the excitation current amplitude of the array, and the excitation current amplitude values are listed in Table 6. According to the optimized excitation current amplitude values in Table 6, the 20-element linear array patterns optimized by different algorithms can be drawn. A comparison of the peak SLL values and null depths are shown in Table 7. Based on the optimized peak SLL and null values in Table 7, it can be determined which algorithm reduces SLL lower and forms deeper nulls. Obviously, the null depth obtained by using the DO algorithm is −131.6 dB, which is 108.9 dB lower than that of a uniform array and 39.58 dB lower than a GWO [37] algorithm-optimized array. Compared to the GWO [37] algorithm-optimized array and uniform array, the null depths obtained with the DO algorithm are substantially higher. The peak SLL obtained using the DO algorithm is −29.39 dB, which is 16.20 dB lower than that of the uniform array and 0.95 dB lower than the peak SLL optimized by the GWO [37] algorithm. Although the DO algorithm slightly widens the main lobe width of the antenna array compared to the GWO [37] algorithm, the peak SLL optimized by the DO algorithm is lower and the nulls are deeper, which is more conducive to suppressing strong interference in the antenna array and, thus, improving the radiation efficiency of the array. The antenna array optimized by the GWO [37] algorithm has poor anti-interference ability. Therefore, the DO algorithm is better than the GWO [37] algorithm in optimizing the performance of the antenna array.

Table 6.
Optimized excitation amplitudes of 2N = 20 elements for Example 4.

Table 7.
Peak SLL and null depths for Example 4.
The population (N) of the DO algorithm is set to 30 and the number of iterations is set to 1000. The array patterns are depicted in Figure 14. Figure 15 displays the 20-element LAA’s 3D radiation patterns (two-dimensional plane rotates 180° around the z axis) before and after DO algorithm optimization.
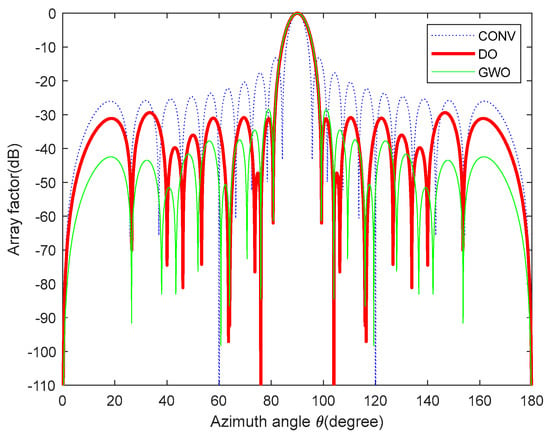
Figure 14.
Array patterns for design Example 4.
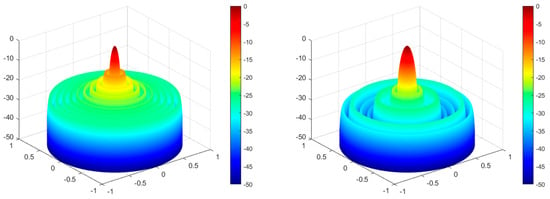
Figure 15.
DO algorithm optimization—3D radiation pattern before and after optimization for design Example 4.
Design Example 5: The fifth example uses DO to realize maximum SLL reduction and notch (i.e., continuous multiple nulls) placement of a 20-element linear array; the region in which the SLL is reduced is θ = [0°, 82°] and θ = [98°, 180°] and it needs to form a notch in the specific direction interval θ [50°, 60°] [120°, 130°]. The population size is 30, and there are 500 iterations in total. Figure 16 shows the original uniform array and the array patterns optimized by three algorithms. The 3D radiation patterns (two-dimensional plane rotates 180° around the z axis) are shown in Figure 17.
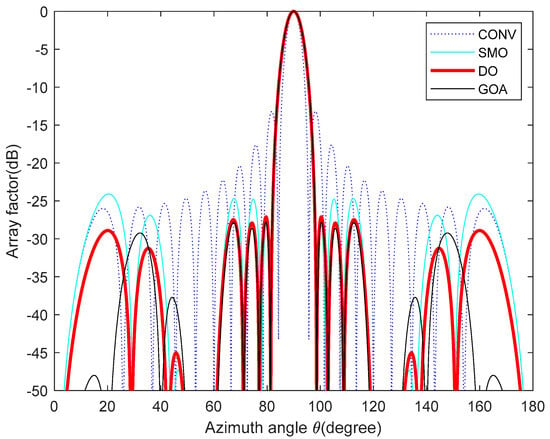
Figure 16.
Array patterns for Example 5.
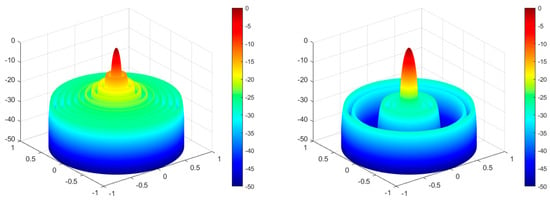
Figure 17.
DO algorithm optimization—3D radiation pattern before and after optimization for design Example 5.
Table 8 shows the peak SLL values and notch depths obtained by a uniform array, the SMO [16] algorithm, GOA [38], and the DO algorithm as well as their corresponding excitation current amplitude values. Based on the amplitude values of the excitation current in the table, the SMO [16] algorithm, GOA [38], and the DO algorithm can all draw corresponding optimized antenna array patterns. According to the results, the DO algorithm can achieve the maximum SLL of −27.1 dB, and the maximum SLL of notch depths is −63.1 dB. The maximum SLL of the DO algorithm-optimized array is 3 dB lower than that of the SMO [16] algorithm-optimized array, and the maximum SLL of notch depths is 6.4 dB and 1.9 dB lower than that of the SMO [16] algorithm-optimized array and the GOA [38]-optimized array, respectively. Therefore, the DO algorithm has more benefits in reducing the maximum SLL and notch depths.

Table 8.
Excitation amplitudes of 20-element linear array after optimization for Example 5.
3.3. Antenna Position Optimization
The DO algorithm is used for pattern synthesis design of linear array antennas to obtain the desired pattern. In order to create the best pattern synthesis with minimum SLL and deep nulls, Examples 6 and 7 in this section show how to optimize the antenna positions xn. It is supposed that In = 1 and φn = 0 for the amplitude and phase of the excitations are uniform.
3.3.1. Minimizing Peak SLL
For minimizing peak SLL, the fitness function is given by Equation (24). It is required to impose an additional restriction on the overall length of the antenna array to retain the main lobe shape and beam width, as seen in the following formula:
The position of the first antenna is fixed at 0.25 λ, the spacing between adjacent elements is 0.5 λ, and the position of the Nth element is fixed at , where the uniform LAA’s standard spacing is indicated by d = 0.5 λ.
Design Example 6: A 2N = 16-element linear array is considered, with the design objective of forming low sidelobes in the regions θ = [0°, 82°] and θ = [98°, 180°]. The population size is 30, and there are 500 iterations in total. Seven algorithms, namely the PSO [39] algorithm, particle swarm optimization and gravitational search algorithm (PSOGSA) [39], whale optimization algorithm (WOA) [39], GOA [39], sparrow search algorithm (SSA) [39], modified sparrow search algorithm (MSSA) [39], and DO algorithm, are used to optimize the position of the array. Table 9 provides a summary of the element positions and the peak SLL values that were optimized using these nature-inspired optimization algorithms. According to the optimized array element positions in Table 9, the optimized antenna array pattern under this model can be drawn. In addition, based on the size of the optimized peak SLL, it is possible to visually compare which algorithm has stronger optimization ability in reducing antenna SLL. More specifically, the conventional method (uniform array) and PSO [39], PSOGSA [39], WOA [39], GOA [39], SSA [39], and MSSA [39] algorithm-optimized arrays provide a peak SLL of −13.1476 dB, −21.3693 dB, −21.8484 dB, −19.1546 dB, −19.9808 dB, −22.0177 dB, and −22.6768 dB, respectively. The DO algorithm-optimized array gives a peak SLL of −22.8766 dB which is 9.729 dB lower and 0.1998 dB lower compared to that of the uniform array and MSSA [39]-optimized array. The array pattern optimized by these algorithms and the 3D radiation patterns (two-dimensional plane rotates 180° around the z axis) of the 16-element LAA before and after DO algorithm optimization are given in Figure 18 and Figure 19.

Table 9.
Sixteen-element LAA with optimized element positions and maximum SLL using different algorithms.
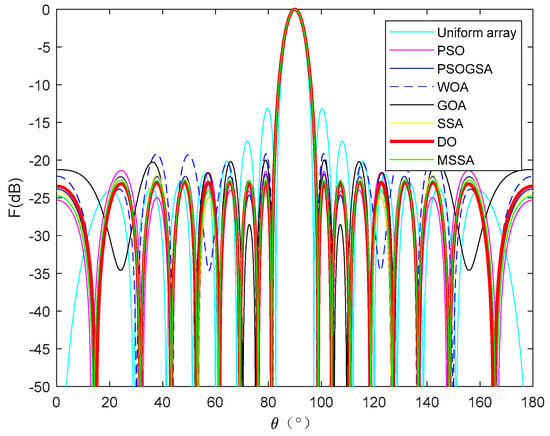
Figure 18.
Array patterns for Example 6.
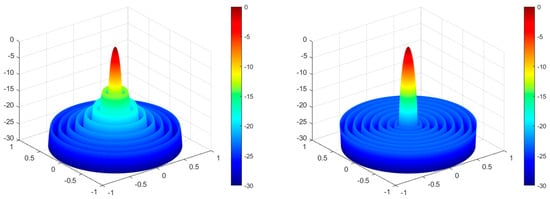
Figure 19.
DO algorithm optimization—3D radiation pattern before and after optimization for design Example 6.
3.3.2. Minimizing Peak SLL and Forming Deep Nulls
Design Example 7: This example shows how to use the DO algorithm to optimize the positions of a 32-element linear array for SLL minimization and the formation of deep nulls. The fitness function used in this case is provided by Equation (25). SLL reduction is desired in the regions θ = [0°, 85°] and θ = [95°, 180°], and deep nulls at θ = 81° and θ = 99° are also desired. The population (N) of the DO algorithm is set to 30 and the number of iterations is set to 1000.
Figure 20 shows the original uniform array and the array direction optimized by CSO [40], GWO [37], and DO algorithms. The 3D radiation patterns (two-dimensional plane rotates 180° around the z axis) are shown in Figure 21. Table 10 provides the optimized positions of the array elements obtained by a uniform array and the CSO [40] algorithm, GWO [37] algorithm, and DO algorithm. According to the optimal array positions obtained by each algorithm in Table 10, their optimal antenna array patterns under the model can be plotted. Table 11 shows the peak SLL values, the null depths, and the FNBW. By comparing the data results in Table 11, the degree to which each algorithm reduces SLL and the depth of nulls formed can be determined. It is very easy to see that the CSO [40] algorithm offers a null depth of −80 dB and the GWO [37] algorithm gives −106 dB nulls. However, the placement of nulls up to −125.1 dB deep at the desired directions (θ = 81° and θ = 99°) is achieved by the DO algorithm; it is seen that the null depth obtained by using the DO algorithm-optimized array is 45.1 dB lower than the CSO [40] algorithm-optimized array and 19.1 dB lower than the GWO [37] algorithm-optimized array, and the FNBW does not exceed the required 10° either. It can also be seen that the peak SLL values provided by CSO [40] algorithm and GWO [37] algorithm are −18.5092 dB and −15.9686 dB; the DO algorithm can reduce the peak SLL value to −20.1012 dB, which is equivalent to a decrease of 1.592 dB compared to the CSO [40] algorithm and 4.1326 dB compared to the GWO [37] algorithm. Thus, the DO algorithm is better than the CSO [40] algorithm and the GWO [37] algorithm in optimizing the performance of the antenna array.
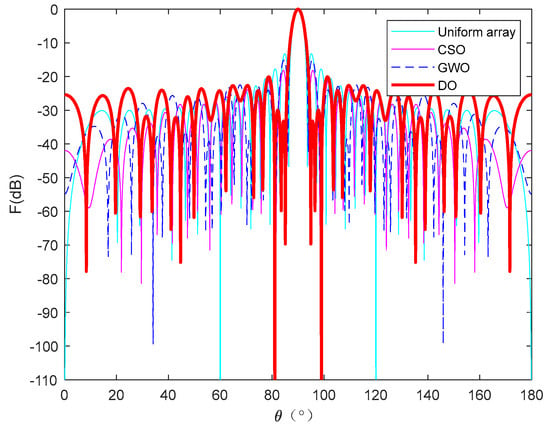
Figure 20.
Array patterns for Example 7.
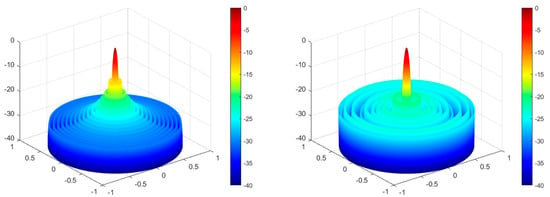
Figure 21.
DO algorithm optimization—3D radiation pattern before and after optimization for design Example 7.

Table 10.
Positions that are optimized for the 32-element array for Example 7.

Table 11.
Peak SLL (dB), null depth (dB) and FNBW (deg) comparison for Example 7.
4. Conclusions
In this paper, the dandelion optimization algorithm’s mathematical model and basic principles are briefly introduced, and it is the first time that the algorithm has been used to optimize a linear antenna array. In order to obtain an array pattern with the lowest SLL and deep nulls in the designated directions, the DO algorithm was used to design six simulation experiments from two situations of optimizing current amplitudes and optimizing array element spacings. In the first two examples, only the sidelobe of the antenna is lowered, and the sidelobe is reduced by a lower degree than other algorithms when the main lobe of the antenna is basically not widened. Examples 3, 4, and 5 use the DO algorithm to optimize the amplitudes of the current to reduce SLL and generate deep nulls and deep notches at specific directions, and the data show that the DO algorithm produces deeper nulls and notches than other algorithms. This is more conducive to the array antenna system in eliminating interference from interference sources. The last two examples involve reducing the sidelobes and generating the deep nulls by optimizing the array element spacing. The results show that the array pattern obtained using the DO algorithm has lower sidelobes and deeper nulls. The six simulation experiments above show that the optimization of the array antenna can not only optimize the current amplitudes of the antenna but also optimizes the positions of the antenna, and the DO algorithm outperforms other existing algorithms discussed here in terms of reducing peak SLL and obtain the depth of nulls. This also explains the viability of the DO algorithm for optimizing antenna arrays and even other electromagnetic problems. Of course, the DO algorithm also has certain limitations. In future work, the authors will focus on improving the DO algorithm by introducing a nonlinear growth factor to overcome its slow convergence speed and tendency to fall into local optima. The improved algorithm should not only be applied to the optimization of linear arrays but also extended to the optimization of planar arrays and even time-modulated arrays for further research. In addition, the authors will no longer be limited to theoretical antenna model simulation optimization but rather closer to real-world engineering applications. We will enrich the resources of our laboratory and strive to link evolutionary algorithms with EM simulation software such as HFSS (Version 2020 R2). We will no longer only use algorithms to optimize antenna models, nor will we solely use HFSS embedded optimization tools to design antenna models. Instead, the two are combined by firstly optimizing the antenna model with an algorithm and secondly outputting the optimization results in HFSS, modeling and designing the antenna model based on the optimization results, and then analyzing the electromagnetic parameters. Finally, efforts were made to create various simple small antenna arrays. Combining theoretical research with practical applications will further promote the development of electromagnetics.
Author Contributions
J.L. (the first author) proposed the idea and conducted simulation experiments to obtain experimental results according to the direction of the research and organized the data and wrote the paper. Y.L. (the corresponding author) is mainly responsible for supervising and reviewing papers, including the correctness of research ideas and the standardization of language expression in the manuscript. W.Z. and T.Z. (the third and fourth authors) built on the details of the completed paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Program No. 62341124), the Yunnan Fundamental Research Projects (Program No. 202201AT070030), the Graduate Research Innovation Fund of Yunnan Normal University (Program No. 009002050205502002), and the Scientific Research Fund of Yunnan Provincial Education Department (Program No. 2024Y150)).
Data Availability Statement
All data generated or analyzed during this study are included in this article. For the other algorithms in this study, the data were taken from the cited references to compare these data with the results obtained by the DO algorithm in this study and to determine the superior performance of the DO algorithm.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, Y.H.; Sun, B.H.; Guo, J.L. A low-cost, single-layer, dual circularly polarized antenna for millimeter-wave applications. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 651–655. [Google Scholar] [CrossRef]
- Bilgic, M.M.; Yegin, K. Modified annular ring antenna for GPS and SDARS automotive applications. IEEE Antennas Wirel. Propag. Lett. 2015, 15, 1442–1445. [Google Scholar] [CrossRef]
- Mobashsher, A.T.; Pretorius, A.J.; Abbosh, A.M. Low-profile vertical polarized slotted antenna for on-road RFID-enabled intelligent parking. IEEE Trans. Antennas Propag. 2019, 68, 527–532. [Google Scholar] [CrossRef]
- Liu, J.L.; Su, T.; Liu, Z.X. High-gain grating antenna with surface wave launcher array. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 706–709. [Google Scholar] [CrossRef]
- Huang, H.; Gao, S.; Lin, S.; Ge, L. A wideband water patch antenna with polarization diversity. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1113–1117. [Google Scholar] [CrossRef]
- Pietrenko-Dabrowska, A.; Koziel, S.; Ullah, U. Reduced-cost two-level surrogate antenna modeling using domain confinement and response features. Sci. Rep. 2022, 12, 4667. [Google Scholar] [CrossRef] [PubMed]
- Pietrenko-Dabrowska, A.; Koziel, S. On EM-driven size reduction of antenna structures with explicit constraint handling. IEEE Access 2021, 9, 165766–165772. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Design-oriented modeling of antenna structures by means of two-level kriging with explicit dimensionality reduction. AEU-Int. J. Electron. Commun. 2020, 127, 153466. [Google Scholar] [CrossRef]
- Sarker, M.A.; Hossain, M.S.; Masud, M.S. Robust beamforming synthesis technique for low side lobe level using taylor excited antenna array. In Proceedings of the 2016 2nd International Conference on Electrical, Computer & Telecommunication Engineering (ICECTE), Rajshahi, Bangladesh, 8–10 December 2016; IEEE: New York, NY, USA, 2016; pp. 1–4. [Google Scholar]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Davis, L.D. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York, NY, USA; Santa Fe, NM, USA, 1991. [Google Scholar]
- Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341. [Google Scholar] [CrossRef]
- Goudos, S.K.; Siakavara, K.; Sahalos, J.N. Novel spiral antenna design using artificial bee colony optimization for UHF RFID applications. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 528–531. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Rajo-Iglesias, E. Ant colony optimization in thinned array synthesis with minimum sidelobe level. IEEE Antennas Wirel. Propag. Lett. 2006, 5, 349–352. [Google Scholar] [CrossRef]
- Al-Azza, A.A.; Al-Jodah, A.A.; Harackiewicz, F.J. Spider monkey optimization: A novel technique for antenna optimization. IEEE Antennas Wirel. Propag. Lett. 2015, 15, 1016–1019. [Google Scholar] [CrossRef]
- Goudos, S.K.; Siakavara, K.; Samaras, T.; Vafiadis, E.E.; Sahalos, J.N. Self-adaptive differential evolution applied to real-valued antenna and microwave design problems. IEEE Trans. Antennas Propag. 2011, 59, 1286–1298. [Google Scholar] [CrossRef]
- Ram, G.; Mandal, D.; Kar, R.; Ghoshal, S.P. Cat swarm optimization as applied to time-modulated concentric circular antenna array: Analysis and comparison with other stochastic optimization methods. IEEE Trans. Antennas Propag. 2015, 63, 4180–4183. [Google Scholar] [CrossRef]
- Darvish, A.; Ebrahimzadeh, A. Improved fruit-fly optimization algorithm and its applications in antenna arrays synthesis. IEEE Trans. Antennas Propag. 2018, 66, 1756–1766. [Google Scholar] [CrossRef]
- Karimkashi, S.; Kishk, A.A. Invasive weed optimization and its features in electromagnetics. IEEE Trans. Antennas Propag. 2010, 58, 1269–1278. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]
- Einstein, A. Investigations on the Theory of the Brownian Movement; Courier Corporation: North Chelmsford, MA, USA, 1956. [Google Scholar]
- Mantegna, R.N. Fast, accurate algorithm for numerical simulation of Levy stable stochastic processes. Phys. Rev. E 1994, 49, 4677. [Google Scholar] [CrossRef]
- Valian, E.; Mohanna, S.; Tavakoli, S. Improved cuckoo search algorithm for global optimization. Int. J. Commun. Inf. Technol. 2011, 1, 31–44. [Google Scholar]
- Yahya, M.; Saka, M.P. Construction site layout planning using multi-objective artificial bee colony algorithm with Levy flights. Autom. Constr. 2014, 38, 14–29. [Google Scholar] [CrossRef]
- Raji, M.F.; Zhao, H.; Monday, H.N. Fast optimization of sparse antenna array using numerical Green’s function and genetic al-gorithm. Int. J. Numer. Model. Electron. Netw. Devices Fields 2020, 33, e2544. [Google Scholar] [CrossRef]
- Balanis, C.A. Microstrip antennas. Antenna Theory Anal. Des. 2005, 3, 811–882. [Google Scholar]
- Khodier, M.M.; Al-Aqeel, M. Linear and circular array optimization: A study using particle swarm intelligence. Prog. Electromagn. Res. B 2009, 15, 347–373. [Google Scholar] [CrossRef]
- Singh, U.; Kumar, H.; Kamal, T.S. Linear array synthesis using biogeography based optimization. Prog. Electromagn. Res. M 2010, 11, 25–36. [Google Scholar] [CrossRef]
- Chatterjee, S.; Chatterjee, S.; Poddar, D.R. Synthesis of linear array using Taylor distribution and Particle Swarm Optimisation. Int. J. Electron. 2015, 102, 514–528. [Google Scholar] [CrossRef]
- Saxena, P.; Kothari, A. Ant lion optimization algorithm to control side lobe level and null depths in linear antenna arrays. AEU-Int. J. Electron. Commun. 2016, 70, 1339–1349. [Google Scholar] [CrossRef]
- Singh, U.; Salgotra, R. Optimal synthesis of linear antenna arrays using modified spider monkey optimization. Arab. J. Sci. Eng. 2016, 41, 2957–2973. [Google Scholar] [CrossRef]
- Subhashini, K.R. Runner-root algorithm to control sidelobe level and null depths in linear antenna arrays. Arab. J. Sci. Eng. 2020, 45, 1513–1529. [Google Scholar] [CrossRef]
- Urvinder, S.; Salgotra, R. Synthesis of linear antenna array using flower pollination algorithm. Neural Comput. Appl. 2018, 29, 435–445. [Google Scholar]
- Hu, K.; Liu, Y.; Zhao, K. Application of chaotic colony predation algorithm in electromagnetics. Phys. Scr. 2023, 98, 105516. [Google Scholar] [CrossRef]
- Saxena, P.; Kothari, A. Optimal pattern synthesis of linear antenna array using grey wolf optimization algorithm. Int. J. Antennas Propag. 2016, 2016, 1205970. [Google Scholar] [CrossRef]
- Wang, H.; Liu, C.; Wu, H.; Li, B.; Xie, X. Optimal pattern synthesis of linear array and broadband design of whip antenna using grasshopper optimization algorithm. Int. J. Antennas Propag. 2020, 2020, 5904018. [Google Scholar] [CrossRef]
- Liang, Q.; Chen, B.; Wu, H.; Ma, C.; Li, S. A novel modified sparrow search algorithm with application in side lobe level reduction of linear antenna array. Wirel. Commun. Mob. Comput. 2021, 2021, 9915420. [Google Scholar] [CrossRef]
- Pappula, L.; Ghosh, D. Linear antenna array synthesis using cat swarm optimization. AEU-Int. J. Electron. Commun. 2014, 68, 540–549. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).