Abstract
The cracking of ultra-long and large concrete structures with strong constraints is a key issue under the action of shrinkage and hydration heat. The length of section pouring during construction is one of the main parameters to control the cracking of concrete. In this paper, the shrinkage test of concrete specimens under the condition of coculture is carried out under the background of the landing gear slide test platform of large aircraft. The measured early shrinkage curve of the expanded concrete is obtained, and the finite element model is established. The effects of the casting thickness, mould temperature, and limited expansion rate on the stress and cracking of super-long and large concrete are studied. The results show that factors such as the casting thickness, mould temperature, and limited expansion rate have significant effects on the limited length of the section after pouring. When the casting thickness is increased by 200%, the limit of the section length is reduced by 42%. When the mould temperature increases by 66.7%, the section length limit decreases by 28.2%, while the value increases by 24.2%, with an increasing expansion rate of 75%. The relationship between the three parameters and the piecewise pouring length is approximately linear. The exact calculation of the section length limit of strongly constrained ultra-long mass concrete under different pouring thicknesses, mould temperatures, and limited expansion rates is derived, and a simplified calculation formula is also proposed through data regression analysis. The errors between them are less than 1.7%, which provides a basis for calculating the section length of strongly constrained ultra-long mass concrete construction.
Keywords:
super-long mass concrete; shrinkage test; strong restraint; segmental length; casting thickness; moulding temperature; restrained expansion rate MSC:
82-05
1. Introduction
The development of unstressed cracks in super-long mass concrete is mainly influenced by two major factors: the shrinkage and heat of hydration. In the process of mass concrete pouring, the cement hydration degree is high and the shrinkage has rapid development and large shrinkage, which are some of the important causes of cracks in the structure. The generation of cracks worsens the mechanical properties and durability of the components and affects the safety of the structure [1,2,3,4]. The shrinkage mechanism and crack resistance of mass concrete under dry conditions were studied, with the belief that the early shrinkage of mass concrete was larger, which would cause greater tensile stress [5,6,7]. If the stress exceeds the tensile strength of the concrete, the structure will crack.
To reduce the early cracks of concrete, methods for reducing the peak temperature of concrete to reduce the tensile stress and thus reduce the generation of cracks were proposed [8,9]. Different types of fiber reinforcements were suggested as additive materials to enhance the tensile strength and prevent the cracking of concrete [10,11,12]. However, these methods can rarely be used in actual mass concrete construction [13] due to the high costs. As a kind of industrial solid waste, fly ash produces a lot of pollution gas every year, and it costs little. In recent years, many studies have shown that concrete prepared with fly ash instead of partial cement can significantly reduce its hydration heat and shrinkage and thus reduce the cracks due to temperature effects. Pitroda et al. [14] studied the performance of concrete under different fly ash content and demonstrated the feasibility of using fly ash instead of cement in concrete productions. Through a comparative experimental study, Kalinski et al. [15] found that replacing ordinary Portland cement with fly ash was a promising method to alleviate the thermal cracking of mass concrete caused by temperature effects. Early hydration heat tests on concrete with different fly ash content were conducted [16,17], and it was found that the addition of fly ash could significantly reduce the early heat release of mass concrete and prevent cracking due to early temperature.
Methods that control the cracks of mass concrete structures subjected to strong restrictions and the shrinkage mechanism between the old and new surfaces are restrained [18,19,20,21]. The shrinkage of new concrete after casting is more different when it is subjected to the strong restraint effect of old concrete than when it is free, and this factor needs to be considered in the calculation. The heat of hydration of mass concrete is affected by the material properties, structural dimensions [22], moulding temperature, and other factors. The temperature field and stress caused by the heat of hydration for different structures were different [23,24,25]. Researchers [26,27,28,29] have theoretically discussed the causes of cracks from the perspective of the actual construction of mass concrete and determined that the casting length of the post-cast segment is important. They also proposed the critical segmental length under special working conditions but did not provide a general recommendation on the segmental length for various working conditions.
The COMAC Changsha Aviation Industry and R and D Base is an important project in the development strategy of “Building an aviation industry city with landing gear system as the leader” in the Hunan Province, China, and is one of the ten major science and technology innovation landmark projects in Changsha City. The taxiway test line platform is a super-long mass concrete structure consisting of a base slab and a runway panel. During the construction, the base slab was poured first, and then the runway panel was poured after a long period. The age difference between the two layers of concrete slabs is large, the deformation of the runway panel is strongly restrained by the base slab under the effect of temperature and shrinkage, and the concrete is subjected to obvious tensile stress. Effectively reducing the level of tensile stress in concrete during construction is the key issue for controlling cracks. At present, the “Standard for the Construction of Massive Concrete” GB50496-2018 [30] only stipulates that the maximum sub-block single size of segmental construction should not exceed 40 m. However, there is no reference standard for the length of the post-cast segment under different working conditions. Selecting the segmental casting length based only on construction experience may cause excessive structural stress, resulting in the formation of a large number of cracks. Therefore, this paper verifies the accuracy of the finite element model through shrinkage tests of concrete specimens and deformation and stress tests of the structure combined with finite element analysis. The effects of the casting thickness, moulding temperature, and restrained expansion rate on the segmental length limit of the post-cast segment are discussed in detail. A theoretical model as well as a numerical model are proposed for calculating the segmental length limits of the post-cast segment of super-long mass concrete under different working conditions, and the predicted results are compared and discussed.
2. Experimental Study and Finite Element Analysis
2.1. Project Description
The total length of the test line of the COMAC large aircraft was 1067 m. The main part of the concrete consisted of a post-cast segment of C40 micro-expansion concrete and a precast C30 concrete base slab with two layers. The size of the post-cast segment was 7.5 m wide and 1.5 m high. The base slab was cast as a whole with a pile foundation, and a permanent expansion joint was reserved for every three segments between the post-cast segments. The structure of the slide rail is shown in Figure 1. In this project, the upper post-cast segment was cast approximately 6 months after the first base slab was cast when the main shrinkage of the base slab in the early stage had been completed. At the same time, the concrete of the post-cast segment was directly laid on the chiselled concrete of the base slab, which had a strong restraining effect on the post-cast segment due to the large stiffness of the base slab and the pile foundation. The large age difference between the upper and lower layers of the concrete would lead to more obvious tensile stresses in the post-cast segment due to the strong interlayer restraint during the process of heat of hydration and shrinkage deformation. If the tensile stresses in the concrete exceed the tensile strength of the concrete at the same age, typical non-structural cracks would appear in the post-cast segment. Considering that the shrinkage stress and temperature stress in the post-cast segment caused by the strong interlayer restraint of two layers of concrete are affected by the segmental casting length of the post-cast segment, determining the segmental length limit of the post-cast zone is highly important for engineering crack resistance.
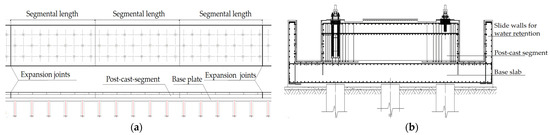
Figure 1.
Slider structure elevation diagram. (a) Elevation view. (b) Cross-sectional view.
2.2. Shrinkage Test Materials and Mixing Proportions
Based on the use of expansive concrete in the post-cast segment of this project, the shrinkage curve of the concrete after the incorporation of the expansion agent could not be calculated using the specifications. To accurately evaluate the effect of shrinkage on the concrete via a stress analysis, it was necessary to measure the shrinkage curve of the concrete through shrinkage tests. The mix ratio parameters of the concrete in this test are shown in Table 1. P-O42.5 Portland cement was selected for the cement, river sand (medium sand), and gravel (5–25 mm, continuous gradation) were selected for the fine and coarse aggregates. The particle size of the aggregates is shown in Table 2, the particle size curve is shown in Figure 2, and the mixing water was tap water. Class I fly ash was selected as the admixture. The fly ash content was determined to be 19.43% by referring to the test results of relevant scholars [31,32,33] and the “Application technical specification of fly ash concrete” GB/T50146-2014 [34]. The chemical composition of the cement is shown in Table 3. A UEA-W-modified low-alkali expansion agent was selected as the expansion agent, and the dosage was determined according to its replacement of the same amount of cementing material.

Table 1.
Concrete ratio parameters.

Table 2.
Aggregate grain size.
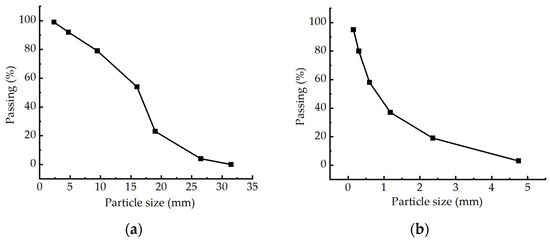
Figure 2.
Grain size curve of the aggregates. (a) Gravel. (b) River sand.

Table 3.
Chemical composition of the cement and fly ash (%).
2.3. Shrinkage Test
For the actual construction of the slide platform, micro-expansion concrete shrinkage tests were carried out at the construction site. The specimens were 100 mm × 100 mm × 515 mm standard-size specimens. One group was plain concrete, and the other group was 0.2% reinforced concrete (consistent with the structural reinforcement rate). The specimens and test equipment are shown in Figure 3a,b. The maintenance conditions were the same as those of the field structure, i.e., the specimens were covered with geotextiles, watered, and moisturized daily for 28 days. The measured temperature and humidity curves are shown in Figure 4a. The early shrinkage strain curves of the concrete specimens were obtained from field tests, as shown in Figure 4b. Under natural field curing conditions, the concrete specimens still showed a certain degree of shrinkage despite the admixture of the expansion agent, and the 360-day shrinkage strain of the plain concrete specimens was 242 με. The shrinkage strain was reduced by approximately 3% after reinforcement, and the shrinkage curves overlapped, indicating that the reinforcement had a reduced effect on the early shrinkage of the concrete when the reinforcement rate was the minimum reinforcement rate, which is consistent with the experimental conclusion obtained by [35]. In the following section, the shrinkage curves of the field slide concrete are used to further analyse the shrinkage and cracking of the actual structure.

Figure 3.
Concrete specimens. (a) Shrinkage specimens. (b) Shrinkage test equipment.
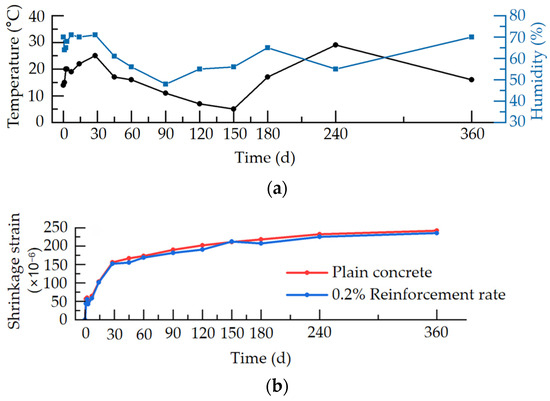
Figure 4.
Shrinkage test. (a) Temperature curve. (b) Humidity curve.
2.4. On-Site Test and Finite Element Analysis
Considering that the concrete shrinkage curve was obtained from actual measurements and that the deformation and stress law of the post-cast segment under strong restraint was not clear, the accuracy of the results of the direct finite element simulation should be verified. Therefore, it was necessary to test the actual deformation and stress state of the post-cast segment to verify the accuracy of the finite element model for further analysis. A 28 m post-cast segment was selected as the test segment at the construction site of the slide rail platform project. The displacement test element and stress test element were installed, and the initial length and initial stress were measured immediately after the sliding platform was cast and moulded. The displacement measurement points were arranged at the four corner points at the bottom of the top slab, as shown in Figure 5a. The change in the distance between the two angles was the displacement. The stress-strain measurement points were arranged at the top, middle, and bottom heights at the two ends and mid-span. The site stress gauge and strain gauge installation diagrams are shown in Figure 5b.
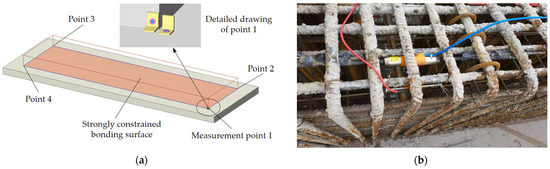
Figure 5.
Schematic of the field test. (a) Field displacement test schematic. (b) On-site stress gauge and strain gauge installation.
Midas/FEA was used to establish a three-dimensional finite element model of the structure, which included two parts: the roof of the C40 micro-expanded concrete after the pouring section and the bottom plate of the C30 concrete before the pouring section. The concrete slab used 3D eight-node solid units, with a total of 3360 units in the top plate and 2816 units in the bottom plate. The rebar used 1D beam units for a total of 170 units. The model divided the grid linearly according to the cell length standard, and the mesh size was 500 mm.
The bottom plate and pile foundation were cast as a whole, and the lower side of the bottom plate imposed fixed constraints. At the same time, convection with the environment was applied to the parts of the roof and bottom plate that were in contact with the external environment. Since the bottom plate was basically stable, the hydration heat was no longer considered, and the part of the bottom plate in contact with the pile foundation was set to a fixed temperature. The basic performance parameters of the concrete and reinforcement in the model are summarized in Table 4.

Table 4.
Material parameters.
The roof was a post-cast section; its shrinkage and creep characteristics should be considered, and shrinkage and creep functions should be introduced into the finite element model. The shrinkage data were input into the model with reference to the “Standard for Construction of Mass Concrete” GB50496-2018 [30] and modified according to the strain time history of the shrinkage test in Section 2.3. The creep coefficient was adopted with reference to [36]. The bottom plate could be considered to be basically stable, and its shrinkage was no longer considered. The contact state of the joint surfaces of two layers of concrete was simulated via symmetric bonding contact, and the stiffness between the contact surfaces was automatically calculated based on a penalty function. The heat of hydration function was introduced to simulate the heat of hydration in the post-pouring section. The heat of hydration data were input into the model with reference to the on-site temperature measurement data, and the action of the condensing tube within 7 days was considered. The concrete tensile strength time histories were calculated according to the “Standard for Construction of Mass Concrete” GB50496-2018 [30] and input into the model, where the concrete tensile strength timescale was calculated according to the following formula:
where ftk(t) is the standard value of the tensile strength of concrete when the age is t, ftk is the standard value of the tensile strength of concrete taken as 2.39 MPa, σ is the maximum allowable tensile stress, and K is the crack prevention safety factor taken as 1.15. The test and model calculation results are shown in Figure 6.
ftk(t) = ftk(1 − 10−0.3t)
σ ≤ ftk(t)/K
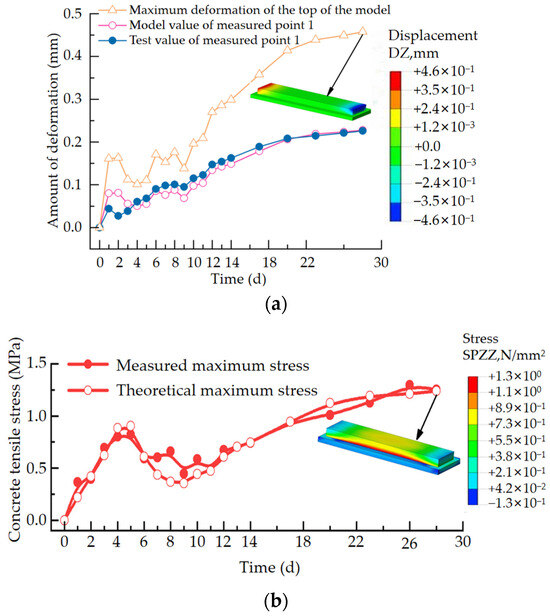
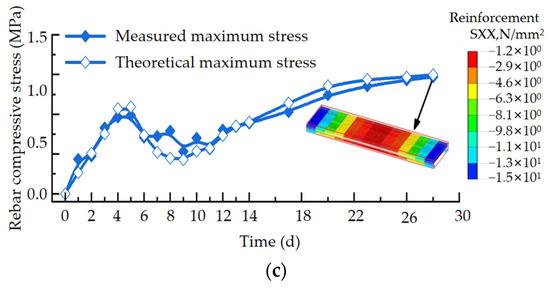
Figure 6.
Structural deformation curve and stress curve. (a) Deformation curve. (b) Concrete stress curve. (c) Rebar compressive stress.
As shown in Figure 6, the deformation curves at the bottom of the structure obtained from the test and the deformation curves obtained from the finite element model match, and the difference between the two was 1.0% at 28 days. The measured stresses of the concrete and reinforcement also had a high degree of agreement with the model results, which indicates that this slide structure model has high accuracy. Based on this model, the stresses in this test section were analysed under field construction conditions with different lengths of post-cast segments. The casting thickness was 1.5 m, the moulding temperature was 30 °C, and the shrinkage strain at 360 days for the reinforcement specimen was taken as the final restrained expansion rate of −0.0235%. According to the comparison between the FEA results and the tensile strength of the concrete, the segmental length limit of the post-cast segment under the construction of the test section of the background project in this paper was 40 m. Considering the safety reserve of engineering design and construction, the final length of the post-cast segment was determined to be 35 m.
3. Length Limits of Strongly Constrained Super-Long Concrete Segments
To determine the segmental length limits of strongly constrained super-long mass concrete under various conditions and to facilitate rapid application using construction units, this paper uses a finite element numerical simulation to explore the effects of parameters such as the casting thickness, moulding temperature, and restrained expansion rate and to establish a general calculation formula. The structural model is the same as that in Section 2.4. The width of the concrete in the post-cast section under the base condition was 7.5 m, the thickness was 1.5 m, the temperature in the mould was 26 °C, and the expansion agent was not mixed (according to the specification, the restrained expansion rate could be taken as −0.04%). The model input parameters are summarized in Table 5. Whether the maximum stress in the post-cast section exceeded the allowable tensile stress was used as the judgement criterion for the segmental length limit.

Table 5.
Model input parameters.
3.1. Casting Thickness
Considering that the minimum size of the concrete structure was not less than 1 m for mass concrete and the general concrete slab thickness was not more than 3 m, five typical casting thicknesses of 1 m, 1.5 m, 2 m, 2.5 m, and 3 m were selected in this section, and the rest of the conditions were the same as those of the foundation. The effect of the casting thickness on the stress and segmental length limit of the post-cast section was studied. By further subdividing the casting thickness based on the results, the relationship curve between the segmental length limit and casting thickness was obtained, and the results are shown in Figure 7.
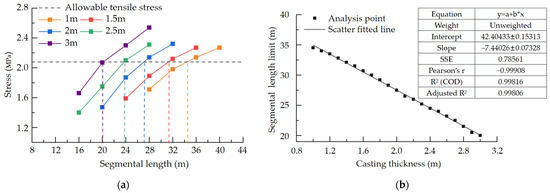
Figure 7.
Influence of the casting thickness on the segmental length limit. (a) Maximum stress of different segmental lengths for post-cast segments of different casting thicknesses. (b) Segmental length limits with casting thickness.
Figure 7a shows that to ensure that the stress in the post-cast section does not exceed the allowable tensile stress of 2.08 MPa, the greater the casting thickness is, the smaller the segmental length. The maximum segmental length was 20 m when the casting thickness was 3 m, and the maximum segmental length was 34.5 m when the casting thickness was 1 m. Under the same segmental length, the maximum stress in the post-cast segment increased with increasing casting thickness. From Figure 7b, it can be seen that when the casting thickness increases, the segmental length limit of the post-pouring section decreases, and the relationship between them is linear. The scattered points were linearly fitted with a scattered distribution according to the law of the segmental length limit under different casting thicknesses, and the fitted R2 (decidable coefficient) was 0.9982, which is a good fit.
3.2. Moulding Temperature
The “Standard for Construction of Mass Concrete” recommends that the moulding temperature of concrete should be controlled below 30 °C. In this section, to study the effect of the entry temperature on the stress and segmental length limit of the post-cast segment, four typical moulding temperatures of 18 °C, 22 °C, 26 °C, and 30 °C were selected, and the rest of the conditions were the same as the base conditions. At the same time, the relationship between the segmental length limit and the moulding temperature was obtained by further changing the moulding temperature, and the results are shown in Figure 8.
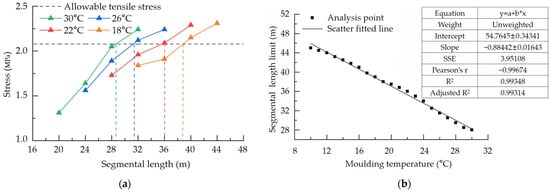
Figure 8.
Influence of moulding temperature on the segmental length limit. (a) Maximum stress of different segment lengths for the post-cast segment at different moulding temperatures. (b) Segmental length limit of the moulding temperature.
From Figure 8a, it can be seen that the lower the mould-in temperature is, the better it is to prevent cracks from developing. To ensure that the stress in the post-cast section does not exceed the allowable tensile stress of 2.08 MPa, the higher the moulding temperature is, the smaller the segmental length. The maximum segmental length was 28 m at 30 °C, and the maximum segmental length reached 39 m at 18 °C. The maximum stress in the post-cast segment increases with increasing moulding temperature for the same segment length. From Figure 8b, it can be seen that the segmental length limit of the post-cast segment decreases when the moulding temperature increases and the relationship between the two is linear. The scattered points were linearly fitted with a scattered distribution according to the law of the segmental length limit under different moulding temperatures, and the fitted R2 was 0.9935, which is a good fit.
3.3. Restrained Expansion Rate
To prevent early cracks due to shrinkage in the post-cast segment of concrete, the use of expansion agents as anti-cracking measures is considered in many mass concrete projects. According to the recommendation of the specification GB50496-2018 “Standard for the Construction of Mass Concrete” for a final shrinkage strain of −0.04% for concrete without an expansion agent, four expansion concrete conditions were selected with final restrained expansion rates of −0.020%, −0.015%, −0.010%, and −0.005% after the incorporation of the expansion agent, and the rest of the conditions were consistent with the base working conditions. The effect of the restrained expansion rate on the stress and segmental length limits of the post-cast segment was investigated. Additionally, after further subdividing the restricted expansion rate, the relationship curve between the segmental length limit and restrained expansion rate was obtained, and the results are shown in Figure 9.
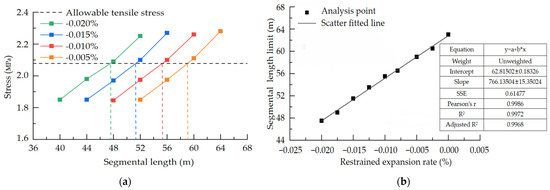
Figure 9.
Influence of the restrained expansion rate on the segmental length limit. (a) Maximum stress of different segmental lengths for the post-cast segments with different restrained expansion rates. (b) Segmental length limit of the restrained expansion rate.
In Figure 9a, to ensure that the stress in the post-cast section does not exceed the allowable tensile stress of 2.08 MPa, the larger the restrained expansion rate is, the larger the segmental length is. The maximum segmental length was 47.5 m when the restrained expansion rate was −0.020%, and the maximum segmental length reached 59 m when the restrained expansion rate was −0.005%. Under the same segment length, the maximum stress in the post-cast segment decreased with an increasing restrained expansion rate. Figure 9b shows that when the restrained expansion rate increases, the segmental length limit of the post-cast segment increases, and the relationship between the two is linear. The scattered points were linearly fitted with a scattered distribution based on the law of segmental length limits at different restrained expansion rates, and the fitted R2 was 0.9972, which indicates a good fit.
3.4. Practical Algorithm for Determining the Segmental Length Limit of Strongly Constrained Super-Long Mass Concrete
In Section 3.1, Section 3.2 and Section 3.2, the effects of the pouring thickness, entering temperature, and limiting expansion rate on the stresses in post-cast sections of super-long mass concrete were investigated, and it was concluded that the length of the post-cast sections was linearly related to these factors under a single factor. Since the casting thickness, temperature entering the mould, and restriction expansion rate are not related to each other, Equations (3)–(5) can be obtained.
where L is the segmental length limit (m) considering one of the factors of pouring thickness, entering temperature, and limiting expansion rate, H is the pouring thickness (m), T is the entering temperature (°C), and the final restrained expansion rate (%) of the standard specimen. If the expansion agent is added, the restrained expansion rate should be measured using the standard test regarding the relevant specification, and the specification can be taken as −0.04% without adding an expansion agent.
L(H) = f(T,α)H + a(T,α),
L(T) = g(H,α)T + b(H,α),
L(α) = m(H,T)α + c(H,T),
To enable the construction unit to quickly determine the segmental length limits of strongly constrained super-long mass concrete, this paper uses three variables, namely, the casting thickness, moulding temperature, and restrained expansion rate, and uses mathematical methods to derive and integrate them into a unified functional expression. The derivation process is briefly described as follows. By setting H = 1 and H = 2 in Equations (3)–(5), respectively, Equations (6) and (7) can be obtained.
f(T,α) + a(T,α) = g(1,α)T + b(1,α) = m(1,T)α + c(1,T)
2f(T,α) + a(T,α) = g(2,α)T + b(2,α) = m(2,T)α + c(2,T)
f(T,α) = g(1,α)T + b(1,α) − a(T,α)
Let T = 1 and T = 2 in Equations (6) and (7), respectively, to obtain Equations (9)–(12).
g(1,α) = [m(1,2) − m(1,1)]α + [c(1,2) − c(1,1)]
b(1,α) = [2m(1,1) − m(1,2)]α + [2c(1,1) − c(1,2)]
g(2,α) = [m(2,2) − m(2,1)]α + [c(2,2) − c(2,1)]
b(1,α) = [2m(2,1) − m(2,2)]α + [2c(2,1) − c(2,2)]
The general expressions of L concerning H, T, and α are provided in Equation (13) by combining Equation (3) with Equations (6)–(12).
L(H, T, α) = {[m(2,2) − m(2,1)]Tα + [c(2,2)-c(2,1)]T − [m(1,2)-m(1,1)]Tα + [c(1,2) − c(1,1)]T
+ [2m(2,1) − m(2,2)]α + 2c(2,1) − c(2,2)}H + {[2m(1,2) − m(1,1)]α + [2c(1,2) − c(1,1)]
− [m(2,2) − m(2,1)]α − c(2,2) + c(2,1)}T + [2m(1,1) − m(1,2)]α − [2m(2,1) − m(2,2)]α
+ 2c(1,1) − c(1,2) − 2c(2,1) + c(2,2)
+ [2m(2,1) − m(2,2)]α + 2c(2,1) − c(2,2)}H + {[2m(1,2) − m(1,1)]α + [2c(1,2) − c(1,1)]
− [m(2,2) − m(2,1)]α − c(2,2) + c(2,1)}T + [2m(1,1) − m(1,2)]α − [2m(2,1) − m(2,2)]α
+ 2c(1,1) − c(1,2) − 2c(2,1) + c(2,2)
The formula contains m(1,1), m(1,2), m(2,1), m(2,2), c(1,1), c(1,2), c(2,1), and c(2,2), for a total of eight unknowns, which can be solved by substituting the finite element calculation data to obtain all the unknowns. The final unified expression for L(H, T, α) in any case is shown in Equation (14).
L(H, T, α) = −0.0625HTα − 0.0025HT + 1.875Hα + 0.0625Tα − 7.575H − 0.9075T + 783.125α + 97.875
Because of the complexity of Equation (14), the calculation is relatively cumbersome when applied to specific engineering analyses. A segmental length limit regression model was fitted based on the results of each condition to facilitate the calculation, and the results are shown in Equation (15).
L(H, T, α) = −7.65H − 0.91T + 786.06α + 97.99
Empirically, the error in the calculation of Equations (14) and (15) is within 1%. The ANOVA results of the regression model are shown in Table 6, which reveals that the P value of the regression model is less than 0.0001, the F value is 13,130.69, and the R2 is 0.9988, indicating that the fitted regression model is highly significant.

Table 6.
Analysis of variance for the segmental length limit polynomial regression model.
The segmental length limits for different H, T, and α values are shown in Figure 10. Taking the post-cast segment of the super-long mass concrete structure of the slide rail in the background of this paper as an example, the segmental length limit calculated using the finite element in Section 2.4 is 40 m under the 1.5 m casting thickness, 30 °C moulding temperature, and −0.0235% restrained expansion rate, and under the same conditions, it is 40.7 m according to the regression model shown in Equation (15), with a relative error of only 1.7%, indicating that the accuracy of the formula is high. Similar to the age difference of super-long mass concrete layered casts or directly on the bedrock of super-long mass concrete projects under the strong constraint of the construction of post-cast sections, according to the actual casting thickness, moulding temperature, and restrained expansion rate, combined with the needs of the project, the accurate calculation of Formula (14) or the approximate calculation of Formula (15) are used to determine the segmental length limit to prevent post-cast section crack development.
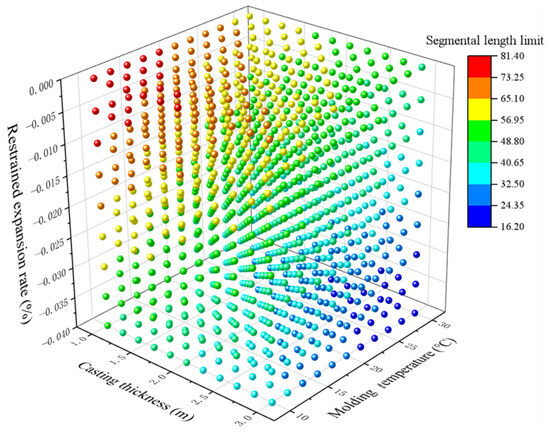
Figure 10.
Limit values of the segmental lengths of the post-cast section under different construction conditions.
4. Conclusions
In this paper, the factors that influence the early stresses of strongly confined super-large concrete structures were investigated through shrinkage tests and stress-strain monitoring combined with finite element analysis. The segmental length limits of post-cast sections under different casting thicknesses, inlet temperatures, and restricted expansion rates under general conditions were discussed, and a general method for calculating the segmental length limits of the post-cast sections was proposed. The main conclusions are listed as follows:
- (1)
- The segmental casting length has a large effect on the stress of strongly constrained super-long mass concrete structures. Increasing the segment length significantly increases the maximum stress in the post-cast segment. Factors such as the casting thickness, moulding temperature, and restrained expansion rate affect the segmental length limit of the post-cast segment. All of the parameters have a linear relationship with the segmental length limit;
- (2)
- The exact formula, as well as the simplified formula for calculating the segmental length limit of the post-cast segment considering the parameters of the casting thickness, moulding temperature, and restrained expansion rate, were derived from the analysis. A comparison between the results calculated from these formulae was conducted, and the maximum error was 1.7%, indicating the high accuracy of the proposed formulae. These formulae can be used to calculate the segmental length of post-cast sections in the construction of strongly constrained super-long mass concrete structures.
Author Contributions
Conceptualization, F.G.; Methodology, F.G.; Software, J.G. and N.Z.; Validation, D.L. and M.L.; Formal analysis, F.G. and D.L.; Investigation, M.N. and J.G.; Data curation, F.G. and D.L.; Writing—original draft preparation, D.L. and J.G.; Writing—review and editing, M.N.; Supervision, N.Z.; Funding acquisition, F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Comac Changsha Aviation Industry and Research and Development Base Project (No: HFW202200153).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, [Dezhou Li], upon reasonable request.
Conflicts of Interest
As for two co-authors from companies, the author Ning Zhang provided the design data and design calculation, and the author Lv Maofeng provided the raw materials and participated in the management and coordination of the experiment. Ning Zhang and Lv Maofeng have not published articles with me or other authors.
References
- Maruyama, I.; Lura, P. Properties of early-age concrete relevant to cracking in massive concrete. Cem. Concr. Res. 2019, 123, 105770. [Google Scholar] [CrossRef]
- Liu, J.; Tian, Q.; Miao, C. Investigation on the plastic shrinkage of cementitious materials under drying conditions: Mechanism and theoretical model. Mag. Concr. Res. 2012, 64, 550–561. [Google Scholar] [CrossRef]
- Hu, Y.H.; Chen, J.; Zou, F. A comparative study of temperature of mass concrete placed in August and November based on on-site measurement. Case Stud. Constr. Mater. 2021, 15, e00694. [Google Scholar] [CrossRef]
- Hamid, H.; Chorzepa, M.G. Quantifying maximum temperature in 17 mass concrete cube specimens made with mixtures including metakaolin and/or slag. Constr. Build. Mater. 2020, 252, 118950. [Google Scholar] [CrossRef]
- Liu, J.; Tian, Q.; Wang, Y.; Li, H.; Xu, W. Evaluation method and mitigation strategies for shrinkage cracking of modern concrete. Engineering 2021, 7, 348–357. [Google Scholar] [CrossRef]
- Klemczak, B.; Batog, M.; Pilch, M.; Żmij, A. Analysis of Cracking Risk in Early Age Mass Concrete with Different Aggregate Types. Procedia Eng. 2017, 193, 234–241. [Google Scholar] [CrossRef]
- Zhu, H.; Hu, Y.; Ma, R. Concrete thermal failure criteria, test method, and mechanism: A review. Constr. Build. Mater. 2021, 283, 122762. [Google Scholar] [CrossRef]
- Li, B.Q.; Wang, Z.H.; Jiang, Y.H. Temperature control and crack prevention during construction in steep slope dams and stilling basins in high-altitude areas. Adv. Mech. Eng. 2018, 10, 1687814017752480. [Google Scholar] [CrossRef]
- Do, T.A.; Hoang, T.T.; Thanh, B.T. Evaluation of heat of hydration, temperature evolution and thermal cracking risk in high-strength concrete at early ages. Case Stud. Therm. Eng. 2020, 21, 100658. [Google Scholar] [CrossRef]
- Shen, D.J.; Liu, X.Z.; Zeng, X. Effect of polypropylene plastic fibers length on cracking resistance of high performance concrete at early age. Constr. Build. Mater. 2020, 244, 117874. [Google Scholar] [CrossRef]
- Kouta, N.; Saliba, J.; Saiyouri, N. Effect of flax fibers on early age shrinkage and cracking of earth concrete. Constr. Build. Mater. 2020, 254, 119315. [Google Scholar] [CrossRef]
- Shen, D.J.; Liu, C.; Wang, M. Effect of polyvinyl alcohol fiber on the cracking risk of high strength concrete under uniaxial restrained condition at early age. Constr. Build. Mater. 2021, 300, 124206. [Google Scholar] [CrossRef]
- Li, X.D.; Yu, Z.P.; Chen, K.X. Investigation of temperature development and cracking control strategies of mass concrete: A field monitoring case study. Case Stud. Constr. Mater. 2023, 18, e02144. [Google Scholar] [CrossRef]
- Pitroda, J.; Zala, L.B.; Umrigar, F.S. Experimental investigations on partial replacement of cement with fly ly-ash in design mix concrete. Int. J. Adv. Eng. Technol. 2012, 3, 126–129. [Google Scholar]
- Kalinski, M.E.; Yerra, P.K. Hydraulic conductivity of compacted cement-stabilized fly ash. Structures 2006, 85, 2330–2336. [Google Scholar] [CrossRef]
- Wei, G.L.; You, Y.J.; Li, P.Y. Study on strength exothermic and hydration evolution of low heat cement mixed with fly ash. Concrete 2022, 2, 54–59. [Google Scholar]
- Shabab, M.E.; Shahzada, K.; Gencturk, B. Synergistic Effect of Fly Ash and Bentonite as Partial Replacement of Cement in Mass Concrete. Innov. Infrastruct. Solut. 2016, 20, 1987–1995. [Google Scholar] [CrossRef]
- He, Y.; Zhang, X.; Hooton, R.D.; Zhang, X. Effects of interface roughness and interface adhesion on new-to-old concrete bonding. Constr. Build. Mater. 2017, 151, 582–590. [Google Scholar] [CrossRef]
- Wei, Y.; Hansen, W. Tensile creep behavior of concrete subject to constant restraint at very early ages. J. Mater. Civ. Eng. 2013, 25, 1277–1284. [Google Scholar] [CrossRef]
- Qin, R.; Hao, H.; Rousakis, T.; Lau, D. Effect of shrinkage reducing admixture on new-to-old concrete interface. Compos. Part B Eng. 2019, 167, 346–355. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, H.; Nie, X.; Tao, M. Experimental study on bond and anchorage of steel bars in precast concrete structures with new-to-old concrete interface. Eng. Struct. 2021, 247, 113086. [Google Scholar] [CrossRef]
- Klemczak, B.; Batog, M.; Giergiczny, Z.; Zmij, A. Complex Effect of Concrete Composition on the Thermo-Mechanical Behaviour of Mass Concrete. Materials 2018, 11, 2207. [Google Scholar] [CrossRef]
- Yu, X.; Chen, J.; Xu, Q.; Zhou, Z. Research on the Influence Factors of Thermal Cracking in Mass Concrete by Model Experiments. KSCE J. Civ. Eng. 2018, 22, 2906–2915. [Google Scholar] [CrossRef]
- Li, Y.; Nie, L.; Wang, B. A numerical simulation of the temperature cracking propagation process when pouring mass concrete. Autom. Constr. 2014, 37, 203–210. [Google Scholar] [CrossRef]
- Smolana, A.; Klemczak, B.; Azenha, M.; Schlicke, D. Experiences and analysis of the construction process of mass foundation slabs aimed at reducing the risk of early age cracks. J. Build. Eng. 2021, 44, 102947. [Google Scholar] [CrossRef]
- Shang, W.; Liu, J.; Wei, Z.; Zhao, H.; Li, L. Research on the critical casting length of oversized concrete monolithic foundation post-cast zone. China Concr. Cem. Prod. 2019, 274, 85–89. [Google Scholar]
- Cha, S.L.; Jin, S.S. Prediction of thermal stresses in mass concrete structures with experimental and analytical results. Constr. Build. Mater. 2020, 258, 120367. [Google Scholar] [CrossRef]
- Smolana, A.; Klemczak, B.; Azenha, M.; Schlicke, D. Early age cracking risk in a massive concrete foundation slab: Comparison of analytical and numerical prediction models with on-site measurements. Constr. Build. Mater. 2021, 301, 124135. [Google Scholar] [CrossRef]
- Cai, Y.; Wang, F.; Zhao, Z.; Lyu, Z.; Wang, Y.; Zou, P. Early-Hydration heat and influencing factor analysis of Large-Volume concrete box girder based on equivalent age. Structures 2023, 50, 1699–1713. [Google Scholar] [CrossRef]
- GB50496-2018; Standard for the Construction of Massive Concrete. Ministry of Housing and Urban-Rural Development of the People’s Republic of China; China Architecture & Building Press: Beijing, China, 2018.
- Choi, Y.S.; Kim, J.G.; Lee, K.M. Corrosion behavior of steel bar embedded in fly ash concrete. Corros. Sci. 2006, 48, 1733–1745. [Google Scholar] [CrossRef]
- Wang, W.; Lu, C.F. Time-varying law of rebar corrosion rate in fly ash concrete. J. Hazard. Mater. 2018, 360, 520–528. [Google Scholar] [CrossRef] [PubMed]
- Liu, H. Influence of high fly ash content on volume stability and durability of high performance concrete. Railw. Eng. 2010, 6, 24–27. [Google Scholar]
- GB/T50146-2014; Application Technical Specification of Fly Ash Concrete. Ministry of Housing and Urban-Rural Development of the People’s Republic of China; China Architecture & Building Press: Beijing, China, 2014.
- Lv, M. Experimental study on the influence of curing conditions and reinforcement ratio on early shrinkage of micro-expanded concrete. Chin. Sci. Technol. J. Database (Full-Text Version) Eng. 2023, 5, 0145–0150. [Google Scholar]
- ACICommittee209. Prediction of Creep, Shrinkage, and Temperature Effects in Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 1992. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).