Method for the Statistical Analysis of the Signals Generated by an Acquisition Card for Pulse Measurement

Abstract

This article shows a method for the statistical analysis of signals. Firstly, this method was applied to analyze the processing of signs generated by an acquisition card for pulse measurement using the synchronous demodulation method. The application of the method allowed the study of each signal consisting of a descriptive statistical analysis, followed by the analysis of the trend and dynamics of the movement using the augmented Dickey–Fuller test and Hurst exponent, respectively. Secondarily, the method presented here supported the comparison between the pulse signals obtained by synchronous demodulation and plethysmography methods. In addition, the residuals from the pulse comparison of both methods were analyzed. To quantify the differences between the signals, these were compared using the mean-squared error, the root-mean-square error, the mean absolute error, the mean error, the mean absolute percentage error, and the mean percentage error. After this research, it was possible to analyze the signals knowing characteristics such as the following: the presence of normal, exponential, lognormal, and uniform distributions, stationary trend, and dynamic movement anti-persistent. The novelty that this article proposes is the use of concepts traditionally used in the study of time series and models of demand administration, now focused on supporting improvements over the different stages of design and conceptualization of signal processing devices.

1. Introduction

There are many different types of human signals, such as electrocardiograms, electroencephalograms, seismocardiography, and photoplethysmograms, among others [1,2,3,4,5,6]. These have an important role in pathological diagnostic processes. To process these signals, noise elimination, feature extraction, and classification are common.

In recent decades, the use of portable devices that allow the acquisition of vital parameters through signals has increased significantly. Miniaturized technologies and powerful signal processing applications make them a non-invasive, cost-effective, and time-saving tool for cardiac monitoring [5]. The physiological signals that are traditionally used to extract information about the cardiovascular system are pulse, blood pressure, arterial oxygen saturation, and respiration, among others. Pulse rate is an essential indicator of cardiovascular health in living beings. It can predict the incidence, progression, and mortality associated with cardiovascular disease. Adequate monitoring can contribute to the prevention, rehabilitation, and evaluation of their behavior.

Wearable devices were the top trend in an electronic survey of health and fitness trends in 2022: they have been estimated to be a $100 billion industry in the US [5]. Market research forecasts growth of heavy future investment in terms of industrial research, to improve the sensors in terms of flexibility, motion, and smart textiles. Within the state of the art, there is a large number of devices whose purpose is the use of signals [7,8,9,10,11]. In addition to health devices, other devices based on the use of signals are being integrated into critical applications, to name a few: remote patient monitoring, space exploration, industry, detection, control, and monitoring systems. As a result of this, other tools must be migrated to the signal monitoring environment and its characterization [12,13,14,15,16,17,18].

For this study, an acquisition card (AC) designed for pulse measurement, obtained as part of the basic science Project with reference to number 0000000287237 CB-2016-01, was used [19]. Within this work, the signals of the time series generated by AC for an environmental signal are analyzed, this signal was taken under normal conditions of pressure and temperature. These signals range from their collection to obtaining pulse measurements. Additionally, the method of synchronous demodulation [20,21,22,23,24] and plethysmography [25,26,27,28,29,30,31] were compared.

The novelty of this document lies in the fact that topics of high statistical importance have been united to develop an accessible and supportive method for developers of biomedical and other concepts based on signals. This research was inspired by the use of statistical tools currently used for the description and comparison of time series and models for demand administration. Considering that the signals studied here are also time series, it was decided to apply some concepts in this new field. We consider it important to mention that we have not identified a document that integrates the topics and scope that this proposes.

The importance of this work lies in analyzing the evolution of the signal with statistical tools according to the treatments it receives. Describing the signal, evaluating its trend, and knowing its movement dynamics allowed the AC developers to support decision-making on features, such as the following: (1) the assignment, integration, or elimination of electronic components, (2) filtering techniques and selection of readings, (3) and the use of external components among others (these aspects will be documented in the design work of the AC system in a document independent of this). The added value of the results obtained lies in the findings on the robustness of the statistical parameters applied here, as well as in the following, in which these allow scrutinizing the characteristics of the signals studied.

The statistical method proposed in this document is formed by three steps which are mentioned below: Step 1. Dataset description and preparation; Step 2. Data processing; and Step 3. Signal characterization.

The descriptive statistical analysis consisted of the use of statistical parameters of tendency and dispersion [32,33,34,35]. Several of the components of the time series signals were analyzed, these were the following:

• Trend analysis, based on the augmented Dickey–Fuller test [36,37];
• Dynamics of movement, from the Hurst exponent [38,39,40].

Additionally, this research addresses some of the most commonly used metrics in measuring the error between two series [41,42,43,44,45,46]. The nomenclature used in this document can be seen in the index presented in Abbreviations.

The rest of the article is presented as follows. Section 2 presents the statistical method for the analysis of the signals step by step. Section 3 presents the results obtained from each of the signals studied as well as the comparison of the pulse signal between the direct synchronization and plethysmography methods. Section 4 discusses the results of the present study, as well as a visualization of future perspectives in light of the findings presented here. And finally, in Section 5 shows the conclusions.

1.1. Methods for Measuring Pulse

Pulse waves and pulse rate are important indicators of cardiovascular health. Several developments in contactless methods have been documented. Table 1 contains some of the many exciting ones.

Table 1. Several developments for pulse measurement: description, advantages, disadvantages in recent years.

Development	Description	Advantages	Disadvantages	Year/References
Cardiac pulse detection by a pulse train using the synchronous Demodulation Technique.	In this document, the operating principle is presented, together with the mathematical demonstration of the theory on which the method for the treatment and recovery of the heart rate signal is based.	The method is presented in mathematical form.	The number of dates must be expanded.	2023/Project with reference to number 0000000287237 CB-2016-01
This method uses a low-power millimeter wave radar system.	It uses a low-power millimeter wave radar system with a transmission power of less than 6 dBm.	In a 20 min monitoring experiment, 96.96% accuracy is reached by this method.	These low-power devices make it impossible to maintain the echo intensity at an optimal level, making accurate and reliable monitoring.	2023/[10]
Use of facial videos.	Robust pulse rate measurements from facial videos in diverse environments.	The method stably detects faces by removing high-frequency components of face coordinate signals derived from noise factors.	The method uses the average of interval values between detected peak points.	2022/[7]
Several capacitive coupling methods.	The system is composed of a set of capacitive electrodes manufactured on a standard printed circuit board.	The system may cause inconvenience, such as foreign body sensations.	This presents weak detection signals.	2021/[8]
The method is to use microwave or millimeter wave Doppler radar as a non-contact hear-rate measurement system.	This method uses ultra-wideband or millimeter wave signals and focuses on detection on the skin surface.	This method can obtain information about the diastole and systole of the heart, as well as the surface of the skin.	Their effectiveness in vehicle environments remains unclear.	2021/[9]
Non-contact, automated cardiac pulse measurements using video imaging and blind source separation.	The authors used bland-Altman and correlation analysis, to compare the cardiac pulse rate extracted from videos recorded by a basic webcam to an FDA-approved finger blood volume pulse sensor.	High precision and correlation were achieved (even with the presence of motion).	It is possible that the linearity assumed is not representative of the true underlying mixture in the signals.	2010/[11]

1.2. Pulse by the Synchronous Demodulation

The synchronous detection method is based on the theory of radio communication, where the phase of an unknown signal is recovered by the correlation of this signal with a sinusoidal signal of the same frequency [19,20].

Synchronous demodulation is the signal recovery method of choice when the input envelope signal is modulated by either a pure sine wave or a square wave [21].

The synchronous detection technique requires that the signal meets certain requirements to determine the phase and amplitude of an input signal at a given frequency [22]. The signal can be analyzed by electronic or digital procedures. A procedure of the application of synchronous detection in pulse detection can be found in [23], where they present a low-duty cycle signal which is improved by data processing to achieve optimal pulse.

1.3. Pulse by Plethysmography Method

The photoplethysmography technique is widely known and a wide range of technologies have been developed around it [24]. One of the main reasons for using the technique is to avoid the use of additional equipment in signal monitoring [25]. Plethysmography [26,27,28] is a technique that allows visualizing the variation in blood volume changes as a result of low variations, thus allowing the detection and measurement of cardiac pulse, oxygen levels, and other biomedical variables [26]. The operating principle is very simple: a light source illuminates the skin then after it interacts with the skin either by transmission or by reflection, and the results are collected to be processed. The interaction of the light with the skin is somewhat complex [29]. Many factors affect the quantity of light received by the sensor, for example, the effect of pressure on the sensor [30]. Although the technique to process the signal through the plethysmography method is well known, a single light source is used for the general case of obtaining a cardiac pulse. The photoplethysmography technique allows the signal to be analyzed by a digital procedure, although extensive instrumentation has already been developed [24].

1.4. Descriptive Statistics

Descriptive statistics according to the number of attributes analyzed are classified as univariate and multivariate exploration.

As is known, measures of central tendency are statistical measures that aim to summarize a set of values in a single value. Some examples of these are the mean, the mode, and the median. On the other hand, dispersion measures are numbers that indicate whether the variable moves a lot, a little, or more or less than another. Within this research the following were used [31,32,33,34]:

• The mean, which is calculated from the sum of each of the signal data divided by the total data; see Equation (1):

$$\overline{\mathrm{x}}=\frac{1}{\mathrm{n}}\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{i}}$$

(1)

where x is each value and n is the amount of data.

And as measures of dispersion, we used the following:

• The standard deviation (σ) is defined as a measure of the dispersion by which points differ from the mean. And in which a low value indicates that the points are very close to the mean, while a high deviation shows that the points are spread over a larger range of values. σ is calculated from Equation (2):

$$\mathsf{\sigma }=\sqrt{\frac{{\sum _{\mathrm{i}=1}^{\mathrm{n}}({\mathrm{x}}_{\mathrm{i}}-\overline{\mathrm{x}})}^2}{\mathrm{n}-1}}$$

(2)

• The variation coefficient (CV) is used to compare data sets belonging to different populations, allowing a measure of dispersion that eliminates possible distortions of the means of two or more populations. CV is calculated from Equation (3):

$$\mathrm{C}\mathrm{V}=\frac{\mathsf{\sigma }}{\overline{\mathrm{x}}}\times 100$$

(3)

• A scatterplot is one of the most powerful yet simple visual plots available. Scatterplots can also indicate the existence of patterns or groups of clusters in the data and identify outliers in the data [31].
• A quantile-to-quantile plot (Q-Q plot) is a graph that tests the conformity between the empirical distribution and the given theoretical distribution. A Q-Q plot is used to verify if data follow a particular distribution or if two given data sets have the same distribution. If the distributions are the same, the graph is a line. The further the obtained results are from the 45° diagonal, the further the empirical distribution from the theoretical one. The extreme points have a greater variability than those in the center of the distribution [32].

1.5. Augmented Dickey–Fuller Test

The augmented Dickey–Fuller test is one of the most widely used statistical tests. The ADF test extends the Dickey–Fuller test equation to include higher-order regressive terms in the model, this adds more thoroughness to the test. However, the null hypothesis remains the same as the Dickey–Fuller test. ADF belongs to a category of tests called “unit root tests” and is used to test whether a given time series is stationary. When a unit root occurs, it means that the time series is non-stationary. Furthermore, the number of unit roots contained in the series corresponds to the number of differentiation operations necessary to make the series stationary. Therefore, it can be said that the series with a trend is called non-stationary with a unit root and the series without a trend is a stationary series characterized by not having a unit root [33].

The following is also known [34]:

The null hypothesis should be rejected when the p-value ≤ significance level or if the test statistic ≤ critical value. Therefore, the data provide evidence that they are stationary.

The null hypothesis should not be rejected when the p-value > significance level or if the test statistic > critical value. Therefore, the data provide no evidence that they are stationary.

1.6. Hurst Exponent

The Hurst exponent is used in time series analysis and fractal analysis as a measure of the long-term memory of a time series. H quantifies the relative tendency of a time series to regress strongly from the mean or to cluster in one direction. In other words, measures how chaotic or unpredictable a time series is, allowing one to quantify how persistent a pattern remains over time by measuring its degree of autocorrelation [38]. H ranges between 0 and 1 [36,37,38], where the following applies.

If 0 ≤ H ≤ 0.5, we have an anti-persistent series, which is often called mean-reverting. That is, if the series has been above a certain value that serves as the long-term average in the previous period, it is more likely that it will be below in the following period and vice versa. This series is considered to have pink noise, which is common in nature and is related to relaxation processes (dynamic equilibrium) as well as turbulence. Then, the time series represents an anti-persistent process with oscillations. An anti-persistent time series exhibits volatility.

If H = 0.5 is uncorrelated. The data is independent; therefore, it is said that there is no memory. If it is a random series that meets all the characteristics of standard Brownian motion, then it is said to have white noise. Therefore, the time series represents a process without dependencies or a random bed.

If 0.5 < H ≤ 1, the series is persistent, and it reinforces the trend. That is, if the series was above (or below) its long-term average in the previous period, it is most likely that it will continue above (or below) in the following period. Therefore, the time series represents a persistent process in which the trend of previous stages is maintained. That is, the time series is self-similar.

If H = 1, the series is deterministic. In this interval, the noise color is black. It represents a long-term cyclical processes.

1.7. Metrics to Measure the Error between Two Series

The comparison between two series is important because it allows us to recognize those characteristics that match or differ. In this section, some of the parameters most commonly used for this purpose are mentioned in [40,41]. A quantification of performance metrics is presented in [18]. These parameters have been used separately in the comparison of scenarios of multiple areas and purposes, some of which can be seen in [43,44,45,46,47,48].

For the comparison of the error (residual) between two time series, if ${\mathrm{x}}_{\mathrm{t}}$ corresponds to the values of the time series 1 and ${\mathrm{y}}_{\mathrm{t}}$ corresponds to the time series 2 (where t is the time period), the error between the both series is as follows (see Equation (4)):

$${\mathrm{e}}_{\mathrm{t}}{=\mathrm{x}}_{\mathrm{t}}-{\mathrm{y}}_{\mathrm{t}}$$

(4)

When evaluating the performance for multiple observations, say n, there will be n error terms. We can define the following standard error measures as below.

The mean squared error (MSE) measures the mean error between the series x and series y; see Equation (5). The range of the MSE is (0, α); the perfect value of MSE is 0, indicating total similitude between the series that were compared.

$$\mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{\mathrm{n}}\sum _{\mathrm{t}=1}^{\mathrm{n}}{\left({\mathrm{e}}_{\mathrm{t}}\right)}^2$$

(5)

The root mean square error (RMSE) measures the average magnitude of error between the series x and series y (see Equation (6)). The range for RMSE is (0, α); the smaller the RMSE value is, the higher the similarity between the two compared series. The units of RMSE are the same as the original units.

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=[{\sum }_{\mathrm{t}=1}^{\mathrm{n}}{\left({\mathrm{e}}_{\mathrm{t}}\right)}^2/\mathrm{n}{]}^{1/2}$$

(6)

The mean absolute error (MAE) is a metric used to measure the average magnitude of the absolute errors between the series x with respect to series y; see Equation (7). The MAE range is (0, α); the smaller the MAE value is, the higher the accuracy of the prediction model. The units of MAE are the same as the original units.

$$\mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{\mathrm{n}}\sum _{\mathrm{t}=1}^{\mathrm{n}}\left|{\mathrm{e}}_{\mathrm{t}}\right|$$

(7)

The mean error (ME) measures the mean error between the series that were compared (see Equation (8)). The ME range is (−α, +α). The perfect value of the ME is 0. Other values indicate little similarity as they move further from the origin. The percentage-dependent metrics measure the size of the error in percentage terms of similarity between two series.

$$\mathrm{M}\mathrm{E}=\sum _{\mathrm{t}=1}^{\mathrm{n}}{\mathrm{e}}_{\mathrm{t}}/\mathrm{n}$$

(8)

The mean absolute percentage error (MAPE) is a measure of the prediction accuracy of a forecasting method in statistics. It usually expresses the accuracy as a ratio, defined by Equation (9):

$$MAPE=\sum _{t=1}^n\frac{\left(x_t-y_t\right)}{y_t}\cdot \frac{100}{n}$$

(9)

The mean percentage error (MPE) measures the percentage error between two series; see Equation (10).

$$\mathrm{M}\mathrm{P}\mathrm{E}=\sum _{\mathrm{t}=1}^{\mathrm{n}}\mathrm{a}\mathrm{b}\mathrm{s}\left[\frac{\left({\mathrm{x}}_{\mathrm{t}}-{\mathrm{y}}_{\mathrm{t}}\right)}{{\mathrm{x}}_{\mathrm{t}}}\right]\cdot \frac{100}{\mathrm{n}}$$

(10)

2. Statistical Method for Analysis of Signal

The method proposed for the statistical analysis of the signals generated by the AC consists of three steps (see Figure 1).

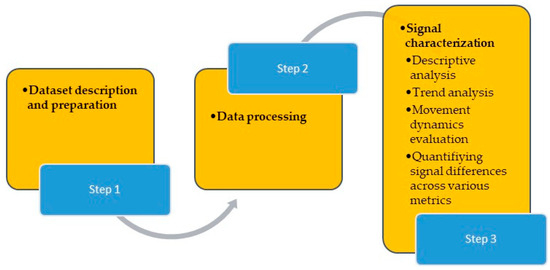
Figure 1. Statistical method for analysis of the signals.

• Step 1. Dataset description and preparation

In this study, an AC designed for pulse measurement was used. Its operation includes the microprocessor (PIC16F1615), through the pulse width modulation (PWM) function, generates a pulses train with a frequency of 122 Hz that forms a square wave composed of 8 pulses of red light and 8 pulses of infrared light spaced by 5.12 × 10⁻⁴ s; its capacity allows the storage of 127,984 units of data. The same microprocessor controls an infrared led on/off system (VSMD6694). This control allowed one led to remain on for a period of 8 pulses, while another remained on and vice versa. The emission of the beams hits the surface of the environmental signal through the optical fiber. Once it interacts with the environmental signal, the reflected light is collected by another optical fiber and processed by a sensor (TEMD7000) connected to a trans-impedance circuit (ADA4505-2AEMZ) and amplified to convert it into a digital signal (s₁). s₁ is the signal from the interaction of the beam with the skin: it is square and noisy. The processor sent the data to memory (CY15V104QN). The LED control process, data collection, and storage were carried out for 65.52 s (1.09 min). The signal sampling frequency was 1950 Hz. Once stored, the data were retrieved and emptied into a computer and processed. At this point, a low-pass filter was applied (s₂) (the filter has a dual purpose: to eliminate noise and transform the square signal into a sine wave to apply the synchronous detection technique) to later define the sine function with the same frequency of the analyzed signal (s₃), as well as the cosine function (s₄), and to also later calculate the pulse by direct synchronization (s₅). With the objective of a comparison between the signals of the pulse by the methods of direct synchronization and plethysmography, (s₆) was calculated too. See Figure 2, where the fluxes of the signal were calculated by both methods. Within this work, the signals of the time series generated by AC for an environmental signal were analyzed, this signal was taken under normal conditions of pressure and temperature.

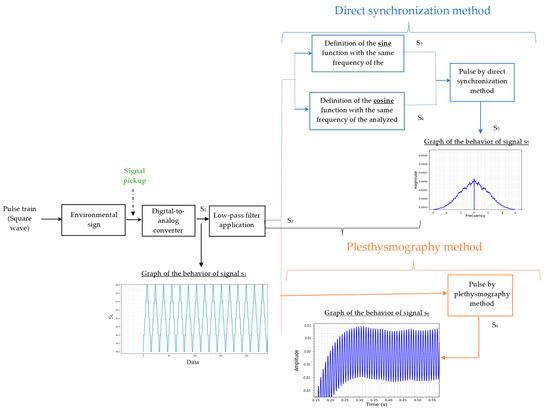
Figure 2. Processing of signal evolution during pulse measurement using AC.

The AC has the characteristic that it can work with or without connection to the computer since, according to its design, it can be used with individuals from different ecosystems. For this research, the card has been used connected to the computer (see Figure 3a). Tera Term 4.105 is the software that AC uses to interact with the computer: this allows you to work with an interface to obtain information, as well as to manipulate the AC. Some of the commands it has are as follows: w: write in FRAM 4 Mb; r: read from FRAM. 4 Mb; etc. (see Figure 3b). The data of s₁ were extracted from the AC with a .txt extension from Tera Term and later processed.

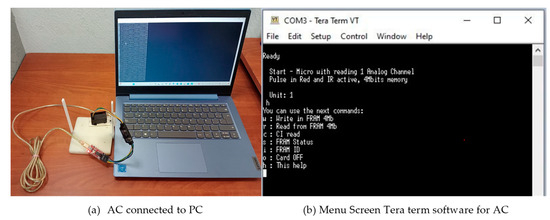
Figure 3. Interaction AC-PC and menu screen tera term software. (a) AC connected to PC; (b) Menu Screen Tera term software for AC.

• Step 2. Data processing

The data processing was carried out with the software Python; this allowed the information to be extracted for each of the signals and for us to process the calculation of each of the statistical parameters (see Table 2).

Table 2. Statistics evaluated for each signal.

Characteristics	Statistical Parameters of Tendency and Dispersion
Descriptive statistical analysis	Type of data distribution, Q-Q plots, Histograms, Box and $\mathrm{whisker}\mathrm{plots}\overline{\mathrm{x}}$, σ, CV,
Trend analysis	ADF
Dynamics of movement	H
Metric in measuring the error	MSE, RMSE, MAE, ME, MAPE, MPE, residual graphs

• Step 3. Signal characterization

Finally, the evolution of each of the signals was described.

3. Results

The behavior of the descriptive statistics used in this research for all signals was measured in volts. Firstly, the results obtained for the signals by the direct synchronization method are shown. The graphical methods used to detect the type of distribution in the signals showed the presence of more than one. Figure 4, Figure 5 and Figure 6 have been focused on showing the distribution of the data of the signals processed to obtain the pulse by the direct synchronization method. In Figure 4, the normal distribution Q-Q plot shows that, although the signals $\left(s_1,\dots ,s_5\right)$ had a normal distribution to the center, this behavior was different in the right and left tails in all cases. In Figure 5, the Q-Q plots of uniform distribution show the signals again $\left(s_1,\dots ,s_5\right)$. Figure 6 show the histogram of the signals $\left(s_1,\dots ,s_5\right)$. The graphical form of the histograms of signals s₂, s₅ and s₆, could confuse the reader. Therefore, to correct this, the minimum value with the opposite sign of each series was added to each value and the Box–Cox transformation was subsequently obtained (see Table 3). Figure 7, Figure 8 and Figure 9 show the Box–Cox transformation histogram for s₂, s₅ and, s₆, respectively.

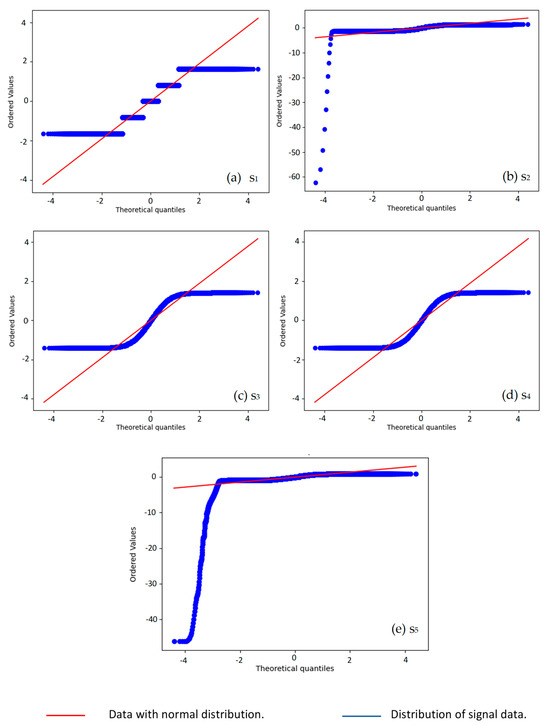
Figure 4. Q-Q normal distribution plots for the signals using the direct synchronization method.

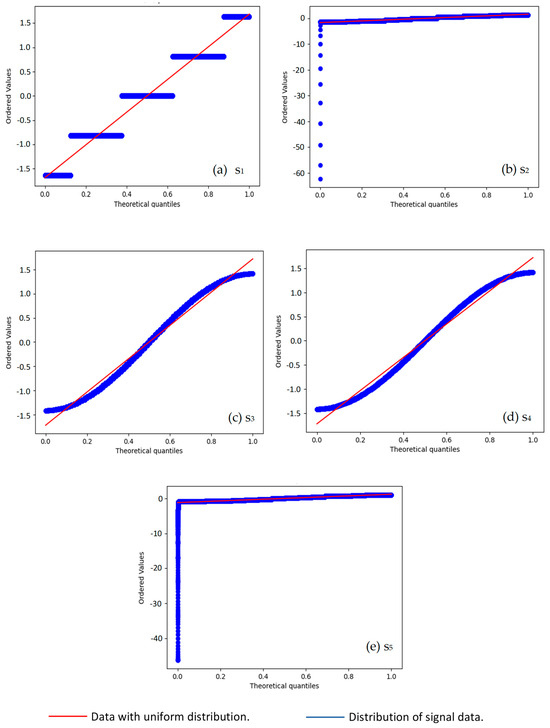
Figure 5. Q-Q uniform distribution plots for the signals using direct synchronization method.

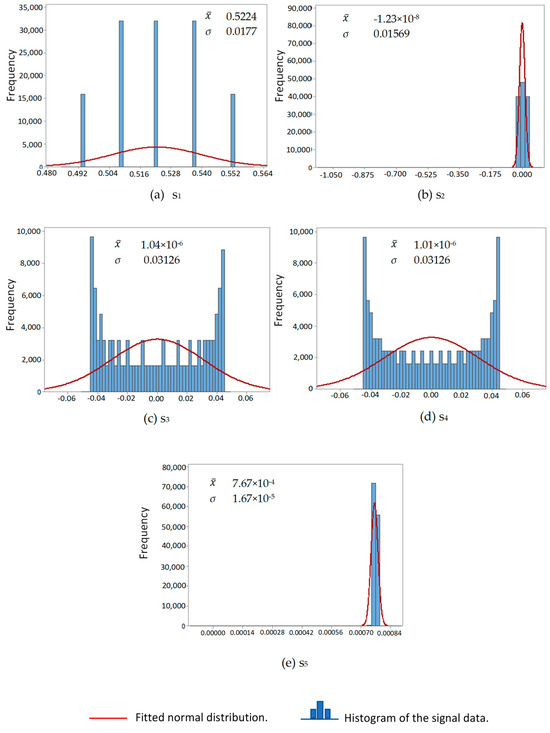
Figure 6. Histograms for the signals using direct synchronization method.

Table 3. Box–Cox transformation of the signal.

Signal	Minimum Value	Box-Cox Transformation
S2	−0.98	$s_{2_{\left(t\right)}}^{3.3}$
S5	−0.00000000001	$s_{5_{\left(t\right)}}^{1.35}$
S6	−0.98	$s_{6_{\left(t\right)}}^{1.44}$

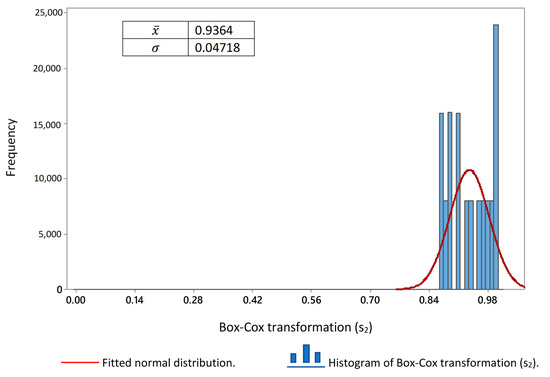
Figure 7. Box–Cox transformation(s₂) histogram.

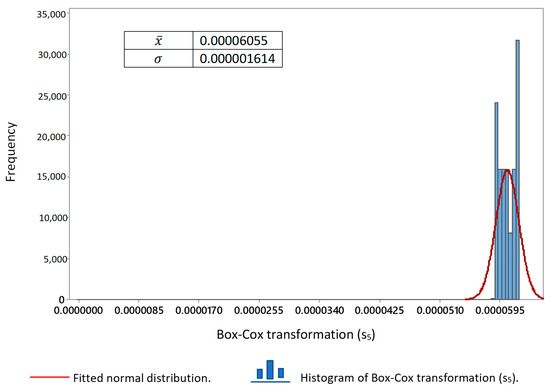
Figure 8. Box–Cox transformation(s₅) histogram.

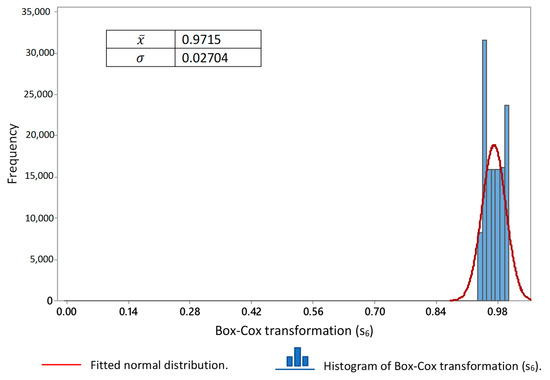
Figure 9. Box–Cox transformation(s₆) histogram.

Once the existence of more than one distribution in the data was known, the signal data were analyzed with Promodel’s stat fit tool from 30 samples of 50 data. The identified distribution is shown in Table 4. Distributions were presented in all signals except in s_1, where the exponential distribution was not presented. Figure 10 shows the box and whisker plot for the signals, respectively $\left(s_1,\dots ,s_5\right),$ starting from $s_1$ with ${\overline{x}}_{s_1}=0.5224$, which, when normalized, takes average values tending to zero $\left({\overline{x}}_{s_2}=-1.23\times {10}^{-8},{\overline{x}}_{s_3}=1.04\times {10}^{-6},{\overline{x}}_{s_4}=1.01\times {10}^{-6}\right)$ to finish taking values for the pulse distribution, with ${\overline{x}}_{s_5}=7.67\times {10}^{-4}$. In Figure 10, it can be seen that the distribution of the data is centered for all cases and tends towards zero for the signals $s_2,\dots ,s_5$. In the cases of signals $s_2$ and $s_5$, extreme points are shown in the lower whisker (represented graphically as a sequence of asterisks).

Table 4. CV-value and detected distribution for the signals obtained by direct synchronization method.

Signal	CV-Value	Detected Distribution
s1	3.4	Normal Lognormal Uniform
s2	−127 × 106	Uniform Normal Lognormal Exponential (oscillating)
s3	3 × 106	Uniform Normal Lognormal Exponential (oscillating)
s4	3 × 106	Normal Lognormal Uniform Exponential (oscillating)
s5	2.16	Uniform Normal Lognormal Exponential (oscillating)

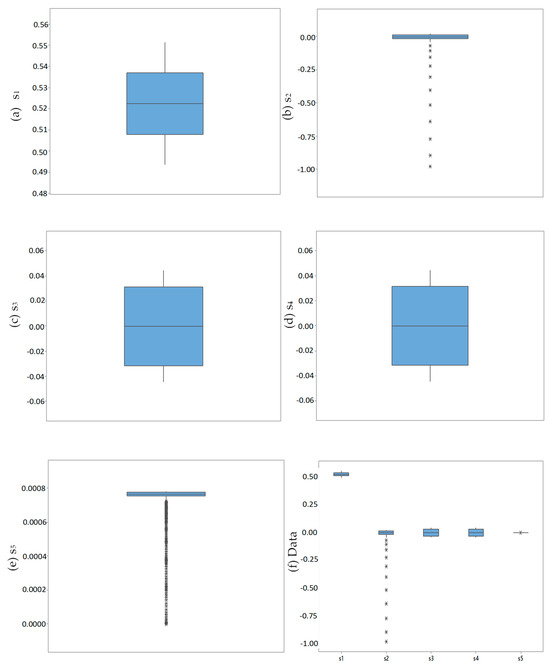
Figure 10. Box and whisker plot for the signals obtained using direct synchronization method.

To compare the dispersion between the evaluated signals, CV was used in this research (see Table 4). CV-values were for s₁ = 3.4 and s₅ = 2.16. Therefore, s₅ presents less dispersion than s₁; this is because s₅ has already been treated. Concerning CV-values for s₂, s₃, s_4, and s_6, this parameter becomes misleading because the small values of the mean make it highly sensitive. Therefore, in these cases, its use is not recommended.

The trend analysis was calculated by the augmented Dickey–Fuller Test and is shown in Table 5 for each of the signals. Therefore, when p-values ≤ 0.05, the decision is to reject the null hypothesis. As a consequence, in all signals, the results provide evidence that the signs were stationary. This same thing can be concluded when observing the critical values. In the same table (third column), H is calculated. The dynamics of movement with H < 0.5 for all the signals shows that the memory of each of these is anti-persistent. Therefore, such characteristic exhibits oscillations and high volatility. That is, if the series has been above a certain value that serves as the long-term average in the previous period, it is more likely that it will be below it in the following period or vice versa. In other words, all signals have pink noise.

Table 5. Augmented Dickey–Fuller test and Hurt exponent for the signals obtained by direct synchronization method.

Signal	ADF Calculated	ADF Result	H Calculated	H Results
s1	Test: −113.15556052161811 p-value: 0.0 Critical values: {‘1%’: −3.4304010901041226, ‘5%’: −2.8615625810800256, ‘10%’: −2.566782019109249}	s1 is stationary	0.01	The memory of s1 is anti-persistent.
s2	Test: −1068.923788266477 p-value: 0.0 Critical values: {‘1%’: −3.4304010905032816, ‘5%’: −2.8615625812564462, ‘10%’: −2.566782019203152}	s2 is stationary	0.32	The memory of s2 is anti-persistent.
s3	Test: −13585028329382.6 p-value: 0.0 Critical values: {‘1%’: −3.4304010905032816, ‘5%’: −2.8615625812564462, ‘10%’: −2.566782019203152}	s3 is stationary	0.00	The memory of s3 is anti-persistent.
s4	Test: −13583953241809.928 p-value: 0.0 Critical values: {‘1%’: −3.4304010905032816, ‘5%’: −2.8615625812564462, ‘10%’: −2.566782019203152}	s4 is stationary	0.00	The memory of s4 is anti-persistent.
s5	Test: −311.9388497424053 p-value: 0.0 Critical values: {‘1%’: −3.4304010913016176, ‘5%’: −2.8615625816092964, ‘10%’: −2.566782019390962}	s5 is stationary	0.33	The memory of s5 is anti-persistent.

Table 6 shows the comparison between signals of the MSE, RMSE, MAE, and ME metrics (in vertical order). We decided to show the complete table considering that the ME values vary in sign due to the order in which the signals were compared. Regarding the values that these parameters take, in general, there is a tendency to decrease as the signals evolve.

Table 6. Comparative of MSE, RMSE, MAE, and ME values between the signals obtained by direct synchronization method.

Statistical	Signal
	s1	s2	s3	s4	s5
s1		0.273	0.274	0.274	0.272
		0.522	0.523	0.523	0.523
		0.522	0.522	0.522	0.522
		0.522	0.522	0.522	0.521
s2	0.273		0.001	0.001	0.0002
	0.522		0.034	0.035	0.016
	0.522		0.029	0.029	0.013
	−0.522		−1.052 × 10−6	−1.022 × 10−6	−7.77 × 10−4
s3	0.274	0.001		0.002	0.001
	0.523	0.034		0.044	0.031
	0.522	0.029		0.039	0.028
	−0.522	1.052 × 10−6		−3.037 × 10−8	−7.65 × 10−4
s4	0.274	0.001	0.002		0.001
	0.523	0.035	0.044		0.031
	0.522	0.029	0.039		0.028
	−0.522	1.022 × 10−6	3.037 ×10−8		−7.65 × 10−4
s5	0.272	0.0002	0.001	0.001
	0.523	0.016	0.031	0.031
	0.522	0.013	0.028	0.028
	−0.521	7.77 × 10−4	7.65 × 10−4	7.65 × 10−4

Table 7 shows MAPE and MPE values for the signals $s_1,..,s_5$; some of the values could not be calculated because, as is known, “division by zero is a division in which the divisor is equal to zero”, and it does not have a well-defined result. Therefore, the result was what has been named in the table as DIV/0”. On the other hand, the calculated values lacked objectivity due to the sensitivity of these parameters to small values. Regarding the comparison between the same signals, the values were not placed in Table 6 and Table 7 because, logically, these show total similarity while MAPE and MPE showed the same incidence of sensitivity already mentioned.

Table 7. Comparative of MAPE and MPE values between the signals obtained by direct synchronization method.

Statistical	Signal
	s1	s2	s3	s4	s5
s1		9966.33	4950.28	DIV/0	DIV/0
		100.02	99.99	99.99	99.85
s2	100.02		175.08	DIV/0	DIV/0
	9966.23		547.6	547.5	100.25
s3	99.99	547.6		+DIV/0	DIV/0
	4650.28	175.08		402.7	101.23
s4	99.99	547.5	402.7		DIV/0
	DIV/0	DIV/0	DIV/0		DIV/0
s5	99.85	100.25	101.73	DIV/0
	DIV/0	DIV/0	DIV/0	DIV/0

Secondly, the results obtained for the signals by the plethysmography method are shown. Table 8 shows that the signal of pulse for plethysmography is anti-persistent. Therefore, this signal has pink noise.

Table 8. Augmented Dickey–Fuller test and Hurt exponent for signals of plethysmography (s₆).

Signal	ADF Calculated	ADF Result	H Calculated	H Results
s6	Test: −311.93884974369644 p-value: 0.0 Critical values {‘1%’: −3.4304010913016176, ‘5%’: −2.8615625816092964, ‘10%’: −2.566782019390962}	s6 is stationary	0.33	The memory of s1 is anti-persistent.

Figure 11a–c show that data have more than one distribution. Therefore, his fit was verified with Promodel´s stat fit and the distribution of s₆ is shown in Table 9. The distributions for s₆ are uniform, normal, lognormal, and in the center exponential. Figure 11d shows the existence of extreme points on the lower whisker.

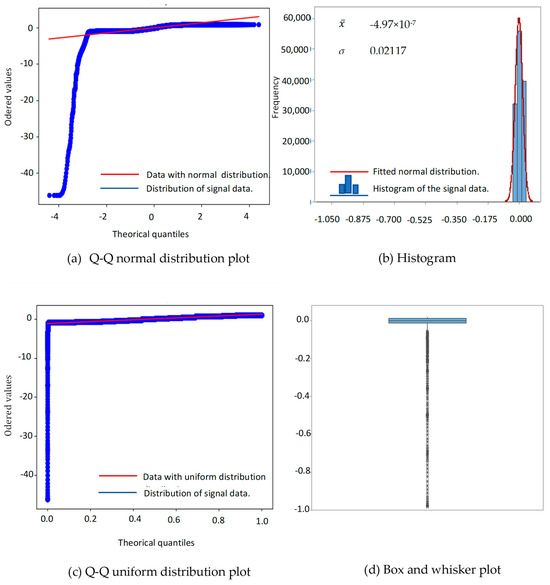
Figure 11. Q-Q normal distribution plot, histogram, Q-Q uniform distribution plot and box and whisker plot of pulse obtained by plethysmography method (s₆).

Table 9. Comparative statistical parameter between the signals of pulse by direct synchronization (s₅) and plethysmography (s₆) methods.

Characteristic	Pulse by Synchronization Method (s5)			Pulse by Plethysmography Method (s6)
Descriptive Analysis	Statistical	Value		Statistical	Value
	$\overline{x}$	7.67 × 10−4		$\overline{x}$	−4.97 × 10−7
	σ	1.67 × 10−5		σ	0.02117
	CV	2.16		CV	Non-robust
	Detected distribution	Initial data	Lognormal Normal Uniform	Detected distribution	Initial data	Lognormal Normal Uniform
		Central data	Uniform Normal Lognormal Exponential		Central data	Uniform Normal Lognormal Exponential
		Final data	Uniform Normal Lognormal		Final data	Uniform Normal Lognormal
	Distribution dates	Box and whisker plot shows outlier data in the bottom tail		Distribution dates	Box and whisker plot shows outlier data in the bottom tail
Trend analysis	Stationary			Stationary
Dynamics of movement	Anti-persistent (The signals have pink noise)			Anti-persistent (The signals have pink noise)
Measuring the error	Error			Value
	MSE			0.0004
	RMSE			0.021
	MAE			0.013
	ME			−7.67 × 10−4
	MAPE			DIV/0
	MPE			102.86

Finally, the results obtained for both signals are compared. Table 9 shows the comparative statistical parameters between the signals of pulse by the direct synchronization (s₅) and plethysmography (s₆) methods. Both methods show normal, uniform, lognormal, and exponential distribution (in this case, samples were taken of the total data of the signals, defining them in three categories: initial data, central data, and final data). On the other hand, the behavior of the means is close to zero with a low standard deviation. And the signals are stationary and anti-persistent. The errors between the series have the following values: MSE = 0.0004, RMSE = 0.021, MAE = 0.013, ME = −7.67×10⁻⁴, MAPE = DIV/0 and MPE = 102.86, the latter being little use.

Figure 12 shows the histogram of the $e_t$ whit Box–Cox transformation. For this, first the smallest value of the series was added to each residue and then the transformation Box–Cox was applied = $e_t^{1.44}$. For this data the parameters statistics were $\overline{x}=0.97044$, $\mathrm{Q}1=0.94984$, $\mathrm{m}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}=0.96882,$ $\mathrm{Q}3=0.98948$, $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}=0.99917$, $\sigma =0.02701$, ${\sigma }^2=0.000729$ and $CV=2.78$.

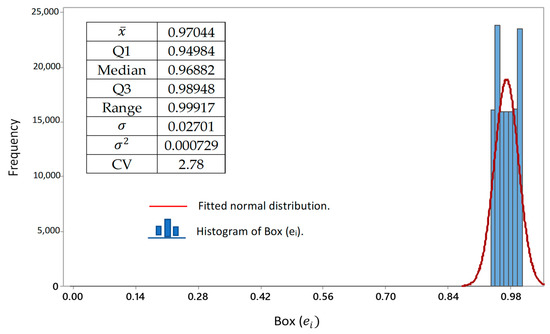
Figure 12. Histogram of the residuals transformed by Box–Cox.

4. Discussion

In this study, the novelty lies in the application of topics commonly used in the field of study of time series and demand management models, now focused on the analysis of signals based on a useful and simple method. So the added value lies in the findings we have had regarding the robustness of the statistics parameters used here, as well as in the following, in which these parameters will allow scrutinizing the characteristics of the signals studied.

In a time series self-similarity can be found, defined, and quantified. In this case, the number of data that made up the time series studied in this document should be increased since the current capacity of the AC limits the amount of data. Therefore, a greater number of data would open the possibility that patterns or behaviors can be identified, considering that self-similarity can occur in a longer time horizon.

In this document, the study of a series of signals was presented in which their descriptive characteristics, trends, and movement dynamics could be known using the following topic: $\overline{x}$, $\sigma$, $\mathrm{C}\mathrm{V}$, data distribution, $\mathrm{A}\mathrm{D}\mathrm{F}$, and $\mathrm{H},$ as well as a Q-Q plot, histogram, and box and whisker plot. Additionally, MSE, RMSE, MAE, and ME were applied. It was possible to calculate the change that each signal, as well as compare the pulses obtained by direct synchronization and plethysmography. Regarding the metrics MAPE and MPE, their scope must be improved and, far from allowing the quantification of the error between two series, they should be able to be comparable regardless of the population in which they have been applied, adhering to strategies that strengthen work with small values. The next studies are focused on the development of a set of metrics where data normalization plays an important role in strengthening these parameters.

The use of graphical enriched the analysis in such a way that in future research the behaviors of the distribution could be used as fingerprints regarding time to relate them to the response of the signals to various controllable variables.

The advantages of the proposed method are as follows:

• It is easy to use and interpret;
• Allows you to describe the signals in a simple way;
• Enables developers to have a tuning tool during the development stages;
• It is an alternative to evaluate the function of systems that emit, process, or collect signals before being implemented in the system or ecosystem of the study individuals;
• As it is a methodology made up of solid statistical tools, its efficient use is supported.

The disadvantages of the proposed method are as follows:

• The metric evaluated to measure the error between two series, MAPE and MPE, are not satisfactory when taking values such as 0, or very small ones; therefore, is not recommended in this scenario. And ME values vary in sign due to the order in which the signals were compared. Therefore, evaluating it once in the series comparison is enough.

The experience regarding the introduction of topics from one field of study to another that this project allowed is satisfactory. It implies an immediate strengthening of the area of application, so the migration of statistical tools in this project aims to influence the development of instruments that work with the principle of using signals.

5. Conclusions

In recent decades, the use of portable devices that allow the acquisition of vital parameters through signals has increased significantly. Market research forecasts growth with heavy future investment in terms of industrial research, to improve the sensors in terms of flexibility, motion, and smart textiles. The use of validity protocols within the validation of this equipment should be of interest to developers, manufacturers, consumers and scientists to evaluate the characteristics of the device and its accuracy.

This document shows a method for the statistical analysis of signals generated by an acquisition card for pulse measurement. This method can be applied as a protocol for validating the behavior of systems in which the inputs and outputs are signals because it proposes a series of steps that can be applied in an economical and simple way.

At the end of this research, it was possible to demonstrate that the signals obtained by direct synchronization and plethysmography methods present similar behaviors. The study of each signal consisted of a descriptive statistical analysis, followed by the analysis of the trend and dynamics of the movement using the Dickey–Fuller test and Hurst exponent, respectively.

Within this investigation, it was possible to analyze several descriptive statistics parameters for each signal among which stand out: histograms (Box–Cox transformations), Q-Q plots, and box and whisker plots, $\overline{x}$, $\sigma$, $CV$. ADF allowed us to statistically reiterate that the signals evaluated here are seasonal, while H showed that the memory of all the evaluated signals was anti-persistent, which exhibited oscillations and high volatility, a situation that did not allow for knowing the self-similarity. On the other hand, metrics for the comparison of the behavior of the series were used, and below we comment on their contribution. Regarding MSE, RMSE, MAE, and ME in general, there was a tendency to decrease. ME presented positive and negative values according to the position that the series took. MAPE and MPE showed little robustness to the small values of the signals and its use did not add value to the study. The use of residual graphs turned out to be very beneficial in evaluating the behavior of the error over time for the comparison of two series.