On Lagrangian Grassmannian Variety and Plücker Matrices

Abstract

The Plücker matrix $B_{L(n,E)}$ of the Lagrangian Grassmannian $L(n,E)$, is determined by the linear envelope $⟨L(n,E)⟩$ of the Lagrangian Grassmannian. The linear envelope $⟨L(n,E)⟩$ is the intersection of linear relations of Plücker of Lagrangian Grassmannian, defined here. The Plücker matrix $B_{L(n,E)}$ is a direct sum of the incidence matrix of the configuration of subsets. These matrices determine the isotropy index $r_n$ and $r_n$-atlas which are invariants associated with the symplectic vector space E.

1. Introduction

Given E a symplectic vector space of dimension $2n$, the set $L(n,E)$ of all Lagrangian subspaces of E is called the Lagrangian Grassmannian of E. These spaces have a prominent role in symplectic geometry that, in the words of Dusa McDuff “Symplectic geometry: is the geometry of closed skew-symmetric form, $[\cdots ]$ thus symplectic geometry is essentially topological in nature $[\cdots ]$”, see [1]. In this article it is shown that the Lagrangian Grassmannian $L(n,E)$ has a rich algebraic structure when we assign a coordinate system known as Plücker coordinates. For this we prove the existence of a matrix $B_{L(n,E)}$, whose kernel contains all the Lagrangian subspaces of E. This matrix is built with the minimal family of linear form in ${\left({\wedge }^{n}E\right)}^{*}$ that nullify the Lagrangian Grassmannian under Plücker inclusion. another way of seeing $B_{L(n,E)}$ is as a sum of matrices of the family $\{{\mathcal{L}}_{r_n},{\mathcal{L}}_{r_n-1},\dots ,{\mathcal{L}}_2\}$ where ${\mathcal{L}}_{r_n-k}$, is a $(0,1)$-matrix, sparce, with $r_n-k$-ones in each row and $r_n-(k+1)$-ones in each column where $k=0,\dots ,r_n-2$ and $r_n=\lfloor \frac{n+2}{2}\rfloor$ is an index that measures the degree of isotropy in E. In this paper, we have:

In Section 3 and Section 4 we construct a family of homogeneous polynomial equations whose solutions parameterize the elements of $L(n,E)$, we call this family of polynomials Plücker relations of Lagrangian Grassmannian. In Section 5 and Section 6 we show that the linear relations of Plücker of the Lagrangian-Grassmannain is the minimal family, up to linear combination, of homogeneous linear polynomials that nullify $L(n,E)$.

In Section 7 calculate the matrix $B_{L(n,E)}$ associated with the linear envelope $\langle L(n,E)\rangle$ of $L(n,E)$, we call this the Plücker matrix of the Lagrangian Grassmannian. We can see that $B_{L(n,E)}$ is the incidence matrix of a family of subsets of the set of indices $I(n,2n)$ and so $B_{L(n,E)}$ is a direct sum of submatrices, each belonging to the set $\{{\mathcal{L}}_{r_n},{\mathcal{L}}_{r_n-1},\dots ,{\mathcal{L}}_2\}$. Where ${\mathcal{L}}_k$ is a sparce matrix of zeroes and ones with k-ones in each row and $k-1$-ones in each column.

Section 8 the isotropy index $r_n:=\lfloor \frac{n+2}{2}\rfloor$ is studied as an invariant of $L(n,E)$ and that, among other things, allows us to compare Lagrangian Grassmannian.

De Concini and Lakshmibai [1981] [2] show that the Lagrangian Grassmannian $L(n,E)$ is defined by quadratic relations. These relations are obtained by expressing $L(n,E)$ as a linear section of $G(n,E)$, so $L(n,E)=G(n,E)\cap \mathbb{P}\left(L\left({\omega }_n\right)\right)$, where $\mathbb{P}\left(L\left({\omega }_n\right)\right)$ is the projectivization of a vector space $L_{{\omega }_n}$ such that ${\wedge }^{n}E\simeq L_{{\omega }_n}\oplus {\wedge }^{n-2}E$, where $L_{{\omega }_n}$ is $S_{p_{2n}}\left(\mathbb{F}\right)$-representation of highest weight ${\omega }_n=h_1^{*}+\cdots +h_n^{*}$, and where $L(n,E)\subset \mathbb{P}\left(L\left({\omega }_n\right)\right)$ see [3] (pages 182–184), [2,4].

The advantage of our approach is that we have the equations $\{Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}}\}$ that define $L(n,E)$ as a projective variety and with this we obtain a totally explicit information of $L(n,E)$ as a linear section of the Grassmannian $G(n,E)$ (see Theorem 6) and in this way, we can give a connection with matrix theory and symplectic geometry which opens a computational horizon in these topics. In [5] we show that the homogeneous linear functionals $\{{\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n,2n)\}$ also allow us to describe the k-Grassmannian-Isotropic $IG(k,E)$, of a symplectic vector space E of dimension $2n$ and we give the Plücker matrix of $IG(k,E)$ which is a generalization of $B_{L(n,E)}$. The following bibliography is relevant for this research in [6,7,8,9,10] we can see a few results about $L(n,E)$. See [9,11,12,13,14], where you can see some applications of $\{{\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n,2n)\}$.

2. Preliminaries

Using terminology and definitions as given in [15,16], let E be an vector space defined over an arbitrary field $\mathbb{F}$. A symplectic form is a bilinear map

$$\langle ,\rangle :E\times E⟶\mathbb{F}$$

that satisfies

$$\begin{array}{ccc}\hfill \langle v,w\rangle & =-\langle w,v\rangle \hfill & \hfill forallv,w\in E\\ \hfill \langle v,v\rangle & =0\hfill & \hfill forallv\in E\\ \hfill andif\langle v,w\rangle & =0\hfill & \hfill forallv\in E\Rightarrow w=0\end{array}$$

and it is said to be skew-symmetric nondegenerate. $(E,\langle ,\rangle )$ is called a symplectic vector space, a symplectic vector space E is necessarily of even dimension and there is a basis $e_1,\dots ,e_n,u_1,\dots u_n$ of E such that

$$\langle e_i,e_j\rangle =\langle u_i,u_j\rangle =0y\langle e_i,u_j\rangle ={\delta }_{ij}$$

where ${\delta }_{ij}$ is the Kroneker delta function. A subspace $U\subseteq E$ is said to be isotropic if $\langle u,u^{\prime }\rangle =0$ for all $u,u^{\prime }\in U$. A subspace $L\subset E$ is said to be Lagrangian subspace if L is isotropic and $dim\left(L\right)=n$. The collection of Lagrangian subspace of E, we call it Lagrangian Grassmannian of E or simply Lagrangian Grassmannian we denote it by $L(n,E)$. A subspace $W\subset E$ is a symplectic subspace of E if the symplectic form in E when restricted to W remains symplectic.

Indices

Let m be an integer we denote

$$\left[m\right]:=\{1,2,\dots ,m\}$$

(1)

to the set of the first m integers. Let m and ℓ be positive integers such that $\mathsf{\ell }<m$ as usual in the literature $C_{\mathsf{\ell }}^m$ denotes binomial coefficient. If $\alpha =({\alpha }_1,\dots ,{\alpha }_{\mathsf{\ell }})\in {\mathbb{N}}^{\mathsf{\ell }}$ then, $supp\left\{\alpha \right\}:=\{{\alpha }_1,\cdots ,{\alpha }_{\mathsf{\ell }}\}$. If $s\ge 1$ is a positive integer and $\Sigma \subset \mathbb{N}$ is a non-empty set, we define the sets

$$C_s(\Sigma ):=\{\alpha =({\alpha }_1,\dots ,{\alpha }_s)\in {\mathbb{N}}^s:{\alpha }_1<\cdots <{\alpha }_{s}andsupp\left\{\alpha \right\}\subseteq \Sigma \}$$

(2)

if $|\Sigma |=m$ then $|C_s(\Sigma )|=C_{\mathsf{\ell }}^m$; with this notation if $\mathsf{\ell }<m$ we define $I(\mathsf{\ell },m)=C_{\mathsf{\ell }}\left(\left[m\right]\right)$. So we have

$$I(\mathsf{\ell },m)=\{\alpha =({\alpha }_1,\dots ,{\alpha }_s):1\le {\alpha }_1<\cdots <{\alpha }_{\mathsf{\ell }}\le m\}.$$

(3)

We say

$$\alpha =({\alpha }_1,\dots ,{\alpha }_s)\in C_s(\Sigma )$$

(4)

if there is a permutation $\sigma$ such that arrange the elements of $supp\left\{\alpha \right\}$ in increasing order so we have $(\sigma \left({\alpha }_1\right),\dots ,\sigma \left({\alpha }_s\right))\in C_s(\Sigma )$.

if $\alpha$ and $\beta$ are elements of $C_s(\Sigma )$ then we say that

$$\alpha =\beta \iff \mathrm{s}upp\left\{\alpha \right\}=\mathrm{s}upp\left\{\beta \right\}.$$

(5)

Let $\alpha \in I(n,2n)$, suppose there are $i,j\in supp\alpha$ such that $i+j=2n+1$ in this case $j=2n-i+1$ and we write this pair as $P_i=(i,2n-i+1)$ so we define the set

$${\Sigma }_n:=\left\{P_1,\dots ,P_n\right\}$$

(6)

and if $\alpha \in I(n,2n)$ such that $\{i,2n-i+1\}\subset supp\left\{\alpha \right\}$, then we say that $P_i\in supp\left\{\alpha \right\}$ and that $P_i\in supp\left\{\alpha \right\}\cap {\Sigma }_m$, note that $|supp{P}_{\beta }|=2|supp\beta |$.

If $k\le n$ is a even integer with notation similar to (2) we define

$$C_{\frac{k}{2}}\left({\Sigma }_n\right):=\{P_{\beta }=(P_{{\beta }_1},\dots ,P_{{\beta }_{\frac{k}{2}}}):P_{{\beta }_i}\in {\Sigma }_{n}and1\le {\beta }_1<\dots <{\beta }_{\frac{k}{2}}\le n\}.$$

(7)

If $1\le a_1<a_2<\cdots <a_{2k}\le 2n$ such that $a_i+a_j\ne 2n+1$ then we define

$${\Sigma }_{a_1,\dots ,a_{2k}}={\Sigma }_n-\{P_{a_1},\cdots ,P_{a_{2k}}\}$$

(8)

so $|{\Sigma }_{a_1,\dots ,a_{2k}}|=n-2k$.

We define the sets

$$\begin{array}{c}(a_1,\dots ,a_{2k})\times C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right):=\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}:=\{(a_1,\dots ,a_{2k},P_{\theta })\in I(n-2,2n)|P_{\theta }\in C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)\}\hfill \end{array}$$

(9)

similarly we define $(a_1,\dots ,a_{2k+1})\times C_{\frac{n-(2k+3)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right).$

Lemma 1.

(A) 

Let $n\ge 4$ be an even number such that $r_n=\frac{n+2}{2}$, then

$$I(n-2,2n)=C_{\frac{n-2}{2}}\left({\Sigma }_n\right)\cup (\bigcup _{k=1}^{r_n-2}\bigcup _{\begin{array}{c}1\le a_1<\cdots <a_{2k}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}(a_1,\dots ,a_{2k})\times C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)).$$

(10)

(B) 

Let $n\ge 5$ be an odd and such that $r_n=\frac{n+1}{2}$, then

$$\begin{array}{c}I(n-2,2n)=\bigcup _{j=1}^n{C}_{\frac{n-3}{2}}({\Sigma }_n-\left\{P_j\right\})\times \left\{j\right\}\cup \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\cup (\bigcup _{k=1}^{r_n-2}\bigcup _{\begin{array}{c}1\le a_1<\cdots <a_{2k+1}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}(a_1,\dots ,a_{2k+1})\times C_{\frac{n-(2k+3)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right)).\hfill \end{array}$$

(11)

Proof. 

(A) Let $n\ge 4$ even integer and let $r_n=\frac{n+2}{2}$, then it is it is enough to prove the inclusion ⊆. If $supp\left\{{\alpha }_{rs}\right\}\subseteq {\Sigma }_n$ then it exists $P_{\theta }\in C_{\frac{n-2}{2}}\left({\Sigma }_n\right)$ such that ${\alpha }_{rs}=P_{\theta }\in C_{\frac{n-2}{2}}\left({\Sigma }_n\right)$. If $1\le |supp\left\{{\alpha }_{rs}\right\}\cap {\Sigma }_n|<\frac{n}{2}$ there are $P_{\theta }\in C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)$ and $(a_1,\dots ,a_{2k})$ such that $1\le a_1<\dots ,<a_{2k}\le 2n$ and ${\alpha }_{rs}=(a_1,\dots ,a_{2k},P_{\theta })\in (a_1,\dots ,a_{2k})\times C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)$.

(B) If $n\ge 5$ odd integer and let $r_n=\frac{n+1}{2}$, analogously it is sufficient to show the ⊆.

Let ${\alpha }_{rs}\in I(n-3,2n)$ then if $1\le |supp\left\{{\alpha }_{rs}\right\}\cap {\Sigma }_n|\le \frac{n-3}{2}$, if $|supp\left\{{\alpha }_{rs}\right\}\cap {\Sigma }_n|=\frac{n-3}{2}$ then ${\alpha }_{rs}=(P_{\theta },j)$ with $P_{\theta }\in C_{\frac{n-3}{2}}({\Sigma }_n-\left\{P_j\right\})$.

If $1\le |supp\left\{{\alpha }_{rs}\right\}\cap {\Sigma }_n|<\frac{n-3}{2}$ then it exists $1\le a_1<\cdots <a_{2k+1}\le 2n$ such that $a_i+a_j\ne 2n$ and $P_{\theta }\in C_{\frac{n-(2k+3)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right)$ with ${\alpha }_{rs}=(a_1,\dots ,a_{2k+1},P_{\theta })\in (a_1,\dots ,a_{2k+1})\times C_{\frac{n-(2k+3)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right)$

with which the demonstration ends. □

Given a canonical basis $\mathcal{B}=\{e_1,\dots ,e_n,u_1,\dots u_n\}$, see [15], of symplectic vector space E, in this article, we redefine its elements as follows $e_{2n}:=u_1,e_{2n-1}:=u_2,\dots e_{n+1}:=u_n$ and we have $\mathcal{B}=\{e_1,\dots ,e_{2n}\}$ such that

$$\langle e_i,e_j\rangle =\left\{\begin{array}{cc}1\hfill & \mathrm{if}j=2n-i+1,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(12)

For $\alpha =({\alpha }_1,\dots ,{\alpha }_n)\in I(n,2n)$, write

$$\begin{array}{cc}\hfill e_{\alpha }& :=e_{{\alpha }_1}\wedge \cdots \wedge e_{{\alpha }_n},\hfill \\ \hfill e_{{\alpha }_{rs}}& :=e_{{\alpha }_1}\wedge \cdots \wedge {\widehat{e}}_{{\alpha }_r}\wedge \cdots \wedge {\widehat{e}}_{{\alpha }_s}\wedge \cdots \wedge e_{{\alpha }_n},\hfill \end{array}$$

where ${\widehat{e}}_{{\alpha }_k}$ means that the corresponding term is omitted.

Denote by ${\wedge }^{n}E$ the n-th exterior power of E, which is generated by $\{e_{\alpha }:\alpha \in I(n,2n)\}$. For $w={\sum }_{\alpha \in I(n,2n)}{p}_{\alpha }{e}_{\alpha }\in {\wedge }^{n}E$, the coefficients $p_{\alpha }$ are the Plücker coordinates of w, see also [17] (p. 42). Writing $w\in {\wedge }^{n}E$ as $w={\sum }_{\alpha \in I(n,2n)}{P}_{\alpha }{e}_{\alpha }$, the vector

$$w_{\rho }={\left[p_{\alpha }\right]}_{\alpha \in I(n,2n)}\in \mathbb{P}\left({\wedge }^{n}E\right)$$

(13)

we call the Plücker vector of w.

3. Contraction Map

In this section, E is a symplectic vector space of dimension $2n$.

Definition 1.

The contraction map is defined as the linear transformation

$$f:{\wedge }^{n}E\to {\wedge }^{n-2}E$$

$$f(w_1\wedge \cdots \wedge w_n)=\sum _{1\le r<s\le n}\langle w_r,w_s\rangle {(-1)}^{r+s-1}{w}_1\wedge \cdots \wedge {\widehat{w}}_r\wedge \cdots \wedge {\widehat{w}}_s\wedge \cdots \wedge w_n$$

where $\widehat{w}$ means that the corresponding term is omitted; see [18] (p. 283).

Lemma 2.

Let f the contraction map, and $w={\sum }_{\alpha \in I(n,2n)}{X}_{\alpha }{e}_{\alpha }\in {\wedge }^{n}E$ arbitrary element, in coordinates of Plücker, then the contraction map

$$f\left(w\right)=\sum _{{\alpha }_{rs}\in I(n-2,2n)}(\sum _{i=1}^n{X}_{({\alpha }_{rs},P_i)})e_{{\alpha }_{rs}}$$

where $X_{{\alpha }_{rs}{P}_i}$ disappears from the equation ${\sum }_{i=1}^n{X}_{({\alpha }_{rs},P_i)}$ if $\left|supp\right\{{\alpha }_{rs}{P}_i\left\}\right|\ne n$.

Proof. 

Let $w={\sum }_{\alpha \in I(n,2n)}{X}_{\alpha }{e}_{\alpha }\in {\wedge }^{n}E$ arbitrary element then

$$\begin{array}{cc}\hfill f\left(w\right)=& \sum _{\alpha \in I(n,2n)}{X}_{\alpha }f\left(e_{\alpha }\right)\hfill \\ \hfill =& \sum _{\alpha \in I(n,2n)}{X}_{\alpha }(\sum _{1\le r<s\le n}\langle e_{{\alpha }_r},e_{{\alpha }_s}\rangle {\left(-1\right)}^{r+s-1}{e}_{{\alpha }_{rs}})\hfill \\ \hfill =& \sum _{1\le r<s\le n}(\sum _{i=1}^n{X}_{({\alpha }_{rs},(i,2n-i+1))}\langle e_i,e_{2n-i+1}\rangle {\left(-1\right)}^{[i+2n-i+1]-1})e_{{\alpha }_{rs}}\hfill \\ \hfill =& \sum _{{\alpha }_{rs}\in I(n-2,2n)}(\sum _{i=1}^n{X}_{({\alpha }_{rs},P_i)})e_{{\alpha }_{rs}}\hfill \end{array}$$

where clearly $X_{\left({\alpha }_{rs}{P}_i\right)}$ disappears from the equation if $\left|supp\right\{{\alpha }_{rs}{P}_i\left\}\right|\ne n.$

Let $\psi :E⟶E$ a symplectomorphism that sends the symplectic basis ${\left\{e_i\right\}}_{i=1}^{2n}$ in the symplectic basis ${\left\{{ϵ}_i\right\}}_{i=1}^{2n}$ such that $\psi \left(e_i\right)={ϵ}_i$ then let us consider the following linear transformations defined in generators ${\psi }^n:{\wedge }^{n}E⟶{\wedge }^{n}E$ such that ${\psi }^n\left(e_{\alpha }\right)={ϵ}_{\alpha }$ and ${\psi }^{n-2}:{\wedge }^{n-2}E⟶{\wedge }^{n-2}E$ such that ${\psi }^{n-2}\left(e_{{\alpha }_{rs}}\right)={ϵ}_{{\alpha }_{rs}}.$

Lemma 3.

Let $f:{\wedge }^{n}E⟶{\wedge }^{n-2}E$ the contraction map then the following diagram commutes

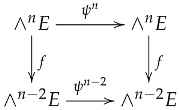that is to say $f\circ {\psi }^n={\psi }^{n-2}\circ f.$

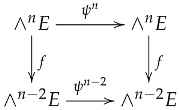
4. Plücker Relations of Lagrangian Grassmannian

For an m-dimensional vector space E, denote by $G(\mathsf{\ell },E)$ the set of vector subspaces of dimension ℓ of E. The Grassmannian $G(\mathsf{\ell },E)$ is a algebraic variety of dimension $\mathsf{\ell }(m-\mathsf{\ell })$ and can be embedded in a projective space ${\mathbb{P}}^{c-1}$, where $c=\left(\genfrac{}{}{0pt}{}{m}{\mathsf{\ell }}\right)$ by Plücker embedding. The Plücker embedding is the injective mapping $\rho :G(\mathsf{\ell },E)\to \mathbb{P}\left({\wedge }^{\mathsf{\ell }}E\right)$ given on each $W\in G(\mathsf{\ell },E)$ by choosing a basis $w_1,\dots ,w_{\mathsf{\ell }}$ of W and then mapping the vector subspace $W\in G(\mathsf{\ell },E)$ to the tensor $w_1\wedge \cdots \wedge w_{\mathsf{\ell }}\in {\wedge }^{\mathsf{\ell }}E$. Since choosing a different basis of W changes the tensor $w_1\wedge \cdots \wedge w_{\mathsf{\ell }}$ by a nonzero scalar, this tensor is a well-defined element in the projective space $\mathbb{P}\left({\wedge }^{\mathsf{\ell }}E\right)\simeq {\mathbb{P}}^{N-1}$, where $N=C_{\mathsf{\ell }}^m={dim}_{\mathbb{F}}\left({\wedge }^{\mathsf{\ell }}E\right)$. If $w={\sum }_{\alpha \in I(\mathsf{\ell },m)}{P}_{\alpha }{e}_{\alpha }\in \mathbb{P}\left({\wedge }^{\mathsf{\ell }}E\right)$, then $w\in G(\mathsf{\ell },E)$ if and only if for each pair of tuples $1\le {\alpha }_1<\cdots <{\alpha }_{\mathsf{\ell }-1}\le m$ and $1\le {\beta }_1<\cdots <{\beta }_{\mathsf{\ell }+1}\le m$, the Plücker coordinates of w satisfy the Plücker relations

$$Q_{\alpha ,\beta }:=\sum _{i=1}^{\mathsf{\ell }+1}{(-1)}^i{P}_{{\alpha }_1\cdots {\alpha }_{\mathsf{\ell }-1}{\beta }_i}{P}_{{\beta }_1,{\beta }_2\cdots \widehat{{\beta }_i}\cdots {\beta }_{\mathsf{\ell }+1}}=0,$$

(14)

where $\widehat{{\beta }_i}$ means that the corresponding term is omitted and where $\alpha =({\alpha }_1,\dots ,{\alpha }_{\mathsf{\ell }-1})\in I(\mathsf{\ell }-1,m)$, $\beta =({\beta }_1,\cdots ,{\beta }_i,\dots ,{\beta }_{\mathsf{\ell }+1})\in I(\mathsf{\ell }+1,m)$, see [17] (Section 4) and [19]. Under the inclusion of Plücker the Lagrangian Grassmannian is given by

$$\begin{array}{c}L(n,E)=\{w_1\wedge \cdots \wedge w_n\in G(n,E):\langle w_i,w_j\rangle =0\mathrm{for}\mathrm{all}1\le i<j\le n\}\end{array}$$

(15)

Lemma 4.

$L(n,E)=G(n,E)\cap kerf.$

Proof. 

Using the Definition 1 we clearly have $L(n,E)\subseteq G(n,E)\cap kerf$ given that $\langle w_r,w_s\rangle =0$ for all $1\le r<s\le 2n$.

Let $v_1\wedge \cdots \wedge v_n\in G(n,E)\cap kerf$ then ${\{w_1\wedge \cdots \wedge {\widehat{w}}_r\wedge \cdots \wedge {\widehat{w}}_s\wedge \cdots \wedge w_n\}}_{1\le r<s\le 2n}$ is a family of linearly independent vectors in ${\wedge }^{n-2}E$ more over by hypothesis $f(w_1\wedge \cdots \wedge w_n)=0$ then $\langle w_r,w_s\rangle =0$ for all $1\le r<s\le 2n$ and so $G(n,E)\cap kerf\subseteq L(n,E)$. □

The proof of the following lemma is a consequence of the Lemma 2 where the kernel of the contraction map f is characterized as follows

Lemma 5.

Let $w={\sum }_{\alpha \in I(n,2n)}{X}_{\alpha }{e}_{\alpha }\in {\wedge }^{n}E$ written in Plücker coordinates, then we have

$$w\in kerf\iff \sum _{i=1}^n{X}_{{\alpha }_{rs}{P}_i}=0,\mathit{for}\mathit{all}{\alpha }_{rs}\in I(n-2,2n).$$

where $X_{{\alpha }_{rs}{P}_i}$ disappears from the equation if $\left|supp\right\{{\alpha }_{rs}{P}_i\left\}\right|\ne n.$

For all ${\alpha }_{rs}\in I(n-2,2n)$ we define a homogeneous linear polynomial

$$\begin{array}{c}{\Pi }_{{\alpha }_{rs}}=\sum _{i=1}^n{c}_{{\alpha }_{rs}{P}_i}{X}_{{\alpha }_{rs}{P}_i}\in {\left({\wedge }^{n}E\right)}^{*}\end{array}$$

(16)

where

$$c_{{\alpha }_{rs}{P}_i}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\left|\mathrm{supp}\right\{{\alpha }_{rs}{P}_i\left\}\right|=n,\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

Remark 1.

Throughout this article, we write the Equation (16) simply as

$$\begin{array}{c}{\Pi }_{{\alpha }_{rs}}=\sum _{i=1}^n{X}_{{\alpha }_{rs}{P}_i}\end{array}$$

(17)

where the addend $X_{{\alpha }_{rs}{P}_i}$ disappears from the Equation (17) if $\left|supp\right\{{\alpha }_{rs}{P}_i\left\}\right|\ne n.$

Corollary 1.

$kerf$ is independent of the symplectic basis and

$$kerf=\bigcap _{{\alpha }_{rs}\in I(n-2,2n)}ker{\Pi }_{{\alpha }_{rs}}.$$

(18)

Proof. 

From the Lemma 2, we have $f\circ {\psi }^n={\psi }^{n-2}\circ f$ so then $kerf\circ {\psi }^n=ker{\psi }^{n-2}\circ f=kerf$ since ${\psi }^{n-2}$ is an isomorphism and then $kerf={\bigcap }_{{\alpha }_{rs}\in I(n-2,2n)}ker{\Pi }_{{\alpha }_{rs}}$. □

Following [20] for definitions of algebraic set, we have below that $kerf$, $G(n,E)$ and $L(n,E)$ are algebraic sets in $\mathbb{P}\left({\wedge }^{n}E\right)$

$$\begin{array}{c}kerf=Z\langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle .\end{array}$$

(19)

So we have to $G(n,E)$ is an algebraic set of

$$\begin{array}{c}G(n,E)=Z\langle Q_{\alpha ,\beta }:\alpha \in I(\mathsf{\ell }-1,m),\beta \in I(\mathsf{\ell }+1,m)\rangle \end{array}$$

(20)

see (14).

Theorem 1.

Let E symplectic vector space of dimension $2n$ then

$$L(n,E)=Z\langle Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}}\rangle$$

where $Q_{\alpha ,\beta }$ and ${\Pi }_{{\alpha }_{rs}}$ are as in (14) and (16), respectively.

Proof. 

Of Lemma 4, (20) and (19) we have

$$\begin{array}{cc}\hfill L(n,E)& =G(n,E)\cap kerf\hfill \\ \hfill & =Z\langle Q_{\alpha ,\beta }\rangle \cap Z\langle {\Pi }_{{\alpha }_{rs}}\rangle \hfill \\ \hfill & =Z\langle Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}}\rangle \hfill \end{array}$$

□

Definition 2.

To the set of homogeneous polynomials

$$\begin{array}{c}\{Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}}\}\end{array}$$

(21)

where $\alpha =({\alpha }_1,\dots ,{\alpha }_{n-1})\in I(n-1,2n)$, $\beta =({\beta }_1,\dots {\beta }_i,\dots ,{\beta }_{n+1})\in I(n+1,2n)$, we call it relations of Pücker of Lagrangian Grassmannian. To the set of linear homogeneous polynomials

$$\begin{array}{c}\{{\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\}\end{array}$$

(22)

we call it linear relations of Plücker of the Lagrangian Grassmannian.

Example 1.

In the case $L(2,E)$ we have the relations of Plücker of Lagrangian Grassmannian

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}Q:=X_{12}{X}_{34}-X_{13}{X}_{24}+X_{14}{X}_{23}\hfill & =0\hfill \\ \Pi :=X_{14}+X_{23}\hfill & =0\hfill \end{array}\right.\end{array}$$

(23)

Example 2.

The linear relations of Plücker of $L(3,E)$ are

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\Pi }_1=X_{P_2,1}+X_{P_3,1}\hfill \\ {\Pi }_2=X_{P_1,2}+X_{P_3,2}\hfill \\ {\Pi }_3=X_{P_1,3}+X_{P_2,3}\hfill \\ {\Pi }_4=X_{P_1,4}+X_{P_5,4}\hfill \\ {\Pi }_5=X_{P_1,5}+X_{P_3,5}\hfill \\ {\Pi }_6=X_{P_2,6}+X_{P_3,6}\hfill \end{array}\right..\end{array}$$

(24)

Example 3.

In the case $L(4,E)$ it was shown in [21] (example 4) that linear relations $\{{\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(2,8)\}$ consists of 28 homogeneous linear equations in 70 variables.

Ideal of $L(n,E)$

The ideal of $L(n,E)$ in $\mathbb{F}{\left[X_{\alpha }\right]}_{\alpha \in I(n,2n)}$ is defines by

$$I\left(L(n,E)\right)=\{f\in \mathbb{F}{\left[X_{\alpha }\right]}_{\alpha \in I(n,2n)}:f\left(w\right)=0forallw\in L(n,E)\}.$$

(25)

Proposition 1.

If the field of definition of the symplectic vector, space E is algebraically closed then

$$I\left(L(n,E)\right)=\sqrt{〈Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}}〉}$$

so $L(n,E)$ is a projective variety.

Proof. 

By the Theorem 1 we have $L(n,E)=Z\langle Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}}\rangle$ and by Hilbert’s Nullstellensatz theorem, see [20] (Theorem 1.3 A), the result is fulfilled. □

Let ${\mathbb{F}}_q$ be a finite field with q elements, and denote by ${\overline{\mathbb{F}}}_q$ an algebraic closure of ${\mathbb{F}}_q$. For a vector space E over ${\mathbb{F}}_q$ of finite dimension k, let $\overline{E}=E{\otimes }_{{\mathbb{F}}_q}{\overline{\mathbb{F}}}_q$ be the corresponding vector space over the algebraically closed field ${\overline{\mathbb{F}}}_q$. We will be considering algebraic varieties in the projective space $\mathbb{P}\left(\overline{E}\right)={\mathbb{P}}^{k-1}\left({\overline{\mathbb{F}}}_q\right)$. Recall that a projective variety $X\subseteq {\mathbb{P}}^{k-1}\left({\overline{\mathbb{F}}}_q\right)$ is defined over the finite field ${\mathbb{F}}_q$ if its vanishing ideal can be generated by polynomials with coefficients in ${\mathbb{F}}_q$. If E is a symplectic vector space, of dimension $2n$ define over a finite field ${\mathbb{F}}_q$, then the rational points of $L(n,E)$ are defined as the set

$$L(n,E)\left({\mathbb{F}}_q\right):=Z\langle Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}},x_{ϵ}^q-x_{ϵ}\rangle$$

where $\alpha \in I(n-1,2n)$, $\beta \in I(n+1,2n)$, ${\alpha }_{rs}\in I(n-2,2n)$ and $ϵ\in I(n,2n)$ more over

$$|L(n,E)\left({\mathbb{F}}_q\right)|={\Pi }_{i=1}^n(1+q^i)$$

(26)

see [22] (Prop. 2.14).

We define the ideal $I_{{\overline{\mathbb{F}}}_q}\subset \mathbb{F}{\left[x_{\alpha }\right]}_{\alpha \in I(n,2n)}$ as

$$I_{{\overline{\mathbb{F}}}_q}=〈Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}},g_{ϵ}〉$$

(27)

where $\alpha \in I(n-1,2n),\beta \in I(n+1,2n),{\alpha }_{rs}\in I(n-2,2n),ϵ\in I(n,2n)$ y $g_{ϵ}=x_{ϵ}^q-x_{ϵ}.$

Lemma 6.

The ideal $I_{{\overline{\mathbb{F}}}_q}$ is radical

Proof. 

The ideal $I_{{\overline{\mathbb{F}}}_q}$ is zero-dimensional since the set of solutions to the homogeneous polynomial equations

$$\left|Sol\right\{Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}},g_{ϵ}\left\}\right|<\infty$$

given that (26) implies $\left|Sol\right\{Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}},g_{ϵ}\left\}\right|=|L(n,E)\left({\mathbb{F}}_q\right)|$ moreover $g_{ϵ}=q{x}_{ϵ}^{q-1}-1=-1$ so $gcd(g_{ϵ},g_{ϵ}^{\prime })=1$, and by Seindeber’s lemma, ver [23] (Proposition 3.7.15), $I_{{\overline{\mathbb{F}}}_q}$ is radical. □

Let ${\Re }_t:=Z\langle h_1,h_2,\dots ,h_t\rangle \le \mathbb{P}\left({\wedge }^{n}E\right)$ a hyperplane of codimension t, we say that $L(n,E)\cap {\Re }_t$ is a linear section of the Lagrangian Grassmannian and let

$$I_t:=\langle Q_{\alpha ,\beta },{\Pi }_{rs},x_{ϵ}^q-x_{ϵ},h_1,h_2,\dots ,h_t\rangle .$$

Lemma 7.

Suppose the basis field ${\mathbb{F}}_q$ is perfect then the linear section of the Lagrangian Grassmannian satisfies $|L(n,E)\left({\mathbb{F}}_q\right)\cap {\Re }_t|={dim}_{{\mathbb{F}}_q}\frac{\mathbb{F}{\left[x_{\alpha }\right]}_{\alpha \in I(n,2n)}}{I_t}.$

Proof. 

Given the $|L(n,E)\cap {\Re }_t|\le |L(n,E)|$ then the ideal $I_r$ is zero dimensional, $mcd(g_{\alpha },g_{\alpha }^{\prime })=1$, thus by Seindeber’s lemma we have that the ideal $I_t$ is radical. □

5. Factorable Morphisms

Let $1\le \cdots <{\overline{\alpha }}_k<\cdots <2n-{\overline{\alpha }}_k+1<\cdots \le 2n$ two integers, we define

$$\mathcal{S}:=\left[2n\right]-\{{\overline{\alpha }}_k,2n-{\overline{\alpha }}_k+1\}$$

(28)

with the notation (2) we define

$$I_{{\overline{\alpha }}_k}(n-1,2n-2):=C_{n-1}\left\{\mathcal{S}\right\}.$$

(29)

Let

$${\varphi }_{{\overline{\alpha }}_k}:=\{(\beta ,{\overline{\alpha }}_k)\in I(n,2n):\beta \in I_{{\overline{\alpha }}_k}(n-1,2n-2)\}.$$

(30)

For $e_{{\overline{\alpha }}_k}\in \mathcal{B}$ be a basic vector and let $\mathsf{\ell }=\langle e_{{\overline{\alpha }}_k}\rangle \subset E$ generated by the vector $e_{{\overline{\alpha }}_k}$ and

$$\mathcal{U}\left(\mathsf{\ell }\right)=\{W\in L(n,E):\mathsf{\ell }\subseteq W\}.$$

(31)

In [16] (Lemma 1.4.38) it shows that there is a one-to-one correspondence between $\mathcal{U}\left(\mathsf{\ell }\right)$ and $L(n-1,{\mathsf{\ell }}^{\perp }/\mathsf{\ell })$, where ${\mathsf{\ell }}^{\perp }/\mathsf{\ell }$ is a symplectic vector space of dimension $2n-2$, generated by the symplectic basis $\{e_1+\mathsf{\ell },\dots ,{\widehat{e}}_{{\overline{\alpha }}_k}+\mathsf{\ell },\dots ,{\widehat{e}}_{2n-{\overline{\alpha }}_k+1}+\mathsf{\ell },\dots ,e_{2n}+\mathsf{\ell }\}$, recall ^{^} means that the term was omitted.

As consequence we have $\mathcal{U}\left(\mathsf{\ell }\right){=}_{-}\wedge e_{{\overline{\alpha }}_k}\left(L(n-1,{\mathsf{\ell }}^{\perp }/\mathsf{\ell })\right)$ and

$$\mathcal{U}\left(\mathsf{\ell }\right)=L(n-1,{\mathsf{\ell }}^{\perp }/\mathsf{\ell })\wedge e_{{\overline{\alpha }}_k}$$

(32)

so in Plücker coordinates we have

$$\mathcal{U}\left(\mathsf{\ell }\right)=(w\in L(n,E):w=\sum _{(\beta ,{\overline{\alpha }}_k)\in {\varphi }_{{\overline{\alpha }}_k}}{p}_{(\beta ,{\overline{\alpha }}_k)}{e}_{(\beta ,{\overline{\alpha }}_k)}).$$

(33)

$X_{\beta }:={\left(e_{\beta }+\mathsf{\ell }\right)}^{*}$ denotes the basis vector of the dual vector space ${\left({\wedge }^{n-1}{\mathsf{\ell }}^{\perp }/\mathsf{\ell }\right)}^{*}$ and $X_{\beta }\wedge X_{{\overline{\alpha }}_k}:=e_{(\beta ,{\overline{\alpha }}_k)}^{*}$ the basis vector of dual vector space ${\left({\wedge }^{n}E\right)}^{*}$. Now with this notation we define in generators an injective linear transformation

$$\begin{array}{c}\hfill \xi :{\left({\wedge }^{n-1}({\mathsf{\ell }}^{\perp }/\mathsf{\ell })\right)}^{*}⟶{\left({\wedge }^{n}E\right)}^{*}\\ \hfill X_{\beta }⟼X_{\beta }\wedge X_{{\overline{\alpha }}_k}\end{array}$$

(34)

with $\beta \in I_{{\overline{\alpha }}_k}(n-1,2n-2)$ and $X_{\beta }\wedge X_{{\overline{\alpha }}_k}=X_{(\beta ,{\overline{\alpha }}_k)}$.

Definition 3.

We say that $h={\sum }_{\alpha \in I(n,2n)}{A}_{\alpha \in I(n,2n)}{X}_{\alpha \in I(n,2n)}\in {\left({\wedge }^{n}E\right)}^{*}$ is factored if $h=h_0\wedge X_{{\overline{\alpha }}_k}$ for some $h_0\in {({\wedge }^{n-1}{\mathsf{\ell }}^{\perp }/\mathsf{\ell })}^{*}$ where $\mathsf{\ell }=\langle e_{{\overline{\alpha }}_k}\rangle$ and $1\le {\overline{\alpha }}_k\le 2n$. We say h satisfies the factoring property if there are at least one coefficient $A_{\overline{\alpha }}\ne 0$ and there are at least one element ${\overline{\alpha }}_k\in supp\left\{\overline{\alpha }\right\}$ such that $2n-{\overline{\alpha }}_k+1\notin supp\left\{\overline{\alpha }\right\}.$

Example 4.

The homogeneous linear polynomials given in the Example 2 are factored

$$\begin{array}{cc}\hfill {\Pi }_1& =(X_{P_2}+X_{P_3})\wedge X_1\hfill \\ \hfill {\Pi }_2& =(X_{P_1}+X_{P_3})\wedge X_2\hfill \\ \hfill {\Pi }_3& =(X_{P_1}+X_{P_2})\wedge X_3\hfill \\ \hfill {\Pi }_4& =(X_{P_1}+X_{P_5})\wedge X_4\hfill \\ \hfill {\Pi }_5& =(X_{P_1}+X_{P_3})\wedge X_5\hfill \\ \hfill {\Pi }_6& =(X_{P_2}+X_{P_3})\wedge X_6\hfill \end{array}$$

Proposition 2.

Let $h\in {\left({\wedge }^{n}E\right)}^{*}$ such that $h\left(L\right(n,E\left)\right)=0$ and $h=h_0\wedge X_{{\overline{\alpha }}_k}$ is factored. Then $h_0\left(L(n-1,{\mathsf{\ell }}^{\perp }/\mathsf{\ell })\right)=0$ where $\mathsf{\ell }=\langle e_{{\overline{\alpha }}_k}\rangle$.

Proof. 

$\mathcal{U}\left(\mathsf{\ell }\right)=L(n-1,{\mathsf{\ell }}^{\perp }/\mathsf{\ell })\wedge e_{\overline{\alpha }}\subseteq L(n,E)$ then $h\left(\mathcal{U}\right(\mathsf{\ell }\left)\right)=0$ and

$$\begin{array}{cc}\hfill h\left(\mathcal{U}\right(\mathsf{\ell }\left)\right)& =h(L(n-1,{\mathsf{\ell }}^{\perp }/\mathsf{\ell })\wedge e_{{\overline{\alpha }}_k})\hfill \\ \hfill & =(h_0\wedge X_{{\overline{\alpha }}_k})(L(n-1,{\mathsf{\ell }}^{\perp }/\mathsf{\ell })\wedge e_{{\overline{\alpha }}_k})\hfill \\ \hfill & =h_0\left(L(n-1,{\mathsf{\ell }}^{\perp }/\mathsf{\ell })\right)·X_{{\overline{\alpha }}_k}\left(e_{{\overline{\alpha }}_k}\right)\hfill \\ \hfill & =0\hfill \end{array}$$

$h_0\left(L(n-1,{\mathsf{\ell }}^{\perp }/\mathsf{\ell })\right)=0.$□

We denote by ${\beta }_{rs}=({\beta }_1,\dots ,{\widehat{\beta }}_r,\dots ,{\widehat{\beta }}_s,\dots ,{\beta }_{n-1})\in I_{{\overline{\alpha }}_k}(n-3,2n-2)$, where ^{^} means that the corresponding term is omitted. We define

$${\Pi }_{({\beta }_{rs},{\overline{\alpha }}_k)}:=\sum _{i=1}^n{X}_{({\beta }_{rs},{\overline{\alpha }}_k)P_i}$$

(35)

an element of in ${\left({\bigwedge }^{n}E\right)}^{*}$ such that $\left|supp\right\{({\beta }_{rs},{\overline{\alpha }}_k)P_i\left\}\right|=n.$

Lemma 8.

Let ${\beta }_{rs}\in I_{{\overline{\alpha }}_k}(n-3,2n-2)$ where $1\le r<s\le 2n$ and $r,s\in \mathcal{S}$ see (28) then

$$\mathcal{U}\left(\mathsf{\ell }\right)\subseteq \bigcap _{{\beta }_{rs}\in I_{{\overline{\alpha }}_k}(n-3,2n-2)}ker{\Pi }_{({\beta }_{rs},{\overline{\alpha }}_k)}.$$

Proof. 

Let $w\in \mathcal{U}\left(\mathsf{\ell }\right)$ be from (33) we have $w={\sum }_{\beta \in I_{{\overline{\alpha }}_k}(n-1,2n-2)}{X}_{(\beta ,{\overline{\alpha }}_k)}{e}_{(\beta ,{\overline{\alpha }}_k)}$ and $f\left(w\right)=0$ for f contraction map, we have

$$f\left(w\right)=\sum _{\beta \in I_{{\overline{\alpha }}_k}(n-1,2n-2)}{X}_{(\beta ,{\overline{\alpha }}_k)}f\left(e_{(\beta ,{\overline{\alpha }}_k)}\right)=$$

$$=\sum _{\beta \in I_{{\overline{\alpha }}_k}(n-1,2n-2)}{X}_{(\beta ,{\overline{\alpha }}_k)}(\sum _{1\le r<s\le n}\langle e_{{\alpha }_r},e_{{\alpha }_s}\rangle {(-1)}^{r+s-1}{e}_{{(\beta ,{\overline{\alpha }}_k)}_{rs}})$$

$$=\sum _{1\le r<s\le n}(\sum _{1\le {\rho }_1<{\rho }_2\le n}{X}_{({\beta }_{rs},{\overline{\alpha }}_k,{\rho }_1,{\rho }_2)}\langle e_{{\rho }_1},e_{{\rho }_2}\rangle {(-1)}^{{\rho }_1+{\rho }_2-1})e_{{(\beta ,{\overline{\alpha }}_k)}_{rs}}=0$$

then

$$\sum _{1\le {\rho }_1<{\rho }_2\le n}{X}_{({\beta }_{rs},{\overline{\alpha }}_k,{\rho }_1,{\rho }_2)}{(-1)}^{{\rho }_1+{\rho }_2-1}\langle e_{{\rho }_1},e_{{\rho }_2}\rangle =0.$$

where ${\beta }_{rs}\in I_{{\overline{\alpha }}_k}(n-3,2n-2)$ and as stated before $({\beta }_{rs},{\overline{\alpha }}_k,{\rho }_1,{\rho }_2)\in I(n,2n)$. Now $\langle e_{{\rho }_1},e_{{\rho }_2}\rangle =1$ iff ${\rho }_1+{\rho }_2=2n+1$, note that with this condition we have ${(-1)}^{{\rho }_1+{\rho }_2-1}=1$. Renaming ${\rho }_1=i$, we have ${\rho }_2=2n-i+1$. Then

$$\sum _{1\le {\rho }_1<{\rho }_2\le n}{X}_{({\beta }_{rs},{\overline{\alpha }}_k){\rho }_1{\rho }_2}=\sum _{i=1}^n{X}_{\left({\beta }_{rs}{\overline{\alpha }}_k\right)P_i}=0$$

for all ${\beta }_{rs}\in I_{{\overline{\alpha }}_k}(n-3,2n-2)$, that is $\mathcal{U}\left(\mathsf{\ell }\right)\subseteq ker{\Pi }_{({\beta }_{rs},{\overline{\alpha }}_k)}$ where

$${\Pi }_{({\beta }_{rs},{\overline{\alpha }}_k)}:=\sum _{i=1}^n{X}_{\left({\beta }_{rs}{\overline{\alpha }}_k\right)P_i}$$

(36)

for all $({\beta }_{rs},{\overline{\alpha }}_k)\in I_{{\overline{\alpha }}_k}(n-3,2n-2)\times \left\{{\overline{\alpha }}_k\right\}.$ □

Remark 2.

Note that

$$\{{\Pi }_{({\beta }_{rs},{\overline{\alpha }}_k)}:{\beta }_{rs}\in I_{{\overline{\alpha }}_k}(n-3,2n-2)\}\subseteq \{{\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\}$$

for all $1\le r<s\le 2n-2$.

6. Linear Envelope of $\mathit{L}(\mathit{n},\mathit{E})$

In this section, E is a symplectic vector space of dimension $2n$.

$$\mathcal{H}:=\langle h\in {\left({\wedge }^{n}E\right)}^{*}:h\left(L(n,E)\right)=0\rangle$$

(37)

Remark 3.

Sometimes in (37), it is necessary to distinguish the even case from the odd case so we write ${\mathcal{H}}_{even}^n\subset {\left({\wedge }^{n}E\right)}^{*}$ to n even number and ${\mathcal{H}}_{odd}^n\subset {\left({\wedge }^{n}E\right)}^{*}$ for n odd number.

Lemma 9.

$\mathcal{H}$ is a nontrivial vector subspace of ${\left({\wedge }^{n}E\right)}^{*}$

Proof. 

The proof follows from (18) given that $L(n,E)\subset kerf$, so $\langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$ is a vector subspace of $\mathcal{H}$. □

Let $h\in \mathcal{H}$ to the set $H_h:=kerh$ we call it a hyperplane containing $L(n,E)$.

Definition 4.

The Linear Envelope $〈L(n,E)〉$ of $L(n,E)$ is the smallest linear variety that contains $L(n,E)$ in $\mathbb{P}\left({\wedge }^{n}E\right).$

The proof of the following corollary follows directly from the Definition 4.

Corollary 2.

$〈L(n,E)〉={\bigcap }_{h\in \mathcal{H}}{H}_h.$

Proposition 3.

Let $h={\sum }_{\alpha \in I(n,2n)}{A}_{\alpha }{X}_{\alpha }\in \mathcal{H}$ and $A_{\overline{\alpha }}\ne 0$ a coefficient different from zero of h then it exists $\{{\overline{\alpha }}_i,{\overline{\alpha }}_j\}\subseteq supp\left\{\overline{\alpha }\right\}$ such that ${\overline{\alpha }}_i+{\overline{\alpha }}_j=2n+1$.

Proof. 

Suppose that for each $\{{\overline{\alpha }}_i,{\overline{\alpha }}_j\}\subseteq supp\left\{\overline{\alpha }\right\}$ you have to ${\overline{\alpha }}_i+{\overline{\alpha }}_j\ne 2n+1$ this means that $\langle e_{{\overline{\alpha }}_i},e_{{\overline{\alpha }}_j}\rangle =0$ then $e_{\overline{\alpha }}=e_{{\overline{\alpha }}_1}\wedge \cdots \wedge e_{{\overline{\alpha }}_n}\in L(n,E)$ and so then $h\left(e_{\overline{\alpha }}\right)=A_{\overline{\alpha }}=0$ which is a contradiction. Then there are $\{{\overline{\alpha }}_i,{\overline{\alpha }}_j\}\subseteq supp\left\{\overline{\alpha }\right\}$ such that ${\overline{\alpha }}_i+{\overline{\alpha }}_j=2n+1$. □

For each $P_{\theta }\in C_{\frac{n-2}{2}}\left({\Sigma }_n\right)$, we define

$$h_{P_{\theta }}=\sum _{i=1}^n{A}_{P_{\theta }{P}_i}{X}_{P_{\theta }{P}_i}$$

(38)

for each $(a_1,\dots ,a_{2k},P_{\theta })\in \left\{(a_1,\dots ,a_{2k})\right\}\times C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)$ we define

$$h_{(a_1,\dots ,a_{2k},P_{\theta })}=\sum _{i=1}^n{A}_{(a_1,\dots ,a_{2k},P_{\theta })}{X}_{(a_1,\dots ,a_{2k},P_{\theta })}.$$

(39)

Similarly

for each $1\le j\le n$ and $(P_{\theta },j)\in C_{\frac{n-3}{2}}({\Sigma }_n-\left\{P_j\right\})\times \left\{j\right\}$ we define

$$h_{P_{(\theta ,j)}}=\sum _{i=1}^n{A}_{(P_{\theta },j,P_i)}{X}_{(P_{\theta },j,P_i)}$$

(40)

for each $(a_1,\dots ,a_{2k+1},P_{\theta })\in \left\{(a_1,\dots ,a_{2k+1})\right\}\times C_{\frac{n-(2k+3)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right)$ we define

$$h_{(a_1,\dots ,a_{2k+1},P_{\theta })}=\sum _{i=1}^n{A}_{(a_1,\dots ,a_{2k+1},P_{\theta })}{X}_{(a_1,\dots ,a_{2k+1},P_{\theta }).}$$

(41)

Corollary 3.

Let E symplectic vector space of dimention $2n$

(i) 

If $n\ge 4$ even, $r_n=\frac{n+2}{2}$ and let $h\in {\mathcal{H}}_{even}^n$ then

$$h=\sum _{P_{\theta }\in C_{\frac{n-2}{2}}\left({\Sigma }_n\right)}{h}_{P_{\theta }}+\sum _{k=1}^{r_n-2}\sum _{(a_1,\dots ,a_{2k},P_{\theta })}{h}_{(a_1\dots ,a_{2k},P_{\theta })}$$

with $P_{\theta }\in C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)$ such that $1\le a_1<\cdots <a_{2k}\le 2n$ and $a_i+a_j\ne 2n+1$.

(ii) 

If $n\ge 5$ odd, $r_n=\frac{n+1}{2}$ and let $h\in {\mathcal{H}}_{odd}^n$ then

$$h=\sum _{j=1}^n\sum _{(P_{\theta },j)\in C_{\frac{n-3}{2}}({\Sigma }_n-\left\{P_j\right\})\times \left\{j\right\}}{h}_{(P_{\theta },j)}+\sum _{k=1}^{r_n-2}\sum _{(a_1,\dots ,a_{2k+1},P_{\theta })}{h}_{(a_1\dots ,a_{2k+1},P_{\theta })}$$

with $P_{\theta }\in C_{\frac{n-(2k+3)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right)$ such that $1\le a_1<\cdots <a_{2k+1}\le 2n+1$ and $a_i+a_j\ne 2n+1.$

Proof. 

The proof follows directly from the Lemma 1 and Proposition 3. □

Lemma 10.

Let E symplectic vector space of dimension 4, and $h\in {\left({\wedge }^{2}E\right)}^{*}$ such that $h\left(L\right(2,E\left)\right)=0$ then $h=A\Pi$ for A a non-zero constant and $\Pi :=X_{P_1}+X_{P_2}$.

Proof. 

Clearly by Proposition 3 each $h\in {\mathcal{H}}_{even}^2$ it is of the form $h=A_{14}{X}_{14}+A_{23}{X}_{23}$ it is easy see that $e_{12}+e_{14}-e_{23}+e_{34}\in L(2,E)$ since it satisfies the Equation (24) more over $h(e_{12}+e_{14}-e_{23}+e_{34})=A_{14}-A_{23}=0$ consequently $h=A\Pi$ where $A=A_{14}=A_{23}$.

□

Theorem 2.

Let E symplectic vector space of dimension $2n$, $h\in {\left({\wedge }^{n}E\right)}^{*}$ such that $h\left(L\right(n,E\left)\right)=0$ and $h=h_0\wedge X_{{\overline{\alpha }}_k}$ is factored then $h\in {\langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle }_{\mathbb{F}}$.

Proof. 

The proof is by induction on n. If $n=2$ it follows from Lemma 10.

We induction hypothesis is, let $E^{\prime }$ symplectic vector space of dimension $2m$ with $m<n$ and $h_0\in {\left({\wedge }^m{E}^{\prime }\right)}^{*}$ such that $h_0\left(L(m,E^{\prime })\right)=0$ then $h_0\in \langle {\Pi }_{{\beta }_{rs}}:{\beta }_{rs}\in I(n-3,2n-2)\rangle$.

If $h\in {\left({\wedge }^{n}E\right)}^{*}$ such that $h\left(L\right(n,E\left)\right)=0$ and $h=h_0\wedge X_{{\overline{\alpha }}_k}$ is factored, then by Lemma 2 $h_0\left(L(n-1,{\mathsf{\ell }}^{\perp }/\mathsf{\ell })\right)=0$ where $\mathsf{\ell }=\langle e_{{\overline{\alpha }}_k}\rangle$ then by induction step $h_0\in \langle {\Pi }_{{\beta }_{rs}}:{\beta }_{rs}\in I_{\overline{\alpha }}(n-3,2n-2)\rangle$ so $h=h_0\wedge X_{{\overline{\alpha }}_k}\in \langle {\Pi }_{{\beta }_{rs}}\wedge X_{{\overline{\alpha }}_k}:{\beta }_{rs}\in I_{\overline{\alpha }}(n-3,2n-2)\rangle \subseteq \langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$. □

Proposition 4.

Let $h={\sum }_{\alpha \in I(n,2n)}{A}_{\alpha }{X}_{\alpha }\in {\left({\wedge }^{n}E\right)}^{*}$ such that $h\left(L\right(n,E\left)\right)=0$ and satisfies the factoring property from the Definition 3, then $h\in \langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$ or $h=h^{\prime }+h^{\prime \prime }$, where $h^{\prime }\in \langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$ and $h^{\prime \prime }$ satisfies that $supp\left\{\alpha \right\}\subset {\Sigma }_n$ for all coefficients $A_{\alpha }\ne 0$ moreover $h^{\prime \prime }\left(L(n,E)\right)=0$.

Proof. 

The proof is by induction on n. If $n=2$ it follows from Lemma 10.

Induction Step): Let $E^{\prime }$ symplectic vector space of dimension $2m$ with $m<n$ and $h_0\in {\left({\wedge }^m{E}^{\prime }\right)}^{*}$ such that $h_0\left(L(m,E^{\prime })\right)=0$ then $h_0\in \langle {\Pi }_{{\beta }_{rs}}:{\beta }_{rs}\in I(n-3,2n-2)\rangle$.

Let $A_{\overline{\alpha }}$ a non-zero coefficient that satisfies the factoring property, from the Definition 3, then there is ${\overline{\alpha }}_k\in supp\left\{\overline{\alpha }\right\}$ but $2n-{\overline{\alpha }}_k+1\notin supp\left\{\overline{\alpha }\right\}$. Now let ${\varphi }_{{\overline{\alpha }}_k}=\{(\beta ,{\overline{\alpha }}_k)\in I(n,2n):\beta \in I_{{\overline{\alpha }}_k}(n-1,2n-2)\}$ as in (30). So if $h={\Sigma }_{\alpha \in I(n,2n)}{A}_{\alpha }{X}_{\alpha }\in {\left({\wedge }^{n}E\right)}^{*}$ then $h={\Sigma }_{\alpha \in {\varphi }_{{\overline{\alpha }}_k}}{A}_{\alpha }{X}_{\alpha }+{\Sigma }_{\alpha \in {\varphi }_{{\overline{\alpha }}_k}^c}{A}_{\alpha }{X}_{\alpha }$ where $I(n,2n)={\varphi }_{{\overline{\alpha }}_k}\cup {\varphi }_{{\overline{\alpha }}_k}^c$. We define homogeneous linear polynomials $h^{\prime }:={\Sigma }_{\alpha \in {\varphi }_{{\overline{\alpha }}_k}}{A}_{\alpha }{X}_{\alpha }$ and $h^{\prime \prime }:={\Sigma }_{\alpha \in {\varphi }_{{\overline{\alpha }}_k}^c}{A}_{\alpha }{X}_{\alpha }$ such that $h^{\prime },h^{\prime \prime }\in {\left({\wedge }^{n}E\right)}^{*}$ and $h=h^{\prime }+h^{\prime \prime }$ so $h^{\prime }={\sum }_{(\beta ,{\overline{\alpha }}_k)\in {\varphi }_{{\overline{\alpha }}_k}}{A}_{(\beta ,{\overline{\alpha }}_k)}{X}_{(\beta ,{\overline{\alpha }}_k)}$ and $h^{\prime \prime }={\sum }_{\alpha \in {\varphi }_{{\overline{\alpha }}_k}^c}{A}_{\alpha }{X}_{\alpha }$. Note that $h^{\prime }\ne 0$, because as we mentioned before $\overline{\alpha }\in {\varphi }_{{\overline{\alpha }}_k}$, from (33) we have that $h^{\prime \prime }\left(\mathcal{U}\left(\mathsf{\ell }\right)\right)=0$ that is $h\left(\mathcal{U}\left(\mathsf{\ell }\right)\right)=h^{\prime }\left(\mathcal{U}\left(\mathsf{\ell }\right)\right)$, since $h\left(L\right(n,E\left)\right)=0$ we obtain $h^{\prime }\left(\mathcal{U}\left(\mathsf{\ell }\right)\right)=0$ moreover $h^{\prime }=h_0\wedge X_{{\overline{\alpha }}_k}$ with $h_0={\sum }_{\beta \in I_{{\overline{\alpha }}_k}(n-1,2n-2)}{A}_{\beta }{X}_{\beta }\in {({\wedge }^{n-1}{\mathsf{\ell }}^{\perp }/\mathsf{\ell })}^{*}$ where $A_{\beta }=A_{(\beta ,{\overline{\alpha }}_k)}$ then by Proposition 2 we have $h_0\left(L(n-1,{\mathsf{\ell }}^{\perp }/\mathsf{\ell })\right)=0$ then $h^{\prime }=h_0\wedge X_{{\overline{\alpha }}_k}\in \langle {\Pi }_{{\beta }_{rs}}\wedge X_{{\overline{\alpha }}_k}:{\beta }_{rs}\in I_{{\overline{\alpha }}_k}(n-3,2n-2)\}\rangle \subseteq \langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$. Given that $h^{\prime \prime }\left(L(n,E)\right)=(h-h^{\prime })\left(L(n,E)\right)=0$ and if $h^{\prime \prime }$ satisfies the factoring property from the Definition 3 continuing recursively in the same way, the process ends in a finite number of steps in $h\in \langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$ or $h=h^{\prime }+h^{\prime \prime }$, where $h^{\prime }\in \langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$ and $h^{\prime \prime }\ne 0$ with $supp\left\{\alpha \right\}\subset {\Sigma }_n$ for all coefficients $A_{\alpha }\ne 0$ and $h^{\prime \prime }\left(L(n,E)\right)=0$. □

Corollary 4.

Let E symplectic vector space of dimension $2n$

(a) If $n\ge 5$ odd then ${\mathcal{H}}_{odd}^n=\langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$

(b) If $h\in {\mathcal{H}}_{even}^n$ then $h=h^{\prime }+h^{\prime \prime }$ such that $h^{\prime }\in {\langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle }_{\mathbb{F}}$ and $h^{\prime \prime }$ satisfies that $supp\left\{\alpha \right\}\subset {\Sigma }_n$ for all coefficients $A_{\alpha }\ne 0$ and $h^{\prime \prime }\left(L(n,E)\right)=0.$

Proof. 

(a) If $h\in {\mathcal{H}}_{odd}^n$ then by Corollary 3$\left(ii\right)$

$$h=\sum _{j=1}^n\sum _{(P_{\theta },j)\in C_{\frac{n-3}{2}}({\Sigma }_n-\left\{P_j\right\})\times \left\{j\right\}}{h}_{(P_{\theta },j)}+\sum _{k=1}^{r-2}\sum _{(a_1,\dots ,a_{2k+1},P_{\theta })}{h}_{(a_1\dots ,a_{2k+1},P_{\theta })}$$

with $P_{\theta }\in C_{\frac{n-2(k+3)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right)$ such that $1\le a_1<\cdots <a_{2k+1}\le 2n+1$ and $a_i+a_j\ne 2n+1$ satisfies the factoring property for all non-zero coefficients of h then by Proposition 4 we have $h\in \langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$

(b) If $h\in {\mathcal{H}}_{even}^n$ then by Corollary 3 we have $h=h^{\prime }+h^{\prime \prime }$ where $h^{\prime }={\sum }_{P_{\theta }\in C_{\frac{n-2}{2}}\left({\Sigma }_n\right)}{h}_{P_{\theta }}$ and $h^{\prime \prime }={\sum }_{k=1}^{r-2}{\sum }_{(a_1,\dots ,a_{2k},P_{\theta })}{h}_{(a_1\dots ,a_{2k},P_{\theta })}$ with $P_{\theta }\in C_{\frac{n-2(k+3)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right)$ such that $1\le a_1<\cdots <a_{2k+1}\le 2n+1$ and $a_i+a_j\ne 2n+1$. Clearly $h^{\prime \prime }$ satisfies factoring property of the Definition 3 for all non-zero coefficients of $h^{\prime \prime }$, so by Proposition 4 we have $h^{\prime \prime }\in {\langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle }_{\mathbb{F}}$ and each coefficient $A_{P_{\theta }}\ne 0$ of $h^{\prime }$ satisfies that $supp\left\{P_{\theta }\right\}\subset C_{\frac{n-2}{2}}\left({\Sigma }_n\right)$ and $h^{\prime }\left(L(n,E)\right)=0$. □

For $P_{\theta }:=(P_{{\theta }_1},\dots ,P_{{\theta }_{\frac{n}{2}}})\in C_{\frac{n}{2}}\left({\Sigma }_n\right)$ an arbitrary element where $1\le {\theta }_1<\cdots <{\theta }_{\frac{n}{2}}\le n$ we say that

$${\theta }_1=minsupp\left\{P_{\theta }\right\}$$

(42)

For $\varnothing \ne \Omega \subseteq C_{\frac{n}{2}}\left({\Sigma }_n\right)$ an arbitrary subset then there are a partition of $\Omega$ of the form

$$\Omega =\bigcup _{j=1}^t{\Omega }_{k_j}$$

(43)

where

$${\Omega }_{k_j}:=\{P_{\theta }\in \Omega :k_j=minsupp\left\{P_{\theta }\right\}\}$$

(44)

to $j\in \{1,\dots ,t\}$ and $1\le k_1<\cdots <k_t\le n$.

$$h_{\Omega }=\sum _{j=1}^t(\sum _{P_{\overline{\theta }}^j\in {\Omega }_{k_j}}(\sum _{i=1}^r{A}_{P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_i}^j}{X}_{P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_i}^j})).$$

(45)

where $P_{\overline{\theta }}^j:=P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_i}^j$

Lemma 11.

Let E symplectic vector space of dimention $2n$, $\Omega \subseteq C_{\frac{n-2}{2}}\left({\Sigma }_n\right)$ non-empty set and $h_{\Omega }\in {\left({\wedge }^{n}E\right)}^{*}$ such that $h_{\Omega }\left(L(n,E)\right)=0$ then $h_{\Omega }\in \langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$.

Proof. 

Let $h_{\Omega }={\sum }_{j=1}^t({\sum }_{P_{\overline{\theta }}^j\in {\Omega }_{k_j}}({\sum }_{i=1}^r{A}_{P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_i}^j}{X}_{P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_i}^j}))$ and without loss of generality we can assume that $A_{P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_1}^j}\ne 0$ for all $j\in \{1,\dots ,t\}$. Now let $\overline{\Pi }:={\sum }_{j=1}^t({\sum }_{P_{\overline{\theta }}^j\in {\Omega }_{k_j}}{A}_{P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_1}^j}{\Pi }_{P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j})\in \langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$ We define

$$\begin{array}{cc}\hfill {\overline{h}}_{\Omega }:& =h_{{\cup }_{j=1}^t{\Omega }_{k_j}}-\overline{\Pi }\hfill \\ \hfill & =\sum _{j=1}^t(\sum _{P_{\overline{\theta }}^j\in {\Omega }_{k_j}}(\sum _{i=2}^r(A_{P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_i}^j}-A_{P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_1}^j})X_{P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_i}^j{k}_j})\wedge X_{2n-k_j+1}\hfill \end{array}$$

then for each $1\le j\le t$ we define

$$h_{(0,k_j)}:=\sum _{P_{\theta }^j\in {\Omega }_{k_j}}(\sum _{i=2}^r(A_{P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_i}^j}-A_{P_{k_j},P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_1}^j})X_{P_{{\theta }_2}^j,\dots P_{{\theta }_{\frac{n-2}{2}}}^j{P}_{{ϵ}_i}^j{k}_j}$$

such that

$${\overline{h}}_{\Omega }=\sum _{j=1}^t(h_{(0,k_j)}\wedge X_{2n-k_j+1})$$

(46)

Let $1\le j_0\le t$ a fixed element, ${\mathsf{\ell }}_{j_0}=\langle e_{j_0}\rangle \subseteq E$ and $L(n-1,{\mathsf{\ell }}_{j_0}^{\perp }/{\mathsf{\ell }}_{j_0})\wedge e_{2n-k_{j_0}+1}\subset L(n,E)$ then

$$\begin{array}{c}{\overline{h}}_{\Omega }(L(n-1,{\mathsf{\ell }}_{j_0}^{\perp }/{\mathsf{\ell }}_{j_0})\wedge e_{2n-k_{j_0}+1})=\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=(\sum _{j=1}^t(h_{(0,k_j)}\wedge X_{2n-k_{j_0}+1}))(L(n-1,{\mathsf{\ell }}_{j_0}^{\perp }/{\mathsf{\ell }}_{j_0})\wedge e_{2n-k_{j_0}+1})=\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=h_{(0,k_{j_0})}(L(n-1,{\mathsf{\ell }}_{j_0}^{\perp }/{\mathsf{\ell }}_{j_0}))·X_{2n-j_0+1}(e_{2n-j_0+1})=\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=h_{(0,k_{j_0})}(L(n-1,{\mathsf{\ell }}_{j_0}^{\perp }/{\mathsf{\ell }}_{j_0})).\hfill \end{array}$$

Moreover, ${\overline{h}}_{\Omega }\left(L(n,E)\right)=0$ implies $h_{(0,k_{j_0})}\left(L(n-1,{\mathsf{\ell }}_{j_0}^{\perp }/{\mathsf{\ell }}_{j_0})\right)=0$ so by Corollary 4$\left(a\right)$ given that $n-1$ is odd number and $h_{(0,k_{j_0})}\in {({\wedge }^{n-1}{\mathsf{\ell }}_{j_0}^{\perp }/{\mathsf{\ell }}_{j_0})}^{*}$ we have $h_0\in \langle {\Pi }_{{\beta }_{rs}}:{\beta }_{rs}\in I_{k_{j_0}}(n-3,2n-2)\rangle$ so

$$\begin{array}{cc}\hfill h_{(0,k_{j_0})}\wedge X_{2n-k_{j_0}+1}& \in \langle {\Pi }_{({\beta }_{rs},k_{2n-j_0+1})}:({\beta }_{rs},k_{2n-j_0+1})\in I(n-2,2n)\rangle \hfill \\ \hfill & \subseteq \langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle \hfill \end{array}$$

then ${\overline{h}}_{\Omega }={\sum }_{j=1}^t(h_{(0,k_j)}\wedge X_{2n-k_j+1})\in \langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\rangle$. □

Corollary 5.

If $n\ge 4$ even then ${\mathcal{H}}_{even}^n=\langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n,2n)\rangle$.

Proof. 

By Corollary 4(b) and by the Lemma 11, we have $\langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n,2n)\rangle \subseteq {\mathcal{H}}_{even}^n$. □

Theorem 3.

Let E be a symplectic vector space of dimension $2n$ then

(I) 

$\mathcal{H}=\langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n,2n)\rangle$

(II) 

$\langle L(n,E)\rangle =\mathbb{P}(kerf)$.

Proof. 

$\left(I\right)$ From the Corollary 4$\left(a\right)$ and Corollary 5 we have $\mathcal{H}=\langle {\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n,2n)\rangle$

$\left(II\right)$ By (I) above, Corollary 2 and (18) we have

$$\langle L(n,E)\rangle =\bigcap _{h\in \mathbb{H}}{H}_h=\bigcap _{{\alpha }_{rs}\in I(n-2,2n)}ker{\Pi }_{{\alpha }_{rs}}=kerf.$$

□

Lemma 12.

Let $g:{\wedge }^{n}E⟶{\wedge }^{n-2}E$ a linear transformation such that $g\left(L\right(n,E\left)\right)=0$ then $g(kerf)=0$.

Proof. 

$g\left(L\right(n,E\left)\right)=0$ we have $L(n,E)\subseteq kerg$ so $kerf\subseteq kerg$ that is $g(kerf)=0$. □

Corollary 6.

Suppose the contraction map f is surjective and suppose $G:{\wedge }^{n}E⟶{\wedge }^{n-2}E$ is a surjective linear transformation that vanishes $L(n,E)$ then there exists a unique isomorphism such that $G=h\circ f$.

Proof. 

By Lemma 12 we have $kerf\subseteq kerG$, more over $kerf=kerG$ since both have the same dimension because f and G are surjective, then there exists a unique linear isomorphism h that makes the following diagram commute.

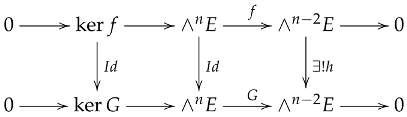and so we have to $G=h\circ f$. □

Corollary 7.

Suppose the contraction map f is surjective then

(i) 

If H is a matrix of order $C_{n-2}^{2n}\times C_n^{2n}$ and maximum rank that annuls $L(n,E)$, then $H=P{B}_{L(n,E)}$, where P is an invertible matrix.

(ii) 

Suppose that there exists R matrix such that $L(n,E)=G(n,E)\cap kerR$. Then $R=P{B}_{L(n,E)}$ where P is an invertible matrix.

Proof. 

The proof of (i) follows directly from the Lemma 6. For the (ii) suppose that $R=\left(\begin{array}{c}{h}_1\\ h_2\\ ⋮\\ h_{ϵ}\end{array}\right)$ is a rank matrix $ϵ$ such that $L(n,E)=G(n,E)\cap kerR$, then $L(n,E)\subset kerR$ and $ϵ\le C_{n-2}^n$. If $ϵ=C_{n-2}^n$ the affirmation is followed by the previous clause of this lemma. Now suppose that $t<C_{n-2}^n$ then $ker{B}_{L(n,E)}⊊kerR$; this implies that

$$\begin{array}{cc}\hfill L(n,E)& =G(n,E)\cap ker{B}_{L(n,E)}\hfill \\ \hfill & ⊊G(n,E)\cap kerR\hfill \\ \hfill & =L(n,E),\hfill \end{array}$$

which is a contradiction and therefore $ϵ=C_{n-2}^n$. □

7. The Plücker Matrix of the Lagrangian Grassmannian

Definition 5.

Let E symplectic vector space of dimension $2n$ defined over an arbitrary field $\mathbb{F}$ arbitrary. The matrix

$$B_{L(n,E)}$$

(47)

of order $C_{n-2}^{2n}\times C_n^{2n}$ associated to the linear equations system $\{{\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\}$ we call the Plücker matrix of the Lagrangian Grassmannian.

The main result of this section is

Theorem 4.

Let E symplectic vector space of dimension $2n$ and let $r_n=\lfloor \frac{n+2}{2}\rfloor$, then there exists a family

$$\mathcal{A}=\{{\mathcal{L}}_{r_n},{\mathcal{L}}_{r_n-1},\dots ,{\mathcal{L}}_2\}$$

of $(0,1)$-matrices, regular, sparse such that

(A) 

If $n\ge 4$ be an even integer and $1\le k\le r_n-2$, then

$$B_{L(n,E)}={\mathcal{L}}_{r_n}\oplus \underset{k=1}{\overset{r_n-2}{⨁}}(\underset{\begin{array}{c}1\le a_1<\cdots <a_{2k}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}{⨁}{\mathcal{L}}_{r_n-k}^{(a_1,\cdots ,a_{2k})})$$

where ${\mathcal{L}}_{r_n-k}^{(a_1,\cdots ,a_{2k})}$ is a copy of ${\mathcal{L}}_{r_n-k}$, for each $1\le k\le r_n-2$.

(B) 

If $n\ge 5$ be an odd integer then $B_{L(n,E)}$

$$B_{L(n,E)}={\mathcal{L}}_{r_n}^n\oplus \underset{k=1}{\overset{r_n-2}{⨁}}(\underset{\begin{array}{c}1\le a_1<a_2<\cdots <a_{2k+1}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}{⨁}{\mathcal{L}}_{r_n-k}^{(a_1,a_2,\cdots ,a_{2k+1})})$$

where ${\mathcal{L}}_{r_n-k}^{(a_1,a_2,\cdots ,a_{2k+1})}$ is a copy of ${\mathcal{L}}_{r_n-k}$ for each $1\le k\le r_n-2$ and ${\mathcal{L}}_{r_n}^n={\mathcal{L}}_{r_n}\oplus \cdots \oplus {\mathcal{L}}_{r_n}$n-times.

7.1. Configuration of Subsets

Following [24] (p. 3) we call $X=\{x_1,\dots ,x_n\}$ an n-set. Now let $X_1,X_2,\cdots ,X_m$ be m distinct subsets of the n-set X. We refer to this collection of subsets of an n-set as a configuration of subsets. We set $a_{ij}=1$ if $x_j\in X_i$ and we set $a_{ij}=0$ if $x_j\notin X_i$. The resulting $(m\times n)$-matrix $A=\left(a_{i,j}\right)$, $i=1,\dots ,m$, $j=1,\dots ,n$ of size m by n is the incidence matrix for the configurations of subsets $X_1,X_2,\cdots ,X_m$ of the n-set X. The $1^{\prime }$s in row i of A display the elements in the subsets $X_j$ and the $1^{\prime }$s in column j display the occurrences of the element $x_j$ among the subsets. If a matrix A has all its coefficients equal 0 or 1 is called a $(0,1)$-matrix. Give a $(0,1)$-matrix A we say that is regular if the number of 1’s is fixed in each column and has a fixed number of 1’s in each row. If A is not regular we say that is irregular see [10,25,26], for more information. A sparse matrix is a $(0,1)$-matrix in which most of the elements are zero.

Configuration of Incidence

Let $S=\{s_1\dots ,s_n\}$ an n-set and $S_1,\dots ,S_m$ be m subsets of the n-set S and $\mathcal{L}$ the $m\times n$ incidence matrix, for the configuration of subsets $S_1,\dots ,S_m$. The pair

$$(S,S_i{)}_{i=1}^m$$

(48)

we call configuration of incidence of S. If $(S^{\prime },S_i^{\prime }{)}_{i=1}^m$,where $S^{\prime }=\{s_1^{\prime }\dots ,s_n^{\prime }\}$, is other configuration of incidence then they are isomorphic if and only if there is a bijection

$$\psi :S⟶S^{\prime }$$

$$\psi \left(s_i\right)=s_i^{\prime }$$

such that $\psi \left(S_i\right)=S_i^{\prime }$ for all $i=1,\dots ,m$ and note $\mathcal{L}={\mathcal{L}}^{\prime }$ where $\mathcal{L}$ and ${\mathcal{L}}^{\prime }$ are $(m\times n)$-incidence matrices.

Let $(S^{\prime },S_i^{\prime }{)}_{i=1}^m$ be an incidence configuration, with S an n-set and $\left\{a\right\}$ a set of cardinality 1 then using the Cartesian product we define the Cartesian incidence configuration as follows

$$a\times {(S,S_i)}_{i=1}^m:={(\left\{a\right\}\times S,S_{(a,i)})}_{i=1}^m$$

(49)

where $S_{(a,i)}:=\left\{a\right\}\times S_i$.

Lemma 13.

The Cartesian incidence configuration $\left\{x\right\}\times {(S,S_i)}_{i=1}^m$ is isomorphic to ${(S,S_i)}_{i=1}^m$ and they have the same incidence matrix.

Proof. 

Since $|\left\{x\right\}\times {(S,S_i)}_{i=1}^m|=|{(S,S_i)}_{i=1}^m|$ then the projection mapping

$$\psi :\left\{x\right\}\times {(S,S_i)}_{i=1}^m⟶{(S,S_i)}_{i=1}^m$$

$$(x,s)⟼s$$

is one–one and clearly ${\psi }_{|\left\{x\right\}\times S_i}=S_i$; thus, the configurations are isomorphic. Moreover, $(x,s)\in \left\{x\right\}\times S_i$ if and only if $s\in S_i$ and so both configurations have the same incidence matrix. □

Let $m\ge 2$ even integer, $r_m=\frac{m+2}{2}$ and ${\Sigma }_m=\{P_1,\dots ,P_m\}$ as in (6)

$${(C_{\frac{m}{2}}\left({\Sigma }_m\right),S_{P_{\alpha }})}_{P_{\alpha }\in C_{\frac{m-2}{2}}\left({\Sigma }_m\right)}$$

(50)

where $C_{\frac{m}{2}}\left({\Sigma }_m\right)$ and $C_{\frac{m}{2}}^m$-set and

$$S_{P_{\alpha }}=\{P_{\beta }\in C_{\frac{m}{2}}\left({\Sigma }_m\right):supp\left\{\alpha \right\}\subset supp\left\{\beta \right\}\},$$

(51)

a configuration of subsets of $C_{\frac{m}{2}}\left({\Sigma }_m\right)$.

Remark 4.

Note that $S_{\alpha }=\{P_{\beta }\in C_{\frac{m}{2}}\left({\Sigma }_m\right):|supp\left\{\alpha \right\}\cap supp\left\{\beta \right\}|=\frac{m-2}{2}\}$.

7.2. Properties

Let $m\ge 4$ even integer, given the incidence configuration (50)

$${(C_{\frac{m}{2}}\left({\Sigma }_m\right),S_{P_{\alpha }})}_{P_{\alpha }\in C_{\frac{m-2}{2}}\left({\Sigma }_m\right)}$$

let $r_m=\frac{m+2}{2}$ then we have

Lemma 14.

For all $P_{\alpha }\in C_{\frac{m-2}{2}}\left({\Sigma }_m\right)$ we have $|S_{P_{\alpha }}|=r_m$.

Proof. 

If $P_{\beta }\in S_{P_{\alpha }}$ and $\left|supp\left\{\alpha \right\}\right|=\frac{m-2}{2}$ then

$$\begin{array}{cc}\hfill |S_{P_{\alpha }}|& =\left|\right\{\beta \in I(m/2,m):supp\left\{\beta \right\}=supp\left\{\alpha \right\}\cup \left\{i\right\}with1\le i\le m\left\}\right|\hfill \\ \hfill & =\left|\right\{i\in \left[m\right]:\left|supp\right\{\alpha \}\cup \{i\left\}\right|=m/2\left\}\right|\hfill \\ \hfill & =m-\left|supp\right\{\alpha \left\}\right|\hfill \\ \hfill & =m-\frac{m-2}{2}\hfill \\ \hfill & =\frac{m+2}{2}\hfill \end{array}$$

□

Lemma 15.

Let $P_{\alpha }$ and $P_{\overline{\alpha }}$ two different elements of $C_{\frac{m-2}{2}}\left({\Sigma }_m\right)$ then

$$S_{P_{\alpha }}\cap S_{P_{\overline{\alpha }}}\ne \varnothing ifandonlyif|supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\}|=\frac{m-4}{2}.$$

Proof. 

$\Rightarrow ):$ Let $P_{\beta }\in S_{P_{\alpha }}\cap S_{P_{\overline{\alpha }}}$. Then there are two different positive integers N and M such that $supp\left\{\alpha \right\}\cup \left\{N\right\}=supp\left\{\beta \right\}=supp\left\{\overline{\alpha }\right\}\cup \left\{M\right\}$, also $supp\left\{\alpha \right\}-\left\{M\right\}=supp\left\{\beta \right\}-\{N,M\}=supp\left\{\overline{\alpha }\right\}-\left\{N\right\}$, as a consequence we have to $supp\left\{\beta \right\}-\{N,M\}=supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\}$ so $|supp\left\{P_{\alpha }\right\}\cap supp\left\{P_{\overline{\alpha }}\right\}|=|supp\left\{P_{\beta }\right\}|-|\{N,M\}|=\frac{m-4}{2}$

$\Leftarrow ):$ Suppose $|supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\}|=\frac{m-4}{2}$ then there exist M, N distinct positive integers such that $\left\{M\right\}=supp\left\{\alpha \right\}-supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\}$ and $\left\{N\right\}=supp\left\{\overline{\alpha }\right\}-supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\}$ and so it exists $P_{\beta }\in C_{\frac{m}{2}}\left({\Sigma }_m\right)$ such that $supp\left\{\beta \right\}=(supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\})\cup \{N,M\}$ then we have $P_{\beta }\in S_{P_{\alpha }}\cap S_{P_{\overline{\alpha }}}$ and so $S_{P_{\alpha }}\cap S_{P_{\overline{\alpha }}}\ne \varnothing$. □

Corollary 8.

Let $P_{\alpha }$ and $P_{\overline{\alpha }}$ be two different of $C_{\frac{m-2}{2}}\left({\Sigma }_n\right)$ then $|S_{P_{\alpha }}\cap S_{P_{\overline{\alpha }}}|\le 1$.

Proof. 

Be $P_{\beta }\in S_{P_{\alpha }}\cap S_{P_{\overline{\alpha }}}$ then there are two positive integers N and M different such that $supp\left\{\alpha \right\}\cup \left\{N\right\}=supp\left\{\beta \right\}=supp\left\{\overline{\alpha }\right\}\cup \left\{M\right\}$, also $supp\left\{\alpha \right\}-\left\{M\right\}=supp\left\{\beta \right\}-\{N,M\}=supp\left\{\overline{\alpha }\right\}-\left\{N\right\}$, as a consequence we have to $supp\left\{\beta \right\}=(supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\}) \cup \{N,M\}$ clearly $(supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\})\cup \left\{M\right\}\subset supp\left\{\alpha \right\}$ then for Lemma 15 we have $|(supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\})\cup \left\{M\right\}|=\frac{m-4}{2}+1=\frac{m-2}{2}$ so we have to $supp\left\{\alpha \right\}=(supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\})\cup \left\{M\right\}$, analogously we have to $supp\left\{\overline{\alpha }\right\}=(supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\})\cup \left\{N\right\}$. Suppose there is another $P_{{\beta }^{\prime }}\in S_{P_{\alpha }}\cap S_{P_{\overline{\alpha }}}$ then there exist $M^{\prime }$ y $N^{\prime }$ distinct positive integers such that $supp\left\{{\beta }^{\prime }\right\}=supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\}\cup \{N^{\prime },M^{\prime }\}$, as $supp\left\{\alpha \right\}\subseteq supp\left\{{\beta }^{\prime }\right\}$ then $(supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\})\cup \left\{M\right\}\subseteq (supp\left\{\alpha \right\}\cap supp\left\{\overline{\alpha }\right\})\cup \{N^{\prime },M^{\prime }\}$ then $M\in \{N^{\prime },M^{\prime }\}$. Analogously, $supp\left\{\overline{\alpha }\right\}\subseteq supp\left\{{\beta }^{\prime }\right\}$, and so we have to $N\in \{N^{\prime },M^{\prime }\}$ so $\{N,M\}=\{N^{\prime },M^{\prime }\}$ then $supp\left\{\beta \right\}=supp\left\{{\beta }^{\prime }\right\}$ so by (5) we have $|S_{P_{\alpha }}\cap S_{P_{\overline{\alpha }}}|\le 1.$ □

Corollary 9.

If $S_{P_{\alpha }}=S_{P_{\overline{\alpha }}}$ then $P_{\alpha }=P_{\overline{\alpha }}.$

Proof. 

Suppose $S_{P_{\alpha }}=S_{P_{\overline{\alpha }}}$ and $P_{\alpha }\ne P_{\overline{\alpha }}$ then by Corollary 8 we have to $|S_{P_{\alpha }}\cap S_{P_{\overline{\alpha }}}|\le 1$; however, this is not possible since by Lemma 14, $|S_{P_{\alpha }}\cap S_{P_{\overline{\alpha }}}|=|S_{P_{\alpha }}|=r_m$ but $m\ge 4$ and so $r_m\ge 3$ which implies that $P_{\alpha }=P_{\overline{\alpha }}.$ □

We call $w_{P_{\alpha }}$ the intersection count of the $S_{P_{\alpha }}$

Lemma 16.

$w_{P_{\alpha }}=r_m-1$

Proof. 

Clearly $P_{\beta }\in S_{P_{\alpha }}$ if and only if $\alpha \in C_{\frac{m-2}{2}}\left\{supp\left\{\beta \right\}\right\}$, so the number subsets $S_{P_{\alpha }}$ that contain $P_{\beta }$ is equal to

$$|C_{\left(\frac{m-2}{2}\right)}\left\{supp\left\{\beta \right\}\right\}|=C_{(m-2)/2}^{m/2}=m/2=r_m-1$$

in consequence we have $w_{P_{\alpha }}=r_m-1$ □

Let us denote by

$${\mathcal{L}}_{r_m}$$

(52)

the $C_{\frac{m-2}{2}}^m\times C_{\frac{m}{2}}^m$-incidence matrix from ${(C_{\frac{m}{2}}({\Sigma }_m),S_{P_{\alpha }})}_{P_{\alpha }\in C_{\frac{m-2}{2}}({\Sigma }_m)}$

Proposition 5.

Let $2\le m$ even positive integer and let $r_m=\frac{m+2}{2}$ then

(a) 

${\mathcal{L}}_{r_m}$ has $r_m$-ones in each row;

(b) 

${\mathcal{L}}_{r_m}$ has $r_m-1$-ones in each column;

(c) 

every two lines have at most one 1 in common;

(d) 

${\mathcal{L}}_{r_m}$ is sparse.

Proof. 

The case $m=2$ generates the matrix ${\mathcal{L}}_2$ which trivially satisfies all the statements of this statement. So we assume that $m\ge 4$ for the rest of the proof.

(a): the $1^{\prime }s$ in row $P_{\alpha }$ of ${\mathcal{L}}_{r_m}$ display the elements in the subset $S_{P_{\alpha }}$ so by Lemma 14 each row has exactly $r_m$ ones in each row.

(b): the $1^{\prime }s$ in the column $P_{\beta }$ display the occurrences of the elements of $S_{P_{\alpha }}$ among the subsets, which follows from Lemma 16.

(c): follows directly from Corollary 8.

(d): The density of ones in the matrix is given by $r_m\times C_{\frac{m-2}{2}}^m=(r_m-1)\times C_{\frac{m}{2}}^m$

$$\frac{r_m}{C_{\frac{m}{2}}^m}=\frac{r_m-1}{C_{\frac{m-2}{2}}^m}$$

which approaches zero as m approaches infinity. □

Definition 6.

Let $n\ge 2$ is an integer and $r_n=\lfloor \frac{n+2}{2}\rfloor$ we define the $r_n$-atlas

$$\mathcal{A}:=\{{\mathcal{L}}_{r_n},{\mathcal{L}}_{r_n-1},\dots ,{\mathcal{L}}_2\}$$

(53)

of incidence matrices corresponding to the family

$${\left\{{\left(C_{\frac{m}{2}}\left({\Sigma }_m\right),S_{P_{\alpha }}\right)}_{P_{\alpha }\in C_{\frac{m-2}{2}}\left({\Sigma }_m\right)}\right\}}_{m=2}^n$$

(54)

of incidence configurations.

7.3. Cartesian Configurations

For $n\ge 4$ even, $r_n=\frac{n+2}{2}$, $1\le k\le r_n-2$ and $1\le a_1<a_2<\cdots <a_{2k}\le 2n$ such that $a_i+a_j\ne 2n+1$ then we define ${\Sigma }_{a_1,\dots ,a_{2k}}={\Sigma }_n-\{P_{a_1},\cdots ,P_{a_{2k}}\}$ as in (8). We define an Cartesian incidence configuration as in (49)

$$(a_1,\dots ,a_{2k})\times {\left(C_{\frac{n-2k}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right),S_{(a_1,\dots ,a_{2k},P_{\alpha })}\right)}_{P_{\alpha }\in C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)}$$

(55)

where

$$\left\{(a_1,\dots ,a_{2k})\right\}\times C_{\frac{n-2k}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)$$

is an $C_{\frac{n-2k}{2}}^{n-2k}$-set and the subsets are

$$S_{(a_1,\dots ,a_{2k},P_{\alpha })}:=\{(a_1,\dots ,a_{2k},P_{\beta }):supp\left\{\alpha \right\}\subset supp\left\{\beta \right\}\}$$

(56)

for all $P_{\alpha }\in C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)$.

Lemma 17.

For $n\ge 4$ even, $r_n=\frac{n+2}{2}$, $1\le k\le r_n-2$ and $1\le a_1<a_2<\cdots <a_{2k}\le 2n$ such that $a_i+a_j\ne 2n+1$ then the incidence matrix of (55) is ${\mathcal{L}}_{r_n-k}^{a_1,\dots ,a_{2k}}={\mathcal{L}}_{r_n-k}$ an element of $\mathcal{A}.$

Proof. 

As $|{\Sigma }_{a_1,\dots ,a_{2k}}|=n-2k$ if we make $m=n-2k$ and $r_m=\frac{m+2}{2}$, clearly $2\le n-2k\le n-2$ and $r_m=r_n-k$. A simple calculation shows that $2\le r_m\le r_n-1$, then renumber the elements of ${\Sigma }_{a_1,\dots ,a_{2k}}=\{P_1,\dots ,P_m\}$ so by the Lemma 13 the incidence configuration

$$(a_1,\dots ,a_{2k})\times {\left(C_{\frac{n-2k}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right),S_{(a_1,\dots ,a_{2k},P_{\alpha })}\right)}_{P_{\alpha }\in C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)}$$

is isomorphic to

$${\left(C_{\frac{m}{2}}\left({\Sigma }_m\right),S_{P_{\alpha }}\right)}_{P_{\alpha }\in C_{\frac{m-2}{2}}\left({\Sigma }_m\right)}$$

so also for the Lemma 13 both have the same $C_{\frac{n-(2k+1)}{2}}^{n-2k}\times C_{\frac{n-2k}{2}}^{n-2k}$ incidence matrix ${\mathcal{L}}_{r_m}={\mathcal{L}}_{r_n-k}$. We denote this matrix by

$${\mathcal{L}}_{r_n-k}^{a_1,\dots ,a_{2k}}={\mathcal{L}}_{r_n-k}.$$

(57)

□

For $n\ge 5$ odd and $r_n=(n+1)/2$ and $j\in \{1,\dots ,n\}$, we define an Cartesian incidence configuration as in (49)

$$j\times {\left(C_{\frac{n-1}{2}}({\Sigma }_n-\left\{P_j\right\}),S_{(j,P_{\alpha })}\right)}_{P_{\alpha }\in C_{\frac{n-3}{2}}({\Sigma }_n-\left\{P_j\right\})}$$

(58)

where

$$\left\{j\right\}\times C_{\frac{n-1}{2}}({\Sigma }_n-\left\{P_j\right\})$$

is a $C_{\frac{n}{2}}^n$-set and its subsets $S_{(j,P_{\alpha })}$ are defined by

$$S_{(j,P_{\alpha })}=\{(j,P_{\beta }):supp\left\{\alpha \right\}\subset supp\left\{\beta \right\}\}$$

(59)

with $P_{\alpha }\in C_{\frac{n-3}{2}}({\Sigma }_n-\left\{P_j\right\})$.

For $n\ge 5$ odd and $r_n=\frac{n+1}{2}$, $1\le k\le r_n-2$, consider $1\le a_1<a_2<\cdots <a_{2k+1}\le 2n$ such that $a_i+a_j\ne 2n+1$ we define ${\Sigma }_{a_1,\dots ,a_{2k+1}}={\Sigma }_n-\{P_{a_1},\dots ,P_{a_{2k+1}}\}$, as in (8).

We define a Cartesian incidence configuration as in (49)

$$(a_1,\dots ,a_{2k+1})\times {\left(C_{\frac{n-(2k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right),S_{(a_1,\dots ,a_{2k+1},P_{\alpha })}\right)}_{P_{\alpha }\in C_{\frac{n-(2k+3)}{2}}\left({\Sigma }_{a_1\dots ,a_{2k+1}}\right)}$$

(60)

where

$$\left\{(a_1,\dots ,a_{2k+1})\right\}\times C_{\frac{n-(2k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right)$$

is $C_{\frac{n-(2k+1)}{2}}^{n-(2k+1)}$-set where the family of subsets is given by

$$S_{(a_1,\dots ,a_{2k+1},P_{\alpha })}=\{(a_1,\dots ,a_{2k+1},P_{\beta }):supp\left\{\alpha \right\}\subset supp\left\{\beta \right\}\}$$

(61)

for all $P_{\alpha }\in C_{\frac{n-2(k+3)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)$.

Lemma 18.

(a) 

The incidence matrix (58) is ${\mathcal{L}}_{r_n}$

(b) 

The $C_{\frac{n-(2k+3)}{2}}^{n-(2k+1)}\times C_{\frac{n-(2k+1)}{2}}^{n-(2k+1)}$ incidence matrix (60) is ${\mathcal{L}}_{r_m}^{(a_1,\dots ,a_{2k+1})}={\mathcal{L}}_{r_n-k}$ and is an element of $\mathcal{A}$.

Proof. 

For the proof of (a) If we do $m=n-1$ and define ${\Sigma }_m={\Sigma }_n-\left\{P_j\right\}$ so on

$$j\times {\left(C_{\frac{n-1}{2}}({\Sigma }_n-\left\{P_j\right\}),S_{(j,P_{\alpha })}\right)}_{(j,P_{\alpha })\in C_{\frac{n-3}{2}}({\Sigma }_n-\left\{P_j\right\})}$$

$$\cong {\left(C_{\frac{m}{2}}\left({\Sigma }_m\right),S_{P_{\alpha }}\right)}_{P_{\alpha }\in C_{\frac{m-2}{2}}\left({\Sigma }_m\right)}$$

so both have the same incidence matrix ${\mathcal{L}}_{r_n}={\mathcal{L}}_{r_m}$. Given that $r_m=\frac{m+2}{2}=\frac{n+1}{2}=r_n$, we denote the incidence matrix (58) by

$${\mathcal{L}}_{r_n}^{\left\{j\right\}}={\mathcal{L}}_{r_m}$$

(62)

and part (a) has been proved.

For the proof of (b), clearly $|{\Sigma }_{a_1,\dots ,a_{2k+1}}|=n-(2k+1)$ if we do $m=(n-1)+2k$ and $r_m=\frac{m+2}{2}$, clearly we have that $r_m=r_n-k$. Now if we rename the elements of ${\Sigma }_{a_1,\dots ,a_{2k+1}}=\{P_1,\dots ,P_m\}$ then

$$(a_1,\dots ,a_{2k+1})\times {\left(C_{\frac{n-(2k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right),S_{P_{\alpha }}\right)}_{P_{\alpha }\in C_{\frac{n-(2k+3)}{2}}\left({\Sigma }_{a_1\dots ,a_{2k+1}}\right)}$$

is isomorphic to the incidence configuration

$${(C_{\frac{m}{2}}\left({\Sigma }_m\right),S_{P_{\alpha }})}_{P_{\alpha }\in C_{\frac{m-2}{2}}\left({\Sigma }_m\right)}$$

then ${\mathcal{L}}_{r_m}^{(a_1,\dots ,a_{2k+1})}={\mathcal{L}}_{r_n-k}$ note that $2\le m\le m-3$ implies that $2\le r_m\le r_n-1$. □

For all ${\alpha }_{rs}\in I(n-2,2n)$ making a change in the notation we rewrite (16) as

$$\begin{array}{c}{\Pi }_{{\alpha }_{rs}}=\sum _{i=1}^n{c}_{{\alpha }_{rs}{P}_i}{X}_{{\alpha }_{rs}{P}_i}\end{array}$$

(63)

where

$$c_{{\alpha }_{rs}{P}_i}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\left|supp\right\{{\alpha }_{rs}{P}_i\left\}\right|=n,\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

For each ${\alpha }_{rs}\in I(n,2n)$, consider

$$S_{{\alpha }_{rs}}=\{{\alpha }_{rs}{P}_i\in I(n-2,2n)\times {\Sigma }_n:|supp\left\{{\alpha }_{rs}{P}_i\right\}|=n\}.$$

(64)

Remark 5.

Note that depending on where ${\alpha }_{rs}\in I(n-2,2n)$ is, we have $S_{{\alpha }_{rs}}$ is equal to (51), (56), (59) or (61), respectively.

7.4. Function $\phi$

For $n\ge 4$, we consider

$$\begin{array}{c}\phi :I(n-2,2n)\to {\{0,1\}}^{C_n^{2n}}\end{array}$$

(65)

$$\begin{array}{c}\left({\alpha }_{rs}\right)\mapsto {\left(c_{\beta }\right)}_{\beta \in I(n,2n)};where\end{array}$$

(66)

$$\begin{array}{c}{c}_{\beta }=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\beta \in S_{{\alpha }_{rs}}\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(67)

Clearly

$$B_{L(n,E)}=\phi \left(I(n-2,2n)\right)$$

(68)

up to permutation of rows.

Lemma 19.

The function φ is injective.

Proof. 

Let ${\alpha }_{rs},{\alpha }_{rs}^{\prime }\in I(n-2,2n)$ such that $\phi \left({\alpha }_{rs}\right)=\phi \left({\alpha }_{rs}^{\prime }\right)$ then ${\left(c_{\beta }\right)}_{\beta \in I(n,2n)}={\left(c_{\beta }^{\prime }\right)}_{\beta \in I(n,2n)}$ this implies $S_{{\alpha }_{rs}}=S_{{\alpha }_{rs}^{\prime }}$ and by Corollary 9 we have ${\alpha }_{rs}={\alpha }_{rs}^{\prime }$ □

Corollary 10.

Let $n\ge 4$ integer even, $r_n=\frac{n+2}{2}$ then

(a) 

$\phi (C_{\frac{n-2}{2}}({\Sigma }_n))={\mathcal{L}}_{r_n}$

(b) 

$\phi ((a_1,\dots ,a_{2k})\times C_{\frac{n-2k}{2}}({\Sigma }_{a_1,\dots ,a_{2k}}))={\mathcal{L}}_{r_n-k}^{(a_1,\dots ,a_{2k})}$

Let $n\ge 5$ odd integer, $r_n=\frac{n+1}{2}$ then

(c) 

$\phi (\left\{j\right\}\times C_{\frac{n-2}{2}}({\Sigma }_n-\left\{P_j\right\}))={\mathcal{L}}_{r_n}^j$ for all $j=1,\dots ,n$

(d) 

$\phi ((a_1,\dots ,a_{2k+1})\times C_{\frac{n-2(k+1)}{2}}({\Sigma }_{a_1,\dots ,a_{2k+1}}))={\mathcal{L}}_{r_n-k}^{(a_1,\dots ,a_{2k+1})}$

Proof. 

The proof follows directly from the Lemma 19 and Remark 5. □

7.5. Proof of the Theorem 4

(A) by Lemma 1 we have

$$\begin{array}{cc}\hfill I(n-2,2n)& =C_{\frac{n-2}{2}}\left({\Sigma }_n\right)\cup (\bigcup _{k=1}^{r_n-2}\bigcup _{\begin{array}{c}1\le a_1<\cdots <a_{2k}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}(a_1,\dots ,a_{2k})\times C_{\frac{n-2(k-1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)).\hfill \end{array}$$

since $\phi$ is injective we have a partition in the image, so

$$\begin{array}{c}\hfill \phi (C_{\frac{n-2}{2}}\left({\Sigma }_n\right))\bigcup (\bigcup _{k=1}^{r_n-2}\bigcup _{\begin{array}{c}1\le a_1<\cdots <a_{2k}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}\phi {(}_{(a_1,\dots ,a_{2k})\times C_{\frac{n-2(k-1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)})).\end{array}$$

Associating the corresponding matrix, using the Corollary 10, we have that

$$\begin{array}{cc}\hfill B_{L(n,E)}& ={\mathcal{L}}_{r_n}\oplus \underset{k=1}{\overset{r_n-2}{⨁}}(\underset{\begin{array}{c}1\le a_1<\cdots <a_{2k}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}{⨁}{\mathcal{L}}_{r_n-k}^{(a_1,\cdots ,a_{2k})}).\hfill \end{array}$$

Part (B) Proceeding as in part (A) of this proof, we have

$$\begin{array}{c}\hfill \bigcup _{j=1}^n(\left\{j\right\}\times C_{\frac{n}{2}}\left({\Sigma }_n\right))\cup (\bigcup _{k=1}^{r_n-2}\bigcup _{\begin{array}{c}1\le a_1<\cdots <a_{2k+1}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}(a_1,\dots ,a_{2k+1})\times C_{\frac{n-2k+3)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right))\end{array}$$

we obtain

$$\begin{array}{c}{\phi }_{\left(I\right(n-2,2n\left)\right)}=\bigcup _{j=1}^n\phi (\left\{j\right\}\times C_{\frac{n-2}{2}}\left({\Sigma }_n\right))\cup \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\bigcup _{k=1}^{r_n-2}(\bigcup _{\begin{array}{c}1\le a_1<a_2<\dots <a_{2k+1}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}{\phi }_{((a_1,\dots ,a_{2k+1})\times C_{\frac{n-(2k+3)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right))})\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{B}_{L(n,E)}=\underset{j=1}{\overset{n}{⨁}}{\mathcal{L}}_{r_n}^j\oplus \underset{k=1}{\overset{r_n-2}{⨁}}(\underset{\begin{array}{c}1\le a_1<\dots <a_{2k+1}\le a_{2n}\\ a_i+a_j\ne 2n+1\end{array}}{⨁}{\mathcal{L}}_{r_n-k}^{(a_1,a_2,\dots ,a_{2k+1})}).\hfill \end{array}$$

Example 5.

Let E be a symplectic vector space of dimension 12 and $r_6=\frac{6+2}{2}=4$ then his $r_6$-atlas is given by the triplet of matrices

$$\mathcal{A}=\{{\mathcal{L}}_4,{\mathcal{L}}_3,{\mathcal{L}}_2\}$$

where

and

$${\mathcal{L}}_3=\left(\begin{array}{cccccc}1& 1& 1& 0& 0& 0\\ 1& 0& 0& 1& 1& 0\\ 0& 1& 0& 1& 0& 1\\ 0& 0& 1& 0& 1& 1\end{array}\right).$$

${\mathcal{L}}_2$ is a row matrix filled with zeros and with only two entries equal to 1.

The matrix $B_{L(6,E)}$, of size $\left(\genfrac{}{}{0pt}{}{12}{4}\right)\times \left(\genfrac{}{}{0pt}{}{12}{6}\right)$, associated to the homogeneous system $\Pi =\{{\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(4,12)\}$ can be given by a block diagonal matrix as follows

$$\begin{array}{cc}{B}_{L(6,E)}\hfill & ={\mathcal{L}}_4\oplus (\underset{\genfrac{}{}{0pt}{}{1\le {\alpha }_1<{\alpha }_2\le 12}{{\alpha }_1+{\alpha }_2\ne 13}}{⨁}{\mathcal{L}}_3^{({\alpha }_1,{\alpha }_2)})\oplus (\underset{\genfrac{}{}{0pt}{}{1\le {\alpha }_1<{\alpha }_2<{\alpha }_3<{\alpha }_4\le 12}{{\alpha }_i+{\alpha }_j\ne 13}}{⨁}{\mathcal{L}}_2^{({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4)}),\hfill \end{array}$$

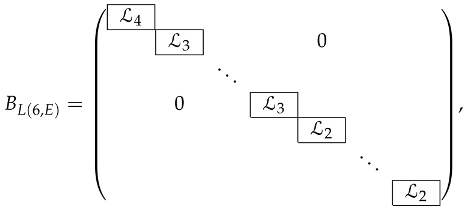where there are 1 matrix ${\mathcal{L}}_4$, 60 submatrices ${\mathcal{L}}_3$, and 240 submatrices ${\mathcal{L}}_2$.

Example 6.

Let E be a symplectic vector space of dimension 14 and $r_7=\lfloor \frac{7+2}{2}\rfloor =4$ then his 4-atlas is given by

$$\mathcal{A}=\{{\mathcal{L}}_4,{\mathcal{L}}_3,{\mathcal{L}}_2\}$$

$$\begin{array}{c}\hfill B_{L(7,E)}=\underset{i=1}{\overset{7}{⨁}}{\mathcal{L}}_4^{\left\{i\right\}}\oplus (\underset{\genfrac{}{}{0pt}{}{1\le a_1<a_2<a_3\le 14}{a_i+a_j\ne 15}}{⨁}{\mathcal{L}}_3^{\left(a_1{a}_2{a}_3\right)})\oplus (\underset{\genfrac{}{}{0pt}{}{1\le a_1<a_2<\dots <a_4<a_5\le 14}{a_i+a_j\ne 15}}{⨁}{\mathcal{L}}_2^{\left(a_1{a}_2{a}_3{a}_4{a}_5\right)}),\end{array}$$

where ${\mathcal{L}}_4^{\left\{i\right\}}={\mathcal{L}}_4$, ${\mathcal{L}}_3^{\left(a_1{a}_2{a}_3\right)}={\mathcal{L}}_3$ and ${\mathcal{L}}_2^{\left(a_1{a}_2{a}_3{a}_4{a}_5\right)}={\mathcal{L}}_2$.

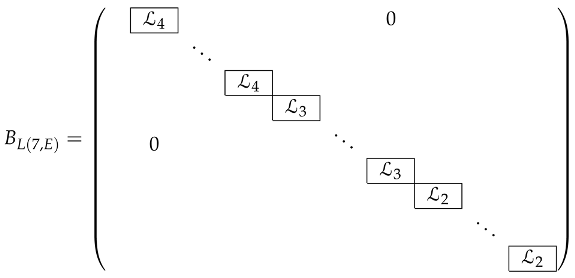
8. Isotropy Index ${\mathit{r}}_{\mathit{n}}$ and ${\mathit{r}}_{\mathit{n}}$-Atlas

Definition 7.

Let E symplectic vector space of dimension $2n$; we call $r_n=\lfloor \frac{n+2}{2}\rfloor$ isotropy index of E.

Let $B_{L(n,E)}$ as Equation (47) and using notation as in (13) and ${\left[\right]}_{\alpha \in I(n,2n)}^T$ denotes the transposed vector.

Lemma 20.

Let f be the contraction map, then $f{\left(w\right)}_{\rho }=B_{L(n,E)}{\left(w_{\rho }\right)}^T$.

Proof. 

Let $w={\sum }_{\alpha \in I(n,2n)}{X}_{\alpha }{e}_{\alpha }\in {\wedge }^{n}E$ and ρ Plücker embedding we denote $w_{\rho }={\left[X_{\alpha }\right]}_{\alpha \in I(n,2n)}$, it as in (13), then by Lemma 2 and by Equation (68) the following diagram commutes i.e., $\rho \circ f=B_{L(n,E)}\circ \rho$

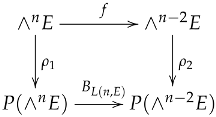so we have

$$\begin{array}{cc}\hfill ({\rho }_2\circ f)\left(w\right)& ={\rho }_2({\displaystyle \sum _{{\alpha }_{rs}\in I(n-2,2n)}}({\displaystyle \sum _{i=1}^n}{X}_{({\alpha }_{rs},P_i)})e_{{\alpha }_{rs}})\hfill \\ \hfill & ={\left[{\displaystyle \sum _{i=1}^n}{X}_{({\alpha }_{rs},P_i)}\right]}_{{\alpha }_{rs}\in I(n-2,2n)}\hfill \\ \hfill & =B_{L(n,E)}{[X_{\alpha }]}_{\alpha \in I(n,2n)}^T\hfill \\ \hfill & =B_{L(n,E)}{\left(w_{{\rho }_1}\right)}^T\hfill \end{array}$$

which proves commutativity so ${\rho }_2\circ f=B_{L(n,E)}\circ {\rho }_1$.

□

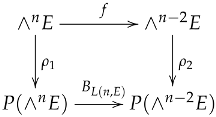
Corollary 11.

$kerf$ is isomorphic to $ker{B}_{L(n,E)}$ as vector spaces.

Proof. 

From the Lemma 20 we have ${\rho }_1(kerf)\subset ker{B}_{L(n,E)}$, and both have the same dimension so $kerf\cong ker{B}_{L(n,E)}$ is an isomorphism of vector spaces. □

The following corollary follows directly from the Lemma 20.

Corollary 12.

Let E symplectic vector spaces of dimension $2n$ then

$$dimkerf=C_n^{2n}-rank{B}_{L(n,E)}$$

Moreover, $C_n^{2n}-C_{n-2}^{2n}\le dimkerf\le C_n^{2n}-1$.

Theorem 5.

Let E symplectic vector space of dimension $2n$ defined over an arbitrary field $\mathbb{F}$ and $r_n=\lfloor \frac{n+2}{2}\rfloor$ the isotropy index.

Then, the following are equivalent:

(a) $Char\mathbb{F}=0$ or $Char\mathbb{F}\ge r_n$

(b) $rank{B}_{L(n,E)}=C_{n-2}^{2n}$

(c) $dimkerf=C_n^{2n}-C_{n-2}^{2n}$

(d) $dim\mathcal{H}=C_{n-2}^{2n}$ and $\{{\Pi }_{{\alpha }_{rs}}:{\alpha }_{rs}\in I(n-2,2n)\}$ is a base of $\mathcal{H}$.

Proof. 

(a) and (b) are equivalent by [27] (Theorem 6).

(b) and (c) are equivalent by Corollary 11 and by Corollary 12.

(c) and (d) are equivalent by Theorem 3. □

We say that the embedding rank $er\left(L\right(n,E\left)\right)$ of $L(n,E)$ is the dimension of the linear envelope $\langle L(n,E)\rangle$.

Lemma 21.

Embedding rank of $L(n,E)$ is $er\left(L(n,E)\right)=C_n^{2n}-rank{B}_{L(n,E)}$.

Proof. 

We have that

$$\begin{array}{cc}\hfill er\left(L\right(n,E\left)\right)& =dim\langle L(n,E)\rangle \hfill \\ \hfill & =dimkerf\hfill \\ \hfill & =C_n^{2n}-rank{B}_{L(n,E)}\hfill \end{array}$$

□

Corollary 13.

Let E a symplectic vector space of dimension $2n$, let f the contraction map the isotropy index $r_n=\lfloor \frac{n+2}{2}\rfloor$ are equivalent

(1) 

f is surjective

(2) 

$er\left(L(n,E)\right)=C_n^{2n}-C_{n-2}^{2n}$

(3) 

$rank{B}_{L(n,E)}=C_{n-2}^{2n}$

(4) 

char$\mathbb{F}=0$ or char$\mathbb{F}\ge r_n$

(5) 

$rank{\mathcal{L}}_{r_n-k}$ is maximum for everything $0\le k\le r_n-2$.

Proof. 

(1) is equivalent (2), (2) is equivalent (3) given that $dimkerf=dimkerB$ y $dimkerf=\left(\genfrac{}{}{0pt}{}{2n}{n}\right)-rankB$.

(3) is equivalent (4) is followed from [27] (Theorem 6) and finally (3) is equivalent (5) is obvious. □

Example 7.

By Corollary 12 $dimkerf=70-rank{B}_{L(4,8)}$, the order of $B_{L(4,8)}$ is $28\times 70$ and by Theorem 4, ${\mathcal{L}}_3$ is a submatrix of $B_{L(4,8)}$ and it is also easy to see that

$${\mathcal{L}}_3=\left(\begin{array}{cccccc}1& 1& 1& 0& 0& 0\\ 1& 0& 0& 1& 1& 0\\ 0& 1& 0& 1& 0& 1\\ 0& 0& 1& 0& 1& 1\end{array}\right)\sim \left(\begin{array}{cccccc}1& 0& 0& 1& 1& 0\\ 0& 1& 0& 1& 0& 1\\ 0& 0& 1& 0& 1& 1\\ 0& 0& 0& 2& 2& 2\end{array}\right).$$

and

$$rank{B}_{L(4,8)}=\left\{\begin{array}{cc}28\hfill & \mathrm{if}\mathrm{char}\mathbb{F}\ge 3\hfill \\ 27\hfill & \mathrm{if}\mathrm{char}\mathbb{F}=2\hfill \end{array}\right.$$

Example 8.

Consider the matrices ${\mathcal{L}}_4$ and ${\mathcal{L}}_3$ in a field ${\mathbb{F}}_2$. By elementary matrix operations we have

$${\mathcal{L}}_4\sim \left(\begin{array}{cccccccccccccccccccc}\mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{1}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\\ \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\\ \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{1}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{1}& \mathsf{0}& \mathsf{0}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{1}& \mathsf{0}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{1}& \mathsf{0}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{1}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{1}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{1}& \mathsf{1}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\end{array}\right)$$

This matrix we denote by $\left(id\right|A_3^3)$.

As we saw in the Example 7, ${\mathcal{L}}_3$ in ${\mathbb{F}}_2$ it is of the form

$${\mathcal{L}}_3\sim \left(\begin{array}{cccccc}\hfill \mathsf{1}& \mathsf{0}& \mathsf{0}\hfill & \mathsf{1}& \mathsf{1}& \mathsf{0}\\ \hfill \mathsf{0}& \mathsf{1}& \mathsf{0}\hfill & \mathsf{1}& \mathsf{0}& \mathsf{1}\\ \hfill \mathsf{0}& \mathsf{0}& \mathsf{1}\hfill & \mathsf{0}& \mathsf{1}& \mathsf{1}\\ \hfill \mathsf{0}& \mathsf{0}& \mathsf{0}\hfill & \mathsf{0}& \mathsf{0}& \mathsf{0}\end{array}\right)$$

and we denote by $\left(Id\right|A_2^2)$.

In [18] (Corollary 1.2) can find a more general case of Theorem 5 also see [28] for some examples where $n=2,3,4,5,6$, and 7.

Let E be a symplectic vector space of dimension $2n$ and let $r_n=\lfloor \frac{n+2}{2}\rfloor$ consider the family of matrices given in (53)

$$\mathcal{A}=\{{\mathcal{L}}_{r_n},{\mathcal{L}}_{r_n-1},\dots ,{\mathcal{L}}_2\}$$

(69)

and we call the $r_n$-atlas of $L(n,E)$.

Lemma 22.

Let n integer and let E and $\overline{E}$ symplectic vector spaces of dimension $2n$ and $2m$, respectively, then

$$r_n=r_{m}ifandonlyifn=morm=n+1.$$

Proof. 

$\Rightarrow )$ If both m and n are even integers or if both m and n odd integers then $n=m$.

Suppose that n is even integer and $m=2k+1$ is odd integer. If $r_n=r_m$ then $\lfloor \frac{n+2}{2}\rfloor =\lfloor \frac{2k+1+2}{2}\rfloor$ so $\frac{n+2}{2}=\frac{2k+2}{2}$ what it implies $n=2k$ so $m=n+1$.

$\Leftarrow )$ If $n=m$ then $r_n=r_m$. Now if $m=n+1$ then $r_m=\lfloor \frac{m+2}{2}\rfloor =\lfloor \frac{n+1+2}{2}\rfloor =\frac{n+2}{2}=r_n.$ □

Corollary 14.

(a) If E and $\overline{E}$ both are symplectic vector spaces of dimension $2n$ so they share the same $r_n$-atlas.

(b) Let E symplectic vector space of dimension $2n$ and let $\overline{E}$ symplectic vector space of dimension $2(n+1)$ then both spaces share the same $r_n$-atlas.

Proof. 

The proof follows directly from the Lemma 22. □

Example 9.

Let $E_1$ and $E_2$ two symplectic vector spaces of dimension $2n$ defined over a field $\mathbb{F}$ and isotropy index $r_n=\lfloor \frac{n+2}{2}\rfloor$. If char$\mathbb{F}$=0 or char$\mathbb{F}\ge r$ then $E_1$ and $E_2$ they share

(a) the same isotropy index $r_n$;

(b) the same $r_n$-atlas $\{{\mathcal{L}}_{r_n},\dots ,{\mathcal{L}}_2\}$;

(c) the same Plücker relations $\{Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}}\}$ of the Lagrangian Grassmannian variety.

Example 10.

Consider the symplectic vector spaces ${\mathbb{R}}^6\oplus {\left({\mathbb{R}}^6\right)}^{*}$ and ${\mathbb{F}}_2^6\oplus {\left({\mathbb{F}}_2^6\right)}^{*}$, two symplectic vector space non-symplectomorphisms, them

(a) They share the same isotropy index $r_6=\frac{6+2}{2}=4$.

(b) They share the same Plücker relations $\{Q_{\alpha ,\beta },{\Pi }_{{\alpha }_{rs}}\}$ of the Lagrangian Grassmannian variety.

However, they do not share the same 4-atlas so we have:

the 4-atlas of ${\mathbb{R}}^6\oplus {\left({\mathbb{R}}^6\right)}^{*}$ is $\{{\mathcal{L}}_4,{\mathcal{L}}_3,{\mathcal{L}}_2\}$ see Example 5

but the 4-atlas of ${\mathbb{F}}_2^6\oplus {\left({\mathbb{F}}_2^6\right)}^{*}$ is $\{\left(id\right|A_3^3),\left(id\right|A_2^2\},{\mathcal{L}}_2\}$ see Example 8.

Hypersurfaces in $L(n,E)$

The linear sections of the Lagrangian-Grassmannian $L(n,E)$ have applications in other fields of mathematics see [14]. Using the notation ${\Re }_{{\alpha }_{rs}}:=Z\langle {\Pi }_{{\alpha }_{rs}}\rangle \subset \mathbb{P}\left({\wedge }^{n}E\right)$ we define the following linear varieties.

Definition 8.

Let $n\ge 4$ even integer then

(a) 

$\Re :={\bigcap }_{{\alpha }_{rs}\in C_{\frac{n-2}{2}}\left({\Sigma }_n\right)}{\Re }_{{\alpha }_{rs}}$

(b) 

${\Re }_{C_{\frac{n-2(k+1)}{2}}}^{(a_1,\dots ,a_{2k})}:={\bigcap }_{{\alpha }_{rs}\in C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k}}\right)}{\Re }_{{\alpha }_{rs}}$

Let $n\ge 5$ odd integer then

(c) 

${\Re }^n:={\bigcap }_{{\alpha }_{rs}\in {\bigcup }_{j=1}^n\left\{j\right\}\times C_{\frac{n-2}{2}}\left({\Sigma }_n\right)}{\Re }_{{\alpha }_{rs}}$

(d) 

${\Re }_{C_{\frac{n-2(k+1)}{2}}}^{(a_1,\dots ,a_{2k+1})}:={\bigcap }_{{\alpha }_{rs}\in C_{\frac{n-2(k+1)}{2}}\left({\Sigma }_{a_1,\dots ,a_{2k+1}}\right)}{\Re }_{{\alpha }_{rs}}$

Theorem 6.

Let E be a symplectic vector space of dimension $2n$ then $L(n,E)$ is intersection of linear sections of the Grassmannian variety and is included in a projective space of a direct sum of matrix kernels

(A) 

If $n\ge 4$ even integer and let $r_n=\frac{n+2}{2}$, then

$$\begin{array}{cc}\hfill L(n,E)& =(G(n,E)\cap \Re )\cap (\bigcap _{k=1}^{r_n-2}\bigcap _{\begin{array}{c}1\le a_1<\cdots <a_{2k}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}(G(n,E)\cap {\Re }_{C_{\frac{n-2k}{2}}}^{(a_1,\dots ,a_{2k})}))\hfill \\ \hfill & \subseteq \mathbb{P}(ker{\mathcal{L}}_{r_n}\oplus \underset{k=1}{\overset{r_n-2}{⨁}}(\underset{\begin{array}{c}1\le a_1<\cdots <a_{2k}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}{⨁}ker{\mathcal{L}}_{r_n-k}^{(a_1,\cdots ,a_{2k})}))\hfill \end{array}$$

(B) 

If $n\ge 5$ odd integer and let $r_n=\frac{n+1}{2}$, then

$$\begin{array}{cc}\hfill L(n,E)& =(G(n,E)\cap {\Re }^n)\cap (\bigcap _{k=1}^{r_n-2}\bigcap _{\begin{array}{c}1\le a_1<\cdots <a_{2k+1}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}(G(n,E)\cap {\Re }_{C_{\frac{n-2k}{2}}}^{(a_1,\dots ,a_{2k+1})}))\hfill \\ \hfill & \subseteq \mathbb{P}(ker{\mathcal{L}}_{r_n}^n\oplus \underset{k=1}{\overset{r_n-2}{⨁}}(\underset{\begin{array}{c}1\le a_1<a_2<\cdots <a_{2k+1}\le 2n\\ a_i+a_j\ne 2n+1\end{array}}{⨁}ker{\mathcal{L}}_{r_n-k}^{(a_1,a_2,\cdots ,a_{2k+1})})).\hfill \end{array}$$