Vibration Characteristics of a Functionally Graded Viscoelastic Fluid-Conveying Pipe with Initial Geometric Defects under Thermal–Magnetic Coupling Fields
Abstract
1. Introduction
2. Mathematical Model
3. Solution Methods
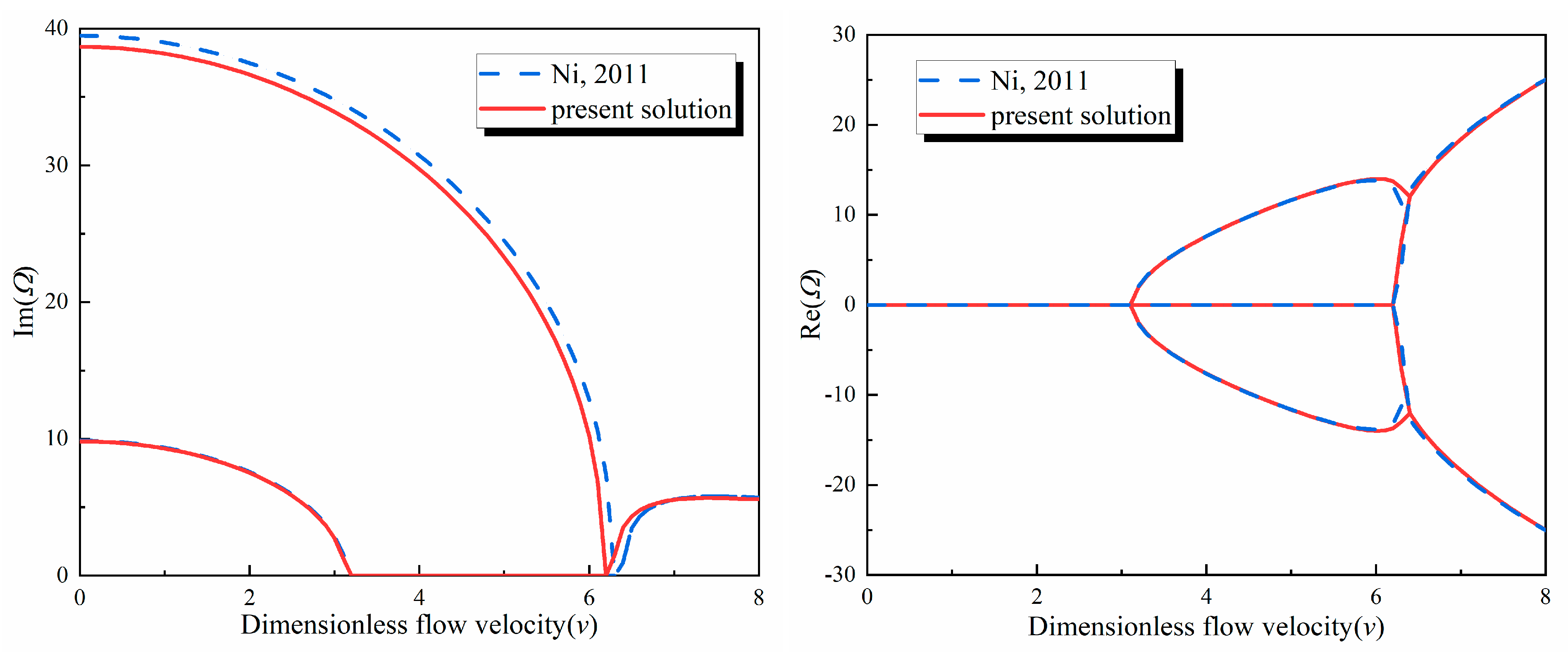
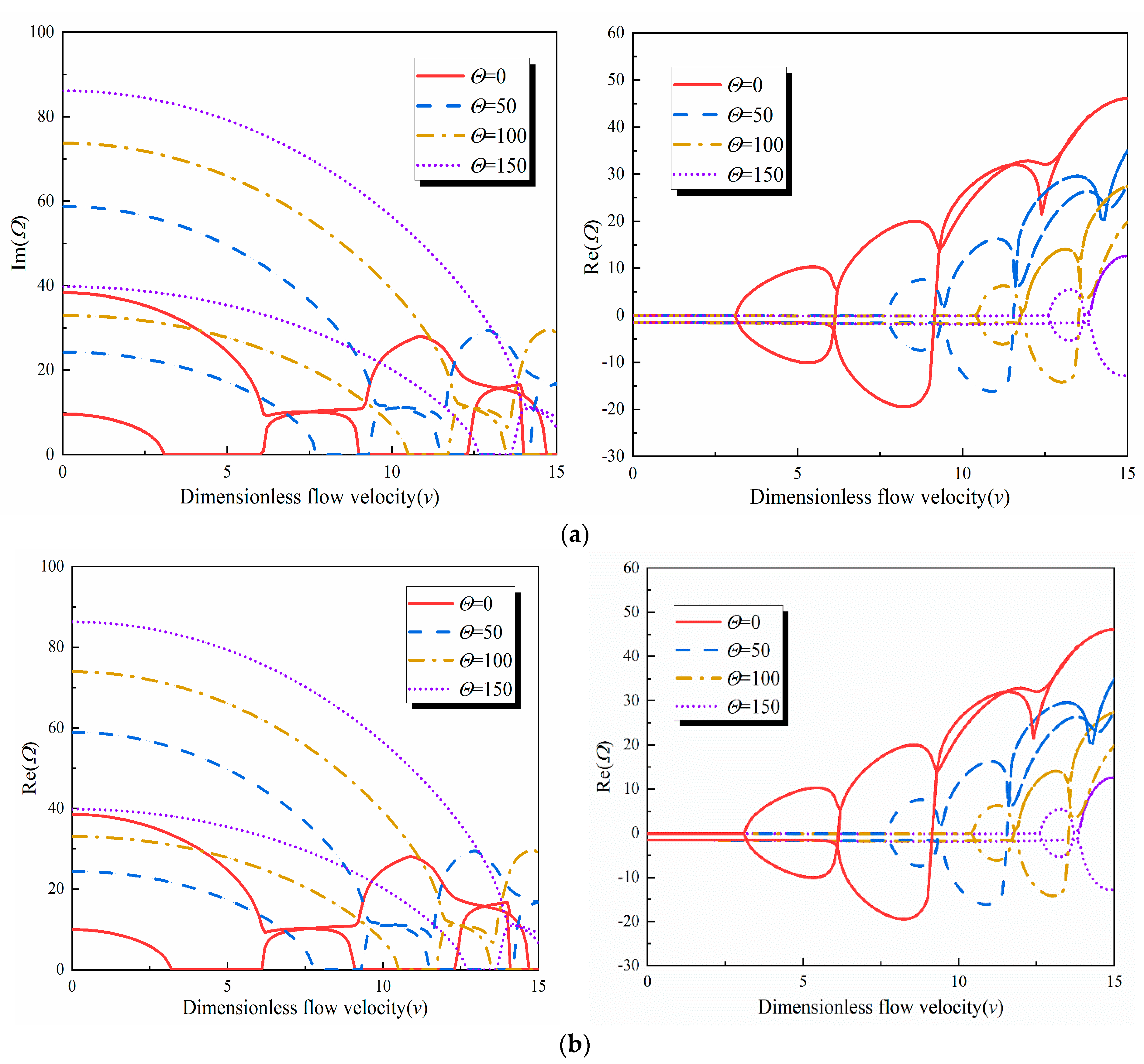
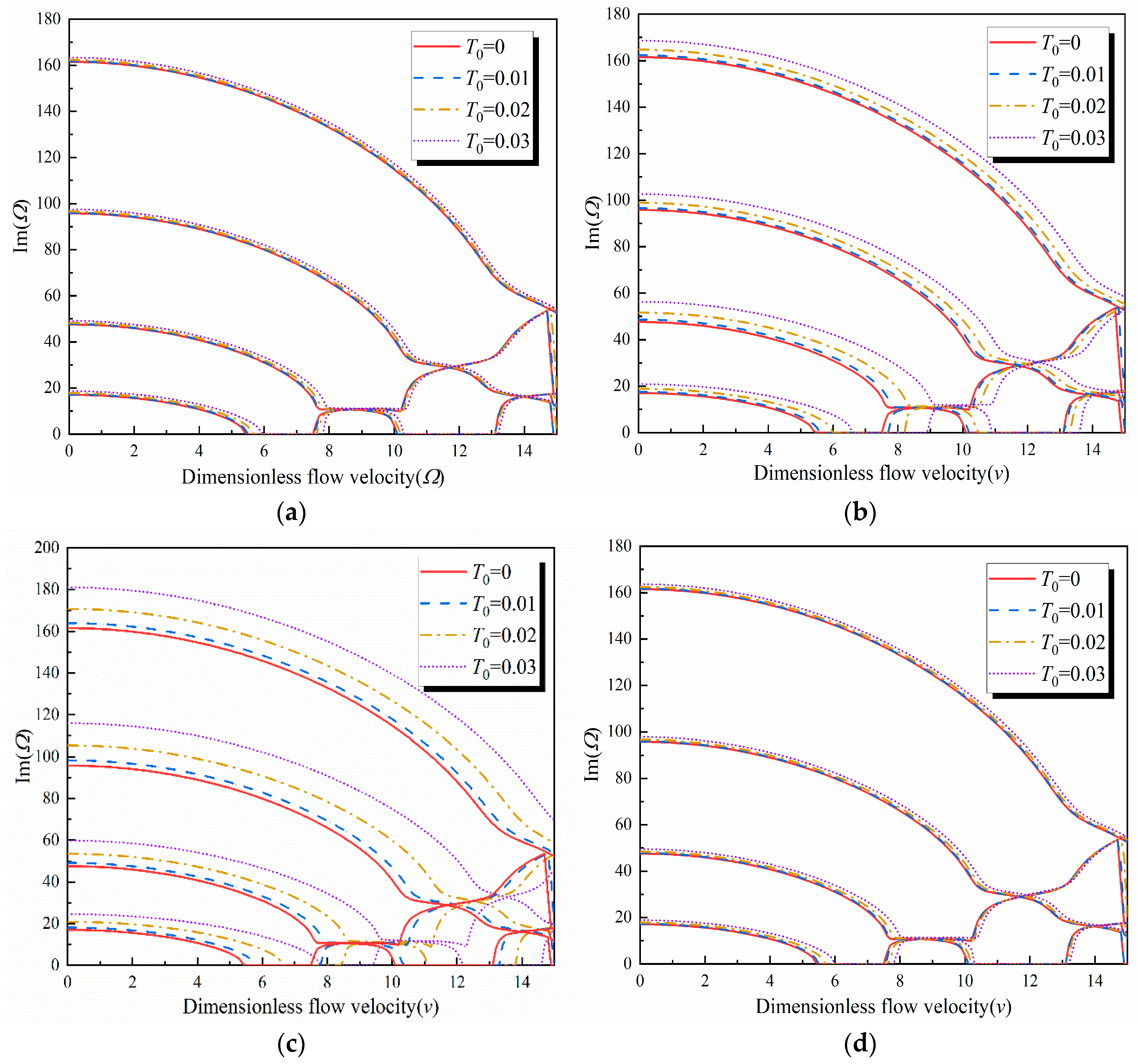
4. Calculation Example
5. Conclusions
- The presence of initial geometric defects does not eliminate the influence of temperature and magnetic fields on the stability of the FGV fluid-conveying pipe. Specifically, the stability of the FGV fluid-conveying pipe decreases with increasing temperature but increases with increasing magnetic field intensity. When both the temperature difference and magnetic field intensity increase simultaneously, they counterbalance each other.
- The natural frequencies of each order of pipes with different types of initial geometric defects increase with the amplitude of the initial geometric defect. For pipes with initial geometric defects of the quadratic parabolic and half-sinusoidal wave types, the change in amplitude primarily influences the first-order imaginary part. For initial geometric defects of the single-sinusoidal wave type, the change in amplitude has the most evident effect on the second-order imaginary part. When initial geometric defects take the form of a half-sinusoidal wave, the third-order imaginary part is most influenced by changes in amplitude.
- As the power-law exponent increases, the first two imaginary parts of the system increase, with the most significant variation occurring in the range of 0–10. This phenomenon arises because an increase in the power-law exponent results in a rapid rise in the elastic modulus of the pipe, subsequently leading to a substantial increase in the stiffness of the pipe system and enhanced stability. With further increase in the power-law exponent, the stiffness of the pipe undergoes only slight changes, and the system gradually achieves greater stability. Therefore, the careful selection of the power-law exponent is important for pipe design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Flowchart of the Analysis Performed in This Study

Appendix B. Solving Equilibrium Position
References
- Païdoussis, M.P.; Issid, N.T. Dynamic stability of pipes conveying fluid. J. Sound Vib. 1974, 33, 267–294. [Google Scholar] [CrossRef]
- Dai, H.L.; Wang, L.; Qian, Q.; Ni, Q. Vortex-induced vibrations of pipes conveying pulsating fluid. Ocean Eng. 2014, 77, 12–22. [Google Scholar] [CrossRef]
- Aldraihem, O.J. Analysis of the dynamic stability of collar-stiffened pipes conveying fluid. J. Sound Vib. 2007, 300, 453–465. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, T. Post-buckling behavior and nonlinear vibration analysis of a fluid-conveying pipe composed of functionally graded material. Compos. Struct. 2018, 185, 393–400. [Google Scholar] [CrossRef]
- Jin, J.D. Stability and chaotic motions of a restrained pipe conveying fluid. J. Sound Vib. 1997, 208, 427–439. [Google Scholar] [CrossRef]
- Kheiri, M. Nonlinear dynamics of imperfectly-supported pipes conveying fluid. J. Fluids Struct. 2020, 93, 102850. [Google Scholar] [CrossRef]
- Li, S.; Karney, B.W.; Liu, G. FSI research in pipeline systems—A review of the literature. J. Fluids Struct. 2015, 57, 277–297. [Google Scholar] [CrossRef]
- Erdogan, F. Fracture mechanics of functionally graded materials. Compos. Eng. 1995, 5, 753–770. [Google Scholar] [CrossRef]
- Imek, M. Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories. Nucl. Eng. Des. 2010, 240, 697–705. [Google Scholar] [CrossRef]
- Fallah, A.; Aghdam, M.M. Nonlinear free vibration and post-buckling analysis of functionally graded beams on nonlinear elastic foundation. Eur. J. Mech. A Solids 2011, 30, 571–583. [Google Scholar] [CrossRef]
- Shen, H.; Païdoussis, M.P.; Wen, J.; Yu, D.; Wen, X. The beam-mode stability of periodic functionally-graded-material shells conveying fluid. J. Sound Vib. 2014, 333, 2735–2749. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Ungbhakorn, V. Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities. Aerosp. Sci. Technol. 2014, 32, 111–120. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Q.; Li, M.; Li, Y. Nonlinear free and forced vibrations of porous functionally graded pipes conveying fluid and resting on nonlinear elastic foundation. Compos. Struct. 2020, 252, 112672. [Google Scholar] [CrossRef]
- Khodabakhsh, R.; Saidi, A.R.; Bahaadini, R. An analytical solution for nonlinear vibration and post-buckling of functionally graded pipes conveying fluid considering the rotary inertia and shear deformation effects. Appl. Ocean Res. 2020, 101, 102277. [Google Scholar] [CrossRef]
- Xu, W.; Pan, G.; Moradi, Z.; Shafiei, N. Nonlinear forced vibration analysis of functionally graded non-uniform cylindrical microbeams applying the semi-analytical solution. Compos. Struct. 2021, 275, 114395. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Analyzing FG shells with large deformations and finite rotations. World J. Eng. 2019, 16, 636–647. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Stability analysis of frame having FG tapered beam-column. Int. J. Steel Struct. 2019, 19, 446–468. [Google Scholar] [CrossRef]
- Masoodi, A.R.; Ghandehari, M.A.; Tornabene, F.; Dimitri, R. Natural frequency response of FG-CNT coupled curved beams in thermal conditions. Appl. Sci. 2024, 14, 687. [Google Scholar] [CrossRef]
- Rajidi, S.R.; Gupta, A.; Panda, S. Vibration characteristics of viscoelastic sandwich tube conveying fluid. Mater. Today Proc. 2020, 28, 2440–2446. [Google Scholar] [CrossRef]
- Amirinezhad, H.; Tarkashvand, A.; Talebitooti, R. Acoustic wave transmission through a polymeric foam plate using the mathematical model of functionally graded viscoelastic (FGV) material. Thin-Walled Struct. 2020, 148, 106466. [Google Scholar] [CrossRef]
- Deng, J.Q.; Liu, Y.S.; Zhang, Z.J.; Liu, W. Stability analysis of multi-span viscoelastic functionally graded material pipes conveying fluid using a hybrid method. Eur. J. Mech. A Solids 2017, 65, 257–270. [Google Scholar] [CrossRef]
- Deng, J.Q.; Liu, Y.; Zhang, Z.; Liu, W. Size-dependent vibration and stability of multi-span viscoelastic functionally graded material nanopipes conveying fluid using a hybrid method. Compos. Struct. 2017, 179, 590–600. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Abaei, A.R.; Ilkhani, M.R. Free vibrations of functionally graded viscoelastic cylindrical panel under various boundary conditions. Compos. Struct. 2015, 126, 1–15. [Google Scholar] [CrossRef]
- Pinnola, F.P.; Barretta, R.; de Sciarra, F.M.; Pirrotta, A. Analytical solutions of viscoelastic nonlocal Timoshenko beams. Mathematics 2022, 10, 477. [Google Scholar] [CrossRef]
- Fu, G.M.; Tuo, Y.H.; Zhang, H.; Su, J.; Sun, B.; Wang, K.; Lou, M. Effects of material characteristics on nonlinear dynamics of viscoelastic axially functionally graded material pipe conveying pulsating fluid. J. Mar. Sci. Appl. 2023, 22, 247–259. [Google Scholar] [CrossRef]
- Akintoye, O.O.; Oyediran, A.A. The effect of various boundary conditions on the nonlinear dynamics of slightly curved pipes under thermal loading. Appl. Math. Model. 2020, 87, 332–350. [Google Scholar] [CrossRef]
- Fu, Y.M.; Zhong, J.; Shao, X.F.; Chen, Y. Thermal postbuckling analysis of functionally graded tubes based on a refined beam model. Int. J. Mech. Sci. 2015, 96–97, 58–64. [Google Scholar] [CrossRef]
- Ghorbanpour Arani, A.; Haghparast, E.; Ghorbanpour Arani, A.H. Size-dependent vibration of double-bonded carbon nanotube-reinforced composite microtubes zconveying fluid under longitudinal magnetic field. Polym. Compos. 2016, 37, 1375–1383. [Google Scholar] [CrossRef]
- Ma, T.; Mu, A. Study on the stability of functionally graded simply supported fluid-conveying microtube under multi-physical fields. Micromachines 2022, 13, 895. [Google Scholar] [CrossRef]
- Lu, Q.S.; To, C.W.S.; Huang, K.L. Dynamic stability and bifurcation of an alternating load and magnetic field excited magnetoelastic beam. J. Sound Vib. 1995, 181, 873–891. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Gao, Y.W.; Zheng, X.; Jiang, Q. Buckling and post-buckling of a ferromagnetic beam-plate induced by magnetoelastic interactions. Int. J. Non-Linear Mech. 2000, 35, 1059–1065. [Google Scholar] [CrossRef]
- Wu, G.Y. The analysis of dynamic instability and vibration motions of a pinned beam with transverse magnetic fields and thermal loads. J. Sound Vib. 2005, 284, 343–360. [Google Scholar] [CrossRef]
- Hosseini, M.; Sadeghi-Goughari, M. Vibration and instability analysis of nanotubes conveying fluid subjected to a longitudinal magnetic field. Appl. Math. Model. 2016, 40, 2560–2576. [Google Scholar] [CrossRef]
- Pisarski, D.; Konowrocki, R.; Szmidt, T. Dynamics and optimal control of an electromagnetically actuated cantilever pipe conveying fluid. J. Sound Vib. 2018, 432, 420–436. [Google Scholar] [CrossRef]
- Zhong, J.; Fu, Y.M.; Wan, D.T.; Li, Y. Nonlinear bending and vibration of functionally graded tubes resting on elastic foundations in thermal environment based on a refined beam model. Appl. Math. Model. 2016, 40, 7601–7614. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, J.L.; She, G.L.; Jing, Y.; Pu, H. Nonlinear free vibration analysis of functionally graded carbon nanotube reinforced fluid-conveying pipe in thermal environment. Steel Compos. Struct. 2022, 45, 641–652. [Google Scholar] [CrossRef]
- Li, Z.M.; Qiao, P. Buckling and postbuckling behavior of shear deformable anisotropic laminated beams with initial geometric imperfections subjected to axial compression. Eng. Struct. 2015, 85, 277–292. [Google Scholar] [CrossRef]
- Ding, H.X.; She, G.L.; Zhang, Y.W. Nonlinear buckling and resonances of functionally graded fluid-conveying pipes with initial geometric imperfection. Eur. Phys. J. Plus 2022, 137, 1329. [Google Scholar] [CrossRef]
- Liu, H.; Lv, Z.; Tang, H.J. Nonlinear vibration and instability of functionally graded nanopipes with initial imperfection conveying fluid. Appl. Math. Model. 2019, 76, 133–150. [Google Scholar] [CrossRef]
- Zhu, B.; Chen, X.C.; Guo, Y.; Li, Y.-H. Static and dynamic characteristics of the post-buckling of fluid-conveying porous functionally graded pipes with geometric imperfections. Int. J. Mech. Sci. 2021, 189, 105947. [Google Scholar] [CrossRef]
- Farshidianfar, A.; Soltani, P. Nonlinear flow-induced vibration of a SWCNT with a geometrical imperfection. Comput. Mater. Sci. 2012, 53, 105–116. [Google Scholar] [CrossRef]
- Tong, G.J.; Liu, Y.S.; Cheng, Q.; Dai, J. Stability analysis of cantilever functionally graded material nanotube under thermo-magnetic coupling effect. Eur. J. Mech. A Solids 2020, 80, 103929. [Google Scholar] [CrossRef]
- Hamed, H.; Tawfik, M.; Negm, H.M. Thermal buckling and nonlinear flutter behavior of shape memory alloy hybrid composite plates. J. Vib. Control 2011, 17, 489–503. [Google Scholar] [CrossRef]
- Matouk, H.; Bousahla, A.A.; Houari, H.; Bourada, F.; El Abbas, A.B.; Tounsi, A.; Mahmound, S.R.; Benrahou, K.H. Investigation on hygro-thermal vibration of P-FG and symmetric S-FG nanobeam using integral Timoshenko beam theory. Adv. Nano Res. 2020, 8, 293–305. [Google Scholar] [CrossRef]
- Zhen, Y.X.; Gong, Y.F.; Tang, Y. Nonlinear vibration analysis of a supercritical fluid-conveying pipe made of functionally graded material with initial curvature. Compos. Struct. 2021, 268, 113980. [Google Scholar] [CrossRef]
- Ni, Q.; Zhang, Z.L.; Wang, L. Application of the differential transformation method to vibration analysis of pipes conveying fluid. Appl. Math. Comput. 2011, 217, 7028–7038. [Google Scholar] [CrossRef]
- Loghman, E.; Kamali, A.; Bakhtiari-Nejad, F.; Abbaszadeh, M. Nonlinear free and forced vibrations of fractionally modeled viscoelastic FGM micro-beam. Appl. Math. Model. 2021, 92, 297–314. [Google Scholar] [CrossRef]
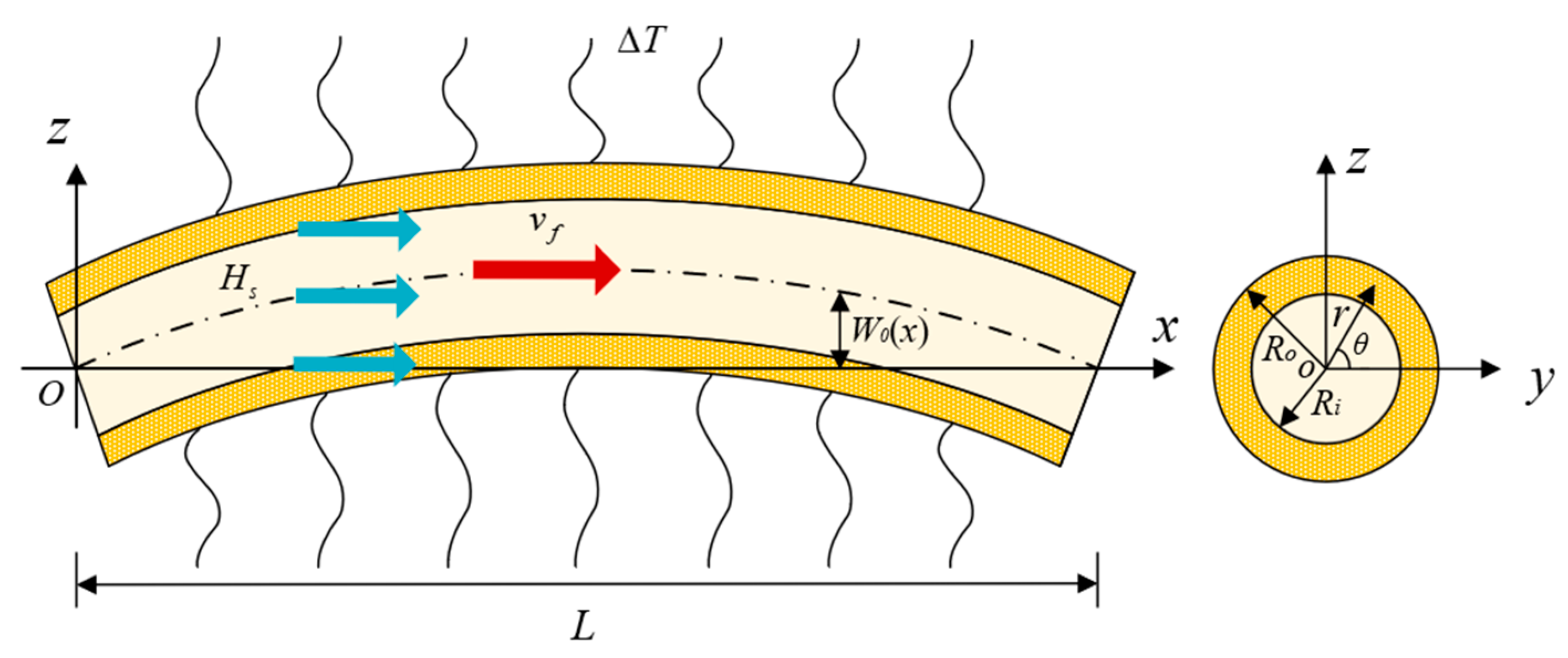



| Notation | Name (Inner Surface) | Value | Notation | Name (Outer Surface) | Value |
|---|---|---|---|---|---|
| Density | Density | ||||
| Young’s modulus | 427 GPa | Young’s modulus | 69 GPa | ||
| Coefficient of thermal expansion | Coefficient of thermal expansion |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Wang, Z.-M. Vibration Characteristics of a Functionally Graded Viscoelastic Fluid-Conveying Pipe with Initial Geometric Defects under Thermal–Magnetic Coupling Fields. Mathematics 2024, 12, 840. https://doi.org/10.3390/math12060840
Ma Y, Wang Z-M. Vibration Characteristics of a Functionally Graded Viscoelastic Fluid-Conveying Pipe with Initial Geometric Defects under Thermal–Magnetic Coupling Fields. Mathematics. 2024; 12(6):840. https://doi.org/10.3390/math12060840
Chicago/Turabian StyleMa, Yao, and Zhong-Min Wang. 2024. "Vibration Characteristics of a Functionally Graded Viscoelastic Fluid-Conveying Pipe with Initial Geometric Defects under Thermal–Magnetic Coupling Fields" Mathematics 12, no. 6: 840. https://doi.org/10.3390/math12060840
APA StyleMa, Y., & Wang, Z.-M. (2024). Vibration Characteristics of a Functionally Graded Viscoelastic Fluid-Conveying Pipe with Initial Geometric Defects under Thermal–Magnetic Coupling Fields. Mathematics, 12(6), 840. https://doi.org/10.3390/math12060840





