Numerical Investigation of Double-Diffusive Convection in an Irregular Porous Cavity Subjected to Inclined Magnetic Field Using Finite Element Method

Abstract

Purpose—This study aims to perform an in-depth analysis of double-diffusive natural convection (DDNC) in an irregularly shaped porous cavity. We investigate the convective heat transfer process induced by the lower wall treated as a heat source while the side walls of the enclosure are maintained at a lower temperature and concentration, and the remaining wall is adiabatic. Various factors, such as the Rayleigh number, Darcy effects, Hartmann number, Lewis number and effects of magnetic inclination are evaluated for their influence on flow dynamics and heat distribution. Design/methodology/approach—After validating the results, the FEM (finite element method) is used to simulate the flow pattern, temperature variations, and concentration by solving the nonlinear partial differential equations with the modified Rayleigh number (10⁴ ≤ Ra ≤ 10⁷), Darcy number (10⁻⁴ ≤ Da ≤ 10⁻¹), Lewis number $(0.1\le Le\le 10)$, and Hartmann number $\left(0\le Ha\le 40\right)$ as the dimensionless operating parameters. Findings—The finding shows that the patterns of convection and the shape of the isotherms within porous enclosures are notably affected by the angle of the applied magnetic field. This study enhances our understanding of how double-diffusive natural convection (DDNC) operates in these enclosures, which helps improve heating and cooling technologies in various engineering fields. Research limitations/implications—Numerical and experimental extensions of the present study make it possible to investigate differences in thermal performance as a result of various curvatures, orientations, boundary conditions, and the use of three-dimensional analysis and other working fluids. Practical implications—The geometry configurations used in this study have wide-ranging applications in engineering fields, such as in heat exchangers, crystallization, microelectronics, energy storage, mixing, food processing, and biomedical systems. Originality/value—This study shows how an inclined magnetic field affects double-diffusive natural convection (DDNC) within a porous system featuring an irregularly shaped cavity, considering various multiphysical conditions.

1. Introduction

Double-diffusive natural convection (DDNC) refers to the combined effects of buoyancy-driven fluid flow and the simultaneous transport of heat and mass. Different flow patterns and convective cells develop in DDNC fluids due to buoyancy forces caused by temperature and concentration variations. There are several uses for natural convection, including in geothermal systems [1,2], chemical engineering, crystal formation, and separation processes [3,4]. Natural convection is the movement of fluid driven by buoyancy force due to mass and heat transfer. In engineering applications, natural convection is important for cooling systems, sun collectors, and many other thermal devices that need to move heat efficiently. Natural convection is a fundamental mechanism for heat transfer in geothermal systems, as the heat is transferred from the hotter regions to the cooler regions, and buoyancy forces are generated, leading to the formation of convective cells and flow patterns. This phenomenon has numerous industrial applications and natural processes including contaminant transport [5,6], drying methods [7], and chemical reactors [8]. An irregular cavity can further complicate the natural convection patterns in geothermal systems, resulting in complex flow and heat transfer phenomena. The interplay between natural convection and the irregularities of the cavity can have an important impact on the efficiency and performance of the system. The complex interplay between heat and mass transfer, porous effects, and irregular cavities has generated significant interest among researchers in various fields, from geothermal systems to chemical engineering. Numerous studies have examined cavities of varying shapes, such as, trapezoids [9,10], triangles [11,12,13], irregular wall cavities [14], and more unusual shapes [15]. Izadi et al. [16] conducted a detailed discussion on mixed convection in enclosures of various shapes and summarized the key findings regarding the enhancement of heat transfer and the effects on pumping power. The dynamics of fluid movement and thermal conduction in these cavities and how they are affected by their shape were the focus of these analyses. All the above studies conclude that the Soret and Dufour effects are two critical physical phenomena that significantly influence the thermal, diffusive transport characteristics and the fluid flow behavior in DDNC. The study of thermal and diffusive transport characteristics in porous media under DDNC was first initiated by Bejan et al. [17]. They analyzed the effect of Lewis numbers in a porous medium. Later on, Goyeau et al. [18] analyzed an enclosure filled with a saturated porous medium and applied the Darcy–Brinkman model to describe the flow within it. They investigated the impact of porosity and Darcy’s number on double-diffusive natural convection (DDNC) within the porous cavity. The simulation findings from their study indicated that while the influence of porosity on the heat and mass transfer rate was negligible at low Darcy numbers, a higher porosity significantly increased the rates of thermal energy transfer and mass transport at high Darcy numbers. Mondal et al. [19] investigated non-steady-state DDNC in porous media and examined the variation in the buoyancy ratio on heat and mass transfer rate. Chamkha et al. [20] studied DDNC in a tilted porous cavity using the finite difference method (FDM). Their results demonstrated that thermal and diffusive transport is affected not only by Darcy’s number and the buoyancy ratio but also by the tilt angle and aspect ratio of a square cavity. Moreover, porous media in cavities used in industrial production are often accompanied by a composite layer. Numerical research on DDNC in a porous cavity with irregular porosity was discussed by He et al. [21], which comprised two parallel porous layers having distinct porosity levels. The investigation conducted by Vijaybabu et al. [22] focused on analyzing the influence of MHD (magnetohydrodynamic) and porous circular cylinders on DDNC and an irreversibility analysis within an enclosure. The researcher Astanina et al. [23] focused on thermogravitational convection in a porous cube with a non-uniform heating of the vertical wall. The mathematical modeling of fluid flow in the heated center of a wavy-shaped cavity as discussed by Rashid et al. [24], focusing on the thermal and diffusive transport in a MHD Casson fluid flow. This study is part of the significant attention given to DDNC in various fields, such as oceanography, metallurgy, and astrophysics.

Magnetohydrodynamics is an important physical phenomenon that has garnered a lot of interest due to its numerous applications in various fields, including engineering and environmental sciences. Numerous studies have investigated the influence of magnetohydrodynamics on heat transfer in enclosures to assess the impact of magnetic fields on heat transfer, whether it occurs via conduction or convection. An FEM was investigated by Rahman et al. [25] to explore the combined impact of magnetohydrodynamics and joule heating on DDNC within a horizontal channel featuring an open enclosure. Teamah et al. [26] explored the effects of the magnetic field and heat source on the DDNC flow in a rectangular enclosure. The researchers observed that increasing the magnetic field resulted in a decrease in fluid circulation and thermal and diffusive transport rates within the cavity. Kumar et al. [27] studied the thermal and diffusive transport in the 2D MHD free convection process, considering the thermal diffusion. The process occurred in a Darcy porous enclosure in a stratified thermal and mass fluid. Bayareh et al. [28] explored the effects of magnetic fields on the thermodynamic efficiency of nanofluid-filled cavities, detailing the role of AI in optimizing system performance and forecasting future advancements. Seyyedi et al. [29] discussed natural convection and entropy generation within a square inclined cavity affected by magnetohydrodynamic (MHD) forces, revealing peaks in entropy generation at specific inclination angles and Hartmann numbers. Ali et al. [30] explained the MHD behavior of mixed convection in a hexagonal enclosure.

The main objective of this research is to investigate the heat and mass transfer in an irregularly shaped porous cavity using the finite element method. To the best of our knowledge, based on a thorough literature review, there are no studies on irregularly shaped enclosures using hybrid mesh techniques. The hybrid mesh consists of both triangular and rectangular shapes. The novelty of the work lies in how an inclined magnetic field influences double-diffusive natural convection (DDNC) within a porous system with an irregularly shaped cavity, taking into account various multiphysical conditions. Therefore, various parameters can be utilized to control heat and mass transfer. This study has applications in heat exchangers, crystallization, microelectronics, food processing, and biomedical systems.

2. Mathematical Formulation

The domain analyzed in this study is a two-dimensional, irregular enclosure with a fluid-permeated porous medium, assumed to be incompressible and steady, and subjected to an inclined magnetic field, as shown in Figure 1. The porous medium contains a mixture of an inert fluid and a solute, which undergoes mass transfer. The side walls and horizontal walls of the cavity are maintained at different constant concentrations and temperatures, resulting in a DDNC problem. The lowest concentration and temperature are along the side walls and the highest ones along the horizontal wall. The enclosure’s upper wall is adiabatic.

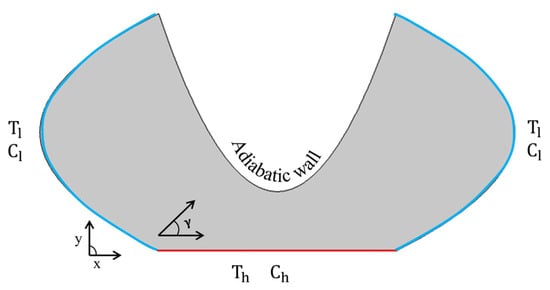
Figure 1. Sketch view of the model.

Governing Equations

Considering the above assumptions, the dimensional equations for continuity, momentum, energy, and concentration can be shown as [31].

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$\rho \left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)+\frac{\partial p}{\partial x}=\mu \left(\frac{{\partial }^{2}u}{{\partial x}^2}+\frac{{\partial }^{2}u}{{\partial y}^2}\right)-\frac{\mu }{K}u+{\xi }_x$$

(2)

$$\rho \left(u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)+\frac{\partial p}{\partial y}=\mu \left(\frac{{\partial }^{2}v}{{\partial x}^2}+\frac{{\partial }^{2}v}{{\partial y}^2}\right)-\frac{\mu }{K}v+{\xi }_y$$

(3)

where ${\xi }_x$ and ${\xi }_y$ represent force terms called the Boussinesq approximation and magnetic field, which contain

$${\xi }_x=-\varrho B_0^2\left(u·{sin}^2\gamma -v·sin\gamma cos\gamma \right)$$

$${\xi }_y=-\varrho B_0^2\left(v·{cos}^2\gamma -u·cos\gamma sin\gamma \right)+\rho g\left[{{\beta }_T\left(T-T_l\right)+\beta }_c\left(c-c_l\right)\right]$$

$$\frac{1}{\varsigma }\left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=\left(\frac{{\partial }^{2}T}{{\partial x}^2}+\frac{{\partial }^{2}T}{{\partial y}^2}\right)$$

(4)

$$\frac{1}{D}\left(u\frac{\partial c}{\partial x}+v\frac{\partial c}{\partial y}\right)=\left(\frac{{\partial }^{2}c}{{\partial x}^2}+\frac{{\partial }^{2}c}{{\partial y}^2}\right)$$

(5)

$\varsigma$ is a diffusion coefficient and $D$ is the magnetic diffusivity.

To convert the dimensional equations into a nondimensional form, the following dimensionless parameter were used [32,33]:

Dimensionless parameter	Definition
Rayleigh number	$Ra=\frac{{\rho }^2{\beta }_{T}g{H}^3∆TPr}{v^2}$
Lewis number	$Le=\frac{\varsigma }{D}$
Prandtl number	$P_r=\frac{v}{a}$
Darcy number	$Da=\frac{K}{H^2}$
Hartmann number	$Ha=BH\sqrt{\frac{\varrho }{\mu }}$
Temperature	$\theta =\frac{\left(T-T_l\right)}{\left(T_h-T_l\right)}$
Fluid pressure	$P=\frac{p}{\rho {\alpha }^2}$
Velocity	$U=\frac{uH}{\alpha },V=\frac{vH}{\alpha }$

The dimensionless form of Equations (1)–(5) are

$$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0$$

(6)

$$U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}+\frac{\partial P}{\partial X}=P_r\left(\frac{{\partial }^{2}U}{{\partial X}^2}+\frac{{\partial }^{2}U}{{\partial Y}^2}\right)-\frac{P_r}{Da}U+{\xi }_X,$$

(7)

$$U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}+\frac{\partial P}{\partial Y}=P_r\left(\frac{{\partial }^{2}V}{{\partial X}^2}+\frac{{\partial }^{2}V}{{\partial Y}^2}\right)-\frac{P_r}{Da}V+{\xi }_Y$$

(8)

where $P_r=\frac{\mu }{\rho }$

$$\begin{array}{c}{\xi }_X={{Ha}^{2}P}_r\left(sin\gamma cos\gamma V-{sin}^2\gamma U\right),\\ {\xi }_Y={{Ha}^{2}P}_r\left(sin\gamma cos\gamma U-{cos}^2\gamma V\right)+P_{r}Ra\left(NC+\theta \right) \end{array}$$

$$U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y}=\left(\frac{{\partial }^2\theta }{{\partial X}^2}+\frac{{\partial }^2\theta }{{\partial Y}^2}\right)$$

(9)

$$Le\left(U\frac{\partial C}{\partial X}+V\frac{\partial C}{\partial Y}\right)=\left(\frac{{\partial }^{2}C}{{\partial X}^2}+\frac{{\partial }^{2}C}{{\partial Y}^2}\right)$$

(10)

The dimensionless boundary conditions are

Cold wall	$C=0$, $\theta =0$	$U=0, V=0$
Hot wall	$C=1$, $\theta =1$	$U=0, V=0$
Remaining wall	$C_n=0$. ${\theta }_n=0$	$U=0, V=0$

The average values in question can be determined by performing an integration over the heated section.

The averaged Nusselt number is

$${Nu}_{av}={\int }_0^{1}Nu dY$$

(11)

The averaged Sherwood Number is

$${Sh}_{av}={\int }_0^{1}Sh dY$$

(12)

The local Nusselt number ${Nu}_{lo}$ and local Sherwood Number ${Sh}_{lo}$ are computed through the equation

$${Nu}_{lo}=-{\left(\frac{\partial \theta }{\partial n}\right)}_s$$

(13)

$${Sh}_{lo}=-{\left(\frac{\partial C}{\partial n}\right)}_s$$

(14)

where (s) refers to the surface of the region, and (n) represents the normal direction to the surface.

In addition, the kinetic energy (total) is

$$K.E.=\frac{1}{2}{\int }_{\Omega }{‖U‖}^{2}d\Omega$$

(15)

3. Numerical Methodology

Several computational techniques have been developed to determine the dynamics of fluid movement and heat transfer rates in different types of enclosures. In this investigation, the FEM is utilized to discretize and solve Equations (6)–(10) along with their corresponding boundary conditions [34,35]. The FEM is acknowledged as a highly efficient computational scheme for obtaining optimized solutions. The research carried out by [36] focused on comparing the FVM and the FDM for the simulation of lid-driven cavity flow. The finite element approach creates a discrete nonlinear system of equations by discretizing equations using a weak formulation. The resulting nonlinear system is solved using the Newton method, whereas the linear inner system is solved directly using the PARDISO program. LU matrix factorization is used in the solver to improve computational efficiency and reduce the required iterations for convergence, resulting in faster and more accurate solutions for complex systems of equations. The iterative process, combined with discretization techniques, greatly reduces the required iterations for obtaining accurate solutions, enhancing computational efficiency. The finite element method employs variable-specific discretization schemes: a second-order one for velocity elements and a linear-order one for temperature and solute concentration, optimizing accuracy and computational efficiency. This approach yields optimized solutions and enhances the understanding of the underlying physics. The computational domain is discretized using a non-uniform mesh comprising triangular and rectangular elements, enabling a flexible representation of irregular geometries. To ensure accuracy in critical areas, a higher density of mesh points is allocated. Figure 2 illustrates the combined use of rectangular and triangular elements in the hybrid finite element grid. This hybrid mesh configuration effectively balances accuracy and computational efficiency, thereby enhancing solution precision. Prior to simulating the model under consideration, the current code was first tested by applying it to previously reported models. The grid independence was established, and the code’s validation was demonstrated through a comparison of the average Nusselt number with the findings from [32,37], using $Ha=25, Le=2.5, Pr=6.8, Ra={10}^5$, and various $\beta$ values as outlined in Table 1. The results are in Figure 3, demonstrating the effectiveness and applicability of the current code. Figure 4 represents the systematic approach employed to implement the proposed methodology.

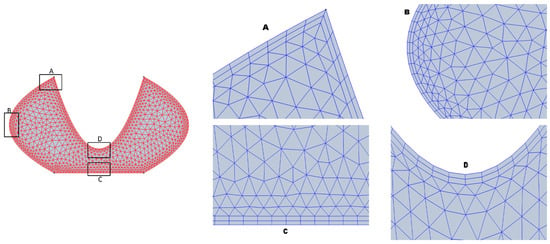
Figure 2. Mesh analysis at different positions, highlighting the specific mesh region (A–D).

Table 1. Comparison of average Nusselt number for $Ha=25, Ra={10}^5, Pr=6.8, Le=2.5$ with previous studies for different values of $\beta$.

$\mathit{\beta }$	[37]	[32]	Present
0.1	2.39023	2.38986	2.2821
1	3.81168	3.81194	3.7710
5	4.27511	4.27587	4.2651
10	4.35470	4.35556	4.3120

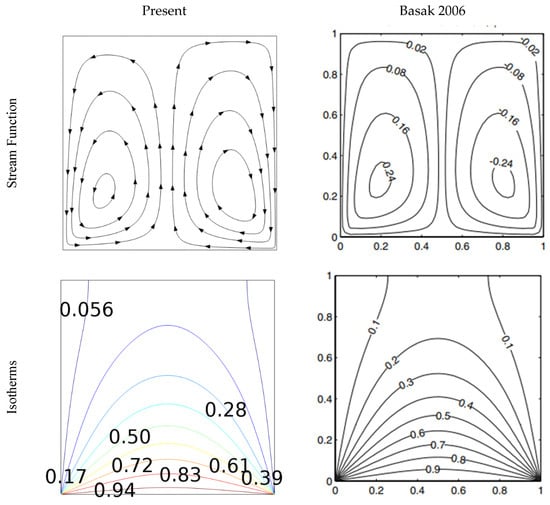
Figure 3. Comparison of the results with Basak et al. [38] in terms of streamlines and isotherms; $P_r=0.71 \mathrm{a}\mathrm{n}\mathrm{d} Ra={10}^6, Da={10}^{-5}$.

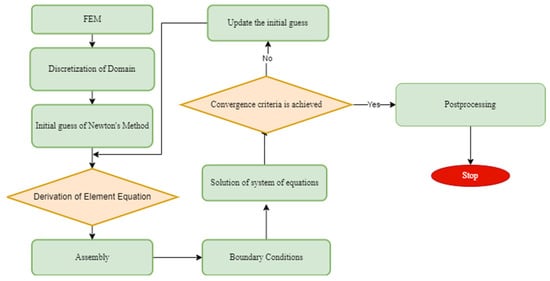
Figure 4. FEM flow chart.

Grid Convergence

To evaluate the impact of grid configuration on simulation results, it is an essential step to investigate the correlation between the number of grid points and ${Nu}_{avg}$. To achieve this, the impact of different grid points on the averaged Nusselt number was evaluated for $Ha=25, Ra=10^5, \gamma =0^o, Le=0.1, Da=0.1$ at an extrafine level. It was observed that any grid structure was finer when ${Nu}_{avg}$, ${Sh}_{avg}$, and $K.E.$ remained constant, as shown in Table 2. As a result, we chose a uniform grid of level 8.

Table 2. Grid independence tests for ${Nu}_{avg}$ for $Ra=10^5,\gamma =0^o,Ha=25,Le=0.1,Da=0.1$.

Grid	NEL	DOFs	${\mathbf{N}\mathbf{u}}_{\mathbf{a}\mathbf{v}\mathbf{g}}$	Error [%]
Fine	3352	32076	7.31940	7.69
Finer	9516	88550	7.88235	5.91
Extrafine	24908	226590	8.37816	0.003
Extremely Fine	34284	306286	8.37847

4. Result and Discussions

This section presents a detailed analysis of the numerical investigation conducted on natural convection in a 2D laminar flow regime within an irregular enclosure under Darcy’s impact. The results are compiled by examining the impact of the Hartmann number $0\le Ha\le 40,$ Darcy number (${10}^{-4}\le Da\le {10}^{-1}$), Lewis number ($0.1\le Le\le 10$), and Rayleigh number (${10}^4\le Ra\le {10}^7$) on the flow. The streamlines, isotherms, and isoconcentration are presented.

4.1. Impact of Rayleigh’s Number

Figure 5 shows contour maps of velocity streamlines, isotherms, and isoconcentration for different Rayleigh numbers in the range ${10}^4\le Ra\le {10}^7$ at $Ha=25, Le=0.1, Da=0.1$. At lower Rayleigh numbers, the flow is stable and streamlined, with evenly spaced isotherms and isoconcentration lines indicating a uniform heat and mass distribution. As the Rayleigh number increases, the streamlines become more complex, indicating a transition from stable laminar flow to a more dynamic regime, possibly approaching turbulence. This is further evidenced by the increasingly intricate isotherm and isoconcentration patterns, suggesting enhanced fluid mixing. The temperature remains the highest at the lower wall and the lowest at the side walls, consistent with the imposed boundary conditions, while the adiabatic upper wall shows no temperature change due to its insulation. The plots indicate that as the Rayleigh number (Ra) increases, buoyancy forces grow stronger, shifting the dominant heat transfer mechanism from conduction to convection. This results in improved thermal mixing and convection, which can impact the effectiveness of thermal systems such as heat exchangers and cooling units. Figure 6 represents the impact of Ra on the averaged Sherwood number, averaged Nusselt number, and total kinetic energy. Apparently, ${Nu}_{avg}$ and ${Sh}_{avg}$ rises with $Ra$, and the maximum values of ${Nu}_{avg}$, ${Sh}_{avg}$ and $K.E$ are 14.5, 32 and $8\times {10}^3$ for ${10}^4\le Ra\le {10}^6$.

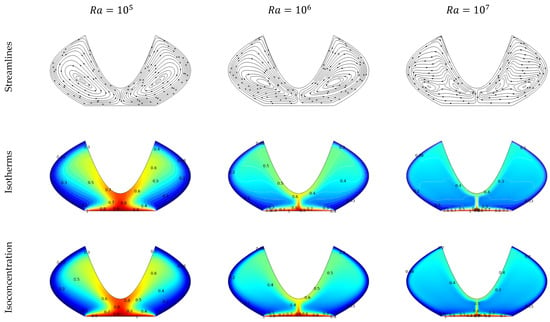
Figure 5. Variations in flow dynamics, temperature fields, and solute dispersion depicted through streamlines, isotherms, and isoconcentration profiles across different Rayleigh numbers (Ra).

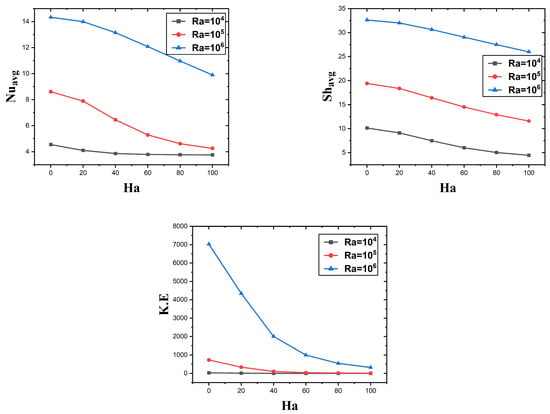
Figure 6. The graph displays the impact of Ra on the average Nusselt number, average Sherwood number, and total kinetic energy.

4.2. Impact of Lewis’s Number

The effect of varying Le $(1\le Le\le 10)$ on momentum, isotherms, and isoconcentration is illustrated in Figure 7. It demonstrates that there is no considerable change in momentum when the Lewis number increases because it is not directly associated with diffusion. The fluid rotates clockwise due to the lower wall being heated, and the side walls have a minimum temperature. At low Lewis numbers, the flow exhibits smooth velocity streamlines with uniform isoconcentration and isotherm contours, indicating a balanced distribution of concentration and temperature. As Le increases, the flow becomes more complex, characterized by intricate velocity streamlines that signify enhanced fluid mixing and convection. Consequently, the flow pattern becomes highly irregular, resulting in improved convective transport within the system. High Lewis numbers increase thermal diffusivity relative to mass diffusivity. The fluid concentration distribution may change. Fluid concentrations on the hot side increase with the Lewis number. Figure 8 illustrates that when Le increases, the mean Nusselt number increase for $0.1\le Le\le 1,$ and the heat transfer rate decreases for $1\le Le\le 5$.

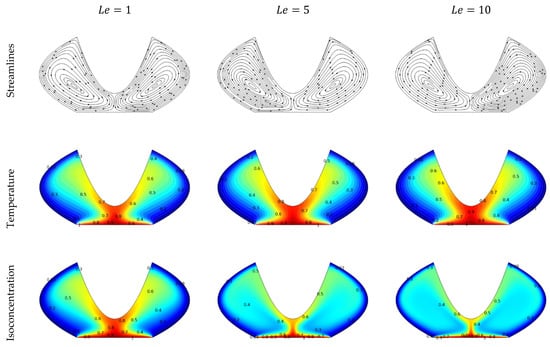
Figure 7. Flow patterns, thermal distribution, and concentration fields within an enclosure for different Lewis numbers (Le), displaying streamlines, temperature contours and concentration distributions.

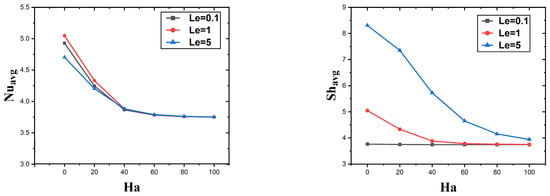
Figure 8. The graph displays the impact of Le on the Nusselt number (averaged) and Sherwood number (averaged).

Table 3 represents the numerical values of ${Nu}_{avg}$, ${Sh}_{avg},$ and $K.E.$ for the parameters $Ha=25, Le=1, Da=0.02, \gamma =0^o, Ra=10^5$. When $Le$ increaes, the number ${Nu}_{avg}$ and K.E. decrease, but the mass transfer rate increases. For a low Hartmann number, ${Nu}_{avg}$, ${Sh}_{avg}$, and K.E. have their maximum value when the $Ha$ mass transfer rate, the heat transfer rate, and total energy decrease. This table also shows that the value of ${Nu}_{avg}$, ${Sh}_{avg}$, and K.E. increases with increasing $Da,\gamma$, and $Ra$.

Table 3. Comparative numerical values of Nusselt number (averaged), Sherwood number (averaged), and kinetic energy (total) for various physical parameters.

$\mathit{L}\mathit{e}$	$\mathit{\gamma }$	$\mathit{R}\mathit{a}$	$\mathit{D}\mathit{a}$	$\mathit{H}\mathit{a}$	${\mathit{N}\mathit{u}}_{\mathit{a}\mathit{v}\mathit{g}}$	${\mathit{S}\mathit{h}}_{\mathit{a}\mathit{v}\mathit{g}}$	$\mathit{K}\mathit{E}$
1	$0^{\mathrm{o}}$	$10^5$	0.02	25	9.9430	9.9441	523.8414
0.1	-	-	-	-	9.9034	5.2336	647.8792
5	-	-	-	-	9.0698	15.6499	294.8795
10	-	-	-	-	8.7665	19.0674	253.2713
-	${15}^{\mathrm{o}}$	-	-	-	9.3401	9.3413	439.5714
-	${30}^{\mathrm{o}}$	-	-	-	9.3477	9.3488	471.8329
-	${45}^{\mathrm{o}}$	-	-	-	9.9732	9.9744	612.1477
-	-	$10^3$	-	-	4.9731	4.9741	0.0700
-	-	$10^4$	-	-	5.3781	5.3791	10.6999
-	-	$10^6$	-	-	16.4802	16.4821	6513.5956
-	-	-	0.0002	-	5.3800	5.3810	9.2370
-	-	-	0.002	-	8.5885	5.5896	229.3243
-	-	-	0.2	-	10.1091	10.1103	587.1623
-	-	-	-	0	10.8920	10.8923	1366.3958
-	-	-	-	50	8.1211	8.1222	134.800
-	-	-	-	75	6.6340	6.6351	38.6461
-	-	-	-	100	5.7814	5.7824	13.1207

4.3. Impact of Darcy’s Number

The streamlines, isoconcentration, and isotherms for various value of Da $\left(0.0001, 0.001, 0.01\right)$ at $\left(Ha=25, Le=0.1, Ra=10^5\right)$ are presented in Figure 9 for an irregular enclosure. Figure 9 shows how the Darcy number (Da) affects an enclosure’s flow, heat, and mass transfer. As Da increases, the streamlines show more dynamic flow, indicating reduced flow resistance. The isotherms transition from tightly packed at low Da to more dispersed at high Da, suggesting enhanced thermal mixing.

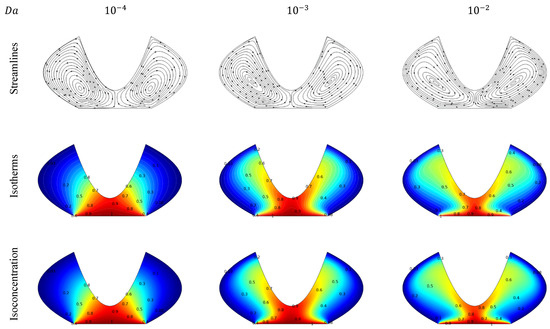
Figure 9. The figure represents the impact of Darcy’s number on velocity streamlines, isotherms, and isoconcentrations.

The isoconcentration contours also become less stratified with a higher Da, reflecting better solute mixing. These changes reveal that a higher Da, indicative of a more permeable medium, promotes more effective heat and mass transfer, important for the design of porous media systems. In engineering applications, a high Da might be beneficial in processes requiring efficient thermal management, while a low Da might be desirable where minimal mixing is needed to maintain concentration gradients. Figure 10 illustrates the impact of Darcy’s number on heat transfer rate and mass transfer rate. It can be seen that when the Darcy number rises, the mass transfer rate and heat transfer rate will increase.

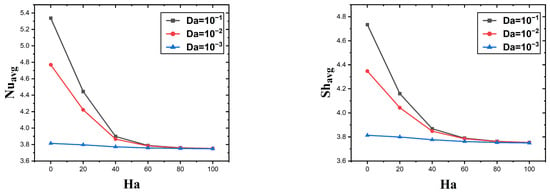
Figure 10. The graph displays the impact of Da on the Nusselt number (averaged) and Sherwood number (averaged).

4.4. Impact of Inclined Angle

Figure 11 demonstrates streamlines, isoconcentration, and isotherms for distinct values of the inclination angle $\gamma$ with $Ha=25, Ra=10^5, Le=0.1, Da=0.1$. From Figure 11, the flow pattern inside the cavity can be described by a series of counterclockwise convection vortices. Temperatures rise on hot walls with an increasing inclined angle in isothermal systems. When the inclined angle increases, the concentration becomes more spread out and diffuse. The angle of inclination significantly influences the thermal efficiency and fluid dynamics in systems utilizing magnetic fields, impacting applications ranging from magnetic refrigeration to chemical processing. Designing enclosures, particularly for cooling systems, demands careful consideration of the inclination angle to optimize thermal control and maintain precise temperature gradients.

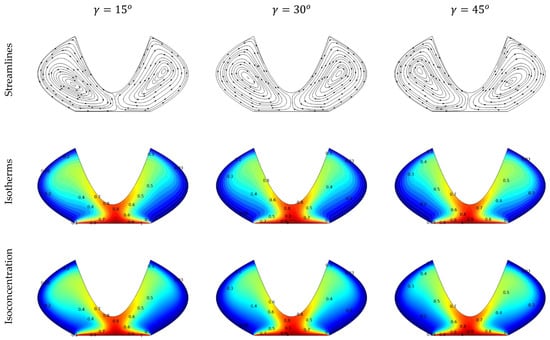
Figure 11. Effect of varying inclined angle ($\gamma$) on the flow structure, temperature distribution, and concentration levels within an enclosure, depicted through streamlines, isotherms, and isoconcentration contours.

4.5. Impact of Hartmann’s Number

Streamlines, isotherms, and isoconcentration distributions for different Hartmann numbers (Ha) are shown in Figure 12. The existence of a magnetic field makes Ha an important factor, due to the fact that it reduces the velocity profile and promotes a laminar flow phase. Hartmann’s number is written as $Ha=BH\sqrt{\frac{\varrho }{\mu }}$. An increase in the value of Ha typically leads to the Lorentz force damping the fluid motion, which can suppress turbulence and result in a more uniform and potentially laminar flow structure. This may lead to a more uniform temperature distribution and a reduction in kinetic energy. In terms of concentration, an increase in Hartmann number can lead to a decrease in concentration gradients as the flow becomes more laminar.

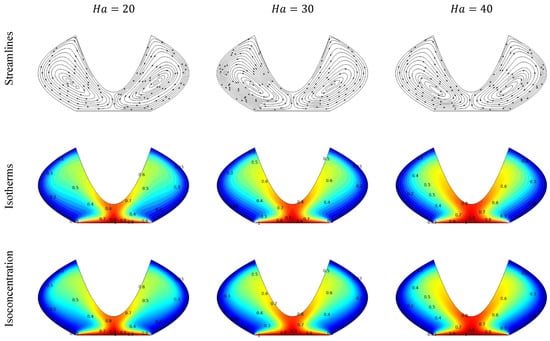
Figure 12. Influence of an increasing Hartmann number (Ha) on fluid motion, thermal stratification, and concentration distribution within an enclosure, presented through streamlines, isotherms, and isoconcentration plots.

5. Conclusions

In this study, the behavior of DDNC in an irregular cavity was explored and investigated. The investigation demonstrated that the flow characteristics were considerably influenced by the thermophysical properties of the fluid. The study also revealed that the inclination angle, Hartmann number, Lewis number, and Rayleigh number affected the flow, magnetic effects, heat transfer, and mass transfer in the cavity. The numerical analysis demonstrated that the flow inside the cavity is 2D and incompressible. This investigation provides significant insights into the behavior of DDNC in an irregular cavity, which could be useful for various engineering applications. The major outcomes of this investigation include the following:

• The heat transfer rate, mass transfer rate, and total kinetic energy increase with the rise in the Rayleigh number.
• In a specific range, $0.1\le Le\le 1$, when the Lewis number rises, the mean Nusselt number and total energy decrease, but the mean Sherwood number increases.
• As the Rayleigh number increases, the isotherms and isoconcentration lines become more distorted, the concentration and temperature gradients become steeper. With the formation of plumes and vortices, the flow becomes more turbulent and complex.
• The findings indicate that the velocity of fluid flow decreases because of porous media flow resistance increasing the Darcy number. The velocity lines of the fluid become more densely packed, resulting in a more laminar flow.
• ${Nu}_{avg}$, ${Sh}_{avg}$, and K.E. increase when the Darcy number rises.
• The flow pattern within the cavity can be described by a series of counterclockwise convection vortices, and temperatures rise on hot walls with the increases in the inclined angle.