1. Introduction
Recently, the model-free adaptive control (MFAC) method has attracted extensive attention; it does not need the specific dynamic characteristics of the control system, only input and output data [
1]. Thanks to its fewer identification parameters and fewer calculations, as well as its wide range of applications, MFAC plays an important role in many fields and applications [
2].
Different from the existing stability analysis for discrete-time (stochastic) systems [
3,
4,
5], the main idea of MFAC is to use the concept of a pseudo-gradient to replace the general discrete-time nonlinear system with a series of dynamic linear time-varying models. In MFAC, the dynamic linear time-varying model has three main forms, namely, compact-form dynamic linearization (CFDL) [
6], partial-form dynamic linearization (PFDL) [
7], and full-form dynamic linearization (FFDL) [
8]. In particular, by utilizing only input–output data information, equivalent models can be derived by means of the concept of a pseudo-partial derivative (PPD). Thus, the learning law can be established by treating the PPD as a time-varying parameter [
9,
10].
Using a virtual equivalent dynamic linearization data model, the time-varying PPD estimation algorithm was designed in [
11], where the internal stability of the FFDL linearization-based MFAC scheme was rigorously presented. In [
12], a new type of MFAC method based on an adaptive forgetting factor was proposed. In [
13], by taking the affine structure of the ultra-local model and the extended state observer (ESO), a local PFDL-based ESO-MFAC was proposed to improve control performance. In order to make the MFAC scheme have a better performance, a PID-like MFAC with discrete (ESO) sparked interest in [
14]. It is worth pointing out that the above-mentioned work did not consider high-order PPD estimation.
High-order MFAC is an important branch of MFAC which uses more information to further improve control performance. In [
15], a high-order estimation algorithm was used to estimate the value of PPD. An improved high-order MFAC method was proposed in [
16], which not only considered more control knowledge than the previous time, but also used more information from the previous time in the estimation algorithm.
Fractional-order control is popular in controlling nonlinear systems [
17]. In [
18], a data driven model has been established and a discrete time fractional order reaching law was studied. In [
19], a fractional order data-driven model was proposed, which related the first variation of the output signal with the fractional order variation of the input one. A fractional data-driven model was presented in [
20], where the instantaneous gain from the fractional output variation to the input one was computed by means of a fuzzy inference system.
These observations motivate our current study. The main contributions of this paper can be summarized into two aspects: (1) both the error and its rate of change are introduced in the control input criterion function, which incorporates a fractional-order operator. Three weighting coefficients are executed to enhance the system capacity of track abrupt signals and mitigate sudden external disturbance; (2) by using the high-order PPD estimation scheme based on previous input and output data, a fractional-order MFAC with high order estimation to enhance convergence is developed.
The rest of this paper is organized as follows: some preliminaries and the problem formulation are presented in
Section 2. The data-driven control algorithm is given in
Section 3. A theoretical analysis of the enhanced convergent condition is derived in
Section 4.
Section 5 provides numerical simulations to illustrate the validity of the designed method. Finally, some conclusions are drawn in
Section 6.
2. System Description
In this paper, we consider the following uncertain discrete-time nonlinear system:
where
indexes the discrete time and
T is the terminal time instant.
is the control input at time instant
k and
is the system output at time instant
k.
are two unknown positive integers.
Definition 1 ([
21]).
The fractional discrete approximation of the G-L derivative for is defined aswhere is the fractional order, is the set of real numbers, h is set to 1 as a sampling time, and is a number of samples for which the approximation of the derivative is calculated. The fractional binomial term in (
2) can be obtained from the following relation:
The following assumptions are considered for the system (
1).
Assumption 1. There exist positive constants and such that and .
Assumption 2. For any , the nonlinear function satisfies the Lipschitz condition, that is,where , l is a Lipschitz constant. Remark 1. The above assumptions are rather standard, and they are taken for granted by several schemes for the control of discrete-time systems. Assumption 1 gives a limit on the system input and output change rate. From a practical point of view, Assumption 2 implies that the output variation depends linearly on the input variation.
By virtue of the second assumption, the dynamic model of (
1) can be expressed as
where
satisfies
.
establishes a dynamic relationship between the input and output data of the system. Therefore, the rapid identification of
becomes particularly crucial. This issue will be addressed in the next section. In this paper, we exclusively address the case of
.
Remark 2. When , degenerates to the conventional integer-order cases. aligns with the standard pseudo-partial derivative in CFDL. For , due to the short-memory characteristics of a fractional-order operator [
21]
, the controller compensates for more information from the previous time; therefore, the robustness of the system’s equivalent model can be enhanced. This contributes to a smoother execution of dynamic linearization, enabling a faster convergence of the estimated to the desired . Assumption 3. For any , the PPD satisfies (or ), where ε is a relatively small positive constant.
Remark 3. Most of the plants, in practice, can satisfy Assumption 3. Its practical meaning is obvious, that is, the plant output should increase (or decrease) when the corresponding control input increases.
3. Design of Model-Free Adaptive Fractional-Order Controller
The following improved calculation criteria are considered:
where
and
represent the tracking error and its rate of change, respectively.
is the desired trajectory.
and
are positive weight coefficients in
.
is a penalty factor, which is used in order to limit the control input variation.
Remark 4. In the input criterion function (6), the first term is the square of the output error. The second term is the rate of change of the error at two adjacent moments. This is used to reduce the impact of excessive changes in the criterion function calculation by the output data. Substituting (
5) into the criterion function (
6), we can obtain
Through calculating, this yields
Using the optimal technique, one can have
where, as a step factor,
is designed to make the controller more universal [
22].
Thus, an improved model-free adaptive fractional-order controller (I-MFAFOC) can be expressed by
Remark 5. Unlike other high-order algorithms designed based on the control input [
13,
14,
16]
, the I-MFAFOC algorithm (10) uses to update the control input . On the other hand, compared to the algorithm in [
16]
, the improved algorithm does not need to set the weight coefficients for the previous control inputs . Since
is unknown, the following universal criteria function with the estimated parameter are defined:
where
is the weight factor.
is the estimated value of
. Equation (
11) indicates that the target-constrained input should be minimized, while the tracking error converges to a minimum; this implies that
will converge to
.
In this paper, for enhancing tracking performance, a high-order parameter estimation algorithm for PPD (HOPPD) is proposed here by updating the criterion function (
11) as follows:
where
is the high-order degree and
are weighting coefficients with
.
Based on the derivation of (
12), as below, and
, the estimation algorithm is expressed by (
13)
where
is the step length to make the algorithm more flexible [
22].
To ensure that the dynamic linearization model is always true, the following reset algorithm is applied:
Therefore, the overall control strategy of the proposed high-order PPD-based improved model-free adaptive fractional-order controller (HOPPD-I-MFAFOC) is delineated in Equations (
14)–(
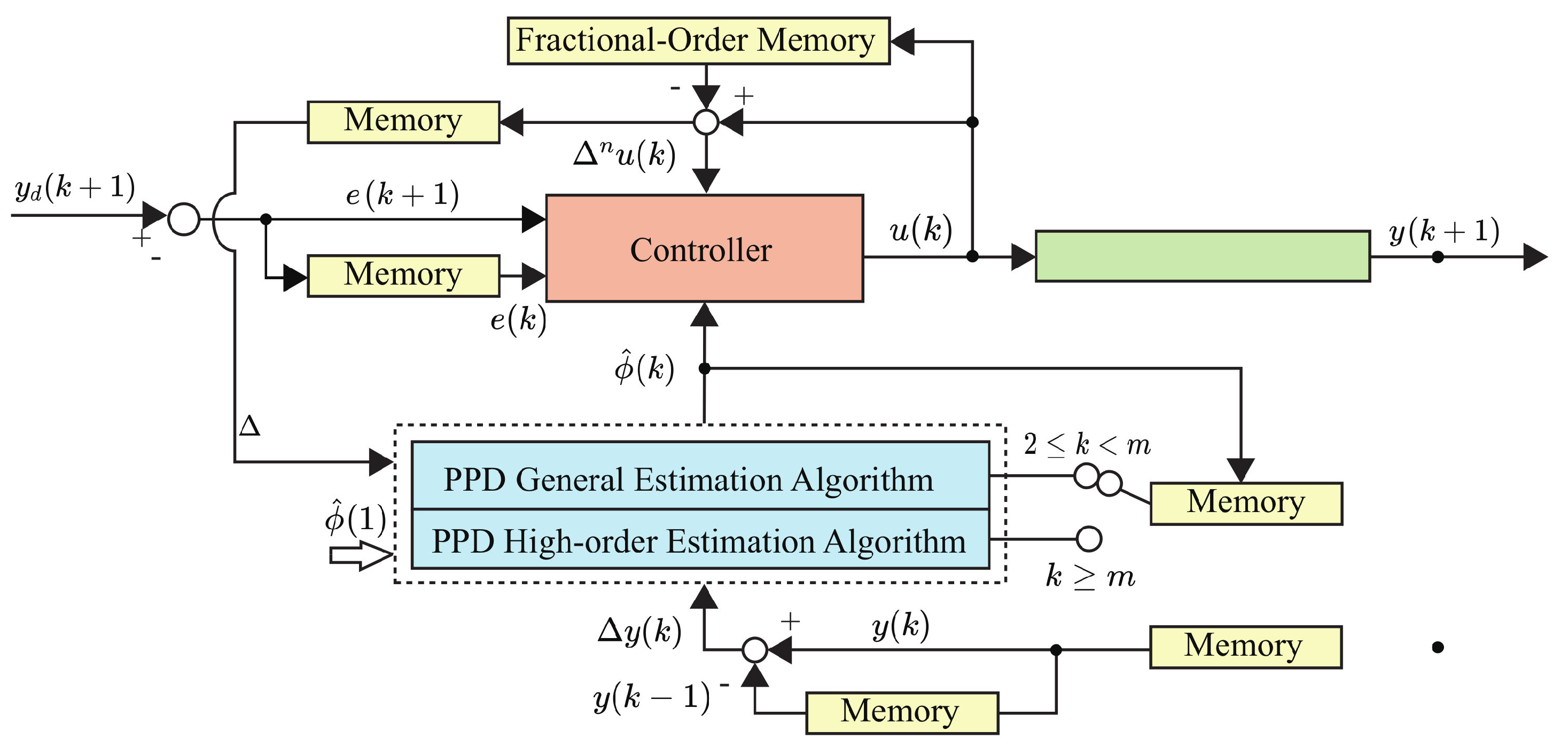
16). The controller diagram is depicted in
Figure 1 with the following two key points. (1) The PPD is derived using a high-order estimation algorithm. (2) The fractional-order controller is used to provide a better performance.
In comparison with traditional MFAC, HOPPD-I-MFAFOC incorporates more historical input and output data, enriching the gain parameters by involving due to the inclusion of a fractional-order and high-order algorithm.
Remark 6. For practical realization, the number of samples taken into consideration has to be reduced to the predefined number and in the experiment [23]. Remark 7. In the first instance, an initial value needs to be assigned to . Since the calculation of relies on the previous m instances, it can only be computed when . Therefore, the high-order estimation algorithm (15) is applied for . However, in the case of , where no previous instances are available, the original estimation algorithm in (16) is utilized. Remark 8. The application of weighting coefficients in the high-order estimation algorithm (15) is analogous to the use of a forgetting factor. Consequently, they can set . 5. Numerical Examples
In this section, to validate the effectiveness of the proposed method, two numerical examples are presented.
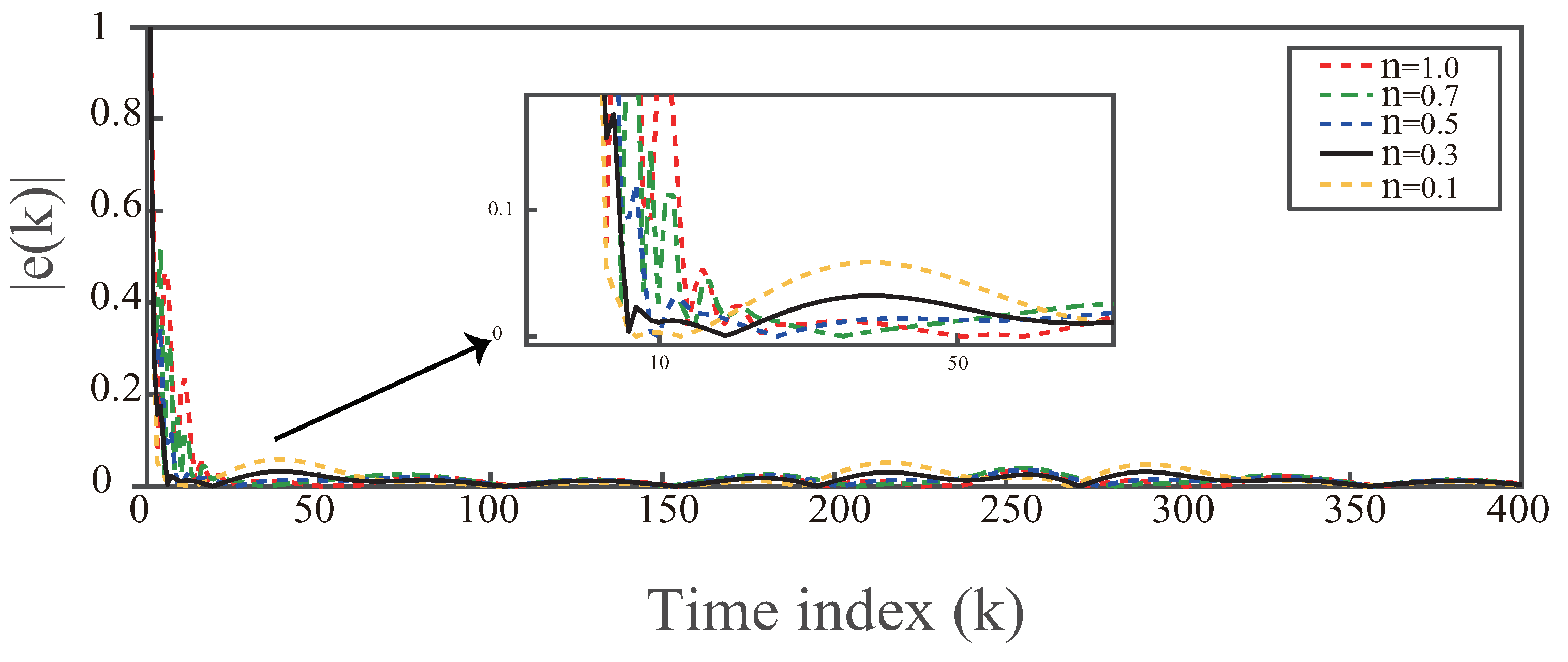
Example 1. An unknown plant replaced by a differencing equation is represented as follows: The tracking trajectory is given as The controller parameters are , , , and . The predefined number is fixed at . The fractional-order is set as . The high-order estimation is configured with , and the weighting coefficients are , , and . The high-order estimation algorithm commences at . The initial PPD is uniformly set as for all controllers. Moreover, the weighting coefficients is chosen as .
Figure 2 illustrates the tracking performance of each controller in response to the given reference signal.
Table 1 presents a comparison of the Sum Square Error (SSE) and Sum Square Control (SSC) between fractional-order and tuned integer order. The results indicate that the I-MFAFOC method shortens the response time and reduces SSE to a certain extent, but requires an increased control effort. The HOPPD-MFAFOC method reduces the overshoot of the tracking signal and decreases SSC to a certain extent, but increases SSE. The HOPPD-I-MFAFOC method achieves a reduction in SSE and SSC, to a certain extent, simultaneously. Moreover, all three fractional-order control methods mentioned above significantly outperform the traditional MFAC method.
Example 2. To demonstrate the effectiveness of the proposed control method in tracking smooth reference signals, a comparative experiment was conducted as follows. The system (36) contains time-varying parameters and uncertain disturbance : Define the desired trajectory as The HOPPD-I-MFAFOC method is applied to control the system (
37) in simulation experiments. The controller parameters are
and
. The predefined number is set to
. A comparison between fractional-order and tuned integer order with respect to SSE and SSC is presented in
Table 2. The tracking performance of each controller is shown in
Figure 3.
The fractional order is chosen as . The order of the high-order estimation is specified as , with weighting coefficients . The high-order estimation algorithm commences at . The initial PPD is uniformly set as for all controllers, and the weight factor is defined as .
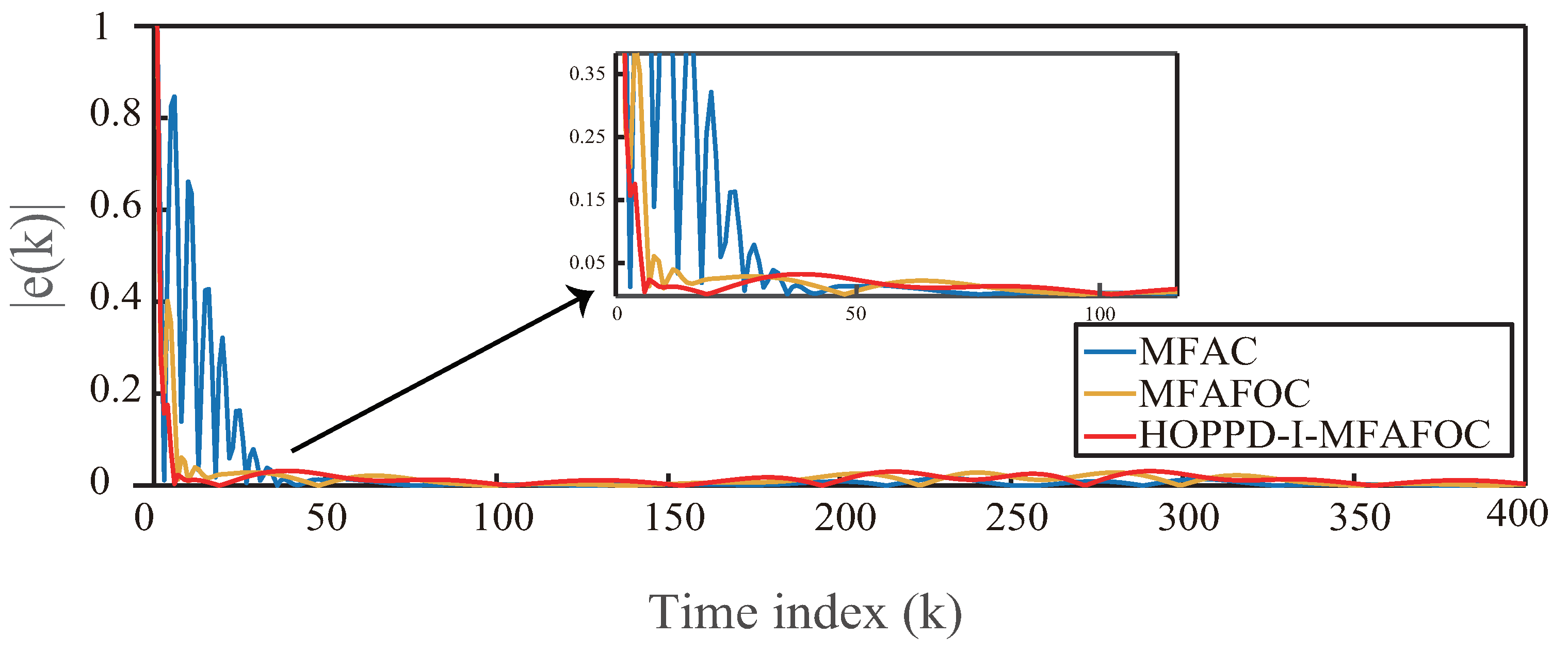
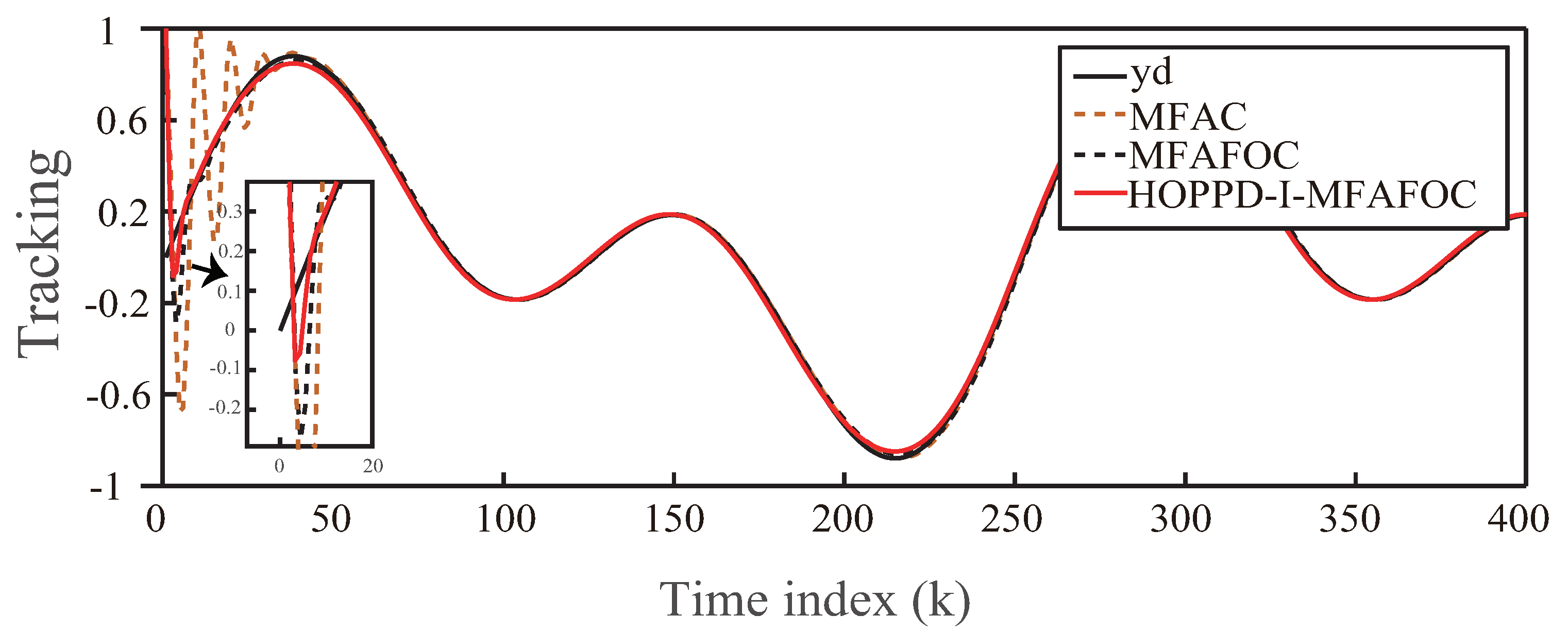
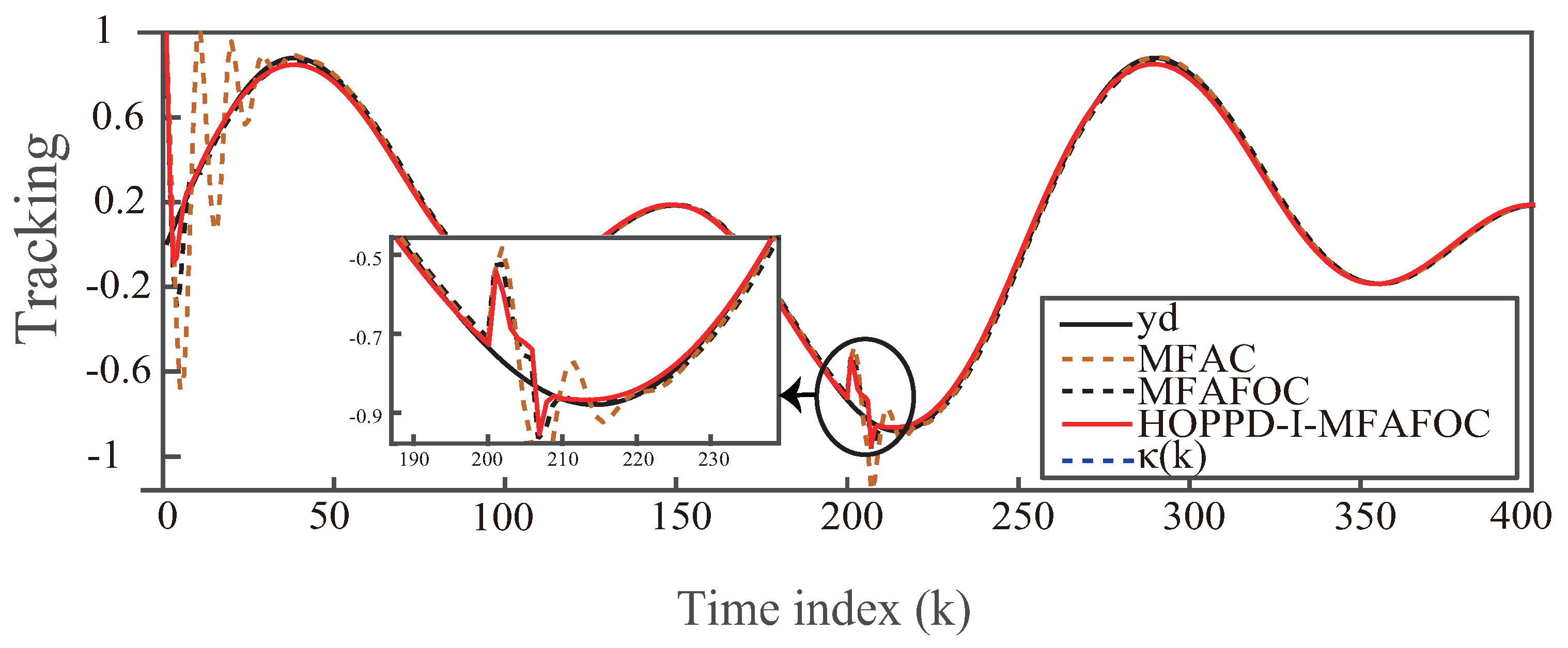
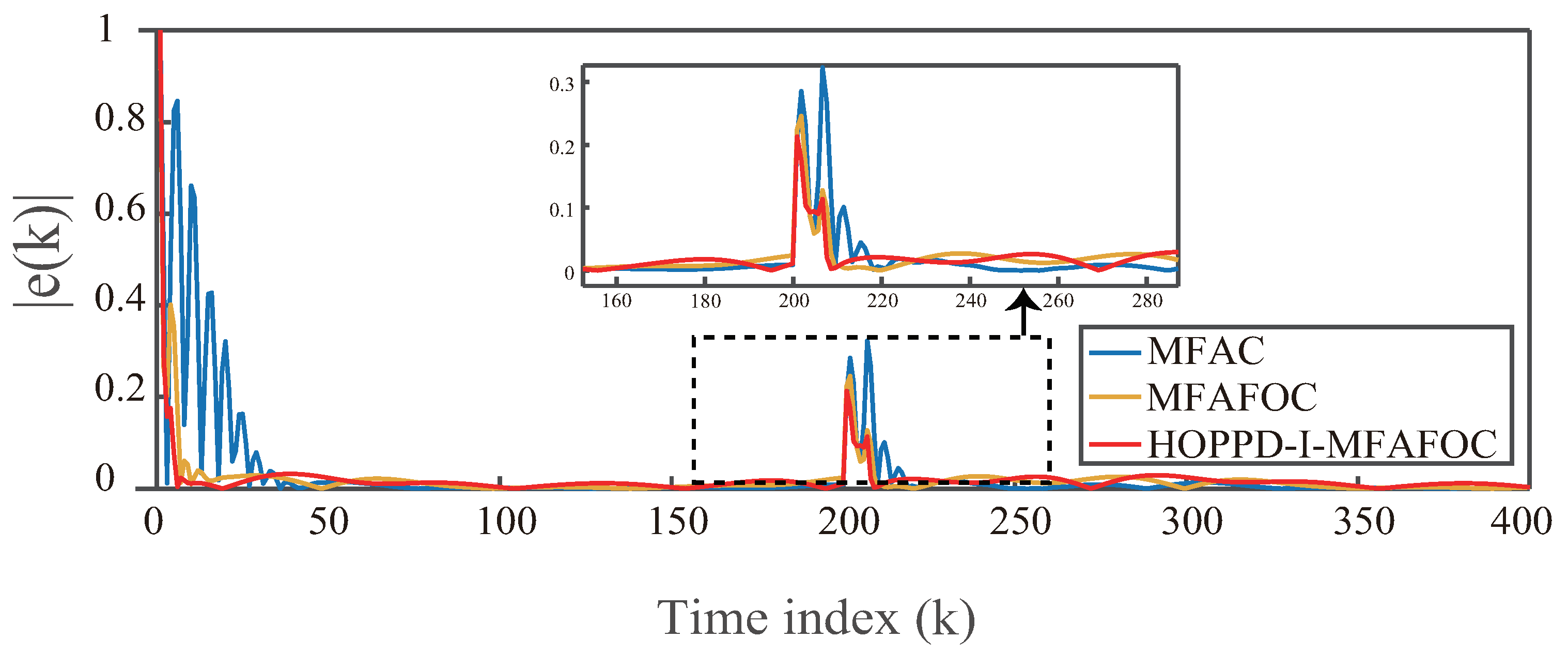
Figure 4 and
Figure 5 provide a trajectory tracking comparison among the MFAC, MFAFOC, and HOPPD-I-MFAFOC methods for the ideal case. The MFAC parameters are set to
and
, demonstrating superior performance. Additionally, performance enhancements are evident when comparing SSE and SSC indices in
Table 3. The results indicate that HOPPD-I-MFAFOC exhibits a 19.46% reduction in SSE and a 13.18% reduction in SSC compared to MFAFOC in tracking the target signal.
Figure 6 and
Figure 7 demonstrate the robustness of the method, verified by introducing an uncertain disturbance based on repeating the experiment described above. The experiment illustrates the enhanced robustness of the new control method. Additionally,
Table 4 provides a comparison between the MFAC, MFAFOC, and HOPPD-I-MFAFOC methods in terms of SSC and SSE for the case with a disturbance. The results show that HOPPD-I-MFAFOC exhibits a 26.43% reduction in SSE and a 9.71% reduction in SSC compared to MFAFOC in tracking the target signal.